Real-Time Probabilistic Flood Forecasting Using Multiple Machine Learning Methods
Abstract
1. Introduction
2. Probabilistic Forecasting and Machine Learning Methods
2.1. Probabilistic Forecasting Method
2.2. Support Vector Regression
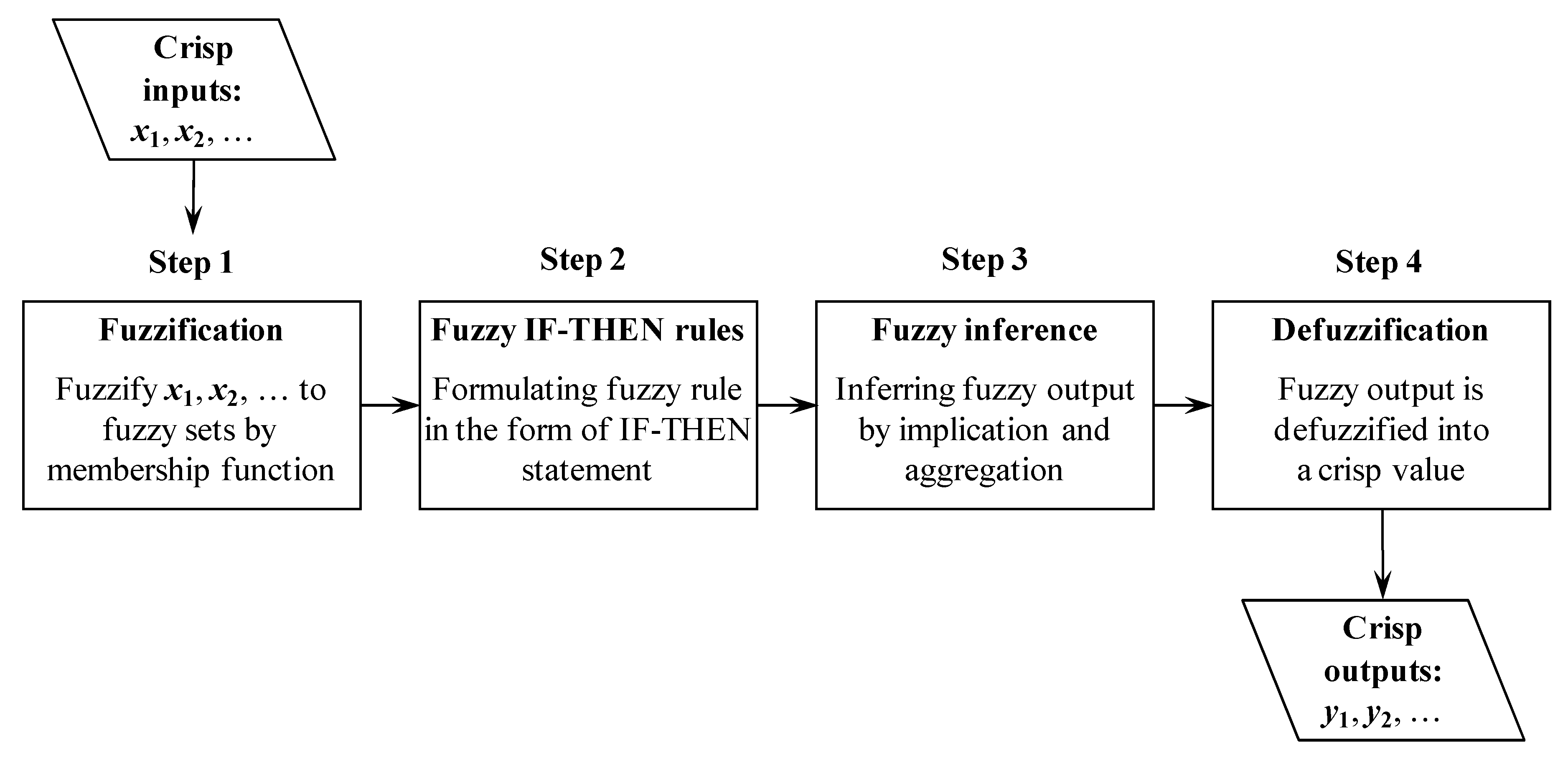
2.3. Fuzzy Inference Model
2.4. Defuzzification Into a Probability Distribution
2.5. k-Nearest Neighbors Method
3. Deterministic Forecasting
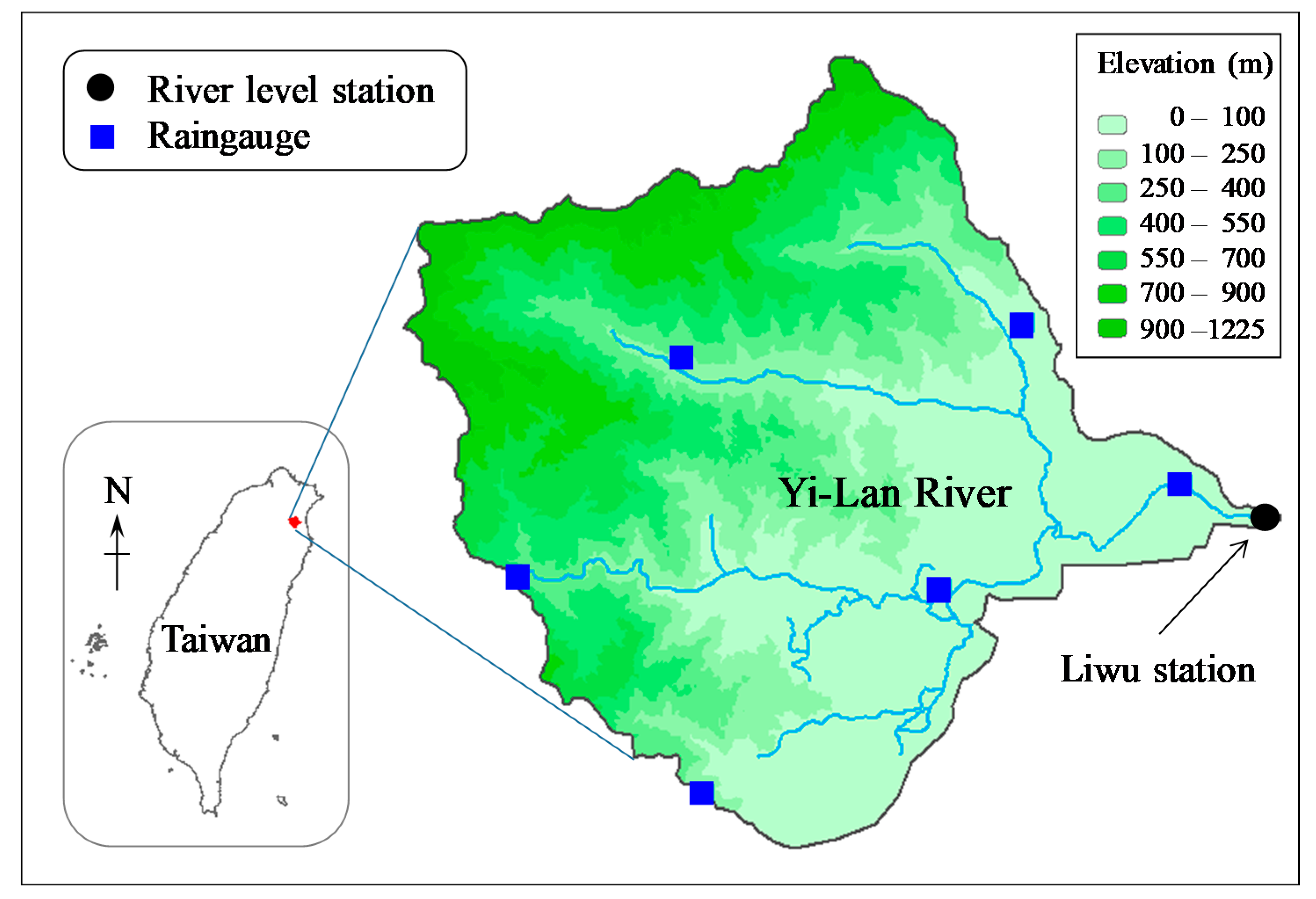
3.1. Study Area and Data
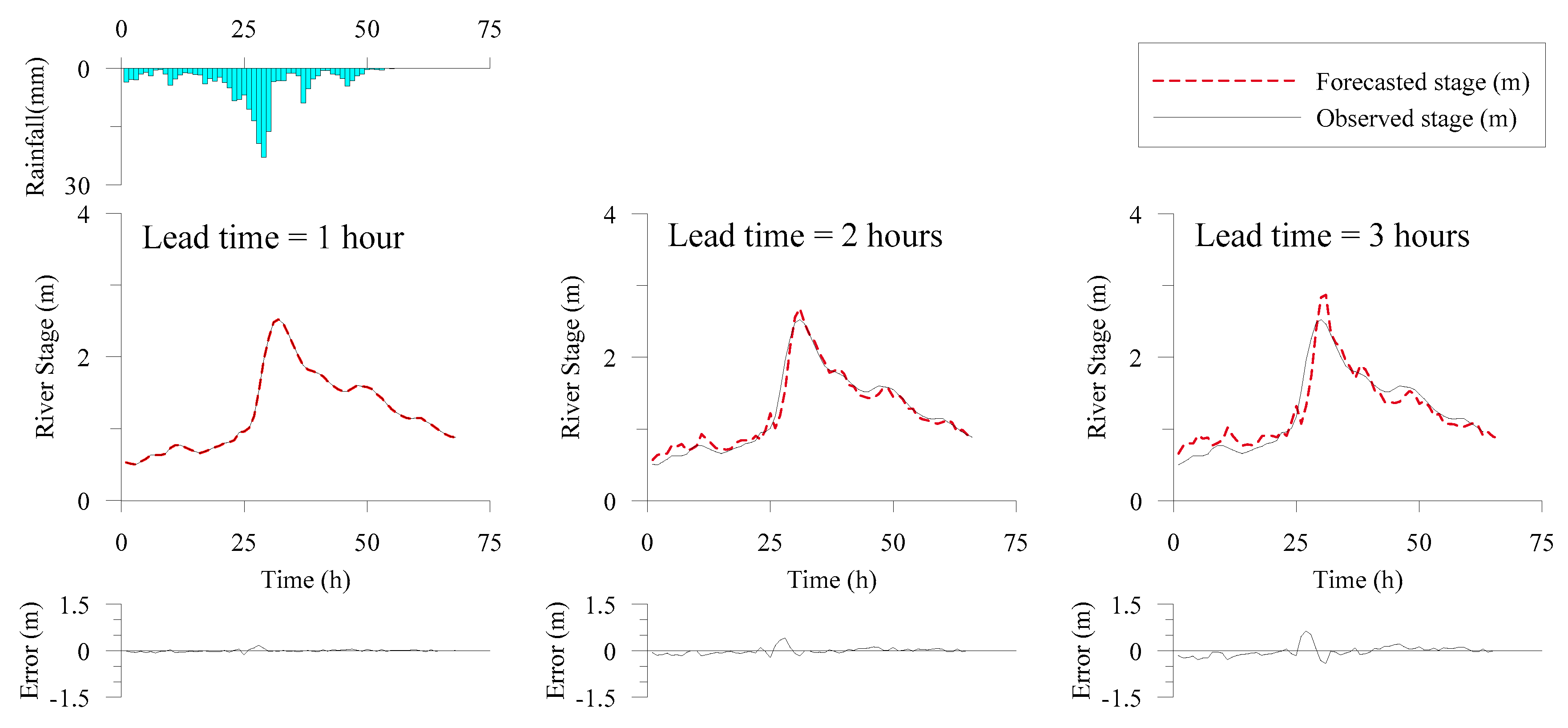
3.2. Deterministic Model Development and Forecasting
4. Probabilistic Forecasting
4.1. Probabilistic Model Development
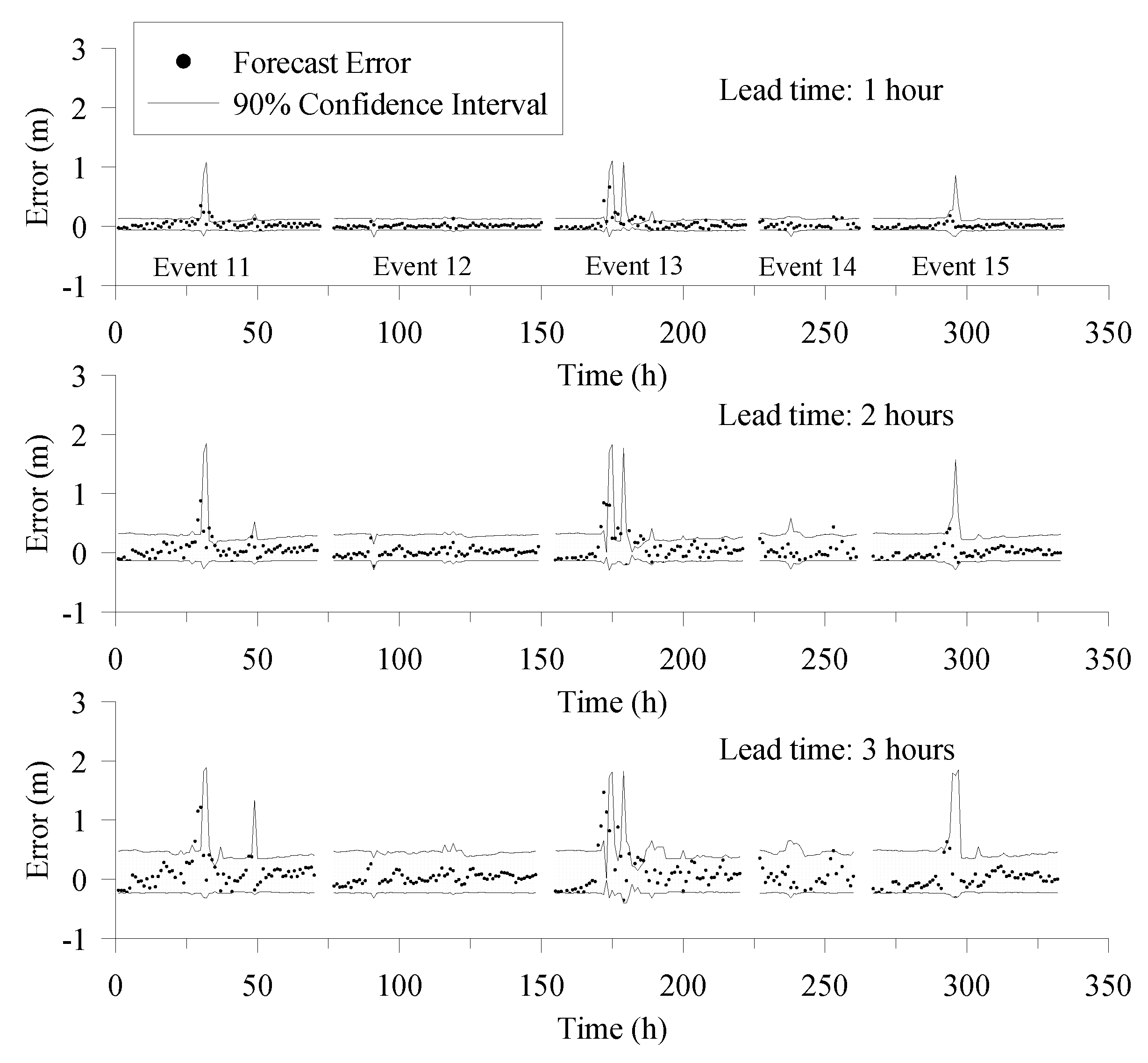
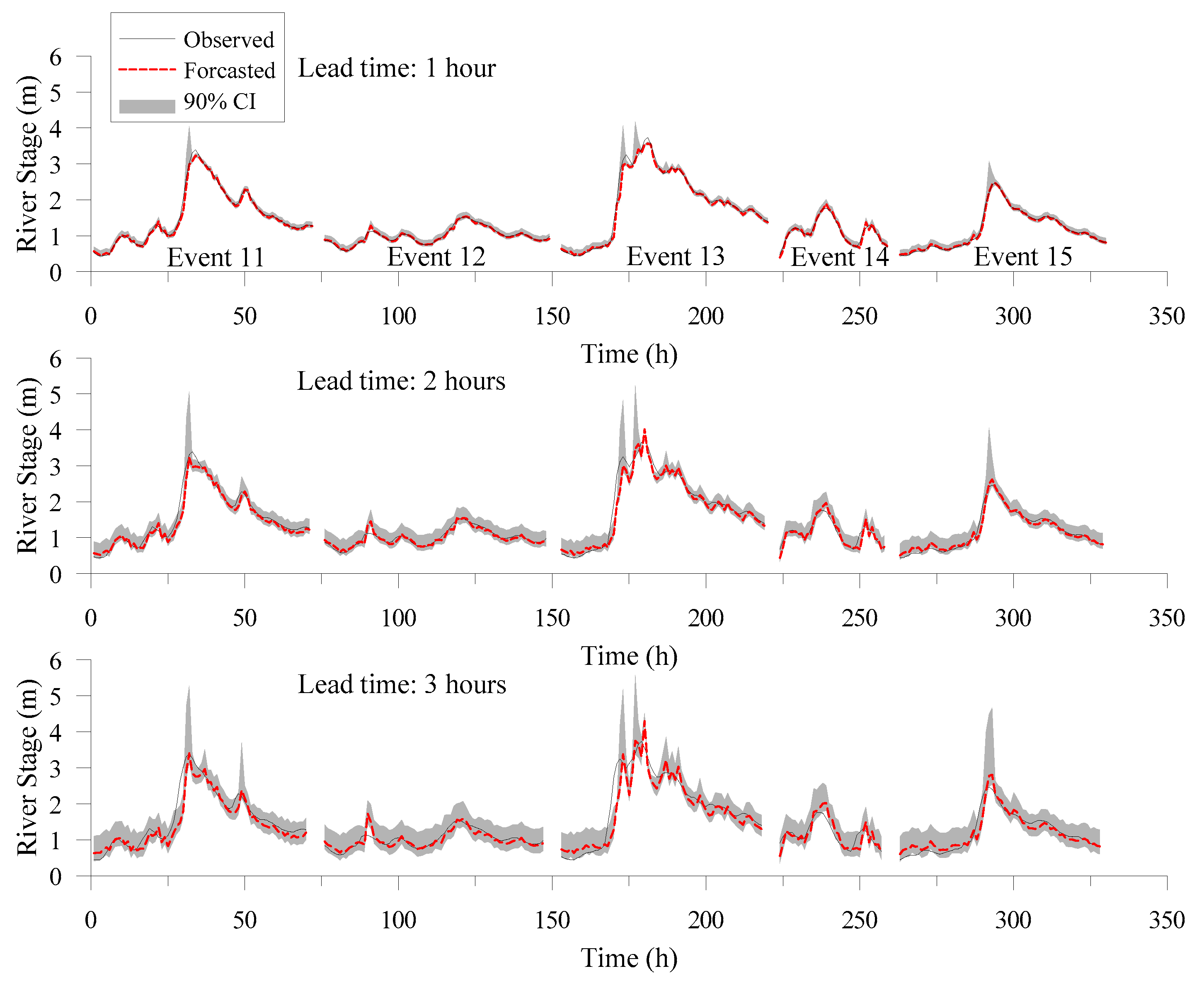
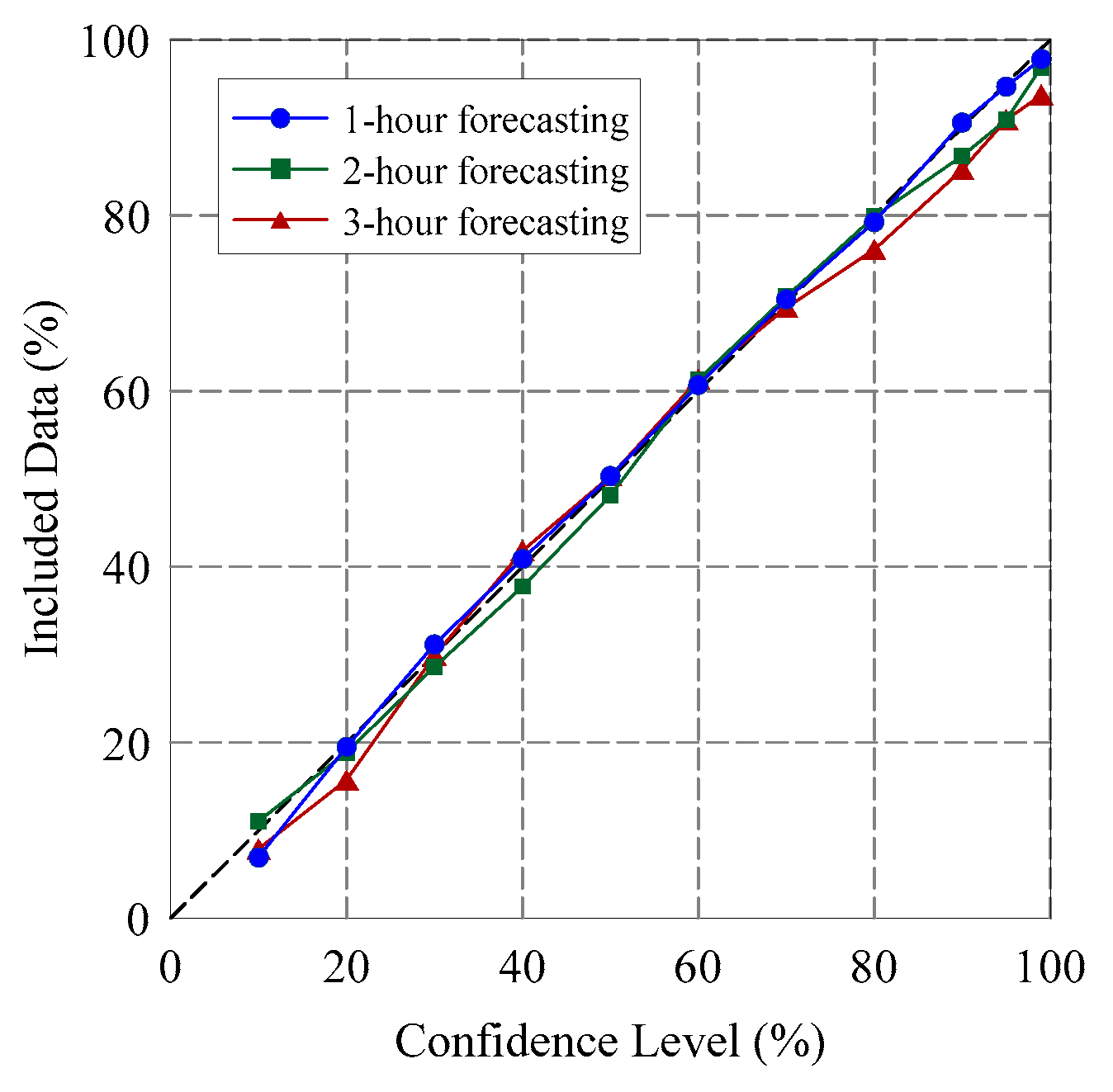
4.2. Probabilistic Forecasting Results
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Chen, S.T.; Yu, P.S. Real-Time probabilistic forecasting of flood stages. J. Hydrol. 2007, 340, 63–77. [Google Scholar] [CrossRef]
- Krzysztofowicz, R. The case for probabilistic forecasting in hydrology. J. Hydrol. 2001, 249, 2–9. [Google Scholar] [CrossRef]
- Krzysztofowicz, R. Bayesian theory of probabilistic forecasting via deterministic hydrologic model. Water Resour. Res. 1999, 35, 2739–2750. [Google Scholar] [CrossRef]
- Krzysztofowicz, R. Bayesian system for probabilistic river stage forecasting. J. Hydrol. 2002, 268, 16–40. [Google Scholar] [CrossRef]
- Krzysztofowicz, R.; Maranzano, C.J. Bayesian system for probabilistic stage transition forecasting. J. Hydrol. 2004, 299, 15–44. [Google Scholar] [CrossRef]
- Biondi, D.; De Luca, D.L. Performance assessment of a Bayesian Forecasting System (BFS) for real-Time flood forecasting. J. Hydrol. 2013, 479, 51–63. [Google Scholar] [CrossRef]
- Georgakakos, K.P.; Seo, D.-J.; Gupta, H.; Schaake, J.; Butts, M.B. Towards the characterization of streamflow simulation uncertainty through multimodel ensembles. J. Hydrol. 2004, 298, 222–241. [Google Scholar] [CrossRef]
- Diomede, T.; Davolio, S.; Marsigli, C.; Miglietta, M.M.; Moscatello, A.; Papetti, P.; Tiziana Paccagnellal, T.; Andrea Buzzi, A.; Malguzzi, P. Discharge prediction based on multi-Model precipitation forecasts. Meteorol. Atmos. Phys. 2008, 101, 245–265. [Google Scholar] [CrossRef]
- Davolio, S.; Miglietta, M.M.; Diomede, T.; Marsigli, C.; Morgillo, A.; Moscatello, A. A meteo-Hydrological prediction system based on a multi-Model approach for precipitation forecasting. Nat. Hazard. Earth Syst. 2008, 8, 143–159. [Google Scholar] [CrossRef]
- Beven, K.J.; Binley, A. The future of distributed models: Model calibration and uncertainty prediction. Hydrol. Process. 1992, 6, 279–298. [Google Scholar] [CrossRef]
- Franks, S.W.; Gineste, P.; Beven, K.J.; Merot, P. On constraining the predictions of a distributed model: The incorporation of fuzzy estimates of saturated areas into the calibration process. Water Resour. Res. 1998, 34, 787–797. [Google Scholar] [CrossRef]
- Hunter, N.M.; Bates, P.D.; Horritt, M.S.; de Roo, A.P.J.; Werner, M.G.F. Utility of different data types for calibrating flood inundation models within a GLUE framework. Hydrol. Earth Syst. Sci. 2005, 9, 412–430. [Google Scholar] [CrossRef]
- Fan, F.M.; Collischonn, W.; Quiroz, K.J.; Sorribas, M.V.; Buarque, D.C.; Siqueira, V.A. Flood forecasting on the Tocantins River using ensemble rainfall forecasts and real-time satellite rainfall estimates. J. Flood Risk Manag. 2016, 9, 278–288. [Google Scholar] [CrossRef]
- Han, S.; Coulibaly, P. Probabilistic flood forecasting using hydrologic uncertainty processor with ensemble weather forecasts. J. Hydrometeorol. 2019, 20, 1379–1398. [Google Scholar] [CrossRef]
- Leandro, J.; Gander, A.; Beg, M.N.A.; Bhola, P.; Konnerth, I.; Willems, W.; Carvalho, R.; Disse, M. Forecasting upper and lower uncertainty bands of river flood discharges with high predictive skill. J. Hydrol. 2019, 576, 749–763. [Google Scholar] [CrossRef]
- Montanari, A.; Brath, A. A stochastic approach for assessing the uncertainty of rainfall-Runoff simulations. Water Resour. Res. 2004, 40, W01106. [Google Scholar] [CrossRef]
- Tamea, S.; Laio, F.; Ridolfi, L. Probabilistic nonlinear prediction of river flows. Water Resour. Res. 2005, 41, W09421. [Google Scholar] [CrossRef]
- Weerts, A.H.; Winsemius, H.C.; Verkade, J.S. Estimation of predictive hydrological uncertainty using quantile regression: Examples from the National Flood Forecasting System (England and Wales). Hydrol. Earth Syst. Sci. 2011, 15, 255–265. [Google Scholar] [CrossRef]
- Teschl, R.; Randeu, W.L.; Teschl, F. Improving weather radar estimates of rainfall using feed-Forward neural networks. Neural Netw. 2007, 20, 519–527. [Google Scholar] [CrossRef]
- Chen, S.T.; Yu, P.S.; Liu, B.W. Comparison of neural network architectures and inputs for radar rainfall adjustment for typhoon events. J. Hydrol. 2011, 405, 150–160. [Google Scholar] [CrossRef]
- Chang, F.J.; Chiang, Y.M.; Chang, L.C. Multi-Step-Ahead neural networks for flood forecasting. Hydrolog. Sci. J. 2007, 52, 114–130. [Google Scholar] [CrossRef]
- Jhong, Y.D.; Chen, C.S.; Lin, H.P.; Chen, S.T. Physical hybrid neural network model to forecast typhoon floods. Water 2018, 10, 632. [Google Scholar] [CrossRef]
- Lin, G.F.; Wu, M.C. An RBF network with a two-Step learning algorithm for developing a reservoir inflow forecasting model. J. Hydrol. 2011, 405, 439–450. [Google Scholar] [CrossRef]
- Sattari, M.T.; Yurekli, K.; Pal, M. Performance evaluation of artificial neural network approaches in forecasting reservoir inflow. Appl. Math. Model. 2012, 36, 2649–2657. [Google Scholar] [CrossRef]
- Bray, M.; Han, D. Identification of support vector machines for runoff modelling. J. Hydroinform. 2004, 6, 265–280. [Google Scholar] [CrossRef]
- Yu, P.S.; Chen, S.T.; Chang, I.F. Support vector regression for real-time flood stage forecasting. J. Hydrol. 2006, 328, 704–716. [Google Scholar] [CrossRef]
- Lin, G.F.; Chou, Y.C.; Wu, M.C. Typhoon flood forecasting using integrated two-Stage support vector machine approach. J. Hydrol. 2013, 486, 334–342. [Google Scholar] [CrossRef]
- Chen, S.T.; Yu, P.S.; Tang, Y.H. Statistical downscaling of daily precipitation using support vector machines and multivariate analysis. J. Hydrol. 2010, 385, 13–22. [Google Scholar] [CrossRef]
- Yang, T.C.; Yu, P.S.; Wei, C.M.; Chen, S.T. Projection of climate change for daily precipitation: A case study in Shih-Men Reservoir catchment in Taiwan. Hydrol. Process. 2011, 25, 1342–1354. [Google Scholar] [CrossRef]
- Chen, S.T.; Yu, P.S. Pruning of support vector networks on flood forecasting. J. Hydrol. 2007, 347, 67–78. [Google Scholar] [CrossRef]
- Chen, S.T. Mining informative hydrologic data by using support vector machines and elucidating mined data according to information entropy. Entropy 2015, 17, 1023–1041. [Google Scholar] [CrossRef]
- Lin, G.F.; Chen, G.R.; Wu, M.C.; Chou, Y.C. Effective forecasting of hourly typhoon rainfall using support vector machines. Water Resour. Res. 2009, 45. [Google Scholar] [CrossRef]
- Chen, S.T. Multiclass support vector classification to estimate typhoon rainfall distribution. Disaster Adv. 2013, 6, 110–121. [Google Scholar]
- Yu, P.S.; Chen, S.T.; Wu, C.C.; Lin, S.C. Comparison of grey and phase-Space rainfall forecasting models using fuzzy decision method. Hydrolog. Sci. J. 2004, 49, 655–672. [Google Scholar] [CrossRef]
- Yu, P.S.; Chen, S.T.; Chen, C.J.; Yang, T.C. The potential of fuzzy multi-Objective model for rainfall forecasting from typhoons. Nat. Hazards 2005, 34, 131–150. [Google Scholar] [CrossRef]
- Alvisi, S.; Mascellani, G.; Franchini, M.; Bardossy, A. Water level forecasting through fuzzy logic and artificial neural network approaches. Hydrol. Earth Syst. Sci. 2006, 10, 1–17. [Google Scholar] [CrossRef]
- Chen, C.S.; Jhong, Y.D.; Wu, T.Y.; Chen, S.T. Typhoon event-Based evolutionary fuzzy inference model for flood stage forecasting. J. Hydrol. 2013, 490, 134–143. [Google Scholar] [CrossRef]
- Wolfs, V.; Willems, P. A data driven approach using Takagi-Sugeno models for computationally efficient lumped floodplain modeling. J. Hydrol. 2013, 503, 222–232. [Google Scholar] [CrossRef]
- Lohani, A.K.; Goel, N.K.; Bhatia, K.K.S. Improving real time flood forecasting using fuzzy inference system. J. Hydrol. 2014, 509, 25–41. [Google Scholar] [CrossRef]
- Chen, C.S.; Jhong, Y.D.; Wu, W.Z.; Chen, S.T. Fuzzy time series for real-time flood forecasting. Stoch. Env. Res. Risk A 2019, 33, 645–656. [Google Scholar] [CrossRef]
- Toth, E.; Brath, A.; Montanari, A. Comparison of short-Term rainfall prediction models for real-Time flood forecasting. J. Hydrol. 2000, 239, 132–147. [Google Scholar] [CrossRef]
- Coulibaly, P.; Haché, M.; Fortin, V.; Bobée, B. Improving daily reservoir inflow forecasts with model combination. J. Hydrol. Eng. 2005, 10, 91–99. [Google Scholar] [CrossRef]
- Sharif, M.; Burn, D.H. Simulating climate change scenarios using an improved k-nearest neighbor model. J. Hydrol. 2006, 325, 179–196. [Google Scholar] [CrossRef]
- Sapin, J.; Rajagopalan, B.; Saito, L.; Caldwell, R.J. A k-Nearest neighbor based stochastic multisite flow and stream temperature generation technique. Environ. Modell. Softw. 2017, 91, 87–94. [Google Scholar] [CrossRef]
- Vapnik, V.N. The Nature of Statistical Learning Theory; Springer: New York, NY, USA, 1995. [Google Scholar]
- Vapnik, V.N. Statistical Learning Theory; Wiley: New York, NY, USA, 1998. [Google Scholar]
- Reddy, C.S.; Raju, K.V.S.N. An improved fuzzy approach for COCOMO’s effort estimation using Gaussian membership function. J. Softw. 2009, 4, 452–459. [Google Scholar] [CrossRef]
- Yu, P.S.; Chen, S.T. Updating real-Time flood forecasting using a fuzzy rule-Based model. Hydrolog. Sci. J. 2005, 50, 265–278. [Google Scholar] [CrossRef][Green Version]
- Chen, S.T. Probabilistic forecasting of coastal wave height during typhoon warning period using machine learning methods. J. Hydroinform. 2019, 21, 343–358. [Google Scholar] [CrossRef]
- Filev, D.; Yager, R.R. A generalized defuzzification method via BAD distributions. Int. J. Intell. Syst. 1991, 6, 687–697. [Google Scholar] [CrossRef]
- Solomatine, D.P.; Dulal, K.N. Model trees as an alternative to neural networks in rainfall-Runoff modelling. Hydrolog. Sci. J. 2003, 48, 399–411. [Google Scholar] [CrossRef]

| Event No. | Name of Typhoon or Storm | Date | Rainfall Duration (h) | Peak Flood Stage (m) | Total Rainfall (mm) | Note |
|---|---|---|---|---|---|---|
| 1 | Jelawat | 26 September 2012 | 96 | 1.22 | 85.2 | Calibration |
| 2 | Trami | 20 August 2013 | 71 | 2.14 | 196.3 | Calibration |
| 3 | Kongrey | 31 August 2013 | 44 | 1.69 | 138.0 | Calibration |
| 4 | Usagi | 20 September 2013 | 60 | 1.71 | 76.4 | Calibration |
| 5 | Fitow | 4 October 2013 | 67 | 1.62 | 118.5 | Calibration |
| 6 | Matmo | 21 July 2014 | 79 | 2.28 | 156.9 | Calibration |
| 7 | Storm 0809 | 09 August 2014 | 133 | 1.22 | 145.6 | Calibration |
| 8 | Fungwong | 20 September 2014 | 147 | 2.91 | 364.8 | Calibration |
| 9 | Dujuan | 27 September 2015 | 86 | 4.23 | 188.2 | Calibration |
| 10 | Meranti | 14 September 2016 | 72 | 1.69 | 103.9 | Calibration |
| 11 | Megi | 26 September 2016 | 77 | 3.39 | 158.5 | Validation |
| 12 | Storm 0601 | 1 June 2017 | 79 | 1.34 | 122.3 | Validation |
| 13 | Storm 1013 | 13 October 2017 | 73 | 4.41 | 351.3 | Validation |
| 14 | Maria | 10 July 2018 | 41 | 1.47 | 107.4 | Validation |
| 15 | Yutu | 1 November 2018 | 73 | 2.52 | 219.9 | Validation |
| Lead Time | RMSE (m) | CE |
|---|---|---|
| 1 hour | 0.07 | 0.99 |
| 2 hours | 0.15 | 0.97 |
| 3 hours | 0.25 | 0.93 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nguyen, D.T.; Chen, S.-T. Real-Time Probabilistic Flood Forecasting Using Multiple Machine Learning Methods. Water 2020, 12, 787. https://doi.org/10.3390/w12030787
Nguyen DT, Chen S-T. Real-Time Probabilistic Flood Forecasting Using Multiple Machine Learning Methods. Water. 2020; 12(3):787. https://doi.org/10.3390/w12030787
Chicago/Turabian StyleNguyen, Dinh Ty, and Shien-Tsung Chen. 2020. "Real-Time Probabilistic Flood Forecasting Using Multiple Machine Learning Methods" Water 12, no. 3: 787. https://doi.org/10.3390/w12030787
APA StyleNguyen, D. T., & Chen, S.-T. (2020). Real-Time Probabilistic Flood Forecasting Using Multiple Machine Learning Methods. Water, 12(3), 787. https://doi.org/10.3390/w12030787





