Evaluating the Water Holding Capacity of Multilayer Soil Profiles Using Hydrus-1D and Multi-Criteria Decision Analysis
Abstract
1. Introduction
2. Materials and Methods
2.1. Research Area
2.2. Soil Column Experiments
2.3. Hydrus-1D Simulation
2.3.1. Governing Equation
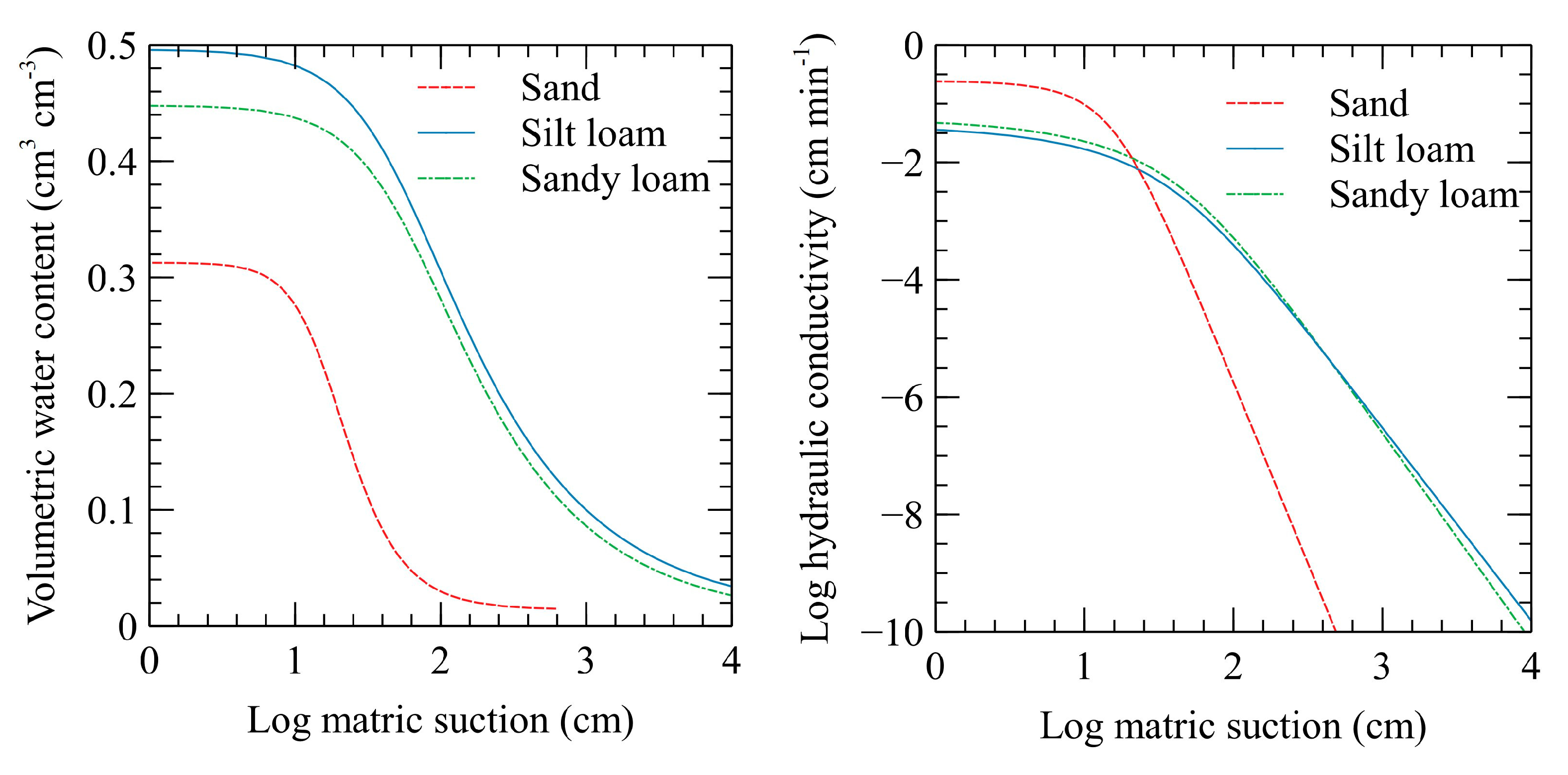
2.3.2. Soil Hydraulic Parameters
2.3.3. Particle Swarm Optimization
2.3.4. Initial and Boundary Conditions
2.3.5. Model Performance Evaluation
2.4. Multi-Criteria Decision Analysis Methods
2.4.1. AHP
2.4.2. TOPSIS
2.4.3. GRA
2.4.4. Criteria Weights
3. Results and Discussion
3.1. Calibration and Validation of Hydrus-1D
3.2. Water Infiltration Rate and Cumulative Infiltration of Different Soil Profiles
3.3. Wetting Front of Different Soil Profiles
3.4. Water Distribution with Different Soil Profiles
3.5. Evaluation of Soil Profiles
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Li, M.S. Ecological restoration of mineland with particular reference to the metalliferous mine wasteland in China: A review of research and practice. Sci. Total Environ. 2006, 357, 38–53. [Google Scholar] [CrossRef] [PubMed]
- Xiao, W.; Lv, X.; Zhao, Y.; Sun, H.; Li, J. Ecological resilience assessment of an arid coal mining area using index of entropy and linear weighted analysis: A case study of Shendong Coalfield, China. Ecol. Indic. 2020, 109, 105843. [Google Scholar] [CrossRef]
- Lv, X.; Xiao, W.; Zhao, Y.; Zhang, W.; Li, S.; Sun, H. Drivers of spatio-temporal ecological vulnerability in an arid, coal mining region in Western China. Ecol. Indic. 2019, 106, 105475. [Google Scholar] [CrossRef]
- Shrestha, R.K.; Lal, R. Ecosystem carbon budgeting and soil carbon sequestration in reclaimed mine soil. Environ. Int. 2006, 32, 781–796. [Google Scholar] [CrossRef] [PubMed]
- Yan, W.M.; Chiu, C.F.; Yuen, K.V. Prediction and modeling of permeability function and its application to the evaluation of breakthrough suction of a two-layer capillary barrier. Can. Geotech. J. 2017, 54, 778–788. [Google Scholar] [CrossRef]
- Miller, D.E.; Gardner, W.H. Water infiltration into stratified soil 1. Soil Sci. Soc. Am. J. 1962, 26, 115–119. [Google Scholar] [CrossRef]
- Alfnes, E.; Kinzelbach, W.; Aagaard, P. Investigation of hydrogeologic processes in a dipping layer structure: 1. The flow barrier effect. J. Contam. Hydrol. 2004, 69, 157–172. [Google Scholar] [CrossRef]
- Hübner, R.; Günther, T.; Heller, K.; Noell, U.; Kleber, A. Impacts of a capillary barrier on infiltration and subsurface stormflow in layered slope deposits monitored with 3-D ERT and hydrometric measurements. Hydrol. Earth Syst. Sci. 2017, 21, 5181–5199. [Google Scholar] [CrossRef]
- Tan, S.H.; Wong, S.W.; Chin, D.J.; Lee, M.L.; Ong, Y.H.; Chong, S.Y.; Kassim, A. Soil column infiltration tests on biomediated capillary barrier systems for mitigating rainfall-induced landslides. Environ. Earth Sci. 2018, 77, 589. [Google Scholar] [CrossRef]
- Zettl, J.D.; Barbour, S.L.; Huang, M.; Si, B.C.; Leskiw, L.A. Influence of textural layering on field capacity of coarse soils. Can. J. Soil Sci. 2011, 91, 133–147. [Google Scholar] [CrossRef]
- Huang, M.; Barbour, L.S.; Elshorbagy, A.; Zettl, J.D.; Si, B.C. Infiltration and drainage processes in multi-layered coarse soils. Can. J. Soil Sci. 2011, 91, 169–183. [Google Scholar] [CrossRef]
- Huang, M.; Barbour, L.S.; Elshorbagy, A.; Zettl, J.D.; Si, B.C. Water availability and forest growth in coarse-textured soils. Can. J. Soil Sci. 2011, 91, 199–210. [Google Scholar] [CrossRef]
- Huang, M.; Spies, J.; Barbour, S.L.; Si, B.C.; Zettl, J. Impact of textural layering on water retention within drained sand profiles. Soil Sci. 2013, 178, 496–504. [Google Scholar] [CrossRef]
- Si, B.; Dyck, M.; Parkin, G.W. Flow and transport in layered soils. Can. J. Soil Sci. 2011, 91, 127–132. [Google Scholar] [CrossRef]
- Jha, R.K.; Sahoo, B.; Panda, R.K. Modeling the water and nitrogen transports in a soil–paddy–atmosphere system using HYDRUS-1D and lysimeter experiment. Paddy Water Environ. 2017, 15, 831–846. [Google Scholar] [CrossRef]
- Ma, Y.; Feng, S.; Song, X. Evaluation of optimal irrigation scheduling and groundwater recharge at representative sites in the North China Plain with SWAP model and field experiments. Comput. Electron. Agric. 2015, 116, 125–136. [Google Scholar] [CrossRef]
- Karandish, F.; Šimůnek, J. An application of the water footprint assessment to optimize production of crops irrigated with saline water: A scenario assessment with HYDRUS. Agric. Water Manag. 2018, 208, 67–82. [Google Scholar] [CrossRef]
- Chen, M.; Willgoose, G.R.; Saco, P.M. Spatial prediction of temporal soil moisture dynamics using HYDRUS-1D. Hydrol. Process. 2014, 28, 171–185. [Google Scholar] [CrossRef]
- Azad, N.; Behmanesh, J.; Rezaverdinejad, V.; Abbasi, F.; Navabian, M. Developing an optimization model in drip fertigation management to consider environmental issues and supply plant requirements. Agric. Water Manag. 2018, 208, 344–356. [Google Scholar] [CrossRef]
- Li, X.; Chang, S.X.; Salifu, K.F. Soil texture and layering effects on water and salt dynamics in the presence of a water table: A review. Environ. Rev. 2014, 22, 41–50. [Google Scholar] [CrossRef]
- Wu, Q.F.; Fan, J.; Yang, X.L.; Pan, Y.W.; Wang, Y.F.; Qiao, Y.Q.; Wang, S. Experiment and simulation of Infiltration from layered soils in open pit mine in Jin-Shaan-Meng adjacent region. Acta Pedol. Sin. 2015, 52, 86–96. [Google Scholar]
- Brunetti, G.; Šimůnek, J.; Piro, P. A comprehensive numerical analysis of the hydraulic behavior of a permeable pavement. J. Hydrol. 2016, 540, 1146–1161. [Google Scholar] [CrossRef]
- Zambrano-Bigiarini, M.; Rojas, R. A model-independent Particle Swarm Optimisation software for model calibration. Environ. Model. Softw. 2013, 43, 5–25. [Google Scholar] [CrossRef]
- Vaidya, O.S.; Kumar, S. Analytic hierarchy process: An overview of applications. Eur. J. Oper. Res. 2006, 169, 1–29. [Google Scholar] [CrossRef]
- Behzadian, M.; Khanmohammadi Otaghsara, S.; Yazdani, M.; Ignatius, J. A state-of the-art survey of TOPSIS applications. Expert Syst. Appl. 2012, 39, 13051–13069. [Google Scholar] [CrossRef]
- Tscheikner-Gratl, F.; Egger, P.; Rauch, W.; Kleidorfer, M. Comparison of multi-criteria decision support methods for integrated rehabilitation prioritization. Water 2017, 9, 68. [Google Scholar] [CrossRef]
- Ramya, S.; Devadas, V. Integration of GIS, AHP and TOPSIS in evaluating suitable locations for industrial development: A case of Tehri Garhwal district, Uttarakhand, India. J. Clean. Prod. 2019, 238, 117872. [Google Scholar] [CrossRef]
- Zhu, S.; Li, D.; Feng, H.; Gu, T.; Zhu, J. AHP-TOPSIS-based evaluation of the relative performance of multiple neighborhood renewal projects: A case study in Nanjing, China. Sustainability 2019, 11, 4545. [Google Scholar] [CrossRef]
- Wang, J.; Huang, Y.; Long, H.; Hou, S.; Xing, A.; Sun, Z. Simulations of water movement and solute transport through different soil texture configurations under negative-pressure irrigation. Hydrol. Process. 2017, 31, 2599–2612. [Google Scholar] [CrossRef]
- Bonfante, A.; Basile, A.; Acutis, M.; De Mascellis, R.; Manna, P.; Perego, A.; Terribile, F. SWAP, CropSyst and MACRO comparison in two contrasting soils cropped with maize in Northern Italy. Agric. Water Manag. 2010, 97, 1051–1062. [Google Scholar] [CrossRef]
- Jiang, J.; Feng, S.; Huo, Z.; Zhao, Z.; Jia, B. Application of the SWAP model to simulate water-salt transport under deficit irrigation with saline water. Math. Comput. Model. 2011, 54, 902–911. [Google Scholar] [CrossRef]
- Hillel, D.; Talpaz, H. Simulation of soil water dynamics in layered soils. Soil Sci. 1977, 123, 54–62. [Google Scholar] [CrossRef]
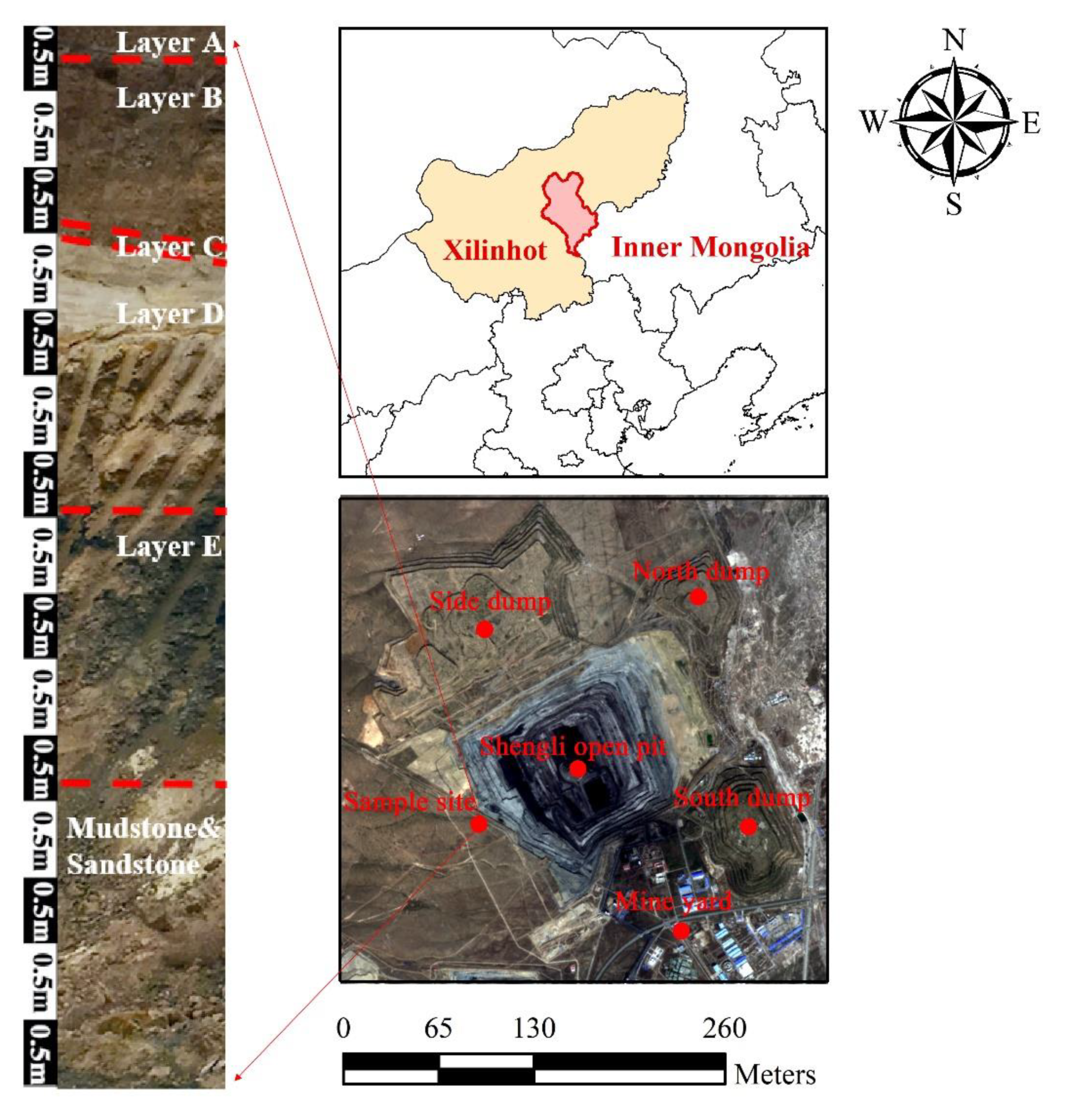











| Sample | Clay (%) | Silt (%) | Sand (%) | Texture | Bulk Density (g cm−3) | Porosity (%) | The Proportion of Total Profile (%) |
|---|---|---|---|---|---|---|---|
| Layer A | 4.55 | 37.73 | 57.72 | Sandy Loam | 1.23 | 0.51 | 4.6% |
| Layer B | 4.43 | 34.04 | 61.54 | Sandy Loam | 1.59 | 0.39 | 21.8% |
| Layer C | 3.32 | 21.8 | 74.87 | Loamy Sand | 1.72 | 0.33 | 2.2% |
| Layer D | 0.15 | 2.69 | 97.16 | Sand | 1.54 | 0.37 | 35.6% |
| Layer E | 7.44 | 71.72 | 20.83 | Silt Loam | 1.22 | 0.51 | 35.9% |
| Intensity of Importance | Definition |
|---|---|
| 1 | Equal importance |
| 3 | Moderate importance |
| 5 | Strong importance |
| 7 | Very strong importance |
| 9 | Extreme importance |
| 2, 4, 6, 8 | Intermediate values between the two adjacent judgments |
| Dataset | Soil Profile | RMSE | NSE | MAE |
|---|---|---|---|---|
| Validation data | SL-S-SiL | 0.0170 ± 0.0036 | 0.9840 ± 0.0090 | 0.0118 ± 0.0041 |
| Calibration data | SL-SiL | 0.0265 ± 0.0045 | 0.9662 ± 0.0261 | 0.0192 ± 0.0052 |
| SL-S | 0.0107 ± 0.0031 | 0.9900 ± 0.0087 | 0.0066 ± 0.0019 | |
| SL-SiL-S | 0.0207 ± 0.0044 | 0.9679 ± 0.0111 | 0.0135 ± 0.0025 |
| Soil Texture | Parameters | Initial Values | Lower Boundary | Upper Boundary | Optimized Values |
|---|---|---|---|---|---|
| Sandy loam | (cm3 cm−3) | 0.000 | 0.00 | 0.050 | 0.003 |
| (cm3 cm−3) | 0.440 | 0.374 | 0.506 | 0.450 | |
| (cm−1) | 0.020 | 0.017 | 0.023 | 0.019 | |
| 1.530 | 1.301 | 1.761 | 1.514 | ||
| (cm min−1) | 0.500 | 0.051 | 0.069 | 0.06 | |
| Sand | (cm3 cm−3) | 0.000 | 0.00 | 0.050 | 0.007 |
| (cm3 cm−3) | 0.310 | 0.264 | 0.357 | 0.312 | |
| (cm−1) | 0.055 | 0.047 | 0.063 | 0.059 | |
| 2.500 | 2.125 | 2.875 | 2.599 | ||
| (cm min−1) | 0.500 | 0.213 | 0.288 | 0.238 | |
| Silt loam | (cm3 cm−3) | 0.00 | 0.000 | 0.050 | 0.016 |
| (cm3 cm−3) | 0.470 | 0.400 | 0.541 | 0.479 | |
| (cm−1) | 0.020 | 0.017 | 0.023 | 0.021 | |
| 1.400 | 1.190 | 1.610 | 1.462 | ||
| (cm min−1) | 0.500 | 0.034 | 0.046 | 0.045 |
| Profiles | Type | Initial Infiltration (cm min−1) | Steady Infiltration Rate (cm min−1) | Accumulation Infiltration (cm) |
|---|---|---|---|---|
| SL-SiL | Measured | 0.8 | 0.04 | 38.5 |
| Simulated | 0.3 | 0.05 | 44.0 | |
| SL-S | Measured | 0.5 | 0.08 | 27.0 |
| Simulated | 0.3 | 0.07 | 28.4 | |
| SL-S-SiL | Measured | 0.9 | 0.06 | 34.7 |
| Simulated | 0.3 | 0.05 | 39.2 | |
| SL-SiL-S | Measured | 0.9 | 0.06 | 32.9 |
| Simulated | 0.3 | 0.06 | 36.6 |
| Profile | Data Type | Infiltration Time of Each Layer (min) | |||
|---|---|---|---|---|---|
| First Layer | Second Layer | Third Layer | Total Time | ||
| SL-SiL | Measured | 77.1 | 469.0 | — | 546.1 |
| Simulated | 96.0 | 546.0 | — | 642.0 | |
| SL-S | Measured | 79.2 | 224.2 | — | 303.4 |
| Simulated | 96.0 | 235.5 | — | 331.5 | |
| SL-S-SiL | Measured | 79.8 | 105.8 | 259.2 | 444.8 |
| Simulated | 96.0 | 99.0 | 288.0 | 483.0 | |
| SL-SiL-S | Measured | 83.1 | 193.1 | 154.2 | 430.4 |
| Simulated | 96.0 | 204.0 | 165.0 | 465.0 | |
| Indices | Description | Unit |
|---|---|---|
| Index 1 | Steady infiltration rate | cm min−1 |
| Index 2 | Accumulation infiltration amount | cm |
| Index 3 | Breakthrough time of wetting front | min |
| Index 4 | Total profile moisture | mm |
| Index 5 | Total profile moisture at 7d | mm |
| Index 6 | Water moisture of first layer at 7d | mm |
| Profile | Index 1 | Index 2 | Index 3 | Index 4 | Index 5 | Index 6 |
|---|---|---|---|---|---|---|
| SL-S | 0.07 | 28.4 | 331.5 | 353 | 137 | 95.0 |
| SL-SiL | 0.05 | 44.0 | 642.0 | 481 | 285 | 74.0 |
| SL-S-SiL | 0.05 | 39.2 | 483.0 | 426 | 222 | 95.0 |
| SL-SiL-S | 0.06 | 36.6 | 465.0 | 408 | 224 | 86.0 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, X.; Zhao, Y.; Liu, H.; Xiao, W.; Chen, S. Evaluating the Water Holding Capacity of Multilayer Soil Profiles Using Hydrus-1D and Multi-Criteria Decision Analysis. Water 2020, 12, 773. https://doi.org/10.3390/w12030773
Wang X, Zhao Y, Liu H, Xiao W, Chen S. Evaluating the Water Holding Capacity of Multilayer Soil Profiles Using Hydrus-1D and Multi-Criteria Decision Analysis. Water. 2020; 12(3):773. https://doi.org/10.3390/w12030773
Chicago/Turabian StyleWang, Xin, Yanling Zhao, Huifang Liu, Wu Xiao, and Shuzhao Chen. 2020. "Evaluating the Water Holding Capacity of Multilayer Soil Profiles Using Hydrus-1D and Multi-Criteria Decision Analysis" Water 12, no. 3: 773. https://doi.org/10.3390/w12030773
APA StyleWang, X., Zhao, Y., Liu, H., Xiao, W., & Chen, S. (2020). Evaluating the Water Holding Capacity of Multilayer Soil Profiles Using Hydrus-1D and Multi-Criteria Decision Analysis. Water, 12(3), 773. https://doi.org/10.3390/w12030773






