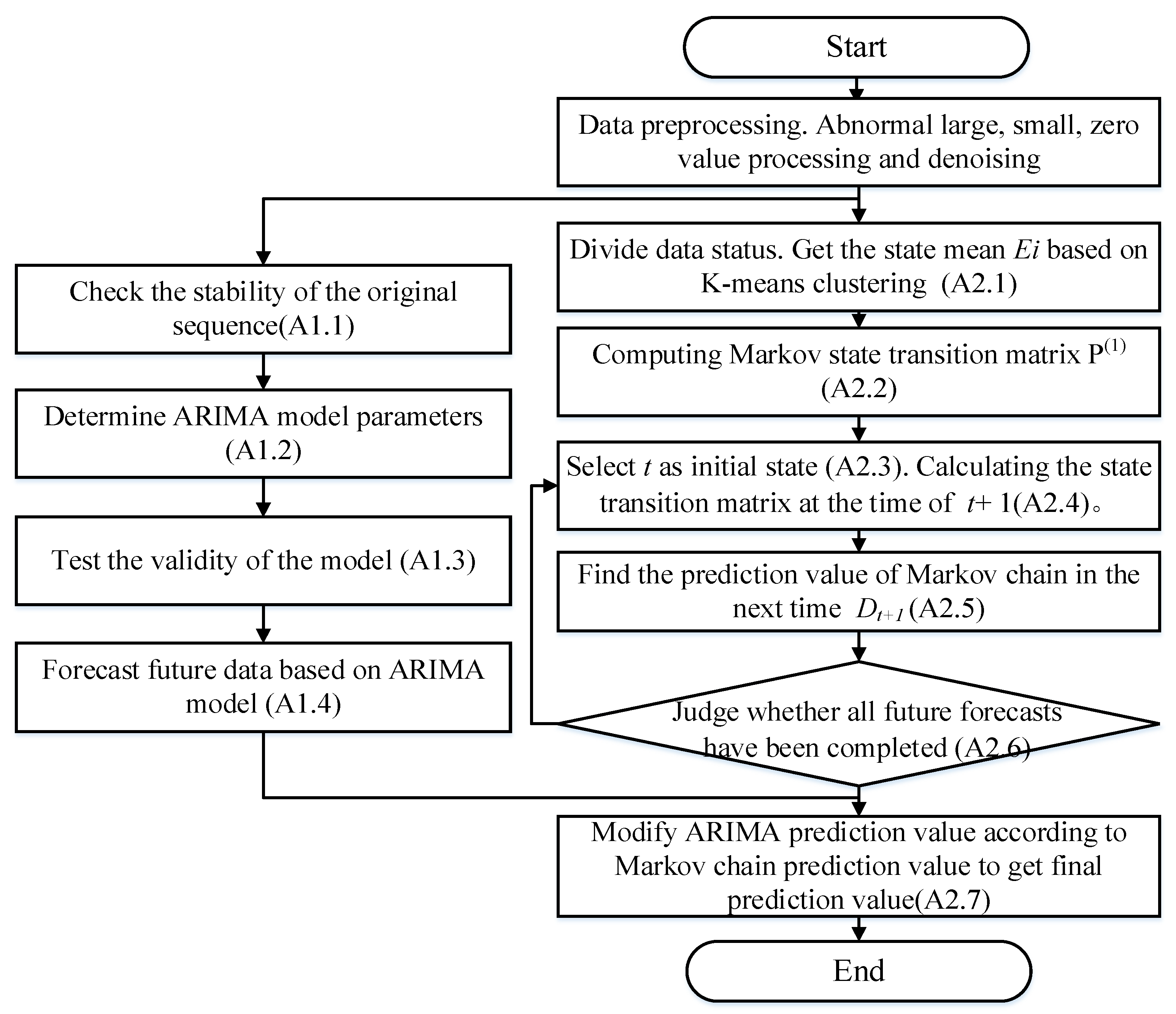
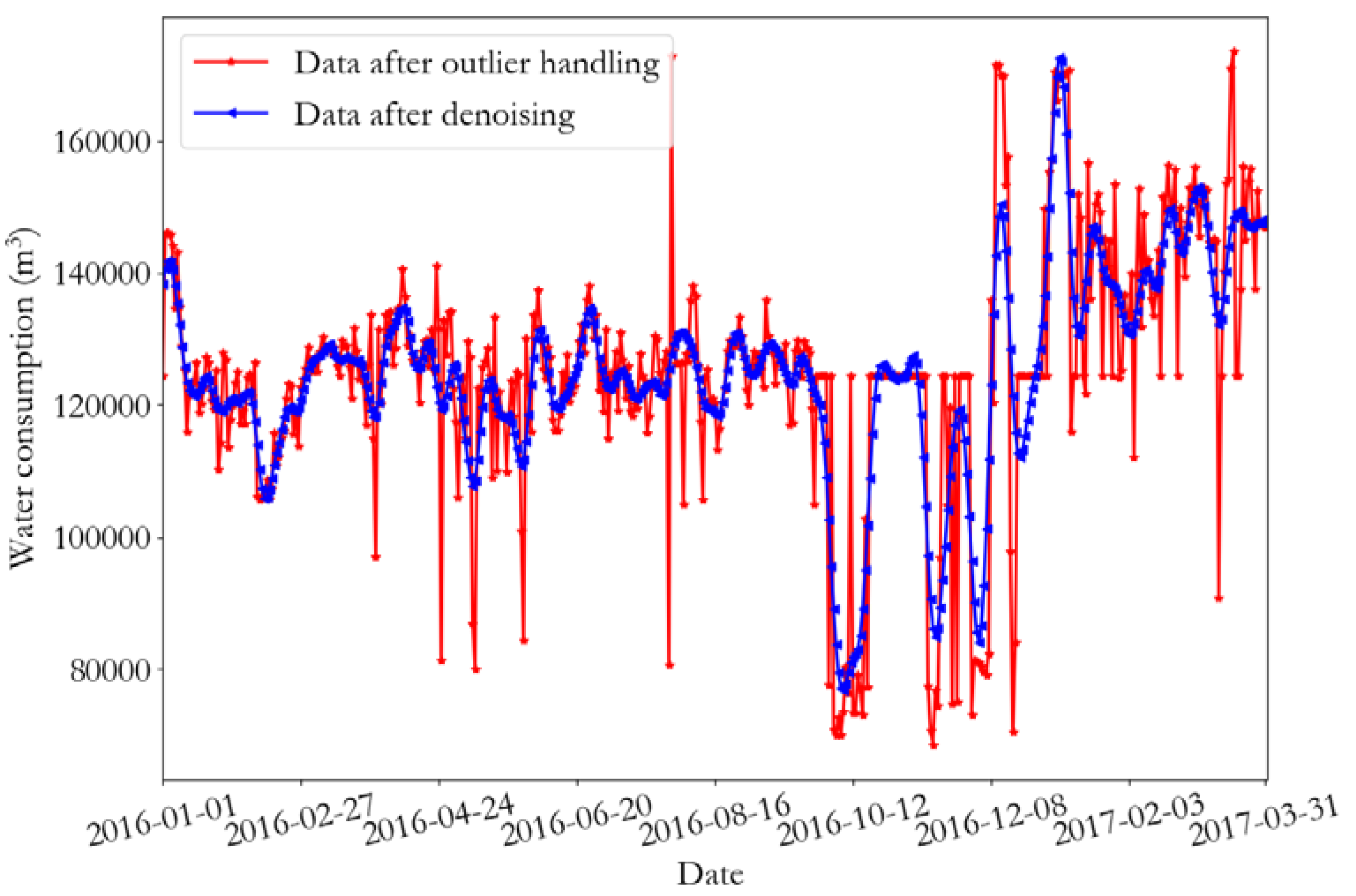
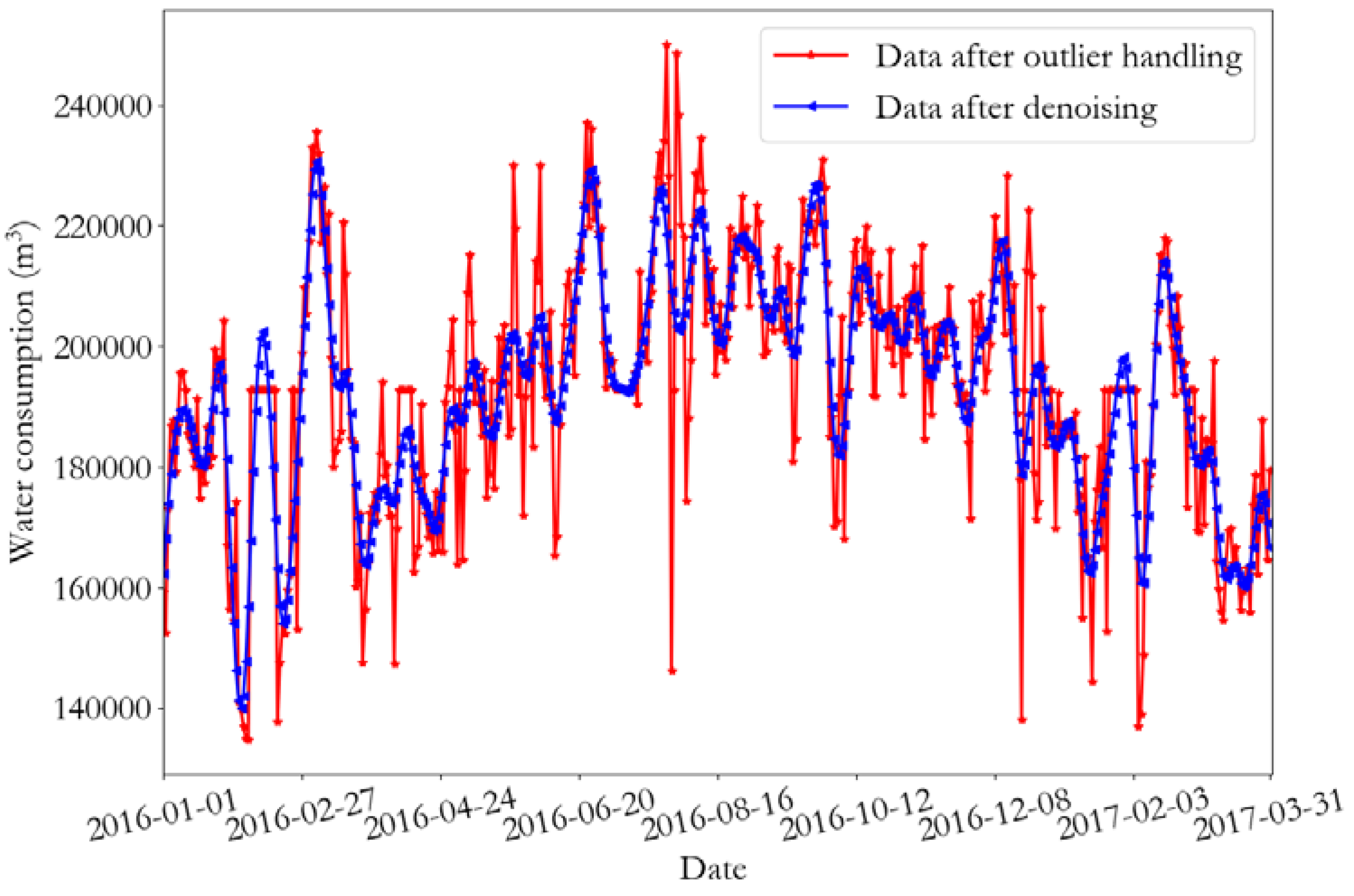
The effectiveness of the proposed algorithm is verified by examples. The daily water intake data of some water monitoring points in Guangdong Province from 2016 to 2017 were selected for the experiment. The daily water consumption data from January to December 2016 was used to build the model, and the data from January 2017 was used to test the validity of the model.
4.2. Model Validation
Firstly, the ARIMA analysis was performed on data 1 of the monitoring point. The water consumption data X
1 of the monitoring point 1 fluctuated within a wide range. To eliminate the fluctuation trend of its time series, the data sequence of X
1 was differentially processed and data sequence of DX
1 was obtained. As can be seen from
Figure 6, the sequence after the first-order difference fluctuated steadily, around the mean value.
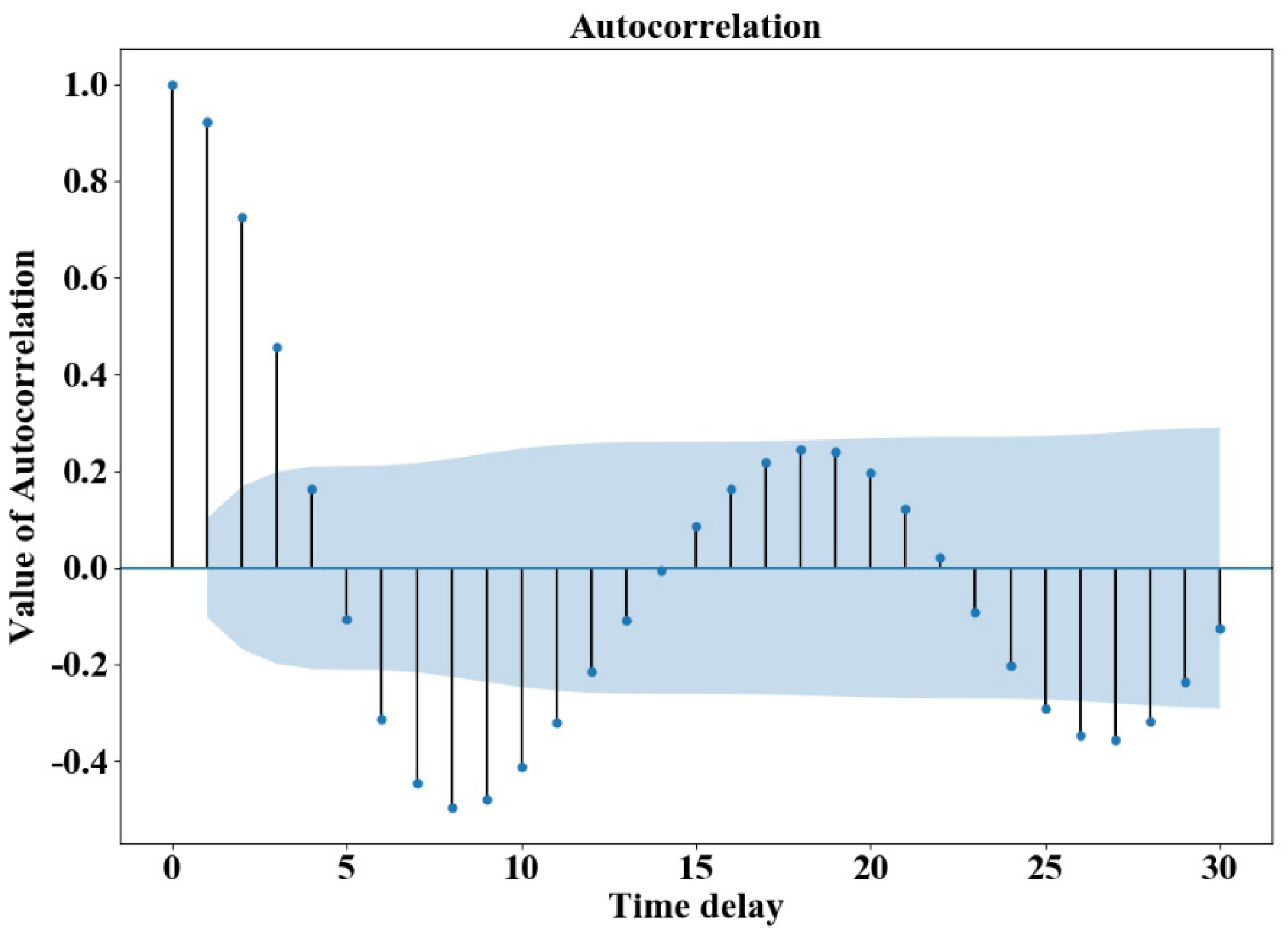
Figure 7 displays the autocorrelation diagram after the first-order difference of the water consumption sequence. It can be seen from the figure that the autocorrelation coefficient is greater than zero for a long time, indicating the presence of a strong property between the sequences. The stationary state of the Augmented Dickey-Fuller (ADF) unit root test sequence was selected (see
Table 3). The
p-value of the unit root test was less than 0.05, suggesting the sequence after the first difference was a stationary sequence.
Further, it is necessary to judge whether there is correlation between the sequence data. If the sequence is white noise sequence, there is no information to be extracted, and the analysis of the sequence needs to be terminated. White noise test was conducted for the data after the first-order difference, and the results are shown in
Table 4. The output
p value is far less than 0.05, so the first-order difference sequence is a stationary non-white noise sequence.
The ARIMA model was fitted on the first-order stationary white noise sequence. The relative optimal model identification method was used to calculate the BIC information of all combinations of ARIMA (
p, 1,
q) at
p and
q less than or equal to 5. The model parameter with the minimum BIC information was selected and the BIC matrix
bic_mat was as follows:
When p value is 2 and q value is 2, the minimum BIC value is 5178.98. Then the sequence was fitted and analyzed with the model of ARIMA (2, 1, 2). The p-value of the white noise test around the residual was 0.93, which is white noise; therefore, the model is valid.
The same method was adopted to determine the water consumption data fitting model of monitoring point 2. The time sequence after the first-order difference of monitoring point 2 fluctuated stably around the mean value, as shown in
Figure 8. And
Figure 9 displays the autocorrelation diagram after the first-order difference of the water consumption sequence at monitoring point 2. The ADF unit root was selected to check the stable state of the sequence, and the results are shown in
Table 5. The unit root test
p-value was less than 0.05, which suggests the sequence after the first-order difference was a stationary sequence. The white noise test was carried out on the data after the first-order difference, and the results are shown in
Table 6. As it can be observed from the results, the output
p-value was far less than 0.05; therefore, the sequence after the first-order difference was a stationary non-white noise sequence. It was determined that the ARIMA (
p, 1,
q) was less than or equal to 5 BIC information of all combinations. The
p and
q values, corresponding to the minimum BIC value, were all 2, and then the sequence was also fitted and analyzed with the model of ARIMA (2, 1, 2). The white noise test
p-value of the residual was 0.90, which was white noise; thus, the model passed the test and is valid.
The longer the prediction period of the ARIMA model, the larger the prediction error, which causes error accumulation. Therefore, the proposed error correction method based on the Markov chain was used to correct the prediction results from the ARIMA model.
Firstly, on the basis of the Markov model, the training data were counted, and the state transition matrix and the one-step state transition value under each state were obtained. Subsequently, the future data prediction value was obtained as the future data trend. Then, the modified values were calculated on the basis of the prediction results of the Markov model.
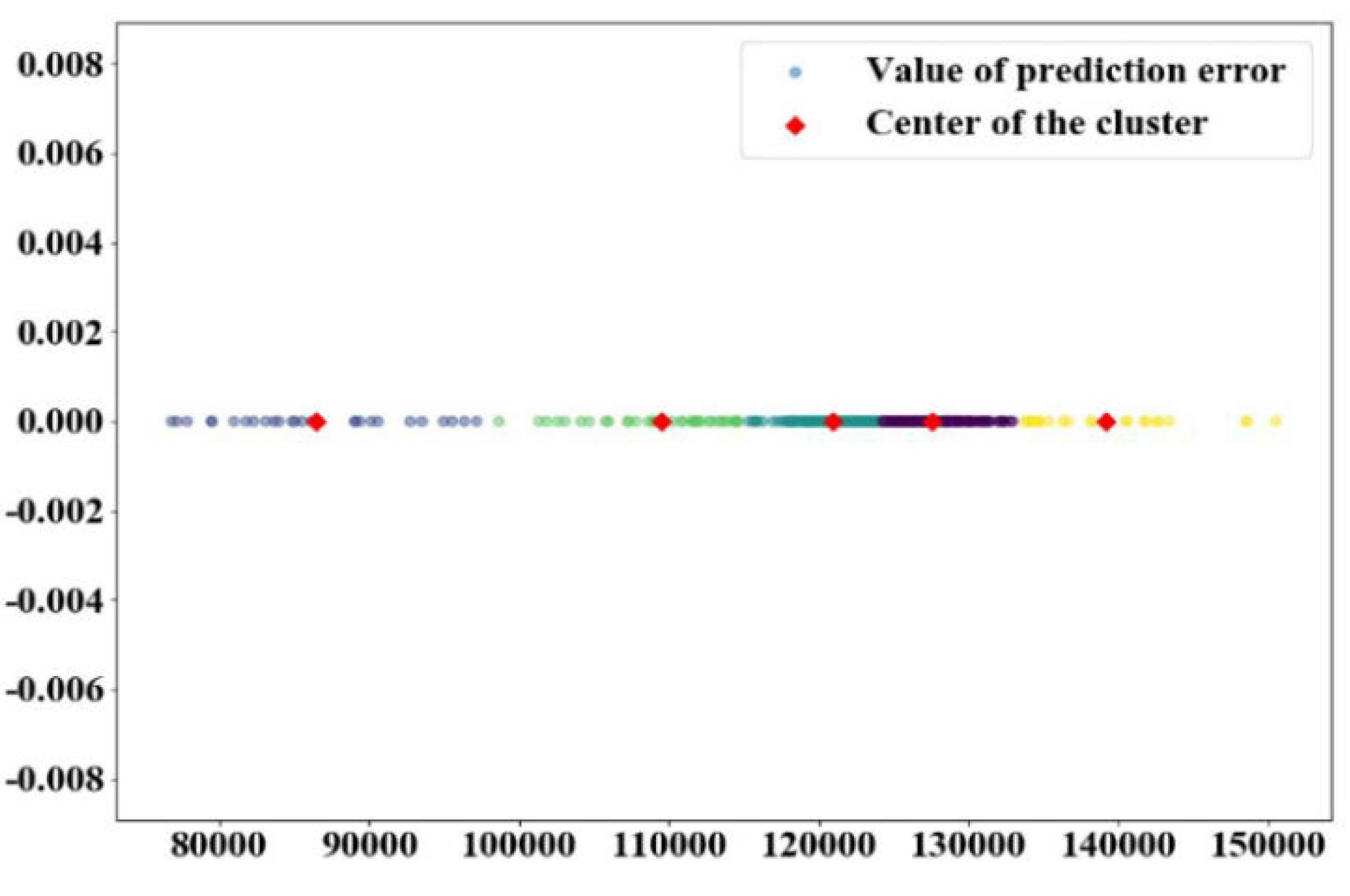
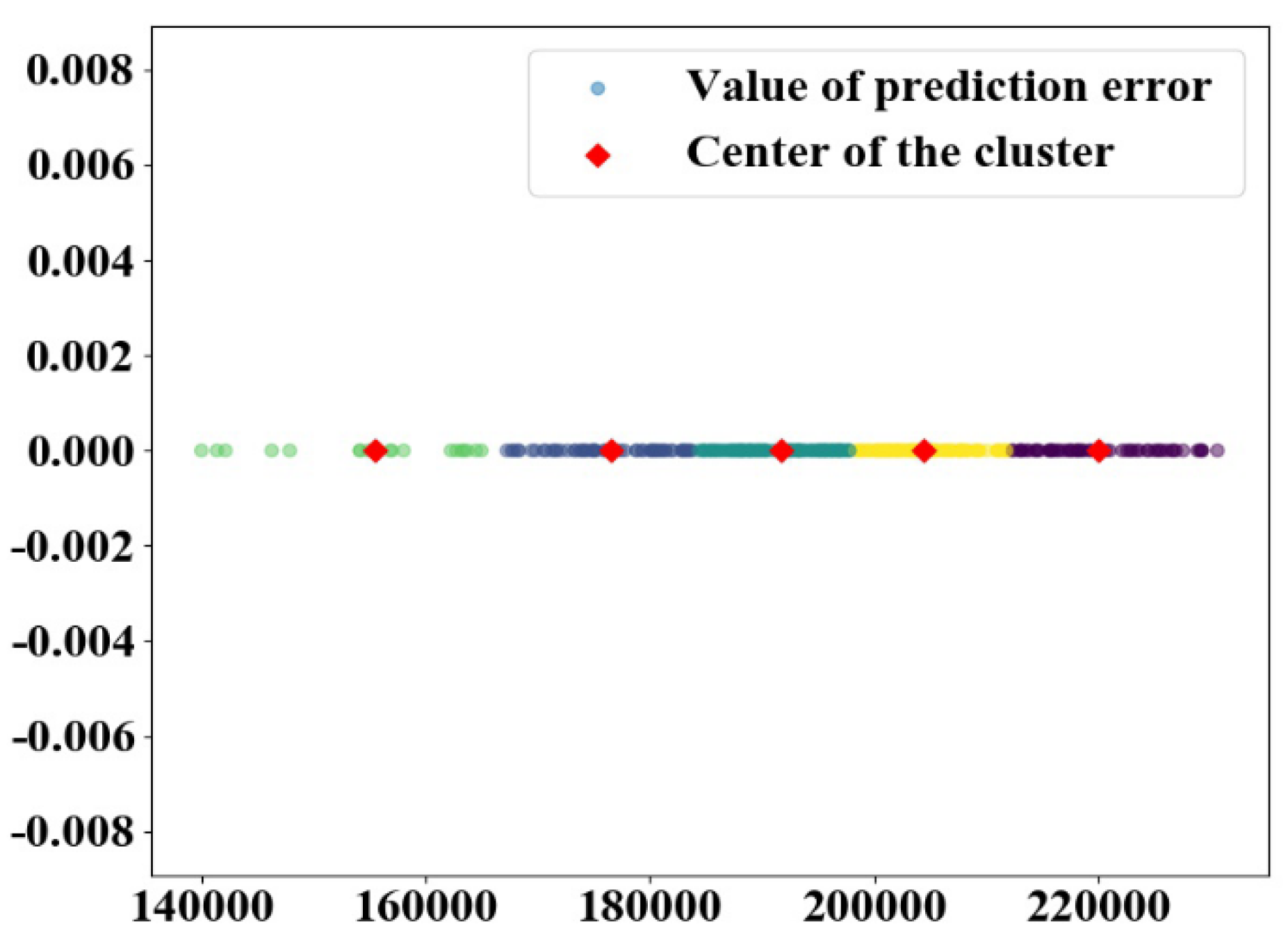
In the prediction based on the Markov chain, the state of data sequence was set to 5, and
k-means algorithm was used to divide the state of data sequence. The cluster diagram of water consumption of monitoring point 1 and 2 are demonstrated in
Figure 10 and
Figure 11, respectively. The cluster center points of monitoring point 1 were the vector of [127561.19 86415.6 120963.62 109515.03 139121.21].
The Markov chain one-step state probability matrix of daily water consumption data at monitoring point 1 and point 2 are presented in the following equation, respectively, as follows:
Given the significance level 0.01, = 32 can be obtained by looking at the table. According to Equations (2) and (3), the statistical value of monitoring point 1 and 2 are 700.81 and 1268.14, respectively. Therefore, the Markov model can be used to predict the daily water consumption in future.
If the water consumption data of monitoring point 1 on that day is known, the state vector is set as P0 = [0,0,0,0,1], according to the water consumption data, then the state vector of the next day is P1 = . According to Equation (6), the predicted value is [127114.01 88890.54 121126.54 109786.08 137019.38]. In the same way, the prediction value of the next n days is calculated, accordingly, on the basis of the method of the modified ARIMA model, that is, combining the predicted value of the Markov chain to modify the predicted result of the ARIMA in proportion.
To test the prediction performance of the proposed model, the following prediction algorithms were compared and analyzed, which included the ARIMA prediction, the Markov prediction, and the modified ARIMA model (ARIMA-M).
In order to measure the stability and adaptability of the prediction model, root mean square error (RMSE) and coefficient of determination (
R2), and the relative prediction error (RE) were selected as the evaluation indexes. The RMSE reflects the difference between the original value and the estimated value. The smaller the value, the closer the predicted value is to the real value, and the better the prediction effect. The
R2 can represent the whole fitting degree of the prediction model. The closer the
R2 is to 1, the better the fitting degree of the prediction value to the observation value, and the better the prediction performance of the model. The RE is the ratio of absolute error to the real value. The relative error reflects the reliability of the prediction. If the true real value and the predicted value of data
r are
Ti and Y
i, respectively,
N is the number of predicted samples, and the average value of all data values is
, then RMSE can be calculated through Equation (12), and
R2 and RE can be expressed by Equations (13) and (14).
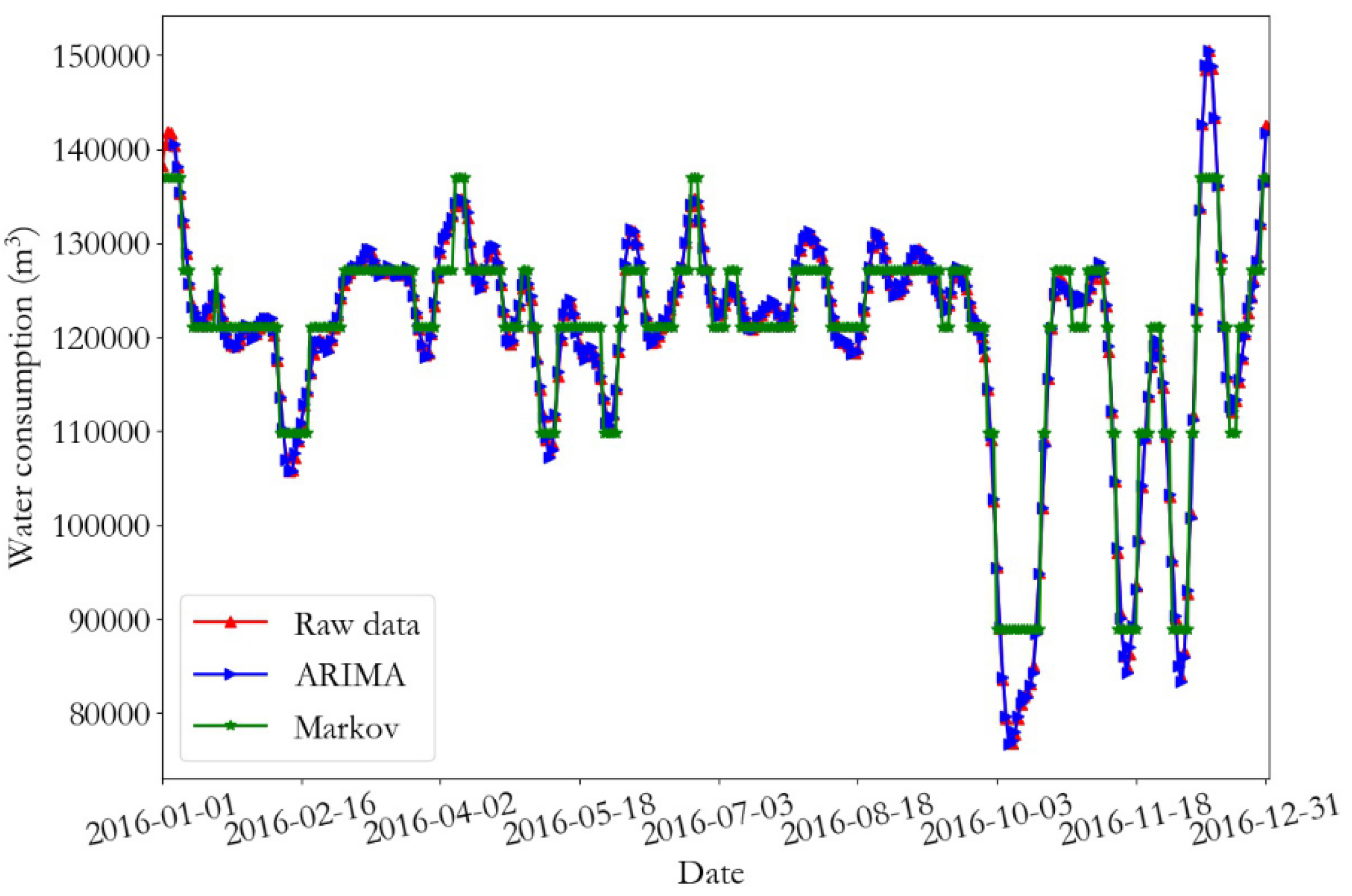
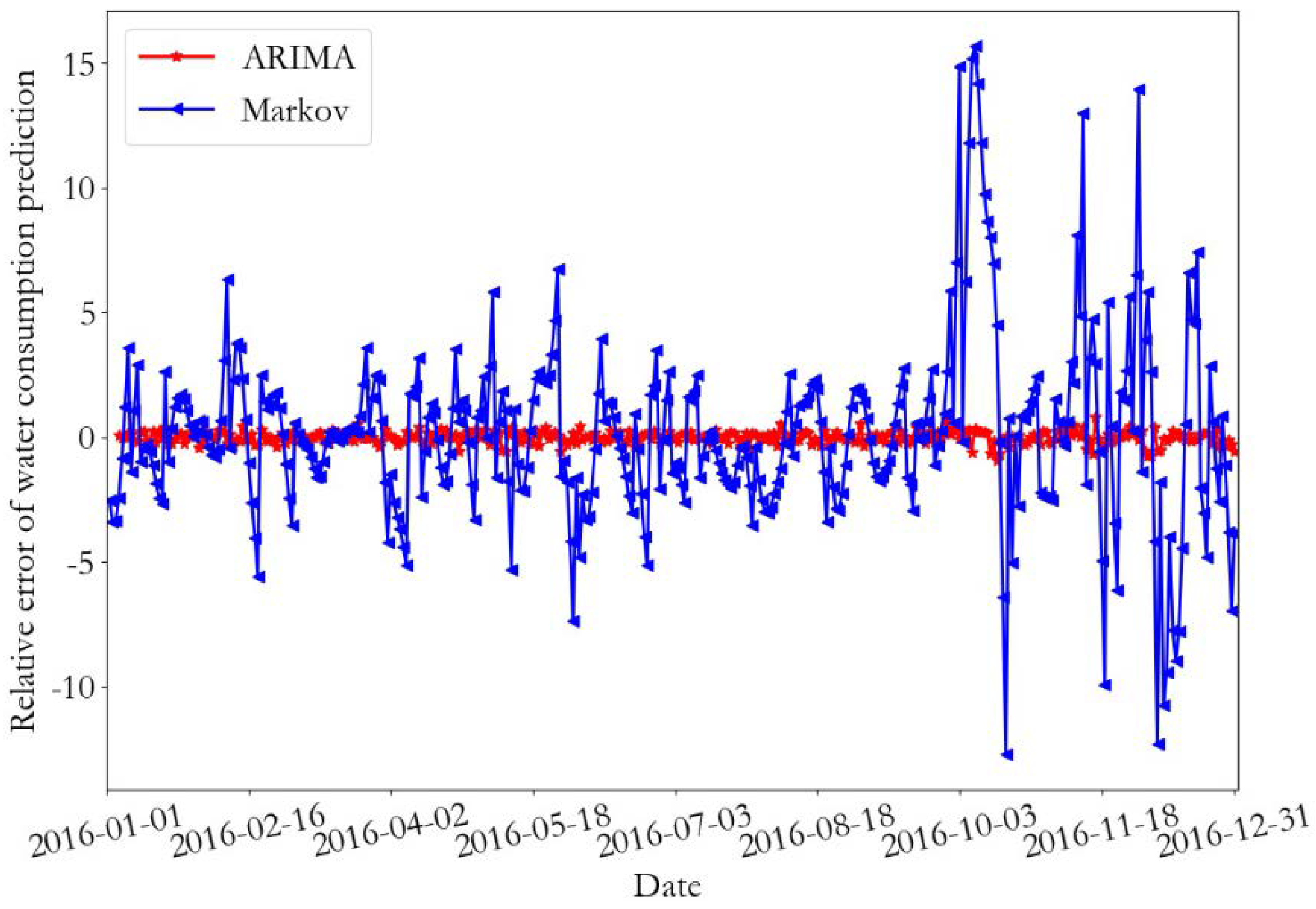
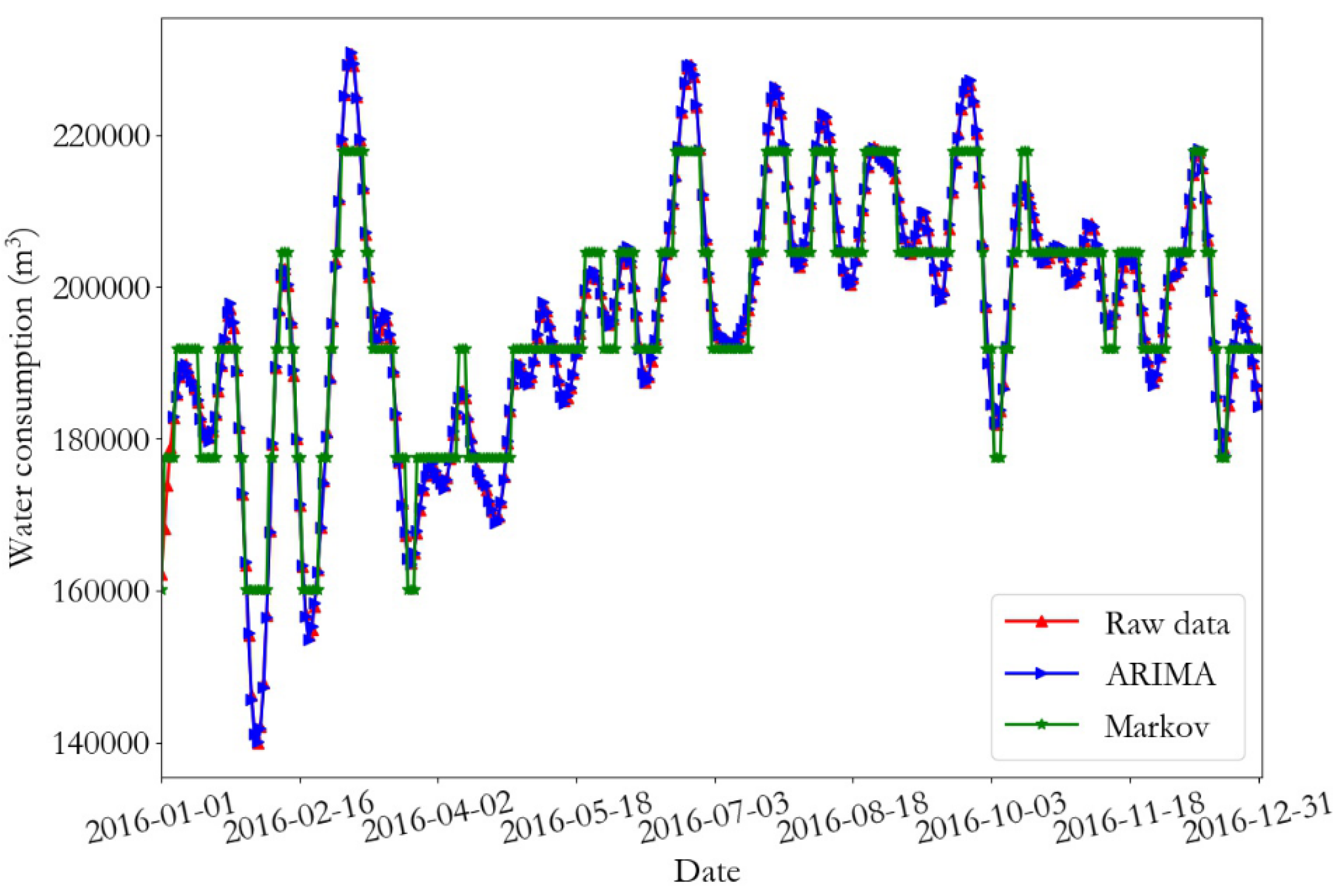
The prediction results and the relative error of the training data of monitoring point 1 are presented in
Figure 12 and
Figure 13, respectively. In addition, the prediction results and relative error curves of the training data of monitoring point 2 are demonstrated in
Figure 14 and
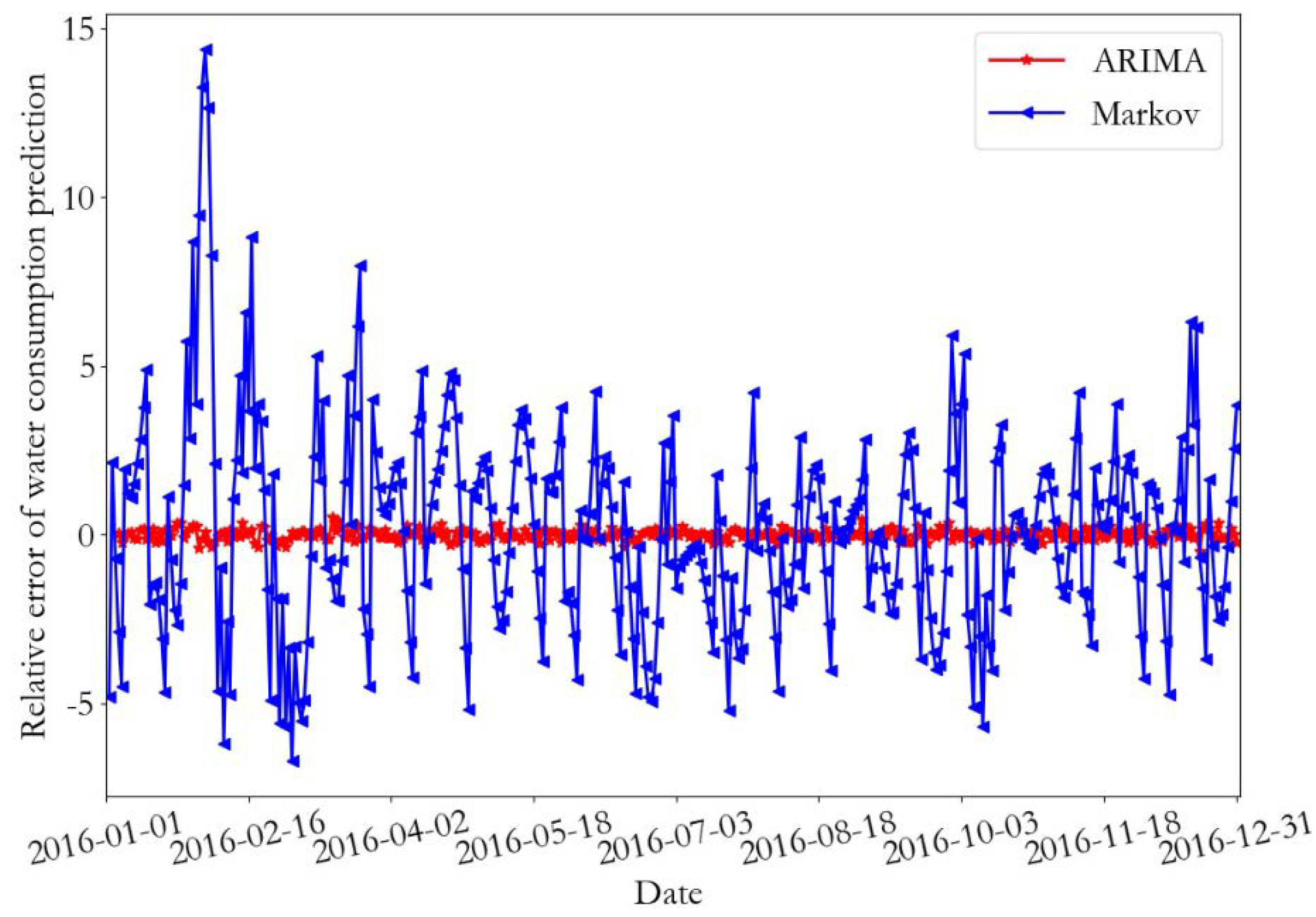
Figure 15, respectively. From the prediction results of the training data, it can be seen that the daily water consumption data of the two monitoring points predicted by the ARIMA were close to the real data value, and the overall trend predicted by the Markov was consistent with the predicted data; however, some errors were present. According to the error curve, it can be seen that the error of the ARIMA prediction was close to 0, and the error value of the Markov prediction at monitoring point 1 fluctuated between −12 and 15. Furthermore, the error value of the Markov prediction at monitoring point 2 fluctuated between −8 and 14.
Table 7 and
Table 8 show the prediction error of the ARIMA and the Markov model on the training dataset for monitoring point 1 and 2, respectively. According to the prediction data of monitoring point, the relative error (RE) of the ARIMA prediction was less than 0.2, and the coefficient of determination (
R2) was close to 1; therefore, the training dataset can be better fitted by this model. The training data mean square error, coefficient of determination, and relative error rate of the Markov model were much larger than those of the ARIMA model. The relative errors of the Markov model for monitoring point 1 and monitoring point 2 were about 13 and 18 times that of the ARIMA, respectively. Therefore, the ARIMA model provided good fitting results for the training data, and the relative error RE of the Markov prediction was less than 2.5%, which can meet the requirements of the daily water consumption data prediction.
Therefore, the ARIMA and Markov combined data prediction model (ARIMA_M) can be used for the daily water consumption data prediction. The ARIMA model can fit the training data with high prediction accuracy. The Markov model can predict the trend of water consumption data on the basis of the training data of water consumption.
On the basis of the training set of daily water consumption, the ARIMA and Markov prediction models can be obtained by training. The ARIMA and the proposed ARIMA-M correction algorithm were used to predict the data of 20 days from 1 to 20 January 2017, in order to verify the validity of the model.
Table 9 demonstrates the predicted values and errors of monitoring point 1 during the following 10 days. According to the future forecast data, the relative error RE of the ARIMA-M forecast can be reduced by 15.77%, compared to the ARIMA forecast.
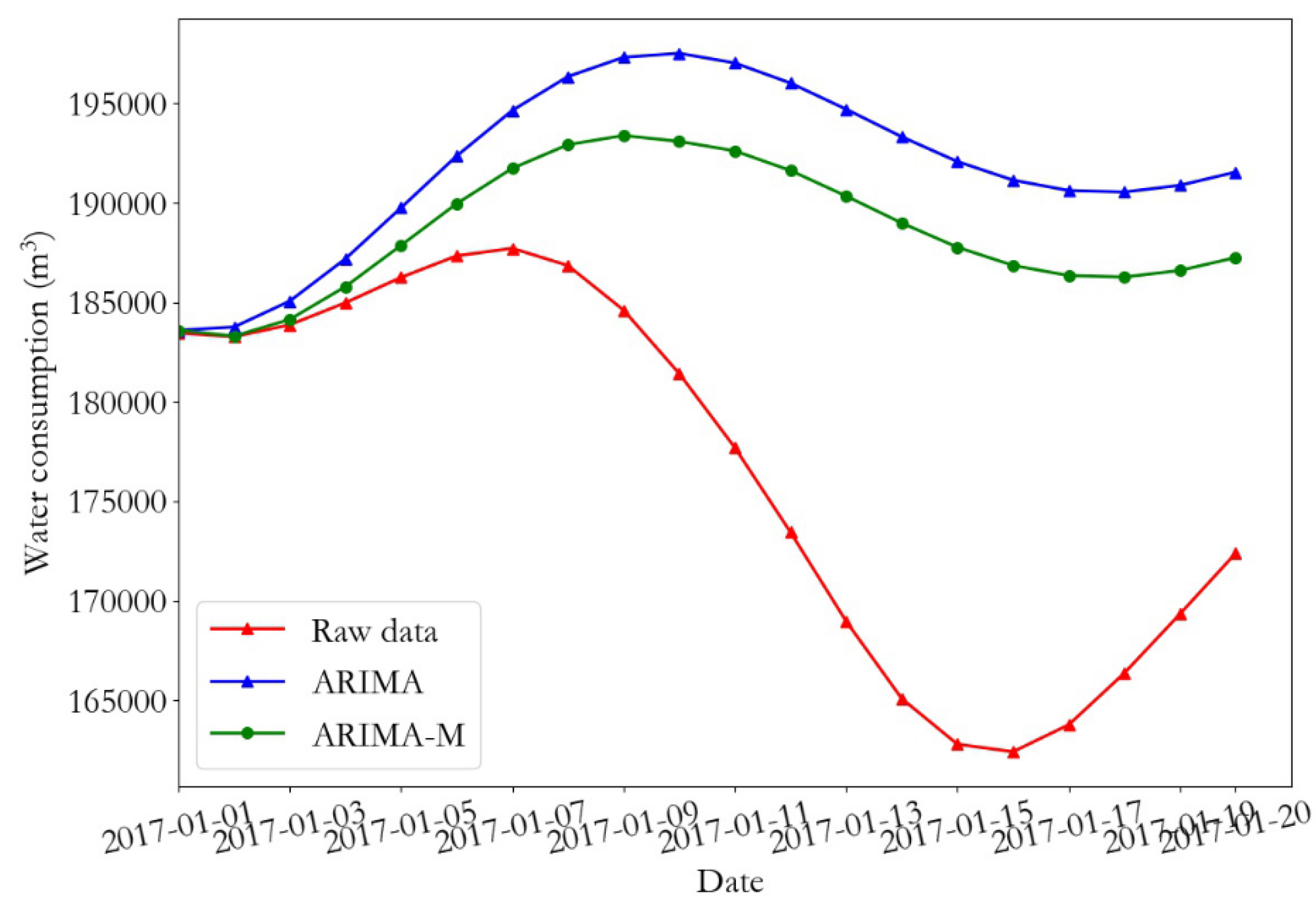
Figure 16 represents the total water consumption change and the relative error curve of monitoring point 2 for the following 20 days.
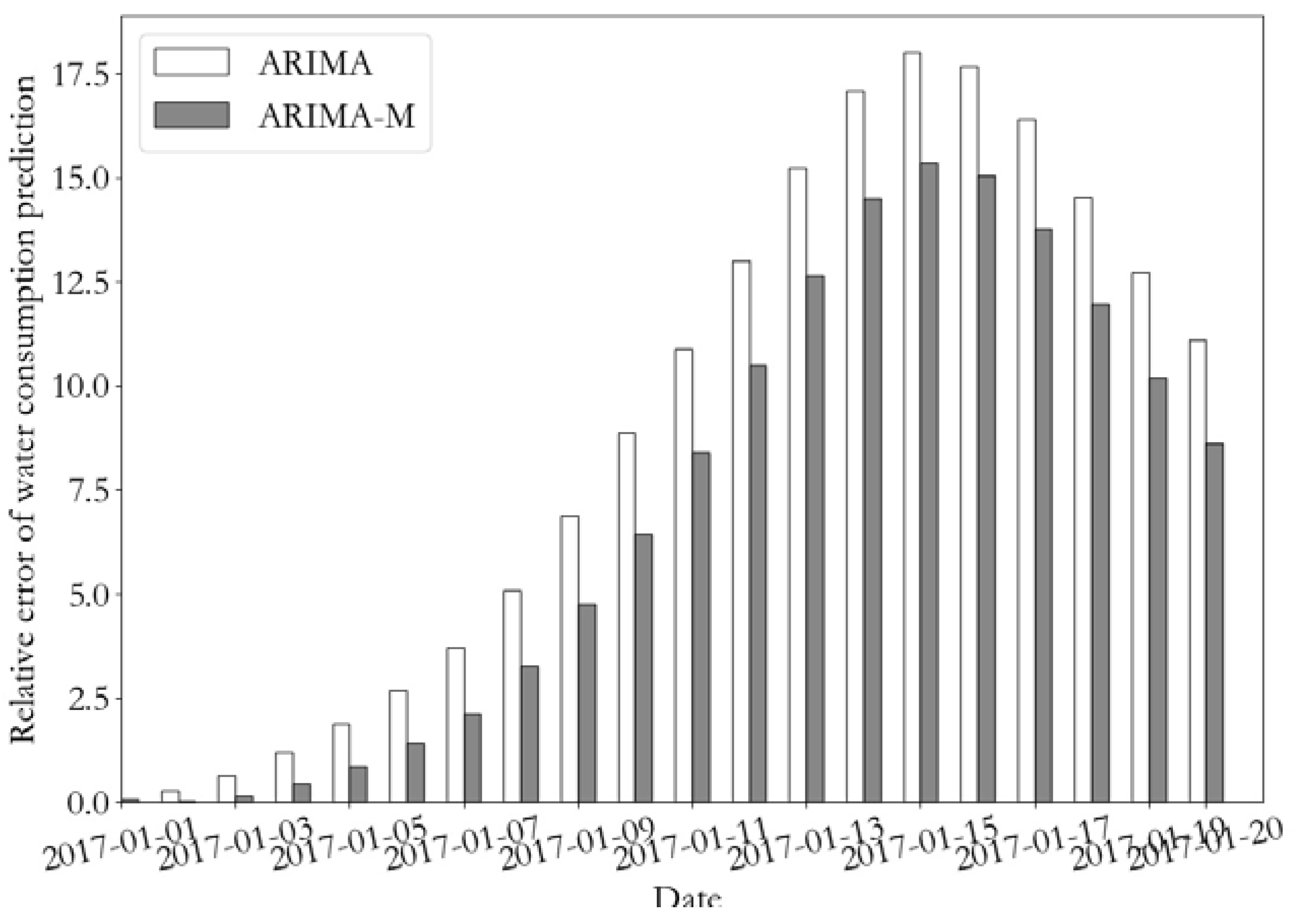
Figure 17 shows the prediction error curve of water consumption of monitoring point 2 for the following 20 days using the ARIMA and ARIMA-M algorithms. It can be seen from the figure that the predicted value of the test data using the ARIMA-M model was closer to the real value, and that the prediction error was lower.
The prediction error of the ARIMA and the proposed ARIMA-M model in the overall test set of monitoring points 1 and 2 are presented in
Table 10 and
Table 11, respectively. It can be observed from the table that compared to the training data that the prediction error of the test data was greatly increased. At monitoring point 1, the RMSE reached to 14,085, the
R2 value was only −0.04, and the relative error reached 8.07. Using ARIMA-M, the RMSE of the predicted value of the test set was decreased by 25%,
R2 was increased by more than 10 times, and relative error was decreased by 24.4%, in comparison with the traditional ARIMA. For monitoring point 2, compared to the ARIMA, the RMSE of predicted value on ARIMA-M test set and the relative error were reduced by 18.4% and 13%, respectively.
According to the above analysis, the ARIMA model can provide a better fit for the changes of daily water consumption data of monitoring points, wheras the Markov can predict the trend of daily water consumption data within a certain error range. However, due to the randomness nature of the water consumption data, the prediction accuracy of the above model for the unknown data decreased, and the proposed ARIMA-M model can be used (1) to correct the deviation of the future daily water consumption prediction data, (2) to reduce the over fitting of the ARIMA model on the training data set, (3) to improve the prediction accuracy of the data, and (4) to provide data support for the decision makers, on the basis of daily water consumption data prediction value.