Incorporating Rainwater Harvesting Systems in Iran’s Potable Water-Saving Scheme by Using a GIS-Simulation Based Decision Support System
Abstract
1. Introduction
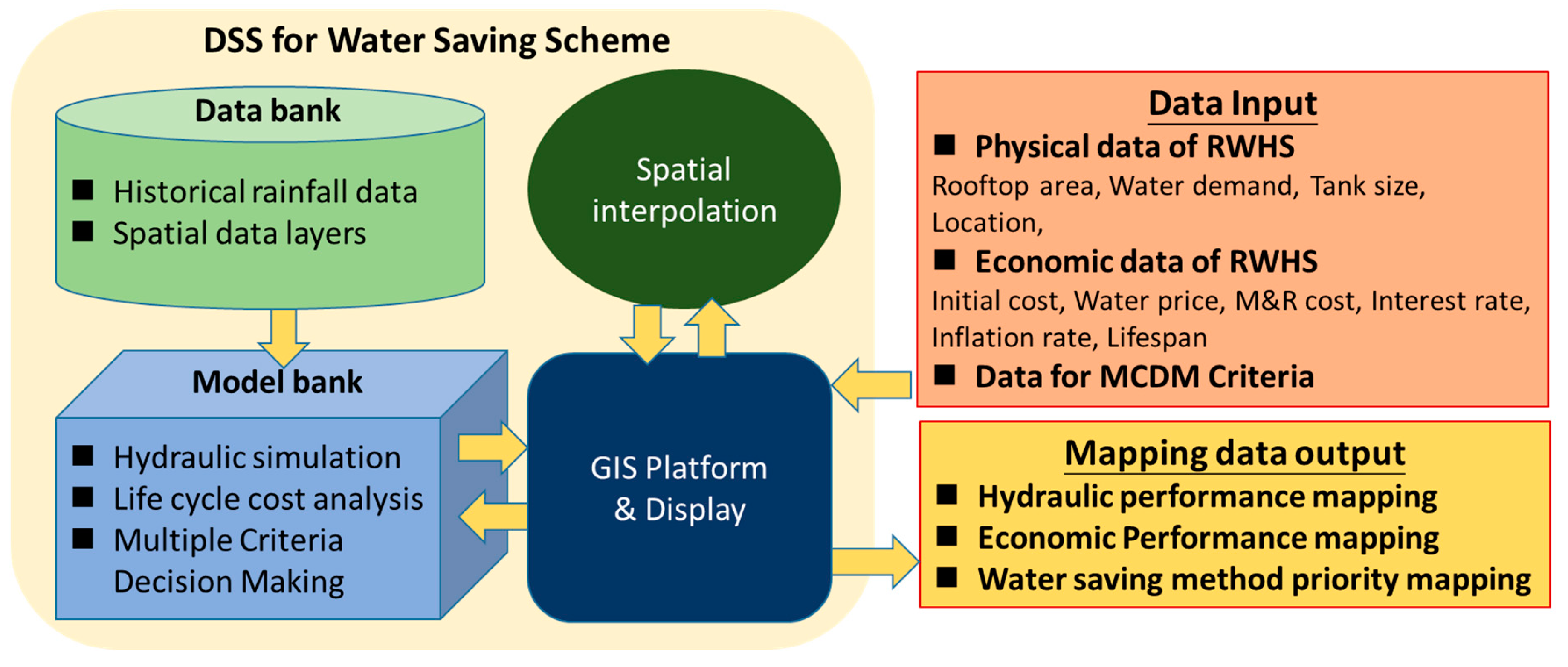
2. Methodology and Material of the DSS for the Water-Saving Scheme
2.1. System Description
2.2. Data Bank
2.3. Hydraulic Simulation
2.4. Economic Analysis (Life Cycle Cost Analysis)
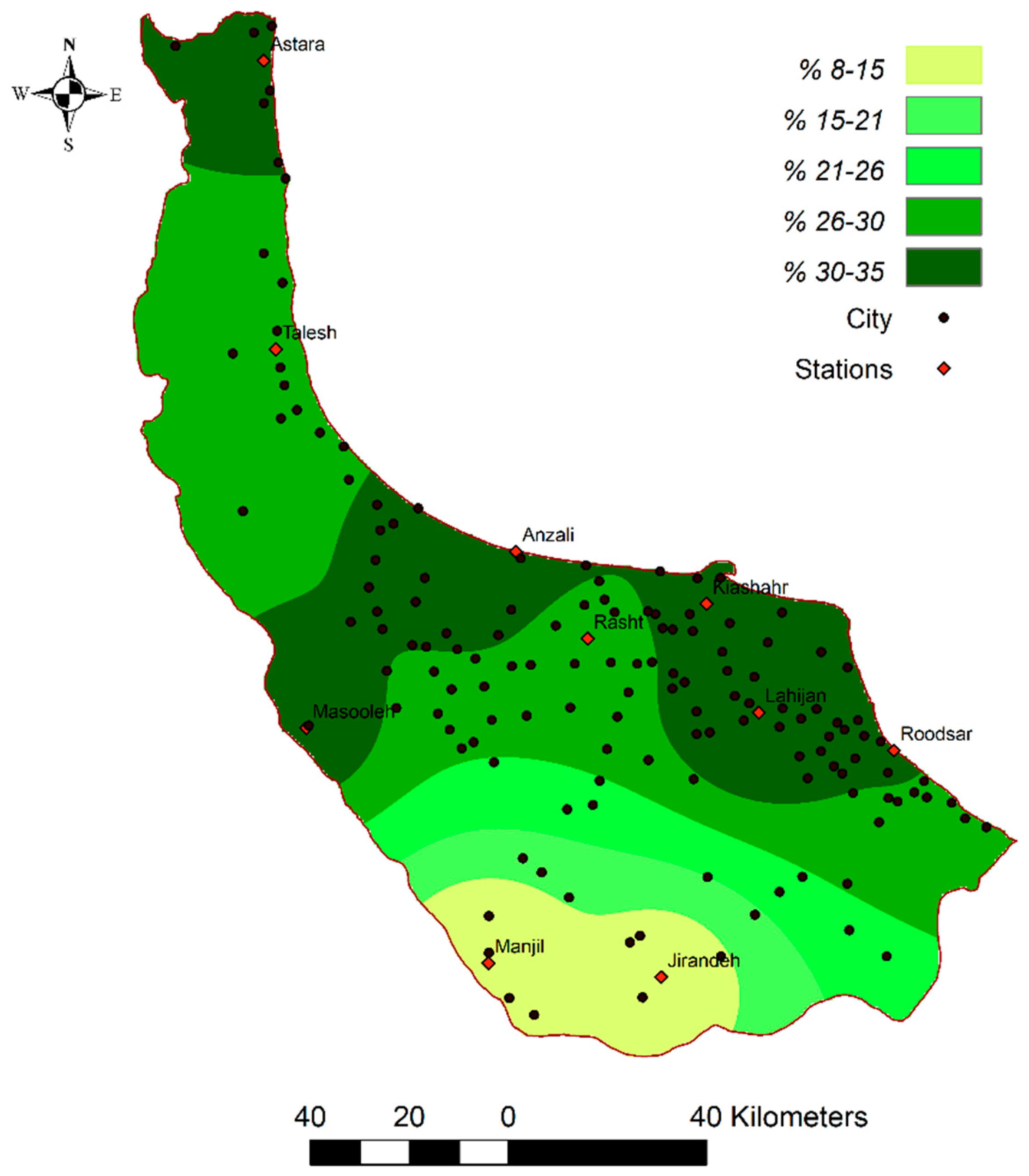
2.5. Spatial Analysis
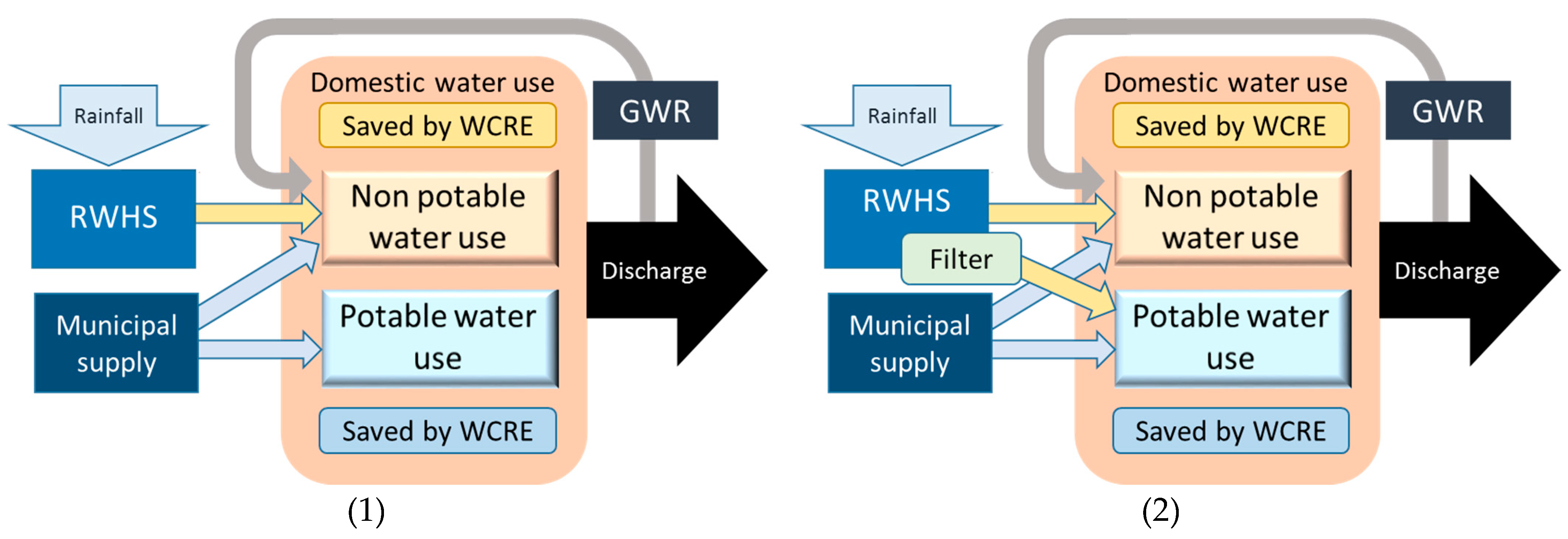
2.6. Modified RWHS Design in Arid Water-Saving Schemes
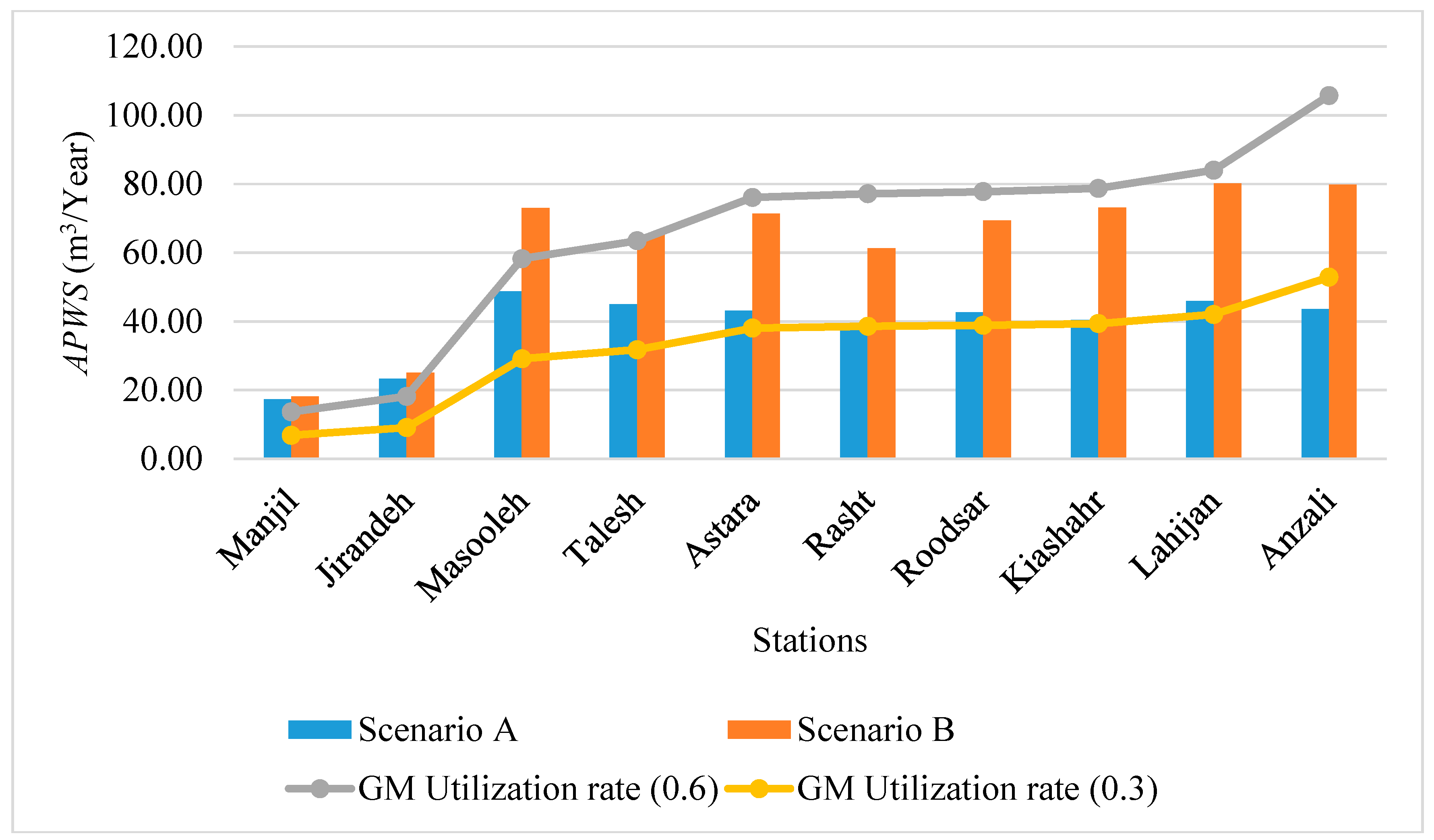
- Scenario A: Typical RWHSs that supply only for domestic non-potable use, i.e., toilet flushing, with daily water demand per person as 24% × 157 L.
- Scenario B: Modified RWHSs are for both potable and non-potable domestic uses by adding a drinkable filter. Therefore, the water demand for such a system is calculated as 157 L per person.
2.7. Multiple Criteria Decision Making
3. Results and Discussion
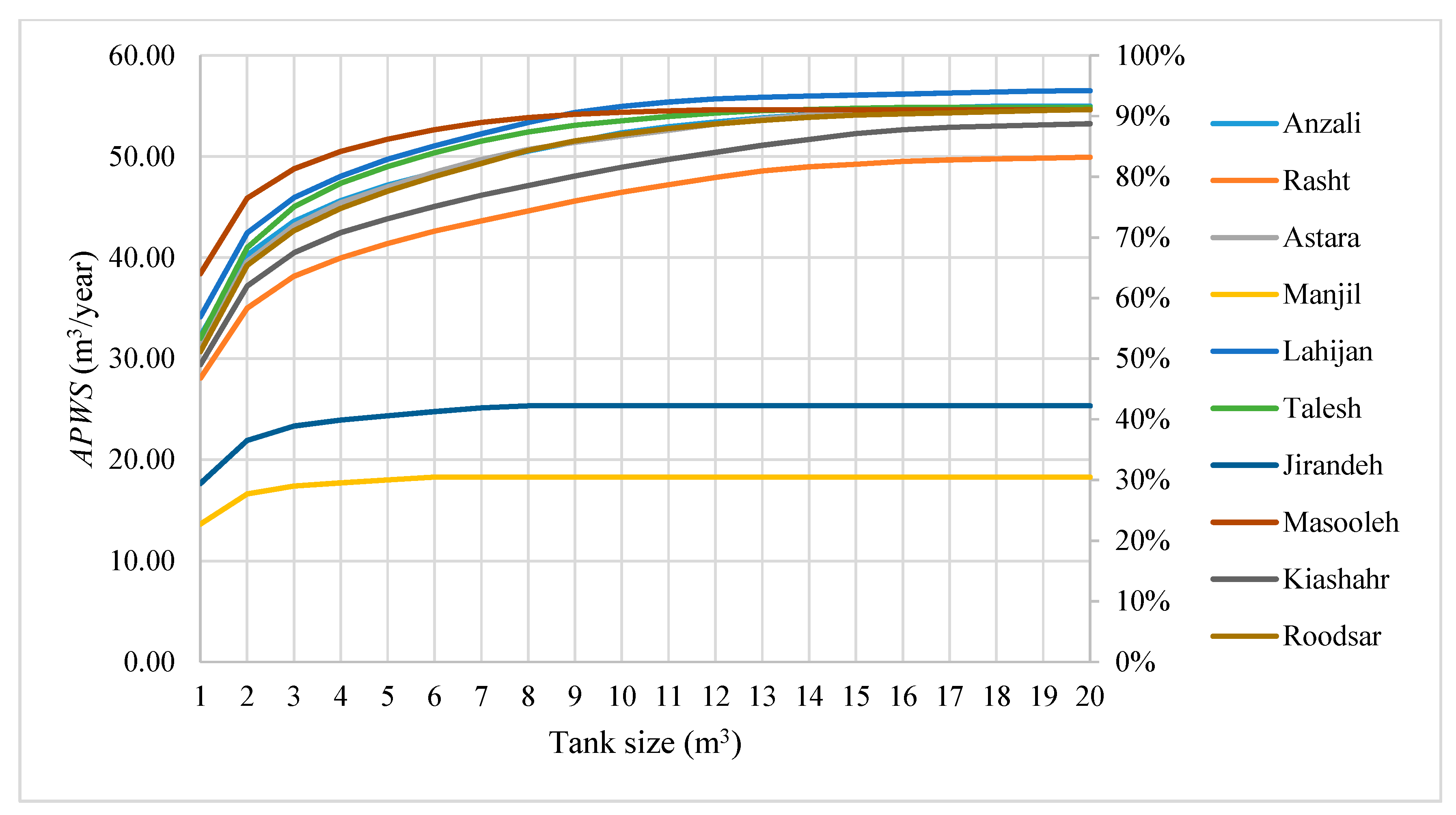
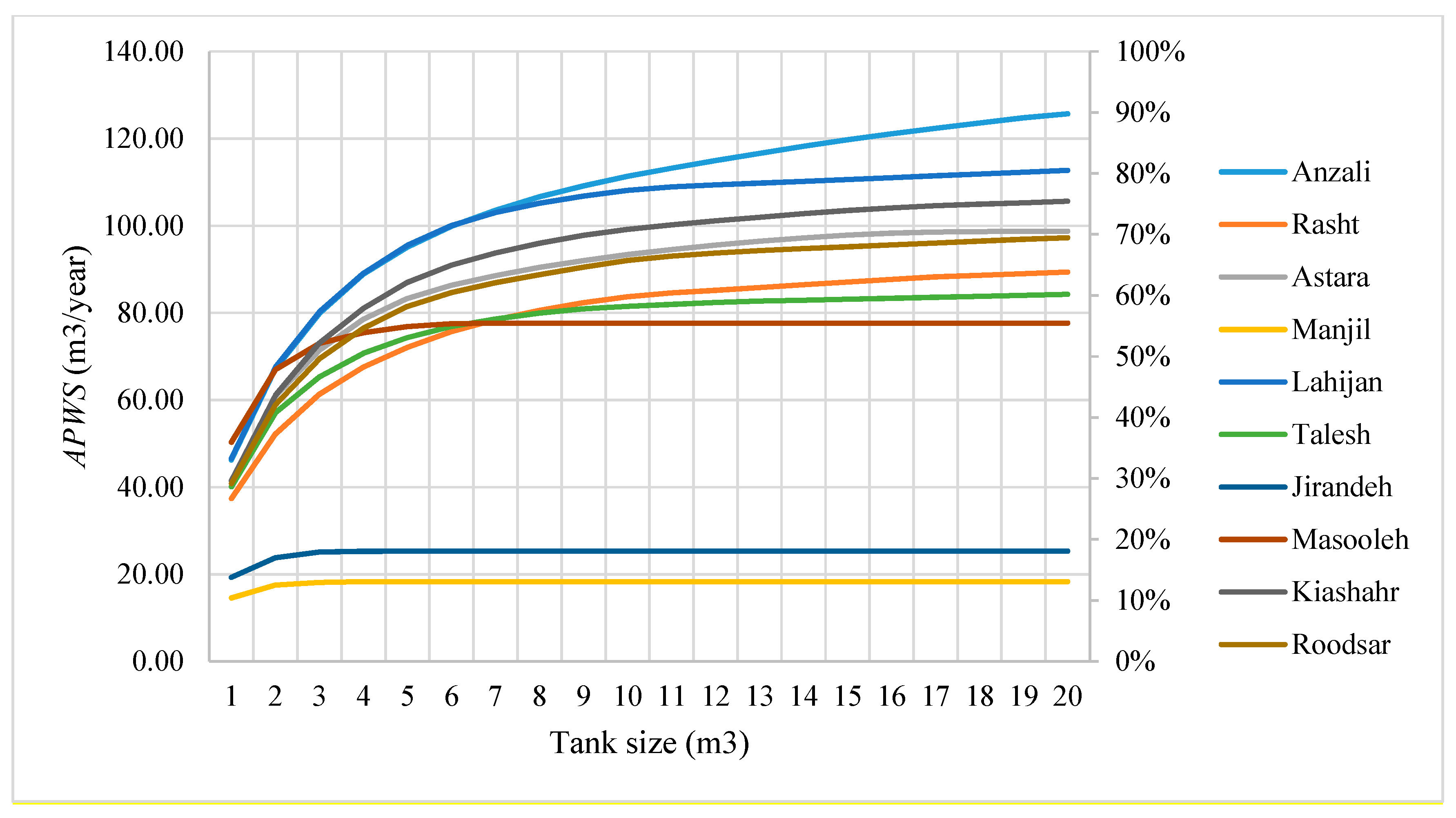
3.1. Result of Hydraulic Simulation
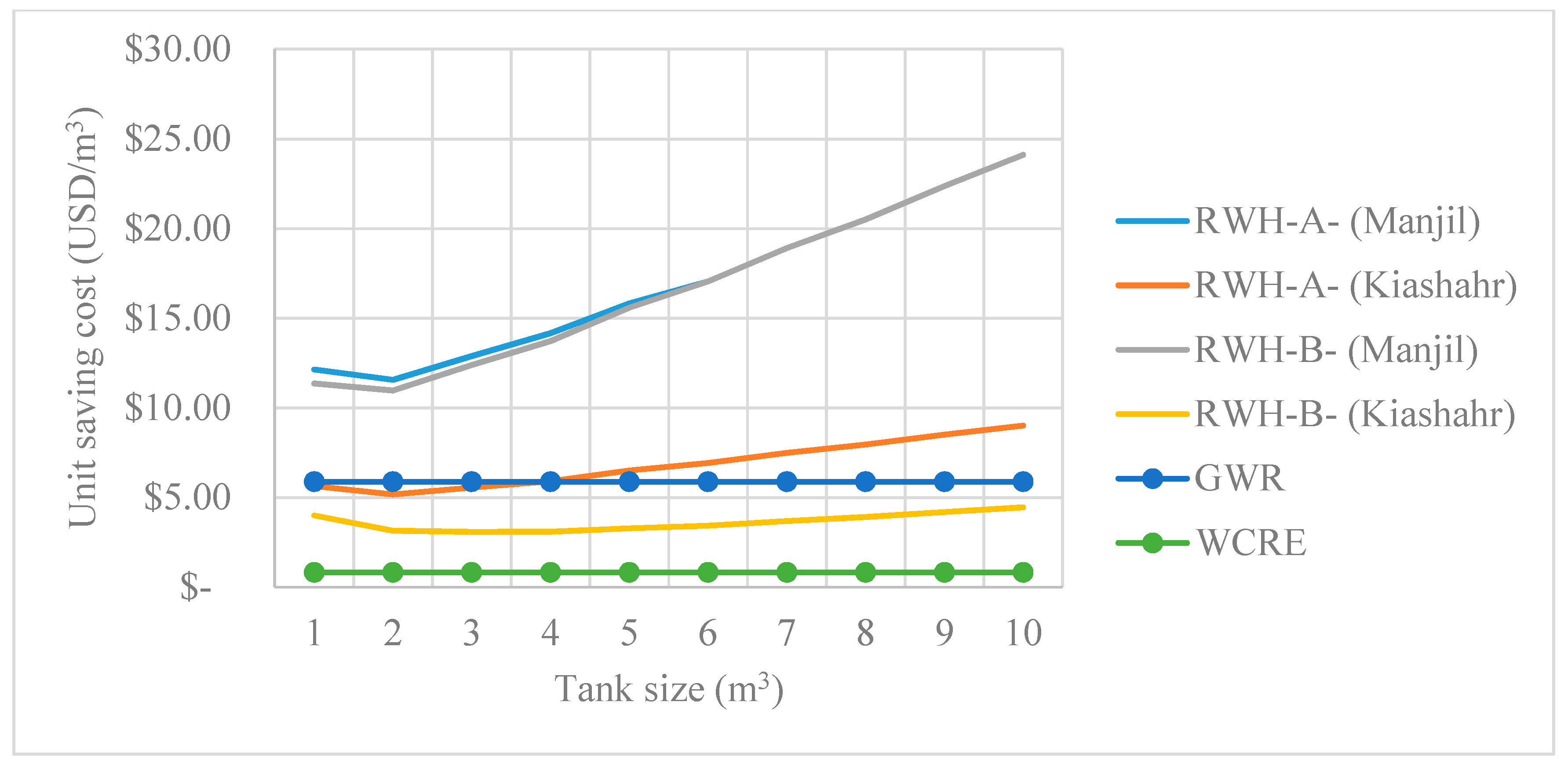
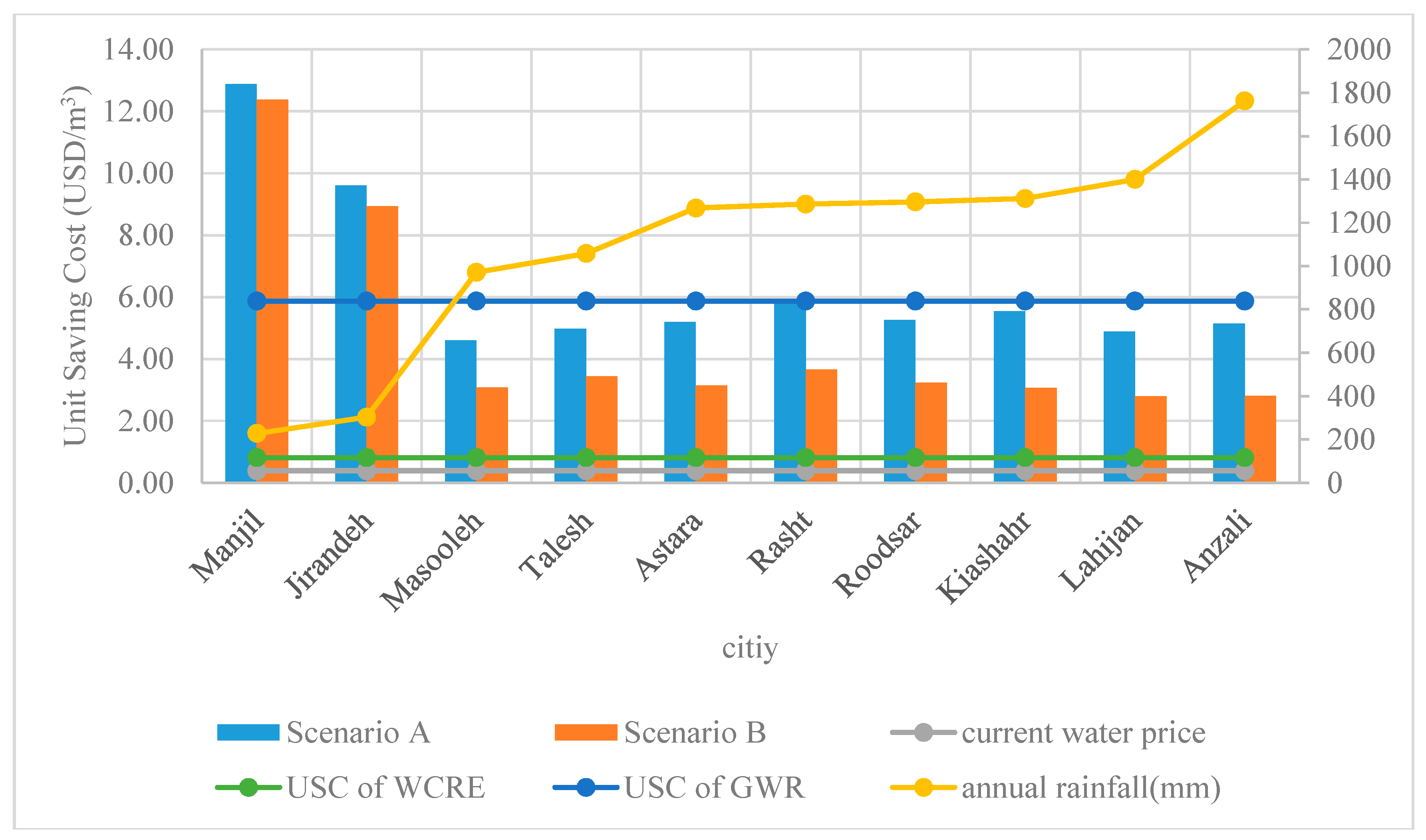
3.2. Results of Economic Analysis
3.3. Results of MCDM and Associated Spatial Interpolation
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
References
- Christian Amos, C.; Rahman, A.; Mwangi Gathenya, J. Economic analysis and feasibility of rainwater harvesting systems in urban and peri-urban environments: A review of the global situation with a special focus on Australia and Kenya. Water 2016, 8, 149. [Google Scholar] [CrossRef]
- Moniruzzaman, M.; Imteaz, M.A. Generalized equations, climatic and spatial variabilities of potential rainwater savings: A case study for Sydney. Resour. Conserv. Recycl. 2017, 125, 139–156. [Google Scholar] [CrossRef]
- Imteaz, M.A.; Moniruzzaman, M. Spatial variability of reasonable government rebates for rainwater tank installations: A case study for Sydney. Resour. Conserv. Recycl. 2018, 133, 112–119. [Google Scholar] [CrossRef]
- Leong, J.Y.C.; Chong, M.N.; Poh, P.E.; Hermawan, A.; Talei, A. Longitudinal assessment of rainwater quality under tropical climatic conditions in enabling effective rainwater harvesting and reuse schemes. J. Clean. Prod. 2017, 143, 64–75. [Google Scholar] [CrossRef]
- Leong, J.Y.C.; Oh, K.S.; Poh, P.E.; Chong, M.N. Prospects of hybrid rainwater-greywater decentralised system for water recycling and reuse: A review. J. Clean. Prod. 2017, 142, 3014–3027. [Google Scholar] [CrossRef]
- Nguyen, D.C.; Han, M.Y. Proposal of simple and reasonable method for design of rainwater harvesting system from limited rainfall data. Resour. Conserv. Recycl. 2017, 126, 219–227. [Google Scholar] [CrossRef]
- Silva, C.M.; Sousa, V.; Carvalho, N.V. Evaluation of rainwater harvesting in Portugal: Application to single-family residences. Resour. Conserv. Recycl. 2015, 94, 21–34. [Google Scholar] [CrossRef]
- Li, Y.; Ye, Q.; Liu, A.; Meng, F.; Zhang, W.; Xiong, W.; Wang, P.; Wang, C. Seeking urbanization security and sustainability: Multi-objective optimization of rainwater harvesting systems in China. J. Hydrol. 2017, 550, 42–53. [Google Scholar] [CrossRef]
- Ghisi, E.; Cardoso, K.A.; Rupp, R.F. Short-term versus long-term rainfall time series in the assessment of potable water savings by using rainwater in houses. J. Environ. Manag. 2012, 100, 109–119. [Google Scholar] [CrossRef]
- Campisano, A.; Butler, D.; Ward, S.; Burns, M.J.; Friedler, E.; DeBusk, K.; Fisher-Jeffes, L.N.; Ghisi, E.; Rahman, A.; Furumai, H.; et al. Urban rainwater harvesting systems: Research, implementation and future perspectives. Water Res. 2017, 115, 195–209. [Google Scholar] [CrossRef]
- Fonseca, C.R.; Hidalgo, V.; Díaz-Delgado, C.; Vilchis-Francés, A.Y.; Gallego, I. Design of optimal tank size for rainwater harvesting systems through use of a web application and geo-referenced rainfall patterns. J. Clean. Prod. 2017, 145, 323–335. [Google Scholar] [CrossRef]
- Nachshon, U.; Netzer, L.; Livshitz, Y. Land cover properties and rain water harvesting in urban environments. Sustain. Cities Soc. 2016, 27, 398–406. [Google Scholar] [CrossRef]
- Gwenzi, W.; Dunjana, N.; Pisa, C.; Tauro, T.; Nyamadzawo, G. Water quality and public health risks associated with roof rainwater harvesting systems for potable supply: Review and perspectives. Sustain. Water Qual. Ecol. 2015, 6, 107–118. [Google Scholar] [CrossRef]
- Amos, C.C.; Rahman, A.; Karim, F.; Gathenya, J.M. A scoping review of roof harvested rainwater usage in urban agriculture: Australia and Kenya in focus. J. Clean. Prod. 2018, 202, 174–190. [Google Scholar] [CrossRef]
- Adham, A.; Riksen, M.; Ouessar, M.; Ritsema, C. A methodology to assess and evaluate rainwater harvesting techniques in (semi-) arid regions. Water 2016, 8, 198. [Google Scholar] [CrossRef]
- Madani, K.; AghaKouchak, A.; Mirchi, A. Iran’s socio-economic drought: challenges of a water-bankrupt nation. Iran. Stud. 2016, 49, 997–1016. [Google Scholar] [CrossRef]
- Mohsen, B. Mesgaran, Pooya Azadi, A National Adaptation Plan for Water Scarcity in Iran, Working Paper 6, Stanford Iran 2040 Project; Stanford university: Stanford, CA, USA, August 2018. [Google Scholar]
- Castonguay, A.C.; Urich, C.; Iftekhar, M.S.; Deletic, A. Modelling urban water management transitions: A case of rainwater harvesting. Environ. Model. Softw. 2018, 105, 270–285. [Google Scholar] [CrossRef]
- Examin the Latest State of Drinking Water in Different Aspects. 2018. Available online: http://www.WaterCM.ir (accessed on 19 September 2019). (In Persian).
- Lee, K.E.; Mokhtar, M.; Mohd Hanafiah, M.; Abdul Halim, A.; Badusah, J. Rainwater harvesting as an alternative water resource in Malaysia: Potential, policies and development. J. Clean. Prod. 2016, 126, 218–222. [Google Scholar] [CrossRef]
- Chiu, Y.-R.; Liaw, C.-H. Designing rainwater harvesting systems for large-scale potable water saving using spatial information system. In International Conference on Computer Supported Cooperative Work in Design; Springer: Berlin/Heidelberg, Germany, 2008; pp. 653–663. [Google Scholar]
- Marinoski, A.K.; Rupp, R.F.; Ghisi, E. Environmental benefit analysis of strategies for potable water savings in residential buildings. J. Environ. Manag. 2018, 206, 28–39. [Google Scholar] [CrossRef]
- Kosovac, A.; Hurlimann, A.; Davidson, B. Water Experts’ Perception of Risk for New and Unfamiliar Water Projects. Water 2017, 9, 976. [Google Scholar] [CrossRef]
- Martin, E.A.; Buchberger, S.G.; Chakraborty, D. Reliability of harvested rainfall as an auxiliary source of non-potable water. Procedia Eng. 2015, 119, 1119–1128. [Google Scholar] [CrossRef][Green Version]
- Okoye, C.O.; Solyalı, O.; Akıntuğ, B. Optimal sizing of storage tanks in domestic rainwater harvesting systems: A linear programming approach. Resour. Conserv. Recycl. 2015, 104, 131–140. [Google Scholar] [CrossRef]
- Ghisi, E. Parameters Influencing the sizing of rainwater tanks for use in houses. Water Resour. Manag. 2010, 24, 2381–2403. [Google Scholar] [CrossRef]
- Liaw, C.-H.; Chiang, Y.-C. Dimensionless analysis for designing domestic rainwater harvesting systems at the regional level in northern taiwan. Water 2014, 6, 3913–3933. [Google Scholar] [CrossRef]
- Ward, S.; Memon, F.A.; Butler, D. Rainwater harvesting: Model-based design evaluation. Water Sci. Technol. 2010, 61, 85–96. [Google Scholar] [CrossRef] [PubMed]
- Chiu, Y.-R.; Tsai, Y.-L.; Chiang, Y.-C. Designing rainwater harvesting systems cost-effectively in a urban water-energy saving scheme by using a gis-simulation based design system. Water 2015, 7, 6285–6300. [Google Scholar] [CrossRef]
- Dumit Gómez, Y.; Teixeira, L.G. Residential rainwater harvesting: Effects of incentive policies and water consumption over economic feasibility. Resour. Conserv. Recycl. 2017, 127, 56–67. [Google Scholar] [CrossRef]
- Bashar, M.Z.I.; Karim, M.R.; Imteaz, M.A. Reliability and economic analysis of urban rainwater harvesting: A comparative study within six major cities of Bangladesh. Resour. Conserv. Recycl. 2018, 133, 146–154. [Google Scholar] [CrossRef]
- Jing, X.; Zhang, S.; Zhang, J.; Wang, Y.; Wang, Y. Assessing efficiency and economic viability of rainwater harvesting systems for meeting non-potable water demands in four climatic zones of China. Resour. Conserv. Recycl. 2017, 126, 74–85. [Google Scholar] [CrossRef]
- Liaw, C.-H.; Tsai, Y.-L.; Cheng, M.-S. Assessing flood mitigation alternatives in Shijr area in metropolitan Taipei. J. Am. Water Resour. Assoc. 2006, 42, 311–322. [Google Scholar] [CrossRef]
- Tsai, Y.-L.; Chiu, Y.-R. Urban storm runoff utilization strategy and volume analysis in multi-purpose rainwater detention-retention systems. Shuikexue Jinzhan/Adv. Water Sci. 2012, 23, 341–345. [Google Scholar]
- Yang, X.; Xie, X.; Liu, D.L.; Ji, F.; Wang, L. Spatial interpolation of daily rainfall data for local climate impact assessment over greater sydney region. Adv. Meteorol. 2015, 2015, 1–12. [Google Scholar] [CrossRef]
- Hargreaves, A.J.; Farmani, R.; Ward, S.; Butler, D. Modelling the future impacts of urban spatial planning on the viability of alternative water supply. Water Res. 2019, 162, 200–213. [Google Scholar] [CrossRef] [PubMed]
- DeOreo, W.B.; Mayer, P.W.; Dziegielewski, B.; Kiefer, J.C. Residential End Uses of Water, Version 2, Executive Report; Water Research Foundation: Alexandria, VA, USA, April 2016. for more information about this project, please visit www.waterrf.org/4309.
- Danescu, T.; Chira, A. Professional Judgment and Reticence to Apply Sampling Techniques. Procedia Econ. Financ. 2014, 15, 1253–1258. [Google Scholar] [CrossRef][Green Version]
- Statistical Center of Iran, the Results of the Survey of Expenditure and Household Income Statistics. 2018. Available online: https://www.amar.org.ir/ (accessed on 12 November 2019).
- Younesloo, S. Research Project Guideline to Using Graywater for Non-Drinking Uses; Ministry of Road & Urban Development; Road, Housing & Urban Development Research Center: Tehran, Iran, 2017; Additional information: http://pub.bhrc.ac.ir.
- Leong, J.Y.C.; Chong, M.N.; Poh, P.E.; Vieritz, A.; Talei, A.; Chow, M.F. Quantification of mains water savings from decentralised rainwater, greywater, and hybrid rainwater-greywater systems in tropical climatic conditions. J. Clean. Prod. 2018, 176, 946–958. [Google Scholar] [CrossRef]
- Sepehri, M.; Malekinezhad, H.; Ilderomi, A.R.; Talebi, A.; Hosseini, S.Z. Studying the effect of rain water harvesting from roof surfaces on runoff and household consumption reduction. Sustain. Cities Soc. 2018, 43, 317–324. [Google Scholar] [CrossRef]
- Pavolová, H.; Bakalár, T.; Kudelas, D.; Puškárová, P. Environmental and economic assessment of rainwater application in households. J. Clean. Prod. 2019, 209, 1119–1125. [Google Scholar] [CrossRef]
- Alinezhad, A.; Khalili, J. New Methods and Applications in Multiple Attribute Decision Making (Madm); International Series in Operations Research Management Science; Springer International Publishing: Cham, Switzerland, 2019; Volume 277, ISBN 978-3-030-15008-2; ISBN 978-3-030-15009-9. [Google Scholar]
- Zavadskas, E.K.; Podvezko, V. Integrated determination of objective criteria weights in MCDM. Int. J. Inf. Technol. Decis. Mak. 2016, 15, 267–283. [Google Scholar] [CrossRef]
- Olson, D.L. Comparison of weights in TOPSIS models. Math. Comput. Model. 2004, 40, 721–727. [Google Scholar] [CrossRef]
- Lani, N.H.M.; Syafiuddin, A.; Yusop, Z.; binti Adam, U.; bin Mat Amin, M.Z. Performance of small and large scales rainwater harvesting systems in commercial buildings under different reliability and future water tariff scenarios. Sci. Total Environ. 2018, 636, 1171–1179. [Google Scholar] [CrossRef] [PubMed]
- López Zavala, M.Á.; Vega, R.C.; Miranda, R.A.L. Potential of rainwater harvesting and greywater reuse for water consumption reduction and wastewater minimization. Water 2016, 8, 264. [Google Scholar] [CrossRef]
- Vargas, D.; Dominguez, I.; Ward, S.; Oviedo-Ocaña, E.R. Assisting global rainwater harvesting practitioners: A decision support tool for tank sizing method selection under uncertainty. Environ. Sci. Water Res. Technol. 2019, 5, 506–520. [Google Scholar] [CrossRef]
- Water consumption Management Guide; National water & wastewater Engineering company of Iran. 2009. Available online: http://www.WaterCM.ir (accessed on 4 November 2019). (In Persian).
- Saaty, T.L. How to make a decision: The analytic hierarchy process. Eur. J. Oper. Res. 1990, 48, 9–26. [Google Scholar] [CrossRef]


| Area (km2) | County | Households | Population | Average Annual Precipitation (mm) | Renewable Water Volume (BCM *) | Average Available Fresh Water per Capita (m3) | |
|---|---|---|---|---|---|---|---|
| Guilan Province | 14,041 | 16 | 777,684 | 2,530,696 | 1061 | 9.2 | 2776 |
| Iran | 1,648,195 | - | - | 83,332,671 | 250 | 130 | 1659 |
| World | 510,072,000 | - | - | 7.65 billion | 750 | 36,100 | 5932 |
| Exchange Rate | Interest Rate | Inflation Rate | Annual Water and Electricity Inflation * | Water Price ($) | Electricity Price ($) | Life Cycle (Years) |
|---|---|---|---|---|---|---|
| 1 USD$ = 42,000 IRR | 15% | 10% | 7% | 0.39 | 0.02 | 25 |
| Initial cost | Including preparation and installation of a typical domestic rainwater harvesting system: Water catchment, Water transfer, Water storage, Water purification, End use | |||||
| Maintenance | Scenario A: 5% of initial cost due to periodic cleaning and services Scenario B: 10% of initial cost due to monthly and seasonal maintenance and cleaning tank and pipes and changing purification components such as filters | |||||
| Operation | Pump type, Hours per day, Annual electricity consumption, Scenario A, Scenario B | |||||
| APWS1 | AAS2 | Initial Cost 3 | BCR 4 | Supported by 5 Government | Social Benefits 6 | Environmental 7 Benefits | |
|---|---|---|---|---|---|---|---|
| RWH-A | * | * | * | * | 3 | 5 | 3 |
| RWH-B | * | * | * | * | 3 | 5 | 5 |
| GWR | 47.1 | $18.37 | $1040 | --- | 4 | 3 | 4 |
| WCRE | 79.4 | $30.98 | $260 | --- | 5 | 2 | 2 |
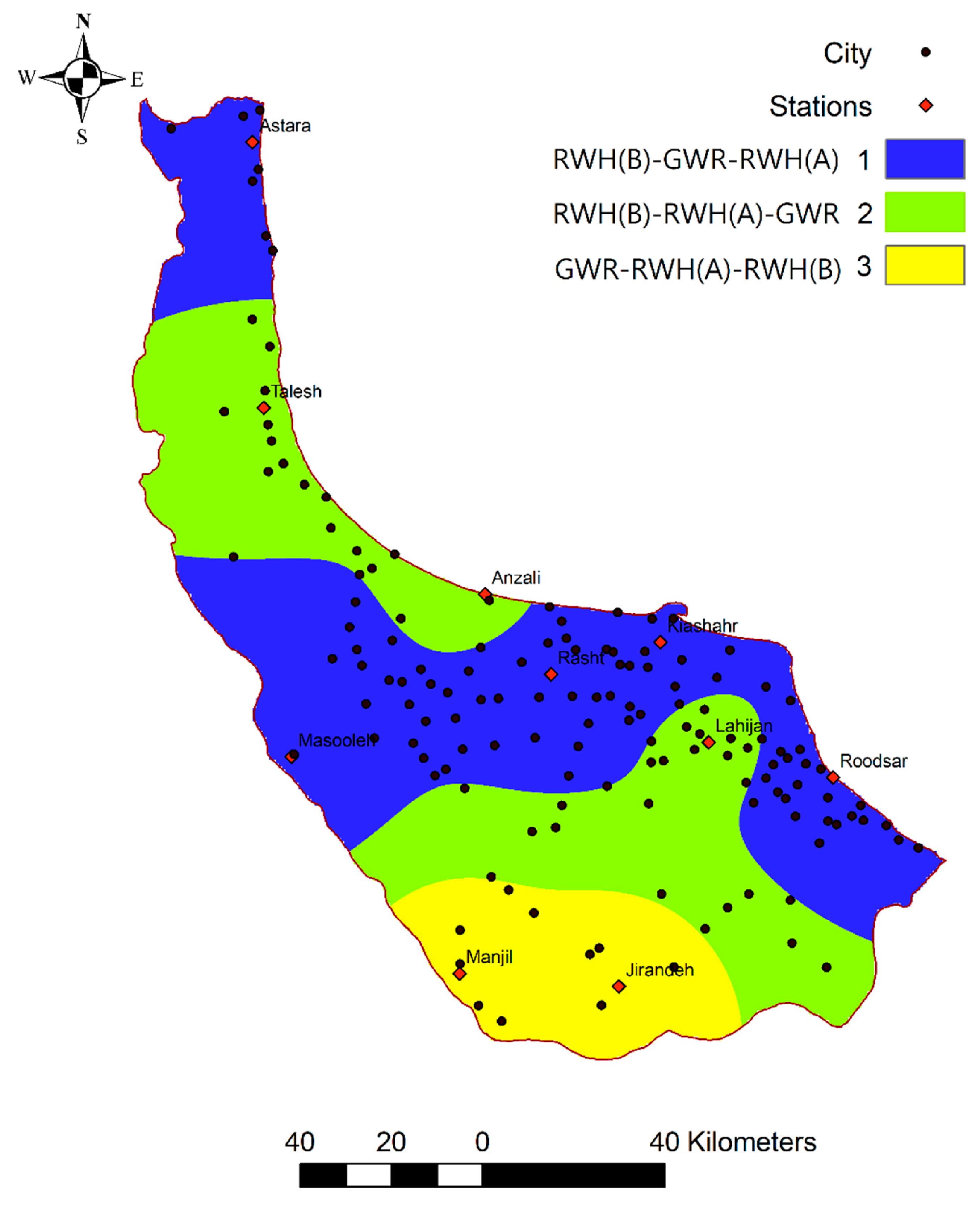
| Types | Order | Stations |
|---|---|---|
| Type 1 | WCRE -RWH(B)-GWR-RWH(A) | Rasht, Astara, Masooleh, Kiashahr, Roodsar |
| Type 2 | WCRE -RWH(B)-RWH(A)-GWR | Anzali, Lahijan, Talesh |
| Type 3 | WCRE -GWR-RWH(A)-RWH(B) | Manjil, Jirandeh |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chiu, Y.-R.; Aghaloo, K.; Mohammadi, B. Incorporating Rainwater Harvesting Systems in Iran’s Potable Water-Saving Scheme by Using a GIS-Simulation Based Decision Support System. Water 2020, 12, 752. https://doi.org/10.3390/w12030752
Chiu Y-R, Aghaloo K, Mohammadi B. Incorporating Rainwater Harvesting Systems in Iran’s Potable Water-Saving Scheme by Using a GIS-Simulation Based Decision Support System. Water. 2020; 12(3):752. https://doi.org/10.3390/w12030752
Chicago/Turabian StyleChiu, Yie-Ru, Kamaleddin Aghaloo, and Babak Mohammadi. 2020. "Incorporating Rainwater Harvesting Systems in Iran’s Potable Water-Saving Scheme by Using a GIS-Simulation Based Decision Support System" Water 12, no. 3: 752. https://doi.org/10.3390/w12030752
APA StyleChiu, Y.-R., Aghaloo, K., & Mohammadi, B. (2020). Incorporating Rainwater Harvesting Systems in Iran’s Potable Water-Saving Scheme by Using a GIS-Simulation Based Decision Support System. Water, 12(3), 752. https://doi.org/10.3390/w12030752





