Temporal Pattern Analysis of Local Rainstorm Events in China During the Flood Season Based on Time Series Clustering
Abstract
1. Introduction
2. Materials and Methods
2.1. Rainfall Data
2.2. Methods
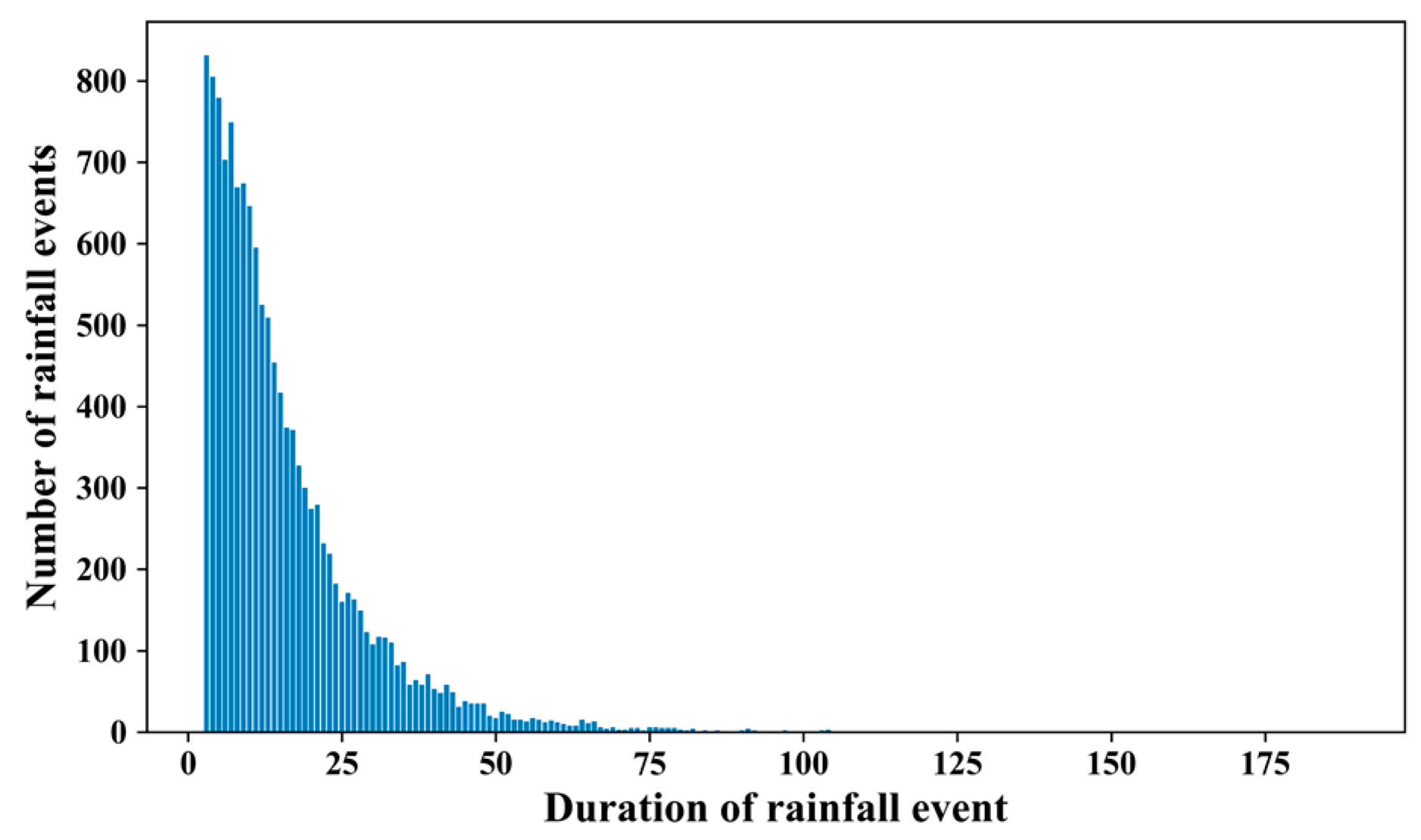
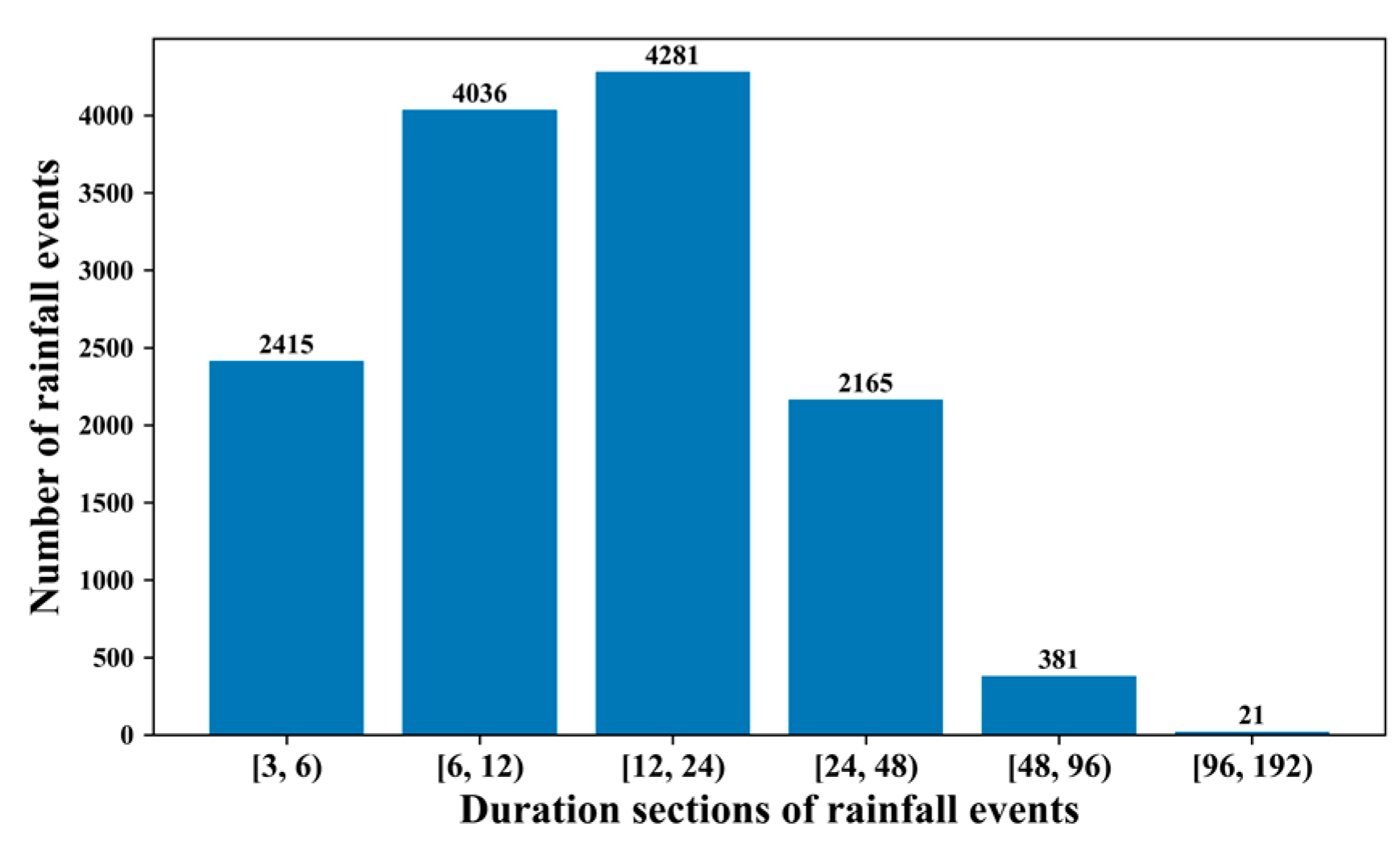
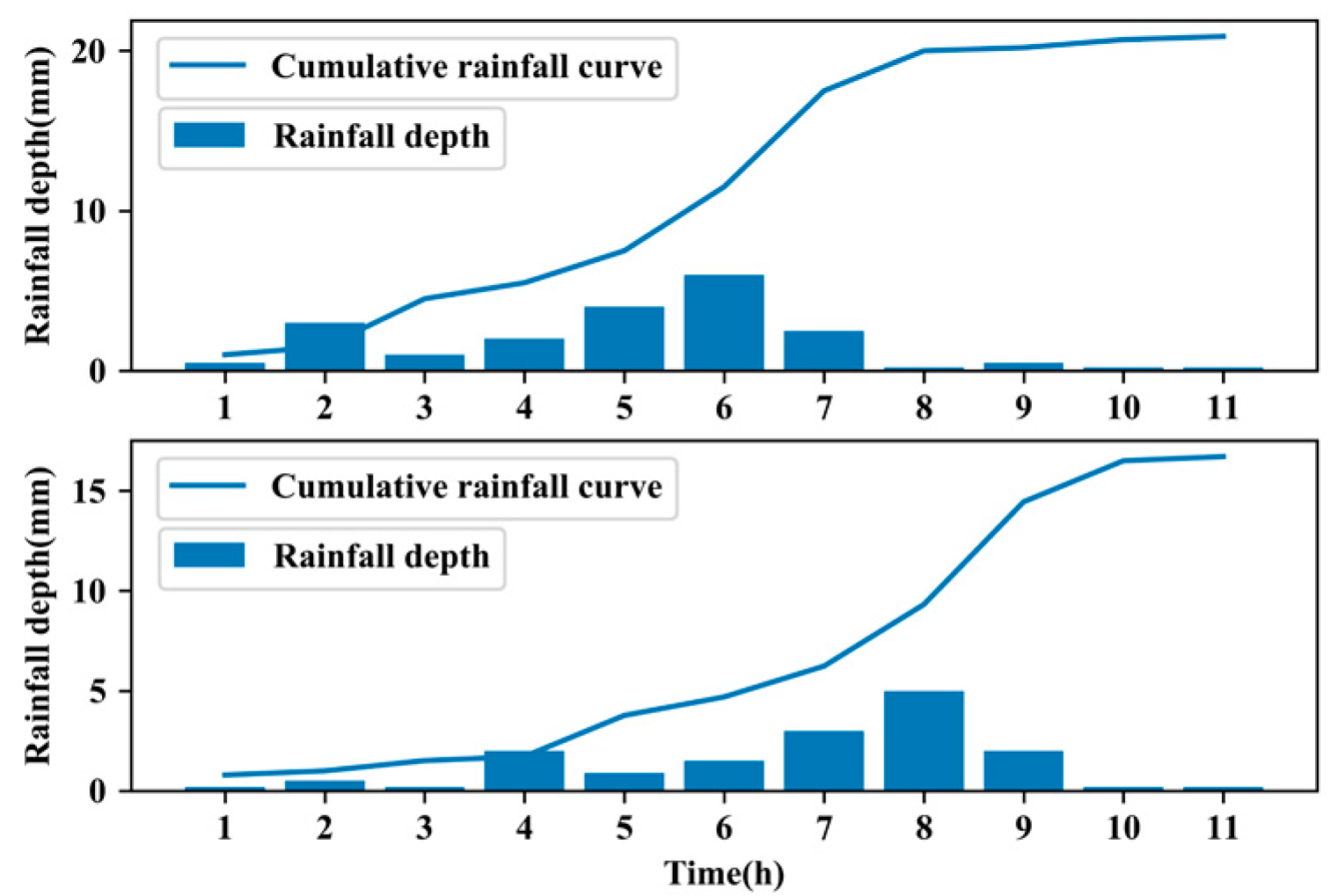
2.2.1. Standardization and Grouping of Rainfall Time Series
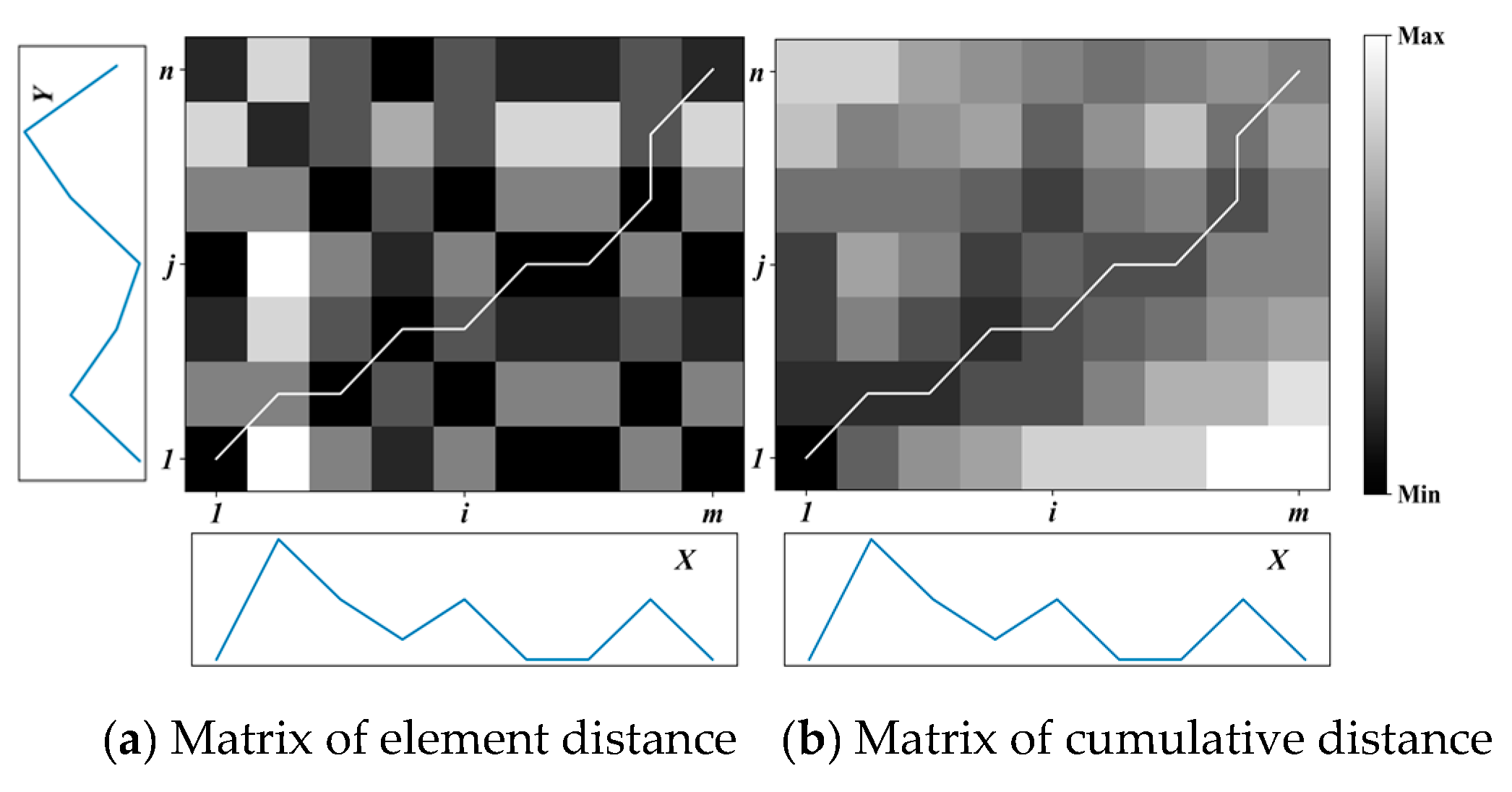
2.2.2. Time Series Clustering
- (1)
- Each element in the time series set is taken as an initial cluster. For a set with elements , the initial cluster , in which ;
- (2)
- Calculate the distance matrix , whose element and , is the distance between cluster and ;
- (3)
- Find the closest two clusters and and merge them: . Renumber the clusters and delete the th row and th column of matrix ;
- (4)
- Repeat the previous step until all clusters merge into one cluster, and then a clustering tree is obtained.
2.2.3. Extraction of Representative Temporal Patterns
3. Results and Discussion
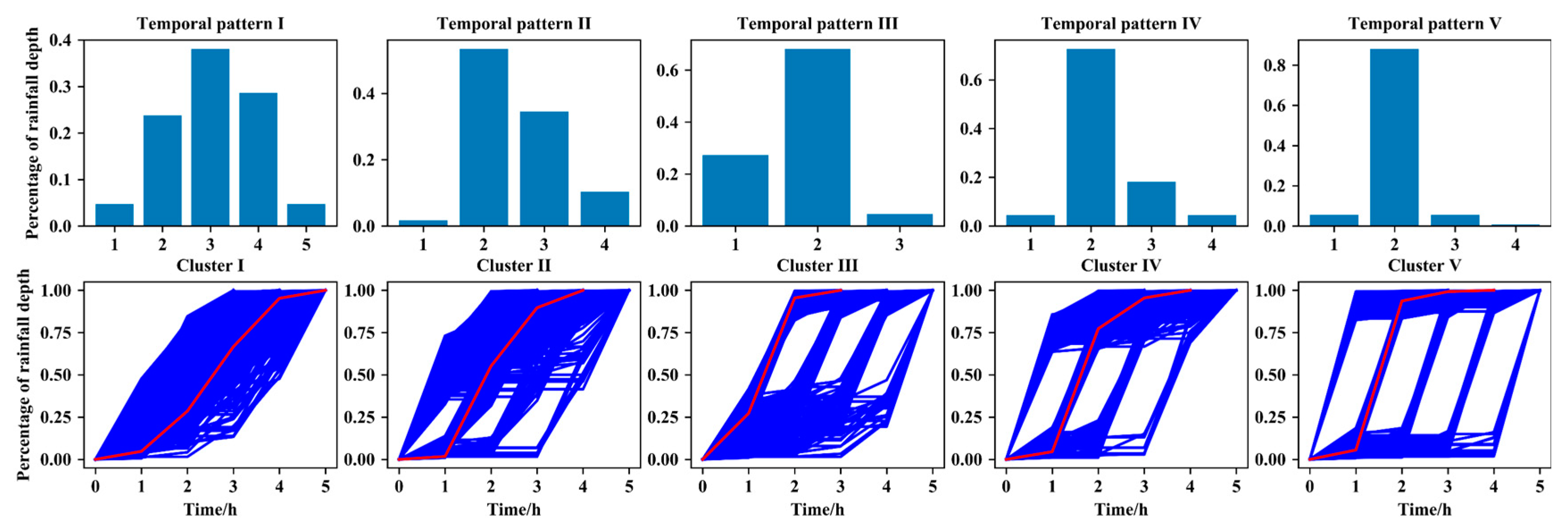
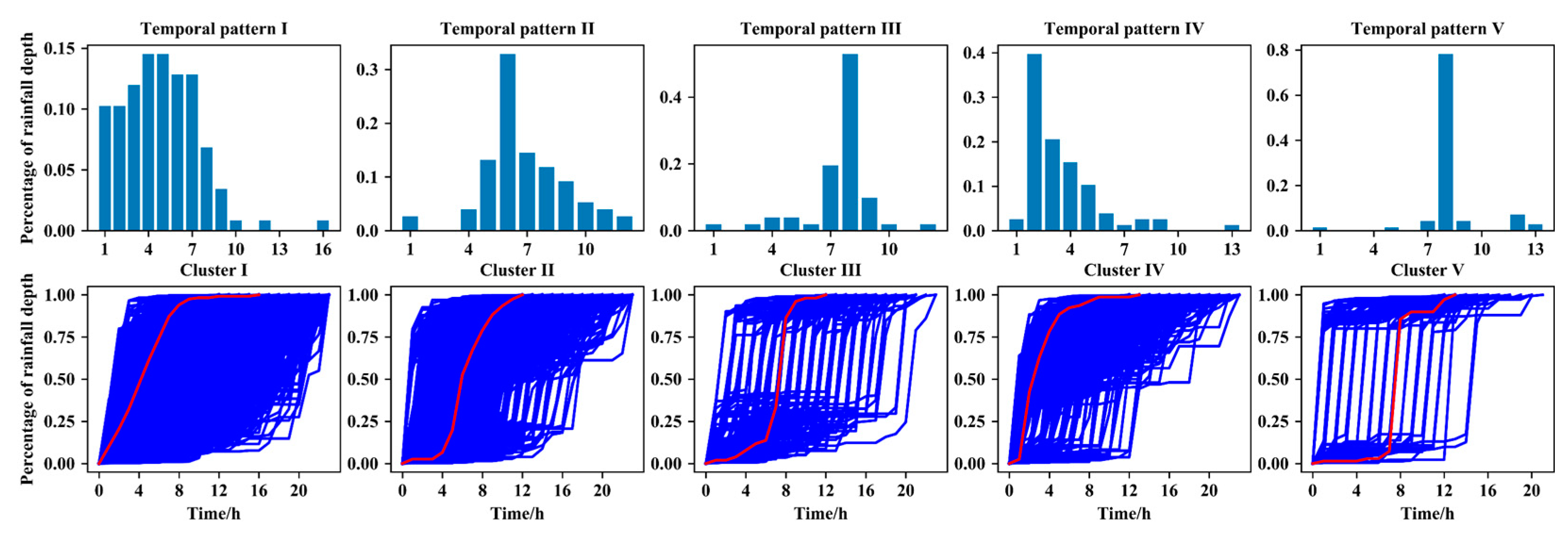
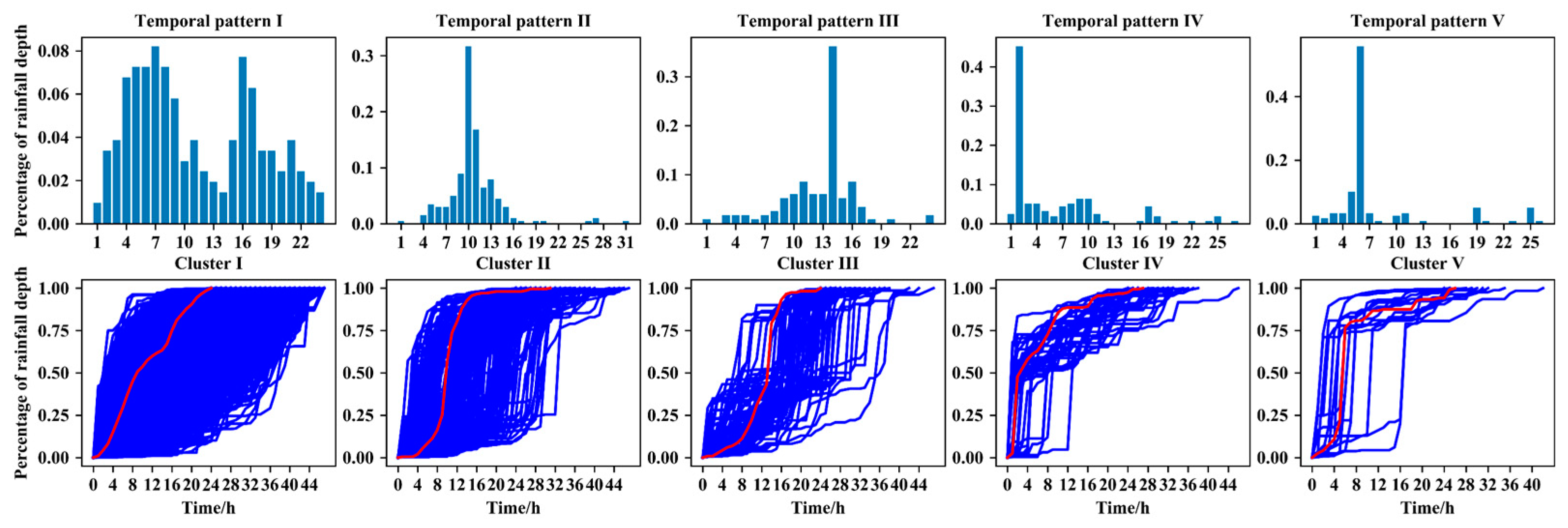
3.1. Representative Temporal Patterns
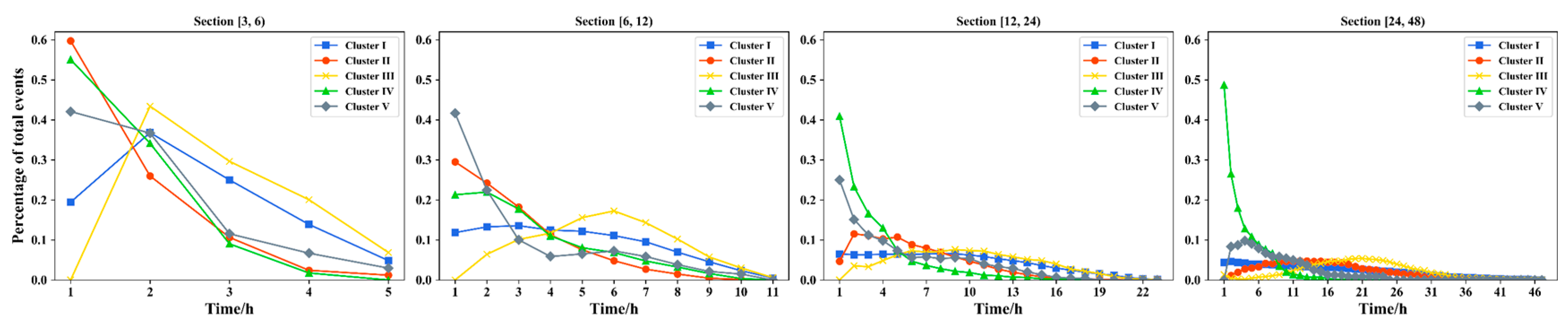
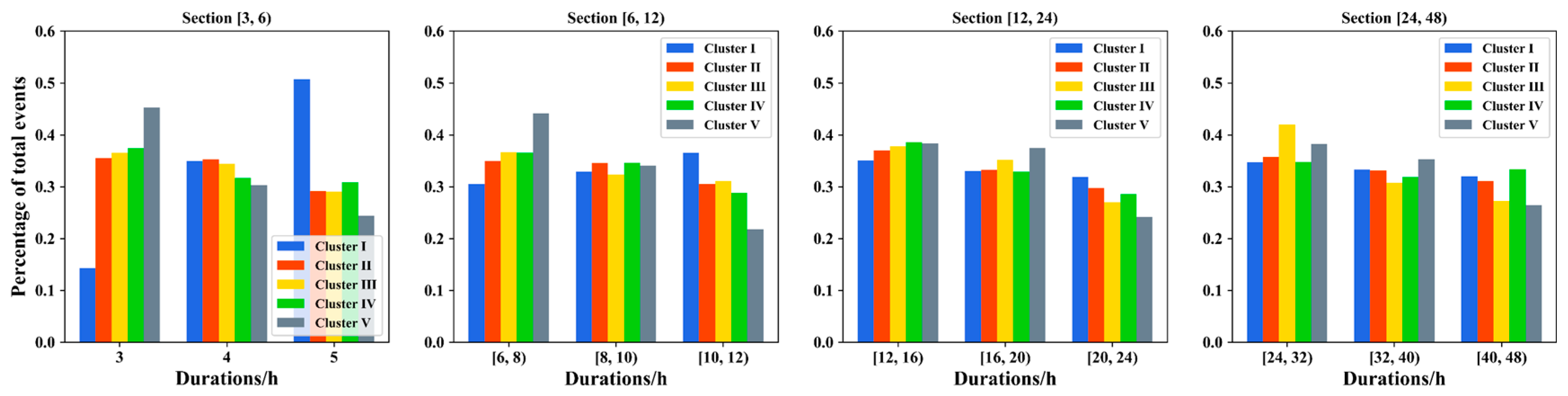
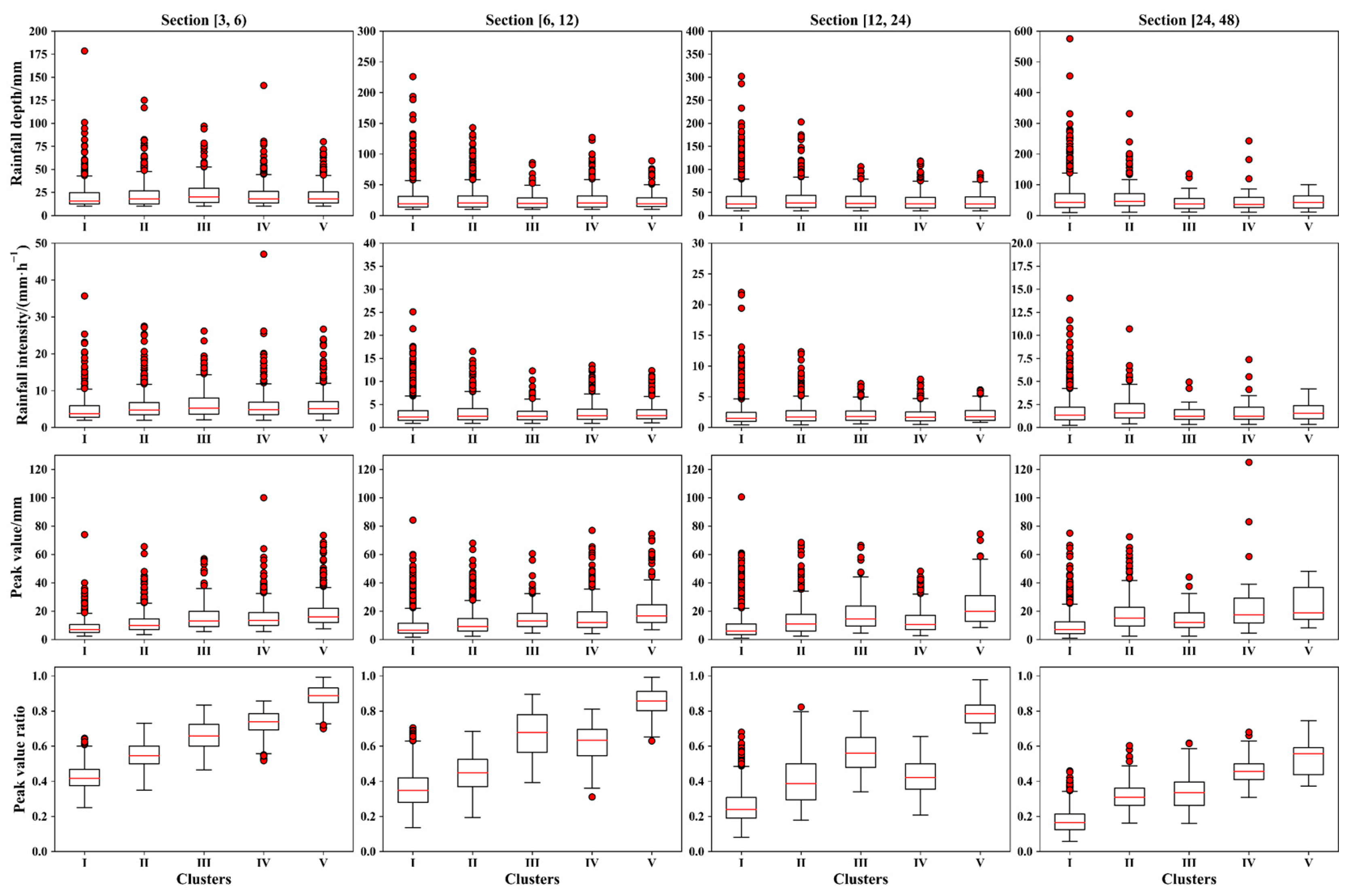
3.2. Statistical Characteristics of the Clusters and Temporal Patterns
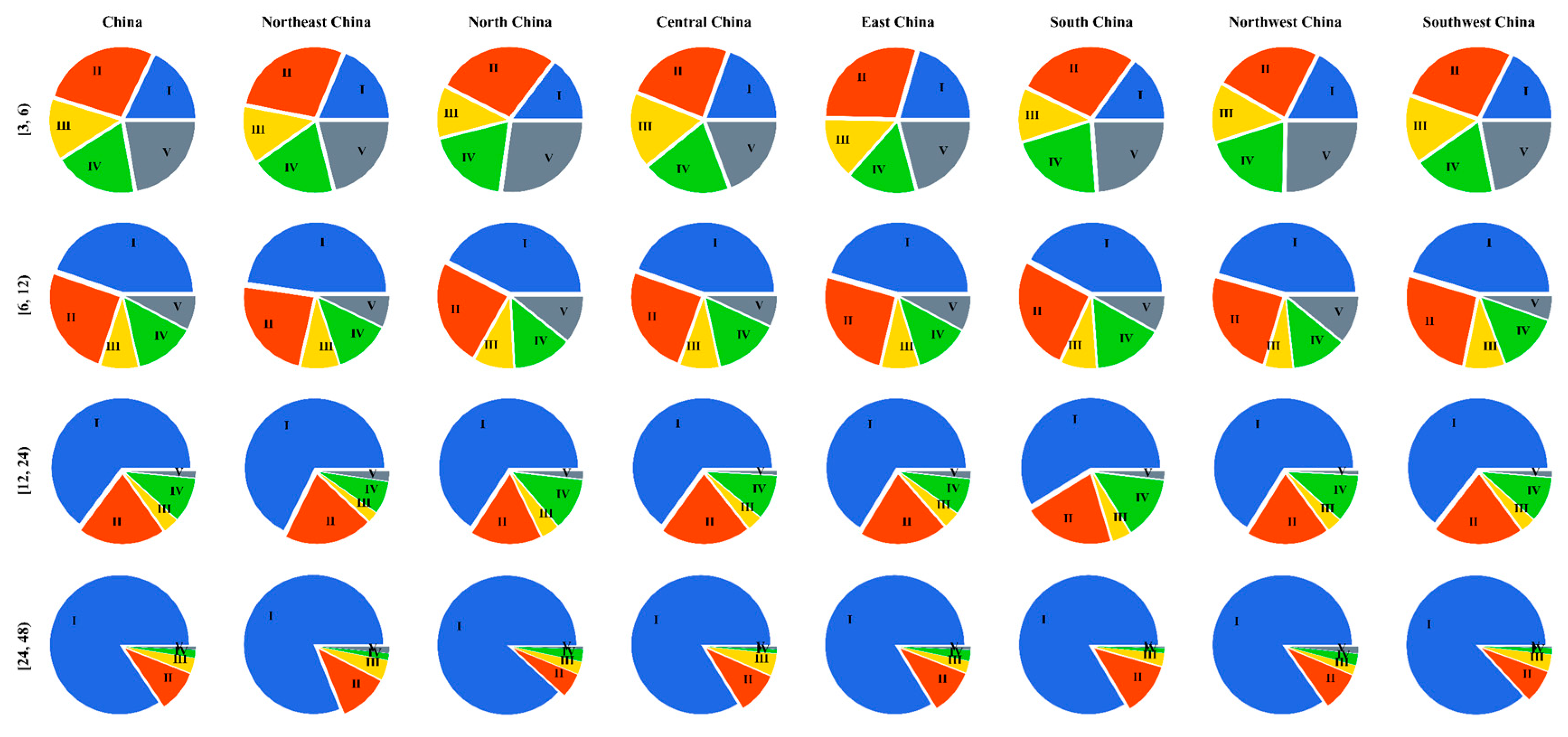
3.3. Regional Analysis of Rainstorm Characteristics
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Douinot, A.; Roux, H.; Garambois, P.A.; Larnier, K.; Labat, D.; Dartus, D. Accounting for rainfall systematic spatial variability in flash flood forecasting. J. Hydrol. 2016, 541, 359–370. [Google Scholar] [CrossRef]
- Hou, J.; Guo, K.; Wang, Z.; Jing, H.; Li, D. Numerical simulation of design storm pattern effects on urban flood inundation. Adv. Water Sci. 2017, 28, 820–828. [Google Scholar]
- Yin, S.; Wang, Y.; Xie, Y.; Liu, A. Characteristics of intra-storm temporal pattern over China. Adv. Water Sci. 2014, 25, 617–624. [Google Scholar]
- Dunkerley, D. Effects of rainfall intensity fluctuations on infiltration and runoff: Rainfall simulation on dryland soils, Fowlers Gap, Australia. Hydrol. Process. 2012, 26, 2211–2224. [Google Scholar] [CrossRef]
- Jain, S.K.; Singh, R.D.; Seth, S.M. Design flood estimation using GIS supported GIUH approach. Water Resour. Manag. 2000, 14, 369–376. [Google Scholar] [CrossRef]
- Máca, P.; Torfs, P. The influence of temporal rainfall distribution in the flood runoff modelling. Soil Water Res. 2009, 4, S102–S110. [Google Scholar] [CrossRef]
- Lin, M.; Chen, X.; Chen, Y. Regression Analysis of Flood Response to the Spatial and Temporal Variability of Storm in the Jinjiangxixi Watershed. Resour. Sci. 2011, 33, 2226–2231. [Google Scholar]
- Bezak, N.; Sraj, M.; Mikos, M. Copula-based IDF curves and empirical rainfall thresholds for flash floods and rainfall-induced landslides. J. Hydrol. 2016, 541, 272–284. [Google Scholar] [CrossRef]
- Forestieri, A.; Caracciolo, D.; Arnone, E.; Noto, L.V. Derivation of rainfall thresholds for flash flood warning in a Sicilian basin using a hydrological model. In Proceedings of the 12th International Conference on Hydroinformatics, Incheon, Korea, 21–26 August 2016; Kim, J.H., Kim, H.S., Yoo, D.G., Jung, D., Song, C.G., Eds.; Elsevier Science B.V.: Amsterdam, The Netherlands, 2016; pp. 818–825. [Google Scholar]
- Norbiato, D.; Borga, M.; Esposti, S.D.; Gaume, E.; Anquetin, S. Flash flood warning based on rainfall thresholds and soil moisture conditions: An assessment for gauged and ungauged basins. J. Hydrol. 2008, 362, 274–290. [Google Scholar] [CrossRef]
- Yuan, W.L.; Liu, M.Q.; Wan, F. Study on the impact of rainfall pattern in small watersheds on rainfall warning index of flash flood event. Nat. Hazards 2019, 97, 665–682. [Google Scholar] [CrossRef]
- Zhai, X.Y.; Guo, L.; Liu, R.H.; Zhang, Y.Y. Rainfall threshold determination for flash flood warning in mountainous catchments with consideration of antecedent soil moisture and rainfall pattern. Nat. Hazards 2018, 94, 605–625. [Google Scholar] [CrossRef]
- Li, J.; Wu, S.; Zhao, X.; Yin, W.; Zhang, S.; Li, M.; Li, J. Analysis on the effect of rain type selection on LID measures. Water Wastewater Eng. 2018, 44, 21–27. [Google Scholar]
- Pedrozo-Acuna, A.; Moreno, G.; Mejia-Estrada, P.; Paredes-Victoria, P.; Brena-Naranjo, J.A.; Meza, C. Integrated approach to determine highway flooding and critical points of drainage. Transp. Res. Part D Transp. Environ. 2017, 50, 182–191. [Google Scholar] [CrossRef]
- Rahman, A.; Weinmann, P.E.; Hoang, T.M.T.; Laurenson, E.M. Monte Carlo simulation of flood frequency curves from rainfall. J. Hydrol. 2002, 256, 196–210. [Google Scholar] [CrossRef]
- Rahman, A.; Islam, M.; Rahman, K.; Khan, S.; Shrestha, S. Investigation of design rainfall temporal patterns in the Gold Coast region of Queensland. Australas. J. Water Resour. 2006, 10, 49–61. [Google Scholar] [CrossRef]
- Liu, Z.; Yang, D.; Hu, J. Dynamic critical rainfall-based torrential flood early warning for medium-small rivers. J. Beijing Norm. Univ. Nat. Sci. (China) 2010, 46, 317–321. [Google Scholar]
- Hapuarachchi, H.A.P.; Wang, Q.J.; Pagano, T.C. A review of advances in flash flood forecasting. Hydrol. Process. 2011, 25, 2771–2784. [Google Scholar] [CrossRef]
- Cheng, W. A review of rainfall thresholds for triggering flash floods. Adv. Water Sci. 2013, 24, 901–908. [Google Scholar]
- Miao, Q.H.; Yang, D.W.; Yang, H.B.; Li, Z. Establishing a rainfall threshold for flash flood warnings in China’s mountainous areas based on a distributed hydrological model. J. Hydrol. 2016, 541, 371–386. [Google Scholar] [CrossRef]
- Georgakakos, K.P. A generalized stochastic hydrometeorological model for flood and flash-flood forecasting: 1. Formulation. Water Resour. Res. 1986, 22, 2083–2095. [Google Scholar] [CrossRef]
- Georgakakos, K.P. A generalized stochastic hydrometeorological model for flood and flash-flood forecasting: 2. Case-Studies. Water Resour. Res. 1986, 22, 2096–2106. [Google Scholar] [CrossRef]
- Mogil, H.M.; Monro, J.C.; Groper, H.S. NWS flash flood warning and disaster preparedness programs. Bull. Am. Meteorol. Soc. 1978, 59, 690–699. [Google Scholar] [CrossRef]
- Nikolopoulos, E.I.; Anagnostou, E.N.; Borga, M.; Vivoni, E.R.; Papadopoulos, A. Sensitivity of a mountain basin flash flood to initial wetness condition and rainfall variability. J. Hydrol. 2011, 402, 165–178. [Google Scholar] [CrossRef]
- Yin, S.Q.; Xie, Y.; Nearing, M.A.; Guo, W.L.; Zhu, Z.Y. Intra-Storm temporal patterns of rainfall in china using huff curves. Trans. ASABE 2016, 59, 1619–1632. [Google Scholar]
- El-Sayed, E.A.H. Development of synthetic rainfall distribution curves for Sinai area. Ain Shams Eng. J. 2018, 9, 1949–1957. [Google Scholar] [CrossRef]
- Keifer, C.; Chu, H. Synthetic Storm Pattern for Drainage Design. J. Hydraul. Div. 1957, 83, 1–25. [Google Scholar]
- Hershfield, D.M. Extreme rainfall relationships. J. Hydraul. Div. 1962, 88, 73–92. [Google Scholar]
- Huff, F.A. Time distribution of rainfall in heavy storms. Water Resour. Res. 1967, 3, 1007–1019. [Google Scholar] [CrossRef]
- Pilgrim, D.H.; Cordery, I. Rainfall temporal patterns for design floods. J. Hydraul. Div. 1975, 101, 81–95. [Google Scholar]
- Yen, B.C.; Chow, V.T. Design hyetographs for small drainage structures. J. Hydraul. Div. 1980, 106, 1055–1076. [Google Scholar]
- USDA. Urban Hydrology for Small Watersheds; Technical Release TR-55; National Resources Conservation Service: Washington, DC, USA, 1986. [Google Scholar]
- Wu, S.J.; Yang, J.C.; Tung, Y.K. Identification and stochastic generation of representative rainfall temporal patterns in Hong Kong territory. Stoch. Environ. Res. Risk Assess. 2006, 20, 171–183. [Google Scholar] [CrossRef]
- Terranova, O.G.; Iaquinta, P. Temporal properties of rainfall events in Calabria (Southern Italy). Nat. Hazards Earth Syst. Sci. 2011, 11, 751–757. [Google Scholar] [CrossRef]
- Ghassabi, Z.; Kamali, G.A.; Meshkatee, A.H.; Hajam, S.; Javaheri, N. Time distribution of heavy rainfall events in south west of Iran. J. Atmos. Sol. Terr. Phys. 2016, 145, 53–60. [Google Scholar] [CrossRef]
- Jun, C.Y.; Qin, X.S.; Lu, W. Temporal Pattern Analysis of Rainstorm Events for Supporting Rainfall Design in a Tropical City. In New Trends in Urban Drainage Modelling: UDM 2018; Mannina, G., Ed.; Springer International Publishing: Berlin/Heidelberg, Germany, 2019; pp. 380–384. [Google Scholar]
- Berndt, D.J.; Clifford, J. Using Dynamic Time Warping to Find. Patterns in Time Series. In Proceedings of the AAAI-94 Workshop on Knowledge Discovery in Databases, Seattle, WA, USA, 31 July–1 August 1994. [Google Scholar]
- Berndt, D.J.; Clifford, J. Finding Patterns in Time Series: A Dynamic Programming Approach. In Advances in Knowledge Discovery and Data Mining; MIT Press: Cambridge, MA, USA, 1996; pp. 229–248. [Google Scholar]
- Gavrilov, M.; Anguelov, D.; Indyk, P.; Motwani, R. Mining the stock market: Which measure is best? In Proceedings of the KDD-2000, Sixth ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Boston, MA, USA, 20–23 August 2000; pp. 487–496. [Google Scholar]
- Goldin, D.Q.; Kanellakis, P.C. On similarity queries for time-series data: Constraint specification and implementation. In Proceedings of the Principles and Practice of Constraint Programming—CP ʹ95: First International Conference, Cassis, France, 19–22 September 1995. [Google Scholar]
- Rafiei, D.; Mendelzon, A. Efficient Retrieval of Similar Time Sequences Using DFT. In Proceedings of the 5th International Conference on Foundations of Data Organizations and Algorithms (FODO ʹ98), Kobe, Japan, 12–13 November 1998. [Google Scholar]
- Sakoe, H.; Chiba, S. Dynamic-Programming algorithm optimization for spoken word recognition. IEEE Trans. Acoust. Speech Signal. Process. 1978, 26, 43–49. [Google Scholar] [CrossRef]
- Jain, A.K. Data clustering: 50 years beyond K-means. Pattern Recognit. Lett. 2010, 31, 651–666. [Google Scholar] [CrossRef]
- Tian, Z.; Ramakrishnan, R.; Livny, M. BIRCH: An efficient data clustering method for very large databases. ACM Sigmod Rec. 1996, 25, 103–114. [Google Scholar]
- Darkins, R.; Cooke, E.J.; Ghahramani, Z.; Kirk, P.D.W.; Wild, D.L.; Savage, R.S. Accelerating Bayesian Hierarchical Clustering of Time Series Data with a Randomised Algorithm. PLoS ONE 2013, 8, 8. [Google Scholar] [CrossRef]
- Schliep, A.; Schonhuth, A.; Steinhoff, C. Using hidden Markov models to analyze gene expression time course data. Bioinformatics 2003, 19, i255–i263. [Google Scholar] [CrossRef]
- Xiong, Y.M.; Yeung, D.Y. Mixtures of ARMA models for model-based time series clustering. In Proceedings of the 2002 IEEE International Conference on Data Mining, Maebashi City, Japan, 9–12 December 2002; IEEE Computer Soc.: Los Alamitos, CA, USA, 2002. [Google Scholar]
- Begum, N.; Ulanova, L.; Dau, H.A.; Wang, J.; Keogh, E. A General Framework for Density Based Time Series Clustering Exploiting a Novel Admissible Pruning Strategy. IEEE Trans. Knowl. Data Eng. 2016. Available online: https://arxiv.org/abs/1612.00637 (accessed on 6 March 2020).
- Keogh, E. A Fast and Robust Method for Pattern Matching in Time Series Databases. In Proceedings of the 9th International Conference on Tools with Artificial Intelligence, Newport Beach, CA, USA, 3–8 November 1997. [Google Scholar]
- Wang, Q.; Megalooikonomou, V. A dimensionality reduction technique for efficient time series similarity analysis. Inf. Syst. 2008, 33, 115–132. [Google Scholar] [CrossRef]
- Chan, K.P.; Fu, A.W.C. Efficient time series matching by wavelets. In Proceedings of the 15th International Conference on Data Engineering, Sydney, Australia, 23–26 March 1999; IEEE Computer Soc.: Los Alamitos, CA, USA, 1999. [Google Scholar]
- Lin, J.; Keogh, E.; Wei, L.; Lonardi, S. Experiencing SAX: A novel symbolic representation of time series. Data Min. Knowl. Discov. 2007, 15, 107–144. [Google Scholar] [CrossRef]
- Ye, L.X.; Keogh, E. Time Series Shapelets: A New Primitive for Data Mining. In Proceedings of the Kdd-09: 15th Acm Sigkdd Conference on Knowledge Discovery and Data Mining, Paris, France, 29 June–1 July 2009; Assoc Computing Machinery: New York, NY, USA, 2009. [Google Scholar]
- Itakura, F. Minimum Prediction Residual principle applied to speech recognition. IEEE Trans. Acoust. Speech Signal. Process. 1975, AS23, 67–72. [Google Scholar] [CrossRef]
- Yi, B.K.; Jagadish, H.V.; Faloutsos, C. Efficient retrieval of similar time sequences under time warping. In Proceedings of the 14th International Conference on Data Engineering, Orlando, FL, USA, 23–27 February 1998; IEEE Computer Soc.: Los Alamitos, CA, USA, 1998. [Google Scholar]
- Kim, S.W.; Park, S.; Chu, W.W. An index-based approach for similarity search supporting time warping in large sequence databases. In Proceedings of the 17th International Conference on Data Engineering, Heidelberg/Germany, Germany, 2–6 April 2001; IEEE Computer Soc.: Los Alamitos, CA, USA, 2001. [Google Scholar]
- Keogh, E. Exact indexing of Dynamic Time Warping. In Proceedings of the Twenty-Eighth International Conference on Very Large Data Bases, Hong Kong, China, 20–23 August 2002; pp. 406–417. [Google Scholar]
- Keogh, E.; Ratanamahatana, C.A. Exact indexing of dynamic time warping. Knowl. Inf. Syst. 2005, 7, 358–386. [Google Scholar] [CrossRef]





| Geographical Zones | Latitude and Longitude Range of Stations | Scope of Flood Season | No. of Stations | No. of Events |
|---|---|---|---|---|
| Northeast China | 41.1° N–47.9° N 123.4° E–132° E | June–September | 18 | 1255 |
| North China | 36.1° N–42.5° N 111.2° E–118.6° E | June–September | 21 | 1384 |
| Central China | 25° N–30.1° N 110.9° E–112.9° E | April–October | 6 | 1150 |
| East China | 24.5° N–33.2° N 114.9° E–121° E | April–September | 26 | 4958 |
| South China | 22.9° N–26° N 109.1° E–114.1° E | April–October | 8 | 2027 |
| Northwest China | 32.4° N–39° N 107.1° E–110.4° E | June–October | 9 | 782 |
| Southwest China | 23.4° N–32.5° N 99.3° E–108.3° E | May–October | 11 | 1743 |
| Duration Section | Clusters | No. of Events (Percentage) | Intensity /mm | Peak Value /mm | Rainfall Depth /mm | Ratio of Peak Value to Rainfall Depth |
|---|---|---|---|---|---|---|
| [3, 6) | Cluster I | 432 (17.9%) | 3.8 | 7 | 15.5 | 41.70% |
| Cluster II | 658 (27.2%) | 4.8 | 10 | 18 | 54.50% | |
| Cluster III | 334 (13.8%) | 5.2 | 13.1 | 20 | 65.80% | |
| Cluster IV | 454 (18.8%) | 4.8 | 13.5 | 18 | 73.90% | |
| Cluster V | 537 (22.2%) | 5.1 | 16 | 18 | 88.70% | |
| [6, 12) | Cluster I | 1805 (44.7%) | 2.3 | 6.5 | 19 | 34.8% |
| Cluster II | 1023 (25.3%) | 2.4 | 9 | 20.4 | 44.8% | |
| Cluster III | 342 (8.5%) | 2.4 | 13 | 19.8 | 67.8% | |
| Cluster IV | 554 (13.7%) | 2.6 | 12 | 20 | 63.3% | |
| Cluster V | 312 (7.7%) | 2.6 | 16.5 | 19 | 85.7% | |
| [12, 24) | Cluster I | 2775 (64.8%) | 1.5 | 6 | 24.5 | 23.80% |
| Cluster II | 854 (19.9%) | 1.7 | 11 | 26.8 | 38.70% | |
| Cluster III | 150 (3.5%) | 1.8 | 14.5 | 25.8 | 56.10% | |
| Cluster IV | 438 (10.2%) | 1.7 | 10.5 | 25.5 | 42.10% | |
| Cluster V | 64 (1.5%) | 1.8 | 19.8 | 24.8 | 78.60% | |
| [24, 48) | Cluster I | 1828 (84.4%) | 1.3 | 7 | 43 | 16.50% |
| Cluster II | 208 (9.6%) | 1.6 | 15 | 46.3 | 30.80% | |
| Cluster III | 74 (3.4%) | 1.2 | 12 | 37.8 | 33.60% | |
| Cluster IV | 39 (1.8%) | 1.2 | 17.5 | 36 | 45.60% | |
| Cluster V | 16 (0.7%) | 1.5 | 18.8 | 42.4 | 55.70% | |
| [48, 96) | Cluster I | 320 (84%) | 1.5 | 9.2 | 92.2 | 10.3% |
| Cluster II | 36 (9.4%) | 1.5 | 12.8 | 75 | 17.2% | |
| Cluster III | 25 (6.6%) | 1.8 | 19 | 105 | 20.9% |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, F. Temporal Pattern Analysis of Local Rainstorm Events in China During the Flood Season Based on Time Series Clustering. Water 2020, 12, 725. https://doi.org/10.3390/w12030725
Wang F. Temporal Pattern Analysis of Local Rainstorm Events in China During the Flood Season Based on Time Series Clustering. Water. 2020; 12(3):725. https://doi.org/10.3390/w12030725
Chicago/Turabian StyleWang, Fan. 2020. "Temporal Pattern Analysis of Local Rainstorm Events in China During the Flood Season Based on Time Series Clustering" Water 12, no. 3: 725. https://doi.org/10.3390/w12030725
APA StyleWang, F. (2020). Temporal Pattern Analysis of Local Rainstorm Events in China During the Flood Season Based on Time Series Clustering. Water, 12(3), 725. https://doi.org/10.3390/w12030725





