Abstract
Use of surrogacy remains a useful method for prioritizing research on representatives of at-risk groups of fishes, yet quantifiable evidence in support of its use is generally not available. Blade strike impact represents one of the most traumatic stressors experienced by fish during non-volitional movements through hydropower turbines. Here, we use data generated from laboratory trials on blade strike impact experiments to directly test use of surrogacy for salmonid and clupeid fishes. Results of logistic regression indicated that a -taxonomic (genus) variable was not a significant predictor of mortality among large rainbow trout and brook trout. Similar results were found for young-of-the-year shad species, but genus-level taxonomy was a significant predictor of mortality while species was not. Multivariate analysis of morphometric data showed that shad clustered together based on similarities in fish shape which was also closely associated with genus. Logistic regression including size as a major covariate suggested total fish length was not a significant predictor of mortality, yet dose–response data suggest differential susceptibility to lower strike velocities. We suggest that use of surrogacy among species is justifiable but should be avoided within a species since the effects of size remain unclear.
This manuscript has been authored by UT-Battelle, LLC under Contract No. DE-AC05-00OR22725 with the US Department of Energy. The United States Government retains and the publisher, by accepting the article for publication, acknowledges that the United States Government retains a non-exclusive, paid-up, irrevocable, world-wide license to publish or reproduce the published form of this manuscript, or allow others to do so, for United States Government purposes. The Department of Energy will provide public access to these results of federally sponsored research in accordance with the DOE Public Access Plan (http://energy.gov/downloads/doe-public-access-plan).
1. Introduction
Downstream passage of fish through hydropower facilities represents a direct threat to migratory fishes worldwide. The threat is magnified globally because most of the largest rivers in the world are impounded, which impedes natural movement of riverine fishes [1]. Fish passing through hydropower turbines are exposed to a suite of injurious or lethal stressors, including rapid decompression, cavitation, shear forces, and impact with structures such as turbine blades [2,3,4,5]. Field trials are often used to estimate morbidity and mortality rates of turbine-passed fish related to turbine characteristics or dam operation parameters; however, these trials are incapable of linking a specific stressor to risk of injury or death because exact exposure conditions are unknown. Physical impact of the turbine blade with fish (e.g., blade strike) is one of the most injurious stressors fish must endure [6]. The risk and severity of injury is also dependent on turbine type, design, and operations, which makes it difficult to apply inferences from one facility to another. Two of the most common turbine types are Francis and propeller type turbines (e.g., Kaplan) [7], with higher rates of mortality observed in Francis compared to propeller turbines [8,9]. Blade leading edge thickness and strike velocity are two important turbine blade characteristics; maximum runner velocity data are generally available, but blade thickness descriptions are more difficult to obtain as they are often considered proprietary by turbine manufacturers [10,11]. In general, thicker blades are less injurious than thinner blades and faster velocities are more damaging than slower velocities [10,11,12,13,14]. Understanding how turbine type or associated characteristics impact survival of fishes is important, but rates of mortality are also affected by how the fish interacts with the turbine.
Other aspects of blade strike impact linked to with interactions with fish include the strike location (e.g., the head, mid-body, or tail), fish orientation (dorsal, lateral, or ventral surface), and angle of blade strike impact. Previous laboratory work suggests that mid-body, lateral strikes perpendicular to the body have the highest mortality rates and represent the worst-case scenario for blade strike [11,13,15]. Strikes of this nature are likely more fatal because the impact and forces acting on biological tissue occurs closer to the fish’s center of gravity where major organs are found. Glancing strikes at shallow angles or impacts to the tail are much less traumatic and mortality rates are low even with thinner blades moving at higher velocities [10,11,12]. Regardless, estimates of overall mortality must also include how the fish interacts with the turbine blade as it passes through the turbine.
Traits of the fish itself (e.g., size and species) also impact overall susceptibility to turbine blade impact during non-volitional movements through turbines. Fish size has been linked with differential rates of mortality so that larger fish often experience higher rates of mortality given other factors such as blade leading edge thickness and velocity remain constant [10,12]. Size-based trends likely vary by species because other work found that rates of mortality in different species were high overall, regardless of size, because smaller individuals were as susceptible to blade strike as larger individuals [13]. Inherent differences in body shape, morphology, and the musculoskeletal system observed among riverine fishes may impact overall susceptibility to blade strike.
Estimating mortality as a function of turbine blade and fish characteristics is important as turbine manufacturers and dam operators strive to increase survival of turbine-passed fish. To better inform design of turbines, biological data must be gathered for as many blade strike conditions as possible and reported in mathematical terms. Biological response data are often conveyed in terms of dose–response relationships, i.e., predicted rate of mortality (the response) against blade leading edge thickness or strike velocity (the dose) [11,13]. Dose–response relationships can be applied to stressor exposure distributions for a particular turbine type or turbine operation. Stressor exposure distributions express the likelihood that a fish will encounter various magnitudes of a stressor while passing through the turbine and can be estimated from computational fluid dynamics (CFD) models of theoretical particles passing through hydropower turbines [16,17]. Comparing dose–response relationships to exposure distributions can better inform design of safer hydropower turbines. In practice, opportunities to improve passage survival may occur during mandatory relicensing of hydropower projects that occurs every 30 to 50 years through the Federal Energy Regulatory Committee (FERC). Relicensing often requires environmental assessments that include investigating solutions meant to mitigate impacts of fish passage for species at highest risk of entrainment. Dose–response data for stressors like blade strike (and others) are incredibly useful to meet that end but are limited by data availability for most species of concern.
The remarkable diversity of fishes species makes it impossible to study all species, so methods have been developed to group and study fish with shared functional traits. In this way, one can study an entire community of riverine fishes without the need to capture, hold, and experiment on every species found in that system. Taxonomic groupings form the basis of this understanding by placing species into hierarchical groups (i.e., genera, family, etc.) based on shared genetic and morphological traits [18]. Furthermore, shared traits among group members allow researchers to investigate fewer, representative or surrogate species instead of every member of the group. Species surrogacy―use of one species in place of another because the targeted species is rare, difficult to collect, or protected by law―has been used in many fields including research on hydropower impacts [19]. For example, species prioritization via surrogacy and traits-based methods has been applied to assess which riverine fishes are at the greatest risk of entrainment [19,20]. This prioritization has also led to targeted, full-scale laboratory experimentation on representative species most likely to experience adverse effects during turbine passage. In fact, mortality data available on blade strike currently are the result of research on surrogate species that best represent at-risk taxonomic groups of fishes [11,13]. Another potential application of surrogacy is assessing whether data from one size group can realistically represent another within the same species. The beneficial aspects of surrogacy are obvious, but there is a paucity of data available to suggest using surrogacy for hydropower related studies is reliable.
Fishes in the salmonid and clupeid families are great test species for surrogacy because both groups contain predominantly anadromous species impacted by hydropower dams [21,22]. Representatives of both families are easy to collect, can be maintained in captivity, and are of conservation concern globally. Salmon, trout, and chars within Salmonidae are well known for their anadromous migrations and juvenile fish within this family are at high risk of turbine passage when smolts migrate downstream to the ocean [22]. Members of Clupeidae, including shad and herring, are also anadromous and many species are threatened throughout much of their native range globally [23]. Both families also contain multiple species and genera which present additional opportunities for testing application of surrogacy at different taxonomic levels.
The objectives of this study are to (1) determine whether taxonomic variables (species, genus, or neither) for salmonid and clupeid fishes are important predictors of mortality, (2) analyze and compare morphometric data for juvenile shad species to test what taxonomic level best captures similarities in fish shape, (3) test whether and how total length impacts predicted mortality within a species, and (4) use these analyses to directly test application of surrogacy via blade strike dose–response data. More specifically, we will use non-linear regression analyses to directly test surrogacy by including species or genus terms in one model compared to another which excludes taxonomic terms. Evidence in support of surrogacy may include selection of a parsimonious model that excludes a species or genus term, thereby suggesting that species dose–response data may adequately predict mortality of salmonid or clupeid fishes in general when exposed to simulated blade strike impact. Clupeid morphometric data will be used to estimate fish shape based on relative location of morphological landmarks (e.g., snout, head, fins, etc.). Fish shape is the best approximation of species available because detailed musculoskeletal and biomechanical data related to blade strike impact are unavailable. Further support of surrogacy would be achieved if shad morphology data are grouped together based on similarities in body shape at higher taxonomic levels (e.g., genus and above). To that end, shad species grouped together based on shared morphology may also be presumed to have similar dose–response relationships related to blade strike impact. Lastly, non-linear regression analysis will also be used to test whether total length (e.g., fish size) is a significant predictor of mortality and therefore assess whether dose–response data should always be separated by fish size within each species. Combined, these analyses offer a quantifiable way to test whether surrogacy can be used reliably for salmonid and clupeid blade strike dose–response data.
2. Materials and Methods
2.1. Fish Collection and Care
Most fishes used in blade strike impact trials were acquired locally and transported back to the Aquatic Ecology Laboratory (Oak Ridge National Laboratory, Oak Ridge, Tennessee, USA) to be used in experiments between June to November 2019. One hundred sixty large (mean total length [TL] = 25.8 ± 2.4 cm and mass = 152.0 ± 48.1 g) rainbow trout, Oncorhynchus mykiss, and 155 large (mean TL = 24.2 ± 2.4 cm and mass = 131.1 ± 39.1 g) brook trout, Salvelinus fontinalis, were obtained from United States Fisheries and Wildlife Service (USFWS) Dale Hollow National Fish Hatchery. An additional 67 large rainbow (n = 227 total) were obtained from a Tennessee Wildlife Resource Agency (TWRA) state hatchery (Tellico Trout Hatchery, Tellico Plains, Tennessee, USA). We also acquired 161 small (mean TL = 11.4 ± 1.0 cm and 13.6 ± 4.4 g) rainbow trout from another TWRA hatchery (Buffalo Springs Trout Hatchery, Rutledge, Tennessee, USA). Lastly, 92 gizzard shad, Dorosoma cepedanium, with mean TL of 16.0 ± 0.6 cm and mass of 31.5 ± 3.8 g were purchased from a local bait shop (Big Fish Outfitters, Lenoir City, Tennessee, USA). All fish were distributed equally into separate 680 L, dual-hull fiberglass, circular tanks that received constant water supply and aeration. Fish were fed daily except 24 h prior to experimentation to prevent fouling of the housing tank and blade strike apparatus.
Shad used in blade strike trials were obtained with the help of South Carolina Department of Natural Resource (SCDNR) fisheries biologists. More specifically, young-of-the-year (YOY) American shad, Alosa sapidissima, were targeted by boat electrofishing during nighttime field collections from Lake Moultrie and Lake Marion, South Carolina, USA on 7 to 10 October 2019. Fish were transported back to the SCDNR hatchery (Dennis Wildlife Center Fish Hatchery, Bonneau, South Carolina, USA) where they were housed until experimentation. While American shad were the target species, sympatric blueback herring, Alosa aestivalis, were inadvertently included in the American shad samples. YOY of both species have remarkably similar morphology at this life stage and are difficult to distinguish without additional handling. We initially waited to identify species until after experimentation to avoid handling stress but eventually were able to identify species through quick visual inspection immediately prior to immersion in anesthesia. A total of 43 American shad (mean TL = 8.5 ± 0.5 cm and mass = 5.35 ± 0.97 g) and 116 blueback herring (mean TL = 7.2 ± 0.4 cm and mass = 3.13 ± 0.47 g) were collected and used in the blade strike impact study. Transport and housing of both shad species required holding fish in 4–8‰ sodium chloride solution to minimize stress and increase survival. Back at the SCDNR hatchery where strike trials were conducted, groups of fish (50–100 individuals) were housed in 680–1420 L fiberglass tanks which received constant water supply and aeration. Fish were held ~12 h prior to experimentation to confirm fish were healthy following capture and transportation stress.
Additional shad were collected from local reservoirs in Tennessee or South Carolina described previously for use in morphological analysis in October and November 2019. YOY fish (≤10.0 cm TL), i.e., American shad, gizzard shad, and threadfin shad (Dorosoma pretenense) along with blueback herring, were targeted to limit the effects of size in our analysis. Eight blueback herring and 11 American shad were collected by boat electrofisher during the collection of fish used in blade strike trials. Eight threadfin shad and 13 gizzard shad were collected via boat electrofisher from Melton Hill Lake near Oak Ridge, Tennessee, USA. Upon arrival at the hatchery facility or laboratory, fish were euthanized via overdose of 250 ppm clove oil by dissolving pure clove oil extract (NOW® 100% Pure Clove Oil, Item #051193, www.gnc.com) in 95% ethanol (1:10) followed by dilution to desired concentration using dechlorinated water. After euthanasia, fish were refrigerated at 4 °C until individual fish were processed.
2.2. Blade Strike Experimentation and Analyses
Simulated blade strike trials were performed using a spring-powered blade strike apparatus that propelled a turbine blade through water to impact fish (Figure 1). Blades had a semicircular leading edge with leading edge widths of 26, 52, or 76 mm. Strike impact velocities ranged from 4.7 to 9.7 m/s which approximate typical turbine passage conditions according to Bevelhimer et al. [11]. Other major strike variables included location (mid-body [M] or head [H]), orientation (lateral [L], dorsal [D], or ventral [V]), and angle (45, 90, or 135°) of blade strike impact [13] (Figure 1, p. 59). A high-speed camera (Model IL4, Fastec Imaging, San Diego, California, USA) and stroboscope (Nova-Pro 300, Monarch Instrument, Amherst, New Hampshire, USA) were synchronized, and recorded each blade strike impact at 1000 fps perpendicular to the blade path to confirm strike impact conditions. Impact velocity was estimated (±0.1 m/s) by reviewing four high-speed videos, i.e., one before and after each exposure group and two actual treatment fish within the exposure group, using Kinovea software (v0.8.15, www.kinovea.org). Each treatment group was a combination of one variable from each exposure category (e.g., blade width, impact velocity, location, etc.) and contained 15–20 treatment fish and 3 control fish. Control fish were pooled together by species or size group within species for analysis.
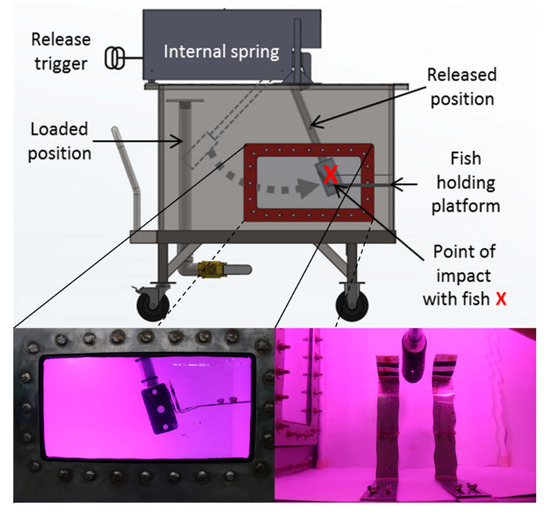
Figure 1.
A diagram of the apparatus used to simulate turbine blade strike. The top panel shows the entire apparatus and approximate path and impact point of the blade with anesthetized fish. The bottom left panel is a side view through the viewing window and the bottom right panel is a top view through the lid—both show the simulated turbine blade and holding platform where fish were positioned during trials.
The blade strike protocol used in this study followed that described in Saylor et al. [13], though modifications were necessary to accommodate our test species. Fish were anesthetized in 14 L of clove oil solution until reaching deep anesthesia characterized by loss of equilibrium, infrequent gill ventilation, and lack of movement [24]. Concentrations of clove oil were 25–30 ppm for rainbow trout, American shad, and blueback herring or 40 ppm for brook trout and gizzard shad [25,26]. Anesthetized fish were randomly assigned as treatment or control and placed into the blade strike apparatus. At this point, fish were placed on brackets containing rubber tubing to gently hold fish in place but allowed free movement following impact with the blade. Exact treatment groups and exposure conditions varied among species (Table A1). Controls were treated in the exact same way as treatment fish but did not receive simulated blade strike. Following blade strike, both trout species and gizzard shad were individually tagged in the mandible using labeled tag fasteners (PAG, 52 mm Fine Tagging Barb Fasteners, www.amazon.com). Because of their small size, American shad and blueback herring were not tagged to avoid additional handling stress, but were instead placed into individually labeled, plastic containers, containing 4 L of 4–8‰ sodium chloride solution and constant aeration. Individuals of all species were monitored every 15 min for 1 h and were removed early if fish exhibited signs of severe distress, i.e., consistent inability to maintain upright position, labored and erratic swimming, excessive hemorrhaging, or obvious signs of spinal fracture. Individuals were categorized as (1) survivor with no signs of distress, (2) moribund and removed early, (3) moribund at 1-h mark, or (4) direct death marked by cessation of gill ventilation. All fish were placed in 250 ppm euthanasia solution of clove oil and water until gill ventilations were not observed for at least 10 min, removed from the euthanasia bath, and placed on ice. Following euthanasia, external examinations and necropsies were performed and observed injuries were recorded following Saylor et al. [13]. Survivors observed with severe injuries, including internal decapitation or vertebral fractures, were considered ecologically dead, i.e., incapable of avoiding predation or acquiring food. Here, mortality was considered any category 2, 3, or 4 fish and any survivor observed with severe injuries. Necropsies were performed by the assessor without knowledge of treatment category.
Mortality rates were calculated for each treatment group and used to generate dose–response relationships according to species or size-group. Dose–response analyses predicted mortality as a function of impact velocity according to the following log-logistic equation [27]:
where f(x; b, c, d, e) is the predicted rate of mortality, b is the inclination point or slope of the curve, c is the lower bound fixed at 0.0, d is upper bound fixed at 1.0, and e is the effective dose (of velocity in m/s) at which 50% of the population would be predicted to experience mortality (i.e., E50 value). Dose–response curves were generated for fish that were struck with the same blade on the mid-body, lateral surface at 90°, and had at least four impact velocity treatments. Dose–response analyses were performed using the “drc” package [27] in R v3.6.1 [28]. All statistical decisions were based on α = 0.05. Curves were produced for large rainbow trout and brook trout, small rainbow trout, gizzard shad, and Alosa spp.; American shad and blueback hearing were combined (Alosa spp.) because samples sizes in each treatment group were low compared to other species.
We used logistic regression and model selection criteria to test species surrogacy using generalized linear models (glm) with a logit link function in R v3.6.1 [28]. Logistic regression analyses were performed on mortality as the binary predictor variable against continuous variables (e.g., blade impact velocity [m/s] or fish size [cm]) and categorical variables including species or genus, blade width (26 or 52 mm), location (M or H), orientation (L or D), and angle (90 or 135°). Variables were considered significant predictors of mortality when p < 0.05. We used a train to test ratio of 80:20 to assess model performance using package “ROCR” to create receiver operating plots (ROCs) and area under the curve (AUC) estimates to test the ability of our models to predict mortality. Akaike Information Criterion (AIC), Second order Akaike Information Criteria (AICc), and Informational and Complexity (ICOMP) criterion were calculated using package “MuMin” [29] to compare logistic models. We performed three analyses to help determine whether species or fish size were necessary parameters of the most parsimonious models that predicted mortality. The first analysis compared two models associated with large rainbow trout and brook trout data struck with the 52 mm blade, where both models included velocity, location, orientation, angle of impact, and total length variables (n = 276). The two models differed in that one included a species (e.g., RBT and BKT) term in the predictive model of mortality while the other did not. The second analysis included small and large rainbow trout data only for fish struck on the mid-body, lateral surface at 90° (n = 197). Both models included blade width and velocity terms, but only one included total length in the final predictive model. The third analysis included blade strike data for gizzard shad, American shad, and blueback herring that were struck with the 52 mm blade on the mid-body, lateral surface at 90° (n = 158). Major variables in both models included strike velocity and total length, but one model included species (GZS, AMS, or BBH) while the other included a genus (Dorosoma or Alosa) term to test which taxonomic level would best predict mortality. If two competing models had similar criteria values (i.e., within 2 units), we selected the model containing the fewest parameters because it required the least complexity to account for comparable levels of variation [30]. These analyses provide an opportunity to directly test whether species or size terms are necessary predictors of mortality and help objectively determine whether dose–response data from one species or size group can be used as a surrogate for another.
2.3. Fish Morphology Measurements and Analyses
The subsample of shad (n = 40 across all species) was used to estimate fish shape via morphometric analysis of body landmarks. Initial measurements included total and standard length (±0.1 cm) as well as mass (±0.01 g). Three sets of measurements were taken, namely, (1) lengths relative to snout tip, (2) body depths, and (3) body widths at each landmark. Major landmarks were identified to approximate body shape of each species including the anterior edge of the eye (e.g., snout) and posterior margin of operculum (e.g., head), as well as the leading edge of the dorsal, pectoral, pelvic, anal, and caudal fins (Figure 2). We used a fish measuring board (±0.1 cm; Fish Measuring Board, Mini, Model #118-E40, Wildco, Yulee, Florida, USA) to estimate lengths and digital calipers (±0.01 mm; iGaging Origin Cal Digital Calipers, Model #100-032-901WB, Brownells Inc., Grinnell, Iowa, USA) for body depth and width measurements. Condition factor (K) was calculated according to Cone [31] using the following equation:
where M is mass in grams and TL is total length in centimeters. Individuals with a condition factor >3 standard deviations above or below the species average were considered outliers and excluded from analysis—only one gizzard shad met these criteria and was removed from further analysis. Raw measurement data were not used so each landmark measurement was converted to a proportion of maximum body length, depth, or width.
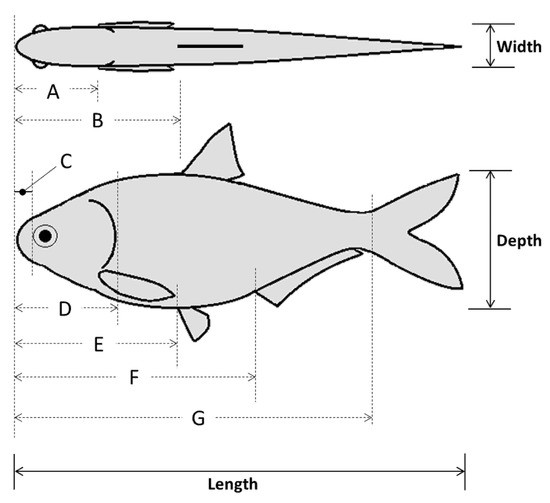
Figure 2.
Diagram of major body landmarks from which morphometric measurements were taken related to body length, depth, and width (solid lines). Dashed vertical lines correspond to landmarks including pectoral fin (A), dorsal fin (B), snout (C), head (D), pelvic fin (E), anal fin (F), and caudal fin (G). Horizontal dashed lines represent length measurements between the snout tip and each landmark, while body depth and width measurements were taken on the body at each landmark (i.e., near vertical lines).
Morphometric data were analyzed using multivariate methods to assess similarities in body shape according to taxonomic level among clupeid fishes. A total of 39 fish (four species) and 22 variables were used including a species term and 21 morphometric variables—seven landmark proportions each for body length, depth, and width. We used a principal component analysis (PCA) to determine which of the 21 morphometric variables accounted for the most variation in our data set. A scree plot was created to visualize percentage of variation explained with each successive principal component to help prioritize which PCs would be used in the cluster analysis. Results of the PCA were then used to perform a hierarchical clustering on principal components (HCPC) analysis to test how shad may cluster or group according to similarities (or dissimilarities) in body shape. Hierarchical clustering was performed using Ward’s linkage method to measure dissimilarity between clusters because it produced the highest agglomerative coefficient. The gap statistic and the silhouette method were used to determine optimal number of clusters while a factor map was created to visualize clusters. Both PCA and HCPC analyses were performed using packages “FactoMineR” and “factoextra” in R v3.6.1 [28].
3. Results
3.1. Blade Strike Impact
We successfully tested 752 individuals and 34 blade strike impact treatments across all species included in this study. Mortality varied by species, but our data suggest large brook and rainbow trout were most susceptible, followed by all clupeids, and small rainbow trout representing the most resistant group in this study. Brook trout mortality occurred at the lowest velocity of 4.9 m/s, while small rainbow trout were observed with a few survivors at velocities up to 8.7 m/s when struck on mid-body, lateral surface at 90°. Blades with thicker leading edges had lower estimated mortality in both small and large rainbow trout (26 > 52 mm) and Alosa (26 > 52 > 76 mm). Mortality associated with the thickest blade (e.g., 76 mm) remained below 25% at velocities up to 9.4 m/s in Alosa, while mortality with the thinnest blade (e.g., 26 mm) was nearly always fatal at velocities near 6.6 m/s in small and large rainbow trout. Mid-body strikes on the dorsal surface at 90° had higher mortality than strikes to the lateral surface, while lateral strikes at 135° had lower mortality compared to those at 90° in both large rainbow trout and brook trout. Smaller rainbow trout had a lower mortality rate of 15.8% at 6.7 m/s compared with 55% in larger individuals exposed to the same velocity. None of the control fishes of any species died during anesthesia, handling, or observation so that the mortality rate of control fish was 0.0 (Table A1).
Trends in the number of survivors that contained major injuries varied by species and size with very few injured survivors in large trout (<7% of all survivors) compared to nearly 70% observed in gizzard shad. We also observed 20% to 25% of all survivors among the smallest fish tested (Alosa and rainbow trout) with major injuries. Major injuries were most often observed as vertebral fractures (up to five separate fractures) near the point of impact regardless of species, size, or treatment group. In contrast, internal decapitation was most often associated with lateral strikes to the head at 90° or in combination with vertebral fractures when struck on the mid-body, lateral surface of trout but was mostly absent in shad. Among trout (both species and sizes), injuries to muscle and kidney tissue near the vertebral fractures were also observed along with multiple rib fractures. Noticeable hemorrhaging and formation of clots in the buccal and opercular chambers in trout were observed in the same fish with vertebrate factures, especially those closer the head. Noticeable damage to the eyes was observed in Alosa in the form of exophthalmia (n = 8) and in extreme cases complete amputation of one eye (n = 6) at the highest velocity (e.g., 9.7 m/s). All fishes that experienced eye amputation were considered dead within the first 15 min of observation and were also observed with complete vertebral fractures during necropsy.
3.2. Dose–Response Curves
Log-logistic regression of mortality against blade strike velocity produced dose–response curves for each species that covered a 2.0 m/s velocity range (Figure 3). The blade strike velocity range for gizzard shad was greater (e.g., 3.4 m/s) than other species but no mortalities were observed at the lowest velocity group of 4.7 m/s, suggesting that its range was also closer to 2.0 m/s. Overall shape of the curves (and inherent relationship therein) were similar for both species of large trout but small rainbow trout had much different curve structure (Figure 3A), while gizzard shad and Alosa spp. Data produced curves of similar shape (Figure 3B). Gizzard shad and brook trout curves produced the lowest ED50 values of 5.7 and 6.0 m/s, respectively. The highest ED50 values were predicted for the small rainbow trout (7.1 m/s) and Alosa (7.9 m/s) regressions, while large rainbow trout fell in the middle with a value of 6.6 m/s. Values for the point of inclination or steepness of the curve (b), were the lowest in large rainbow trout and brook trout and steepness increased with average total length of fish regardless of species. The highest steepness values were observed with small rainbow trout (−29.33) and Alosa (−37.31), suggesting that smaller changes in velocity are associated with comparatively higher probabilities of mortality than other species. All parameter estimates were considered significant for all species included in our dose–response analyses (Table 1).
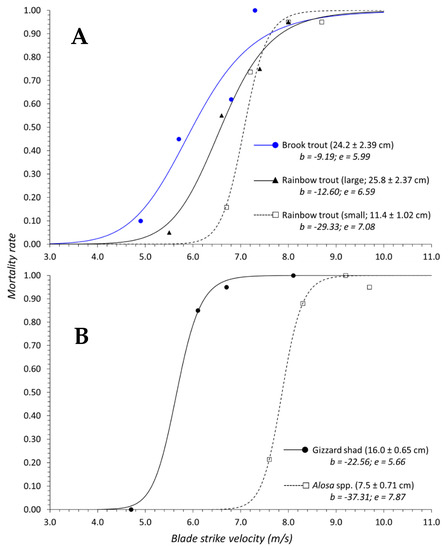
Figure 3.
Graphs of dose–response curves using log-logistic regression to predict mortality according to blade strike velocity (m/s). Curves were produced for (A) small (black; dashed line; open squares) and large rainbow trout (black; solid line; closed triangles) and brook trout (blue; solid line; closed circles) or (B) gizzard shad (black; solid line; closed circles) and Alosa spp. (black; dashed line; open squares).

Table 1.
Results of log-logistic regression of mortality against blade strike impact velocity for each species, size class within a species, or combination of species.
3.3. Logisitic Regression Analyses
The logistic regression of large rainbow trout and brook trout suggested blade strike characteristics were significant predictors of mortality, and the species term was not included in the accepted model. Both models tested had AIC, AICc, and ICOMP values that were less than one unit apart (Table 2) so the Trouts.m2 model that did not have a species term was accepted because it required less complexity to explain comparable levels of variation in our data. Interestingly, the model that contained the species term also indicated that species (rainbow trout or brook trout) was not a significant predictor of mortality (Table 2). Significant predictors of mortality in the accepted model included velocity, orientation, angle of impact, and total length while location was not significant. Variables with the greatest significant effect on mortality were velocity and impact angle. For every 1.0 m/s increase in strike velocity, fish were ~6 times more likely to die (at average total length, constant orientation and impact angle). While total length was a significant predictor of mortality for large rainbow trout and brook trout, the odds of survival was predicted to increase by 20% for every 1.0 cm increase in fish length at average velocity and constant location, orientation, and impact angle (Table 2). Our data suggest that species is not an important predictor of mortality for both rainbow trout and brook trout compared to velocity when exposed to similar blade strike conditions. The ROC curve and AUC value for Trouts.m2 suggest this model has high specificity and properly classified mortality as a function of blade strike characteristics without including species (Figure 4A).

Table 2.
Results of a logistic regression of mortality and strike impact conditions including adult rainbow trout and brook trout data (Trouts), small and large rainbow trout (RBT), and data for gizzard shad, American shad, and blueback herring (Shads).
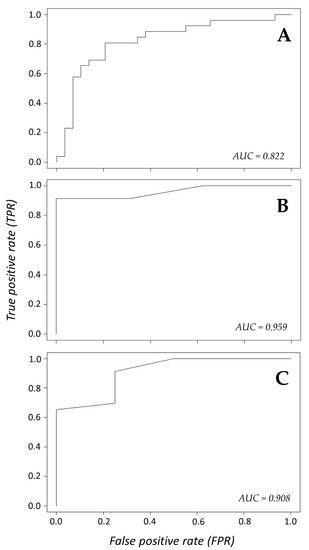
Figure 4.
Receiver operating (ROC) plots with area under the curve (AUC) values depicting specificity of logistic regression models used to predict mortality as a result of blade strike conditions. Logistic models were produced for large rainbow trout and brook trout (A), small and large rainbow trout (B), or gizzard shad, American shad, and blueback herring (C).
Analysis of rainbow trout data that included both small and large individuals found that blade velocity and leading-edge width significantly influenced mortality among trout, but the effect of total length was not as clear. One small rainbow trout was removed from the data set as an outlier because its standardized residual was greater than 3.00, i.e., making the final sample size equal to 197. Both models produced selection criteria values that were within 2.0 units of one another; however, AIC and AICc criteria suggested the model with total length was best (RBT.m1) while ICOMP values were lowest when excluding the total length term (RBT.m2; Table 2). The total length term in RBT.m1 was not considered significant, but the p-value (0.061) was just above the 95% confidence level used here. The odds of mortality would be slightly higher (~7%) for every 1.0 cm increase in total length of rainbow trout when blade width was held constant and at average velocity. The combination of non-significance, small change in odds of mortality, and lower ICOMP value suggests that the RBT.m2 model excluding total length would be best. This model had an AUC value of 0.959, suggesting that it adequately classified mortalities and the ROC plot indicates high specificity of the RBT.m2 model that did not include total length (Figure 4B).
The shad logistic regression suggested mortality was significantly influenced by velocity and the model with a genus (Dorosoma vs. Alosa) term accounted for variation slightly better than species (GZS vs. AMS vs. BBH). Importantly, fish total length was not considered significant for either model and was not included in the most parsimonious model of our shad blade strike data. Like the analyses above, all selection criteria values were within 2.0 units of one another, but the Shads.m8 model had slightly lower criteria values (Table 2). The genus term was considered a significant predictor of mortality (p < 0.001) and the model suggested the Dorosoma species were ~6000 times more likely to experience mortality compared to Alosa species when struck on the mid-body, lateral surface at 90° and average velocity. While we chose the model containing the genus term, the alternative model that had a species term (Shads.m6) also predicted that gizzard shad was more susceptible than the other shad species. Interestingly, even though species was considered a significant predictor of mortality (p < 0.001), this was only true for gizzard shad compared to blueback herring in Shads.m6. Blueback herring was significantly indistinguishable from American shad (p = 0.622), i.e., predicted mortality is the same for both species. The combination of lower selection criteria and observation of non-significance between American shad and blueback herring suggests that the model containing a genus-level taxonomic term will adequately predict mortality among shad. Furthermore, the ROC plot and an AUC value of 0.908 suggests that our accepted model (Shads.m8) has high specificity and properly classified mortality as a function of velocity and genus (Figure 4C).
Initial analyses of morphometric data suggested that discrepancies in size affected our analysis of body proportions, but also predict two clusters which align with genus-level taxonomy instead of species. All gizzard shad used in this analysis were ~4.0 cm longer on average than the other species and at least one larger threadfin shad (12.2 cm) was used as well. The effect of size was evident in a biplot of these data, where all gizzard shad are grouped separately and the largest threadfin (TFS17) was included within an ellipse that overlaps with American shad and blueback herring ellipses (Figure 5A). Similarly, the HCPC analysis suggested three clusters best represented these morphometric data—gizzard shad and threadfin shad each clustered separately, and the single large threadfin shad was included in the third cluster containing American shad and blueback herring (Figure 5B). To that end, we removed all gizzard shad and the largest threadfin shad from further analysis because the effect of size may confound interpretations of our morphometric data since smaller gizzard shad were not available for our analysis. The result of excluding gizzard and threadfin data left proportional morphometric data for 26 fish across all species (TL < 10.0 cm) to be used in another set of PCA and HCPC analyses. The results of PCA suggest that 50% of the variation in these morphometric data was described by the first three dimensions while over 75% was explained by including up to six dimensions (Figure 6). Twelve of the 21 morphometric variables explained more variation than would be expected if all variables contributed equally, and no single variable appeared to be more important than the others. The HCPC analysis using six principal components produced two clusters, one representing the combination of American shad and blueback herring (i.e., Alosa) and the second representing threadfin shad (Figure 7). Both the average silhouette method (Figure A1A) and gap statistic (Figure A1B) indicate that two clusters are optimal for our shad data. Combined, these multivariate analyses suggest that use of Alosa is permissible for blade strike studies since YOY of both American shad and blueback herring have similar overall body shape at this life stage.
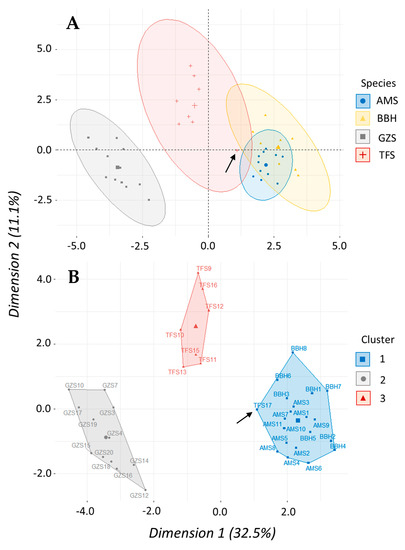
Figure 5.
Initial results of the principal component analysis and hierarchical clustering on principal components using morphometric data collected from American (AMS), blueback (BBH), gizzard (GZS), and threadfin (TFS) shad. (A) Biplot showing ellipses encircling individual fish considered part of that group according to PCA. (B) Cluster factor map showing results of HCPC analysis that produced three clusters. Gizzard shad and threadfin shad #17 (black arrow) were all ~4.0 cm larger on average than other shad species so all gizzard shad and TFS17 data were removed from the final analysis to preclude the confounding effects of fish size.
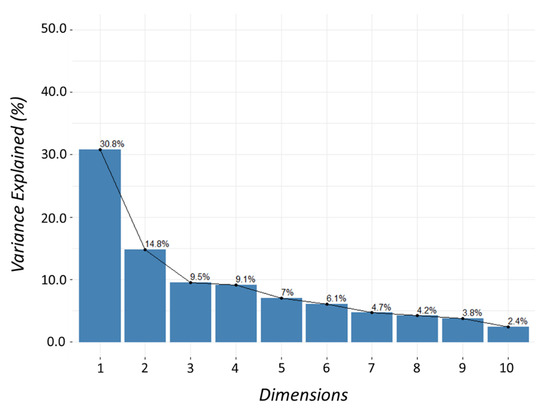
Figure 6.
Scree plot produced from the principal component analysis of shad morphometric data containing one species term and 21 morphometric variables.
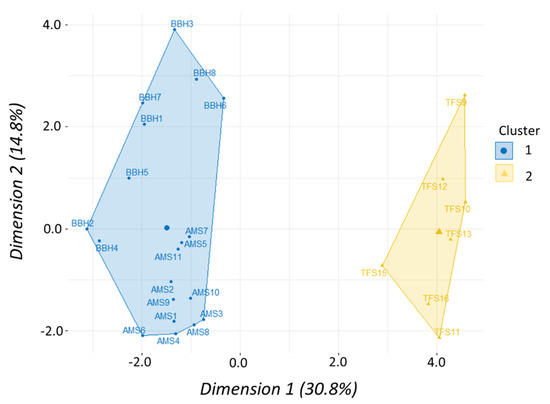
Figure 7.
Cluster factor map produced from hierarchical clustering on six principal components for American shad (AMS), blueback herring (BBH), and threadfin shad (TFS) morphometric data.
4. Discussion
Results of our analyses suggest use of surrogacy for blade strike data is acceptable, i.e., dose–response data for one species should sufficiently represent another, though the exact taxonomic application varies by family. Within Salmonidae, we tested large fish from two of the three most common genera in North America (i.e., Oncorhynchus and Salvelinus) and logistic regression indicated that inclusion of genus was not necessary to predict mortality. In terms of surrogacy using dose–response data, this suggests that combining response data for both species into a singular curve should adequately represent this family. The dose–response curves for each species are also quite similar and the confidence bands for both curves overlap across the entire velocity range (Figure 8A). Within Clupeidae, surrogacy seems equally applicable, but taxonomic level did significantly influence predicted mortality. The accepted logistic model for our shad data indicated species-level taxonomy within a genus was not important, but genus-level taxonomy within a family was a significant predictor of mortality (Table 2). This is especially evident in the logistic regression that suggested gizzard shad were three orders of magnitude more likely to experience death when compared to Alosa spp. (Table 2). Similarly, morphometric data showed shad within Alosa had a proportionally similar shape that was distinctly separate from Dorosoma (Figure 7). While the shad dose–response curves have similar shapes, the ED50 value for gizzard shad occurred at velocities 2.2 m/s slower than Alosa spp. which also suggests gizzard shad is more susceptible to blade strike (Figure 3B). The discrepancy in mortality susceptibility could be related to size differences since gizzard shad were ~4.0 cm longer on average than other shad species. In this way, we suggest that the dose–response curve for Alosa spp. data remains useful as is, but the dose–response curve for gizzard shad must be kept to represent Dorosoma.
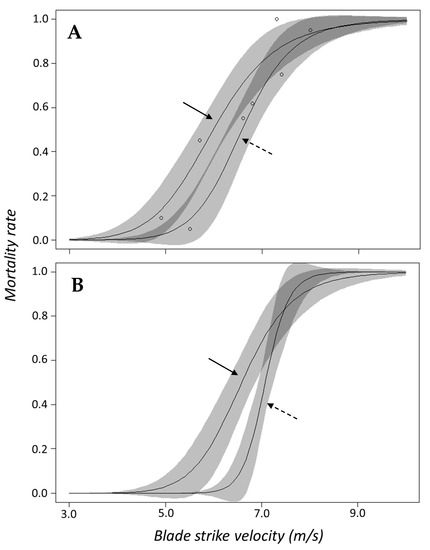
Figure 8.
Plot of dose–response curves for (A) large rainbow (solid arrow) and brook (dashed arrow) trout and (B) small (dashed arrow) and large (solid arrow) rainbow trout which highlights the 95% confidence bands for each curve.
Based on available data, use of surrogacy for larger salmonids or YOY Alosa spp. is justifiable with two caveats. First, while rainbow trout and brook trout should represent the salmonid family well, it is unclear whether inclusion of data from other diverse genera (i.e., Salmo) would show similar responses to blade strike. This study also did not include comparison between species within the same genus, though results of the logistic regression suggests species is likely not an important predictor of mortality. Differences in species may become apparent if more treatment conditions other than mid-body, lateral strikes at 90° were included in regression models. For example, mortality for rainbow and brook trout struck on the mid-body, dorsal surface at 90° both experienced high, but unequal rates of mortality (Table A1). Inclusion of multiple blade leading widths or strike velocities for mid-body, dorsal or 135° strikes could also help further separate a species effect. To date, mid-body, lateral strikes at 90° prioritized in this study have consistently been associated with higher overall mortality regardless of species [10,11,12,13]. Blade strike laboratory data for threadfin shad were also not available which could help elucidate if species within Dorosoma have similar responses to blade strike velocity. Second, surrogacy in this case is supported for trout with total length from 16.5 to 31.5 cm (i.e., size range for both species of large trout tested in this study), and shad dose–response data may only be applicable to YOY American shad and blueback herring because smaller gizzard shad were unavailable. Sizes of both trout and shad data are, however, broadly representative of the size ranges that pass through hydropower turbines as they migrate downstream to their native coastal habitat. Regardless, application of our dose–response curves to markedly smaller or larger size groups of trout or shad is not advisable pending the collection and analysis of more varied size data.
Application of surrogacy within rainbow trout as a function of body size may also be possible but the evidence is less conclusive. Both rainbow trout models suggested that total length was not a significant predictor of mortality, even if values were close to significant (e.g., RBT.m1; Table 1) because the odds of mortality were nearly the same across all sizes of rainbow trout. In addition, a logistic regression of only mortality and total length suggested that fish size remained a non-significant predictor of mortality. This simplistic model also did not properly account for variation in our data considering the AIC value was much higher (184.06) compared to our accepted model (Table 2). A similar trend was detected in Saylor et al. [13] who found that size was not a significant contributor of mortality in bluegill compared to blade leading edge width or velocity. The lack of significance in bluegill was attributed to the marked susceptibility of the species overall, but smaller fish experienced mortality at lower velocities than larger fish [13]. In contrast, the shapes of small and large dose–response curves appear to be different and the confidence intervals of both do not overlap at lower velocities (Figure 8B). Other researchers studying similarly sized rainbow trout (i.e., 10.0 to 25.0 cm fork length) found that larger fish had markedly higher rates of mortality compared to smaller trout [10,12]. We found similar trends when large (~25.0 cm) trout struck by a 52 mm blade had noticeably higher mortality compared to small (~10.0 cm) trout (Groups 2 and 11; Table A1); however, the thinnest 26 mm blade caused ~100% mortality regardless of trout size in this study (Groups 6 and 15; Table A1). Work by EPRI et al. [10,12] did not make statistical comparisons between treatment groups or model responses simultaneously over their entire data set, which limits more direct comparisons with this study. In the absence of more conclusive agreement between this analysis and previous studies, dose–response relationships within the same species should be treated separately, i.e., surrogacy according to size is not advisable for rainbow trout. To that end, understanding how size effects mortality within a species remains unclear and suggests trends in size are also linked closely with fish species.
5. Conclusions
Our use of surrogacy in this study should help turbine manufacturers and researchers better understand the effects of turbine passage stressors by increasing inference space of blade strike data. Brook trout data should be a suitable representative to species like bull trout, Salvelinus confluentus, which is threatened throughout much of its native range in North America [32,33]. Additional dose–response data for Salmo spp. or multiple, similarly sized Dorosoma spp. would better inform application of surrogacy but is unwarranted because there is currently no evidence to suggest other species within either genus would respond markedly different from species tested here, though fish length has a confounding effect on mortality. Our use of morphometric analyses and fish shape is the best approximation of species available for blade strike analyses currently, but future work should investigate the biomechanical properties of the fish musculoskeletal system including how scales, skeletal complexity, and center of gravity affect whole-fish flexibility. For example, early work by Turnpenny [15] measured each species’ center of gravity and found that injury and mortality rates were higher when the blade struck the fish’s center gravity, i.e., a direct strike. Biomechanical data may account for fish species better than body shape alone in models used to predict mortality caused by blade strike impact. Understanding the effects of size remains a challenge; however, use of dose–response data from one size class as a surrogate for that species may be the only option in absence of desired data. Otherwise, size and species can be easily accounted for by adjusting model parameters (both b and e) based on changes in mortality linked with other treatment conditions. Our methods prefer inclusion of fewer fish in more treatment groups to extend our inference space of blade strike data. Smaller sample sizes increase total variation in our regression models, but we also cover more possible blade strike scenarios which can better inform a species’ total passage risk. In certain scenarios, it may be beneficial to use actual species’ dose–response models (when available) if that species is of great concern. Alternatively, enough insight may be gained by use of surrogate data that represent average genus- or family-level responses, or for circumstances where data do not exist. Regardless, our data will help populate and broaden the application of the Biological Performance Assessment (BioPA) model [34] and the Hydropower Biological Evaluation Toolset (HBET) [35] which are available to turbine manufacturers and/or project managers attempting to design safer hydropower turbines that can ameliorate impacts of turbine passage without stark losses in electricity production.
Author Contributions
Conceptualization, R.S., D.S., M.B. and B.P.; methodology, R.S., M.B. and B.P.; formal analysis, R.S.; investigation, R.S., D.S. and M.B.; writing—original draft preparation, R.S.; writing—review and editing, D.S., M.B. and B.P.; supervision, M.B. and B.P. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the United States Department of Energy’s Water Power Technologies Office at Oak Ridge National Laboratory (ORNL/UT-Battelle, LLC), under contract number DE-AC05-00OR22725.
Acknowledgments
This manuscript has been authored by UT-Battelle, LLC under Contract No. DE-AC05-00OR22725 with the US Department of Energy. Fish use approval was granted by the ORNL Institutional Animal Care and Use Committee [protocol #0461]. The authors would like to thank Bill Post, Jarrett Gibbons, and all the fisheries biologists, hatchery technicians, and field crews from the South Carolina Department of Natural Resources Dennis Wildlife Center and Fish Hatchery for research space, onsite housing, and collection of American shad and blueback herring. We thank Andrew Currie and Steven Arms (United States Fish and Wildlife Service Dale Hollow National Fish Hatchery) for rainbow and brook trout. We also must thank John Ellis and Roger Bitz (Tellico and Buffalo Springs State Hatcheries, respectively, Tennessee Wildlife Resource Agency) for additional rainbow trout. Special thanks to Rebecca Brink (ORNL) for assistance with laboratory trials and Evin Carter (ORNL), Brett Pflugrath (Pacific Northwest National Laboratory, PNNL), Ryan Harnish (PNNL), and Robert Mueller (PNNL) for reviewing this article. We also thank Lara Aston and Alison Colotelo (PNNL) and Shelaine Curd (ORNL) for project management.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A

Table A1.
Experimental overview of the study including 34 treatment groups and five control (C) groups for rainbow trout (large and small), brook trout, gizzard shad, and Alosa spp. (species data combined because sample sizes of American shad and blueback herring were small. Mean total length (TL) is reported with standard deviation (SD) with units of centimeter (cm). Blade strike characteristics included blade width (BW; mm), velocity (Vel; m/s), location (Loc, with M; mid-body or H; head), orientation (Ort, with L; lateral, D; dorsal, and V; ventral), impact angle (Ang). The total number in each group (N) is reported with counts (Mort) and rates (MR) of mortalities. Analyses include dose–response (DR) and logistic regression (LR) used in this study. P-values are calculated for Chi-square tests with Yates correction using the following equation [1]: and compared each treatment to the species’ control group. We assumed α = 0.05; significant comparisons are in bold.
Table A1.
Experimental overview of the study including 34 treatment groups and five control (C) groups for rainbow trout (large and small), brook trout, gizzard shad, and Alosa spp. (species data combined because sample sizes of American shad and blueback herring were small. Mean total length (TL) is reported with standard deviation (SD) with units of centimeter (cm). Blade strike characteristics included blade width (BW; mm), velocity (Vel; m/s), location (Loc, with M; mid-body or H; head), orientation (Ort, with L; lateral, D; dorsal, and V; ventral), impact angle (Ang). The total number in each group (N) is reported with counts (Mort) and rates (MR) of mortalities. Analyses include dose–response (DR) and logistic regression (LR) used in this study. P-values are calculated for Chi-square tests with Yates correction using the following equation [1]: and compared each treatment to the species’ control group. We assumed α = 0.05; significant comparisons are in bold.
| No. | Spp | TL ± SD (cm) | BW | Vel | Loc | Ort | Ang | N | Mort | MR | Analyses | p-Value |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| C | Rainbow trout | 25.8 ± 2.37 | -- | -- | -- | -- | -- | 26 | 0 | 0.0 | -- | -- |
| 1 | 52 | 5.5 | M | L | 90 | 20 | 1 | 5.0 | DR; LR | 0.447 | ||
| 2 | 52 | 6.6 | M | L | 90 | 20 | 11 | 55.0 | DR; LR | <0.001 | ||
| 3 | 52 | 7.4 | M | L | 90 | 20 | 15 | 75.0 | DR; LR | <0.001 | ||
| 4 | 52 | 8.0 | M | L | 90 | 20 | 19 | 95.0 | DR; LR | <0.001 | ||
| 5 | 52 | 6.6 | M | L | 135 | 21 | 9 | 42.9 | LR | <0.001 | ||
| 6 | 26 | 6.6 | M | L | 90 | 20 | 20 | 100.0 | LR | <0.001 | ||
| 7 | 52 | 6.6 | M | D | 90 | 20 | 16 | 80.0 | LR | <0.001 | ||
| 8 | 52 | 6.6 | M | V | 90 | 20 | 6 | 30.0 | LR | 0.005 | ||
| 9 | 52 | 6.6 | H | L | 90 | 20 | 4 | 20.0 | LR | 0.032 | ||
| 10 | 52 | 7.4 | H | L | 90 | 20 | 16 | 80.0 | LR | <0.001 | ||
| C | Rainbow trout | 11.4 ± 1.02 | C | C | C | C | C | 21 | 0 | 0.0 | -- | -- |
| 11 | 52 | 6.7 | M | L | 90 | 19 | 3 | 15.8 | DR; LR | 0.098 | ||
| 12 | 52 | 7.2 | M | L | 90 | 19 | 14 | 73.7 | DR; LR | <0.001 | ||
| 13 | 52 | 8.0 | M | L | 90 | 20 | 19 | 95.0 | DR; LR | <0.001 | ||
| 14 | 52 | 8.7 | M | L | 90 | 20 | 19 | 95.0 | DR; LR | <0.001 | ||
| 15 | 26 | 6.6 | M | L | 90 | 20 | 18 | 90.0 | LR | 0.002 | ||
| C | Brook trout | 24.2 ± 2.39 | -- | -- | -- | -- | -- | 20 | 0 | 0.0 | -- | -- |
| 16 | 52 | 4.9 | M | L | 90 | 20 | 2 | 10.0 | DR; LR | 0.234 | ||
| 17 | 52 | 5.7 | M | L | 90 | 20 | 9 | 45.0 | DR; LR | 0.001 | ||
| 18 | 52 | 6.8 | M | L | 90 | 21 | 13 | 61.9 | DR; LR | <0.001 | ||
| 19 | 52 | 7.3 | M | L | 90 | 20 | 20 | 100.0 | DR; LR | <0.001 | ||
| 20 | 52 | 6.8 | M | D | 90 | 19 | 17 | 89.5 | LR | <0.001 | ||
| 21 | 52 | 6.8 | H | L | 90 | 20 | 13 | 65.0 | LR | <0.001 | ||
| 22 | 52 | 6.8 | M | L | 135 | 15 | 5 | 33.3 | LR | 0.011 | ||
| C | Gizzard shad | 16.0 ± 0.65 | -- | -- | -- | -- | -- | 12 | 0 | 0.0 | -- | -- |
| 23 | 52 | 4.7 | M | L | 90 | 20 | 0 | 0.0 | DR; LR | 1.000 | ||
| 24 | 52 | 6.1 | M | L | 90 | 20 | 17 | 85.0 | DR; LR | <0.001 | ||
| 25 | 52 | 6.7 | M | L | 90 | 20 | 19 | 95.0 | DR; LR | <0.001 | ||
| 26 | 52 | 8.1 | M | L | 90 | 20 | 20 | 100.0 | DR; LR | <0.001 | ||
| C | Alosa spp. | 7.5 ± 0.71 | -- | -- | -- | -- | -- | 29 | 0 | 0.0 | -- | -- |
| 27 | 52 | 7.1 | M | L | 90 | 2 | 0 | 0.0 | LR | -- | ||
| 28 | 52 | 7.6 | M | L | 90 | 14 | 3 | 21.4 | DR; LR | 1.000 | ||
| 29 | 52 | 8.3 | M | L | 90 | 25 | 22 | 88.0 | DR; LR | 0.026 | ||
| 30 | 52 | 9.2 | M | L | 90 | 17 | 17 | 100.0 | DR; LR | <0.001 | ||
| 31 | 52 | 9.7 | M | L | 90 | 20 | 19 | 95.0 | DR; LR | <0.001 | ||
| 32 | 26 | 8.2 | M | L | 90 | 17 | 17 | 100.0 | -- | <0.001 | ||
| 33 | 76 | 8.1 | M | L | 90 | 19 | 2 | 10.5 | -- | 0.148 | ||
| 34 | 76 | 9.4 | M | L | 90 | 16 | 3 | 18.8 | -- | 0.037 |
Note: Data containing (--) indicate that this column was not applicable to this treatment group. Control fish for all species were not used in dose–response or logistic regression analyses and p-values were not reported because treatment groups are compared to control groups to generate statistical inferences.
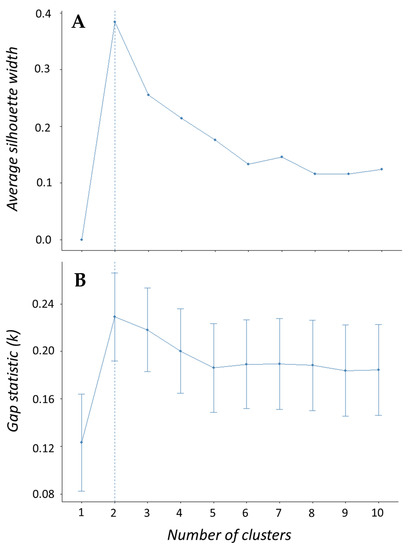
Figure A1.
Graph depicting two common methods to determine optimal number of clusters to be used in a hierarchical cluster analysis. Methods include (A) average silhouette, which measures how well data lies within each cluster so that higher values indicate better fit, and (B) the gap statistic, which compares intracluster variation to a null reference and clusters with highest values representing the greatest distance from uniform.
References
- Silva, A.T.; Lucas, M.C.; Castro-Santos, T.; Katopodis, C.; Baumgartner, L.J.; Thiem, J.D.; Aarestrup, K.; Pompeu, P.S.; O’Brien, G.C.; Braun, D.C.; et al. The future of fish passage science, engineering, and practice. Fish Fish. 2018, 19, 340–362. [Google Scholar] [CrossRef]
- Neitzel, D.; Dauble, D.D.; Cada, G.F.; Richmond, M.C.; Guensch, G.R.; Mueller, R.R.; Abernethy, C.S.; Amidan, B. Survival estimates for juvenile fish subjected to a laboratory-generated shear environment. Trans. Am. Fish. Soc. 2004, 133, 447–454. [Google Scholar] [CrossRef]
- Čada, G.; Loar, J.; Garrison, L.; Fisher, R.; Neitzel, D. Efforts to Reduce Mortality to Hydroelectric Turbine-Passed Fish: Locating and Quantifying Damaging Shear Stresses. Environ. Manag. 2006, 37, 898–906. [Google Scholar] [CrossRef]
- George, S.D.; Baldigo, B.P.; Smith, M.J.; McKeown, D.M.; Faulring, J.W. Variations in water temperature and implications for trout populations in the Upper Schoharie Creek and West Kill, New York, USA. J. Freshw. Ecol. 2015, 31, 93–108. [Google Scholar] [CrossRef]
- Colotelo, A.H.; Goldman, A.E.; Wagner, K.A.; Brown, R.S.; Deng, Z.D.; Richmond, M.C. A comparison of metrics to evaluate the effects of hydro-facility passage stressors on fish. Environ. Rev. 2017, 25, 1–11. [Google Scholar] [CrossRef]
- Čada, G.F. The development of advanced hydroelectric turbines to improve fish passage survival. Fisheries 2001, 26, 14–23. [Google Scholar] [CrossRef]
- Uria-Martinez, R.; Johnson, M.M.; O’Connor, P.W.; Samu, N.M.; Witt, A.M.; Battey, H.; Welch, T.; Bonnet, M.; Wagoner, S. 2017 Hydropower Market Report; EERE: Oak Ridge, TN, USA, 2018. [Google Scholar]
- Fu, T.; Deng, Z.D.; Duncan, J.P.; Zhou, D.; Carlson, T.J.; Johnson, G.E.; Hou, H. Assessing hydraulic conditions through Francis turbines using an autonomous sensor device. Renew. Energy 2016, 99, 1244–1252. [Google Scholar] [CrossRef]
- Martinez, J.J.; Deng, Z.D.; Titzler, P.S.; Duncan, J.P.; Lu, J.; Mueller, R.P.; Tian, C.; Trumbo, B.A.; Ahmann, M.L.; Renholds, J.F. Hydraulic and biological characterization of a large Kaplan turbine. Renew. Energy 2019, 131, 240–249. [Google Scholar] [CrossRef]
- EPRI, (Electric Power Research Institute). Evaluation of the Effects of Turbine Blade Leading Edge Design on Fish Survival; EPRI: Palo Alto, CA, USA, 2008; Volume 5. [Google Scholar]
- Bevelhimer, M.S.; Pracheil, B.M.; Fortner, A.M.; Saylor, R.; Deck, K.L. Mortality and Injury Assessment for Three Species of Fish Exposed to Simulated Turbine Blade Strike. Can. J. Fish. Aquat. Sci. 2019, 76, 2350–2363. [Google Scholar] [CrossRef]
- EPRI, (Electric Power Research Institute). 2010 Tests Examining Survival of Fish Struck By Turbine Blades; EPRI: Palo Alto, CA, USA, 2011; Volume 12. [Google Scholar]
- Saylor, R.; Fortner, A.; Bevelhimer, M. Quantifying mortality and injury susceptibility for two morphologically disparate fishes exposed to simulated turbine blade strike. Hydrobiologia 2019, 842, 55–75. [Google Scholar] [CrossRef]
- Turnpenny, A.W.H. Mechanisms of Fish Damage in Low Head Turbines: An Experimental Appraisal. In Fish Migration and Fish Bypasses; Jungwirth, M., Schmutz, S., Weiss, S., Eds.; Blackwell Publishing Ltd.: Malden, MA, USA, 1998; pp. 300–314. [Google Scholar]
- Turnpenny, A.W.H.; Davis, M.H.; Fleming, J.M.; Davies, J.K. Experimental Studies Relating to the Passage of Fish and Shrimps Through Tidal Power Turbines; CORE: Southampton, UK, 1992. [Google Scholar]
- Romero-Gomez, P.; Richmond, M.C. Movement and collision of Lagrangian particles in hydro-turbine intakes: A case study. J. Hydraul. Res. 2017, 1686, 1–15. [Google Scholar] [CrossRef]
- Harding, S.F.; Richmond, M.C.; Mueller, R.P. Experimental observation of inertial particles through idealized hydroturbine distributor geometry. Water 2019, 11, 471. [Google Scholar] [CrossRef]
- Nelson, J.S.; Grande, T.C.; Wilson, M.V.H. Fishes of the World, 5th ed.; John Wiley & Sons: Hoboken, NJ, USA, 2016. [Google Scholar]
- Pracheil, B.M.; McManamay, R.A.; Bevelhimer, M.S.; DeRolph, C.R.; Čada, G.F. A traits-based approach for prioritizing species for monitoring and surrogacy selection. Endanger. Species Res. 2016, 31, 243–258. [Google Scholar] [CrossRef]
- Čada, G.F.; Schweizer, P.E. The Application of Traits-Based Assessment Approaches to Estimate the Effects of Hydroelectric Turbine Passage on Fish Populations; Oak Ridge National Laboratory: Oak Ridge, TN, USA, 2012; Volume 4. [Google Scholar]
- Grubbs, R.D.; Kraus, R.T. Fish Migration. In Encyclopedia of Animal Behavior; Breed, M.D., Moore, J., Eds.; Elsevier Academic Press: San Diego, CA, USA, 2010; pp. 715–724. [Google Scholar]
- Binder, T.R.; Cooke, S.J.; Hinch, S.G. Physiological Specializations of Different Fish Groups: Fish Migrations. In Encyclopedia of Fish Physiology: From Genome to Environment; Farrell, A.P., Cech, J.J., Jr., Richards, J.G., Stevens, E.D., Eds.; Elsevier Inc.: San Diego, CA, USA, 2011; pp. 1921–1952. [Google Scholar]
- Waldman, J.R.; Limburg, K.E. The world’s shads: Summary of their status, conservation, and research needs. In Biodiversity, Status, and Conservation of the World’s Shads; Symposium 35; Limburg, K.E., Waldman, J.R., Eds.; American Fisheries Society: Bethesda, MD, USA, 2003; pp. 363–369. [Google Scholar]
- Sneddon, L.U. Clinical Anesthesia and Analgesia in. J. Exot. Pet Med. 2012, 21, 32–43. [Google Scholar] [CrossRef]
- Javahery, S.; Nekoubin, H.; Moradlu, A.H. Effect of anaesthesia with clove oil in fish (review). Fish Physiol. Biochem. 2012, 38, 1545–1552. [Google Scholar] [CrossRef]
- Priborsky, J.; Velisek, J. A Review of Three Commonly Used Fish Anesthetics. Rev. Fish. Sci. Aquac. 2018, 26, 417–442. [Google Scholar] [CrossRef]
- Ritz, C.; Baty, F.; Streibig, J.C.; Gerhard, D. Dose-response analysis using R. PLoS ONE 2015, 10, 1–13. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Stastical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2019. [Google Scholar]
- Barton, K. MuMIn: Multi-Model Interfernce. Available online: https://cran.r-project.org/package=MuMIn (accessed on 21 December 2019).
- Sakamoto, Y.; Ishiguro, M.; Kitagawa, G. Akaike Information Criterion Statistics; KTK Scientific Publishers: Tokyo, Japan, 1986. [Google Scholar]
- Cone, R.S. The Need to Reconsider the Use of Condition Indices in Fishery Science. Trans. Am. Fish. Soc. 1989, 118, 510–514. [Google Scholar] [CrossRef]
- U.S. Fish and Wildlife Service. Recovery Plan for the Coterminous United States Population of Bull Trout (Salvelinus Confluentus); U.S. Fish and Wildlife Service: Portland, OR, USA, 2015; Volume 179.
- Dunham, J.B.; Rieman, B.E. Metapopulation structure of bull trout: Influences of physical, biotic, and geometrical landscape characteristics. Ecol. Appl. 1999, 9, 642–655. [Google Scholar] [CrossRef]
- Richmond, M.C.; Serkowski, J.A.; Radowski, C.; Strickler, B.; Weisbeck, M.; Dotson, C. Computational Tools to Assess Turbine Biological Performance. Hydroreview 2014, 33, 1–6. [Google Scholar]
- Hou, H.; Deng, Z.; Martinez, J.; Fu, T.; Duncan, J.; Johnson, G.; Lu, J.; Skalski, J.; Townsend, R.; Tan, L. A Hydropower Biological Evaluation Toolset (HBET) for Characterizing Hydraulic Conditions and Impacts of Hydro-Structures on Fish. Energies 2018, 11, 990. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).