Coupling SWAT Model and CMB Method for Modeling of High-Permeability Bedrock Basins Receiving Interbasin Groundwater Flow
Abstract
1. Introduction
2. Materials and Methods
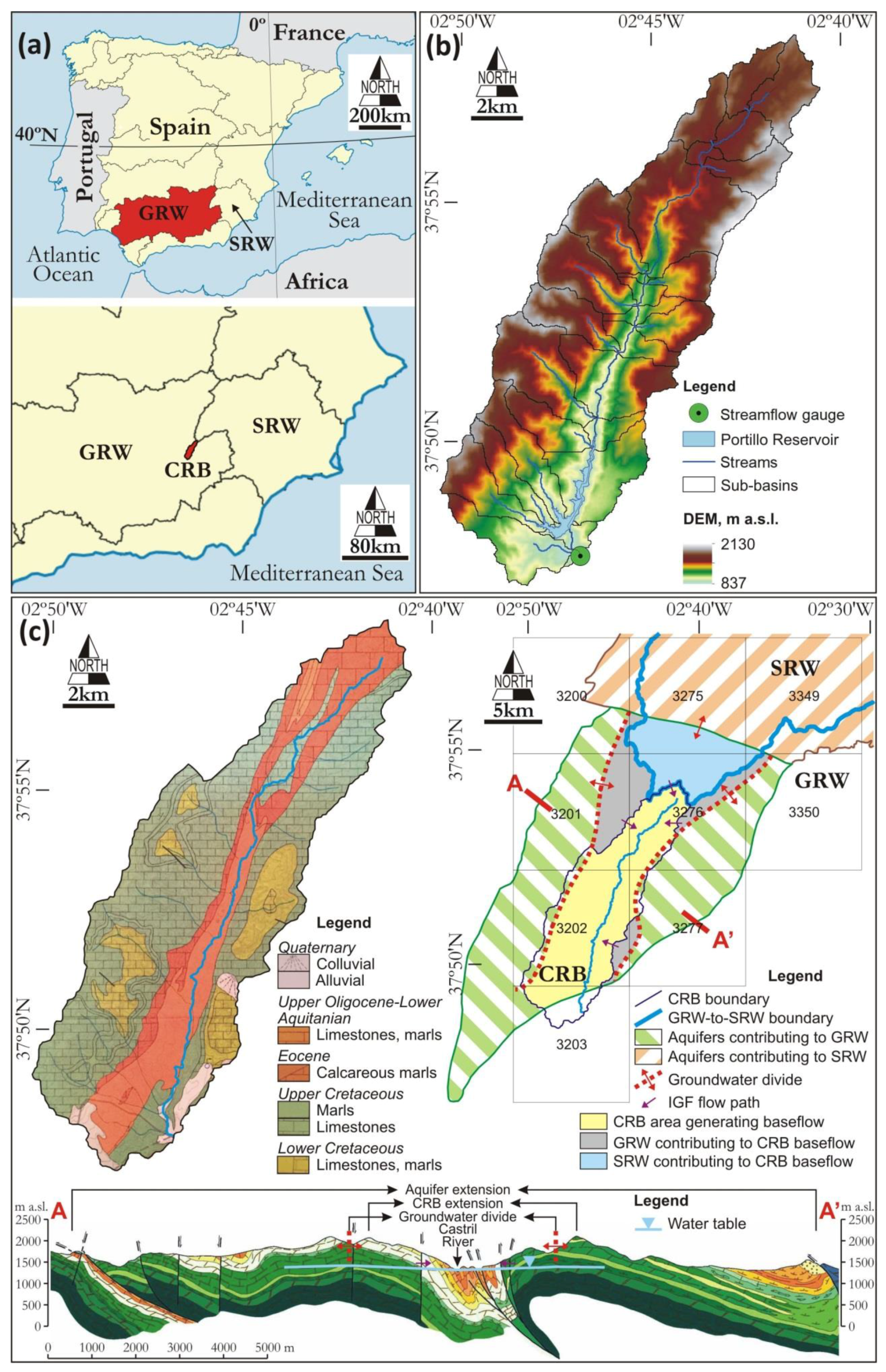
2.1. Study Area
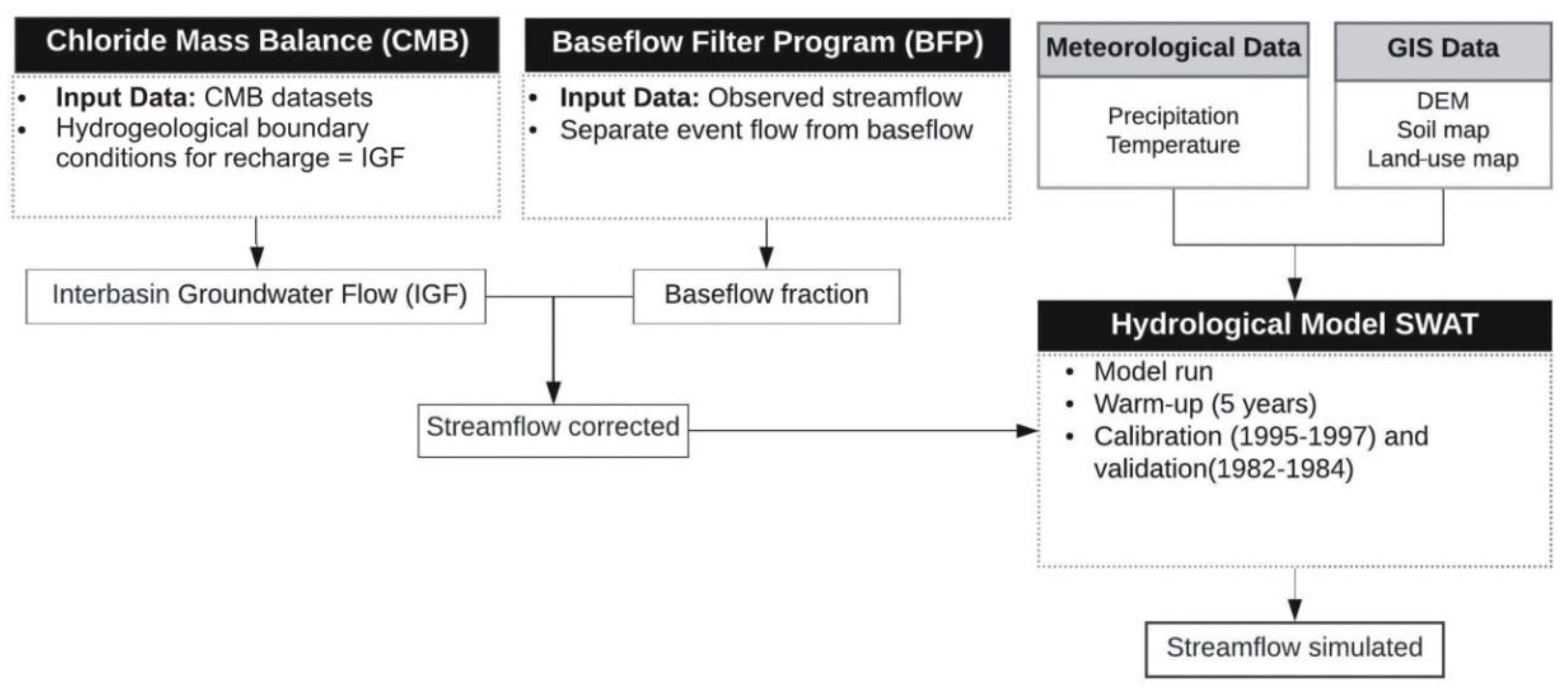
2.2. Overall Model Description
2.3. CMB Method
2.3.1. CMB Method Application for Aquifer Recharge over Continental Spain
2.3.2. IGF Series Generation
2.4. BFLOW Program
2.5. SWAT Model
2.5.1. Description of the SWAT Model
2.5.2. Data, Model Set-Up, Calibration, and Validation
3. Results and Discussion
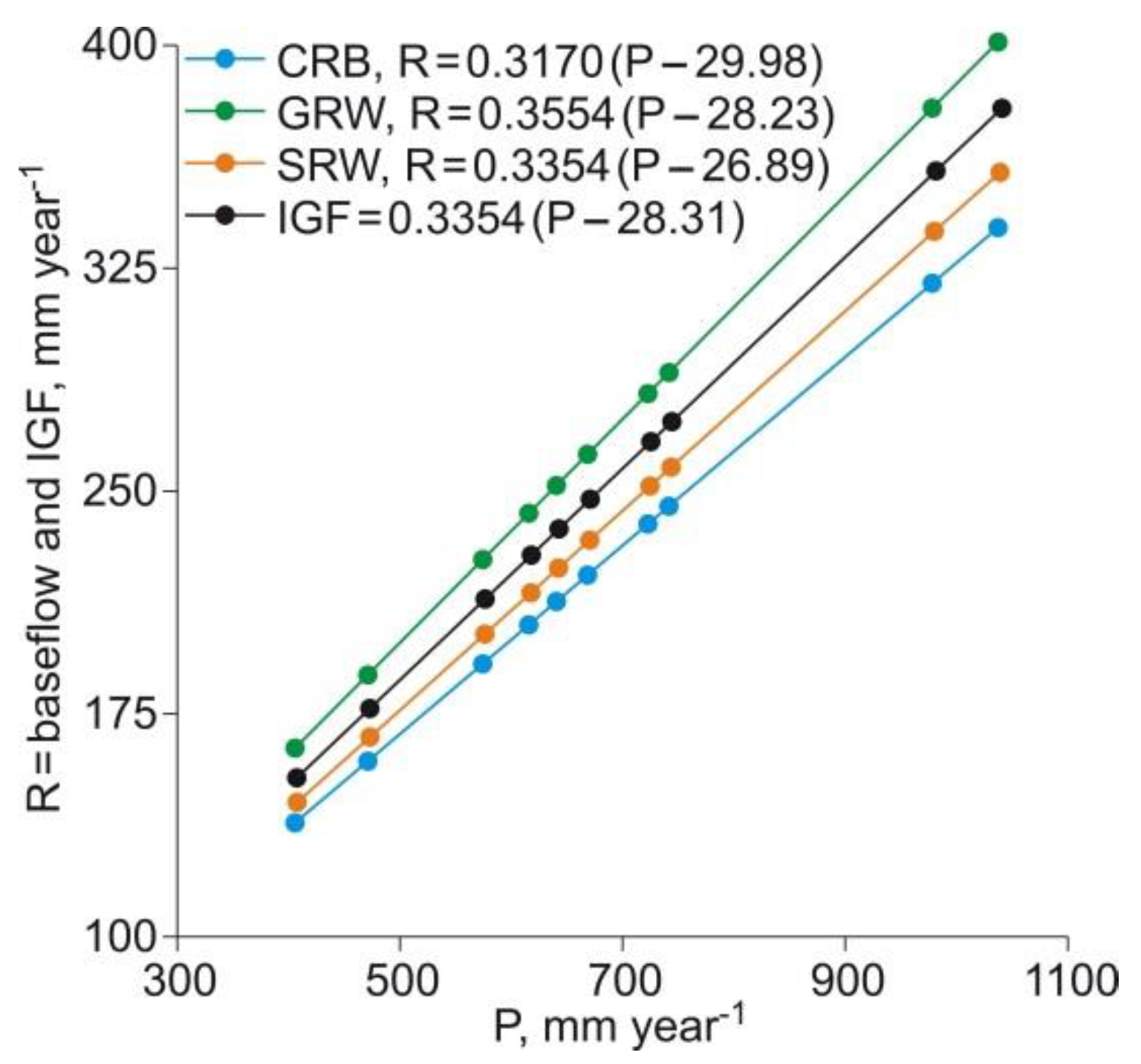
3.1. Using the CMB Datasets to Estimate IGF
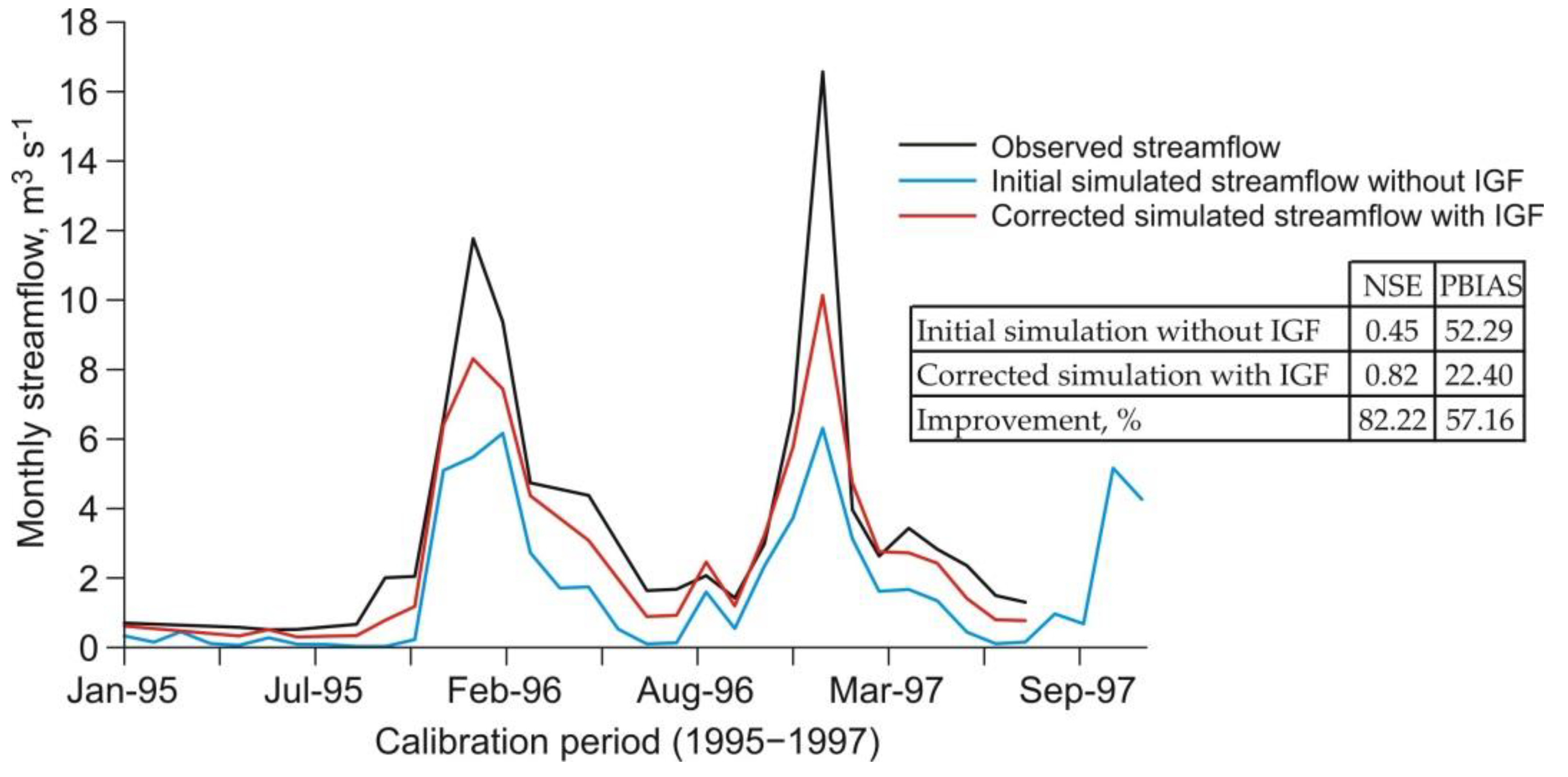
3.2. Comparison of SWAT Model Results with and without IGF
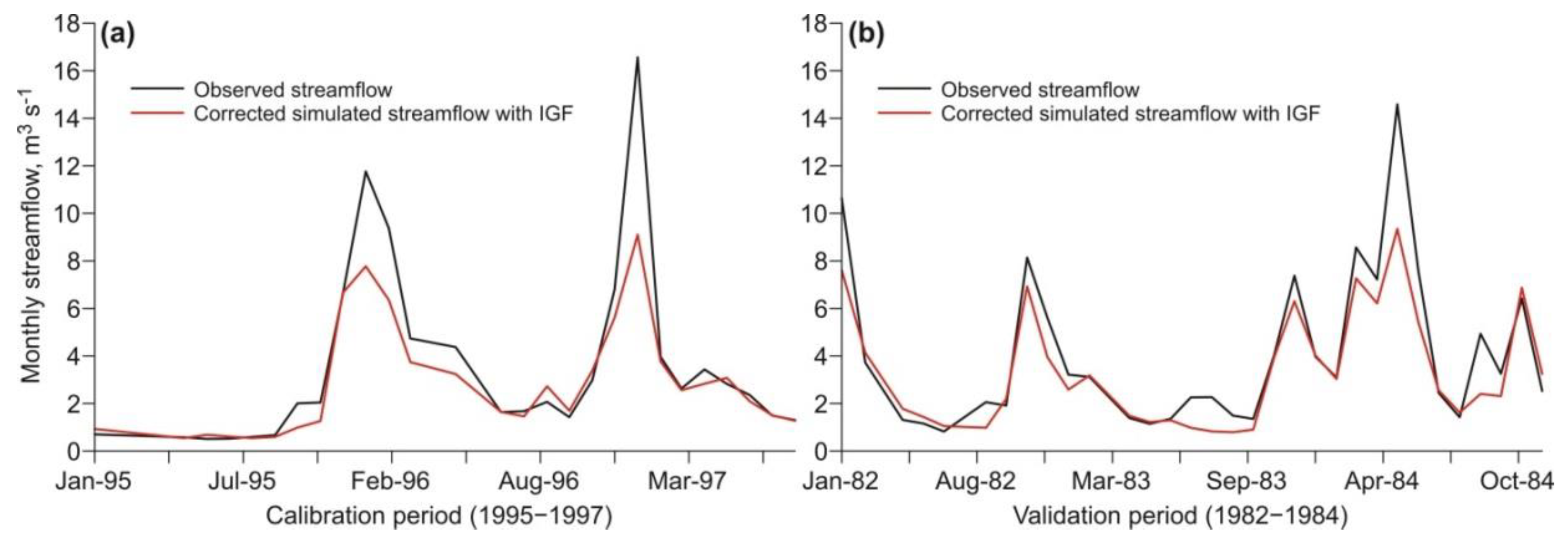
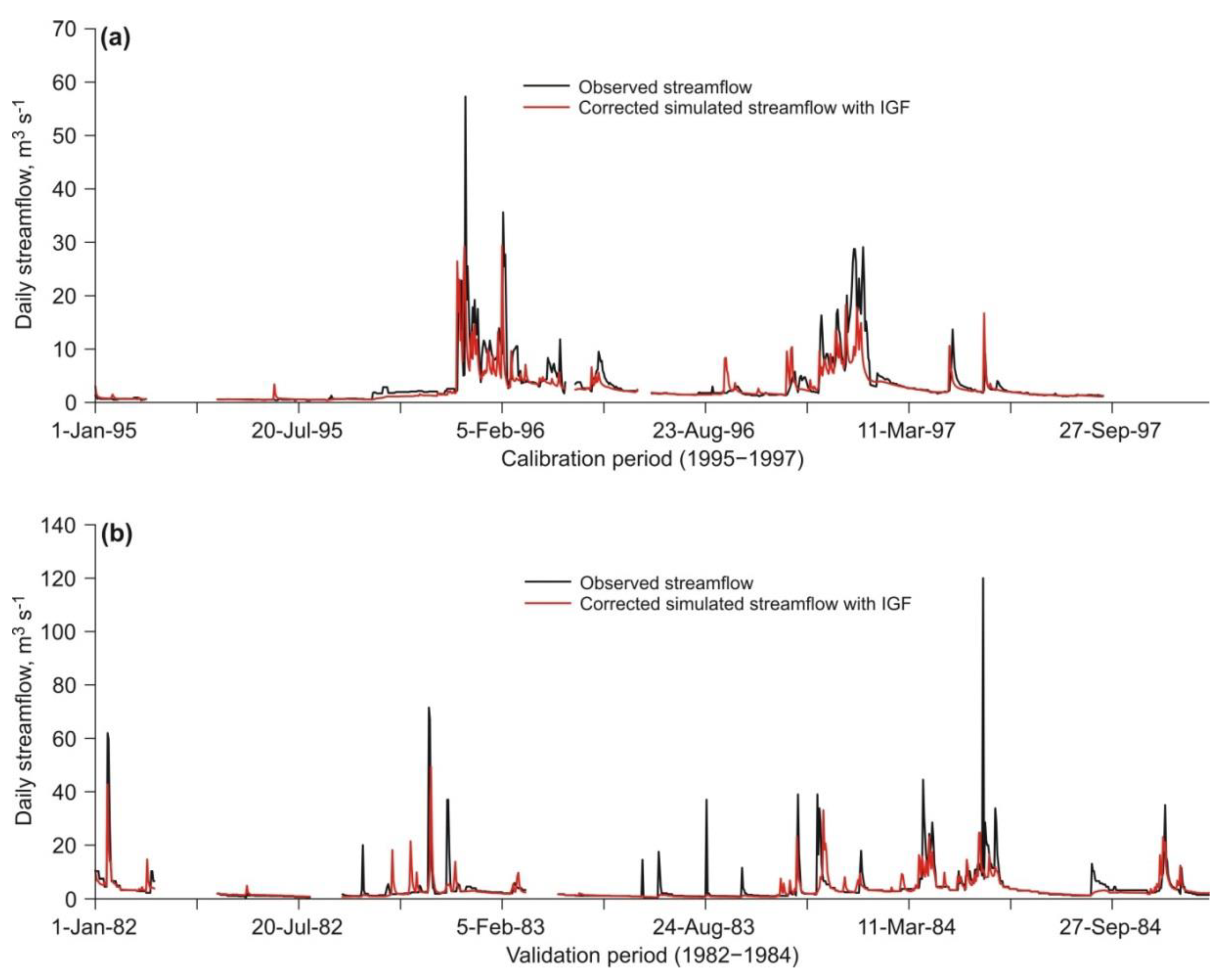
3.3. Calibration and Validation of SWAT Model Including IGF
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Trolle, D.; Hamilton, D.P.; Hipsey, M.R.; Bolding, K.; Bruggeman, J.; Mooij, W.M.; Janse, J.H.; Nielsen, A.; Jeppesen, E.; Elliott, A.; et al. A community–based framework for aquatic ecosystem models. Hydrobiologia 2012, 683, 25–34. [Google Scholar] [CrossRef]
- Hojberg, A.L.; Refsgaard, J.C. Model uncertainty-parameter uncertainty versus conceptual models. Water Sci. Technol. 2005, 52, 177–186. [Google Scholar] [CrossRef] [PubMed]
- Beven, K. Towards integrated environmental models of everywhere: Uncertainty, data and modelling as a learning process. Hydrol. Earth Syst. Sci. 2007, 11, 460–467. [Google Scholar] [CrossRef]
- Alcalá, F.J.; Martínez-Valderrama, J.; Robles-Marín, P.; Guerrera, F.; Martín-Martín, M.; Raffaelli, G.; Tejera de León, J.; Asebriy, L. A hydrological-economic model for sustainable groundwater use in sparse-data drylands: Application to the Amtoudi Oasis in southern Morocco, northern Sahara. Sci. Total Environ. 2015, 537, 309–322. [Google Scholar] [CrossRef]
- Francesconi, W.; Srinivasan, R.; Pérez-Miñana, E.; Willcock, S.P.; Quintero, M. Using the Soil and Water Assessment Tool (SWAT) to model ecosystem services: A systematic review. J. Hydrol. 2016, 535, 625–636. [Google Scholar] [CrossRef]
- Arnold, J.G.; Srinivasan, R.; Muttiah, R.S.; Williams, J.R. Large area hydrologic modeling and assessment Part I: Model development. J. Am. Water Resour. Assoc. 1998, 34, 73–89. [Google Scholar] [CrossRef]
- Molina-Navarro, E.; Andersen, H.E.; Nielsen, A.; Thodsen, H.; Trolle, D. Quantifying the combined effects of land use and climate changes on stream flow and nutrient loads: A modelling approach in the Odense Fjord catchment (Denmark). Sci. Total Environ. 2018, 621, 253–264. [Google Scholar] [CrossRef]
- Blanco-Gómez, P.; Jimeno-Sáez, P.; Senent-Aparicio, J.; Pérez-Sánchez, J. Impact of Climate Change on Water Balance Components and Droughts in the Guajoyo River Basin (El Salvador). Water 2019, 11, 2360. [Google Scholar] [CrossRef]
- Senent-Aparicio, J.; Liu, S.; Pérez-Sánchez, J.; López-Ballesteros, A.; Jimeno-Sáez, P. Assessing Impacts of Climate Variability and Reforestation Activities on Water Resources in the Headwaters of the Segura River Basin (SE Spain). Sustainability 2018, 10, 3277. [Google Scholar] [CrossRef]
- Fu, B.; Merritt, W.S.; Croke, B.F.W.; Weber, T.R.; Jakeman, A.J. A review of catchment-scale water quality and erosion models and a synthesis of future prospects. Environ. Model. Softw. 2019, 114, 75–97. [Google Scholar] [CrossRef]
- Luo, Y.; Arnold, J.; Allen, P.; Chen, X. Baseflow simulation using SWAT model in an inland river basin in Tianshan Mountains, Northwest China. Hydrol. Earth Syst. Sci. 2012, 16, 1259–1267. [Google Scholar] [CrossRef]
- Ficklin, D.L.; Luo, Y.; Zhang, M. Watershed Modelling of Hydrology and Water Quality in the Sacramento River Watershed, California. Hydrol. Process. 2012, 27, 236–250. [Google Scholar] [CrossRef]
- Genereux, D.P.; Jordan, M.T.; Carbonell, D. A pired-watershed budget study to quantify interbasin groundwater flow in a lowland rain forest. Costa Rica. Water Resour. Res. 2005, 41, W04011. [Google Scholar] [CrossRef]
- Nguyen, V.T.; Dietrich, J.; Uniyal, B. Modeling interbasin groundwater flow in karst areas: Model development, application, and calibration strategy. Environ. Modell. Softw. 2020, 124, 104606. [Google Scholar] [CrossRef]
- Zanon, C.; Genereux, D.P.; Oberbauer, S.F. Use of a watershed hydrologic model to estimate interbasin groundwater flow in a Costa Rican rainforest. Hydrol. Process. 2014, 28, 3670–3680. [Google Scholar] [CrossRef]
- Rahayuningtyas, C.; Wu, R.S.; Anwar, R.; Chiang, L.C. Improving avswat stream flow simulation by incorporating groundwater recharge prediction in the upstream Lesti watershed, East Java, Indonesia. Terr. Atmos. Ocean. Sci. 2014, 25, 881–892. [Google Scholar] [CrossRef]
- Han, M.; Zhao, C.Y.; Šimůnek, J.; Feng, G. Evaluating the impact of groundwater on cotton growth and root zone water balance using Hydrus-1D coupled with a crop growth model. Agric. Water Manag. 2015, 160, 64–75. [Google Scholar] [CrossRef]
- Obuobie, E. Estimation of Groundwater Recharge in the Context of Future Climate Change in the White Volta River Basin, West Africa. Germany. Ph.D. Thesis, Rheinischen Friedrich-Wilhelms-Universität, Bonn, Germany, 2008; 165p. [Google Scholar]
- Alcalá, F.J.; Martín-Martín, M.; Guerrera, F.; Martínez-Valderrama, J.; Marín, P.R. A feasible methodology for groundwater resource modelling for sustainable use in sparse-data drylands: Application to the Amtoudi Oasis in the northern Sahara. Sci. Total Environ. 2018, 630, 1246–1257. [Google Scholar] [CrossRef]
- Kim, N.W.; Chung, I.M.; Won, Y.S.; Arnold, J.G. Development and application of the integrated SWAT-MODFLOW model. J. Hydrol. 2008, 356, 1–16. [Google Scholar] [CrossRef]
- Bouaziz, L.; Weerts, A.; Schellekens, J.; Sprokkereef, E.; Stam, J.; Savenije, H.; Hrachowitz, M. Redressing the balance: Quantifying net intercatchment groundwater flows. Hydrol. Earth Syst. Sci. 2018, 22, 6415–6434. [Google Scholar] [CrossRef]
- Palanisamy, B.; Workman, S.R. Hydrologic modeling of flow through sinkholes located in streambeds of Cane Run stream, Kentucky. J. Hydrol. Eng. 2014, 20, 04014066. [Google Scholar] [CrossRef]
- Malagó, A.; Efstathiou, D.; Bouraoui, F.; Nikolaidis, N.P.; Franchini, M.; Bidoglio, G.; Kritsotakis, M. Regional scale hydrologic modeling of a karst-dominant geomorphology: The case study of the island of Crete. J. Hydrol. 2016, 540, 64–81. [Google Scholar] [CrossRef]
- Baffaut, C.; Benson, V.W. Modeling flow and pollutant transport in a karst watershed with SWAT. Trans. ASABE 2009, 52, 469–479. [Google Scholar] [CrossRef]
- Nikolaidis, N.P.; Bouraoui, F.; Bidoglio, G. Hydrologic and geochemical modeling of a karstic Mediterranean watershed. J. Hydrol. 2013, 477, 129–138. [Google Scholar] [CrossRef]
- Alcalá, F.J.; Cantón, Y.; Contreras, S.; Were, A.; Serrano-Ortiz, P.; Puigdefábregas, J.; Solé-Benet, A.; Custodio, E.; Domingo, F. Diffuse and concentrated recharge evaluation using physical and tracer techniques: Results from a semiarid carbonate massif aquifer in southeastern Spain. Environ. Earth Sci. 2011, 63, 541–557. [Google Scholar] [CrossRef]
- Andreu, J.M.; Alcalá, F.J.; Vallejos, Á.; Pulido-Bosch, A. Recharge to aquifers in SE Spain: Different approaches and new challenges. J. Arid Environ. 2011, 75, 1262–1270. [Google Scholar] [CrossRef]
- Rutledge, A.T.; Mesko, T.O. Estimated Hydrologic Characteristics of Shallow Aquifer Systems in the Valley and Ridge, the Blue Ridge, and the Piedmont Physiographic Provinces Based on Analysis of Streamflow Recession and Base Flow; U.S. Geological Survey: Reston, VA, USA, 1996; 58p.
- Lim, K.J.; Engel, B.A.; Tang, Z.; Choi, J.; Kim, K.S.; Muthukrishnan, S.; Tripathy, D. Automated web GIS based hydrograph analysis tool, WHAT. J. Am. Water Resour. Assoc. 2005, 1407–1416. [Google Scholar] [CrossRef]
- Plesca, I.; Timbe, E.; Exbrayat, J.-F.; Windhorst, D.; Kraft, P.; Crespo, P.; Vaché, K.B.; Frede, H.-G.; Breuer, L. Model intercomparison to explore catchment functioning: Results from a remote montane tropical rainforest. Ecol. Model. 2012, 239, 3–13. [Google Scholar] [CrossRef]
- Lee, J.; Kim, J.; Jang, W.S.; Lim, K.J.; Engel, B.A. Assessment of Baseflow Estimates Considering Recession Characteristics in SWAT. Water 2018, 10, 371. [Google Scholar] [CrossRef]
- Lerner, D.N.; Issar, A.S.; Simmers, I. Groundwater recharge. A guide to understanding and estimating natural recharge. In IAH International Contributions to Hydrogeology; Heise: Hannover, Germany, 1990; 345p. [Google Scholar]
- Batelaan, O.; De Smedt, F. GIS-based recharge estimation by coupling surface-subsurface water balances. J. Hydrol. 2007, 337, 337–355. [Google Scholar] [CrossRef]
- Alcalá, F.J.; Custodio, E. Spatial average aquifer recharge through atmospheric chloride mass balance and its uncertainty in continental Spain. Hydrol. Process. 2014, 28, 218–236. [Google Scholar] [CrossRef]
- Scanlon, B.R.; Healy, R.W.; Cook, P.G. Choosing appropriate techniques for quantifying groundwater recharge. Hydrogeol. J. 2002, 10, 18–39. [Google Scholar] [CrossRef]
- McMahon, P.B.; Plummer, L.N.; Bohlke, J.K.; Shapiro, S.D.; Hinkle, S.R. A comparison of recharge rates in aquifers of the United States based on groundwater-based data. Hydrogeol. J. 2011, 19, 779–800. [Google Scholar] [CrossRef]
- Claasen, H.C.; Reddy, M.M.; Halm, D.R. Use of the chloride ion in determining hydrologic-basin water budgets: A 3-year case study in the San Juan Mountains, Colorado, USA. J. Hydrol. 1986, 85, 49–71. [Google Scholar] [CrossRef]
- Dettinger, M.D. Reconnaissance estimates of natural recharge to desert basins in Nevada, USA, by using chloride-balance calculations. J. Hydrol. 1989, 106, 55–78. [Google Scholar] [CrossRef]
- Wood, W.W.; Sanford, W.E. Chemical and isotopic methods for quantifying ground-water recharge in a regional, semiarid environment. Ground Water 1995, 33, 458–468. [Google Scholar] [CrossRef]
- Sami, K.; Hughes, D.A. A comparison of recharge estimates to a fractured sedimentary aquifer in South Africa from a chloride mass balance and an integrated surface-subsurface model. J. Hydrol. 1996, 179, 111–136. [Google Scholar] [CrossRef]
- Scanlon, B.R.; Keese, K.E.; Flint, A.L.; Flint, L.E.; Gaye, C.B.; Edmunds, W.M.; Simmers, I. Global synthesis of groundwater recharge in semiarid and arid regions. Hydrol. Process. 2006, 20, 3335–3370. [Google Scholar] [CrossRef]
- Alcalá, F.J.; Custodio, E. Natural uncertainty of spatial average aquifer recharge through atmospheric chloride mass balance in continental Spain. J. Hydrol. 2015, 524, 642–661. [Google Scholar] [CrossRef]
- Paz, C.; Alcalá, F.J.; Carvalho, J.M.; Ribeiro, L. Current uses of ground penetrating radar in groundwater-dependent ecosystems research. Sci. Total Environ. 2017, 595, 868–885. [Google Scholar] [CrossRef]
- Capel-Molina, J.J. Los Climas de España; Oikos-Tau: Barcelona, Spain, 1981; 403p. [Google Scholar]
- Trigo, R.; Pozo-Vázquez, D.; Osborn, T.; Castro-Díez, Y.; Gámiz-Fortis, S.; Esteban-Parra, M. North Atlantic oscillation influence on precipitation, river flow and water resources in the Iberian peninsula. Int. J. Climatol. 2004, 24, 925–944. [Google Scholar] [CrossRef]
- Vanderlinden, K.; Giraldez, J.V.; Van Meirvenne, M. Assessing Reference Evapotranspiration by the Hargreaves Method in Southern Spain. J. Irrig. Drain. Eng. 2004, 130, 184–191. [Google Scholar] [CrossRef]
- Azéma, J.; Foucault, A.; Fourcade, E.; García–Hernández, M.; González–Donoso, J.M.; Linares, D.; López–García, A.C.; Rivas, P.; Vera, J.A. Las Microfacies del Jurásico y Cretácico de las Zonas Externas de las Cordilleras Béticas; Servicio de Publicaciones de la Universidad de Granada: Granada, Spain, 1979. [Google Scholar]
- Vera, J.A. Geología de España, 1st ed.; Sociedad Geológica de España e Instituto Geológico y Minero de España, Ministerio de Educación y Ciencia: Madrid, Spain, 2004; 884p. [Google Scholar]
- Sanz de Galdeano, C.; Peláez, J.A. La Cuenca de Guadix–Baza. Estructura, Tectónica Activa, Sismicidad, Geomorfología y Dataciones Existentes; Universidad de Granada–CSIC: Granada, Spain, 2007; 351p. [Google Scholar]
- IGME. Hydrogeological Map of Spain, Scale 1:200,000; Sheet nº 78, Baza; Geological Survey of Spain, Memory and Maps. 1988. Available online: http://info.igme.es/cartografiadigital/tematica/Hidrogeologico200.aspx (accessed on 20 January 2020).
- IGME. Hydrogeological Map of Spain, Scale 1:200,000. Sheet nº 71, Villacarrillo; Geological Survey of Spain, Memory and Maps. 1995. Available online: http://info.igme.es/cartografiadigital/tematica/Hidrogeologico200.aspx (accessed on 20 January 2020).
- IGME. Proyecto para la actualización de la infraestructura hidrogeológica de las Unidades 05.01 Sierra de Cazorla, 05.02 Quesada-Castril, 07.07 Sierras de Segura-Cazorla y el Carbonatado de la Loma de Úbeda; Geological Survey of Spain and General Directorate for Water Planning; Ministry of Industry: Madrid, Spain, 2001. (In Spanish) [Google Scholar]
- Peralta-Maraver, I.; López-Rodríguez, M.J.; de Figueroa, J.T. Structure, dynamics and stability of a Mediterranean river food web. Mar. Freshwater Res. 2017, 68, 484–495. [Google Scholar] [CrossRef]
- Alcalá, F.J.; Custodio, E. Atmospheric chloride deposition in continental Spain. Hydrol. Process. 2008, 22, 3636–3650. [Google Scholar] [CrossRef]
- Alcala, F.J.; Custodio, E. Using the Cl/Br ratio as a tracer to identify the origin of salinity in aquifers in Spain and Portugal. J. Hydrol. 2008, 359, 189–207. [Google Scholar] [CrossRef]
- Hurrell, J.W. Decadal trends in the North Atlantic Oscillation, regional temperatures and precipitation. Nature 1995, 269, 676–679. [Google Scholar] [CrossRef]
- Raposo, J.R.; Dafonte, J.; Molinero, J. Assessing the impact of future climate change on groundwater recharge in Galicia-Costa, Spain. Hydrogeol. J. 2013, 21, 459–479. [Google Scholar] [CrossRef]
- Barberá, J.A.; Jódar, J.; Custodio, E.; González-Ramón, A.; Jiménez-Gavilán, P.; Vadillo, I.; Pedrera, A.; Martos-Rosillo, S. Groundwater dynamics in a hydrologically-modified alpine watershed from an ancient managed recharge system (Sierra Nevada National Park, Southern Spain): Insights from hydrogeochemical and isotopic information. Sci. Total Environ. 2018, 640–641, 874–893. [Google Scholar] [CrossRef]
- Pulido-Velazquez, D.; Collados-Lara, A.J.; Alcalá, F.J. Assessing impacts of future potential climate change scenarios on aquifer recharge in continental Spain. J. Hydrol. 2018, 567, 803–819. [Google Scholar] [CrossRef]
- Nathan, R.J.; McMahon, T.A. Evaluation of automated techniques for base-flow and recession analyses. Water Resour. Res. 1990, 26, 1465–1473. [Google Scholar] [CrossRef]
- Arnold, J.G.; Allen, P.M.; Muttiah, R.; Bernhardt, G. Automated Base Flow Separation and Recession Analysis Techniques. Ground Water 1995, 33, 1010–1018. [Google Scholar] [CrossRef]
- Meaurio, M.; Zabaleta, A.; Angel, J.; Srinivasan, R.; Antigüedad, I. Evaluation of SWAT models performance to simulate streamflow spatial origin. The case of a small forested watershed. J. Hydrol. 2015, 525, 326–334. [Google Scholar] [CrossRef]
- Arnold, J.G.; Allen, P.M. Automated Methods for Estimating Baseflow and Ground Water Recharge from Streamflow Records. JAWRA J. Am. Water Resour. Assoc. 1999, 35, 411–424. [Google Scholar] [CrossRef]
- Senent-Aparicio, J.; Pérez-Sánchez, J.; Carrillo-García, J.; Soto, J. Using SWAT and Fuzzy TOPSIS to Assess the Impact of Climate Change in the Headwaters of the Segura River Basin (SE Spain). Water 2017, 9, 149. [Google Scholar] [CrossRef]
- Jimeno-Sáez, P.; Senent-Aparicio, J.; Pérez-Sánchez, J.; Pulido-Velazquez, D. A Comparison of SWAT and ANN models for daily runoff simulation in different climatic zones of peninsular Spain. Water 2018, 10, 192. [Google Scholar] [CrossRef]
- Abbaspour, K.C.; Rouholahnejad, E.; Vaghefi, S.; Srinivasan, R.; Yang, H.; Kløve, B. A continental-scale hydrology and water quality model for Europe: Calibration and uncertainty of a high-resolution large-scale SWAT model. J. Hydrol. 2015, 524, 733–752. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Wilson, B.N.; Douglas-Mankin, K.R.; Arnold, J.G.; Gowda, P.H. Hydrologic and water quality models: Use, calibration, and validation. Trans. ASABE 2012, 55, 1241–1247. [Google Scholar] [CrossRef]
- Hargreaves, G.H.; Samani, Z.A. Estimating potential evapotranspiration. J. Irrig. Drain. Div. ASCE 1982, 108, 225–230. [Google Scholar]
- Arnold, J.G.; Kiniry, J.R.; Srinivasan, R.; Williams, J.R.; Haney, E.B.; Neitsch, S.L. Soil and Water Assessment Tool—Input/Output Documentation—Version 2012. Available online: http://swat.tamu.edu/documentation/ (accessed on 20 December 2019).
- Moral, F.; Cruz-Sanjulian, J.J.; Olias, M. Geochemical evolution of groundwater in the carbonate aquifers of Sierra de Segura (Betic Cordillera, Southern Spain). J. Hydrol. 2008, 360, 281–296. [Google Scholar] [CrossRef]
- Senent-Aparicio, J.; Jimeno-Sáez, P.; Bueno-Crespo, A.; Pérez-Sánchez, J.; Pulido-Velazquez, D. Coupling machine-learning techniques with SWAT model for instantaneous peak flow prediction. Biosyst. Eng. 2019, 177, 67–77. [Google Scholar] [CrossRef]
- Krause, P.; Boyle, D.P.; Base, F. Comparison of different efficiency criteria for hydrological model assessment. Adv. Geosci. 2005, 5, 89–97. [Google Scholar] [CrossRef]

| Statistic and Equation 1 | Description |
|---|---|
| NSE indicates a perfect match between observed and simulated data, and ranges from −∞ to 1. Higher than 0.5 is considered satisfactory. | |
| lnNSE is the logarithmic form of the model efficiency coefficient. NSE emphasizes the high flows, and lnNSE emphasizes the low flows. | |
| R2 indicates the degree of linear relationship between simulated and observed data, and ranges from 0 to 1. Higher than 0.5 is considered a satisfactory result. | |
| PBIAS calculates the average tendency of the simulated data to be higher or lower than their observed counterparts. The optimal value is 0, and an acceptable one is between ±25. | |
| RMSE = 0 indicates a perfect match between observed and simulated data. Increasing RMSE values indicate that matching is getting worse. | |
| RSR is RMSE relative to standard deviation of the observed data, and ranges from 0 to ∞. The lower the RSR, the lower the RMSE and the better the model performance. Lower than 0.7 is acceptable. |
| Cell 1 | CRB | GRW | SRW | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| S | P 2 | CVP | R | CVR | S | P | CVP | R | CVR | S | P | CVP | R | CVR | |
| 3200 | 3.2 | 894 | 0.31 | 315 | 0.27 | 0.8 | 894 | 0.31 | 315 | 0.27 | |||||
| 3201 | 10.4 | 909 | 0.33 | 332 | 0.27 | 20.2 | 909 | 0.33 | 332 | 0.27 | |||||
| 3202 | 60.6 | 693 | 0.34 | 229 | 0.28 | 4.8 | 693 | 0.34 | 229 | 0.28 | |||||
| 3203 | 7.1 | 486 | 0.35 | 143 | 0.27 | ||||||||||
| 3275 | 1.0 | 813 | 0.32 | 276 | 0.27 | 21.7 | 813 | 0.32 | 276 | 0.27 | |||||
| 3276 | 22.0 | 668 | 0.33 | 206 | 0.29 | 14.5 | 668 | 0.33 | 206 | 0.29 | 25.0 | 668 | 0.33 | 206 | 0.29 |
| 3277 | 1.8 | 517 | 0.35 | 153 | 0.30 | 1.1 | 517 | 0.35 | 153 | 0.30 | |||||
| 3349 | 0.1 | 687 | 0.32 | 212 | 0.27 | 0.5 | 687 | 0.32 | 212 | 0.27 | |||||
| 3350 | 2.0 | 612 | 0.33 | 186 | 0.28 | 0.5 | 612 | 0.33 | 186 | 0.28 | |||||
| Sum | 101.9 | 46.9 | 48.4 | ||||||||||||
| SWA 3 | 692 | 0.34 | 227 | 0.28 | 787 | 0.33 | 269 | 0.28 | 736 | 0.32 | 239 | 0.28 | |||
| Parameter 1 | CRB | GRW | SRW |
|---|---|---|---|
| Δm | −0.67 | −0.66 | −0.67 |
| Δσ | −0.73 | −0.71 | −0.72 |
| mC | 227 | 269 | 239 |
| σC | 63.1 | 74.9 | 66.8 |
| Year | P 1 | Psi 1 | R, CRB 1 | R, GRW | R, SRW | IGF, GRW+SRW 2 |
|---|---|---|---|---|---|---|
| 1996 | 1037.9 | 1.76 | 338.5 | 401.4 | 357.1 | 378.9 |
| 1997 | 978.9 | 1.47 | 319.8 | 379.2 | 337.3 | 357.9 |
| 1998 | 472.3 | −1.08 | 159.2 | 188.7 | 167.4 | 177.9 |
| 1999 | 575.4 | −0.56 | 191.9 | 227.5 | 202.0 | 214.6 |
| 2000 | 669.5 | −0.09 | 221.7 | 262.9 | 233.6 | 248.0 |
| 2001 | 742.6 | 0.28 | 244.9 | 290.4 | 258.1 | 274.0 |
| 2002 | 616.8 | −0.35 | 205.0 | 243.1 | 215.9 | 229.3 |
| 2003 | 723.7 | 0.19 | 238.9 | 283.3 | 251.8 | 267.3 |
| 2004 | 641.5 | −0.23 | 212.9 | 252.4 | 224.2 | 238.1 |
| 2005 | 406.9 | −1.40 | 138.5 | 164.1 | 145.5 | 154.7 |
| Mean 3 | 686.6 | 227.1 | 269.3 | 239.3 | 240.1 | |
| SD | 199.2 | 63.1 | 74.9 | 66.8 | 66.8 | |
| CV | 0.29 | 0.28 | 0.28 | 0.28 | 0.28 |
| Parameter 1 | Description | Range Used in Calibration | Fitted Value |
|---|---|---|---|
| r_CN2.mgt | Soil Conservation Service (SCS) runoff curve number | −0.1 to 0.1 | 0.08 |
| v_ALPHA_BF.gw | Baseflow alpha factor (day−1) | 0 to 1 | 0.11 |
| a_GW_DELAY.gw | Groundwater delay time (day) | 0 to 60 | 2.82 |
| a_GWQMN.gw | Threshold depth of water in the shallow aquifer for return flow to occur (mm) | −200 to 1000 | 898.00 |
| v_GW_REVAP.gw | Groundwater revap coefficient | 0.02 to 0.1 | 0.09 |
| a_RCHRG_DP.gw | Deep aquifer percolation fraction | −0.05 to 0.05 | 0.04 |
| a_REVAPMN.gw | Threshold depth of water in shallow aquifer for revap or percolation to deep aquifer to occur (mm) | −500 to 500 | −61.00 |
| v_CANMX.hru | Maximum canopy storage (mm) | 0 to 8 | 0.47 |
| v_EPCO.bsn | Plant uptake compensation factor | 0.5 to 1 | 0.56 |
| v_ESCO.bsn | Soil evaporation compensation factor | 0.3 to 0.8 | 0.61 |
| r_SOL_AWC.sol | Available water capacity of the soil layer (mm H2O/mm soil) | −0.02 to 0.02 | −0.02 |
| v_LAT_TTIME.hru | Lateral flow travel time (day) | 0 to 180 | 76.50 |
| v_SLSOIL.hru | Slope length for lateral subsurface flow (m) | 0 to 150 | 1.35 |
| r_SLSUBBSN.hru | Average slope length (m) | −0.5 to 0.5 | 0.08 |
| r_HRU_SLP.hru | Average slope steepness (m/m) | −0.5 to 0.5 | 0.40 |
| v_OV_N.hru | Manning’s ‘n’ value for overland flow | 0.01 to 1 | 0.61 |
| r_CH_S1.sub | Average slope of tributary channels (m/m). | −0.5 to 0.5 | 0.26 |
| v_CH_N1.sub | Manning’s ‘n’ value for the tributary channels | 0.01 to 30 | 1.68 |
| r_CH_S2.rte | Average slope of main channel along the channel length (m/m) | −0.5 to 0.5 | −0.04 |
| v_CH_N2.rte | Manning’s ‘n’ value for the main channel | 0.01 to 0.3 | 0.04 |
| v_SURLAG.bsn | Surface runoff lag coefficient | 0.05 to 24 | 20.71 |
| Statistic | Time Step | Calibration | Validation |
|---|---|---|---|
| NSE | Monthly | 0.77 | 0.8 |
| R2 | Monthly | 0.92 | 0.89 |
| PBIAS | Monthly | 19.82 | 17.25 |
| RSR | Monthly | 0.48 | 0.44 |
| lnNSE | Daily | 0.81 | 0.64 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Senent-Aparicio, J.; Alcalá, F.J.; Liu, S.; Jimeno-Sáez, P. Coupling SWAT Model and CMB Method for Modeling of High-Permeability Bedrock Basins Receiving Interbasin Groundwater Flow. Water 2020, 12, 657. https://doi.org/10.3390/w12030657
Senent-Aparicio J, Alcalá FJ, Liu S, Jimeno-Sáez P. Coupling SWAT Model and CMB Method for Modeling of High-Permeability Bedrock Basins Receiving Interbasin Groundwater Flow. Water. 2020; 12(3):657. https://doi.org/10.3390/w12030657
Chicago/Turabian StyleSenent-Aparicio, Javier, Francisco J. Alcalá, Sitian Liu, and Patricia Jimeno-Sáez. 2020. "Coupling SWAT Model and CMB Method for Modeling of High-Permeability Bedrock Basins Receiving Interbasin Groundwater Flow" Water 12, no. 3: 657. https://doi.org/10.3390/w12030657
APA StyleSenent-Aparicio, J., Alcalá, F. J., Liu, S., & Jimeno-Sáez, P. (2020). Coupling SWAT Model and CMB Method for Modeling of High-Permeability Bedrock Basins Receiving Interbasin Groundwater Flow. Water, 12(3), 657. https://doi.org/10.3390/w12030657








