A Normal Cloud Model-Based Method for Risk Assessment of Water Inrush and Its Application in a Super-Long Tunnel Constructed by a Tunnel Boring Machine in the Arid Area of Northwest China

Abstract

Tunnel water inrush is complex, fuzzy, and random, and it is affected by many factors, such as hydrology, geology, and construction. However, few papers have considered the impact of dynamic monitoring on water inrush in previous research. In this study, considering geological, hydrological, and construction factors, as well as dynamic monitoring, a new multi-index evaluation method is proposed to analyze the risk of tunnel water inrush based on the normal cloud model. A new weight algorithm combining analytic hierarchy process and entropy method is used to calculate the index weight. The certainty degree of each evaluation index belonging to the corresponding cloud can be obtained by the cloud model theory. The final level of tunnel water inrush is determined via the synthetic certainty degree. The proposed method is applied to analyze the risk of water inrush in the SS (Shuang-san) tunnel constructed by a tunnel boring machine in the arid area of Northwest China. The evaluation results are not only basically identical to the results calculated by the ideal point and gray relation projection methods, but also agree well with the actual excavation results. This demonstrates that this new risk assessment method of water inrush has high accuracy and feasibility. Simultaneously, it also provides a new research idea to analyze the probability of tunnel water inrush and can provide a reference for related projects.

1. Introduction

Water inrush has great perniciousness in tunnel excavation [1,2]; particularly for a tunnel constructed by a tunnel boring machine (TBM), it may not only submerge the mechanical equipment of the TBM, which is worth tens of millions of dollars, but also seriously endanger the safety and life of the builders in the tunnel [3,4]. For the construction of tunnels in arid areas, water inrush also leads to a decline in groundwater level, surface vegetation degradation, and land desertification [5]. Therefore, predicting the risk of water inrush and reducing its harm are of great significance for regional sustainable development.

Water inrush in tunnels is affected by many factors, such as hydrology, geology, and construction, and it is complex, fuzzy, and random. In recent years, many researchers and engineers have made great efforts to assess the risk of tunnel water inrush, and have developed various methods of analysis, including the geological analysis method [6], the analytic hierarchy process (AHP) method [7,8], the neural network method [9,10], the geographic information system (GIS) method [11,12], and the fuzzy synthetic evaluation method [13,14]. Although these methods provide a theoretical basis to analyze the risk of water inrush, there still have some shortcomings. For example, due to the limitation of previous exploration technology, the geological analysis method cannot accurately obtain the hydrogeological conditions along the tunnel. The neural network method needs a large amount of historical data to construct learning samples in the evaluation process. The GIS method is mainly based on topography, geomorphology, and other factors to determine the risk of water inrush, which ignores the complexity of water inrush. Although the fuzziness and randomness of water inrush are taken into account in the above methods, few scholars have considered the impact of dynamic monitoring on water inrush in the evaluation process. In this study, based on detailed geological, hydrological, construction, and dynamic monitoring data of the SS (Shuang-san) tunnel, which is a super-long tunnel constructed by a TBM in the arid area of Northwest China, a new multi-index evaluation method is proposed to analyze the risk of tunnel water inrush based on the normal cloud model. The aim of this method is to further improve the accuracy of the risk prediction of water inrush.

The structure of this paper is designed as follows: Section 2 introduces the engineering background of the study area. Section 3 proposes a new risk assessment method of water inrush based on the cloud model and the comprehensive weight algorithm. Section 4 discusses the evaluation results of the proposed cloud model method by comparing them with other methods. Section 5 verifies that the actual excavation situations are consistent with the evaluation results. Finally, Section 6 summarizes the research of this paper.

2. Study Area

Engineering Background

The SS tunnel is located at the junction of the northern region of the Tianshan Mountains and the Jungger Basin in Xinjiang Province, China, as shown in Figure 1. It is a typical long tunnel with a length of 31.5 km and a longitudinal slope of 1/5000, 22.7 km of which was constructed by a TBM. The excavation diameter is 5.5 m, the ground elevation along the line is 775–1005 m, the topography is not undulating, the relative height difference is 5–35 m and the overburden thickness is 80–295 m. The geological structure of the SS tunnel mainly consists of Tuffaceous sandstone and lithic tuff from SD52+500 to SD50+300, small-scale faults and joint fissures are well developed, and the width of the fault zones is 0.3–5 m. The geological section of the SS tunnel is presented as Figure 2. The surface water above the tunnel is not abundant, and there is no river passing nearby. The groundwater is mainly fissure water stored in the rock mass, but the water is abundant. It is very likely that large water inrush would occur during the TBM construction, which would seriously threaten construction safety. Actually, water inrush occurred many times in the SS tunnel during the 19 months from August 2017 to February 2019, which seriously affected the tunneling efficiency of the TBM, as shown in Figure 3. Accordingly, there is a need to assess the risk level of water inrush in this section of the SS tunnel and provide risk warning for the subsequent tunneling of the TBM.

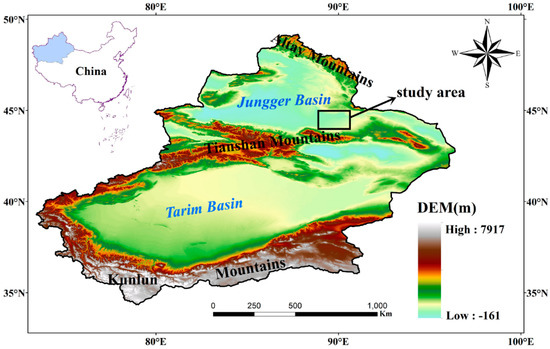
Figure 1. The geographical location of the study area.

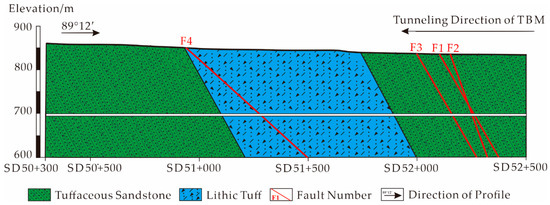
Figure 2. The geological profile of the SS (Shuang-san) tunnel from SD52+500 to SD50+300. TBM, tunnel boring machine.

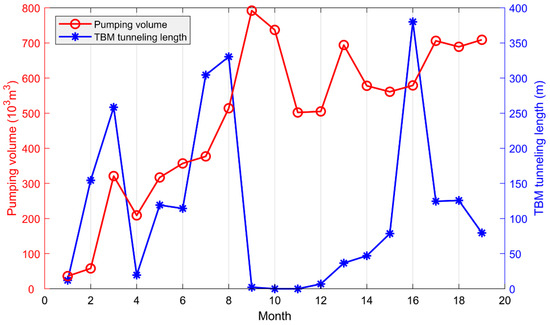
Figure 3. The measured data of the TBM monthly tunneling length and monthly pumping volume of the SS (Shuang-san) tunnel during the 19 months from August 2017 to February 2019.

3. Risk Assessment of Water Inrush

The occurrence of tunnel water inrush not only endangers engineering construction in arid areas, but also has an important irreversible impact on the ecological environment at the top of the tunnel. Consequently, analyzing the risk of tunnel water inrush has important engineering practical value in arid areas.

A new risk analysis method, based on the normal cloud theory, is proposed to analyze the risk of water inrush, as presented in Figure 4. First, a complete evaluation index system and evaluation criteria of water inrush risk assessment are determined. Second, the numerical characteristics of the cloud are calculated by the normal cloud model theory. Third, the weight of each evaluation index is calculated by a comprehensive weight calculating algorithm. Finally, the comprehensive certainty degree is determined by the comprehensive weight and certainty degree belonging to the corresponding level. Then, the risk level of water inrush can be determined.

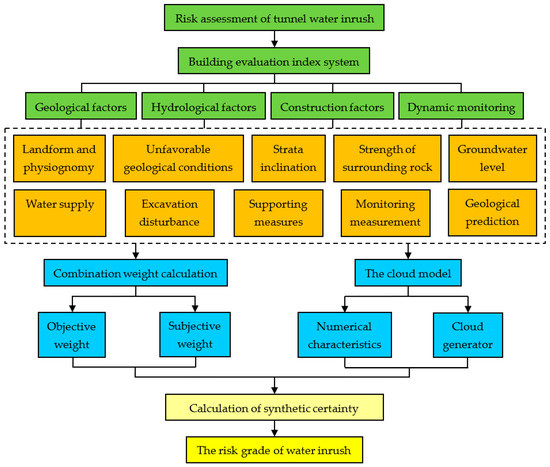
Figure 4. The risk assessment process of tunnel water inrush based on a normal cloud model.

3.1. Evaluation Index System

In actual engineering, there are many factors that cause water inrush, and the reasons are very complicated. According to previous research results [15,16,17], these factors can be categorized into hydrological factors (Q₁), geological factors (Q₂), construction factors (Q₃), and dynamic monitoring (Q₄). In this paper, ten factors were selected to establish the assessment index system for water inrush, including landform and physiognomy (C₁), unfavorable geological conditions (C₂), strata inclination (C₃), strength of the surrounding rock (C₄), groundwater level (C₅), water supply (C₆), excavation disturbance (C₇), supporting measures (C₈), monitoring measurement (C₉), and geological prediction (C₁₀). C₁~C₄ are geological factors, C₅ and C₆ are hydrological factors, C₇ and C₈ are construction factors, and C₉ and C₁₀ correspond to dynamic monitoring. In the established evaluation system, C₃, C₄, and C₅ are quantitative indices, and the index values were obtained by the measured data of the project. The other indices are qualitative indices, and the index values are determined by the expert scoring method. Combined with water inrush classification of the tunnel, the ten risk assessment indices were divided into four levels: low risk (I), medium risk (II), high risk (III), and higher risk (IV), as shown in Table 1.

Table 1. Assessment indices and classification criteria for water inrush.

Assessment Indices	I (Low Risk)	II (Medium Risk)	III (High Risk)	IV (Higher Risk)
Landform and physiognomy (C1)	<25	25~50	50~75	75~100
Unfavorable geological conditions (C2)	<25	25~50	50~75	75~100
Strata inclination (C3)	<10	10~35	35~75	75~90
Strength of surrounding rock (C4)	(BQ) > 450	350 < (BQ) ≤ 450	250 < (BQ) ≤ 350	(BQ) ≤ 250
Groundwater level (C5)	<10	10~30	30~60	>60
Water supply (C6)	<25	25~50	50~75	75~100
Excavation disturbance (C7)	<25	25~50	50~75	75~100
Supporting measures (C8)	85~100	70~85	60~70	<60
Monitoring measurement (C9)	85~100	70~85	60~70	<60
Geological prediction (C10)	85~100	70~85	60~70	<60

C₅ refers to the height difference between the tunnel floor and the groundwater level, and C₃ and C₅ are measured in meters and degrees, respectively. BQ refers to the basic quality of surrounding rock.

3.1.1. Landform and Physiognomy (C₁)

Landform and physiognomy reflect the fluctuation characteristics of the terrain above the tunnel. Under different geographic and geomorphic conditions, the possibility of tunnel water inrush is different. If the terrain above the tunnel fluctuates greatly and there is a large area of depression, the possibility of tunnel water inrush is large. Conversely, if the terrain above the tunnel fluctuates little and the landform is relatively flat, the possibility of tunnel water inrush is small. In the present study, the proportion of negative landform area above the tunnel was quantified [18], and it was divided into four levels: Without negative landform (0~25), small-scale negative landform (25~50), medium-scale negative landform (50~75), and large-scale negative landform (75~100), as shown in Table 1.

3.1.2. Unfavorable Geological Conditions (C₂)

Faults and large fissures not only bring difficulties to construction, but also are important unfavorable geological conditions that cause water inrush. Because of the existence of faults and fissures, the spatial distribution balance of water originally stored in the strata is destroyed in the process of tunnel construction, which easily leads to groundwater inrush in the tunnel along these paths. According to the degree of fault and fissure development in the strata [19], the unfavorable geological conditions was divided into four levels in this paper: non-developed strata (0~25), weakly developed strata (25~50), medially developed strata (50~75), and strongly developed strata (75~100), as shown in Table 1.

3.1.3. Strata Inclination (C₃)

Strata development is complex and changeable in a tunnel, and the trend of strata has an effect on the flow of groundwater. The permeability of groundwater is anisotropic in rock strata, which is smaller in the vertical direction than in the horizontal direction. In this study, the angle (0~90°) between the trend of rock strata and the axis of the tunnel, α, was selected as the strata inclination, and the strata inclination was divided into four grades: 0~10°, 10~35°, 35~75°, and 75~90° [15], as shown in Table 1.

3.1.4. Strength of Surrounding Rock (C₄)

In the process of tunnel construction, the strength of the surrounding rock is an important reference index for the risk of water inrush and construction safety. If the integrity of the surrounding rock is poor, the surrounding rock is prone to collapse and result in deformation in tunnel construction, and the risk of water inrush is high. According to the size of the surrounding rock classification standard (BQ), the strength of surrounding rock was divided into four levels in this paper: (BQ) > 450, 350 < (BQ) ≤ 450, 250 < (BQ) ≤ 350 and (BQ) ≤ 250 [20], as shown in Table 1.

3.1.5. Groundwater Level (C₅)

For underground engineering excavation, the distribution characteristics of groundwater are not only closely related to water inrush, but are also one of the important driving factors. Meanwhile, when water inrush occurs, groundwater not only erodes the surrounding rock, but is also the carrier of material movement [21,22]. When the groundwater level is high, the water pressure is higher, and the risk of water inrush is greater. In this paper, the height difference $h$ between the tunnel floor and the groundwater level are defined as the effective groundwater level, and $h$ is classified into four grades: 0 < $h$ ≤ 10 m, 10 < $h$ ≤ 30 m, 30 <$h$ ≤ 60 m and $h$ > 60 m [23].

3.1.6. Water Supply (C₆)

Generally, rivers, surface precipitation, lakes, and groundwater in rock mass are the main supply of the water sources of water inrush, and adequate water supply may lead to large scale and long duration of water inrush. Therefore, when analyzing the cause of water inrush, we should not only analyze the flow characteristics of groundwater in the rock mass, but also consider the potential threat of water supply to tunnel water inrush. If the water supply capacity is strong, the possibility of tunnel water inrush is high [16,24]. Based on the supply capacity of water resources, it was divided into four levels in this paper: weaker supply capacity (0~25), weak supply capacity (25~50), strong supply capacity (50~75), and stronger supply capacity (75~100), as shown in Table 1.

3.1.7. Excavation Disturbance (C₇)

Construction factors have great uncertainty in the process of tunnel construction. The construction parameters, technical level of builders and engineering management may affect the construction quality of the tunnel. If the construction scheme is not reasonable, the excavation disturbance to the tunnel will be larger, and the possibility of water inrush will be greater. Therefore, it is necessary to formulate a reasonable excavation scheme to minimize the disturbance to surrounding rock. According to the disturbance degree of the surrounding rock during tunnel excavation, it was divided into four grades in this paper: smaller disturbance (0~25), small disturbance (25~50), large disturbance (50~75), and larger disturbance (75~100), as shown in Table 1.

3.1.8. Supporting Measure (C₈)

The original balance of the strata around the tunnel is destroyed during tunnel construction, causing the deformation or collapse of the surrounding rock. The timeliness and rigidity of the supporting are important indicators to measure whether the supporting measures are reasonable. Reasonable supporting measures are critical to ensuring the safety of tunnel construction, in addition, it can prevent the weathering of the surrounding rock and reduce the impact of groundwater on the tunnel construction [25]. Based on the rationality of the supporting measure, it was divided into four grades: unreasonable (0~60), basically reasonable (60~70), reasonable (70~85), and more reasonable (85~100), as shown in Table 1.

3.1.9. Monitoring Measurement (C₉)

The hydrogeological conditions and the deformation of the surrounding rock dynamically change in time and space in the process of tunnel construction, and monitoring measurement is an important means to capture these dynamic changes. According to continuous field observation and measurement, we can obtain a lot of feedback information, such as seepage and displacement of the surrounding rock, which is of great significance for us to analyze the potential risk of water inrush. According to the rationality of monitoring measurement scheme, it was divided into four grades in this paper: unreasonable (0~60), basically reasonable (60~70), reasonable (70~85), and more reasonable (85~100), as shown in Table 1.

3.1.10. Geological Prediction (C₁₀)

Advanced geological forecast is one of the important technical methods to detect the risk of water inrush when the tunnel crosses the water-rich section [18]. A reasonable geological prediction method can not only effectively detect the water storage situation of the rock mass in front of the tunnel face, but can also provide an early risk warning for the builders. This gives technicians enough time to formulate a detailed pretreatment scheme to minimize the probability of water inrush, and then reduce the adverse impact of water inrush on tunnel construction. According to the rationality of the geological prediction method, it was divided into four grades in this paper: unreasonable (0~60), basically reasonable (60~70), reasonable (70~85), and more reasonable (85~100), as shown in Table 1.

3.2. The Normal Cloud Model

The cloud model proposed by Li is a mathematical theory that is used to analyze the uncertainty problem, which is based on the probability statistics method and the fuzzy set theory [26,27]. It can achieve a good conversion between a qualitative concept and its quantitative instantiations. So far, it has been widely applied in the stability classification of surrounding rocks, evaluation of water-use efficiency, prevention and control of disaster, and other areas [28,29,30].

3.2.1. Cloud and Cloud Droplets

Let $U$ be a quantitative universe of discourse, which can be described by precise numerical values, and $A$ is a qualitative concept of $U$. Assume that there is a quantitative number $x\in U$, and $x$ is a random realization of concept $A$. For arbitrary element $x$, there is a random variable with stabilization tendency, called the certainty degree $\mu (x)$ [31,32]. The parameter $\mu (x)$ can be estimated as [33,34]:

$$\begin{array}{c}\mu :U\to \left[0,1\right]\hspace{1em}\forall x\in U\to \mu (x)\end{array}$$

(1)

where the distribution of $x$ on $U$ is called a cloud, and each $(x, \mu (x))$ is a cloud drop.

According to the definition of cloud, cloud is composed of numerous cloud drops, and it can transform the qualitative concept into a quantitative value. Each cloud drop is a quantitative representation of a qualitative concept in the $U$ space. The certainty degree of a cloud drop reflects the fuzziness and randomness of a concept.

3.2.2. Numerical Characteristics of Cloud

Theoretically, the distribution of $x$ on $U$ can be described by the cloud numerical characteristics $(E_x,E_n,H_e)$. The expected value ($E_x$) represents the central value of the concept in the $U$ space. Entropy ($E_n)$ is the uncertainty measurement of the qualitative concept, which reflects the value range of the distribution of cloud drops. The dispersion degree of cloud drops can be indicated by Hyper entropy ($H_e$), which can reflect the uncertainty degree of $E_n$ and control the thickness of cloud drops [35,36]. For instance, Figure 5 shows a normal cloud diagram, in which the cloud numerical characteristics are $E_x=0,$ $E_n=2,$ and $H_e=0.2$.

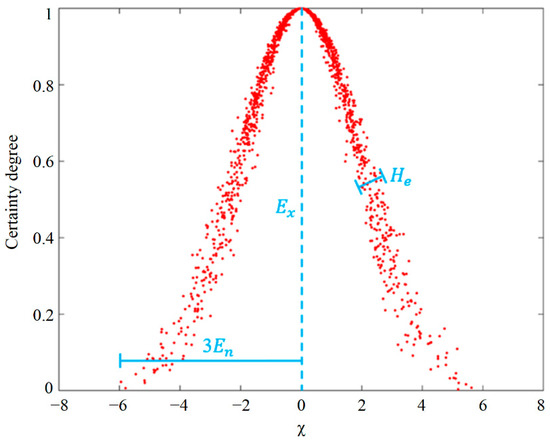
Figure 5. A normal cloud model with parameters $E_x=0$, $E_n=2$, and $H_e=0.2$.

The three cloud numerical characteristics are calculated by Formulas (2)–(4):

$$\begin{array}{c}{E}_x=\frac{C_{max}+C_{min}}{2}\end{array}$$

(2)

$$\begin{array}{c}{E}_n=\frac{C_{max}-C_{min}}{6}\end{array}$$

(3)

$$\begin{array}{c}{H}_e=k\end{array}$$

(4)

where $C_{max} \mathrm{and} C_{min}$ are the maximum and minimum boundary values of the corresponding grade standard, respectively. Based on the practical situation, $k$ can be set as an appropriate constant (k < 0.5) to ensure that the cloud thickness is appropriate. In this paper, $k$ was 0.01 [37]. If a variable has only an upper or lower limit, such as $(-\infty ,c_{min}]$ or $[c_{max},+\infty )$, the boundary parameters can be determined by the maximum and minimum values of the variable.

3.2.3. Cloud Generator

Cloud generator is a tool to implement the conversion between the qualitative index and the quantitative index. The cloud generator is divided into forward cloud generator (FCG) and backward cloud generator (BCG), as shown in Figure 6. The FCG maps from qualitative to quantitative, it can generate a large number of cloud drops to form a cloud diagram by inputting the cloud numerical characteristics $(E_x,E_n,H_e)$. In contrast, the BCG can convert quantitative values into the qualitative a concept [38,39].

Figure 6. Two different types of cloud generators. (a) forward cloud generator; (b) backward cloud generator.

In this study, the forward cloud generator was used to analyze the risk of water inrush. If a variable $x\in A$ is a random realization of the concept $A$ and obeys the Gaussian distribution $x~N(E_x,{\acute{E_n}}^2)$, and $\acute{E_n}$ obeys the Gaussian distribution $\acute{E_n}~N(E_n,H_e^2)$. The certainty degree of $x$ to $A$, $\mu (x)$, satisfies [27]:

$$\begin{array}{c}\mu (x)=e^{-\frac{{(x-E_x)}^2}{2{\acute{E_n}}^2}}\end{array}$$

(5)

where $\acute{E_n}$ is a normally distributed random number, the distribution of $x$ in $U$ is called a normal cloud.

The specific algorithm of the forward normal cloud model is as follows:

• Calculate expectation $E_x$, entropy $E_n$, and hyper entropy $H_e$;
• Generate a normally distributed random number $\acute{E_{ni}}$ with expectation $E_{ni}$ and variance $H_{ei}$: $\acute{E_{ni}}~N(E_{ni},H_{ei}^2)$;
• Generate a normally distributed random number $x_i$ with expectation $E_{xi}$ and variance $\acute{E_{ni}}$: $x_i~N(E_{xi},{\acute{E_{ni}}}^2)$;
• Calculate the certainty degree of $x_i$, $\mu (x_i)=e^{-\frac{{(x_i-E_{xi})}^2}{2{\acute{E_{ni}}}^2}}$;
• Generate a cloud drop ($x_i, \mu (x_i)$), and repeat steps 1 to 5 until N cloud drops are generated.

3.3. Evaluation Index Weight Calculation

3.3.1. Subjective Weight Calculation

The analytic hierarchy process (AHP), proposed by Saaty, is an effective method to analyze complicated decisions [40]. It can analyze the underlying logical relationship of the study objects in quantitative terms. Moreover, AHP has been widely applied in many fields. In this study, the specific algorithm of AHP is shown below:

Firstly, according to the established evaluation index system, the relative importance of any two indices at each level is analyzed by the 1~9 scale method (see Table 2) [41]. Then, the judgment matrix $M$ can be constructed by the Formula (6).

$$\begin{array}{c}M=\left[\begin{array}{cccc}\frac{M_1}{M_1}& \frac{M_1}{M_2}& \cdots & \frac{M_1}{M_n}\\ \frac{M_2}{M_1}& \frac{M_2}{M_2}& \cdots & \frac{M_2}{M_n}\\ ⋮& ⋮& \ddots & ⋮\\ \frac{M_n}{M_1}& \frac{M_n}{M_2}& \cdots & \frac{M_n}{M_n}\end{array}\right]=\left[\begin{array}{cccc}{M}_{11}& M_{12}& \cdots & M_{1n}\\ M_{21}& M_{22}& \cdots & M_{2n}\\ ⋮& ⋮& \ddots & ⋮\\ M_{n1}& M_{n2}& \cdots & M_{nn}\end{array}\right]\end{array}$$

(6)

Table 2. The 1~9 scale method of analytic hierarchy process (AHP).

$\mathbf{Value} \mathbf{of} {\mathit{M}}_{\mathit{i}\mathit{j}}$	Two-by-Two Comparison
1	$M_i$ and $M_j$ are equally important
3	$M_i$ is slightly more important than $M_j$
5	$M_i$ is more important than $M_j$
7	$M_i$ is substantially more important than $M_j$
9	$M_i$ is absolutely more important than $M_j$
2, 4, 6, 8	the middle value of two adjacent judgements
Explanation	When $M_j$ and $M_i$ are compared, the value is the reciprocal of $M_i$ and $M_j$ scalar.

Secondly, the weight vector and the maximum eigenvalues of $M$ can be calculated as:

$$\begin{array}{c}{w}_i=\sqrt[n]{{\displaystyle {\displaystyle \prod }_{j=1}^n}{M}_{ij}}/{\displaystyle {\displaystyle \sum }_{i=1}^n}\sqrt[n]{{\displaystyle {\displaystyle \prod }_{j=1}^n}{M}_{ij}}\hspace{1em}(i=1,2,\cdots n)\end{array}$$

(7)

$$\begin{array}{c}{\lambda }_{max}={\displaystyle {\displaystyle \sum }_{i=1}^n}\frac{{(Mw)}_i}{n{w}_i}\end{array}$$

(8)

where $w_i$ is the weight of the $i$th assessment index, $M$ is the judgment matrix, $n$ is the dimension of judgment matrix $M$, and ${\lambda }_{max}$ is the maximum eigenvalue of $M$.

Finally, to ensure the accuracy of the results, the consistency of judgment matrix $M$ should be verified by Formula (9).

$$\begin{array}{c}CR=\frac{({\lambda }_{max}-n)/(n-1)}{RI}\end{array}$$

(9)

where $RI$ is the random consistency index value. The values of $RI$ are shown in Table 3.

Table 3. The random consistency index values.

n	1	2	3	4	5	6	7	8	9	10
$RI$	0	0	0.58	0.90	1.12	1.24	1.32	1.41	1.45	1.49

If $CR$ is less than 0.1, it indicates that the judgment matrix satisfies the consistency requirement, and therefore the normalized eigenvector can be used as the weight vector.

3.3.2. Objective Weight Calculation

Water inrush is a dynamic process affected by many factors, and the process is highly uncertain. In the information theory, entropy is an index to measure the disorder and degree of confusion of a system. It can not only objectively reflect the amount of effective information provided by the data, but can also measure the uncertainty of the system. The smaller the entropy value of an evaluation index, the greater the amount of effective information provided by the index, and the greater the weight of the index. This method can avoid human interference in the calculation process as much as possible so that the weight assignment is more in line with engineering practice [42,43].

Assuming that there are $m$ cases of tunnel water inrush and $n$ evaluation indices, the original data matrix $X={(x_{ij})}_{m\times n}$ can be constructed as:

$$\begin{array}{c}X=\left[\begin{array}{cccc}{x}_{11}& x_{12}& \cdots & x_{1n}\\ x_{21}& x_{22}& \cdots & x_{2n}\\ ⋮& ⋮& \ddots & ⋮\\ x_{m1}& x_{m2}& \cdots & x_{mn}\end{array}\right]\end{array}$$

(10)

In order to eliminate the influence of dimension in the different types of data, the original data should be standardized. The larger an index value, the lower the risk, and the standardization is calculated by the following formula:

$$\begin{array}{c}{b}_{ij}=\frac{x_{ij}-min\left\{x_{ij}\right\}}{max\left\{x_{ij}\right\}-min\left\{x_{ij}\right\}}\end{array}$$

(11)

The smaller an index value, the lower the risk, and the standardization can be calculated as:

$$\begin{array}{c}{b}_{ij}=\frac{max\left\{x_{ij}\right\}-x_{ij}}{max\left\{x_{ij}\right\}-min\left\{x_{ij}\right\}}\end{array}$$

(12)

With Formulas (11) and (12), the normalized matrix $B={(b_{ij})}_{m\times n}$ can be obtained:

$$\begin{array}{c}B=\left[\begin{array}{cccc}{b}_{11}& b_{12}& \cdots & b_{1n}\\ b_{21}& b_{22}& \cdots & b_{2n}\\ ⋮& ⋮& \ddots & ⋮\\ b_{m1}& b_{m2}& \cdots & b_{mn}\end{array}\right]\end{array}$$

(13)

According to the definition of entropy, the entropy value of the $j$th evaluation index is calculated by Equations (14) and (15):

$$\begin{array}{c}{r}_{ij}=(1+b_{ij})/{\displaystyle {\displaystyle \sum }_{i=1}^m}(1+b_{ij})\end{array}$$

(14)

$$\begin{array}{c}{E}_j=-{(ln m)}^{-1}{\displaystyle {\displaystyle \sum }_{i=1}^m}{r}_{ij} ln r_{ij}\end{array}$$

(15)

The weight of the $j$th evaluation index can be determined by the following formula:

$$\begin{array}{c}{w}_j=\frac{1-E_j}{{{\displaystyle \sum }}_{j=1}^n(1-E_j)}\end{array}$$

(16)

3.3.3. Combination Weight Calculation

The calculation of the combination weight is used to integrate the above two weights so that the weight reflects both the subjective experience and the objective facts. The calculation method is as follows:

$$\begin{array}{c}p=\beta w_i+(1-\beta )w_j\end{array}$$

(17)

where $p$ is the combination weight of the evaluation indices, and $\beta$ is the weight coefficient. $\beta$ can be determined by expert scoring. If the decisions prefer expert experience, $\beta \in \left[0.5, 1\right]$. If the decisions prefer measured data, $\beta \in \left[0, 0.5\right]$ [25,44]. For example, if experts give $\left[{\beta }_1,{\beta }_2, {\beta }_3\right]=\left[0.6, 0.7, 0.6\right]$, then the weight coefficient is $\beta =\frac{{\beta }_1+{\beta }_2+{\beta }_3}{3}=0.63$.

3.4. Calculation of the Synthetic Certainty Degree

According to the forward normal cloud generator, the normal cloud model for the risk assessment of water inrush can be generated, and the certainty degree of $x$ belonging to the corresponding cloud can also be calculated. Then, combined with the combination weights calculated by Formula (17), the synthetic certainty degree, $U$, can be calculated by Formula (18).

$$\begin{array}{c}U={\displaystyle {\displaystyle \sum }_i^n}\mu (x)p_i\end{array}$$

(18)

where $p_i$ is the combination weight of the $i$th evaluation index, and $\mu (x)$ is the certainty degree of the $i$th assessment index.

4. Results and Discussion

In this study, the SS tunnel from SD52+160 to SD50+617 was selected as the research area. According to the actual geological survey and the hydrological conditions of the SS tunnel, the research area was divided into ten sections. Moreover, based on the actual hydrogeological investigation, construction, management, advance geological forecasting, and the expert scoring method, the risk factor parameter values of water inrush in the ten samples could be obtained, as shown in Table 4.

Table 4. The risk factor parameter values of water inrush in the SS (Shuang-san) tunnel.

Sample	C1	C2	C3	C4	C5	C6	C7	C8	C9	C10
SD52+160–SD52+135	45	85	66	320	104	30	70	55	65	50
SD52+135–SD52+060	40	80	62	320	102	20	65	60	70	50
SD52+060–SD51+980	20	45	60	400	115	10	40	85	80	85
SD51+980–SD51+917	10	35	63	330	112	10	45	80	80	80
SD51+917–SD51+280	10	20	62	380	115	10	30	90	85	90
SD51+280–SD51+264	15	85	60	300	118	10	80	65	75	40
SD51+264–SD51+212	20	50	55	280	113	10	60	70	75	65
SD51+212–SD51+170	10	60	54	340	108	10	65	75	75	70
SD51+170–SD50+660	10	15	65	380	117	10	35	90	80	90
SD50+660–SD50+617	10	35	62	420	120	10	40	80	80	80

4.1. Weight Calculation

4.1.1. Subjective Weight Calculation Based on AHP

Based on the established assessment index system of water inrush in this study, the judgment matrix $M$ can be obtained by AHP.

$$\begin{array}{c}M=\left[\begin{array}{cccccccccc}1& 1/4& 5& 4& 1/3& 1/3& 5& 7& 6& 1\\ 4& 1& 6& 5& 2& 3& 6& 8& 7& 4\\ 1/5& 1/6& 1& 1/3& 1/5& 1/5& 2& 2& 2& 1/6\\ 1/4& 1/5& 3& 1& 1/5& 1/4& 3& 4& 5& 1/4\\ 3& 1/2& 5& 5& 1& 2& 6& 7& 7& 3\\ 3& 1/3& 5& 4& 1/2& 1& 5& 6& 6& 3\\ 1/5& 1/6& 1/2& 1/3& 1/6& 1/5& 1& 2& 3& 1/5\\ 1/7& 1/8& 1/2& 1/4& 1/7& 1/6& 1/2& 1& 2& 1/6\\ 1/6& 1/7& 1/2& 1/5& 1/7& 1/6& 1/3& 1/2& 1& 1/5\\ 1& 1/4& 6& 4& 1/3& 1/3& 5& 6& 5& 1\end{array}\right]\end{array}$$

(19)

Then, the weight vector and the maximum eigenvalues of $M$ can be calculated by Formulas (7) and (8). The AHP-based weight of each assessment index is presented in Table 5, where ${\lambda }_{max}=$ 10.8765. In addition, $RI=$ 1.49 and $CR=$ 0.0654 < 0.1.

Table 5. Weights of the assessment indices of water inrush.

Index	C1	C2	C3	C4	C5
AHP-based Weight	0.1084	0.2672	0.0320	0.0541	0.2043
Entropy-based Weight	0.1029	0.1287	0.1005	0.0985	0.1074
Combination Weight	0.1062	0.2118	0.0594	0.0719	0.1655
Index	C6	C7	C8	C9	C10
AHP-based Weight	0.1591	0.0290	0.0210	0.0180	0.1067
Entropy-based Weight	0.0771	0.1010	0.1037	0.0720	0.1082
Combination Weight	0.1263	0.0578	0.0541	0.0396	0.1073

4.1.2. Objective Weight Calculation Based on Entropy

For the evaluation indices of C₁~C₃ and C₅~C₇, the smaller the value, the lower the risk of water inrush. For the evaluation indices of C₄ and C₈~C₁₀, the larger the value, the lower the risk of water inrush. Based on the evaluation index values of water inrush in Table 4, the normalized matrix $B$ can be obtained by Formulas (11) and (12).

$$\begin{array}{c}B=\left[\begin{array}{cccccccccc}0.0000& 0.0000& 0.0000& 0.2857& 0.8889& 0.0000& 0.2000& 0.0000& 0.0000& 0.2000\\ 0.1429& 0.0714& 0.3333& 0.2857& 1.0000& 0.5000& 0.3000& 0.1429& 0.2500& 0.2000\\ 0.7143& 0.5714& 0.5000& 0.8571& 0.2778& 1.0000& 0.8000& 0.8571& 0.7500& 0.9000\\ 1.0000& 0.7143& 0.2500& 0.3571& 0.4444& 1.0000& 0.7000& 0.7143& 0.7500& 0.8000\\ 1.0000& 0.9286& 0.3333& 0.7143& 0.2778& 1.0000& 1.0000& 1.0000& 1.0000& 1.0000\\ 0.8571& 0.0000& 0.5000& 0.1429& 0.1111& 1.0000& 0.0000& 0.2857& 0.5000& 0.0000\\ 0.7143& 0.5000& 0.9167& 0.0000& 0.3889& 1.0000& 0.4000& 0.4286& 0.5000& 0.5000\\ 1.0000& 0.3571& 1.0000& 0.4286& 0.6667& 1.0000& 0.3000& 0.5714& 0.5000& 0.6000\\ 1.0000& 1.0000& 0.0833& 0.7143& 0.1667& 1.0000& 0.9000& 1.0000& 0.7500& 1.0000\\ 1.0000& 0.7143& 0.3333& 1.0000& 0.0000& 1.0000& 0.8000& 0.7143& 0.7500& 0.8000\end{array}\right]\end{array}$$

(20)

With Formulas (14)–(16), the entropy-based weight of each assessment index can be calculated, as presented in Table 5.

4.1.3. Combination Weight Calculation

According to the calculation results of the AHP-based weight and the entropy-based weight, the combination weight of each assessment index can be calculated by Formula (17). In this study, $\beta$ was taken as 0.6. The calculation results of the index weight are presented in Table 5.

4.2. Cloud Model of Water Inrush

According to the assessment index values and classification criteria of water inrush, the cloud numerical characteristics $(E_x,E_n,H_e)$ of different risk levels can be calculated by Formulas (2)–(4), as shown in Table 6.

Table 6. Cloud numerical characteristics $(E_x,E_n,H_e)$ of each assessment index.

Index	I	II	III	IV
C1	(12.5, 4.1667, 0.01)	(37.5, 4.1667, 0.01)	(62.5, 4.1667, 0.01)	(87.5, 4.1667, 0.01)
C2	(12.5, 4.1667, 0.01)	(37.5, 4.1667, 0.01)	(62.5, 4.1667, 0.01)	(87.5, 4.1667, 0.01)
C3	(5, 1.6667, 0.01)	(22.5, 4.1667, 0.01)	(55, 6.6667, 0.01)	(82.5, 2.5, 0.01)
C4	(550, 33.3333, 0.01)	(400, 16.6667, 0.01)	(300, 16.6667, 0.01)	(125, 41.6667, 0.01)
C5	(5, 1.6667, 0.01)	(20, 3.3333, 0.01)	(45, 5, 0.01)	(90, 10, 0.01)
C6	(12.5, 4.1667, 0.01)	(37.5, 4.1667, 0.01)	(62.5, 4.1667, 0.01)	(87.5, 4.1667, 0.01)
C7	(12.5, 4.1667, 0.01)	(37.5, 4.1667, 0.01)	(62.5, 4.1667, 0.01)	(87.5, 4.1667, 0.01)
C8	(92.5, 2.5, 0.01)	(77.5, 2.5, 0.01)	(65, 1.6667, 0.01)	(30, 10, 0.01)
C9	(92.5, 2.5, 0.01)	(77.5, 2.5, 0.01)	(65, 1.6667, 0.01)	(30, 10, 0.01)
C10	(92.5, 2.5, 0.01)	(77.5, 2.5, 0.01)	(65, 1.6667, 0.01)	(30, 10, 0.01)

Then, the certainty degree of each assessment index belonging to different risk levels can be calculated by the forward cloud generator, as shown in Table 7. Combined with the combination weight of each evaluation index, the synthetic certainty degree can be calculated by Formula (18), as shown in Table 8. The risk level of water inrush was determined by the maximum synthetic certainty degree, and the distributions of the certainty degrees of each evaluation index in the four risk levels of water inrush are illustrated in Figure 7. In Figure 7, the X-axis is the value of each assessment index, and the Y-axis is the corresponding value of the certainty degree.

Table 7. Certainty degrees of assessment indices C₁~C₁₀.

Sample	C1	C2	C3	C4	C5
SD52+160–SD52+135	0.1987	0.8350	0.2579	0.4864	0.3761
SD52+135–SD52+060	0.8366	0.1959	0.5776	0.4864	0.4871
SD52+060–SD51+980	0.1944	0.1987	0.7557	1.0000	0.0441
SD51+980–SD51+917	0.8359	0.8355	0.4875	0.1985	0.0888
SD51+917–SD51+280	0.8359	0.1944	0.5776	0.4869	0.0441
SD51+280–SD51+264	0.8355	0.8350	0.7557	1.0000	0.0199
SD51+264–SD51+212	0.1944	0.0112	1.0000	0.4873	0.0707
SD51+212–SD51+170	0.8359	0.8352	0.9888	0.0562	0.1985
SD51+170–SD50+660	0.8359	0.8355	0.3264	0.4869	0.0259
SD50+660–SD50+617	0.8359	0.8355	0.5776	0.4860	0.0110
Sample	C6	C7	C8	C9	C10
SD52+160–SD52+135	0.2022	0.1975	0.0442	1.0000	0.1355
SD52+135–SD52+060	0.1944	0.8352	0.0113	0.0111	0.1355
SD52+060–SD51+980	0.8359	0.8355	0.0111	0.6036	0.0111
SD51+980–SD51+917	0.8359	0.1984	0.6036	0.6036	0.6036
SD51+917–SD51+280	0.8359	0.1966	0.6038	0.0111	0.6038
SD51+280–SD51+264	0.8359	0.1979	1.0000	0.6047	0.6064
SD51+264–SD51+212	0.8359	0.8352	0.0111	0.6047	1.0000
SD51+212–SD51+170	0.8359	0.8357	0.6047	0.6047	0.0118
SD51+170–SD50+660	0.8359	0.8361	0.6038	0.6036	0.6038
SD50+660–SD50+617	0.8359	0.8355	0.6036	0.6036	0.6036

Table 8. Calculation results of the different evaluation methods applied to the SS (Shuang-san) tunnel.

Sample	Synthetic Certainty Degree				The Cloud Model Method	Ideal Point Method	Gray Relation Projection Method
	U(I)	U(II)	U(III)	U(IV)
SD52+160–SD52+135	0	0.0466	0.1013	0.2561	IV	IV	IV
SD52+135–SD52+060	0.0245	0.0889	0.1180	0.1373	IV	III	IV
SD52+060–SD51+980	0.1260	0.1880	0.0449	0.0073	II	II	III
SD51+980–SD51+917	0.1943	0.3098	0.0432	0.0147	II	II	II
SD51+917–SD51+280	0.3334	0.0464	0.0343	0.0073	I	II	II
SD51+280–SD51+264	0.1943	0.0240	0.1709	0.2567	IV	IV	IV
SD51+264–SD51+212	0.1262	0.0240	0.2530	0.0117	III	III	III
SD51+212–SD51+170	0.1943	0.0567	0.2893	0.0329	III	III	III
SD51+170–SD50+660	0.4688	0.1072	0.0194	0.0043	I	II	II
SD50+660–SD50+617	0.1943	0.3816	0.0343	0.0018	II	II	II

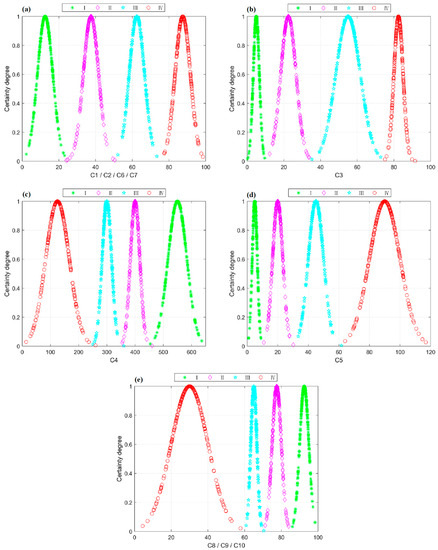
Figure 7. Cloud of each assessment index generated by the forward cloud generator. (a) landform and physiognomy (C₁), unfavorable geological conditions (C₂), water supply (C₆), and excavation disturbance (C₇); (b) strata inclination (C₃); (c) strength of the surrounding rock (C₄); (d) groundwater level (C₅); (e) supporting measures (C₈), monitoring measurement (C₉), and geological prediction (C₁₀).

4.3. Risk Level Assessment

In order to assess the reliability of the cloud model, the ideal point and gray relation projection methods were compared in this paper [45,46,47]. The evaluation results calculated by different methods are shown in Table 8.

Based on the comparative analysis of the evaluation results in Table 8, the results calculated by the three methods are exactly same in the sections of SD52+160–SD52+135, SD51+980–SD51+917, SD51+280–SD51+264, SD51+264–SD51+212, SD51+212–SD51+170 and SD50+660–SD50+617. The final levels of SD52+160–SD52+135 and SD51+280–SD51+264 are IV, the risk levels of SD51+264–SD51+212 and SD51+212–SD51+170 are III, and the final levels of SD51+980–SD51+917 and SD50+660–SD50+617 are II.

Moreover, the synthetic certainty degree of the SD52+135–SD52+060 section belonging to the different risk levels is: U(IV) = 0.1373, U(III) = 0.1180, U(II) = 0.0889, and U(I) = 0.0245. Hence, the probability of water inrush in this section is level IV (very high), which is the same as the evaluation result calculated by the gray relation projection method. The evaluation result calculated by the ideal point method is level III, which is lower than the above two methods, and the final level of SD52+135–SD52+060 is IV. The maximum synthetic certainty degree of SD52+060–SD51+980 is: U(II) = 0.1880. This shows that the result calculated by the normal cloud model is of level II, which is the same as the result of the ideal point method and is lower than the result of the gray relation projection method. Therefore, the final level of SD52+060–SD51+980 is II. The synthetic certainty degree of SD51+917–SD51+280 and SD51+170–SD50+660 belonging to the different risk levels is U(I) > U(II) > U(III) > U(IV). Compared with the results calculated by the ideal point and gray relation projection methods, the result calculated by the normal cloud model is lower, and the final levels of SD51+917–SD51+280 and SD51+170–SD50+660 are I.

In summary, the 70% (7/10) final levels are the same as the ideal point and gray relation projection method. It can be seen that the final results calculated by the three methods have high consistency.

5. Excavation Verification

According to the statistical analysis of the location and the volume of water inrush in the SS tunnel, within the study area from SD52+160 to SD50+617, the measured maximum water inrush volumes of the ten samples are presented as Figure 8.

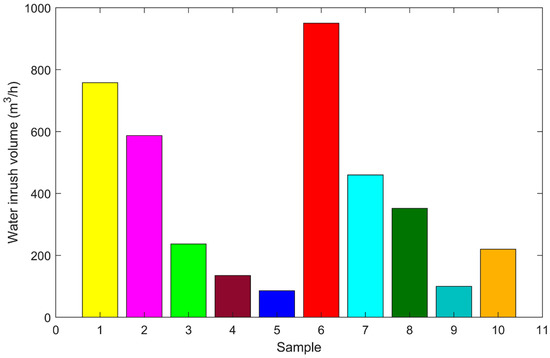
Figure 8. The measured maximum water inrush volume of the ten samples in the SS (Shuang-san) tunnel.

In view of the advanced geological prediction result of the complex frequency conductivity method, the risk of water inrush is very high for SD52+160, as seen in Figure 9. Obvious water inrush appears on the tunnel face when the TBM reaches SD52+160, as seen in Figure 10a, and the measured maximum water inrush volume is 758 m³/h. Moreover, large-scale water inrush also appears on the right wall of SD52+090 and SD51+265, as seen in Figure 10b,c, and the measured maximum water inrush volume is 587 m³/h and 950 m³/h, respectively. Several outflow points of water inrush occur at the TBM shield of SD50+660, as seen in Figure 10d, and the measured maximum water inrush volume is 220 m³/h. Therefore, the evaluation results calculated by the proposed cloud model method show high consistency with the actual excavation situations, which demonstrates that this risk assessment method is of high accuracy and reliability for practical engineering.

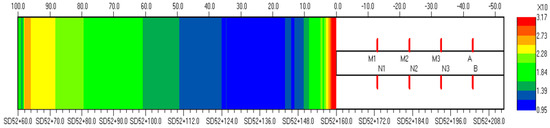
Figure 9. The advanced geological prediction result of the complex frequency conductivity method at SD52+160.

Figure 10. Practical situation of water inrush in the SS (Shuang-san) tunnel. (a) water inrush at SD52+160; (b) water inrush at SD52+090; (c) water inrush at SD51+265; (d) water inrush at SD50+660.

6. Conclusions

Considering geological, hydrological, and construction factors, as well as dynamic monitoring, a new multi-index evaluation method was proposed in this paper to analyze the risk of tunnel water inrush based on the normal cloud model. The weight coefficients of the assessment indicators were calculated by the objective and subjective weights, and the certainty degree of each assessment indicator belonging to the corresponding cloud was obtained by the normal cloud generator. The risk level of water inrush was determined by the comprehensive determination degree.

The proposed evaluation method was applied to assess the risk of water inrush in the SS tunnel constructed by a TBM in the arid area of Northwest China. The evaluation results are not only consistent with the results of the ideal point and gray relation projection methods, but also agree well with the actual excavation situations. This demonstrates that this new risk evaluation method of water inrush has high accuracy and reliability and can provide a reference for related projects.

Since water inrush is characterized as complex, fuzzy, and random, the application of cloud theory to the risk prediction of water inrush is only a preliminary attempt, and there are still some issues to be further studied, such as the flow mechanism and distribution characteristics of groundwater in the fractures of the surrounding rock. In addition, it is worth exploring the introduction of the multi-dimensional cloud model into the risk analysis of water inrush.