Deriving a Bayesian Network to Assess the Retention Efficacy of Riparian Buffer Zones
Abstract
1. Introduction
2. Materials and Methods
2.1. Data Collection and Preprocessing
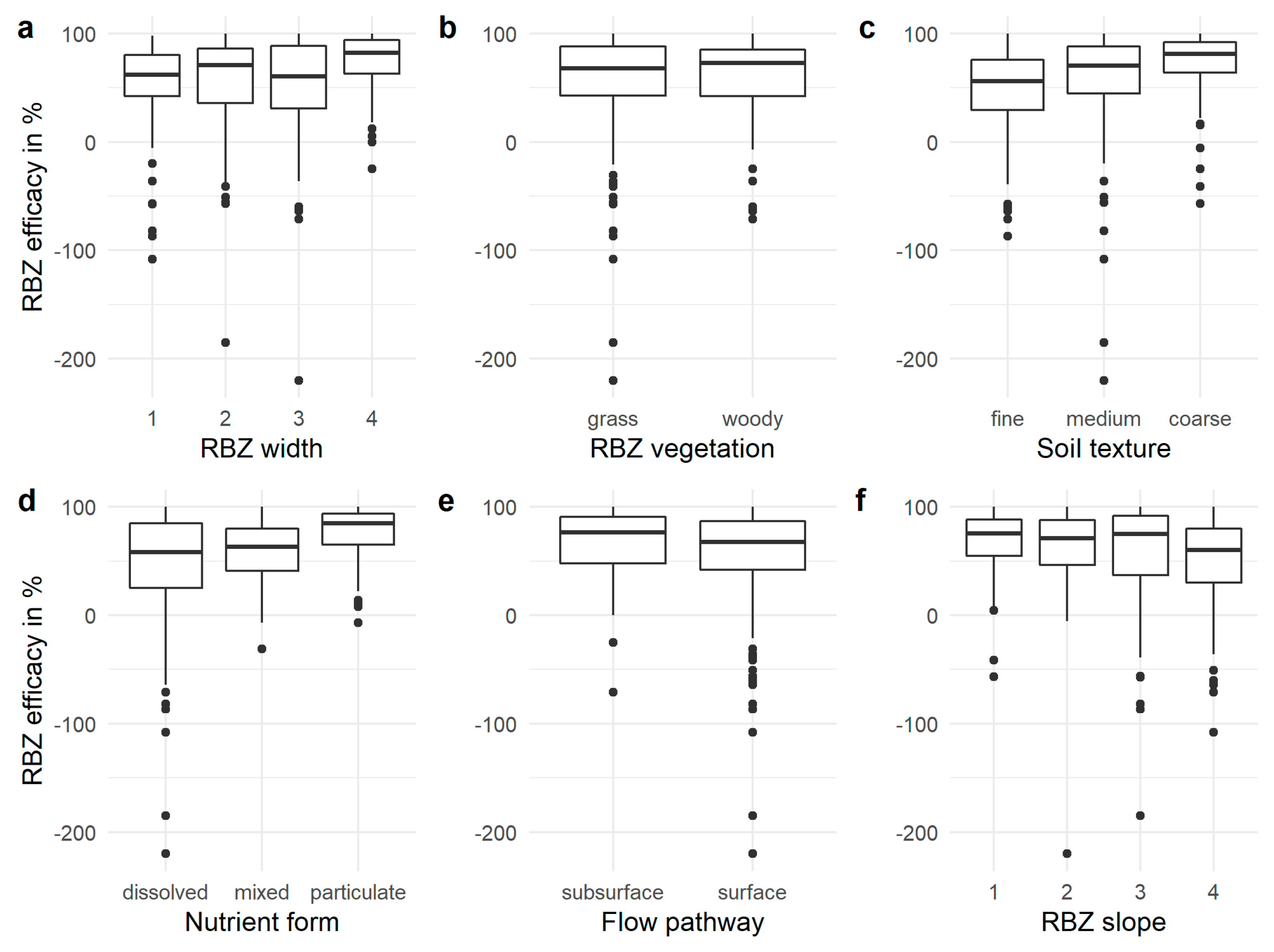
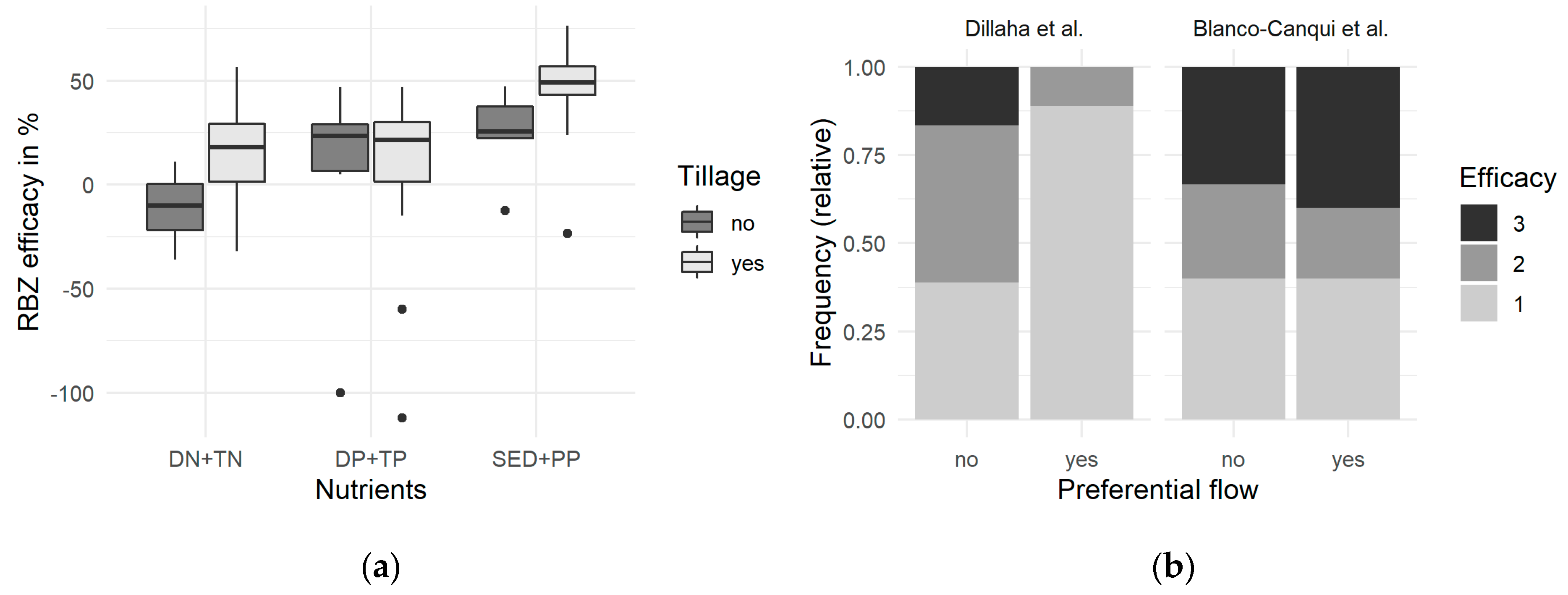
- RBZ width and nutrient form: after entering the RBZ, the velocity of surface runoff decreases due to surface roughness and soil infiltration [22,49,50]. This results in a lower transport capacity and a deposition of sediment and particulate nutrients, which is an important process for their retention [40]. Positive yet variable relationships of RBZ width and efficacy have widely been acknowledged in reviews and guidelines (e.g., [19,33,48]) with broader RBZ being needed to efficiently retain dissolved nutrients compared to sediment [46].
- RBZ vegetation, flow pathway, and nutrient form: dense aboveground vegetation increases the hydraulic roughness and reduces the transport capacity of water for particles, while dense root systems favor soil permeability, porosity, infiltration, and, thus, the sorption of dissolved nutrients (DN, DP) to soil particles as well as their uptake by plants [45,51]. Previous studies reported contrasting results in respect to the efficacy of grassed and woody RBZ [12,52,53]. Most probably, this is due the large number of processes and complex interactions among nutrients, plants, soil, and micro-organisms [54].
- Soil texture, flow pathway, and nutrient form: the larger the soil particles, the faster they settle under given flow conditions. While most of the coarse sediment can be retained even in narrow RBZ, the retention of fine sediment requires soil infiltration in RBZ which are more than 15–20 m wide in order to be effective [12,23,55]. In addition, soil composition (e.g., texture) is decisive for P sorption, hydraulic conductivity and, thus, for surface runoff, soil moisture storage, as well as residence time of nutrients in the root zone [40,47,51,56,57]. While sandy soils favor infiltration, surface flow predominates on clayey soils.
- RBZ slope and width: RBZ are expected to be less effective in reducing the transport capacity of water flow as well as in trapping sediments and nutrients in steep terrain [13,23,40] thus requiring broader buffers on steeper slopes [48]. Due to the experimental design and data availability, the influence of slope was not significant in other studies (e.g., [47,58]). RBZ slope was used in some regression models as an independent variable (e.g., [13,48]).
2.2. Aggregating the Nutrient Forms
2.3. BN Design—Nodes and States
2.4. BN Training and Evaluation—Importance of Nodes and State Definition
2.5. Implementation
3. Results
3.1. Aggregating the Nutrient Forms
3.2. Variability of RBZ Efficacy and Importance of Nodes
3.3. Cross-Validation and Evaluation of BNs
4. Discussion
4.1. BN Cross-Validation and Evaluation
4.2. Further BN Development
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Le Moal, M.; Gascuel-Odoux, C.; Ménesguen, A.; Souchon, Y.; Étrillard, C.; Levain, A.; Moatar, F.; Pannard, A.; Souchu, P.; Lefebvre, A.; et al. Eutrophication: A new wine in an old bottle? Sci. Total Environ. 2019, 651, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Evans, A.E.V.; Mateo-Sagasta, J.; Qadir, M.; Boelee, E.; Ippolito, A. Agricultural water pollution: Key knowledge gaps and research needs. Curr. Opin. Environ. Sust. 2019, 36, 20–27. [Google Scholar] [CrossRef]
- FAO; IMWI. More People, More Food, Worse Water? A Global Review of Water Pollution from Agriculture; Mateo-Sagasta, J., Marjani Zadeh, S., Turral, H., Eds.; FAO: Rome, Italy; IMWI: Colombo, Sri Lanka, 2018; p. 207. [Google Scholar]
- Diamantini, E.; Lutz, S.R.; Mallucci, S.; Majone, B.; Merz, R.; Bellin, A. Driver detection of water quality trends in three large European river basins. Sci. Total Environ. 2018, 612, 49–62. [Google Scholar] [CrossRef] [PubMed]
- Schwarzenbach, R.P.; Egli, T.; Hofstetter, T.B.; von Gunten, U.; Wehrli, B. Global Water Pollution and Human Health. Annu. Rev. Environ. Resour. 2010, 35, 109–136. [Google Scholar] [CrossRef]
- Withers, P.J.A.; Neal, C.; Jarvie, H.P.; Doody, D.G. Agriculture and Eutrophication: Where Do We Go from Here? Sustainability 2014, 6, 5853. [Google Scholar] [CrossRef]
- Fischer, P.; Pöthig, R.; Venohr, M. The degree of phosphorus saturation of agricultural soils in Germany: Current and future risk of diffuse P loss and implications for soil P management in Europe. Sci. Total Environ. 2017, 599, 1130–1139. [Google Scholar] [CrossRef] [PubMed]
- European Environment Agency. European Waters: Assessment of Status and Pressures 2018; Publications Office of the European Union: Luxembourg, Luxembourg, 2018; p. 85. [Google Scholar]
- Stutter, M.I.; Chardon, W.J.; Kronvang, B. Riparian Buffer Strips as a Multifunctional Management Tool in Agricultural Landscapes: Introduction. J. Environ. Qual. 2012, 41, 297–303. [Google Scholar] [CrossRef]
- Feld, C.K.; Fernandes, M.R.; Ferreira, M.T.; Hering, D.; Ormerod, S.J.; Venohr, M.; Gutiérrez-Cánovas, C. Evaluating riparian solutions to multiple stressor problems in river ecosystems-A conceptual study. Water Res. 2018, 139, 381–394. [Google Scholar] [CrossRef]
- Mander, Ü.; Tournebize, J.; Tonderski, K.; Verhoeven, J.T.A.; Mitsch, W.J. Planning and establishment principles for constructed wetlands and riparian buffer zones in agricultural catchments. Ecol. Eng. 2017, 103, 296–300. [Google Scholar] [CrossRef]
- Dorioz, J.-M.; Wang, D.; Poulenard, J.; Trevisan, D. The effect of grass buffer strips on phosphorus dynamics—A critical review and synthesis as a basis for application in agricultural landscapes in France. Agric. Ecosyst. Environ. 2006, 117, 4–21. [Google Scholar] [CrossRef]
- Zhang, X.; Liu, X.; Zhang, M.; Dahlgren, R.A.; Eitzel, M. A review of vegetated buffers and a meta-analysis of their mitigation efficacy in reducing nonpoint source pollution. J. Environ. Qual. 2010, 39, 76–84. [Google Scholar] [CrossRef] [PubMed]
- Muñoz-Carpena, R.; Parsons, J.E.; Gilliam, J.W. Modeling hydrology and sediment transport in vegetative filter strips. J. Hydrol. 1999, 214, 111–129. [Google Scholar] [CrossRef]
- Lowrance, R.; Altier, L.S.; Williams, R.G.; Inamdar, S.P.; Sheridan, J.M.; Bosch, D.D.; Hubbard, R.K.; Thomas, D.L. REMM: The Riparian Ecosystem Management Model. J. Soil Water Conserv. 2000, 55, 27–34. [Google Scholar]
- Hassanzadeh, Y.T.; Vidon, P.G.; Gold, A.J.; Pradhanang, S.M.; Addy Lowder, K. RZ-TRADEOFF: A New Model to Estimate Riparian Water and Air Quality Functions. Water 2019, 11, 769. [Google Scholar] [CrossRef]
- Weissteiner, C.J.; Bouraoui, F.; Aloe, A. Reduction of nitrogen and phosphorus loads to European rivers by riparian buffer zones. Knowl. Manag. Aquat. Ecosyst. 2013, 408, 15. [Google Scholar] [CrossRef]
- Hook, P.B. Sediment retention in rangeland riparian buffers. J. Environ. Qual. 2003, 32, 1130–1137. [Google Scholar] [CrossRef]
- Lee, P.; Smyth, C.; Boutin, S. Quantitative review of riparian buffer width guidelines from Canada and the United States. J. Environ. Manag. 2004, 70, 165–180. [Google Scholar] [CrossRef]
- Broadmeadow, S.; Nisbet, T.R. The effects of riparian forest management on the freshwater environment: A literature review of best management practice. HESS 2004, 8, 286–305. [Google Scholar] [CrossRef]
- Dosskey, M.G.; Helmers, M.J.; Eisenhauer, D.E. A design aid for determining width of filter strips. J. Soil Water Conserv. 2008, 63, 232–241. [Google Scholar] [CrossRef]
- Gumiere, S.J.; Le Bissonnais, Y.; Raclot, D.; Cheviron, B. Vegetated filter effects on sedimentological connectivity of agricultural catchments in erosion modelling: A review. ESPL 2011, 36, 3–19. [Google Scholar] [CrossRef]
- Liu, X.; Zhang, X.; Zhang, M. Major factors influencing the efficacy of vegetated buffers on sediment trapping: A review and analysis. J. Environ. Qual. 2008, 37, 1667–1674. [Google Scholar] [CrossRef] [PubMed]
- Yuan, Y.; Bingner, R.L.; Locke, M.A. A review of effectiveness of vegetative buffers on sediment trapping in agricultural areas. Ecohydrology 2009, 2, 321–336. [Google Scholar] [CrossRef]
- Mayer, P.M.; Reynolds, S.K.; McCutchen, M.D.; Canfield, T.J. Meta-analysis of nitrogen removal in riparian buffers. J. Environ. Qual. 2007, 36, 1172–1180. [Google Scholar] [CrossRef] [PubMed]
- Barton, D.N.; Kuikka, S.; Varis, O.; Uusitalo, L.; Henriksen, H.J.; Borsuk, M.; de la Hera, A.; Farmani, R.; Johnson, S.; Linnell, J.D. Bayesian networks in environmental and resource management. Integr. Environ. Assess. Manag. 2012, 8, 418–429. [Google Scholar] [CrossRef]
- Borsuk, M.E.; Stow, C.A.; Reckhow, K.H. A Bayesian network of eutrophication models for synthesis, prediction, and uncertainty analysis. Ecol. Model. 2004, 173, 219–239. [Google Scholar] [CrossRef]
- Kelly, R.A.; Jakeman, A.J.; Barreteau, O.; Borsuk, M.E.; ElSawah, S.; Hamilton, S.H.; Henriksen, H.J.; Kuikka, S.; Maier, H.R.; Rizzoli, A.E.; et al. Selecting among five common modelling approaches for integrated environmental assessment and management. Environ. Model. Softw. 2013, 47, 159–181. [Google Scholar] [CrossRef]
- Marcot, B.G.; Penman, T.D. Advances in Bayesian network modelling: Integration of modelling technologies. Environ. Model. Softw. 2019, 111, 386–393. [Google Scholar] [CrossRef]
- Phan, T.D.; Smart, J.C.R.; Capon, S.J.; Hadwen, W.L.; Sahin, O. Applications of Bayesian belief networks in water resource management: A systematic review. Environ. Model. Softw. 2016, 85, 98–111. [Google Scholar] [CrossRef]
- McVittie, A.; Norton, L.; Martin-Ortega, J.; Siameti, I.; Glenk, K.; Aalders, I. Operationalizing an ecosystem services-based approach using Bayesian Belief Networks: An application to riparian buffer strips. Ecol. Econ. 2015, 110, 15–27. [Google Scholar] [CrossRef]
- Castelle, A.J.; Johnson, A.W.; Conolly, C. Wetland and stream buffer size requirements-a review. J. Environ. Qual. 1994, 23, 878–882. [Google Scholar] [CrossRef]
- Collins, A.L.; Hughes, G.; Zhang, Y.; Whitehead, J. Mitigating diffuse water pollution from agriculture: Riparian buffer strip performance with width. CAB Rev. Perspect. Agric. Veter. Sci. Nutr. Nat. Resour. 2009, 4, 15. [Google Scholar] [CrossRef]
- Dodd, R.J.; Sharpley, A.N. Conservation practice effectiveness and adoption: Unintended consequences and implications for sustainable phosphorus management. Nutr. Cycl. Agroecosyst. 2016, 104, 373–392. [Google Scholar] [CrossRef]
- Dosskey, M.G. Toward quantifying water pollution abatement in response to installing buffers on crop land. Environ. Manag. 2001, 28, 577–598. [Google Scholar] [CrossRef] [PubMed]
- Dosskey, M.G.; Vidon, P.; Gurwick, N.P.; Allan, C.J.; Duval, T.P.; Lowrance, R. The Role of Riparian Vegetation in Protecting and Improving Chemical Water Quality in Streams. JAWRA 2010, 46, 261–277. [Google Scholar] [CrossRef]
- Hickey, M.B.C.; Doran, B. A review of the efficiency of buffer strips for the maintenance and enhancement of riparian ecosystems. Water Qual. Res. J. Can. 2004, 39, 311–317. [Google Scholar] [CrossRef]
- Hill, A.R. Nitrate removal in stream riparian zones. J. Environ. Qual. 1996, 25, 743–755. [Google Scholar] [CrossRef]
- Hill, A.R. Groundwater nitrate removal in riparian buffer zones: A review of research progress in the past 20 years. Biogeochemistry 2019, 143, 347–369. [Google Scholar] [CrossRef]
- Hoffmann, C.C.; Kjaergaard, C.; Uusi-Kämppä, J.; Hansen, H.C.B.; Kronvang, B. Phosphorus retention in riparian buffers: Review of their efficiency. J. Environ. Qual. 2009, 38, 1942–1955. [Google Scholar] [CrossRef]
- Krutz, L.J.; Senseman, S.A.; Zablotowicz, R.M.; Matocha, M.A. Reducing herbicide runoff from agricultural fields with vegetative filter strips: A review. Weed Sci. 2005, 53, 353–367. [Google Scholar] [CrossRef]
- Lacas, J.-G.; Voltz, M.; Gouy, V.; Carluer, N.; Gril, J.-J. Using grassed strips to limit pesticide transfer to surface water: A review. Agron. Sustain. Dev. 2005, 25, 253–266. [Google Scholar] [CrossRef]
- Mayer, P.M.; Reynolds, S.K., Jr.; Canfield, T.J. Riparian Buffer Width, Vegetative Cover, and Nitrogen Removal Effectiveness; EPA/600/R-05/118; U.S. Environmental Protection Agency: Washington, DC, USA, 2005; p. 27. [Google Scholar]
- Polyakov, V.; Fares, A.; Ryder, M.H. Precision riparian buffers for the control of nonpoint source pollutant loading into surface water: A review. Environ. Rev. 2005, 13, 129–144. [Google Scholar] [CrossRef]
- Roberts, W.M.; Stutter, M.I.; Haygarth, P.M. Phosphorus retention and remobilization in vegetated buffer strips: A review. J. Environ. Qual. 2012, 41, 389–399. [Google Scholar] [CrossRef] [PubMed]
- Sweeney, B.W.; Newbold, J.D. Streamside Forest Buffer Width Needed to Protect Stream Water Quality, Habitat, and Organisms: A Literature Review. JAWRA 2014, 50, 560–584. [Google Scholar] [CrossRef]
- Valkama, E.; Usva, K.; Saarinen, M.; Uusi-Kämppä, J. A Meta-Analysis on Nitrogen Retention by Buffer Zones. J. Environ. Qual. 2018. [Google Scholar] [CrossRef]
- Wenger, S. A Review of the Scientific Literature on Riparian Buffer Width, Extent and Vegetation; Office of Public Service and Outreach, Institute of Ecology: Athens, GA, USA, 1999; p. 59. [Google Scholar]
- Borin, M.; Vianello, M.; Morari, F.; Zanin, G. Effectiveness of buffer strips in removing pollutants in runoff from a cultivated field in North-East Italy. Agric. Ecosyst. Environ. 2005, 105, 101–114. [Google Scholar] [CrossRef]
- Fiener, P.; Auerswald, K. Effectiveness of grassed waterways in reducing runoff and sediment delivery from agricultural watersheds. J. Environ. Qual. 2003, 32, 927–936. [Google Scholar] [CrossRef] [PubMed]
- Pärn, J.; Pinay, G.; Mander, Ü. Indicators of nutrients transport from agricultural catchments under temperate climate: A review. Ecol. Indic. 2012, 22, 4–15. [Google Scholar] [CrossRef]
- King, S.E.; Osmond, D.L.; Smith, J.; Burchell, M.R.; Dukes, M.; Evans, R.O.; Knies, S.; Kunickis, S. Effects of Riparian Buffer Vegetation and Width: A 12-Year Longitudinal Study. J. Environ. Qual. 2016, 45, 1243–1251. [Google Scholar] [CrossRef]
- Osborne, L.L.; Kovacic, D.A. Riparian vegetated buffer strips in water-quality restoration and stream management. Freshw. Biol. 1993, 29, 243–258. [Google Scholar] [CrossRef]
- Yang, F.; Yang, Y.; Li, H.; Cao, M. Removal efficiencies of vegetation-specific filter strips on nonpoint source pollutants. Ecol. Eng. 2015, 82, 145–158. [Google Scholar] [CrossRef]
- Schauder, H.; Auerswald, K. Long-term trapping efficiency of a vegetated filter strip under agricultural use. J. Plant Nutr. Soil Sci. 1992, 155, 489–492. [Google Scholar] [CrossRef]
- Vidon, P.; Hill, A.R. Denitrification and patterns of electron donors and acceptors in eight riparian zones with contrasting hydrogeology. Biogeochemistry 2004, 71, 259–283. [Google Scholar] [CrossRef]
- Barling, R.D.; Moore, I.D. Role of buffer strips in management of waterway pollution: A review. Environ. Manag. 1994, 18, 543–558. [Google Scholar] [CrossRef]
- Darch, T.; Carswell, A.; Blackwell, M.S.A.; Hawkins, J.M.B.; Haygarth, P.M.; Chadwick, D. Dissolved Phosphorus Retention in Buffer Strips: Influence of Slope and Soil Type. J. Environ. Qual. 2015, 44, 1216–1224. [Google Scholar] [CrossRef] [PubMed]
- Chen, S.H.; Pollino, C.A. Good practice in Bayesian network modelling. Environ. Model. Softw. 2012, 37, 134–145. [Google Scholar] [CrossRef]
- Nojavan, A.F.; Qian, S.S.; Stow, C.A. Comparative analysis of discretization methods in Bayesian networks. Environ. Model. Softw. 2017, 87, 64–71. [Google Scholar] [CrossRef]
- Marcot, B.G. Metrics for evaluating performance and uncertainty of Bayesian network models. Ecol. Model. 2012, 230, 50–62. [Google Scholar] [CrossRef]
- Moe, S.J.; Haande, S.; Couture, R.-M. Climate change, cyanobacteria blooms and ecological status of lakes: A Bayesian network approach. Ecol. Model. 2016, 337, 330–347. [Google Scholar] [CrossRef]
- Team, R.C. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2017. [Google Scholar]
- Scutari, M. Learning Bayesian Networks with the bnlearn R Package. J. Stat. Softw. 2010, 35, 1–22. [Google Scholar] [CrossRef]
- Therneau, T.; Atkinson, B.; Ripley, B. rpart: Recursive Partitioning and Regression Trees. 1–11 April 2017. Available online: https://cran.r-project.org/web/packages/rpart/index.html (accessed on 14 June 2019).
- Højsgaard, S. Graphical Independence Networks with the gRain Package for R. J. Stat. Softw. 2012, 1. [Google Scholar] [CrossRef]
- Zhao, Q.; Zhang, Y.; Xu, S.; Ji, X.; Wang, S.; Ding, S. Relationships between Riparian Vegetation Pattern and the Hydraulic Characteristics of Upslope Runoff. Sustainability 2019, 11. [Google Scholar] [CrossRef]
- Kelly, J.M.; Kovar, J.L.; Sokolowsky, R.; Moorman, T.B. Phosphorus uptake during four years by different vegetative cover types in a riparian buffer. Nutr. Cycl. Agroecosyst. 2007, 78, 239–251. [Google Scholar] [CrossRef]
- Missaoui, A.M.; Boerma, H.R.; Bouton, J.H. Genetic variation and heritability of phosphorus uptake in Alamo switchgrass grown in high phosphorus soils. Field Crops Res. 2005, 93, 186–198. [Google Scholar] [CrossRef]
- Oniśko, A.; Druzdzel, M.J.; Wasyluk, H. Learning Bayesian network parameters from small data sets: Application of Noisy-OR gates. Int. J. Approx. Reason. 2001, 27, 165–182. [Google Scholar] [CrossRef]
- Pitchforth, J.; Mengersen, K. A proposed validation framework for expert elicited Bayesian Networks. Expert Syst. Appl. 2013, 40, 162–167. [Google Scholar] [CrossRef]
- Cooper, J.R.; Gilliam, J.W. Phosphorus redistribution from cultivated fields into riparian areas. Soil Sci. Soc. Am. J. 1987, 51, 1600–1604. [Google Scholar] [CrossRef]
- Stutter, M.I.; Langan, S.J.; Lumsdon, D.G. Vegetated buffer strips can lead to increased release of phosphorus to waters: A biogeochemical assessment of the mechanisms. Environ. Sci. Technol. 2009, 43, 1858–1863. [Google Scholar] [CrossRef]
- Uusi-Kämppä, J.; Jauhiainen, L. Long-term monitoring of buffer zone efficiency under different cultivation techniques in boreal conditions. Agric. Ecosyst. Environ. 2010, 137, 75–85. [Google Scholar] [CrossRef]
- Uusi-Kämppä, J. Phosphorus purification in buffer zones in cold climates. Ecol. Eng. 2005, 24, 491–502. [Google Scholar] [CrossRef]
- Shipitalo, M.J.; Bonta, J.V.; Dayton, E.A.; Owens, L.B. Impact of Grassed Waterways and Compost Filter Socks on the Quality of Surface Runoff from Corn Fields. J. Environ. Qual. 2010, 39, 1009–1018. [Google Scholar] [CrossRef]
- Newbold, J.D.; Herbert, S.; Sweeney, B.W.; Kiry, P.; Alberts, S.J. Water Quality Functions of a 15-Year-Old Riparian Forest Buffer System. JAWRA 2010, 46, 299–310. [Google Scholar] [CrossRef]
- Dillaha, T.A.; Sherrard, J.H.; Lee, D.; Mostaghimi, S.; Shanholtz, V.O. Evaluation of vegetative filter strips as a best management practice for feed lots. J. Water Pollut. Control Fed. 1988, 60, 1231–1238. [Google Scholar]
- Kassam, A.; Friedrich, T.; Derpsch, R. Global spread of Conservation Agriculture. Int. J. Environ. Stud. 2019, 76, 29–51. [Google Scholar] [CrossRef]
- Prestele, R.; Hirsch, A.L.; Davin, E.L.; Seneviratne, S.I.; Verburg, P.H. A spatially explicit representation of conservation agriculture for application in global change studies. Glob. Chang. Biol. 2018, 24, 4038–4053. [Google Scholar] [CrossRef] [PubMed]
- Jarvie, H.P.; Johnson, L.T.; Sharpley, A.N.; Smith, D.R.; Baker, D.B.; Bruulsema, T.W.; Confesor, R. Increased Soluble Phosphorus Loads to Lake Erie: Unintended Consequences of Conservation Practices? J. Environ. Qual. 2017, 46, 123–132. [Google Scholar] [CrossRef] [PubMed]
- Daryanto, S.; Wang, L.; Jacinthe, P.-A. Impacts of no-tillage management on nitrate loss from corn, soybean and wheat cultivation: A meta-analysis. Sci. Rep. 2017, 7, 12117. [Google Scholar] [CrossRef]
- Eghball, B.; Gilley, J.E.; Kramer, L.A.; Moorman, T.B. Narrow grass hedge effects on phosphorus and nitrogen in runoff following manure and fertilizer application. J. Soil Water Conserv. 2000, 55, 172–176. [Google Scholar]
- Raffaelle, J.B., Jr.; McGregor, K.C.; Foster, G.R.; Cullum, R.F. Effect of narrow grass strips on conservation reserve land converted to cropland. Trans. ASAE 1997, 40, 1581–1587. [Google Scholar] [CrossRef]
- Dillaha, T.A.; Sherrard, J.H.; Lee, D.; Shanholtz, V.O.; Mostaghimi, S.; Magette, W.L. Use of Vegetative Filter Strips to Minimize Sediment and Phosphorus Losses from Feedlots; Phase 1, Experimental Plot Studies; Virginia Polytechnic Institute and State University Blacksburg: Blacksburg, VA, USA, 1986; p. 68. [Google Scholar]
- Blanco-Canqui, H.; Gantzer, C.J.; Anderson, S.H. Performance of grass barriers and filter strips under interrill and concentrated flow. J. Environ. Qual. 2006, 35, 1969–1974. [Google Scholar] [CrossRef]
- White, M.J.; Arnold, J.G. Development of a simplistic vegetative filter strip model for sediment and nutrient retention at the field scale. Hydrol. Process. 2009, 23, 1602–1616. [Google Scholar] [CrossRef]
- Vidon, P.G.F.; Hill, A.R. Landscape controls on nitrate removal in stream riparian zones. WRR 2004, 40. [Google Scholar] [CrossRef]
- Habibiandehkordi, R.; Lobb, D.A.; Sheppard, S.C.; Flaten, D.N.; Owens, P.N. Uncertainties in vegetated buffer strip function in controlling phosphorus export from agricultural land in the Canadian prairies. Environ. Sci. Pollut. Res. 2017, 24, 18372–18382. [Google Scholar] [CrossRef] [PubMed]
- Verstraeten, G.; Poesen, J.; Gillijns, K.; Govers, G. The use of riparian vegetated filter strips to reduce river sediment loads: An overestimated control measure? Hydrol. Process. 2006, 20, 4259–4267. [Google Scholar] [CrossRef]
- Helmers, M.J.; Eisenhauer, D.E.; Dosskey, M.G.; Franti, T.G.; Brothers, J.M.; McCullough, M.C. Flow pathways and sediment trapping in a field-scale vegetative filter. Trans. ASAE 2005, 48, 955–968. [Google Scholar] [CrossRef]
- Dosskey, M.G.; Helmers, M.J.; Eisenhauer, D.E.; Franti, T.G.; Hoagland, K.D. Assessment of concentrated flow through riparian buffers. J. Soil Water Conserv. 2002, 57, 336–343. [Google Scholar]
- Daniels, R.B.; Gilliam, J.W. Sediment and chemical load reduction by grass and riparian filters. Soil Sci. Soc. Am. J. 1996, 60, 246–251. [Google Scholar] [CrossRef]
- Yadav, B.; Hatfield, K. Stream network conflation with topographic DEMs. Environ. Model. Softw. 2018, 102, 241–249. [Google Scholar] [CrossRef]
- Hösl, R.; Strauss, P.; Glade, T. Man-made linear flow paths at catchment scale: Identification, factors and consequences for the efficiency of vegetated filter strips. Landsc. Urban Plan. 2012, 104, 245–252. [Google Scholar] [CrossRef]
- Beven, K.J.; Kirkby, M.J. A physically based, variable contributing area model of basin hydrology. Hydrol. Sci. B 1979, 24, 43–69. [Google Scholar] [CrossRef]
- Beven, K. TOPMODEL: A critique. Hydrol. Process. 1997, 11, 1069–1085. [Google Scholar] [CrossRef]
- De Vente, J.; Poesen, J.; Arabkhedri, M.; Verstraeten, G. The sediment delivery problem revisited. Prog. Phys. Geogr. 2007, 31, 155–178. [Google Scholar] [CrossRef]
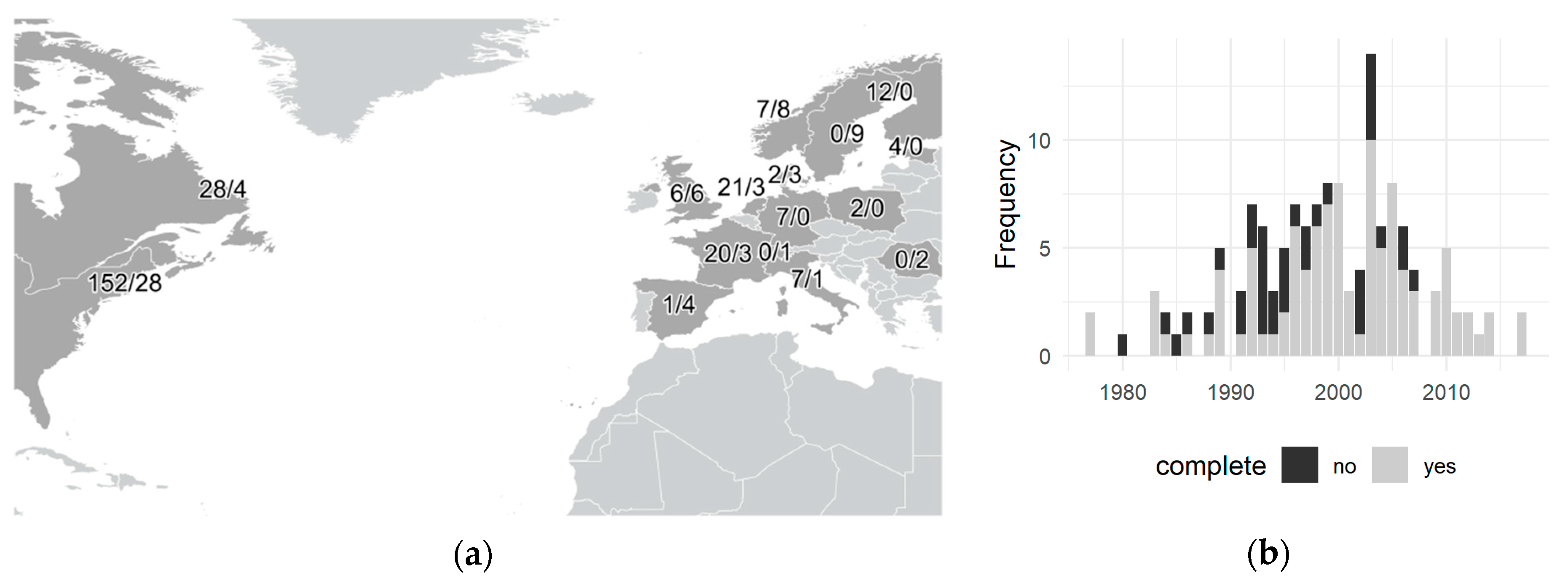
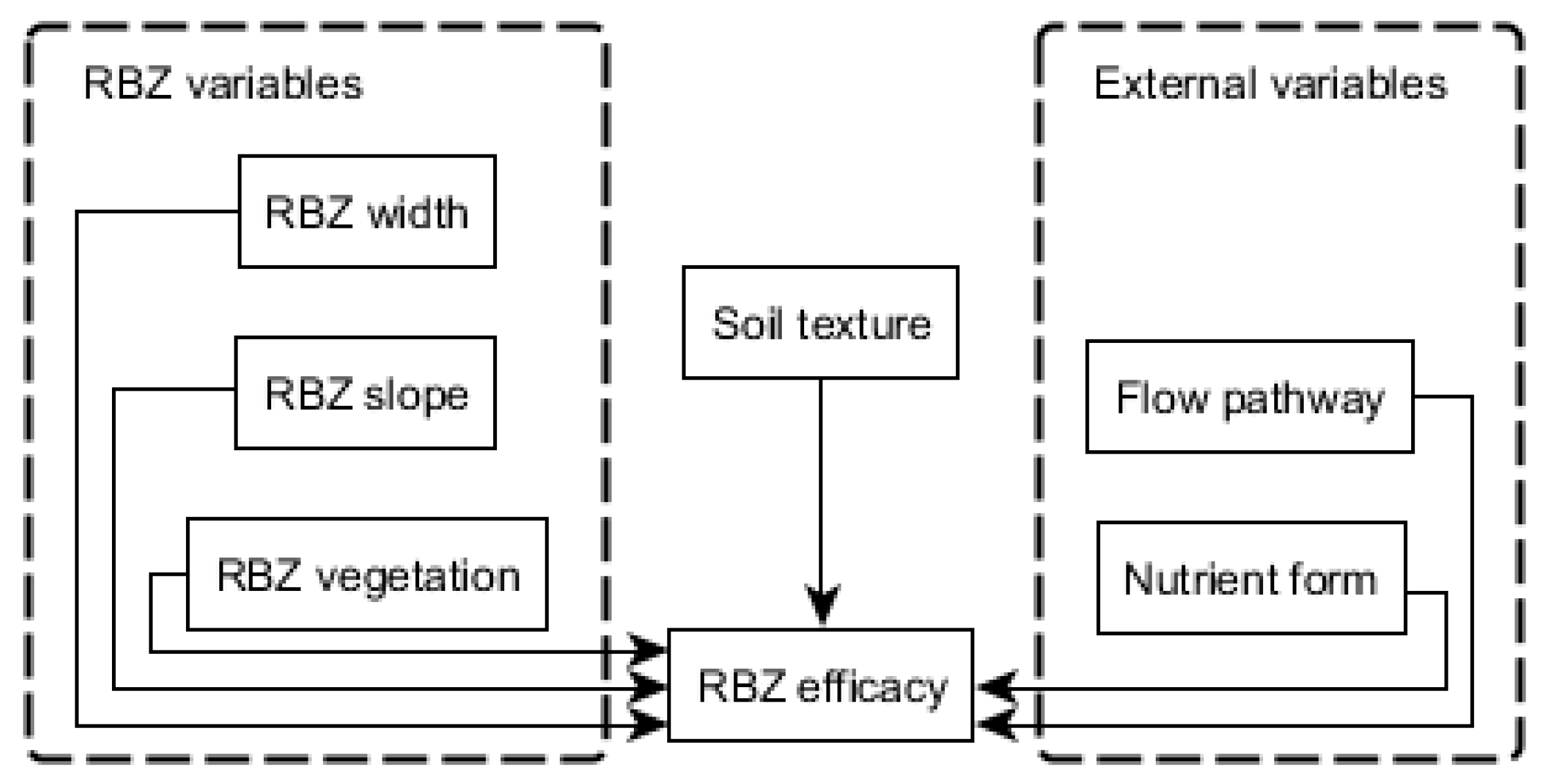
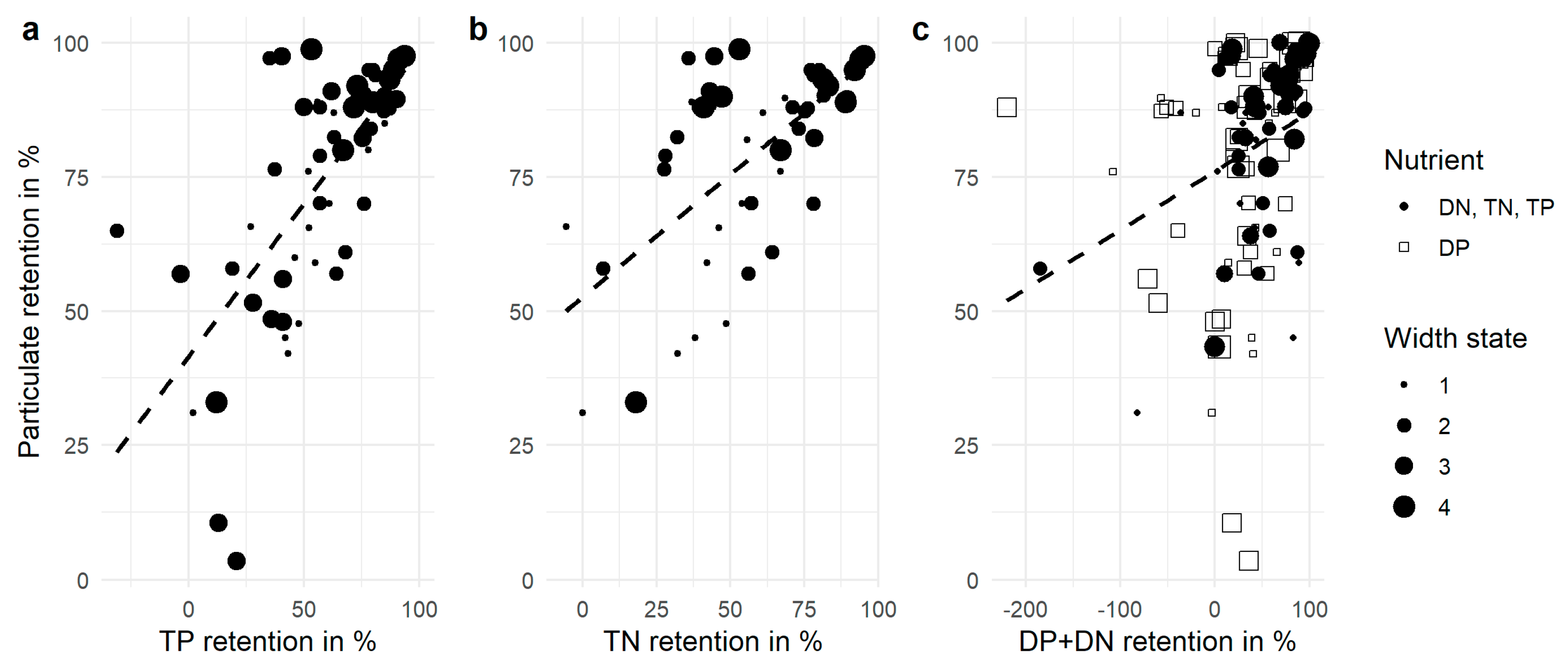
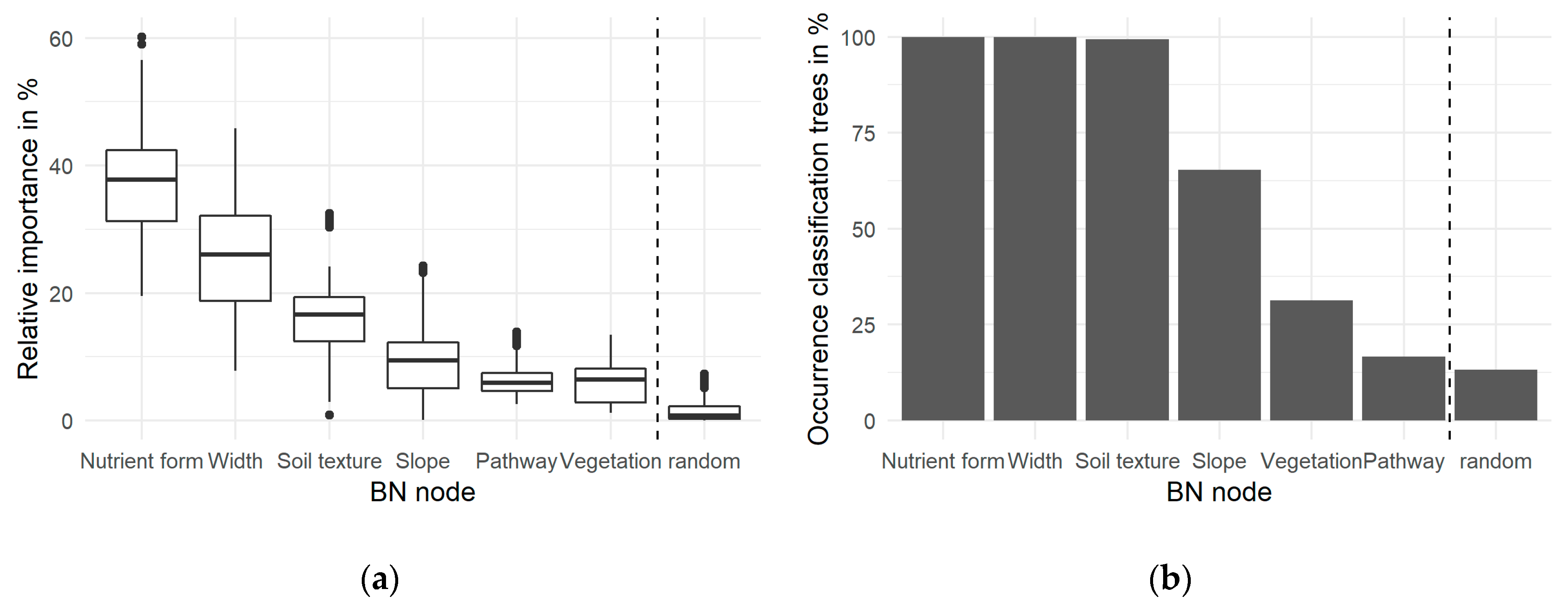
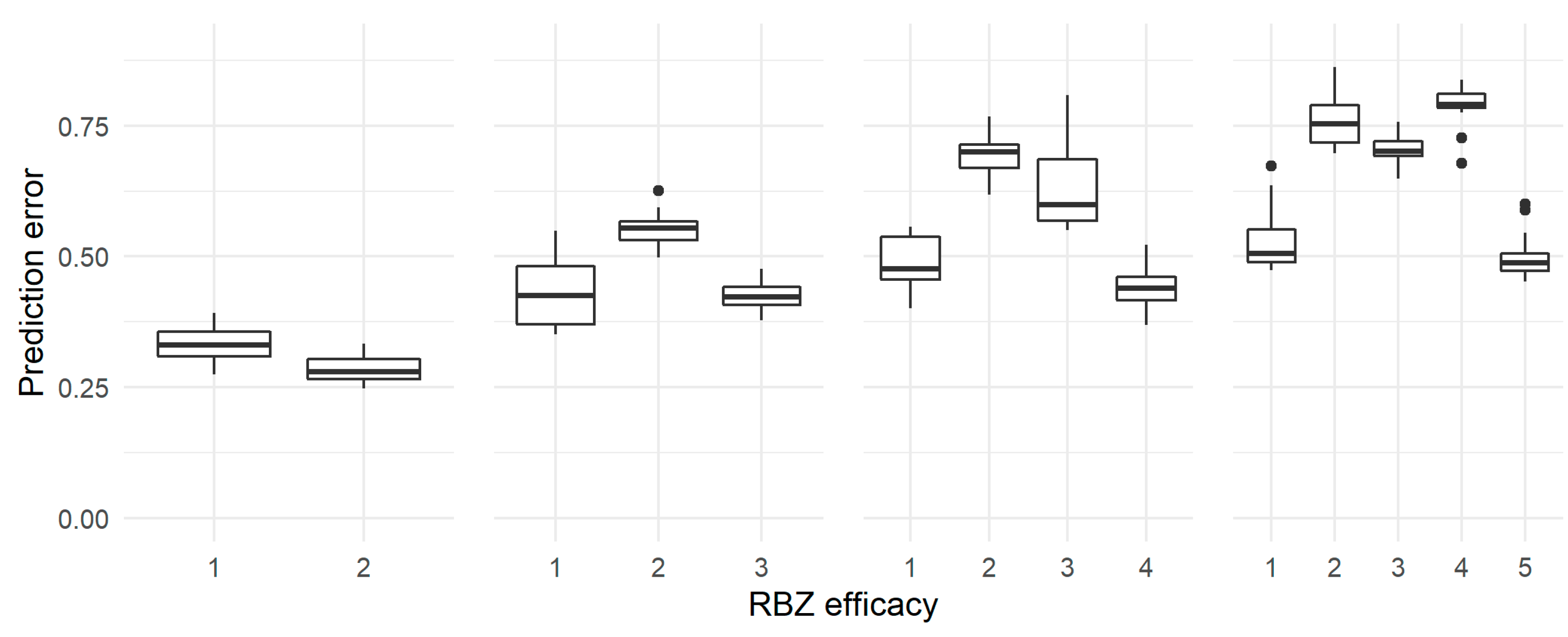
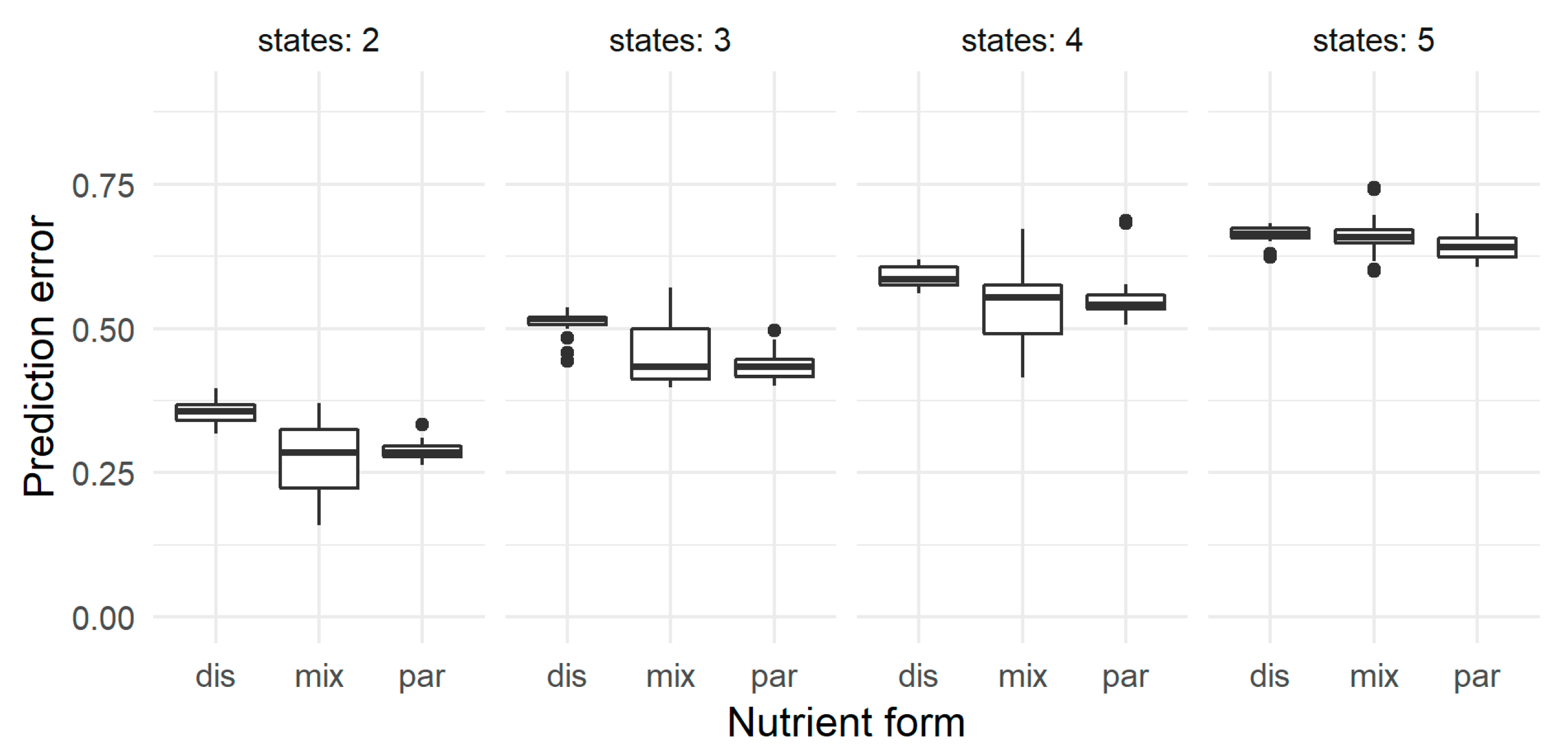
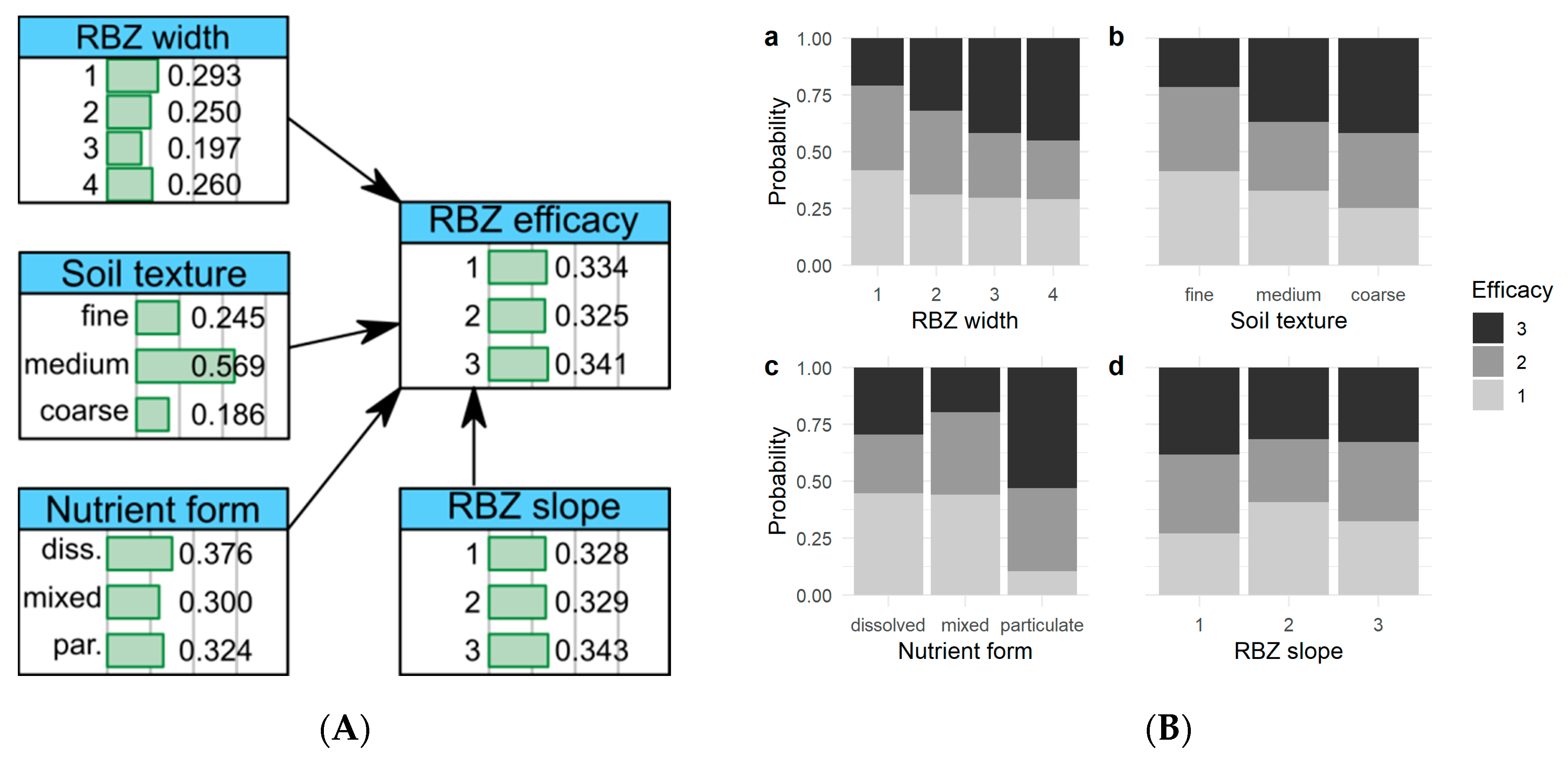
| Variable (Node) | Unit | States | Definition | Data per State |
|---|---|---|---|---|
| RBZ width | m | 1, 2 | <10, 10–220 | 315, 265 |
| 1, 2, 3 | <5.1, <10.1, 10.1–220 | 170, 214, 196 | ||
| 1, 2, 3, 4 | <5.1, <10, <15, 15–220 | 170, 145, 114, 151 | ||
| RBZ vegetation | - | Grass | Including e.g., giant cane | 433 |
| Woody | With shrubs and trees | 147 | ||
| Soil texture | - | Fine, medium, coarse | Clayey (fL, CL, SiC, C, SC), silty-loamy (L, SiL, Si, SCL), sandy (SL, cL, S, SSi, LS) 1 | 142, 330, 108 |
| Fine, coarse | Clayey, silty to sandy | 142, 408 | ||
| Nutrient form | - | Particulate | Particulate P (PP), sediment | 188 (17 + 171) |
| Mixed | Total P (TP) and N (TN) | 174 (95 + 79) | ||
| Dissolved | Dissolved P (DP) 2 and N (DN) 3 | 218 (87 + 131) | ||
| Flow pathway | - | Surface | Surface runoff | 480 |
| Subsurface | (Including) groundwater | 100 | ||
| RBZ slope | % | 1, 2 | <5, 5–22 | 262, 318 |
| 1, 2, 3 | <3.1, <7.5, 7.5–22 | 190, 191, 199 | ||
| 1, 2, 3, 4 | <3, <5, <10, 10–22 | 124, 138, 157, 161 | ||
| RBZ efficacy | % | 1, 2 | <68.3, ≥68.3 | 290, 290 |
| 1, 2, 3 | <55, <82.3, ≥82.3 | 193, 193, 194 | ||
| 1, 2, 3, 4 | <42.6, <68.3, <87.5, ≥87.5 | 145, 145, 145, 145 | ||
| 1, 2, 3, 4, 5 | <35.5, <60.6, <78.5, <89.8, ≥89.8 | 116, 116, 115, 117, 116 |
| Value | Complete (Count) | Incomplete (Count) |
|---|---|---|
| Studies 1 | 104 | 36 |
| Datasets | 269 | 72 |
| Efficacy values | 580 | 98 |
| Countries 2 | 13 | 12 |
| Variables (nodes) | All | Slope, soil texture |
| BN | RBZ Efficacy | Node | Mean Prediction Error | Significance (p Value) 1 | |||
|---|---|---|---|---|---|---|---|
| Number of States | Two States | Three States | Four States | 2 < 3 2 | 3 < 4 | ||
| Complete | 2 | RBZ slope | 0.32 | 0.26 | 0.31 | 0.031* | 0.984 |
| 3 | 0.51 | 0.45 | 0.46 | 0.016* | 0.656 | ||
| 4 | 0.59 | 0.55 | 0.56 | 0.016* | 0.844 | ||
| 5 | 0.67 | 0.65 | 0.64 | 0.016* | 0.109 | ||
| 2 | RBZ width | 0.32 | 0.31 | 0.30 | 0.031* | 0.031* | |
| 3 | 0.47 | 0.47 | 0.47 | 0.719 | 0.109 | ||
| 4 | 0.59 | 0.55 | 0.55 | 0.016* | 0.922 | ||
| 5 | 0.67 | 0.66 | 0.64 | 0.281 | 0.016* | ||
| 2 | Soil texture | 0.32 | 0.30 | - | 0.002** | - | |
| 3 | 0.48 | 0.47 | - | 0.010** | - | ||
| 4 | 0.58 | 0.55 | - | 0.002** | - | ||
| 5 | 0.66 | 0.65 | - | 0.002** | - | ||
| Simplified | 2 | RBZ slope | 0.30 | 0.30 | 0.30 | 0.219 | 0.984 |
| 3 | 0.48 | 0.46 | 0.48 | 0.016* | 1 | ||
| 4 | 0.55 | 0.54 | 0.56 | 0.500 | 1 | ||
| 5 | 0.64 | 0.64 | 0.64 | 0.578 | 0.844 | ||
| 2 | RBZ width | 0.30 | 0.30 | 0.30 | 0.047* | 0.781 | |
| 3 | 0.48 | 0.47 | 0.47 | 0.047* | 0.953 | ||
| 4 | 0.58 | 0.53 | 0.54 | 0.016* | 0.844 | ||
| 5 | 0.64 | 0.64 | 0.64 | 0.656 | 0.219 | ||
| 2 | Soil texture | 0.30 | 0.30 | - | 0.963 | - | |
| 3 | 0.47 | 0.48 | - | 0.898 | - | ||
| 4 | 0.55 | 0.55 | - | 0.980 | - | ||
| 5 | 0.64 | 0.64 | - | 0.590 | - | ||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gericke, A.; Nguyen, H.H.; Fischer, P.; Kail, J.; Venohr, M. Deriving a Bayesian Network to Assess the Retention Efficacy of Riparian Buffer Zones. Water 2020, 12, 617. https://doi.org/10.3390/w12030617
Gericke A, Nguyen HH, Fischer P, Kail J, Venohr M. Deriving a Bayesian Network to Assess the Retention Efficacy of Riparian Buffer Zones. Water. 2020; 12(3):617. https://doi.org/10.3390/w12030617
Chicago/Turabian StyleGericke, Andreas, Hong Hanh Nguyen, Peter Fischer, Jochem Kail, and Markus Venohr. 2020. "Deriving a Bayesian Network to Assess the Retention Efficacy of Riparian Buffer Zones" Water 12, no. 3: 617. https://doi.org/10.3390/w12030617
APA StyleGericke, A., Nguyen, H. H., Fischer, P., Kail, J., & Venohr, M. (2020). Deriving a Bayesian Network to Assess the Retention Efficacy of Riparian Buffer Zones. Water, 12(3), 617. https://doi.org/10.3390/w12030617




