Modeling of Future Extreme Storm Surges at the NW Mediterranean Coast (Spain)
Abstract
1. Introduction
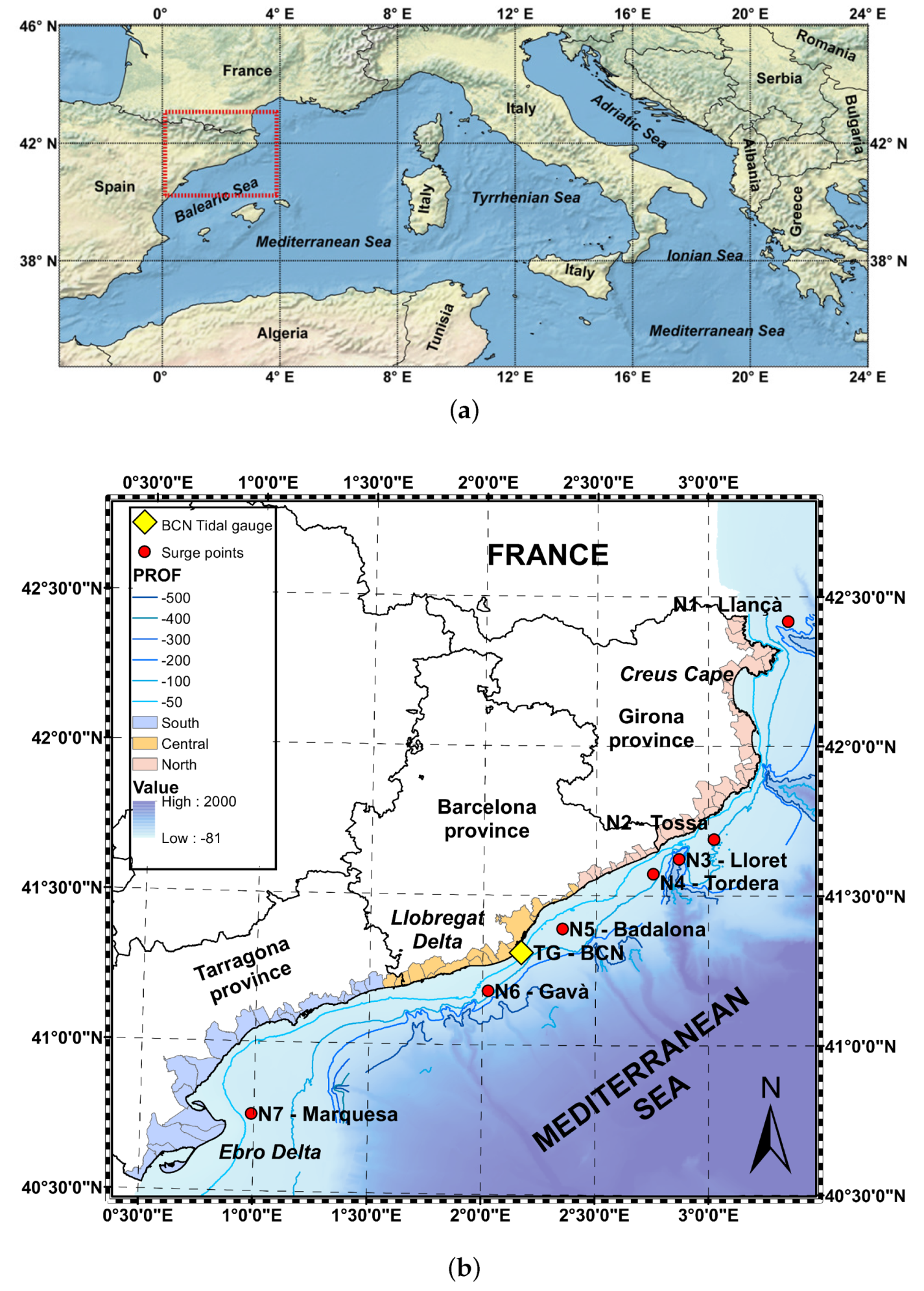
2. Study Area
3. Theoretical Background and Methods
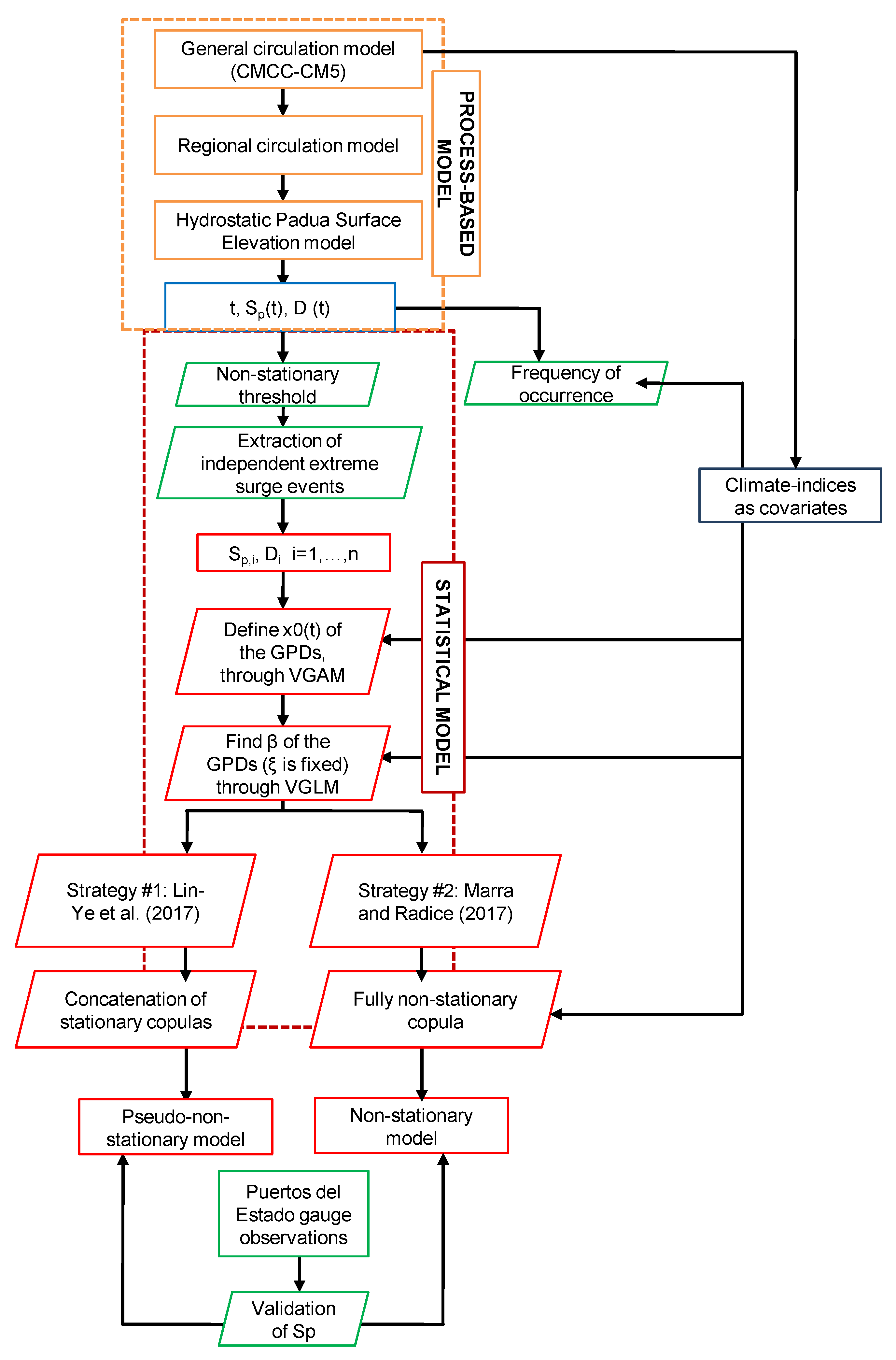
3.1. The Process-Based Model
3.2. Statistical Model
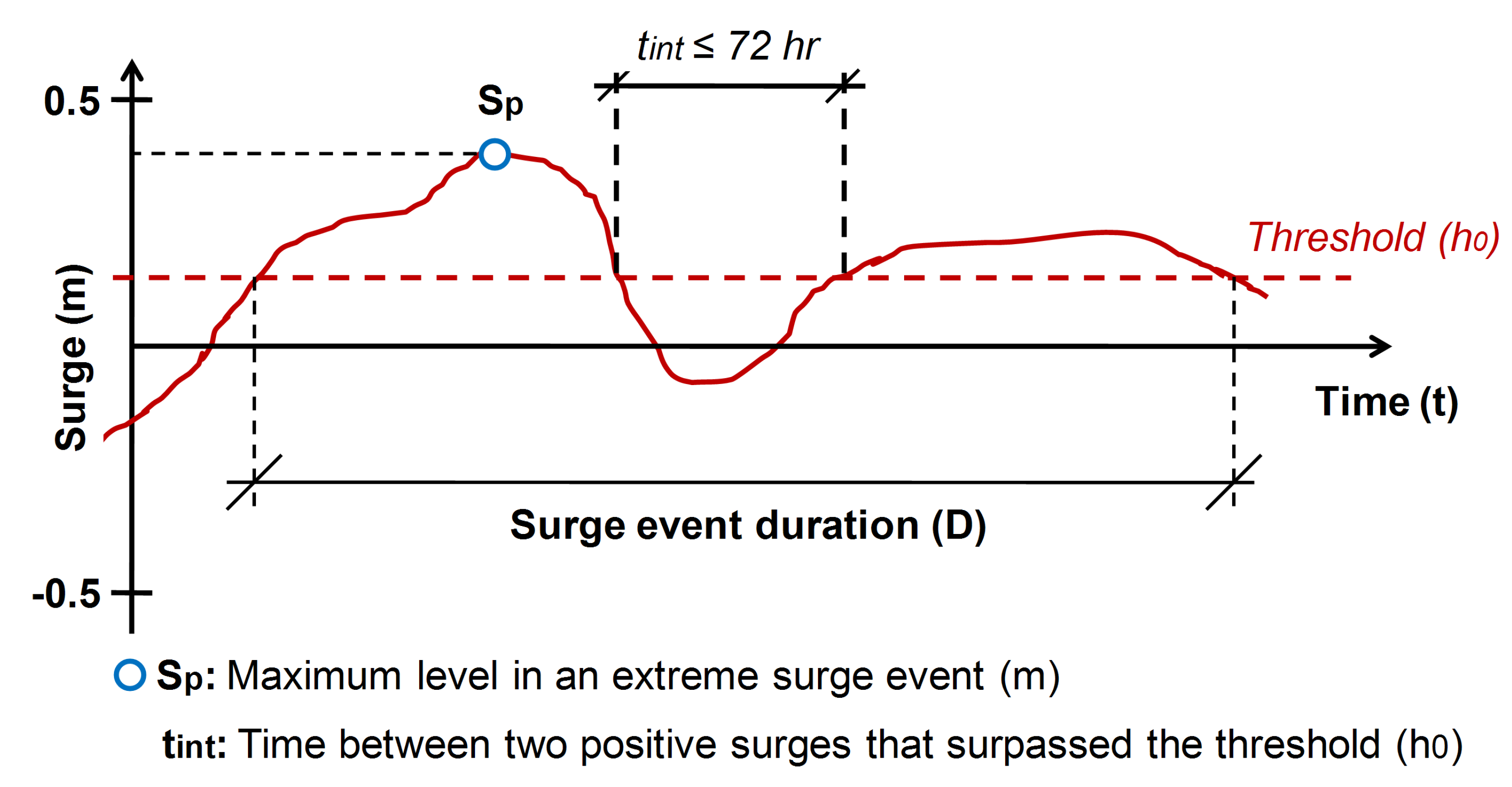
3.2.1. Commonalities of the Two Strategies
3.2.2. Differences of the Two Strategies for Modeling Dependence
3.3. Validation of the Non-Stationary Statistical Model
4. Results
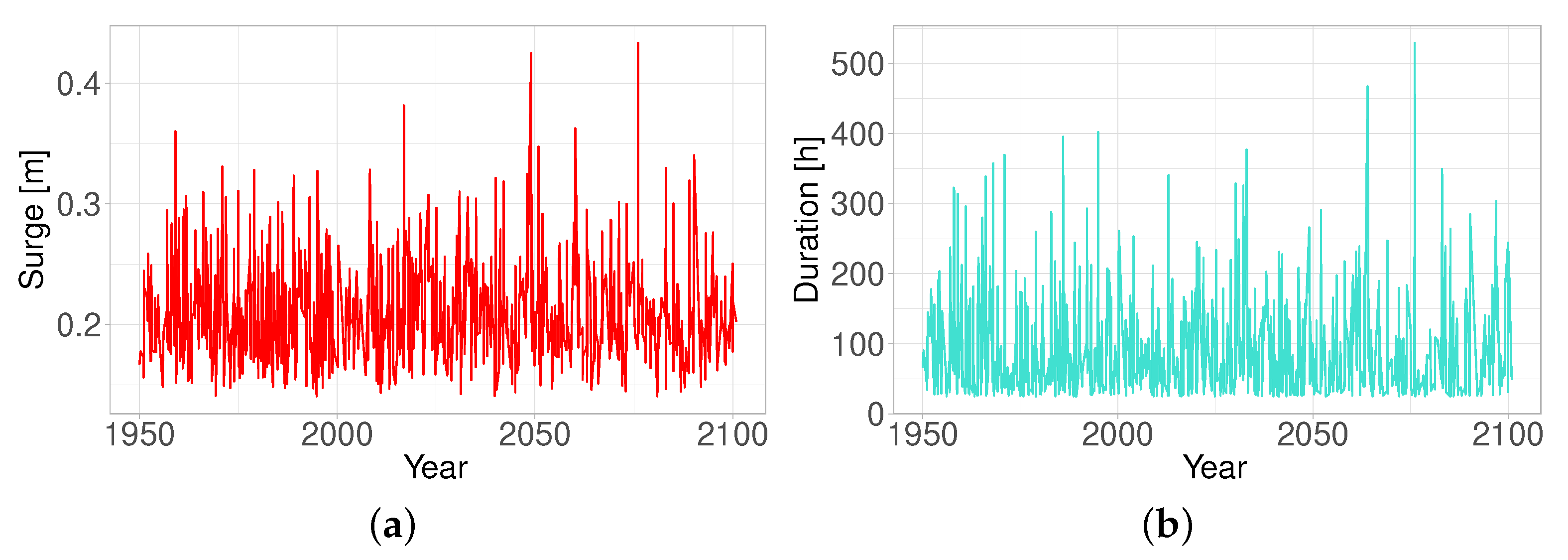
4.1. Process-Based Model
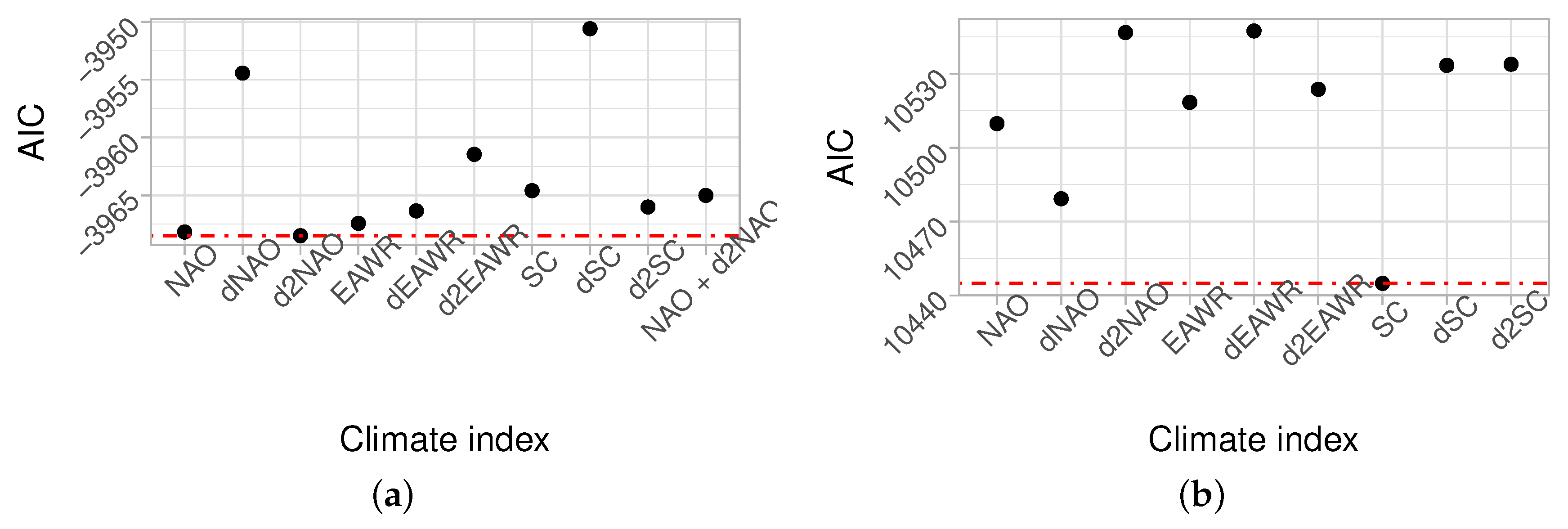
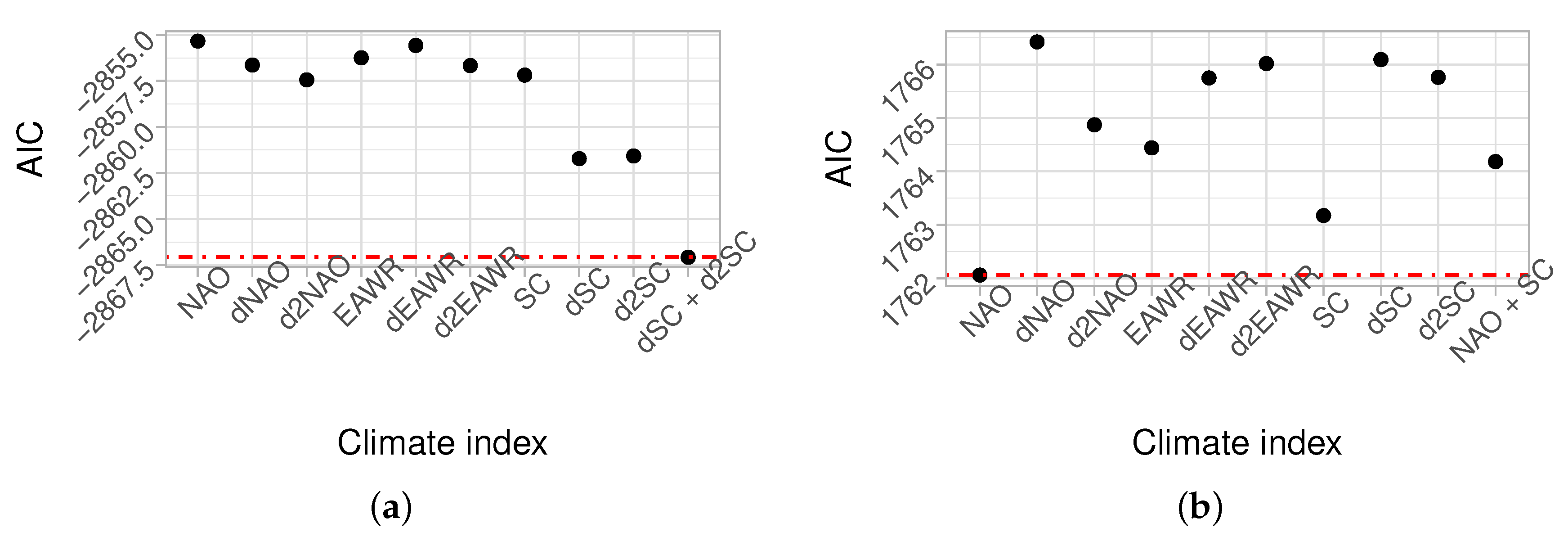
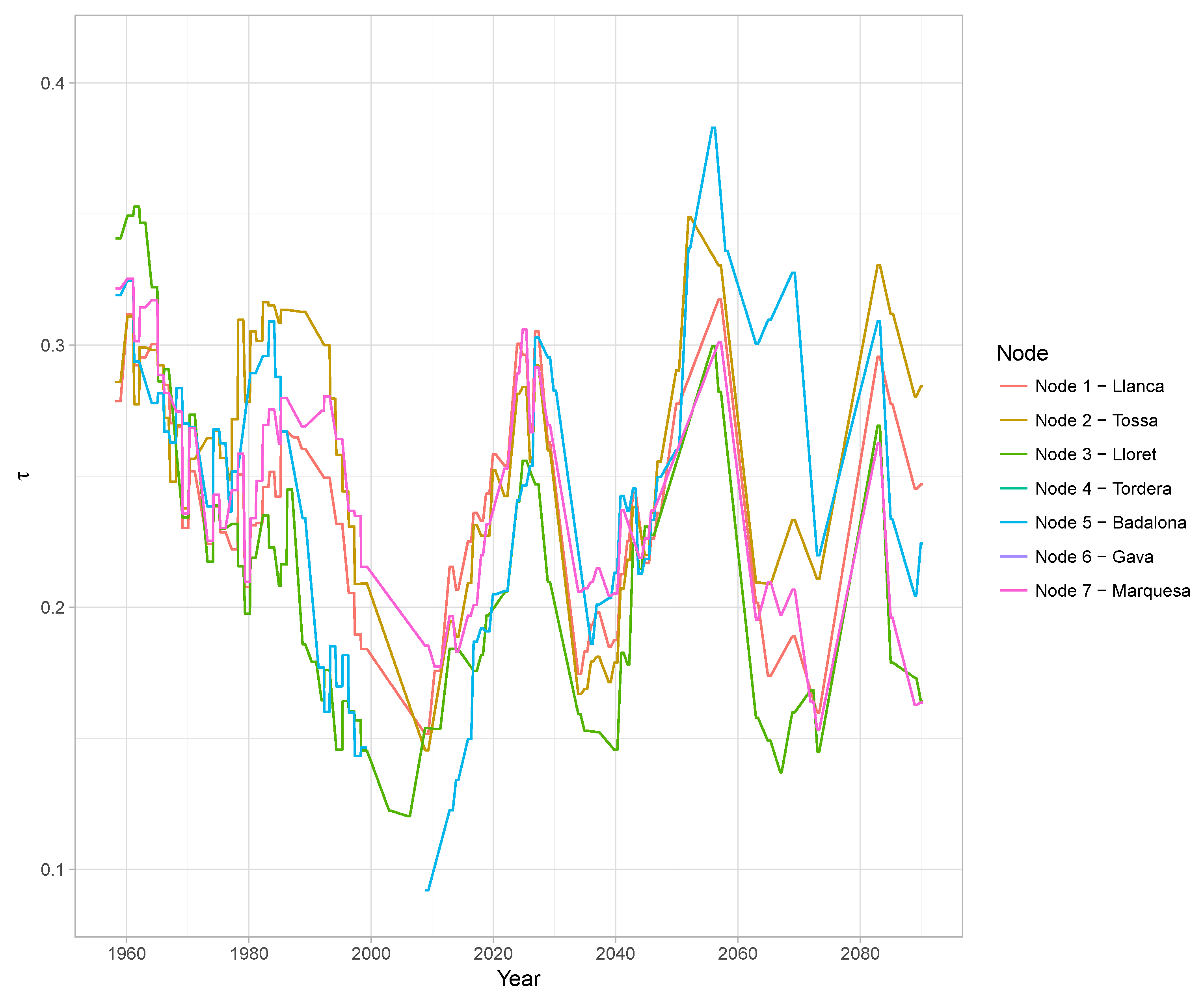
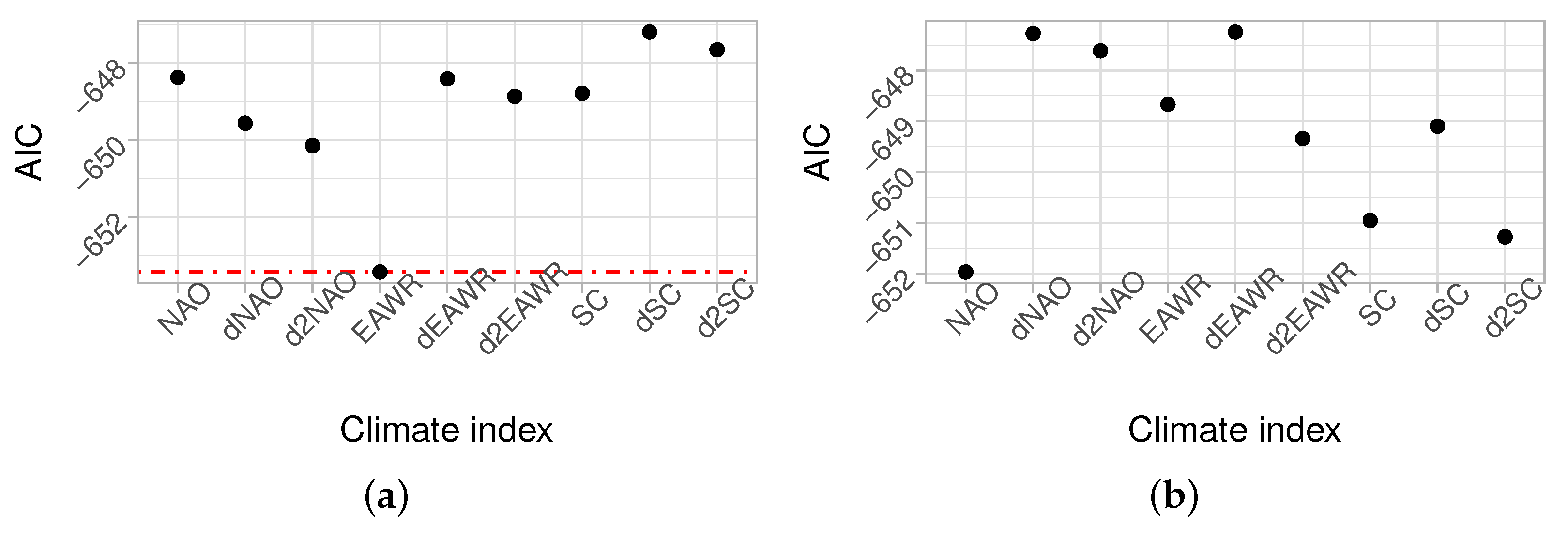
4.2. Non-Stationary Statistical Models
5. Discussion
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| AIC | Akaike Information Criterion |
| CMIP5 | Coupled Model Intercomparison Project 5 |
| East Atlantic Pattern | |
| GCM | General Circulation Model |
| GPD | Generalized Pareto Distribution |
| HYPSE | Hydrostatic Padua Surface Elevation Model |
| North Atlantic Oscillation | |
| Probability Distribution Function | |
| RCM | Regional Circulation Model |
| REDMAR | RED de MAReográfos (Spanish Acronym for Puertos del Estado Tidal Monitoring Network) |
| Scandinavian Pattern | |
| SWH | Significant Wave Height |
| VGAM | Vectorial Generalized Additive Model |
| VGLM | Vectorial Generalized Linear Model |
References
- Bolaños, R.; Jordà, G.; Cateura, J.; López, J.; Puigdefàbregas, J.; Gómez, J.; Espino, M. The XIOM: 20 years of a regional coastal observatory in the Spanish Catalan coast. J. Mar. Syst. 2009, 77, 237–260. [Google Scholar] [CrossRef]
- Soomere, T.; Pindsoo, K. Spatial variability in the trends in extreme storm surges and weekly-scale high water levels in the eastern Baltic Sea. Cont. Shelf Res. 2016, 115, 53–64. [Google Scholar] [CrossRef]
- Brown, J.D.; Spencer, T.; Moeller, I. Modeling storm surge flooding of an urban area with particular reference to modeling uncertainties: A case study of Canvey Island, United Kingdom. Water Resour. Res. 2007, 43. [Google Scholar] [CrossRef]
- Hinkel, J.; Lincke, D.; Vafeidis, A.T.; Perrette, M.; Nicholls, R.J.; Tol, R.S.J.; Marzeion, B.; Fettweis, X.; Ionescu, C.; Levermann, A. Coastal flood damage and adaptation costs under 21st century sea-level rise. Proc. Natl. Acad. Sci. USA 2014, 111, 3292–3297. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H.; Cheng, W.C.; Qiu, X.X.; Feng, X.B.; Gong, W.P. Tide-surge interaction along the east coast of the Leizhou Peninsula, South China Sea. Cont. Shelf Res. 2017, 142, 32–49. [Google Scholar] [CrossRef]
- Ullmann, A.; Pirazzoli, P.A.; Tomasin, A. Sea surges in Camargue: Trends over the 20th century. Cont. Shelf Res. 2007, 27, 922–934. [Google Scholar] [CrossRef]
- Staneva, J.; Wahle, K.; Koch, W.; Behrens, A.; Fenoglio-Marc, L.; Stanev, E.V. Coastal flooding: Impact of waves on storm surge during extremes - a case study for the German Bight. Nat. Hazards Earth Sys. Sci. 2016, 16, 2373–2389. [Google Scholar] [CrossRef]
- Sánchez-Arcilla, A.; García-León, M.; Gracia, V.; Devoy, R.; Stanica, A.; Gault, J. Managing coastal environments under climate change: Pathways to adaptation. Sci. Total Environ. 2016, 572, 1336–1352. [Google Scholar] [CrossRef]
- Krien, Y.; Testut, L.; Islam, A.K.M.S.; Bertin, X.; Durand, F.; Mayet, C.; Tazkia, A.R.; Becker, M.; Calmant, S.; Papa, F.; et al. Towards improved storm surge models in the northern Bay of Bengal. Cont. Shelf Res. 2017, 135, 58–73. [Google Scholar] [CrossRef]
- Grases, A.; Gracia, V.; García-León, M.; Lin-Ye, J.; Sierra, J.P. Coastal Flooding and Erosion under a Changing Climate: Implications at a Low-Lying Coast (Ebro Delta). Water 2020, 12, 346. [Google Scholar] [CrossRef]
- Silva, A.T.; Naghettini, M.; Portela, M.M. On some aspects of peaks-over-threshold modeling of floods under nonstationarity using climate covariates. Stoch. Environ. Res. Risk Assess. 2016, 30, 207–224. [Google Scholar] [CrossRef]
- Du, T.; Xiong, L.H.; Xu, C.Y.; Gippel, C.J.; Guo, S.; Liu, P. Return period and risk analysis of nonstationary low-flow series under climate change. J. Hydrol. 2015, 527, 234–250. [Google Scholar] [CrossRef]
- Vousdoukas, M.I.; Voukouvalas, E.; Annunziato, A.; Giardino, A.; Feyen, L. Projections of extreme storm surge levels along Europe. Clim. Dyn. 2016, 1–20. [Google Scholar] [CrossRef]
- Conte, D.; Lionello, P. Characteristics of large positive and negative surges in the Mediterranean Sea and their attenuation in future climate scenarios. Glob. Planet. Chang. 2013, 111, 159–173. [Google Scholar] [CrossRef]
- Marcos, M.; Jordà, G.; Gomis, D.; Pérez, B. Changes in storm surges in southern Europe from a regional model under climate change scenarios. Glob. Planet. Chang. 2011, 77, 116–128. [Google Scholar] [CrossRef]
- Barnston, A.G.; Livezey, R.E. Classification, Seasonality and Persistence of Low-Frequency Atmospheric Circulation Patterns. Mon. Weather Rev. 1987, 115, 1083–1126. [Google Scholar] [CrossRef]
- Hurrell, J.W.; Deser, C. North Atlantic climate variability: The role of the North Atlantic Oscillation. J. Marine Syst. 2009, 78, 28–41. [Google Scholar] [CrossRef]
- Lionello, P.; Malanotte-Rizzoli, P.; Boscolo, R. Mediterranean Climate Variability; Elsevier: Amsterdam, The Netherlands, 2006; Volume 4. [Google Scholar]
- Lionello, P.; Sanna, A. Mediterranean wave climate variability and its links with NAO and Indian Monsoon. Clim. Dyn. 2005, 25, 611–623. [Google Scholar] [CrossRef]
- Lionello, P.; Cogo, S.; Galati, M.; Sanna, A. The Mediterranean surface wave climate inferred from future scenario simulations. Glob. Planet. Change 2008, 63, 152–162. [Google Scholar] [CrossRef]
- Lin-Ye, J.; García-León, M.; Gràcia, V.; Ortego, M.I.; Lionello, P.; Sánchez-Arcilla, A. Multivariate statistical modeling of future marine storms. Appl. Ocean Res. 2017, 65, 192–205. [Google Scholar] [CrossRef]
- Trigo, R.M.; Osborn, T.J.; Corte-Real, J.M. The North Atlantic Oscillation influence on Europe: Climate impacts and associated physical mechanisms. Clim. Res. 2002, 20, 9–17. [Google Scholar] [CrossRef]
- Ulbrich, U.; Lionello, P.; Belusic, D.; Jacobeit, J.; Knippertz, P.; Kuglitsch, F.G.; Leckebusch, G.C.; Luterbacher, J.; Maugeri, M.; Maheras, P.; et al. 5—Climate of the Mediterranean: Synoptic Patterns, Temperature, Precipitation, Winds, and Their Extremes. In The Climate of the Mediterranean Region; Lionello, P., Ed.; Elsevier: Oxford, UK, 2012; pp. 301–346. [Google Scholar] [CrossRef]
- Lionello, P.; Galati, M.B. Links of the significant wave height distribution in the Mediterranean sea with the Northern Hemisphere teleconnection patterns. Adv. Geosci. 2008, 17, 13–18. [Google Scholar] [CrossRef]
- Tsimplis, M.N.; Shaw, A.G.P.; Flather, R.A.; Woolf, D.K. The influence of the North Atlantic Oscillation on the sea-level around the northern European coasts reconsidered: The thermosteric effects. Philos. Trans. A Math. Phys. Eng. Sci. 2006, 364, 845–856. [Google Scholar] [CrossRef] [PubMed]
- Woodworth, P.; Flather, R.A.; Williams, J.A.; Wakelin, S.L.; Jevrejeva, S. The dependence of U.K. extreme sea levels and storm surges on the North Atlantic Oscillation. Cont. Shelf Res. 2007, 27, 935–946. [Google Scholar] [CrossRef]
- Cid, A.; Menéndez, M.; Castanedo, S.; Abascal, A.J.; Méndez, F.J.; Medina, R. Long-term changes in the frequency, intensity and duration of extreme storm surge events in southern Europe. Clim. Dyn. 2016, 46, 1503–1516. [Google Scholar] [CrossRef]
- Lionello, P.; Conte, D.; Marzo, L.; Scarascia, L. The contrasting effect of increasing mean sea level and decreasing storminess on the maximum water level during storms along the coast of the Mediterranean Sea in the mid 21st century. Glob. Planet. Chang. 2016, 151, 80–91. [Google Scholar] [CrossRef]
- Wadey, M.P.; Haigh, I.D.; Brown, J.M. A century of sea level data and the UK’s 2013/14 storm surges: An assessment of extremes and clustering using the Newlyn tide gauge record. Ocean Sci. 2014, 10, 1031–1045. [Google Scholar] [CrossRef]
- Wakelin, S.L.; Woodworth, P.L.; Flather, R.A.; Williams, J.A. Sea-level dependence on the NAO over the NW European Continental Shelf. Geophy. Res. Lett. 2003, 30. [Google Scholar] [CrossRef]
- Hemer, M.A.; Trenham, C.E. Evaluation of a CMIP5 derived dynamical global wind wave climate model ensemble. Ocean Model. 2016, 103, 190–203. [Google Scholar] [CrossRef]
- Trenberth, K.; Fasullo, J.; Shepherd, T. Attribution of climate extreme events. Nat. Clim. Chang. 2015, 5, 725–730. [Google Scholar] [CrossRef]
- Campos, Á.; García-Valdecasas, J.M.; Molina, R.; Castillo, C.; Álvarez-Fanjul, E.; Staneva, J. Addressing Long-Term Operational Risk Management in Port Docks under Climate Change Scenarios—A Spanish Case Study. Water 2019, 11, 2153. [Google Scholar] [CrossRef]
- Marcos, M.; Tsimplis, M.N.; Shaw, A.G.P. Sea level extremes in southern Europe. J. Geophys. Res. Oceans 2009, 114. [Google Scholar] [CrossRef]
- Lionello, P.; Conte, D.; Reale, M. The effect of cyclones crossing the Mediterranean region on sea level anomalies on the Mediterranean Sea coast. Nat. Hazards Earth Syst. Sci. 2019, 19, 1541–1564. [Google Scholar] [CrossRef]
- De Michele, C.; Salvadori, G.; Passoni, G.; Vezzoli, R. A multivariate model of sea storms using copulas. Coast. Eng. 2007, 54, 734–751. [Google Scholar] [CrossRef]
- Wahl, T.; Mudersbach, C.; Jensen, J. Assessing the hydrodynamic boundary conditions for risk analyses in coastal areas: A multivariate statistical approach based on Copula functions. Nat. Hazards Earth Syst. Sci. 2012, 12, 495–510. [Google Scholar] [CrossRef]
- Corbella, S.; Stretch, D.D. Simulating a multivariate sea storm using Archimedean copulas. Coast. Eng. 2013, 76, 68–78. [Google Scholar] [CrossRef]
- Masina, M.; Lamberti, A.; Archetti, R. Coastal flooding: A copula based approach for estimating the joint probability of water levels and waves. Coast. Eng. 2015, 97, 37–52. [Google Scholar] [CrossRef]
- Woollings, T.; Blackburn, M. The North Atlantic jet stream under climate change and its relation to the NAO and EA patterns. J. Clim. 2012, 25, 886–902. [Google Scholar] [CrossRef]
- Marra, G.; Radice, R. Bivariate copula additive models for location, scale and shape. Comp. Stat. Data Anal. 2017, 112, 99–113. [Google Scholar] [CrossRef]
- Stocker, T.; Qin, D.; Plattner, G.K.; Tignor, M.; Allen, S.; Boschung, J.; Nauels, A.; Xia, Y.; Bex, V.; Midgley, P. IPCC, 2013: Summary for Policymakers. In Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2013. [Google Scholar]
- Scoccimarro, E.; Gualdi, S.; Bellucci, A.; Sanna, A.; Fogli, P.G.; Manzini, E.; Vichi, M.; Oddo, P.; Navarra, A. Effects of Tropical Cyclones on Ocean Heat Transport in a High-Resolution Coupled General Circulation Model. J. Clim. 2011, 24, 4368–4384. [Google Scholar] [CrossRef]
- Butterworth, S. On the theory of filter amplifiers. Wireless Eng. 1930, 7, 536–541. [Google Scholar]
- Rockel, B.; Will, A.; Hense, A. The Regional Climate Model COSMO-CLM (CCLM). Meteorol. J. 2008, 17, 347–348. [Google Scholar] [CrossRef]
- Lionello, P.; Mufato, R.; Tomasin, A. Sensitivity of free and forced oscillations of the Adriatic Sea to sea level rise. Clim. Res. 2005, 29, 23–29. [Google Scholar] [CrossRef][Green Version]
- Egozcue, J.J.; Pawlowsky-Glahn, V.; Ortego, M.I.; Tolosana-Delgado, R. The effect of scale in daily precipitation hazard assessment. Nat. Hazards Earth Sys. Sci. 2006, 6, 459–470. [Google Scholar] [CrossRef]
- Yee, T.W.; Wild, C.J. Vector Generalized Additive Models. J. R. Stat. Soc. Series B. Methodol. 1996, 58, 481–493. [Google Scholar] [CrossRef]
- Fessler, J. Nonparametric fixed-interval smoothing with vector splines. Signal Process. IEEE Trans. 1991, 39, 852–859. [Google Scholar] [CrossRef]
- Hastie, T.J.; Tibshirani, R.J. Generalized Additive Models; CRC Press: Boca Raton, FL, USA, 1990; Volume 43. [Google Scholar]
- Rigby, R.A.; Stasinopoulos, D.M. Generalized additive models for location, scale and shape. J. R. Stat. Soc. Series C Appl. Stat. 2005, 54, 507–554. [Google Scholar] [CrossRef]
- Yee, T.W.; Stephenson, A.G. Vector generalized linear and additive extreme value models. Extremes 2007, 10, 1–19. [Google Scholar] [CrossRef]
- Coles, S. An introduction to Statistical Modeling of Extreme Values; Springer: London, UK, 2001; pp. 801–804. [Google Scholar]
- Koenker, R. Quantile Regression; Econometric Society Monographs; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- Northrop, P.J.; Jonathan, P. Threshold modeling of spatially dependent non-stationary extremes with application to hurricane-induced wave heights. Environmetrics 2011, 22, 799–809. [Google Scholar] [CrossRef]
- Jonathan, P.; Ewans, K.; Randell, D. Joint modeling of extreme ocean environments incorporating covariate effects. Coast. Eng. 2013, 79, 22–31. [Google Scholar] [CrossRef]
- Akaike, H. Factor analysis and AIC. Psychometrika 1987, 52, 317–332. [Google Scholar] [CrossRef]
- Tamura, Y.; Sato, T.; Ooe, M.; Ishiguro, M. A procedure for tidal analysis with a Bayesian information criterion. Geophys. J. Int. 1991, 104, 507–516. [Google Scholar] [CrossRef]
- Sklar, A. Fonctions dé Repartition à n Dimension et Leurs Marges; Université Paris 8: Paris, France, 1959. [Google Scholar]
- Nelsen, R. An Introduction to Copulas; Springer Science & Business Media: New York, NY, USA, 2007. [Google Scholar]
- Okhrin, O.; Okhrin, Y.; Schmid, W. On the structure and estimation of hierarchical Archimedean copulas. J. Econom. 2013, 173, 189–204. [Google Scholar] [CrossRef]
- Lin-Ye, J.; García-León, M.; Gràcia, V.; Sánchez-Arcilla, A. A multivariate statistical model of extreme events: An application to the Catalan coast. Coast. Eng. 2016, 117, 138–156. [Google Scholar] [CrossRef]
- Kendall, M. A new measure of rank correlation. Biometrika 1937, 6, 83–93. [Google Scholar]
- Salvadori, G.; De Michele, C.; Durante, F. On the return period and design in a multivariate framework. Hydrol. Earth Syst. Sci. 2011, 15, 3293–3305. [Google Scholar] [CrossRef]
- Joe, H. Dependence Modeling with Copulas; Chapman and Hall/CRC: London, UK, 2014. [Google Scholar]
- Salvadori, G.; De Michele, C.; Kottegoda, N.T.; Rosso, R. Extremes in Nature: An Approach Using Copulas; Springer Science & Business Media: Amsterdam, The Netherlands, 2007; Volume 56. [Google Scholar]
- Kullback, S. Information Theory and Statistics; Courier Corporation: Chelmsford, MA, USA, 1997. [Google Scholar]
- Aitchison, J. On criteria for measures of compositional difference. Math. Geol. 1992, 24, 365–379. [Google Scholar] [CrossRef]
- Pawlowsky-Glahn, V.; Egozcue, J.J.; Tolosana-Delgado, R. Modeling and Analysis of Compositional Data; John Wiley & Sons: Hoboken, NJ, USA, 2015. [Google Scholar]
- Aitchison, J. The statistical analysis of compositional data. J. R. Stat. Soc. Ser. B Methodol. 1982, 44, 139–177. [Google Scholar] [CrossRef]
- Egozcue, J.J.; Pawlowsky-Glahn, V.; Mateu-Figueras, G.; Barceló-Vidal, C. Isometric logratio transformations for compositional data analysis. Math. Geol. 2003, 35, 279–300. [Google Scholar] [CrossRef]
- Pawlowsky-Glahn, V.; Egozcue, J.J. Geometric approach to statistical analysis on the simplex. Stoch. Environ. Res. Risk Assess. 2001, 15, 384–398. [Google Scholar] [CrossRef]
- Obermann-Hellhund, A.; Conte, D.; Somot, S.; Torma, C.Z.; Ahrens, B. Mistral and Tramontane wind systems in climate simulations from 1950 to 2100. Clim. Dyn. 2018, 50, 693–703. [Google Scholar] [CrossRef]
- Ullmann, A.; Moron, V. Weather regimes and sea surge variations over the Gulf of Lions (French Mediterranean coast) during the 20th century. Int. J. Clim. 2008, 28, 159–171. [Google Scholar] [CrossRef]
- Bertin, X.; Li, K.; Roland, A.; Bidlot, J.R. The contribution of short-waves in storm surges: Two case studies in the Bay of Biscay. Cont. Shelf Res. 2015, 96, 1–15. [Google Scholar] [CrossRef]
- Brown, J.M.; Wolf, J. Coupled wave and surge modeling for the eastern Irish Sea and implications for model wind-stress. Cont. Shelf Res. 2009, 29, 1329–1342. [Google Scholar] [CrossRef]
- Marcos, M.; Rohmer, J.; Vousdoukas, M.I.; Mentaschi, L.; Le Cozannet, G.; Amores, A. Increased Extreme Coastal Water Levels Due to the Combined Action of Storm Surges and Wind Waves. Geophys. Res. Lett. 2019, 46, 4356–4364. [Google Scholar] [CrossRef]
- Mase, H.; Tsujio, D.; Yasuda, T.; Mori, N. Stability analysis of composite breakwater with wave-dissipating blocks considering increase in sea levels, surges and waves due to climate change. Ocean Eng. 2013, 71, 58–65. [Google Scholar] [CrossRef]
- Tsimplis, M.N.; Álvarez-Fanjul, E.; Gomis, D.; Fenoglio-Marc, L.; Pérez, B. Mediterranean Sea level trends: Atmospheric pressure and wind contribution. Geophys. Res. Lett. 2005, 32, L20602. [Google Scholar] [CrossRef]
- Ullmann, A.; Pirazzoli, P.; Moron, V. Sea surges around the Gulf of Lions and atmospheric conditions. Glob. Planet. Chang. 2008, 63, 203–214. [Google Scholar] [CrossRef]
- Vanem, E. Joint statistical models for significant wave height and wave period in a changing climate. Mar. Struct. 2016, 49, 180–205. [Google Scholar] [CrossRef]

| D | ||||
|---|---|---|---|---|
| Both strategies | Storm surge threshold | () | ||
| Frequency | () | |||
| Location parameter () of the generalized Pareto distribution | – | – | ||
| Strategy #1: Lin-Ye | Scale parameter of the generalized Pareto distribution | () | () | |
| Strategy #2: Marra-Radice | () | – | ||
| Kendall’s of the copula | () | |||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin-Ye, J.; García-León, M.; Gràcia, V.; Ortego, M.I.; Lionello, P.; Conte, D.; Pérez-Gómez, B.; Sánchez-Arcilla, A. Modeling of Future Extreme Storm Surges at the NW Mediterranean Coast (Spain). Water 2020, 12, 472. https://doi.org/10.3390/w12020472
Lin-Ye J, García-León M, Gràcia V, Ortego MI, Lionello P, Conte D, Pérez-Gómez B, Sánchez-Arcilla A. Modeling of Future Extreme Storm Surges at the NW Mediterranean Coast (Spain). Water. 2020; 12(2):472. https://doi.org/10.3390/w12020472
Chicago/Turabian StyleLin-Ye, Jue, Manuel García-León, Vicente Gràcia, María Isabel Ortego, Piero Lionello, Dario Conte, Begoña Pérez-Gómez, and Agustín Sánchez-Arcilla. 2020. "Modeling of Future Extreme Storm Surges at the NW Mediterranean Coast (Spain)" Water 12, no. 2: 472. https://doi.org/10.3390/w12020472
APA StyleLin-Ye, J., García-León, M., Gràcia, V., Ortego, M. I., Lionello, P., Conte, D., Pérez-Gómez, B., & Sánchez-Arcilla, A. (2020). Modeling of Future Extreme Storm Surges at the NW Mediterranean Coast (Spain). Water, 12(2), 472. https://doi.org/10.3390/w12020472






