Dynamic Evapotranspiration Alters Hyporheic Flow and Residence Times in the Intrameander Zone
Abstract
1. Introduction
2. Materials and Methods
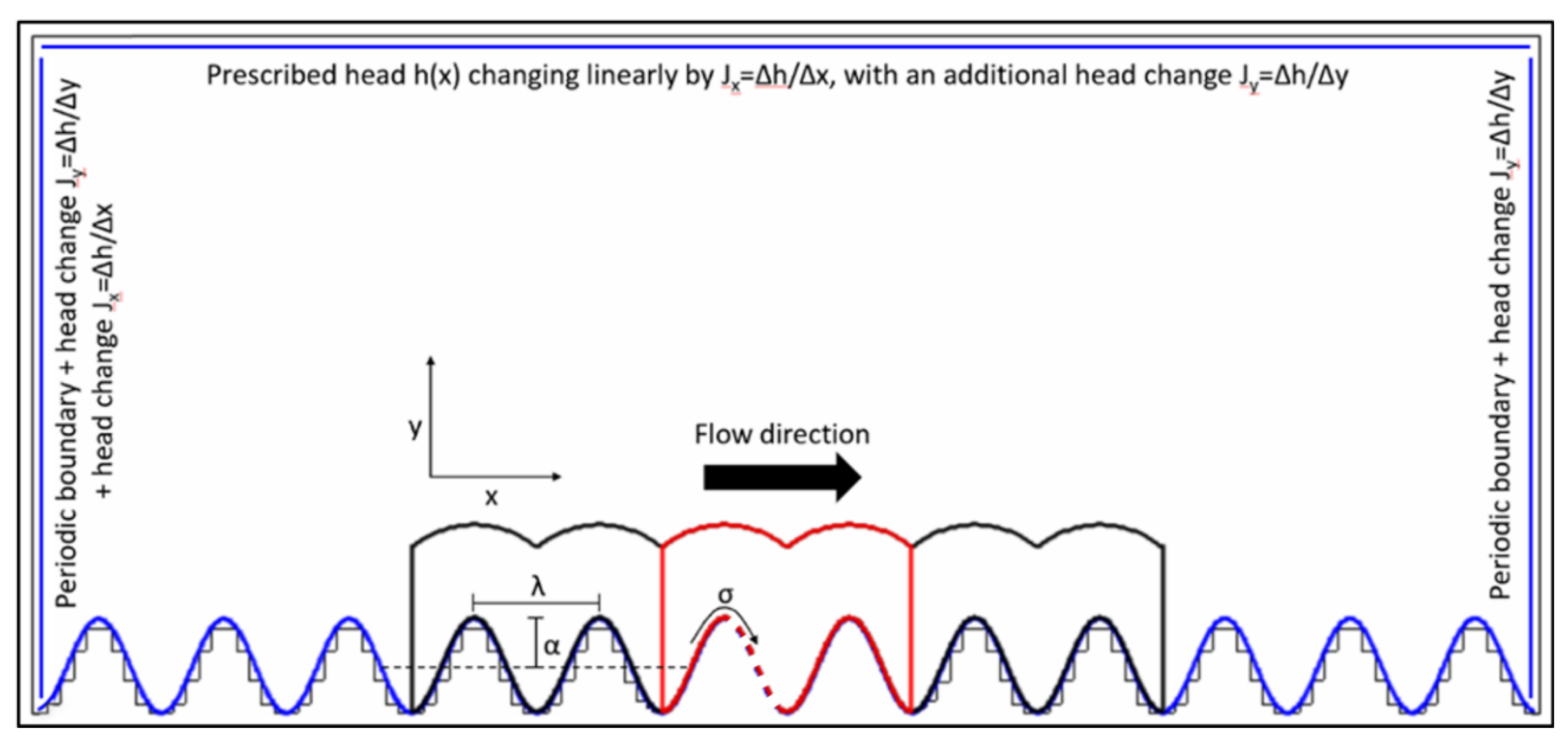
2.1. Conceptual Model
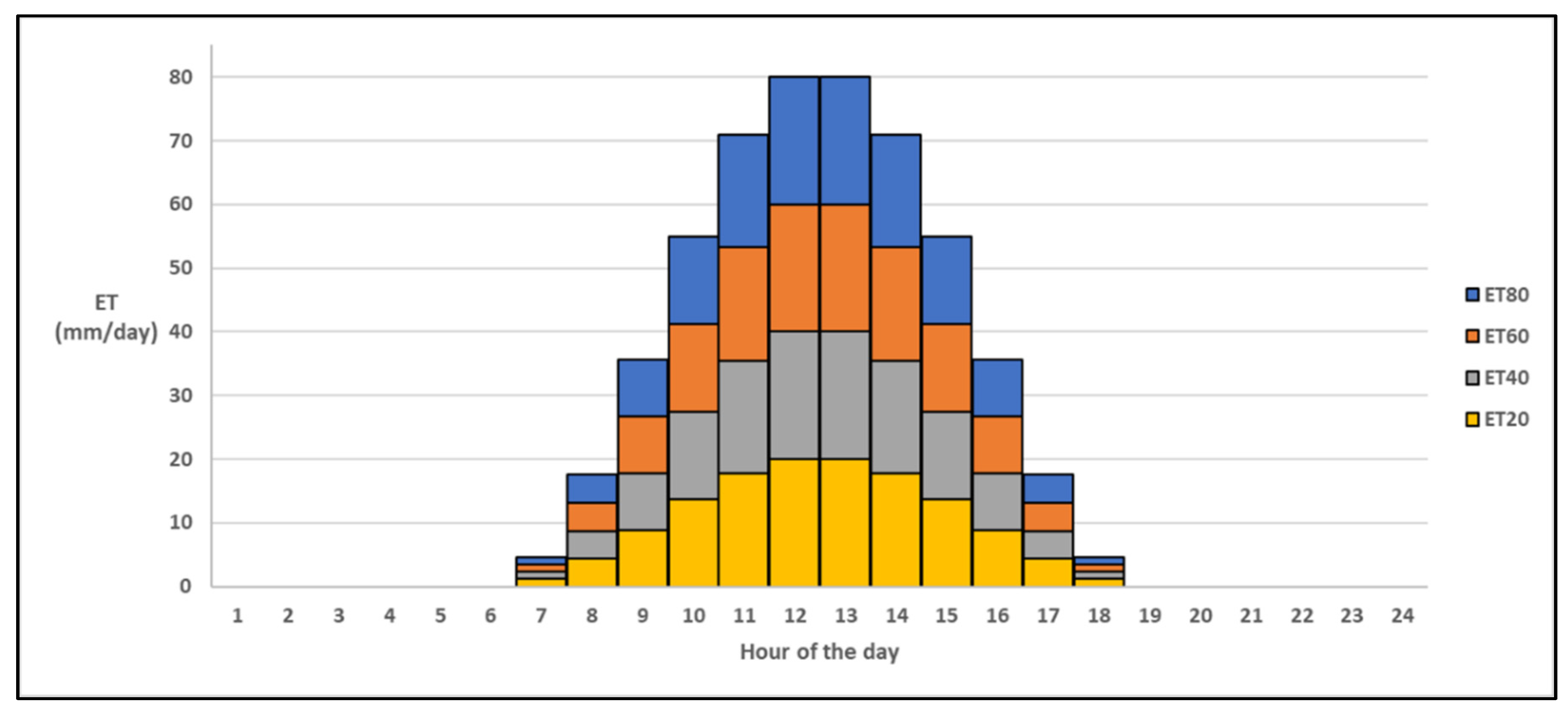
2.2. Modeling Scenarios
2.3. Characterization of the Hyporheic Exchange
3. Results
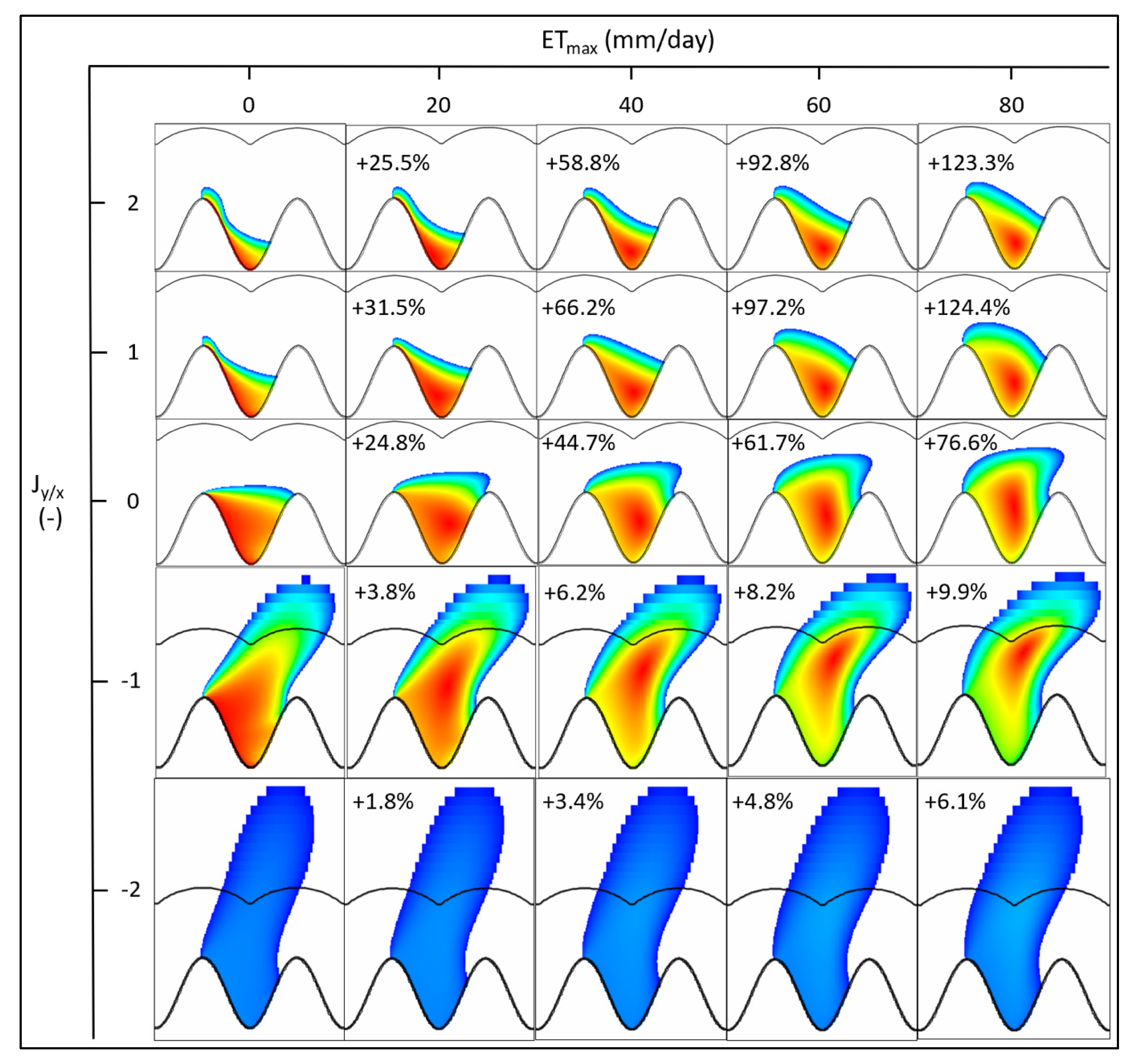
3.1. Hyporheic Zone Area
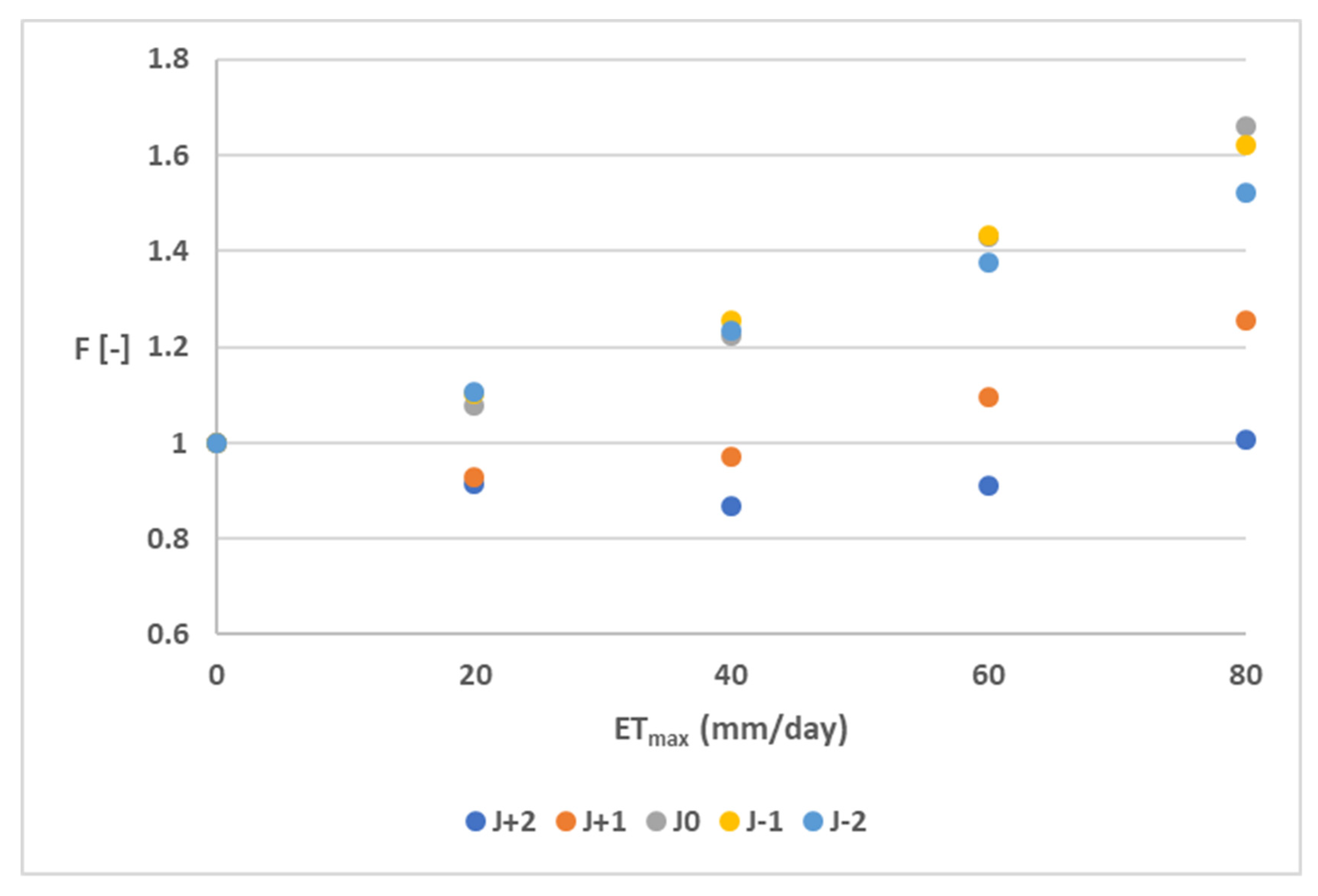
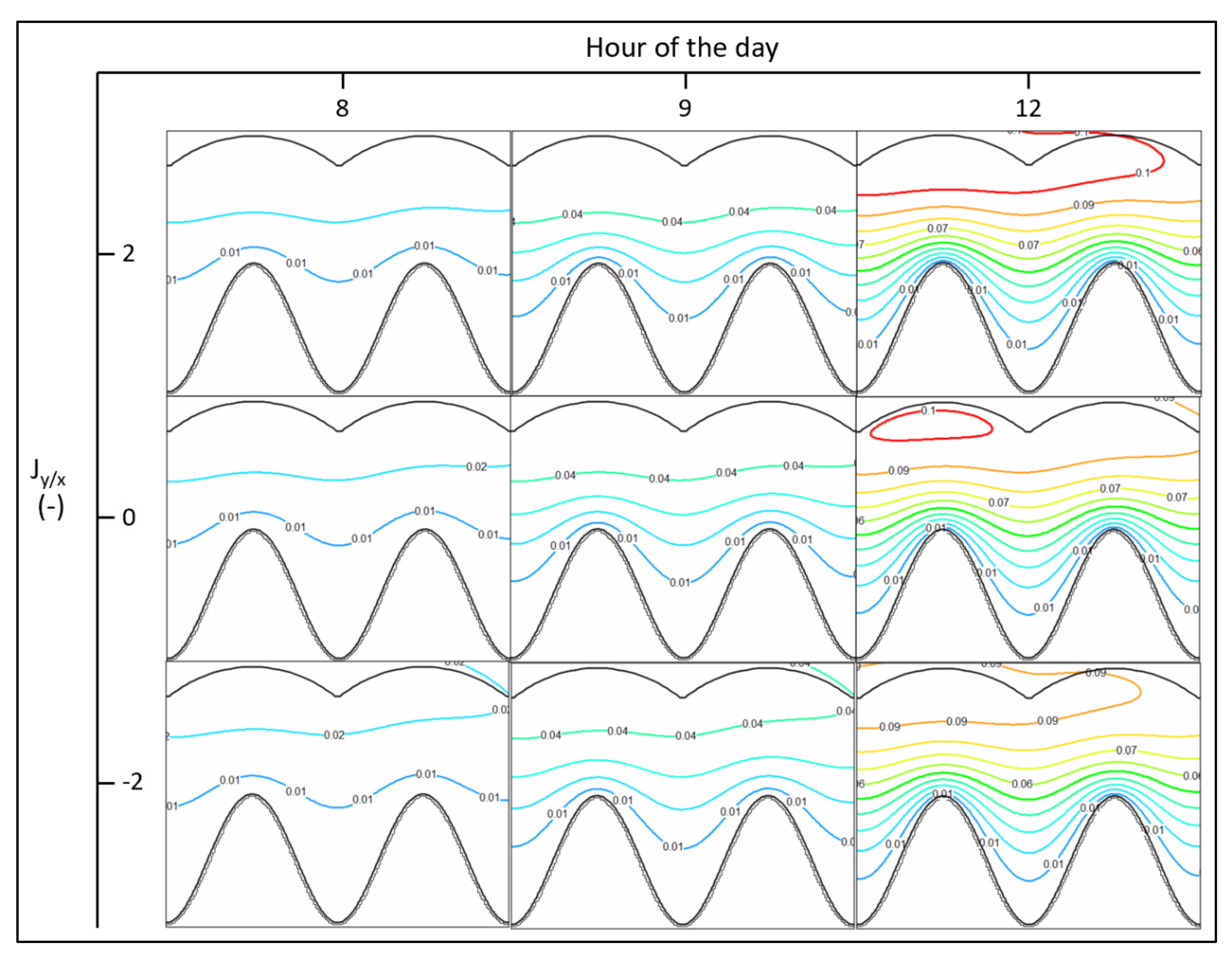
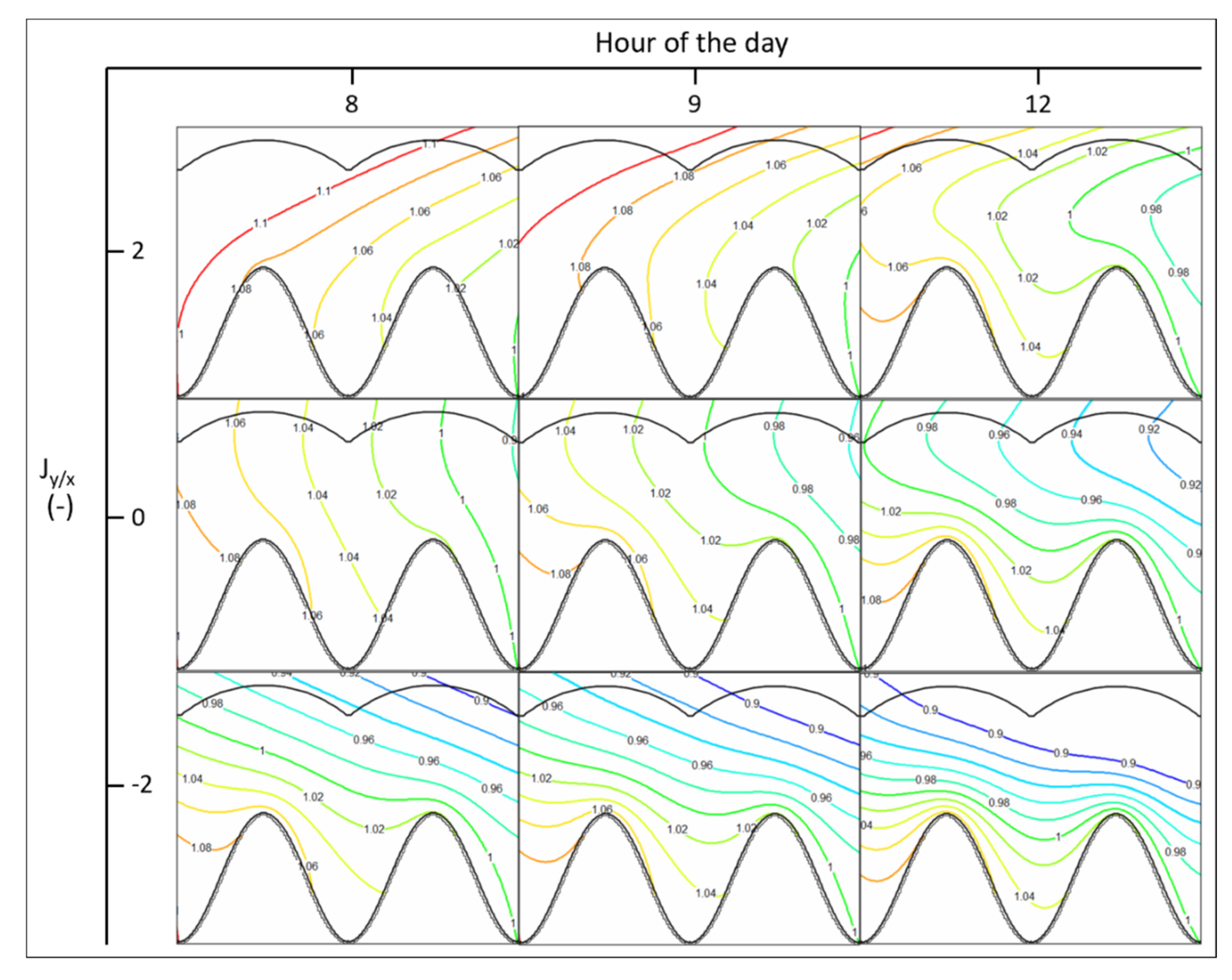
3.2. Net Groundwater Flux
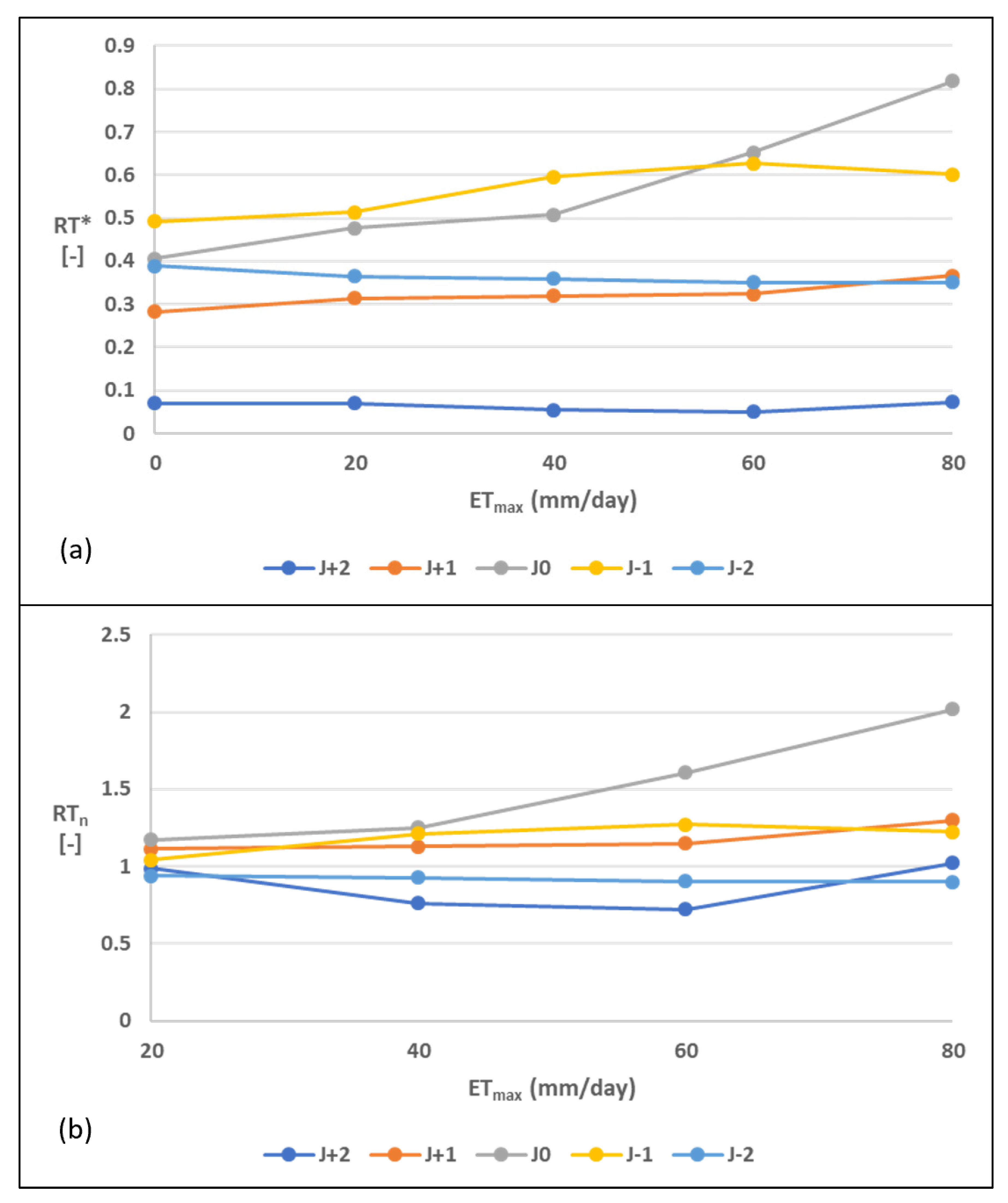
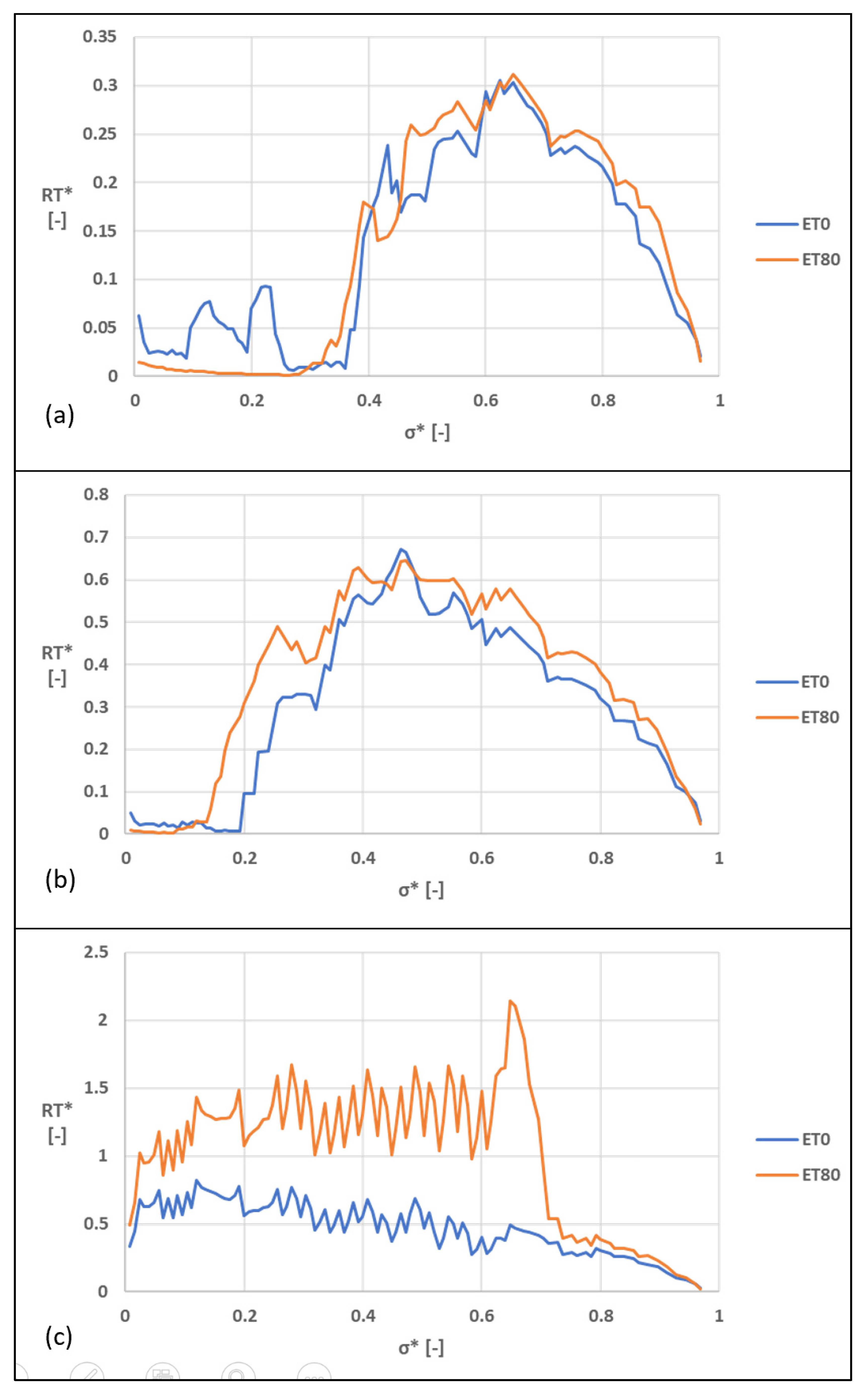
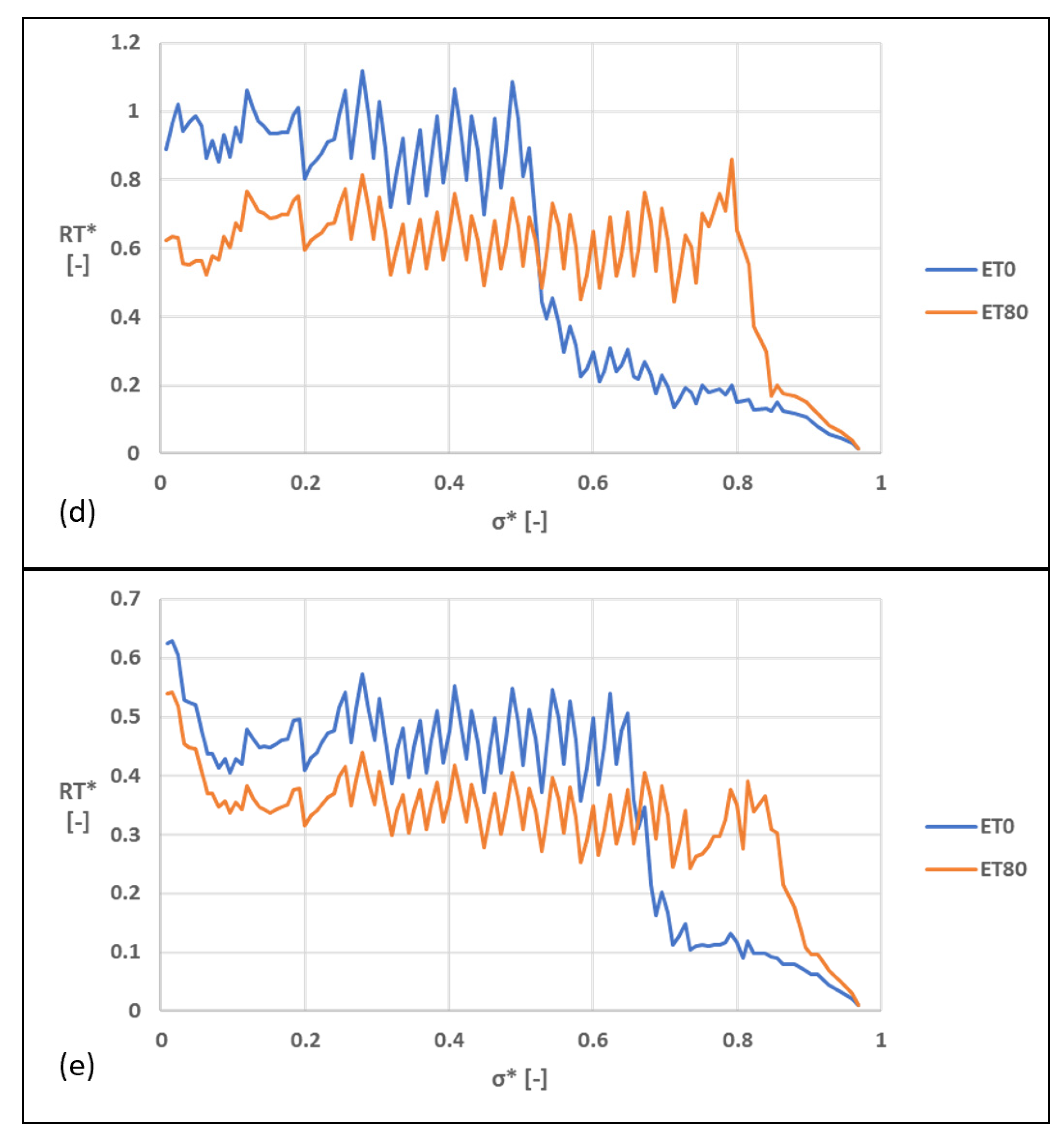
3.3. Residence Time
3.4. Drawdown and Head
3.5. Aquifer Sensitivity
4. Discussion
4.1. Hyporheic Zone Area
4.2. Net Groundwater Flux
4.3. Residence Time
4.4. Model Assumptions and Limitations
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Brunke, M.; Gonser, T. The ecological significance of exchange processes between rivers and groundwater. Freshwater Biol. 1997, 37, 1–33. [Google Scholar] [CrossRef]
- Hendricks, S.P. Microbial ecology of the hyporheic zone—A perspective integrating hydrology and biology. J. North Am. Benthological Soc. 1993, 12, 70–78. [Google Scholar] [CrossRef]
- Harvey, J.W.; Bencala, K.E. The effect of streambed topography on surface-subsurface water exchange in mountain catchments. Water Resour. Res. 1993, 29, 89–98. [Google Scholar] [CrossRef]
- Boano, F.; Revelli, R.; Ridolfi, L. Bedform-induced hyporheic exchange with unsteady flows. Adv. Water Resour. 2007, 30, 148–156. [Google Scholar] [CrossRef]
- Alexander, R.B.; Böhlke, J.K.; Boyer, E.W.; David, M.B.; Harvey, J.W.; Mulholland, P.J.; Seitzinger, S.P.; Tobias, C.R.; Tonitto, C.; Wollheim, W.M. Dynamic modeling of nitrogen losses in river networks unravels the coupled effects of hydrological and biogeochemical processes. Biogeochemistry 2009, 93, 91–116. [Google Scholar] [CrossRef]
- Fuller, C.C.; Harvey, J.W. Reactive uptake of trace metals in the hyporheic zone of a mining-contaminated stream, Pinal Creek, Arizona. Environ. Sci. Technol. 2000, 34, 1150–1155. [Google Scholar] [CrossRef]
- National Research Council. Riparian Areas: Functions and Strategies for Management; The National Academies Press: Washington, DC, USA, 2002. [Google Scholar]
- Boulton, A.J. Hyporheic Rehabilitation in Rivers: Restoring Vertical Connectivity. Freshwater Biol. 2007, 52, 632–650. [Google Scholar] [CrossRef]
- Boulton, A.J.; Datry, T.; Kasahara, T.; Mutz, M.; Stanford, J.A. Ecology and management of the hyporheic zone: Stream-groundwater interactions of running waters and their floodplains. J. N. Am. Benthol. Soc. 2010, 29, 26–40. [Google Scholar] [CrossRef]
- McClain, M.E.; Boyer, E.W.; Dent, C.L.; Gergel, S.E.; Grimm, N.B.; Groffman, P.M.; Hart, S.C.; Harvey, J.W.; Johnston, C.A.; Mayorga, E.; et al. Biogeochemical hot spots and hot moments at the interface of terrestrial and aquatic ecosystems. Ecosystems 2003, 6, 301–312. [Google Scholar] [CrossRef]
- Cardenas, M.B. Stream-aquifer interactions and hyporheic exchange in gaining and losing sinuous streams. Water Resour. Res. 2009b, 45, W06429. [Google Scholar] [CrossRef]
- Harvey, J.W.; Böhlke, J.K.; Voytek, M.A.; Scott, D.; Tobias, C.R. Hyporheic zone denitrification: Controls on effective reaction depth and contribution to whole-stream mass balance. Water Resour. Res. 2013, 49, 6298–6316. [Google Scholar] [CrossRef]
- Boano, F.; Demaria, A.; Revelli, R.; Ridolfi, L. Biogeochemical zonation due to intrameander hyporheic flow. Water Resour. Res. 2010, 46, W02511. [Google Scholar] [CrossRef]
- Gomez, J.D.; Wilson, J.L.; Cardenas, M.B. Residence time distributions in sinuosity-driven hyporheic zones and their biogeochemical effects. Water Resour. Res. 2012, 48, W09533. [Google Scholar] [CrossRef]
- O’Connor, B.L.; Harvey, J.W. Scaling hyporheic exchange and its influence on biogeochemical reactions in aquatic ecosystems. Water Resour. Res. 2008, 44, W12423. [Google Scholar] [CrossRef]
- Boano, F.; Harvey, J.W.; Marion, A.; Packman, A.I.; Revelli, R.; Ridolfi, L.; Wörman, A. Hyporheic flow and transport processes: Mechanisms, models, and biogeochemical implications. Rev. Geophys. 2014, 52, 603–679. [Google Scholar] [CrossRef]
- Buffington, J.; Tonina, D. Hyporheic exchange in mountain rivers ii: Effects of channel morphology on mechanics, scales, and rates of exchange. Geogr. Compass 2009, 3, 1038–1062. [Google Scholar] [CrossRef]
- Tonina, D.; Buffington, J.M. Hyporheic exchange in mountain rivers i: Mechanics and environmental effects. Geogr. Compass 2009, 3, 1063–1086. [Google Scholar] [CrossRef]
- Cardenas, M.B. A model for lateral hyporheic flow based on valley slope and channel sinuosity. Water Resour. Res. 2009, 45, W01501. [Google Scholar] [CrossRef]
- Cardenas, M.B. The effect of river bend morphology on flow and timescales of surface water-groundwater exchange across pointbars. J. Hydrol. 2008, 362, 134–141. [Google Scholar] [CrossRef]
- Revelli, R.; Boano, F.; Camporeale, C.; Ridolfi, L. Intra-meander hyporheic flow in alluvial rivers. Water Resour. Res. 2008, 44, W12428. [Google Scholar] [CrossRef]
- Boano, F.; Camporeale, C.; Revelli, R.; Ridolfi, L. Sinuosity driven hyporheic exchange in meandering rivers. Geophys. Res. Lett. 2006, 33, L18406. [Google Scholar] [CrossRef]
- Wondzell, S.M.; Gooseff, M.N.; McGlynn, B.L. An analysis of alternative conceptual models relating hyporheic exchange flow to diel fluctuations in discharge during baseflow recession. Hydrol. Proc. 2010, 24, 686–694. [Google Scholar] [CrossRef]
- White, W.N. A Method of Estimating Groundwater Supplies Based on Discharge by Plants and Evaporation from Soil—Results of Investigation in Escalante Valley, Utah; U.S. Geological Survey Water-Supply Paper; US Government Printing Office: Washington, DC, USA, 1932; Volume 659, 105p. [Google Scholar]
- Duke, J.R.; White, J.D.; Allen, P.M.; Muttiah, R.S. Riparian influence on hyporheic-zone formation downstream of a small dam in the Blackland Prairie region of Texas. Hydrol. Process. 2007, 21, 141–150. [Google Scholar] [CrossRef]
- Lautz, L.K. Estimating groundwater evapotranspiration rates using diurnal water-table fluctuations in a semi-arid riparian zone. Hydrogeol. J. 2008, 16, 483–497. [Google Scholar] [CrossRef]
- Yue, W.; Wang, T.; Franz, T.E.; Chen, X. Spatiotemporal patterns of water table fluctuations and evapotranspiration induced by riparian vegetation in a semiarid area. Water Resour. Res. 2016, 52, 1948–1960. [Google Scholar] [CrossRef]
- Butler, J.J., Jr.; Kluitenberg, G.J.; Whittemore, D.O.; Loheide II, S.P.; Jin, W.; Billinger, M.A.; Zhan, X. A field investigation of phreatophyte-induced fluctuations in the water table. Water Resour. Res. 2007, 43, W02404. [Google Scholar] [CrossRef]
- Gomez-Velez, J.D.; Wilson, J.L.; Cardenas, M.B.; Harvey, J.W. Flow and residence times of dynamic stream bank storage and sinuosity-driven hyporheic exchange. Water Resour. Res. 2017, 53, 8572–8595. [Google Scholar] [CrossRef]
- Gomez, J.D.; Wilson, J.L. Age distributions and dynamically changing hydrologic systems: Exploring topography-driven flow. Water Resour. Res. 2013, 49, 1503–1522. [Google Scholar] [CrossRef]
- Larsen, L.; Harvey, J.W.; Magilo, M.M. Dynamic hyporheic exchange at intermediate timescales: Testing the relative importance of evapotranspiration and flood pulses. Water Resour. Res. 2014, 50, 318–335. [Google Scholar] [CrossRef]
- Zarnetske, J.P.; Haggerty, R.; Wondzell, S.M.; Baker, M.A. Dynamics of nitrate production and removal as a function of residence time in the hyporheic zone. J. Geophys. Res. 2011, 116, G01025. [Google Scholar] [CrossRef]
- Zheng, C.; Wang, P.P. MT3DMS A Modular Three-Dimensional Multi-Species Transport Model for Simulation of Advection, Dispersion and Chemical Reactions of Contaminants in Groundwater Systems; Documentation and User’s Guide; US Army Engineer Research and Development Center Contract Report SERDP-99-1; US Army Corps of Engineers: Washington, DC, USA, 1999; 202p. [Google Scholar]
- Pollock, D.W. User Guide for MODPATH Version 6—A Particle-Tracking Model for MODFLOW; US Geological Survey Techniques and Methods 6–A41; US Department of the Interior: Reston, VA, USA, 2012; 58p. [Google Scholar]
- Welsch, D.J. Riparian forest buffers: Function and Design for Protection and Enhancement of Water Resources; US Department of Agriculture, Forest Service, Northern Area State & Private Forestry: Radnor, PA, USA, 1991; NA-PR-07-91. [Google Scholar]
- Winston, R.B. ModelMuse—A Graphical user Interface for MODFLOW-2005 and PHAST; US Geological Survey Techniques and Methods 6-A29; US Department of the Interior: Reston, VA, USA, 2009; 52p. [Google Scholar]
- Harbaugh, A.W. MODFLOW-2005: The U.S. Geological Survey Modular Ground-Water Model: The Ground-Water Flow Process; US Geological Survey Techniques and Methods 6-A16; US Department of the Interior: Reston, VA, USA, 2005; variously p. [Google Scholar]
- Solyu, M.E.; Lenters, J.D.; Istanbulluoglu, E.; Loheide, S.P. On evapotranspiration and shallow groundwater fluctuations: A Fourier-based improvement to the White method. Water Resour. Res. 2012, 48, W06506. [Google Scholar] [CrossRef]
- Fan, J.; Oestergaard, K.T.; Guyot, A.; Lockington, D.A. Estimating groundwater recharge and evapotranspiration from water table fluctuations under three vegetation covers in a coastal sandy aquifer of subtropical Australia. J. Hydrol. 2014, 519, 1120–1129. [Google Scholar] [CrossRef]
- Baird, K.J.; Maddock, T. Simulating riparian evapotranspiration: A new methodology and application for groundwater models. J. Hydrol. 2005, 312, 176–190. [Google Scholar] [CrossRef]
- Shah, N.; Nachabe, M.; Ross, M. Extinction depth and evapotranspiration from ground water under selected land covers. Ground Water 2007, 45, 329–338. [Google Scholar] [CrossRef] [PubMed]
- Carroll, R.W.H.; Pohll, G.M.; Morton, C.G.; Huntington, J.L. Calibrating a basin-scale groundwater model to remotely sensed estimates of groundwater evapotranspiration. J. Am. Water Resour. Assoc. 2015, 1–14. [Google Scholar] [CrossRef]
- Ihaka, R.; Gentleman, R. R: A language for data analysis and graphics. J. Comput. Graph. Stat. 1996, 5, 299–314. [Google Scholar]
- Triska, F.J.; Kennedy, V.C.; Avanzino, R.J.; Zellweger, G.W.; Bencala, K.E. Retention and transport of nutrients in a third-order stream in northwest California: Hyporheic processes. Ecology 1989, 70, 1893–1905. [Google Scholar] [CrossRef]
- Wohl, E. Rivers in the Landscape: Science and Management, 1st ed.; John Wiley & Sons, Ltd.: Chichester, West Sussex, UK, 2014; pp. 133–147. [Google Scholar]
- Kasahara, T.; Hill, A.R. Lateral hyporheic zone chemistry in an artificially constructed gravel bar and a re-meandered stream channel, southern Ontario, Canada. J. Am. Water Resour. Assoc. 2007, 43, 1257–1269. [Google Scholar] [CrossRef]
- Kasahara, T.; Hill, A.R. Modeling the effects of lowland stream restoration projects on stream-subsurface water exchange. Ecol. Eng. 2008, 32, 310–319. [Google Scholar] [CrossRef]
- Gomez-Velez, J.D.; Harvey, J.W. A hydrogeomorphic river network model predicts where and why hyporheic exchange is important in large basins. Geophys. Res. Lett. 2014, 41, 6403–6412. [Google Scholar] [CrossRef]
- Heeren, D.M.; Fox, G.A.; Fox, A.K.; Storm, D.E.; Miller, R.B.; Mittelstet, A.R. Divergence and flow direction as indicators of subsurface heterogeneity and stage-dependent storage in alluvial floodplains. Hydrol. Process. 2014, 28, 1307–1317. [Google Scholar] [CrossRef][Green Version]
- Shamsuddin, M.K.N.; Sulaiman, W.N.A.; Ramli, M.F.; Kusin, F.M. Vertical hydraulic conductivity of riverbank and hyporheic zone sediment at Muda River riverbank filtration site, Malaysia. Appl. Water. Sci. 2019, 9. [Google Scholar] [CrossRef]
- Loheide, S.P. A method for estimating subdaily evapotranspiration of shallow groundwater using diurnal water table fluctuations. Ecohydrology 2008, 1, 59–66. [Google Scholar] [CrossRef]
| Parameter | Symbol and Units | Constant Value |
|---|---|---|
| Sinuosity | S, (-) | 1.87 |
| Wavelength | λ, m | 40 |
| Down-valley water table gradient | Jx, (-) | 0.00125 |
| Hydraulic conductivity | K, m/h | 3.5 |
| Porosity | φ, (-) | 0.25 |
| Specific yield | Sy, (-) | 0.20 |
| Longitudinal dispersivity | αL, m | 10 |
| Start Time Step | End Time Step | MODFLOW | MT3DMS | MODPATH |
|---|---|---|---|---|
| −1 | 0 | Steady-state | Inactive | Inactive |
| 0 | 1 | Transient | Steady-state | Inactive |
| 1 | 720 | Transient | Transient | Inactive |
| 720 | 721 | Transient | Transient | Particles released |
| 721 | 744 | Transient | Transient | Particles travel |
| 744 | variable | Transient | Transient | Particles travel |
| Jy/x | Head Contour Azimuth, ° | Head Gradient, % | ||||
|---|---|---|---|---|---|---|
| 6th h | 12th h | Δ | 6th h | 12th h | Δ | |
| 2 | 117 | 82 | 35 | 0.115 | 0.179 | 0.064 |
| 1 | 117 | 75 | 42 | 0.114 | 0.213 | 0.099 |
| 0 | 96 | 70 | 26 | 0.125 | 0.253 | 0.128 |
| −1 | 65 | 65 | 0 | 0.185 | 0.307 | 0.122 |
| −2 | 65 | 65 | 0 | 0.256 | 0.376 | 0.120 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kruegler, J.; Gomez-Velez, J.; Lautz, L.K.; Endreny, T.A. Dynamic Evapotranspiration Alters Hyporheic Flow and Residence Times in the Intrameander Zone. Water 2020, 12, 424. https://doi.org/10.3390/w12020424
Kruegler J, Gomez-Velez J, Lautz LK, Endreny TA. Dynamic Evapotranspiration Alters Hyporheic Flow and Residence Times in the Intrameander Zone. Water. 2020; 12(2):424. https://doi.org/10.3390/w12020424
Chicago/Turabian StyleKruegler, James, Jesus Gomez-Velez, Laura K. Lautz, and Theodore A. Endreny. 2020. "Dynamic Evapotranspiration Alters Hyporheic Flow and Residence Times in the Intrameander Zone" Water 12, no. 2: 424. https://doi.org/10.3390/w12020424
APA StyleKruegler, J., Gomez-Velez, J., Lautz, L. K., & Endreny, T. A. (2020). Dynamic Evapotranspiration Alters Hyporheic Flow and Residence Times in the Intrameander Zone. Water, 12(2), 424. https://doi.org/10.3390/w12020424






