Numerical Simulation of Frost Heave of Concrete Lining Trapezoidal Channel Under an Open System
Abstract
:1. Introduction
2. Frost Heave Model and Analysis Method
2.1. Basic Assumption
- (1)
- The concrete lining is an isotropic material.
- (2)
- Since the dimension of the lining channel along the water delivery direction is much larger than the cross-sectional area and the cross-section is symmetric, the lining force in the water conveyance direction and the heat conduction process of the channel base do not change. Thus, the analysis of the expansion failure can be simplified to a plane strain problem [18].
- (3)
- The heat transported by the migration of moisture to the frozen zone is negligible.
- (4)
- There is no overlying load above the foundation of the channel, and the ice pressure is 0.
2.2. Heat Conduction Equation
2.3. Moisture Transfer Equation
2.4. Moisture Migration Driving Force
2.5. Stress–Strain Equation
2.6. Contact Behavior Between Foundation Soil and Concrete
3. Finite Element Model Calculation and Parameter Selection
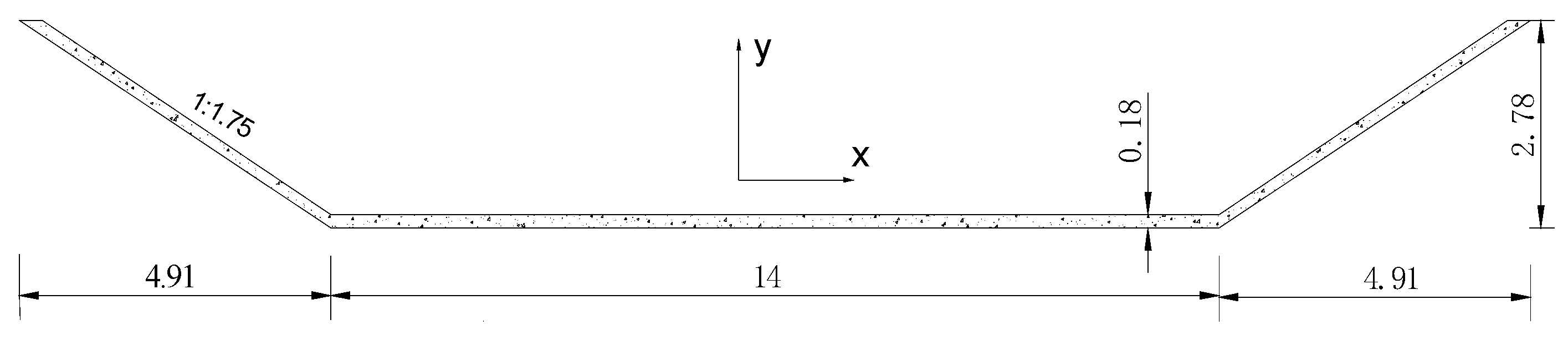
3.1. Channel Prototype
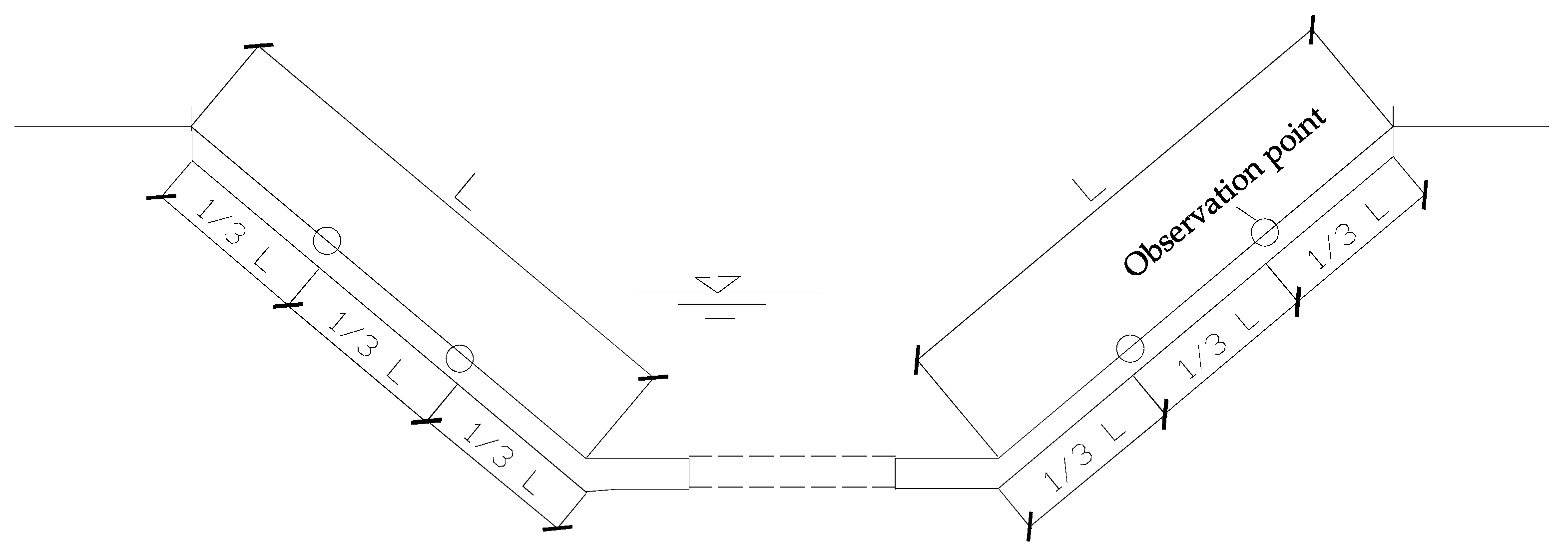
3.2. Upper Boundary Condition
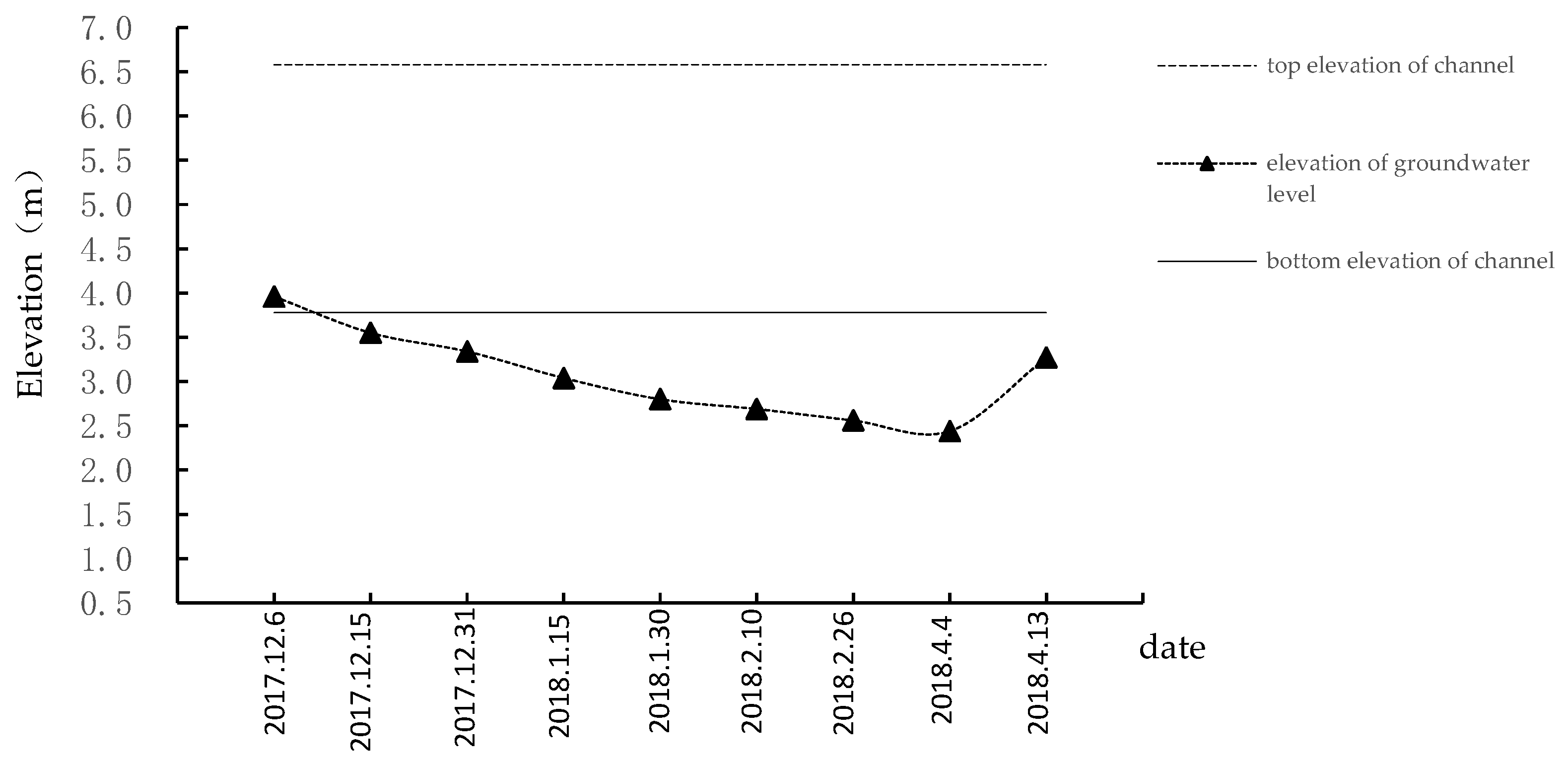
3.3. Lower Boundary Condition
3.4. Finite Element Model Calculation and Parameter Selection
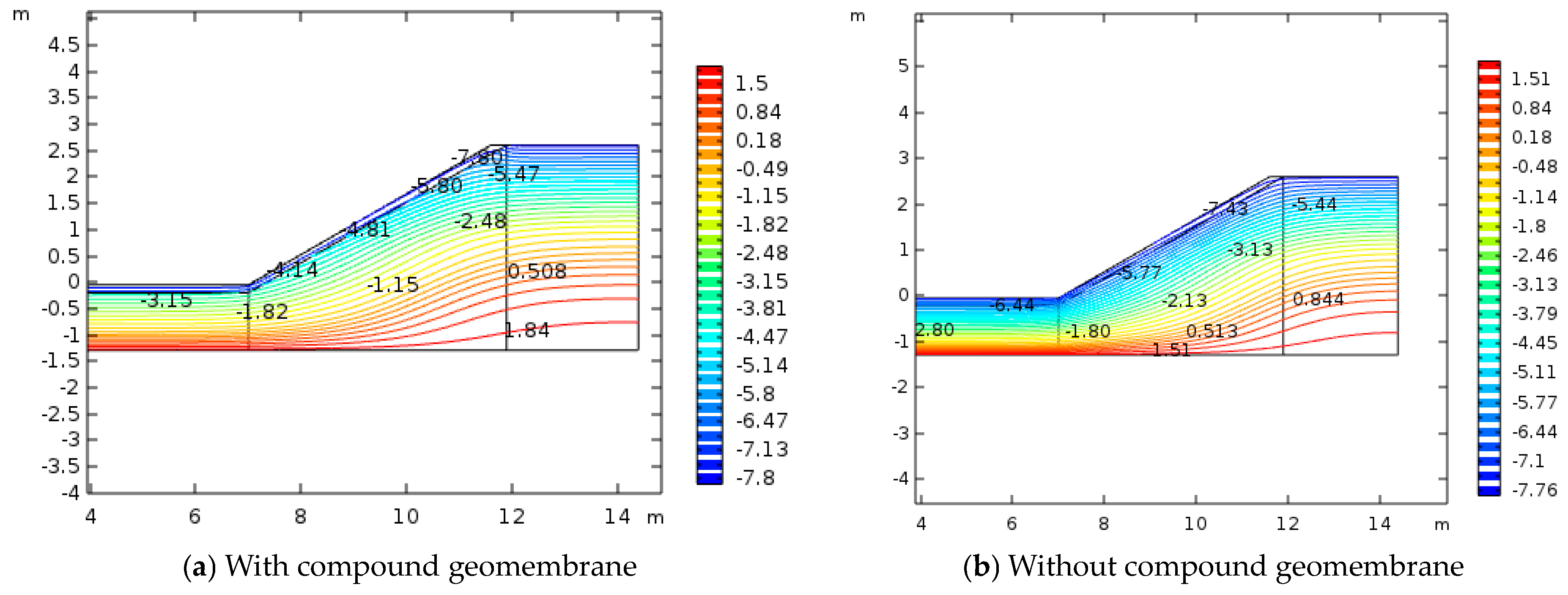
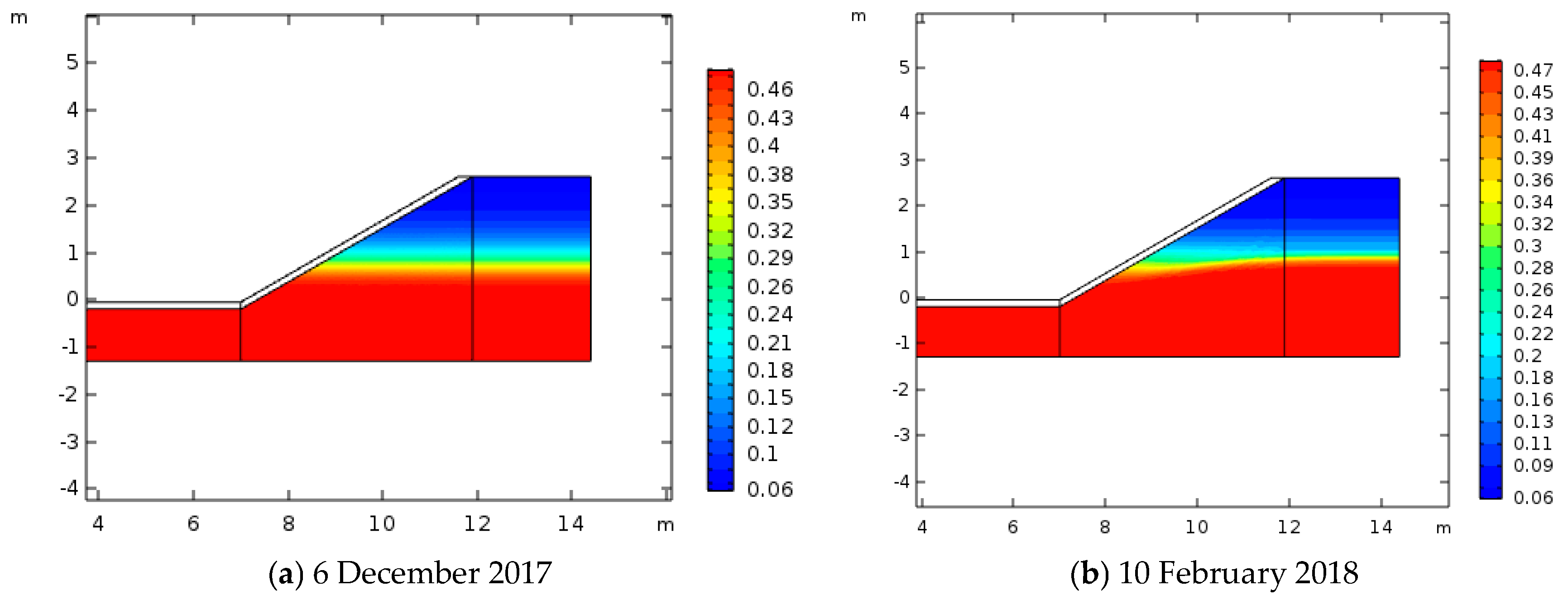
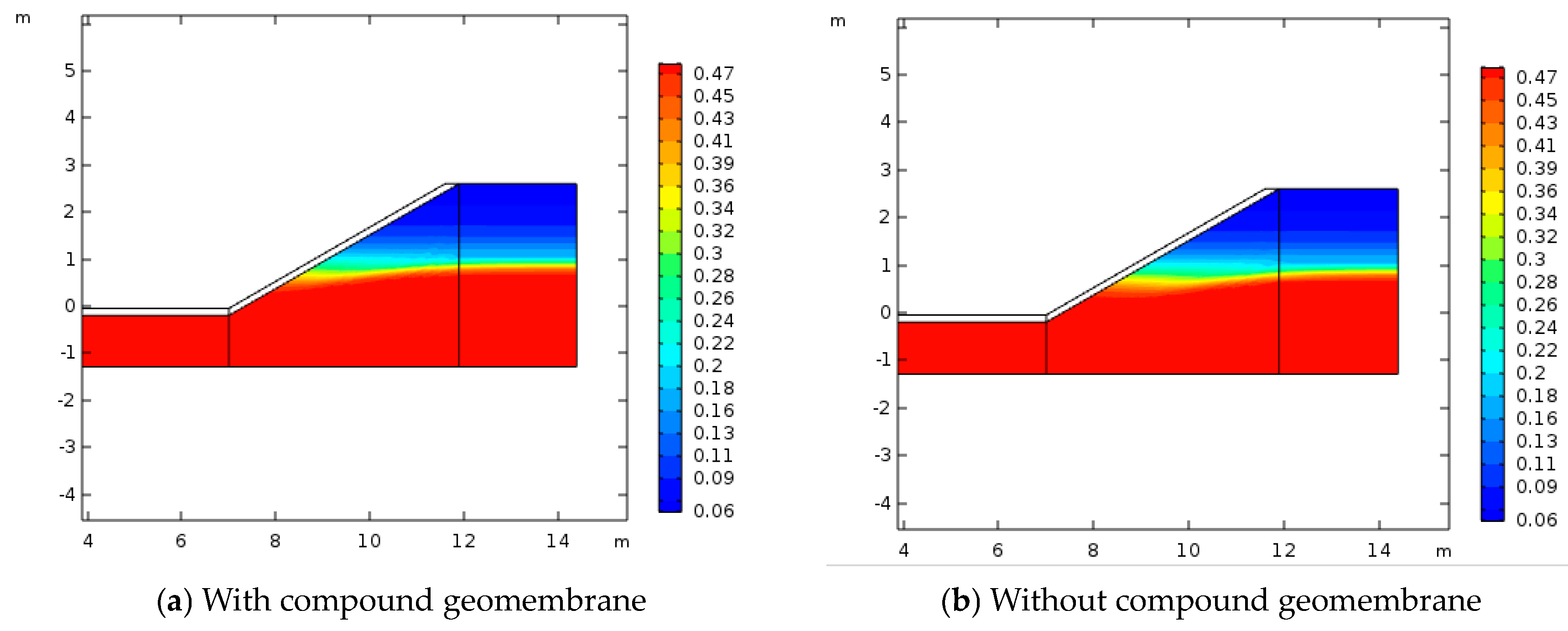
4. Discussion
Distribution Law of Frost Heave in Basic Soil
5. Conclusions
- (1)
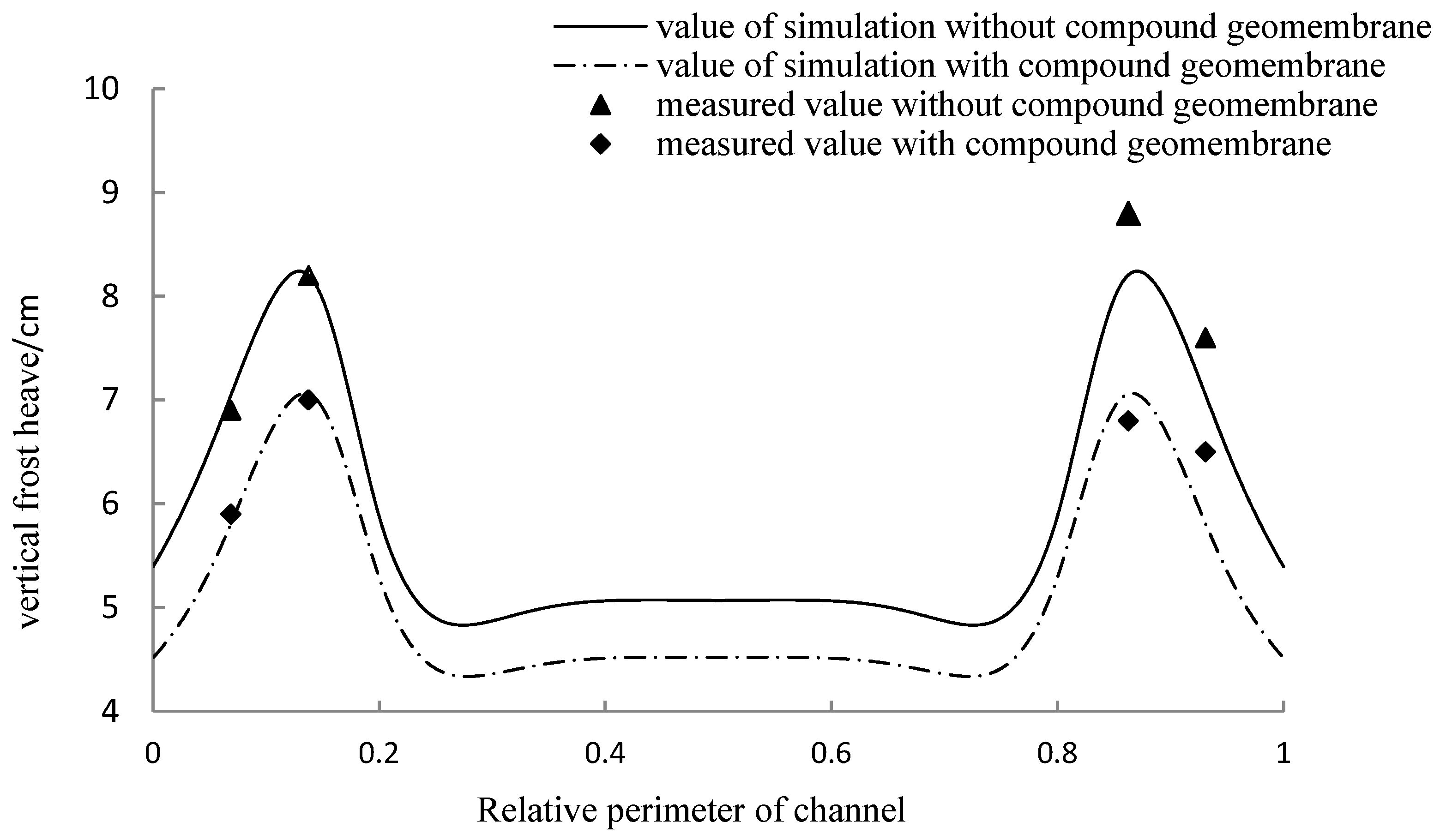
- A hydrothermal three-field coupling simulation was carried out on the trapezoidal channel with a compound geomembrane on the lower side of the lining. The simulation also considered the influence of groundwater-level changes on the temperature field and the effect of capillary action on water migration. The simulation results were basically consistent with the measurements, revealing the frost heave distribution of the trapezoidal channel. According to the simulation results, the amount of frost heaving of the base soil reached a maximum at a length of one-third of the slope from the bottom of the channel at 8.243 cm. In the bottom and top of the channel, the frost heave was small.
- (2)
- The addition of the compound geomembrane had little effect on the moisture transfer, but it could change the distribution of the temperature in the base soil to a large extent. Therefore, the main reason why the frost heaving of the channel reduced was that it can form thermal resistance between the concrete lining and base soil. The frost heave decreased by 14.3% and 15.5% at a distance of one-third from the bottom of the channel along the slope and at the top of the channel, respectively.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Xu, X.Z.; Wang, J.C.; Zhang, L.X. Frozen Soil Physics; Science Press: Beijing, China, 2001. [Google Scholar]
- Ma, W.; Wang, D.Y. Frozen Soil Mechanics; Science Press: Beijing, China, 2014. [Google Scholar]
- Song, Q.L.; He, W.Q.; Li, G.; Zhao, H.W.; Zhang, Y.F. The research on insulation and frost heave control for concrete lining canal. J. Irrig. Drain. 2015, 34, 43–48. [Google Scholar]
- Hao, J.C.; Lou, Z.K.; Gao, F. Numerical simulation and slope coefficient optimization of frost heave of trapezoidal channel. J. Irrig. Drain. 2017, 36, 81–86. [Google Scholar]
- Mu, S.; Ladanyi, B. Modeling of coupled heat, moisture and stress field in freezing soil. Cold Reg. Sci. Tech. 1987, 14, 237–246. [Google Scholar] [CrossRef]
- Masters, I.; Pao, W.K.S.; Lewis, R.W. Coupling temperature to a double-porosity model of deformable porous media. Int. J. Numer. Methods Eng. 2000, 49, 421–438. [Google Scholar] [CrossRef]
- Li, S.Y.; Zhang, M.Y.; Pei, W.S.; Lai, Y.M. Experimental and numerical simulations on heat-water-mechanics interaction mechanism in a freezing soil. Appl. Therm. Eng. 2018, 132, 209–220. [Google Scholar] [CrossRef]
- Bai, R.Q.; Lai, Y.M.; Zhang, M.Y.; Gao, J.Q. Water-vapor-heat behavior in a freezing unsaturated coarse-grained soil with a closed top. Cold Reg. Sci. Tech. 2018, 155, 120–126. [Google Scholar] [CrossRef]
- He, Z.Y.; Zhang, S.; Teng, J.D.; Yao, Y.P.; Sheng, D.C. A coupled model for liquid water-vapor-heat migration in freezing soils. Cold Reg. Sci. Tech. 2018, 148, 22–28. [Google Scholar] [CrossRef]
- Zhu, Z.W.; Ning, J.G.; Ma, W. Constitutive model and numerical analysis for the coupled problem of water, temperature and stress fields in the process of soil freeze-thaw. Eng. Mech. 2007, 24, 138–144. [Google Scholar]
- Mao, X.S.; Li, N.; Wang, B.G.; Hu, C.S. Analysis model of stress and deformation of permafrost Subgrade with phase changing. J. Traffic Transp. Eng. 2007, 7, 58–62. [Google Scholar]
- Huo, X.L.; Chen, S.G.; Wei, M.M.; Xiao, X. Study on frozen-thaw stability of subgrade in seasonal frozen soil with phase changing. Cons. Tech. 2013, 42, 93–96. [Google Scholar]
- Wang, T.H.; Hu, C.S.; Ning, L. Simulation method for calculating stress and deformation of highway embankment on frozen soil area. Cold Reg. Sci. Tech. 2005, 42, 89–95. [Google Scholar] [CrossRef]
- Li, Z.; Liu, S.H.; Feng, Y.T.; Liu, K.; Zhang, C.C. Numerical study on the effect of frost heave prevention with different canal lining structures in seasonally frozen ground regions. Cold Reg. Sci. Tech. 2013, 85, 242–249. [Google Scholar] [CrossRef]
- Li, S.Y.; Zhang, M.Y.; Tian, Y.B.; Pei, W.S.; Zhong, H. Experimental and numerical investigations on frost damage mechanism of a canal in cold regions. Cold Reg. Sci. Tech. 2015, 116, 1–11. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, Z.Z.; Wang, Y.; Liu, Q.H.; Guo, R.; Xiao, M. Frost heave model of canal considering influence of moisture migration and phase transformation on temperature field. Trans. Chin. Soc. Agric. Eng. 2016, 32, 83–88. [Google Scholar]
- Wang, Z.Z.; Liu, S.J.; Wang, Y.; Liu, Q.H.; Ge, J.R. Size effect on frost heave damage for lining trapezoidal canal with arc-bottom in cold regions. J. Hydraul. Eng. 2018, 49, 803–813. [Google Scholar]
- Zienkiewicz, O.C.; Taylor, R.L.; Fox, D. The Finite Element Method for Solid and Structural Mechanics, 7th ed.; Elsevier: Singapore, 2013. [Google Scholar]
- Jame, Y.W.; Norum, D.I. Heat and mass transfer in a freezing unsaturated porous medium. Water Resour. Res. 1980, 16, 811–819. [Google Scholar] [CrossRef]
- Zhou, J.Z.; Li, D.Q. Numerical analysis of coupled water, heat and stress in saturated freezing soil. Cold Reg. Sci. Tech. 2012, 72, 43–49. [Google Scholar] [CrossRef]
- Konrad, J.M.; Morgenstern, N.R. Prediction of frost heave in the laboratory during transient freezing. Can. Geotech. J. 1982, 19, 250–259. [Google Scholar] [CrossRef]
- Kay, B.D.; Groenevelt, P.H. On the interaction of water and heat transport in frozen and unfrozen soils: Basic theory; the vapor phase. Soil Sci. Soc. Am. J. 1974, 38, 395–400. [Google Scholar] [CrossRef]
- Peck, R.B.; Hansen, W.E.; Thornburn, T.H. Foundation Engineering, 2nd ed.; Wiley: New York, NY, USA, 1974. [Google Scholar]
- Wang, Z.Z.; Shao, J.D.; Jiang, Y.J.; Zhang, C.Q. Nonlinear finite element analysis of interaction of orthotropic frozen ground and construction. China Civ. Eng. J. 1999, 32, 55–60. [Google Scholar]
- Cai, Z.W. Study on Thermal Conductivity of Filled Polypropylene. Master’s Thesis, Zhongshan University, Guangzhou, China, June 2005. [Google Scholar]
- Liu, W.M.; He, P.; Zhang, Z. A calculation method of thermal conductivity of soils. J. Glaciol. Geocryol. 2002, 24, 770–773. [Google Scholar]
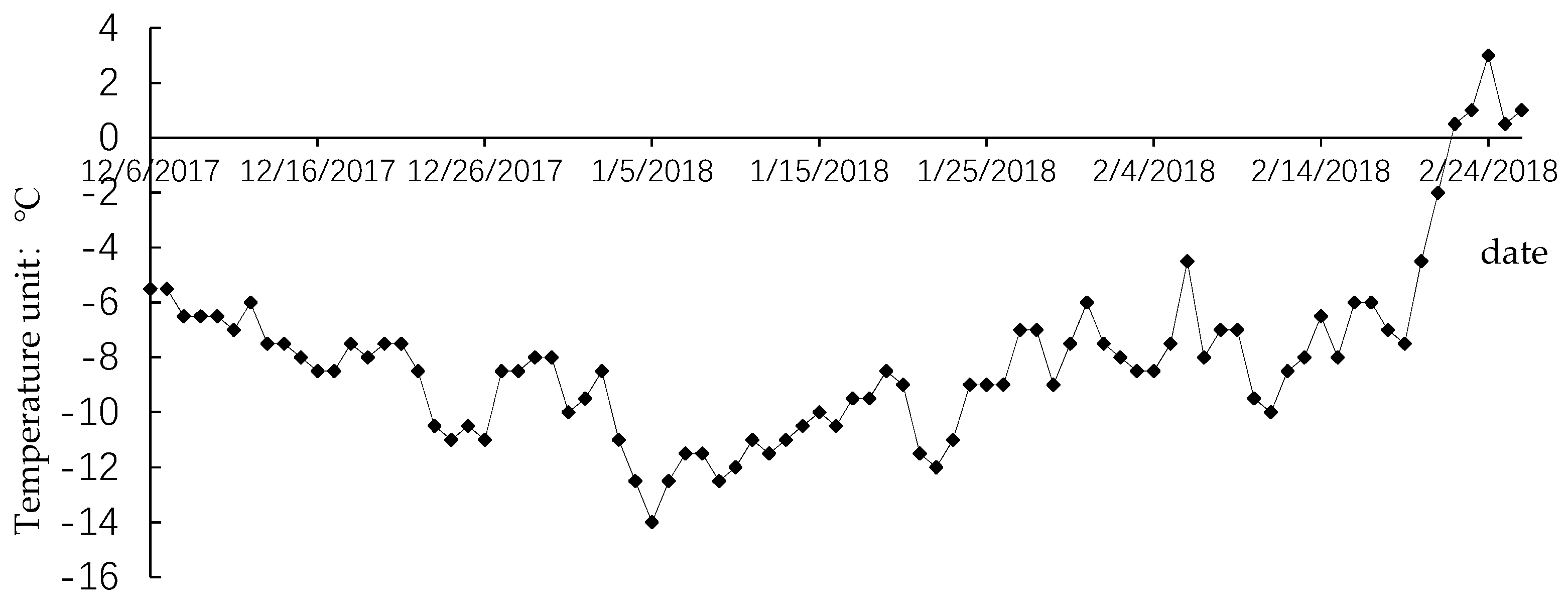

| Date | Height Difference (m) | Ground Temperature (°C) | Temperature Gradient (°C m−1) | Equivalent Height Difference (m) | Equivalent Temperature (°C) |
|---|---|---|---|---|---|
| 6 December 2017 | 2.62 | −5.5 | 2.10 | 1.27 | 2.67 |
| 15 December 2018 | 3.03 | −8.0 | 2.64 | 0.86 | 2.27 |
| 31 December 2018 | 3.24 | −10.0 | 3.09 | 0.65 | 2.01 |
| 15 January 2018 | 3.54 | −10.0 | 2.82 | 0.35 | 0.99 |
| 30 January 2018 | 3.78 | −7.5 | 1.98 | 0.11 | 0.22 |
| 10 February 2018 | 3.89 | −9.5 | 2.44 | 0 | 0.00 |
| Properties | Value | |||
|---|---|---|---|---|
| Temperature/°C | −1 | −2 | −3 | −5 |
| Elastic modulus/MPa | 19 | 26 | 33 | 46 |
| Material | Thickness (mm) | Number of Layers | Thermal Conductivity (W/(m·K)) | Specific Heat Capacity (kJ/(kg·K)) | Density (kg/m3) |
|---|---|---|---|---|---|
| Geotextile | 3 | 2 | 0.241 | 1.88 | 133 |
| PE film | 0.3 | 1 | 0.16 | 0.9 | 1400 |
| air | 8 | 1 | 0.02 | 1.003 | 1.29 |
| Material | Thermal Conductivity (W/(m·K)) | Specific Heat Capacity (kJ/(kg·K)) | Density (kg/m3) |
|---|---|---|---|
| Concrete | 1.58 | 0.97 | 2250 |
| Ice | 2.2 | 2.1 | 917 |
| Soil | 1.5 | 0.92 | 1390 |
| Water | 0.6 | 4.2 | 1000 |
| Air | 0.02 | 1.003 | 1.29 |
| Lining Form | One-Third of the West Slope | Two-Thirds of the West Slope | One-Third of the East Slope | Two-Thirds of the East Slope |
|---|---|---|---|---|
| With geomembrane | 1.45% | 0.07% | 6.93% | 6.72% |
| Without geomembrane | 1.69% | 0.86% | 3.82% | 3.33% |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mo, T.; Lou, Z. Numerical Simulation of Frost Heave of Concrete Lining Trapezoidal Channel Under an Open System. Water 2020, 12, 335. https://doi.org/10.3390/w12020335
Mo T, Lou Z. Numerical Simulation of Frost Heave of Concrete Lining Trapezoidal Channel Under an Open System. Water. 2020; 12(2):335. https://doi.org/10.3390/w12020335
Chicago/Turabian StyleMo, Tengfei, and Zongke Lou. 2020. "Numerical Simulation of Frost Heave of Concrete Lining Trapezoidal Channel Under an Open System" Water 12, no. 2: 335. https://doi.org/10.3390/w12020335
APA StyleMo, T., & Lou, Z. (2020). Numerical Simulation of Frost Heave of Concrete Lining Trapezoidal Channel Under an Open System. Water, 12(2), 335. https://doi.org/10.3390/w12020335





