Elevation Dependence of the Impact of Global Warming on Rainfall Variations in a Tropical Island
Abstract
:1. Introduction
2. Materials and Methods
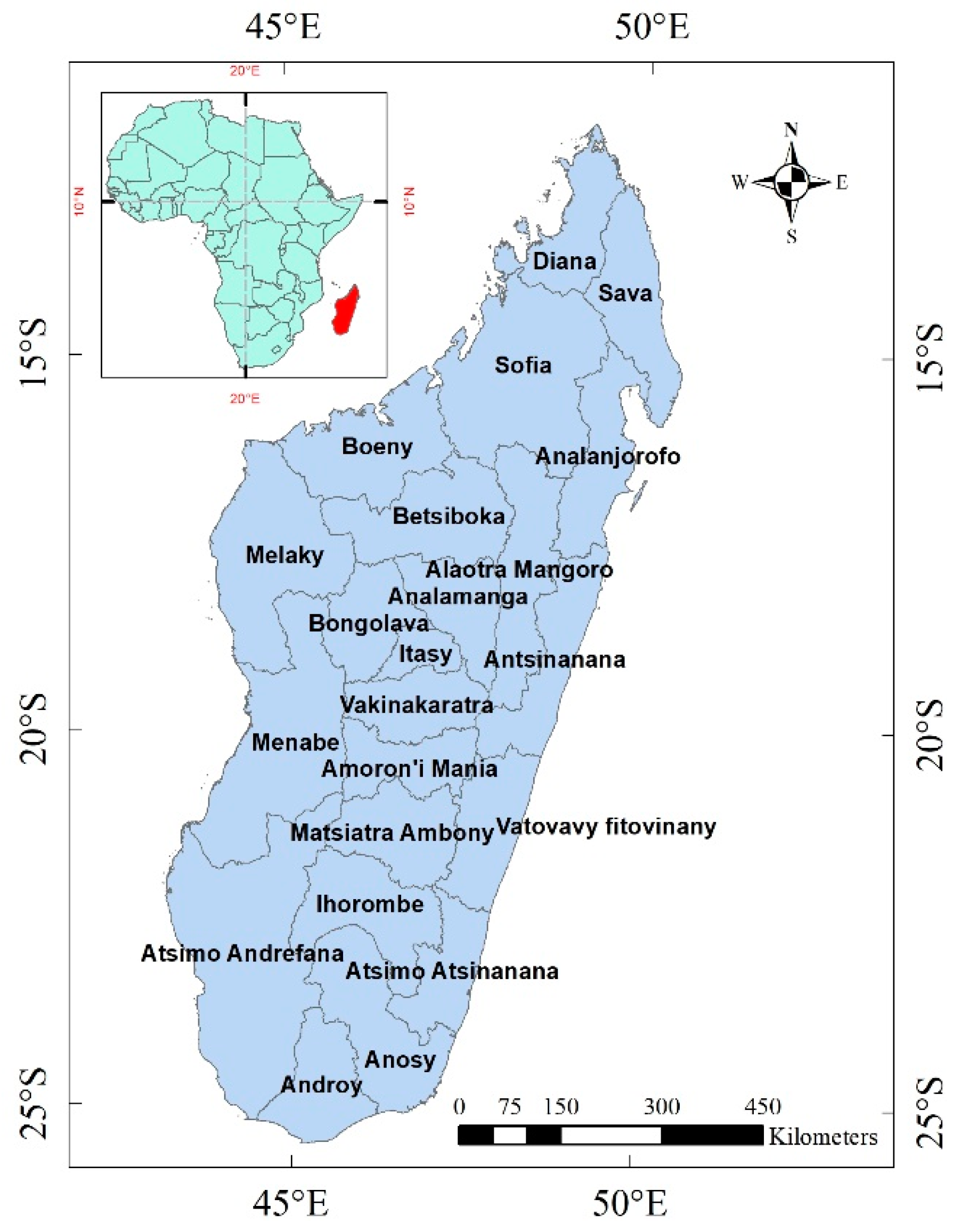
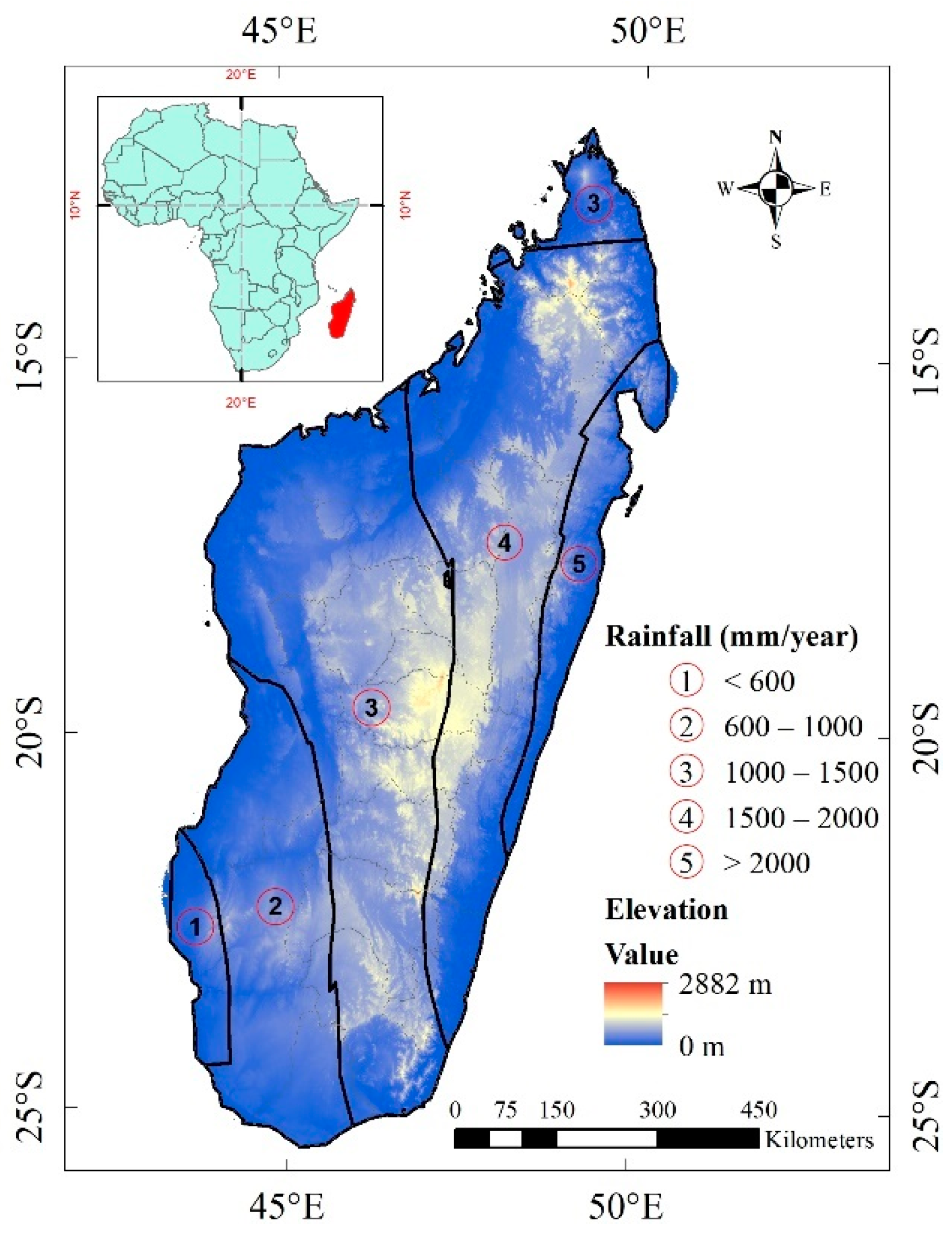
2.1. Description of the Study Area
2.2. Data Source
2.3. Methods
2.3.1. The MK Test and Sen’s Slope Estimator
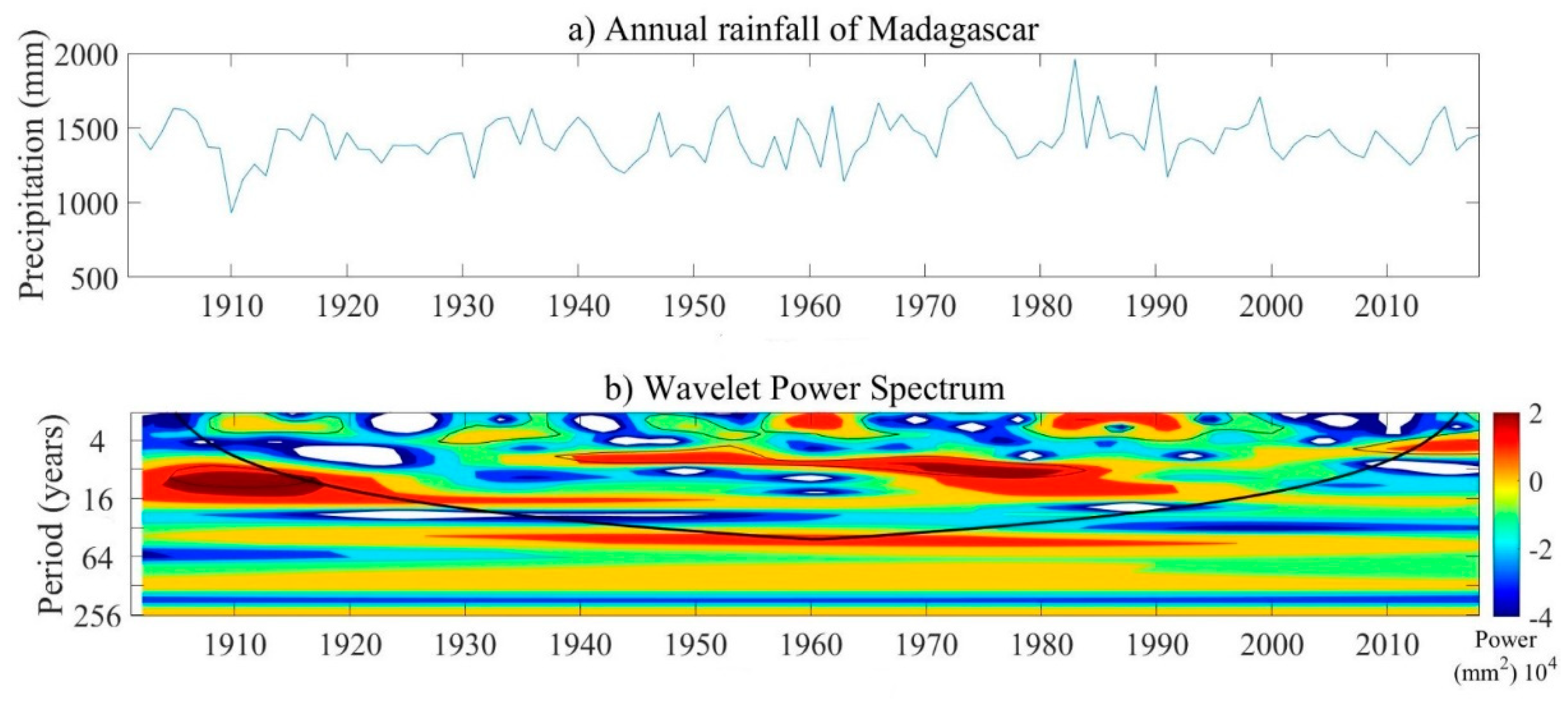
2.3.2. Continuous Wavelet Transform
2.3.3. Elevation Dependence of Temperature Trends and Rainfall Trends
3. Results and Discussions
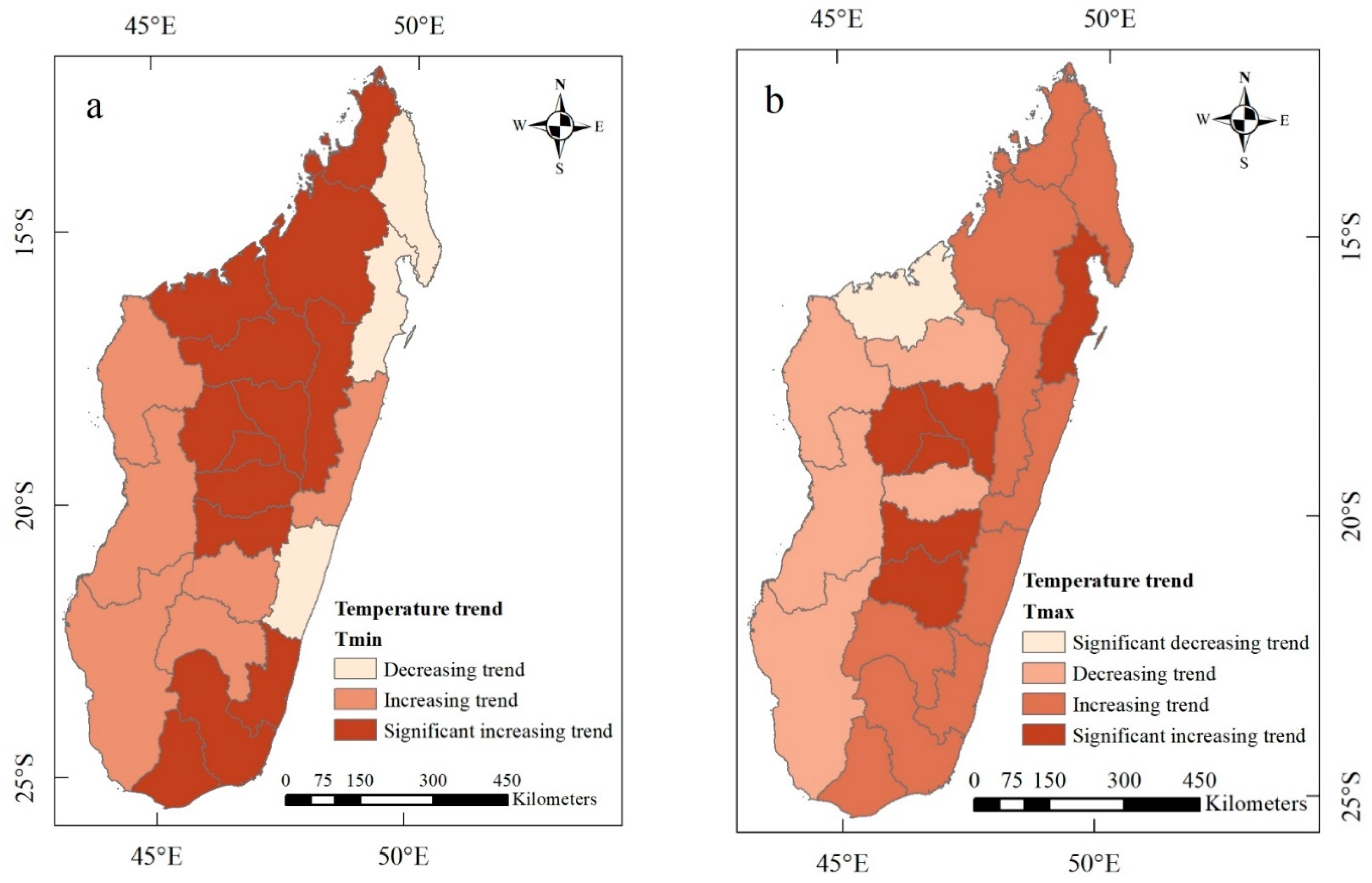
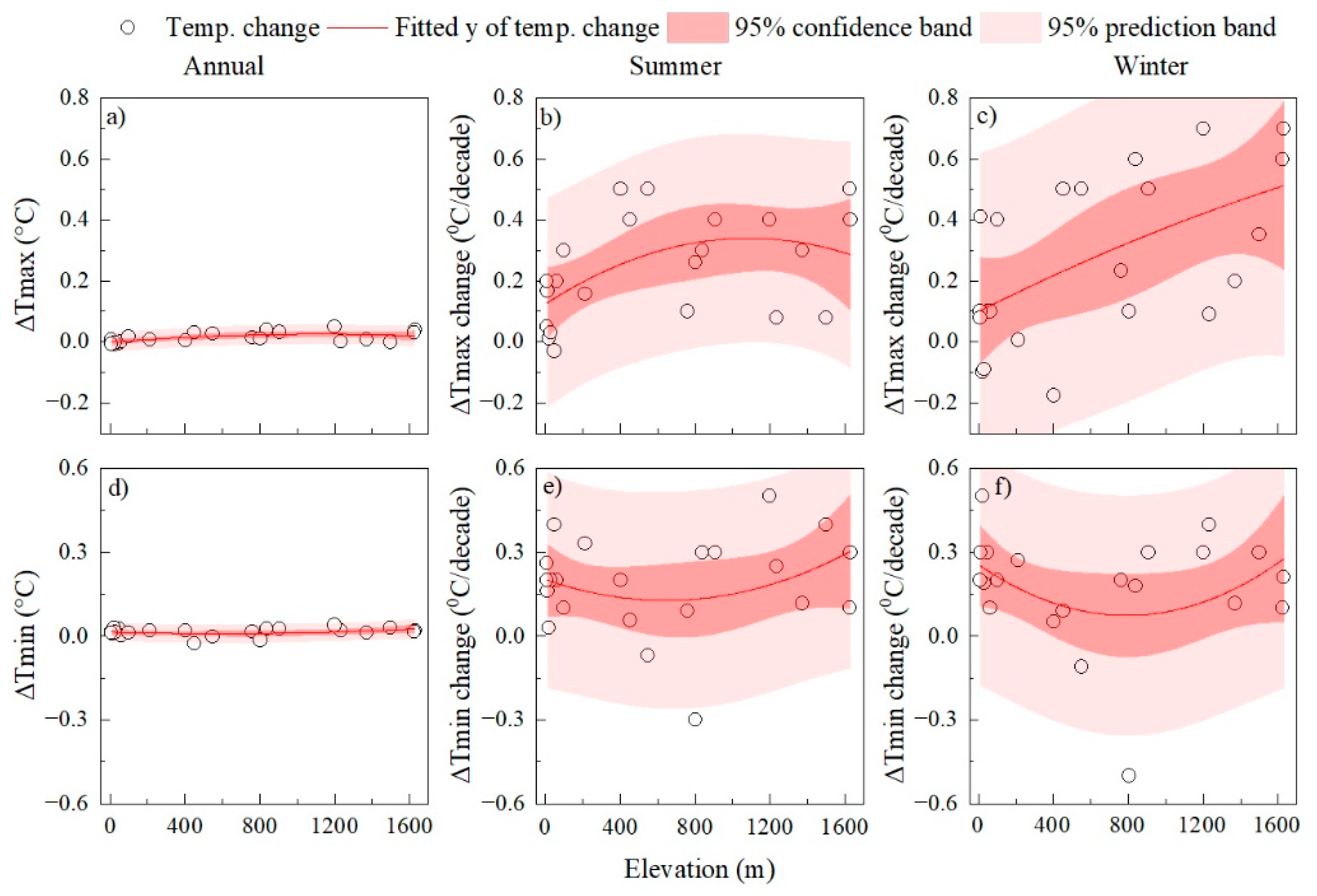
3.1. The Warming in Madagascar
3.2. Changes in Annual Rainfall
3.2.1. Increases in Annual Average Rainfall of Madagascar
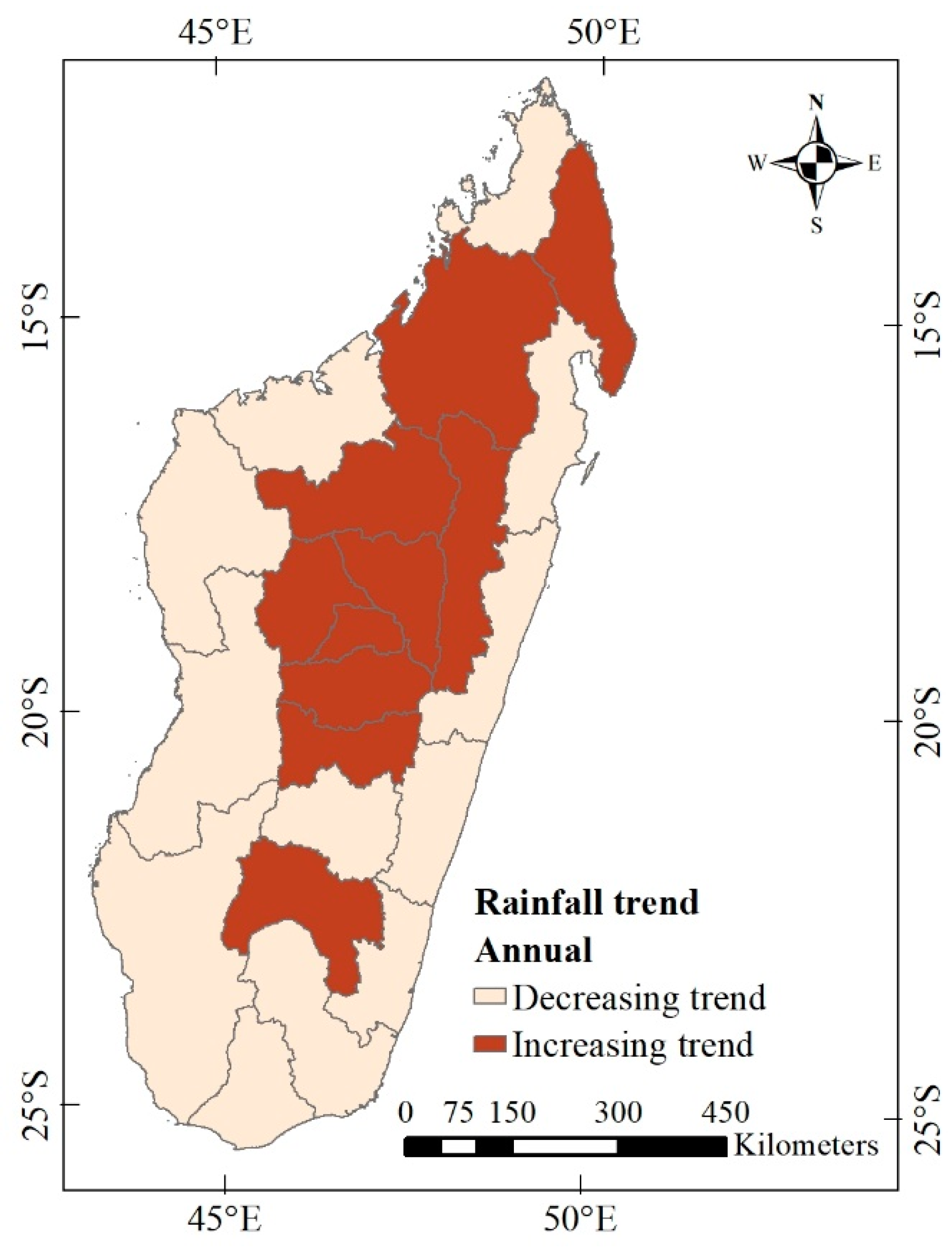
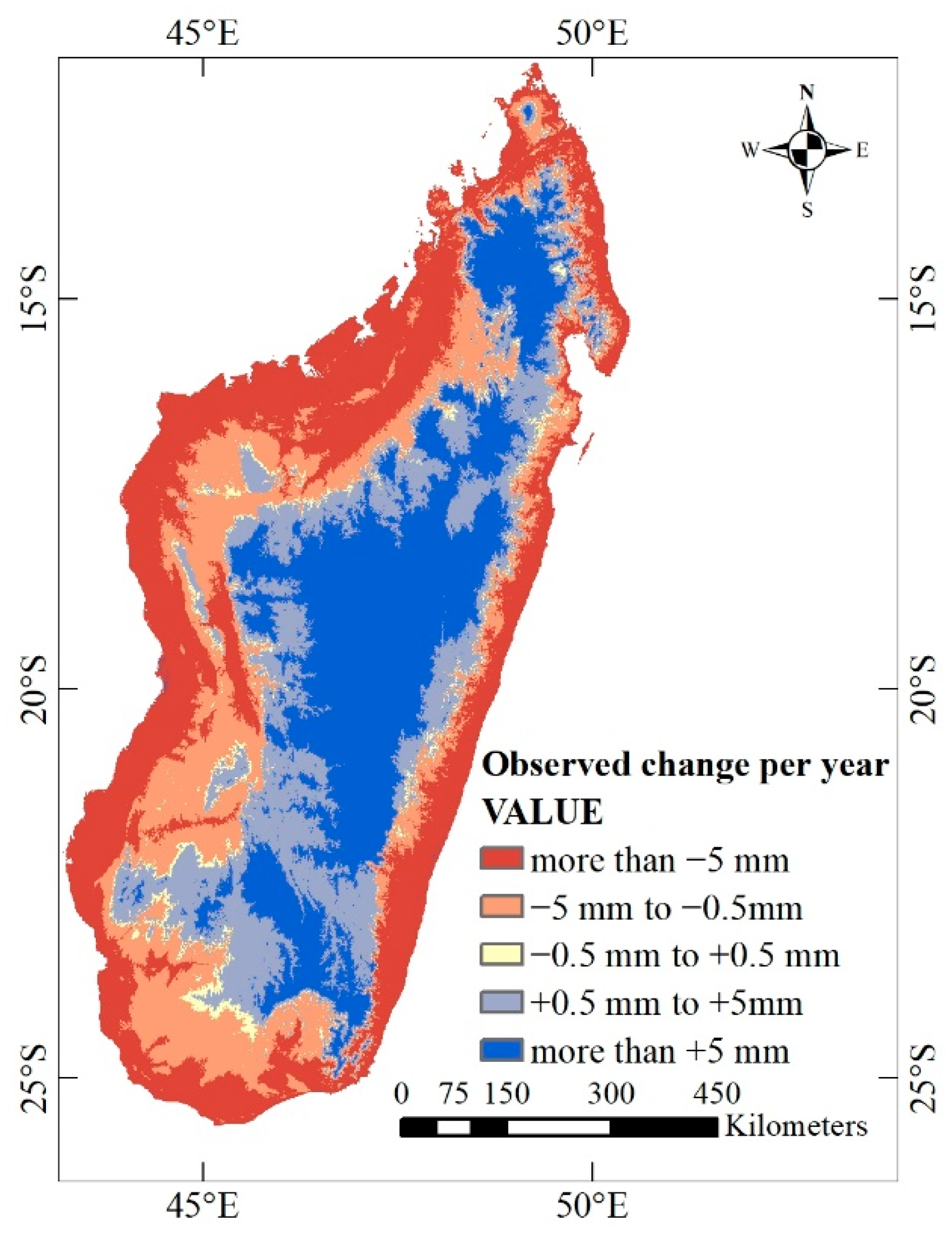
3.2.2. Changes in regional annual rainfall of Madagascar
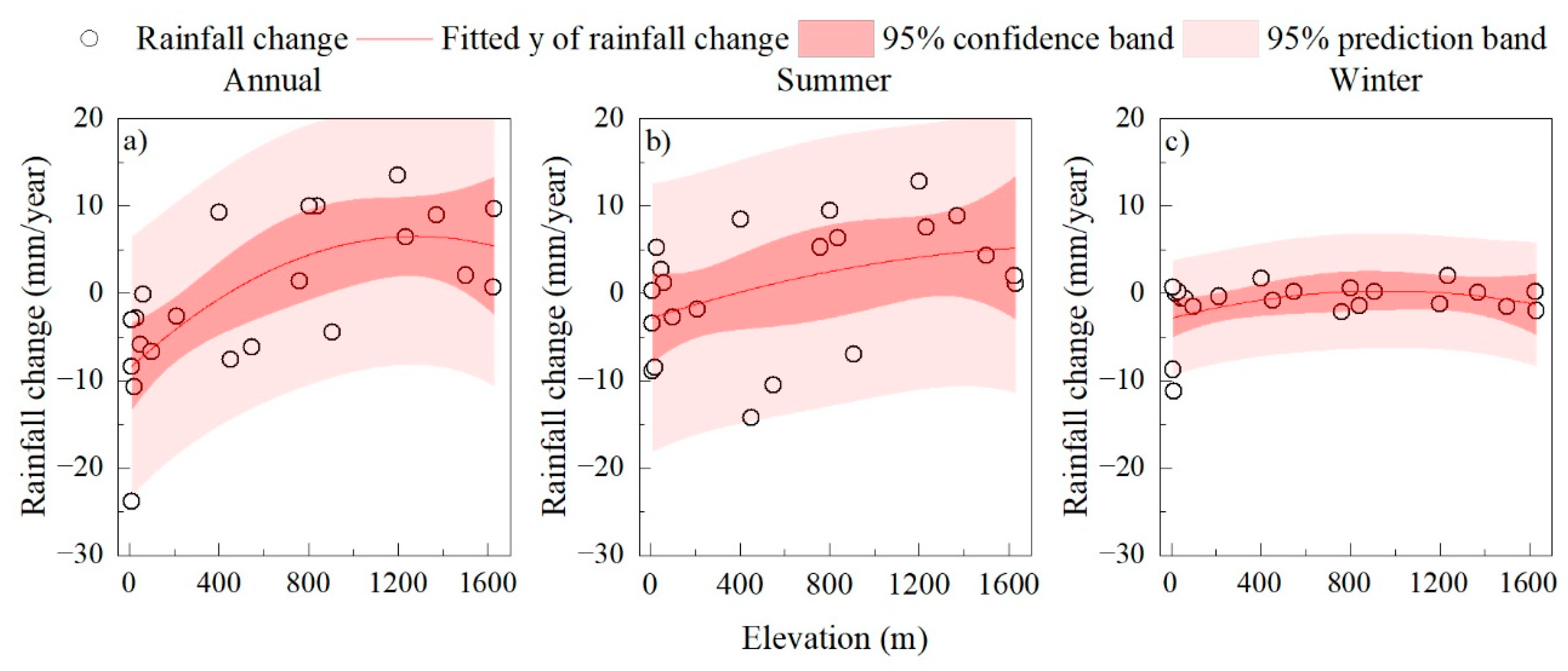
3.2.3. Correlation between Elevation and Annual Rainfall Variation
3.3. The Phenomenon of Wet becomes Wetter and the Warmer Becomes Wetter
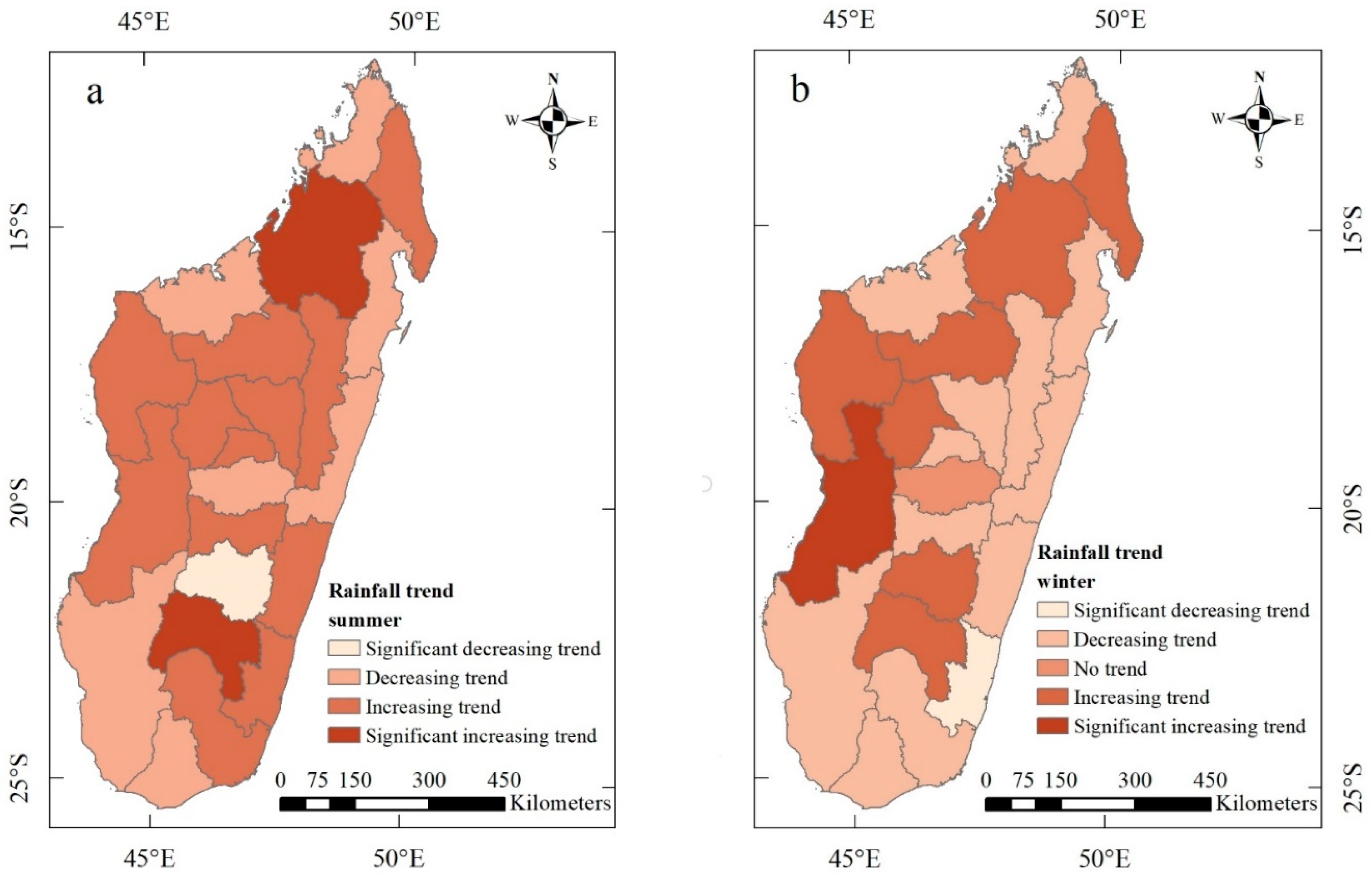
3.3.1. Changes in Regional Seasonal Rainfall
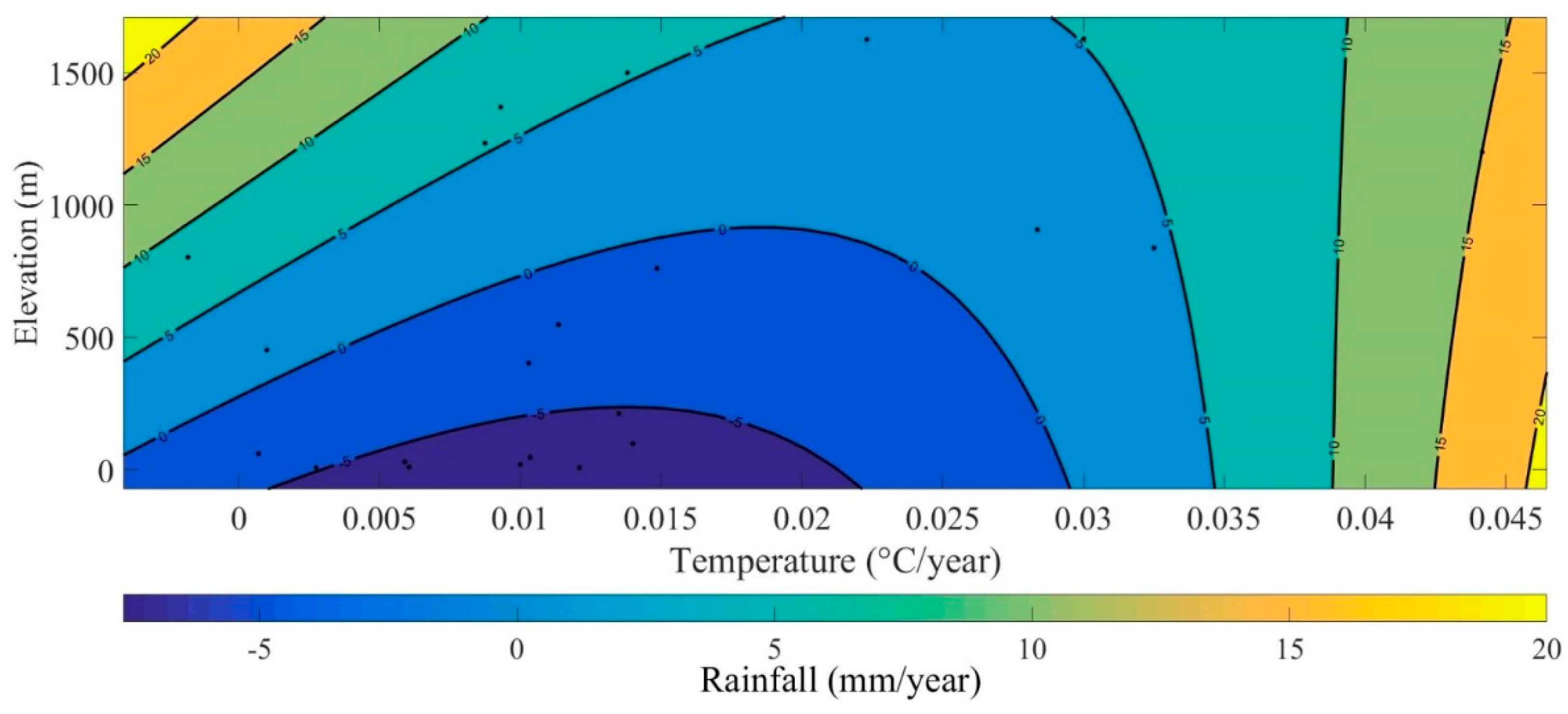
3.3.2. Correlation between Rainfall, Temperature, and Elevation
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
References
- NASA. Available online: https://climate.nasa.gov/vital-signs/global-temperature/ (accessed on 19 July 2020).
- Ahmadalipour, A.; Moradkhani, H.; Castelletti, A.; Magliocca, N. Future drought risk in Africa: Integrating vulnerability, climate change, and population growth. Sci. Total Environ. 2019, 662, 672–686. [Google Scholar] [CrossRef] [PubMed]
- Fujihara, Y.; Tanaka, K.; Watanabe, T.; Nagano, T.; Kojiri, T. Assessing the impacts of climate change on the water resources of the Seyhan River Basin in Turkey: Use of dynamically downscaled data for hydrologic simulations. J. Hydrol. 2008, 353, 33–48. [Google Scholar] [CrossRef]
- IPCC. Climate Change 2014: Synthesis Report. Contribution of Working Groups I, II and III to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; IPCC: Geneva, Switzerland, 2014; p. 151. [Google Scholar]
- Zhu, Y.; Lin, Z.; Wang, J.; Zhao, Y.; He, F. Impacts of Climate Changes on Water Resources in Yellow River Basin, China. Procedia Eng. 2016, 154, 687–695. [Google Scholar] [CrossRef] [Green Version]
- Huang, Y.; Cai, J.; Yin, H.; Cai, M. Correlation of precipitation to temperature variation in the Huanghe River (Yellow River) basin during 1957–2006. J. Hydrol. 2009, 372, 1–8. [Google Scholar] [CrossRef]
- Yang, P.; Xia, J.; Zhang, Y.; Hong, S. Temporal and spatial variations of precipitation in Northwest China during 1960–2013. Atmos. Res. 2017, 183, 283–295. [Google Scholar] [CrossRef]
- Ahmadalipour, A.; Moradkhani, H. Multi-dimensional assessment of drought vulnerability in Africa: 1960–2100. Sci. Total Environ. 2018, 644, 520–535. [Google Scholar] [CrossRef]
- Sannigrahi, S.; Zhang, Q.; Joshi, P.; Sutton, P.C.; Keesstra, S.; Roy, P.; Pilla, F.; Basu, B.; Wang, Y.; Jha, S.; et al. Examining effects of climate change and land use dynamic on biophysical and economic values of ecosystem services of a natural reserve region. J. Clean. Prod. 2020, 257, 120424. [Google Scholar] [CrossRef]
- Chen, Y.; Liu, A.; Cheng, X. Quantifying economic impacts of climate change under nine future emission scenarios within CMIP6. Sci. Total Environ. 2020, 703, 134950. [Google Scholar] [CrossRef]
- Epule, T.E.; Ford, J.D.; Lwasa, S. Projections of maize yield vulnerability to droughts and adaptation options in Uganda. Land Use Policy 2017, 65, 154–163. [Google Scholar] [CrossRef]
- Morishima, W.; Akasaka, I. Seasonal trends of rainfall and surface temperature over southern Africa. Afr. Study Monogr. 2010, 40, 67–76. [Google Scholar]
- Vera, J.F.R.; Mera, Y.E.Z.; Pérez-Martin, M. Adapting water resources systems to climate change in tropical areas: Ecuadorian coast. Sci. Total Environ. 2020, 703, 135554. [Google Scholar] [CrossRef] [PubMed]
- Muluneh, A.; Stroosnijder, L.; Keesstra, S.; Biazin, B. Adapting to climate change for food security in the Rift Valley dry lands of Ethiopia: Supplemental irrigation, plant density and sowing date. J. Agric. Sci. 2017, 155, 703–724. [Google Scholar] [CrossRef]
- Nematchoua, M.K.; Ricciardi, P.; Orosa, J.A.; Buratti, C. A detailed study of climate change and some vulnerabilities in Indian Ocean: A case of Madagascar Island. Sustain. Cities Soc. 2018, 41, 886–898. [Google Scholar] [CrossRef] [Green Version]
- Joly, F. Le climat de Madagascar. L’inf. Geogr. 1941, 5, 76–80. [Google Scholar] [CrossRef]
- Tadross, M.; Randriamarolaza, L.; Yip, Z.K. Climate Change in Madagascar; Recent past and future; World Bank: Washington, DC, USA, 2008; pp. 1–18. [Google Scholar]
- Middletown, J.; McMaster, D. Africa. Available online: https://www.britannica.com/place/Africa (accessed on 28 May 2020).
- Xu, F.; Liu, H.; Peng, H.; Niu, C.; Liu, J. Temperature and precipitation trends and their links with elevation in the Hengduan Mountain region, China. Clim. Res. 2018, 75, 163–180. [Google Scholar] [CrossRef]
- Yao, J.; Yang, Q.; Mao, W.; Zhao, Y.; Xu, X. Precipitation trend–Elevation relationship in arid regions of the China. Glob. Planet. Chang. 2016, 143, 1–9. [Google Scholar] [CrossRef]
- Yu, H.; Wang, L.; Yang, R.; Yang, M.; Gao, R. Temporal and spatial variation of precipitation in the Hengduan Mountains region in China and its relationship with elevation and latitude. Atmos. Res. 2018, 213, 1–16. [Google Scholar] [CrossRef]
- Zeng, W.; Yu, Z.; Wu, S.; Qin, J. Changes in annual, seasonal and monthly precipitation events and their link with elevation in Sichuan province, China. Int. J. Clim. 2015, 36, 2303–2322. [Google Scholar] [CrossRef]
- Qing, Y.; Zhu-Guo, M.; Liang, C. A Preliminary Analysis of the Relationship between Precipitation Variation Trends and Altitude in China. Atmos. Ocean. Sci. Lett. 2011, 4, 41–46. [Google Scholar] [CrossRef]
- Rashid, M.; Beecham, S.; Chowdhury, R.K. Assessment of trends in point rainfall using Continuous Wavelet Transforms. Adv. Water Resour. 2015, 82, 1–15. [Google Scholar] [CrossRef]
- Torrence, C.; Compo, G. A practical guide to Wavelet Analysis. J. Am. Meteorol. Soc. 1998, 79, 61–78. [Google Scholar] [CrossRef] [Green Version]
- Roushangar, K.; Alizadeh, F.; Adamowski, J.F. Exploring the effects of climatic variables on monthly precipitation variation using a continuous wavelet-based multiscale entropy approach. Environ. Res. 2018, 165, 176–192. [Google Scholar] [CrossRef] [PubMed]
- Kendall, M.G. Rank Correlation Methods, 5th ed.; Griffin, C., Ed.; Oxford University Press: London, UK, 1975; ISBN 978-0195208375. [Google Scholar]
- Mann, H.B. Nonparametric tests against trend. Econometrica 1945, 13, 245–259. [Google Scholar] [CrossRef]
- Animashaun, I.; Oguntunde, P.; Akinwumiju, A.; Olubanjo, O. Rainfall Analysis over the Niger Central Hydrological Area, Nigeria: Variability, Trend, and Change point detection. Sci. Afr. 2020, 8, e00419. [Google Scholar] [CrossRef]
- Asare-Nuamah, P.; Botchway, E. Understanding climate variability and change: Analysis of temperature and rainfall across agroecological zones in Ghana. Heliyon 2019, 5, e02654. [Google Scholar] [CrossRef] [Green Version]
- Valipour, M.; Bateni, S.; Sefidkouhi, M.A.G.; Raeini-Sarjaz, M.; Singh, V.P. Complexity of Forces Driving Trend of Reference Evapotranspiration and Signals of Climate Change. Atmosphere 2020, 11, 1081. [Google Scholar] [CrossRef]
- Gentilucci, M.; Bisci, C.; Burt, P.; Fazzini, M.; Vaccaro, C. Interpolation of Rainfall through Polynomial Regression in the Marche Region (Central Italy). In Geospatial Technologies for All; Lecture Notes in Geoinformation and Cartography, Mansourian, A., Pilesjö, P., Harrie, L., van Lammeren, R., Eds.; Springer International Publishing: Cham, Switzerland, 2018; pp. 55–73. [Google Scholar]
- Tattersall, I.; Sussman, R.W. Notes on Topography, Climate, and Vegetation of Madagascar. In Lemur Biology; Tattersall, I., Sussman, R.W., Eds.; Springer: Boston, MA, USA, 1975; pp. 13–21. [Google Scholar]
- Chu, H.; Wei, J.; Qiu, J.; Li, Q.; Wang, G. Identification of the impact of climate change and human activities on rainfall-runoff relationship variation in the Three-River Headwaters region. Ecol. Indic. 2019, 106, 105516. [Google Scholar] [CrossRef]
- Güçlü, Y.S. Multiple Şen-innovative trend analyses and partial Mann-Kendall test. J. Hydrol. 2018, 566, 685–704. [Google Scholar] [CrossRef]
- Joshi, N.; Gupta, D.; Suryavanshi, S.; Adamowski, J.F.; Madramootoo, C.A. Analysis of trends and dominant periodicities in drought variables in India: A wavelet transform based approach. Atmos. Res. 2016, 182, 200–220. [Google Scholar] [CrossRef]
- Mullick, R.A.; Nur, R.M.; Alam, J.; Islam, K.A. Observed trends in temperature and rainfall in Bangladesh using pre-whitening approach. Glob. Planet. Chang. 2019, 172, 104–113. [Google Scholar] [CrossRef]
- Samarakoon, S.; Dharmagunawardhane, H.; Kularatne, T. Analysis of rainfall trend using mann–kendall test and the sen’s slope estimator: A case study in Matale district in Sri Lanka. Int. J. Agric. Environ. Res. 2017, 6, 131–138. [Google Scholar]
- Umar, D.; Ramli, M.; Aris, A.Z.; Jamil, N.R.; Aderemi, A.A. Evidence of climate variability from rainfall and temperature fluctuations in semi-arid region of the tropics. Atmos. Res. 2019, 224, 52–64. [Google Scholar] [CrossRef]
- Yin, Y.; Xu, C.; Chen, H.; Li, L.; Xu, H.; Li, H.; Jain, S.K. Trend and concentration characteristics of precipitation and related climatic teleconnections from 1982 to 2010 in the Beas River basin, India. Glob. Planet. Chang. 2016, 145, 116–129. [Google Scholar] [CrossRef]
- Sen, P.K. Estimates of the regression coefficient based on Kendall’s Tau. J. Am. Stat. Assoc. 1968, 63, 1379–1389. [Google Scholar] [CrossRef]
- Theil, H. A rank-invariant method of linear and polynomial regression analysis. In Henri Theil’s Contributions to Economics and Econometrics; Springer: Dordrecht, The Netherlands, 1992; pp. 345–381. [Google Scholar]
- Santos, C.A.G.; Ideiao, S.M.A. Application of the Wavelet Transform for Analysis of Precipitation and Runoff 439 Time Series; IAHS Publ.: Wallington, UK, 2006; p. 303. [Google Scholar]
- Lau, K.M.; Weng, H. Climate signal detection using wavelet transform: How to make a time series sing. Bull. Am. Meteorol Soc. 1995, 76, 32391–32402. [Google Scholar] [CrossRef] [Green Version]
- Sokol, Z.; Bližňák, V. Areal distribution and precipitation–altitude relationship of heavy short-term precipitation in the Czech Republic in the warm part of the year. Atmos. Res. 2009, 94, 652–662. [Google Scholar] [CrossRef]
- Dahri, Z.H.; Ludwig, F.; Moors, E.; Ahmad, B.; Khan, A.; Kabat, P. An appraisal of precipitation distribution in the high-altitude catchments of the Indus basin. Sci. Total Environ. 2016, 289–306. [Google Scholar] [CrossRef] [Green Version]
- Palazzi, E.; Filippi, L.; Von Hardenberg, J. Insights into elevation-dependent warming in the Tibetan Plateau-Himalayas from CMIP5 model simulations. Clim. Dyn. 2017, 48, 3991–4008. [Google Scholar] [CrossRef] [Green Version]
- Sanchez-Moreno, J.F.; Mannaerts, C.M.; Jetten, V. Influence of topography on rainfall variability in Santiago Island, Cape Verde. Int. J. Clim. 2013, 34, 1081–1097. [Google Scholar] [CrossRef]
- Nicholson, S.E.; Nash, D.J.; Chase, B.M.; Grab, S.W.; Shanahan, T.M.; Verschuren, D.; Asrat, A.; Lézine, A.-M.; Umer, M. Temperature variability over Africa during the last 2000 years. Holocene 2013, 23, 1085–1094. [Google Scholar] [CrossRef] [Green Version]
- Niang, I.; Abdrabo, M.; Essel, A.; Lennard, C.; Padgham, J.; Urquhart, P. Africa in Climate Change 2014: Impacts, Adaptation, and Vulnerability, Part B: Regional Aspects; Contribution of Working Group II to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2014; pp. 1199–1295. [Google Scholar]
- Hulme, M.; Doherty, R.; Ngara, T.; New, M.; Lister, D. African climate change: 1900-2100. Clim. Res. 2001, 17, 145–168. [Google Scholar] [CrossRef] [Green Version]
- Ongoma, V.; Chen, H. Temporal and spatial variability of temperature and precipitation over East Africa from 1951 to 2010. Theor. Appl. Clim. 2017, 129, 131–144. [Google Scholar] [CrossRef]
- Collins, J.M. Temperature Variability over Africa. J. Clim. 2011, 24, 3649–3666. [Google Scholar] [CrossRef] [Green Version]
- Mountain Research Initiative EDW Working Group; Pepin, N.; Bradley, R.S.; Diaz, H.F.; Baraer, M.; Caceres, E.B.; Forsythe, N.; Fowler, H.J.; Greenwood, G.; Hashmi, M.Z.; et al. Elevation-dependent warming in mountain regions of the world. Nat. Clim. Chang. 2015, 5, 424–430. [Google Scholar] [CrossRef] [Green Version]
- Wang, Q.; Fan, X.; Wang, M.-B. Recent warming amplification over high elevation regions across the globe. Clim. Dyn. 2013, 43, 87–101. [Google Scholar] [CrossRef] [Green Version]
- Fan, Z.-X.; Bräuning, A.; Thomas, A.; Li, J.-B.; Cao, K.-F. Spatial and temporal temperature trends on the Yunnan Plateau (Southwest China) during 1961–2004. Int. J. Clim. 2010, 31, 2078–2090. [Google Scholar] [CrossRef]
- Gebrechorkos, S.H.; Hülsmann, S.; Bernhofer, C. Long-term trends in rainfall and temperature using high-resolution climate datasets in East Africa. Sci. Rep. 2019, 9, 1–9. [Google Scholar] [CrossRef] [Green Version]
- Thomas, N.; Nigam, S. Twentieth-Century Climate Change over Africa: Seasonal Hydroclimate Trends and Sahara Desert Expansion. J. Clim. 2018, 31, 3349–3370. [Google Scholar] [CrossRef]
- Nicholson, S.E.; Funk, C.; Fink, A.H. Rainfall over the African continent from the 19th through the 21st century. Glob. Planet. Chang. 2018, 165, 114–127. [Google Scholar] [CrossRef]
- Santos, C.A.G.; Da Silva, R.M.; Akrami, S.A. Rainfall Analysis in Klang River Basin Using Continuous Wavelet Transform. J. Urban Environ. Eng. 2016, 10, 3–10. [Google Scholar] [CrossRef]
- Janowiak, J.E. An Investigation of Interannual Rainfall Variability in Africa. J. Clim. 1988, 1, 240–255. [Google Scholar] [CrossRef]
- Nicholson, S.E.; Entekhabi, D. The quasi-periodic behavior of rainfall variability in Africa and its relationship to the southern oscillation. Theor. Appl. Clim. 1986, 34, 311–348. [Google Scholar] [CrossRef]
- Niedzielski, T. El Niño/Southern Oscillation and Selected Environmental Consequences. In Machine Learning in Geosciences; Elsevier: Amsterdam, The Netherlands, 2014; Volume 55, pp. 77–122. [Google Scholar]
- Trenberth, K. Changes in precipitation with climate change. Clim. Res. 2011, 47, 123–138. [Google Scholar] [CrossRef] [Green Version]
- Cerdà, A. Relationships between climate and soil hydrological and erosional characteristics along climatic gradients in Mediterranean limestone areas. Geomorphology 1998, 25, 123–134. [Google Scholar] [CrossRef]
- Cerdà, A. Effect of climate on surface flow along a climatological gradient in Israel: A field rainfall simulation approach. J. Arid. Environ. 1998, 38, 145–159. [Google Scholar] [CrossRef]
- Putnam, A.; Broecker, W.S. Human-induced changes in the distribution of rainfall. Sci. Adv. 2017, 3, e1600871. [Google Scholar] [CrossRef] [Green Version]
- Ambrosino, C.; Chandler, R.E.; Todd, M.C. Southern African Monthly Rainfall Variability: An Analysis Based on Generalized Linear Models. J. Clim. 2011, 24, 4600–4617. [Google Scholar] [CrossRef]
- Keesstra, S.; Nunes, J.P.; Saco, P.M.; Parsons, A.J.; Poeppl, R.; Masselink, R.; Cerda, A. The way forward: Can connectivity be useful to design better measuring and modelling schemes for water and sediment dynamics? Sci. Total Environ. 2018, 644, 1557–1572. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tanteliniaina, M.F.R.; Chen, J.; Adyel, T.M.; Zhai, J. Elevation Dependence of the Impact of Global Warming on Rainfall Variations in a Tropical Island. Water 2020, 12, 3582. https://doi.org/10.3390/w12123582
Tanteliniaina MFR, Chen J, Adyel TM, Zhai J. Elevation Dependence of the Impact of Global Warming on Rainfall Variations in a Tropical Island. Water. 2020; 12(12):3582. https://doi.org/10.3390/w12123582
Chicago/Turabian StyleTanteliniaina, Mirindra Finaritra Rabezanahary, Jia Chen, Tanveer M. Adyel, and Jun Zhai. 2020. "Elevation Dependence of the Impact of Global Warming on Rainfall Variations in a Tropical Island" Water 12, no. 12: 3582. https://doi.org/10.3390/w12123582
APA StyleTanteliniaina, M. F. R., Chen, J., Adyel, T. M., & Zhai, J. (2020). Elevation Dependence of the Impact of Global Warming on Rainfall Variations in a Tropical Island. Water, 12(12), 3582. https://doi.org/10.3390/w12123582




