Optimization of Hydrologic Response Units (HRUs) Using Gridded Meteorological Data and Spatially Varying Parameters
Abstract
:1. Introduction
2. Methodology
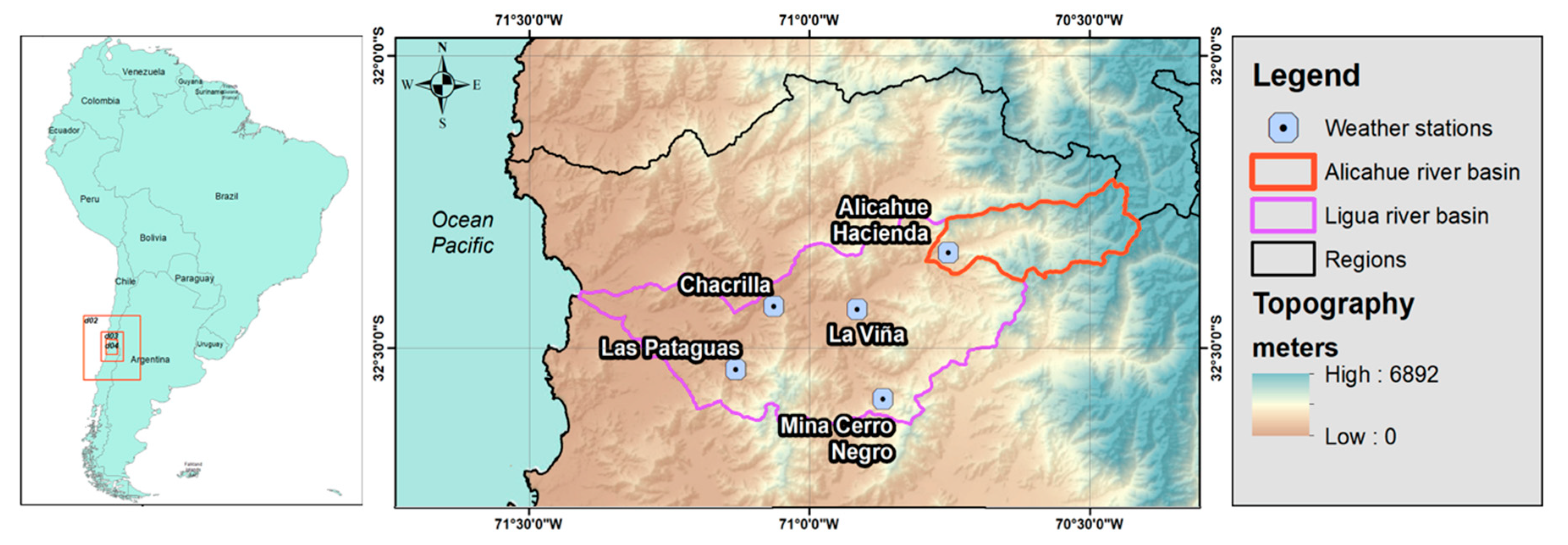
2.1. Area of the Study Case
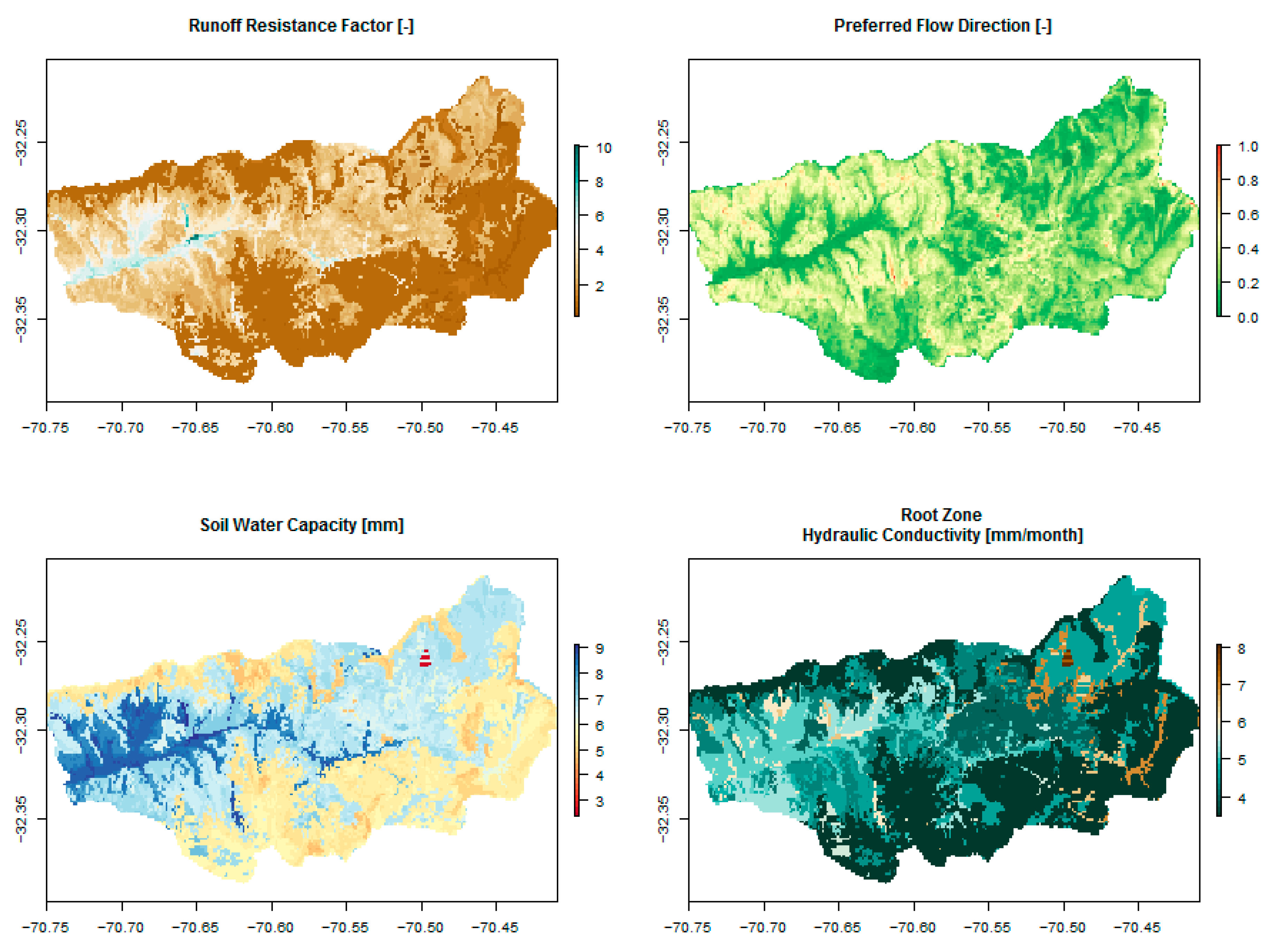
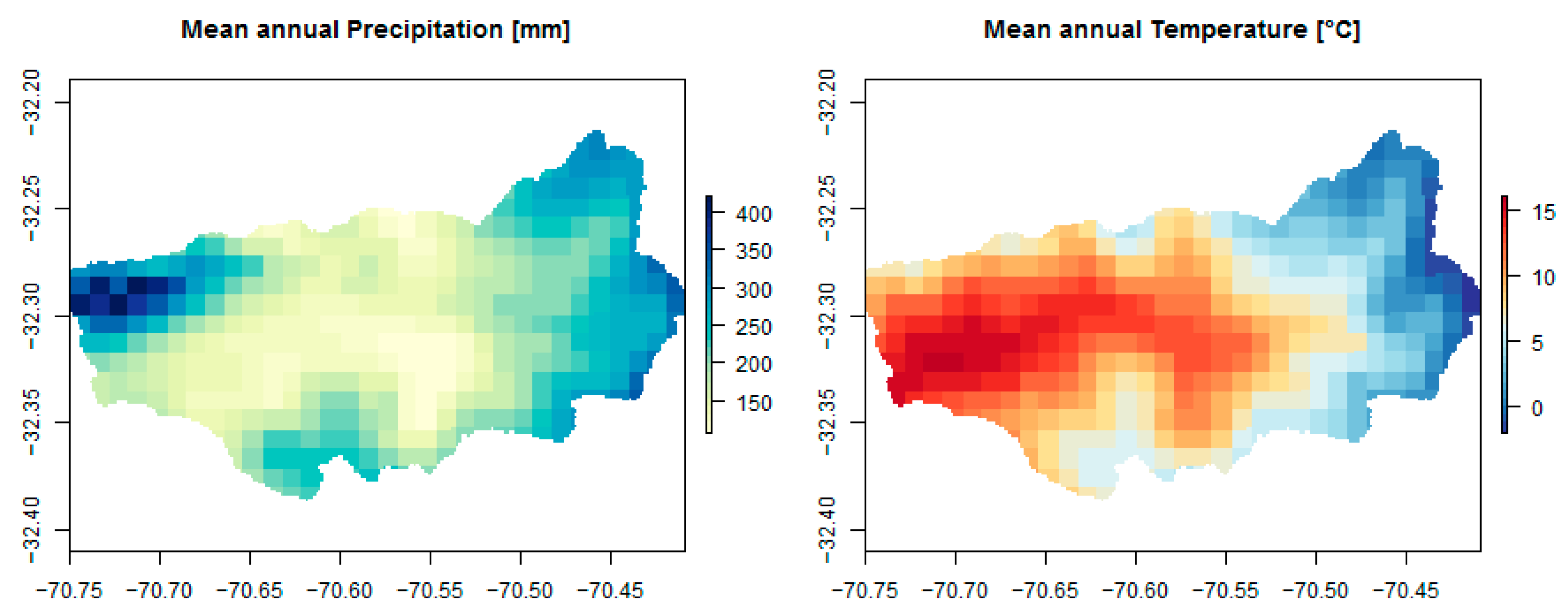
2.2. Hydrologic Parameters and Meteorological Datasets
2.3. Clustering Processes and HRU Delineation
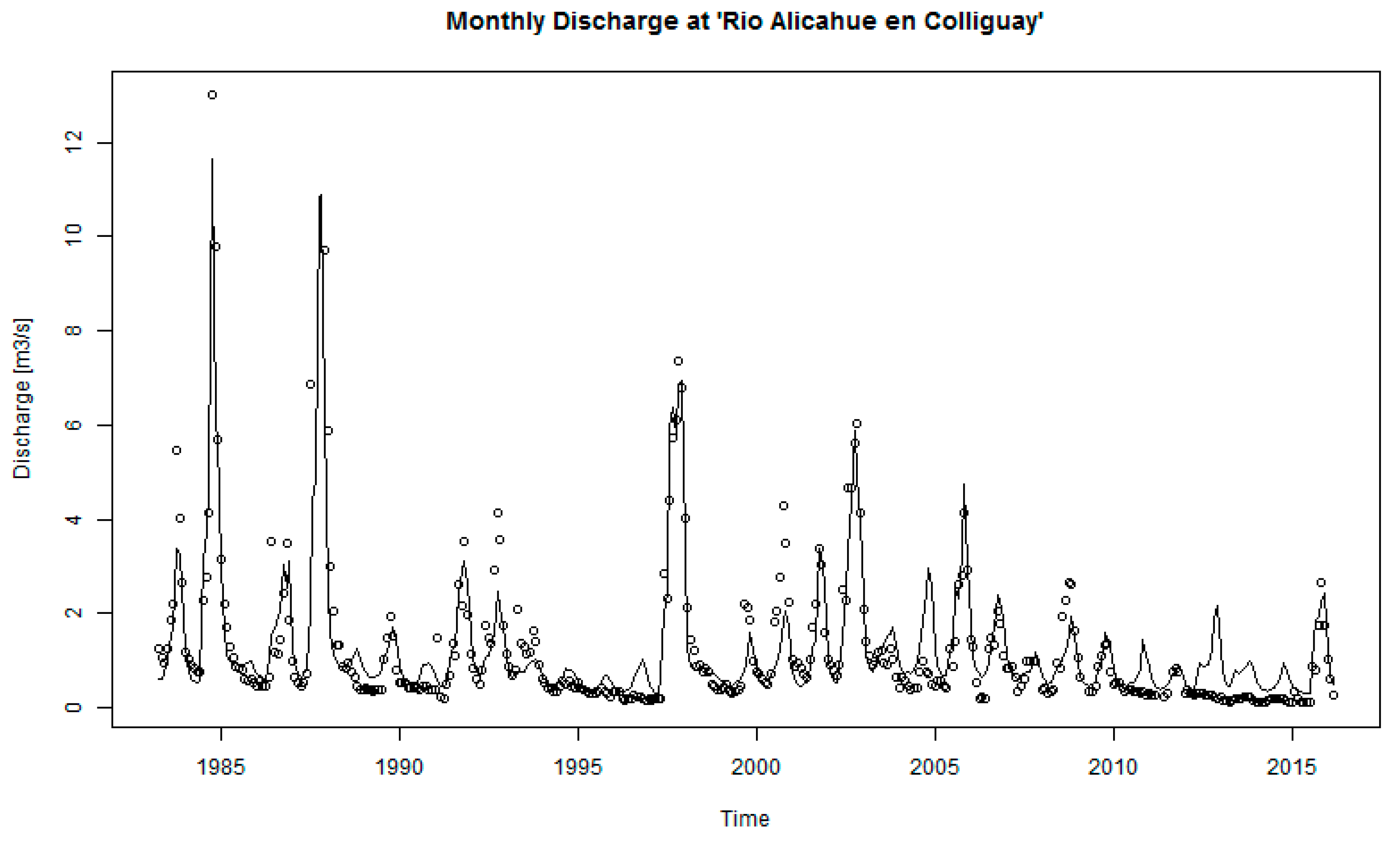
2.4. Hydrological Model Setup and Simulations
3. Results
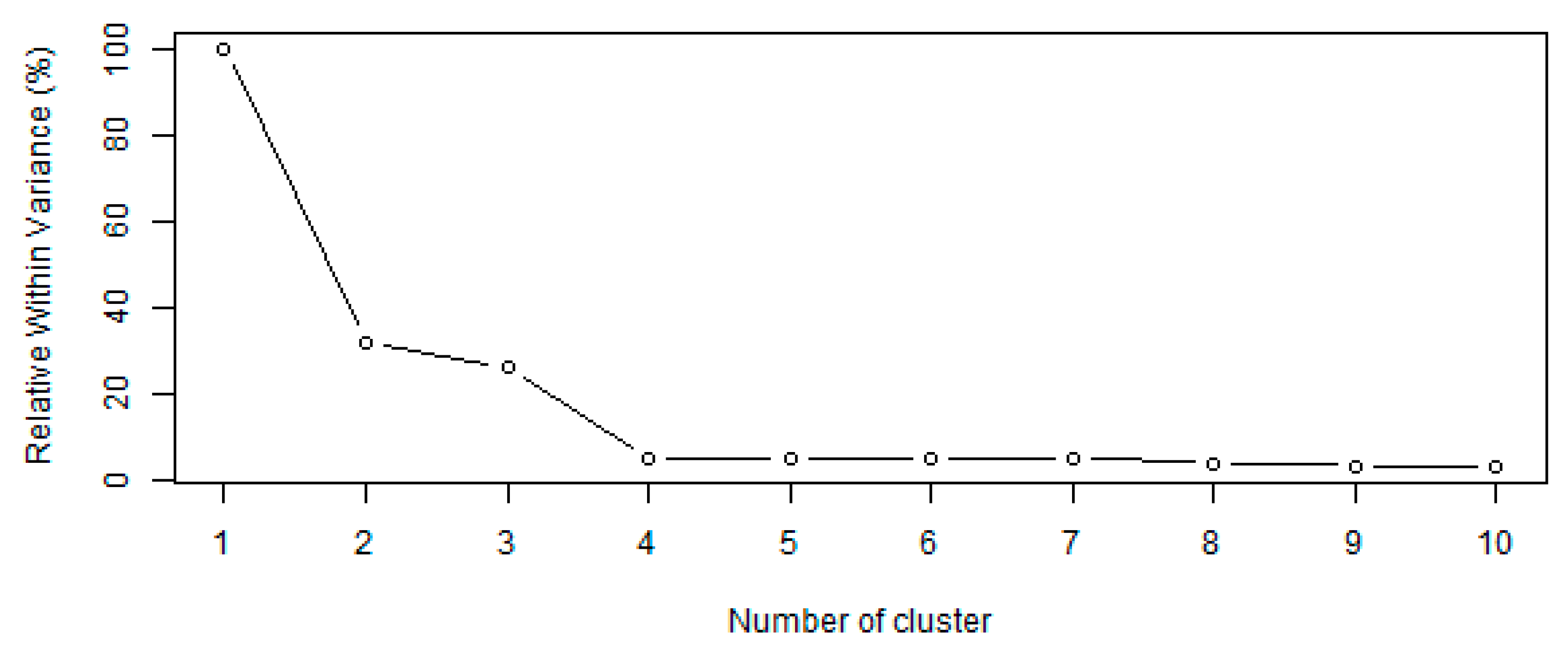
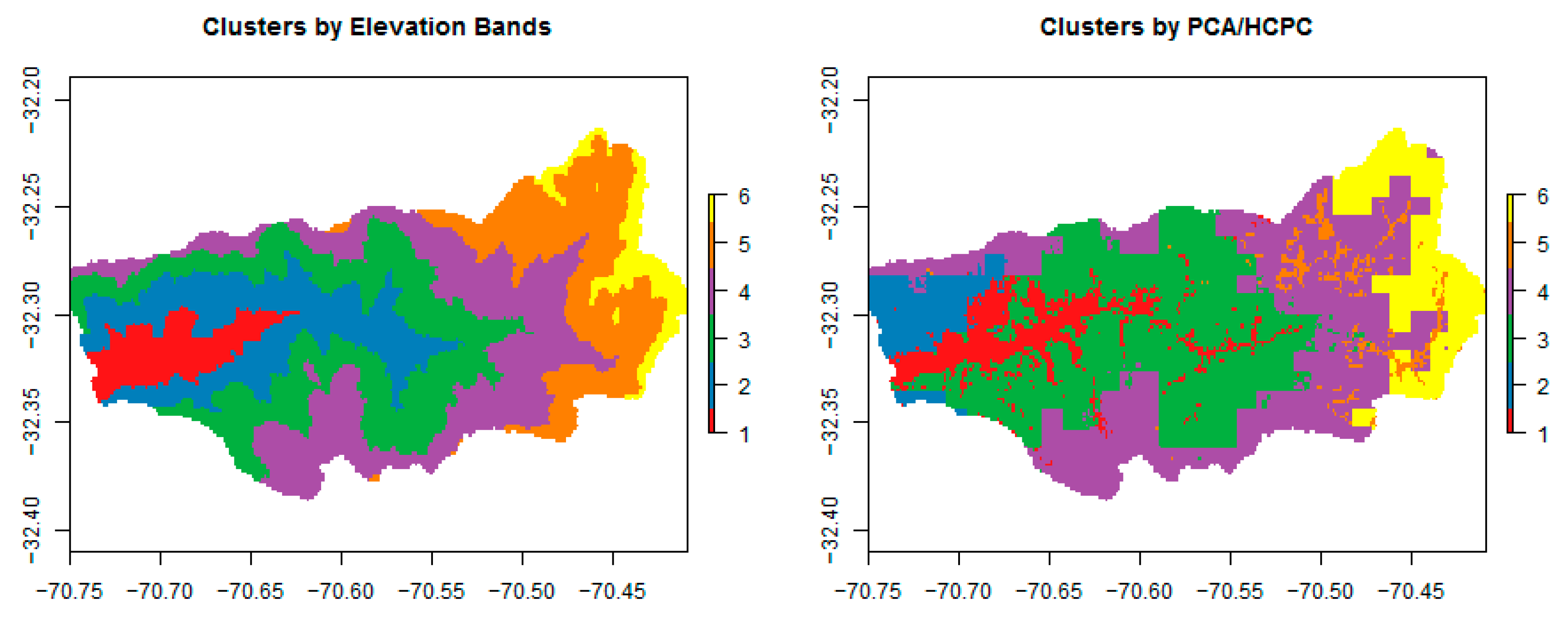
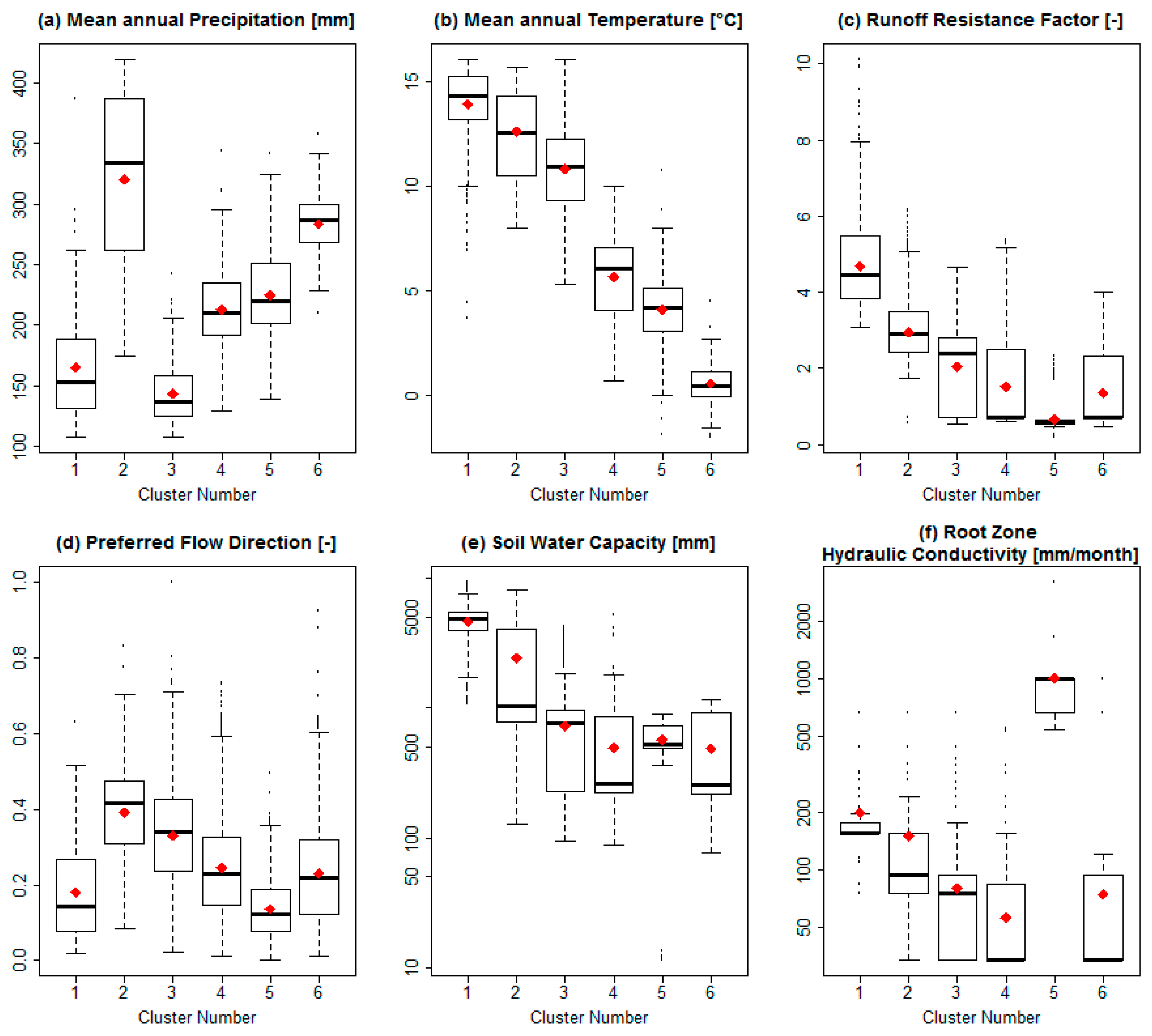
3.1. PCA and Cluster Analysis
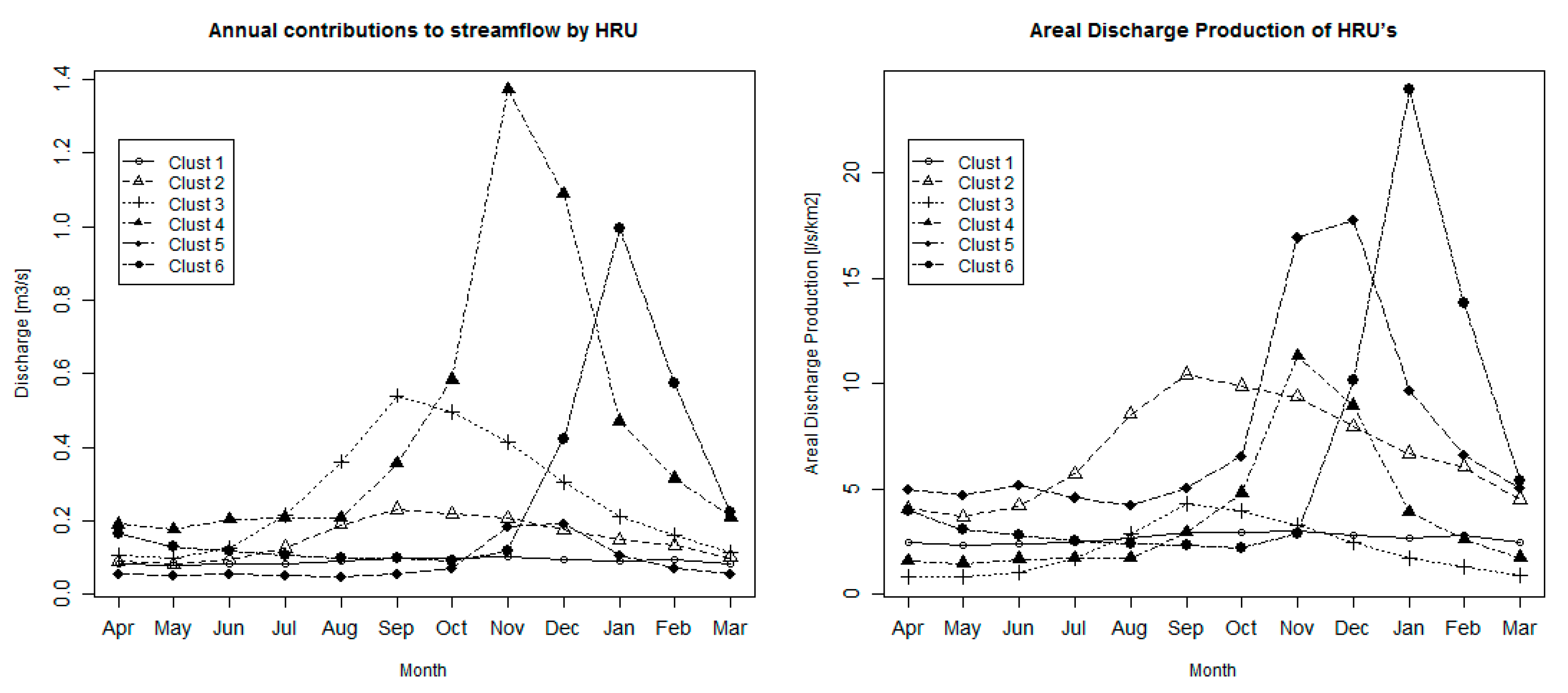
3.2. Hydrological Modeling and HRU Contribution
4. Discussion
4.1. Methodology and Data Uncertainties in the Dataset Preparation
4.2. Clustering Method and Results
4.3. Discharge Independence in the Hydrologic Modeling
5. Conclusions and Further Developments
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Leavesley, G.; Lichty, R.; Troutman, B.; Saindon, L. Precipitation-Runoff Modeling System; User’s Manual; US Department of the Interior: Washington, DC, USA, 1983. [Google Scholar] [CrossRef] [Green Version]
- Flügel, W.-A. Delineating hydrological response units by geographical information system analyses for regional hydrological modelling using PRMS/MMS in the drainage basin of the River Bröl, Germany. Hydrol. Process. 1995, 9, 423–436. [Google Scholar] [CrossRef]
- Pilz, T.; Francke, T.; Bronstert, A. lumpR 2.0.0: An R package facilitating landscape discretisation for hillslope-based hydrological models. Geosci. Model Dev. 2017, 10, 3001–3023. [Google Scholar] [CrossRef] [Green Version]
- Savvidou, E.; Efstratiadis, A.; Koussis, A.D.; Koukouvinos, A.; Skarlatos, D. The Curve Number Concept as a Driver for Delineating Hydrological Response Units. Water 2018, 10, 194. [Google Scholar] [CrossRef] [Green Version]
- Höge, M.; Wöhling, T.; Nowak, W. A Primer for Model Selection: The Decisive Role of Model Complexity. Water Resour. Res. 2018, 54, 1688–1715. [Google Scholar] [CrossRef]
- Nijzink, R.C.; Hutton, C.; Pechlivanidis, I.G.; Capell, R.; Arheimer, B.; Freer, J.; Han, D.; Wagener, T.; McGuire, K.; Savenije, H.H.G.; et al. The evolution of root-zone moisture capacities after deforestation: A step towards hydrological predictions under change? Hydrol. Earth Syst. Sci. 2016, 20, 4775–4799. [Google Scholar] [CrossRef] [Green Version]
- Orth, R.; Dutra, E.; Pappenberger, F. Improving Weather Predictability by Including Land Surface Model Parameter Uncertainty. Mon. Weather. Rev. 2016, 144, 1551–1569. [Google Scholar] [CrossRef]
- Dehotin, J.; Braud, I. Which spatial discretization for distributed hydrological models? Proposition of a methodology and illustration for medium to large-scale catchments. Hydrol. Earth Syst. Sci. 2008, 12, 769–796. [Google Scholar] [CrossRef] [Green Version]
- Haghnegahdar, A.; Tolson, B.A.; Craig, J.R.; Paya, K.T. Assessing the performance of a semi-distributed hydrological model under various watershed discretization schemes. Hydrol. Process. 2015, 29, 4018–4031. [Google Scholar] [CrossRef]
- Han, J.; Huang, G.; Zhang, H.; Li, Z.; Li, Y. Effects of watershed subdivision level on semi-distributed hydrological simulations: Case study of the SLURP model applied to the Xiangxi River watershed, China. Hydrol. Sci. J. 2013, 59, 108–125. [Google Scholar] [CrossRef]
- Haverkamp, S.; Fohrer, N.; Frede, H.-G. Assessment of the effect of land use patterns on hydrologic landscape functions: A comprehensive GIS-based tool to minimize model uncertainty resulting from spatial aggregation. Hydrol. Process. 2005, 19, 715–727. [Google Scholar] [CrossRef]
- Young, C.A.; Escobar-Arias, M.I.; Fernandes, M.; Joyce, B.; Kiparsky, M.; Mount, J.F.; Mehta, V.K.; Purkey, D.; Viers, J.H.; Yates, D. Modeling the Hydrology of Climate Change in California’s Sierra Nevada for Subwatershed Scale Adaptation1. JAWRA J. Am. Water Resour. Assoc. 2009, 45, 1409–1423. [Google Scholar] [CrossRef]
- Yates, D.; Sieber, J.; Purkey, D.; Huber-Lee, A. 21—A Demand-, Priority-, and Preference-Driven Water Planning Model. Part 1: Model Characteristics. Water Int. 2005, 30, 487–500. [Google Scholar] [CrossRef]
- Bonelli, S.; Vicuna, S.; Meza, F.J.; Gironás, J.; Barton, J.R. Incorporating climate change adaptation strategies in urban water supply planning: The case of central Chile. J. Water Clim. Chang. 2014, 5, 357–376. [Google Scholar] [CrossRef]
- Vicuña, S.; Garreaud, R.D.; McPhee, J. Climate change impacts on the hydrology of a snowmelt driven basin in semiarid Chile. Clim. Chang. 2011, 105, 469–488. [Google Scholar] [CrossRef]
- Skamarock, W.C.; Klemp, J.B.; Dudhia, J.; Gill, D.O.; Barker, D.M.; Duda, M.G.; Huang, X.-Y.; Wang, W.; Powers, J.G. A Description of the Advanced Research WRF Version 3. Available online: http://opensky.ucar.edu/islandora/object/technotes%3A500/datastream/PDF/view (accessed on 9 October 2018).
- Tachikawa, T.; Kaku, M.; Iwasaki, A.; Gesch, D.B.; Oimoen, M.J.; Zhang, Z.; Danielson, J.J.; Krieger, T.; Curtis, B.; Haase, J.; et al. ASTER Global Digital Elevation Model Version—Summary of Validaton Results. NASA Land Processes Distributed Active Archive Center. 2011. Available online: http://www.jspacesystems.or.jp/ersdac/GDEM/ver2Validation/Summary_GDEM2_validation_report_final.pdf (accessed on 17 March 2015).
- Martínez, E.; Flores, J.; Retamal, M.; Ahumada, I.; Brito, S. Informe Técnico Final Monitoreo de Cambios, Corrección Cartográfica y Actualización del Catastro de Bosque Nativo en las Regiones de Valparaíso, Metropolitana y Libertador Bernardo O’Higgins.; Centro de Información de Recursos Naturales (CIREN): Santiago, Chile, 2013. [Google Scholar]
- Garreaud, R. Impact of the Variability of Snowline in Winter Discharge Peaks in Basins of Mixed Regime in Central Chile; Sociedad Chilena de Ingeniería Hidráulica: Santiago, Chile, 1992. (In Spanish) [Google Scholar]
- Purkey, D.R.; Joyce, B.; Vicuña, S.; Hanemann, M.W.; Dale, L.L.; Yates, D.; Dracup, J.A. Robust analysis of future climate change impacts on water for agriculture and other sectors: A case study in the Sacramento Valley. Clim. Chang. 2007, 87, 109–122. [Google Scholar] [CrossRef]
- Hijmans, R.J. Geosphere: Spherical Trigonometry; Version 1.5-7; R Package. Available online: https://CRAN.R-project.org/package=geosphere (accessed on 11 May 2017).
- Jolliffe, I.T.; Cadima, J. Principal component analysis: A review and recent developments. Philos. Trans. R. Soc. A: Math. Phys. Eng. Sci. 2016, 374, 20150202. [Google Scholar] [CrossRef]
- Jolliffe, I.T. Principal Components as a Small Number of Interpretable Variables: Some Examples; Springer: New York, NY, USA, 1986; pp. 50–63. [Google Scholar] [CrossRef]
- Zuśka, Z.; Kopcińska, J.; Dacewicz, E.; Skowera, B.; Wojkowski, J.; Ziernicka-Wojtaszek, A. Application of the principal component analysis (PCA) method to assess the impact of meteorological elements on concentrations of particulate matter (PM10): A case study of the mountain valley (the Sacz Basin, Poland). Sustainability 2019, 11, 6740. [Google Scholar] [CrossRef] [Green Version]
- Jolliffe, I.T. Principal Component Analysis, 2nd ed.; Springer: Verlag, NY, USA, 2002; Volume 98, p. 487. [Google Scholar] [CrossRef]
- Lê, S.; Josse, J.; Husson, F. FactoMineR: An R Package for Multivariate Analysis. J. Stat. Softw. 2008, 25, 1–8. [Google Scholar]
- Team, R.C. A Language and Environment for Statistical Computing. 2019. Available online: https://www.r-project.org/ (accessed on 15 September 2019).
- Husson, F.; Julie, J.; Jérôme, P. Technical Report—Agrocampus Principal component methods -hierarchical clustering—Partitional clustering: Why would we need to choose for visualizing data? Appl. Math. Dep. Agrocampus. 2010, 1, 1–17. [Google Scholar]
- Fouedjio, F. A hierarchical clustering method for multivariate geostatistical data. Spat. Stat. 2016, 18, 333–351. [Google Scholar] [CrossRef]
- Kalnay, E.; Kanamitsu, M.; Kistler, R.; Collins, W.; Deaven, D.; Gandin, L.; Iredell, M.; Saha, S.; White, G.; Woollen, J.; et al. The NCEP/NCAR 40-Year Reanalysis Project. Bull. Am. Meteorol. Soc. 1996, 77, 437–471. [Google Scholar] [CrossRef] [Green Version]
- Alvarez-Garreton, C.; Mendoza, P.A.; Boisier, J.P.; Addor, N.; Galleguillos, M.; Zambrano-Bigiarini, M.; Lara, A.; Puelma, C.; Cortes, G.; Garreaud, R.D.; et al. The CAMELS-CL dataset: Catchment attributes and meteorology for large sample studies—Chile dataset. Hydrol. Earth Syst. Sci. 2018, 22, 5817–5846. [Google Scholar] [CrossRef] [Green Version]
- DGA: Actualización del Balance Hídrico Nacional, SIT N° 417. Santiago. 2017. Available online: http://documentos.dga.cl/REH5796v1.pdf (accessed on 1 August 2019).
- Kolmogorov, A. Curves in a Hilbert space that are invariant under the one-parameter group of motions. Dokl. Akad. Nauk SSSR. 1940, 26, 6–9. [Google Scholar]
- Hurst, H.E. Long-term storage capacity of reservoirs. Trans. Amer. Soc. Civil Eng. 1951, 116, 770–799. [Google Scholar]
- Koutsoyiannis, D. Hurst-Kolmogorov Dynamics and Uncertainty1. JAWRA J. Am. Water Resour. Assoc. 2011, 47, 481–495. [Google Scholar] [CrossRef]
- Dimitriadis, P.; Koutsoyiannis, D. Stochastic synthesis approximating any process dependence and distribution. Stoch. Environ. Res. Risk Assess. 2018, 32, 1493–1515. [Google Scholar] [CrossRef]
| Dim.1 | Dim.2 | Dim.3 | Dim.4 | Dim.5 | |
|---|---|---|---|---|---|
| Explained Variance (%) | 50.7 | 16.1 | 11.9 | 5.9 | 5.0 |
| Variables | Contribution to each dimension (%) | ||||
| Temp | 28.2 | 0.1 | 0.7 | 0.2 | 5.1 |
| Albedo | 11.5 | 1.1 | 5.6 | 1.6 | 10.0 |
| Wind Speed | 10.8 | 1.3 | 0.6 | 0.0 | 8.5 |
| Precipitation | 10.7 | 41.5 | 22.6 | 0.0 | 0.6 |
| Evapotranspiration | 10.2 | 2.2 | 1.5 | 0.5 | 12.3 |
| Net Radiation | 9.7 | 3.5 | 9.6 | 1.4 | 10.7 |
| Relative Humidity | 9.5 | 5.6 | 1.4 | 1.0 | 0.0 |
| Runoff Resistance Coefficient | 4.9 | 13.9 | 10.5 | 12.1 | 2.5 |
| Soil Water Capacity | 4.1 | 20.3 | 6.4 | 4.4 | 9.7 |
| Preferred Flow Direction | 0.3 | 4.7 | 32.1 | 0.4 | 35.6 |
| Root Zone Hydraulic Conductivity | 0.0 | 5.7 | 9.0 | 78.3 | 5.0 |
| Scenario | NSE | RMSE |
|---|---|---|
| HRU_01 | 0.58 | 4.1% |
| HRU_02 | 0.71 | 4.3% |
| HRU_03 | 0.72 | 3.6% |
| HRU_04 | 0.77 | 3.5% |
| HRU_05 | 0.78 | 3.2% |
| HRU_06 | 0.79 | 3.1% |
| HRU_07 | 0.78 | 3.1% |
| HRU_08 | 0.77 | 3.1% |
| HRU_09 | 0.76 | 3.2% |
| HRU_10 | 0.74 | 3.2% |
| Goal | 1.00 | 0.0% |
| Cluster 1 | Cluster 2 | Cluster 3 | Cluster 4 | Cluster 5 | Cluster 6 | |
|---|---|---|---|---|---|---|
| Area (km2) | 34.0 | 22.1 | 125.2 | 121.7 | 10.9 | 41.5 |
| % over total area | 9.6% | 6.2% | 35.2% | 34.2% | 3.1% | 11.7% |
| Elevation (m.a.s.l.) | 1483 | 1460 | 2063 | 2080 | 2837 | 2951 |
| Precipitation (mm) | 204 | 413 | 175 | 269 | 287 | 357 |
| Evapotranspiration (mm) | 126 | 203 | 110 | 154 | 50 | 161 |
| Evapotranspiration/Precipitation (–) | 0.62 | 0.49 | 0.63 | 0.57 | 0.17 | 0.45 |
| Discharge | ||||||
| Mean (m3/s) | 0.09 | 0.15 | 0.26 | 0.45 | 0.08 | 0.26 |
| % over total discharge | 7% | 12% | 20% | 35% | 6% | 20% |
| Standard deviation (m3/s) | 0.03 | 0.11 | 0.30 | 0.77 | 0.08 | 0.47 |
| Coefficient of variation | 0.34 | 0.76 | 1.16 | 1.72 | 0.99 | 1.79 |
| Hydrograph centroid (month index) | 9.65 | 9.85 | 9.79 | 10.57 | 10.35 | 11.49 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Poblete, D.; Arevalo, J.; Nicolis, O.; Figueroa, F. Optimization of Hydrologic Response Units (HRUs) Using Gridded Meteorological Data and Spatially Varying Parameters. Water 2020, 12, 3558. https://doi.org/10.3390/w12123558
Poblete D, Arevalo J, Nicolis O, Figueroa F. Optimization of Hydrologic Response Units (HRUs) Using Gridded Meteorological Data and Spatially Varying Parameters. Water. 2020; 12(12):3558. https://doi.org/10.3390/w12123558
Chicago/Turabian StylePoblete, David, Jorge Arevalo, Orietta Nicolis, and Felipe Figueroa. 2020. "Optimization of Hydrologic Response Units (HRUs) Using Gridded Meteorological Data and Spatially Varying Parameters" Water 12, no. 12: 3558. https://doi.org/10.3390/w12123558





