Determination of Deep Learning Model and Optimum Length of Training Data in the River with Large Fluctuations in Flow Rates
Abstract
:1. Introduction
2. Methods
2.1. Applied DNN Models
2.1.1. Convolution Neural Network (CNN)
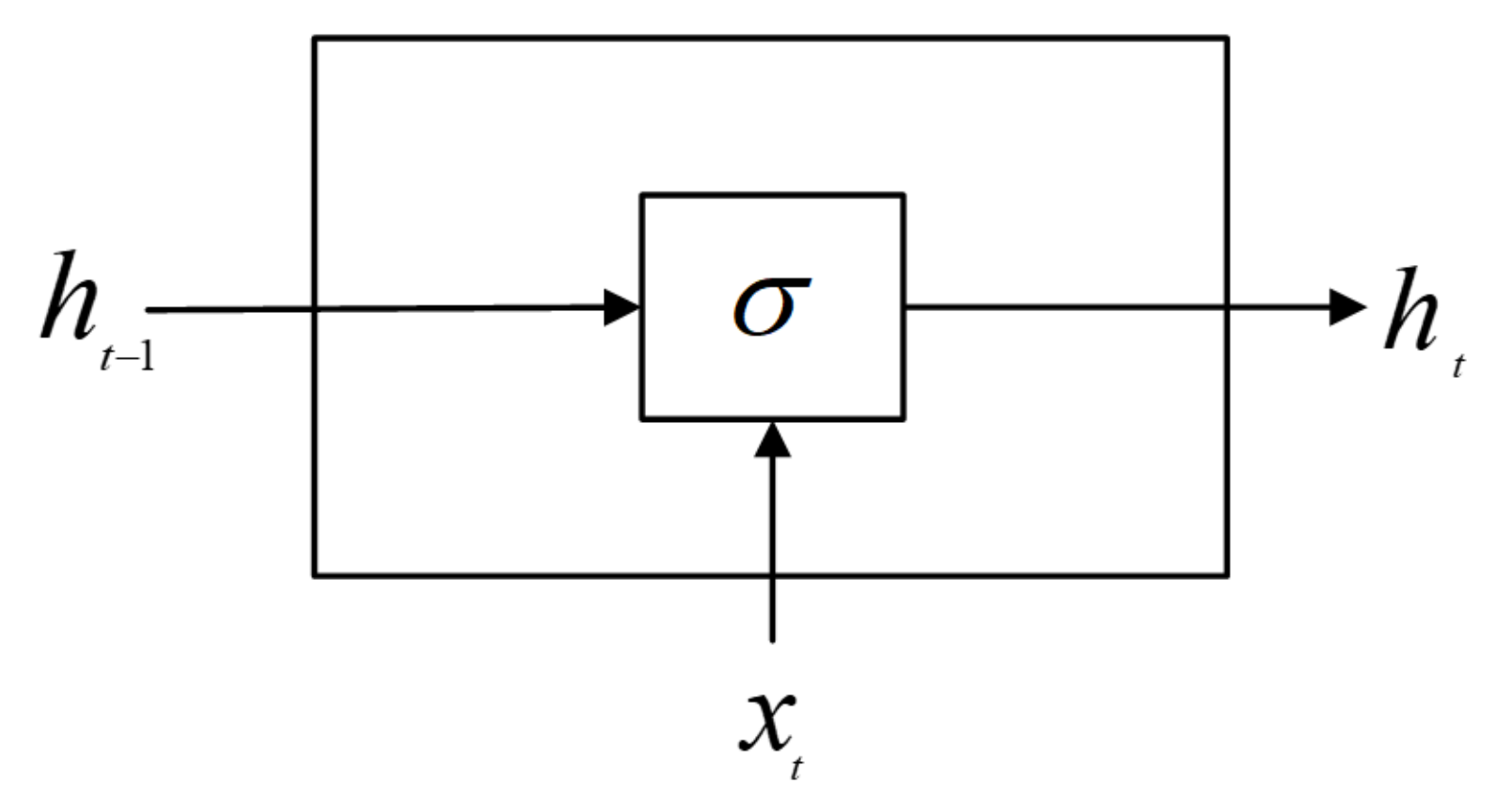
2.1.2. Simple Recurrent Neural Network (Simple RNN)
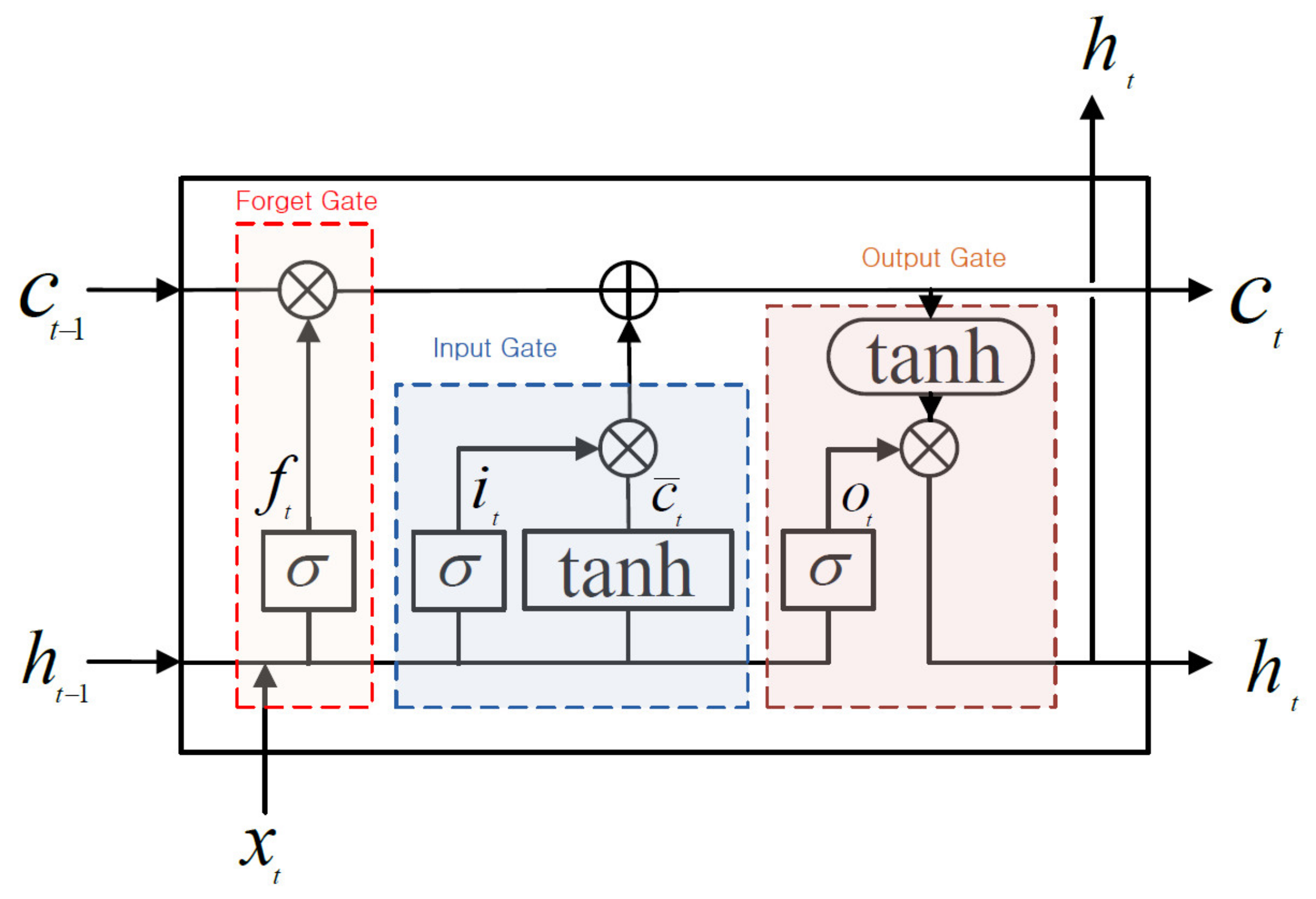
2.1.3. Long Short-Term Memory (LSTM)
2.1.4. Bidirectional LSTM (Bi-LSTM)
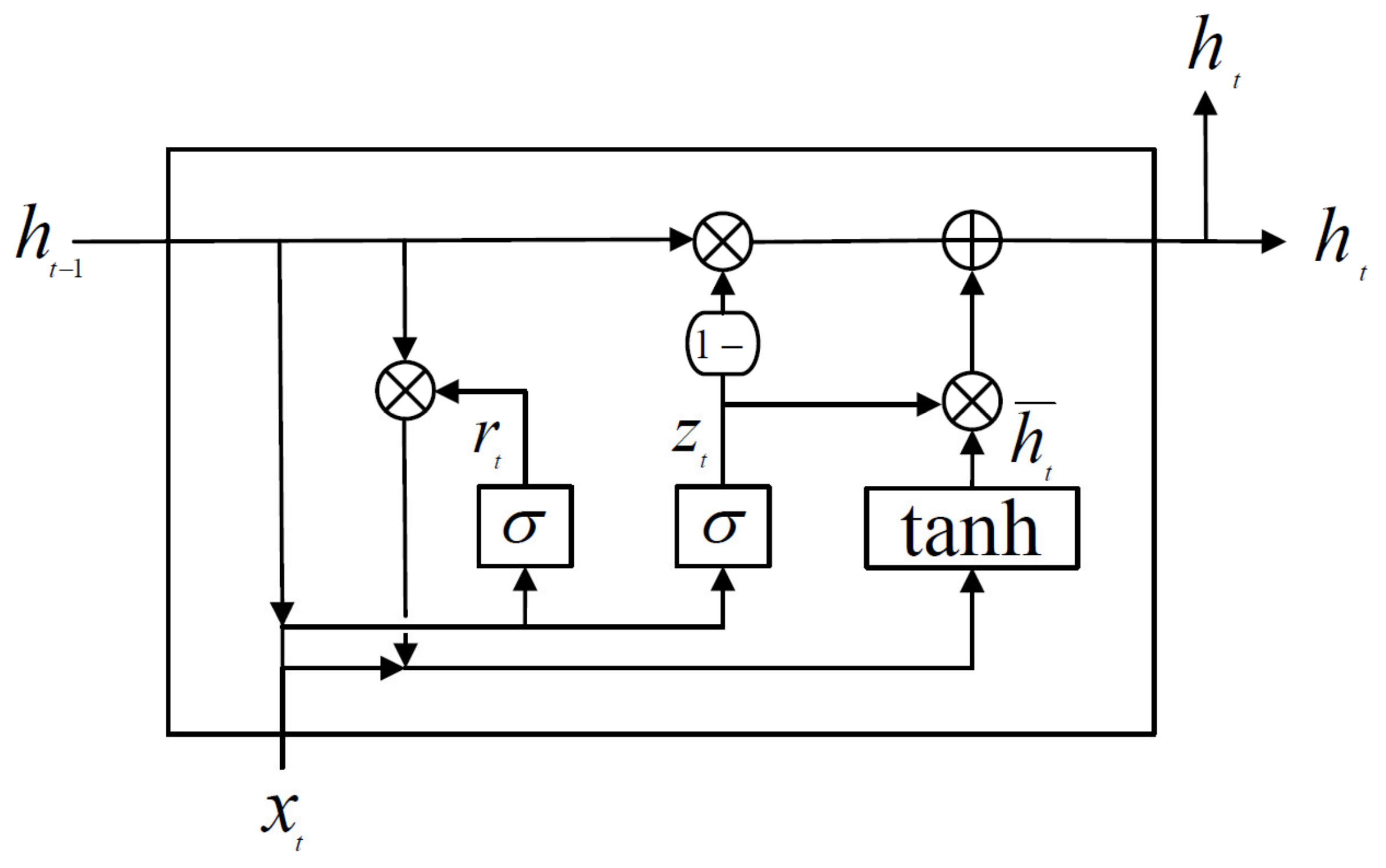
2.1.5. Gated Recurrent Unit (GRU)
2.2. Application of Models
3. Study Area and Data
3.1. Study Area
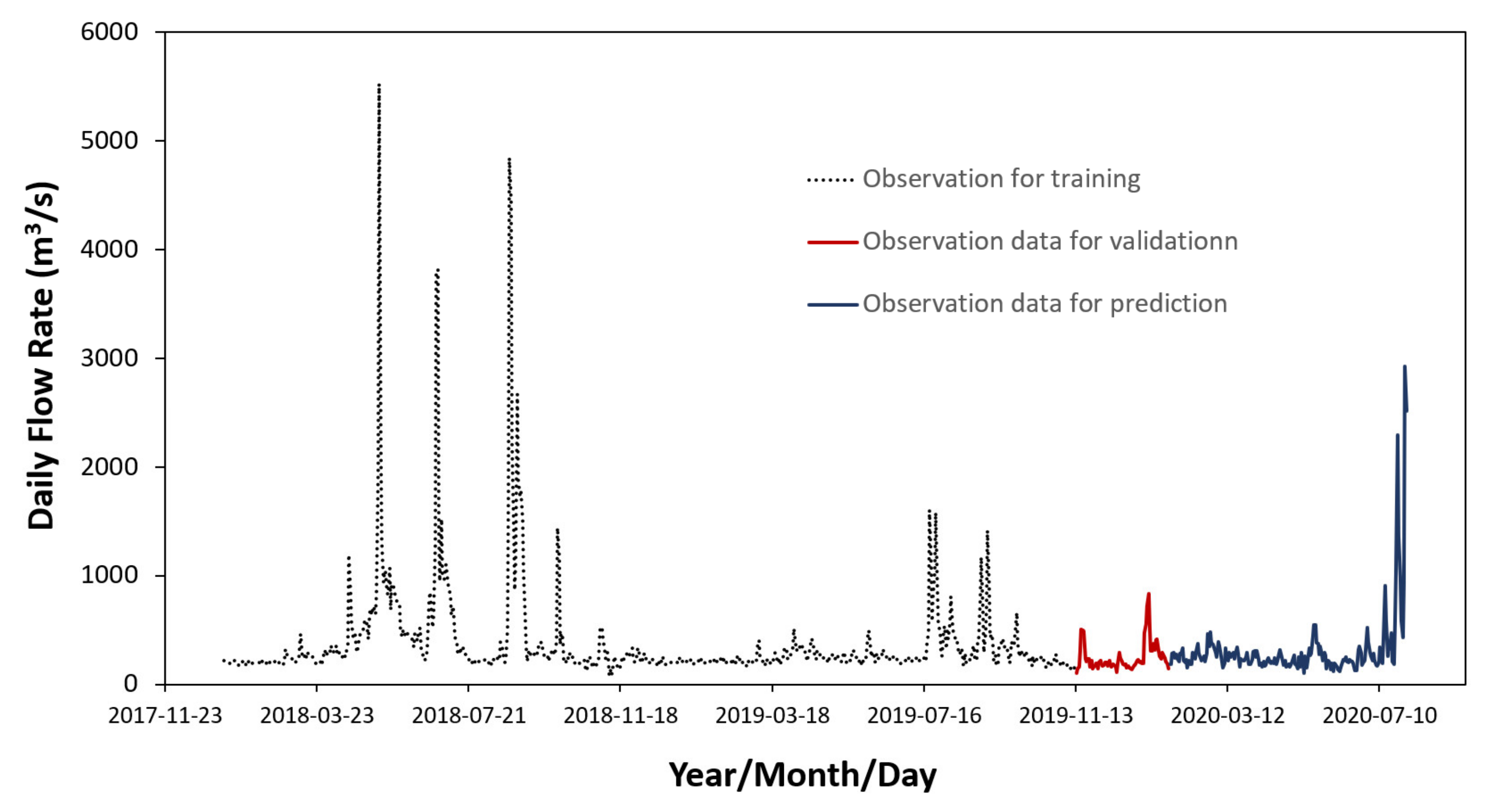
3.2. Hydrologic Data
3.3. Composition of Models
3.4. Model Performace Indicators
- (1)
- Mean Absolute Error (MAE)
- (2)
- Mean Squared Error (MSE)
- (3)
- Root Mean Squared Error (RMSE)
- (4)
- Coefficient of determination
- (5)
- Nash-Sutcliffe model Efficiency coefficient (NSE)
4. Results
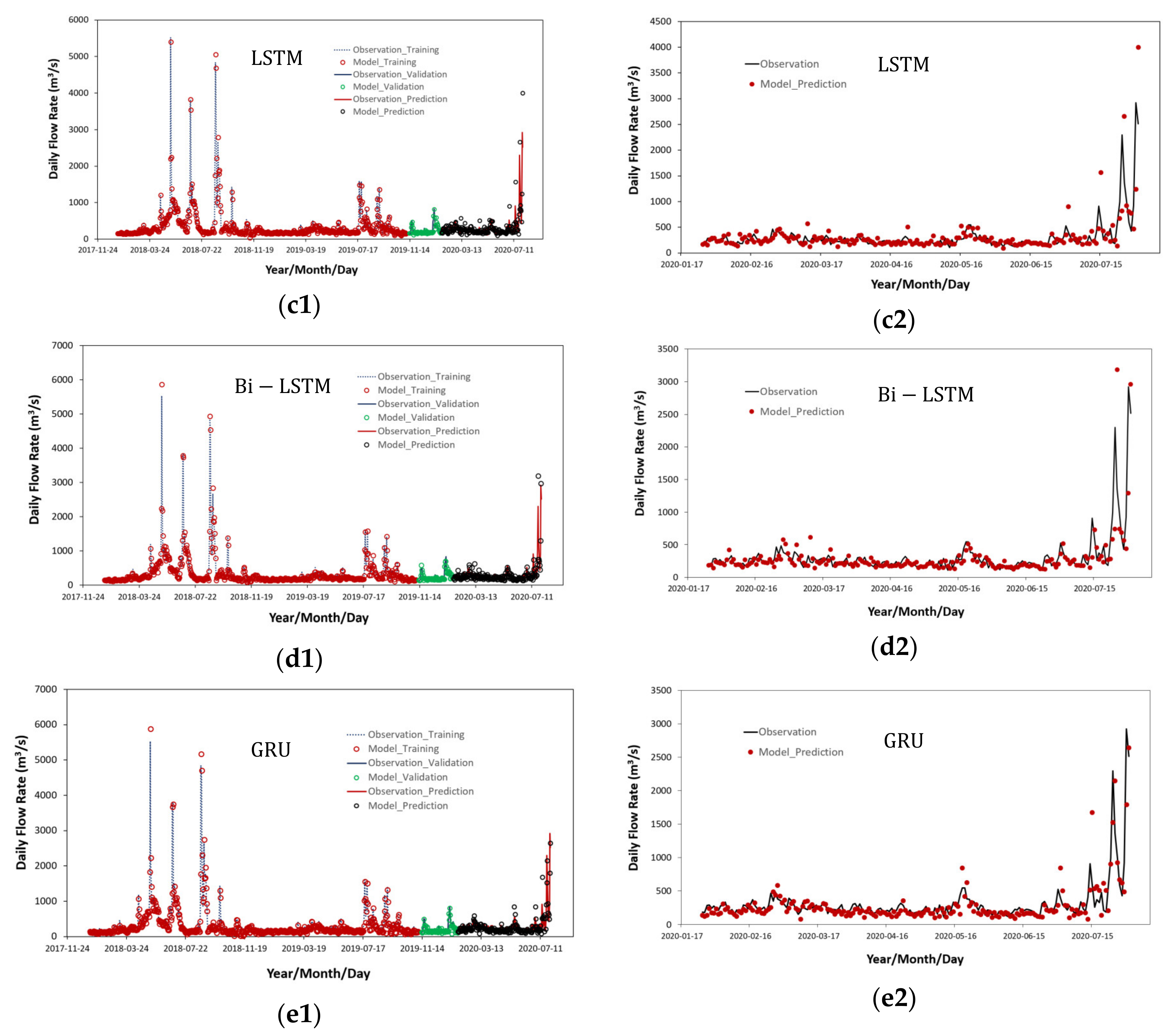
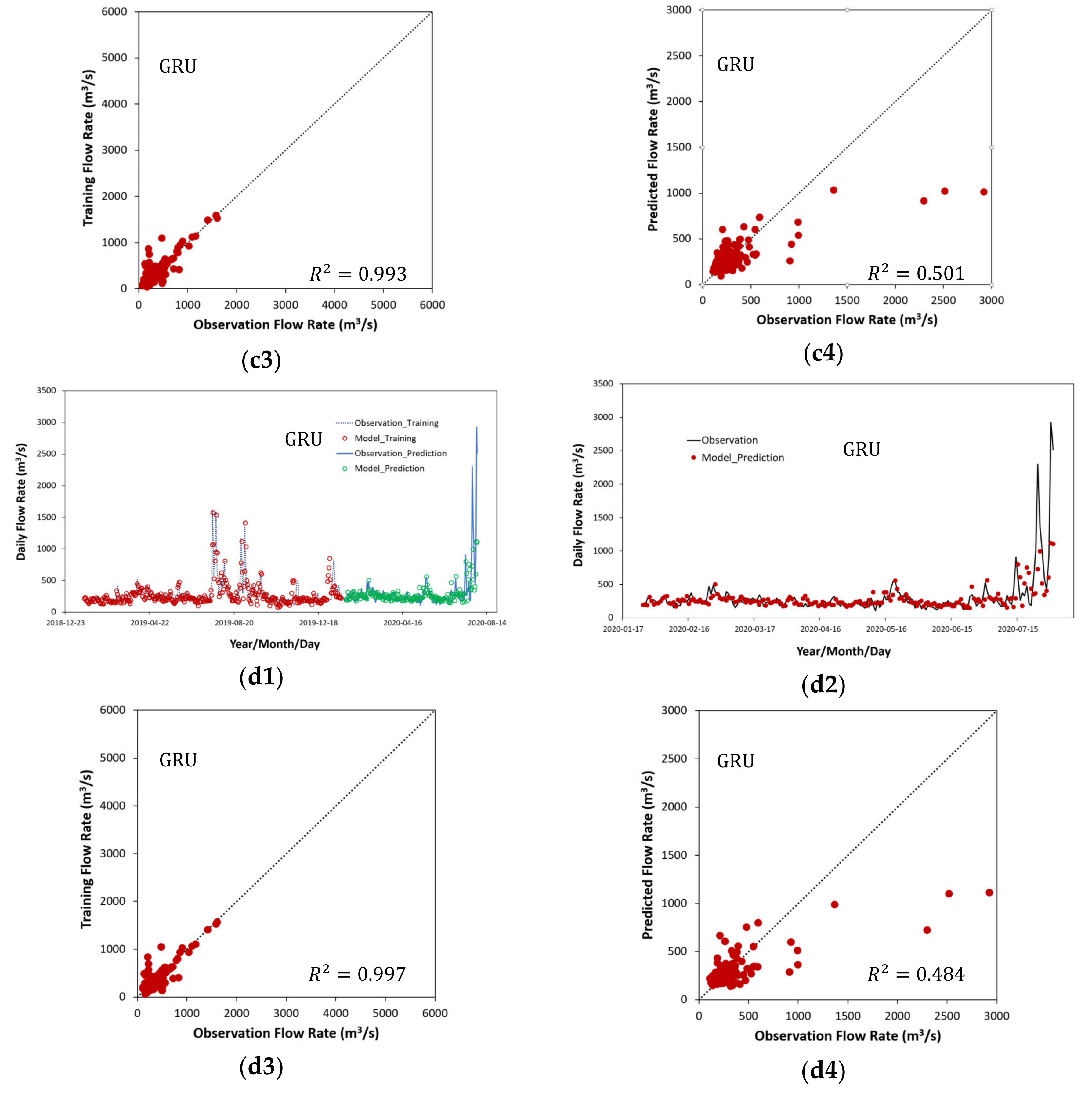
4.1. Results on Traning, Validation and Prediction Using Various Time Series Deep Learning Models
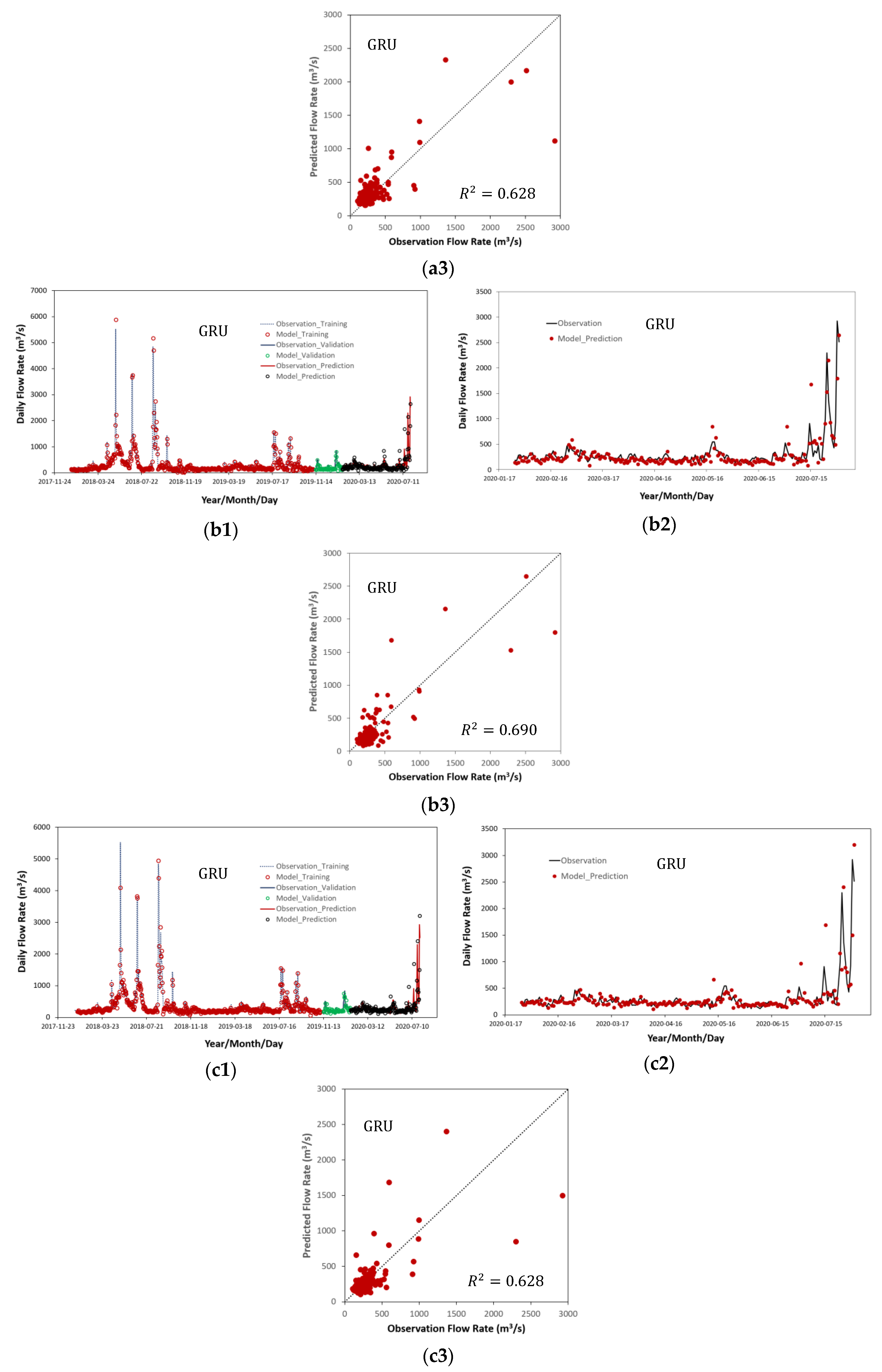
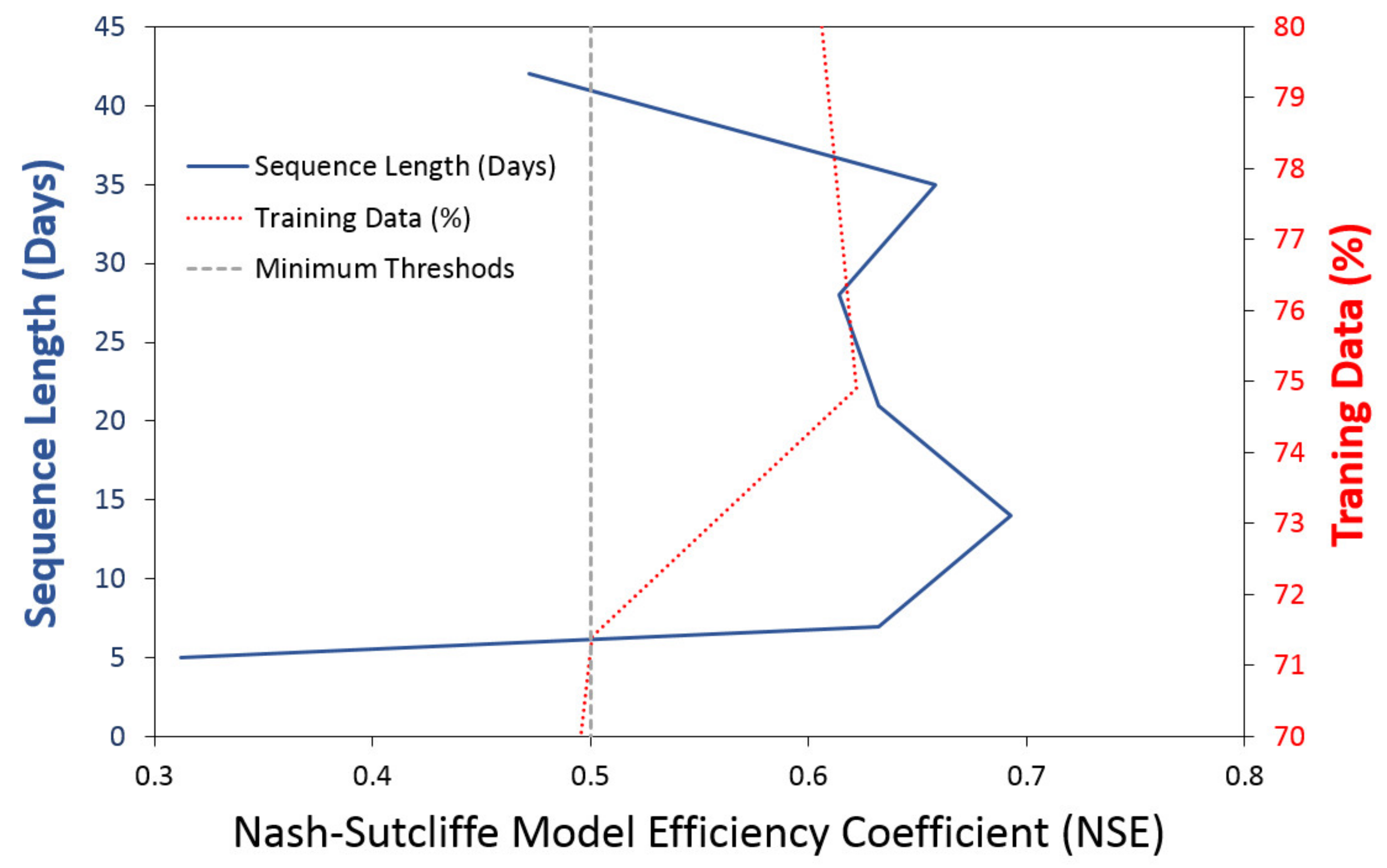
4.2. Training and Prediction Results of Sequence Length Variation Using GRU
4.3. GRU Performance with Changes in Length of Training Data and Prediction Data
5. Discussion
5.1. Comparison with Previous Studies
- Most of the DNN studies used in previous water resources engineering [10,11,12,13,14,15,16,17,18,19,20,21,22] were mainly used by RNN, Bi-LSTM and LSTM models to predict time series data. The GRU model had similar accuracy as the LSTM model but as shown in Figure 5, the GRU model is simplified by omitting the cell state calculation rather than using 3 gates in the LSTM model and can effectively calculate the large flow rates.
- As seen in previous studies [10,11,12], most applications of deep learning technology in the field of water resources engineering were focused on predicting the water levels in streams and the inflows into dams with small variation in hydraulic variables. When DNN models were learning time series data with very high seasonal fluctuations, relatively accurate predictions were possible for low flow rates but the accuracy at high flow rates were significantly reduced. Thus, unlike previous studies for flood runoff prediction, if the variation between the minimum and maximum values of the time series data is very large, the predicted accuracy of the time series data becomes very inaccurate and vulnerable. In this study, LSTM and GRU models were able to achieve better results than other RNN models when the seasonal fluctuations in the flow rate of urban streams were very large. Among them, GRU model results were the best.
- In most areas of water resources engineering [9,13,14,15,16,17,18,19,20,21,22], the time series data of any length were utilized as input data without proper consideration of the sequence length of the data in the calculation of the DNN models, which can predict water levels and flow rates. However, it is essential to verify the change in accuracy according to the sequence length of time series data that directly affects the forecast results. In this study, NSE was selected as 0.5 as the minimum threshold for sequence length. The range of sequence length applicable to the Han River (, which had a very large flow fluctuation, was 7 to 35 days and in the case of 14 days, the most optimal prediction of the flow rates could be obtained.
- When the length of the observation data of flow rates is not sufficiently secured, the length of the minimum input time series flow data to be learned must be determined in order to predict the flood flow rates for a specified period of time with minimum accuracy (. In previous studies [10,11,12,13,14,15,16,17,18,19,20,21,22], the lengths of training data and forecast data were arbitrarily determined. But in this study, if the length of the training data was determined within the range of 74.9% to 80% of the total data length, the forecast results were also accurately predicted in high flow rates.
5.2. Critical Conditions of Deep Learning to Ensure Reliability
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Lee, K.S. Rehabilitation of the Hydrologic Cycle in the Anyangcheon Watershed, Sustainable Water Resources Research Center; Ministry of Education, Science and Technology: Seoul, Korea, 2007. [Google Scholar]
- Lee, K.S.; Chung, E.S. Development of integrated watershed management schemes for an intensively urbanized region in Korea. J. Hydro Environ. Res. 2007, 1, 95–109. [Google Scholar] [CrossRef]
- Henonin, J.; Russo, B.; Mark, O.; Gourbesville, P. Real-time urban flood forecasting and modelling—A state of the art. J. Hydroinform. 2013, 15, 717–736. [Google Scholar] [CrossRef]
- Carter, R.W.; Godfrey, R.G. Storage and Flood Routing; Manual of Hydrology: Part 3. Flood-Flow Techniques, Geological Survey Water-Supply Paper 1543-B, Methods and Practices of the Geological Survey; US Department of the Interior: Washington, DC, USA, 1960. [Google Scholar]
- Moussa, R.; Bocquillon, C. Approximation zones of the Saint-Venant equations for flood routing with overbank flow. Hydrol. Earth Syst. Sci. 2000, 4, 251–260. [Google Scholar] [CrossRef] [Green Version]
- Kim, B.; Sanders, B.; Famiglietti, J.S.; Guinot, V. Urban flood modeling with porous shallow-water equations: A case study of model errors in the presence of anisotropic porosity. J. Hydrol. 2015, 523, 680–692. [Google Scholar] [CrossRef] [Green Version]
- Biscarini, C.; Francesco, S.D.; Ridolfi, E.; Manciola, P. On the simulation of floods in a narrow bending valley: The Malpasset Dam break case study. Water 2016, 8, 545. [Google Scholar] [CrossRef] [Green Version]
- Nkwunonwo, U.C.; Whitworth, M.; Baily, B. A review of the current status of flood modelling for urban flood risk management in the developing countries. Sci. Afr. 2020, 7, 1–15. [Google Scholar] [CrossRef]
- Ghumman, A.R.; Ghazaw, Y.M.; Sohail, A.R.; Watanabe, K. Runoff forecasting by artificial neural network and conventional model. Alex. Eng. J. 2011, 50, 345–350. [Google Scholar] [CrossRef] [Green Version]
- Kim, S.; Tachikawa, Y. Real-time river-stage prediction with artificial neural network based on only upstream observation data. J. Jpn. Soc. Civ. Eng. Ser. B1 Hydraul. Eng. 2018, 74, I_1375–I_1380. [Google Scholar] [CrossRef]
- Tran, Q.-K.; Song, S.-K. Water level forecasting based on deep learning: A use case of Trinity River-Texas-the United States. J. KIISE 2017, 44, 607–612. [Google Scholar] [CrossRef]
- Yoo, H.; Lee, S.O.; Choi, S.; Park, M. A study on the data driven neural network model for the prediction of time series data: Application of water surface elevation forecasting in Hangang River Bridge. J. Korean Soc. Disaster Secur. 2019, 12, 73–82. [Google Scholar]
- Elumalai, V.; Brindha, K.; Sithole, B.; Lakshmanan, E. Spatial interpolation methods and geostatistics for mapping groundwater contamination in a coastal area. Environ. Sci. Pollut. Res. 2017, 21, 11601–11617. [Google Scholar] [CrossRef] [PubMed]
- Kumar, D.N.; Raju, K.S.; Sathish, T. River flow forecasting using recurrent neural networks. Water Resour. Manag. 2004, 18, 143–161. [Google Scholar] [CrossRef]
- Firat, M. Comparison of artificial intelligence techniques for river flow forecasting. Hydrol. Earth Syst. Sci. 2008, 12, 123–139. [Google Scholar] [CrossRef] [Green Version]
- Sattari, M.T.; Yurekli, K.; Pal, M. Performance evaluation of artificial neural network approaches in forecasting reservoir inflow. Appl. Math. Model. 2012, 36, 2649–2657. [Google Scholar] [CrossRef]
- Chen, P.-A.; Chang, L.-C.; Chang, L.-C. Reinforced recurrent neural networks for multi-step-ahead flood forecasts. J. Hydrol. 2013, 497, 71–79. [Google Scholar] [CrossRef]
- Park, M.K.; Yoon, Y.S.; Lee, H.H.; Kom, J.H. Application of recurrent neural network for inflow prediction into multi-purpose dam basin. J. Korea Water Resour. Assoc. 2018, 51, 1217–1227. [Google Scholar]
- Zhang, D.; Peng, Q.; Lin, J.; Wang, D.; Liu, X.; Zhuang, J. Simulating reservoir operation using a recurrent neural network algorithm. Water 2019, 11, 865. [Google Scholar] [CrossRef] [Green Version]
- Mok, J.-Y.; Choi, J.-H.; Moon, Y.-I. Prediction of multipurpose dam inflow using deep learning. J. Korea Water Resour. Assoc. 2020, 53, 97–105. [Google Scholar]
- Zhang, D.; Lin, J.; Peng, Q.; Wang, D.; Yang, T.; Sorooshian, S.; Liu, X.; Zhuang, J. Modeling and simulating of reservoir operation using the artificial neural network, support vector regression, deep learning algorithm. J. Hydrol. 2018, 565, 720–736. [Google Scholar] [CrossRef] [Green Version]
- Apaydin, H.; Feizi, H.; Sattari, M.T.; Colak, M.S.; Shamshirband, S.; Chau, K.-W. Comparative analysis of recurrent neural network architectures for reservoir inflow forecasting. Water 2020, 12, 1500. [Google Scholar] [CrossRef]
- Hatami, N.; Gavet, Y.; Debayle, J. Classification of time-series images using deep convolutional neural networks. In Proceedings of the Tenth International Conference on Machine Vision (ICMV 2017), Vienna, Austria, 13 April 2018; Volume 10696. [Google Scholar]
- Wang, Z.; Oates, T. Encoding time series as images for visual inspection and classification using tiled convolutional neural networks. In Proceedings of the Twenty-Ninth AAAI Conference on Artificial Intelligence, Austin, TX, USA, 25–26 January 2015. [Google Scholar]
- Bengio, Y.; Simard, P.; Frasconi, P. Learning long-term dependencies with gradient descent is difficult. IEEE Trans. Neural Netw. 1994, 5, 157–166. [Google Scholar] [CrossRef] [PubMed]
- Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Graves, A.; Schmidhuber, J. Framewise phoneme classification with bidirectional LSTM and other neural network architectures. Neural Netw. 2005, 18, 602–610. [Google Scholar] [CrossRef] [PubMed]
- Zhao, R.; Yan, R.; Wang, J.; Mao, K. Learning to monitor machine health with convolutional bi-directional LSTM networks. Sensors 2017, 17, 273. [Google Scholar] [CrossRef]
- Cho, K.; Van Merrienboer, B.; Bahdanau, D.; Bengio, Y. On the Properties of Neural Machine Translation: Encoder–Decoder Approaches. In Proceedings of the SSST-8, Eighth Workshop on Syntax, Semantics and Structure in Statistical Translation, Doha, Qatar, 7 October 2014; pp. 103–111. [Google Scholar]
- Seoul Metropolitan Government. Study on River Management by Universities; Seoul Metropolitan Government: Seoul, Korea, 2013.
- Seoul Metropolitan Government. Statistical Yearbook of Seoul; Seoul Metropolitan Government: Seoul, Korea, 2004.
- Ministry of Construction and Transportation. Master Plan for River Modification of the Han River Basin; Ministry of Construction and Transportation: Sejong City, Korea, 2002.
- Water Resources Management Information System. Available online: http://www.wamis.go.kr (accessed on 1 August 2020).
- Google Earth. Available online: http://www.google.com/maps (accessed on 15 October 2020).
- Weather Data Portal. Available online: https://data.kma.go.kr/cmmn/main.do (accessed on 1 August 2020).
- Lee, J.S. Water Resources Engineering; Goomibook: Seoul, Korea, 2008. [Google Scholar]
- Anaconda. Available online: https://www.anaconda.com (accessed on 1 August 2020).
- TensorFlow. Available online: https://www.tensorflow.org (accessed on 1 August 2020).
- Moriasi, D.N.; Arnold, J.G.; Van Liew, M.W.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Model evaluation guidelines for systematic quantification of accuracy in watershed simulations. Soil Water Div. ASABE 2007, 50, 885–900. [Google Scholar]
- Segura-Beltrán, F.; Sanchis-Ibor, C.; Morales-Hernández, M.; González-Sanchis, M.; Bussi, G.; Ortiz, E. Using post-flood surveys and geomorphologic mapping to evaluate hydrological and hydraulic models: The flash flood of the Girona River (Spain) in 2007. J. Hydrol. 2016, 541, 310–329. [Google Scholar] [CrossRef] [Green Version]
- Kastridis, A.; Kirkenidis, C.; Sapountzis, M. An integrated approach of flash flood analysis in ungauged Mediterranean watersheds using post-flood surveys and unmanned aerial vehicles. Hydrol. Process. 2020, 34, 4920–4939. [Google Scholar] [CrossRef]
- Narbondo, S.; Gorgoglione, A.; Crisci, M.; Chreties, C. Enhancing physical similarity approach to predict runoff in ungauged watersheds in sub-tropical regions. Water 2020, 12, 528. [Google Scholar] [CrossRef] [Green Version]
- Chen, H.; Luo, Y.; Potter, C.; Moran, P.J.; Grieneisen, M.L.; Zhang, M. Modeling pesticide diuron loading from the San Joaquin watershed into the Sacramento-San Joaquin Delta using SWAT. Water Res. 2017, 121, 374–385. [Google Scholar] [CrossRef]
- Chiew, F.; Stewardson, M.J.; McMahon, T. Comparison of six rainfall-runoff modelling approaches. J. Hydrol. 1993, 147, 1–36. [Google Scholar] [CrossRef]
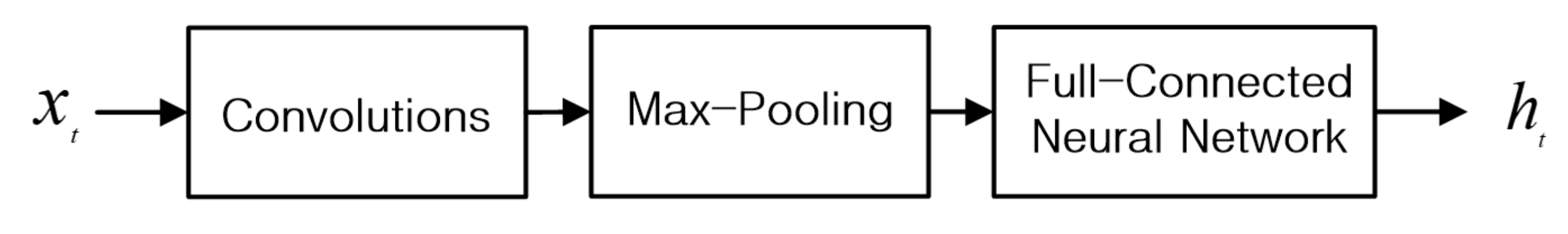




| Length of River (km) |
Basin Area | Mean Rainfall (mm/Year) |
Mean Streamflow |
|---|---|---|---|
| 494.44 | 25,953.60 | 1313.42 | 355.97 |
|
Minimum Flow Rate | Maximum Flow Rate | Average Flow Rate | Coefficient of Flow Fluctuation (CFF) |
Standard Deviation of Flow Rate |
|---|---|---|---|---|
| 78.60 | 5527.19 | 355.97 | 70.32 | 425.84 |
| Model | Activation Function | Input Layer | Hidden Layer 1 | Dropout | Hidden Layer 2 | Dense Layer 1 | Dense Layer 2 |
|---|---|---|---|---|---|---|---|
| CNN | ReLU | Conv1D | Conv1D 5 units/ Max Pooling 5 units | 0.25 | Flatten 10 units | 25 units | 1 unit |
| Simple RNN | ReLU | Simple RNN | Simple RNN 50 units | 0.25 | Simple RNN 50 units | 25 units | 1 unit |
| LSTM | ReLU | LSTM | LSTM 50 units | 0.25 | LSTM 50 units | 25 units | 1 unit |
| Bi-LSTM | ReLU | Bi-LSTM | Bi-LSTM 50 units | 0.25 | Bi-LSTM 50 units | 25 units | 1 unit |
| GRU | ReLU | GRU | GRU 50 units | 0.25 | GRU 50 units | 25 units | 1 unit |
| Performance Rating | ||
|---|---|---|
| Very good | ||
| Good | ||
| Satisfactory | ||
| Unsatisfactory |
| Model | Computational State | MAE | MSE | RMSE | NSE | |
|---|---|---|---|---|---|---|
| CNN | Training | 113.53 | 133.55 | 11.56 | 0.557 | 0.557 |
| Validation | 69.37 | 492.59 | 22.19 | 0.512 | 0.525 | |
| Prediction | 92.83 | 101.53 | 10.08 | 0.526 | 0.527 | |
| Simple RNN | Training | 107.32 | 6633.79 | 81.45 | 0.864 | 0.868 |
| Validation | 93.10 | 5951.47 | 77.15 | 0.133 | 0.348 | |
| Prediction | 123.89 | 3315.69 | 57.58 | 0.418 | 0.435 | |
| LSTM | Training | 25.06 | 74.89 | 8.69 | 0.994 | 0.994 |
| Validation | 57.69 | 154.21 | 12.42 | 0.473 | 0.477 | |
| Prediction | 114.93 | 4.72 | 2.17 | 0.394 | 0.394 | |
| Bi-LSTM | Training | 27.61 | 285.04 | 16.88 | 0.994 | 0.994 |
| Validation | 44.69 | 293.10 | 17.12 | 0.748 | 0.752 | |
| Prediction | 102.68 | 672.41 | 25.93 | 0.466 | 0.469 | |
| GRU | Training | 50.90 | 2201.17 | 46.92 | 0.984 | 0.984 |
| Validation | 66.63 | 2643.39 | 51.41 | 0.513 | 0.576 | |
| Prediction | 102.19 | 753.54 | 27.45 | 0.691 | 0.693 |
| Sequence Length (Days) | Computational State | MAE | MSE | RMSE | NSE | |
|---|---|---|---|---|---|---|
| 4 | Training | 75.33 | 2534.94 | 50.35 | 0.961 | 0.961 |
| Validation | 85.25 | 3889.03 | 62.36 | 0.257 | 0.389 | |
| Prediction | 123.63 | 3309.35 | 57.53 | 0.291 | 0.312 | |
| 7 | Training | 42.84 | 534.27 | 23.11 | 0.986 | 0.986 |
| Validation | 62.42 | 1158.18 | 34.03 | 0.612 | 0.636 | |
| Prediction | 101.69 | 979.24 | 31.29 | 0.628 | 0.632 | |
| 14 | Training | 50.90 | 2201.17 | 46.92 | 0.984 | 0.984 |
| Validation | 66.63 | 2643.39 | 51.41 | 0.513 | 0.576 | |
| Prediction | 102.19 | 753.54 | 27.45 | 0.690 | 0.693 | |
| 21 | Training | 31.38 | 3.66 | 1.91 | 0.975 | 0.975 |
| Validation | 62.74 | 17.74 | 4.21 | 0.549 | 0.549 | |
| Prediction | 101.69 | 979.24 | 31.29 | 0.628 | 0.632 | |
| 28 | Training | 31.84 | 180.78 | 13.45 | 0.992 | 0.992 |
| Validation | 66.18 | 707.03 | 26.59 | 0.515 | 0.534 | |
| Prediction | 104.28 | 833.30 | 28.87 | 0.611 | 0.614 | |
| 35 | Training | 25.78 | 10.05 | 3.17 | 0.994 | 0.994 |
| Validation | 56.21 | 593.75 | 24.37 | 0.507 | 0.522 | |
| Prediction | 95.73 | 0.10 | 0.32 | 0.658 | 0.658 | |
| 42 | Training | 41.26 | 368.71 | 19.20 | 0.988 | 0.988 |
| Validation | 52.11 | 319.11 | 52.11 | 0.700 | 0.705 | |
| Prediction | 104.13 | 147.80 | 12.16 | 0.471 | 0.472 |
|
Training Data (%) |
Prediction Data (%) | Computational State | MAE | MSE | RMSE | NSE | |
|---|---|---|---|---|---|---|---|
| 80.0 | 20.0 | Training | 30.22 | 300.28 | 17.33 | 0.991 | 0.991 |
| Prediction | 103.13 | 527.31 | 22.96 | 0.604 | 0.606 | ||
| 74.9 | 25.1 | Training | 17.01 | 8.06 | 2.84 | 0.995 | 0.995 |
| Prediction | 98.29 | 117.27 | 10.83 | 0.622 | 0.622 | ||
| 71.4 | 28.6 | Training | 10.91 | 9.04 | 3.01 | 0.993 | 0.993 |
| Prediction | 101.42 | 876.86 | 29.61 | 0.501 | 0.501 | ||
| 66.8 | 33.2 | Training | 8.23 | 2.33 | 1.53 | 0.997 | 0.997 |
| Prediction | 102.15 | 1093.35 | 33.07 | 0.479 | 0.484 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Park, K.; Jung, Y.; Kim, K.; Park, S.K. Determination of Deep Learning Model and Optimum Length of Training Data in the River with Large Fluctuations in Flow Rates. Water 2020, 12, 3537. https://doi.org/10.3390/w12123537
Park K, Jung Y, Kim K, Park SK. Determination of Deep Learning Model and Optimum Length of Training Data in the River with Large Fluctuations in Flow Rates. Water. 2020; 12(12):3537. https://doi.org/10.3390/w12123537
Chicago/Turabian StylePark, Kidoo, Younghun Jung, Kyungtak Kim, and Seung Kook Park. 2020. "Determination of Deep Learning Model and Optimum Length of Training Data in the River with Large Fluctuations in Flow Rates" Water 12, no. 12: 3537. https://doi.org/10.3390/w12123537
APA StylePark, K., Jung, Y., Kim, K., & Park, S. K. (2020). Determination of Deep Learning Model and Optimum Length of Training Data in the River with Large Fluctuations in Flow Rates. Water, 12(12), 3537. https://doi.org/10.3390/w12123537






