The Role of Non-Hydrostatic Effects in Nonlinear Dispersive Wave Modeling
Abstract
1. Introduction
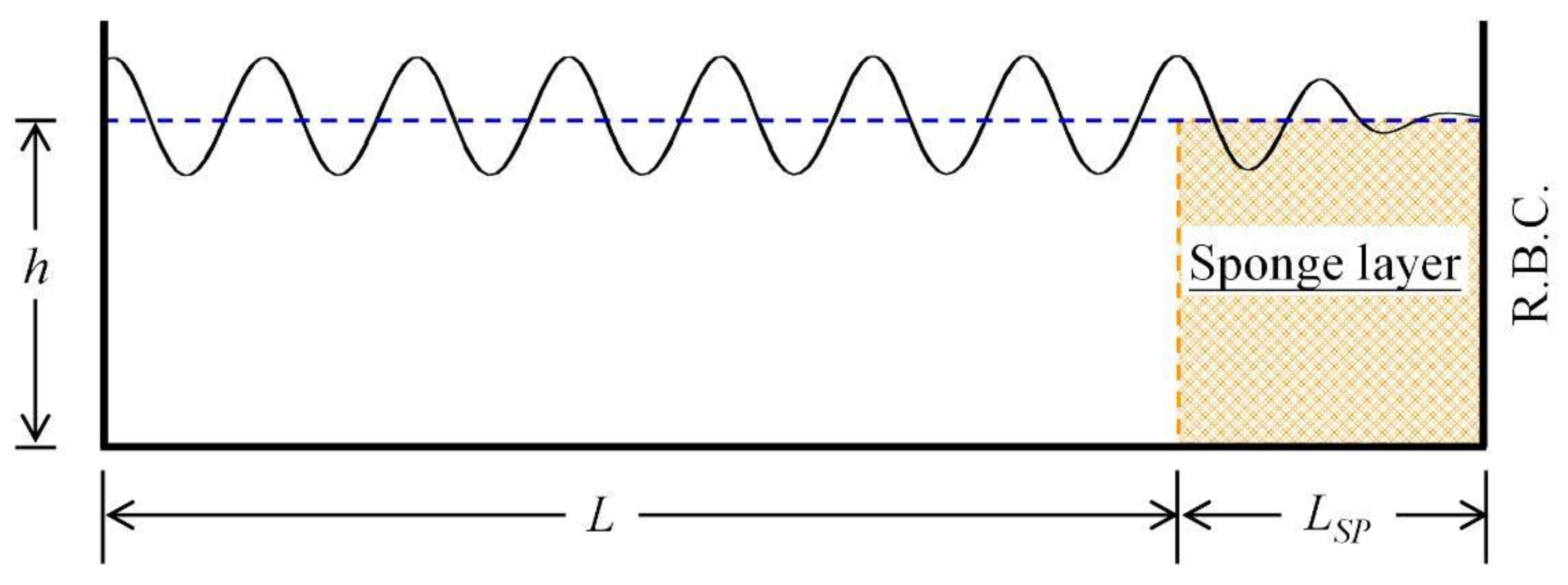
2. Model Description
3. Non-Hydrostatic Effects on Linear/Nonlinear Waves
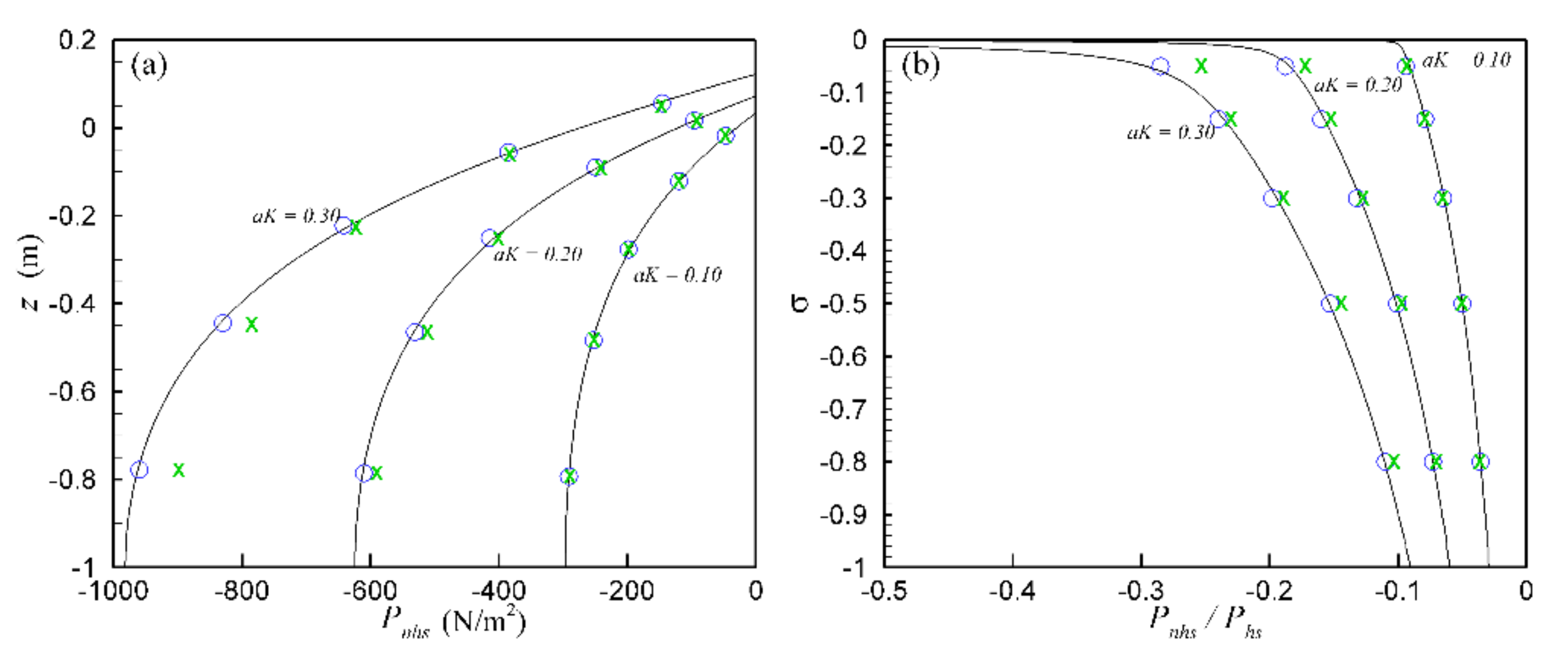
3.1. Linear Wave Dispersion
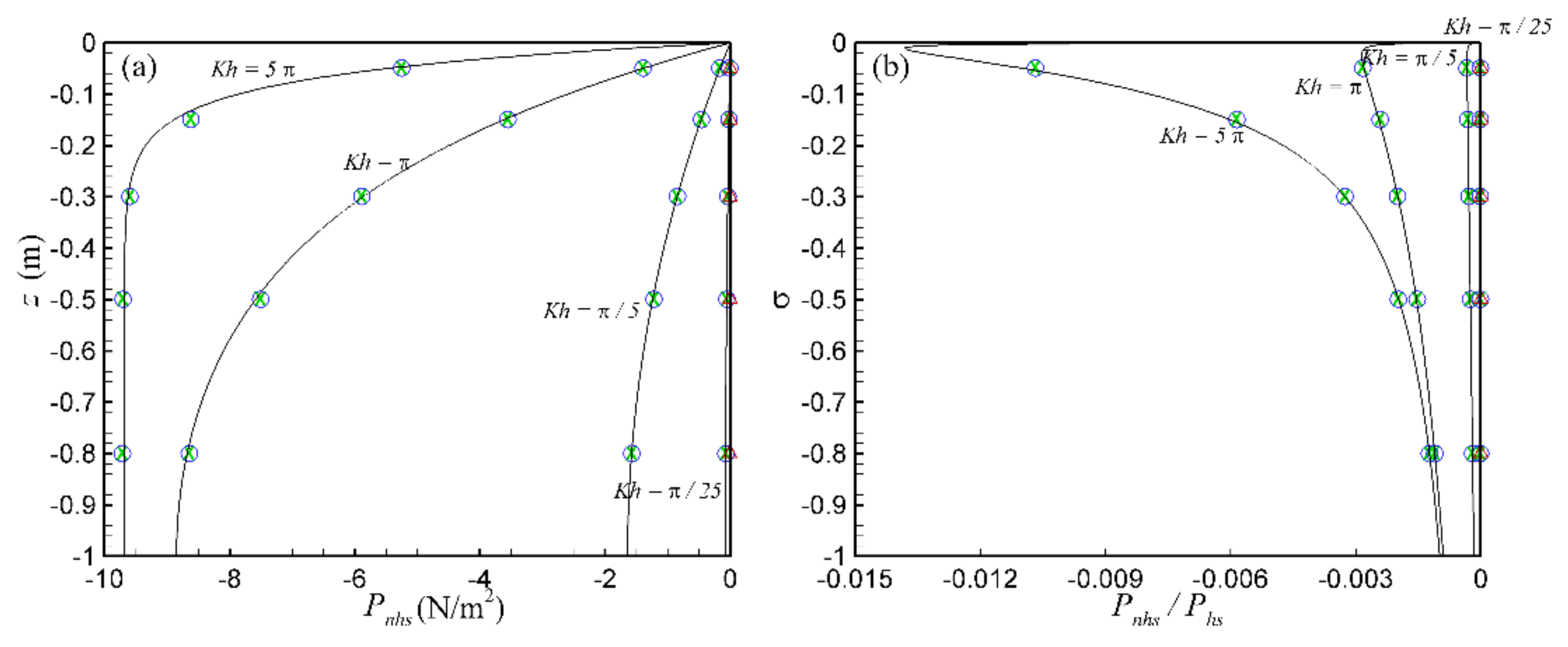
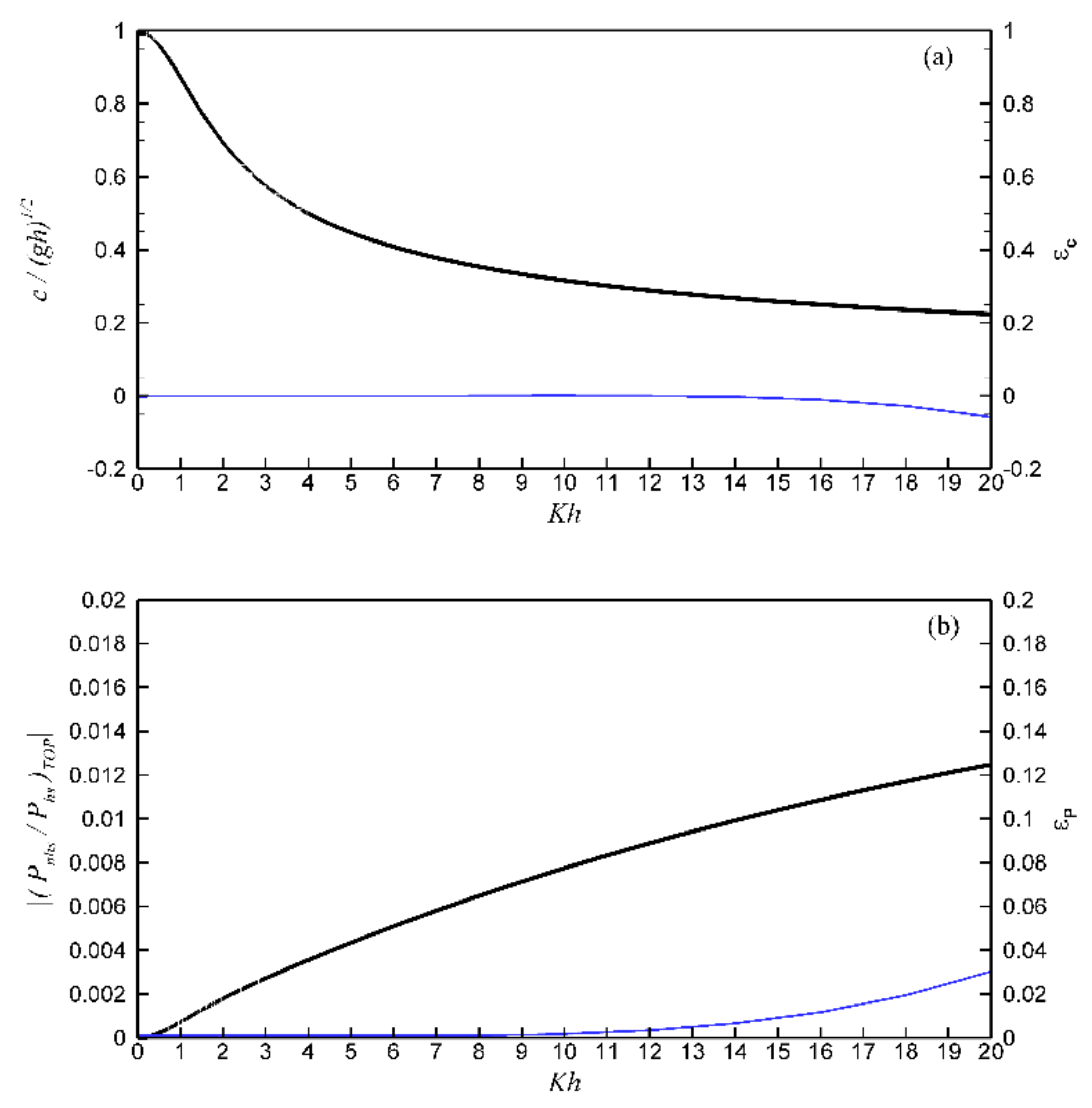
3.1.1. Contribution and Sensitivity Analysis
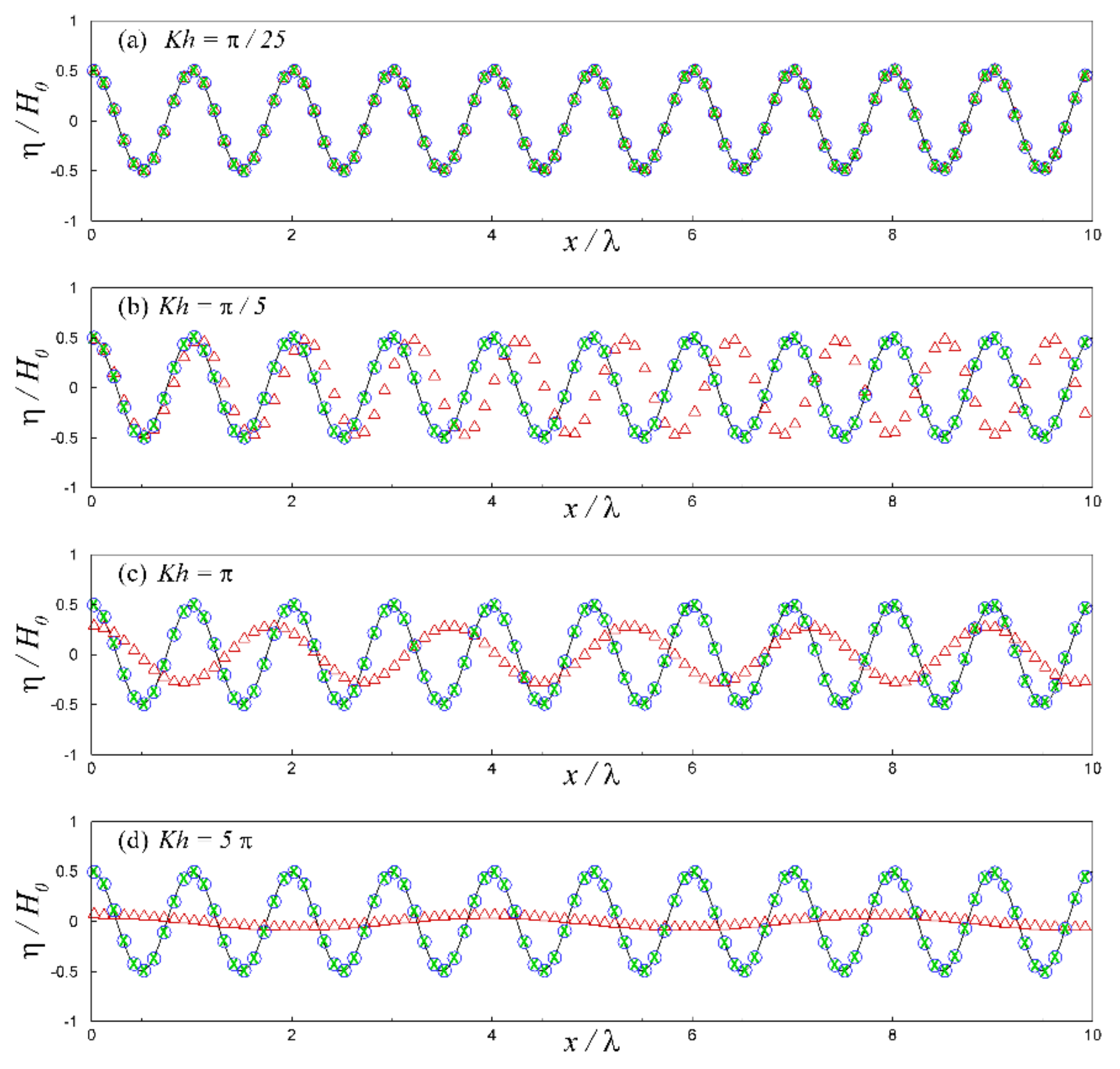
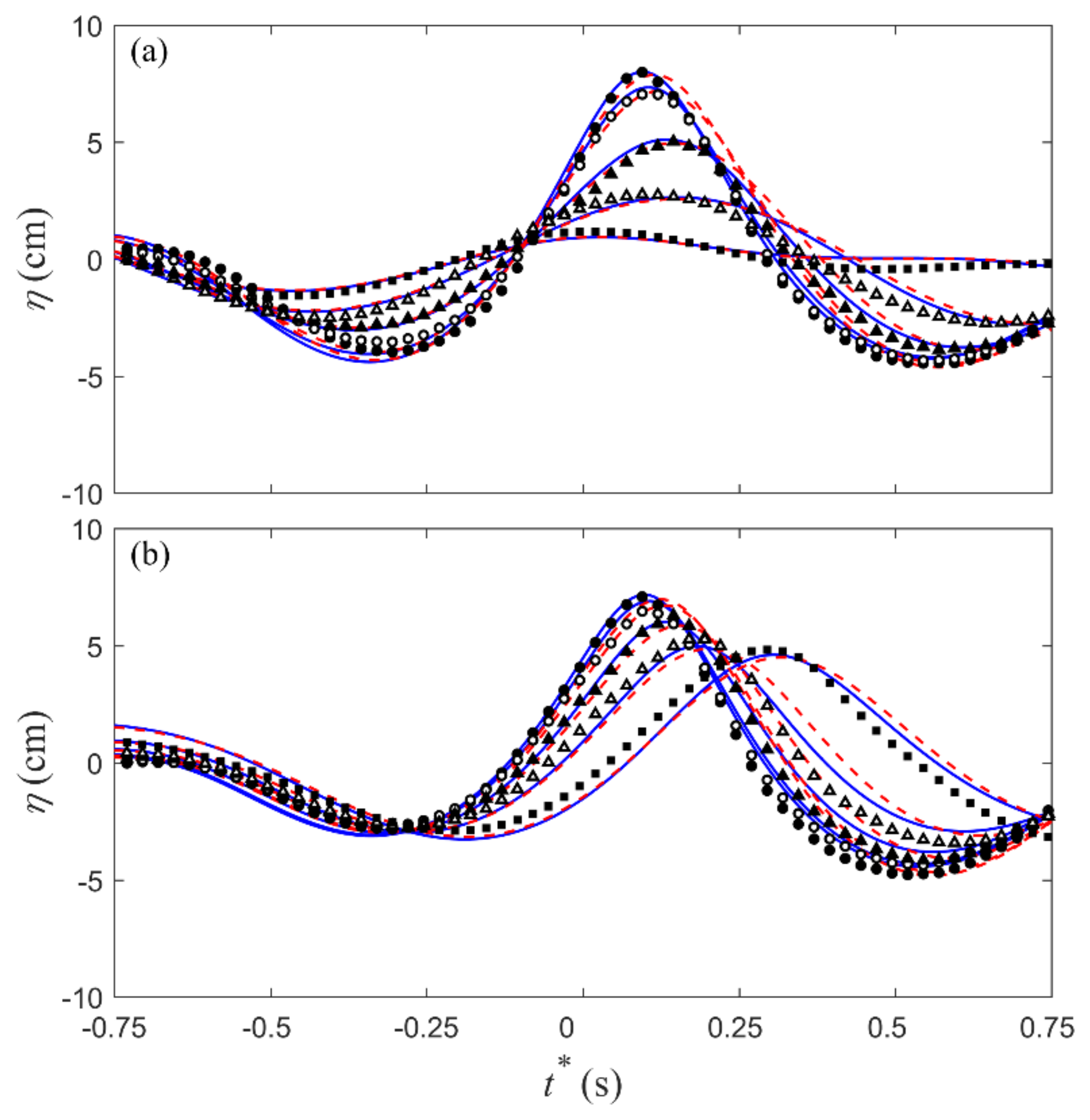
3.1.2. Free-Surface Spatial Profile
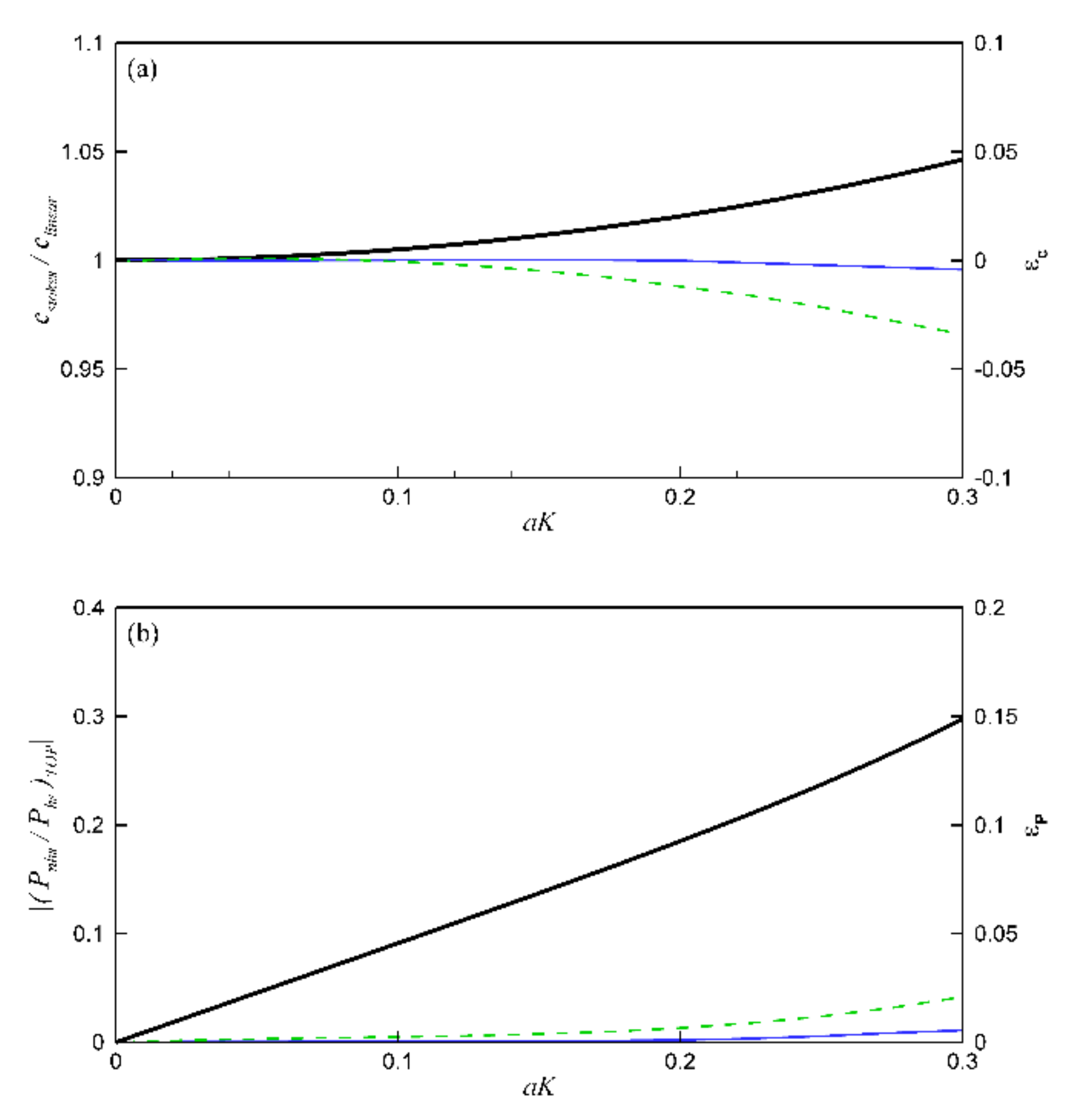
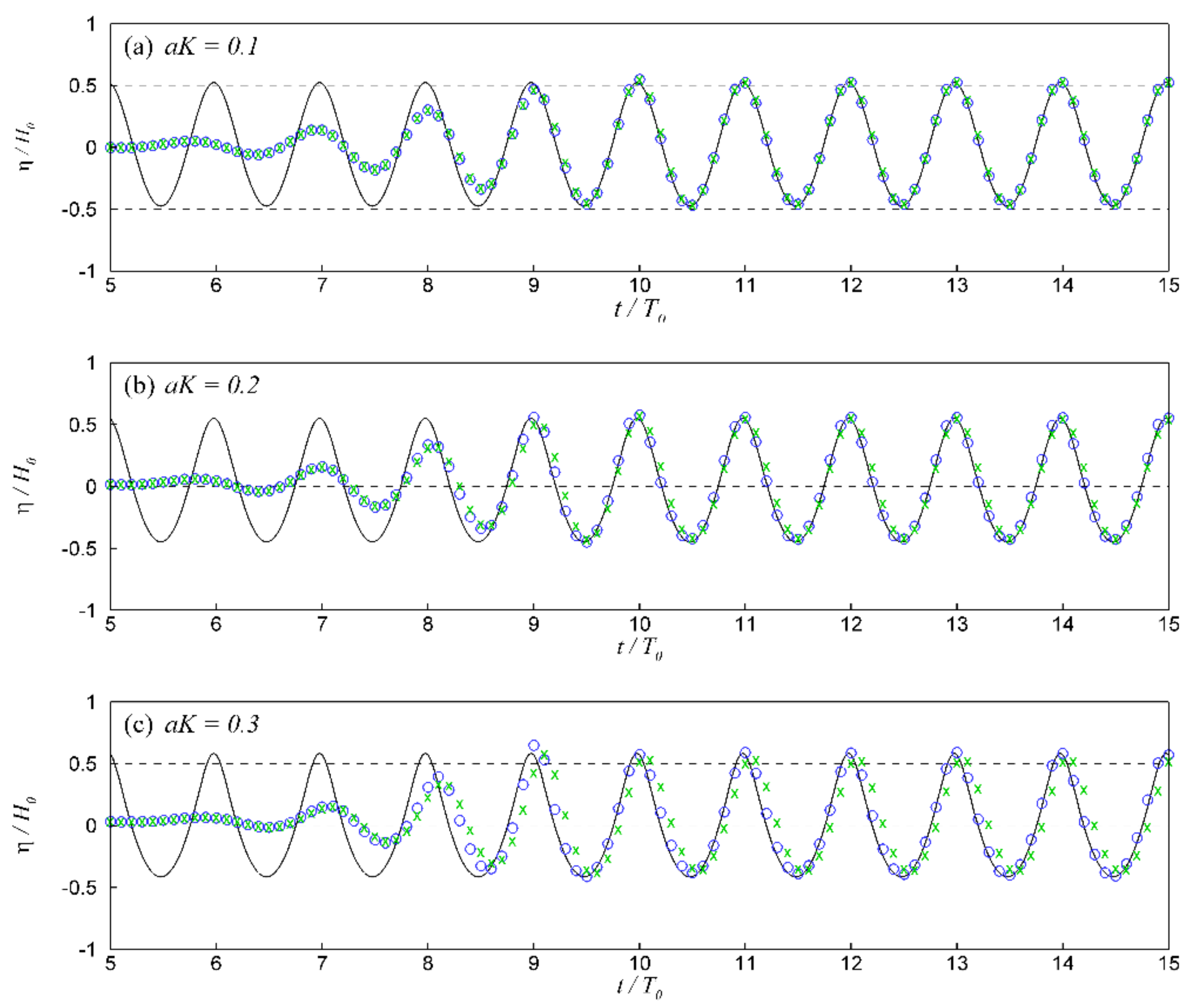
3.2. Wave Non-Linearity
3.2.1. Contribution and Sensitivity Analysis
3.2.2. Free-Surface Time Series
4. Non-Hydrostatic Effects for Waves with Complicated Interactions
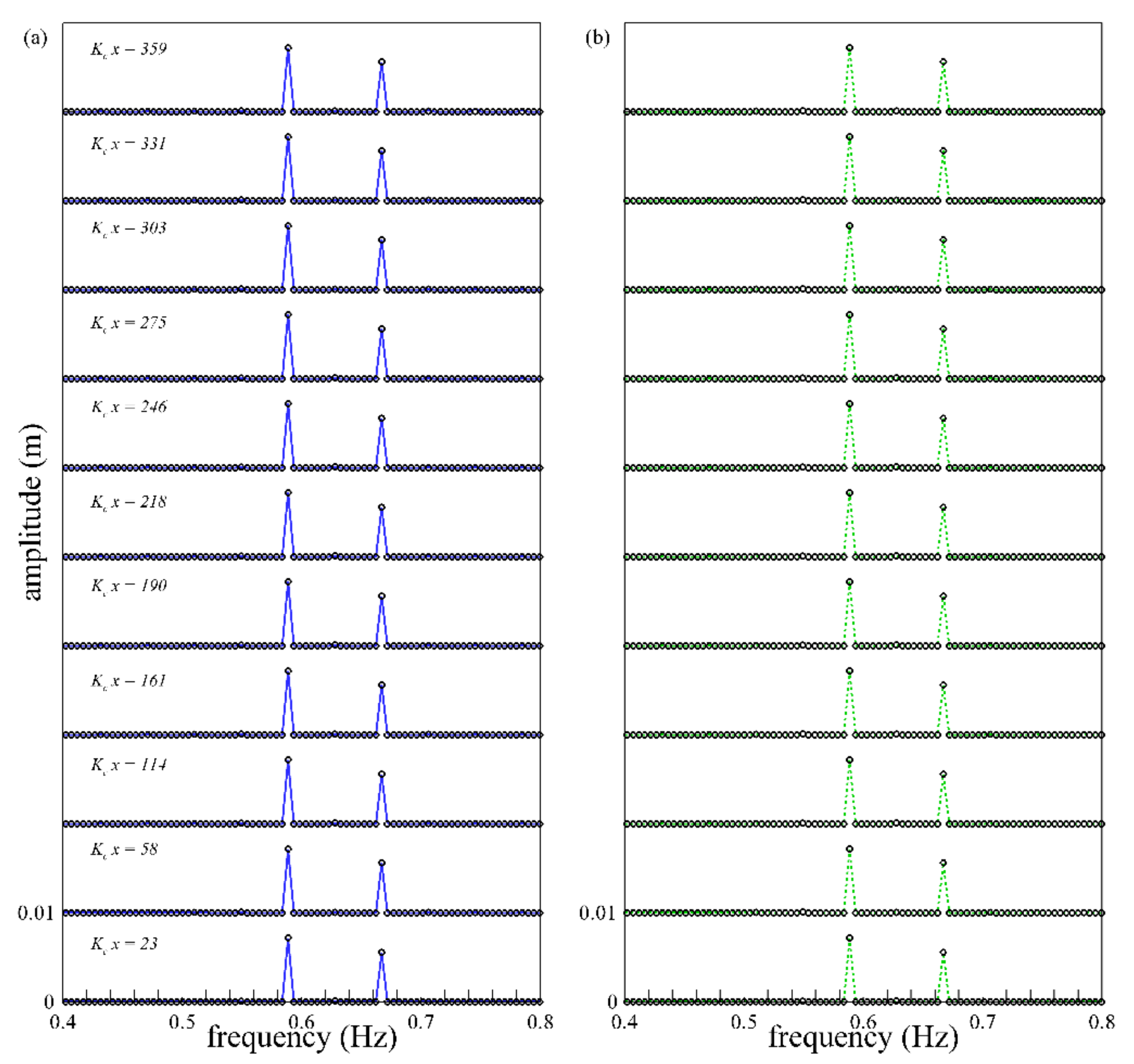
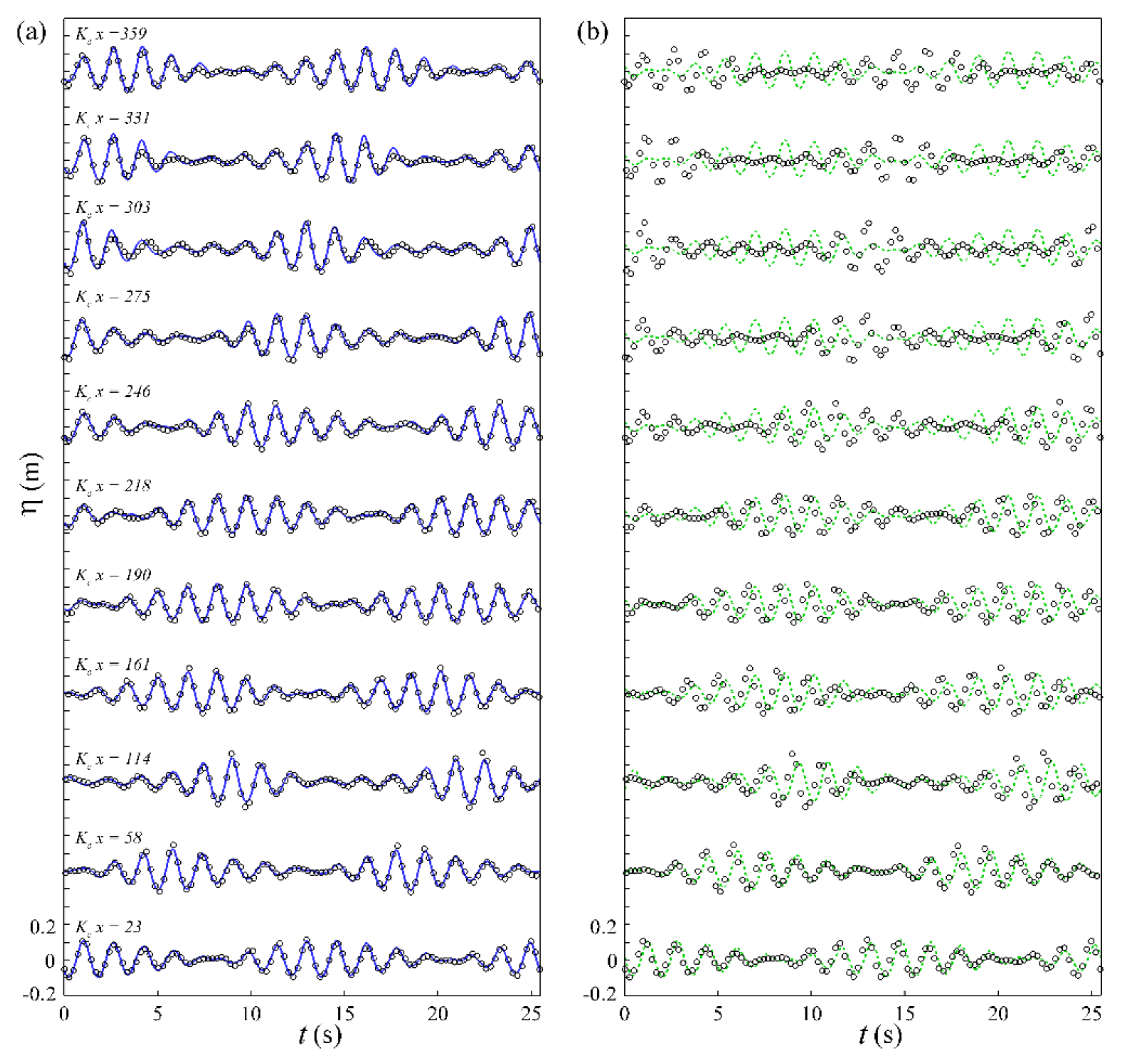
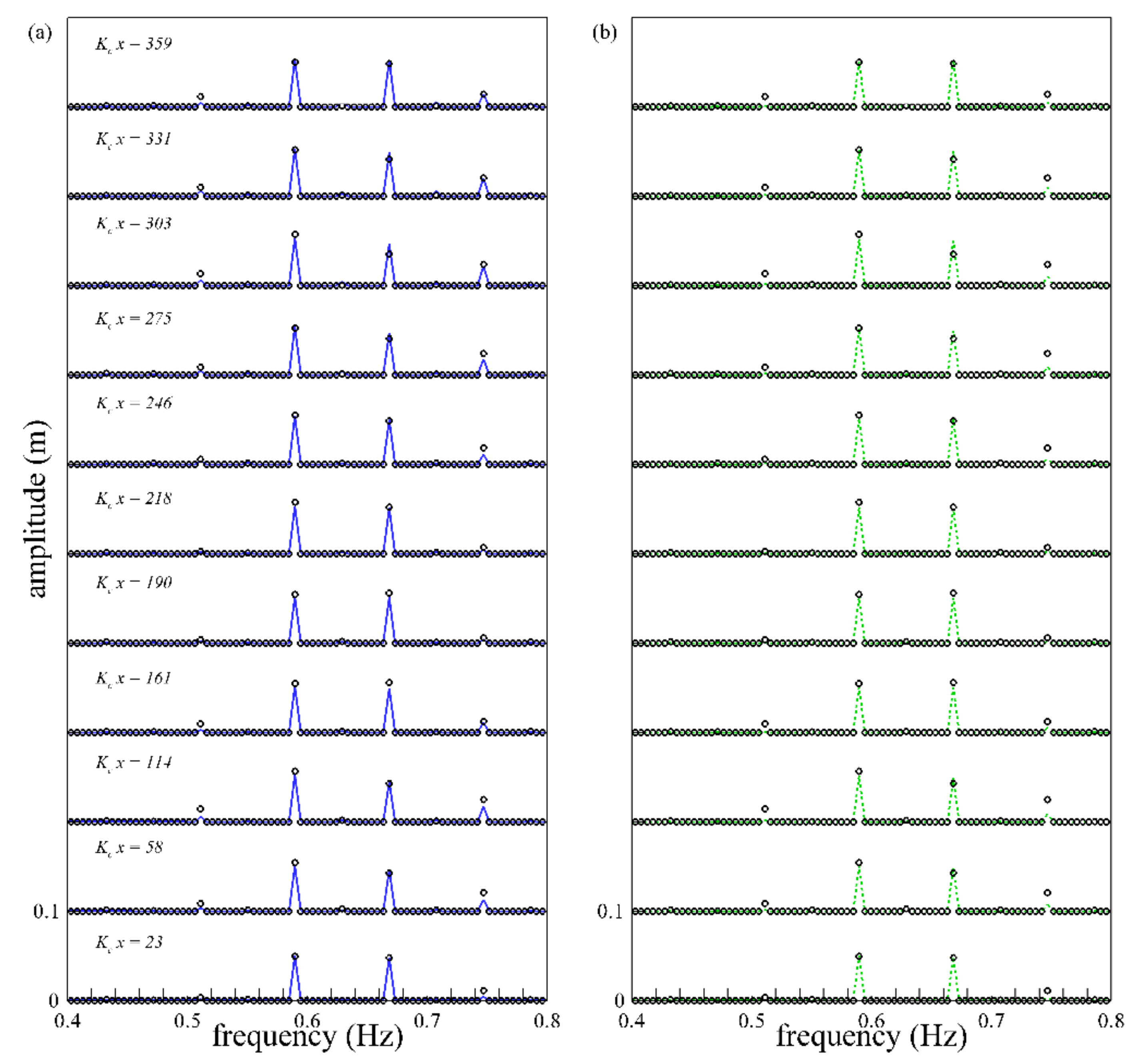
4.1. Bi-Chromatic Waves
4.1.1. Linear Bi-Chromatic Waves
4.1.2. Non-Linear Bi-Chromatic Waves
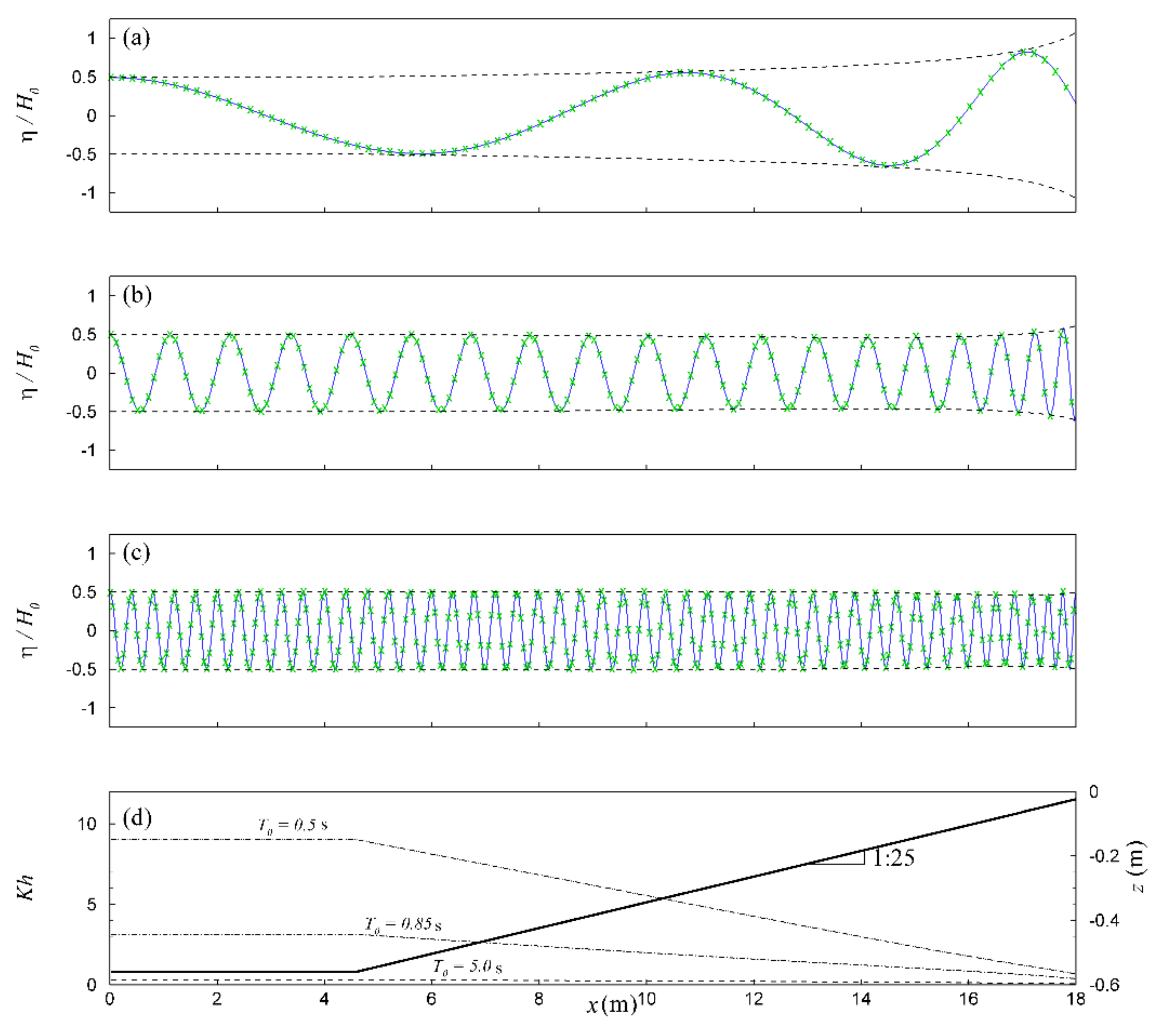
4.2. Wave Shoaling
4.2.1. Linear Wave Shoaling
4.2.2. Non-Linear Wave Shoaling
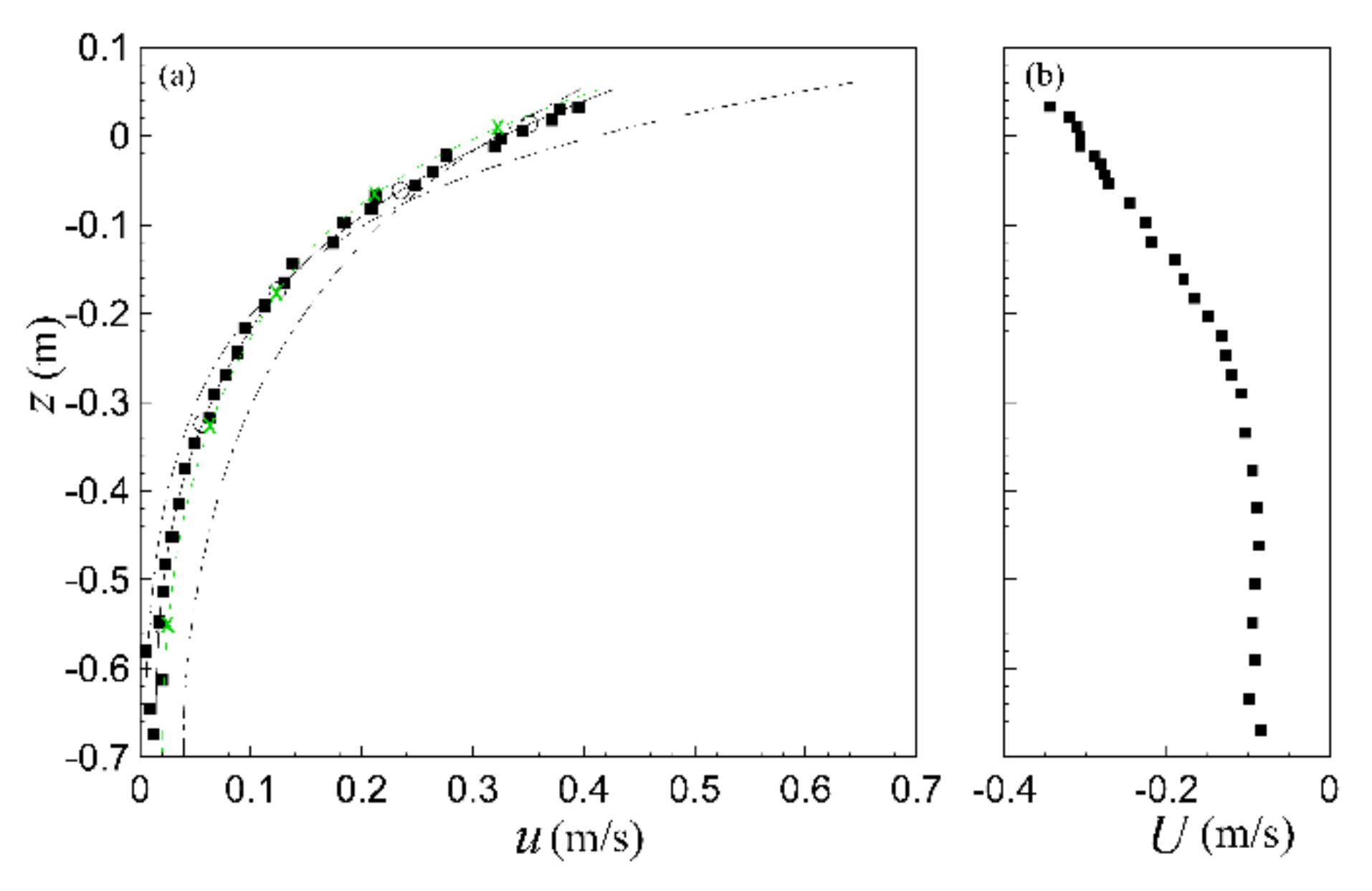
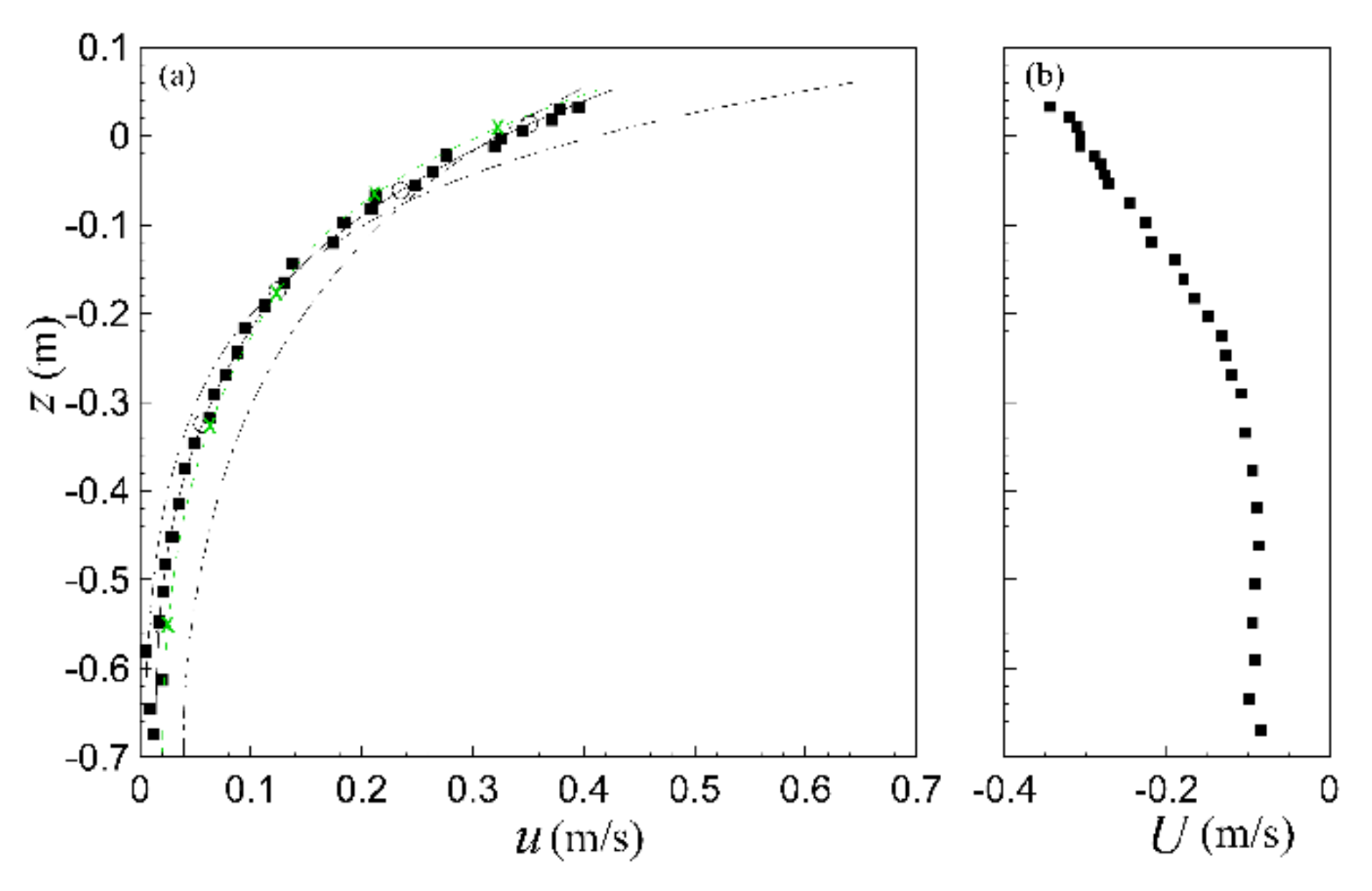
4.3. Non-Linear Wave Interacting with Depth-Varying Current
4.3.1. Interaction with a Negatively Sheared Opposing Current
4.3.2. Interaction with a Positively Sheared Following Current
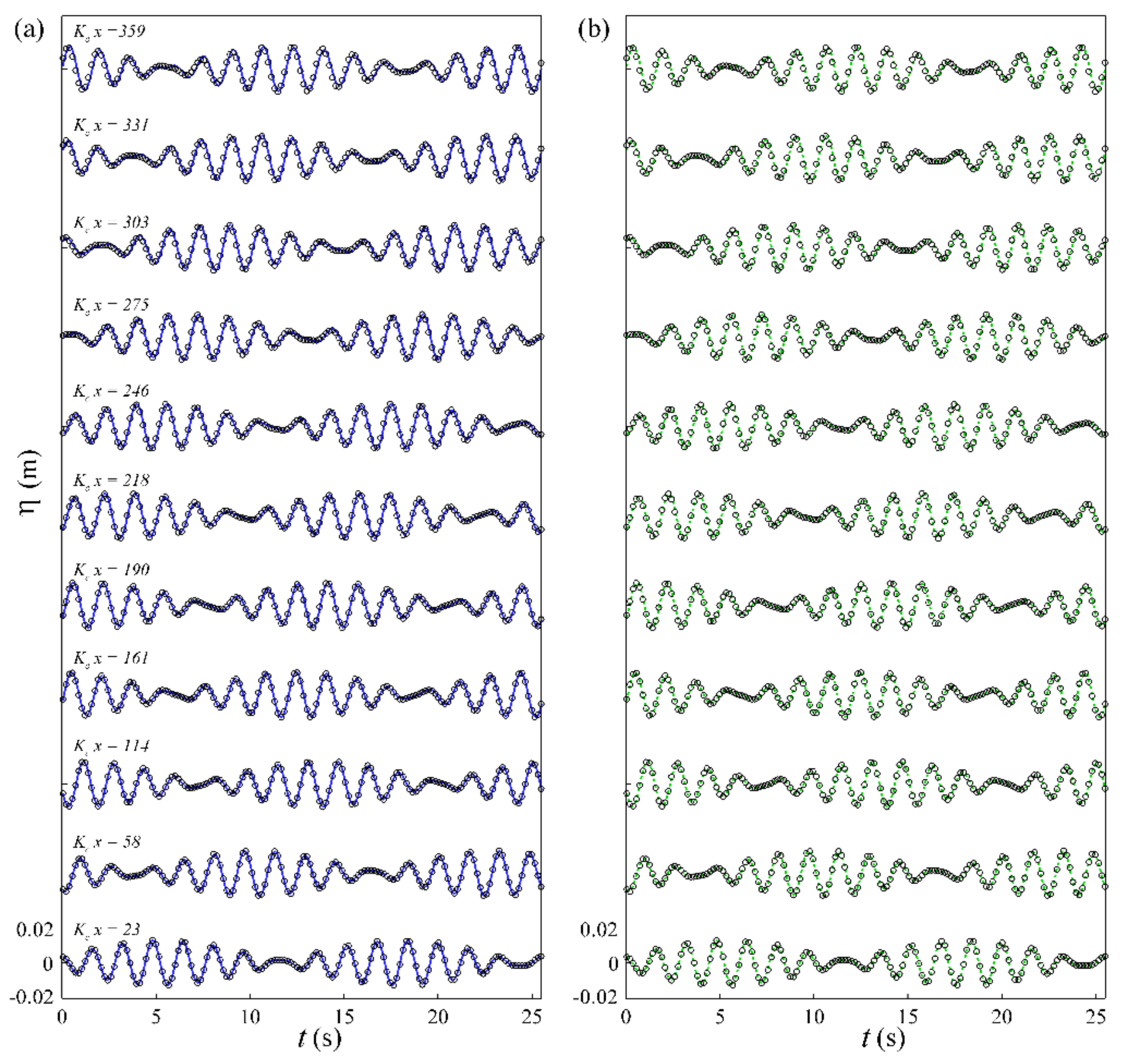
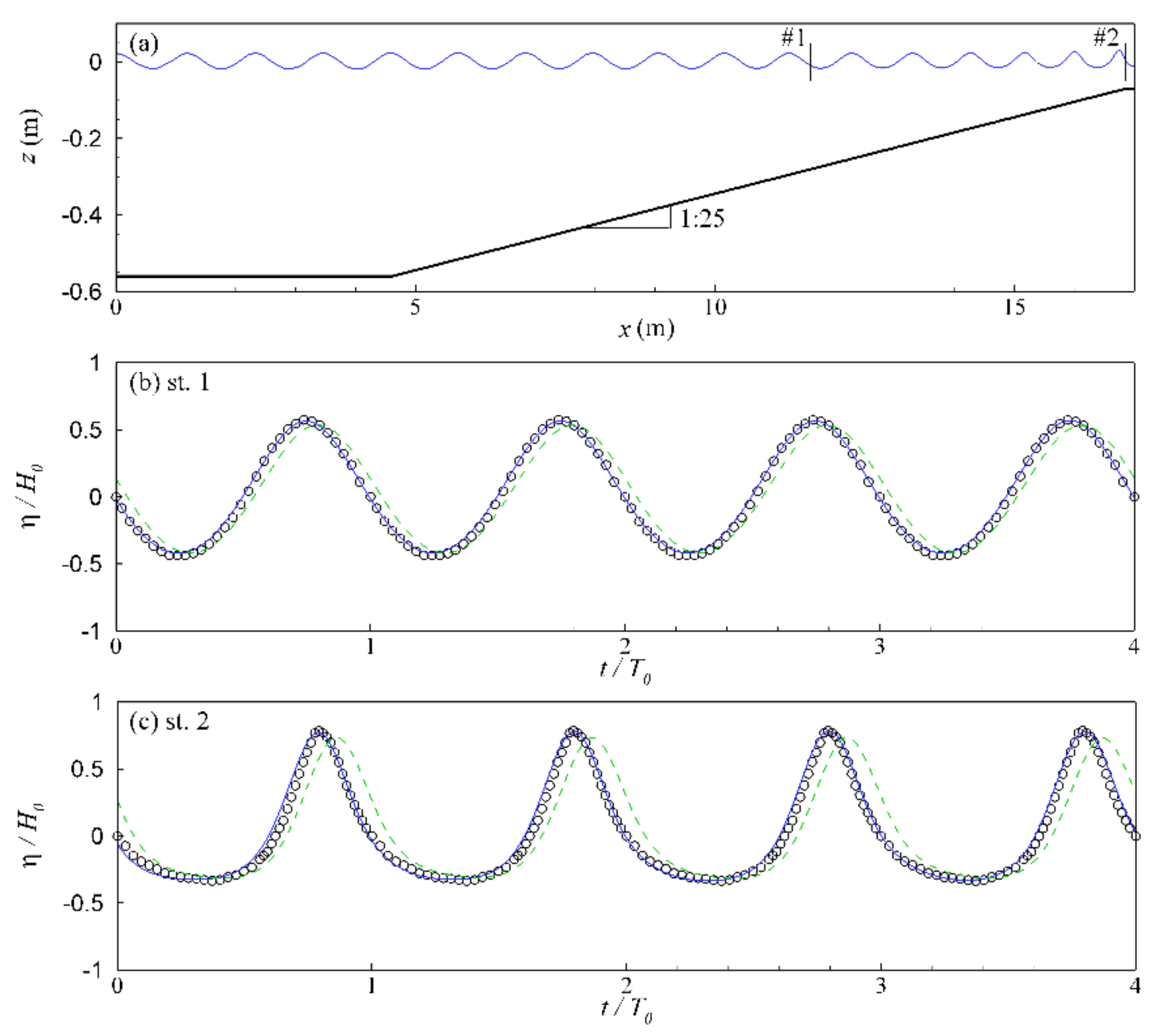
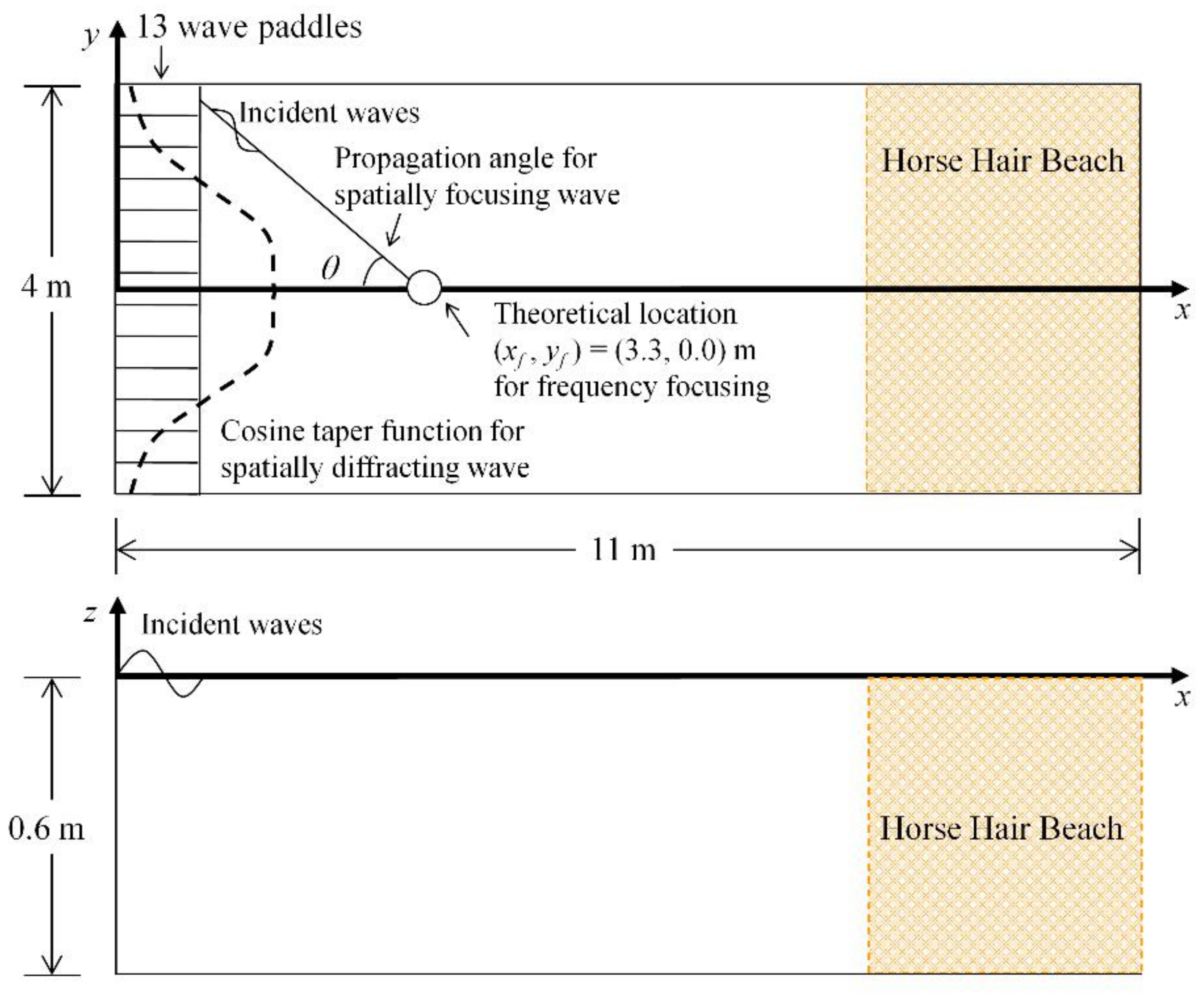
4.4. Spatial Focusing and Diffracting Waves
4.4.1. Spatial Focusing Waves
4.4.2. Spatial Diffracting Waves
5. Summary and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Mei, C.C.; Liu, P.L.F. Surface waves and coastal dynamics. Annu. Rev. Fluid Mech. 1993, 25, 215–240. [Google Scholar] [CrossRef]
- Battjes, J.A. Developments in coastal engineering research. Coast. Eng. 2006, 23, 121–132. [Google Scholar] [CrossRef]
- Cavaleri, L.; Alves, J.H.G.M.; Ardhuin, F.; Babanin, A.; Banner, M.; Belibassakis, K.; Benoit, M.; Donelan, M.; Groeneweg, J.; Herbers, T.H.C.; et al. Wave modelling—The state of the art. Prog. Oceanogr. 2007, 75, 603–674. [Google Scholar] [CrossRef]
- Mei, C.C. The Applied Dynamics of Ocean Surface Waves; Wiley Inter-Science: New York, NY, USA, 1983. [Google Scholar]
- Fenton, J.D. A fifth-order Stokes theory for steady waves. J. Waterw. Port Coast. Ocean Eng. 1985, 111, 216–234. [Google Scholar] [CrossRef]
- Beji, S.; Battjes, J.A. Experimental investigation of wave propagation over a bar. Coast. Eng. 1993, 19, 151–162. [Google Scholar] [CrossRef]
- Melville, W.K. The instability and breaking of deep-waterwaves. J. Fluid Mech. 1982, 115, 165–185. [Google Scholar] [CrossRef]
- Kirby, J.T. Nonlinear, dispersive long waves in water of variable depth. In Gravity Waves in Water of Finite Depth; Advances in Fluid Mechanics, Series; Hunt, J.N., Ed.; Computational Mechanics Publications: Southampton, UK, 1997; Volume 10, pp. 55–125. [Google Scholar]
- Hwung, H.H.; Chiang, W.S. The measurements on wave modulation and breaking. Meas. Sci. Technol. 2005, 16, 1921–1928. [Google Scholar] [CrossRef]
- Ting, C.L.; Chao, W.T.; Young, C.C. Experimental investigation of nonlinear regular wave transformation over a submerged step: Harmonic generation and wave height modulation. Coast. Eng. 2016, 117, 19–31. [Google Scholar] [CrossRef]
- Swan, C.; Cummins, I.P.; James, R.L. An experimental study of two-dimensional surface water waves propagating on depth-varying currents. Part 1. Regular waves. J. Fluid Mech. 2001, 428, 273–304. [Google Scholar] [CrossRef]
- Yao, A.F.; Wu, C.H. Spatial and temporal characteristics of transient extreme wave profiles on depth-varying currents. J. Eng. Mech. 2006, 132, 1015–1025. [Google Scholar] [CrossRef]
- Tsai, W.T.; Yue, D.K.P. Computation of nonlinear free-surface flows. Annu. Rev. Fluid Mech. 1996, 28, 249–278. [Google Scholar] [CrossRef]
- Liu, P.L.F.; Losada, I.J. Wave propagation modeling in coastal engineering. J. Hydraul. Res. 2002, 40, 229–240. [Google Scholar] [CrossRef]
- Choi, D.Y.; Wu, C.H. A new efficient 3D non-hydrostatic free-surface flow model for simulating water wave motions. Ocean Eng. 2006, 33, 587–609. [Google Scholar] [CrossRef]
- Peregrine, D.H. Long waves on a beach. J. Fluid Mech. 1967, 27, 815–827. [Google Scholar] [CrossRef]
- Madsen, P.A.; Sørensen, O.R. A new form of the Boussinesq equations with improved linear dispersion characteristics. Part 2. A slowly-varying bathymetry. Coast. Eng. 1992, 18, 183–204. [Google Scholar] [CrossRef]
- Nwogu, O. Alternative form of Boussinesq equations for nearshore wave propagation. J. Waterw. Port Coast. Ocean Eng. 1993, 119, 618–638. [Google Scholar] [CrossRef]
- Gobbi, M.F.; Kirby, J.T.; Wei, G. A fully nonlinear Boussinesq model for surface waves. II. Extension to O((kh)4). J. Fluid Mech. 2000, 405, 182–210. [Google Scholar] [CrossRef]
- Madsen, P.A.; Bingham, H.B.; Liu, H. A new Boussinesq method for fully nonlinear waves from shallow to deep water. J. Fluid Mech. 2002, 462, 1–30. [Google Scholar] [CrossRef]
- Lynett, P.; Liu, P.L.F. A two-layer approach to wave modeling. Proc. Math. Phys. Eng. Sci. 2004, 460, 2637–32669. [Google Scholar] [CrossRef]
- Berkhoff, J.C.W. 1972 Computation of combined refraction—Diffraction. In Proceedings of the 13th International Conference on Coastal Engineering, Vancouver, BC, Canada, 10–14 July 1972; pp. 471–490. [Google Scholar]
- Nadaoka, K.; Beji, S.; Nakagawa, Y. A fully dispersive weakly nonlinear model for water waves. Proc. Math. Phys. Eng. Sci. 1997, 453, 303–318. [Google Scholar] [CrossRef]
- Smith, R.A. An operator expansion formalism for nonlinear surface waves over variable depth. J. Fluid Mech. 1998, 363, 333–347. [Google Scholar] [CrossRef]
- Longuet-Higgins, M.S.; Cokelet, E.D. The deformation of steep surface waves on water. I A numerical method of computation. Proc. Math. Phys. Eng. Sci. 1976, 95, 1–26. [Google Scholar]
- Dold, J.W.; Peregrine, D.H. Steep unsteady waves: An efficient computational scheme. In Proceedings of the 19th International Conference on Coastal Engineering, Houston, TX, USA, 3–7 September 1984; pp. 955–967. [Google Scholar]
- Ohyama, T.; Nadaoka, K. Development of a numerical wave tank for analysis of nonlinear and irregular wave field. Fluid Dyn. Res. 1991, 8, 231–251. [Google Scholar] [CrossRef]
- Li, B.; Fleming, C.A. A three dimensional multigrid model for fully nonlinear water waves. Coast. Eng. 1997, 30, 235–258. [Google Scholar] [CrossRef]
- Turnbull, M.S.; Borthwick, A.G.L.; Eatock Taylor, R. Numerical wave tank based on a σ-transformed finite element inviscid flow solver. Int. J. Numer. Methods Fluids 2003, 42, 641–663. [Google Scholar] [CrossRef]
- Guyenne, P.; Grilli, S.T. Numerical study of three-dimensional overturning waves in shallow water. J. Fluid Mech. 2006, 547, 361–388. [Google Scholar] [CrossRef]
- Mayer, S.; Garapon, A.; Sørensen, L.S. A fractional step method for unsteady free-surface flow with applications to non-linear wave dynamics. Int. J. Numer. Methods Fluids 1998, 28, 293–315. [Google Scholar] [CrossRef]
- Casulli, V. A semi-implicit finite difference method for non-hydrostatic, free-surface flows. Int. J. Numer. Methods Fluids 1999, 30, 425–440. [Google Scholar] [CrossRef]
- Li, B.; Fleming, C.A. Three-dimensional model of Navier-Stokes equations for water waves. J. Waterw. Port Coast. Ocean Eng. 2001, 127, 16–25. [Google Scholar] [CrossRef]
- Namin, M.M.; Lin, B.; Falconer, R. An implicit numerical algorithm for solving non-hydrostatic free-surface flow problems. Int. J. Numer. Methods Fluids 2001, 35, 341–356. [Google Scholar] [CrossRef]
- Kocyigit, M.B.; Falconer, R.A.; Lin, B. Three-dimensional numerical modeling of free surface flows with non-hydrostatic pressure. Int. J. Numer. Methods Fluids 2002, 40, 1145–1162. [Google Scholar] [CrossRef]
- Chen, X. A fully hydrodynamic model for three-dimensional, free-surface flows. Int. J. Numer. Methods Fluids 2003, 42, 929–952. [Google Scholar] [CrossRef]
- Hsu, T.J.; Liu, P.L.F. Toward modeling turbulent suspension of sand in the nearshore. J. Geophys. Res. Oceans 2004, 109, C06018. [Google Scholar] [CrossRef]
- Wu, C.H.; Young, C.C.; Chen, Q.; Lynett, P.J. Efficient non-hydrostatic modeling of nonlinear waves from shallow to deep water. J. Waterw. Port Coast. Ocean Eng. 2010, 136, 104–118. [Google Scholar] [CrossRef]
- Ma, G.; Shi, F.; Kirby, J.T. Shock-capturing non-hydrostatic model for fully dispersive surface wave processes. Ocean Model. 2012, 43, 22–35. [Google Scholar] [CrossRef]
- Bai, Y.; Cheung, K.F. Dispersion and nonlinearity of multi-layer non-hydrostatic free-surface flow. J. Fluid Mech. 2013, 726, 226–260. [Google Scholar] [CrossRef]
- Stelling, G.; Zijlema, M. An accurate and efficient finite-difference algorithm for non-hydrostatic free-surface flow with application to wave propagation. Int. J. Numer. Methods Fluids 2003, 43, 1–23. [Google Scholar] [CrossRef]
- Zijlema, M.; Stelling, G. Further experiences with computing non-hydrostatic free-surface flows involving water waves. Int. J. Numer. Methods Fluids 2005, 48, 169–197. [Google Scholar] [CrossRef]
- Yuan, H.; Wu, C.H. An implicit 3D fully non-hydrostatic model for free-surface flows. Int. J. Numer. Methods Fluids 2004, 46, 709–733. [Google Scholar] [CrossRef]
- Yuan, H.; Wu, C.H. A two-dimensional vertical non-hydrostatic σ model with an implicit method for free-surface flows. Int. J. Numer. Methods Fluids 2004, 44, 811–835. [Google Scholar] [CrossRef]
- Yuan, H.; Wu, C.H. Fully Nonhydrostatic Modeling of Surface Waves. J. Eng. Mech. 2006, 132, 447–456. [Google Scholar] [CrossRef]
- Ahmadi, A.; Badiei, P.; Namin, M.M. An implicit two-dimensional non-hydrostatic model for free-surface flows. Int. J. Numer. Methods Fluids 2007, 54, 1055–1074. [Google Scholar] [CrossRef]
- Badiei, P.; Namin, M.M.; Ahmadi, A. A three-dimensional non-hydrostatic vertical boundary fitted model for free-surface flows. Int. J. Numer. Methods Fluids 2008, 56, 607–627. [Google Scholar] [CrossRef]
- Young, C.C.; Wu, C.H.; Kuo, J.T.; Liu, W.C. A higher-order σ-coordinate non-hydrostatic model for nonlinear surface waves. Ocean Eng. 2007, 34, 1357–1370. [Google Scholar] [CrossRef]
- Young, C.C.; Wu, C.H.; Liu, W.C.; Kuo, J.T. A higher-order non-hydrostatic s model for simulating non-linear refraction-diffraction of water waves. Coast. Eng. 2009, 56, 919–930. [Google Scholar] [CrossRef]
- Young, C.C.; Wu, C.H. An efficient and accurate non-hydrostatic model with embedded Boussinesq-type like equations for surface wave modeling. Int. J. Numer. Methods Fluids 2009, 60, 27–53. [Google Scholar] [CrossRef]
- Young, C.C.; Wu, C.H. Nonhydrostatic Modeling of Nonlinear Deep-Water Wave Groups. J. Eng. Mech. 2010, 136, 155–167. [Google Scholar] [CrossRef]
- Choi, D.Y.; Wu, C.H.; Young, C.C. An efficient curvilinear non-hydrostatic model for simulating surface water waves. Int. J. Numer. Methods Fluids 2011, 66, 1093–1115. [Google Scholar] [CrossRef]
- Young, C.C.; Chao, W.T.; Ting, C.L. Applicable sloping range and bottom smoothing treatment for σ-based modeling of wave propagation over rapidly varying topography. Ocean Eng. 2016, 125, 261–271. [Google Scholar] [CrossRef]
- Chen, X. A comparison of hydrostatic and nonhydrostatic pressure components in seiche oscillations. Math. Comput. Model. 2005, 41, 887–902. [Google Scholar] [CrossRef]
- Casulli, V.; Stelling, G.S. Numerical simulation of 3D quasi-hydrostatic free-surface flows. J. Hydraul. Eng. 1998, 124, 678–686. [Google Scholar] [CrossRef]
- Bradford, S.F. Godunov-based model for nonhydrostatic wave dynamics. J. Waterw. Port Coast. Ocean Eng. 2005, 131, 226–238. [Google Scholar] [CrossRef]
- Chiang, W.S.; Hsiao, S.C.; Hwung, H.H. Evolution of sidebands in deep-water bichromatic wave trains. J. Hydraul. Res. 2007, 45, 67–80. [Google Scholar] [CrossRef]
- Trulsen, K.; Stansberg, C.T. Spatial evolution of water surface waves: Numerical simulation and experiment of bichromatic waves. In Proceedings of the Eleventh International Offshore and Polar Engineering Conference, Stavanger, Norway, 17–22 June 2001; International Society of Offshore and Polar Engineers: Mountain View, CA, USA, 2001. [Google Scholar]
- Longuet-Higgins, M.S.; Stewart, R.W. Changes in the form of short gravity waves on long waves and tidal currents. J. Fluid Mech. 1960, 8, 565–583. [Google Scholar] [CrossRef]
- Bateman, W.J.D.; Swan, C.; Taylor, P.H. On the efficient numerical simulation of directionally spread surface water waves. J. Comput. Phys. 2001, 174, 277–305. [Google Scholar] [CrossRef]
- Shemer, L.; Jiao, H.; Kit, E.; Agnon, Y. Evolution of a nonlinear wave field along a tank: Experiments and numerical simulations based on the spatial Zakharov equation. J. Fluid Mech. 2001, 427, 107–129. [Google Scholar] [CrossRef]
- Westhuis, J.; van Groesen, E.; Huijsmans, R. Experiments and numerics of bichromatic wave groups. J. Waterw. Port Coast. Ocean Eng. 2001, 127, 334–342. [Google Scholar] [CrossRef]
- Ting, F.C.K.; Kirby, J.T. Observation of undertow and turbulence in a laboratory surf zone. Coast. Eng. 1994, 24, 51–80. [Google Scholar] [CrossRef]
- Peregrine, D.H. Interaction of water waves and currents. Adv. Appl. Mech. 1976, 16, 9–117. [Google Scholar]
- Nepf, H.; Monismith, S. Wave dispersion on a sheared current. Appl. Ocean Res. 1994, 16, 313–316. [Google Scholar] [CrossRef]
- Wu, C.H.; Nepf, H.M. Breaking wave criteria and energy losses for three-dimensional wave breaking. J. Geophys. Res. Oceans 2002, 107, 3177. [Google Scholar] [CrossRef]
- Dean, R.G. Freak waves: A possible explanation. In Water Wave Kinematics; Torum, O., Gudmestad, O.T., Eds.; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1990; pp. 609–612. [Google Scholar]
- Kharif, C.; Pelinovsky, E. Physical mechanisms of the rogue wave phenomenon. Eur. J. Mech. B Fluids 2003, 22, 603–634. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Young, C.-C.; Wu, C.H.; Hsu, T.-W. The Role of Non-Hydrostatic Effects in Nonlinear Dispersive Wave Modeling. Water 2020, 12, 3513. https://doi.org/10.3390/w12123513
Young C-C, Wu CH, Hsu T-W. The Role of Non-Hydrostatic Effects in Nonlinear Dispersive Wave Modeling. Water. 2020; 12(12):3513. https://doi.org/10.3390/w12123513
Chicago/Turabian StyleYoung, Chih-Chieh, Chin H. Wu, and Tai-Wen Hsu. 2020. "The Role of Non-Hydrostatic Effects in Nonlinear Dispersive Wave Modeling" Water 12, no. 12: 3513. https://doi.org/10.3390/w12123513
APA StyleYoung, C.-C., Wu, C. H., & Hsu, T.-W. (2020). The Role of Non-Hydrostatic Effects in Nonlinear Dispersive Wave Modeling. Water, 12(12), 3513. https://doi.org/10.3390/w12123513






