Using Field-Based Monitoring to Enhance the Performance of Rainfall Thresholds for Landslide Warning
Abstract
:1. Introduction
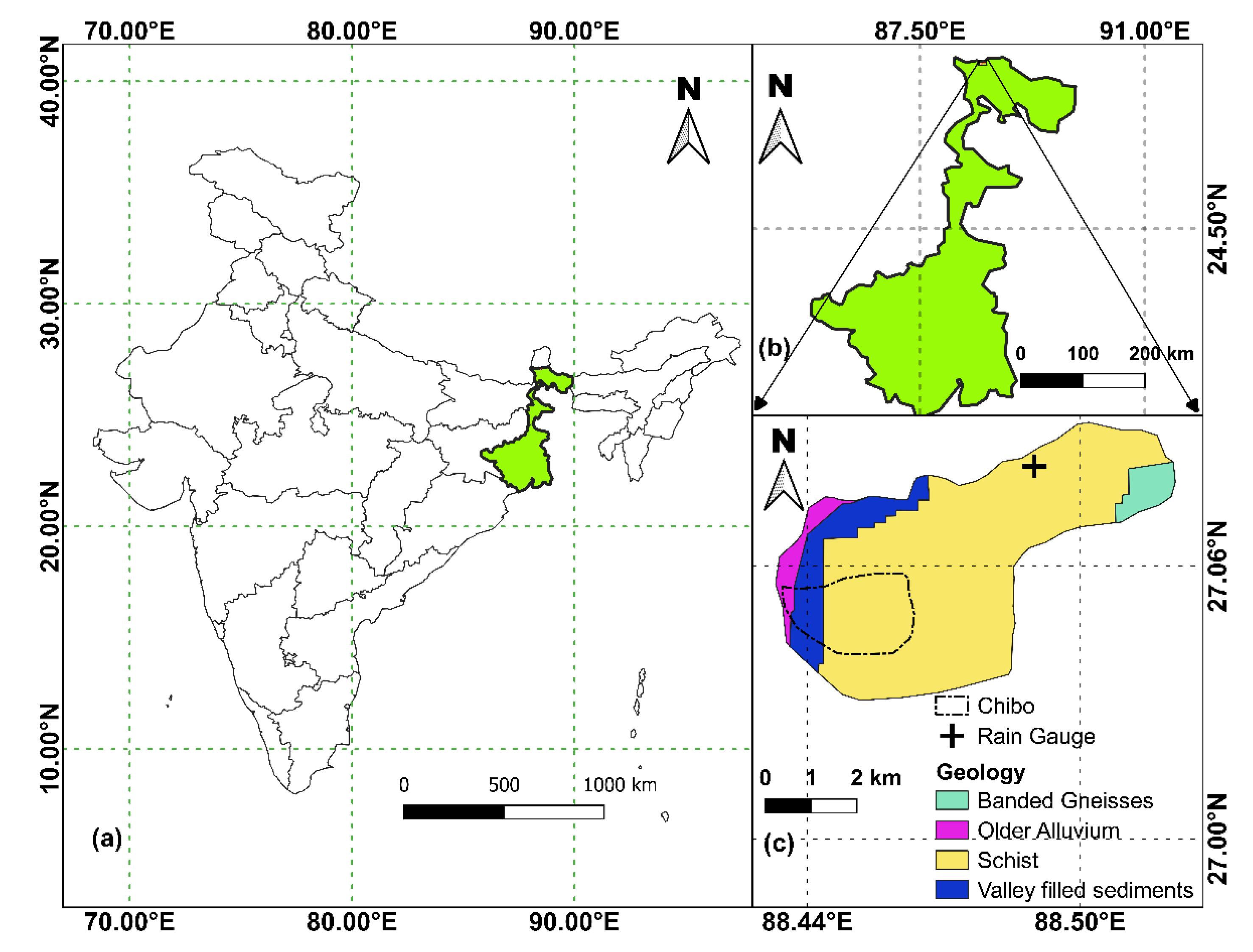
2. Study Area
3. Methodology
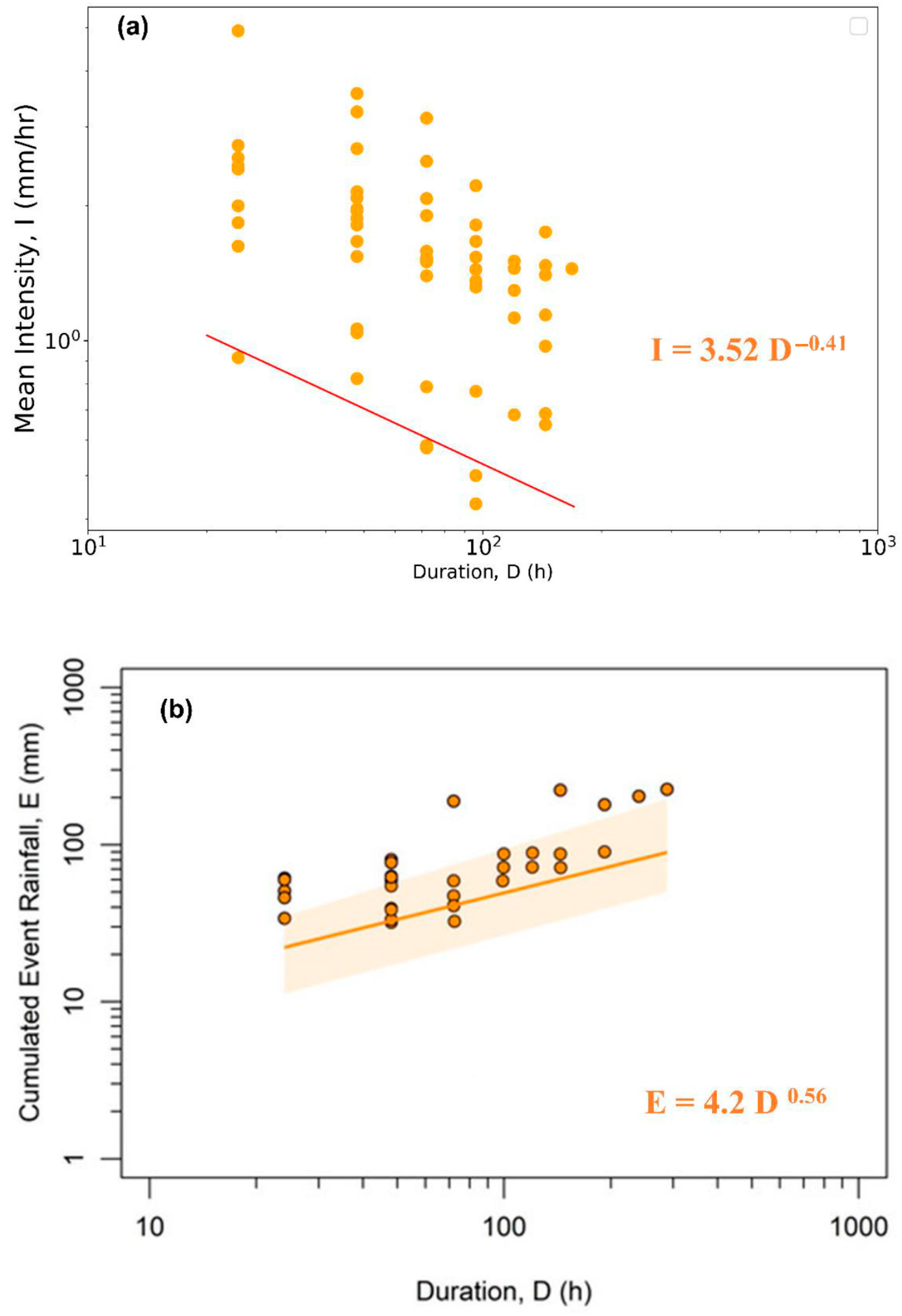
3.1. Empirical Thresholds
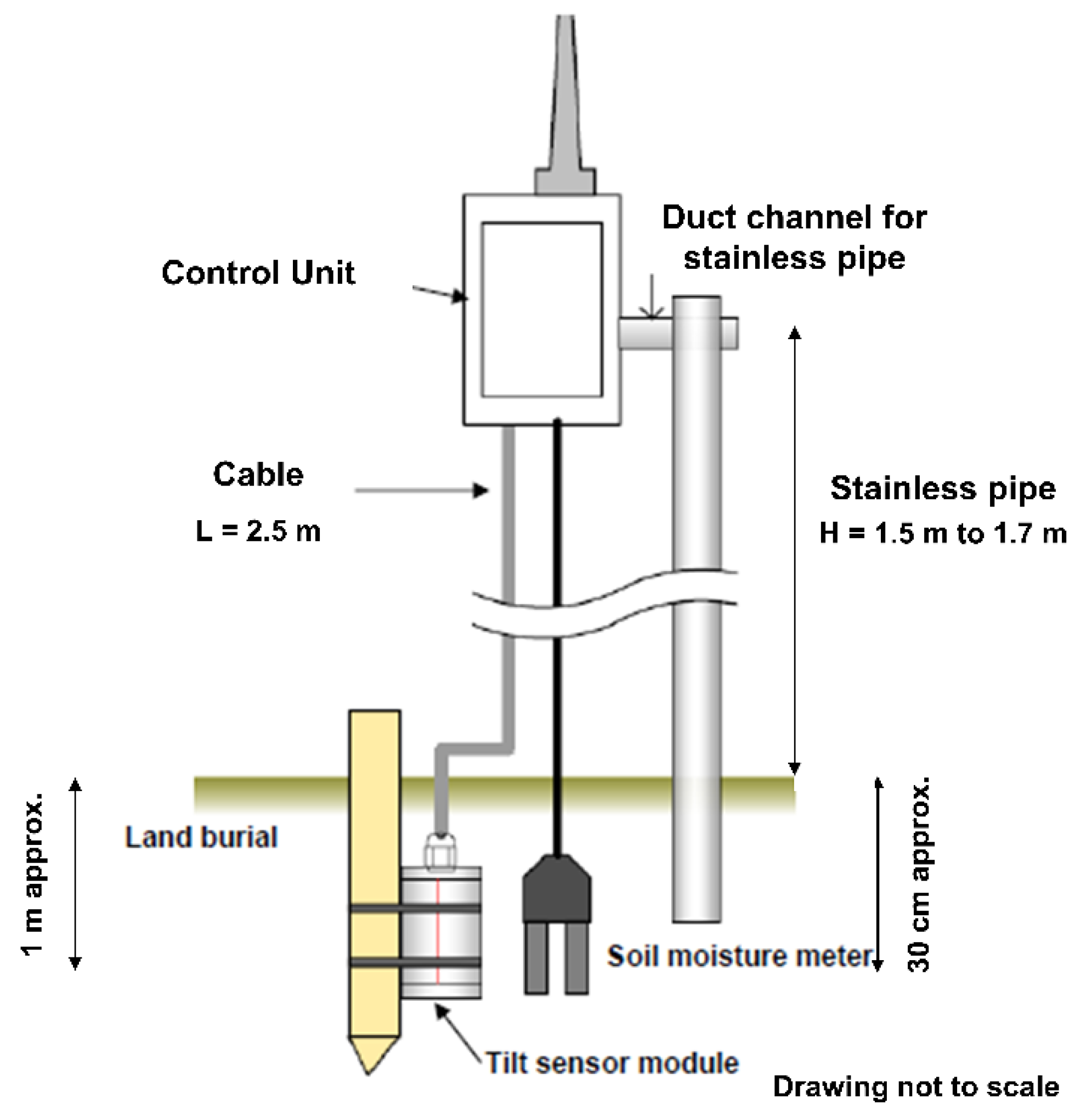
3.2. Field Monitoring System
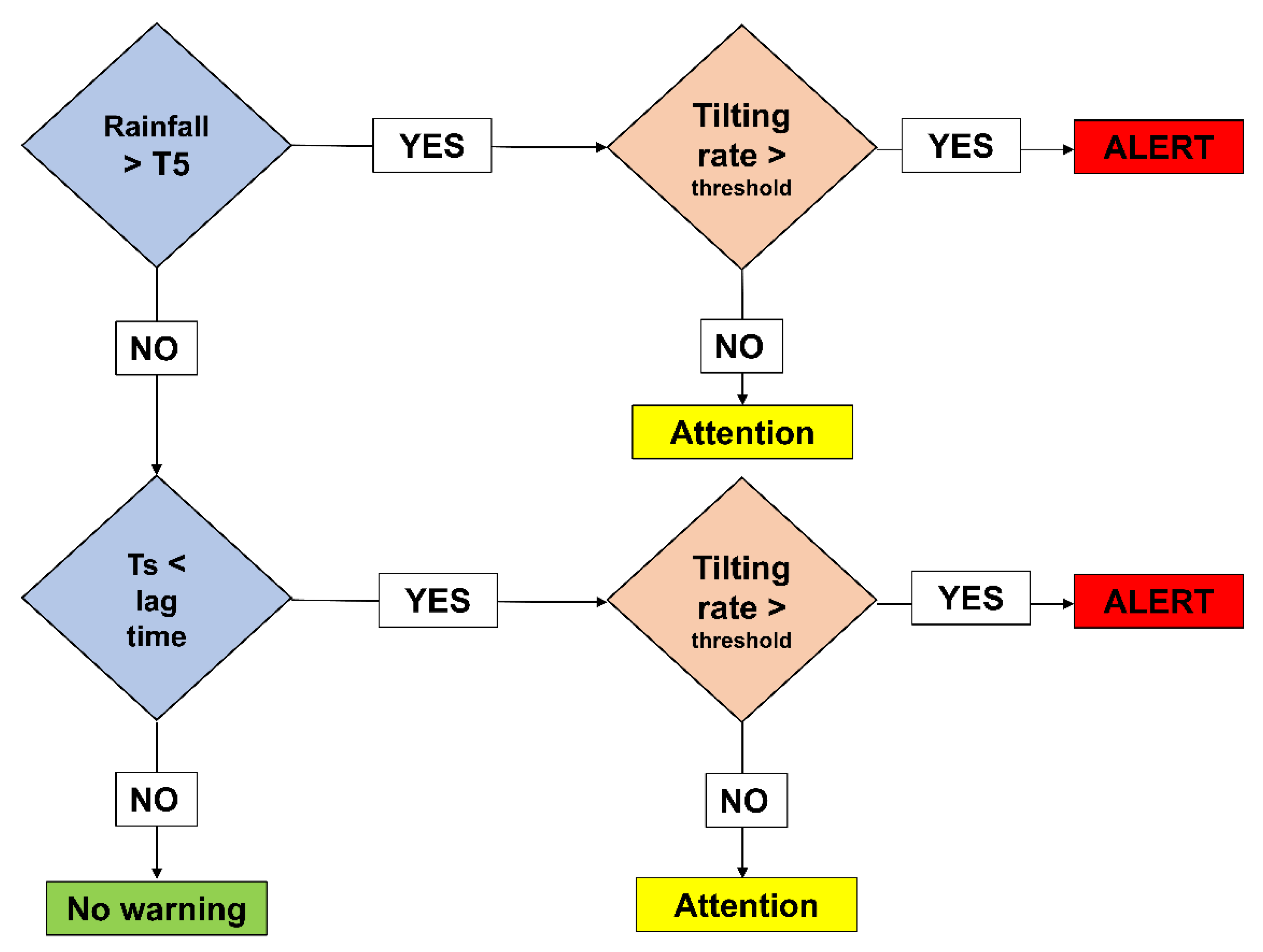
3.3. Combined Use of Field Monitoring Data and Empirical Thresholds
4. Results
4.1. Performance of Empirical Thresholds
4.2. Performance of Tilt Meters
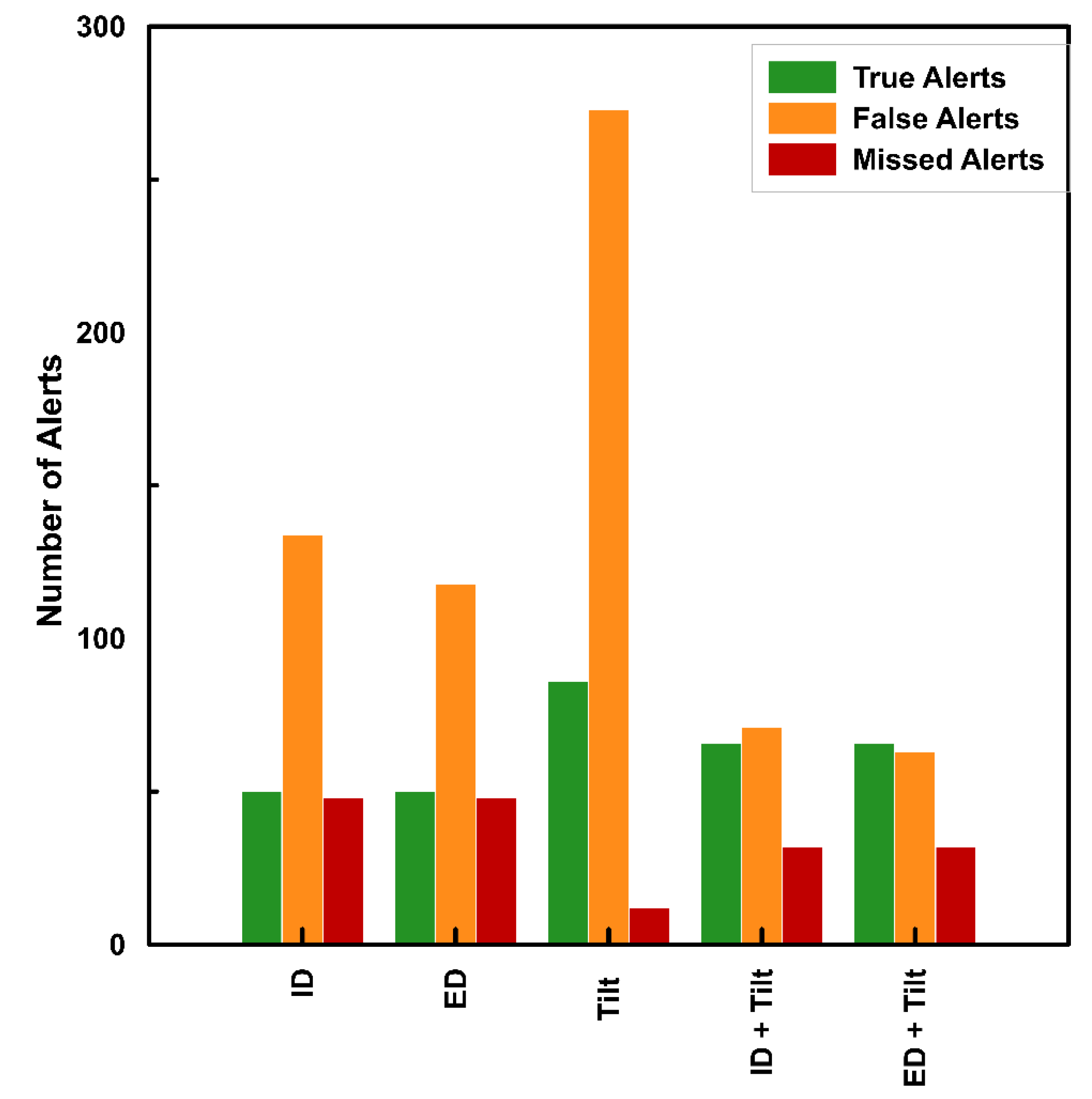
4.3. Performance of Proposed Algorithm
5. Discussion
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Dowling, C.A.; Santi, P.M. Debris flows and their toll on human life: A global analysis of debris-flow fatalities from 1950 to 2011. Nat. Hazards 2014, 71, 203–227. [Google Scholar] [CrossRef]
- Petley, D. Global patterns of loss of life from landslides. Geology 2012, 40, 927–930. [Google Scholar] [CrossRef]
- Devoli, G.; Tiranti, D.; Cremonini, R.; Sund, M.; Boje, S. Comparison of landslide forecasting services in Piedmont (Italy) and Norway, illustrated by events in late spring 2013. Nat. Hazards 2018, 19, 1351–1372. [Google Scholar] [CrossRef] [Green Version]
- Baum, R.L.; Godt, J.W. Early warning of rainfall-induced shallow landslides and debris flows in the USA. Landslides 2010, 7, 259–272. [Google Scholar] [CrossRef]
- Segoni, S.; Piciullo, L.; Gariano, S.L. A review of the recent literature on rainfall thresholds for landslide occurrence. Landslides 2018, 15, 1483–1501. [Google Scholar] [CrossRef]
- Fusco, F.; De Vita, P.; Mirus, B.B.; Baum, R.L.; Allocca, V.; Tufano, R.; Clemente, E.D.I.; Calcaterra, D. Physically based estimation of rainfall thresholds triggering shallow landslides in volcanic slopes of Southern Italy. Water 2019, 11, 1915. [Google Scholar] [CrossRef] [Green Version]
- De Vita, P.; Fusco, F.; Napolitano, E.; Tufano, R. Physically-based models for estimating rainfall triggering debris flows in Campania (Southern Italy). In Advancing Culture of Living with Landslides; Springer International Publishing: Cham, Switzerland, 2017; pp. 289–297. [Google Scholar]
- Napolitano, E.; Fusco, F.; Baum, R.L.; Godt, J.W.; De Vita, P. Effect of antecedent-hydrological conditions on rainfall triggering of debris flows in ash-fall pyroclastic mantled slopes of Campania (southern Italy). Landslides 2016, 13, 967–983. [Google Scholar] [CrossRef]
- Guzzetti, F.; Peruccacci, S.; Rossi, M.; Stark, C.P. Rainfall thresholds for the initiation of landslides in central and southern Europe. Meteorol. Atmos. Phys. 2007, 98, 239–267. [Google Scholar] [CrossRef]
- Caine, N. The rainfall intensity-duration control of shallow landslides and debris flows: An update. Geogr. Ann. Ser. A Phys. Geogr. 1980, 62, 23–27. [Google Scholar]
- Aleotti, P. A warning system for rainfall-induced shallow failures. Eng. Geol. 2004, 73, 247–265. [Google Scholar] [CrossRef]
- Bordoni, M.; Corradini, B.; Lucchelli, L.; Valentino, R.; Bittelli, M.; Vivaldi, V.; Meisina, C. Empirical and physically based thresholds for the occurrence of shallow landslides in a prone area of Northern Italian Apennines. Water 2019, 11, 2653. [Google Scholar] [CrossRef] [Green Version]
- Berti, M.; Martina, M.L.V.; Franceschini, S.; Pignone, S.; Simoni, A.; Pizziolo, M. Probabilistic rainfall thresholds for landslide occurrence using a Bayesian approach. J. Geophys. Res. Earth Surf. 2012, 117, 1–20. [Google Scholar] [CrossRef] [Green Version]
- Guzzetti, F.; Peruccacci, S.; Rossi, M.; Stark, C.P. The rainfall intensity-duration control of shallow landslides and debris flows: An update. Landslides 2008, 5, 3–17. [Google Scholar] [CrossRef]
- Brunetti, M.T.; Peruccacci, S.; Rossi, M.; Luciani, S.; Valigi, D.; Guzzetti, F. Rainfall thresholds for the possible occurrence of landslides in Italy. Nat. Hazards Earth Syst. Sci. 2010, 10, 447–458. [Google Scholar] [CrossRef]
- Dahal, R.K.; Hasegawa, S. Representative rainfall thresholds for landslides in the Nepal Himalaya. Geomorphology 2008, 100, 429–443. [Google Scholar] [CrossRef]
- Peruccacci, S.; Brunetti, M.T.; Luciani, S.; Vennari, C.; Guzzetti, F. Lithological and seasonal control on rainfall thresholds for the possible initiation of landslides in central Italy. Geomorphology 2012, 139–140, 79–90. [Google Scholar] [CrossRef]
- Melillo, M.; Brunetti, M.T.; Peruccacci, S.; Gariano, S.L.; Guzzetti, F. An Algorithm for the objective reconstruction of rainfall events responsible for landslides. In Landslide Dynamics: ISDR-ICL Landslide Interactive Teaching Tools; Fundamentals, Mapping and Monitoring; Springer International Publishing: Cham, Switzerland, 2014; Volume 1, pp. 433–447. [Google Scholar]
- Melillo, M.; Brunetti, M.T.; Peruccacci, S.; Gariano, S.L.; Guzzetti, F. Rainfall thresholds for the possible landslide occurrence in Sicily (Southern Italy) based on the automatic reconstruction of rainfall events. Landslides 2016, 13, 165–172. [Google Scholar] [CrossRef]
- Zhao, B.; Dai, Q.; Han, D.; Dai, H.; Mao, J.; Zhuo, L. Probabilistic thresholds for landslides warning by integrating soil moisture conditions with rainfall thresholds. J. Hydrol. 2019, 574, 276–287. [Google Scholar] [CrossRef]
- Segoni, S.; Rossi, G.; Rosi, A.; Catani, F. Landslides triggered by rainfall: A semi-automated procedure to define consistent intensity-duration thresholds. Comput. Geosci. 2014, 63, 123–131. [Google Scholar] [CrossRef]
- Teja, T.S.; Dikshit, A.; Satyam, N. Determination of rainfall thresholds for landslide prediction using an algorithm-based approach: Case study in the Darjeeling Himalayas, India. Geoscience 2019, 9, 302. [Google Scholar] [CrossRef] [Green Version]
- Abraham, M.T.; Satyam, N.; Rosi, A.; Pradhan, B.; Segoni, S. The selection of rain gauges and rainfall parameters in estimating intensity-duration thresholds for landslide occurrence: Case study from Wayanad (India). Water 2020, 12, 1000. [Google Scholar] [CrossRef] [Green Version]
- Abraham, M.T.; Pothuraju, D.; Satyam, N. Rainfall thresholds for prediction of landslides in Idukki, India: An empirical approach. Water 2019, 11, 2113. [Google Scholar] [CrossRef] [Green Version]
- Gariano, S.L.; Melillo, M.; Peruccacci, S.; Brunetti, M.T. How much does the rainfall temporal resolution affect rainfall thresholds for landslide triggering? Nat. Hazards 2020, 100, 655–670. [Google Scholar] [CrossRef] [Green Version]
- Segoni, S.; Rosi, A.; Fanti, R.; Gallucci, A.; Monni, A.; Casagli, N. A regional-scale landslide warning system based on 20 years of operational experience. Water 2018, 10, 1297. [Google Scholar] [CrossRef] [Green Version]
- Rosi, A.; Canavesi, V.; Segoni, S.; Dias Nery, T.; Catani, F.; Casagli, N. Landslides in the mountain region of rio de Janeiro: A proposal for the semi-automated definition of multiple rainfall thresholds. Geosciences 2019, 9, 203. [Google Scholar] [CrossRef] [Green Version]
- Nikolopoulos, E.I.; Crema, S.; Marchi, L.; Marra, F.; Guzzetti, F.; Borga, M. Impact of uncertainty in rainfall estimation on the identification of rainfall thresholds for debris flow occurrence. Geomorphology 2014, 221, 286–297. [Google Scholar] [CrossRef]
- Bogaard, T.; Greco, R. Invited perspectives: Hydrological perspectives on precipitation intensity-duration thresholds for landslide initiation: Proposing hydro-meteorological thresholds. Nat. Hazards Earth Syst. Sci. 2018, 18, 31–39. [Google Scholar] [CrossRef] [Green Version]
- Wicki, A.; Lehmann, P.; Hauck, C.; Seneviratne, S.I.; Waldner, P.; Stähli, M. Assessing the potential of soil moisture measurements for regional landslide early warning. Landslides 2020, 17, 1881–1896. [Google Scholar] [CrossRef] [Green Version]
- Mirus, B.B.; Becker, R.E.; Baum, R.L.; Smith, J.B. Integrating real-time subsurface hydrologic monitoring with empirical rainfall thresholds to improve landslide early warning. Landslides 2018, 15, 1909–1919. [Google Scholar] [CrossRef]
- Glade, T.; Crozier, M.; Smith, P. Applying probability determination to refine landslide-triggering rainfall thresholds using an empirical “Antecedent Daily Rainfall Model.”. Pure Appl. Geophys. 2000, 157, 1059–1079. [Google Scholar] [CrossRef]
- Rosi, A.; Segoni, S.; Canavesi, V.; Monni, A.; Gallucci, A.; Casagli, N. Definition of 3D rainfall thresholds to increase operative landslide early warning system performances. Landslides 2020, 1–13. [Google Scholar] [CrossRef]
- Martelloni, G.; Segoni, S.; Lagomarsino, D.; Fanti, R.; Catani, F. Snow accumulation/melting model (SAMM) for integrated use in regional scale landslide early warning systems. Hydrol. Earth Syst. Sci. 2013, 17, 1229–1240. [Google Scholar] [CrossRef] [Green Version]
- Wei, X.; Fan, W.; Cao, Y.; Chai, X.; Bordoni, M.; Meisina, C.; Li, J. Integrated experiments on field monitoring and hydro-mechanical modeling for determination of a triggering threshold of rainfall-induced shallow landslides. A case study in Ren River catchment, China. Bull. Eng. Geol. Environ. 2020, 79, 513–532. [Google Scholar] [CrossRef]
- Pecoraro, G.; Calvello, M.; Piciullo, L. Monitoring strategies for local landslide early warning systems. Landslides 2018, 16, 213–231. [Google Scholar] [CrossRef]
- Casagli, N.; Catani, F.; Del Ventisette, C.; Luzi, G. Monitoring, prediction, and early warning using ground-based radar interferometry. Landslides 2010, 7, 291–301. [Google Scholar] [CrossRef]
- Yin, Y.; Zheng, W.; Liu, Y.; Zhang, J.; Li, X. Integration of GPS with InSAR to monitoring of the Jiaju landslide in Sichuan, China. Landslides 2010, 7, 359–365. [Google Scholar] [CrossRef]
- Derron, M.H.; Jaboyedoff, M. LIDAR and DEM techniques for landslides monitoring and characterization. Nat. Hazards Earth Syst. Sci. 2010, 10, 1877–1879. [Google Scholar] [CrossRef]
- Joyce, K.E.; Samsonov, S.V.; Levick, S.R.; Engelbrecht, J.; Belliss, S. Mapping and monitoring geological hazards using optical, LiDAR, and synthetic aperture RADAR image data. Nat. Hazards 2014, 73, 137–163. [Google Scholar] [CrossRef]
- Jaboyedoff, M.; Oppikofer, T.; Abella, A.; Derron, M.; Loye, A.; Metzger, R.; Pedrazzini, A. Use of LIDAR in landslide investigations: A review. Nat. Hazards 2010, 61, 5–28. [Google Scholar] [CrossRef] [Green Version]
- Raspini, F.; Bianchini, S.; Ciampalini, A.; Del Soldato, M.; Montalti, R.; Solari, L.; Tofani, V.; Casagli, N. Persistent Scatterers continuous streaming for landslide monitoring and mapping: The case of the Tuscany region (Italy). Landslides 2019, 16, 2033–2044. [Google Scholar] [CrossRef] [Green Version]
- Angeli, M.G.; Pasuto, A.; Silvano, S. A critical review of landslide monitoring experiences. Eng. Geol. 2000, 55, 133–147. [Google Scholar] [CrossRef]
- Bhattacharya, A.; Mukherjee, K. Review on InSAR based displacement monitoring of Indian Himalayas: Issues, challenges and possible advanced alternatives. Geocarto Int. 2017, 32, 298–321. [Google Scholar] [CrossRef]
- Meisina, C.; Zucca, F.; Notti, D.; Colombo, A.; Cucchi, A.; Savio, G.; Giannico, C.; Bianchi, M. Geological interpretation of PSInSAR data at regional scale. Sensors 2008, 8, 7469–7492. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Abraham, M.T.; Satyam, N.; Pradhan, B.; Alamri, A.M. IoT-based geotechnical monitoring of unstable slopes for landslide early warning in the Darjeeling Himalayas. Sensors 2020, 20, 2611. [Google Scholar] [CrossRef]
- Towhata, I.; Uchimura, T.; Seko, I.; Wang, L. Monitoring of unstable slopes by MEMS tilting sensors and its application to early warning. IOP Conf. Ser. Earth Environ. Sci. 2015, 26, 012049. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.; Tang, H.; Li, C.; Lu, G.; Cai, Y.; Zhang, J.; Tan, F. Design and testing of a flexible inclinometer probe for model tests of landslide deep displacement measurement. Sensors 2018, 18, 224. [Google Scholar] [CrossRef] [Green Version]
- Chen, Y.; Irfan, M.; Uchimura, T.; Zhang, K. Feasibility of using elastic wave velocity monitoring for early warning of rainfall-induced slope failure. Sensors 2018, 18, 997. [Google Scholar] [CrossRef] [Green Version]
- Tao, S.; Uchimura, T.; Fukuhara, M.; Tang, J.; Chen, Y.; Huang, D. Evaluation of soil moisture and shear deformation based on compression wave velocities in a shallow slope surface layer. Sensors 2019, 19, 3406. [Google Scholar] [CrossRef] [Green Version]
- Le Cozannet, G.; Hosford, S.; Douglas, J.; Serrano, J.J.; Coraboeuf, D.; Comte, J. Connecting hazard analysts and risk managers to sensor information. Sensors 2008, 8, 3932–3937. [Google Scholar] [CrossRef]
- Uchimura, T.; Towhata, I.; Wang, L. Miniature ground inclinometer for slope monitoring. In Proceedings of the 14th Asian Regional Conference on Soil Mechanics and Geotechnical Engineering, Hong Kong, China, 23–27 May 2011. [Google Scholar]
- Huang, Y.; Sai, A.; Vasan, S.; Doraiswami, R.; Osterman, M.; Pecht, M. MEMS reliability review. IEEE Trans. Device Mater. Reliabil. 2012, 12, 482–493. [Google Scholar] [CrossRef] [Green Version]
- Jung, H.; Kim, C.J.; Kong, S.H. An optimized MEMS-based electrolytic tilt sensor. Sens. Actuators A Phys. 2007, 139, 23–30. [Google Scholar] [CrossRef]
- Yang, Z.; Cai, H.; Shao, W.; Huang, D.; Uchimura, T.; Lei, X.; Tian, H.; Qiao, J. Clarifying the hydrological mechanisms and thresholds for rainfall-induced landslide: In situ monitoring of big data to unsaturated slope stability analysis. Bull. Eng. Geol. Environ. 2019, 78, 2139–2150. [Google Scholar] [CrossRef]
- Yang, Z.; Shao, W.; Qiao, J.; Huang, D.; Tian, H.; Lei, X.; Uchimura, T. A multi-source early warning system of MEMS based wireless monitoring for rainfall-induced landslides. Appl. Sci. 2017, 7, 1234. [Google Scholar] [CrossRef] [Green Version]
- Froude, M.J.; Petley, D.N. Global fatal landslide occurrence from 2004 to 2016. Nat. Hazards Earth Syst. Sci. 2018, 18, 2161–2181. [Google Scholar] [CrossRef] [Green Version]
- Dikshit, A.; Satyam, N. Rainfall thresholds for the prediction of landslides using empirical methods in Kalimpong, Darjeeling, India. In Proceedings of the JTC1 Workshop on Advances in Landslide Understanding, Barcelona, Spain, 24–26 May 2017. [Google Scholar]
- Dahal, R.K. Rainfall-induced Landslides in Nepal. Int. J. Jpn. Eros. Control Eng. 2012, 5, 1–8. [Google Scholar] [CrossRef] [Green Version]
- Gabet, E.J.; Burbank, D.W.; Putkonen, J.K.; Pratt-sitaula, B.A.; Ojha, T. Rainfall thresholds for landsliding in the Himalayas of Nepal. Geomorphology 2004, 63, 131–143. [Google Scholar] [CrossRef]
- Dikshit, A.; Sarkar, R.; Pradhan, B.; Segoni, S.; Alamri, A.M. Rainfall induced landslide studies in Indian Himalayan region: A critical review. Appl. Sci. 2020, 10, 2466. [Google Scholar] [CrossRef] [Green Version]
- Abraham, M.T.; Satyam, N.; Reddy, S.K.P.; Pradhan, B. Runout modeling and calibration of friction parameters of Kurichermala debris flow, India. Landslides 2020, 1–8. [Google Scholar] [CrossRef]
- Dikshit, A.; Satyam, D.N. Estimation of rainfall thresholds for landslide occurrences in Kalimpong, India. Innov. Infrastruct. Solut. 2018, 3, 24. [Google Scholar] [CrossRef]
- Dikshit, A.; Satyam, N. Probabilistic rainfall thresholds in Chibo, India: Estimation and validation using monitoring system. J. Mt. Sci. 2019, 16, 870–883. [Google Scholar] [CrossRef]
- Abraham, M.T.; Satyam, N.; Pradhan, B.; Alamri, A.M. Forecasting of landslides using rainfall severity and soil wetness: A probabilistic approach for Darjeeling Himalayas. Water 2020, 12, 804. [Google Scholar] [CrossRef] [Green Version]
- Abraham, M.T.; Satyam, N.; Kushal, S.; Rosi, A.; Pradhan, B.; Segoni, S. Rainfall threshold estimation and landslide forecasting for Kalimpong, India using SIGMA model. Water 2020, 12, 1195. [Google Scholar] [CrossRef] [Green Version]
- Dikshit, A.; Sarkar, R.; Satyam, N. Probabilistic approach toward Darjeeling Himalayas landslides—A case study. Cogent Eng. 2018, 5, 1–11. [Google Scholar] [CrossRef]
- Dortch, J.M.; Owen, L.A.; Haneberg, W.C.; Caffee, M.W.; Dietsch, C.; Kamp, U. Nature and timing of large landslides in the Himalaya and Transhimalaya of northern India. Quat. Sci. Rev. 2009, 28, 1037–1054. [Google Scholar] [CrossRef]
- Dikshit, A.; Satyam, D.N.; Towhata, I. Early warning system using tilt sensors in Chibo, Kalimpong, Darjeeling Himalayas, India. Nat. Hazards 2018, 94, 727–741. [Google Scholar] [CrossRef]
- Mukherjee, A.; Mitra, A. Geotechnical study of mass movements along the kalimpong approach road in the Eastern Himalayas. Indian J. Geol. 2001, 73, 271–279. [Google Scholar]
- Save The Hills Blog. Available online: http://savethehills.blogspot.com/ (accessed on 15 September 2020).
- Chuo Kaihatsu Corporation—Company Profile. Available online: http://www.ckcnet.co.jp/ (accessed on 18 October 2020).
- Lin, W.; Shunsaku, N.; Taro, U.; Ikuo, T.; Ling, S.; Shangning, T. An early warning system of unstable slopes by multi-point MEMS tilting sensors and water contents. In Advancing Culture of Living with Landslides; Springer International Publishing: Cham, Switzerland, 2017; pp. 147–154. [Google Scholar]
- Lagomarsino, D.; Segoni, S.; Rosi, A.; Rossi, G.; Battistini, A.; Catani, F.; Casagli, N. Quantitative comparison between two different methodologies to define rainfall thresholds for landslide forecasting. Nat. Hazards Earth Syst. Sci. 2015, 15, 2413–2423. [Google Scholar] [CrossRef] [Green Version]
- Melillo, M.; Brunetti, M.T.; Peruccacci, S.; Gariano, S.L.; Roccati, A.; Guzzetti, F. A tool for the automatic calculation of rainfall thresholds for landslide occurrence. Env. Model. Softw. 2018, 105, 230–243. [Google Scholar] [CrossRef]
- Ivanov, V.; Arosio, D.; Tresoldi, G.; Hojat, A.; Zanzi, L.; Papini, M.; Longoni, L. Investigation on the role of water for the stability of shallow landslides—Insights from experimental tests. Water 2020, 12, 1203. [Google Scholar] [CrossRef] [Green Version]
- Cogan, J.; Gratchev, I. A study on the effect of rainfall and slope characteristics on landslide initiation by means of flume tests. Landslides 2019, 16, 2369–2379. [Google Scholar] [CrossRef]
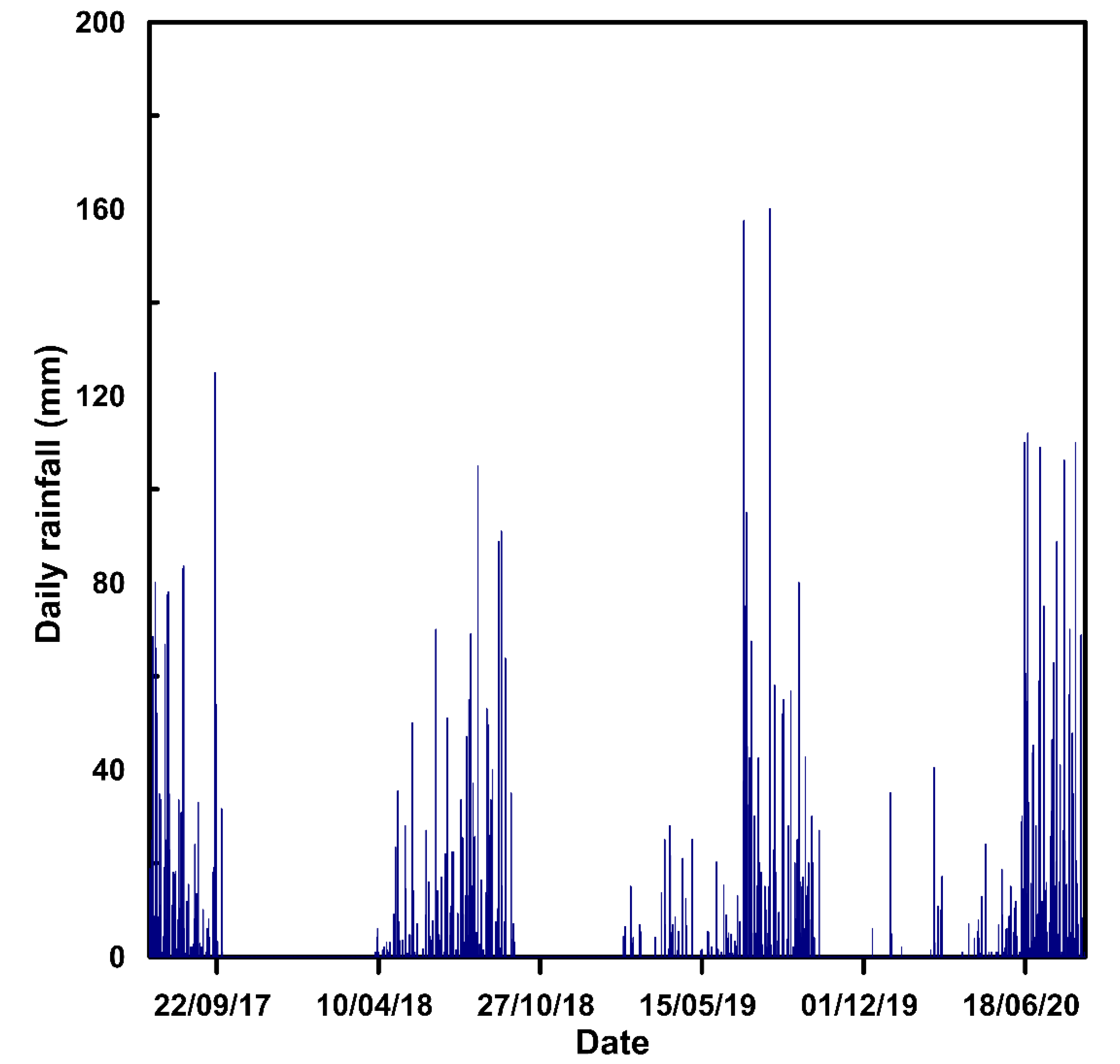

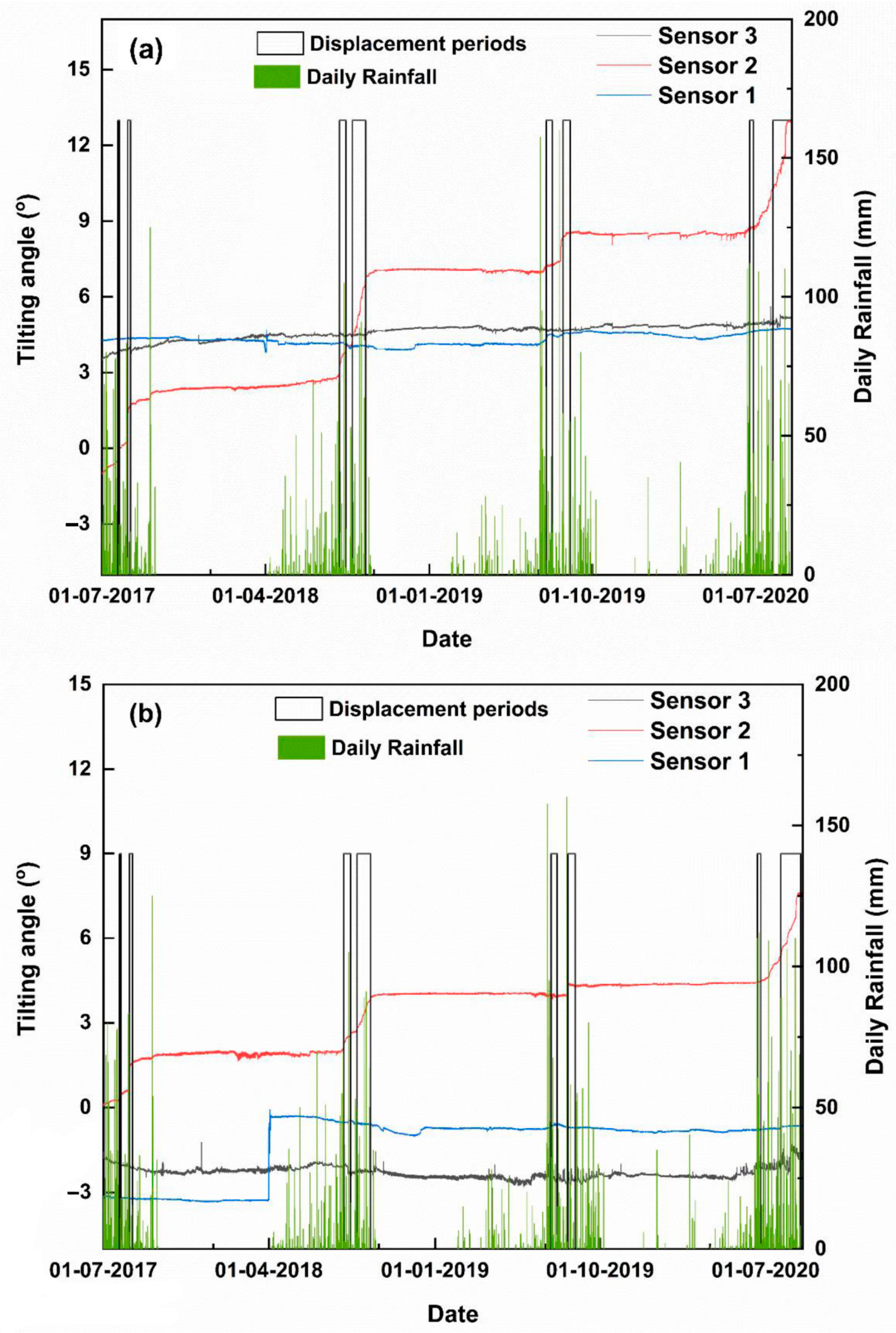

| Month | January | February | March | April | May | June | July | August | September | October | November | December |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Rainfall (mm) | 14.60 | 30.1 | 29.10 | 74.87 | 105.87 | 292.20 | 675.85 | 512.68 | 347.50 | 10.33 | 0.00 | 2.00 |
| Statistical Attributes | ID Threshold [58] | ED Threshold [22] |
|---|---|---|
| a = True positives | 50 | 50 |
| b = False positives | 134 | 118 |
| c = False negatives | 48 | 48 |
| d = True negatives | 926 | 942 |
| Efficiency = (a + d)/(a + b + c + d) | 0.84 | 0.86 |
| Odds ratio = (a + d)/(b + c) | 5.36 | 5.98 |
| Specificity = d/(b + d) | 0.87 | 0.89 |
| Sensitivity = a/(a + c) | 0.51 | 0.51 |
| Likelihood ratio = Sensitivity/(1 − Specificity) | 4.04 | 4.58 |
| Statistical Attributes | Field Monitoring |
|---|---|
| True positives | 86 |
| False positives | 273 |
| False negatives | 12 |
| True negatives | 787 |
| Efficiency | 0.75 |
| Odds ratio | 3.06 |
| Specificity | 0.74 |
| Sensitivity | 0.88 |
| Likelihood ratio | 3.41 |
| Statistical Attributes | ID + Tilt | Variation from ID | ED + Tilt | Variation from ED |
|---|---|---|---|---|
| True positives | 66 | +16 | 66 | +16 |
| False positives | 71 | −63 | 63 | −55 |
| False negatives | 32 | −16 | 32 | −16 |
| True negatives | 989 | +63 | 997 | +55 |
| Efficiency | 0.91 | +0.07 | 0.92 | +0.06 |
| Odds ratio | 10.24 | +4.88 | 11.19 | +5.21 |
| Specificity | 0.93 | +0.06 | 0.94 | +0.05 |
| Sensitivity | 0.67 | +0.16 | 0.67 | +0.16 |
| Likelihood ratio | 10.05 | +6.02 | 11.33 | +6.75 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abraham, M.T.; Satyam, N.; Bulzinetti, M.A.; Pradhan, B.; Pham, B.T.; Segoni, S. Using Field-Based Monitoring to Enhance the Performance of Rainfall Thresholds for Landslide Warning. Water 2020, 12, 3453. https://doi.org/10.3390/w12123453
Abraham MT, Satyam N, Bulzinetti MA, Pradhan B, Pham BT, Segoni S. Using Field-Based Monitoring to Enhance the Performance of Rainfall Thresholds for Landslide Warning. Water. 2020; 12(12):3453. https://doi.org/10.3390/w12123453
Chicago/Turabian StyleAbraham, Minu Treesa, Neelima Satyam, Maria Alexandra Bulzinetti, Biswajeet Pradhan, Binh Thai Pham, and Samuele Segoni. 2020. "Using Field-Based Monitoring to Enhance the Performance of Rainfall Thresholds for Landslide Warning" Water 12, no. 12: 3453. https://doi.org/10.3390/w12123453
APA StyleAbraham, M. T., Satyam, N., Bulzinetti, M. A., Pradhan, B., Pham, B. T., & Segoni, S. (2020). Using Field-Based Monitoring to Enhance the Performance of Rainfall Thresholds for Landslide Warning. Water, 12(12), 3453. https://doi.org/10.3390/w12123453









