A New Runoff Routing Scheme for Xin’anjiang Model and Its Routing Parameters Estimation Based on Geographical Information
Abstract
:1. Introduction
2. Methodology
2.1. Xin’anjiang Model
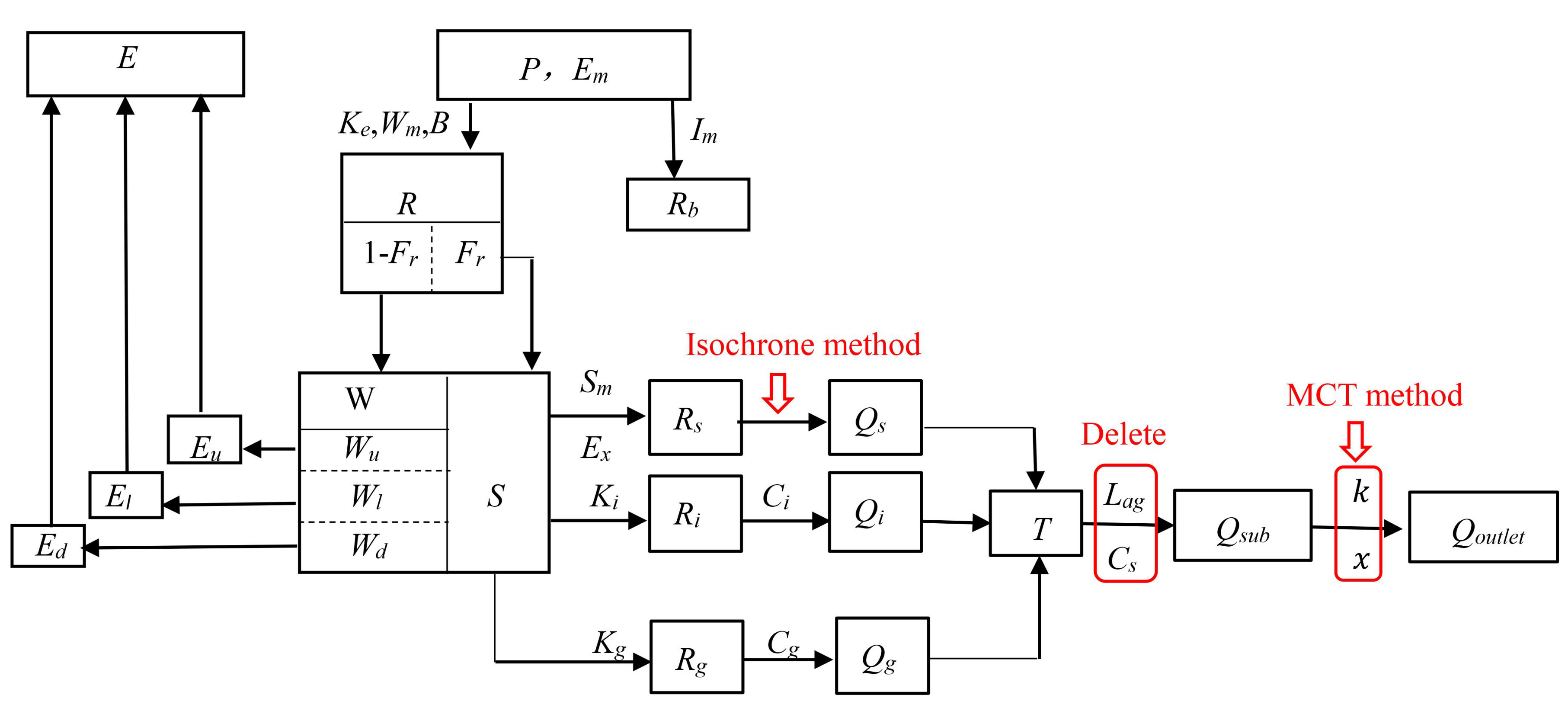
2.2. The New Runoff Routing Scheme
2.2.1. Overland Routing
2.2.2. Interflow and Groundwater Routing
2.2.3. Channel Routing
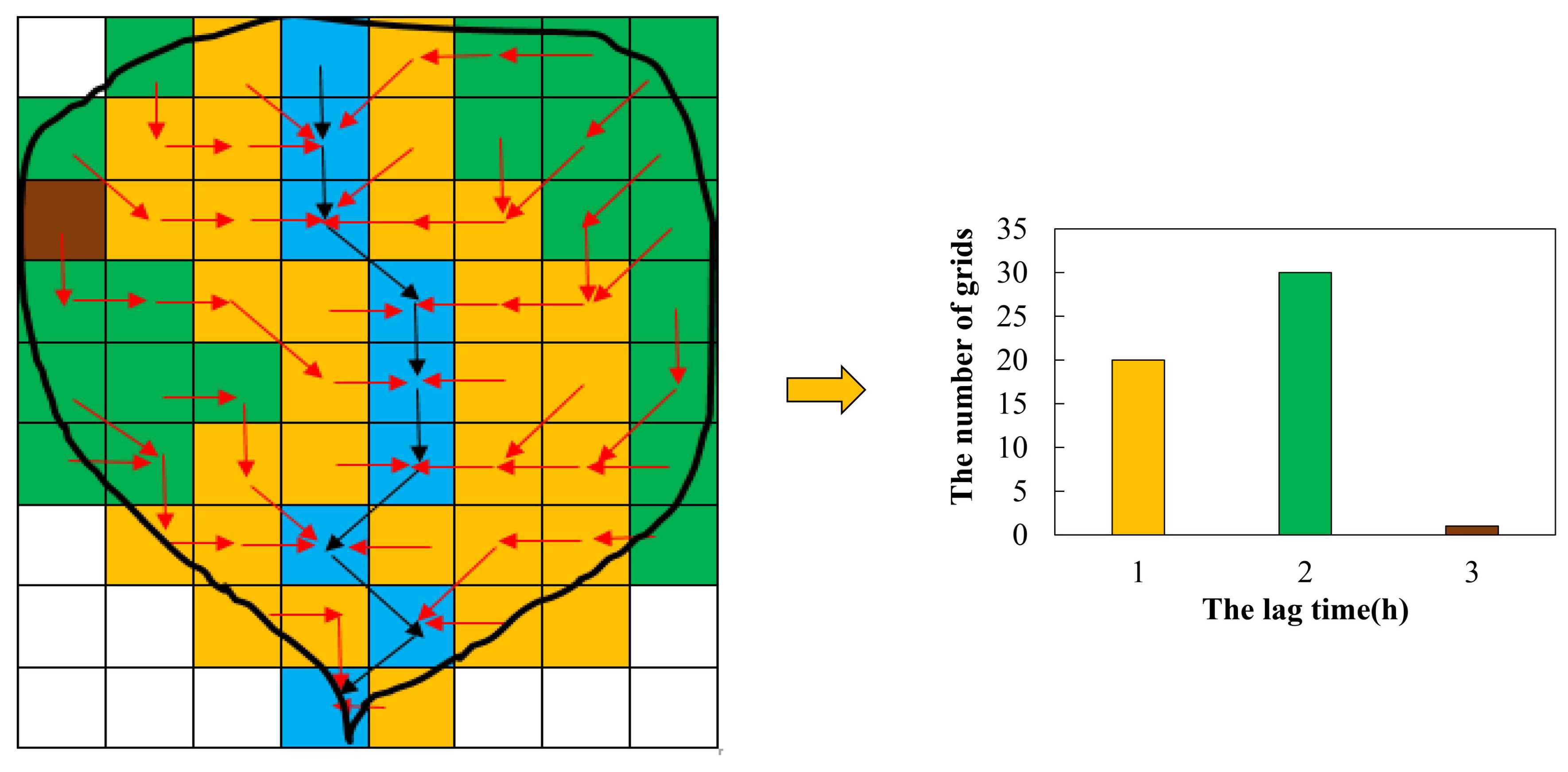
2.2.4. Routing Parameters Estimation for New Routing Scheme
3. Case Studies
3.1. Studies Area
3.2. Model Evaluation and Comparison
4. Results and Discussion
4.1. Parameter Calibration and Estimation
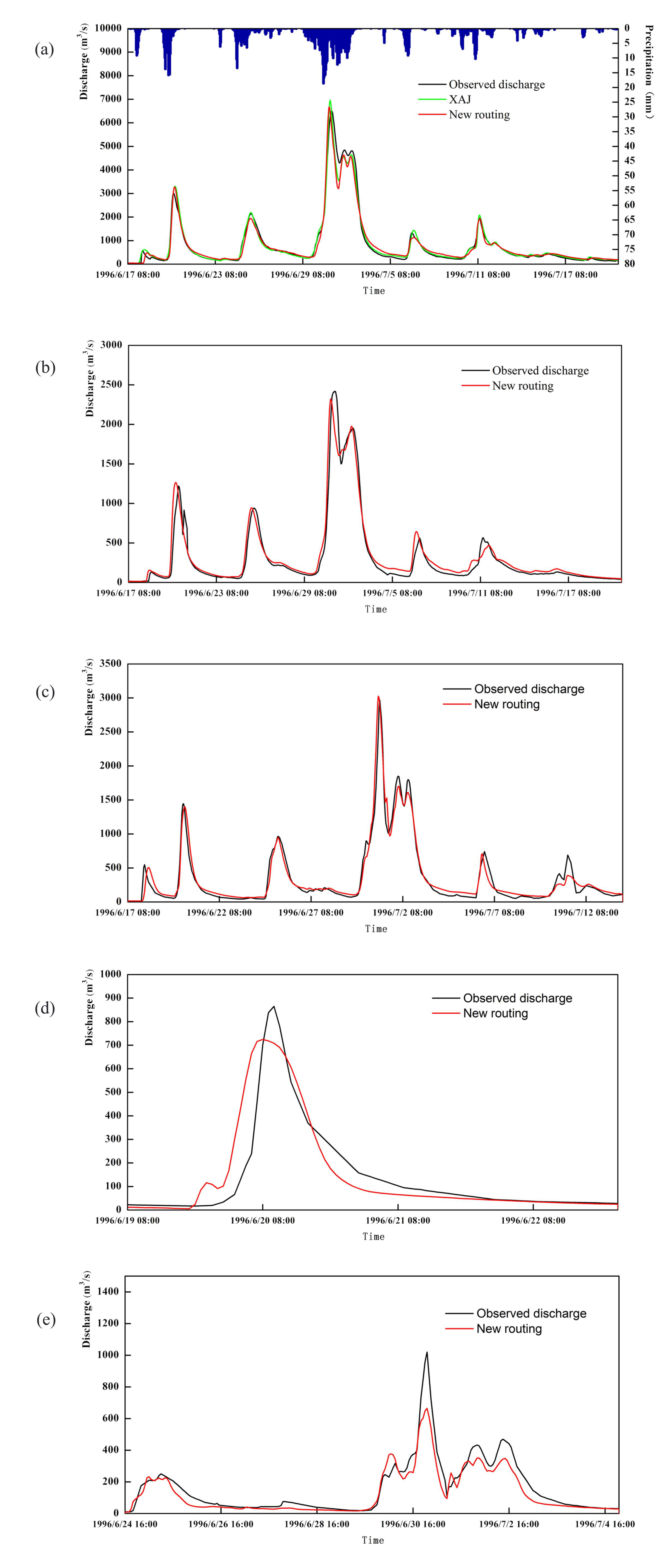
4.2. The Performance of the New Routing Scheme at the Outlet
4.3. The Performance of the New Routing Scheme at the Interior Locations
4.4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Smith, M.B.; Laurine, D.P.; Koren, V.; Reed, S.; Zhang, Z. Hydrologic Model. Calibration in the National Weather Service; American Geophysical Union (AGU): Washington, DC, USA, 2003; Volume 6, pp. 133–152. [Google Scholar]
- Gupta, H.V.; Sorooshian, S.; Hogue, T.S.; Boyle, D.P. Advances in Automatic Calibration of Watershed Models; American Geophysical Union (AGU): Washington, DC, USA, 2003; Volume 6, pp. 9–28. [Google Scholar]
- Seyfried, M.S.; Wilcox, B.P. Scale and the Nature of Spatial Variability: Field Examples Having Implications for Hydrologic Modeling. Water Resour. Res. 1995, 31, 173–184. [Google Scholar] [CrossRef]
- Koren, V.; Reed, S.; Smith, M.; Zhang, Z.; Seo, D.-J. Hydrology laboratory research modeling system (HL-RMS) of the US national weather service. J. Hydrol. 2004, 291, 297–318. [Google Scholar] [CrossRef] [Green Version]
- Beven, K. Changing ideas in hydrology—The case of physically-based models. J. Hydrol. 1989, 105, 157–172. [Google Scholar] [CrossRef]
- Wilcox, B.P.; Rawls, W.J.; Brakensiek, D.L.; Wight, J.R. Predicting runoff from Rangeland Catchments: A comparison of two models. Water Resour. Res. 1990, 26, 2401–2410. [Google Scholar] [CrossRef]
- Loague, K. R-5 revisited: 2. Reevaluation of a quasi-physically based rainfall-runoff model with supplemental information. Water Resource. Res. 1990, 26, 973–987. [Google Scholar] [CrossRef]
- Robinson, J.S.; Sivapalan, M. Catchment-scale runoff generation model by aggregation and similarity analyses. Hydrol. Process. 1995, 9, 555–574. [Google Scholar] [CrossRef]
- Chao, L.; Zhang, K.; Li, Z.; Wang, J.; Yao, C.; Li, Q. Applicability assessment of the CASCade Two Dimensional SEDiment (CASC2D-SED) distributed hydrological model for flood forecasting across four typical medium and small watersheds in China. J. Flood Risk Manag. 2019, 12. [Google Scholar] [CrossRef] [Green Version]
- Reed, S.; Koren, V.; Smith, M.; Zhang, Z.; Moreda, F.; Seo, D.-J.; Participants, A.D. Overall distributed model intercomparison project results. J. Hydrol. 2004, 298, 27–60. [Google Scholar] [CrossRef]
- Moore, R.J.; Cole, S.J.; Bell, V.A.; Jones, D.A. Issues in Flood Forecasting: Ungauged Basins, Extreme Floods and Uncertainty. In Frontiers in Flood Forecasting, Eighth Kovacs Colloquium, June/July 2006, UNESCO, Paris; Tchiguuirinskaia, I., Thein, K.N.N., Hubert, P., Eds.; IAHS Publication: Wallingford, Oxfordshire, UK, 2006; pp. 103–122. [Google Scholar]
- WMO. Manual on Flood Forecasting and Warning. World Meteorological Organization; WMO: Geneva, Switzerland, 2011; p. 1072. [Google Scholar]
- Liu, Y.; Zhang, K.; Li, Z.; Liu, Z.; Wang, J.; Huang, P. A hybrid runoff generation modelling framework based on spatial combination of three runoff generation schemes for semi-humid and semi-arid watersheds. J. Hydrol. 2020, 590. [Google Scholar] [CrossRef]
- Ren-Jun, Z. The Xinanjiang model applied in China. J. Hydrol. 1992, 135, 371–381. [Google Scholar] [CrossRef]
- Zhao, R. Watershed concentration flow of linear time-varying systems. J. China Hydrol. 1991, 4, 22–24. [Google Scholar]
- Xu, Q.; Li, Z.; Chen, X. Study on the parameter laws of watershed flow concentration of Xinanjiang model. Boutiq. China Sci. Technol. Papers Online 2008, 2, 335–338. [Google Scholar]
- Hu, W.; Li, Z.; Zhang, H.; Zhong, L. Study on relationship between recession coefficient of river network and underlying surface for Xin’ anjiang model. Water Resource. Power 2017, 35, 14–17. [Google Scholar]
- McCarthy, G.T. The Unit Hydrograph and Flood Routing. In Proceedings of the Proceedings of Conference of North Atlantic Division, US Army Corps of Engineers, New London, CT, USA, 24 June 1938. [Google Scholar]
- Yao, C.; Li, Z.; Bao, H.; Yu, Z. Application of a developed Grid-Xin’anjiang model to Chinese watersheds for flood forecasting purpose. J. Hydrol. Eng. 2009, 14, 923–934. [Google Scholar] [CrossRef]
- Yao, C.; Li, Z.; Yu, Z.; Zhang, K. A priori parameter estimates for a distributed, grid-based Xinanjiang model using geographically based information. J. Hydrol. 2012, 468, 47–62. [Google Scholar] [CrossRef]
- Yao, C.; Zhang, K.; Yu, Z.; Li, Z.; Li, Q. Improving the flood prediction capability of the Xinanjiang model in ungauged nested catchments by coupling it with the geomorphologic instantaneous unit hydrograph. J. Hydrol. 2014, 517, 1035–1048. [Google Scholar] [CrossRef]
- Beven, K. Rainfall-Runoff Modelling: The Primer, the Seconded; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2012. [Google Scholar]
- Saghafian, B.; Julien, P.Y.; Rajaie, H. Runoff hydrograph simulation based on time variable isochrone technique. J. Hydrol. 2002, 261, 193–203. [Google Scholar] [CrossRef]
- Wen, Z.; Liang, X.; Yang, S. A new multiscale routing framework and its evaluation for land surface modeling applications. Water Resour. Res. 2012, 48. [Google Scholar] [CrossRef]
- Todini, E. A Mass Conservative and Water Storage Consistent Variable Parameter Muskingum-Cunge Approach. Hydrol. Earth Syst. Sci. 2007, 4, 1645–1659. [Google Scholar] [CrossRef] [Green Version]
- Liu, Z.; Todini, E. Towards a comprehensive physically-based rainfall-runoff model. Hydrol. Earth Syst. Sci. 2002, 6, 859–881. [Google Scholar] [CrossRef]
- Rodríguez-Iturbe, I.; Valdés, J.B. The geomorphologic structure of hydrologic response. Water Resour. Res. 1979, 15, 1409–1420. [Google Scholar] [CrossRef] [Green Version]
- Rui, X. Study of determining geomorphologic unit hydrograph by means of probability density functions of path length and slope. Adv. Water Sci. 2003, 14, 602–606. [Google Scholar]
- Xiaofang, R.; Mei, Y.; Fanggui, L.; Xinglong, G. Calculation of watershed flow concentration based on the grid drop concept. Water Sci. Eng. 2008, 1, 1–9. [Google Scholar] [CrossRef] [Green Version]
- Gupta, V.K.; Waymire, E.; Wang, C.T. A representation of an instantaneous unit hydrograph from geomorphology. Water Resour. Res. 1980, 16, 855–862. [Google Scholar] [CrossRef]
- O’Callaghan, J.; Mark, D.M. The extraction of drainage networks from digital elevation data. Comput. Vision Graph. Image Process. 1984, 27, 247. [Google Scholar] [CrossRef]
- Graham, S.T.; Famiglietti, J.S.; Maidment, D.R. Five-minute, 1/2°, and 1° data sets of continental watersheds and river networks for use in regional and global hydrologic and climate system modeling studies. Water Resour. Res. 1999, 35, 583–587. [Google Scholar] [CrossRef] [Green Version]
- Oki, T.; Sud, Y.C. Design of Total Runoff Integrating Pathways (TRIP)—A Global River Channel Network. Earth Interact. 1998, 2, 1–37. [Google Scholar] [CrossRef]
- Wang, M.H.; Hjelmfelt, A.T.; Garbrecht, J. DEM aggregation for watershed modeling. Jawra J. American Water Resource. Assoc. 2010, 36, 579–584. [Google Scholar] [CrossRef]
- Lohmann, D.; Nolte-Holube, R.; Raschke, E. A Large-Scale Horizontal Routing Model to be Coupled to Land Surface Parametrization Schemes. Tellus Ser. A 1996, 48, 708–721. [Google Scholar] [CrossRef]
- Reggiani, P.; Todini, E.; Meißner, D. A conservative flow routing formulation: Déjà vu and the variable-parameter Muskingum method revisited. J. Hydrol. 2014, 519, 1506–1515. [Google Scholar] [CrossRef]
- Gochis, D.J.; Barlage, M.; Dugger, A.; FitzGerald, K.; Karsten, L.; McAllister, M.; McCreight, J.; Mills, J.; RafieeiNasab, A.; Read, L.; et al. The WRF-Hydro Modeling System Technical Description (Version 5.0); Center for Atmospheric Research (NCAR): Boulder, CO, USA, 2018; Available online: http://ral.ucar.edu/sites/default/files/public/WRFHydroV5TechnicalDescription.pdf (accessed on 13 April 2018).
- MWR. Standard for Hydrological Information and Hydrological Forecasting (GB/T 2482-2008); Ministry of Water Resources of the People’s Republic of China, Standards Press of China, Beijing: Beijing, China, 2008; p. 16.
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models part I—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
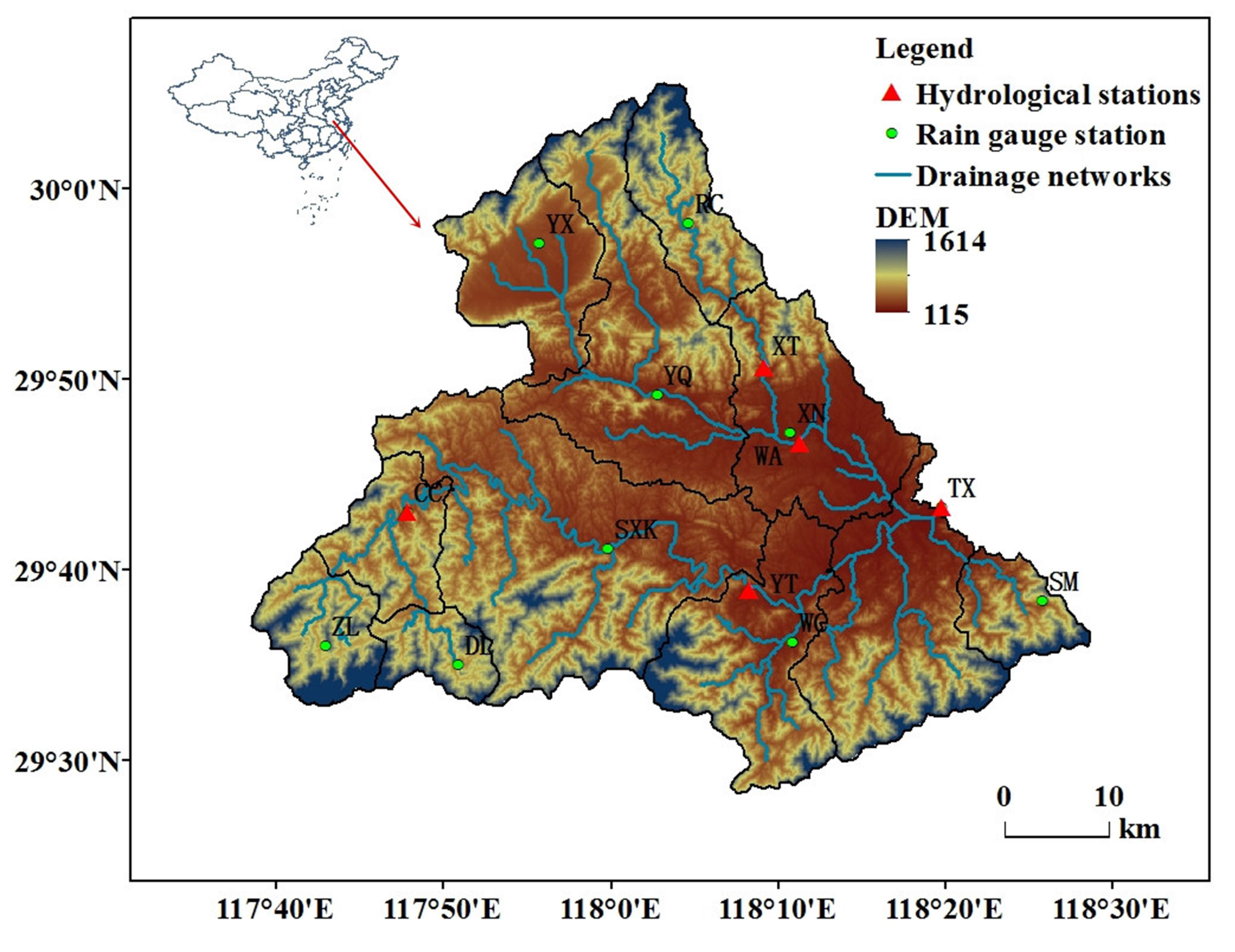
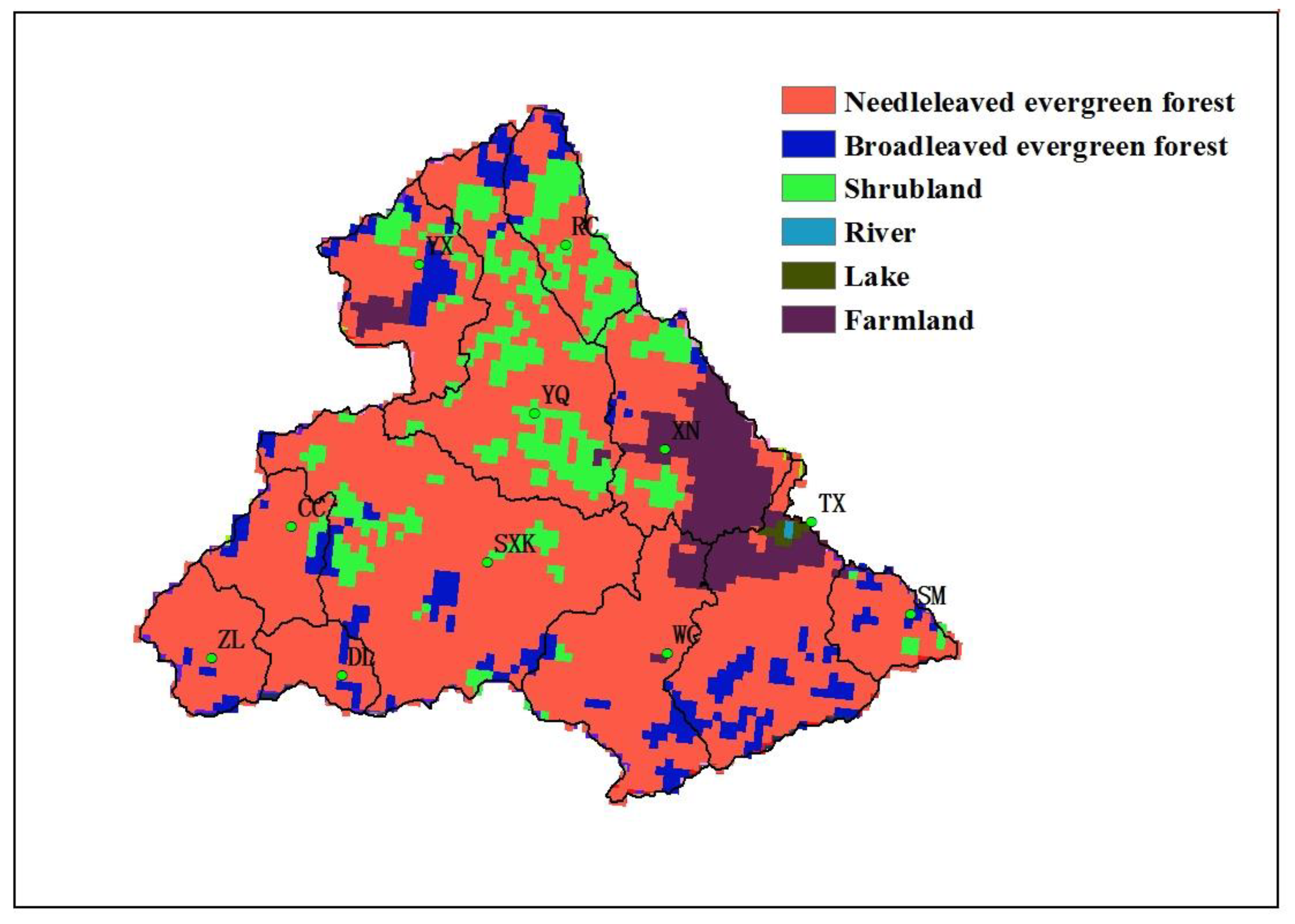
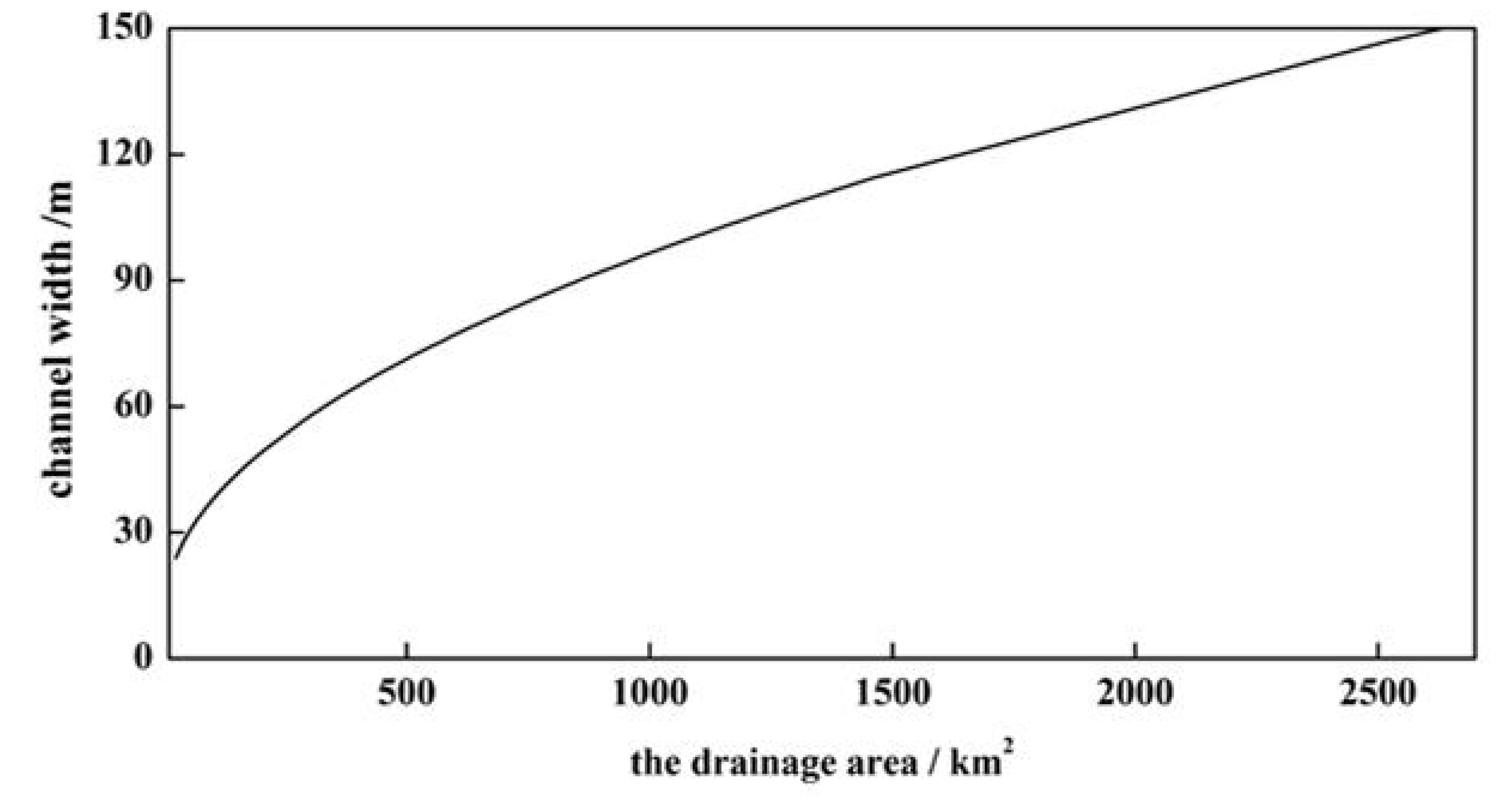

| Station Name | Period for Flood Events | Number of Flood Events |
|---|---|---|
| Tunxi (TX) | 1982–2003 | 33 |
| Yuetan (YT) | 1982–2003 | 33 |
| Wanan (WA) | 1988–2003 | 22 |
| Chengcun (CC) | 1986–1999 | 25 |
| Xinting (XT) | 1986–2000 | 27 |
| Parameter | Description | Parameter Values |
|---|---|---|
| Ke | Ratio of potential evapotranspiration to pan evaporation | 1.08 |
| Wum | Tension water capacity of upper layer (mm) | 20 |
| Wlm | Tension water capacity of lower layer (mm) | 73 |
| C | Evapotranspiration coefficient of deeper layer | 0.08 |
| B | Exponent of distribution of tension water capacity | 0.532 |
| Wm | Tension water capacity (mm) | 120 |
| Im | Ratio of impervious area to the total area of the catchment | 0.0014 |
| Sm | Free water capacity (mm) | 20 |
| Ex | Exponent of distribution of free water capacity (mm) | 1.2 |
| Kg | Outflow coefficient of free water storage to groundwater | 0.35 |
| Ki | Outflow coefficient of free water storage to interflow | 0.35 |
| Cg | Recession constant of groundwater storage | 0.998 |
| Ci | Recession constant of interflow storage | 0.87 |
| CS | Recession constant in the lag-and-route method | 0.9 |
| Lag | Lag time (h) | 2 |
| Muskingum time constant for each sub-reach (h) | 1 | |
| Muskingum weighting factor for each sub-reach | 0.35 |
| Sub Catchments | Overland Roughness | Overland Slope | Channel Roughness |
|---|---|---|---|
| Wucheng (WC) | 0.1275 | 0.015984 | 0.025 |
| Shimen (SM) | 0.1275 | 0.031171 | 0.025 |
| Zuolong (ZL) | 0.1275 | 0.035772 | 0.025 |
| Dalian (DL) | 0.1275 | 0.033066 | 0.025 |
| Tunxi (TX) | 0.055 | 0.023073 | 0.018 |
| Shangxikou (SXK) | 0.2 | 0.023417 | 0.025 |
| Rucun (RC) | 0.1275 | 0.028201 | 0.018 |
| Yixian (YX) | 0.1275 | 0.010486 | 0.018 |
| Yanqian (YQ) | 0.1275 | 0.024971 | 0.018 |
| Xiuning (XN) | 0.03 | 0.079677 | 0.018 |
| Chengcun (CC) | 0.1275 | 0.125944 | 0.025 |
| Station Name | Rain Gauges | Drainage Area (Km2) | Rain Gauges Network Intensity (/Km2) | Qualified Ratio (%) | Average | ||
|---|---|---|---|---|---|---|---|
| RRE | RPE | PTE | NSE | ||||
| Tunxi (TX) | 11 | 2692 | 245 | 100 | 81.3 | 81.3 | 0.92 |
| Yuetan (YT) | 4 | 952 | 238 | 87.9 | 81.8 | 66.7 | 0.88 |
| Wanan (WA) | 4 | 865 | 216 | 63.6 | 72.7 | 86.4 | 0.85 |
| Chengcun (CC) | 3 | 290 | 97 | 88.0 | 88.0 | 96.0 | 0.86 |
| Xinting (XT) | 1 | 184 | 184 | 92.6 | 65.0 | 88.9 | 0.84 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zang, S.; Li, Z.; Yao, C.; Zhang, K.; Sun, M.; Kong, X. A New Runoff Routing Scheme for Xin’anjiang Model and Its Routing Parameters Estimation Based on Geographical Information. Water 2020, 12, 3429. https://doi.org/10.3390/w12123429
Zang S, Li Z, Yao C, Zhang K, Sun M, Kong X. A New Runoff Routing Scheme for Xin’anjiang Model and Its Routing Parameters Estimation Based on Geographical Information. Water. 2020; 12(12):3429. https://doi.org/10.3390/w12123429
Chicago/Turabian StyleZang, Shuaihong, Zhijia Li, Cheng Yao, Ke Zhang, Mingkun Sun, and Xiangyi Kong. 2020. "A New Runoff Routing Scheme for Xin’anjiang Model and Its Routing Parameters Estimation Based on Geographical Information" Water 12, no. 12: 3429. https://doi.org/10.3390/w12123429
APA StyleZang, S., Li, Z., Yao, C., Zhang, K., Sun, M., & Kong, X. (2020). A New Runoff Routing Scheme for Xin’anjiang Model and Its Routing Parameters Estimation Based on Geographical Information. Water, 12(12), 3429. https://doi.org/10.3390/w12123429







