A Model of Ice Wedge Polygon Drainage in Changing Arctic Terrain
Abstract
:1. Introduction
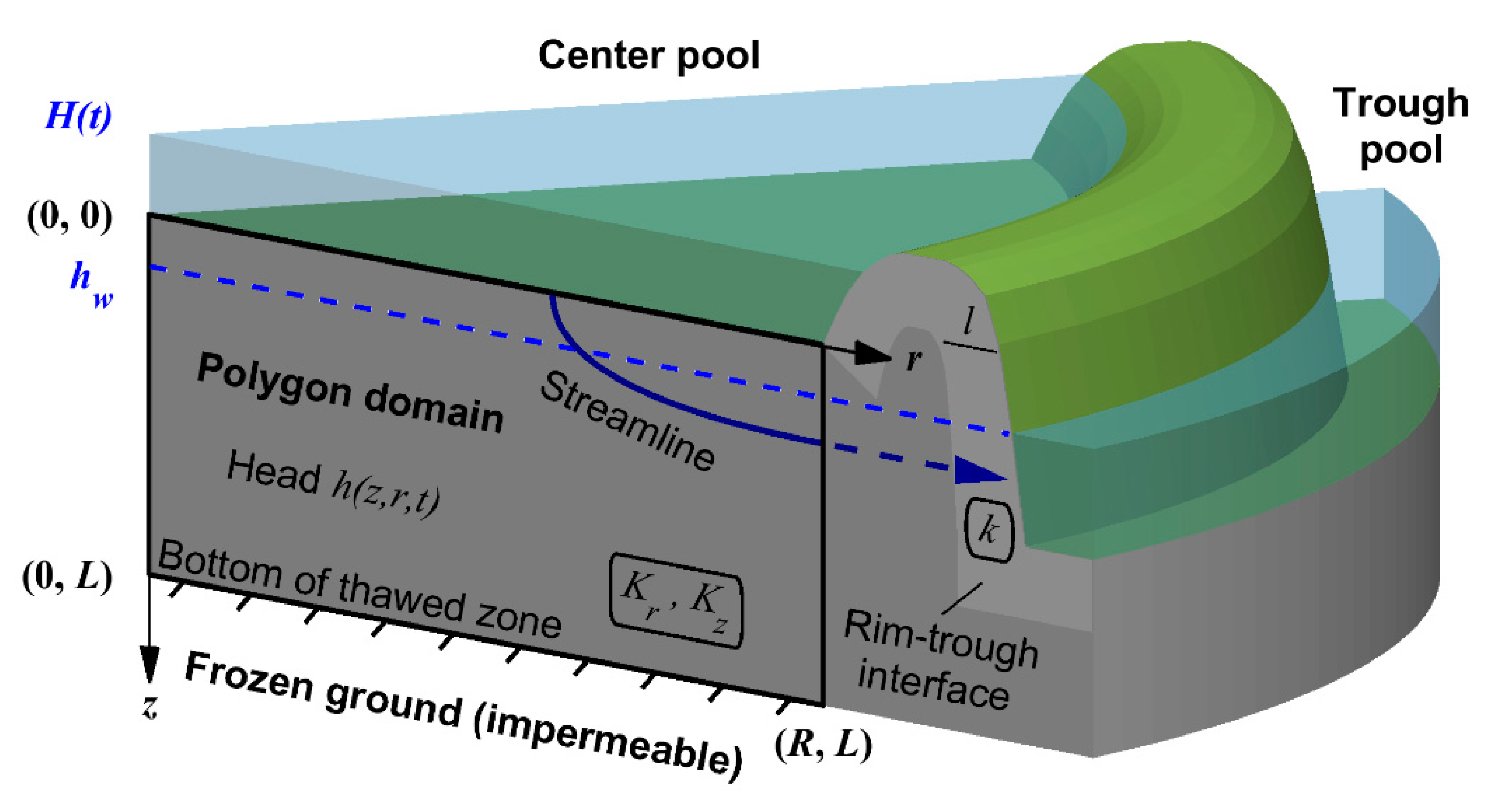
2. Conceptual Model
3. Methods
3.1. Problem Statement For Constant Thaw Depth
3.2. Reduction to Dimensionless Steady-State Problem
3.3. Solutions
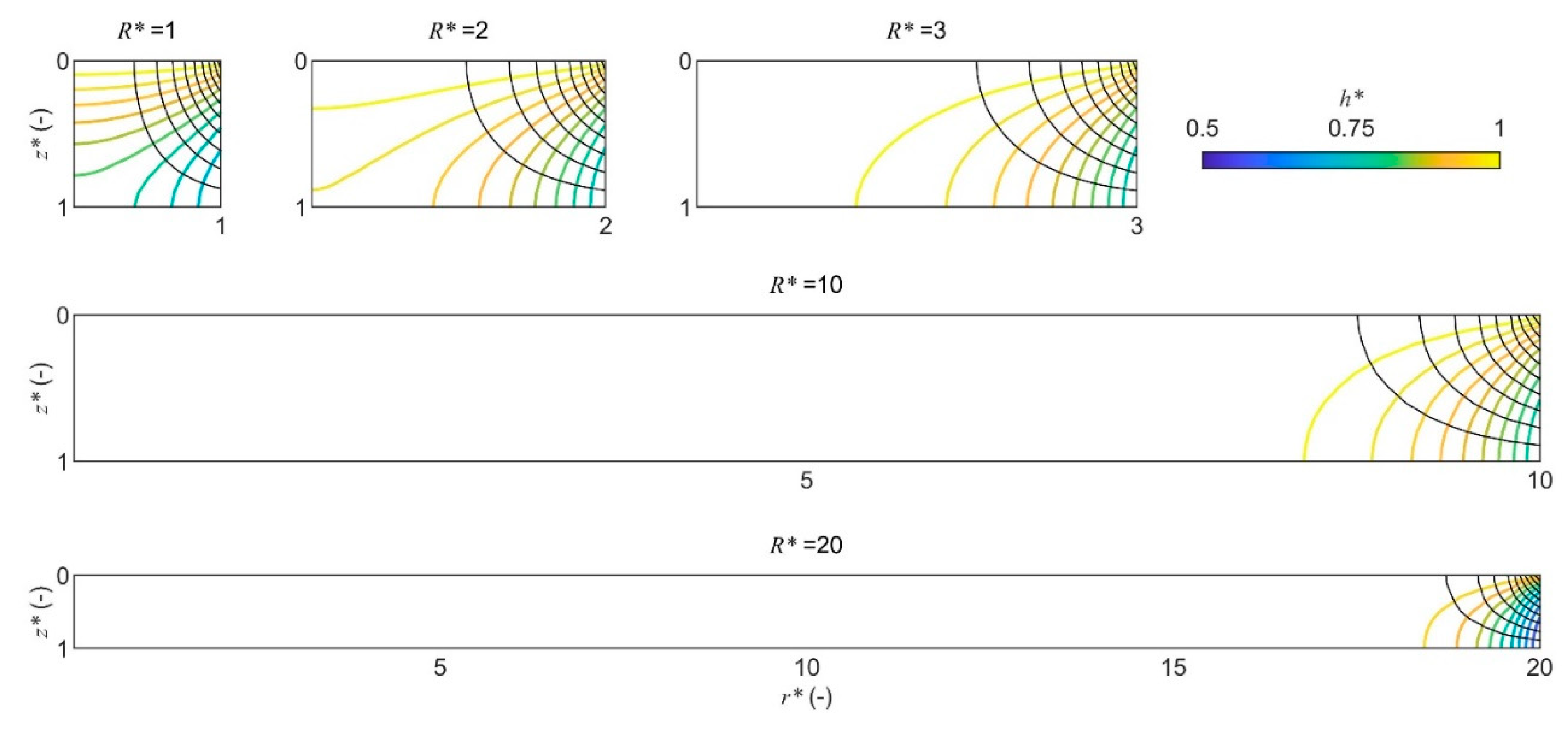
3.3.1. Head h*(r*, z*)
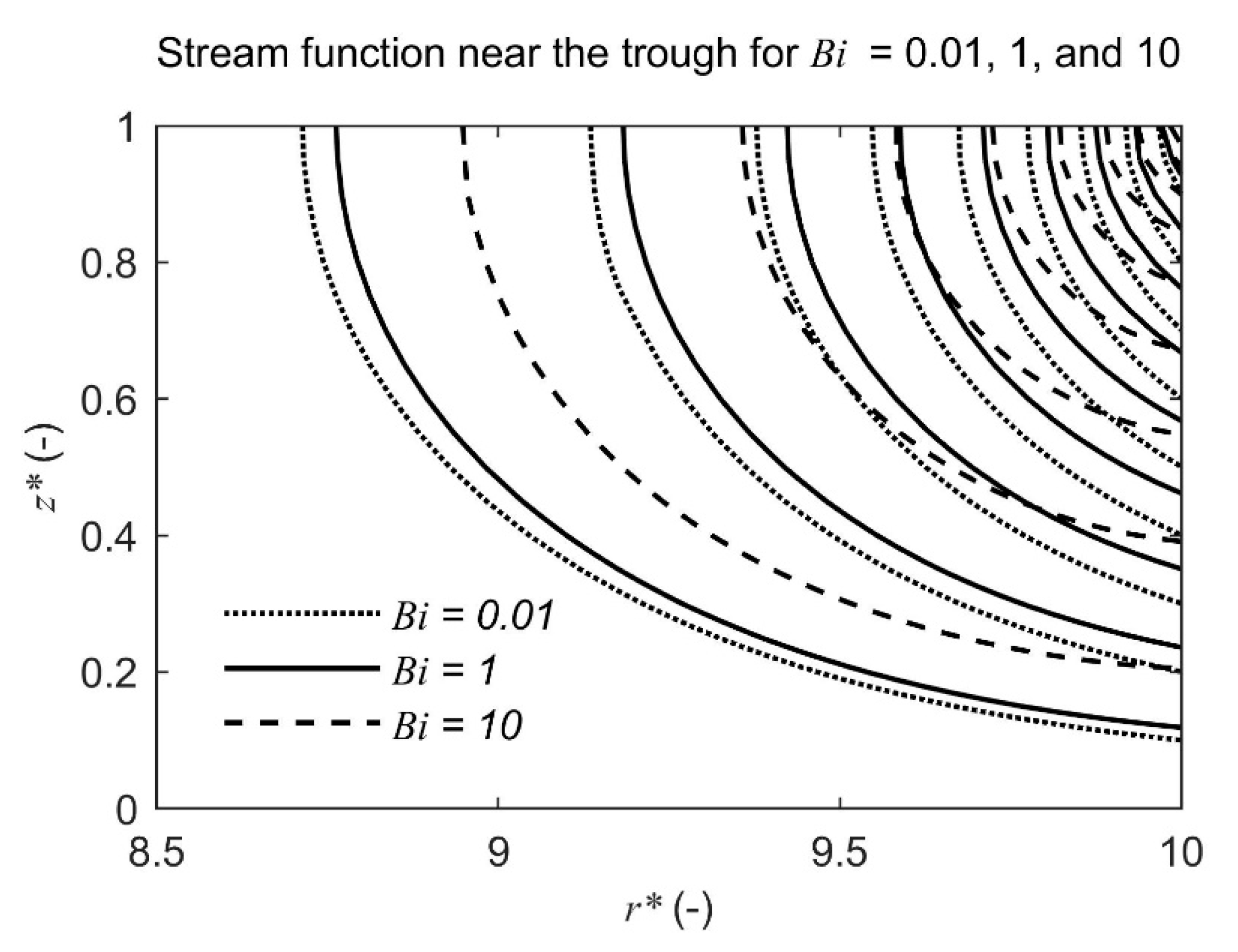
3.3.2. Fluxes and Stokes Stream Function ψ*(r*, z*)
3.3.3. Center Pool Level H(t): Constant Thaw Depth
3.3.4. Center Pool Level H(t): Dynamic Thaw Depth, Analytical Approach
3.3.5. Center Pool Level H(t): Dynamic Thaw Depth, Numerical Approach
3.4. Computation of Solutions
3.5. Model Parameters for Demonstration
3.5.1. Constant Thaw-Layer Thickness
3.5.2. Dynamic Thaw-Layer Thickness
4. Results
4.1. Flow Nets: Head and Flux Distributions
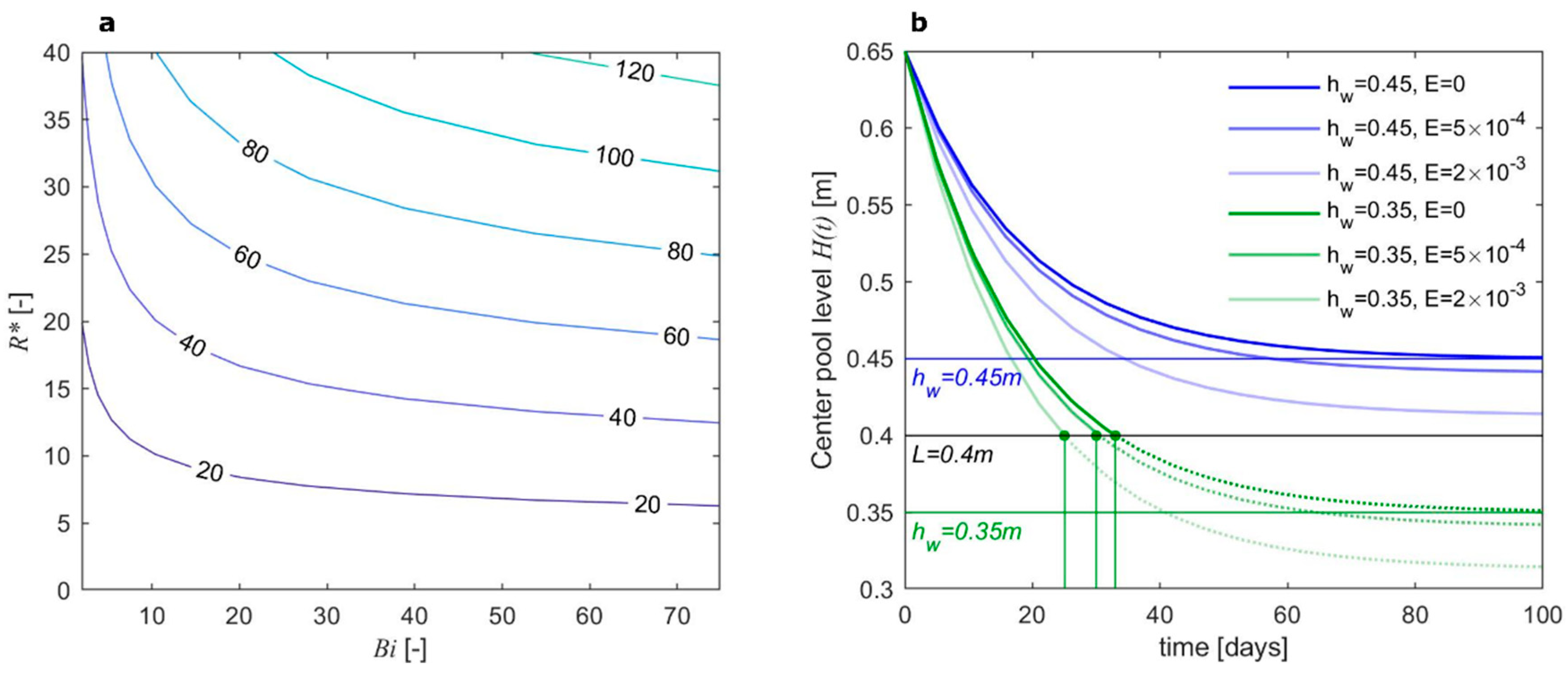
4.2. Water Level Dynamics and the Role of Evapotranspiration
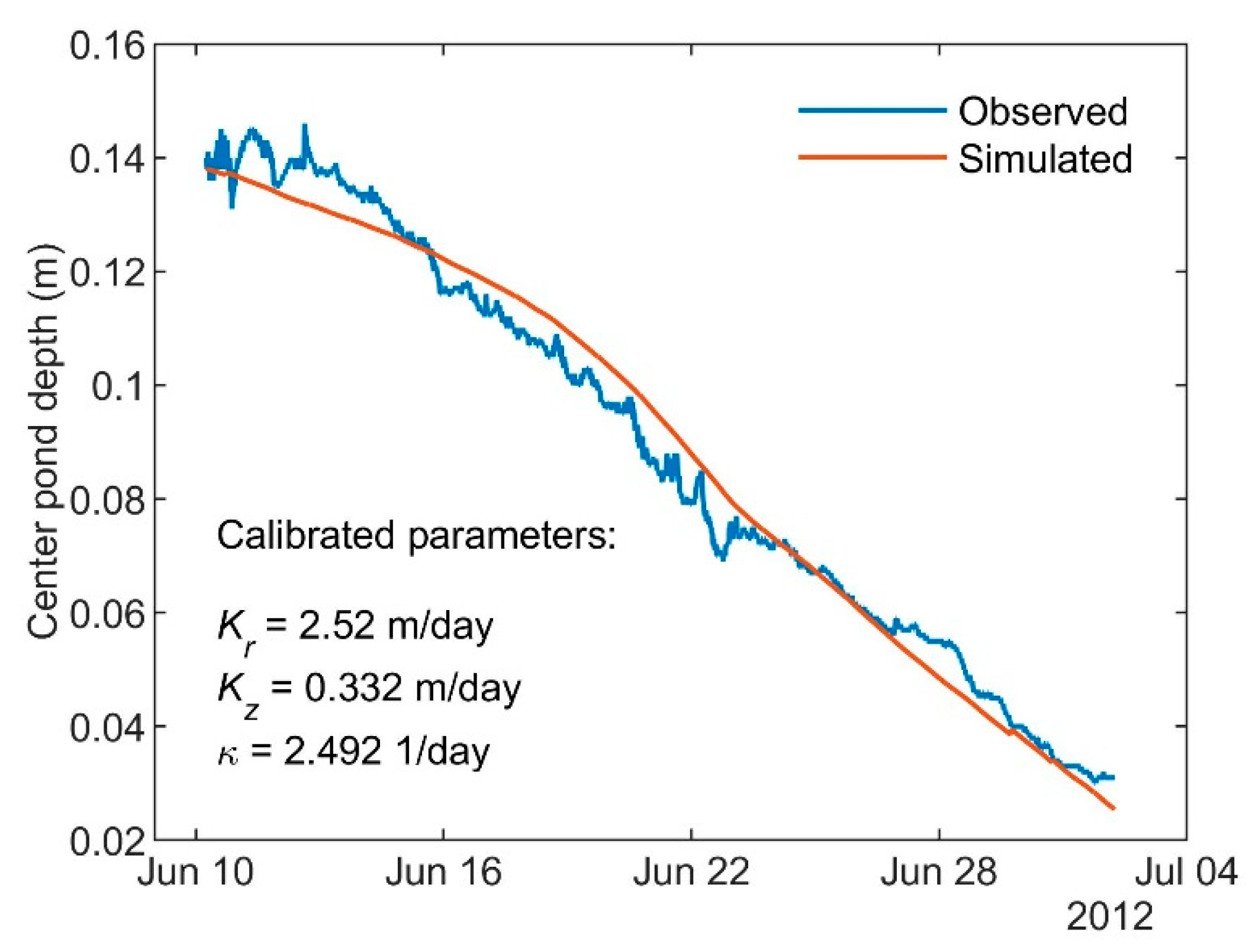
4.3. Calibration of Center Pond Drainage Scenario with Dynamic Thaw-Layer Thickness at Utqiagvik
5. Conclusions
- Polygons are flushed most intensively at the edges for practically all existing physical and geometric parameters. The streamline patterns in this zone change little when the aspect ratio (radius-to-thickness of active layer) exceeds a value of three.
- Anisotropy in hydraulic conductivity (horizontal-to-vertical hydraulic conductivity ratio) has a secondary influence on the intensity of flushing. Increases of anisotropy values counteract the effects of increased geometrical aspect ratio increases and vice versa (as discussed in Appendix B).
- Hydraulic resistance of the drainage interface between the polygon and trough also has some limited, but not overriding influence within the typical range of Arctic tundra conditions.
- Drainage time scales are consistent with observed duration of the center pool drainage within low-centered polygons. The parameter can be used to characterize drainage times from an inundated polygon center.
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Derivation of the Head Distribution and Stokes Stream Function
Appendix B. Role of Hydraulic Resistance of the Polygon-trough Interface and Anisotropy
References
- Jorgenson, M.T.; Shur, Y.L.; Pullman, E.R. Abrupt increase in permafrost degradation in Arctic Alaska. Geophys. Res. Lett. 2006, 33, L024960. [Google Scholar] [CrossRef]
- Liljedahl, A.; Boike, J.; Daanen, R.; Fedorov, A.N.; Frost, G.V.; Grosse, G.; Hinzman, L.D.; Iijma, Y.; Jorgenson, J.C.; Matveyeva, N.; et al. Pan-Arctic ice-wedge degradation in warming permafrost and its influence on tundra hydrology. Nat. Geosci. 2016, 9, 312–318. [Google Scholar] [CrossRef]
- Farquharson, L.M.; Romanovsky, V.E.; Cable, W.L.; Walker, D.A.; Kokelj, S.V.; Nicolsky, D. Climate change drives widespread and rapid thermokarst development in very cold permafrost in the Canadian High Arctic. Geophys. Res. Lett. 2019, 46, 6681–6689. [Google Scholar] [CrossRef] [Green Version]
- Helbig, M.; Boike, J.; Langer, M.; Schreiber, P.; Runkle, B.R.; Kutzbach, L. Spatial and seasonal variability of polygonal tundra water balance: Lena River Delta, northern Siberia (Russia). Hydrogeol. J. 2013, 21, 133–147. [Google Scholar] [CrossRef]
- Liljedahl, A.K.; Wilson, C.J. Ground Water Levels for NGEE Areas A, B, C, and D, Barrow, Alaska, 2012–2014; Next Generation Ecosystems Arctic Data Collection; Oak Ridge National Laboratory, U.S. Department of Energy: Oak Ridge, TN, USA, 2016. [Google Scholar] [CrossRef]
- Koch, J.C.; Gurney, K.; Wipfli, M.S. Morphology-dependent water budgets and nutrient fluxes in Arctic thaw ponds. Permafr. Periglac. Process. 2014, 25, 79–93. [Google Scholar] [CrossRef]
- Koch, J.C.; Jorgenson, M.T.; Wickland, K.P.; Kanevskiy, M.; Striegl, R. Ice wedge degradation and stabilization impact water budgets and nutrient cycling in Arctic trough ponds. J. Geophys. Res. Biogeosci. 2018, 123, 2604–2616. [Google Scholar] [CrossRef]
- Wales, N.A.; Gomez-Velez, J.D.; Newman, B.D.; Wilson, C.J.; Dafflon, B.; Kneafsey, T.J.; Wullschleger, S.D. Understanding the relative importance of vertical and horizontal flow in ice-wedge polygons. Hydrol. Earth Syst. Sci. 2020, 24, 1109–1129. [Google Scholar] [CrossRef]
- Cory, R.M.; Ward, C.P.; Crump, B.C.; Kling, G.W. Sunlight controls water column processing of carbon in arctic fresh waters. Science 2014, 345, 925–928. [Google Scholar] [CrossRef] [PubMed]
- Jan, A.; Coon, E.T.; Painter, S.L.; Garimella, R.; Moulton, J.D. An intermediate-scale model for thermal hydrology in low-relief permafrost-affected landscapes. Comput. Geosci. 2018, 22, 163–177. [Google Scholar] [CrossRef]
- Aas, K.S.; Martin, L.; Nitzbon, J.; Langer, M.; Boike, J.; Lee, H.; Berntsen, T.K.; Westermann, S. Thaw processes in ice-rich permafrost landscapes represented with laterally coupled tiles in a land surface model. Cryosphere 2019, 13, 591–609. [Google Scholar] [CrossRef] [Green Version]
- Nitzbon, J.; Langer, M.; Westermann, S.; Martin, L.; Aas, K.S.; Boike, J. Pathways of ice-wedge degradation in polygonal tundra under different hydrological conditions. Cryosphere 2019, 13, 1089–1123. [Google Scholar] [CrossRef] [Green Version]
- Nitzbon, J.; Westermann, S.; Langer, M.; Martin, L.C.; Strauss, J.; Laboor, S.; Boike, J. Fast response of cold ice-rich permafrost in northeast Siberia to a warming climate. Nat. Commun. 2020, 11, 2201. [Google Scholar] [CrossRef]
- Dobinksi, W. Permafrost active layer. Earth Sci. Rev. 2020, 208, 103301. [Google Scholar]
- Abolt, C.J.; Young, M.H. High-resolution mapping of spatial heterogeneity in ice wedge polygon geomorphology near Prudhoe Bay, Alaska. Sci. Data 2020, 7, 87. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Quinton, W.L.; Hayashi, M.; Carey, S.K. Peat hydraulic conductivity in cold regions and its relation to pore size and geometry. Hydrol. Process. 2008, 22, 2829–2837. [Google Scholar] [CrossRef]
- Abolt, C.J.; Young, M.H.; Caldwell, T.G. Numerical modelling of ice-wedge polygon geomorphic transition. Permafr. Periglac. Process. 2017, 28, 347–355. [Google Scholar] [CrossRef]
- Beckwith, C.W.; Baird, A.; Heathwaite, A.L. Anisotropy and depth-related heterogeneity of hydraulic conductivity in a bog peat. I: Laboratory measurements. Hydrol. Process. 2003, 17, 89–101. [Google Scholar] [CrossRef]
- Chason, D.B.; Siegel, D.I. Hydraulic conductivity and related physical properties of peat, Lost River Peatland, Northern Minnesota. Soil Sci. 1986, 142, 91–99. [Google Scholar] [CrossRef]
- Ebel, B.A.; Koch, J.C.; Walvoord, M.A. Soil physical, hydraulic, and thermal properties in interior Alaska, USA: Implications for hydrologic response to thawing permafrost conditions. Water Resour. Res. 2019, 55, 4427–4447. [Google Scholar] [CrossRef]
- Rodell, M.; Houser, P.R.; Jambor, U.; Gottschalck, J.; Mitchell, K.; Meng, C.-J.; Arsenault, K.; Cosgrove, B.; Radakovich, J.; Entin, M.B.J.K.; et al. The Global Land Data Assimilation System. Bull. Am. Meteorol. Soc. 2004, 85, 381–394. [Google Scholar] [CrossRef] [Green Version]
- Jafarov, E.E.; Marchenko, S.S.; Romanovsky, V.E. Numerical modeling of permafrost dynamics in Alaska using a high spatial resolution dataset. Cryosphere 2012, 6, 613–624. [Google Scholar] [CrossRef] [Green Version]
- Mackowski, D.W. Conduction Heat Transfer, Notes for MECH 7210. Mechanical Engineering Dept., Auburn University, 2020. Available online: http://www.eng.auburn.edu/~dmckwski/mech7210/condbook.pdf (accessed on 24 September 2020).
- Abramowitz, M.; Stegun, I. Handbook of Mathematical Functions: With Formulas, Graphs, and Mathematical Tables; Dover Publications: Mineola, NY, USA, 1965. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zlotnik, V.A.; Harp, D.R.; Jafarov, E.E.; Abolt, C.J. A Model of Ice Wedge Polygon Drainage in Changing Arctic Terrain. Water 2020, 12, 3376. https://doi.org/10.3390/w12123376
Zlotnik VA, Harp DR, Jafarov EE, Abolt CJ. A Model of Ice Wedge Polygon Drainage in Changing Arctic Terrain. Water. 2020; 12(12):3376. https://doi.org/10.3390/w12123376
Chicago/Turabian StyleZlotnik, Vitaly A., Dylan R. Harp, Elchin E. Jafarov, and Charles J. Abolt. 2020. "A Model of Ice Wedge Polygon Drainage in Changing Arctic Terrain" Water 12, no. 12: 3376. https://doi.org/10.3390/w12123376
APA StyleZlotnik, V. A., Harp, D. R., Jafarov, E. E., & Abolt, C. J. (2020). A Model of Ice Wedge Polygon Drainage in Changing Arctic Terrain. Water, 12(12), 3376. https://doi.org/10.3390/w12123376





