A Model of Ice Wedge Polygon Drainage in Changing Arctic Terrain

Abstract

As ice wedge degradation and the inundation of polygonal troughs become increasingly common processes across the Arctic, lateral export of water from polygonal soils may represent an important mechanism for the mobilization of dissolved organic carbon and other solutes. However, drainage from ice wedge polygons is poorly understood. We constructed a model which uses cross-sectional flow nets to define flow paths of meltwater through the active layer of an inundated low-centered polygon towards the trough. The model includes the effects of evaporation and simulates the depletion of ponded water in the polygon center during the thaw season. In most simulations, we discovered a strong hydrodynamic edge effect: only a small fraction of the polygon volume near the rim area is flushed by the drainage at relatively high velocities, suggesting that nearly all advective transport of solutes, heat, and soil particles is confined to this zone. Estimates of characteristic drainage times from the polygon center are consistent with published field observations.

1. Introduction

Polygonal tundra landscapes have experienced rapid change in recent decades. Across the Arctic, an abrupt acceleration in ice wedge degradation has been observed since the second half of the twentieth century [1,2,3]. This melting results in a deepening of troughs at polygon boundaries, which often become inundated. The formation and expansion of flooded troughs, or thermokarst pools (hereafter referred to as trough pools, for short), has profound influence on tundra hydrology and ecological processes. For example, in polygonal terrain with poorly developed (undegraded) troughs, hydrologic simulations suggest that most fluxes of water into and out of the active layer are vertical, either in the form of precipitation or evapotranspiration [2]. After troughs deepen, however, observations indicate that water may drain laterally from the active layer of the polygon interior throughout the summer [4,5,6,7,8]. A common result of this drainage is the flushing of nutrients and other solutes from polygonal soils into trough pools, where they may fertilize plant growth [7]. This flushing may be especially effective at mobilizing dissolved organic carbon, because exposure to sunlight following the discharge of water from tundra soils commonly accelerates oxidation [9].

Given the importance of this transition to tundra hydrology and carbon cycling, a number of studies have begun to incorporate ice wedge degradation into land surface models [10,11,12,13]. However, to our knowledge, very little work offers insights into the dynamics of active layer drainage at the scale of individual polygons (~10 m). Here, we present a three-dimensional axisymmetric transient model of the flow above and inside an inundated low-centered polygon surrounded by flooded troughs, resulting in a simple analytical solution. Within our model, all subsurface flow occurs within a seasonally thawed layer which, depending on the time within the thaw season, is equal to or less thick than the active layer, here defined as the portion of the subsurface which experiences phase change between ice and liquid water [14]. Typically, the thickness of this thawed layer follows a roughly asymptotic trajectory, increasing quickly at the start of the summer, then gradually stabilizing near the active layer thickness late in the season. Accordingly, we studied an idealized (cylindrical) low-centered polygon, with a seasonally thawed depth L, and a radial distance R from the center point to the interior wall of the rims; the depth L can either be treated as constant for simulations of short time duration, or changed dynamically, using numerical or analytical approaches. Our model includes the effects of the polygon geometry, anisotropy, and hydrologic interconnection between the polygon center and the trough, with consideration of evaporation.

Parameterized by published field data from polygonal soils, the model indicates that water movement in the active layer occurs predominantly at the periphery of the polygon center, while the interior conducts very little water. Hence, advective flushing of mass, solutes, and energy is confined primarily to a small region at the edge of the polygon.

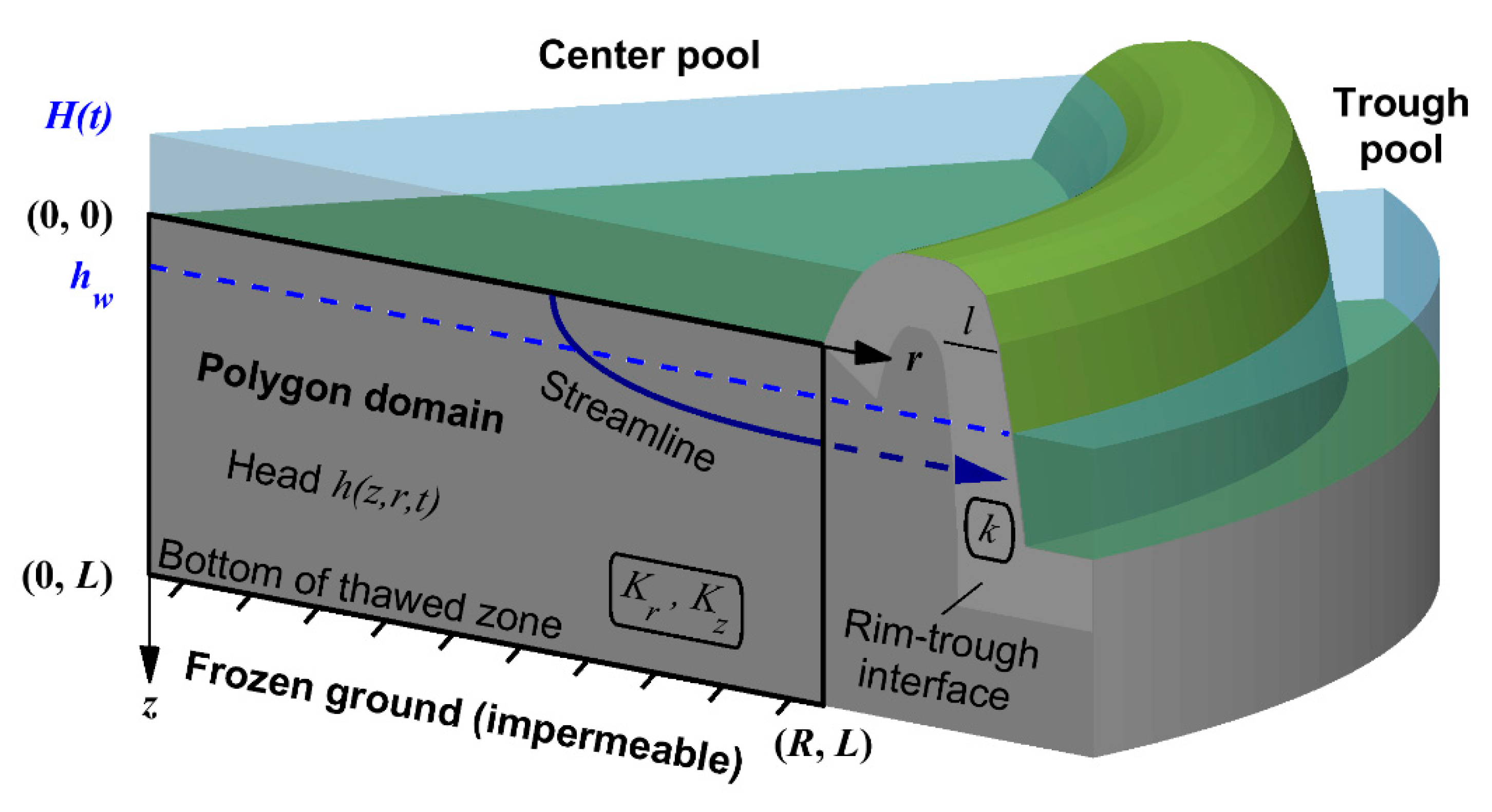
2. Conceptual Model

We consider a three-dimensional axisymmetric transient model of the flow in an inundated, cylindrical, low-centered polygon in which a thermokarst pool had begun to develop, characterized by a thawed layer of depth L, and a distance R from the center point of the polygon to the start of the rim (Figure 1). Pools of water exist both in the center and in the trough.

In cylindrical coordinates $\left(r,z\right)$, the vertical $z$-axis is directed downward from the polygon surface while r is the radial coordinate, which is zero at the polygon center. The datum for the hydraulic head is located at the base of the thawed layer. The pool has a uniform water level, $H\left(t\right)$, which reduces over time t, and is constrained from spilling by a rim separating the center from the trough (Figure 1). The water level in the trough with respect to the datum, h_w, is treated as constant.

Drainage of water through the active layer of the polygon center toward the trough pool is controlled by hydraulic resistance, which is dependent on horizontal and vertical hydraulic conductivity ($K_r$ and $K_z$, respectively), polygon size, and the hydraulic exchange rate between the polygon and trough. The latter is defined by hydraulic resistance of the polygon–trough interface. This resistance is a function of interface thickness l and hydraulic conductivity k. With finer sediments on the interface, one can assume $k<K_r$ (by a factor of about 2) [7]. In general, the thickness l is less than the width of the rim, which may be in the order of several meters [15]. Thus, the flux across the polygon boundary ($r = R$) at each elevation is defined by the difference between the head in the trough (h_w) and the head in the polygon subsurface across from the trough at this elevation, $h\left(R,z,t\right)$. In general, the flux direction may vary.

The value $d = H\left(0\right)-h_w$ represents the initial head difference that drives the drainage. The drainage completion time, $t_{drain}$, is defined by the equation $H\left(t_{drain}\right)= L$.

Hydraulic head inside of the active layer, $h\left(r,z,t\right)$_, responds rapidly to the center pool level at the surface (H(t)) due to the small vertical scale of the active layer. The polygon thickness L(t) may vary from zero to a maximum value of D and can be scaled as follows: L(t) = D$·$f(t), where f(t) is a dimensionless function that varies from 0 to 1 by the end of the season. The thickness of the thawed layer can also be treated as constant for qualitative analyses or simulations of a short time duration.

3. Methods

3.1. Problem Statement For Constant Thaw Depth

In this case, L = D, a constant. Due to the small vertical scale of the polygon, soil compressibility effects on the flow of water through the active layer are neglected in the following flow equation:

$$\frac{K_r}{r}\frac{\partial }{\partial r}\left(r\frac{\partial h}{\partial r}\right) + K_z\frac{{\partial }^{2}h}{\partial z^2} = 0,0 < r < R,0 < z < L$$

(1)

The boundary condition at the z-axis indicates axial symmetry as follows:

$$\frac{\partial h\left(0,z,t\right)}{\partial r} = 0,\hspace{1em}0 < z < L$$

(2)

The boundary condition at the surface is defined by the pool level $H\left(t\right)$:

$$h\left(r,0,t\right) = H\left(t\right),0 < r < R$$

(3)

Exchange of water across the polygon interior/trough interface (i.e., under the rim) can be described using a Robin boundary condition that relates flux to the difference in head at each elevation between the radial boundary and the trough, through the coefficient $\kappa$:

$$-K_r\frac{\partial h\left(R,z,t\right)}{\partial r} = \kappa \left[h\left(R,z,t\right)-h_w\right],\kappa \approx k/l,0<z<L$$

(4)

where $\kappa$ represents the conductance of the interface and rim. When the coefficient $\kappa =0$, the boundary is impermeable to drainage, while $\kappa \to \infty$ when water drains into the trough without added resistance, resulting in the boundary condition $h\left(R,z,t\right)=h_w$ (Figure 1).

The base of the thawed zone at z = L is impermeable due to the frozen substrate:

$$\frac{\partial h\left(r,L,t\right)}{\partial z} = 0,0<r<R$$

(5)

The variable level of water in the center pool is related to the drainage flux across the ground surface. Therefore, an additional equation of the mass balance of the water in the center pool is used, considering evaporative losses E:

$$\pi R^2\frac{dH}{dt} = -2\pi K_z{{\displaystyle \int }}_0^R\frac{\partial h\left(r,0,t\right)}{\partial z}r·dr-\pi R^{2}E,H\left(0\right) = H_0$$

(6)

3.2. Reduction to Dimensionless Steady-State Problem

We introduce new dimensionless coordinates for space ($r^{*}$, $z^{*})$ and time ($t^{*}$) as follows:

$$r^{*} = \frac{r}{L}\sqrt{\frac{K_z}{K_r}},z^{*} = \frac{z}{L},t^{*} = \frac{t}{t_L }$$

(7)

and define functions for head $h^{*}\left(r^{*},z^{*}\right)$ in the thawed zone and center pool depth $H^{*}\left(t^{*}\right)$:

$$h^{*}\left(r^{*},z^{*}\right) = \frac{h\left(r,z,t\right)-h_w}{H\left(t\right)-h_w},H^{*}\left(t^{*}\right) = \frac{H\left(t\right)-h_w}{H_0-h_w}$$

(8)

with dimensionless parameters:

$$R^{*} = \frac{R}{L}\sqrt{\frac{K_z}{K_r}},B{i}^{*} = \frac{\kappa L}{\sqrt{K_r{K}_z}},Q^{*} = {{\displaystyle \int }}_0^{R^{*}}\frac{\partial h^{*}\left(r^{*},0\right)}{\partial z^{*}}{r}^{*}d{r}^{*},E^{*} = \frac{E·t_L}{H_0-h_w}$$

(9)

where the dimensional parameter $t_L$ below represents a characteristic drainage time of the model:

$$t_L = \frac{R^2}{2K_{r}L·Q^{*}}$$

(10)

These substitutions replace time-dependent $h\left(r,z,t\right)$ by the time-independent dimensionless function $h^{*}\left(r^{*},z^{*}\right)$. The time dependence is embedded in $H^{*}\left(t^{*}\right)$ by Equation (8):

$$h\left(r,z,t\right) = \left[H\left(t\right)-h_w\right]·h^{*}\left(r^{*},z^{*}\right)+h_w,H\left(t\right)= \left(H_0-h_w\right)·H^{*}\left(t^{*}\right)+h_w$$

(11)

This transformation relies on the assumption that head inside the thawed zone responds rapidly to changes in the level of the center pool. The resulting boundary value problem for $h^{*}\left(r^{*},z^{*}\right)$ is as follows:

$$\frac{1}{r^{*}}\frac{\partial }{\partial r^{*}}\left(r^{*}\frac{\partial h^{*}}{\partial r^{*}}\right) + \frac{{\partial }^2{h}^{*}}{{\partial z^{*}}^2} = 0,0 < r^{*} < R^{*},0 < z^{*} < 1$$

(12)

$$\frac{\partial h^{*}\left(0,z^{*}\right)}{\partial r^{*}}=0,0<z^{*}<1$$

(13)

$$h^{*}\left(r^{*},0\right) = 1,0 \le r^{*} \le R^{*}$$

(14)

$$-\frac{\partial h^{*}\left(R^{*},z^{*}\right)}{\partial r^{*}} = Bi·h^{*}\left(R^{*},z^{*}\right),0<z^{*}<1$$

(15)

$$\frac{\partial h^{*}\left(r^{*},L\right)}{\partial z^{*}} = 0,0<r^{*}<R^{*}$$

(16)

The dimensionless form of the water balance Equation (6) with initial conditions is:

$$\frac{d{H}^{*}}{d{t}^{*}} = -H^{*}-E^{*},H^{*}\left(0\right)= 1$$

(17)

This equation explains drainage for the duration 0 < t < t_drain.

3.3. Solutions

3.3.1. Head h*(r*, z*)

The solution of the boundary value problem (12)–(16) for $h^{*}\left(r^{*},z^{*}\right)$ can be found by the standard method of separation of variables. Details are presented in Appendix A.

$$h^{*}\left(r^{*},z^{*}\right)=2{\sum }_{n=1}^{\infty }\frac{J_0\left({\lambda }_n{r}^{*}\right)}{{\lambda }_n{R}^{*}\left[J_0\left({\lambda }_n{R}^{*}\right)\left(\frac{{\lambda }_n}{Bi}\right)+J_1\left({\lambda }_n{R}^{*}\right)\right]}\frac{cosh({\lambda }_n\left(1-z\right))}{cosh({\lambda }_n)}$$

(18)

where ${\lambda }_n,n=1,2,\dots$ are roots of the equation.

$${\lambda }_n{J}_1\left({\lambda }_n{R}^{*}\right)=Bi·J_0\left({\lambda }_n{R}^{*}\right),n=1,2,\dots$$

(19)

Values of $h^{*}\left(r^{*},z^{*}\right)$ range from 0 to 1.

3.3.2. Fluxes and Stokes Stream Function ψ*(r*, z*)

One variable of primary interest is the transient drainage rate, $Q\left(t\right)$, which can be calculated using the dimensional parameters and variables in Equations (7) and (8):

$$Q\left(t\right)=-2\pi K_z{\int }_0^R\frac{\partial h\left(r,0,t\right)}{\partial z}rdr=-2\pi K_{r}L\left[H\left(t\right)-h_w\right]·Q^{*}$$

(20)

where the time-independent constant $Q^{*}$ was defined in Equation (9). Using Equations (18) and (19), one obtains:

$$Q^{*}=Q^{*}\left(R^{*},Bi\right)=2{{\displaystyle \sum }}_{n=1}^{\infty }\frac{tanh({\lambda }_n)}{{\lambda }_n\left[{\left(\frac{{\lambda }_n}{Bi}\right)}^2+1\right]}$$

(21)

The axial symmetry of the flow permits effective analysis of the kinematic flow structure inside the polygon using the time-independent Stokes stream function, ${\psi }^{*}\left(r^{*},z^{*}\right)$. This function is related to $h^{*}\left(r^{*},z^{*}\right)$ by conditions of orthogonality of their gradients:

$$\frac{\partial {\psi }^{*}}{\partial r^{*}}\equiv -r^{*}\frac{\partial h^{*}}{\partial z^{*}},\frac{\partial {\psi }^{*}}{\partial z^{*}}\equiv r^{*}\frac{\partial h^{*}}{\partial r^{*}}$$

(22)

subject to the condition:

$${\psi }^{*}\left(0,0\right)=0$$

(23)

The latter equation indicates zero flux at the intersection of the polygon surface ($z=0$) and the symmetry axis. Level curves of the function ${\psi }^{*}\left(r^{*},z^{*}\right)$ are perpendicular to the equipotentials of head $h^{*}\left(r^{*},z^{*}\right)$ for isotropic hydraulic conductivity conditions, which satisfies the Laplace equation at any moment in time. The flow net of streamlines and equipotentials provides a tool for visualizing the flow structure inside the thawed zone.

Using Equations (7), (8), (22), and (23), one obtains:

$$\begin{array}{l}{\psi }^{*}\left(r^{*},z^{*}\right)={{\displaystyle \int }}_0^{r^{*}}\frac{\partial h^{*}\left(r^{*},z^{*}\right)}{\partial z^{*}}{r}^{*}d{r}^{*}\\ =2{{\displaystyle \sum }}_{n=1}^{\infty }\frac{J_1\left({\lambda }_n{r}^{*}\right)r^{*}}{{\lambda }_n{R}^{*}\left[J_0\left({\lambda }_n{R}^{*}\right)\left(\frac{{\lambda }_n}{Bi}\right)+J_1\left({\lambda }_n{R}^{*}\right)\right]}\frac{sinh({\lambda }_n\left(1-z\right))}{cosh({\lambda }_n)}\end{array}$$

(24)

The maximal value of ${\psi }^{*}\left(r^{*},z^{*}\right)$ is located at the point z = 0 and r = R. The normalized dimensionless Stokes stream function varies between 0 and 1:

$${\Psi }^{*}\left(r^{*},z^{*}\right)=\frac{{\psi }^{*}\left(r^{*},z^{*}\right)}{max\left\{{\psi }^{*}\left(r^{*},z^{*}\right)\right\}}=\frac{{\psi }^{*}\left(r^{*},z^{*}\right)}{{\psi }^{*}\left(R^{*},0\right)}$$

(25)

where

$${\psi }^{*}\left(R^{*},0\right)=Q^{*}$$

(26)

Importantly, the positions of streamlines based on the dimensional and dimensionless normalized stream functions do not depend on time, but the flux magnitude does change over time, as defined in Equation (20).

3.3.3. Center Pool Level H(t): Constant Thaw Depth

The solution of the initial value problem (17) for depth H*(t*) is:

$$\frac{H\left(t\right)-h_w}{H_0-h_w} = H^{*}\left(t^{*}\right) = e^{-t^{*}}-E^{*}\left(1-e^{-t^{*}}\right),t^{*}= \frac{t}{t_L}$$

(27)

At large time values, this equation shows that the stabilized water level in the pool, $H_{min},$ is equal to or below the water level in the trough if $h_w$ remains constant:

$$\underset{t\to \infty }{limH\left(t\right) = }{H}_{min} = h_w-E·t_L$$

(28)

In the case of non-zero evaporation from the center pool, the drainage may become reversed, i.e., the trough with constant water level $h_w$ may become a source of water for the center pool.

The center pool will not be drained entirely, if

$$H_{min}= h_w-E·t_L>L$$

(29)

In other cases $H_{min}$ can decrease to the elevation of the polygon surface and satisfy the condition $H\left(t_{drain}\right) = L$. In this case, the time of complete pool drainage continues from Equation (27) as follows:

$$t_{drain} = t_{L}ln\left(1+\frac{H_0-L}{L-h_w+E{t}_L}\right)$$

(30)

3.3.4. Center Pool Level H(t): Dynamic Thaw Depth, Analytical Approach

In this case, L(t) = D$·$f(t), and the problem requires treatment of a moving bottom boundary, which requires additional effort. Equation (6) is amended by using the relationship in Equation (20):

$$\pi R^2\frac{dH}{dt} = -2\pi K_{r}L\left[H\left(t\right)-h_w\right]·Q^{*}-\pi R^{2}E,H\left(0\right) = H_0$$

(31)

Which can be rewritten for integration considering the definitions of t* and H* in Equations (7) and (8) as follows:

$$\frac{d{H}^{*}}{dt*} = -p\left(t^{*}\right)H^{*}-E^{*},H^{*}\left(0\right)=1$$

(32)

The time-dependent coefficient p(t*) here is as follows:

$$p\left(t^{*}\right) = \frac{2K_r\left(H_0-h_w\right)f{Q}^{*}}{R^2}$$

(33)

Which reflects a time-dependent, experimentally determined function f for the active layer. Transient f also creates time dependence in the parameters R* and Q* in Equation (9). Finally, integration of the linear Equation (32) is standard:

$$H^{*}\left(t^{*}\right)=e^{-P\left(t^{*}\right)}-e^{-P\left(t^{*}\right)}{{\displaystyle \int }}_0^{t^{*}}{e}^{P\left(\eta \right)}{E}^{*}\left(\eta \right)d\eta ,P\left(t^{*}\right)={{\displaystyle \int }}_0^{t^{*}}p\left(\xi \right)d\xi$$

(34)

3.3.5. Center Pool Level H(t): Dynamic Thaw Depth, Numerical Approach

As an alternative to the methods described in Section 3.3.4, dynamic seasonally thawed zone thickness can also be accounted for by solving the model in a piecewise fashion, dividing the time domain into discrete timesteps. In this approach, the thawed zone thickness L(t) is represented in table format and treated as forcing data for each timestep. Additionally, this approach permits head in the trough pool to likewise be defined in table format as a function of time, h_w(t). An example using this approach to simulate the early-summer disappearance of a center pond near Utqiagvik, Alaska is presented in Section 4.3.

3.4. Computation of Solutions

Scripts for these calculations have been provided in the Supplementary Material. The methods used to investigate pool dynamics are determined by whether the thaw depth is treated as constant or dynamic.

When the thaw-layer thickness L is steady, a constant value of R* is defined. Flow net calculations start with determining a set of ${\lambda }_n,n=1,2,\dots$ in Equation (19). Convergence of the series in Equations (18) and (24) is generally rapid. Next, the dimensionless head is converted to dimensional format by Equation (11), and constant, dimensionless flux Q* is calculated using specific $R^{*}$ and $Bi$ by Equation (21). This Q* is utilized in estimates of t_L and pool depth dynamics, by Equations (10) or (27). Geometric and soil physical parameters are defined in the opening lines of the scripts and can easily be manipulated by the user. An example of this model is presented in Section 4.2.

When thaw-layer thickness L is dynamic, the function f must be known a priori in analytical or table format. The value of R* becomes time dependent according to Equation (33) because of the continuously changing polygon radius-to-depth ratio. Corresponding ${\lambda }_n,n=1,2,\dots$ differ for each moment of time, together with Q* according to Equation (21). If the function f is not provided as a continuous function, Equation (32) can be solved using a finite-difference approach on a discrete time grid, as described in Section 3.5.2 and Section 4.3.

3.5. Model Parameters for Demonstration

3.5.1. Constant Thaw-Layer Thickness

To demonstrate the use of the model under assumptions of constant thaw-layer thickness, we used ranges for geometric and soil physical parameters of ice-wedge polygons derived from the literature. Based on ice-wedge polygon horizontal scale and vertical thickness from [2,7,16,17], we explored aspect ratios (R/L) ranging from 1 to 20.

Our hydraulic conductivity values are derived from [18], who analyzed peat cores and determined heterogeneous $K_r$ in the range between 0.1 and 10 m/day, but typically on the order of 1 m/day. The anisotropy ratio $K_r/K_z$ had somewhat erratic behavior, often appearing nearly isotropic, but with a range extending from 0.1 and 10. Similar values for hydraulic conductivity were published by [4,7,16,19,20], but these studies generally did not distinguish between $K_r$ and $K_z$. Estimates by [8] for high-centered and low-centered polygons had generally similar magnitudes of $K_r$.

Higher values of $K_r$ and $K_z$ are sometimes observed immediately in the top 0.2–0.3 m (relative to the underlying part of the active layer) by one or two orders of magnitude [16,18]. This scenario may effectively increase the initial effective pool depth and reduce the thickness of the active layer, but will not affect concepts of the model.

For characteristic cases, the maximum center pool depth in low-centered polygons, $H_0$, can be taken in the order of 0.5 m [2,5,15].

3.5.2. Dynamic Thaw-Layer Thickness

In order to validate the model in a scenario characterized by dynamic thaw-layer thickness, we calibrated it to match ponded water levels in a low-centered polygon during an early season drainage event in 2012 at the Barrow Environmental Observatory near Utqiagvik, Alaska (Area A in [5]). We used measured data from the site as boundary conditions for the model, including directly observed trough water levels. Meteorological forcing data consisted of observed precipitation from the Barrow, Alaska National Weather Service ground station and re-analyzed evapotranspiration from NASA’s Global Land Data Assimilation System (GLDAS) [21]. Although the thaw depth was not measured directly in the polygon during the 2012 thaw season, it was measured directly during the 2013 and 2014 thaw seasons. Using the 2013 and 2014 thaw depth measurements and atmospheric conditions, we calibrated a permafrost heat flow model (Geophysical Institute Permafrost Laboratory (GIPL) model) [22] and simulated thaw depths for 2012 using air temperature and snow depth measured at the site. We applied these simulated thaw depths to control the dynamic thaw depth of the model.

In order to incorporate varying precipitation, evapotranspiration, trough water level, and thaw depth, we ran the model in piecewise fashion, restarting the model at each timestep with current boundary conditions. We included data from 6:00 AM, June 10 through 6:00 AM, July 2, 2012 (23 days) during which time the inundated low-centered polygon drained. The data was collected every 15 min, resulting in 2112 timesteps in the analysis.

The adjustable parameters in the calibration were the horizontal and vertical hydraulic conductivity (K_r and K_z), the discharge conductance (κ), and the initial ponded water level (H(0)). We calibrated the model using a Levenberg–Marquardt approach implemented in the Julia LsqFit package (https://github.com/JuliaNLSolvers/LsqFit.jl). The objective function was the sum of the squared errors between the measured and simulated ponded water levels in the polygon center. Regularization terms were added to the objective function to penalize solutions where K_r and κ deviated from physical values. Assuming preferential horizontal (radial) flow, the value of K_z was required to be less than K_r.

4. Results

4.1. Flow Nets: Head and Flux Distributions

To assess the effects of aspect ratio $R/L$ on flow dynamics, we assumed isotropic conditions ($K_r = K_z$), and the coefficient $\kappa = 2.0$ day⁻¹ (assuming k as a fraction of $K_r$ (e.g., 50%) and l on the order of 0.25 m). For a polygon $L = D = 0.5 \mathrm{m}$ thick, several horizontal polygon sizes were considered: R =0.5, 1.0, 1.5, 5.0, and 10.0 m.

The dimensionless parameters are as follows: $Bi = \frac{\kappa L}{\sqrt{K_r{K}_z}} = \frac{2·0.5}{\sqrt{1·1}} = 1$ and $R^{*}= \frac{R}{L}\sqrt{\frac{K_z}{K_r}} = \frac{R}{0.5}\sqrt{1}$= 1, 2, 3, 10, and 20 (Figure 2). The latter two values correspond to commonly observed ice-wedge polygon radii of around 5–10 m. For comparison, the smaller aspect ratios of $R^{*}=1$, 2, and 3 are also shown, to highlight the impact of disparity between radial and vertical scales

The shape of the flow net is steady during the drainage period, while the magnitude of each local velocity vector declines with the depth of water in the center pool, as defined in Equation (20). Considering that each stream tube conducts identical discharge toward the periphery of the polygon, the flux magnitudes near the polygon center and the trough differ by orders of magnitude.

These results indicate that the primary flux region is focused within about two vertical scales from the rim, when aspect ratio is approximately 3.0 or greater. This water flux disparity implies that advection-driven transport of solutes, heat, and soil particles may be concentrated near the periphery of an inundated polygon, while the center remains poorly flushed.

An investigation of model sensitivity to other contributing factors (hydraulic resistance of polygon-trough interface and anisotropy for commonly observed values) indicated that they are secondary to the effect of aspect ratio; these results are discussed in Appendix B.

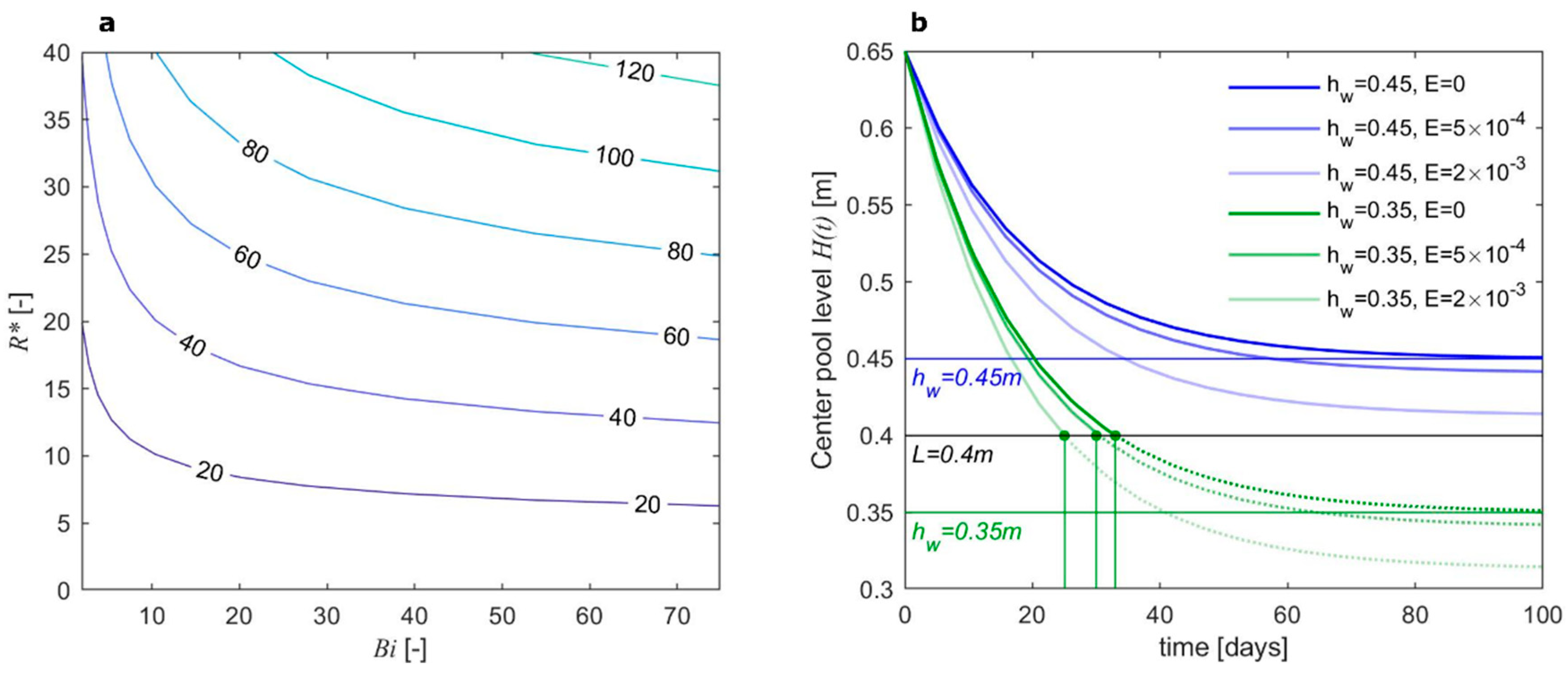
4.2. Water Level Dynamics and the Role of Evapotranspiration

The time scale $t_L$ is defined by Equation (9) through non-dimensional discharge $Q^{*}\left(R^{*},Bi\right)$. For simulations assuming a constant thaw-layer thickness L, we likewise assumed that the water level in the trough h_w remains approximately constant during the time period of interest. Figure 3a indicates that discharge increases linearly with the anisotropy-adjusted aspect ratio, $R^{*}$, for practically any value of $Bi$, the hydraulic conductance of the polygon drainage interface. This general graph can be utilized to evaluate of the polygon drainage dynamics, indicating that discharge is linearly dependent on the anisotropy-adjusted aspect ratio and is only dependent on the drainage interface when its conductance is significantly low.

For illustration, we considered drainage of a typical anisotropic polygon of radius R = 10 m, thickness L = 0.4 m, and rim–trough interface width l ≈ 0.5 m. Conductive properties were as follows: K_r = 1 m/day, K_z = 0.2 m/day, and k = 0.5 m day⁻¹ (i.e., κ = 1.0 day⁻¹). The initial center pool level was H(0) = 0.65 m (i.e., 0.25 m above the ground surface) and the water level in the trough was h_w = 0.45 m. These parameters yielded dimensionless values R* = 16.8 and Bi = 0.89. The characteristic time of this problem was $t_L$ = 18 days. (Sensitivity of results to κ is moderate at these values, as discussed in Appendix B).

Published experimental data on evapotranspiration E in Siberia [4] and Alaska [7] using various field methods indicate typical values on the order of 10⁻³ m day⁻¹. Therefore, we used E = $0.5·{10}^{-3}$m day⁻¹ and E = $2·{10}^{-3}$m day⁻¹ to explore the effect on t_drain values.

In Figure 3b, we show the dynamics of the pool water level following Equation (27). Here, water in the polygon center remains ponded indefinitely (Figure 3b), at the evaporation rates that we considered, because $H_{min}$ > L = 0.4 m according to Equation (29).

The situation changes if the water level in the trough is at lower elevation than in the polygon center, e.g., if h_w = 0.35 m. Equation (27) shows that the pool will drain entirely at any evaporation rate (E = 0, $0.5·{10}^{-3}$, and $2·{10}^{-3}$ m day⁻¹). Corresponding drainage times, calculated from Equation (30) are t_drain = 33, 30, and 25 days, and are similar to typical conditions observed in the Arctic, either at the start of the summer or following a large precipitation event in mid-summer [5,8].

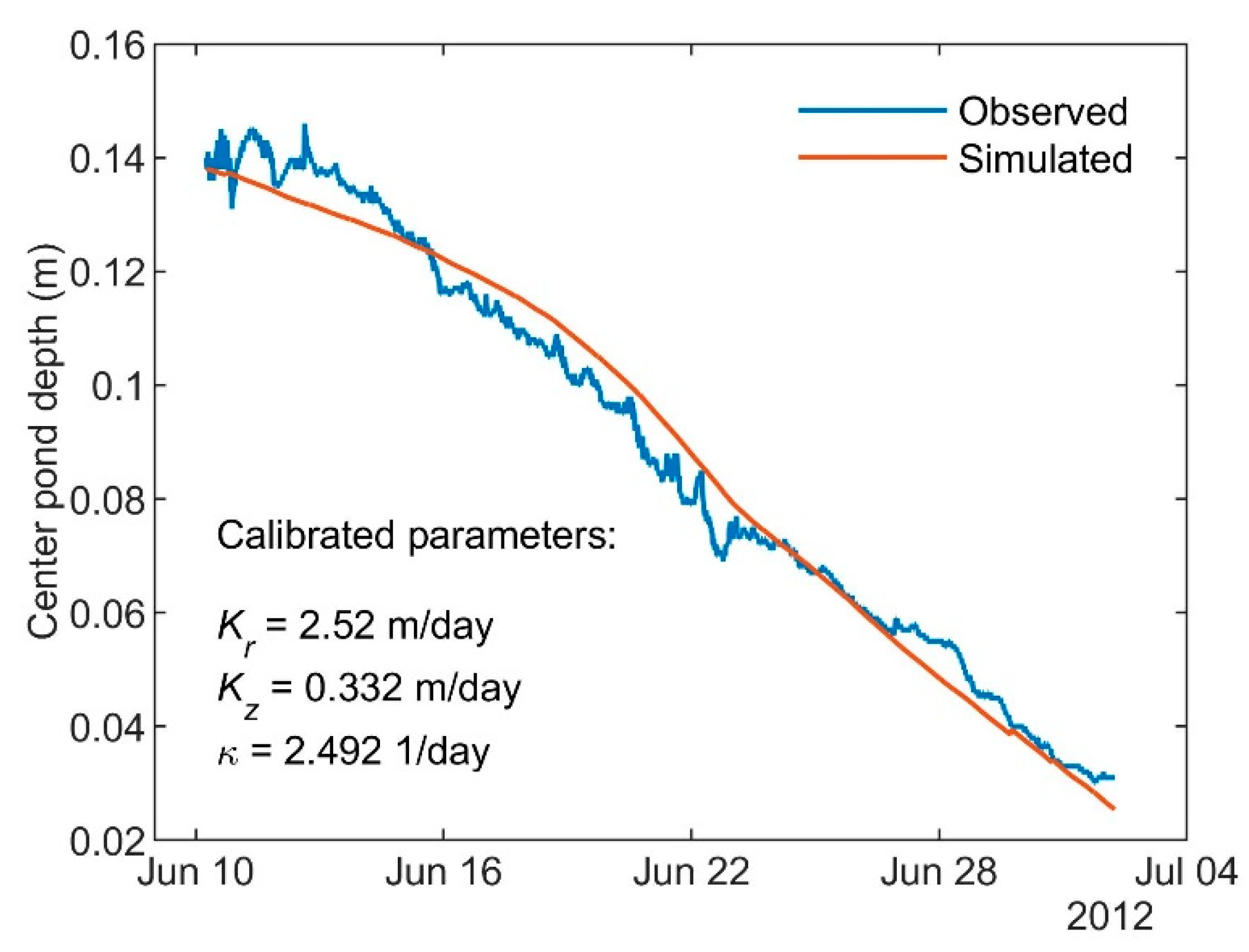
4.3. Calibration of Center Pond Drainage Scenario with Dynamic Thaw-Layer Thickness at Utqiagvik

Figure 4 presents the results of our calibration of the model against head data from the center pool in early summer at an inundated low-centered polygon near Utqiagvik, Alaska [5]. The simulation considered piecewise-linear gradual changes to the thickness of the thawed layer beneath the polygon center and observations of dynamic water level in the trough pool, as described in Section 3.3.5 and Section 3.5.2. The final calibration demonstrates a very close match between observed and simulated head in the center pool, with a root mean squared error of ~0.006 m. Likewise, the calibrated parameters K_r, K_z, and κ fit squarely within the ranges defined in Section 3.5.1, with an anisotropy ratio K_r/K_z of ~7.6. The close match between observed and simulated head and the reasonable calibration of hydraulic parameters affirms the physical realism of our model in a scenario characterized by rapid changes in thaw-layer thickness and trough pool water level. A video illustrating these results is also available online in the Supplementary Material.

5. Conclusions

We developed a hydrodynamic model of inundated low-centered polygon drainage coupled with the center pool water balance and obtained an analytical solution. For conditions typically observed in polygonal tundra, a very strong edge effect was found; only a small fraction of the polygon located near the edges is flushed by the water drained from center pool storage. Confidence in the model is bolstered by the fact that simulated characteristic drainage time estimates are consistent with published observations, and the model accurately simulates the early summer disappearance of the center pond in a low-centered polygon when solved in a piecewise-linear fashion that accounts for dynamic thaw-layer thickness and water level in the trough pool. Some of the key insights derived from the model are:

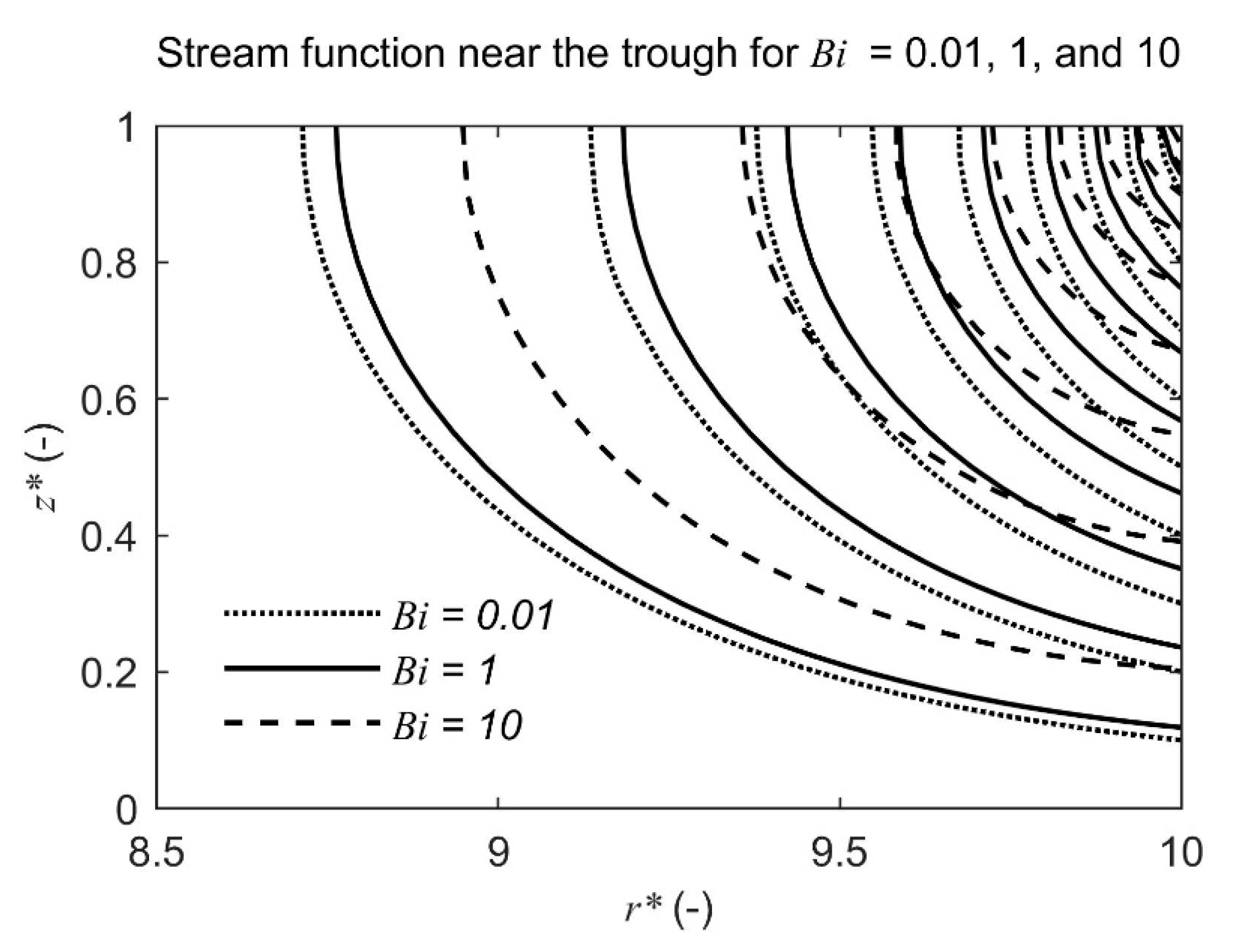
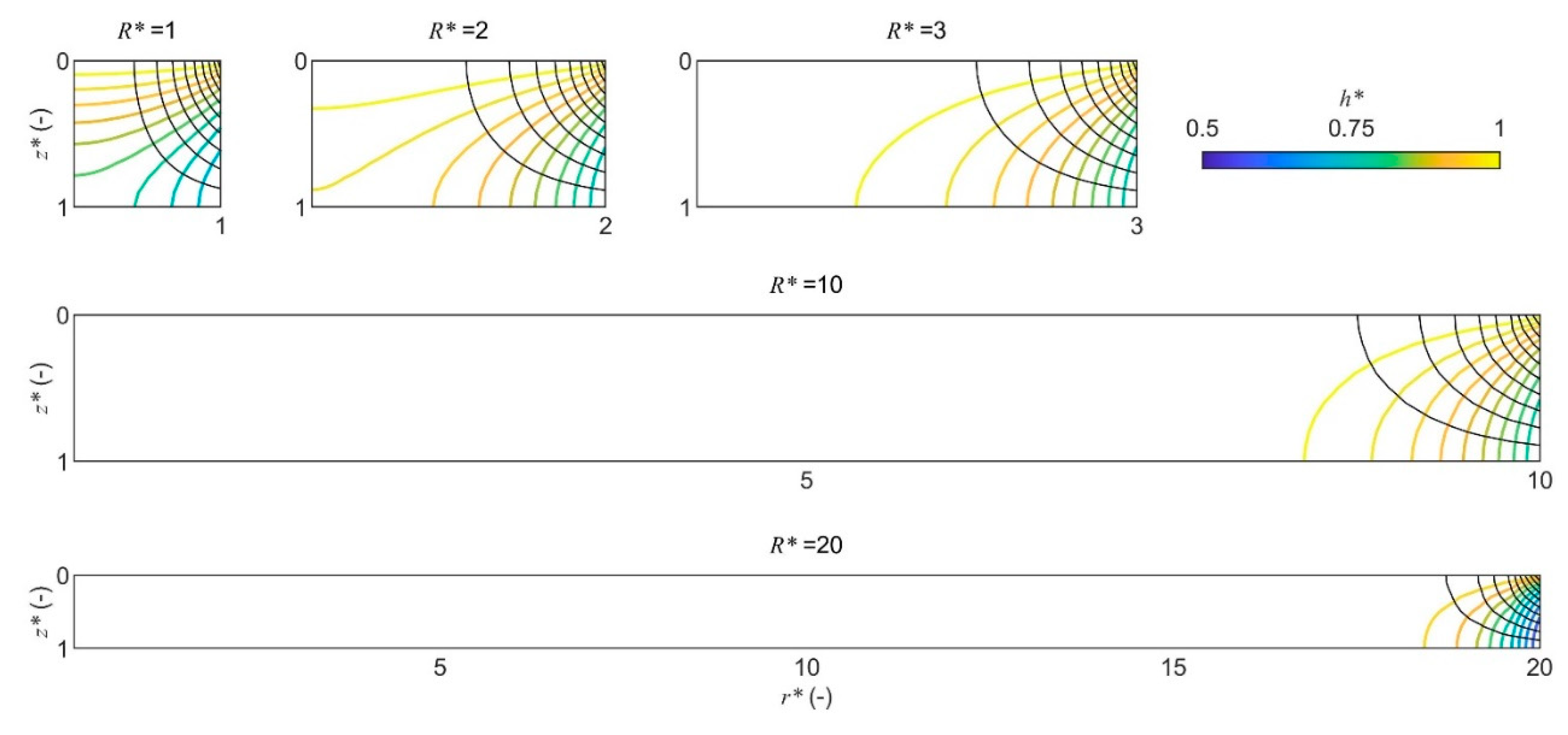
• Polygons are flushed most intensively at the edges for practically all existing physical and geometric parameters. The streamline patterns in this zone change little when the aspect ratio (radius-to-thickness of active layer) exceeds a value of three.
• Anisotropy in hydraulic conductivity (horizontal-to-vertical hydraulic conductivity ratio) has a secondary influence on the intensity of flushing. Increases of anisotropy values counteract the effects of increased geometrical aspect ratio increases and vice versa (as discussed in Appendix B).
• Hydraulic resistance of the drainage interface between the polygon and trough also has some limited, but not overriding influence within the typical range of Arctic tundra conditions.
• Drainage time scales are consistent with observed duration of the center pool drainage within low-centered polygons. The parameter $t_L$ can be used to characterize drainage times from an inundated polygon center.