Estimating IDF Curves Consistently over Durations with Spatial Covariates
Abstract
:1. Introduction
- Under which conditions is the spatial d-GEV approach an improvement compared to the separate application of the GEV for each duration and station?
- Does the spatial d-GEV approach provide reliable estimates at ungauged sites?
2. Methods
2.1. Data
2.2. d-GEV as a Model for Annual Maxima for Different Durations
2.2.1. Station-Wise Model for a Range of Durations (d-GEV)
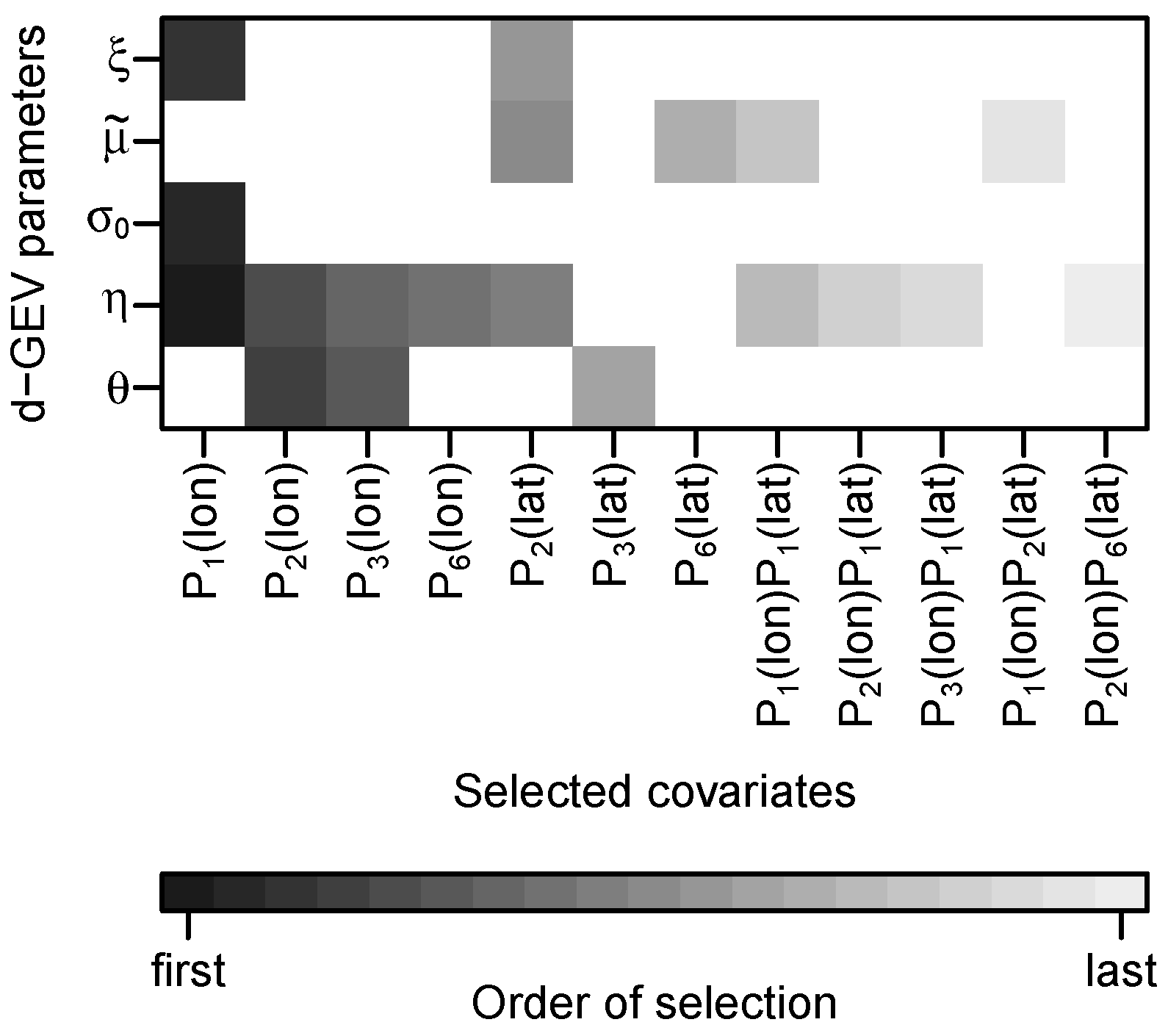
2.2.2. Adding Spatial Covariates
2.3. Model Selection
2.4. Verification
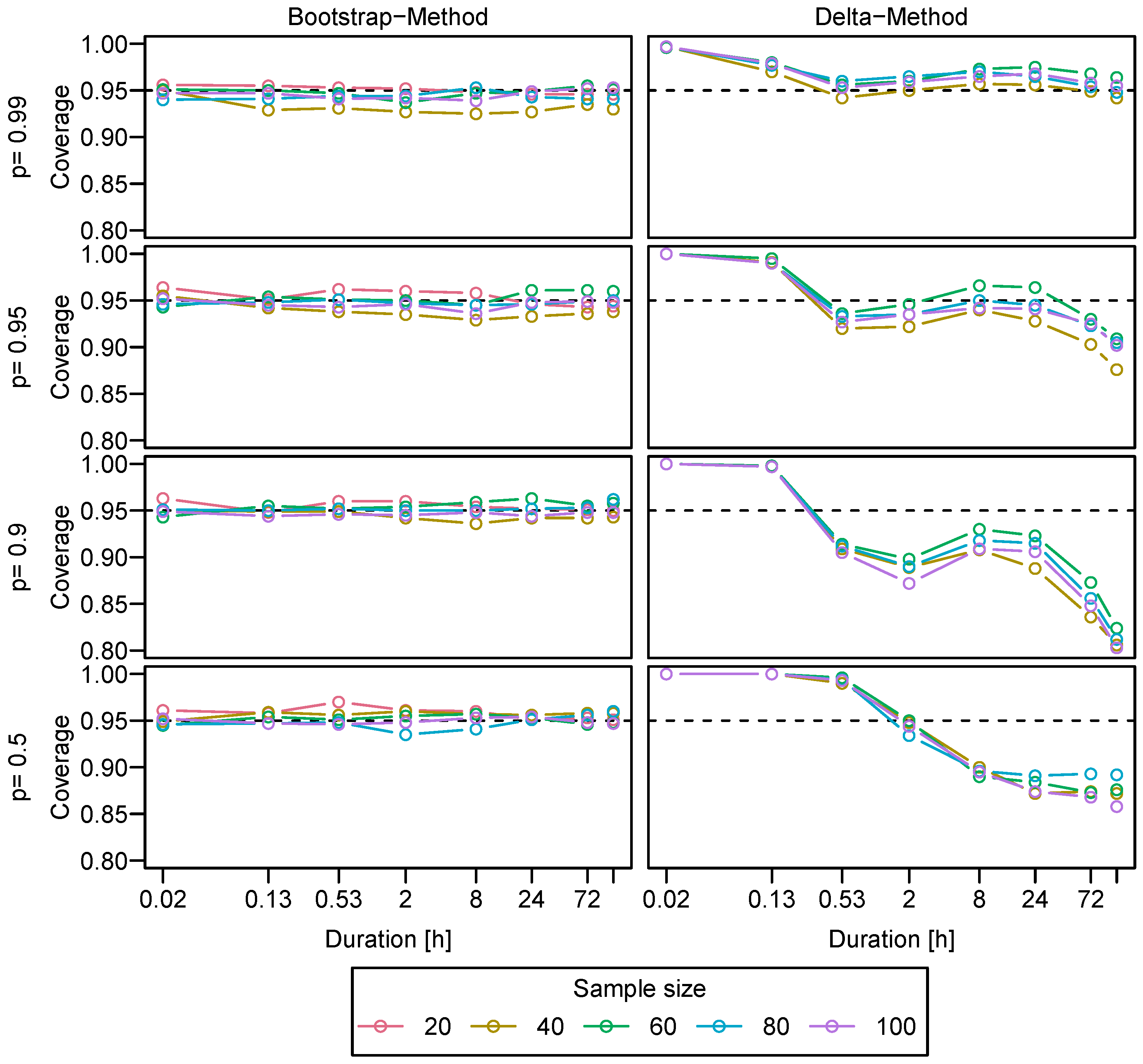
2.5. Confidence Intervals
3. Results
3.1. Model Performance
3.1.1. Overall Performance
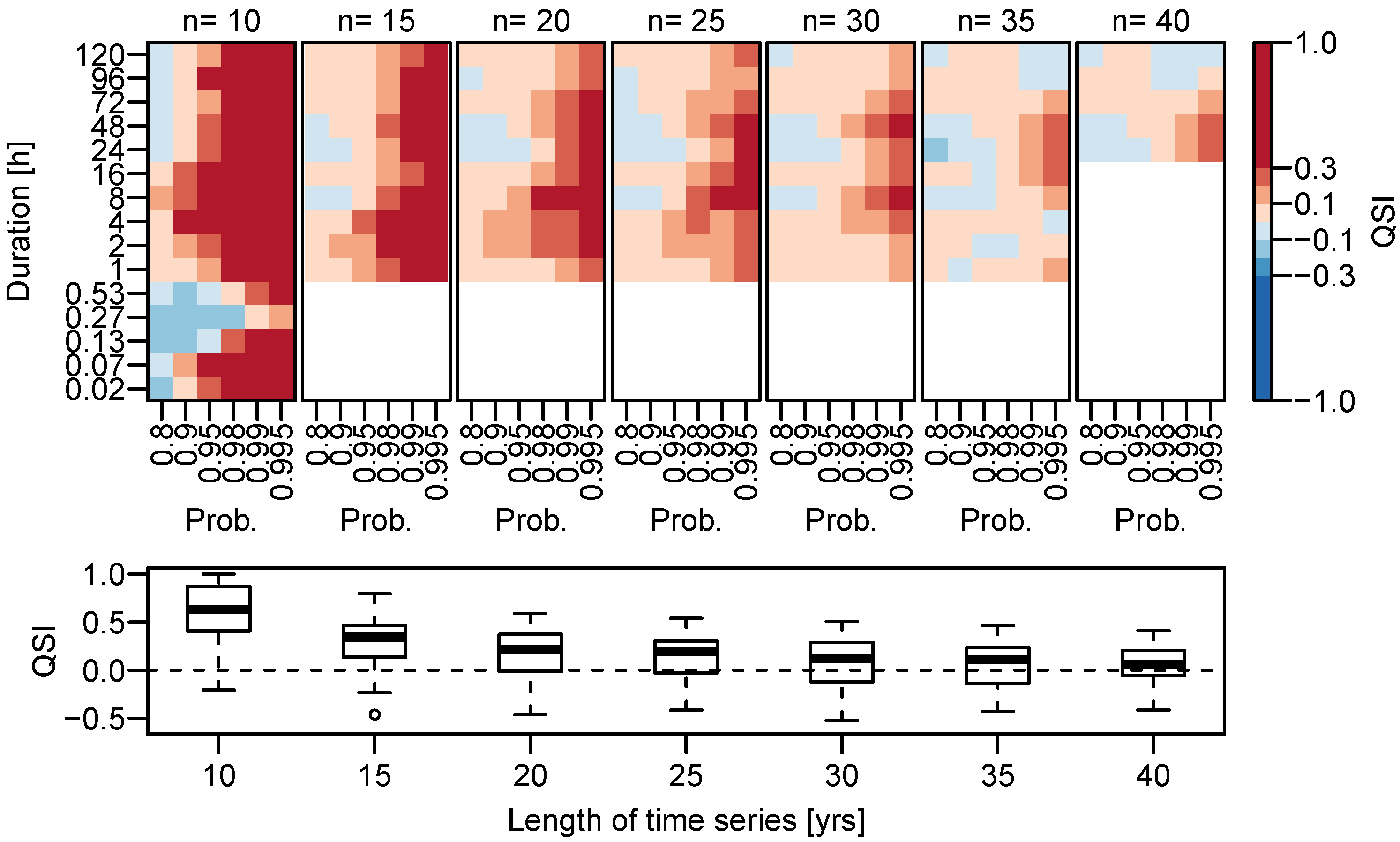
3.1.2. Dependence on Time Series Length
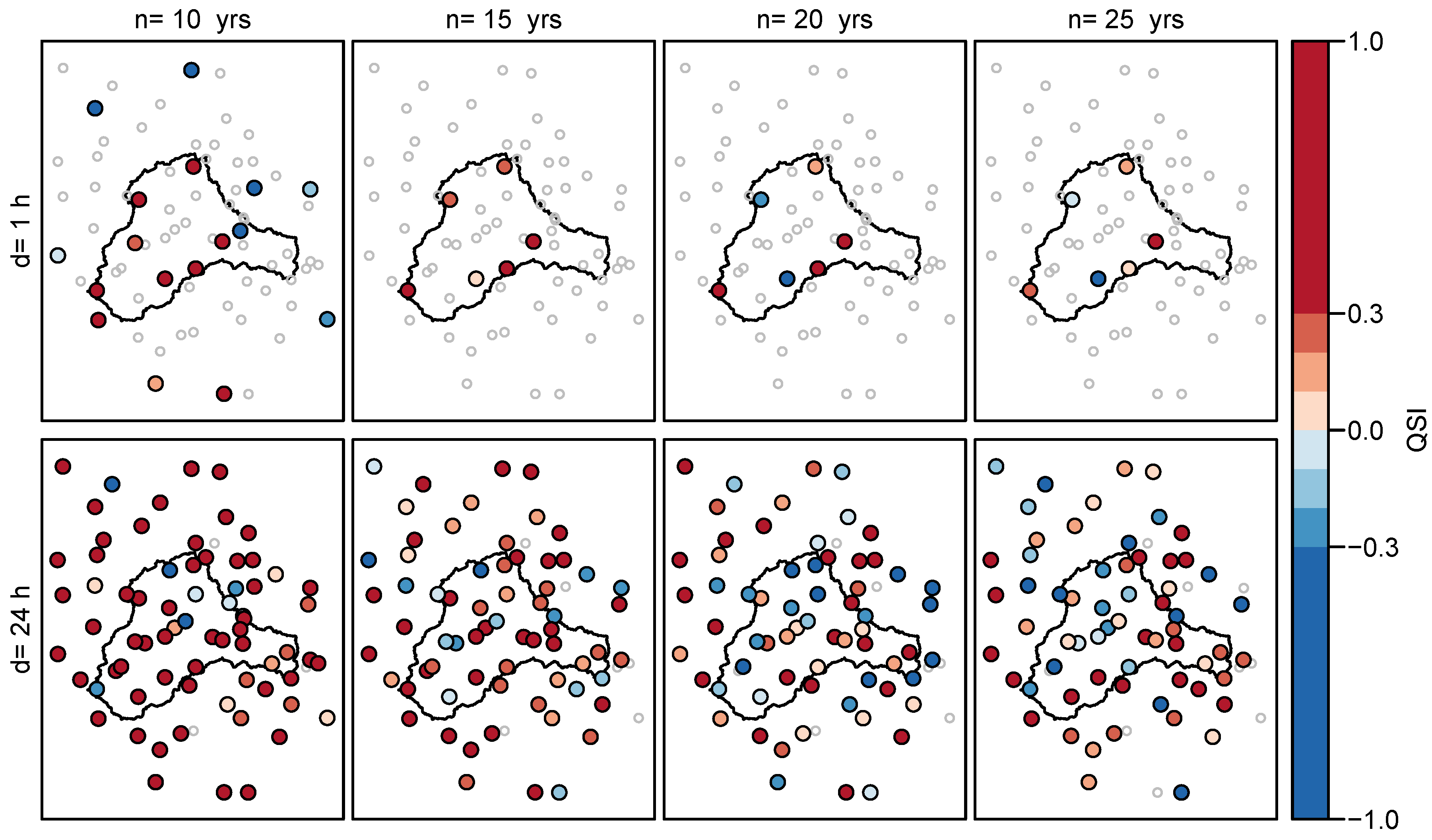
3.1.3. Ungauged Sites
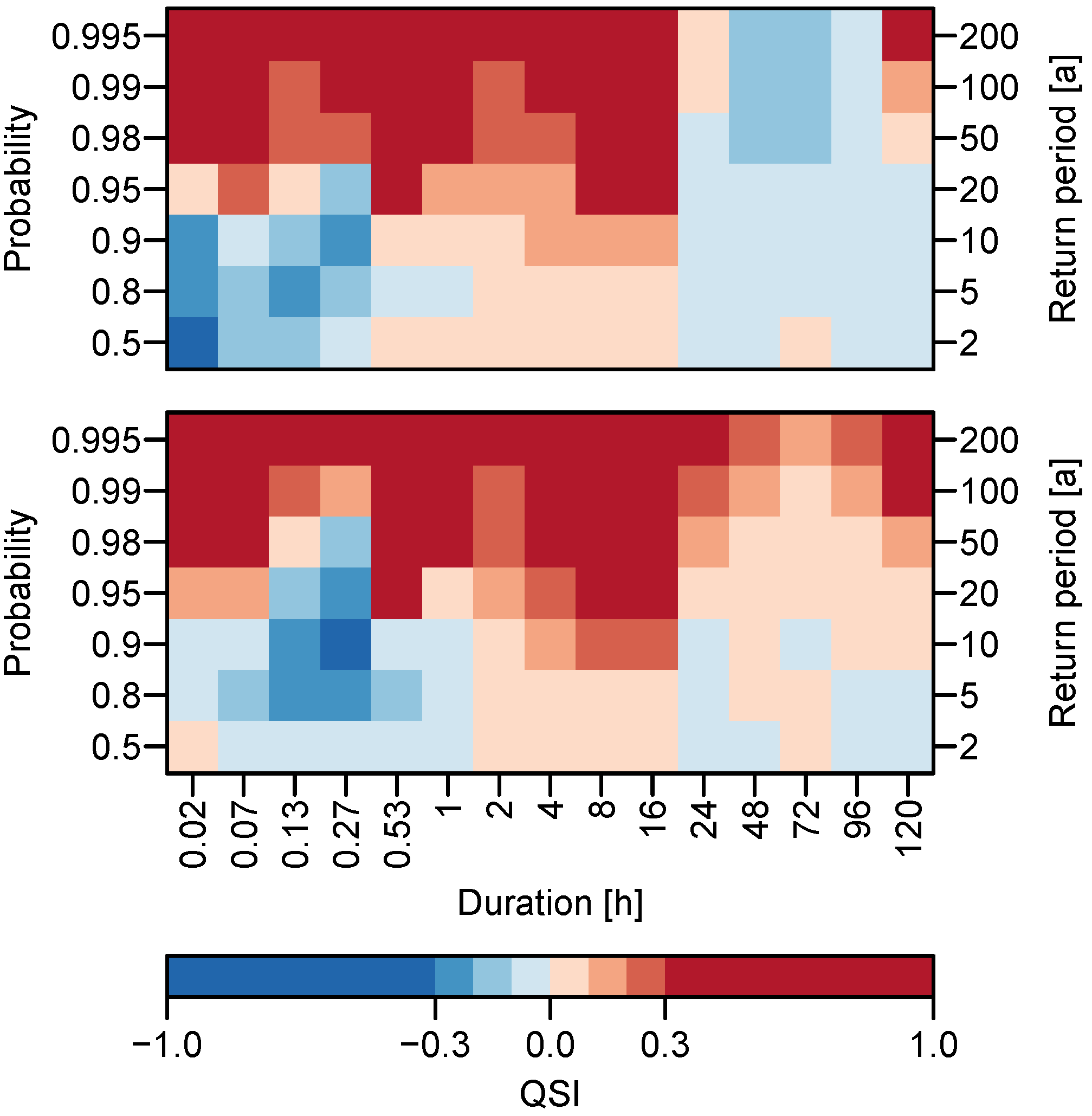
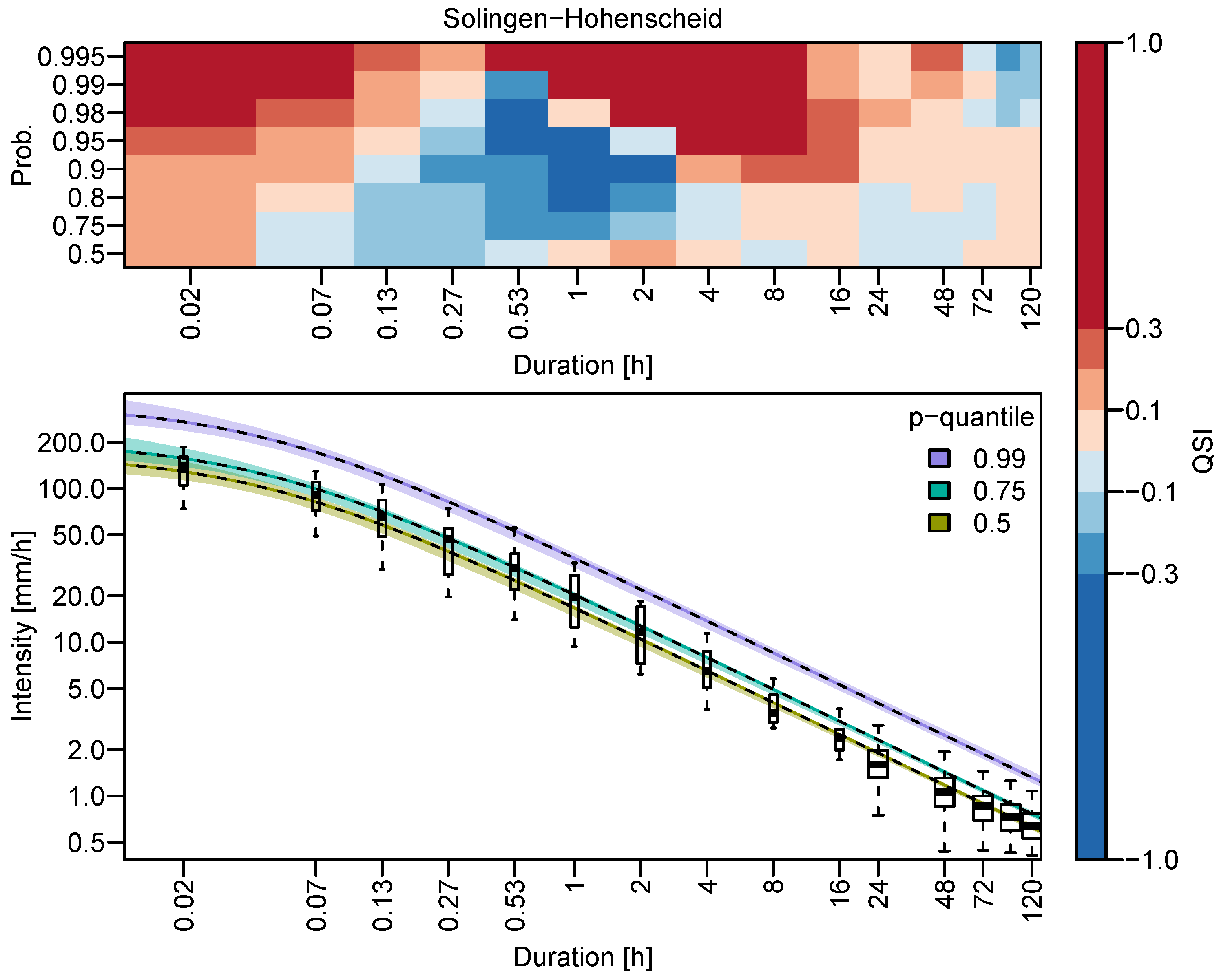
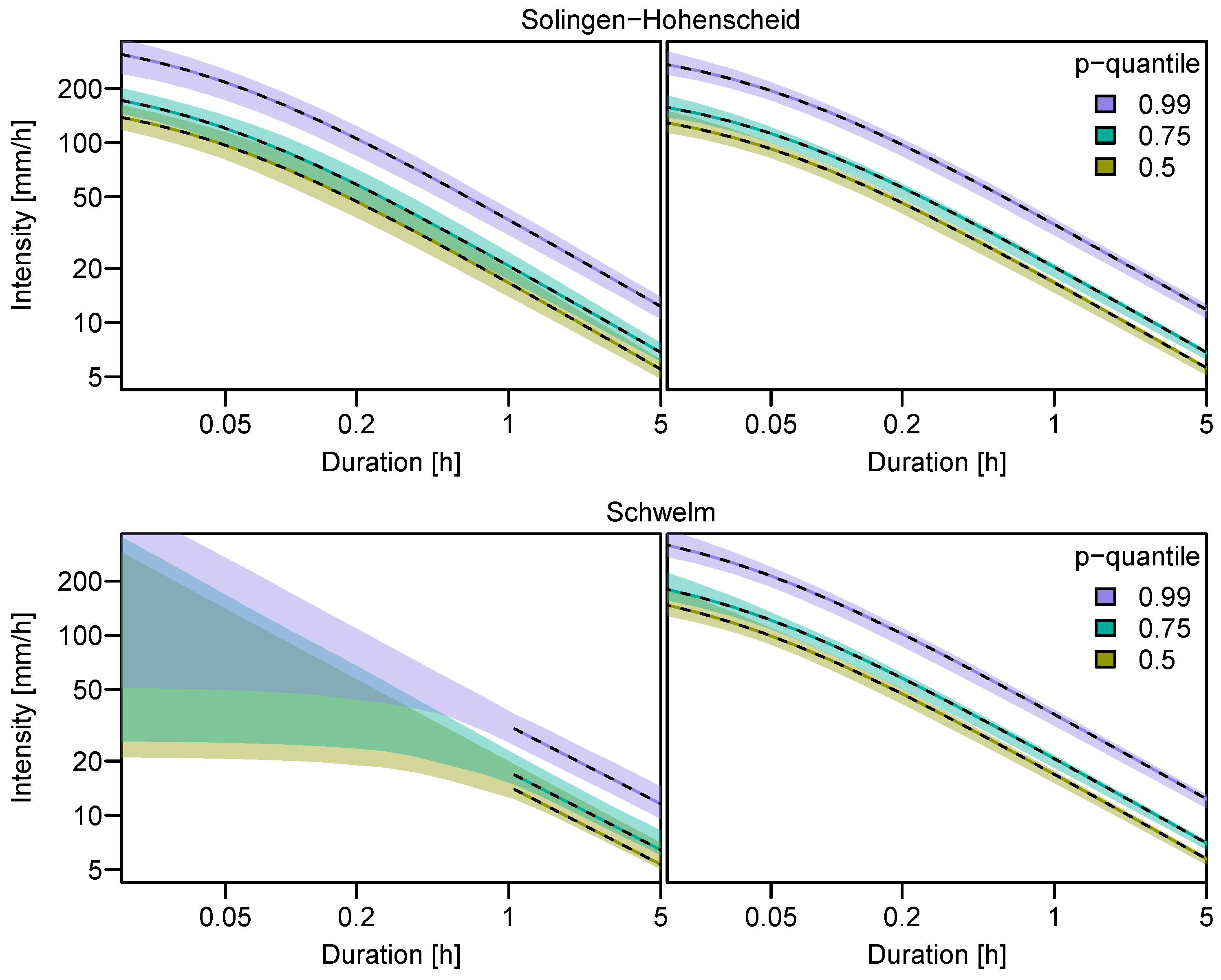
3.2. Quantile Estimation and Uncertainty
4. Discussion
5. Summary
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| BHM | Bayesian Hierarchical Model |
| DWD | German Weather Service (Deutscher Wetterdienst) |
| EVT | Extreme Value Theory |
| GEV | Generalized Extreme Value distribution |
| d-GEV | duration-dependent GEV |
| IDF | Intensity-Duration-Frequency (curve) |
| QS | Quantile Score |
| QSS | Quantile Skill Score |
| QSI | Quantile Skill Index |
| VGLM | Vector generalized linear model |
| VGAM | Vector generalized additive model |
Appendix A. Overview of Verification Variations
- the overall performance
- the dependence of the model performance on the length of the time series used for training the model
- the model performance at ungauged sites.
| Overall Performance | Dependence on Time Series Length | Ungauged Sites | |||||
|---|---|---|---|---|---|---|---|
| Training | Validation | Training | Validation | Training | Validation | ||
| spatial d-GEV | station | () years | 3 years | years | 3 years | - | 3 years |
| remaining stations | all data | - | all data | - | all data | - | |
| GEV | station | () years | 3 years | years | 3 years | years | 3 years |
| remaining stations | - | - | - | - | - | - | |
Appendix B. Coverage of Confidence Intervals
References
- Hattermann, F.F.; Kundzewicz, Z.W.; Huang, S.; Vetter, T.; Gerstengarbe, F.W.; Werner, P. Climatological drivers of changes in flood hazard in Germany. Acta Geophys. 2013, 61, 463–477. [Google Scholar] [CrossRef]
- Seneviratne, S.; Nicholls, N.; Easterling, D.; Goodess, C.; Kanae, S.; Kossin, J.; Luo, Y.; Marengo, J.; McInnes, K.; Rahimi, M.; et al. Changes in climate extremes and their impacts on the natural physical environment. In Managing the Risks of Extreme Events and Disasters to Advance Climate Change Adaptation; Field, C.B., Barros, V., Stocker, T.F., Dahe, Q., Dokken, D.J., Ebi, K.L., Mastrandrea, M.D., Mach, K.J., Plattner, G.K., Allen, S.K., Eds.; Cambridge University Press: Cambridge, UK, 2012; pp. 109–230. [Google Scholar]
- Chow, V.T. Frequency analysis of hydrologic data with special application to rainfall intensities. Univ. Ill. Bull. 1953, 50, 86. [Google Scholar]
- KOSTRA-DWD. Available online: https://www.dwd.de/DE/leistungen/kostra_dwd_rasterwerte/kostra_dwd_rasterwerte.html (accessed on 4 August 2020).
- Junghänel, T.; Ertelund, H.; Deutschländer, T. KOSTRA-DWD-2010R: Berichtzur Revisionderkoordinierten Starkregenregionalisierung und -auswertung des Deutschen Wetterdienstes in der Version 2010; Deutscher Wetterdienst, Abteilung Hydrometeorologie: Offenbach, Germany, 2017.
- Precipitation Frequency Data Server. Available online: https://hdsc.nws.noaa.gov/hdsc/pfds/ (accessed on 15 October 2020).
- Perica, S.; Pavlovic, S.; St. Laurent, M.; Trypaluk, C.; Unruh, D.; Wilhite, O. NOAA Atlas 14: Precipitation-Frequency Atlas of the United States, Volume 11 Version 2.0; U.S. Department of Commerce National Oceanic and Atmospheric Administration National Weather Service: Silver Spring, MD, USA, 2018.
- Hosking, J.R.M.; Wallis, J.R. Regional Frequency Analysis: An Approach Based on L-Moments; Cambridge University Press: Cambridge, UK, 1998; p. 208. [Google Scholar]
- Fukutome, S.; Schindler, A.; Capobianco, A. MeteoSwiss Extreme Value Analyses: User Manual and Documentation, 3rd ed.; Technical Report, 255; Federal Office of Meteorology and Climatology, MeteoSwiss: Zürich, Switzerland, 2018; 80p.
- MeteoSwiss Maps of Extreme Precipitation. Available online: https://www.meteoswiss.admin.ch/home/climate/swiss-climate-in-detail/extreme-value-analyses/maps-of-extreme-precipitation.html (accessed on 15 October 2020).
- Goudenhoofdt, E.; Delobbe, L.; Willems, P. Regional frequency analysis of extreme rainfall in Belgium based on radar estimates. Hydrol. Earth Syst. Sci. 2017, 21, 5385–5399. [Google Scholar] [CrossRef] [Green Version]
- Olsson, J.; Södling, J.; Berg, P.; Wern, L.; Eronn, A. Short-duration rainfall extremes in Sweden: A regional analysis. Hydrol. Res. 2019, 50, 945–960. [Google Scholar] [CrossRef]
- Gaur, A.; Schardong, A.; Simonovic, S.P. Gridded Extreme Precipitation Intensity-Duration-Frequency Estimates for the Canadian Landmass. J. Hydrol. Eng. 2020, 25, 05020006. [Google Scholar] [CrossRef]
- Coles, S. An Introduction to Statistical Modeling of Extreme Values; Springer: New York, NY, USA, 2001. [Google Scholar] [CrossRef]
- Koutsoyiannis, D.; Kozonis, D.; Manetas, A. A mathematical framework for studying rainfall Intensity-Duration-Frequency relationships. J. Hydrol. 1998, 206, 118–135. [Google Scholar] [CrossRef]
- Ritschel, C.; Ulbrich, U.; Névir, P.; Rust, H.W. Precipitation extremes on multiple timescales—Bartlett-Lewis rectangular pulse model and Intensity-Duration-Frequency curves. Hydrol. Earth Syst. Sci. 2017, 21, 6501–6517. [Google Scholar] [CrossRef] [Green Version]
- Lehmann, E.; Phatak, A.; Soltyk, S.; Chia, J.; Lau, R.; Palmer, M. Bayesian hierarchical modelling of rainfall extremes. In Proceedings of the 20th International Congress on Modelling and Simulation, Adelaide, Australia, 1–6 December 2013; pp. 2806–2812. [Google Scholar]
- Van de Vyver, H.; Demarée, G.R. Construction of Intensity-Duration-Frequency (IDF) curves for precipitation at Lubumbashi, Congo, under the hypothesis of inadequate data. Hydrol. Sci. J. J. Sci. Hydrol. 2010, 55, 555–564. [Google Scholar] [CrossRef]
- Stephenson, A.G.; Lehmann, E.A.; Phatak, A. A max-stable process model for rainfall extremes at different accumulation durations. Weather Clim. Extrem. 2016, 13, 44–53. [Google Scholar] [CrossRef] [Green Version]
- Blanchet, J.; Ceresetti, D.; Molinié, G.; Creutin, J.D. A regional GEV scale-invariant framework for Intensity-Duration-Frequency analysis. J. Hydrol. 2016, 540, 82–95. [Google Scholar] [CrossRef]
- Davison, A.C.; Padoan, S.A.; Ribatet, M. Statistical modeling of spatial extremes. Stat. Sci. 2012, 27, 161–186. [Google Scholar] [CrossRef] [Green Version]
- Dyrrdal, A.V.; Lenkoski, A.; Thorarinsdottir, T.L.; Stordal, F. Bayesian hierarchical modeling of extreme hourly precipitation in Norway. Environmetrics 2015, 26, 89–106. [Google Scholar] [CrossRef] [Green Version]
- Fischer, M.; Rust, H.; Ulbrich, U. A spatial and seasonal climatology of extreme precipitation return-levels: A case study. Spat. Stat. 2019, 34. [Google Scholar] [CrossRef]
- Van de Vyver, H. Spatial regression models for extreme precipitation in Belgium. Water Resour. Res. 2012, 48. [Google Scholar] [CrossRef]
- Yee, T.W.; Stephenson, A.G. Vector generalized linear and additive extreme value models. Extremes 2007, 10, 1–19. [Google Scholar] [CrossRef]
- Mélèse, V.; Blanchet, J.; Molinié, G. Uncertainty estimation of Intensity-Duration-Frequency relationships: A regional analysis. J. Hydrol. 2018, 558, 579–591. [Google Scholar] [CrossRef] [Green Version]
- Bentzien, S.; Friederichs, P. Decomposition and graphical portrayal of the quantile score. Q. J. R. Meteorol. Soc. 2014, 140, 1924–1934. [Google Scholar] [CrossRef]
- Wilks, D.S. Statistical Methods in the Atmospheric Sciences; Academic Press: Cambridge, MA, USA, 2011; Volume 100. [Google Scholar]
- Chow, V.T.; Maidment, D.R.; Mays, L.W. Applied Hydrology; McGraw-Hill series in water resources and environmental engineering; Tata McGraw-Hill Education: New York, NY, USA, 1988. [Google Scholar]
- Singh, V. Elementary Hydrology; Prentice Hall: New Jersey, NJ, USA, 1992. [Google Scholar]
- García-Bartual, R.; Schneider, M. Estimating maximum expected short-duration rainfall intensities from extreme convective storms. Phys. Chem. Earth Part B 2001, 26, 675–681. [Google Scholar] [CrossRef]
- Ulrich, J.; Ritschel, C. IDF: Estimation and Plotting of IDF Curves; R package version 2.0.0. 2019. [Google Scholar]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2020. [Google Scholar]
- Tyralis, H.; Langousis, A. Estimation of Intensity-Duration-Frequency curves using max-stable processes. Stoch. Environ. Res. Risk Assess. 2019, 33, 239–252. [Google Scholar] [CrossRef]
- Jurado, O.E.; Ulrich, J.; Rust, H.W. Evaluating the Performance of a Max-Stable Process for Estimating Intensity-Duration-Frequency Curves. 2020; Manuscript submitted for publication. [Google Scholar]
- Pasternack, A.; Grieger, J.; Rust, H.W.; Ulbrich, U. Recalibrating Decadal Climate Predictions—What is an adequate model for the drift? Geosci. Model Dev. Discuss. 2020, 2020, 1–38. [Google Scholar] [CrossRef]
- Arlot, S.; Celisse, A. A survey of cross-validation procedures for model selection. Statist. Surv. 2010, 4, 40–79. [Google Scholar] [CrossRef]
- Hastie, T.; Tibshirani, R.; Friedman, J. Elements of Statistical Learning, 2nd ed.; Stanford University: Stanford, CA, USA, 2009. [Google Scholar] [CrossRef]
- Davison, A.C.; Hinkley, D.V. Bootstrap Methods and Their Application; Number 1; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar]
- Van de Vyver, H. A multiscaling-based Intensity-Duration-Frequency model for extreme precipitation. Hydrol. Process. 2018, 32, 1635–1647. [Google Scholar] [CrossRef]
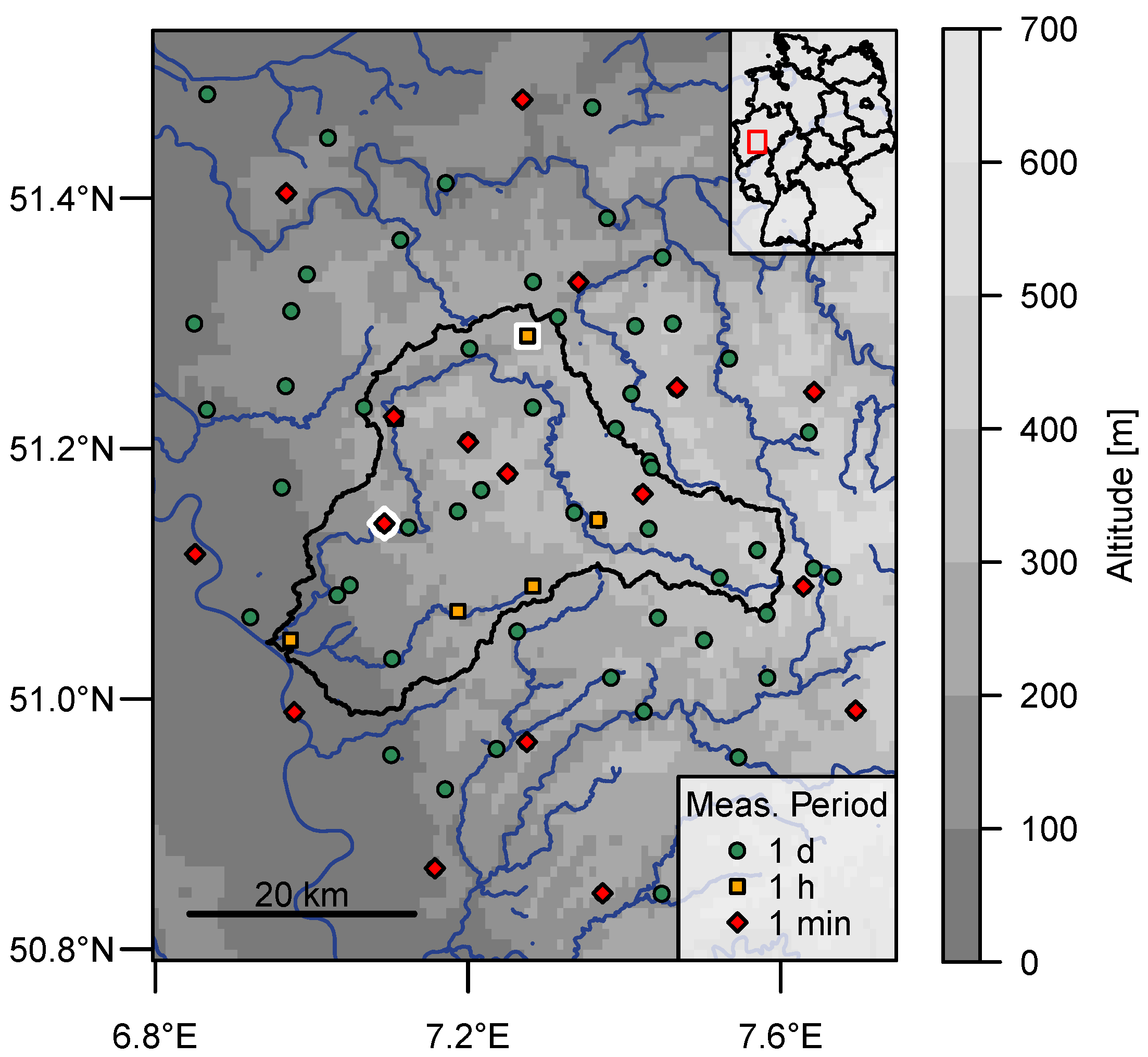

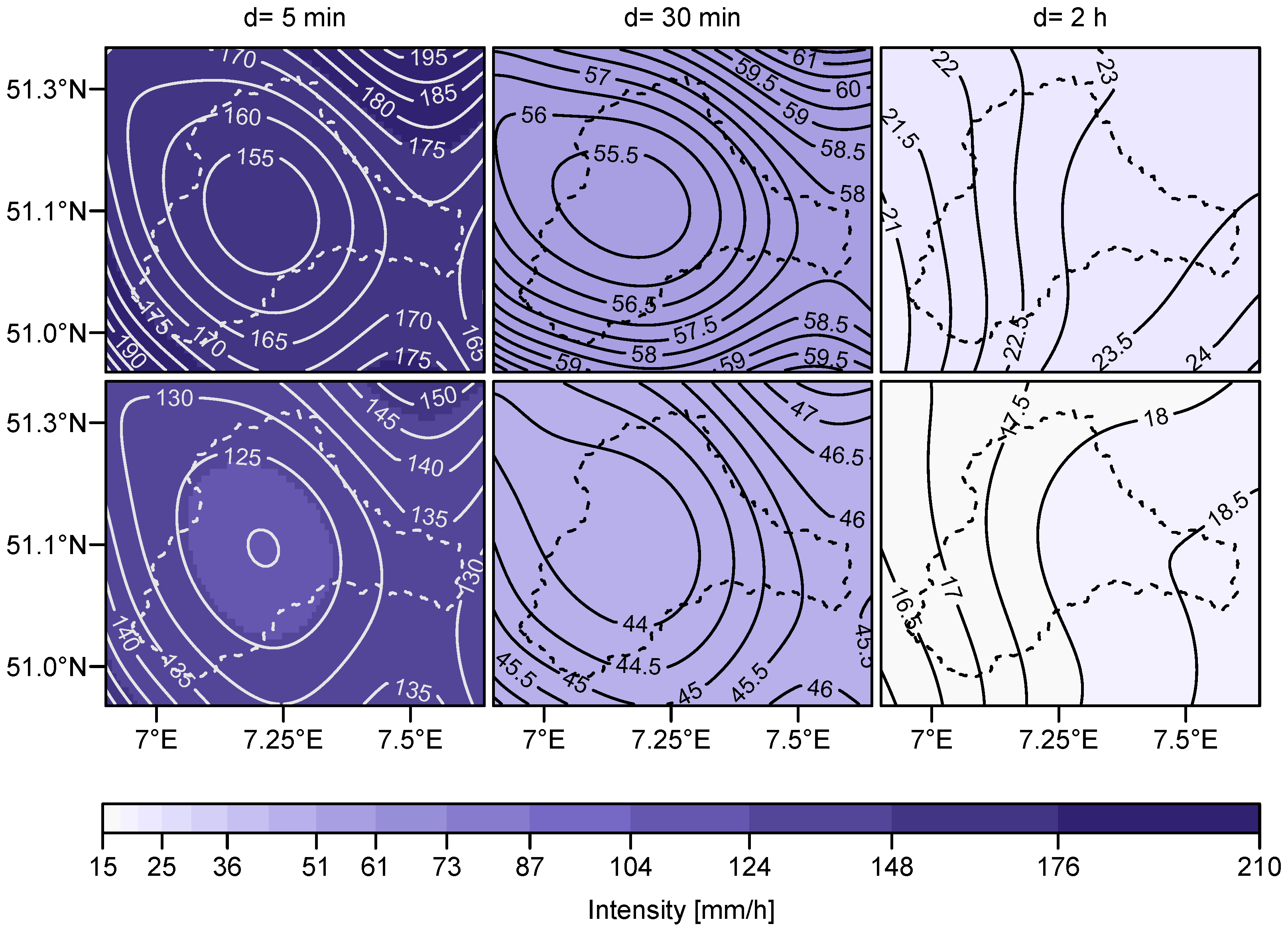
| Provider | Number of Stations | Measuring Interval | Device | Length of Time Series |
|---|---|---|---|---|
| DWD | 69 | 1 day | Hellmann | 9–121 years |
| DWD | 17 | 1 min | Pluvio | 5–14 years |
| WV | 6 | 1 hour | Pluvio | 38 years |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ulrich, J.; Jurado, O.E.; Peter, M.; Scheibel, M.; Rust, H.W. Estimating IDF Curves Consistently over Durations with Spatial Covariates. Water 2020, 12, 3119. https://doi.org/10.3390/w12113119
Ulrich J, Jurado OE, Peter M, Scheibel M, Rust HW. Estimating IDF Curves Consistently over Durations with Spatial Covariates. Water. 2020; 12(11):3119. https://doi.org/10.3390/w12113119
Chicago/Turabian StyleUlrich, Jana, Oscar E. Jurado, Madlen Peter, Marc Scheibel, and Henning W. Rust. 2020. "Estimating IDF Curves Consistently over Durations with Spatial Covariates" Water 12, no. 11: 3119. https://doi.org/10.3390/w12113119
APA StyleUlrich, J., Jurado, O. E., Peter, M., Scheibel, M., & Rust, H. W. (2020). Estimating IDF Curves Consistently over Durations with Spatial Covariates. Water, 12(11), 3119. https://doi.org/10.3390/w12113119






