Barite Scale Formation and Injectivity Loss Models for Geothermal Systems
Abstract
1. Introduction
2. Materials and Methods
2.1. Geochemistry
2.1.1. Fluid Chemistry
2.1.2. Equilibrium Models and Barite Scaling Potential
2.1.3. Crystal Growth Kinetics
2.2. Flow
2.2.1. Reservoir Hydraulics
2.2.2. Reactive Transport Modelling
3. Results
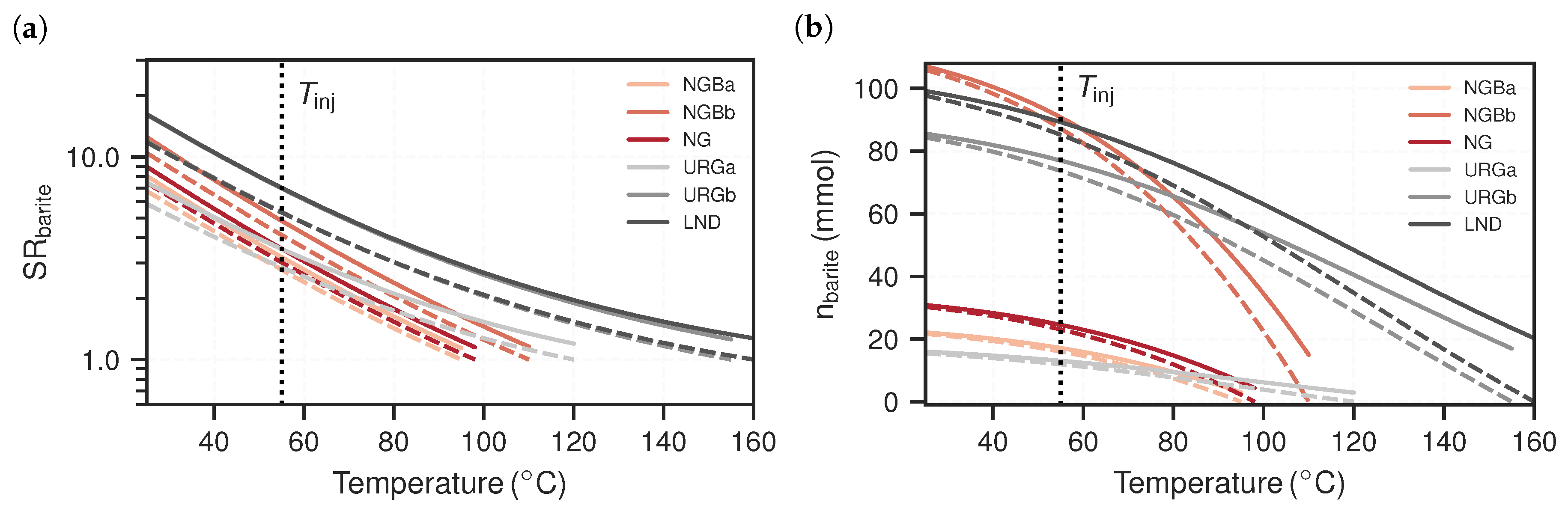
3.1. Equilibrium Models
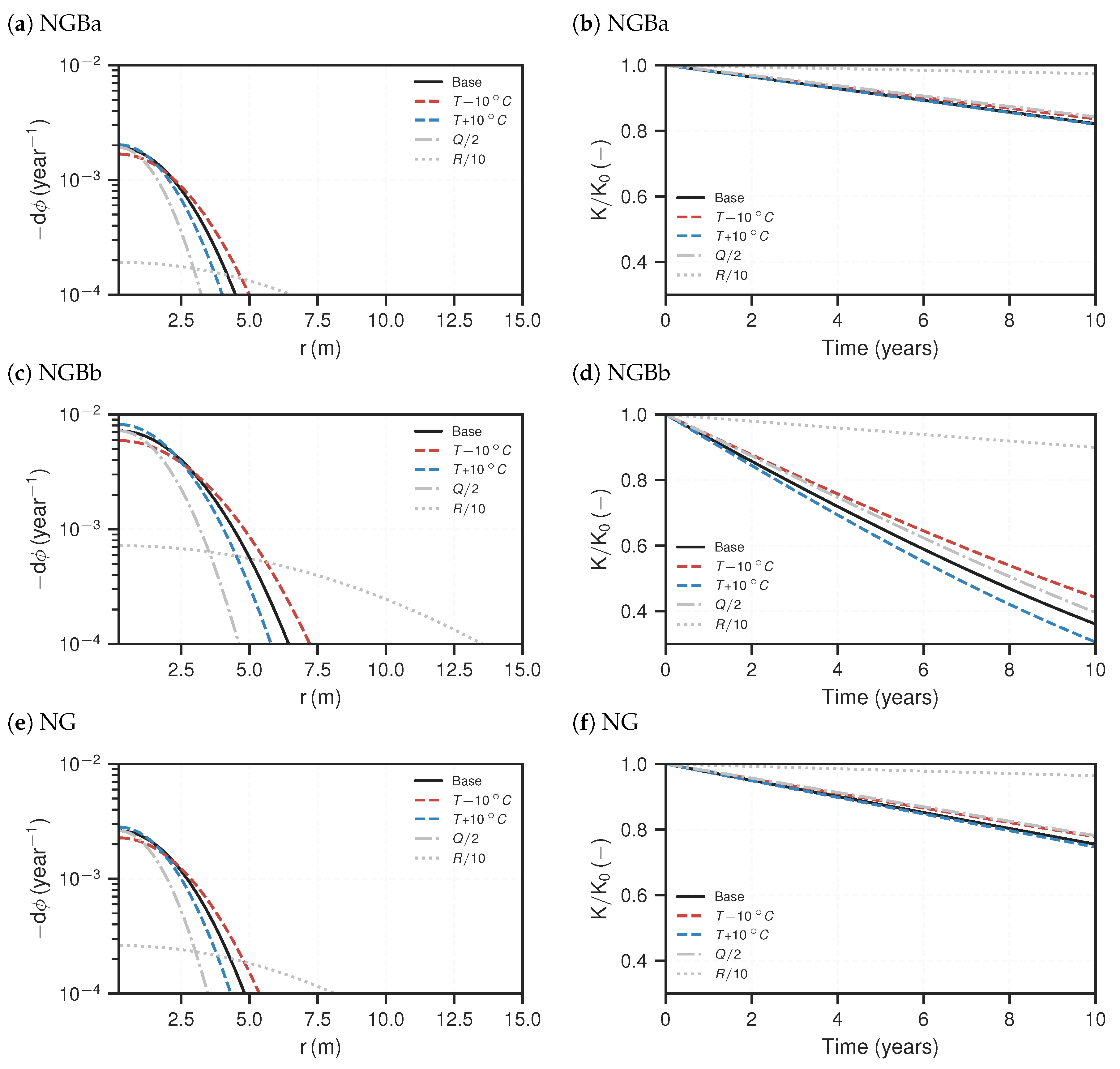
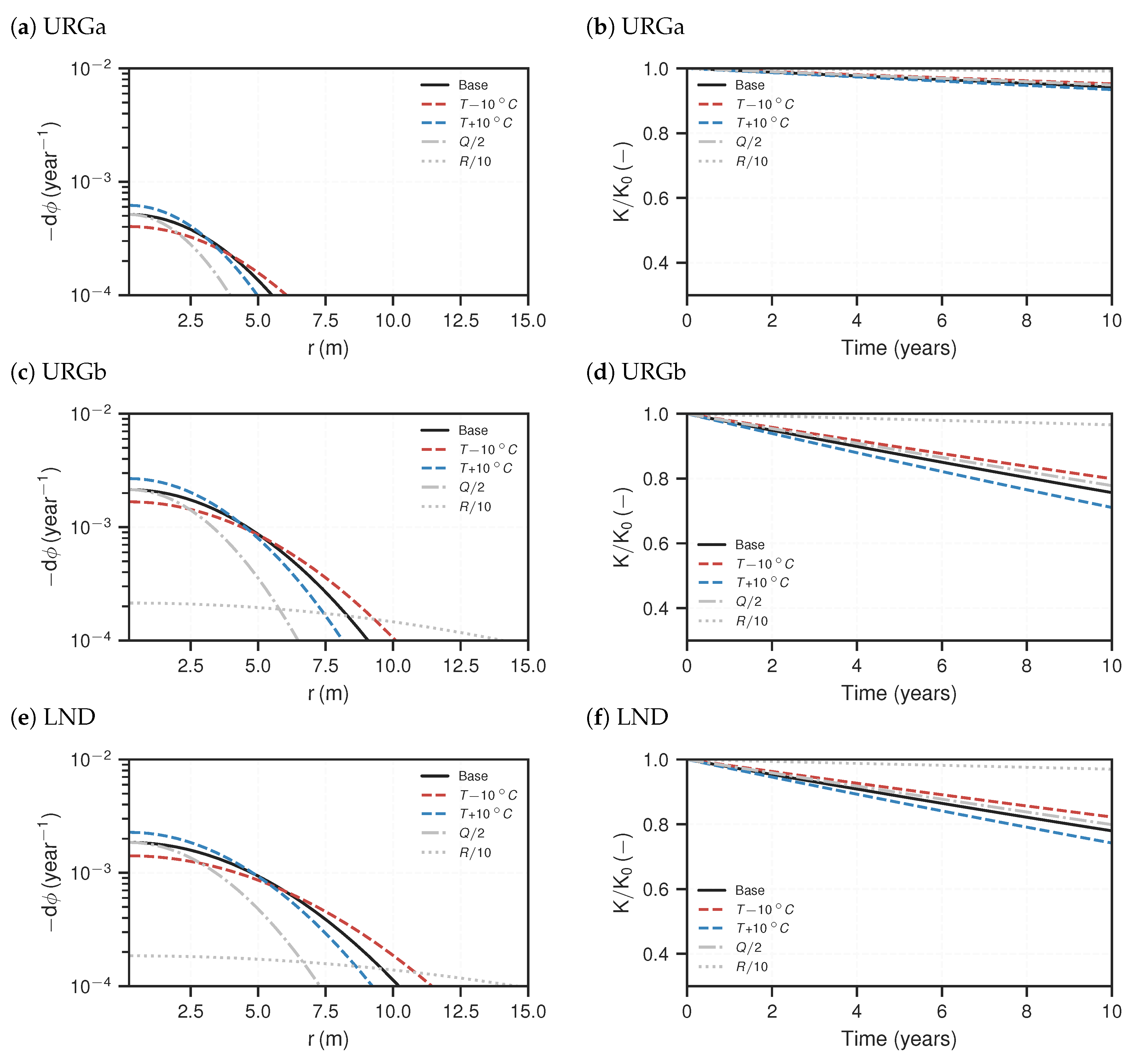
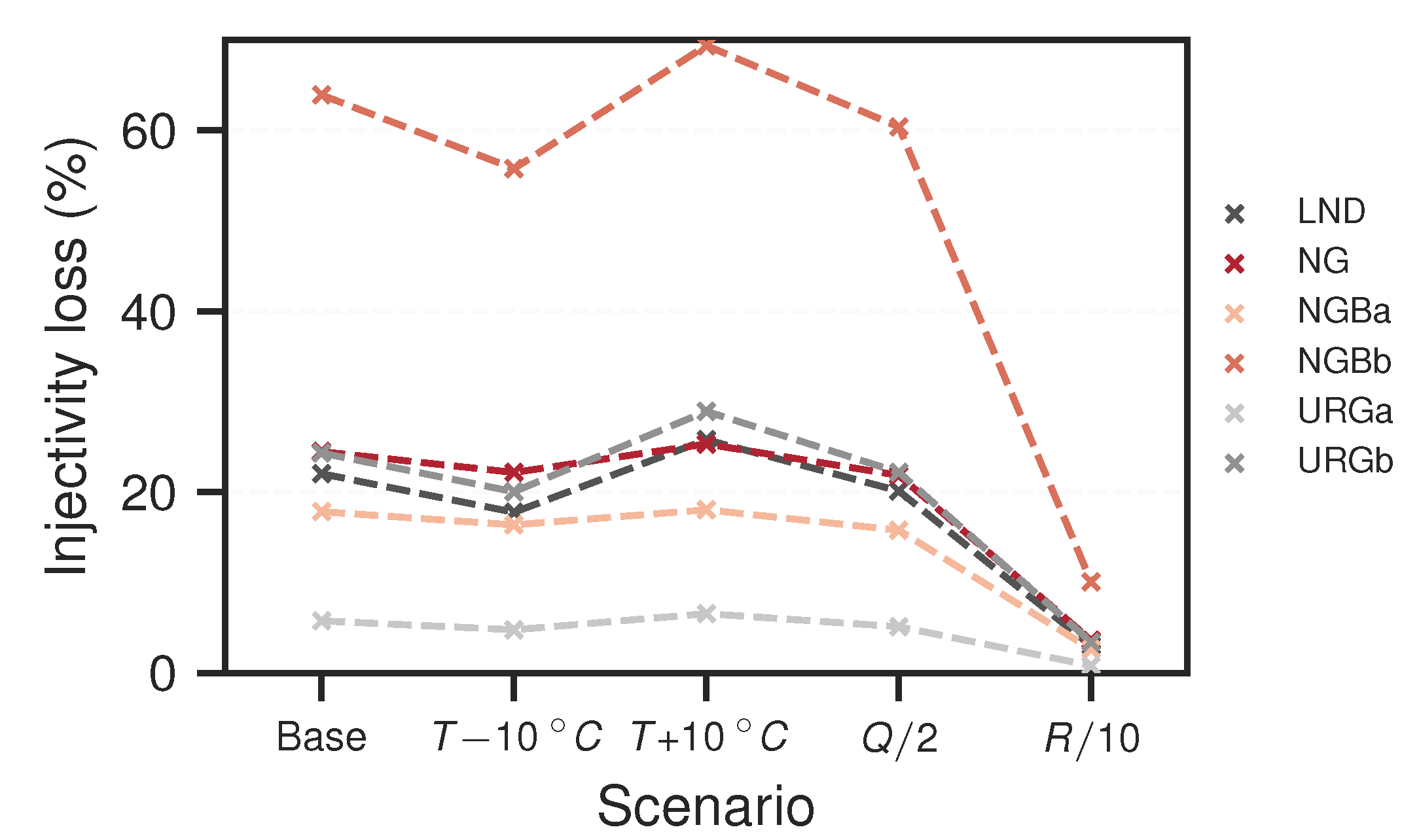
3.2. Reactive Transport Models
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| Abbreviation | Description | Unit |
| Concentration | ||
| Concentration in equilibrium | ||
| Damköhler number | − | |
| Activity coefficient | − | |
| i | Aqueous species or solid | − |
| Ionic strength | ||
| j | Grid node | − |
| J | Injectivity | |
| K | Rock permeability | |
| Initial rock permeability | ||
| Precipitation rate constant | ||
| Solubility constant | ||
| Landau | − | |
| M | Aquifer thickness | |
| Da slope along the r-axis | ||
| Water mass | ||
| Precipitation potential | ||
| Neustadt-Glewe | − | |
| North German Basin | − | |
| P | Pressure | |
| Porosity | − | |
| Initial porosity | − | |
| Volume fraction | − | |
| Q | Flow rate | |
| r | Radial distance from well-centre | |
| R | Barite precipitation rate (surface area normalised) | |
| Characteristic length | ||
| Reach of pressure difference | ||
| Well radius | ||
| Density of solid | ||
| Density of fluid | ||
| s | Water column | |
| S | Specific inner rock surface | |
| Reactive surface area | ||
| Scaling factor for reactive surface area | − | |
| Supersaturation ratio | − | |
| T | Temperature | |
| Injection temperature | ||
| Total dissolved solids | ||
| Upper Rhine Graben | − | |
| V | Flow constant (=Q / 2 M ) | |
| Weight fraction | ||
| Scaling score |
Appendix A. Reactive Transport Simulations
Appendix A.1. Kinetic Rate Constant
| T | |||
|---|---|---|---|
| 25 | |||
| 25 | |||
| 25 | |||
| 25 | |||
| 60 | |||
| 60 | |||
| 60 | |||
| 60 | |||
| 25 |
Appendix A.2. Governing Equations and Analytical Solution

References
- Agemar, T.; Weber, J.; Schulz, R. Deep Geothermal Energy Production in Germany. Energies 2014, 7, 4397–4416. [Google Scholar] [CrossRef]
- Schumacher, S.; Pierau, R.; Wirth, W. Probability of Success Studies for Geothermal Projects in Clastic Reservoirs: From Subsurface Data to Geological Risk Analysis. Geothermics 2020, 83, 101725. [Google Scholar] [CrossRef]
- Wolfgramm, M.; Thorwart, K.; Rauppach, K.; Brandes, J. Zusammensetzung, Herkunft Und Genese Geothermaler Tiefengrundwässer Im Norddeutschen Becken (NDB) Und Deren Relevanz Für Die Geothermische Nutzung. Z. Geol. Wiss. 2011, 339, 173–193. [Google Scholar]
- Pauwels, H.; Fouillac, C.; Fouillac, A.M. Chemistry and Isotopes of Deep Geothermal Saline Fluids in the Upper Rhine Graben: Origin of Compounds and Water-Rock Interactions. Geochim. Cosmochim. Acta 1993, 57, 2737–2749. [Google Scholar] [CrossRef]
- Stober, I.; Wolfgramm, M.; Birner, J. Hydrochemie Der Tiefenwässer in Deutschland. Z. Geol. Wiss. 2013, 42, 339–380. [Google Scholar]
- Naumann, D. Salinare Tiefenwässer in Norddeutschland: Gas- und Isotopengeochemische Untersuchungen zur Herkunft und Geothermische Nutzung; Scientific Technical Report STR00/21; Deutsches GeoForschungsZentrum Potsdam: Potsdam, Germany, 2000. [Google Scholar]
- Sanjuan, B.; Millot, R.; Innocent, C.; Dezayes, C.; Scheiber, J.; Brach, M. Major Geochemical Characteristics of Geothermal Brines from the Upper Rhine Graben Granitic Basement with Constraints on Temperature and Circulation. Chem. Geol. 2016, 428, 27–47. [Google Scholar] [CrossRef]
- Wolfgramm, M.; Seibt, A. Zusammensetzung von Tiefenwässern in Deutschland Und Ihre Relevanz Für Geothermische Anlagenteile. In Proceedings of the Der Geothermiekongress 2011, Rheinstetten, Germany, 11–13 November 2008. [Google Scholar]
- Wolfgramm, M.; Rauppach, K.; Thorwart, K. Mineralneubildung Und Partikeltransport Im Thermalwasserkreislauf Geothermischer Anlagen Deutschlands. Z. Geol. Wiss. 2011, 39, 213–239. [Google Scholar]
- Regenspurg, S.; Feldbusch, E.; Byrne, J.; Deon, F.; Driba, D.L.; Henninges, J.; Kappler, A.; Naumann, R.; Reinsch, T.; Schubert, C. Mineral Precipitation during Production of Geothermal Fluid from a Permian Rotliegend Reservoir. Geothermics 2015, 54, 122–135. [Google Scholar] [CrossRef]
- Nitschke, F.; Scheiber, J.; Kramar, U.; Neumann, T. Formation of Alternating Layered Ba-Sr-Sulfate and Pb-Sulfide Scaling in the Geothermal Plant of Soultz-Sous-Forêts. Neues Jahrb. Mineral. J. Mineral. Geochem. 2014, 191, 145–156. [Google Scholar] [CrossRef]
- Seibt, P.; Kabus, F.; Wolfgramm, M.; Bartels, J.; Seibt, A. Monitoring of Hydrogeothermal Plants in Germany—An Overview. In Proceedings of the World Geothermal Congress, Bali, Indonesia, 25–30 April 2010. [Google Scholar]
- Birner, J.; Seibt, A.; Seibt, P.; Wolfgramm, M. Removing and Reducing Scalings—Practical Experience in the Operation of Geothermal Systems. In Proceedings of the World Geothermal Congress, Melbourne, Australia, 16–24 April 2015. [Google Scholar]
- Scheiber, J.; Seibt, A.; Birner, J.; Genter, A.; Moeckes, W. Application of a Scaling Inhibitor System at the Geothermal Power Plant in Soultz-Sous-Forêts: Laboratory and On-Site Studies. In Proceedings of the European Geothermal Congress, Pisa, Italy, 3–7 June 2013. [Google Scholar]
- Agemar, T.; Schellschmidt, R.; Schulz, R. Subsurface Temperature Distribution in Germany. Geothermics 2012, 44, 65–77. [Google Scholar] [CrossRef]
- Blount, C.W. Barite Solubilities and Thermodynamic Quantities up to 300 ∘C and 1400 Bars. Am. Miner. 1977, 62, 942–957. [Google Scholar]
- Templeton, C.C. Solubility of Barium Sulfate in Sodium Chloride Solutions from 25∘ to 95 ∘C. J. Chem. Eng. Data 1960, 5, 514–516. [Google Scholar] [CrossRef]
- Hörbrand, T.; Baumann, T.; Moog, H.C. Validation of Hydrogeochemical Databases for Problems in Deep Geothermal Energy. Geotherm. Energy 2018, 6. [Google Scholar] [CrossRef]
- Bozau, E.; Häußler, S.; Van Berk, W. Hydrogeochemical Modelling of Corrosion Effects and Barite Scaling in Deep Geothermal Wells of the North German Basin Using PHREEQC and PHAST. Geothermics 2015, 53, 540–547. [Google Scholar] [CrossRef]
- Haarberg, T.; Selm, I.; Granbakken, D.B.; Ostvold, T.; Read, P.; Schmidt, T. Scale Formation in Reservoir and Production Equipment During Oil Recovery: An Equilibrium Model. SPE Prod. Eng. 1992, 7, 75–84. [Google Scholar] [CrossRef]
- Schröder, H.; Teschner, M.; Köhler, M.; Seibt, A.; Krüger, M. Long Term Reliability of Geothermal Plants—Examples from Germany. In Proceedings of the European Geothermal Congress, Unterhaching, Germany, 30 May–1 June 2007. [Google Scholar]
- Lasaga, A.C. Kinetic Theory in the Earth Sciences; Princeton University Press: Oxfordshire, UK, 1998. [Google Scholar]
- Phillips, O.M. Flow and Reactions in Permeable Rocks; Cambridge University Press: Cambridge, UK, 1991. [Google Scholar]
- Beckingham, L.E. Evaluation of Macroscopic Porosity-Permeability Relationships in Heterogeneous Mineral Dissolution and Precipitation Scenarios. Water Resour. Res. 2017, 53, 10217–10230. [Google Scholar] [CrossRef]
- Gardner, G.L.; Nancollas, G.H. Crystal Growth in Aqueous Solution at Elevated Temperatures. Barium Sulfate Growth Kinetics. J. Phys. Chem. 1983, 87, 4699–4703. [Google Scholar] [CrossRef]
- Godinho, J.R.; Stack, A.G. Growth Kinetics and Morphology of Barite Crystals Derived from Face-Specific Growth Rates. Cryst. Growth Des. 2015, 15, 2064–2071. [Google Scholar] [CrossRef]
- Christy, A.G.; Putnis, A. The Kinetics of Barite Dissolution and Precipitation in Water and Sodium Chloride Brines at 44–85 ∘C. Geochim. Cosmochim. Acta 1993, 57, 2161–2168. [Google Scholar] [CrossRef]
- Liu, S.T.; Nancollas, G.H.; Gasiecki, E.A. Scanning Electron Microscopic and Kinetic Studies of the Crystallization and Dissolution of Barium Sulfate Crystals. J. Cryst. Growth 1976, 33, 11–20. [Google Scholar] [CrossRef]
- Nancollas, G.H.; Purdie, N. Crystallization of Barium Sulphate in Aqueous Solution. Trans. Faraday Soc. 1963, 59. [Google Scholar] [CrossRef]
- Ruiz-Agudo, C.; Putnis, C.V.; Ruiz-Agudo, E.; Putnis, A. The Influence of pH on Barite Nucleation and Growth. Chem. Geol. 2015, 391, 7–18. [Google Scholar] [CrossRef]
- Risthaus, P.; Bosbach, D.; Becker, U.; Putnis, A. Barite Scale Formation and Dissolution at High Ionic Strength Studied with Atomic Force Microscopy. Colloids Surf. Physicochem. Eng. Asp. 2001, 191, 201–214. [Google Scholar] [CrossRef]
- Zhen-Wu, B.Y.; Dideriksen, K.; Olsson, J.; Raahauge, P.J.; Stipp, S.L.; Oelkers, E.H. Experimental Determination of Barite Dissolution and Precipitation Rates as a Function of Temperature and Aqueous Fluid Composition. Geochim. Cosmochim. Acta 2016, 194, 193–210. [Google Scholar] [CrossRef]
- Nancollas, G.H.; Liu, S.T. Crystal Growth and Dissolution of Barium Sulfate. Soc. Pet. Eng. J. 1975, 15, 509–516. [Google Scholar] [CrossRef]
- Orywall, P.; Drüppel, K.; Kuhn, D.; Kohl, T.; Zimmermann, M.; Eiche, E. Flow-through Experiments on the Interaction of Sandstone with Ba-Rich Fluids at Geothermal Conditions. Geotherm. Energy 2017, 5, 20. [Google Scholar] [CrossRef]
- Kühn, M.; Frosch, G.; Kölling, M.; Kellner, T. Experimentelle Untersuchungen Zur Barytübersättigung Einer Thermalsole. Grundwasser 1997, 2, 111–117. [Google Scholar] [CrossRef]
- Griffiths, L.; Heap, M.J.; Wang, F.; Daval, D.; Gilg, H.A.; Baud, P.; Schmittbuhl, J.; Genter, A. Geothermal Implications for Fracture-Filling Hydrothermal Precipitation. Geothermics 2016, 64, 235–245. [Google Scholar] [CrossRef]
- Wolfgramm, M.; Rauppach, K.; Seibt, A.; Müller, K.; Canic, T.; Adelhelm, C. Rasterelektronenmikroskopische Untersuchungen von Barytkristallen Nach Fällung Aus Salinarem Modell-Geothermalwasser—Zur Reduzierung von Barytscaling in Geothermischen Anlagen. In Proceedings of the Der Geothermiekongress 2011, Bochum, Germany, 17–19 November 2009. [Google Scholar]
- Canic, T.; Baur, S.; Adelhelm, C.; Rauppach, K.; Wolfgramm, M. Kinetik von Barytausfällungen Aus Geothermalwasser—Einfluss Der Scherung. In Proceedings of the Der Geothermiekongress 2011, Bochum, Germany, 17–19 November 2009. [Google Scholar]
- Baumgärtner, J.; Teza, D.; Hettkamp, T.; Hauffe, P. Stimulierung Tiefer Geothermischer Systeme. BBR Fachmagazine Brunn. Leitungsbau 2010, 61, 13–23. [Google Scholar]
- Bär, K.M. Untersuchung Der Tiefengeothermischen Potenziale von Hessen. Ph.D. Thesis, Technische Universität, Darmstadt, Germany, 2012. [Google Scholar]
- Kühn, M.; Vernoux, J.F.; Kellner, T.; Isenbeck-Schröter, M.; Schulz, H.D. Onsite Experimental Simulation of Brine Injection into a Clastic Reservoir as Applied to Geothermal Exploitation in Germany. Appl. Geochem. 1998, 13, 477–490. [Google Scholar] [CrossRef]
- Parkhurst, D.L.; Appelo, C. Description of Input and Examples for PHREEQC Version 3: A Computer Program for Speciation, Batch-Reaction, One-Dimensional Transport, and Inverse Geochemical Calculations; Report 6-A43; USGS: Reston, VA, USA, 2013.
- Pitzer, K.S. Theoretical Considerations of Solubility with Emphasis on Mixed Aqueous Electrolytes; LBNL Report LBL-21961; Lawrence Berkeley National Laboratory: Berkeley, CA, USA, 1986.
- Wolfgramm, M. Fluidentwicklung und Diagenese im Nordostdeutschen Becken-Petrographie, Mikrothermometrie und Geochemie Stabiler Isotope. Ph.D. Thesis, Martin-Luther-Universität Halle-Wittenberg, Halle, Germany, 2002. [Google Scholar]
- Bruss, D. Zur Herkunft der Erdöle im mittleren Oberrheingraben und ihre Bedeutung für die Rekonstruktion der Migrationsgeschichte und der Speichergesteinsdiagenese; Number 3831 in Berichte des Forschungszentrums Jülich; Forschungszentrum Jülich GmbH Zentralbibliothek, Verlag: Jülich, Germany, 2000. [Google Scholar]
- Kühn, M.; Bartels, J.; Iffland, J. Predicting Reservoir Property Trends under Heat Exploitation: Interaction between Flow, Heat Transfer, Transport, and Chemical Reactions in a Deep Aquifer at Stralsund, Germany. Geothermics 2002, 31, 725–749. [Google Scholar] [CrossRef]
- Wiersberg, T.; Seibt, A.; Zimmer, M. Gas-Geochemische Untersuchungen an Formationsfluiden Des Rotliegend Der Bohrung Groß Schönebeck 3/90; Scientific Technical Report STR04/03; Deutsches GeoForschungsZentrum Potsdam: Potsdam, Germany, 2004. [Google Scholar]
- Seibt, A.; Thorwart, K. Untersuchungen Zur Gasphase Geothermischer Genutzter Tiefenwässer Und Deren Relevanz Für Den Anlagenbetrieb. Z. Geol. Wiss. 2011, 39, 264–274. [Google Scholar]
- Rabbani, A.; Jamshidi, S. Specific Surface and Porosity Relationship for Sandstones for Prediction of Permeability. Int. J. Rock Mech. Min. Sci. 2014, 71, 25–32. [Google Scholar] [CrossRef]
- Beckingham, L.E.; Mitnick, E.H.; Steefel, C.I.; Zhang, S.; Voltolini, M.; Swift, A.M.; Yang, L.; Cole, D.R.; Sheets, J.M.; Ajo-Franklin, J.B.; et al. Evaluation of Mineral Reactive Surface Area Estimates for Prediction of Reactivity of a Multi-Mineral Sediment. Geochim. Cosmochim. Acta 2016, 188, 310–329. [Google Scholar] [CrossRef]
- Dupuit, J. Études Théoriques et Pratiques Sur Le Mouvement Des Eaux Dans Les Canaux Découverts et à Travers Les Terrains Perméables; Technical Report; Dunod: Paris, France, 1863. [Google Scholar]
- Franz, M.; Barth, G.; Zimmermann, J.; Budach, I.; Nowak, K.; Wolfgramm, M. Geothermal Resources of the North German Basin: Exploration Strategy, Development Examples and Remaining Opportunities in Mesozoic Hydrothermal Reservoirs. Geol. Soc. Lond. Spec. Publ. 2018, 469, 193–222. [Google Scholar] [CrossRef]
- Langevin, C.D. Modeling Axisymmetric Flow and Transport. Ground Water 2008, 46, 579–590. [Google Scholar] [CrossRef] [PubMed]
- Bear, J. Dynamics of Fluids in Porous Media. Soil Sci. 1972, 120, 162–163. [Google Scholar] [CrossRef]
- Lichtner, P.C. The Quasi-Stationary State Approximation to Coupled Mass Transport and Fluid-Rock Interaction in a Porous Medium. Geochim. Cosmochim. Acta 1988, 52, 143–165. [Google Scholar] [CrossRef]
- Carman, P.C. Fluid Flow through Granular Beds. Trans. Inst. Chem. Eng. 1937, 15, 150–166. [Google Scholar] [CrossRef]
- Hommel, J.; Coltman, E.; Class, H. Porosity–Permeability Relations for Evolving Pore Space: A Review with a Focus on (Bio-)Geochemically Altered Porous Media. Transp. Porous Media 2018, 124, 589–629. [Google Scholar] [CrossRef]
- Renard, P.; De Marsily, G. Calculating Equivalent Permeability: A Review. Adv. Water Resour. 1997, 20, 253–278. [Google Scholar] [CrossRef]
- Prieto, M. Nucleation and Supersaturation in Porous Media (Revisited). Miner. Mag. 2014, 78, 1437–1447. [Google Scholar] [CrossRef][Green Version]
- He, S.; Oddo, J.E.; Tomson, M.B. The Inhibition of Gypsum and Barite Nucleation in NaCl Brines at Temperatures from 25 to 90 ∘C. Appl. Geochem. 1994, 9, 561–567. [Google Scholar] [CrossRef]
- Pandey, S.; Chaudhuri, A.; Rajaram, H.; Kelkar, S. Fracture Transmissivity Evolution Due to Silica Dissolution/Precipitation during Geothermal Heat Extraction. Geothermics 2015, 57, 111–126. [Google Scholar] [CrossRef]
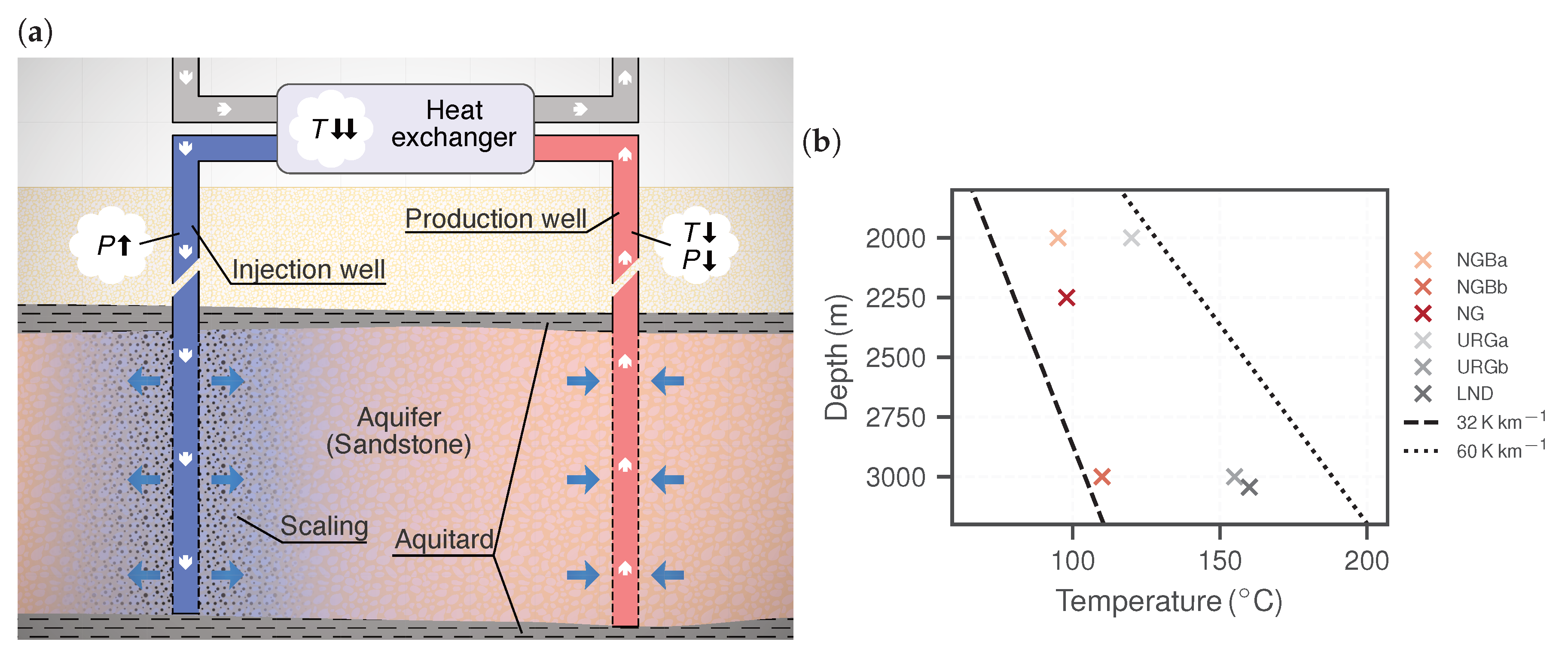
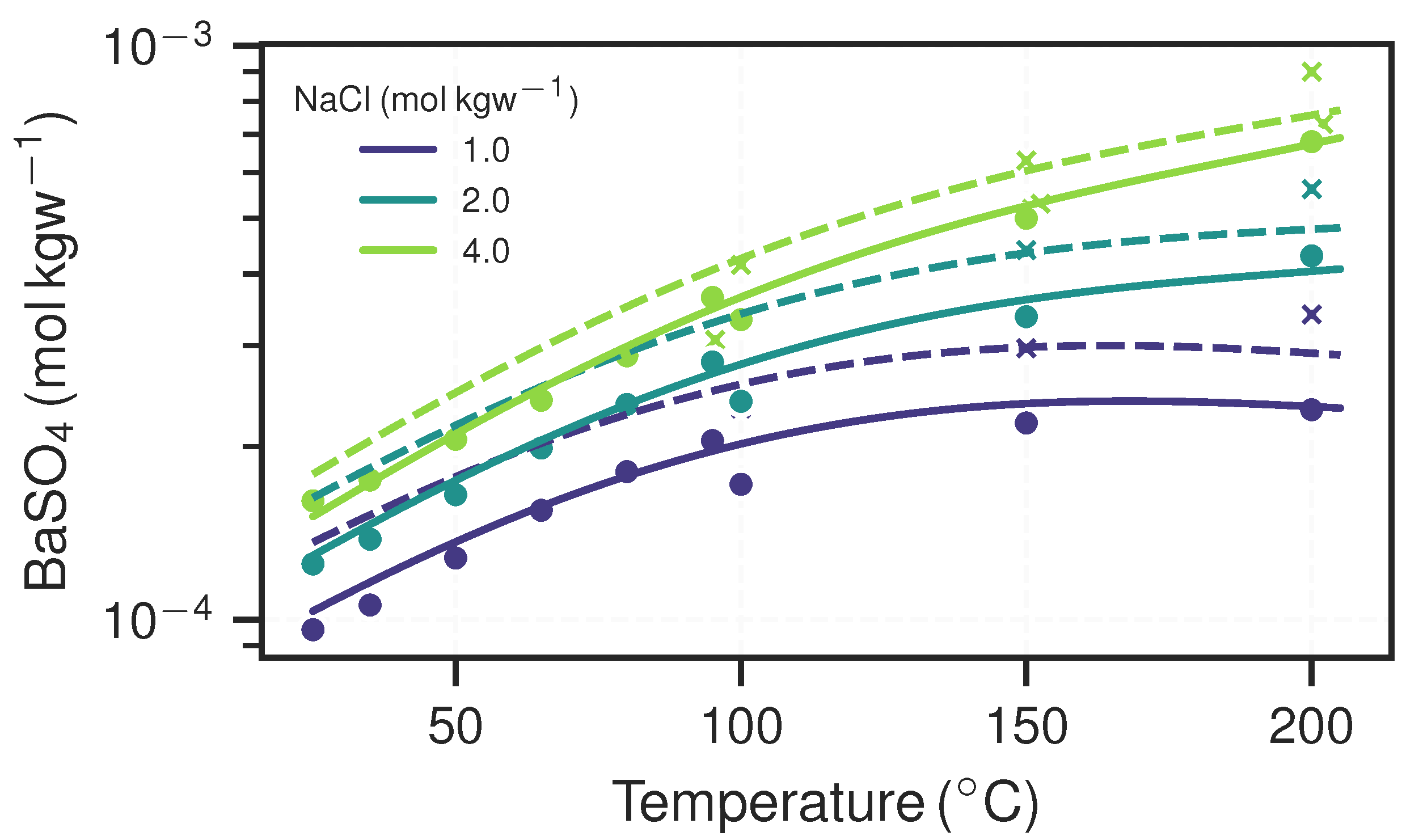
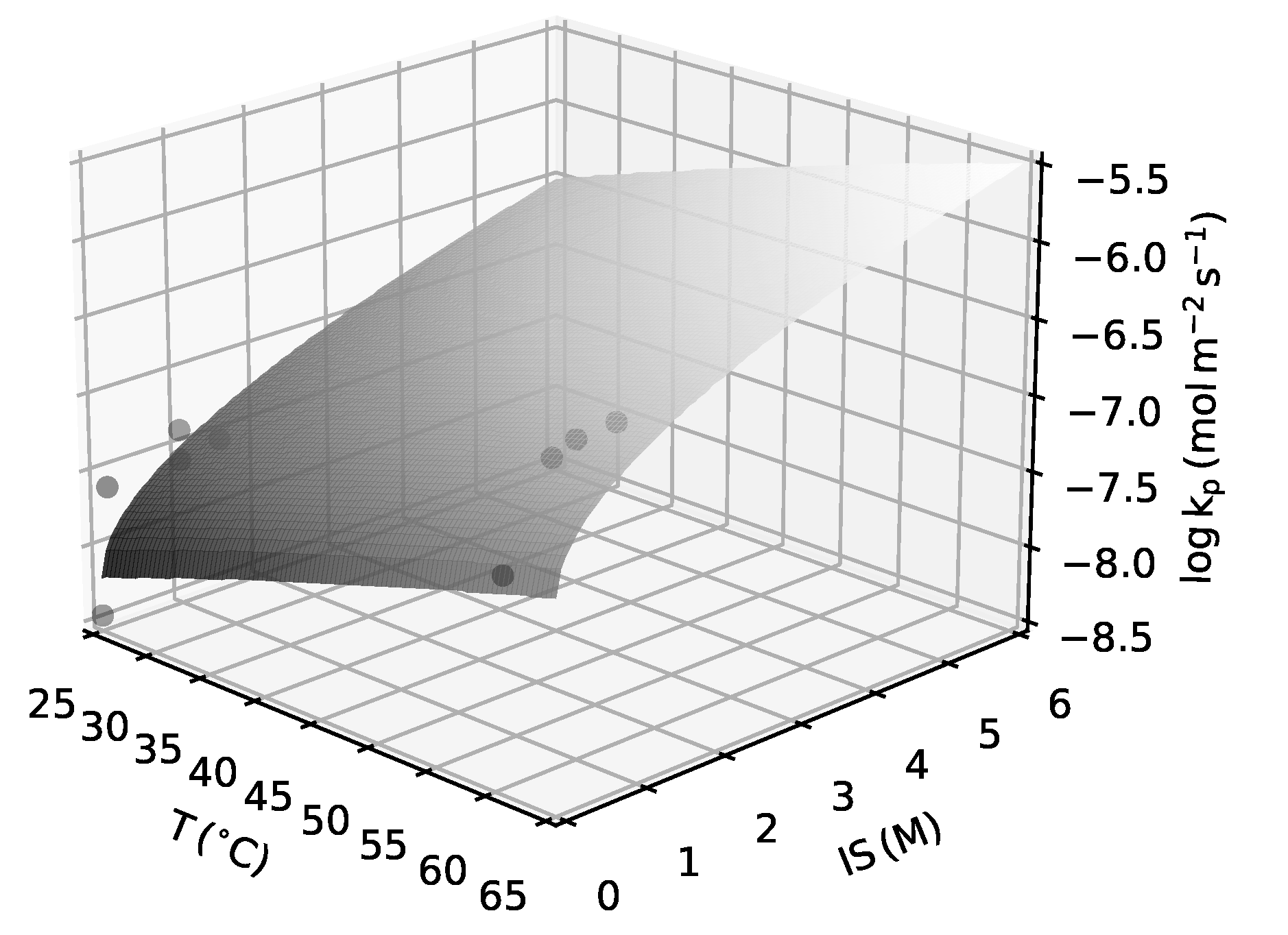
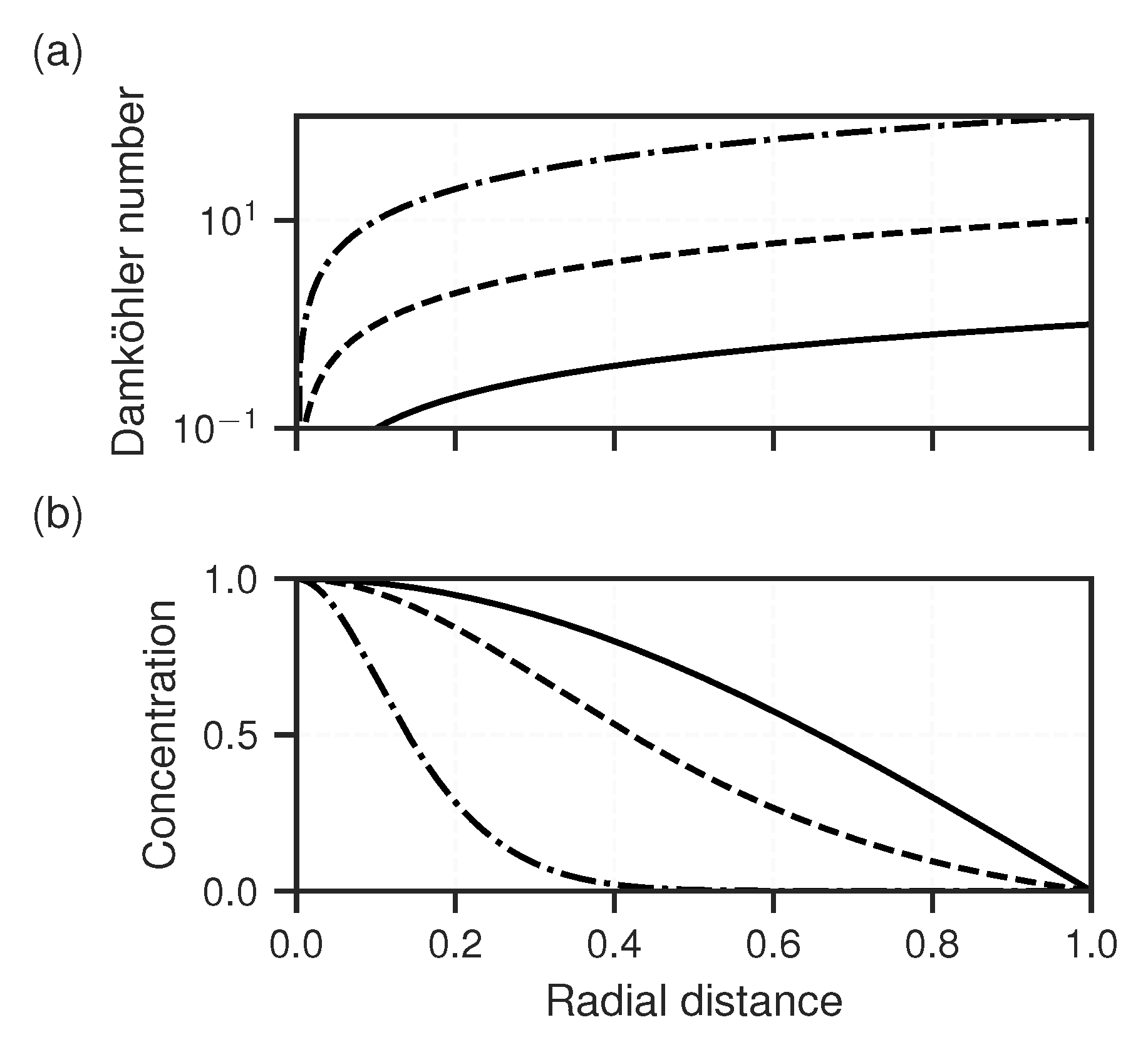
| Parameter | Unit | NGBa | NGBb | NG | URGa | URGb | LND | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Measured | Reservoir | Measured | Reservoir | Measured | Reservoir | Measured | Reservoir | Measured | Reservoir | Measured | Reservoir | ||
| T | 25 | 95 | 25 | 110 | 25 | 98 | 25 | 120 | 25 | 155 | 25 | 160 | |
| P | 0.1 | 20 | 0.1 | 30 | 0.1 | 23 | 0.1 | 20 | 0.1 | 30 | 0.1 | 30 | |
| 1130 | 1110 | 1190 | 1150 | 1150 | 1110 | 1050 | 1000 | 1080 | 1010 | 1070 | 996 | ||
| − | 5.60 | 5.33 | 6.00 | 4.91 | 5.20 | 5.64 | 5.80 | 5.66 | 5.50 | 5.28 | 5.15 | 5.41 | |
| 4.05 | 4.00 | 6.21 | 6.11 | 4.50 | 4.48 | 1.37 | 1.32 | 2.29 | 2.31 | 2.05 | 2.01 | ||
| − | NA | 3.42 | NA | 2.89 | 8.33 | 5.47 | NA | 3.19 | NA | 2.64 | 6.38 | 3.62 | |
| 2.06 | 2.06 | 2.87 | 2.87 | 2.24 | 2.24 | 7.88 | 7.88 | 1.33 | 1.33 | 1.06 | 1.06 | ||
| 3.08 | 3.08 | 4.87 | 4.87 | 3.54 | 3.54 | 8.94 | 8.94 | 1.59 | 1.59 | 1.27 | 1.27 | ||
| 2.11 | 2.15 | 3.49 | 3.47 | 2.33 | 2.37 | 1.03 | 1.04 | 1.82 | 1.77 | 1.99 | 1.96 | ||
| 7.53 | 7.53 | 4.61 | 4.61 | 6.43 | 6.43 | 4.23 | 4.23 | 4.29 | 4.29 | 3.25 | 3.25 | ||
| 5.53 | 3.38 | 8.57 | 5.70 | 5.61 | 3.80 | 2.58 | 2.70 | 4.16 | 8.83 | 5.09 | 1.06 | ||
| NA | 2.71 | NA | 1.30 | 4.43 | 3.77 | NA | 1.89 | NA | 9.53 | 8.69 | 1.10 | ||
| 1.73 | 1.73 | 2.61 | 2.61 | 1.26 | 1.26 | 1.84 | 1.84 | 3.73 | 3.73 | 4.03 | 4.03 | ||
| 3.79 | 3.67 | 5.85 | 5.69 | 4.19 | 4.15 | 1.30 | 1.18 | 2.06 | 2.10 | 1.88 | 1.79 | ||
| 4.04 | 4.04 | 6.73 | 6.73 | 5.30 | 5.30 | 1.29 | 1.29 | 2.61 | 2.61 | 2.84 | 2.84 | ||
| 5.04 | 7.91 | 7.58 | 4.49 | 5.31 | 6.89 | 3.74 | 5.93 | 3.26 | 3.61 | 1.36 | 3.02 | ||
| 3.97 | 3.61 | 5.97 | 4.10 | 7.11 | 8.32 | 4.21 | 4.04 | 7.69 | 7.42 | 4.01 | 4.14 | ||
| NA | 4.15 | NA | 4.25 | NA | 4.16 | NA | 1.09 | NA | 1.89 | 2.75 | 2.12 | ||
| 0.22 | 100 | 500 | 20 | 0.2 |
| Scenario | Parameter | Value | Unit |
|---|---|---|---|
| T | 65 | ||
| T | 45 | ||
| Q | 50 | ||
| 0.01 | − |
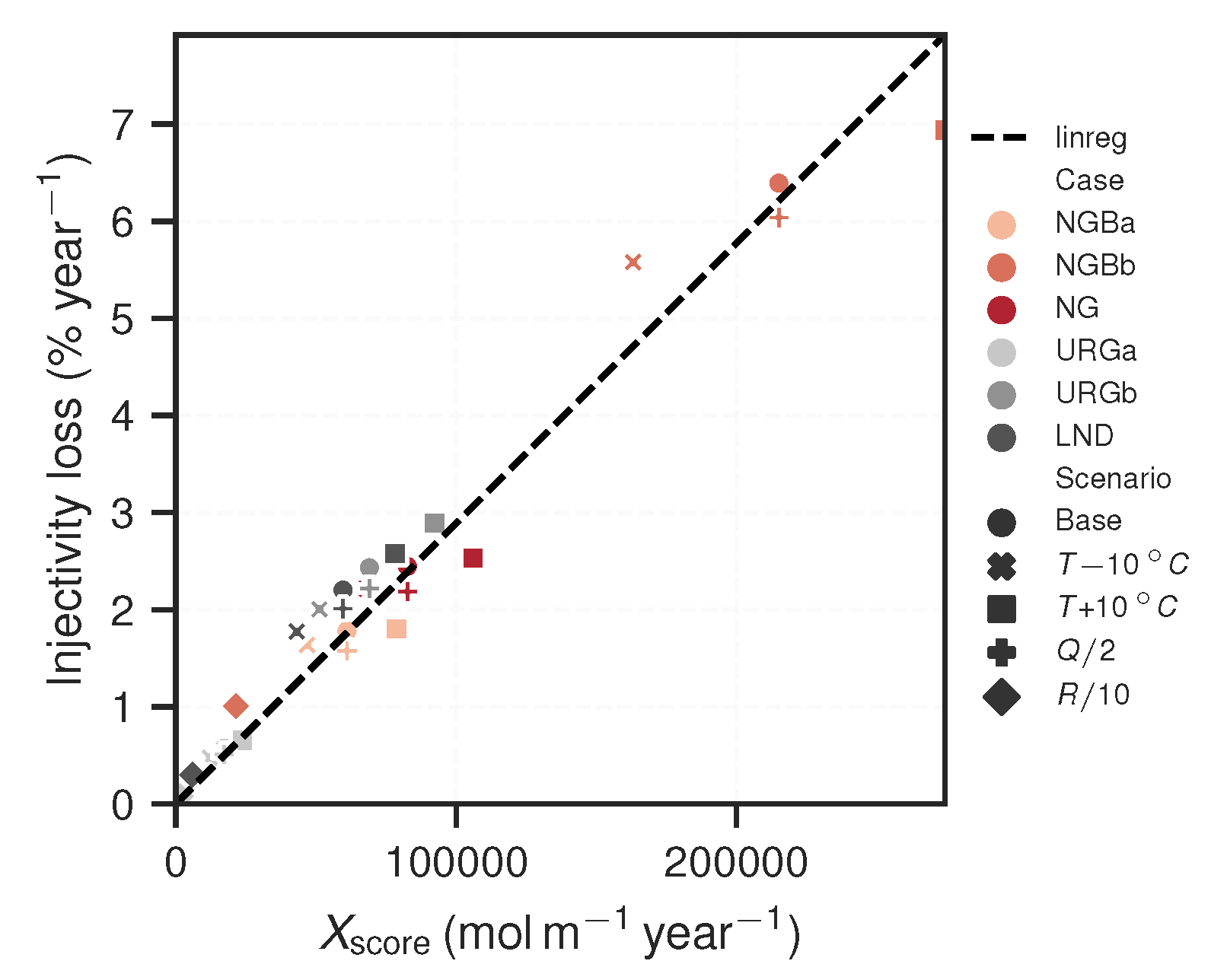
| Scenario | Loss | ||||
|---|---|---|---|---|---|
| Case | |||||
| NGBa | Base | 16 | 4.4 | 0.018 | 6.1 |
| NGBa | 16 | 5.6 | 0.018 | 7.9 | |
| NGBa | 16 | 3.3 | 0.016 | 4.7 | |
| NGBa | 16 | 8.7 | 0.016 | 6.1 | |
| NGBa | 16 | 0.43 | 0.0026 | 0.61 | |
| NGBb | Base | 87 | 2.8 | 0.064 | 22 |
| NGBb | 87 | 3.6 | 0.069 | 27 | |
| NGBb | 87 | 2.1 | 0.056 | 16 | |
| NGBb | 87 | 5.6 | 0.06 | 22 | |
| NGBb | 87 | 0.28 | 0.01 | 2.1 | |
| NG | Base | 23 | 4.1 | 0.024 | 8.3 |
| NG | 23 | 5.3 | 0.025 | 11 | |
| NG | 23 | 3.2 | 0.022 | 6.4 | |
| NG | 23 | 8.2 | 0.022 | 8.3 | |
| NG | 23 | 0.41 | 0.0036 | 0.83 | |
| URGa | Base | 12 | 1.6 | 0.0057 | 1.7 |
| URGa | 12 | 2.3 | 0.0066 | 2.4 | |
| URGa | 12 | 1.2 | 0.0048 | 1.2 | |
| URGa | 12 | 3.3 | 0.0051 | 1.7 | |
| URGa | 12 | 0.16 | 0.0008 | 0.17 | |
| URGb | Base | 74 | 1.1 | 0.024 | 6.9 |
| URGb | 74 | 1.4 | 0.029 | 9.2 | |
| URGb | 74 | 0.79 | 0.02 | 5.1 | |
| URGb | 74 | 2.1 | 0.022 | 6.9 | |
| URGb | 74 | 0.11 | 0.0034 | 0.69 | |
| LND | Base | 85 | 0.8 | 0.022 | 6 |
| LND | 85 | 1 | 0.026 | 7.8 | |
| LND | 85 | 0.58 | 0.018 | 4.3 | |
| LND | 85 | 1.6 | 0.02 | 6 | |
| LND | 85 | 0.08 | 0.003 | 0.6 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tranter, M.; De Lucia, M.; Wolfgramm, M.; Kühn, M. Barite Scale Formation and Injectivity Loss Models for Geothermal Systems. Water 2020, 12, 3078. https://doi.org/10.3390/w12113078
Tranter M, De Lucia M, Wolfgramm M, Kühn M. Barite Scale Formation and Injectivity Loss Models for Geothermal Systems. Water. 2020; 12(11):3078. https://doi.org/10.3390/w12113078
Chicago/Turabian StyleTranter, Morgan, Marco De Lucia, Markus Wolfgramm, and Michael Kühn. 2020. "Barite Scale Formation and Injectivity Loss Models for Geothermal Systems" Water 12, no. 11: 3078. https://doi.org/10.3390/w12113078
APA StyleTranter, M., De Lucia, M., Wolfgramm, M., & Kühn, M. (2020). Barite Scale Formation and Injectivity Loss Models for Geothermal Systems. Water, 12(11), 3078. https://doi.org/10.3390/w12113078





