Significant Extremal Dependence of a Daily North Atlantic Oscillation Index (NAOI) and Weighted Regionalised Rainfall in a Small Island Using the Extremogram
Abstract
1. Introduction
2. Study Area
3. Rainfall and NAO Data
3.1. Daily Rainfall Data
3.2. North Atlantic Oscillation Index (NAOI) Daily Data
4. Methods
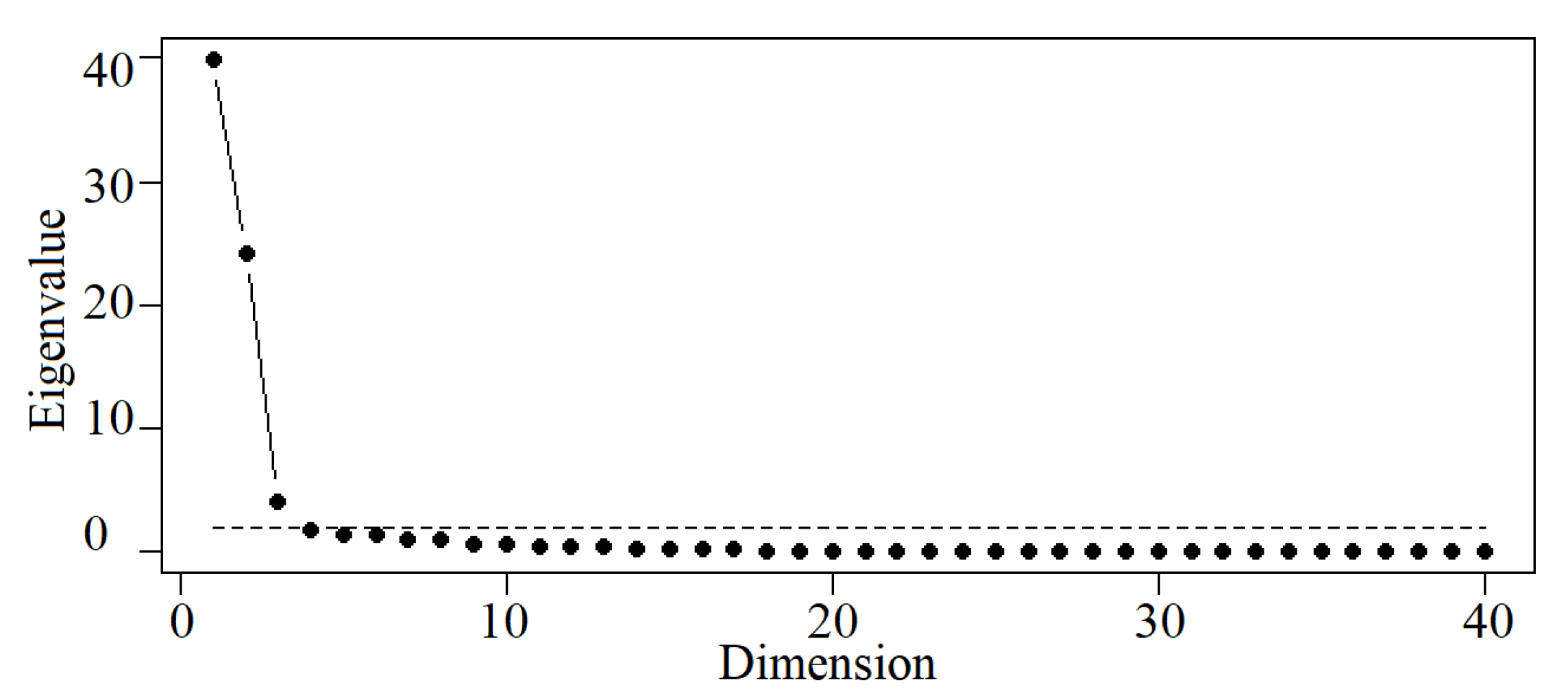
4.1. Regionalisation of the Daily Rainfall Series
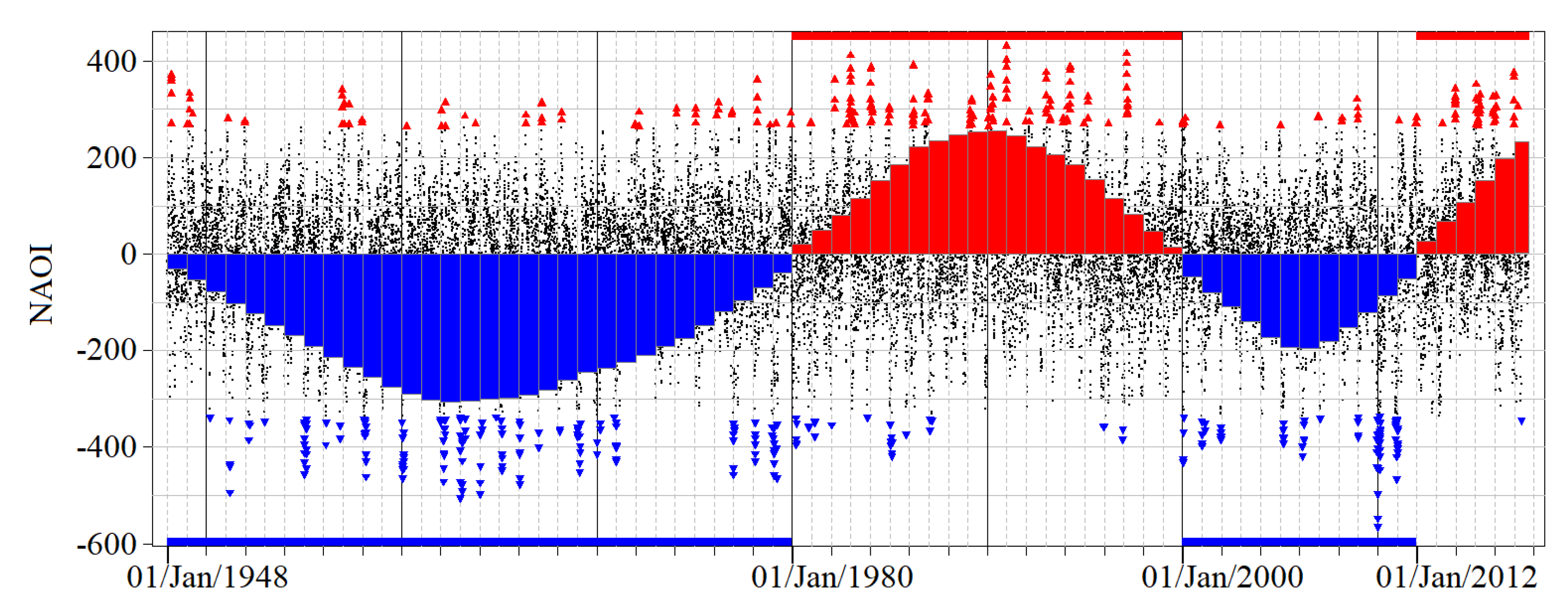
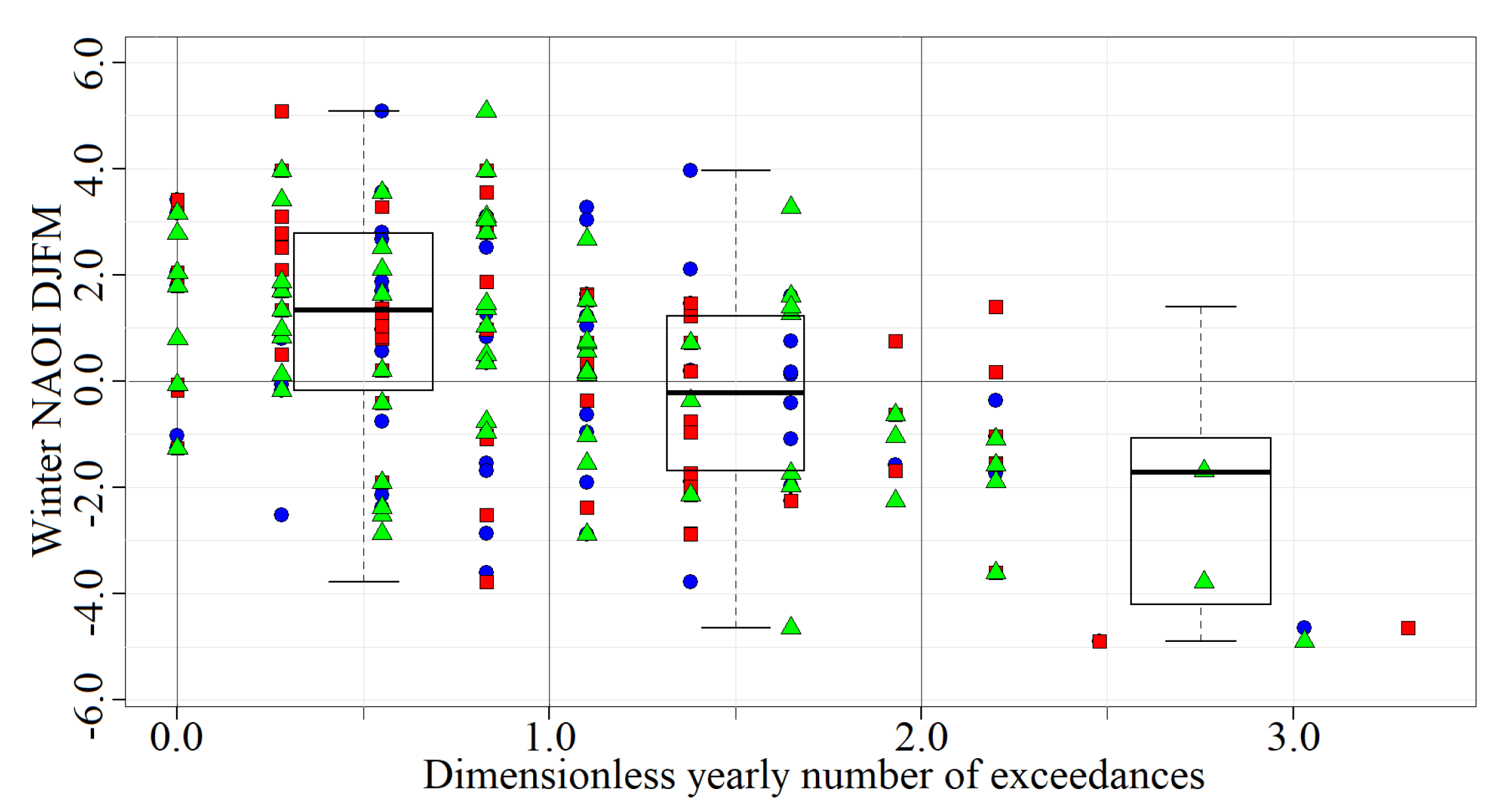
4.2. Dominant Negative and Positive NAO Phases
4.3. Strictly Stationary and Regularly Varying
4.4. Tail-Dependence
4.5. Extremogram
4.6. Cross-Extremogram
5. Results
5.1. Weighted Regionalised Daily Rainfall Series
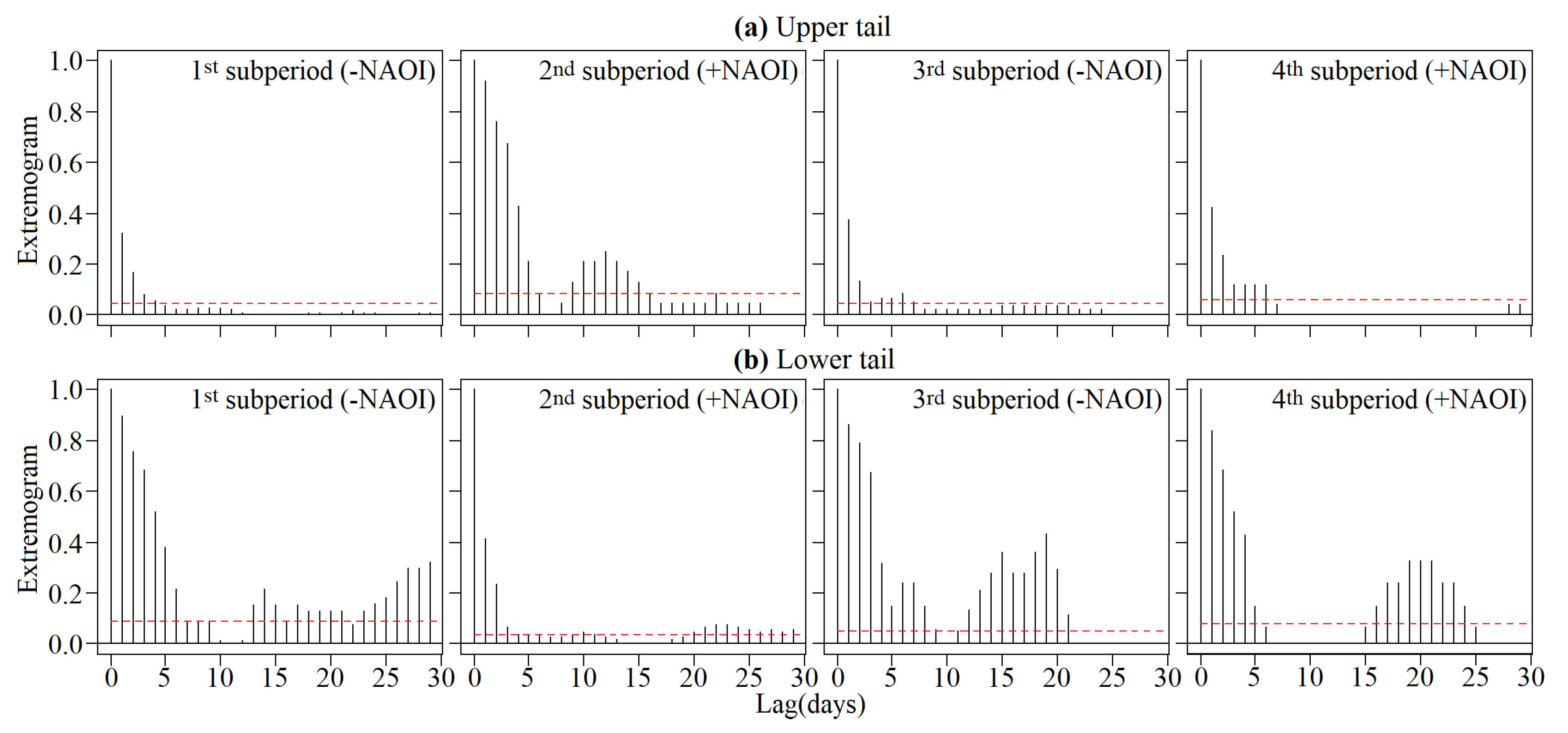
5.2. Dominant Extremal NAOI Subperiods and Their Extremograms
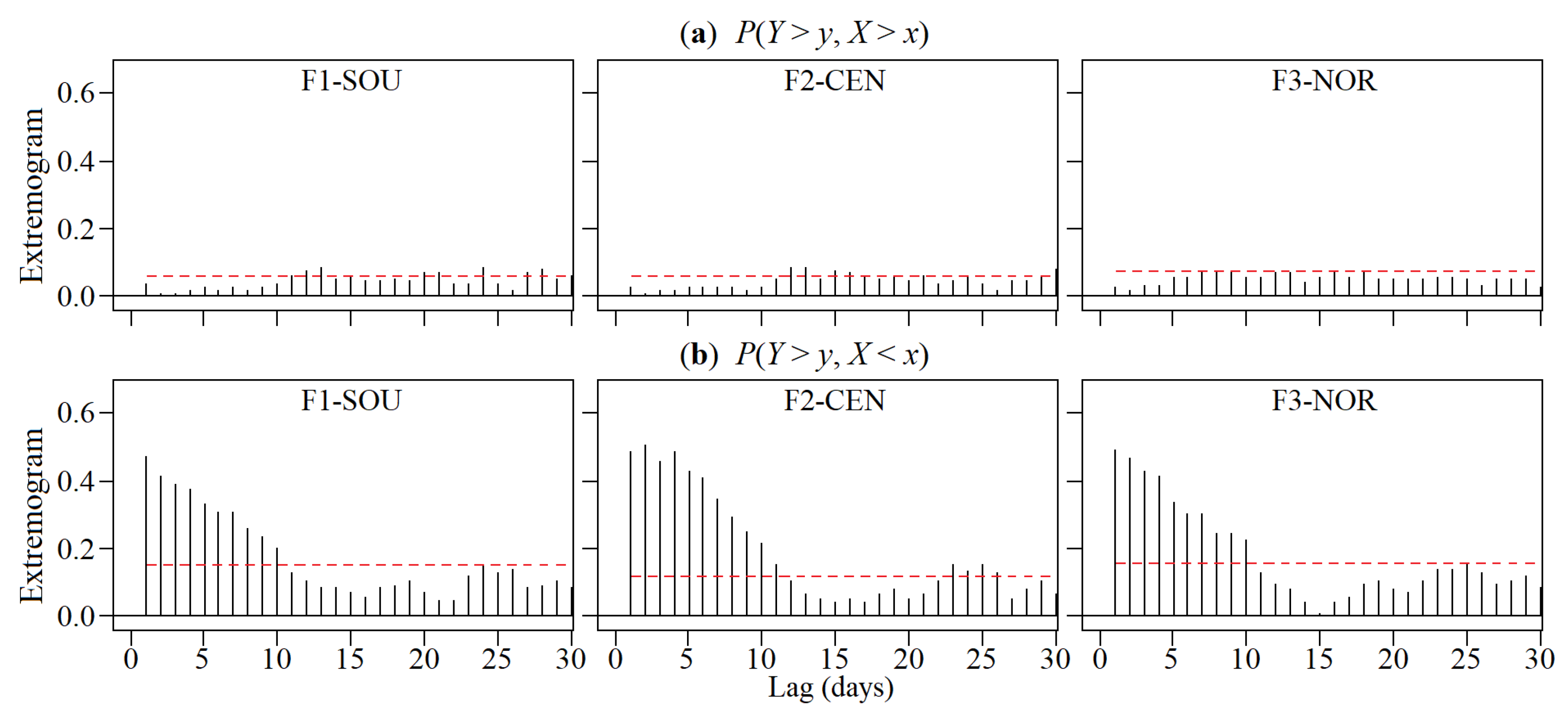
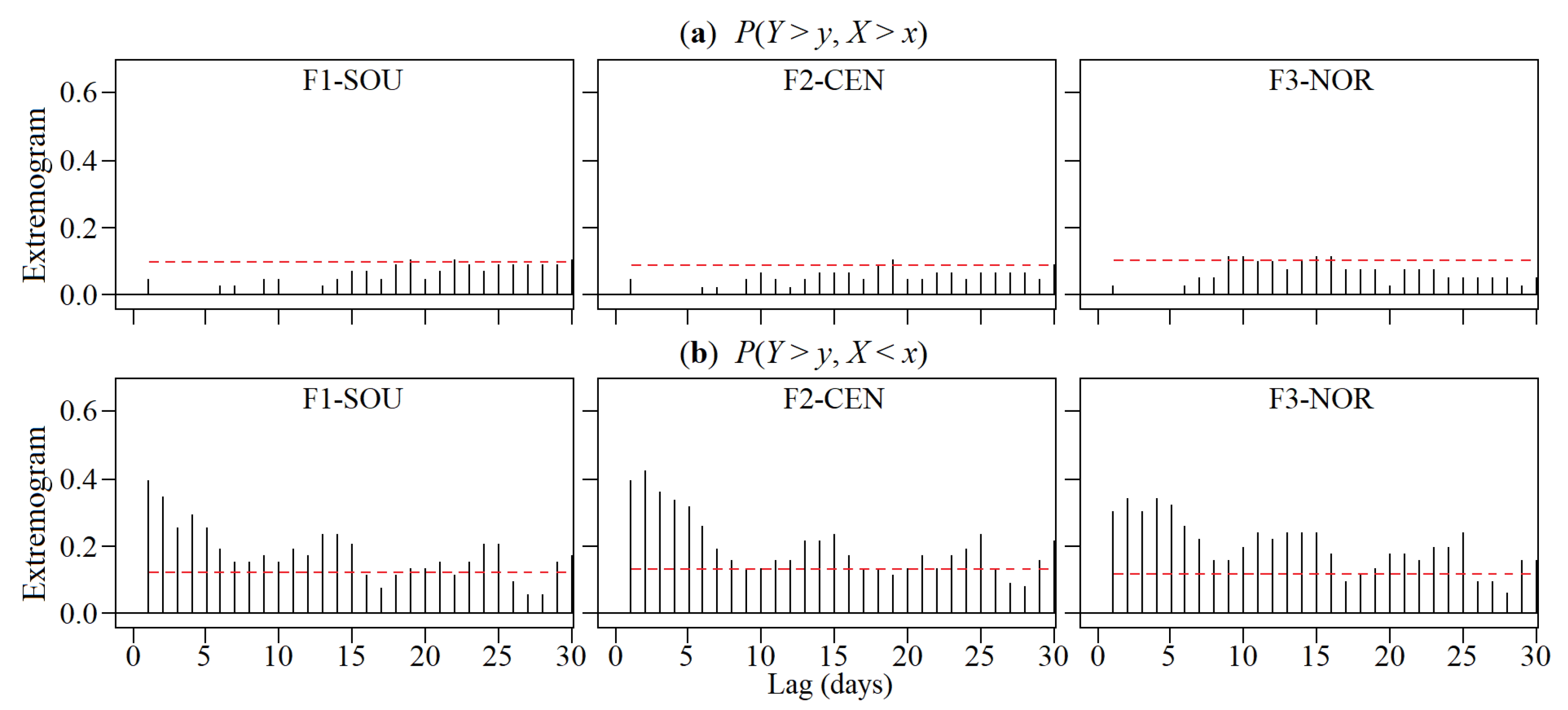
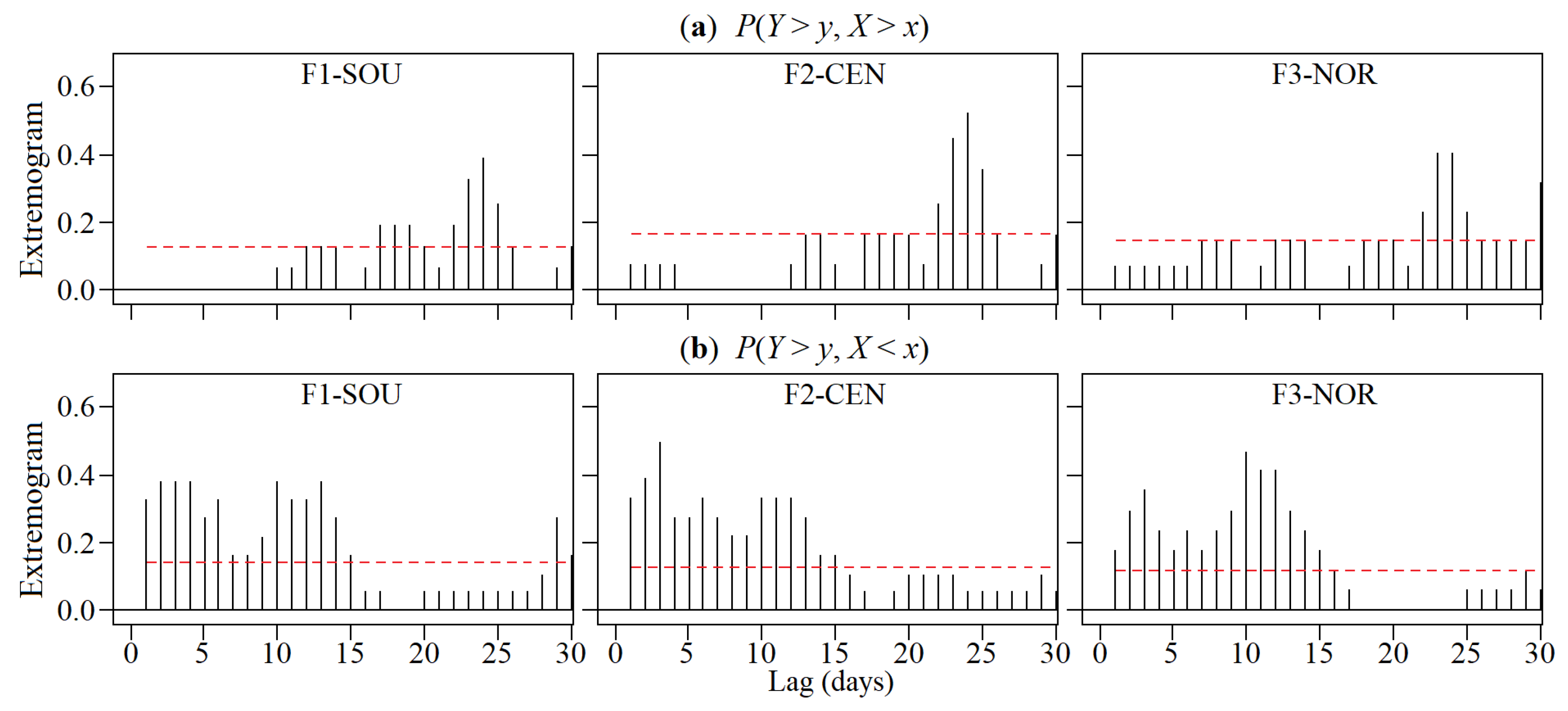
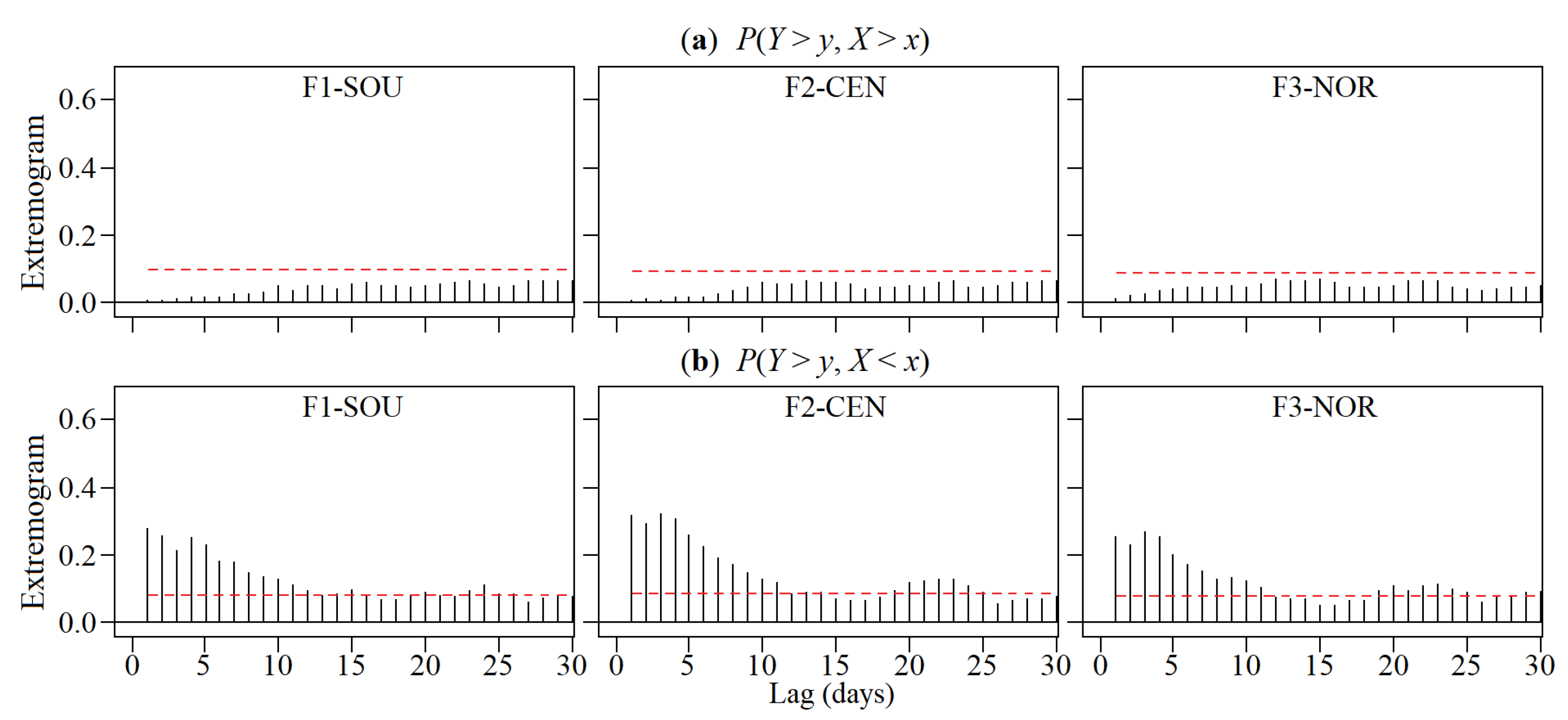
5.3. Extremal Dependence of the Regionalised Rainfall and NAOI via the Cross-Extremogram
5.4. Discussion and Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Boers, N.; Goswami, B.; Rheinwalt, A.; Bookhagen, B.; Hoskins, B.; Kurths, J. Complex networks reveal global pattern of extreme-rainfall teleconnections. Nature 2019, 566, 373–377. [Google Scholar] [CrossRef] [PubMed]
- McCarthy, J.J.; Canziani, O.F.; Leary, N.A.; Dokken, D.J.; White, K.S. (Eds.) Climate Change 2001: Impacts, Adaptation, and Vulnerability: Contribution of Working Group II to the Third Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK, 2001; Volume 2. [Google Scholar]
- Feng, Z.; Leung, L.R.; Hagos, S.; Houze, R.A.; Burleyson, C.D.; Balaguru, K. More frequent intense and long-lived storms dominate the springtime trend in central US rainfall. Nat. Commun. 2016, 7, 1–8. [Google Scholar] [CrossRef] [PubMed]
- Padilla, F.M.; Mommer, L.; de Caluwe, H.; Smit-Tiekstra, A.E.; Visser, E.J.; de Kroon, H. Effects of extreme rainfall events are independent of plant species richness in an experimental grassland community. Oecologia 2019, 191, 177–190. [Google Scholar] [CrossRef] [PubMed]
- Sanches, F.; Verdum, R.; Fisch, G.; Gass, S.L.B.; Rocha, V.M. Extreme Rainfall Events in the Southwest of Rio Grande do Sul (Brazil) and Its Association with the Sandization Process. Am. J. Clim. Chang. 2019, 8, 441. [Google Scholar] [CrossRef]
- Tabari, H.; Madani, K.; Arnbjerg-Nielsen, K.; Willems, P. Disentangling natural and forced components of extreme rainfall hazards over Europe. EGU2019: European Geophysical Union General Assembly 2019, Vienna, 7–12 April 2019. Geophys. Res. Abstr. 2019, 21. [Google Scholar]
- Hanna, E.; Cropper, T.E.; Jones, P.D.; Scaife, A.A.; Allan, R. Recent seasonal asymmetric changes in the NAO (a marked summer decline and increased winter variability) and associated changes in the AO and Greenland Blocking Index. Int. J. Climatol. 2015, 35, 2540–2554. [Google Scholar] [CrossRef]
- Davis, R.A.; Mikosch, T. The extremogram: A correlogram for extreme events. Bernoulli 2009, 15, 977–1009. [Google Scholar] [CrossRef]
- Smolka, A. Natural disasters and the challenge of extreme events: Risk management from an insurance perspective. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2006, 364, 2147–2165. [Google Scholar] [CrossRef]
- Costa, A.C.; Soares, A. Trends in extreme precipitation indices derived from a daily rainfall database for the South of Portugal. Int. J. Climatol. A J. R. Meteorol. Soc. 2009, 29, 1956–1975. [Google Scholar] [CrossRef]
- Soares, P.M.; Cardoso, R.M.; Miranda, P.M.; Viterbo, P.; Belo-Pereira, M. Assessment of the ENSEMBLES regional climate models in the representation of precipitation variability and extremes over Portugal. J. Geophys. Res. Atmos. 2012, 117. [Google Scholar] [CrossRef]
- Santos, M.; Fragoso, M. Precipitation variability in Northern Portugal: Data homogeneity assessment and trends in extreme precipitation indices. Atmos. Res. 2013, 131, 34–45. [Google Scholar] [CrossRef]
- Luna, T.; Rocha, A.; Carvalho, A.; Ferreira, J.; Sousa, J. Modelling the extreme precipitation event over Madeira Island on 20 February 2010. Nat. Hazards Earth Syst. Sci. 2011, 11, 2437–2452. [Google Scholar] [CrossRef]
- Fragoso, M.; Trigo, R.; Pinto, J.; Lopes, S.; Lopes, A.; Ulbrich, S.; Magro, C. The 20 February 2010 Madeira flash-floods: Synoptic analysis and extreme rainfall assessment. Nat. Hazards Earth Syst. Sci. 2012, 12, 715–730. [Google Scholar] [CrossRef]
- Levizzani, V.; Laviola, S.; Cattani, E.; Costa, M.J. Extreme precipitation on the Island of Madeira on 20 February 2010 as seen by satellite passive microwave sounders. Eur. J. Remote Sens. 2013, 46, 475–489. [Google Scholar] [CrossRef]
- Teixeira, J.; Carvalho, A.; Carvalho, M.; Luna, T.; Rocha, A. Sensitivity of the WRF model to the lower boundary in an extreme precipitation event–Madeira island case study. Nat. Hazards Earth Syst. Sci. 2014, 14, 2009–2025. [Google Scholar] [CrossRef]
- Gouveia-Reis, D.; Lopes, L.G.; Mendonça, S. A dependence modelling study of extreme rainfall in Madeira Island. Phys. Chem. Earth Parts A/B/C 2016, 94, 85–93. [Google Scholar] [CrossRef]
- Van Montfort, M.; Witter, J. The generalized Pareto distribution applied to rainfall depths. Hydrol. Sci. J. 1986, 31, 151–162. [Google Scholar] [CrossRef]
- Fan, L.; Chen, D. Trends in extreme precipitation indices across China detected using quantile regression. Atmos. Sci. Lett. 2016, 17, 400–406. [Google Scholar] [CrossRef]
- Acero, F.J.; García, J.A.; Gallego, M.C. Peaks-over-threshold study of trends in extreme rainfall over the Iberian Peninsula. J. Clim. 2011, 24, 1089–1105. [Google Scholar] [CrossRef]
- Veron, S.; Mouchet, M.; Govaerts, R.; Haevermans, T.; Pellens, R. Vulnerability to climate change of islands worldwide and its impact on the tree of life. Sci. Rep. 2019, 9, 1–14. [Google Scholar] [CrossRef]
- Wise, J. The autocorrelation function and the spectral density function. Biometrika 1955, 42, 151–159. [Google Scholar] [CrossRef]
- Osborn, T.J.; Briffa, K.R.; Tett, S.F.; Jones, P.D.; Trigo, R.M. Evaluation of the North Atlantic Oscillation as simulated by a coupled climate model. Clim. Dyn. 1999, 15, 685–702. [Google Scholar] [CrossRef]
- Hurrell, J.W.; Deser, C. North Atlantic climate variability: The role of the North Atlantic Oscillation. J. Mar. Syst. 2010, 79, 231–244. [Google Scholar] [CrossRef]
- Mitchell, D.; Davini, P.; Harvey, B.; Massey, N.; Haustein, K.; Woollings, T.; Jones, R.; Otto, F.; Guillod, B.; Sparrow, S.; et al. Assessing mid-latitude dynamics in extreme event attribution systems. Clim. Dyn. 2017, 48, 3889–3901. [Google Scholar] [CrossRef]
- Uvo, C.B. Analysis and regionalization of northern European winter precipitation based on its relationship with the North Atlantic Oscillation. Int. J. Climatol. A J. R. Meteorol. Soc. 2003, 23, 1185–1194. [Google Scholar] [CrossRef]
- Tabari, H.; Willems, P. Lagged influence of Atlantic and Pacific climate patterns on European extreme precipitation. Sci. Rep. 2018, 8, 5748. [Google Scholar] [CrossRef]
- Trigo, R.M.; Zêzere, J.L.; Rodrigues, M.L.; Trigo, I.F. The influence of the North Atlantic Oscillation on rainfall triggering of landslides near Lisbon. Nat. Hazards 2005, 36, 331–354. [Google Scholar] [CrossRef]
- Cropper, T.; Hanna, E.; Valente, M.A.; Jónsson, T. A daily Azores–Iceland North Atlantic Oscillation index back to 1850. Geosci. Data J. 2015, 2, 12–24. [Google Scholar] [CrossRef]
- Falkland, A.; Custodio, E. Hydrology and water resources of small islands: A practical guide: A contribution to the International Hydrological Programme. Stud. Rep. Hydrol. 1991, 49, i–xiii. [Google Scholar]
- Chazarra, A.; Baceló, A.; Pires, V.; Cunha, S.; Silva, A.; Marques, J.; Carvalho, F.; Mendes, M.; Neto, J.; Mendes, L. Climate Atlas of the Archipelagos of the Canary Islands, Madeira and the Azores: Air Temperature and Precipitation PRECIPITATION (1971–2000); Ministry of Agriculture, Food and Environment, State Meteorological Agency: Madrid, Spain, 2011.
- Espinosa, L.A.; Portela, M.M.; Rodrigues, R. Spatio-temporal variability of droughts over past 80 years in Madeira Island. J. Hydrol. Reg. Stud. 2019, 25, 100623. [Google Scholar] [CrossRef]
- NOAA. Daily Climate Timeseries: NAO: NOAA PSL. Available online: https://psl.noaa.gov/data/timeseries/daily/NAO/ (accessed on 20 February 2020).
- Lyra, G.B.; Oliveira-Júnior, J.F.; Zeri, M. Cluster analysis applied to the spatial and temporal variability of monthly rainfall in Alagoas state, Northeast of Brazil. Int. J. Climatol. 2014, 34, 3546–3558. [Google Scholar] [CrossRef]
- Abatzoglou, J.T.; Redmond, K.T.; Edwards, L.M. Classification of regional climate variability in the state of California. J. Appl. Meteorol. Climatol. 2009, 48, 1527–1541. [Google Scholar] [CrossRef]
- Espinosa, L.A.; Portela, M.M.; Pontes Filho, J.D.; Studart, T.M.d.C.; Santos, J.F.; Rodrigues, R. Jointly Modeling Drought Characteristics with Smoothed Regionalized SPI Series for a Small Island. Water 2019, 11, 2489. [Google Scholar] [CrossRef]
- Ferrelli, F.; Brendel, A.; Aliaga, V.; Piccolo, M.; Perillo, G. Climate regionalization and trends based on daily temperature and precipitation extremes in the south of the Pampas (Argentina). Cuad. De Investig. Geográfica 2019, 45, 393–416. [Google Scholar] [CrossRef]
- Pomee, M.S.; Hertig, E. Statistical downscaling of temperature over the Euro-Mediterranean region: The role of sea surface temperature and soil moisture as additional predictors. Geophys. Res. Abstr. 2019, 21, EGU2019-10012-1. Available online: https://meetingorganizer.copernicus.org/EGU2019/EGU2019-10012-1.pdf (accessed on 25 October 2020).
- Baeriswyl, P.A.; Rebetez, M. Regionalization of precipitation in Switzerland by means of principal component analysis. Theor. Appl. Climatol. 1997, 58, 31–41. [Google Scholar] [CrossRef]
- Álvarez-Rodríguez, J.; Llasat, M.; Estrela, T. Analysis of geographic and orographic influence in Spanish monthly precipitation. Int. J. Climatol. 2017, 37, 350–362. [Google Scholar] [CrossRef]
- Santos, M.; Fragoso, M.; Santos, J.A. Regionalization and susceptibility assessment to daily precipitation extremes in mainland Portugal. Appl. Geogr. 2017, 86, 128–138. [Google Scholar] [CrossRef]
- Fazel, N.; Berndtsson, R.; Uvo, C.B.; Madani, K.; Kløve, B. Regionalization of precipitation characteristics in Iran’s Lake Urmia basin. Theor. Appl. Climatol. 2018, 132, 363–373. [Google Scholar] [CrossRef]
- Raja, N.B.; Aydin, O. Regionalization of precipitation in Mauritius: A statistical approach. Meteorol. Appl. 2019, 26, 711–719. [Google Scholar] [CrossRef]
- Evans, D.G.; Jones, S.M. Detecting Voronoi (area-of-influence) polygons. Math. Geol. 1987, 19, 523–537. [Google Scholar] [CrossRef]
- Abdi, H. Factor rotations in factor analyses. In Encyclopedia for Research Methods for the Social Sciences; Sage: Thousand Oaks, CA, USA, 2003; pp. 792–795. [Google Scholar]
- Kaufman, J.D.; Dunlap, W.P. Determining the number of factors to retain: Q windows-based FORTRAN-IMSL program for parallel analysis. Behav. Res. Methods Instrum. Comput. 2000, 32, 389–395. [Google Scholar] [CrossRef] [PubMed]
- Kaiser, H.F. The application of electronic computers to factor analysis. Educ. Psychol. Meas. 1960, 20, 141–151. [Google Scholar] [CrossRef]
- Cleveland, W.S. Robust locally weighted regression and smoothing scatterplots. J. Am. Stat. Assoc. 1979, 74, 829–836. [Google Scholar] [CrossRef]
- Ledford, A.W.; Tawn, J.A. Modelling dependence within joint tail regions. J. R. Stat. Soc. Ser. B (Stat. Methodol.) 1997, 59, 475–499. [Google Scholar] [CrossRef]
- Langford, E. Quartiles in elementary statistics. J. Stat. Educ. 2006, 14. [Google Scholar] [CrossRef]
- Klein Tank, A.; Peterson, T.; Quadir, D.; Dorji, S.; Zou, X.; Tang, H.; Santhosh, K.; Joshi, U.; Jaswal, A.; Kolli, R.; et al. Changes in daily temperature and precipitation extremes in central and south Asia. J. Geophys. Res. Atmos. 2006, 111. [Google Scholar] [CrossRef]
- Yarnal, B. Synoptic Climatology in Environmental Analysis: A Primer; Belhaven: Jackson, MS, USA, 1993. [Google Scholar]
- Burrough, P.; McDonnell, R. Spatial information systems and geostatistics. Geogr. Inf. Syst. 1998, 333, 330. [Google Scholar]
- Lopes, S.; Fragoso, M.; Lopes, A. Heavy Rainfall Events and Mass Movements in the Funchal Area (Madeira, Portugal): Spatial Analysis and Susceptibility Assessment. Atmosphere 2020, 11, 104. [Google Scholar] [CrossRef]
- Greatbatch, R.J.; Gollan, G.; Jung, T.; Kunz, T. Tropical origin of the severe European winter of 1962/1963. Q. J. R. Meteorol. Soc. 2015, 141, 153–165. [Google Scholar] [CrossRef]
- Draisma, G.; Drees, H.; Ferreira, A.; De Haan, L. Bivariate tail estimation: Dependence in asymptotic independence. Bernoulli 2004, 10, 251–280. [Google Scholar] [CrossRef]
- Ackerman, E.A. The Köppen classification of climates in North America. Geogr. Rev. 1941, 31, 105–111. [Google Scholar] [CrossRef]
- Thornthwaite, C.W. An approach toward a rational classification of climate. Geogr. Rev. 1948, 38, 55–94. [Google Scholar] [CrossRef]
- MacLeod, A.; Korycinska, A. Detailing Köppen–Geiger climate zones at sub-national to continental scale: A resource for pest risk analysis. EPPO Bull. 2019, 49, 73–82. [Google Scholar] [CrossRef]
- DiStefano, C.; Zhu, M.; Mindrila, D. Understanding and using factor scores: Considerations for the applied researcher. Pract. Assess. Res. Eval. 2009, 14, 20. [Google Scholar]
- Kieffer, K.M. Orthogonal versus Oblique Factor Rotation: A Review of the Literature Regarding the Pros and Cons. Available online: https://eric.ed.gov/?id=ED427031 (accessed on 15 May 2020).
- Johannessen, O.M.; Kuzmina, S.I.; Bobylev, L.P.; Miles, M.W. Surface air temperature variability and trends in the Arctic: New amplification assessment and regionalisation. Tellus A Dyn. Meteorol. Oceanogr. 2016, 68, 28234. [Google Scholar] [CrossRef]
- Parracho, A.; Melo-Gonçalves, P.; Rocha, A. Regionalisation of precipitation for the Iberian Peninsula and climate change. Phys. Chem. Earth Parts A/B/C 2016, 94, 146–154. [Google Scholar] [CrossRef]
- Wu, Z.; Xu, H.; Li, Y.; Wen, L.; Li, J.; Lu, G.; Li, X. Climate and drought risk regionalisation in China based on probabilistic aridity and drought index. Sci. Total Environ. 2018, 612, 513–521. [Google Scholar] [CrossRef]
- PRAM. Plano Regional da Água da Regiao Autonoma da Madeira; Relatorio Tecnico; PRAM: Autonomous Region of Madeira, Portugal, 2003. [Google Scholar]
- DLR. Decreto Legislativo Regional 38/2008/M. 20 August 2008. Available online: https://data.dre.pt/eli/declegreg/38/2008/08/20/m/dre/pt/html (accessed on 15 May 2020).
- Liberato, M.L.; Ramos, A.M.; Gouveia, C.M.; Sousa, P.; Russo, A.; Trigo, R.M.; Santo, F.E. Exceptionally extreme drought in Madeira Archipelago in 2012: Vegetation impacts and driving conditions. Agric. For. Meteorol. 2017, 232, 195–209. [Google Scholar] [CrossRef]
- Prada, S.N.; Da Silva, M.O.; Cruz, J.V. Groundwater behaviour in Madeira, volcanic island (Portugal). Hydrogeol. J. 2005, 13, 800–812. [Google Scholar] [CrossRef]
- Hurrell, J.W.; Kushnir, Y.; Visbeck, M. The north Atlantic oscillation. Science 2001, 291, 603–605. [Google Scholar] [CrossRef] [PubMed]
- López-Moreno, J.I.; Vicente-Serrano, S.M. Positive and negative phases of the wintertime North Atlantic Oscillation and drought occurrence over Europe: A multitemporal-scale approach. J. Clim. 2008, 21, 1220–1243. [Google Scholar] [CrossRef]
- Xu, H.; Kim, H.M.; Nye, J.A.; Hameed, S. Impacts of the North Atlantic Oscillation on sea surface temperature on the Northeast US Continental Shelf. Cont. Shelf Res. 2015, 105, 60–66. [Google Scholar] [CrossRef]
- NCAR. The Climate Data Guide: Hurrell North Atlantic Oscillation (NAO) Index, Station-Based (Last Modified 24 Apr 2020). Available online: https://climatedataguide.ucar.edu/ (accessed on 15 May 2020).
- McAdie, A. Monsoon and Trade Winds as Rain Makers and Desert Makers. Geogr. Rev. 1922, 12, 412–419. [Google Scholar] [CrossRef]
- Prada, S.; da Silva, M.O.; Figueira, C.; Meneses, M.; Pontes, A. Fog water collection in Madeira Island (Portugal). In Proceedings of the 4th International Conference on Fog, Fog Collection and Dew, La Serena, Chile, 22–27 July 2007; pp. 22–27. [Google Scholar]
- Trouet, V.; Esper, J.; Graham, N.E.; Baker, A.; Scourse, J.D.; Frank, D.C. Persistent positive North Atlantic Oscillation mode dominated the medieval climate anomaly. Science 2009, 324, 78–80. [Google Scholar] [CrossRef]
- Cattiaux, J.; Vautard, R.; Cassou, C.; Yiou, P.; Masson-Delmotte, V.; Codron, F. Winter 2010 in Europe: A cold extreme in a warming climate. Geophys. Res. Lett. 2010, 37. [Google Scholar] [CrossRef]
- Figueira, C.; de Sequeira, M.M.; Vasconcelos, R.; Prada, S. Cloud water interception in the temperate laurel forest of Madeira Island. Hydrol. Sci. J. 2013, 58, 152–161. [Google Scholar] [CrossRef]
- Serreze, M.C.; Carse, F.; Barry, R.G.; Rogers, J.C. Icelandic low cyclone activity: Climatological features, linkages with the NAO, and relationships with recent changes in the Northern Hemisphere circulation. J. Clim. 1997, 10, 453–464. [Google Scholar] [CrossRef]
- Scaife, A.; Arribas, A.; Blockley, E.; Brookshaw, A.; Clark, R.; Dunstone, N.; Eade, R.; Fereday, D.; Folland, C.; Gordon, M.; et al. Skillful long-range prediction of European and North American winters. Geophys. Res. Lett. 2014, 41, 2514–2519. [Google Scholar] [CrossRef]
- Dai, G.; Mu, M.; Jiang, Z. Evaluation of the forecast performance for North Atlantic Oscillation onset. Adv. Atmos. Sci. 2019, 36, 753–765. [Google Scholar] [CrossRef]
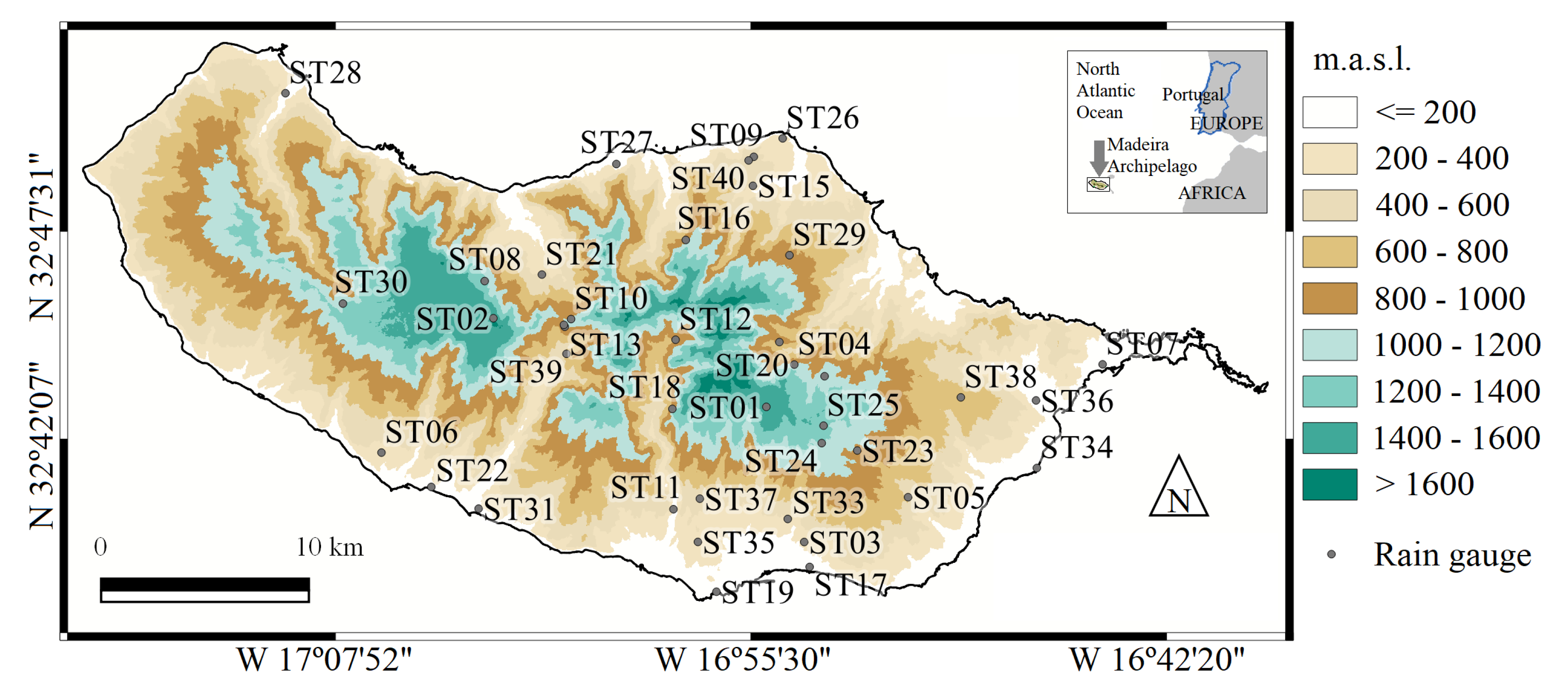
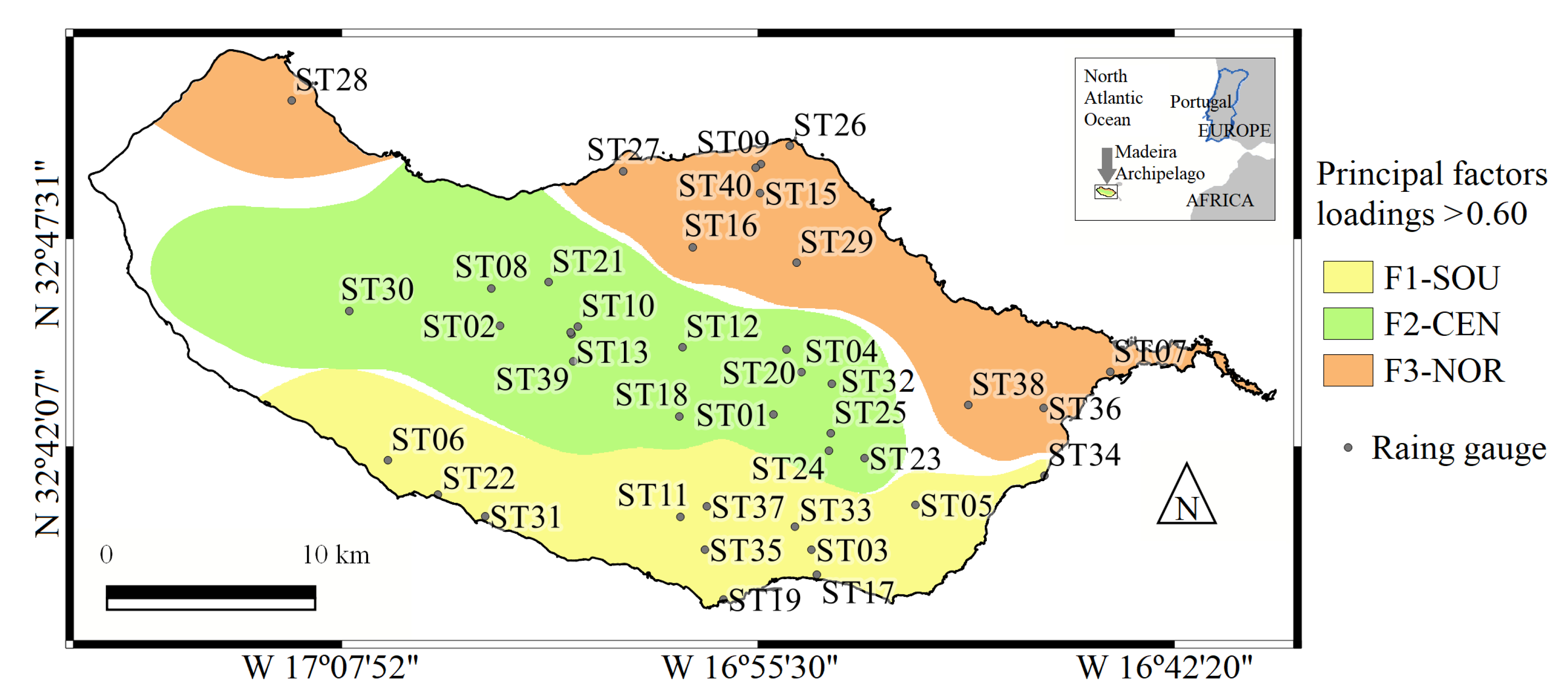


| Code | Name | Coordinate | Elevation (m.a.s.l.) | Areal Influence (km) | Factor-Region | |
|---|---|---|---|---|---|---|
| Latitude N | Longitude W | |||||
| ST01 | Areeiro | 324311 | 165501 | 1610.1 | 13.67 | F2-CEN |
| ST02 | Bica da Cana | 324522 | 170319 | 1560.2 | 22.05 | F2-CEN |
| ST03 | Bom Sucesso | 323943 | 165345 | 292.0 | 6.98 | F1-SOU |
| ST04 | Cabeço do Meio-Nogueira | 324408 | 165355 | 995.3 | 4.07 | F2-CEN |
| ST05 | Camacha-Valparaiso | 324034 | 165031 | 675.2 | 28.57 | F1-SOU |
| ST06 | Canhas | 324139 | 170635 | 400.4 | 25.19 | F1-SOU |
| ST07 | Caniçal | 324414 | 164419 | 16.2 | 11.34 | F3-NOR |
| ST08 | Caramujo | 324609 | 170330 | 1214.5 | 30.41 | F2-CEN |
| ST09 | Cascalho | 324944 | 165530 | 430.4 | 1.83 | F3-NOR |
| ST10 | Chão dos Louros Encumeadas | 324525 | 170104" | 895.2 | 9.54 | F2-CEN |
| ST11 | Covão ETA | 324029 | 165746 | 510.1 | 22.45 | F1-SOU |
| ST12 | Curral das Freiras | 324444 | 165735 | 787.4 | 20.08 | F2-CEN |
| ST13 | Encumeada de São Vicente | 324501 | 170100 | 900.2 | 1.12 | F2-CEN |
| ST14 | Encumeadas Casa EEM | 324514 | 170115 | 1010.5 | 2.32 | F2-CEN |
| ST15 | ETA São Jorge | 324857 | 165533 | 500.5 | 10.42 | F3-NOR |
| ST16 | Fajã Penedo | 324731 | 165736 | 620.5 | 23.83 | F3-NOR |
| ST17 | Funchal Observatório | 323851 | 165332 | 58.2 | 7.08 | F1-SOU |
| ST18 | Lapa Branca-Curral das Freiras | 324308 | 165753" | 610.2 | 22.45 | F2-CEN |
| ST19 | Lido-Cais do Carvão | 323811 | 165611 | 20.5 | 4.98 | F1-SOU |
| ST20 | Lombo Furão | 324456 | 165439 | 994.5 | 13.61 | F2-CEN |
| ST21 | Loural | 324621 | 170145 | 368.1 | 19.37 | F2-CEN |
| ST22 | Lugar de Baixo | 324044 | 170459 | 15.1 | 10.94 | F1-SOU |
| ST23 | Meia Serra | 324207 | 165212 | 115.3 | 12.47 | F2-CEN |
| ST24 | Montado do Pereiro | 324206 | 165302 | 1261.0 | 6.53 | F2-CEN |
| ST25 | Poiso-Posto Florestal | 324246 | 165313 | 1360.2 | 4.60 | F2-CEN |
| ST26 | Ponta de São Jorge | 325001 | 165424 | 266.5 | 6.15 | F3-NOR |
| ST27 | Ponta Delgada | 324916 | 165931 | 123.3 | 17.26 | F3-NOR |
| ST28 | Porto do Moniz | 325057 | 170946 | 64.3 | 80.65 | F3-NOR |
| ST29 | Queimadas | 324659 | 165407 | 881.4 | 34.66 | F3-NOR |
| ST30 | Rabaçal | 324530 | 170751 | 1233.4 | 101.10 | F2-CEN |
| ST31 | Ribeira Brava | 324026 | 170346 | 25.4 | 24.13 | F1-SOU |
| ST32 | Ribeiro Frio | 324351 | 165258 | 1167.1 | 19.07 | F2-CEN |
| ST33 | Sanatório | 324007 | 165402 | 384.1 | 11.75 | F1-SOU |
| ST34 | Santa Catarina | 324136 | 164623 | 49.2 | 7.74 | F1-SOU |
| ST35 | Santa Quitéria ETA | 323939 | 165703 | 321.0 | 9.20 | F1-SOU |
| ST36 | Santana | 324319 | 164627 | 80.4 | 16.46 | F3-NOR |
| ST37 | Santo António | 324036 | 165645 | 525.3 | 10.82 | F1-SOU |
| ST38 | Santo da Serra | 324333 | 164901 | 660.2 | 36.08 | F3-NOR |
| ST39 | Serra de Água | 324431 | 170111 | 573.2 | 24.34 | F2-CEN |
| ST40 | Vale da Lapa | 324937 | 165540 | 347.0 | 5.31 | F3-NOR |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Espinosa, L.A.; Portela, M.M.; Rodrigues, R. Significant Extremal Dependence of a Daily North Atlantic Oscillation Index (NAOI) and Weighted Regionalised Rainfall in a Small Island Using the Extremogram. Water 2020, 12, 2989. https://doi.org/10.3390/w12112989
Espinosa LA, Portela MM, Rodrigues R. Significant Extremal Dependence of a Daily North Atlantic Oscillation Index (NAOI) and Weighted Regionalised Rainfall in a Small Island Using the Extremogram. Water. 2020; 12(11):2989. https://doi.org/10.3390/w12112989
Chicago/Turabian StyleEspinosa, Luis Angel, Maria Manuela Portela, and Rui Rodrigues. 2020. "Significant Extremal Dependence of a Daily North Atlantic Oscillation Index (NAOI) and Weighted Regionalised Rainfall in a Small Island Using the Extremogram" Water 12, no. 11: 2989. https://doi.org/10.3390/w12112989
APA StyleEspinosa, L. A., Portela, M. M., & Rodrigues, R. (2020). Significant Extremal Dependence of a Daily North Atlantic Oscillation Index (NAOI) and Weighted Regionalised Rainfall in a Small Island Using the Extremogram. Water, 12(11), 2989. https://doi.org/10.3390/w12112989







