Analysis on the Characteristics of Dry and Wet Periods in The Yangtze River Basin
Abstract
1. Introduction
2. Study Area and Data
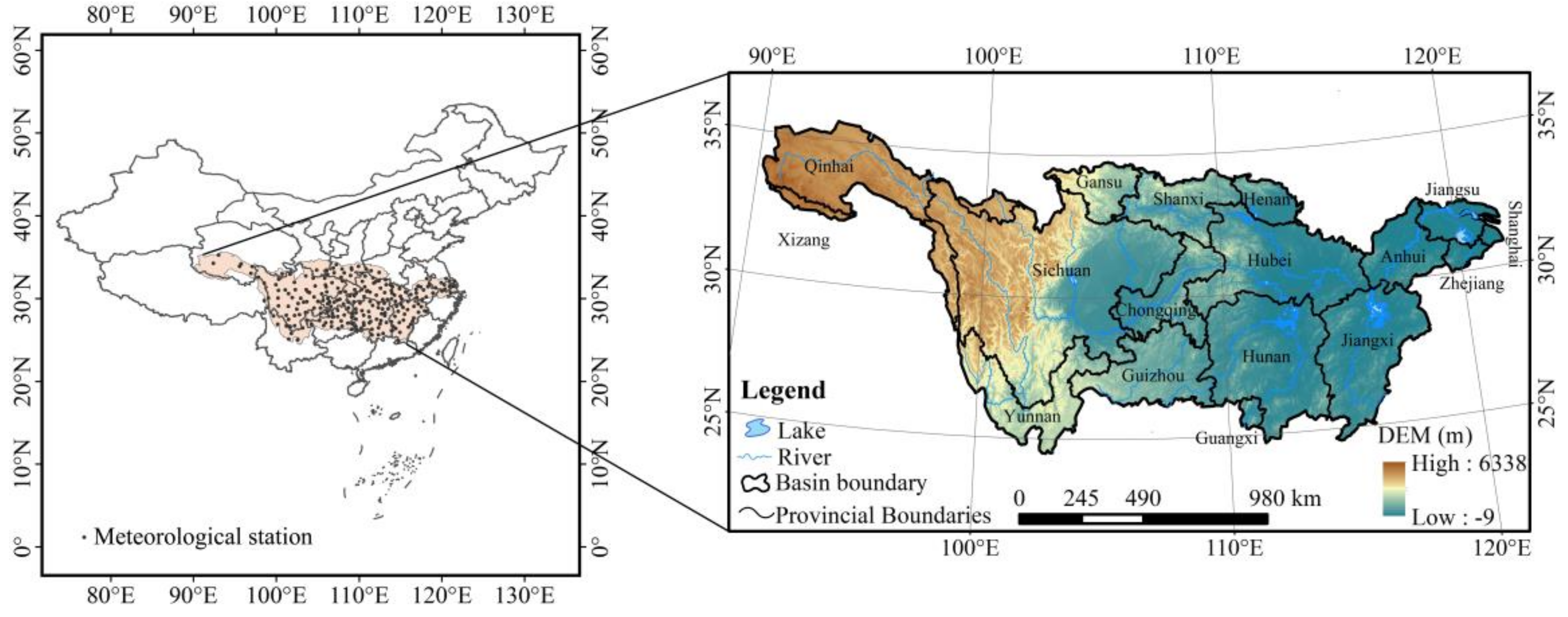
2.1. Study Area
2.2. Data Sources
3. Method
3.1. Calculation of the Standardized Precipitation Evaporation Index
3.2. Empirical Orthogonal Function (EOF) and Rotational Empirical Orthogonal Function (REOF)
3.3. “Take the Minimum” Category
3.4. Linear Trend Rate and Significance Calculation of Drought and Wetness Index
3.5. Definition of Drought and Wetness Events
3.6. Other Methods
4. Results
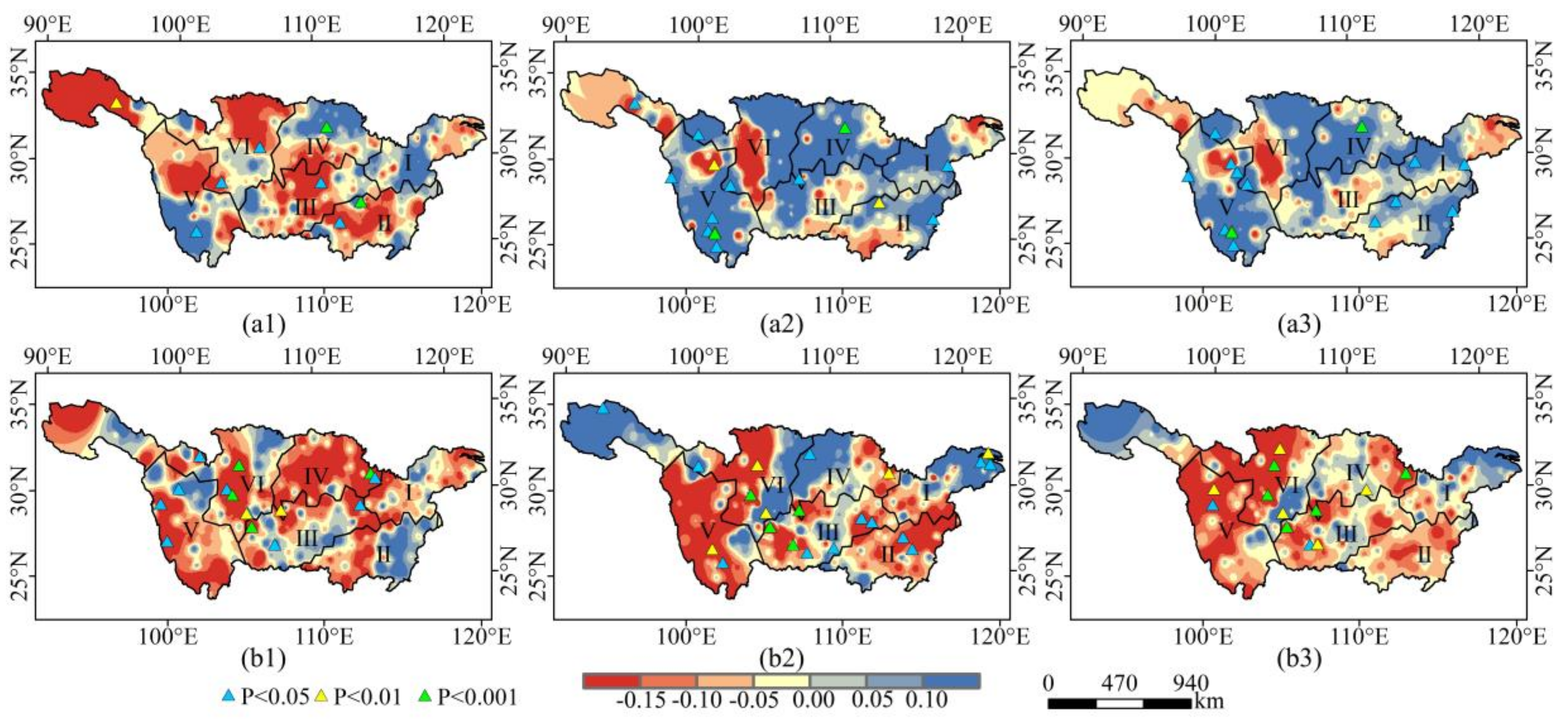
4.1. Spatial Distribution of the Number of Dry/Wet Months and Drought/Wetness Events in the Yangtze River Basin
4.2. Partitioning Based on REOF
4.3. Change Characteristics of Drought and Wetness
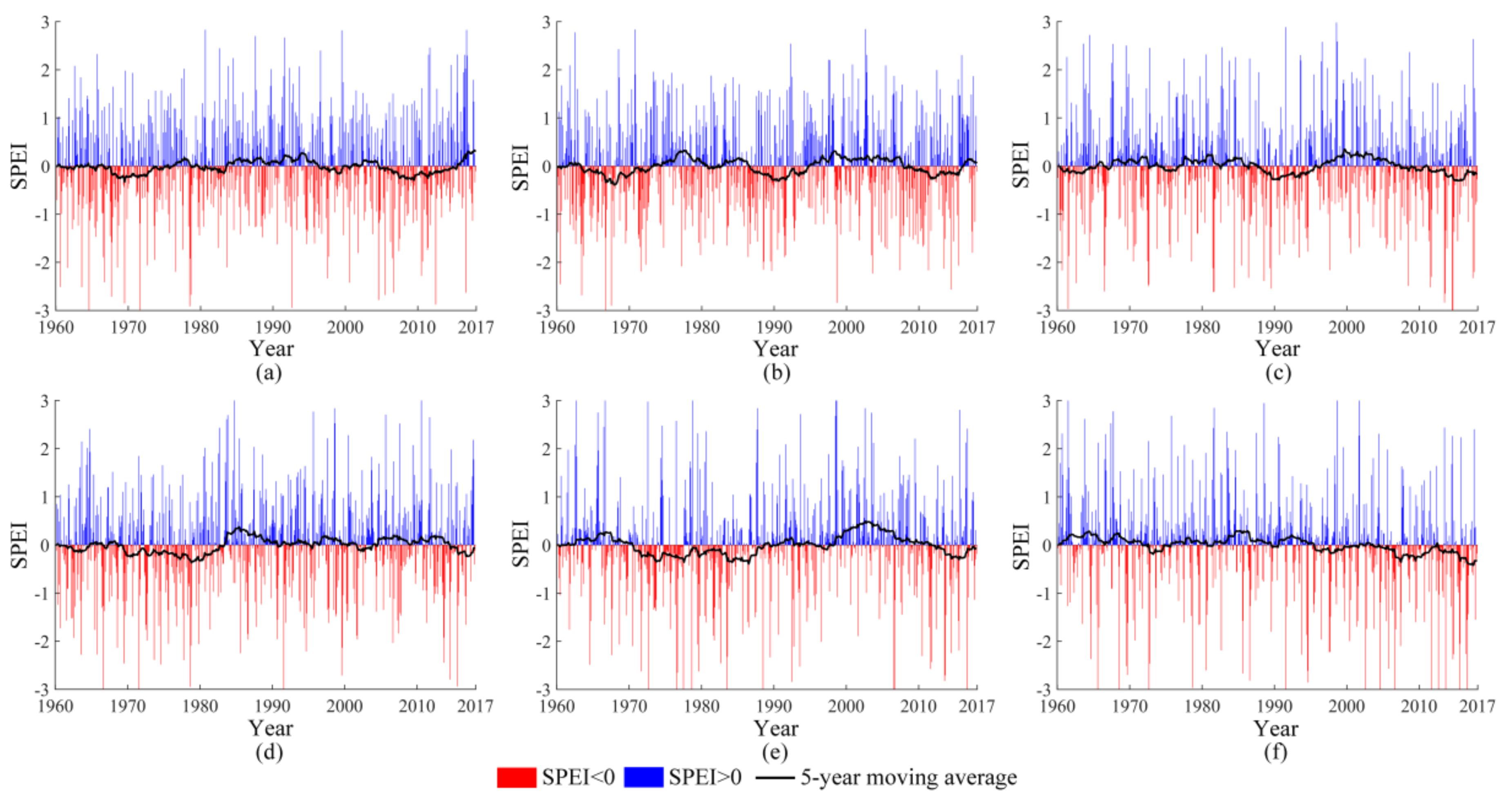
4.3.1. Distribution of Conditions of Drought and Wetness in Each Year-Month
4.3.2. Change Trend of Drought and Wetness Indicators
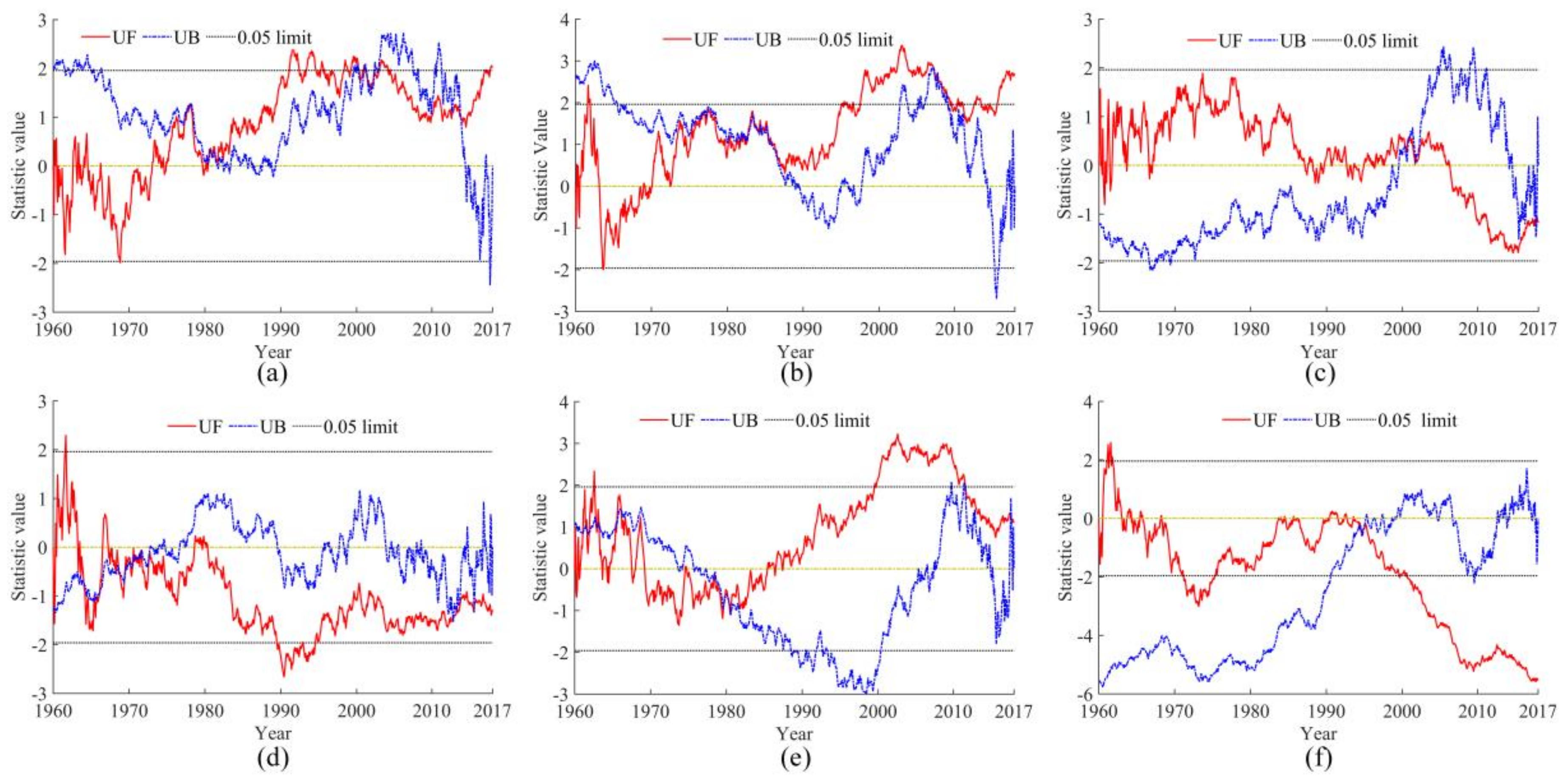
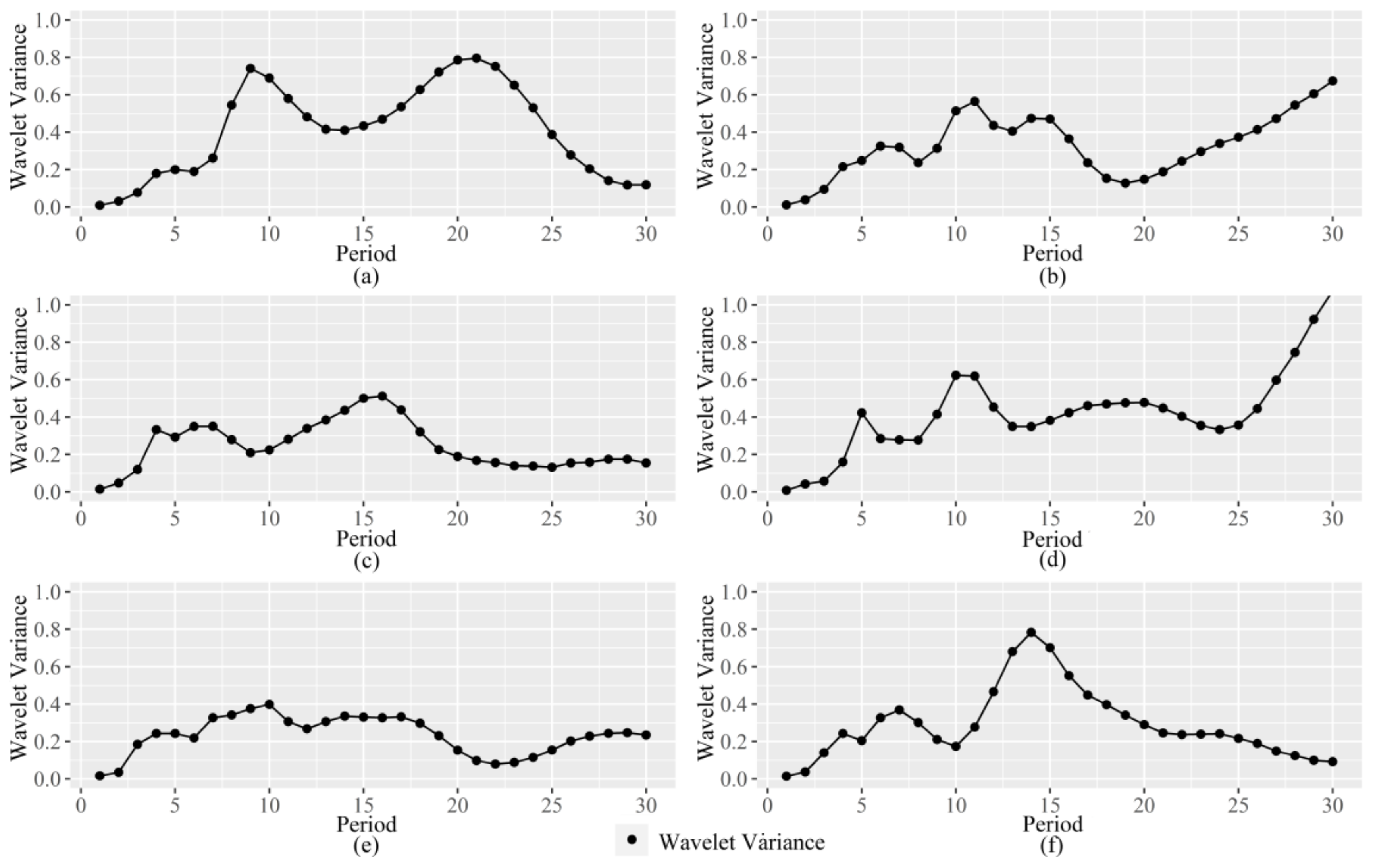
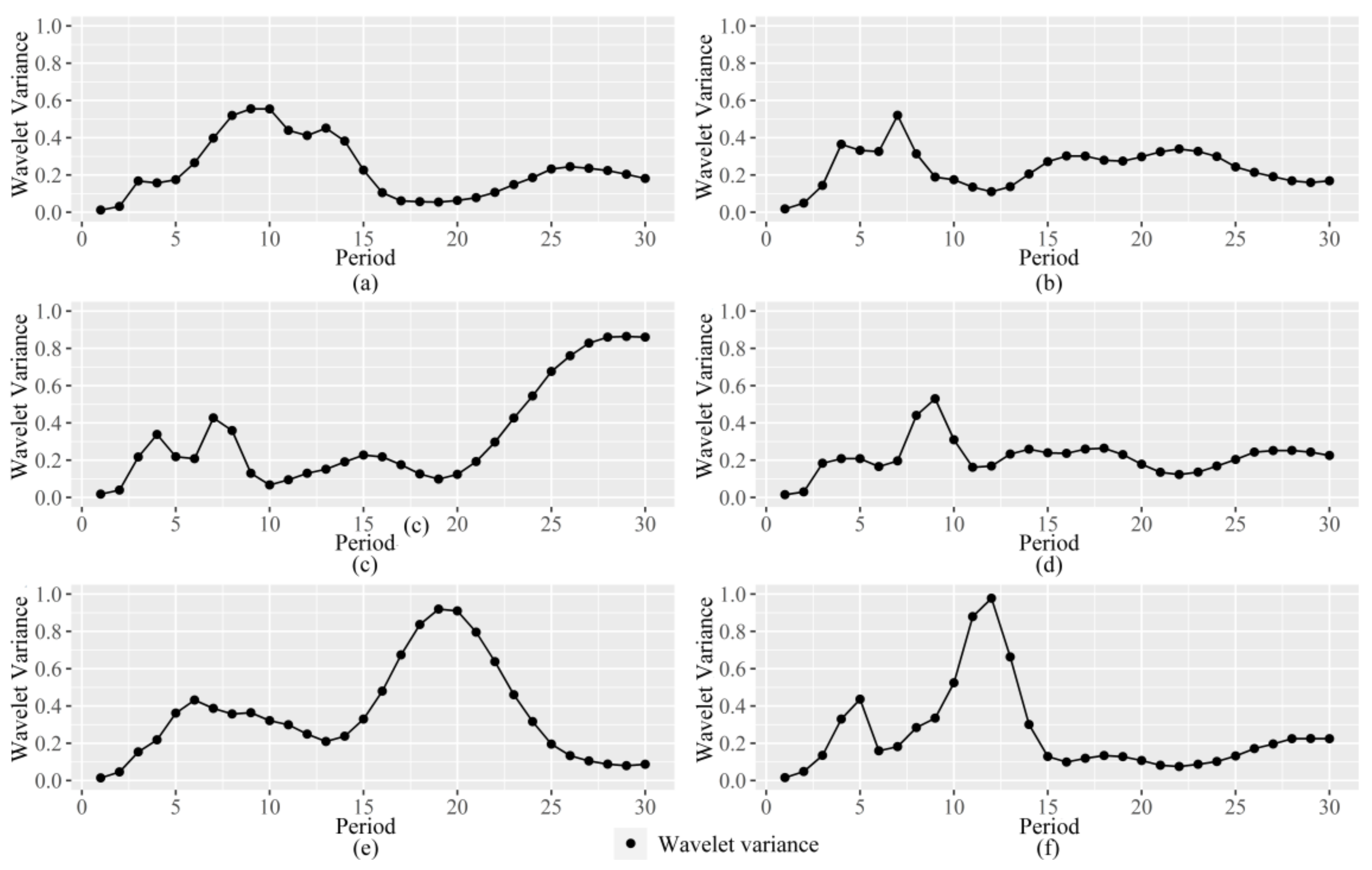
4.3.3. Abrupt Changes and Variation Periods of Drought and Wetness
5. Discussion
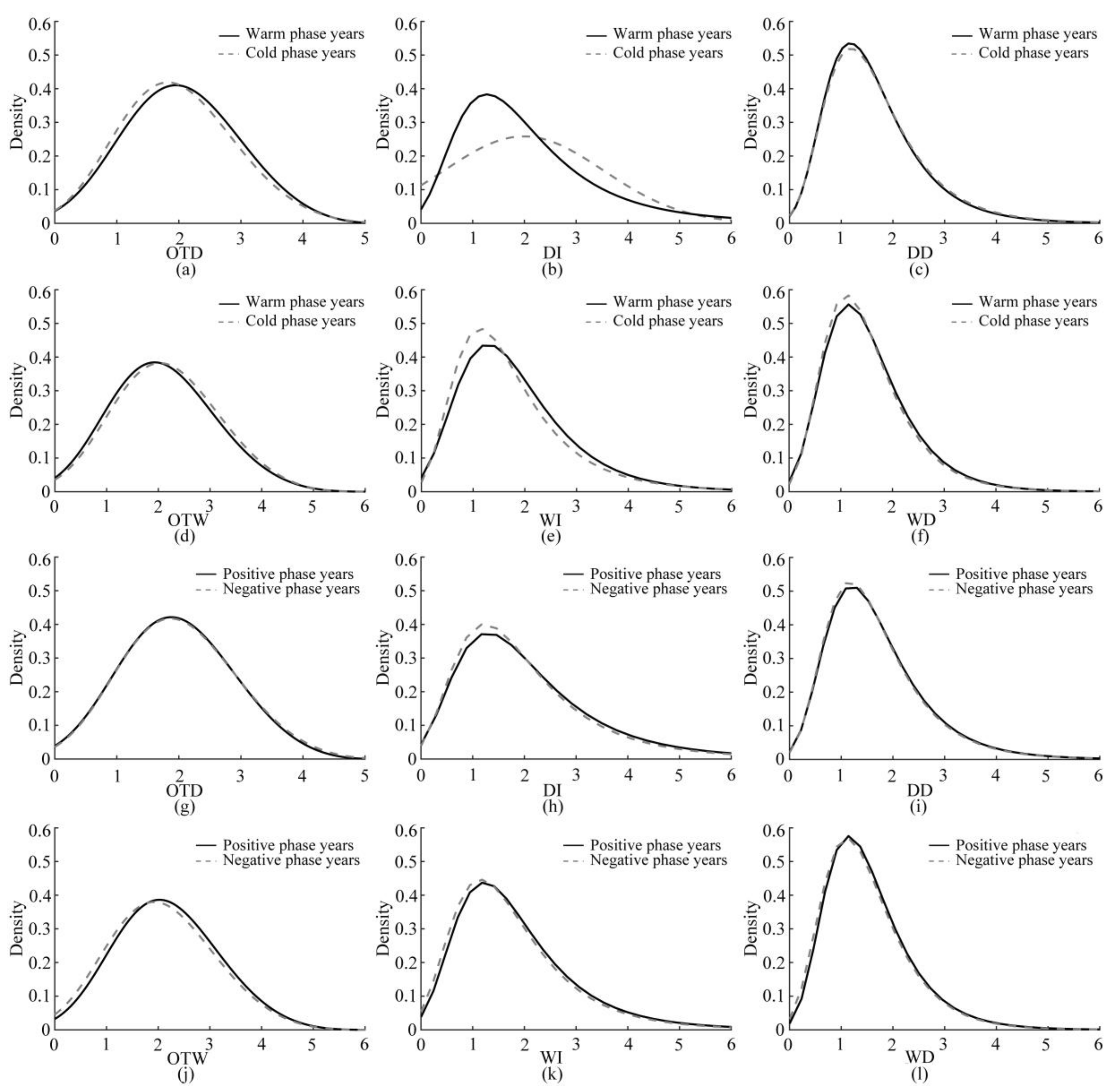
5.1. Effects of AO and ENSO on Drought and Wetness
5.2. Continuity of Drought and Wetness Changes in the Yangtze River Basin
6. Conclusions
- (a)
- The Yangtze River basin is characterized by the coexistence of drought and flooding in the same areas. Areas where there were more dry/wet months at the same levels, are more likely to occur in the same region. There were more mildly and moderately dry months in the middle and lower reaches of the Yangtze River, but also mildly and moderately wet months. The upper reaches of the Yangtze River were prone to extremely dry months as well as extremely wet months.
- (b)
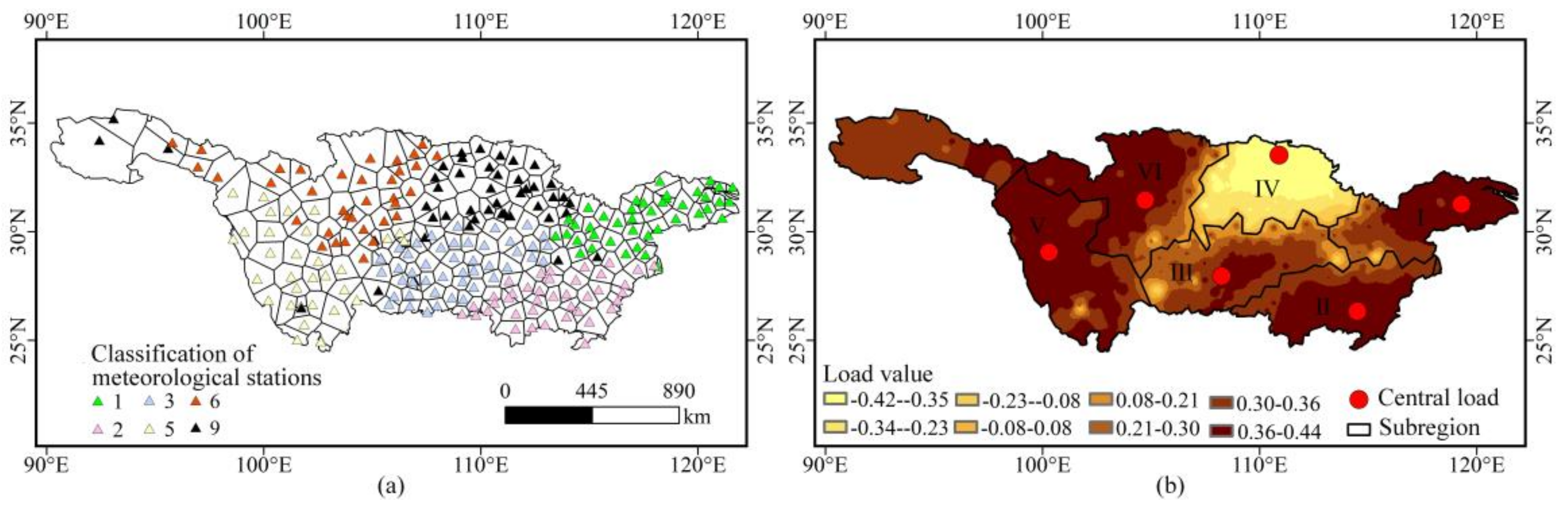
- Using REOF to analyze the drought and wetness conditions of the Yangtze Riverb asin in time and space, it was found that there are six significant patterns in the Yangtze River basin. Through the “Take the minimum“ method and the Tyson polygon, the Yangtze River basin can be divided into six characteristic subregions: east, southeast, south, north, southwest, and northwest.
- (c)
- The distribution of SPEI values for the central load of each pattern from 1960 to 2017 shows that drought and wetness of a higher grade generally occur from May to September. The eastern parrern frequently changed between dry and wet status; the southeastern pattern had more normal periods of dry and wet; the southern pattern had higher levels of wet months; the northwestern pattern was consistent and relatively dry; the northern pattern and the southwestern pattern had a longer period of extreme drought/wetness in the 1970s and 1980s.
- (d)
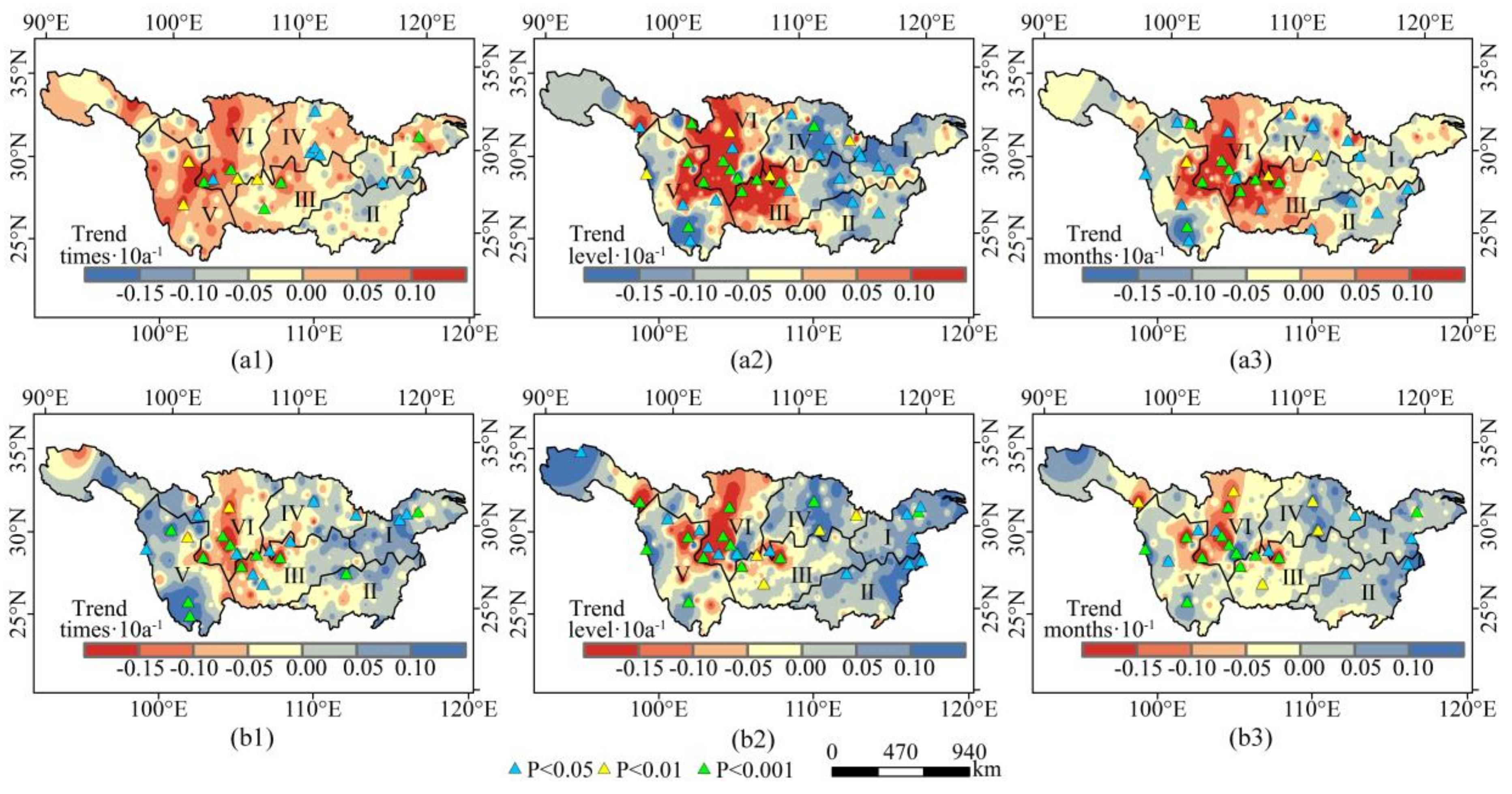
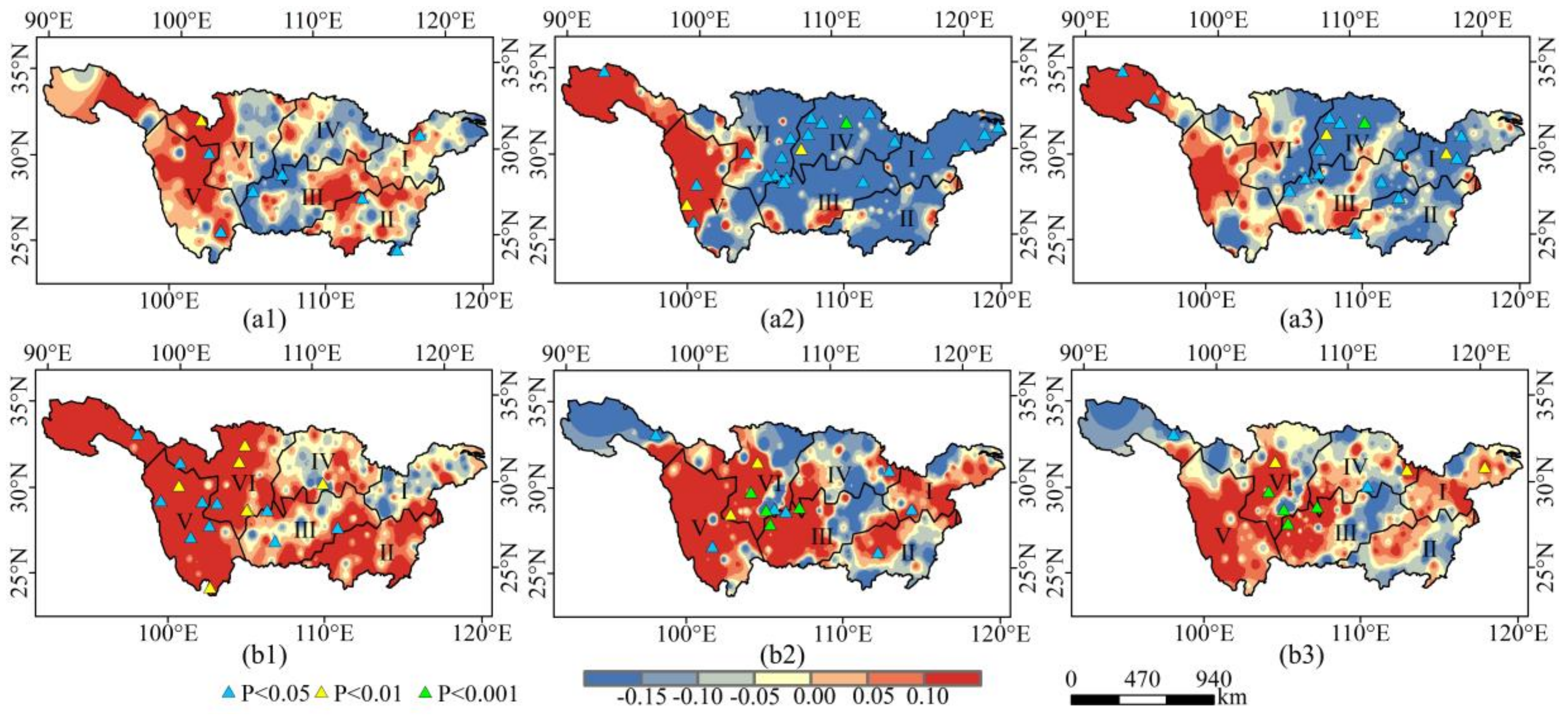
- From 1960 to 2017, the inter-annual change showed that the number of dry months, the OTD, and the DI and DD increased significantly in fewer subregions. However, spatially, the southern part of the Northwestern pattern and the western part of the southern pattern showed a significant decrease in the OTW, WI, and WD, and a significant increase in the OTD, DI, and DD, and this region changed from wetness to dryness in the past 29 years.
- (e)
- According to the 5-year moving average of the central load SPEI value, the subregions I and II had experienced many dry-wet transitions, the subregion III had a long-term normal dry–wet state before 1998, and the subregions IV and VI had a relatively long dry–wet transition. However, these dry and wet state transitions can better correspond to the abrupt change of RPCs.
Author Contributions
Funding
Conflicts of Interest
Abbreviations
References
- Barlow, K.M.; Christy, B.P.; O’Leary, G.J.; Riffkin, P.A.; Nuttall, J.G. Simulating the impact of extreme heat and frost events on wheat crop production: A review. Field Crop. Res. 2015, 171, 109–119. [Google Scholar] [CrossRef]
- El-Zein, A.; Tonmoy, F.N. Assessment of vulnerability to climate change using a multi-criteria outranking approach with application to heat stress in Sydney. Ecol. Indic. 2015, 48, 207–217. [Google Scholar] [CrossRef]
- Huang, H.; Zhang, B.; Ma, S.; Ma, B.; Cui, Y.; Wang, X.; Ma, C.; Chen, K.; Zhang, T. Temporal and spatial variations of meteorological drought and drought risk analysis in Hedong Area of Gansu Province. Chin. J. Agrometeorol. 2020, 41, 459–469. [Google Scholar] [CrossRef]
- Yang, T.; Lu, G.; Li, H.; He, H.; Wang, X. Advances in the study of projection of climate change impacts on hydrological extremes. Adv. Water Sci. 2011, 22, 279–286. [Google Scholar] [CrossRef]
- Allen, M.R.; Ingram, W.J. Constraints on future changes in climate and the hydrologic cycle. Nature 2002, 419, 224–232. [Google Scholar] [CrossRef]
- Rayne, S.; Forest, K. Evidence for increasingly variable Palmer Drought Severity Index in the United States since 1895. Sci. Total Environ. 2016, 544, 792–796. [Google Scholar] [CrossRef]
- Ford, T.W.; Labosier, C.F. Meteorological conditions associated with the onset of flash drought in the Eastern United States. Agric. For. Meteorol. 2017, 247, 414–423. [Google Scholar] [CrossRef]
- Salvati, L.; Sateriano, A.; Zitti, M. Long-term land cover changes and climate variations: A country-scale approach for a new policy target. Land Use Policy 2013, 30, 401–407. [Google Scholar] [CrossRef]
- Plummer, N.; Salinger, M.J.; Nicholls, N.; Suppiah, R.; Hennessy, K.J.; Leighton, R.M.; Trewin, B.; Page, C.M.; Lough, J.M. Changes in Climate Extremes Over the Australian Region and New Zealand During the Twentieth Century. In Weather and Climate Extremes; Springer: Dordrecht, The Netherlands, 1999; pp. 183–202. [Google Scholar]
- Lian, L.; Liu, B. Change characteristics of dry and wet spells in northwest China during the past 58 years. Arid Land Geogr. 2019, 42, 1301–1309. [Google Scholar] [CrossRef]
- Shi, Y.; Shen, Y.; Li, D.; Zhang, G.; Ding, Y.; Hu, R.; Kang, E. Discussion on the present situation of climate change from warm-dry to warm-wet in Northwest China. Q. Sci. 2003, 23, 152–164. [Google Scholar]
- Liu, L.; Zhai, P.; Zheng, Z. Variations in longest consecutive dry days in warm half year over Northern China. Acta Meteorol. Sin. 2008, 66, 474–477. [Google Scholar] [CrossRef]
- Ni, S.; Gu, Y.; Peng, Y.; Liu, J.; Wang, H. Spatio-temporal pattern and evolution trend of drought disaster in China in recent seventy years. J. Nat. Disaster 2019, 28, 176–181. [Google Scholar] [CrossRef]
- Yuan, X.; Wang, L.; Wu, P.; Ji, P.; Sheffield, J.; Zhang, M. Anthropogenic shift towards higher risk of flash drought over China. Nat. Commun. 2019, 10. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Zhou, X.; Xu, Q. Analysis on storm-flood in Yangtze River in 2010 and influence of storage and discharge of Three Gorges Reservoir. Yangtze River 2011, 42, 1–5. [Google Scholar] [CrossRef]
- Chen, X.; Zhou, B.; Zhong, H.; Liu, Y. Climate characteristic of the 2011 spring drought in the mid-lower Yangtze Basin. Resour. Environ. Yangtze Basin 2014, 23, 139–145. [Google Scholar] [CrossRef]
- Yin, Z.; Liu, X.; Zhang, H. Analysis of storm flood occurred in Yangtze River Basin in July 2012. J. China Hydrol. 2014, 34, 81–87. [Google Scholar] [CrossRef]
- Lin, J.; Wang, W.; Cai, X. Analysis of the low-frequency oscillation characteristics over mid-lower reaches of the Yangtze River in 2011 and 2013 based on improved comprehensive meteorological drought index. J. Meteorol. Sci. 2016, 36, 810–818. [Google Scholar] [CrossRef]
- Shan, L.; Zhang, L.; Zhang, Y.; She, D.; Xia, J. Characteristics of dry-wet abrupt alternation events in the middle and lower reaches of the Yangtze River Basin and their relationship with ENSO. J. Geogr. Sci. 2018, 28, 1039–1058. [Google Scholar] [CrossRef]
- Wang, L.; Chen, W. Applicability Analysis of standardized precipitation evapotranspiration index in drought monitoring in China. Plateau Meteorol. 2014, 33, 423–431. [Google Scholar] [CrossRef]
- Palmer, W.C. Meteorological Drought; US Department of Commerce, Weather Bureau: Washington, DC, USA, 1965; pp. 1–58.
- McKee, T.B.; Doesken, N.J.; Kleist, J. The Relationship of Drought Frequency and Duration to Time Scales: Proceedings of Vulnerability; Cambridge University Press: Cambridge, UK, 1993; pp. 100–184. [Google Scholar]
- Vicente-Serrano, S.M.; Beguería, S.; López-Moreno, J.I. A multiscalar drought index sensitive to global warming: The standardized precipitation evapotranspiration index. J. Clim. 2010, 23, 1696–1718. [Google Scholar] [CrossRef]
- Zhang, S.; Zuo, H.; Ren, P.; Xiong, G.; Li, B.; Dong, W.; Wang, L. Application of standardized precipitation evapotranspiration index in China. Clim. Environ. Res. 2013, 18, 617–625. [Google Scholar]
- Zhang, Q.; Tang, H.; Cui, F.; Dai, L. SPEI-based analysis of drought characteristics and trends in Hulun Buir grassland. Acta Ecol. Sin. 2019, 39, 7110–7123. [Google Scholar] [CrossRef]
- Tang, M.; Zhang, B.; Zhang, Y.; Wang, G.; Ma, B.; Jia, Y. Assessment of spring and summer meteorological droughts based on SPEI and SPI in eastern agricultural region of Qinghai Province. J. Nat. Res. 2017, 32, 1029–1042. [Google Scholar] [CrossRef]
- Liu, L.; Niu, Q.; Heng, J.; Li, H.; Xu, Z. Characteristics of dry and wet conversion and dynamic vegetation response in Yarlung Zangbo River basin. Trans. Chin. Soc. Agric. Eng. 2020, 36, 175–184. [Google Scholar] [CrossRef]
- Zhang, D.; Hong, H.; Zhang, Q. Attribution of the changes in annual streamflow in the Yangtze River Basin over the past 146 years. Theor. Appl. Climatol. 2015, 119, 323–332. [Google Scholar] [CrossRef]
- Ma, Q.; Xie, Z.; Chen, F. Temporal and spatial distribution of terrestrial water storage in the Yangtze River Basin during 1982–2005. Clim. Environ. Res. 2011, 16, 429–440. [Google Scholar] [CrossRef]
- Liang, C.; Shen, S. Climatic features of the drought in the Yangtze River Basin and regions to its south disclosed by WAP index. J. Nanjing Univ. Nat. Sci. 2010, 2, 166–174. [Google Scholar] [CrossRef]
- Allen, R.G.; Pereira, L.S.; Raes, D. Crop evapotranspiration: Guidelines for computing crop water requirements. In FAO Irrigation and Drainage Paper No. 56; FAO: Rome, Italy, 1998; pp. 1–15. [Google Scholar]
- Ahmad, M.I.; Sinclair, C.D.; Werritty, A. Log-logistic flood frequency analysis. J. Hydrol. 1988, 98, 205–224. [Google Scholar] [CrossRef]
- Hosking, J.; Wallis, J. Regional Frequency Analysis—An Approach Based on L-Moments; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar]
- Chen, X.; Li, Y.; Yao, N.; Liu, D.; Javed, T.; Liu, C.; Liu, F. Impacts of multi-timescale SPEI and SWDI variations on winter wheat yields. Agric. Syst. 2020, 185, 102955. [Google Scholar] [CrossRef]
- Gao, X.; Zhao, Q.; Zhao, X.; Wu, P.; Pan, W.; Gao, X.; Sun, M. Temporal and spatial evolution of the standardized precipitation evapotranspiration index (SPEI) in the Loess Plateau under climate change from 2001 to 2050. Sci. Total Environ. 2017, 595, 191–200. [Google Scholar] [CrossRef]
- Soh, Y.; Koo, C.; Huang, Y.; Fung, K. Application of artificial intelligence models for the prediction of standardized precipitation evapotranspiration index (SPEI) at Langat River Basin, Malaysia. Comput. Electron. Agric. 2018, 144, 164–173. [Google Scholar] [CrossRef]
- Wei, F. Modern Climate Statistics Diagnosis and Prediction Technology, 2nd ed.; China Meteorological Press: Beijing, China, 2007; pp. 63–65. [Google Scholar]
- Denbo, D.W.; Allen, J.S. Rotary empirical orthogonal function analysis of currents near the Oregon Coast. J. Phys. Oceanogr. 1984, 14, 35–46. [Google Scholar] [CrossRef]
- Wang, H.; Chen, Y.; Pan, Y.; Li, W. Spatial and temporal variability of drought in the arid region of China and its relationships to teleconnection indices. J. Hydrol. 2015, 523, 283–296. [Google Scholar] [CrossRef]
- Zambreski, Z.; Lin, X.; Aiken, R.; Kluitenberg, G.; Pielke, R., Sr. Identification of hydroclimate subregions for seasonal drought monitoring in the U.S. Great Plains. J. Hydrol. 2018, 567, 570–581. [Google Scholar] [CrossRef]
- Richman, M. Review article, rotation of principal components. J. Climatol. 1986, 6, 293–335. [Google Scholar] [CrossRef]
- Hannachi, A.; Jolliffe, I.; Stephenson, D. Empirical orthogonal functions and related techniques in atmospheric science: A review. Int. J. Climatol. 2007, 27, 1119–1152. [Google Scholar] [CrossRef]
- Cai, Y.; Wu, T.; Zhang, W. Spatial and temporal distribution characteristics of heatwave in Sichuan Province based on REOF. J. Nat. Disaster 2018, 27, 201–208. [Google Scholar] [CrossRef]
- Mann, H.B. Nonparametric Tests against Trend. Econometrica 1945, 13, 245–259. [Google Scholar] [CrossRef]
- Kendall, K. Thin-film peeling-the elastic term. J. Phys. D Appl. Phys. 1975, 8, 1449–1452. [Google Scholar] [CrossRef]
- Kendall, M.G. Rank Correlation Measures; Charles Griffin: London, UK, 1975; pp. 325–340. [Google Scholar]
- Han, H.; Hou, J.; Huang, M.; Li, Z.; Xu, K.; Zhang, D.; Bai, G.; Wang, C. Impact of soil and water conservation measures and precipitation on streamflow in the middle and lower reaches of the Hulu River Basin, China. Catena 2020, 195, 104792. [Google Scholar] [CrossRef]
- Yang, Y.; Tian, F. Abrupt change of runoff and its major driving factors in Haihe River Catchment, China. J. Hydrol. 2009, 374, 373–383. [Google Scholar] [CrossRef]
- Mandelbrot, B.B. The Fractal Geometry of Nature; W.H. Freeman: New York, NY, USA, 1982; pp. 232–246. [Google Scholar]
- Gumbel, E.J. Statistical Theory of Extreme Values and Some Practical Applications; Applied Mathematics Series; U.S. National Bureau of Standards: Washington, DC, USA, 1954; Volume 33, p. 51.
- Pearson, K. Notes on the history of correlation. Biometrika 1920, 13, 25–45. [Google Scholar] [CrossRef]
- Cahill, A.T. Determination of changes in Streamflow Variance by means of a Wavelet-Based Test. Water Resour. Res. 2002, 38, 1–14. [Google Scholar] [CrossRef]
- Watson, D.; Philip, G.M. A refinement of Inverse Distance Established interpolation. Geoprocesing 1985, 2, 315–327. [Google Scholar]
- North, G.R.; Bell, T.L.; Cahalan, R.F.; Moeng, F.J. Sampling errors in the estimation of empirical orthogonal functions. Mon. Weather Rev. 1982, 110, 699–706. [Google Scholar] [CrossRef]
- Yulaeva, E.; Wallace, J.M. The signature of ENSO in global temperature and precipitation fields derived from the microwave sounding unit. J. Clim. 1994, 7, 1719–1736. [Google Scholar] [CrossRef]
- Yun, K.; Timmermann, A. Decadal Monsoon-ENSO relationships reexamined. Geophys. Res. Lett. 2018, 45, 2014–2021. [Google Scholar] [CrossRef]
- Dutta, R.; Maity, R. Temporal evolution of hydroclimatic teleconnection and a time-varying model for long-lead prediction of Indian summer monsoon rainfall. Sci. Rep. 2018, 8, 10778. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Wu, M.; Li, D.; Liu, Y.; Li, S. Spatiotemporal decompositions of summer drought in China and Its teleconnection with global sea surface temperatures during 1901–2012. J. Clim. 2017, 30, 6391–6412. [Google Scholar] [CrossRef]
- Gong, D.; Zhu, J.; Wang, S. A significant correlation between the summer precipitation in the Yangtze River basin and the early Arctic oscillation. Chin. Sci. Bull. 2002, 546–549. [Google Scholar] [CrossRef]
- Gong, D.; Wang, S. Influence of Arctic Oscillation on winter climate over China. Acta Geol. Sin. 2003, 559–568. [Google Scholar] [CrossRef]
- Ju, J.; Ren, J.; Lv, J. Effect of interdecadal variation of Arctic Oscillation on temperature increasing in North of East Asian Winter. Plateau Meteol. 2004, 429–434. [Google Scholar] [CrossRef]
- Hu, S.; Zeng, W.; Wang, L.; He, X. Regional frequencies and spatio-temporal characteristics of extreme precipitation over Yangtze River Basin. Resour. Environ. Yangtze Basin 2019, 28, 2008–2018. [Google Scholar] [CrossRef]
- Sun, H.; Zhang, X.; Li, Z.; Liu, F.; Shang, P.; Luo, Z.; Zhou, H. Inhomogeneity distribution of different types of precipitation in the Yangtze River Basin. Resour. Environ. Yangtze Basin 2019, 28, 1422–1433. [Google Scholar] [CrossRef]
- Wang, Q.; Zhang, M.; Wang, S.; Luo, S.; Wang, B.; Zhu, X. Extreme temperature events in Yangtze River Basin during 1962–2011. Acta Geol. Sin. 2013, 68, 611–625. [Google Scholar] [CrossRef]
- Ma, B.; Zhang, B.; Jia, L.; Huang, H. Conditional distribution selection for SPEI-daily and its revealed meteorological drought characteristics in China from 1961 to 2017. Atmos. Res. 2020. [Google Scholar] [CrossRef]
| Mild Drought | Moderate Drought | Severe Drought | Extreme Drought |
|---|---|---|---|
| −1 < SPEI ≤ −0.5 | −1.5 < SPEI ≤ −1 | −2 < SPEI ≤ −1.5 | SPEI ≤ −2 |
| Mild Wetness | Moderate Wetness | Severe Wetness | Extreme Wetness |
| 1 > SPEI ≥ 0.5 | 1.5 > SPEI ≥ 1 | 2 > SPEI ≥ 1.5 | SPEI ≥ 2 |
| Pattern | REOF1 | REOF2 | REOF3 | REOF4 | REOF5 | REOF6 | REOF7 |
|---|---|---|---|---|---|---|---|
| Contribution rate | 21.99% | 11.59% | 8.23% | 5.08% | 4.50% | 2.89% | 2.54% |
| Cumulative contribution rate | 21.99% | 33.58% | 41.81% | 46.89% | 51.39% | 54.27% | 56.81% |
| Is it significant? | Yes | Yes | Yes | Yes | Yes | Yes | No |
| Pattern | REOF1 | REOF2 | REOF3 |
|---|---|---|---|
| Name | The Eastern Pattern | The Southeastern Pattern | The Southern Pattern |
| Representative region | Subregion I | Subregion II | Subregion III |
| Representative station | 58345 | 57896 | 57731 |
| Pattern | REOF4 | REOF5 | REOF6 |
| Name | The Northern pattern | The Southeastern pattern | The Northwestern pattern |
| Representative region | Subregion IV | Subregion V | Subregion VI |
| Representative station | 57154 | 56537 | 56196 |
| Pattern | REOF1 | REOF2 | REOF3 | REOF4 | REOF5 | REOF6 |
|---|---|---|---|---|---|---|
| Station | 58345 | 57896 | 57731 | 57154 | 56357 | 56196 |
| correlation coefficient | 0.83 | 0.78 | 0.72 | −0.79 | 0.65 | 0.6 |
| Significant level | *** | *** | *** | *** | *** | *** |
| Station | Dry Months | OTD | DD | DI |
|---|---|---|---|---|
| 58345 | −0.093 | −0.027 | 0.008 | −0.055 |
| 57896 | −0.162 | −0.090 | −0.098 | −0.104 |
| 57731 | 0.009 | 0.002 | 0.008 | 0.004 |
| 57154 | −0.178 | −0.153 | −0.016 | 0.041 |
| 56357 | −0.129 | −0.048 | −0.038 | 0.047 |
| 56196 | 0.287 | 0.078 | 0.152 | 0.242 |
| Station | Moist Months | OTW | WD | WI |
| 58345 | −0.005 | −0.024 | 0.023 | 0.097 |
| 57896 | 0.122 | −0.017 | 0.044 | 0.048 |
| 57731 | −0.039 | −0.008 | 0.001 | 0.007 |
| 57154 | 0.105 | 0.009 | 0.115 | 0.198 |
| 56357 | 0.247 | 0.103 | 0.084 | 0.040 |
| 56196 | −0.280 | −0.138 | −0.048 | −0.050 |
| Index | Phase | Criterion | Year |
|---|---|---|---|
| ENSO | Warm phase | ≥0.5 °C | 1964 1966 1969 1970 1973 1977 1978 1980 1983 1987 |
| 1988 1992 1995 1998 2003 2005 2007 2010 2015 | |||
| Cold phase | ≤−0.5 °C | 1965 1968 1971 1972 1974 1975 1976 1984 1985 1989 | |
| 1996 1997 1999 2000 2001 2006 2008 2009 2011 | |||
| AO | Positive phase | ≥0.2 °C | 1971 1972 1974 1975 1983 1988 1989 1990 1991 1992 |
| 1994 1998 1999 2001 2006 2007 2008 2011 2015 2017 | |||
| Negative phase | ≤−0.2 °C | 1960 1962 1963 1964 1965 1966 1967 1968 1969 1970 | |
| 1976 1977 1978 1979 1981 1984 1985 1986 1987 1993 | |||
| 1995 1997 2000 2002 2003 2005 2009 2010 |
| Type | Index | 58345 | 57896 | 57731 | 57154 | 56357 | 56196 |
|---|---|---|---|---|---|---|---|
| Drought | OTD | 0.51 | 0.57 | 0.57 | 0.70 | 0.87 | 0.67 |
| DI | 0.66 | 0.61 | 0.55 | 0.53 | 0.67 | 0.63 | |
| DD | 0.65 | 0.59 | 0.50 | 0.55 | 0.69 | 0.58 | |
| Wetness | OTW | 0.54 | 0.53 | 0.50 | 0.39 | 0.80 | 0.61 |
| WI | 0.62 | 0.44 | 0.58 | 0.63 | 0.52 | 0.38 | |
| WD | 0.53 | 0.40 | 0.57 | 0.62 | 0.50 | 0.41 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, H.; Zhang, B.; Cui, Y.; Ma, S. Analysis on the Characteristics of Dry and Wet Periods in The Yangtze River Basin. Water 2020, 12, 2960. https://doi.org/10.3390/w12112960
Huang H, Zhang B, Cui Y, Ma S. Analysis on the Characteristics of Dry and Wet Periods in The Yangtze River Basin. Water. 2020; 12(11):2960. https://doi.org/10.3390/w12112960
Chicago/Turabian StyleHuang, Hao, Bo Zhang, Yanqiang Cui, and Shangqian Ma. 2020. "Analysis on the Characteristics of Dry and Wet Periods in The Yangtze River Basin" Water 12, no. 11: 2960. https://doi.org/10.3390/w12112960
APA StyleHuang, H., Zhang, B., Cui, Y., & Ma, S. (2020). Analysis on the Characteristics of Dry and Wet Periods in The Yangtze River Basin. Water, 12(11), 2960. https://doi.org/10.3390/w12112960







