Wave Force Characteristics and Stability of Detached Breakwaters Consisting of Open Cell Caissons Interlocked via Crushed Stones
Abstract
1. Introduction
2. Experimental Setup and Analysis Methods
2.1. Experimental Setup
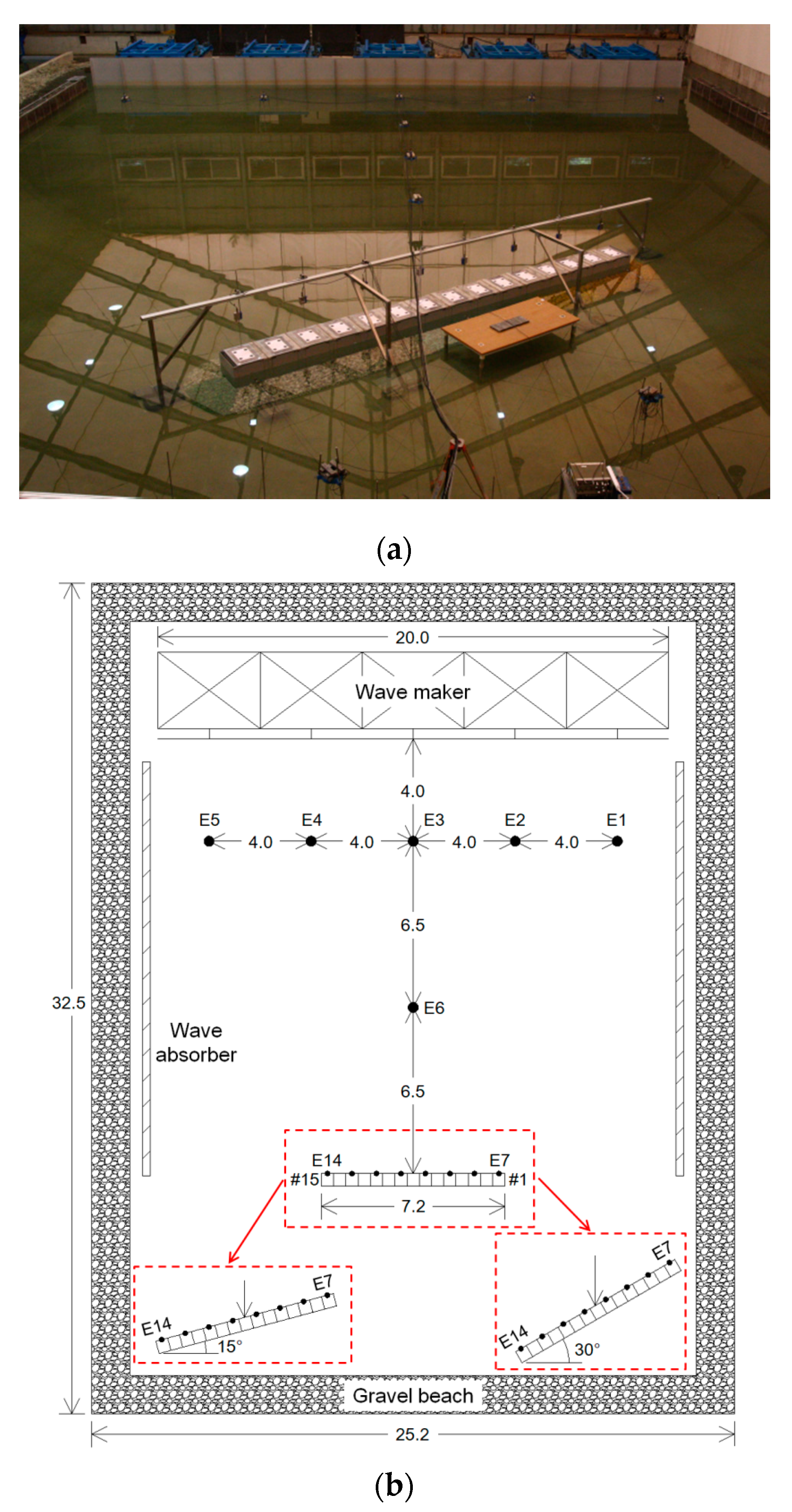
2.1.1. Wave Basin and Model Setup
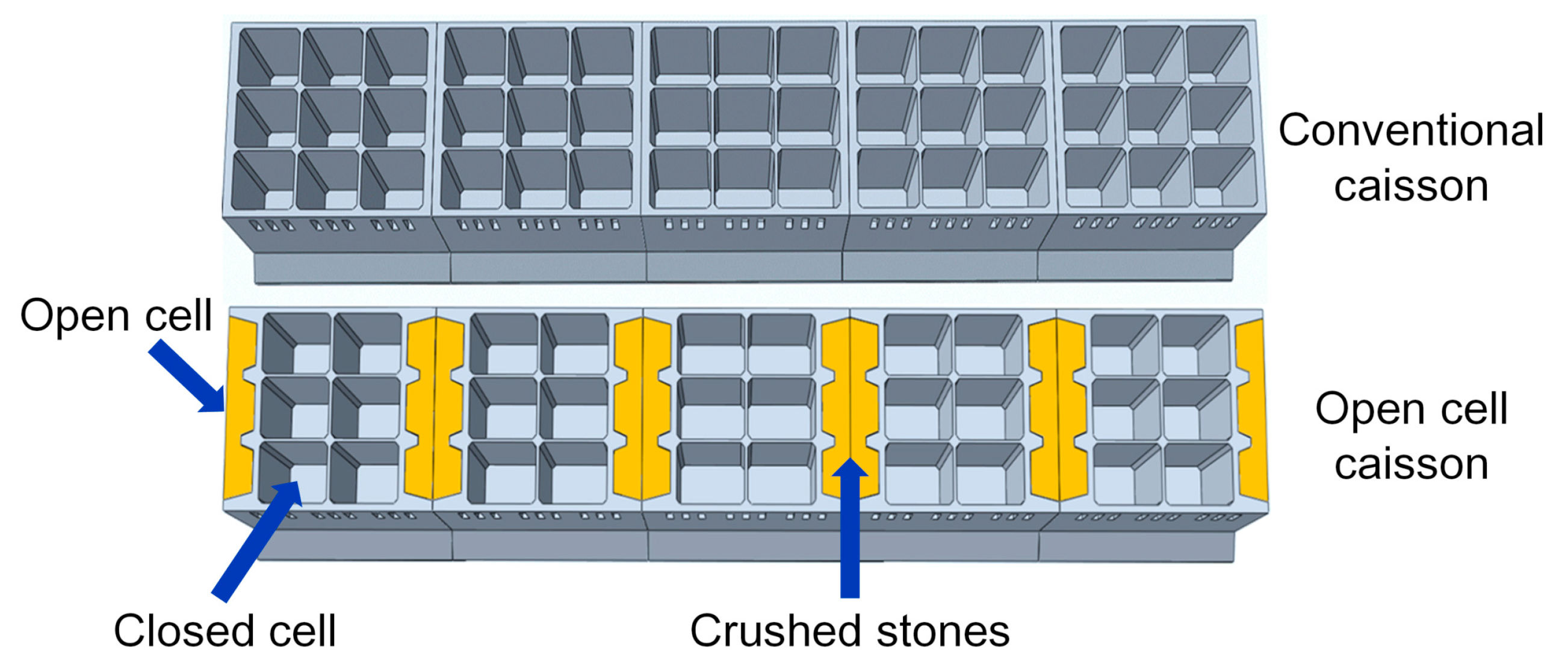
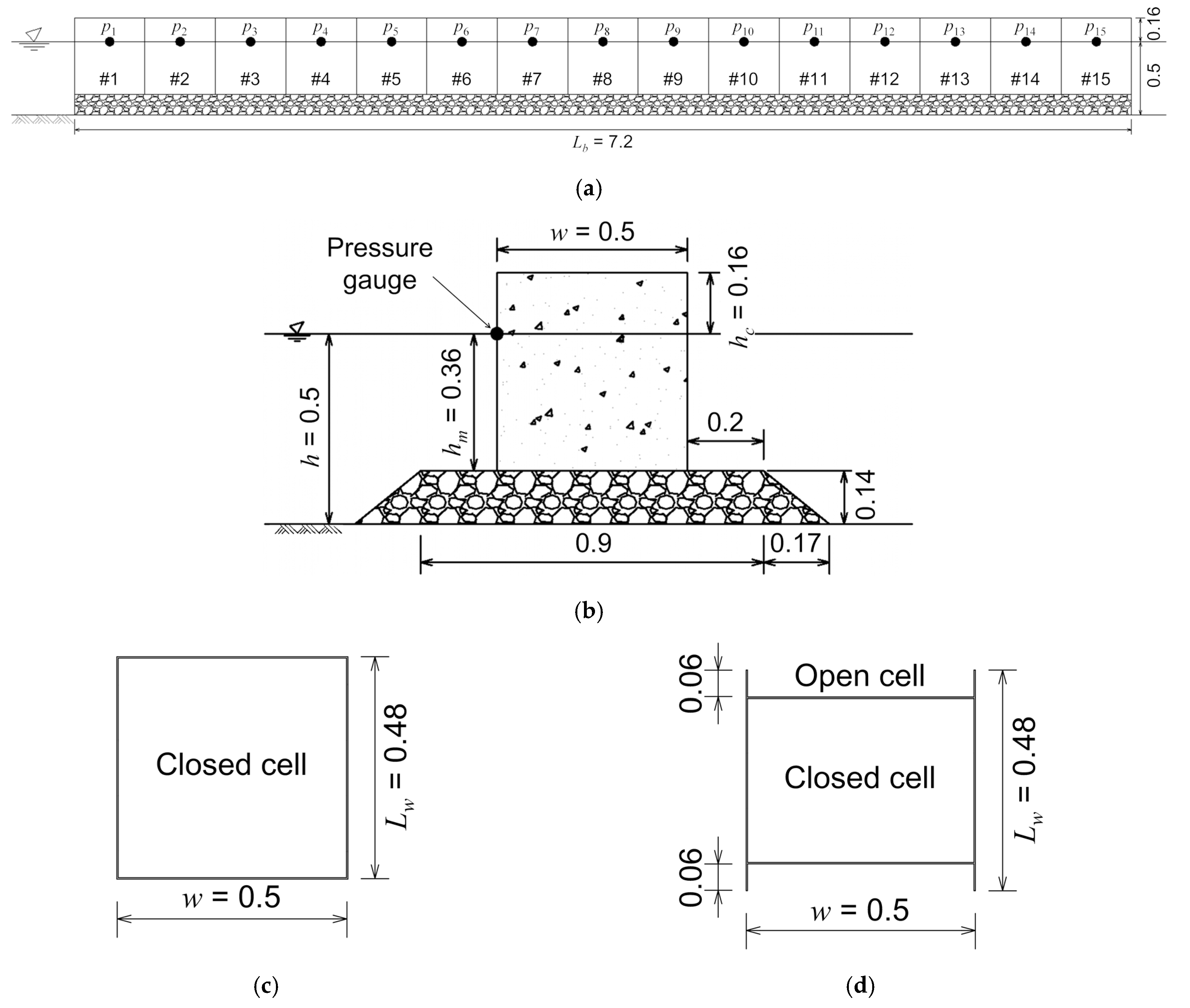
2.1.2. Breakwater Model
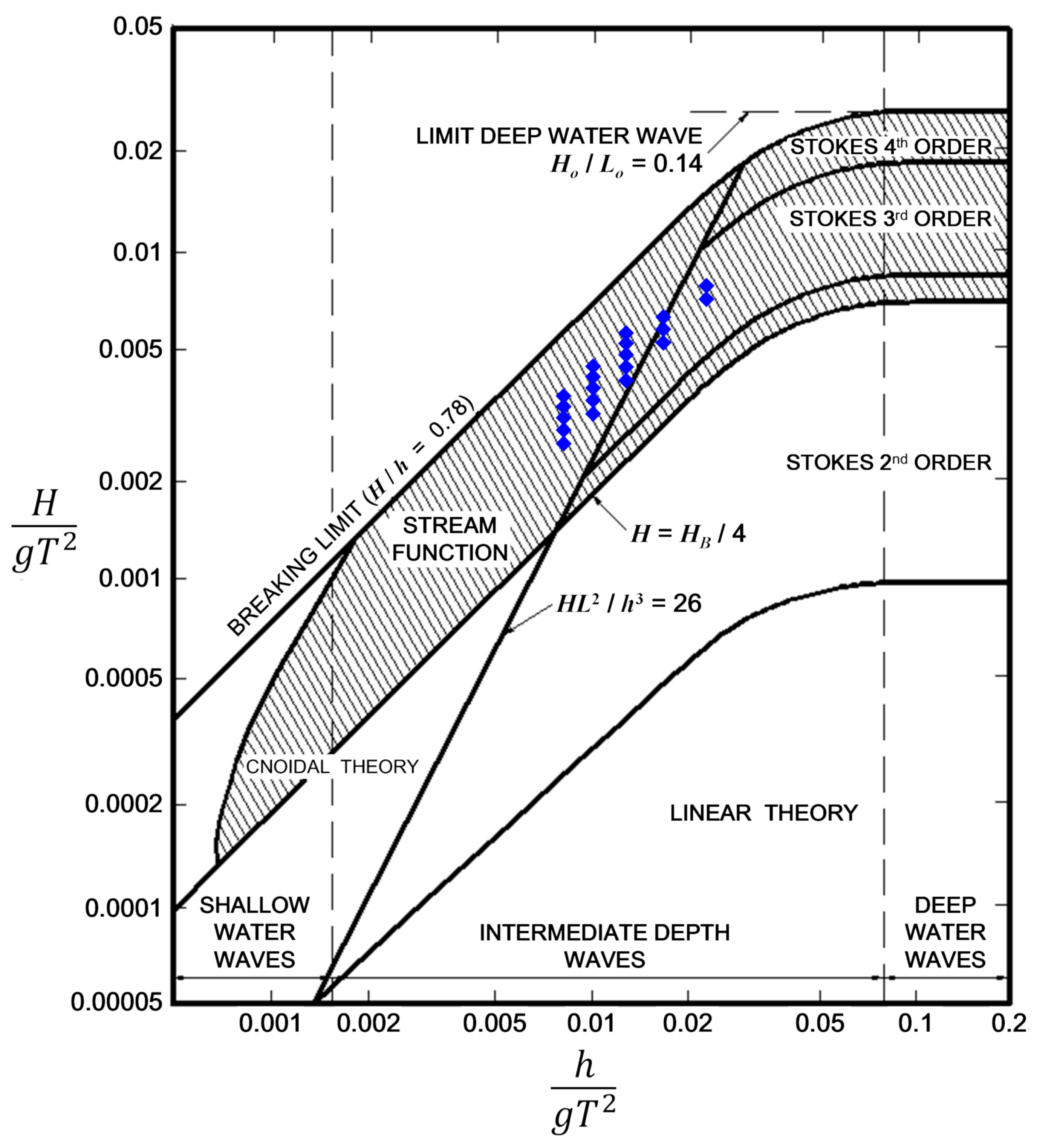
2.1.3. Test Waves
2.2. Analysis Method
2.2.1. Data Acquisition and Analysis
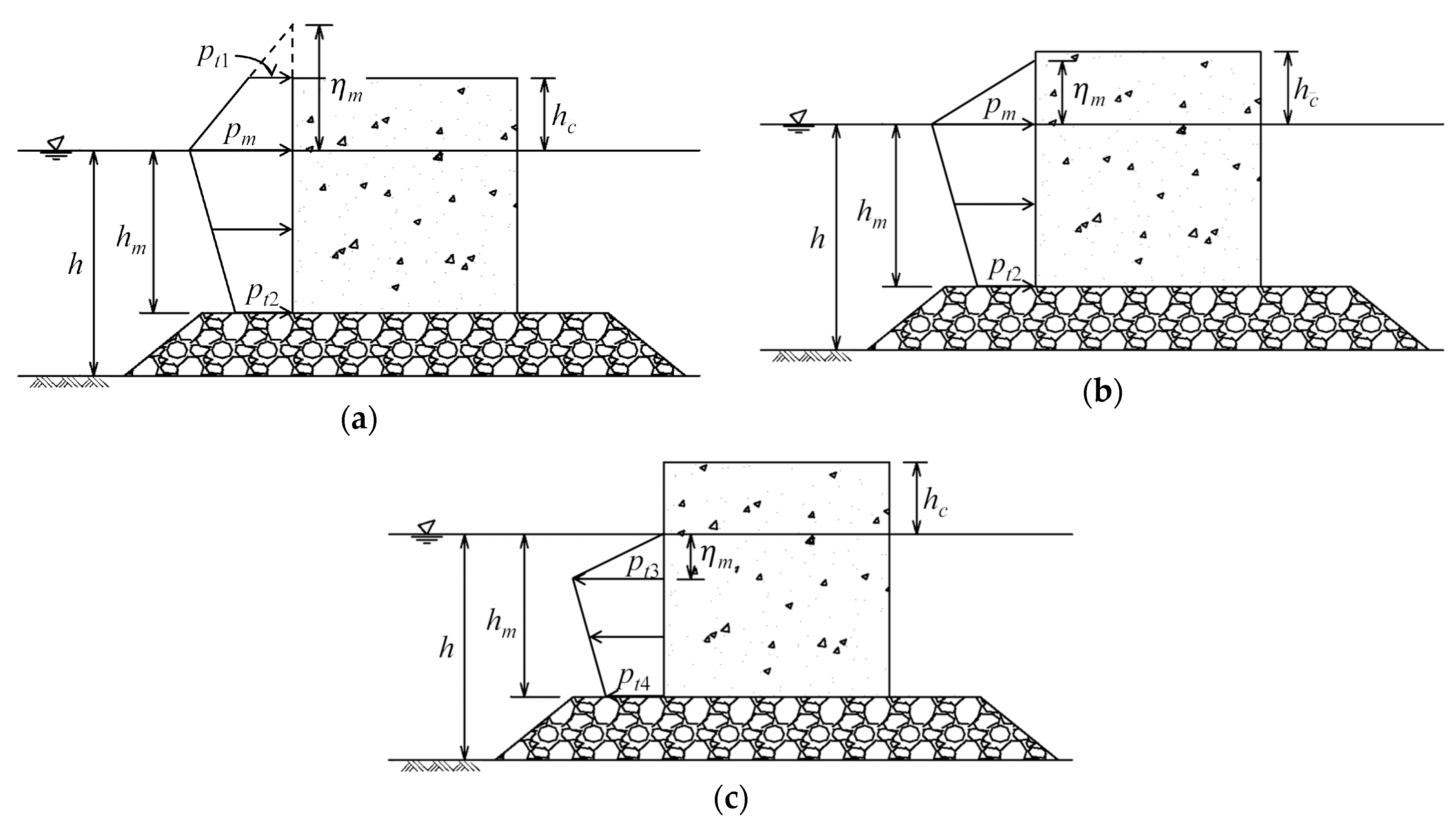
2.2.2. Wave Force Calculation
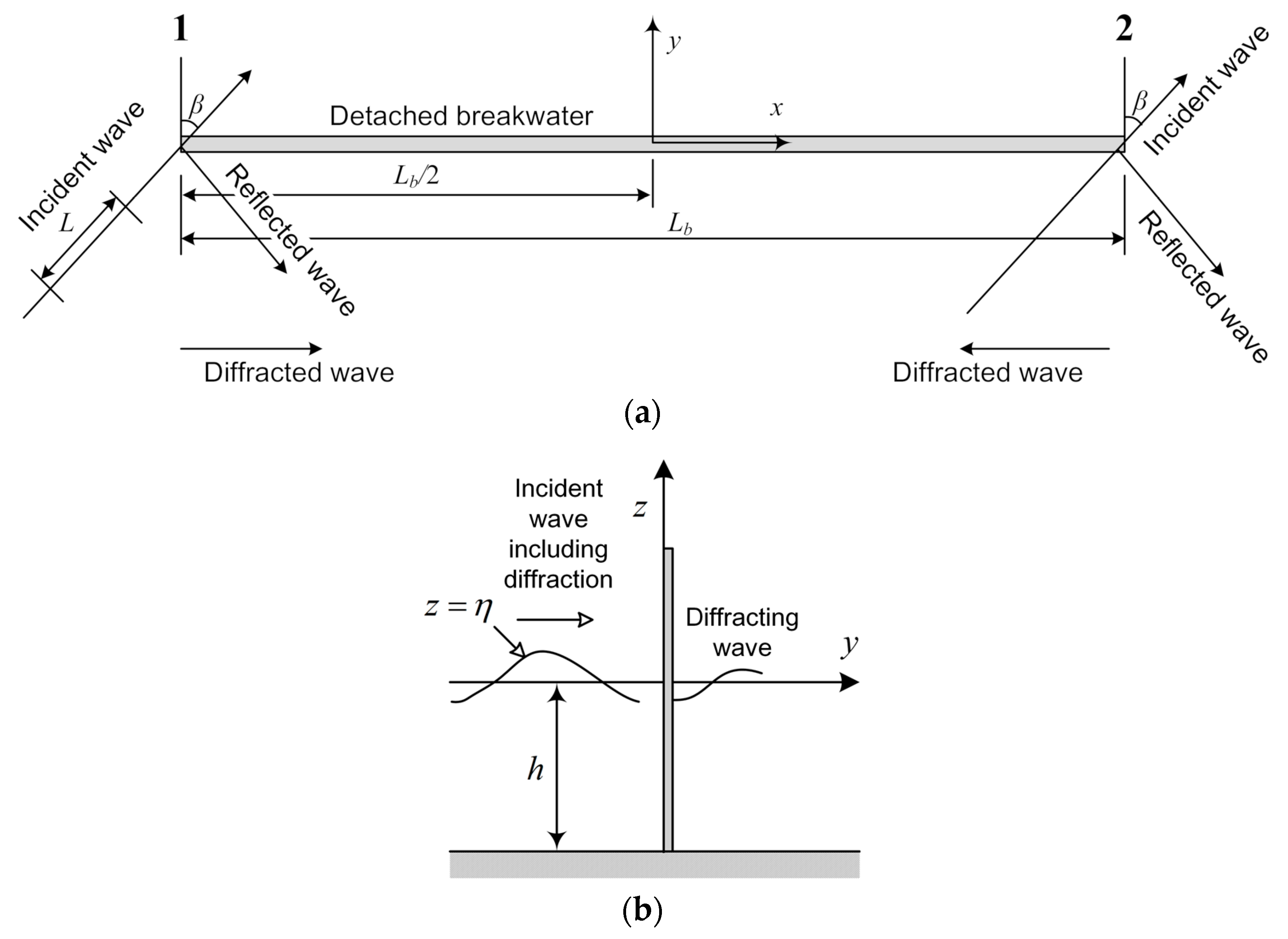
2.2.3. Analytical Solution for Wave Forces
3. Results and Discussion
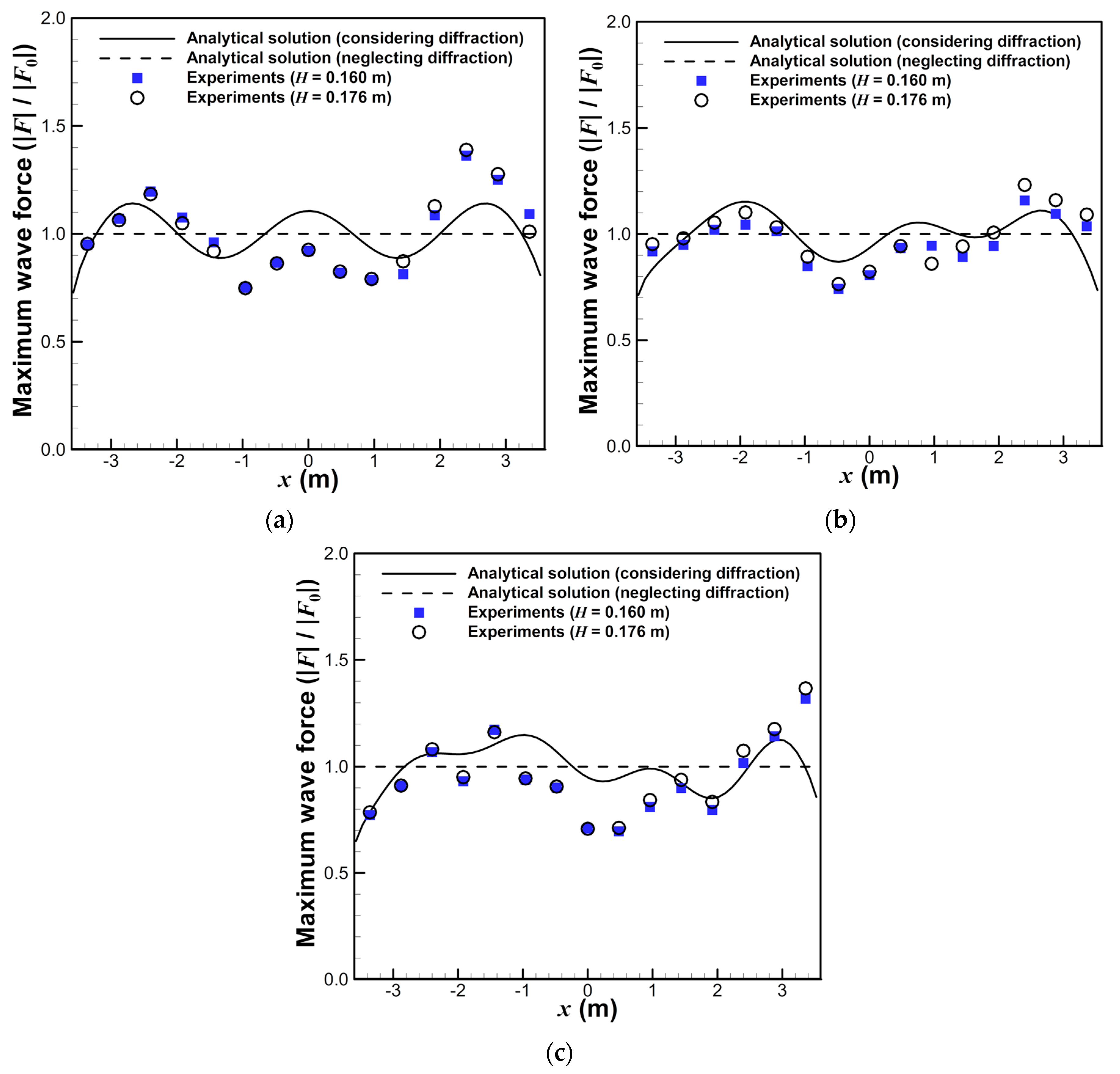
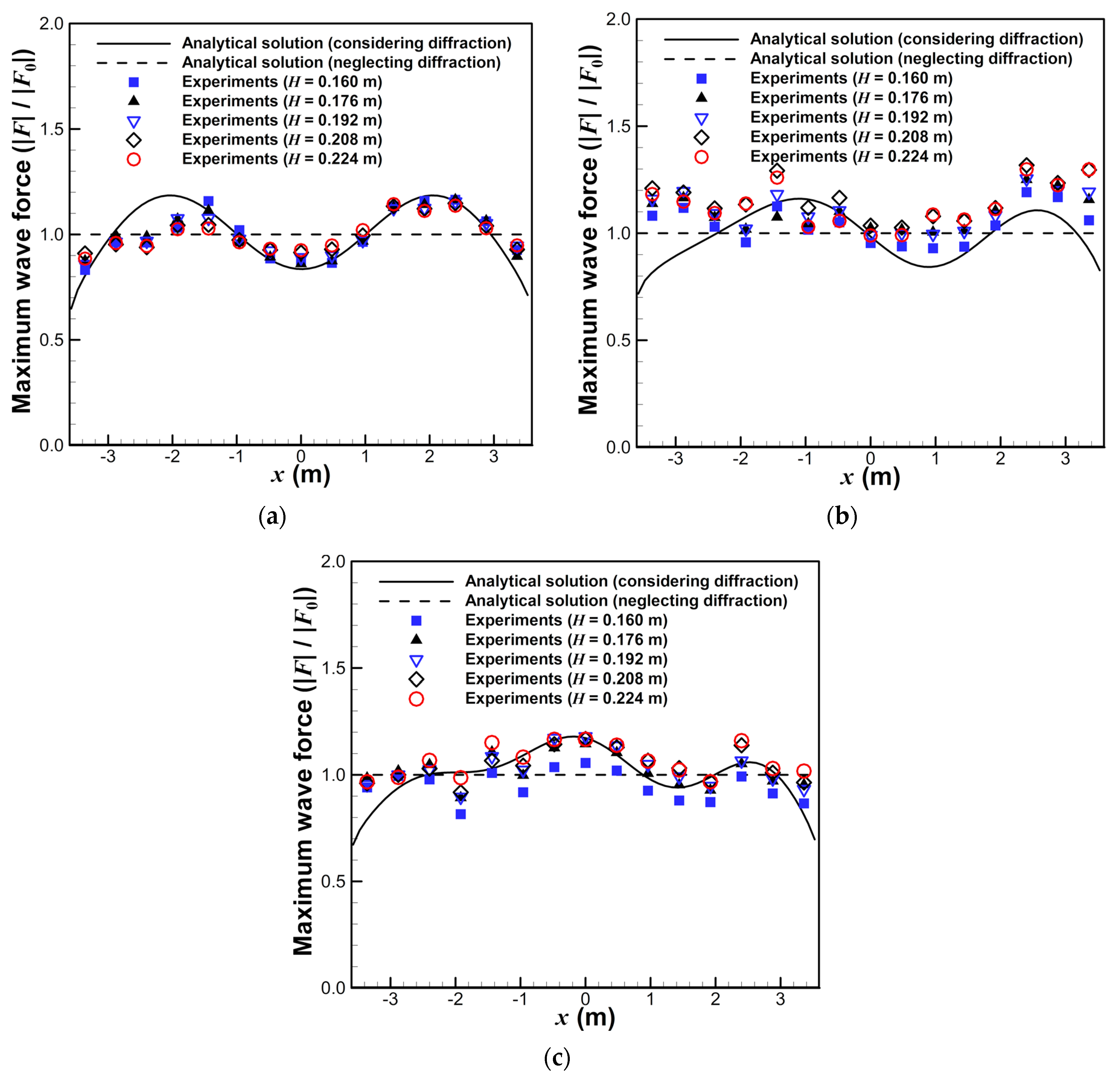
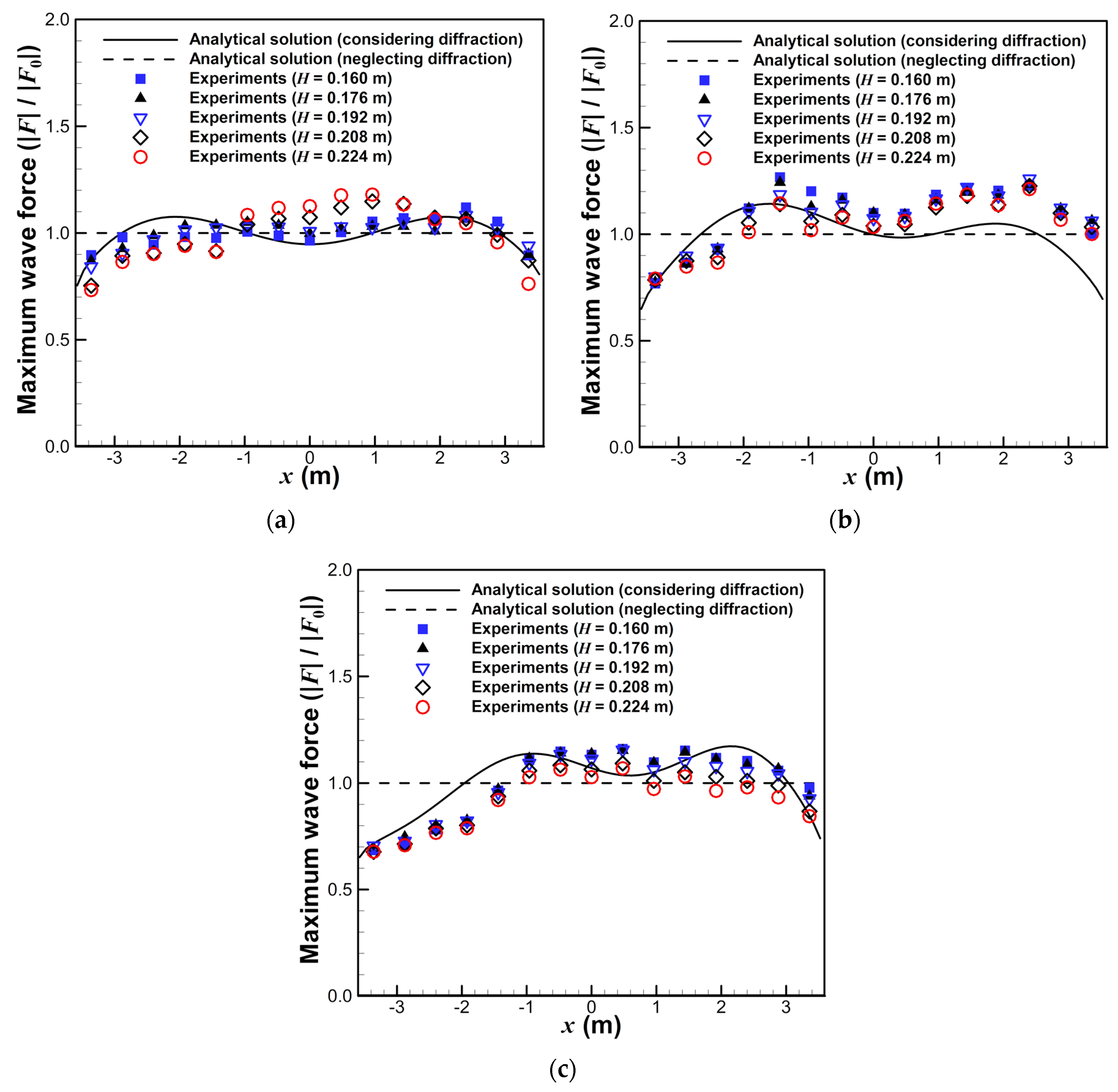
3.1. Maximum Wave Force Per Unit Length
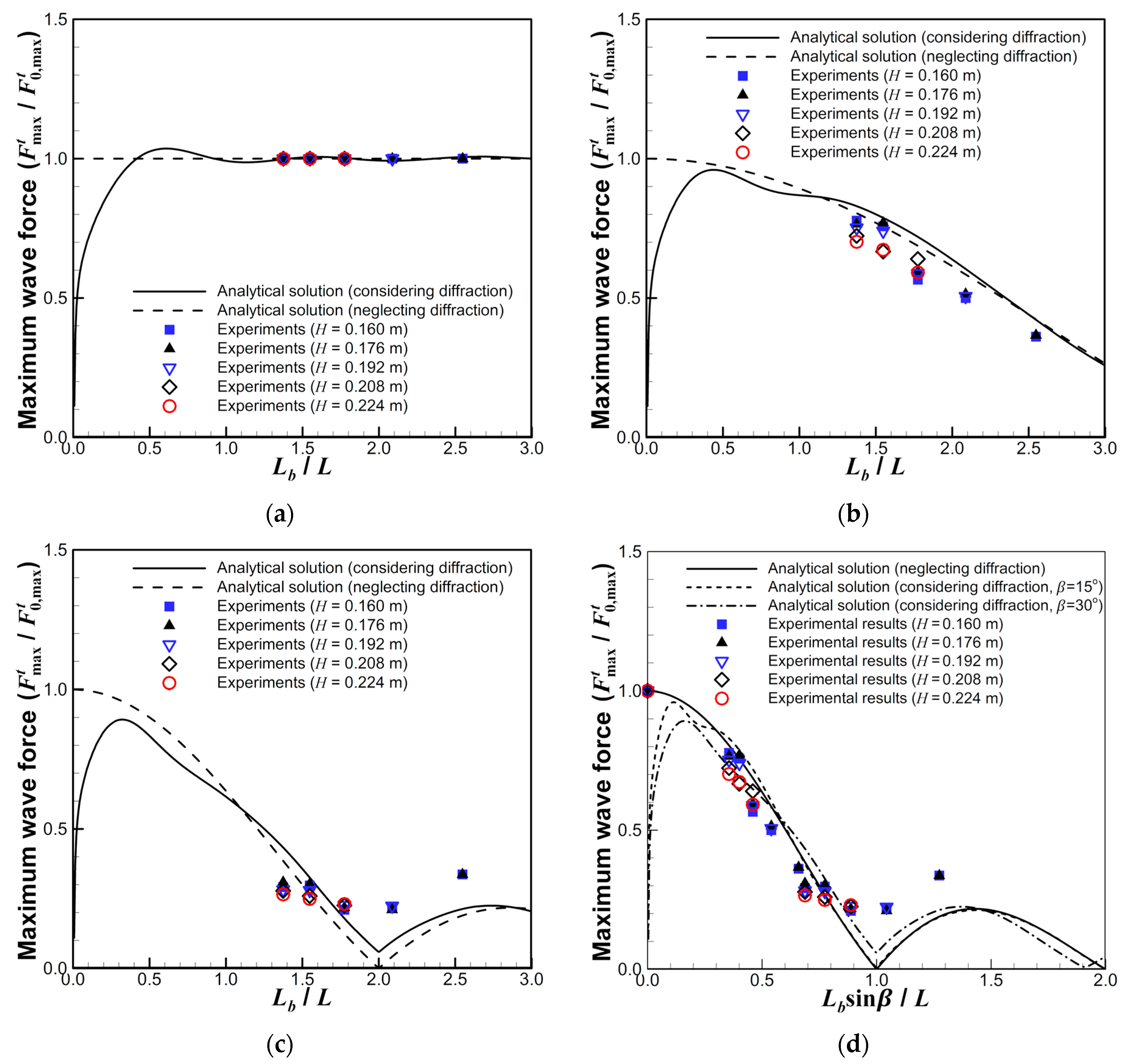
3.2. Wave Force Acting on the Entire Breakwater
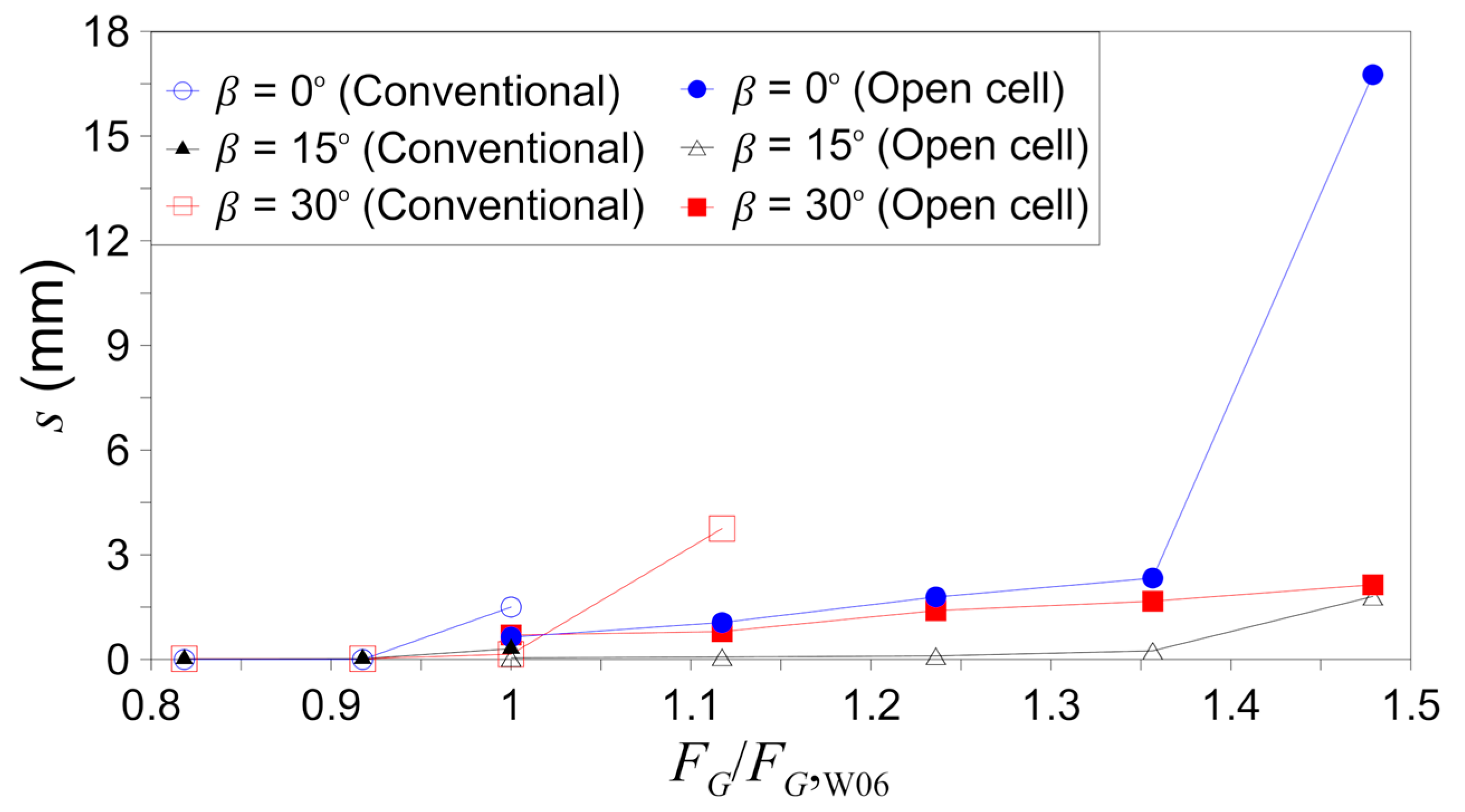
3.3. Stability Against Sliding
4. Conclusions
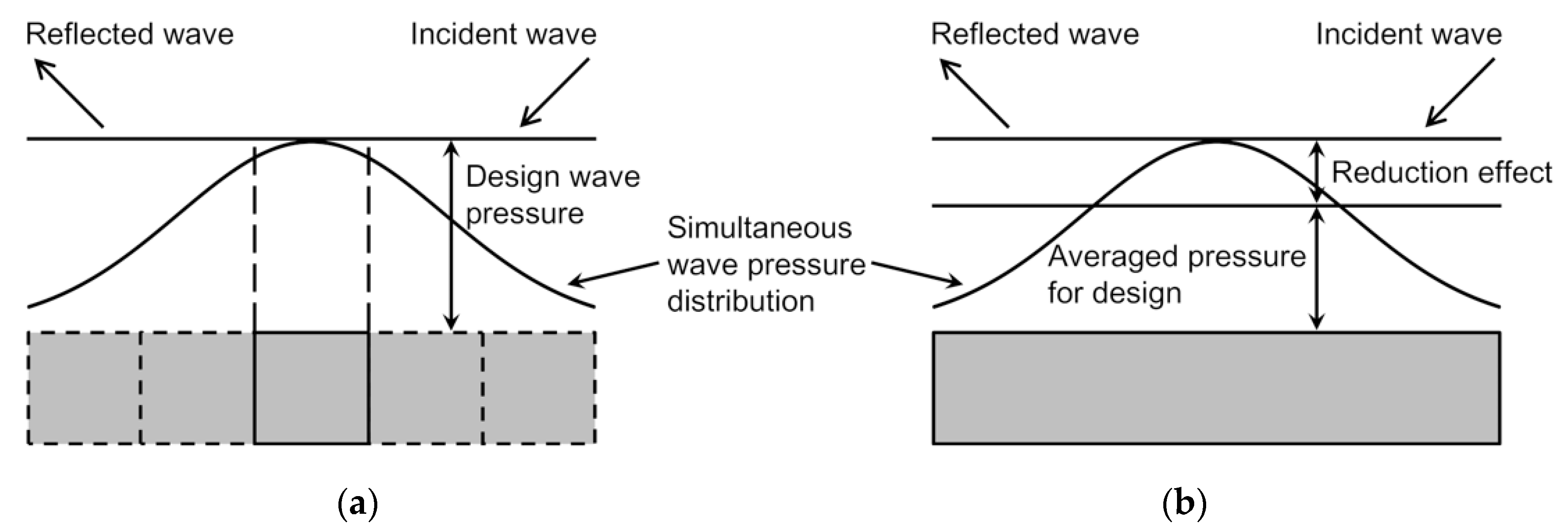
- The wave force acting on the open cell caisson breakwater decreased as the relative length of the breakwater and incident wave angle increased. The reduced force ratio was 0.210 when the relative length of the breakwater () was 0.887. These results demonstrate the effectiveness of the force reduction of open cell caisson breakwaters. In some cases, the relative wave force exceeded 1.0 due to diffraction, and the analytical solution predicted this phenomenon well. Moreover, the diffraction effects were considerable for the conventional caisson breakwater but negligible for the long-detached breakwater () involving open cell caissons.
- When the incident wave was obliquely propagated along the long structure, the acting wave force was reduced, owing to the phase difference of the wave pressures. The open cell caisson breakwater was more stable than the conventional one for oblique and normal incident waves. Specifically, at an incident wave angle of 0° (normal incidence), the open cell caisson breakwater could withstand a relative wave force 35% higher than that tolerated by the conventional caisson breakwater, owing to the frictional resistance force induced by the crushed stones in two open cells facing each other.
- The structures based on open cell caissons could experience excessive deformations before the sliding failure occurred. To prevent this, the deformation of the crushed stones filled in the open cells should be controlled by compacting the crushed stones or by using low-flow mortar to reduce the void.
Author Contributions
Funding
Conflicts of Interest
References
- The Intergovernmental Panel on Climate Change (IPCC). Global Warming of 1.5 °C; Intergovernmental Panel on Climate Change (IPCC): Geneva, Switzerland, 2019.
- Yamada, Y.; Satoh, M.; Sugi, M.; Kodama, C.; Noda, A.T.; Nakano, M.; Nasuno, T. Response of tropical cyclone activity and structure to global warming in a high-resolution global nonhydrostatic model. J. Clim. 2017, 30, 9703–9724. [Google Scholar] [CrossRef]
- Cha, E.J.; Knutson, T.R.; Lee, T.C.; Ying, M.; Nakaegawa, T. Third assessment on impacts of climate change on tropical cyclones in the typhoon committee region–Part II: Future projections. Trop. Cyclone Res. Rev. 2020, 9, 75–86. [Google Scholar] [CrossRef]
- Park, W.S.; Seo, J.; Won, D.; Lee, B.W. Stability assessment formulas for an interlocking caisson breakwater under oblique wave conditions. J. Coastal Res. 2018, 85, 1236–1240. [Google Scholar] [CrossRef]
- DY Engineering. Report of the Working Design Project of Seogwipo Port for the Construction to Repair Damage Caused by the Typhoon; Jeju Special Self-Governing Province: Jeju-do, Korea, 2013. (In Korean) [Google Scholar]
- Trӕtteberg, A. The effects of wave crests on wave forces. In Proceedings of the 11th Conference on Coastal Engineering, London, UK, September 1968; pp. 934–939. [Google Scholar]
- Battjes, J.A. Effects of short-crestedness on wave loads on long structures. Appl. Ocean Res. 1982, 4, 165–172. [Google Scholar] [CrossRef]
- Takahashi, S.; Shimosako, K. Reduction of Wave Force on a Long Caisson of Vertical Breakwater and Its Stability; Technical Notes No. 685 of Port and Harbour Research Institute; Harbour Research Institute: Nagase, Yokosuka, Japan, 1990; pp. 1–20. (In Japanese)
- Burcharth, H.F.; Liu, Z. Force Reduction of Short-Crested Non-Breaking Waves on Caissons; Final Report of Mast III Project PROVERBS (PRObabilistic Design Tools for VERtical BreakwaterS); Technical University of Braunschweig: Braunschweig, Germany, 1999; Volume IIa, Chapter 4.3; pp. 1–26. [Google Scholar]
- Mares-Nasarre, P.; van Gent, M.R.A. Oblique wave attack on rubble mound breakwater crest walls of finite length. Water 2020, 12, 353. [Google Scholar] [CrossRef]
- Jung, J.S.; Lee, C.; Cho, Y.S. Prediction of wave force on a long structure of semi-infinite breakwater type considering diffraction. J. Korean Soc. Coast. Ocean Eng. 2015, 27, 424–433. (In Korean) [Google Scholar] [CrossRef]
- Jung, J.S.; Lee, C.; Cho, Y.S. Distribution of wave forces at points on a vertical structure of semi-infinite breakwater considering diffraction. J. Korean Soc. Coast. Ocean Eng. 2016, 28, 240–249. (In Korean) [Google Scholar] [CrossRef]
- Jung, J.S.; Lee, C. Spatial variation of wave forces along a semi-infinite breakwater due to wave diffraction. In Proceedings of the Conference of Korean Association of Ocean Science Technology Society, Busan, Korea, 22–23 July 2020; p. 683. (In Korean). [Google Scholar]
- Kim, B.H.; Park, W.S.; Lee, J.W.; Jung, J.S. Making long caisson breakwater using interlocking system. Mag. Korean Soc. Civ. Eng. 2010, 58, 65–72. (In Korean) [Google Scholar]
- Seo, J.H.; Yi, J.H.; Park, W.S.; Won, D.H. Dispersion characteristics of wave forces on interlocking caisson breakwaters by cross cables. J. Korean Soc. Coast. Ocean Eng. 2015, 27, 315–323. (In Korean) [Google Scholar] [CrossRef]
- Park, W.S.; Won, D.; Seo, J.; Lee, B.W. Proposal of rotating stability assessment formula for an interlocking caisson breakwater subjected to wave forces. J. Korean Soc. Coast. Ocean Eng. 2020, 32, 11–16. (In Korean) [Google Scholar] [CrossRef]
- Goda, Y. Random seas and design of maritime structures. In Advanced Series on Ocean Engineering, 3rd ed.; World Scientific: Singapore, 2010; Volume 33. [Google Scholar]
- Ministry of Oceans and Fisheries (MOF). KC CODE KDS 64 45 20; Ministry of Oceans and Fisheries: Sejong-si, Korea, 2017. (In Korean)
- U.S. Army Corps of Engineers. Coastal Engineering Manual (CEM), Engineer Manual 1110-2-1100; U.S. Army Corps of Engineers: Washington, DC, USA, 2002.
- Cuomo, G.; Allsop, W.; Bruce, T.; Pearson, J. Breaking wave loads at vertical seawalls and breakwaters. Coast. Eng. 2010, 57, 424–439. [Google Scholar] [CrossRef]
- Facci, A.L.; Falcucci, G.; Agresta, A.; Biscarini, C.; Jannelli, E.; Ubertini, S. Fluid structure interaction of buoyant bodies with free surface flows: Computational modelling and experimental validation. Water 2019, 11, 1048. [Google Scholar] [CrossRef]
- Stagonas, D.; Ravindar, R.; Sriram, V.; Schimmels, S. Experimental evidence of the influence of recurves on wave loads at vertical seawalls. Water 2020, 12, 889. [Google Scholar] [CrossRef]
- Lee, B.W.; Seo, J.; Park, W.-S.; Won, D. A hydraulic experimental study of a movable barrier on a revetment to block wave overtopping. Appl. Sci. 2020, 10, 89. [Google Scholar] [CrossRef]
- Penney, W.G.; Price, A.T. The diffraction theory of sea waves by breakwaters and the shelter afforded by breakwaters. Philos. Trans. R. Soc. Lond. A 1952, 244, 236–253. [Google Scholar]
- Kim, H.; Do, K.D.; Suh, K.D. Scattering of obliquely incident water waves by partially reflecting non-transmitting breakwaters. Ocean Eng. 2011, 38, 148–158. [Google Scholar] [CrossRef]
- Hattori, C.; Shibata, K.; Ohori, K. Disasters of Breakwaters by Wave Action (Part 3); Technical Notes of Port and Harbour Research Institute; Harbour Research Institute: Kanagawa, Japan, 1984; p. 485. (In Japanese)
- Miyai, S.; Ohira, K.; Shiomi, M. Disasters of Breakwaters by Wave Action (Part 4); Technical Notes of Port and Harbour Research Institute; Harbour Research Institute: Kanagawa, Japan, 1993; p. 765. (In Japanese)
- Spinneken, J.; Swan, C. The operation of a 3D wave basin in force control. Ocean Eng. 2012, 55, 88–100. [Google Scholar] [CrossRef]
- Stratigaki, V.; Troch, P.; Stallard, T.; Forehand, D.; Kofoed, J.P.; Folley, M.; Benoit, M.; Babarit, A.; Kirkegaard, J. Wave basin experiments with large wave energy converter arrays to study interactions between the converters and effects on other users in the sea and coastal area. Energies 2014, 7, 701–734. [Google Scholar] [CrossRef]

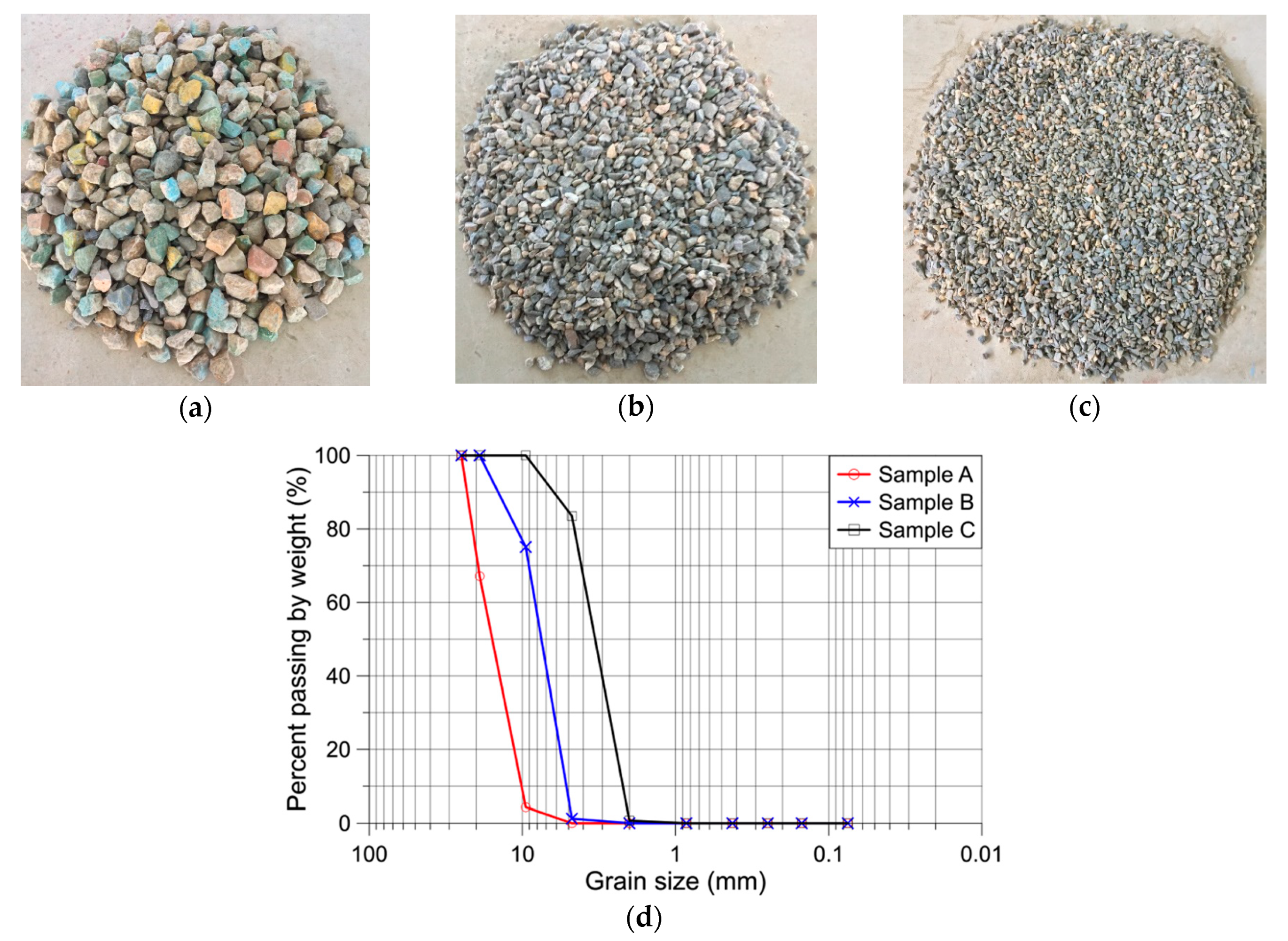

| Sample | D10 (= De, mm) | D30 (mm) | D50 (mm) | D60 (mm) | Cu | Cc | USCS |
|---|---|---|---|---|---|---|---|
| A | 10.359 | 13.383 | 16.408 | 17.920 | 1.730 | 0.965 | GP |
| B | 5.313 | 6.600 | 7.886 | 8.529 | 1.605 | 0.961 | GP |
| C | 2.308 | 2.972 | 3.636 | 3.969 | 1.720 | 0.946 | SP |
| H (m) | 0.160 | 0.176 | 0.192 | 0.208 | 0.224 | |
|---|---|---|---|---|---|---|
| T (s) | ||||||
| 1.50 | W01 (0.0566) | W02 (0.0623) | ||||
| 1.75 | W03 (0.0464) | W04 (0.0510) | W05 (0.0557) | |||
| 2.00 | W06 (0.0395) | W07 (0.0434) | W08 (0.0473) | W09 (0.0513) | W10 (0.0552) | |
| 2.25 | W11 (0.0344) | W12 (0.0378) | W13 (0.0413) | W14 (0.0447) | W15 (0.0482) | |
| 2.50 | W16 (0.0306) | W17 (0.0336) | W18 (0.0367) | W19 (0.0397) | W20 (0.0428) | |
| Case | Conventional Caisson | Open Cell Caisson | ||
|---|---|---|---|---|
| Head | Trunk | Head (Crushed Stones) | Trunk (Crushed Stones) | |
| Self-weight (kN) | 1.80 | 1.20 | 1.89 (0.18) | 0.96 (0.37) |
| Effective self-weight (kN) | 1.19 | 0.57 | 1.19 (0.12) | 0.57 (0.25) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, B.W.; Jung, J.-S.; Park, W.-S.; Yoon, J.-S. Wave Force Characteristics and Stability of Detached Breakwaters Consisting of Open Cell Caissons Interlocked via Crushed Stones. Water 2020, 12, 2873. https://doi.org/10.3390/w12102873
Lee BW, Jung J-S, Park W-S, Yoon J-S. Wave Force Characteristics and Stability of Detached Breakwaters Consisting of Open Cell Caissons Interlocked via Crushed Stones. Water. 2020; 12(10):2873. https://doi.org/10.3390/w12102873
Chicago/Turabian StyleLee, Byeong Wook, Jae-Sang Jung, Woo-Sun Park, and Jae-Seon Yoon. 2020. "Wave Force Characteristics and Stability of Detached Breakwaters Consisting of Open Cell Caissons Interlocked via Crushed Stones" Water 12, no. 10: 2873. https://doi.org/10.3390/w12102873
APA StyleLee, B. W., Jung, J.-S., Park, W.-S., & Yoon, J.-S. (2020). Wave Force Characteristics and Stability of Detached Breakwaters Consisting of Open Cell Caissons Interlocked via Crushed Stones. Water, 12(10), 2873. https://doi.org/10.3390/w12102873






