Evaluation of an Application of Probabilistic Quantitative Precipitation Forecasts for Flood Forecasting
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Basins and Case Selection
2.2. Precipitation Forecasts
2.3. Hydrologic Prediction Model
2.4. Forecast Evaluation Statistics
3. Results
4. Discussion
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Nguyen, P.; Thorstensen, A.; Sorooshian, S.; Hsu, K.; Aghakouchak, A. Flood forecasting and inundation mapping using HiResFlood-UCI and near-real-time satellite precipitation data: The 2008 Iowa flood. J. Hydrometeorol. 2015, 16, 1171–1183. [Google Scholar] [CrossRef]
- Krajewski, W.F.; Ceynar, D.; Demir, I.; GosKa, R.; Kruger, A.; Langel, C.; Mantilla, R.; Niemeier, J.; Quintero, F.; Seo, B.-C.; et al. Real-time flood forecasting and information system for the state of Iowa. Bull. Am. Meteorol. Soc. 2017, 98, 539–554. [Google Scholar] [CrossRef]
- Cuo, L.; Pagano, T.C.; Wang, Q.J. A Review of Quantitative Precipitation Forecasts and Their Use in Short- to Medium-Range Streamflow Forecasting. J. Hydrometeorol. 2011, 12, 713–728. [Google Scholar] [CrossRef]
- Seo, B.C.; Quintero, F.; Krajewski, W.F. High-resolution QPF uncertainty and its implications for flood prediction: A case study for the eastern Iowa flood of 2016. J. Hydrometeorol. 2018, 19, 1289–1304. [Google Scholar] [CrossRef]
- Davolio, S.; Miglietta, M.M.; Diomede, T.; Marsigli, C.; Morgillo, A.; Moscatello, A. A meteo-hydrological prediction system based on a multi-model approach for precipitation forecasting. Nat. Hazards Earth Syst. Sci. 2008, 8, 143–159. [Google Scholar] [CrossRef]
- Wu, J.; Lu, G.; Wu, Z. Flood forecasts based on multi-model ensemble precipitation forecasting using a coupled atmospheric-hydrological modeling system. Nat. Hazards 2014, 74, 325–340. [Google Scholar] [CrossRef]
- Fritsch, J.M.; Carbone, R.E. Improving Quantitative Precipitation Forecasts in the Warm Season: A USWRP Research and Development Strategy. Bull. Am. Meteorol. Soc. 2004, 85, 955–966. [Google Scholar] [CrossRef]
- Gallus, W.A. Rainfall Forecasting. The Challenge of Warm-Season Convective Precipitation Forecasting. In Hydrological Science and Engineering; Wong, T.S.W., Ed.; Nova Science Publishers: Hauppauge, NY, USA, 2012; pp. 129–160. ISBN 978-61942-134-9. [Google Scholar]
- Moser, B.A.; Gallus, W.A.; Mantilla, R. An initial assessment of radar data assimilation on warm season rainfall forecasts for use in hydrologic models. Weather Forecast. 2015, 30, 1491–1520. [Google Scholar] [CrossRef]
- Ebert, E.E.; Damrath, U.; Wergen, W.; Baldwin, M.E. The WGNE Assessment of Short-term Quantitative Precipitation Forecasts. Bull. Am. Meteorol. Soc. 2003, 84, 481–492. [Google Scholar] [CrossRef]
- Cluckie, I.D.; Xuan, Y.; Wang, Y. Uncertainty analysis of hydrological ensemble forecasts in a distributed model utilising short-range rainfall prediction. Hydrol. Earth Syst. Sci. 2009, 13, 293–303. [Google Scholar] [CrossRef]
- Nielsen, E.R.; Schumacher, R.S. Using Convection-Allowing Ensembles to Understand the Predictability of an Extreme Rainfall Event. Mon. Weather Rev. 2016, 144, 3651–3676. [Google Scholar] [CrossRef]
- Duda, J.D.; Gallus, W.A. The impact of large-scale forcing on skill of simulated convective initiation and upscale evolution with convection-allowing grid spacings in the WRF. Weather Forecast. 2013, 28, 994–1018. [Google Scholar] [CrossRef]
- Golding, B.W. Quantitative precipitation forecasting in the UK. J. Hydrol. 2000, 239, 286–305. [Google Scholar] [CrossRef]
- Eckel, F.A.; Mass, C.F. Aspects of Effective Mesoscale, Short-Range Ensemble Forecasting. Weather Forecast. 2005, 20, 328–350. [Google Scholar] [CrossRef]
- Cintineo, R.; Otkin, J.A.; Xue, M.; Kong, F. Evaluating the Performance of Planetary Boundary Layer and Cloud Microphysical Parameterization Schemes in Convection-Permitting Ensemble Forecasts Using Synthetic GOES-13 Satellite Observations. Mon. Weather Rev. 2014, 142, 163–182. [Google Scholar] [CrossRef]
- Banks, R.F.; Tiana-Alsina, J.; Baldasano, J.M.; Rocadenbosch, F.; Papayannis, A.; Solomos, S.; Tzanis, C.G. Sensitivity of boundary-layer variables to PBL schemes in the WRF model based on surface meteorological observations, lidar, and radiosondes during the HygrA-CD campaign. Atmos. Res. 2016, 176–177, 185–201. [Google Scholar] [CrossRef]
- Cloke, H.L.; Pappenberger, F. Ensemble flood forecasting: A review. J. Hydrol. 2009, 375, 613–626. [Google Scholar] [CrossRef]
- Dowell, D.; Alexander, C.; Alcott, T.; Ladwig, T. HRRR Ensemble (HRRRE) Guidance 2018 HWT Spring Experiment. Available online: https://rapidrefresh.noaa.gov/internal/pdfs/2018_Spring_Experiment_HRRRE_Documentation.pdf (accessed on 1 June 2018).
- Avolio, E.; Federico, S.; Miglietta, M.M.; Lo Feudo, T.; Calidonna, C.R.; Sempreviva, A.M. Sensitivity analysis of WRF model PBL schemes in simulating boundary-layer variables in southern Italy: An experimental campaign. Atmos. Res. 2017, 192, 58–71. [Google Scholar] [CrossRef]
- Roberts, B.; Jirak, I.L.; Clark, A.J.; Weiss, S.J.; Kain, J.S. PostProcessing and Visualization Techniques for Convection-Allowing Ensembles. Bull. Am. Meteorol. Soc. 2019, 100, 1245–1258. [Google Scholar] [CrossRef]
- Clark, A.J. Generation of Ensemble Mean Precipitation Forecasts from Convection-Allowing Ensembles. Weather Forecast. 2017, 32, 1569–1583. [Google Scholar] [CrossRef]
- Leith, C.E. Theoretical Skill of Monte Carlo Forecasts. Mon. Weather Rev. 1974, 102, 409–418. [Google Scholar] [CrossRef]
- Buizza, R.; Miller, M.; Palmer, T.N. Stochastic representation of model uncertainties in the ECMWF ensemble prediction system. Q. J. R. Meteorol. Soc. 1999, 460, 2887–2908. [Google Scholar] [CrossRef]
- Werner, K.; Brandon, D.; Clark, M.; Gangopadhyay, S. Incorporating medium-range numerical weather model output into the Ensemble Streamflow Prediction system of the National Weather Service. J. Hydrometeorol. 2005, 6, 101–114. [Google Scholar] [CrossRef]
- Ebert, E.E. Ability of a poor man’s ensemble to predict the probability and distribution of precipitation. Mon. Weather Rev. 2001, 129, 2461–2480. [Google Scholar] [CrossRef]
- Ferraris, L.; Rudari, R.; Siccardi, F. The Uncertainty in the Prediction of Flash Floods in the Northern Mediterranean Environment. J. Hydrometeorol. 2002, 3, 714–727. [Google Scholar] [CrossRef]
- Yan, H.; Gallus, W.A., Jr. An Evaluation of QPF from the WRF, NAM, and GFS Models Using Multiple Verification Methods over a Small Domain. Weather Forecast. 2016, 31, 1363–1379. [Google Scholar] [CrossRef]
- Carlberg, B.; Franz, K.; Gallus, W., Jr. Submitted, A method to account for QPF spatial displacement errors in short-term ensemble streamflow forecasting. Water 2020. [Google Scholar]
- Reed, S.M.; MacFarlane, A. Validation of NWS Hydrologic Ensemble Forecast Service (HEFS) Real-time Products at the Middle Atlantic River Forecast Center. In Proceedings of the 34th Conference on Hydrology, Boston, MA, USA, 12–16 January 2020; American Meteorological Society: Boston, MA, USA, 2020. [Google Scholar]
- Stensrud, D.J.; Yussouf, N. Reliable Probabilistic Quantitative Precipitation Forecasts from a Short-Range Ensemble Forecasting System. Weather Forecast. 2007, 22, 3–17. [Google Scholar] [CrossRef]
- Jeanne-Rose, R.; Madsen, H.; Ole, M. A Methodology for Probabilistic Real-Time Forecasting—An Urban Case Study. J. Hydroinform. 2013, 15, 751–762. [Google Scholar] [CrossRef]
- Thompson, G.; Eidhammer, T. A Study of Aerosol Impacts on Clouds and Precipitation Development in a Large Winter Cyclone. J. Atmos. Sci. 2014, 71, 3636–3658. [Google Scholar] [CrossRef]
- Nakanishi, M.; Niino, H. Development of an improved turbulence closure model for the atmospheric boundary layer. J. Meteorol. Soc. Jpn. 2009, 87, 895–912. [Google Scholar] [CrossRef]
- Skamarock, W.C.; Klemp, J.B.; Dudhia, J.; Gill, D.O.; Barker, D.; Duda, M.G.; Powers, J.G. A Description of the Advanced Research WRF Version 3; Citeseer: Boulder, CO, USA, 2008. [Google Scholar]
- Janjic, Z.; Gall, R. Scientific Documentation of the NCEP Nonhydrostatic Multiscale Model on the B Grid (NMMB). Prt 1 Dynamics; Citeseer: Boulder, CO, USA, 2012. [Google Scholar]
- Environmental Modeling Center, N.W.S. NAM 2017. Available online: https://www.emc.ncep.noaa.gov/NAM/mconf.php (accessed on 1 October 2018).
- Janjić, Z.I. The Step-Mountain Eta Coordinate Model: Further Developments of the Convection, Viscous Sublayer, and Turbulence Closure Schemes. Mon. Weather Rev. 1994, 122, 927–945. [Google Scholar] [CrossRef]
- Hong, S.; Lim, J. The WRF single-moment 6-class microphysics scheme (WSM6). J. Korean Meteorol. Soc. 2006, 42, 129–151. [Google Scholar]
- Hong, S.-Y.; Noh, Y.; Dudhia, J. A New Vertical Diffusion Package with an Explicit Treatment of Entrainment Processes. Mon. Weather Rev. 2006, 134, 2318–2341. [Google Scholar] [CrossRef]
- Aligo, E.B.; Ferrier, J.; Carley, E.; Rogers, M.; Pyle, S.; Weiss, J.; Jirak, I.L. Modified Microphysics for Use in High-Resolution NAM Forecasts. In Proceedings of the 27th Conference on Severe Storms, Madison, WI, USA, 2–7 November 2014. [Google Scholar]
- Azizan, I.; Karin, S.A.B.A.; Raju, S.S.K. Fitting rainfall data by using cubic spline interpolation. In Proceedings of the MATEC Web Conference; EDP Sciences: Paris, France, 2018; Volume 225, p. 9. [Google Scholar]
- Lin, Y.; Mitchell, K.E. The NCEP Stage II/IV hourly preciptiation analysis development and applications. In Proceedings of the 19th Conference on Hydrology, 9–13 January 2005; American Meteorological Society: San Diego, CA, USA, 2005. [Google Scholar]
- Burnash, R.J.C.; Ferral, L.; McGuire, R.A. A Generalized Streamflow Simulation System: Conceptual Models for Digital Computers; Joint Federal and State River Forecast Center, U.S. National Weather Service, and California Department of Water Resources Techinical Report; California Department of Water Resources: Sacramento, CA, USA, 1973.
- Burnash, R.J.C. The NWS River Forecast System-Catchment Modeling. In Computer Models of Watershed Hydrology; Singh, V., Ed.; Water Resources Publication: Lone Tree, CO, USA, 1995; pp. 311–366. [Google Scholar]
- Epstein, E.S. A scoring system for probability forecasts of ranked categories. J. Appl. Meteorol. 1969, 8, 985–987. [Google Scholar] [CrossRef]
- Wilks, D.S. Forecast verification. In Statistical Methods in the Atmospheric Sciences; Academic Press: Boston, MA, USA, 1995; pp. 233–283. ISBN 978-0-12-385022-5. [Google Scholar]
- Murphy, A.H. On the “Ranked Probability Score”. J. Appl. Meteorol. 1969, 8, 988–989. [Google Scholar] [CrossRef]
- Murphy, A.H. A Note on the Ranked Probability Score. J. Appl. Meteorol. 1971, 10, 155–156. [Google Scholar] [CrossRef]
- NWS about WPC’s PQPF and Percentile QPF Products. Available online: https://www.wpc.ncep.noaa.gov/pqpf/about_pqpf_products.shtml (accessed on 8 April 2019).
- UCAR Image Archive—Meteorological Case Study Selection Kit. Available online: http://www2.mmm.ucar.edu/imagearchive/ (accessed on 1 November 2018).
- Clark, M.; Gangopadhyay, S.; Hay, L.; Rajagopalan, B.; Wilby, R. The Schaake Shuffle: A Method for Reconstructing Space—Time Variability in Forecasted Precipitation and Temperature Fields. J. Hydrometeorol. 2004, 5, 243–262. [Google Scholar] [CrossRef]
- Roulin, E.; Vannitsem, S. Postprocessing of Ensemble Precipitation Predictions with Extended Logistic Regression Based on Hindcasts. Mon. Weather Rev. 2012, 140, 874–888. [Google Scholar] [CrossRef]
- Crochemore, L.; Ramos, M.-H.; Papenberger, F. Bias correcting precipitation forecasts to improve the skill of seasonal streamflow forecasts. Hydrol. Earth Syst. Sci. 2016, 20, 3601–3618. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |

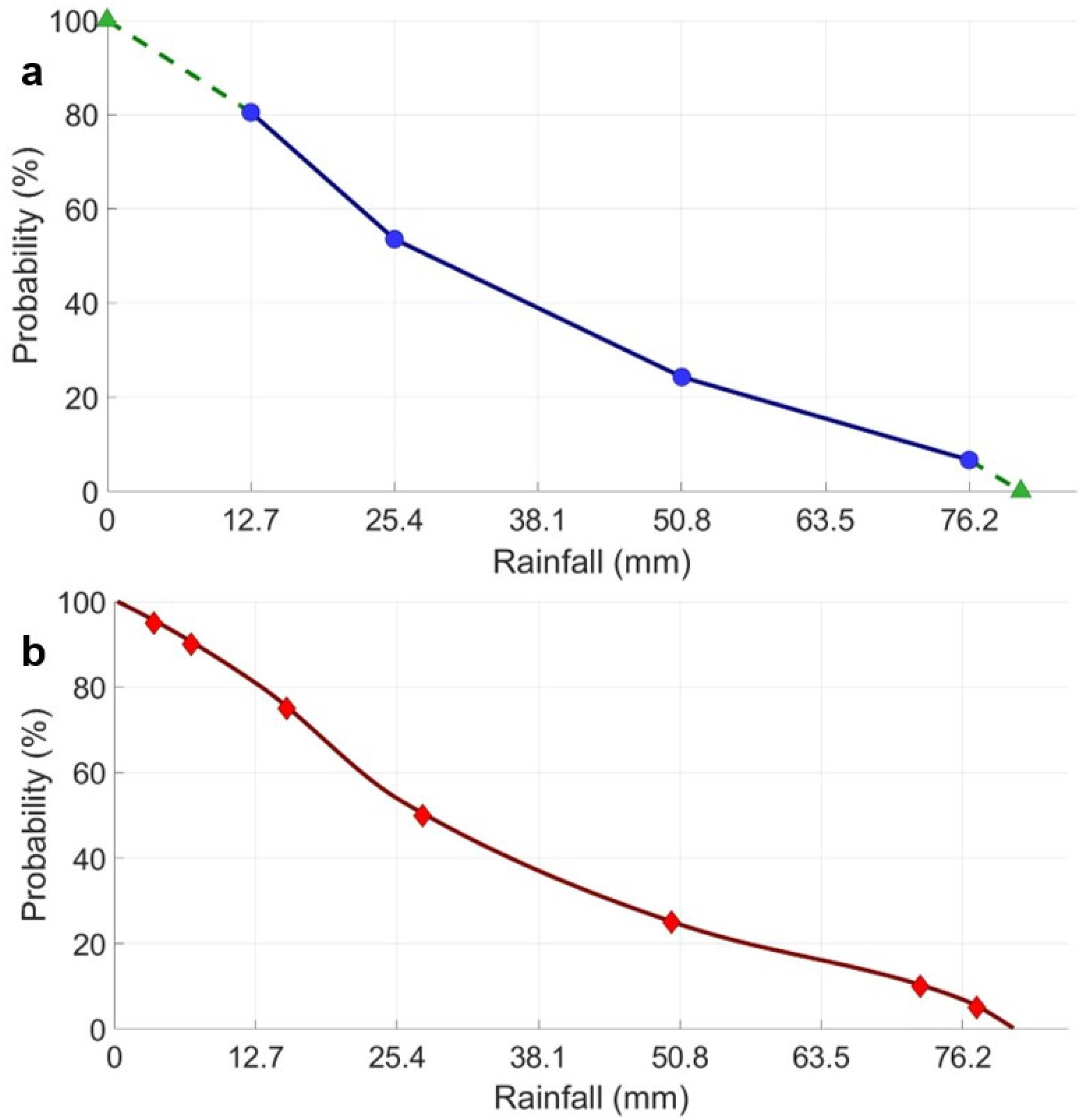
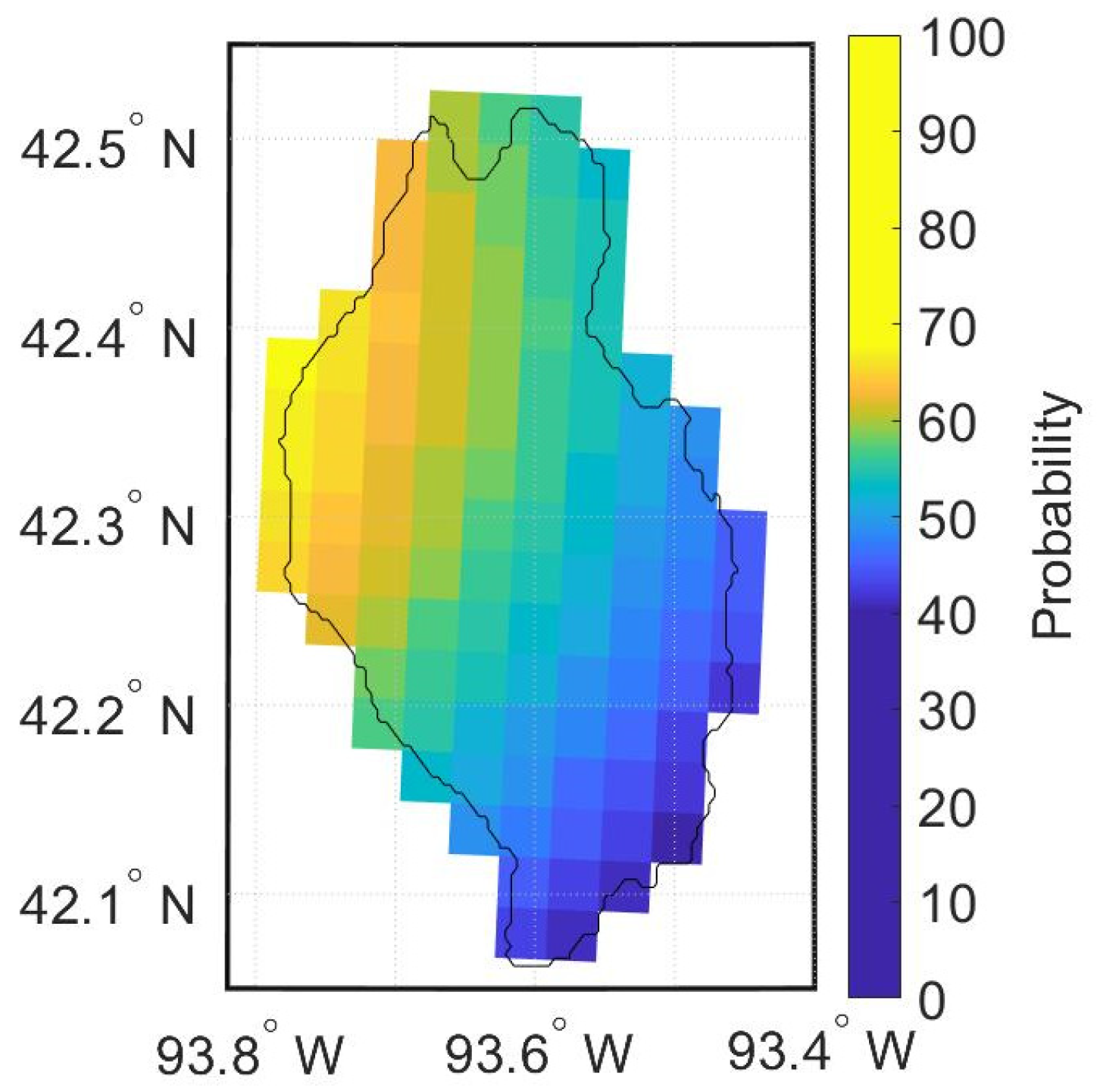
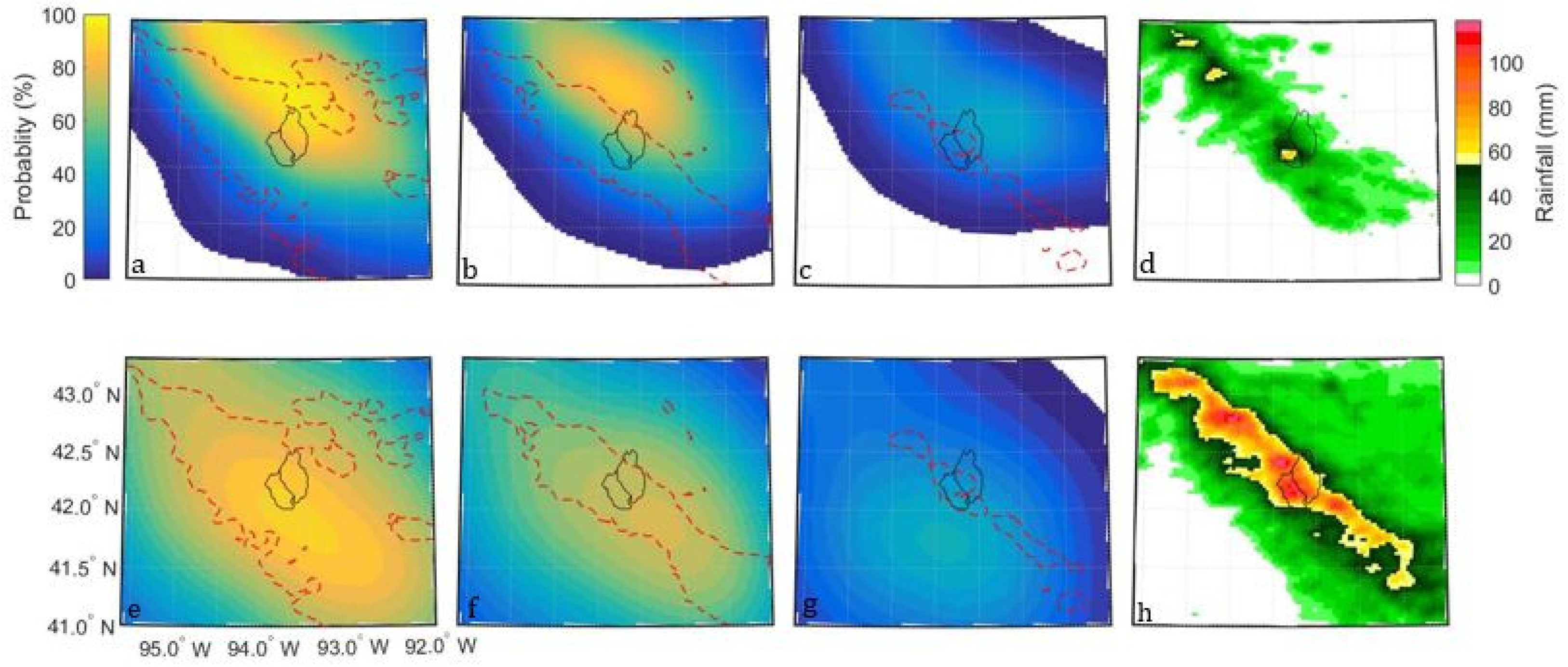

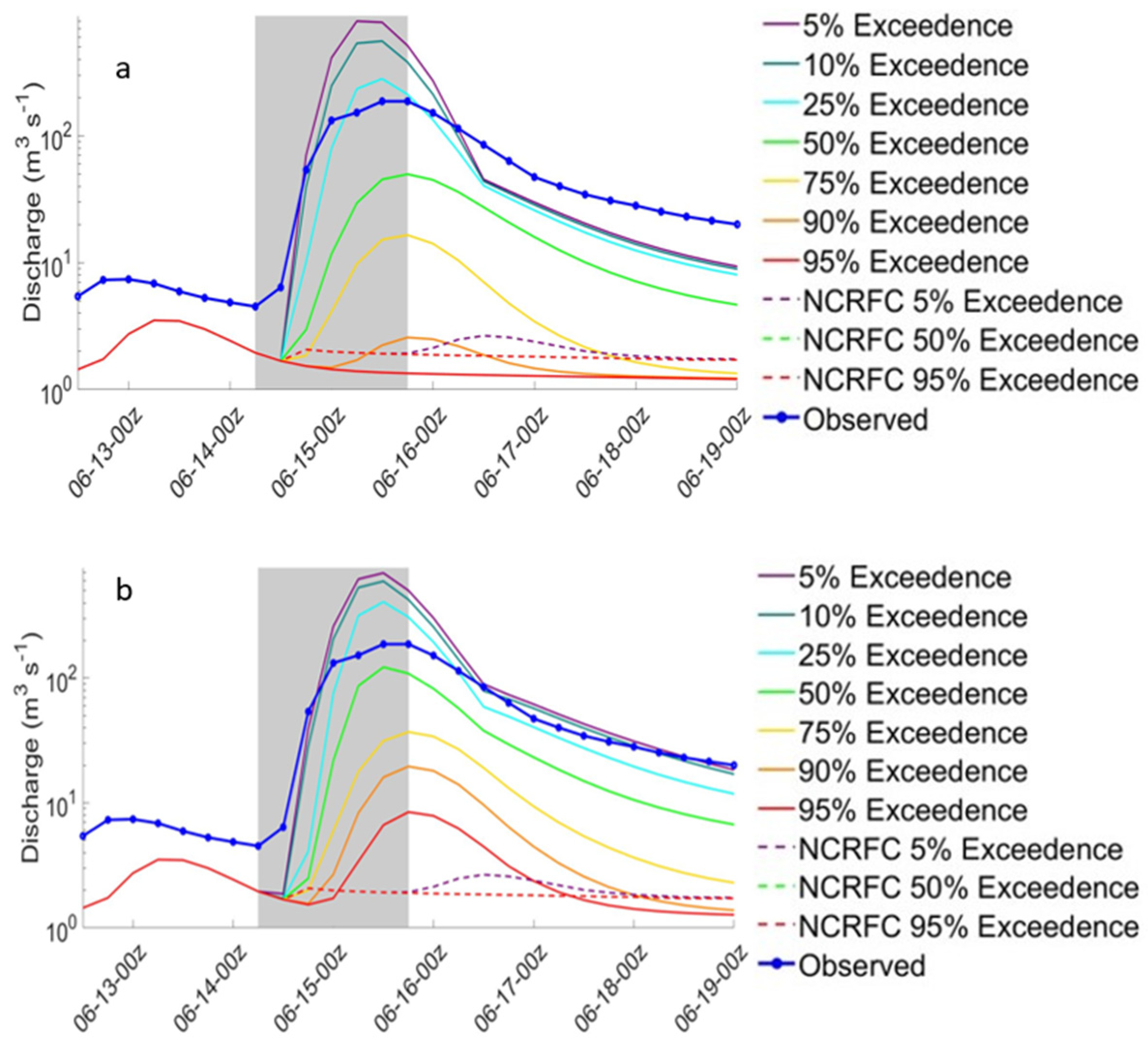
| Basin | Area | USGS Gauge Station | NWS ID | Number of Events |
|---|---|---|---|---|
| Kickapoo at Ontario (WI) | 303 km2 | 05407470 | ONTW3 | 10 |
| Fox River at Waukesha (WI) | 326 km2 | 05543830 | WKEW3 | 11 |
| Turkey River at Spillville (IA) | 458 km2 | 05411600 | SPLI4 | 11 |
| Squaw Creek at Ames (IA) | 528 km2 | 05470500 | AMEI4 | 14 |
| Pecatonica East at Blanchardville (WI) | 572 km2 | 05433000 | BCHW3 | 14 |
| Pecatonica West at Darlington (WI) | 707 km2 | 05432500 | DARW3 | 8 |
| Des Plains at Russell (IL) | 785 km2 | 05527800 | RUSI2 | 6 |
| South Skunk River at Ames (IA) | 816 km2 | 05470000 | AMWI4 | 14 |
| Wapsipinicon River at Tripoli (IA) | 896 km2 | 05420680 | TLPI4 | 7 |
| Volga River at Littleport (IA) | 901 km2 | 05412400 | VLPI4 | 6 |
| Root River at Pilot Mound (MN) | 1463 km2 | 05383950 | PRMM5 | 8 |
| Member | ICs/LBCs | Microphysics | PBL | Grid Spacing | Vert. Levels |
|---|---|---|---|---|---|
| HREF HRW NSSL | NAM/NAM | WSM6 | MYJ | 3.2 km | 40 |
| HREF HRW ARW | RAP/GFS | WSM6 | YSU | 3.2 km | 50 |
| HREF HRW MMB | RAP/GFS | Ferrier-Aligo | MYJ | 3.2 km | 50 |
| HREF NAM CONUS NEST | NAM/NAM | Ferrier-Aligo | MYJ | 3 km | 60 |
| HRRRE 9-MEMBERS | GDAS (with random permutations added) | Thompson aerosol-aware | MYNN | 3 km | 51 |
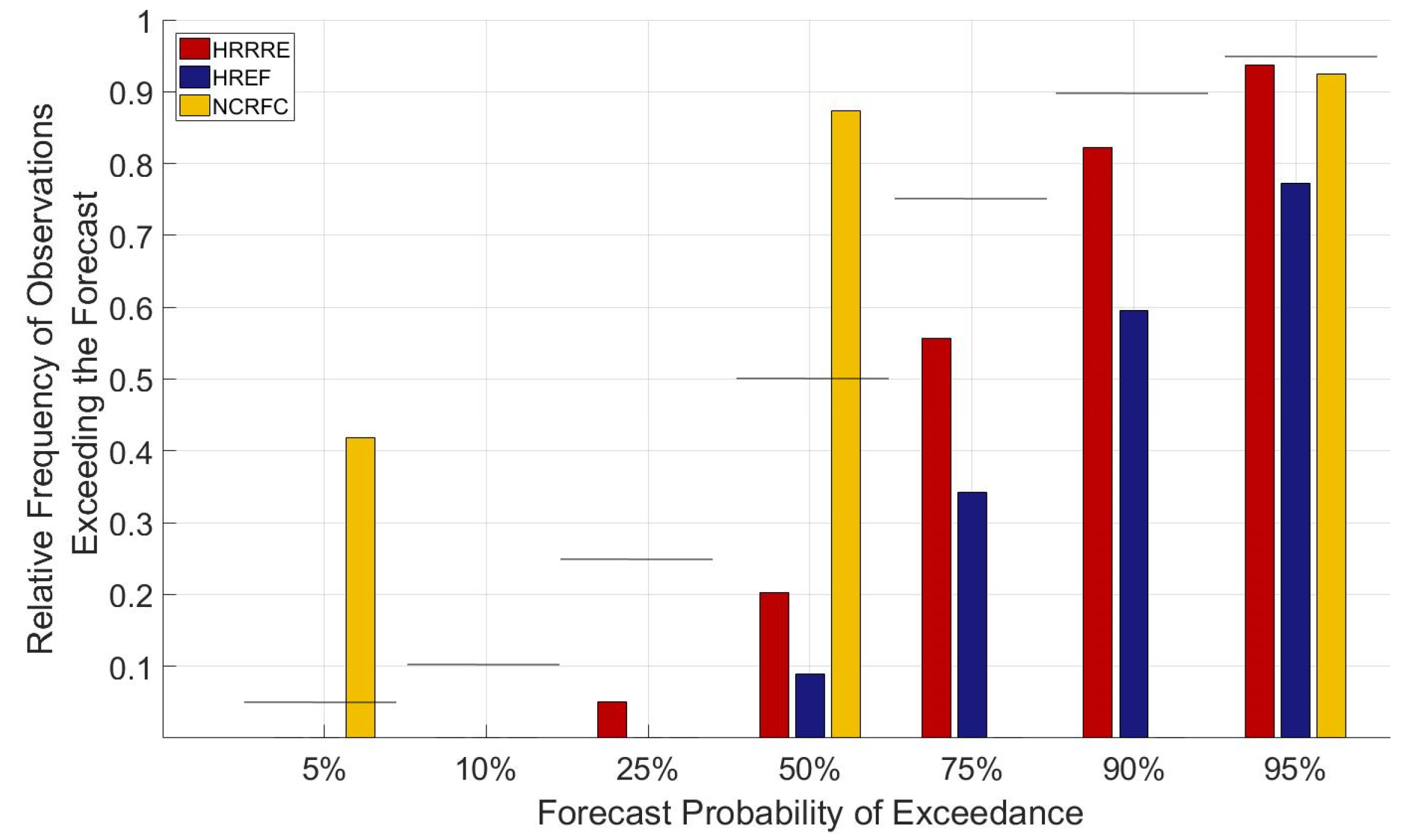
| Probability of Exceedance | 5% | 10% | 25% | 50% | 75% | 90% | 95% | |
|---|---|---|---|---|---|---|---|---|
| Error | HRRRE-based | 818 | 566 | 283 | 95.7 | 9.46 | −20.9 | −28.1 |
| HREF-based | 810 | 666 | 422 | 191 | 53.5 | −2.83 | −17.3 | |
| PD | HRRRE-based | 3330% | 2150% | 1000% | 321% | 47.6% | −26.5% | −43.5% |
| HREF-based | 3470% | 2720% | 1500% | 619% | 175% | 15.8% | −20.7% | |
| Averaged Rainfall | HRRRE | 226 | 176 | 119 | 73.9 | 40.1 | 21.8 | 14.0 |
| HREF | 249 | 215 | 159 | 103 | 61.2 | 34.8 | 23.1 | |
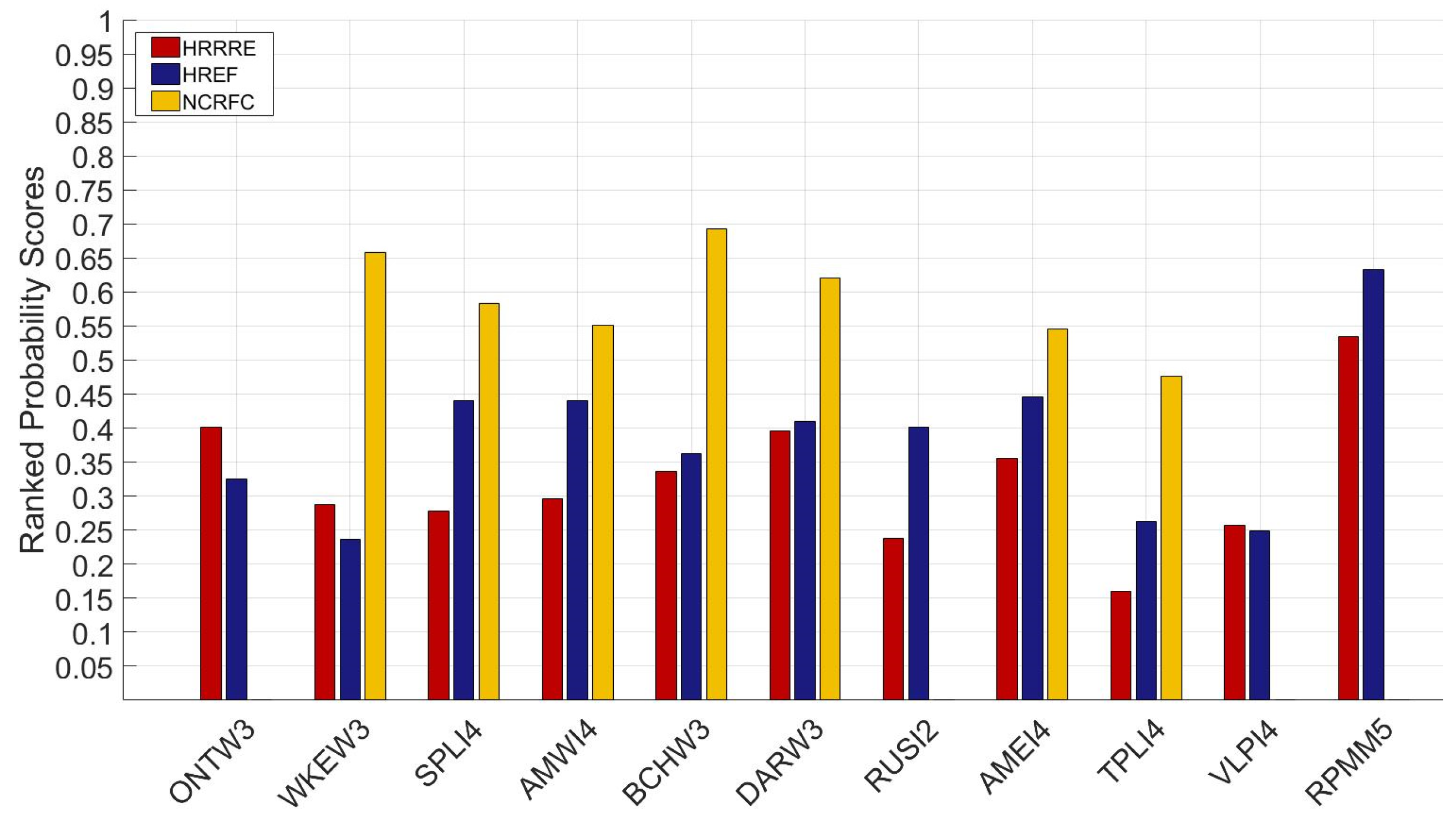
| Average RPS | Standard Deviation RPS | |
|---|---|---|
| HRRRE-based | 0.29 (0.28) | 0.06 (0.10) |
| HREF-based | 0.36 (0.34) | 0.09 (0.12) |
| NCRFC | 0.59 | 0.07 |
| 95% | 90% | 75% | 50% | 25% | 10% | 5% | ||
|---|---|---|---|---|---|---|---|---|
| Skunk River | HRRRE-based | −185 | −185 | −171 | −137 | 94.3 | 371 | 615 |
| HREF-based | −179 | −167 | −150 | −64.6 | 220 | 411 | 507 | |
| Squaw Creek | HRRRE-based | −86.7 | −85.2 | −66.0 | −19.5 | 157 | 402 | 620 |
| HREF-based | −86.4 | −77.9 | −54.7 | −9.60 | 163 | 430 | 561 |
| Probability of Exceedance | 5% | 10% | 25% | 50% | 75% | 90% | 95% |
|---|---|---|---|---|---|---|---|
| HRRRE-based | 60% | 65% | 64% | 62% | 45% | 28% | 22% |
| HREF-based | 74% | 80% | 79% | 79% | 72% | 54% | 48% |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Goenner, A.R.; Franz, K.J.; Jr, W.A.G.; Roberts, B. Evaluation of an Application of Probabilistic Quantitative Precipitation Forecasts for Flood Forecasting. Water 2020, 12, 2860. https://doi.org/10.3390/w12102860
Goenner AR, Franz KJ, Jr WAG, Roberts B. Evaluation of an Application of Probabilistic Quantitative Precipitation Forecasts for Flood Forecasting. Water. 2020; 12(10):2860. https://doi.org/10.3390/w12102860
Chicago/Turabian StyleGoenner, Andrew R., Kristie J. Franz, William A. Gallus Jr, and Brett Roberts. 2020. "Evaluation of an Application of Probabilistic Quantitative Precipitation Forecasts for Flood Forecasting" Water 12, no. 10: 2860. https://doi.org/10.3390/w12102860
APA StyleGoenner, A. R., Franz, K. J., Jr, W. A. G., & Roberts, B. (2020). Evaluation of an Application of Probabilistic Quantitative Precipitation Forecasts for Flood Forecasting. Water, 12(10), 2860. https://doi.org/10.3390/w12102860






