Timescale Methods for Simplifying, Understanding and Modeling Biophysical and Water Quality Processes in Coastal Aquatic Ecosystems: A Review
Abstract
1. Introduction
“Nature is pleased with simplicity. And nature is no dummy.”—Commonly attributed to Isaac Newton
1.1. What Are Timescales?
1.2. Some Fundamental Concepts and Definitions
1.2.1. Constituents, Particles, Parcels, and Types
1.2.2. Lagrangian and Eulerian Descriptions and Approaches
1.3. Transport Timescales
- Residence time—Although the term “residence time” is frequently used to mean a variety of things [88,92,93,94], one of the most common definitions is the time taken by a particle to leave a water body or defined region of interest [92,95,96,97]. Because particles originating at different locations and times within a water body may require different amounts of time to exit, residence time (according to this definition) is a function of location and time [87,92,97]. A strict interpretation of this residence time definition is the time taken to leave a water body for the first time (see Figure 3), an important distinction in tidal systems where oscillatory transport can cause particles to exit and then re-enter the domain of interest one or more times [26,95,98,99]. Numerical simulations currently offer the best methods for estimating time- and position-dependent timescales in realistic domains [66,97,100,101]; however, other (field-based [102,103,104,105], analytic [22,59]) methods may also provide trustworthy estimates, though with less resolution or with additional simplifying assumptions. Other residence time definitions, which are not location- and time-specific, also exist and see wide application (see “flushing time” below).
- Age—Age is defined as the time elapsed since a particle entered a water body or defined region [88,94,96,106]. Because the time to reach a specific location after entering will vary across the water body and over time, age (like residence time, as per our preferred definition above) is also time- and location-specific (see Figure 3). Age is seen as the complement to the location- and time-specific residence time: while age is the time taken since entering to reach location x within a water body, residence time is the time remaining within the water body after reaching location x [87,88,96,106]. Some authors have generalized the common definition for age above, arriving at the following: “the time elapsed since the parcel under consideration left the region in which its age is prescribed to be zero” [63,64].
- Transit time—Transit time has been defined as the total time for a particle to travel across an entire water body or defined region, from entrance to exit [93,96]. Therefore, transit time is the sum of the location- and time-specific age and residence time (see Figure 3). Some authors have taken advantage of the fact that transit time is equivalent to age computed at the downstream boundary or exit of a water body [28,107]. Travel time is similar to transit time, in that it usually references the time taken to travel between two defined points in space [28]. The transit time and location- and time-specific age and residence time are easily derived analytically for a plug flow situation (see Appendix A).
- Exposure time—Exposure time goes forward where the strict definition of residence time stops. While the strict, spatially and temporally variable residence time only accounts for time spent within a defined region until leaving it the first time, exposure time accounts for the total time spent within the domain of interest [87], including “all subsequent re-entries” [95] (see Figure 3). Thus, exposure time may be of particular relevance in systems with oscillatory tidal flows [108]. When computing exposure time with a numerical model, it is important that the computational domain be larger than the domain of interest [95], since transport processes outside the domain of interest control particle re-entry.
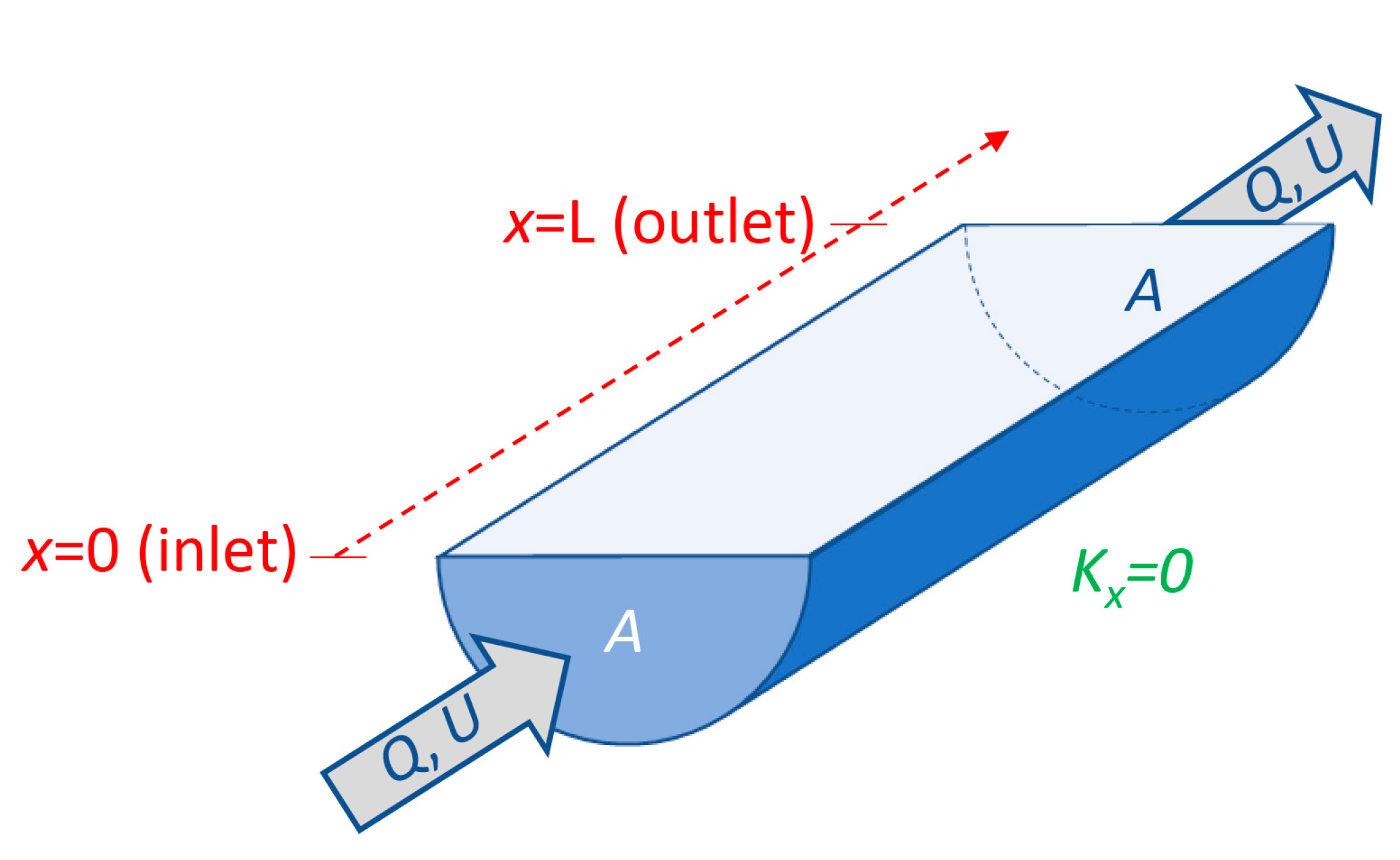
- Flushing time—“Flushing time is a bulk or integrative parameter describing the general exchange characteristics of a waterbody without identifying detailed underlying physical processes or their spatial distribution” ([27], adapted from [87]). There are numerous methods for defining and quantifying flushing times, many of them mathematically quite simple. For example, if advection is expected to dominate exchange between the domain of interest and an adjacent water body (as for a river reach), an advective flushing time may be estimated simply as V/Q, where V is the volume of the domain of interest, and Q is the rate of volumetric flow through it. For this situation, V/Q estimates the time for all water in the domain of interest to be replaced, whereas ½(V/Q) represents the mean time for replacement of the original water. Analogously, if we assume that an estuary behaves similarly to a “plug flow reactor”, i.e., with perfect cross-sectional mixing but zero streamwise mixing, V/Q would represent the time needed to replace all the water initially in the estuary by water entering through its upstream boundary (Figure 4). Some variations on this approach include: (A) substitution of V with freshwater volume Vfw and of Q with freshwater inflow rate Qfw, if one is interested in the time to replace freshwater [52,109] (this is often called the “freshwater fraction method” [58,110]); or (B) substitution of V and Q, respectively, with scalar mass M and scalar flux F (in units (mass/time)), if one is concerned with time for replacement of a scalar quantity [87]. (Incidentally, the V/Q [90,104], Vfw/Qfw [109], and M/F [111] formulations are sometimes called “residence times”.) It should be noted that the V/Q estimate depends on the (sometimes arbitrary) size of the domain of interest [112].
- e-folding flushing time—Another construct for quantifying time for flushing is the e-folding time (τe-fold). This approach capitalizes on the frequently observed exponential-like decrease of constituent mass within a water body over time as it is subjected to flushing. This roughly exponential decrease is often observed in the results of coastal transport simulations [87,100,101,112,113,114,115] (see Figure 5) and tracer experiments [116,117]. Mathematically, the exponential form results from assuming a constant flow rate through a perfectly well-mixed system of constant volume, as for a CSTR (continuously stirred tank reactor) [87]. The well-mixed assumption employed here (Figure 6) is in stark contrast to the plug flow assumption above (Figure 4) and thus may be the more appropriate assumption for estuaries subject to strong (e.g., tidal) dispersive mixing. τe-fold may be obtained as (A) the reciprocal of the specific decay rate calculated from an exponential best-fit to a concentration time series [87,100,112,113] or simply as (B) the time when mass falls to 1/e (37%) of its initial value [114,117]. If the CSTR assumptions are perfectly met, τe-fold = V/Q, but if they are not met (e.g., for basins with bidirectional, tidal exchange flow), V/Q may not accurately characterize the effective flushing time captured by methods (A) or (B) above [87]. Although the well-mixed assumption is almost never satisfied, the e-folding construct is nonetheless employed widely and can work well in representing the net effect of all flushing processes acting on a basin. It is important to note the quantitative difference between this flushing time approach (which characterizes flushing of only 63%, or 1-e−1, of initial mass; Figure 6) and the simple advective V/Q, Vfw/Qfw, and M/F approaches above, whose aim is to characterize 100% replacement of initial mass or volume (Figure 4). Indeed, any perfect CSTR would never truly experience 100% replacement of initial mass, as suggested by the exponential dependency of concentration on time. Even so, for an inert constituent in a well-mixed system, the concentration tends to zero as time tends to infinity, resulting in a finite domain-averaged residence time, which is equal to the e-folding time [88,94,113,118].
- Tidal prism flushing time—Another class of flushing time approaches for estuaries—tidal prism models—prominently acknowledges tides as a flushing agent [119,120]. The most basic form for the tidal prism flushing time is V∙Ttide/Vp [58], where V is estuary volume, Ttide is the tidal period, and Vp is the tidal prism volume (i.e., estuary volume difference between high and low tides). Applications of this general approach may vary in the way V and Vp are defined or calculated [27,110]. Moreover, authors have employed a range of assumptions and adjustments for capturing the influence of freshwater inflow or return flow at the seaward boundary [27,58,119]. Like the e-folding time, the tidal prism flushing (or “turnover” [58,110]) time is based on the assumption of well-mixedness [87,119].
- Turnover time—The V/Q [58], Vfw/Qfw [110], M/F [88,94], e-folding [121], and other bulk approaches [110] are also sometimes called “turnover times.” A relatively new approach for estimating bulk estuary turnover timescales is based on the total exchange flow (TEF) through a cross section at the estuary mouth; TEF is calculated using an isohaline framework [122], and the TEF timescale τTEF may be thought of as “the ratio of the mass of salt in the estuary to the salt flux into the estuary” [110]. (τTEF is also called a “residence time” [122].) In addition to physical processes, the term “turnover time” is frequently applied to biological or geochemical processes as well [62,90,123,124,125].
- Retention time—The term “retention time” is frequently, though not exclusively, used to refer to how long constituents (e.g., nutrients, sediment, organisms) remain within a particular aquatic environment or sub-environment [14,126]. Mechanisms influencing constituent retention can include both hydrodynamic processes (e.g., pools, eddies, and dead zones [14]; stratification and mixing [127]), sedimentation [14], biogeochemical processing [14], and motility of organisms [127]. Hydraulic “retention time” is sometimes treated interchangeably with “residence time” [128] or with expressions described herein as “flushing times” [129].
1.4. What Are Timescales Good for?
- A more meaningful substitute for primitive variables and native process rates: Computed or measured primitive variables (e.g., velocity, pressure, temperature, concentration; also known as state variables) and native process rates (e.g., velocity, production, growth) are not always conducive to interpretation in their raw form [79,89]. (Here, we use the term “native process rate” to refer to the typical rate variable(s) used in connection with a particular process, e.g., velocity or discharge for water movement, or specific growth rate for biomass growth.) On the other hand, diagnostic timescales can incorporate valuable contextual information that native process rates and primitive variables do not. For that reason, timescales can serve as auxiliary variables that might better illuminate a scientific problem [79,89]. For example, the primitive variable “velocity” alone contains no additional problem-specific information that can aid the user in understanding the practical effect of that velocity: it is just a velocity. Whereas the advective timescale τadv—the timescale counterpart to velocity—typically conveys the time needed for a particle to traverse a specified water body or distance (e.g., the time taken by a fisherman’s cooler to travel to the river mouth from the upstream location where it, sadly, fell overboard). Therefore, in comparison to a process rate or primitive variable, a timescale can in many cases take the user farther on an interpretive level by communicating what the process rate, materially, means in the context of the scientific question at hand.
- A common currency for comparing speeds of processes: Timescales provide a common cross-disciplinary currency by which the speed of disparate processes can be compared [23]. For example, consider the observed reduction in the concentration of a decaying pollutant in a river over the first couple days after release. Relevant process rates (e.g., decay (1/time), river discharge (volume/time)) can be transformed into timescales (τdecay, τflush) that can then be directly compared. Therefore, if τdecay is, for instance, 0.2 day and τflush is 30 days, the ~2 order-of-magnitude difference in timescales suggests that decay is a much faster process than river-driven flushing and is likely primarily responsible for any significant concentration reduction in the couple days following pollutant release. Since they all carry the same units, timescales can thus help bridge the gap between scientific disciplines and make quick, back-of-the-envelope assessments of dominant processes possible. Timescale ratios can represent the competition between processes; in some cases, such dimensionless numbers can serve as simple indicators of how an ecosystem might respond to a combination of different physical, biological, or geochemical processes [21,23,25,132,133,134,135,136].
- Distilling numerical model outputs [89,137]: The output files of numerical fluid flow models can be immense. Making sense of all those gigabytes, or even terabytes, of spatially and temporally detailed data is a non-trivial effort [79,137,138]. Timescales can extract the essence from such comprehensive datasets. In contrast to other analysis techniques that might provide spatially (temporally) detailed glimpses of the output at limited points in time (space), timescales can integrate across space and/or time and take advantage of most, if not all, of the results [79,138]. For this reason, timescales derived from the results of complex numerical models may be considered “holistic” [79,138]. Importantly, a model-derived timescale, such as the transit time for a particle through an estuary, may be considered holistic in a second sense: it takes into account all processes and forcings included in the model that influence the transport (e.g., river flow, tides, wind, density gradients, etc.) [139]. It is this second meaning that we refer to hereinafter.
- Comparing systems across space or time: An effective way of enhancing understanding of an aquatic system is through comparison with other systems or through assessing the functioning of a single system under different conditions over time. Timescales can help encapsulate the general physical or ecological state of aquatic systems across space or time, do so in a way that is relatively simple and intuitive, and allow for easy comparisons.
- Building simple(r) models: The partial differential equations (PDEs) governing hydrodynamics and scalar transport are complex, as they are composed of many terms describing multiple influences on momentum and mass balances. Because high-quality (i.e., stable and accurate) numerical solutions to the governing equations can be computationally costly, justifiable simplification of these PDEs is therefore a worthwhile activity. One simplification approach implements timescales of variability in combination with other (e.g., velocity, length, pressure, density) scales to estimate the relative magnitudes of individual terms in time-marching equations [2]; terms that “scale” much smaller than other terms may be justifiably neglected, with the equations reducing to the most essential terms and, hopefully, the numerical solution becoming more tractable and efficient. Another method of simplification involves quantifying the primary processes with timescales, creating dimensionless ratios with those timescales, and then substituting those ratios appropriately into a time- or space-dependent equation. The conversion of a mathematical relationship into dimensionless form can significantly reduce the complexity—and increase the solvability—of the equation [21,23]).
- Assessing connectivity: Transport timescales can contribute substantially to assessments of connectivity between different aquatic systems or subregions within a system [56,95,140,141,142]. In fact, transport timescales can form the basis for one important assessment tool—the “connectivity matrix” [95,140] (see Section 3.4).
- In conceptual models: Timescales are often invoked in conceptual models or qualitative descriptions of how systems work. Even if not quantified or clearly defined, well-known terms such as “residence time” capture a general meaning that a scientific or management audience can conceptually follow. Timescales are frequently used (in mental models, written descriptions, cartoons, schematics, etc.) to qualitatively explain ecological phenomena such as phytoplankton bloom development in coastal systems [6,143], legacy phosphorus across watersheds [14], coastal hypoxia [11], nutrient release from sediments in shallow lakes [144], and eutrophication in lakes [145] and coastal systems [146].
2. How Are Diagnostic Timescales Estimated?
2.1. Combining Process Rates with Other Scales
2.2. Transport Timescales Based on Observational Data
2.2.1. Drifter-Based Experiments
2.2.2. Tracer-Based Experiments
2.3. Transport Timescales Based on Numerical Models
2.3.1. Forward Methods
2.3.2. Backward Methods
3. Timescale Applications for Explaining Ecosystem Processes and Variability in Water Quality
3.1. Timescales in Conceptual Models
3.2. Implementing Timescales in Building Simple Models
3.2.1. Simple Models of the Physical Environment
3.2.2. Simple Ecological Models Using Physical Timescales
3.2.3. Simple Ecological Models Using Physical and Biogeochemical Timescales
3.3. Assessing Relative Speeds or Dominance of Processes
- Estuarine nitrogen processing: In their studies covering several European estuaries, Middelburg and Nieuwenhuize compared water “residence time” estimates to turnover times for particulate nitrogen, nitrate, ammonium [90], and amino acids [123], providing insight into which nutrient forms may become limiting [90] and whether individual forms will be significantly modified during transport through an estuary [90,123].
- Hypoxia development in a tidal river: In their study of the effect of water diversion structures on water quality in a complex, heavily managed tidal environment, Monsen et al. [230] compared 2D model-computed e-folding flushing times to half-lives for biological oxygen demand (BOD) [231]. They found that when a physical barrier was installed on a branch of the San Joaquin River (CA, USA), consequently forcing all flow through the mainstem, flushing times on the mainstem could decrease enough (relative to BOD half-life) to prevent the development of hypoxia, a frequent occurrence in a deep portion of the mainstem San Joaquin.
- Nutrient processing on shelves and export to the open ocean: Sharples et al. [210] compared their global-scale, latitudinally varying estimates of continental shelf residence times (Figure 14A herein) with nutrient processing times (assumed independent of latitude) in a discussion of which shelf regions would be expected to experience more (middle to high latitudes) or less (low latitudes) nitrate removal before exchange with the open ocean occurs.
- Development of a unique estuarine bacterial community: In their study of the Parker River Estuary and Plum Island Sound (MA, USA), Crump et al. [91] studied the conditions for the development of a unique community of estuarine bacterioplankton, as opposed to the advected populations of riverine or marine origin that were prevalent in the estuary. They compared water residence times and bacterial doubling times across seasons and the salinity gradient, finding that a local estuarine community developed at intermediate salinity only in the summer and fall, when water residence time was much longer than average doubling time, thus allowing the local community ample time to develop. In contrast, no local bacterial community developed in spring, when residence time was similar to average doubling time—apparently short enough to prevent the development of new estuarine bacterioplankton populations [91].
- Benthic control of phytoplankton biomass: Several authors have compared benthic grazing timescales to transport and/or phytoplankton growth timescales to understand controls on estuarine aquaculture potential [134] or phytoplankton biomass [25,61,124,232,233,234]. Extending the conceptual model of Dame [233] (who expanded that of Smaal and Prins [234]), Strayer et al. [232] presented a graphical conceptual model (Figure 19A) of phytoplankton regulation as a function of hydrologic residence time on the horizontal axis and bivalve clearance time (i.e., time for a bivalve population to clear the overlying water column of phytoplankton through their pumping) on the vertical axis. They described three regimes within that 2D timescale space, each associated with a different control on phytoplankton biomass (advective loss, bivalve grazing, or phytoplankton growth), stating that the regime boundaries would vary as a function of phytoplankton net growth rate. The Strayer et al. [232] conceptual model (Figure 19A) was used to show how bivalve clearance rates changed as a function of bivalve invasion or population decline. The Strayer et al. [232] conceptual model was later extended through (1) the generalization of the benthic grazing timescale to include potentially any in situ loss process and (2) normalization of the loss and transport timescales by the algal growth timescale (Figure 19B) [23]. The latter model was derived from the simple, dimensionless expression in Equation (7), was consistent with the Strayer model control domains, and showed that the regime boundaries are in fact defined by two timescale ratios, i.e., at = 1, = 1, and = (see description in Section 3.2.3). These conceptual models, together, demonstrate the utility of timescales (and their ratios) in understanding and delineating the conditions under which an ecosystem response (e.g., algal biomass accumulation) is controlled by one of several processes.
3.4. Evaluating Connectivity
- Exposure of marine protected areas (MPAs) to shipping-related pollution: Delpeche-Ellmann et al. [56] analyzed the paths of GPS-tracked surface drifters released in the Gulf of Finland’s main shipping fairway, providing insight into which MPAs on the edges of the Gulf are most likely to be affected by pollutants originating in the fairway, as well as timescales for transport to the MPAs. The transport timescales provide information for environmental managers regarding the time available to respond to pollutant spills and contain them before they reach MPAs.
- “Material connectivity”: Oldham et al. [229] noted that, in the field of hydrology, there have been numerous efforts at characterizing hydrological or hydraulic connectivity between landscapes; whereas, to their knowledge, there had been no attempts to “characterise connectivity in terms of the ‘effectiveness’ of transferring material,” a notion which those authors termed “material connectivity.” They argued that material connectivity must account for both physical transport and biological or chemical processing, since two environments may have strong hydrological connectivity between them but, if material carried by the water undergoes significant removal during transit, the material connectivity may be poor. The ratio of a transport timescale τtran to a reaction or “material processing” timescale τrxn—termed the Damköhler number (Da) in the chemical engineering literature and generalized by Oldham et al. [229]—was proposed to capture the conditions under which material connectivity is strong or weak. For example, when reactions remove a constituent during transit and Da = τtran/τrxn >> 1, transport is very slow compared to in situ loss processes; the constituent material will be substantially lost during transport, resulting in material disconnectivity even under conditions of hydraulic connectivity. On the other hand, if Da << 1, transport is very fast compared to processing, the material behaves essentially conservatively, and material connectivity is therefore strong. Relatedly, Brodie et al. [237] estimated residence times for freshwater and several water quality constituents exported to the Great Barrier Reef and made the case that residence times of pollutants in that system are potentially much greater than those of the water itself, contrary to common assumptions.
- Harmful algal bloom (HAB) initiation in geometrically complex estuaries: Qin and Shen [199] performed both theoretical analyses and 3D numerical modeling to understand the roles of estuary geometry and hydrodynamic connectivity between estuary subregions in determining where HABs are first observed to begin. (For their species of interest, a density of 1000 cells/mL was defined as the HAB threshold). Their idealized analytical model (in which residence time was a key parameter) predicted that the location of first HAB occurrence in a hydraulically interconnected system of two water bodies (e.g., the mainstem of a tidal river and its tributary) is determined by the relative ratios of residence time to volume (τr/V) for the two water bodies. A HAB was predicted to be observed first in the water body with the larger τr/V ratio, i.e., the longer residence time and/or smaller volume. Results from numerical experiments with a 3D transport-reaction model of the lower James River (Figure 22A) were consistent with the theoretical model, demonstrating that—regardless of the initial source location of cells—flushing (represented by model-computed τr) and subregion volume V are indeed dominant factors determining where a HAB is first observed. Specifically, their 3D simulations were initiated with a non-zero algal concentration in the bottom layer of the lower James River mainstem (see Figure 22B), to represent cyst release in that region; initial algal concentrations were zero elsewhere, including in the tributaries. Nonetheless, only a few days were needed for concentrations in the tributaries to be higher than in the mainstem, initiated by cell transport from the mainstem driven by estuarine circulation. Simulated bloom-level densities ultimately developed first in the tributaries (Figure 22D), as predicted by the theoretical model. Both numerical and analytical results are consistent with, and help explain, first occurrences of toxic algal blooms in that system, which are frequently observed in the Lafayette River, a relatively small tributary to the James with a long residence time.
3.5. Comparing Systems across Space or Time
- Ecosystem responses to management actions: To understand changes in hydrodynamics, water quality, and ecosystem processes induced by the installation of a temporary physical salinity-intrusion barrier in the Sacramento-San Joaquin Delta (CA, USA), Kimmerer et al. [62] employed high-speed boat-based isotope mapping (same approach as in [173]) to produce spatial patterns of water age with and without the barrier. Benthic grazing turnover time (i.e., time for benthic bivalve population to filter through the entire overlying water column) was also estimated as one measure of ecosystem response to related changes in salinity.
- Variability and drivers of estuarine flushing: In order to investigate the sensitivity of flushing in Mobile Bay (AL, USA) to river flow, wind, and baroclinic forcing, Du et al. [243] estimated both bulk (e-folding flushing time) and spatially variable (freshwater age) transport timescale metrics using a 3D numerical model. Deriving a simple empirical flushing time–discharge relationship based on a set of sensitivity runs and comparing to previous estimates based on a 2D depth-integrated model [244], they concluded that baroclinic processes reduce flushing times by approximately half. The spatial and temporal transport time patterns produced in these analyses (Figure 24 herein) could serve as valuable information toward interpreting variability in water quality and ecosystem processes.
- Retention of harmful algal cells: Ralston et al. [127] employed a 3D coupled hydrodynamic-biological model of the Nauset Estuary (MA, USA) to explore the physical and biological processes controlling recurrent blooms of the toxic alga Alexandrium fundyense. Implementing an e-folding approach to calculate A. fundyense residence times under a range of conditions, they explored the influence of swimming behavior, spring-neap tidal phase, wind, and stratification on retention of cells in one of the estuary’s salt ponds, concluding that all four processes are major factors determining retention. Although growth and mortality were turned off in these simulations, the computed residence times are particularly holistic, in that they not only include 3D hydrodynamic processes but also organism behavior (see Figure 25 herein).
- Ecosystem transformations by bivalves: The graphical timescale-based conceptual model of Strayer et al. [232] (see Figure 19A and Section 3.3 above) describes the evolution of five aquatic ecosystems in response to major changes in bivalve grazer populations. The process controlling phytoplankton was shown to be capable of shifting between advection, grazing, and algal growth as a function of either bivalve invasion or population decline.
- Hydrologic influence on zooplankton communities: Augmenting an 18-year field dataset with calculated water residence times, Burdis and Hirsch [33] explored several potential environmental drivers of zooplankton community structure in a natural riverine lake. As hypothesized, they found that water residence time was the most important driver of zooplankton abundance and community structure. Similar to Peierls et al. [57] and Hall et al. [238], use of a transport timescale allowed these authors to collapse spatial location and temporally variable hydrology into a single variable associated with each sample.
4. Discussion
4.1. The Timescale “Tower of Babel”
4.2. Holism of Timescales
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Note
Appendix A
References
- Cambridge Learner’s Dictionary; Cambridge University Press: Cambridge, UK, 2019.
- Cushman-Roisin, B.; Beckers, J.-M. Introduction to Geophysical Fluid Dynamics: Physical and Numerical Aspects; Cushman-Roisin, B., Beckers, J.-M., Eds.; Academic Press: Waltham, MA, USA, 2011; Volume 101, pp. 1–828. [Google Scholar]
- Lucas, L.V. Time scale (OR “Timescale”). In Encyclopedia of Estuaries; Kennish, M.J., Ed.; Springer: Dordrecht, The Netherlands, 2016. [Google Scholar]
- Cloern, J.E. Tidal stirring and phytoplankton bloom dynamics in an estuary. J. Mar. Res. 1991, 49, 203–221. [Google Scholar] [CrossRef]
- Litaker, W.; Duke, C.S.; Kenney, B.E.; Ramus, J. Short-term environmental variability and phytoplankton abundance in a shallow tidal estuary. II. Spring and Fall. Mar. Ecol. Prog. Ser. 1993, 94, 141–154. [Google Scholar] [CrossRef]
- Cloern, J.E. Phytoplankton bloom dynamics in coastal ecosystems: A review with some general lessons from sustained investigation of San Francisco Bay, California. Rev. Geophys. 1996, 34, 127–168. [Google Scholar] [CrossRef]
- Jay, D.A.; Geyer, W.R.; Montgomery, D.R. An ecological perspective on estuarine classification. In Estuarine Science: A Synthetic Approach to Research and Practice; Hobbie, J.E., Ed.; Island Press: Washington, DC, USA, 2000; pp. 149–176. [Google Scholar]
- Mostofa, K.M.G.; Liu, C.Q.; Zhai, W.D.; Minella, M.; Vione, D.; Gao, K.S.; Minakata, D.; Arakaki, T.; Yoshioka, T.; Hayakawa, K.; et al. Reviews and Syntheses: Ocean acidification and its potential impacts on marine ecosystems. Biogeosciences 2016, 13, 1767–1786. [Google Scholar] [CrossRef]
- Malamud-Roam, F.P.; Ingram, B.L.; Hughes, M.; Florsheim, J.L. Holocene paleoclimate records from a large California estuarine system and its watershed region: Linking watershed climate and bay conditions. Quat. Sci. Rev. 2006, 25, 1570–1598. [Google Scholar] [CrossRef]
- Cronin, T.M.; Vann, C.D. The sedimentary record of climatic and anthropogenic influence on the Patuxent estuary and Chesapeake Bay ecosystems. Estuaries 2003, 26, 196–209. [Google Scholar] [CrossRef]
- Rabalais, N.N.; Diaz, R.J.; Levin, L.A.; Turner, R.E.; Gilbert, D.; Zhang, J. Dynamics and distribution of natural and human-caused hypoxia. Biogeosciences 2010, 7, 585–619. [Google Scholar] [CrossRef]
- Monismith, S.G.; Kimmerer, W.; Burau, J.R.; Stacey, M. Structure and flow-induced variability of the subtidal salinity field in Northern San Francisco Bay. J. Phys. Oceanogr. 2002, 32, 3003–3019. [Google Scholar] [CrossRef]
- MacCready, P.; Geyer, W.R. Advances in Estuarine Physics. Annu. Rev. Mar. Sci. 2010, 2, 35–58. [Google Scholar] [CrossRef]
- Sharpley, A.; Jarvie, H.P.; Buda, A.; May, L.; Spears, B.; Kleinman, P. Phosphorus legacy: Overcoming the effects of past management practices to mitigate future water quality impairment. J. Environ. Qual. 2013, 42, 1308–1326. [Google Scholar] [CrossRef]
- Blumberg, A.F.; Khan, L.A.; St. John, J.P. Three-dimensional hydrodynamic model of New York Harbor region. J. Hydraul. Eng. 1999, 125, 799–816. [Google Scholar] [CrossRef]
- Wang, L.; Samthein, M.; Erlenkeuser, H.; Grimalt, J.; Grootes, P.; Heilig, S.; Ivanova, E.; Kienast, M.; Pelejero, C.; Pfaumann, U. East Asian monsoon climate during the Late Pleistocene: High-resolution sediment records from the South China Sea. Mar. Geol. 1999, 156, 245–284. [Google Scholar] [CrossRef]
- Breithaupt, J.L.; Smoak, J.M.; Byrne, R.H.; Waters, M.N.; Moyer, R.P.; Sanders, C.J. Avoiding timescale bias in assessments of coastal wetland vertical change. Limnol. Oceanogr. 2018, 63, S477–S495. [Google Scholar] [CrossRef] [PubMed]
- Stacey, M.T.; Burau, J.R.; Monismith, S.G. Creation of residual flows in a partially stratified estuary. J. Geophys. Res. 2001, 106, 13–37. [Google Scholar] [CrossRef]
- Chapin, F.S., III; Woodwell, G.M.; Randerson, J.T.; Rastetter, E.B.; Lovett, G.M.; Baldocchi, D.D.; Clark, D.A.; Harmon, M.E.; Schimel, D.S.; Valentini, R.; et al. Reconciling carbon-cycle concepts, terminology, and methods. Ecosystems 2006, 9, 1041–1050. [Google Scholar] [CrossRef]
- Cohen, A.S. The past is a key to the future: Lessons paleoecological data can provide for management of the African Great Lakes. J. Great Lakes Res. 2018, 44, 1142–1153. [Google Scholar] [CrossRef]
- Shen, J.; Hong, B.; Kuo, A.Y. Using timescales to interpret dissolved oxygen distributions in the bottom waters of Chesapeake Bay. Limnol. Oceanogr. 2013, 58, 2237–2248. [Google Scholar] [CrossRef]
- Andutta, F.P.; Ridd, P.V.; Deleersnijder, E.; Prandle, D. Contaminant exchange rates in estuaries—New formulae accounting for advection and dispersion. Prog. Oceanogr. 2014, 120, 139–153. [Google Scholar] [CrossRef]
- Lucas, L.V.; Thompson, J.K.; Brown, L.R. Why are diverse relationships observed between phytoplankton biomass and transport time? Limnol. Oceanogr. 2009, 54, 381–390. [Google Scholar] [CrossRef]
- Wang, Z.G.; Wang, H.; Shen, J.; Ye, F.; Zhang, Y.L.; Chai, F.; Liu, Z.; Du, J.B. An analytical phytoplankton model and its application in the tidal freshwater James River. Estuar. Coast. Shelf Sci. 2019, 224, 228–244. [Google Scholar] [CrossRef]
- Koseff, J.R.; Holen, J.K.; Monismith, S.G.; Cloern, J.E. Coupled effects of vertical mixing and benthic grazing on phytoplankton populations in shallow, turbid estuaries. J. Mar. Res. 1993, 51, 843–868. [Google Scholar] [CrossRef]
- Delhez, J.M.; de Brye, B.; de Brauwere, A.; Deleersnijder, E. Residence time vs influence time. J. Mar. Syst. 2014, 132, 185–195. [Google Scholar] [CrossRef]
- Lucas, L.V. Implications of estuarine transport for water quality. In Contemporary Issues in Estuarine Physics, 1st ed.; Valle-Levinson, A., Ed.; Cambridge University Press: New York, NY, USA, 2010; pp. 272–306. [Google Scholar]
- Cornaton, F.; Perrochet, P. Groundwater age, life expectancy and transit time distributions in advective-dispersive systems: 1. Generalized reservoir theory. Adv. Water Resour. 2006, 29, 1267–1291. [Google Scholar] [CrossRef]
- Ambrosetti, W.; Barbanti, L.; Sala, N. Residence time and physical processes in lakes. J. Limnol. 2003, 62, 1–15. [Google Scholar] [CrossRef]
- Rueda, F.J.; Cowen, E.A. Residence time of a freshwater embayment connected to a large lake. Limnol. Oceanogr. 2005, 50, 1638–1653. [Google Scholar] [CrossRef]
- Rueda, F.J.; Moreno-Ostos, E.; Armengol, J. The residence time of river water in reservoirs. Ecol. Model. 2006, 191, 260–274. [Google Scholar] [CrossRef]
- McDonald, C.P.; Lathrop, R.C. Seasonal shifts in the relative importance of local versus upstream sources of phosphorus to individual lakes in a chain. Aquat. Sci. 2017, 79, 385–394. [Google Scholar] [CrossRef]
- Burdis, R.M.; Hirsch, J.K. Crustacean zooplankton dynamics in a natural riverine lake, Upper Mississippi River. J. Freshw. Ecol. 2017, 32, 240–258. [Google Scholar] [CrossRef]
- Zwart, J.A.; Sebestyen, S.D.; Solomon, C.T.; Jones, S.E. The Influence of Hydrologic Residence Time on Lake Carbon Cycling Dynamics Following Extreme Precipitation Events. Ecosystems 2017, 20, 1000–1014. [Google Scholar] [CrossRef]
- Vollenweider, R.A. Input-output models: With special reference to the phosphorus loading concept in limnology. Schweiz. Z. Für Hydrol. 1975, 37, 53–84. [Google Scholar] [CrossRef]
- Hester, E.T.; Hammond, B.; Scott, D.T. Effects of inset floodplains and hyporheic exchange induced by in-stream structures on nitrate removal in a headwater stream. Ecol. Eng. 2016, 97, 452–464. [Google Scholar] [CrossRef]
- Seybold, E.; McGlynn, B. Hydrologic and biogeochemical drivers of dissolved organic carbon and nitrate uptake in a headwater stream network. Biogeochemistry 2018, 138, 23–48. [Google Scholar] [CrossRef]
- Benettin, P.; Bertuzzo, E. tran-SAS v1.0: A numerical model to compute catchment-scale hydrologic transport using StorAge Selection function. Geosci. Model Dev. 2018, 11, 1627–1639. [Google Scholar] [CrossRef]
- Remondi, F.; Kirchner, J.W.; Burlando, P.; Fatichi, S. Water flux tracking with a distributed hydrological model to quantify controls on the spatio-temporal variability of transit time distributions. Water Resour. Res. 2018, 54, 3081–3099. [Google Scholar] [CrossRef]
- Rozemeijer, J.; Klein, J.; Hendriks, D.; Borren, W.; Ouboter, M.; Rip, W. Groundwater-surface water relations in regulated lowland catchments; hydrological and hydrochecmical effects of a major change in surface water level management. Sci. Total Environ. 2019, 660, 1317–1326. [Google Scholar] [CrossRef] [PubMed]
- Onderka, M.; Chudoba, V. The wavelets show it—The transit time of water varies in time. J. Hydrol. Hydromech. 2018, 64, 295–302. [Google Scholar] [CrossRef]
- Geyer, W.R.; Signell, R.P. A reassessment of the role of tidal dispersion in estuaries and bays. Estuaries 1992, 15, 97–108. [Google Scholar] [CrossRef]
- Banas, N.S.; Hickey, B.M. Mapping exchange and residence time in a model of Willapa Bay, Washington, a branching, macrotidal estuary. J. Geophys. Res. 2005, 110, C11011. [Google Scholar] [CrossRef]
- Alosairi, Y.; Pokavanich, T. Residence and transport time scales associated with Shatt Al-Arab discharges under various hydrological conditions estimated using a numerical model. Mar. Pollut. Bull. 2017, 118, 85–92. [Google Scholar] [CrossRef]
- Andutta, F.P.; Ridd, P.V.; Wolanski, E. The age and the flushing time of the Great Barrier Reef waters. Cont. Shelf Res. 2013, 53, 11–19. [Google Scholar] [CrossRef]
- Drake, C.W.; Jones, C.S.; Schilling, K.E.; Amado, A.A.; Weber, L.J. Estimating nitrate-nitrogen retention in a large constructed wetland using high-frequency, continuous monitoring and hydrologic modeling. Ecol. Eng. 2018, 117, 69–83. [Google Scholar] [CrossRef]
- White, S.A. Design and season influence nitrogen dynamics in two surface flow constructed wetlands treating nursery irrigation runoff. Water 2018, 10, 8. [Google Scholar] [CrossRef]
- Koszalka, I.M.; Haine, T.W.N.; Magaldi, M.G. Fates and travel times of Denmark Strait overflow water in the Irminger Basin. J. Phys. Oceanogr. 2013, 43, 2611–2628. [Google Scholar] [CrossRef]
- Mouchet, A.; Deleersnijder, E. The leaky funnel model, a metaphor of the ventilation of the World Ocean as simulated in an OGCM. Tellus 2008, 60, 761–774. [Google Scholar] [CrossRef][Green Version]
- Rutherford, K.; Fennel, K. Diagnosing transit times on the northwestern North Atlantic continental shelf. Ocean Sci. 2018, 14. [Google Scholar] [CrossRef]
- Waugh, D.W.; Hall, T.M. Age of stratospheric air: Theory, observations, and models. Rev. Geophys. 2002, 40, 1–26. [Google Scholar] [CrossRef]
- Fischer, H.B.; List, E.J.; Koh, R.C.Y.; Imberger, J.; Brooks, N.H. Mixing in Inland and Coastal Waters; Academic Press: San Diego, CA, USA, 1979. [Google Scholar]
- MacCready, P.; Banas, N.S. Residual circulation, mixing, and dispersion. In Treatise on Estuarine and Coastal Science; Wolansky, E., McLusky, D.S., Eds.; Academic Press: Waltham, MA, USA, 2011; Volume 2, pp. 75–89. [Google Scholar]
- Seitzinger, S.; Harrison, J.A.; Bohlke, J.K.; Bouwman, A.F.; Lowrance, R.; Peterson, B.; Tobias, C.; Van Drecht, G. Denitrification across landscapes and waterscapes: A synthesis. Ecol. Appl. 2006, 16, 2064–2090. [Google Scholar] [CrossRef]
- Stabeno, P.J.; Danielson, S.L.; Kachel, D.G.; Kachel, N.B.; Mordy, C.W. Currents and transport on the Eastern Bering Sea shelf: An integration of over 20 years of data. Deep-Sea Res. Part II 2016, 134, 13–29. [Google Scholar] [CrossRef]
- Delpeche-Ellmann, N.; Torsvik, T.; Soomere, T. Tracks of surface drifters from a major fairway to marine protected areas in the Gulf of Finland. Proc. Est. Acad. Sci. 2015, 64, 226–233. [Google Scholar] [CrossRef]
- Peierls, B.L.; Hall, N.S.; Paerl, H.W. Non-monotonic Responses of Phytoplankton Biomass Accumulation to Hydrologic Variability: A Comparison of Two Coastal Plain North Carolina Estuaries. Estuaries Coasts 2012, 35, 1376–1392. [Google Scholar] [CrossRef]
- Sheldon, J.E.; Alber, M. The calculation of estuarine turnover times using freshwater fraction and tidal prism models: A critical evaluation. Estuaries Coasts 2006, 29, 133–146. [Google Scholar] [CrossRef]
- Deleersnijder, E.; Beckers, J.-M.; Delhez, E.J.M. The residence time of settling particles in the surface mixed layer. Environ. Fluid Mech. 2006, 6, 25–42. [Google Scholar] [CrossRef]
- de Brauwere, A.; Deleersnijder, E. Assessing the parameterization of the settling flux in a depth-integrated model of the fate of decaying and sinking particles, with application to fecal bacteria in the Scheldt Estuary. Environ. Fluid Mech. 2010, 10, 157–175. [Google Scholar] [CrossRef]
- Buzzelli, C.; Parker, M.; Geiger, S.; Wan, Y.; Doering, P.; Haunert, D. Predicting system-scale impacts of oyster clearance on phytoplankton productivity in a small subtropical estuary. Environ. Model. Assess. 2013, 18, 185–198. [Google Scholar] [CrossRef]
- Kimmerer, W.; Wilkerson, F.; Downing, B.; Dugdale, R.; Gross, E.; Kayfetz, K.; Khanna, S.; Parker, A.E.; Thompson, J.K. Effects of drought and the emergency drought barrier on the ecosystem of the California Delta. San Franc. Estuary Watershed Sci. 2019, 17, 1–28. [Google Scholar] [CrossRef]
- Deleersnijder, E.; Campin, J.M.; Delhez, E.J.M. The concept of age in marine modelling I. Theory and preliminary model results. J. Mar. Syst. 2001, 28, 229–267. [Google Scholar] [CrossRef]
- Delhez, E.J.M.; Campin, J.M.; Hirst, A.C.; Deleersnijder, E. Toward a general theory of the age in ocean modelling. Ocean Model. 1999, 1, 17–27. [Google Scholar] [CrossRef]
- de Groot, S.R.; Mazur, P. Non-Equilibrium Thermodynamics; North-Holland Publishing Company: Amsterdam, The Netherlands, 1962; p. 510. [Google Scholar]
- de Brye, B.; de Brauwere, A.; Gourgue, O.; Delhez, E.J.M.; Deleersnijder, E. Water renewal timescales in the Scheldt Estuary. J. Mar. Syst. 2012, 94, 74–86. [Google Scholar] [CrossRef]
- Cox, M.D. An Idealized Model of the World Ocean. 1. The Global-Scale Water Masses. J. Phys. Oceanogr. 1989, 19, 1730–1752. [Google Scholar] [CrossRef]
- Haine, T.W.N.; Hall, T.M. A generalized transport theory: Water-mass composition and age. J. Phys. Oceanogr. 2002, 32, 1932–1946. [Google Scholar] [CrossRef]
- Baretta-Bekker, H.J.G.; Duursma, E.K.; Kuipers, B.R. (Eds.) Tracer. In Encyclopedia of Marine Sciences; Springer: Berlin, Germany, 1998; p. 357. [Google Scholar]
- Batchelor, G.K. An Introduction to Fluid Dynamics, 1st ed.; Cambridge University Press: Cambridge, UK, 2000; p. 615. [Google Scholar]
- Kundu, P.K.; Cohen, I.M. Fluid Mechanics, 3rd ed.; Elsevier Academic Press: San Diego, CA, USA, 2004; p. 759. [Google Scholar]
- Thuburn, J. TVD schemes, positive schemes, and the universal limiter. Mon. Weather Rev. 1997, 125, 1990–1995. [Google Scholar] [CrossRef]
- Gross, E.S.; Koseff, J.R.; Monismith, S.G. Evaluation of advective schemes for estuarine salinity simulations. J. Hydr. Engrgy 1999, 125, 1199–1209. [Google Scholar] [CrossRef]
- van Slingerland, P. An Accurate and Robust Finite Volume Method for the Advection Diffusion Equation. Master’s Thesis, Delft University of Technology, Delft, The Netherlands, 2007. [Google Scholar]
- Hunter, J.R.; Craig, P.D.; Phillips, H.E. On the Use of Random-Walk Models with Spatially-Variable Diffusivity. J. Comput. Phys. 1993, 106, 366–376. [Google Scholar] [CrossRef]
- Visser, A.W. Using random walk models to simulate the vertical distribution of particles in a turbulent water column. Mar. Ecol. Prog. Ser. 1997, 158, 275–281. [Google Scholar] [CrossRef]
- Visser, A.W. Lagrangian modelling of plankton motion: From deceptively simple random walks to Fokker-Planck and back again. J. Mar. Syst. 2008, 70, 287–299. [Google Scholar] [CrossRef]
- van Sebille, E.; Griffies, S.M.; Abernathey, R.; Adams, T.P.; Berloff, P.; Biastoch, A.; Blanke, B.; Chassignet, E.P.; Cheng, Y.; Cotter, C.J.; et al. Lagrangian ocean analysis: Fundamentals and practices. Ocean Model. 2018, 121, 49–75. [Google Scholar] [CrossRef]
- Deleersnijder, E.; Draoui, I.; Lambrechts, J.; Legat, V.; Mouchet, A. Consistent boundary conditions for age calculations. Water 2020, 12, 1274. [Google Scholar] [CrossRef]
- Alessandrini, S.; Ferrero, E. A hybrid Lagrangian-Eulerian particle model for reacting pollutant dispersion in non-homogeneous non-isotropic turbulence. Phys. A 2009, 388, 1375–1387. [Google Scholar] [CrossRef]
- Peyret, R.; Taylor, T.D. Computational Methods for Fluid Flow; Springer: New York, NY, USA, 1983. [Google Scholar]
- Condie, S.A.; Andrewartha, J.R. Circulation and connectivity on the Australian North West Shelf. Cont. Shelf Res. 2008, 28, 1724–1739. [Google Scholar] [CrossRef]
- Thomas, C.J.; Lambrechts, J.; Wolanski, E.; Traag, V.A.; Blondel, V.D.; Deleersnijder, E.; Hanert, E. Numerical modelling and graph theory tools to study ecological connectivity in the Great Barrier Reef. Ecol. Model. 2014, 272, 160–174. [Google Scholar] [CrossRef]
- Frys, C.; St-Amand, A.; Le Henaff, M.; Figueiredo, J.; Kuba, A.; Walker, B.; Lambrechts, J.; Vallaeys, V.; Vincent, D.; Hanert, E. Fine-Scale Coral Connectivity Pathways in the Florida Reef Tract: Implications for Conservation and Restoration. Front. Mar. Sci. 2020, 7. [Google Scholar] [CrossRef]
- Grech, A.; Hanert, E.; McKenzie, L.; Rasheed, M.; Thomas, C.; Tol, S.; Wang, M.Z.; Waycott, M.; Wolter, J.; Coles, R. Predicting the cumulative effect of multiple disturbances on seagrass connectivity. Glob. Chang. Biol. 2018, 24, 3093–3104. [Google Scholar] [CrossRef] [PubMed]
- Paris, C.B.; Helgers, J.; van Sebille, E.; Srinivasan, A. Connectivity Modeling System: A probabilistic modeling tool for the multi-scale tracking of biotic and abiotic variability in the ocean. Environ. Model. Softw. 2013, 42, 47–54. [Google Scholar] [CrossRef]
- Monsen, N.E.; Cloern, J.E.; Lucas, L.V.; Monismith, S.G. A comment on the use of flushing time, residence time, and age as transport time scales. Limnol. Oceanogr. 2002, 47, 1545–1553. [Google Scholar] [CrossRef]
- Takeoka, H. Fundamental concepts of exchange and transport time scales in a coastal sea. Cont. Shelf Res. 1984, 3, 311–326. [Google Scholar] [CrossRef]
- Deleersnijder, E.; Mouchet, A.; Delhez, E.J.M. Diagnostic Timescales in Fluid Flows: From the Tower of Babel to Partial Differential Problems; Université Catholique de Louvain: Louvain-la-Neuve, Belgium, 2018; pp. 1–26. Available online: http://hdl.handle.net/2078.1/196273 (accessed on 10 March 2018).
- Middelburg, J.J.; Nieuwenhuize, J. Uptake of dissolved inorganic nitrogen in turbid, tidal estuaries. Mar. Ecol. Prog. Ser. 2000, 192, 79–88. [Google Scholar] [CrossRef]
- Crump, B.C.; Hopkinson, C.S.; Sogin, M.L.; Hobbie, J.E. Microbial biogeography along an estuarine salinity gradient: Combined influences of bacterial growth and residence time. Appl. Environ. Microb. 2004, 70, 1494–1505. [Google Scholar] [CrossRef]
- Lucas, L.V. Residence time. In Encyclopedia of Estuaries; Kennish, M.J., Ed.; Springer: Dordrecht, The Netherlands, 2016. [Google Scholar]
- Sheldon, J.E.; Alber, M. A comparison of residence time calculations using simple compartment models of the Altamaha River Estuary, Georgia. Estuaries 2002, 25, 1304–1317. [Google Scholar] [CrossRef]
- Bolin, B.; Rodhe, H. A note on the concepts of age distribution and transit time in natural reservoirs. Tellus 1973, 25, 58–62. [Google Scholar] [CrossRef]
- de Brauwere, A.; de Brye, B.; Blaise, S.; Deleersnijder, E. Residence time, exposure time, and connectivity in the Scheldt Estuary. J. Mar. Syst. 2011, 84, 85–95. [Google Scholar] [CrossRef]
- Zimmerman, J.T.F. Mixing and flushing of tidal embayments in the western Dutch Wadden Sea. Part I: Distribution of salinity and calculation of mixing time scales. Neth. J. Sea Res. 1976, 10, 149–191. [Google Scholar] [CrossRef]
- Delhez, E.J.M.; Heemink, A.W.; Deleersnijder, E. Residence time in a semi-enclosed domain from the solution of an adjoint problem. Estuar. Coast. Shelf Sci. 2004, 61, 691–702. [Google Scholar] [CrossRef]
- Delhez, E.J.M. On the concept of exposure time. Cont. Shelf Res. 2013, 71, 27–36. [Google Scholar] [CrossRef]
- Delhez, E.J.M. Transient residence and exposure times. Ocean Sci. 2006, 2, 1–9. [Google Scholar] [CrossRef]
- Rayson, M.D.; Gross, E.S.; Hetland, R.D.; Fringer, O.B. Time scales in Galveston Bay: An unsteady estuary. J. Geophys. Res. Oceans 2016, 121, 2268–2285. [Google Scholar] [CrossRef]
- Defne, Z.; Ganju, N.K. Quantifying the Residence Time and Flushing Characteristics of a Shallow, Back-Barrier Estuary: Application of Hydrodynamic and Particle Tracking Models. Estuaries Coasts 2015, 38, 1719–1734. [Google Scholar] [CrossRef]
- Storlazzi, C.D.; Cheriton, O.M.; Messina, A.M.; Biggs, T.W. Meteorologic, oceanographic, and geomorphic controls on circulation and residence time in a coral reef-lined embayment: Faga’alu Bay, American Samoa. Coral Reefs 2018, 37, 457–469. [Google Scholar] [CrossRef]
- Manning, J.P.; McGillicuddy, D.J.; Pettigrew, N.R.; Churchill, J.H.; Incze, L.S. Drifter Observations of the Gulf of Maine Coastal Current. Cont. Shelf Res. 2009, 29, 835–845. [Google Scholar] [CrossRef]
- Pawlowicz, R.; Hannah, C.; Rosenberger, A. Lagrangian observations of estuarine residence times, dispersion, and trapping in the Salish Sea. Estuar. Coast. Shelf Sci. 2019, 225, 1–16. [Google Scholar] [CrossRef]
- Corcoran, A.A.; Reifel, K.M.; Jones, B.H.; Shipe, R.F. Spatiotemporal development of physical, chemical, and biological characteristics of stormwater plumes in Santa Monica Bay, California (USA). J. Sea Res. 2010, 63, 129–142. [Google Scholar] [CrossRef]
- Lucas, L.V. Age. In Encyclopedia of Estuaries; Kennish, M.J., Ed.; Springer: Dordrecht, The Netherlands, 2016. [Google Scholar]
- Delhez, E.J.M.; Wolk, F. Diagnosis of the transport of adsorbed material in the Scheldt estuary: A proof of concept. J. Mar. Syst. 2013, 128, 17–26. [Google Scholar] [CrossRef]
- Camacho, R.A.; Martin, J.L. Hydrodynamic Modeling of First-Order Transport Timescales in the St. Louis Bay Estuary, Mississippi. J. Environ. Eng. 2013, 139, 317–331. [Google Scholar] [CrossRef]
- Dyer, K.R. Estuaries: A Physical Introduction, 2nd ed.; John Wiley & Sons Ltd.: Chichester, UK, 1997; p. 195. [Google Scholar]
- Lemagie, E.P.; Lerczak, J.A. A Comparison of Bulk Estuarine Turnover Timescales to Particle Tracking Timescales Using a Model of the Yaquina Bay Estuary. Estuaries Coasts 2015, 38, 1797–1814. [Google Scholar] [CrossRef]
- Geyer, W.R.; Morris, J.T.; Pahl, F.G.; Jay, D.A. Interaction between physical processes and ecosystem structure: A comparative approach. In Estuarine Science: A Synthetic Approach to Research and Practice; Hobbie, J.E., Ed.; Island Press: Washington, DC, USA, 2000; pp. 177–206. [Google Scholar]
- Jouon, A.; Douillet, P.; Ouillon, S.; Fraunie, P. Calculations of hydrodynamic time parameters in a semi-opened coastal zone using a 3D hydrodynamic model. Cont. Shelf Res. 2006, 26, 1395–1415. [Google Scholar] [CrossRef]
- Tartinville, B.; Deleersnijder, E.; Rancher, J. The water residence time in the Mururoa atoll lagoon: Sensitivity analysis of a three-dimensional model. Coral Reefs 1997, 16, 193–203. [Google Scholar] [CrossRef]
- Hinrichs, C.; Flagg, C.N.; Wilson, R.E. Great South Bay After Sandy: Changes in Circulation and Flushing due to New Inlet. Estuaries Coasts 2018, 41, 2172–2190. [Google Scholar] [CrossRef]
- Huguet, J.-R.; Brenon, I.; Coulombier, T. Characterisation of the water renewal in a macro-tidal marina using several transport timescales. Water 2019, 11, 2050. [Google Scholar] [CrossRef]
- Wolanski, E.; Mazda, Y.; King, B.; Gay, S. Dynamics, Flushing and Trapping in Hinchinbrook Channel, a Giant Mangrove Swamp, Australia. Estuar. Coast. Shelf Sci. 1990, 31, 555–579. [Google Scholar] [CrossRef]
- Hansen, J.C.R.; Reidenbach, M.A. Turbulent mixing and fluid transport within Florida Bay seagrass meadows. Adv. Water Resour. 2017, 108, 205–215. [Google Scholar] [CrossRef]
- Deleersnijder, E. A Quick Refresher on Exposure and Residence Times in a Well-Mixed Domain; Université Catholique de Louvain: Louvain-la-Neuve, Belgium, 2020; pp. 1–4. Available online: http://hdl.handle.net/2078.1/229804 (accessed on 15 May 2020).
- Sanford, L.P.; Boicourt, W.C.; Rives, S.R. Model for estimating tidal flushing of small embayments. J. Waterw. Port Coast. Ocean Eng. 1992, 118, 635–654. [Google Scholar] [CrossRef]
- van de Kreeke, J. Residence time: Application to small boat basins. J. Waterw. Port Coast. Ocean Eng 1983, 109, 416–428. [Google Scholar] [CrossRef]
- Shen, J.; Haas, L. Calculating age and residence time in the tidal York River using three-dimensional model experiments. Estuar. Coast. Shelf Sci. 2004, 61, 449–461. [Google Scholar] [CrossRef]
- MacCready, P. Calculating Estuarine Exchange Flow Using Isohaline Coordinates. J. Phys. Oceanogr. 2011, 41, 1116–1124. [Google Scholar] [CrossRef]
- Middelburg, J.J.; Nieuwenhuize, J. Nitrogen uptake by heterotrophic bacteria and phytoplankton in the nitrate-rich Thames estuary. Mar. Ecol. Prog. Ser. 2000, 203, 13–21. [Google Scholar] [CrossRef]
- Caraco, N.F.; Cole, J.J.; Raymond, P.A.; Strayer, D.L.; Pace, M.L.; Findlay, S.; Fischer, D.T. Zebra mussel invasion in a large, turbid river: Phytoplankton response to increased grazing. Ecology 1997, 78, 588–602. [Google Scholar] [CrossRef]
- Middelburg, J.J.; Barranguet, C.; Boschker, H.T.S.; Herman, P.M.J.; Moens, T.; Heip, C.H.R. The fate of intertidal microphytobenthos carbon: An in situ C-13-labeling study. Limnol. Oceanogr. 2000, 45, 1224–1234. [Google Scholar] [CrossRef]
- Hong, B.; Liu, Z.H.; Shen, J.; Wu, H.; Gong, W.P.; Xu, H.Z.; Wang, D.X. Potential physical impacts of sea-level rise on the Pearl River Estuary, China. J. Mar. Syst. 2020, 201. [Google Scholar] [CrossRef]
- Ralston, D.K.; Brosnahan, M.L.; Fox, S.E.; Lee, K.D.; Anderson, D.M. Temperature and Residence Time Controls on an Estuarine Harmful Algal Bloom: Modeling Hydrodynamics and Alexandrium fundyense in Nauset Estuary. Estuaries Coasts 2015, 38, 2240–2258. [Google Scholar] [CrossRef]
- Larson, M.; Nunes, A.; Tanaka, H. Semi-analytic model of tidal-induced inlet flow and morphological evolution. Coast. Eng. 2020, 155. [Google Scholar] [CrossRef]
- Chen, Y.H.; Yu, K.F.; Hassan, M.; Xu, C.; Zhang, B.; Gin, K.Y.H.; He, Y.L. Occurrence, distribution and risk assessment of pesticides in a river-reservoir system. Ecotoxicol. Environ. Saf. 2018, 166, 320–327. [Google Scholar] [CrossRef]
- Viero, D.P.; Defina, A. Water age, exposure time, and local flushing time in semi-enclosed, tidal basins with negligible freshwater inflow. J. Mar. Syst. 2016, 156, 16–29. [Google Scholar] [CrossRef]
- Ralston, D.K.; Geyer, W.R. Sediment Transport Time Scales and Trapping Efficiency in a Tidal River. J. Geophys. Res. Earth 2017, 122, 2042–2063. [Google Scholar] [CrossRef]
- Fennel, K.; Testa, J.M. Biogeochemical Controls on Coastal Hypoxia. Annu. Rev. Mar. Sci. 2019, 11, 105–130. [Google Scholar] [CrossRef] [PubMed]
- Gross, E.S.; Koseff, J.R.; Monismith, S.G. Three-dimensional salinity simulations of South San Francisco Bay. J. Hydraul. Eng. 1999, 125, 32–46. [Google Scholar] [CrossRef]
- Kim, J.H.; Hong, S.J.; Lee, W.C.; Kim, H.C.; Eom, K.H.; Jung, W.S.; Kim, D.M. Estimation of the Effect of Flushing Time on Oyster Aquaculture Potential in Jaran Bay. Ocean Sci. J. 2019, 54, 559–571. [Google Scholar] [CrossRef]
- Wolanski, E. Bounded and unbounded boundaries—Untangling mechanisms for estuarine-marine ecological connectivity: Scales of m to 10,000 km—A review. Estuar. Coast. Shelf Sci. 2017, 198, 378–392. [Google Scholar] [CrossRef]
- Golbuu, Y.; Gouezo, M.; Kurihara, H.; Rehm, L.; Wolanski, E. Long-term isolation and local adaptation in Palau’s Nikko Bay help corals thrive in acidic waters. Coral Reefs 2016, 35, 909–918. [Google Scholar] [CrossRef]
- Viero, D.P.; Defina, A. Renewal time scales in tidal basins: Climbing the Tower of Babel. In Sustainable Hydraulics in the Era of Global Change: Advances in Water Engineering and Research, 1st ed.; Erpicum, S., Dewals, B., Archambeau, P., Pirotton, M., Eds.; CRC Press: London, UK, 2016; pp. 338–345. [Google Scholar]
- Deleersnijder, E.; Delhez, E.J.M. Timescale- and tracer-based methods for understanding the results of complex marine models. Estuar. Coast. Shelf Sci. 2007, 74. [Google Scholar] [CrossRef]
- Deleersnijder, E. Classical vs. Holistic Timescales: The Mururoa Atoll Lagoon Case Study; Université Catholique de Louvain: Louvain-la-Neuve, Belgium, 2019; pp. 1–12. Available online: http://hdl.handle.net/2078.1/224391 (accessed on 18 April 2020).
- Mouchet, A.; Cornaton, F.; Deleersnijder, E.; Delhez, E.J.M. Partial ages: Diagnosing transport processes by means of multiple clocks. Ocean Dyn. 2016, 66, 367–386. [Google Scholar] [CrossRef]
- Lin, L.; Liu, Z. Partial residence times: Determining residence time composition in different subregions. Ocean Dyn. 2019, 69, 1023–1036. [Google Scholar] [CrossRef]
- Rypina, I.I.; Fertitta, D.; Macdonald, A.; Yoshida, S.; Jayne, S. Multi-iteration approach to studying tracer spreading using drifter data. J. Phys. Oceanogr. 2017, 47, 339–351. [Google Scholar] [CrossRef]
- Scavia, D.; Field, J.C.; Boesch, D.F.; Buddemeier, R.W.; Burkett, V.; Cayan, D.R.; Fogarty, M.; Harwell, M.A.; Howarth, R.W.; Mason, C.; et al. Climate change impacts on U.S. Coastal and Marine Ecosystems. Estuaries 2002, 25, 149–164. [Google Scholar] [CrossRef]
- Beklioglu, M.; Romo, S.; Kagalou, I.; Quintana, X.; Bécares, E. State of the art in the functioning of shallow Mediterranean lakes: Workshop conclusions. Hydrobiologia 2007, 584, 317–326. [Google Scholar] [CrossRef]
- Schindler, D.W. Recent advances in the understanding and management of eutrophication. Limnol. Oceanogr. 2006, 51, 356–363. [Google Scholar] [CrossRef]
- Cloern, J.E. Our evolving conceptual model of the coastal eutrophication problem. Mar. Ecol. Prog. Ser. 2001, 210, 223–253. [Google Scholar] [CrossRef]
- Oveisy, A.; Boegman, L.; Rao, Y.R. A model of the three-dimensional hydrodynamics, transport and flushing in the Bay of Quinte. J. Great Lakes Res. 2015, 41, 536–548. [Google Scholar] [CrossRef]
- Lopez, C.B.; Cloern, J.E.; Schraga, T.S.; Little, A.J.; Lucas, L.V.; Thompson, J.K.; Burau, J.R. Ecological values of shallow-water habitats: Implications for restoration of disturbed ecosystems. Ecosystems 2006, 9, 422–440. [Google Scholar] [CrossRef]
- Cochran, J.K.; Miquel, J.C.; Armstrong, R.; Fowler, S.W.; Masque, P.; Gasser, B.; Hirschberg, D.; Szlosek, J.; Baena, A.M.R.Y.; Verdeny, E.; et al. Time-series measurements of Th-234 in water column and sediment trap samples from the northwestern Mediterranean Sea. Deep-Sea Res. Partt II 2009, 56, 1487–1501. [Google Scholar] [CrossRef]
- Wang, W.X.; Fisher, N.S.; Luoma, S.N. Kinetic determinations of trace element bioaccumulation in the mussel Mytilus edulis. Mar. Ecol. Prog. Ser. 1996, 140, 91–113. [Google Scholar] [CrossRef]
- Cuetara, J.I.; Burau, J.R. Drifter Studies in Open Shallow Water Habitats of the San Francisco Bay and Delta. Available online: https://archive.usgs.gov/archive/sites/sfbay.wr.usgs.gov/watershed/drifter_studies/index.html (accessed on 11 February 2020).
- Falco, P.; Griffa, A.; Poulain, P.-M.; Zambianchi, E. Transport Properties in the Adriatic Sea as Deduced from Drifter Data. J. Phys. Oceanogr. 2000, 30, 2055–2071. [Google Scholar] [CrossRef]
- Zhou, M.; Niiler, P.P.; Hu, J.-H. Surface currents in the Bransfield and Gerlache Straits, Antarctica. Deep-Sea Res. Part II 2002, 49, 267–280. [Google Scholar] [CrossRef]
- Lacy, J.R. Circulation and Transport in a Semi-Enclosed Estuarine Subembayment. Ph.D. Thesis, Stanford University, Stanford, CA, USA, 2000. [Google Scholar]
- Conomos, T.J.; Peterson, D.H.; Carlson, P.R.; McCulloch, D.S. Movement of Seabed Drifters in the San Francisco Bay Estuary and the Adjacent Pacific Ocean: A Preliminary Report; Geological Survey Circular 637-B; United States Geological Survey: Washington, DC, USA, 1970; pp. 1–8. [Google Scholar]
- Conomos, T.J. Movement of spilled oil as predicted by estuarine nontidal drift. Limnol. Oceanogr. 1975, 20, 159–173. [Google Scholar] [CrossRef]
- Rypina, I.I.; Kirincich, A.; Lentz, S.; Sundermeyer, M. Investigating the Eddy Diffusivity Concept in the Coastal Ocean. J. Phys. Oceanogr. 2016, 46, 2201–2218. [Google Scholar] [CrossRef]
- Poulain, P.M.; Gerin, R.; Mauri, E.; Pennel, R. Wind Effects on Drogued and Undrogued Drifters in the Eastern Mediterranean. J. Atmos. Ocean. Tech. 2009, 26, 1144–1156. [Google Scholar] [CrossRef]
- Perry, R.W.; Pope, A.C.; Romine, J.G.; Brandes, P.L.; Burau, J.R.; Blake, A.R.; Ammann, A.J.; Michel, C.J. Flow-mediated effects on travel time, routing, and survival of juvenile Chinook salmon in a spatially complex, tidally forced river delta. Can. J. Fish. Aquat. Sci. 2018, 75, 1886–1901. [Google Scholar] [CrossRef]
- Vallino, J.J.; Hopkinson, C.S., Jr. Estimation of dispersion and characteristic mixing times in Plum Island Sound Estuary. Estuar. Coast. Shelf Sci. 1998, 46, 333–350. [Google Scholar] [CrossRef]
- Bois, P.; Childers, D.L.; Corlouer, T.; Laurent, J.; Massicot, A.; Sanchez, C.A.; Wanko, A. Confirming a plant-mediated “Biological Tide” in an aridland constructed treatment wetland. Ecosophere 2017, 8, 1–16. [Google Scholar] [CrossRef]
- Nishihara, G.N.; Terada, R.; Shimabukuro, H. Effects of wave energy on the residence times of a fluorescent tracer in the canopy of the intertidal marine macroalgae, Sargassum fusiforme (Phaeophyceae). Phycol. Res. 2011, 59, 24–33. [Google Scholar] [CrossRef]
- Dahlgaard, H.; Herrmann, J.; Salomon, J.C. A Tracer Study of the Transport of Coastal Water from the English-Channel through the German-Bight to the Kattegat. J. Mar. Syst. 1995, 6, 415–425. [Google Scholar] [CrossRef]
- Bailly du Bois, P.; Dumas, F.; Solier, L.; Voiseux, C. In-situ database toolbox for short-term dispersion model validation in macro-tidal seas, application for 2D-model. Cont. Shelf Res. 2012, 36, 63–82. [Google Scholar] [CrossRef]
- Bailly du Bois, P.; Garreau, P.; Laguionie, P.; Korsakissok, I. Comparison between modelling and measurement of marine dispersion, environmental half-time and 137Cs inventories after the Fukushima Daiichi accident. Ocean Dyn. 2014, 64, 361–383. [Google Scholar] [CrossRef]
- Bailly du Bois, P.; Laguionie, P.; Boust, D.; Korsakissok, I.; Didier, D.; Fiévet, B. Estimation of marine source-term following Fukushima Dai-ichi accident. J. Environ. Radioact. 2012, 114, 2–9. [Google Scholar] [CrossRef] [PubMed]
- Bressac, M.; Levy, I.; Chamizo, E.; La Rosa, J.J.; Povinec, P.P.; Gastaud, J.; Oregioni, B. Temporal evolution of 137Cs, 237Np, and 239+240Pu and estimated vertical 239+240Pu export in the northwestern Mediterranean Sea. Sci. Total Environ. 2017, 595, 178–190. [Google Scholar] [CrossRef] [PubMed]
- Uncles, R.J.; Torres, R. Estimating dispersion and flushing time-scales in a coastal zone: Application to the Plymouth area. Ocean Coast Manag. 2013, 72, 3–12. [Google Scholar] [CrossRef]
- Souza, T.A.; Godoy, J.M.; Godoy, M.L.D.P.; Moreira, I.; Carvalho, Z.L.; Salomao, M.S.M.B.; Rezende, C.E. Use of multitracers for the study of water mixing in the Paraiba do Sul River estuary. J. Environ. Radioact. 2010, 101, 564–570. [Google Scholar] [CrossRef]
- Dulaiova, H.; Burnett, W.C. Evaluation of the flushing rates of Apalachicola Bay, Florida via natural geochemical tracers. Mar. Chem. 2008, 109, 395–408. [Google Scholar] [CrossRef]
- Eller, K.T.; Burnett, W.C.; Fitzhugh, L.M.; Chanton, J.P. Radium Sampling Methods and Residence Times in St. Andrew Bay, Florida. Estuaries Coasts 2014, 37, 94–103. [Google Scholar] [CrossRef]
- Black, E.E.; Lam, P.J.; Lee, J.M.; Buesseler, K.O. Insights From the U-238-Th-234 Method Into the Coupling of Biological Export and the Cycling of Cadmium, Cobalt, and Manganese in the Southeast Pacific Ocean. Glob. Biogeochem. Cycles 2019, 33, 15–36. [Google Scholar] [CrossRef]
- Downing, B.D.; Bergamaschi, B.A.; Kendall, C.; Kraus, T.E.C.; Dennis, K.J.; Carter, J.A.; Von Dessonneck, T.S. Using Continuous Underway Isotope Measurements To Map Water Residence Time in Hydrodynamically Complex Tidal Environments. Env. Sci. Technol. 2016, 50, 13387–13396. [Google Scholar] [CrossRef]
- Gross, E.; Andrews, S.; Bergamaschi, B.; Downing, B.; Holleman, R.; Burdick, S.; Durand, J. The Use of Stable Isotope-Based Water Age to Evaluate a Hydrodynamic Model. Water 2019, 11, 2207. [Google Scholar] [CrossRef]
- Choi, K.W.; Lee, J.H.W. Numerical determination of flushing time for stratified water bodies. J. Mar. Syst. 2004, 50, 263–281. [Google Scholar] [CrossRef]
- Safak, I.; Wiberg, P.L.; Richardson, D.L.; Kurum, M.O. Controls on residence time and exchange in a system of shallow coastal bays. Cont. Shelf Res. 2015, 97, 7–20. [Google Scholar] [CrossRef]
- Du, J.B.; Park, K.; Yu, X.; Zhang, Y.L.J.; Ye, F. Massive pollutants released to Galveston Bay during Hurricane Harvey: Understanding their retention and pathway using Lagrangian numerical simulations. Sci. Total Environ. 2020, 704. [Google Scholar] [CrossRef] [PubMed]
- Guillou, N.; Thiebot, J.; Chapalain, G. Turbines’ effects on water renewal within a marine tidal stream energy site. Energy 2019, 189. [Google Scholar] [CrossRef]
- Palazzoli, I.; Leonardi, N.; Jimenez-Robles, A.M.; Fagherazzi, S. Velocity skew controls the flushing of a tracer in a system of shallow bays with multiple inlets. Cont. Shelf Res. 2020, 192. [Google Scholar] [CrossRef]
- Miguel, L.L.A.J.; Castro, J.W.A.; Machava, S.F.A. Dynamics of water exchange and salt flux in the Macuse Estuary, central Mozambique, southern Africa. Afr. J. Mar. Sci. 2019, 41, 203–219. [Google Scholar] [CrossRef]
- Hall, T.M.; Plumb, R.A. Age as a diagnostic of stratospheric transport. J. Geophys. Res. 1994, 99, 1059–1070. [Google Scholar] [CrossRef]
- Holzer, M.; Hall, T.M. Transit-time and Tracer-age Distributions in Geophysical Flows. J. Atmos. Sci. 2000, 57, 3539–3558. [Google Scholar] [CrossRef]
- Cornaton, F.; Perrochet, P. Groundwater age, life expectancy and transit time distributions in advective-dispersive systems; 2. Reservoir theory for sub-drainage basins. Adv. Water Resour. 2006, 29, 1292–1305. [Google Scholar] [CrossRef]
- Delhez, E.J.M.; Deleersnijder, E. The concept of age in marine modelling II. Concentration distribution function in the English Channel and the North Sea. J. Mar. Syst. 2002, 31, 279–297. [Google Scholar] [CrossRef]
- Mercier, C.; Delhez, E.J.M. Diagnosis of the sediment transport in the Belgian Coastal Zone. Estuar. Coast. Shelf Sci. 2007, 74, 670–683. [Google Scholar] [CrossRef]
- Gong, W.P.; Shen, J. A model diagnostic study of age of river-borne sediment transport in the tidal York River Estuary. Environ. Fluid Mech. 2010, 10, 177–196. [Google Scholar] [CrossRef]
- Zhu, L.; Gong, W.; Zhang, H.; Huang, W.; Zhang, R. Numerical study of sediment transport time scales in an ebb-dominated waterway. J. Hydrol. 2020, 591, 125299. [Google Scholar] [CrossRef]
- Radtke, H.; Neumann, T.; Voss, M.; Fennel, W. Modeling pathways of riverine nitrogen and phosphorus in the Baltic Sea. J. Geophys. Res. Ocean. 2012, 117. [Google Scholar] [CrossRef]
- Delhez, E.J.M.; Lacroix, G.; Deleersnijder, E. The age as a diagnostic of the dynamics of marine ecosystem models. Ocean Dyn. 2004, 54, 221–231. [Google Scholar] [CrossRef]
- Liu, Z.; Wang, H.Y.; Guo, X.Y.; Wang, Q.; Gao, H.W. The age of Yellow River water in the Bohai Sea. J. Geophys. Res. Ocean. 2012, 117. [Google Scholar] [CrossRef]
- Andrejev, O.; Myrberg, K.; Lundberg, P.A. Age and renewal time of water masses in a semi-enclosed basin—Application to the Gulf of Finland. Tellus A 2004, 56, 548–558. [Google Scholar] [CrossRef]
- Gourgue, O.; Deleersnijder, E.; White, L. Toward a generic method for studying water renewal, with application to the epilimnion of Lake Tanganyika. Estuar. Coast. Shelf Sci. 2007, 74, 628–640. [Google Scholar] [CrossRef]
- Meier, H.E.M. Modeling the pathways and ages of inflowing salt- and freshwater in the Baltic Sea. Estuar. Coast. Shelf Sci. 2007, 74, 610–627. [Google Scholar] [CrossRef]
- Kärnä, T.; Baptista, A.M. Water age in the Columbia River estuary. Estuar. Coast. Shelf Sci. 2016, 183, 249–259. [Google Scholar] [CrossRef]
- Li, Y.Y.; Feng, H.; Zhang, H.W.; Su, J.; Yuan, D.K.; Guo, L.; Nie, J.; Du, J.L. Hydrodynamics and water circulation in the New York/New Jersey Harbor: A study from the perspective of water age. J. Mar. Syst. 2019, 199. [Google Scholar] [CrossRef]
- Shang, J.C.; Sun, J.; Tao, L.; Li, Y.Y.; Nie, Z.H.; Liu, H.Y.; Chen, R.; Yuan, D.K. Combined Effect of Tides and Wind on Water Exchange in a Semi-Enclosed Shallow Sea. Water 2019, 11, 1762. [Google Scholar] [CrossRef]
- Bendtsen, J.; Gustafsson, K.E.; Soderkvist, J.; Hansen, J.L.S. Ventilation of bottom water in the North Sea-Baltic Sea transition zone. J. Mar. Syst. 2009, 75, 138–149. [Google Scholar] [CrossRef]
- Du, J.B.; Shen, J. Water residence time in Chesapeake Bay for 1980–2012. J. Mar. Syst. 2016, 164, 101–111. [Google Scholar] [CrossRef]
- Qin, Q.B.; Shen, J. Physical transport processes affect the origins of harmful algal blooms in estuaries. Harmful Algae 2019, 84, 210–221. [Google Scholar] [CrossRef]
- Delhez, E.J.M.; Deleersnijder, E. Residence time and exposure time of sinking phytoplankton in the euphotic layer. J. Biol. 2010, 262, 505–516. [Google Scholar] [CrossRef]
- Boyer, J.N.; Fourqurean, J.W.; Jones, R.D. Spatial characterization of water quality in Florida Bay and Whitewater Bay by multivariate analyses: Zones of similar influence. Estuaries 1997, 20, 743–758. [Google Scholar] [CrossRef]
- Paerl, H.W.; Huisman, J. Blooms like it hot. Science 2008, 320, 57–58. [Google Scholar] [CrossRef]
- Rabalais, N.N.; Turner, R.E. Oxygen depletion in the Gulf of Mexico adjacent to the Mississippi River. In Past and Present Water Column Anoxia; Neretin, L.N., Ed.; Springer: Dordrecht, The Netherlands, 2006; pp. 225–245. [Google Scholar]
- Durand, J. A conceptual model of the aquatic food web of the Upper San Francisco Estuary. San Franc. Estuary Watershed Sci. 2015, 13, 1–37. [Google Scholar] [CrossRef]
- Hopkinson, C.S.; Vallino, J.J. The Relationships among Mans Activities in Watersheds and Estuaries—A Model of Runoff Effects on Patterns of Estuarine Community Metabolism. Estuaries 1995, 18, 598–621. [Google Scholar] [CrossRef]
- Battin, T.J.; Kaplan, L.A.; Findlay, S.; Hopkinson, C.S.; Marti, E.; Packman, A.I.; Newbold, J.D.; Sabater, F. Biophysical controls on organic carbon fluxes in fluvial networks. Nat. Geosci. 2008, 1, 95–100. [Google Scholar] [CrossRef]
- Liu, X.; Dunne, J.P.; Stock, C.A.; Harrison, M.J.; Adcroft, A.; Resplandy, L. Simulating Water Residence Time in the Coastal Ocean: A Global Perspective. Geophys. Res. Lett. 2019, 46, 13910–13919. [Google Scholar] [CrossRef]
- England, M.H. The Age of Water and Ventilation Timescales in a Global Ocean Model. J. Phys. Oceanogr. 1995, 25, 2756–2777. [Google Scholar] [CrossRef]
- Liu, X.; (IMSG at NOAA/NWS/NCEP/EMC, College Park, Maryland, USA). Personal communication, 2020.
- Sharples, J.; Middelburg, J.J.; Fennel, K.; Jickells, T.D. What proportion of riverine nutrients reaches the open ocean? Glob. Biogeochem. Cycles 2017, 31, 39–58. [Google Scholar] [CrossRef]
- Mouchet, A.; Deleersnijder, E.; Primeau, F. The leaky funnel model revisited. Tellus A 2012, 64. [Google Scholar] [CrossRef]
- Deleersnijder, E.; Wang, J.; Mooers, C.N.K. A two-compartment model for understanding the simulated three-dimensional circulation in Prince William Sound, Alaska. Cont. Shelf Res. 1998, 18, 279–287. [Google Scholar] [CrossRef][Green Version]
- Abdelrhman, M.A. Simplified modeling of flushing and residence times in 42 embayments in New England, USA, with special attention to Greenwich Bay, Rhode Island. Estuar. Coast. Shelf Sci. 2005, 62, 339–351. [Google Scholar] [CrossRef]
- Dettmann, E.H. Effect of water residence time on annual export and denitrification of nitrogen in estuaries: A model analysis. Estuaries 2001, 24, 481–490. [Google Scholar] [CrossRef]
- Lucas, L.V.; Thompson, J.K. Changing restoration rules: Exotic bivalves interact with residence time and depth to control phytoplankton productivity. Ecosphere 2012, 3, 117. [Google Scholar] [CrossRef]
- Jassby, A.D.; Cloern, J.E.; Cole, B.E. Annual primary production: Patterns and mechanisms of change in a nutrient-rich tidal ecosystem. Limnol. Oceanogr. 2002, 47, 698–712. [Google Scholar] [CrossRef]
- Müller-Solger, A.B.; Jassby, A.D.; Müller-Navarra, D.C. Nutritional quality of food resources for zooplankton (Daphnia) in a tidal freshwater system (Sacramento-San Joaquin River Delta). Limnol. Oceanogr. 2002, 47, 1468–1476. [Google Scholar] [CrossRef]
- Jassby, A.D. Phytoplankton in the Upper San Francisco Estuary: Recent biomass trends, their causes and their trophic significance. San Franc. Estuary Watershed Sci. 2008, 6, 1–24. [Google Scholar]
- Kimmerer, W.J.; Orsi, J.J. Changes in the zooplankton of the San Francisco Bay Estuary since the introduction of the clam Potamocorbula amurensis. In San Francisco Bay: The Ecosystem; Hollibaugh, J.T., Ed.; Pacific Division of the American Association for the Advancement of Science: San Francisco, CA, USA, 1996; pp. 403–424. [Google Scholar]
- Winder, M.; Jassby, A.D. Shifts in zooplankton community structure: Implications for food web processes in the Upper San Francisco Estuary. Estuaries Coasts 2011, 34, 675–690. [Google Scholar] [CrossRef]
- Bennett, A.W.; Moyle, P.B. Where have all the fishes gone? Interactive factors producing fish declines in the Sacramento-San Joaquin Estuary. In San Francisco Bay: The Ecosystem; Hollibaugh, J.T., Ed.; Pacific Division of the American Association for the Advancement of Science: San Francisco, CA, USA, 1996; pp. 519–542. [Google Scholar]
- MacNally, R.; Thomson, J.R.; Kimmerer, W.J.; Feyrer, F.; Newman, K.B.; Sih, A.; Bennett, W.A.; Brown, L.; Fleishman, E.; Culberson, S.D.; et al. Analysis of pelagic species decline in the upper San Francisco Estuary using multivariate autoregressive modeling (MAR). Ecol. Appl. 2010, 20, 1417–1430. [Google Scholar] [CrossRef] [PubMed]
- ICF International. Chapter 3.1 and 3.2—Conservation Strategy. Administrative Draft. Bay Delta Conservation Plan; ICF 00610.10; ICF International: Sacramento, CA, USA, 2012. [Google Scholar]
- ICF International. Chapter 5—Effects Analysis. Administrative Draft. Bay Delta Conservation Plan; ICF 00282.11; ICF International: Sacramento, CA, USA, 2012. [Google Scholar]
- ICF International. Appendix F—Ecological Effects. Working Draft. Bay Delta Conservation Plan; ICF 00282.11; ICF International: Sacramento, CA, USA, 2011. [Google Scholar]
- Nixon, S.W.; Ammerman, J.W.; Atkinson, L.P.; Berounsky, V.M.; Billen, G.; Boicourt, W.C.; Boynton, W.R.; Church, T.M.; Di Toro, D.M.; Elmgren, R.; et al. The fate of nitrogen and phosphorus at the land-sea margin of the North Atlantic Ocean. Biogeochemistry 1996, 35, 141–180. [Google Scholar] [CrossRef]
- Mayorga, E.; Seitzinger, S.P.; Harrison, J.A.; Dumont, E.; Beusen, A.H.W.; Bouwman, A.F.; Fekete, B.M.; Kroeze, C.; Van Drecht, G. Global Nutrient Export from WaterSheds 2 (NEWS 2): Model development and implementation. Environ. Model. Softw. 2010, 25, 837–853. [Google Scholar] [CrossRef]
- Isaac, B.J.; Parente, A.; Galletti, C.; Thornock, J.N.; Smith, P.J.; Tognotti, L. A Novel Methodology for Chemical Time Scale Evaluation with Detailed Chemical Reaction Kinetics. Energy Fuel 2013, 27, 2255–2265. [Google Scholar] [CrossRef]
- Oldham, C.E.; Farrow, D.E.; Peiffer, S. A generalized Damkohler number for classifying material processing in hydrological systems. Hydrol. Earth Syst. Sci. 2013, 17, 1133–1148. [Google Scholar] [CrossRef]
- Monsen, N.E.; Cloern, J.E.; Burau, J.R. Effects of flow diversions on water and habitat quality: Examples from California’s highly manipulated Sacramento-San Joaquin Delta. San Franc. Estuary Watershed Sci. 2007, 5, 1–16. [Google Scholar] [CrossRef]
- Volkmar, E.C.; Dahlgren, R.A. Biological oxygen demand dynamics in the Lower San Joaquin River, California. Environ. Sci. Technol. 2006, 40, 5653–5660. [Google Scholar] [CrossRef]
- Strayer, D.L.; Caraco, N.F.; Cole, J.J.; Findlay, S.; Pace, M.L. Transformation of freshwater ecosystem by bivalves. Bioscience 1999, 49, 19–27. [Google Scholar] [CrossRef]
- Dame, R.F. Ecology of Marine Bivalves: An Ecosystem Approach; CRC Press: Boca Raton, FL, USA, 1996. [Google Scholar]
- Smaal, A.C.; Prins, T.C. The uptake of organic matter and the release of inorganic nutrients by bivalve suspension feeder beds. In Bivalve Filter Feeders in Estuarine and Coastal Ecosystem Processes; Dame, R.F., Ed.; Springer: Berlin, Germany, 1993; Volume 33, pp. 271–298. [Google Scholar]
- Soetaert, K.; Herman, P.M.J. Estimating Estuarine Residence Times in the Westerschelde (the Netherlands) Using a Box Model with Fixed Dispersion Coefficients. Hydrobiologia 1995, 311, 215–224. [Google Scholar] [CrossRef]
- Braunschweig, F.; Martins, F.; Chambel, P.; Neves, R. A methodology to estimate renewal time scales in estuaries: The Tagus Estuary case. Ocean Dyn. 2003, 53, 137–145. [Google Scholar] [CrossRef]
- Brodie, J.; Wolanski, E.; Lewis, S.; Bainbridge, Z. An assessment of residence times of land-sourced contaminants in the Great Barrier Reef lagoon and the implications for management and reef recovery. Mar. Pollut. Bull. 2012, 65, 267–279. [Google Scholar] [CrossRef]
- Hall, N.S.; Paerl, H.W.; Peierls, B.L.; Whipple, A.C.; Rossignol, K.L. Effects of climatic variability on phytoplankton community structure and bloom development in the eutrophic, microtidal, New River Estuary, North Carolina, USA. Estuar. Coast. Shelf Sci. 2013, 117, 70–82. [Google Scholar] [CrossRef]
- Alber, M.; Sheldon, J.E. Use of a date-specific method to examine variability in the flushing times of Georgia estuaries. Estuar. Coast. Shelf Sci. 1999, 49, 469–482. [Google Scholar] [CrossRef]
- Wheat, E.E.; Banas, N.S.; Ruesink, J.L. Multi-day water residence time as a mechanism for physical and biological gradients across intertidal flats. Estuar. Coast. Shelf Sci. 2019, 227. [Google Scholar] [CrossRef]
- Wan, Y.S.; Qiu, C.; Doering, P.; Ashton, M.; Sun, D.T.; Coley, T. Modeling residence time with a three-dimensional hydrodynamic model: Linkage with chlorophyll a in a subtropical estuary. Ecol. Model. 2013, 268, 93–102. [Google Scholar] [CrossRef]
- Delesalle, B.; Sournia, A. Residence Time of Water and Phytoplankton Biomass in Coral-Reef Lagoons. Cont. Shelf Res. 1992, 12, 939–949. [Google Scholar] [CrossRef]
- Du, J.; Park, K.; Shen, J.; Dzwonkowski, B.; Yu, X.; Yoon, B.I. Role of Baroclinic Processes on Flushing Characteristics in a Highly Stratified Estuarine System, Mobile Bay, Alabama. J. Geophys. Res. Oceans 2018, 123, 4518–4537. [Google Scholar] [CrossRef]
- Webb, B.M.; Marr, C. Spatial variability of hydrodynamic timescales in a broad and shallow estuary: Mobile Bay, Alabama. J. Coast. Res. 2016, 32, 1374–1389. [Google Scholar]
- Okubo, A. Diffusion and Ecological Problems: Mathematical Models; Springer: Berlin/Heidelberg, Germany; New York, NY, USA, 1980. [Google Scholar]
- Geyer, W.R.; Chant, R.; Houghton, R. Tidal and spring-neap variations in horizontal dispersion in a partially mixed estuary. J. Geophys. Res. Ocean. 2008, 113. [Google Scholar] [CrossRef]
- Hong, B.; Wang, G.; Xu, H.; Wang, D. Study on the transport of terrestrial dissolved substances in the Pearl River Estuary using passive tracers. Water 2020, 12, 1235. [Google Scholar] [CrossRef]
- Pham Van, C.; de Brye, B.; de Brauwere, A.; Hoitink, A.J.F.T.; Soares-Frazao, S.; Deleersnijder, E. Numerical Simulation of Water Renewal Timescales in the Mahakam Delta, Indonesia. Water 2020, 12, 1017. [Google Scholar] [CrossRef]
- Deleersnijder, E. Toward a Generic Method to Estimate the Water Renewal Rate of a Semi-Enclosed Domain; Université Catholique de Louvain: Louvain-la-Neuve, Belgium, 2011; pp. 1–46. Available online: http://hdl.handle.net/2078.1/155414 (accessed on 21 September 2020).
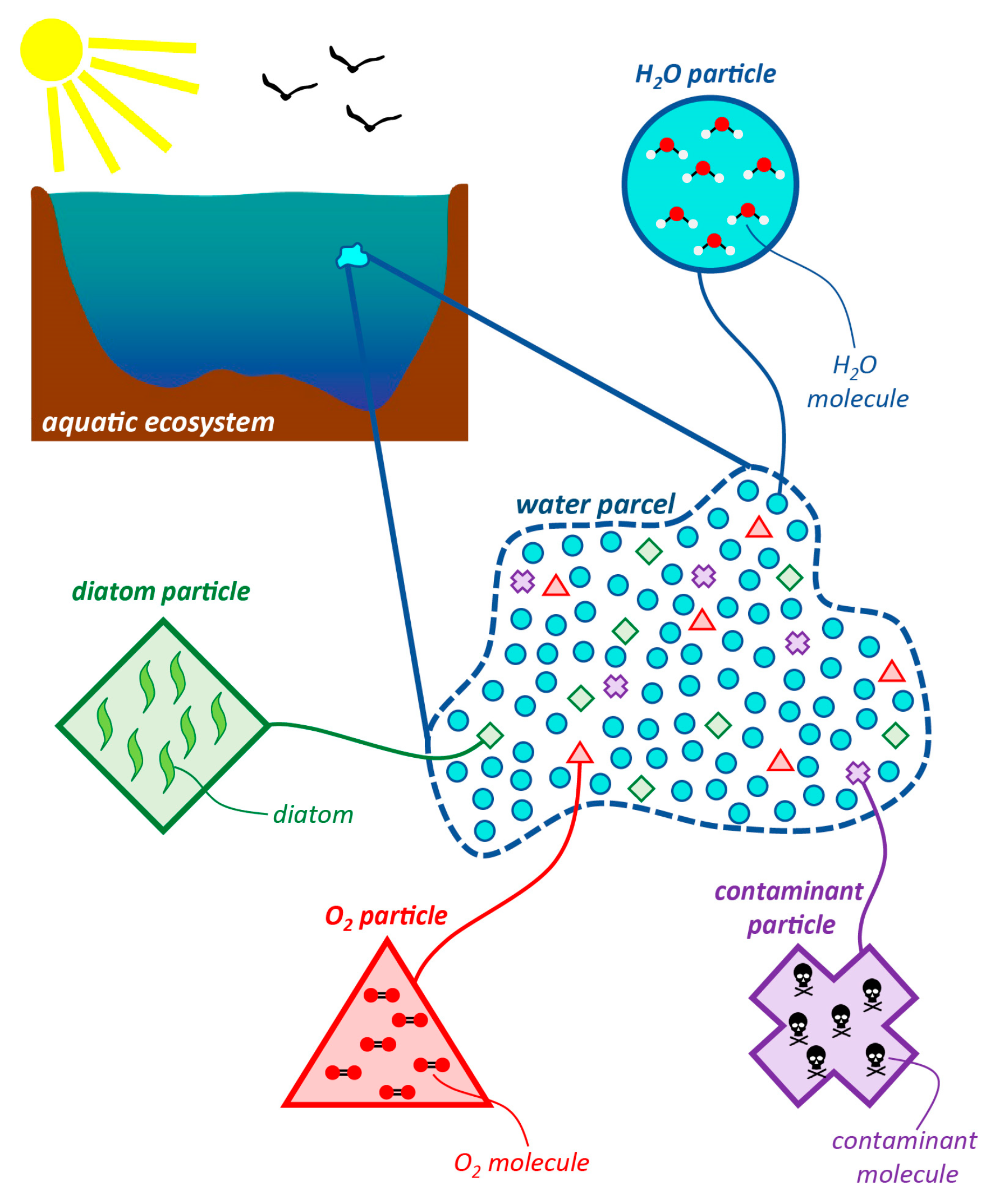
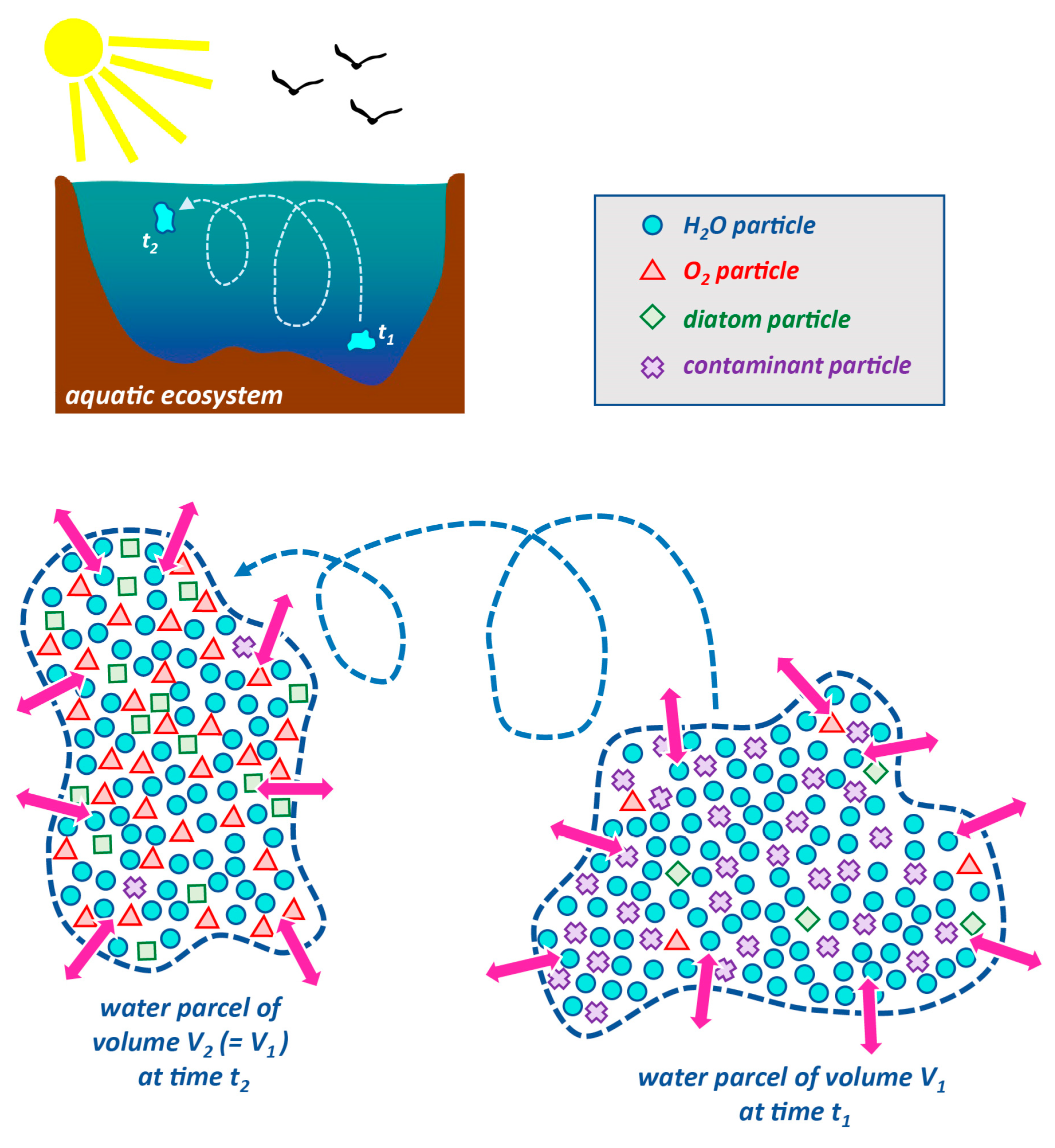
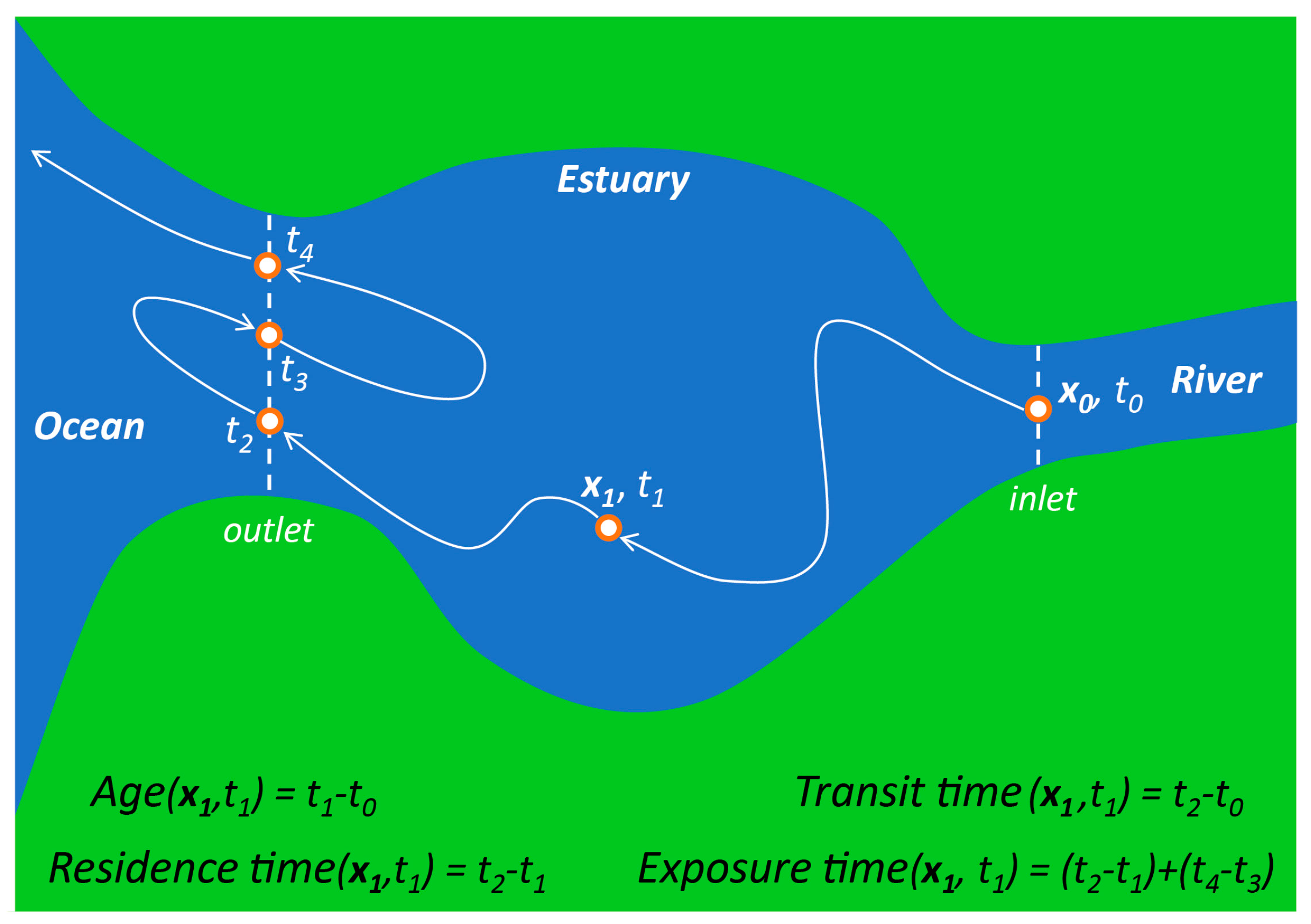



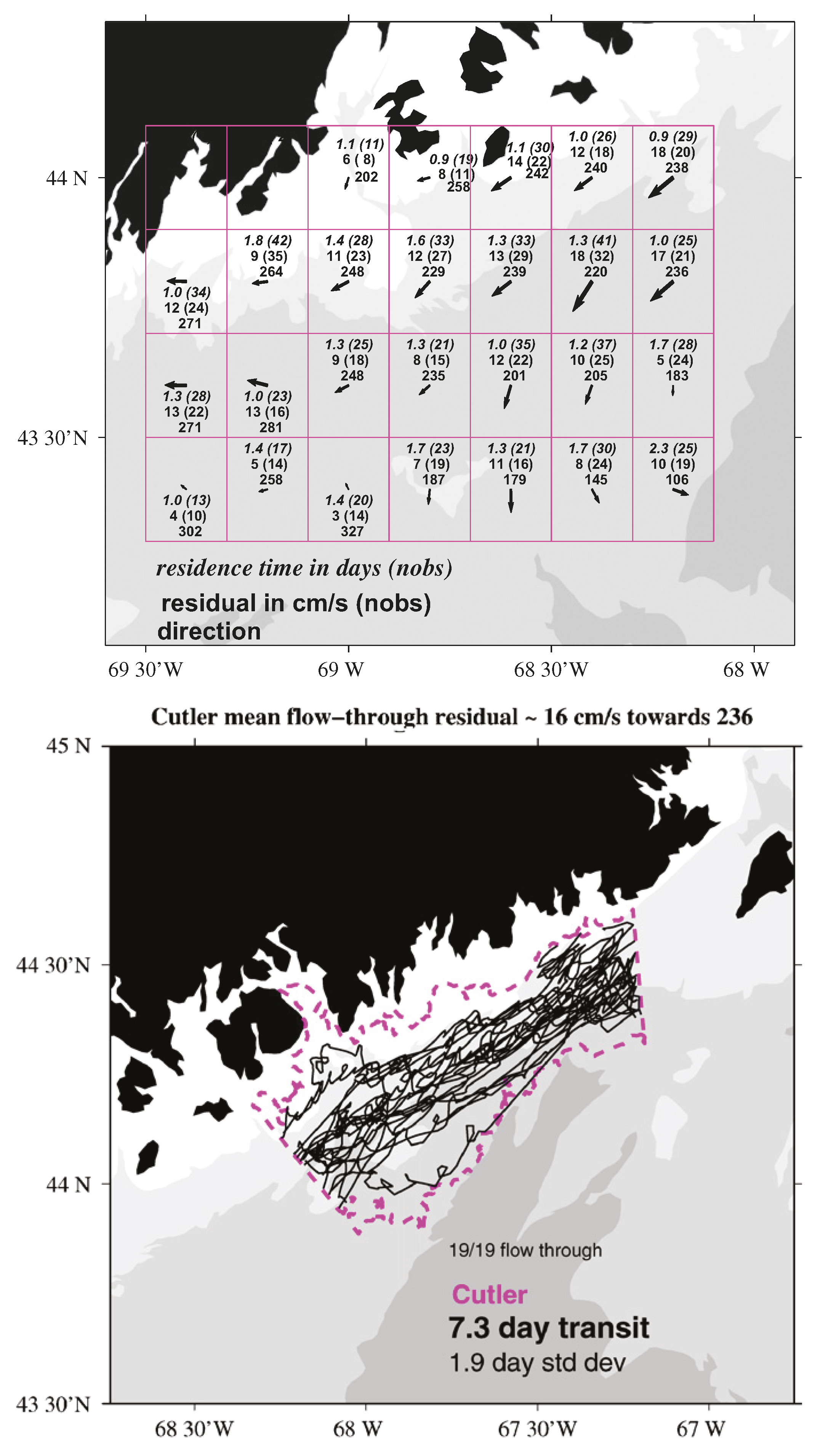
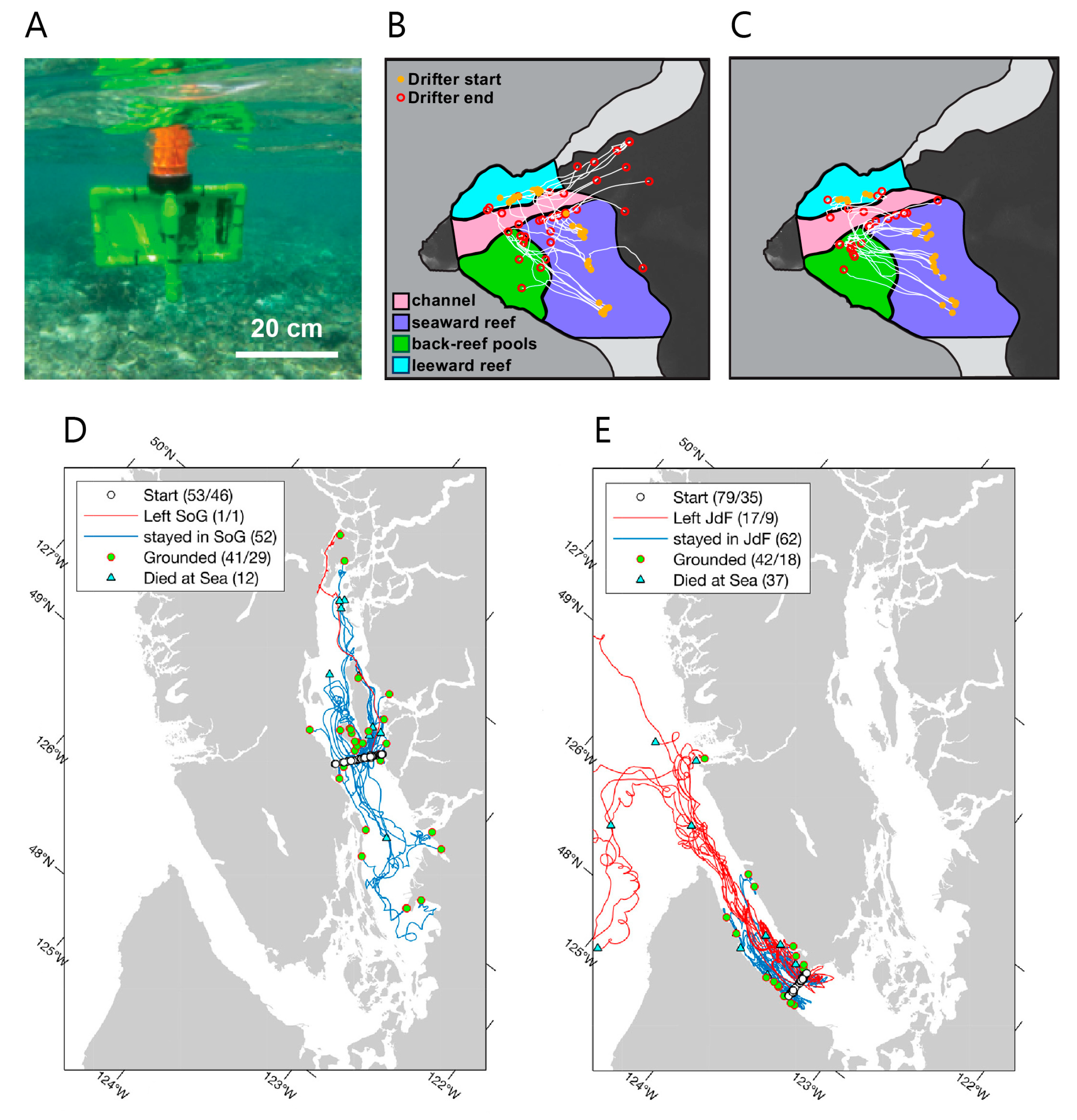
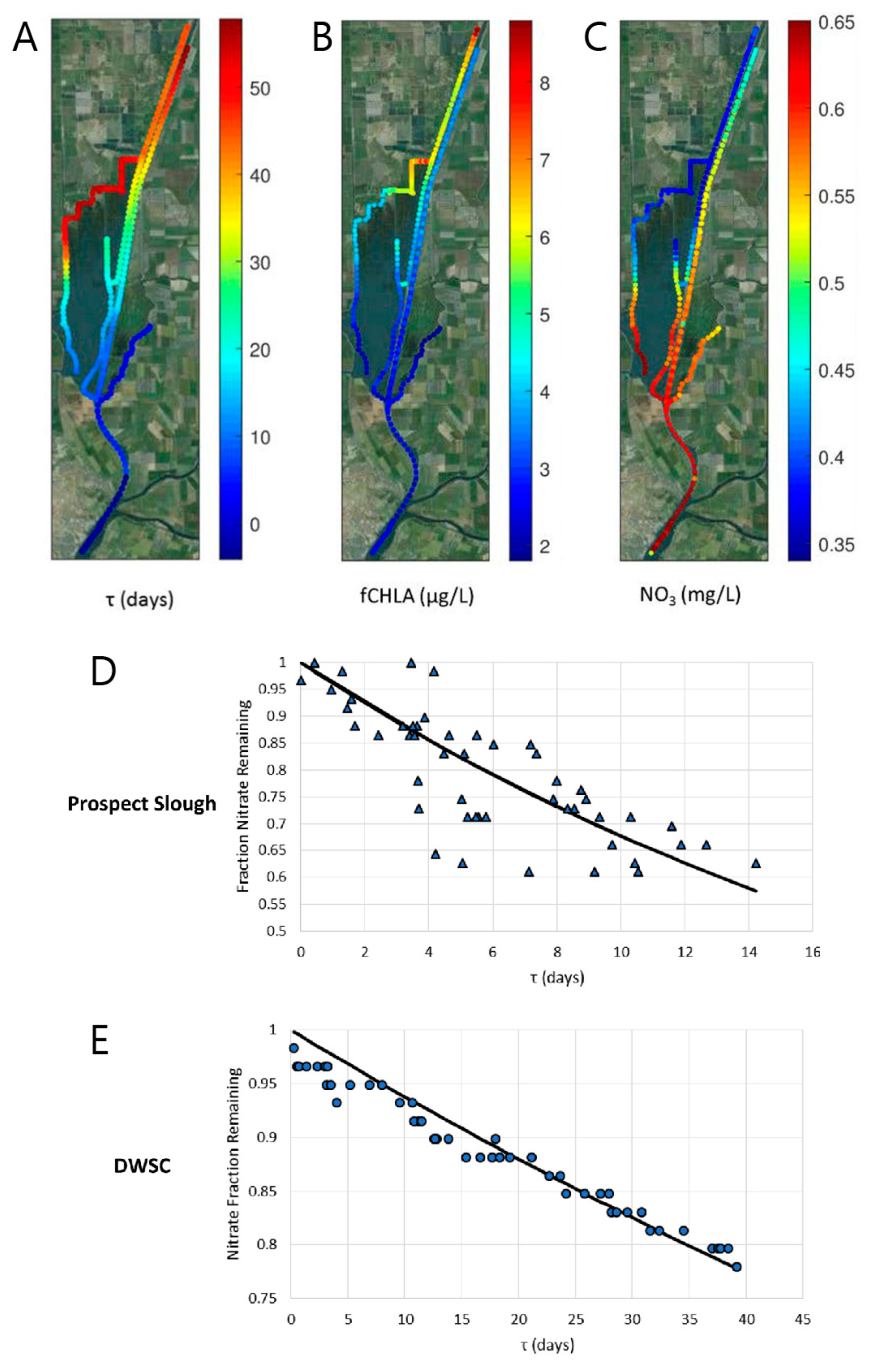
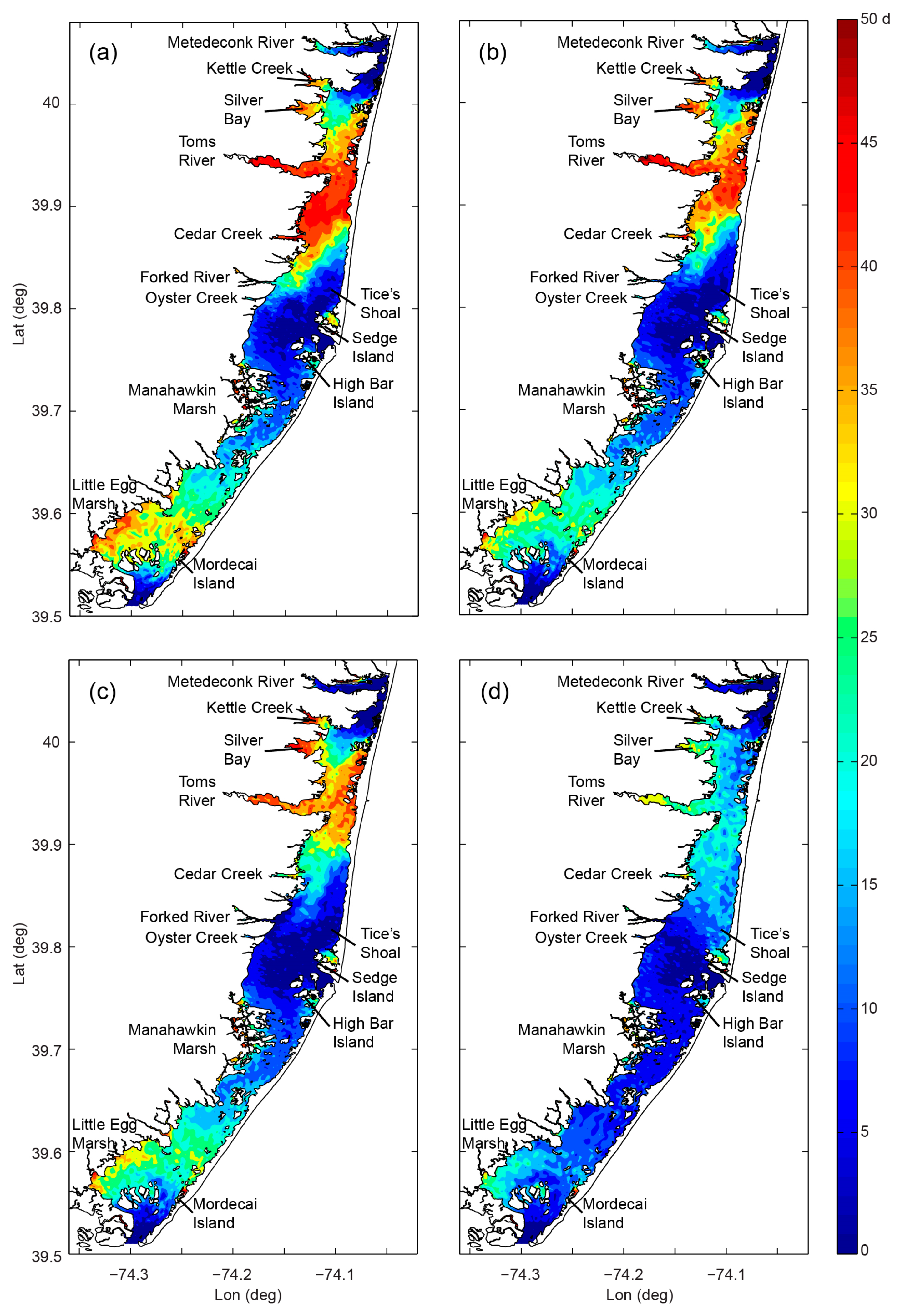

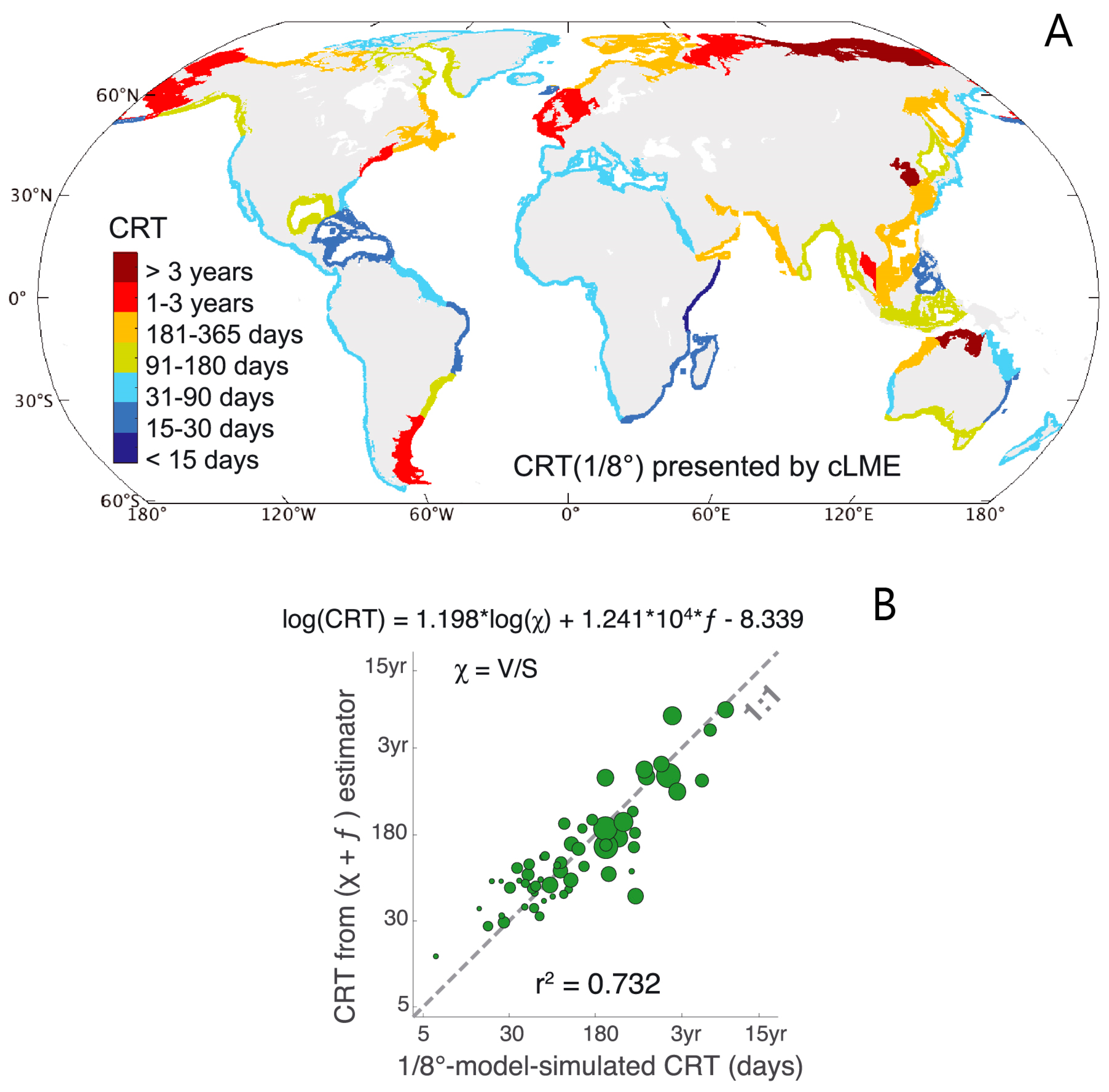

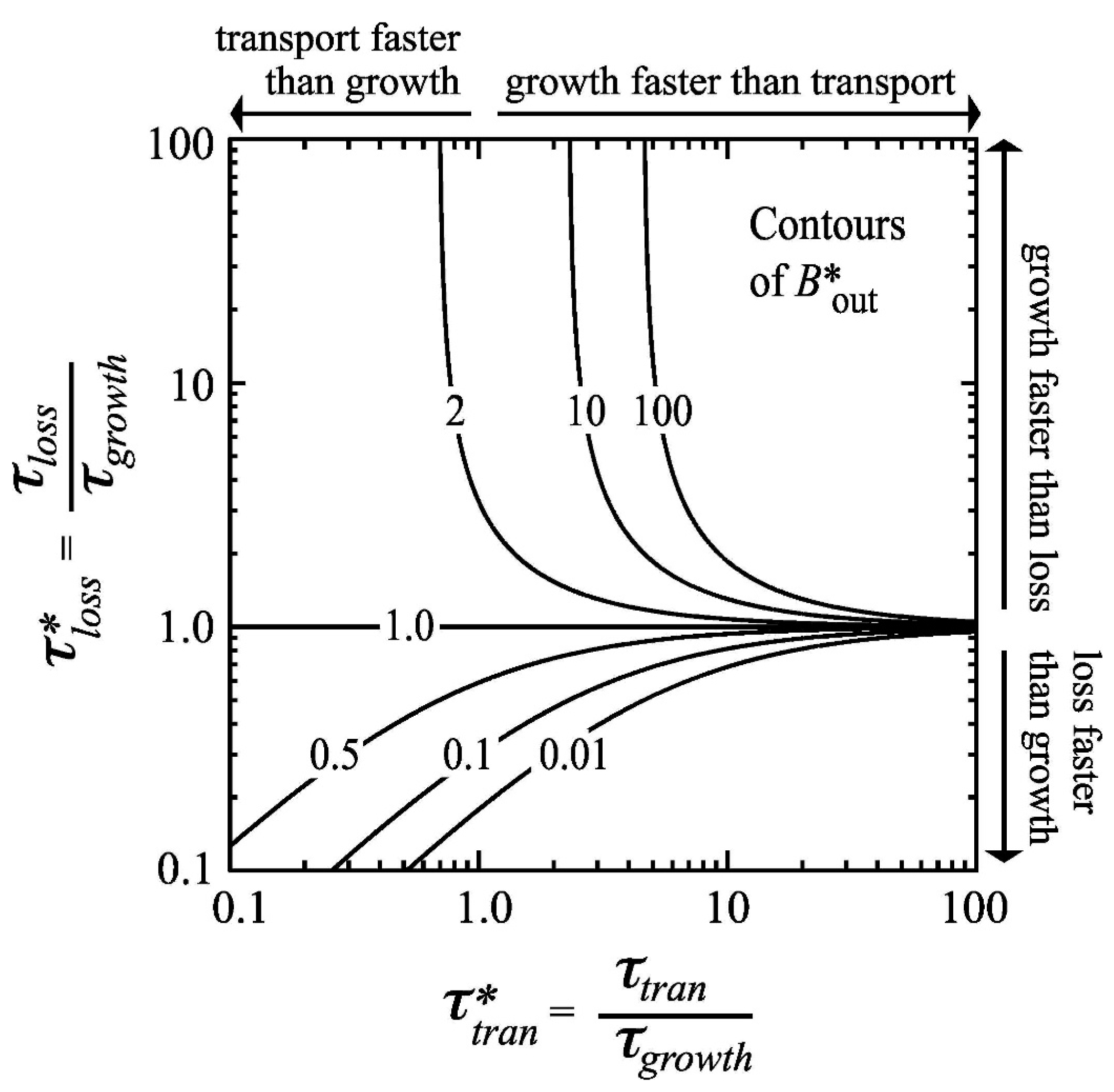

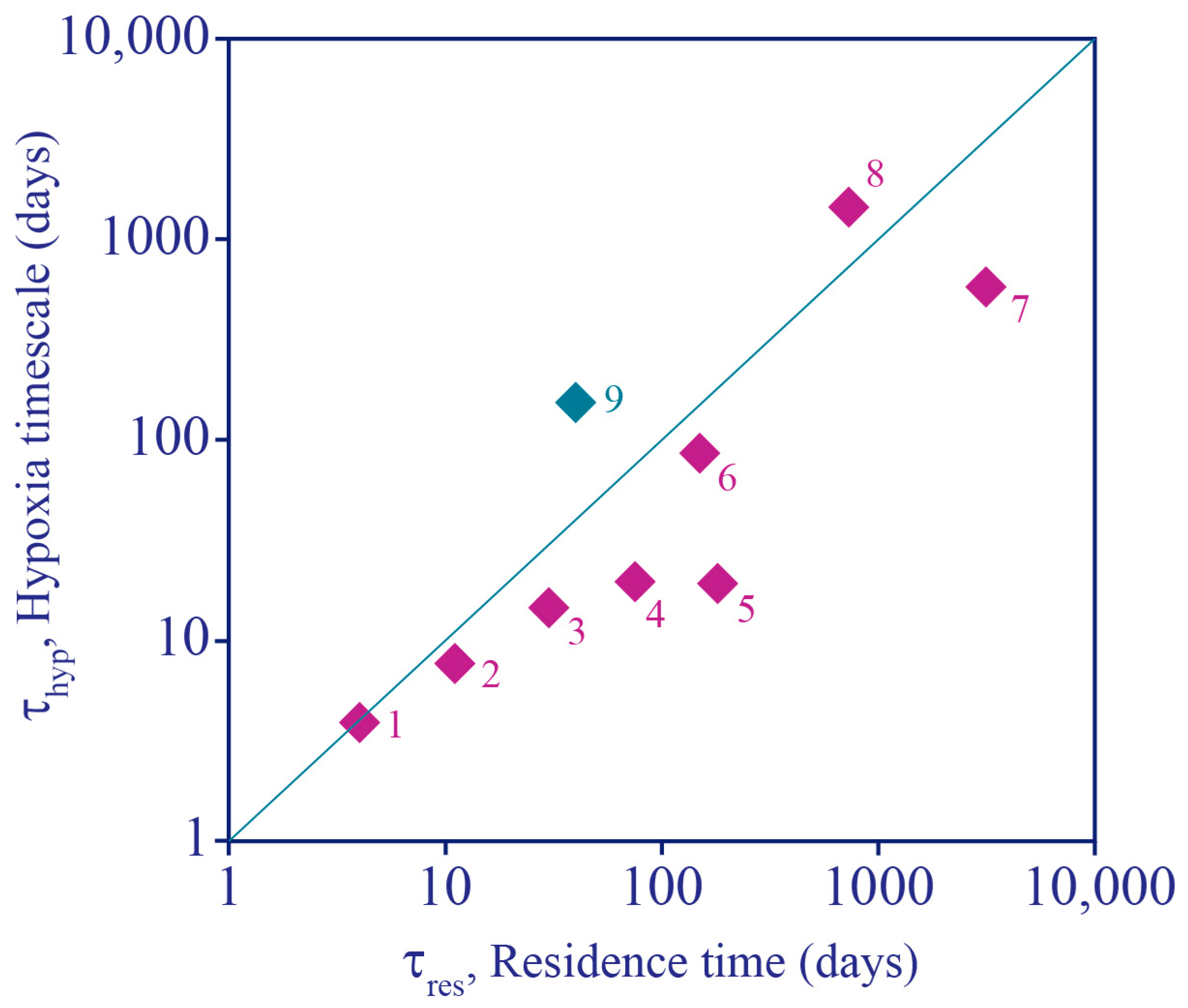
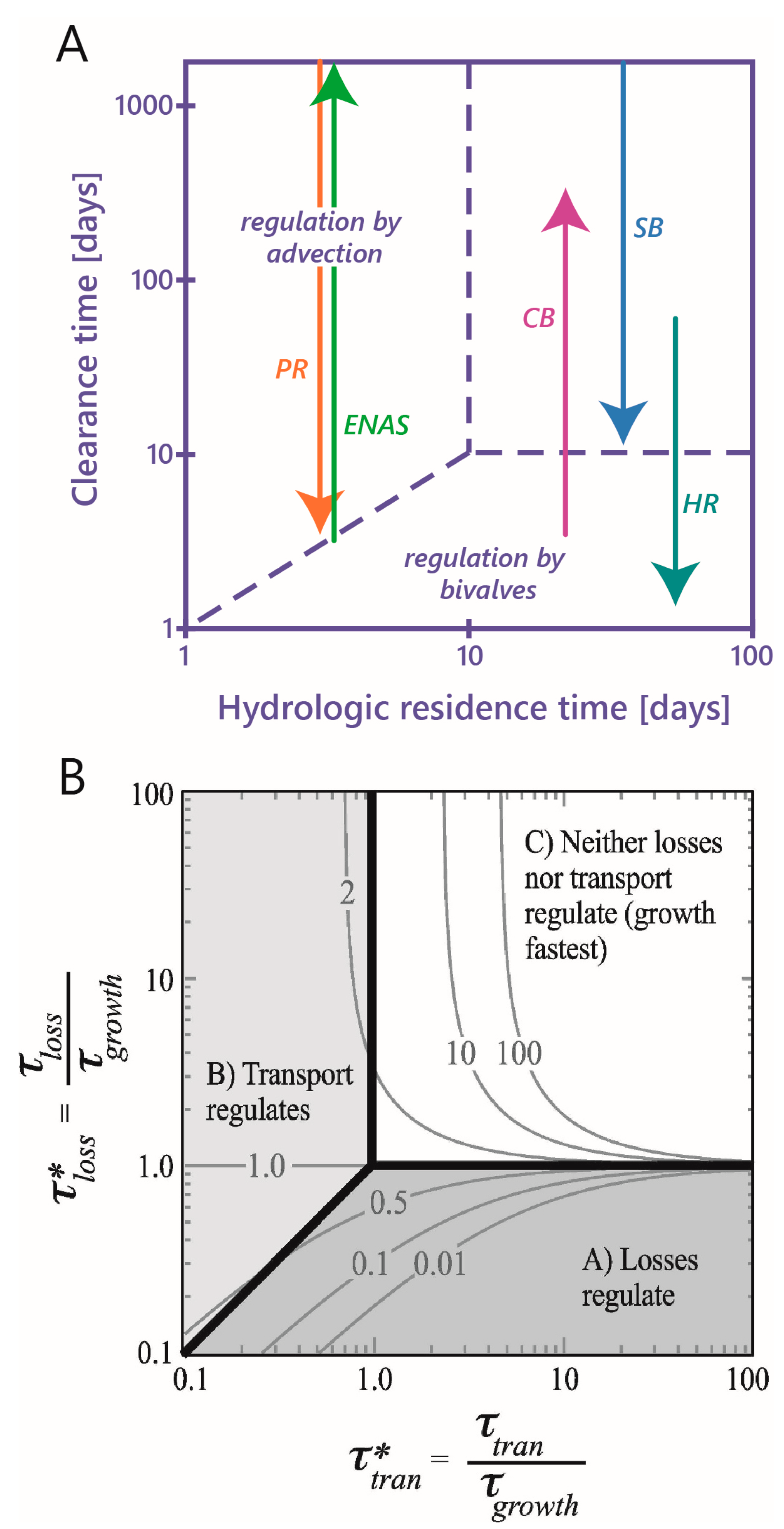
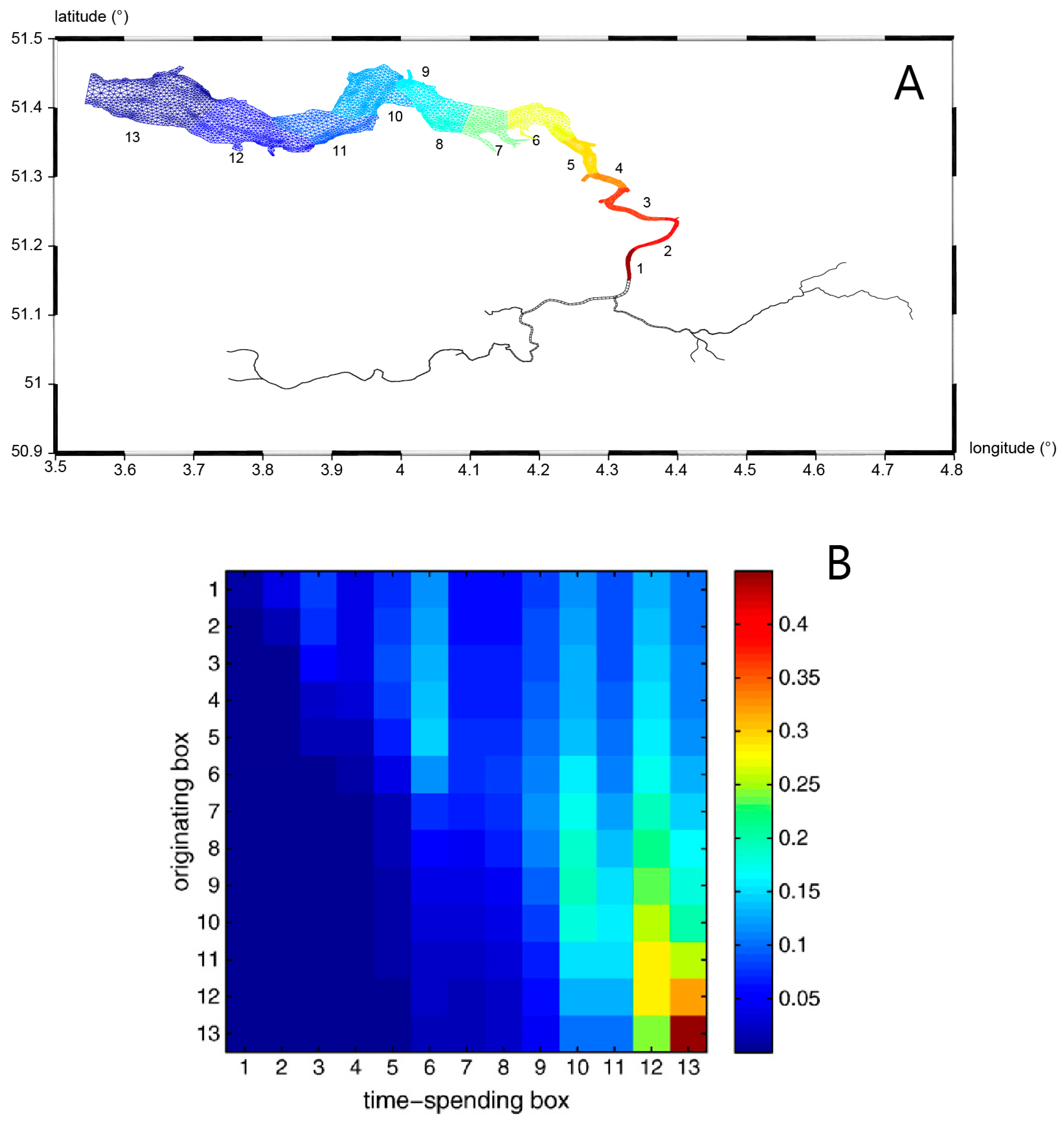
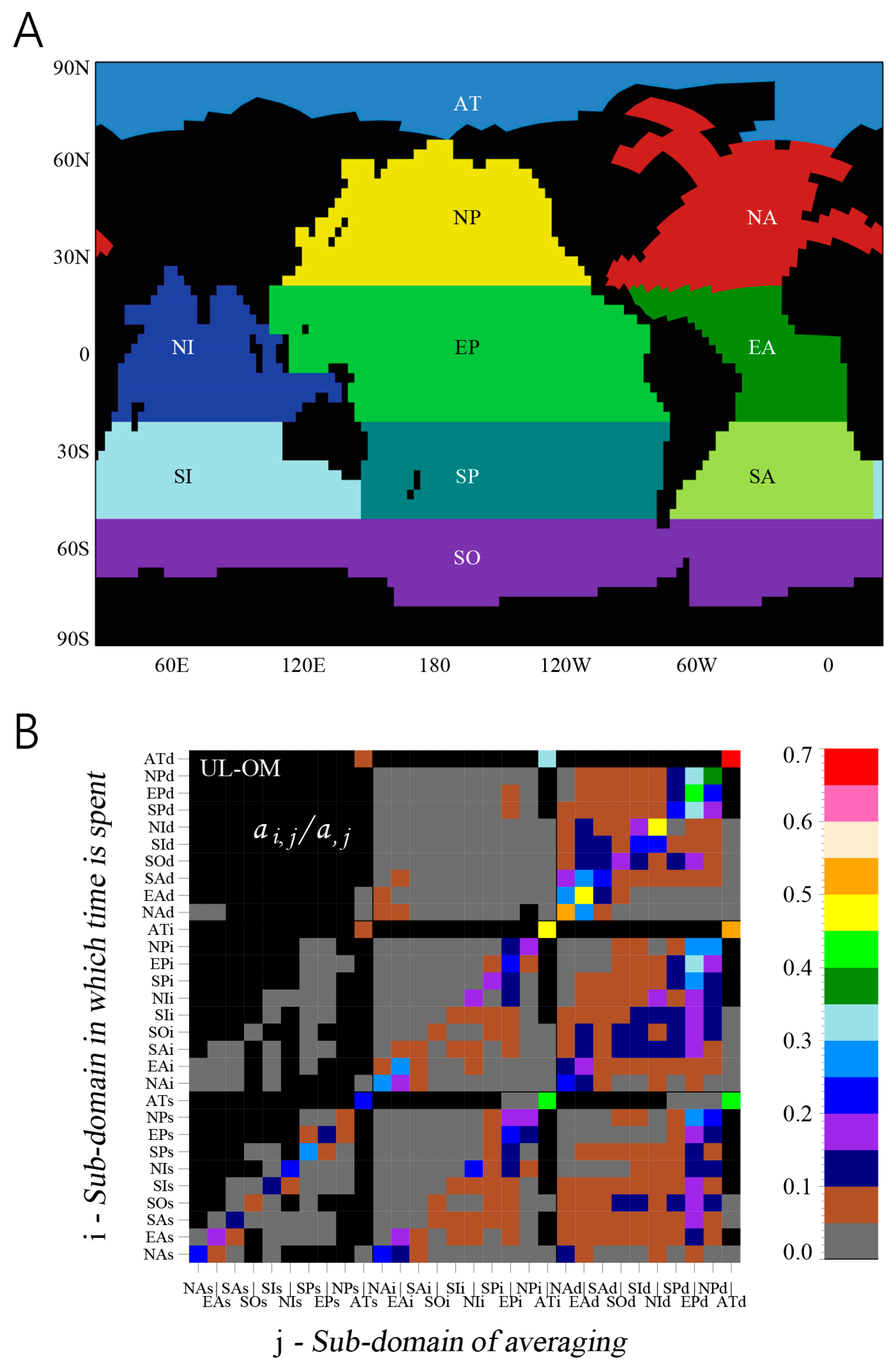
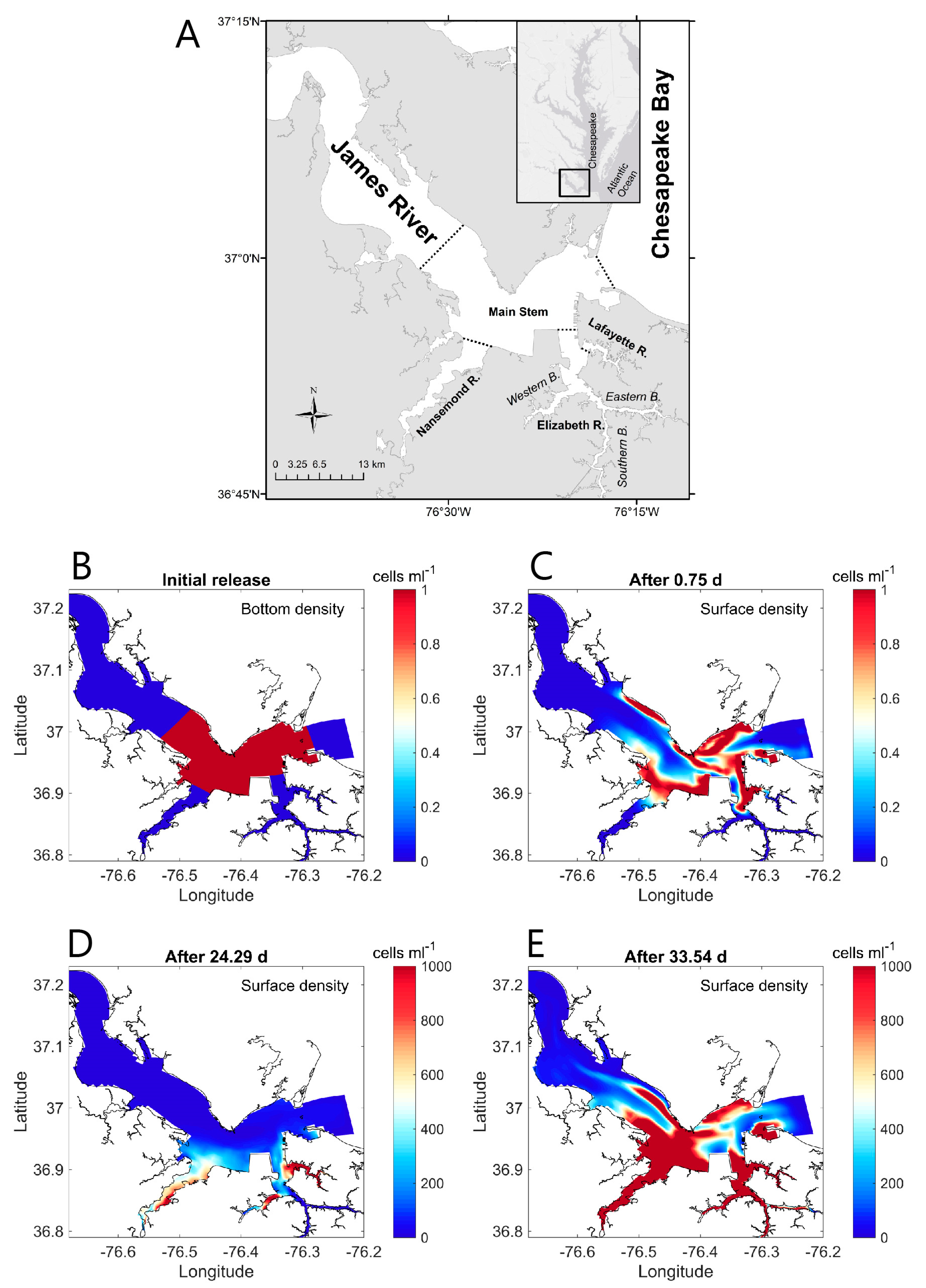
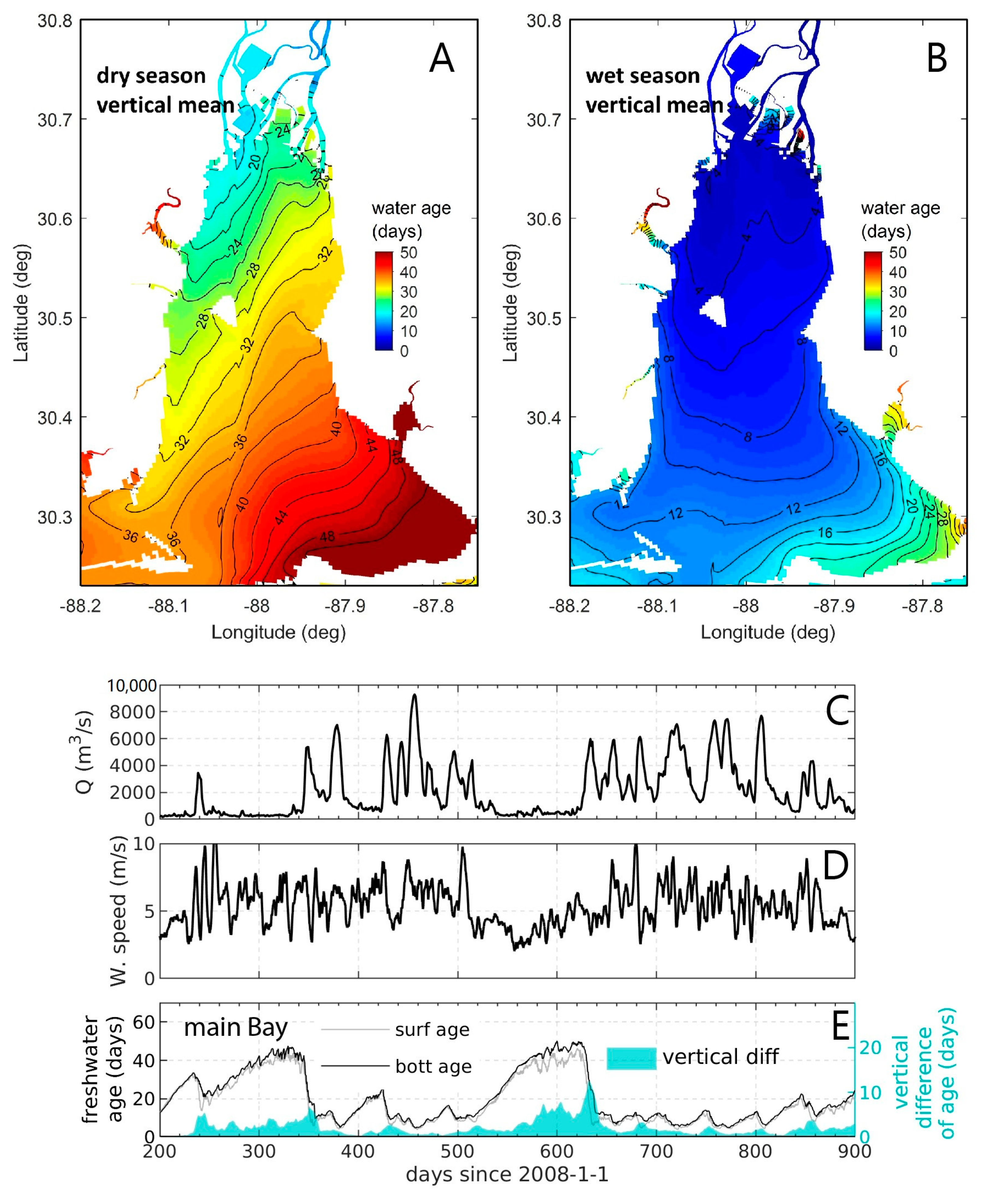
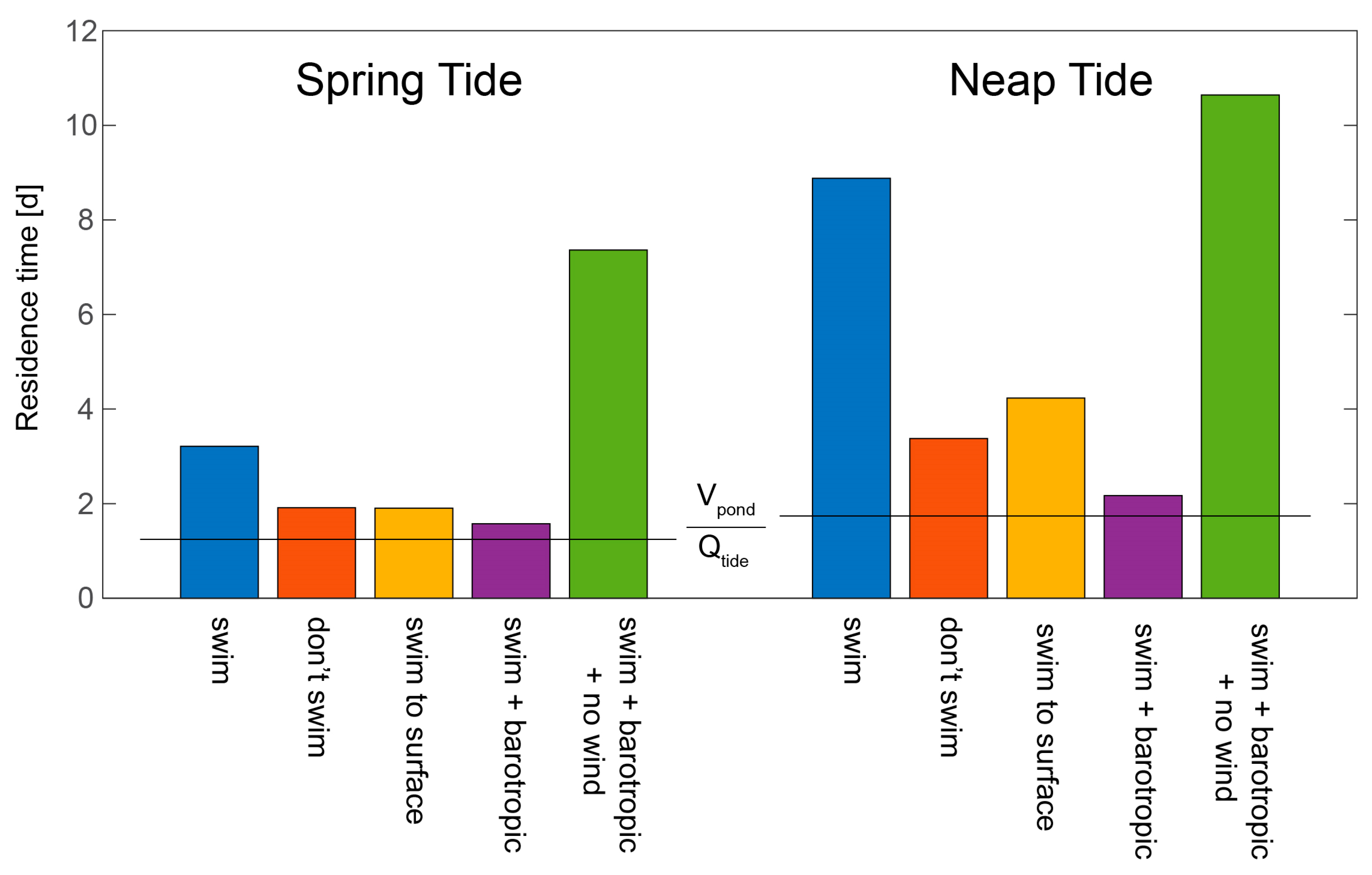
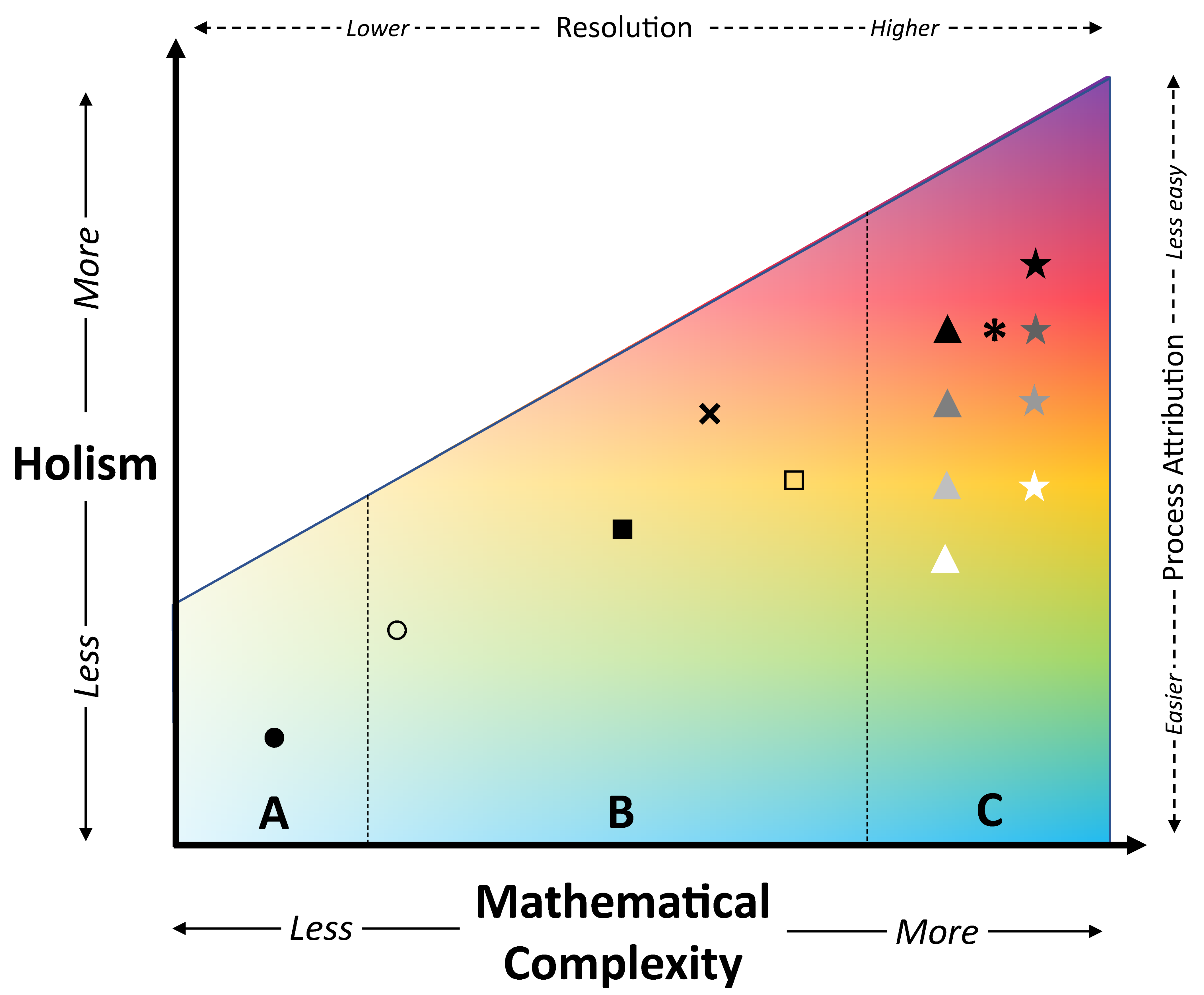
| Process | Native Process Rate | Units | Timescale | Relevant Citations |
|---|---|---|---|---|
| Diffusion/Dispersion/Mixing | Diffusion/Dispersion/Mixing Coefficient (K) | length2/time | L2/K | [42,49,52,59,147] |
| Advection | Velocity (U) | length/time | L/U | [23,49,59] |
| Flushing by river flow | Volumetric flow rate (Q) | length3/time | V/Q | [87] |
| Flushing by scalar flux | Mass flux rate (F) | mass/time | M/F | [42] |
| 1 Growth or decay | Specific growth or decay rate (μ) | 1/time | 1/|μ| | [25] |
| 2 Decay by one-half | Specific decay rate (μdecay) | 1/time | ln(2)/μdecay | [125] |
| 3 Growth by factor of 2 | Specific growth rate (μgrowth) | 1/time | ln(2)/μgrowth | [127] |
| Sinking/settling | Sinking speed (w) | length/time | Lz/w | [59,60] |
| 4 Productivity | Areal Productivity (Pa) | biomass/(length2-time) | Ba/Pa | [125] |
| 4 Benthic consumption | Grazing/Filtration/Clearance rate (BG) | length3/(length2-time) | Lz/BG | [23,25,62,124] |
| Zooplankton grazing | Zooplankton community grazing rate (ZG) | biomass/(length3-time) | Bp/ZG | [23,148] |
| Oxygen consumption | Net oxygen consumption rate (CDO) | mass O2/(length3-time) | DO/CDO | [21,132] |
| 4 Nutrient uptake | Nutrient uptake rate (υ) | mass nutrient/(length3-time) | η/υ | [90] |
| Author(s) | Water Body | Time Period/Conditions | Timescale(approach) | Value | |
|---|---|---|---|---|---|
| Jouon et al. [112] | SW lagoon of New Caledonia | Constant, moderate trade wind | V/Q 1 | 6.8 d | 2 |
| Mean residence time 2 | 10.8 d | ||||
| e-folding 3 | 11.4 d | ||||
| Lemagie and Lerczak [110] | Yaquina Bay (USA) | Q = 10 m3/s, Ao = 125 cm | TEF 1,4 | 3.96 tc | 26 |
| Tidal prism 1,4 | 1.27 tc | ||||
| Freshwater fraction 1,4 | 12.63 tc | ||||
| Transit (e-folding) 2,4 | 32.6 tc | ||||
| Flushing (e-folding) 2,4 | 5.16 tc | ||||
| Monsen et al. [87] | Mildred Island (USA) | June 1999 (low flow) | V/Q 5 | 31-50 d | 17–28 |
| e-folding 6 | 7.7 d | ||||
| 7 | 8.3–9.1 d | ||||
| Mean age 6,8 | 1.8 d | ||||
| Oveisy et al. [147] | Bay of Quinte (Canada) | Summer 2004 | e-folding 3,10 | 44 d | 14 |
| V/Q 1,9,11 | 64 d | ||||
| Residence time 2,10 | 52 d | ||||
| Dispersion 3,10 | 1.7 y | ||||
| Rayson et al. [100] | Galveston Bay (USA) | Mid–late April 2009 (peak flow) | Freshwater fraction 1 | ~10 d | 2 |
| TEF 1,12 | ~20 d | ||||
| Mean residence time 2,12 | ~20 d | ||||
| e-folding 2,12 | ~20 d | ||||
| Mean age 3,12 | ~20 d | ||||
| Rayson et al. [100] | Galveston Bay (USA) | Late July 2009 (low flow) | Freshwater fraction 1,12 | ~200 d | 10 |
| TEF 1,12 | ~20 d | ||||
| Mean residence time 2,12 | ~25 d | ||||
| e-folding 2,12 | ~50 d | ||||
| Mean age 3,12 | ~30 d | ||||
| Tartinville et al. [113] | Mururoa atoll Lagoon (French Polynesia) | Tides, wind, hoa inflow, stratification | L/U 1 | 8.3 d | 1113 |
| L/U’ 1 | 5.3 d | ||||
| Diffusion 13 | 5900 d | ||||
| e-folding 2 | 114 d |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lucas, L.V.; Deleersnijder, E. Timescale Methods for Simplifying, Understanding and Modeling Biophysical and Water Quality Processes in Coastal Aquatic Ecosystems: A Review. Water 2020, 12, 2717. https://doi.org/10.3390/w12102717
Lucas LV, Deleersnijder E. Timescale Methods for Simplifying, Understanding and Modeling Biophysical and Water Quality Processes in Coastal Aquatic Ecosystems: A Review. Water. 2020; 12(10):2717. https://doi.org/10.3390/w12102717
Chicago/Turabian StyleLucas, Lisa V., and Eric Deleersnijder. 2020. "Timescale Methods for Simplifying, Understanding and Modeling Biophysical and Water Quality Processes in Coastal Aquatic Ecosystems: A Review" Water 12, no. 10: 2717. https://doi.org/10.3390/w12102717
APA StyleLucas, L. V., & Deleersnijder, E. (2020). Timescale Methods for Simplifying, Understanding and Modeling Biophysical and Water Quality Processes in Coastal Aquatic Ecosystems: A Review. Water, 12(10), 2717. https://doi.org/10.3390/w12102717






