The GEOframe-NewAge Modelling System Applied in a Data Scarce Environment
Abstract
1. Introduction
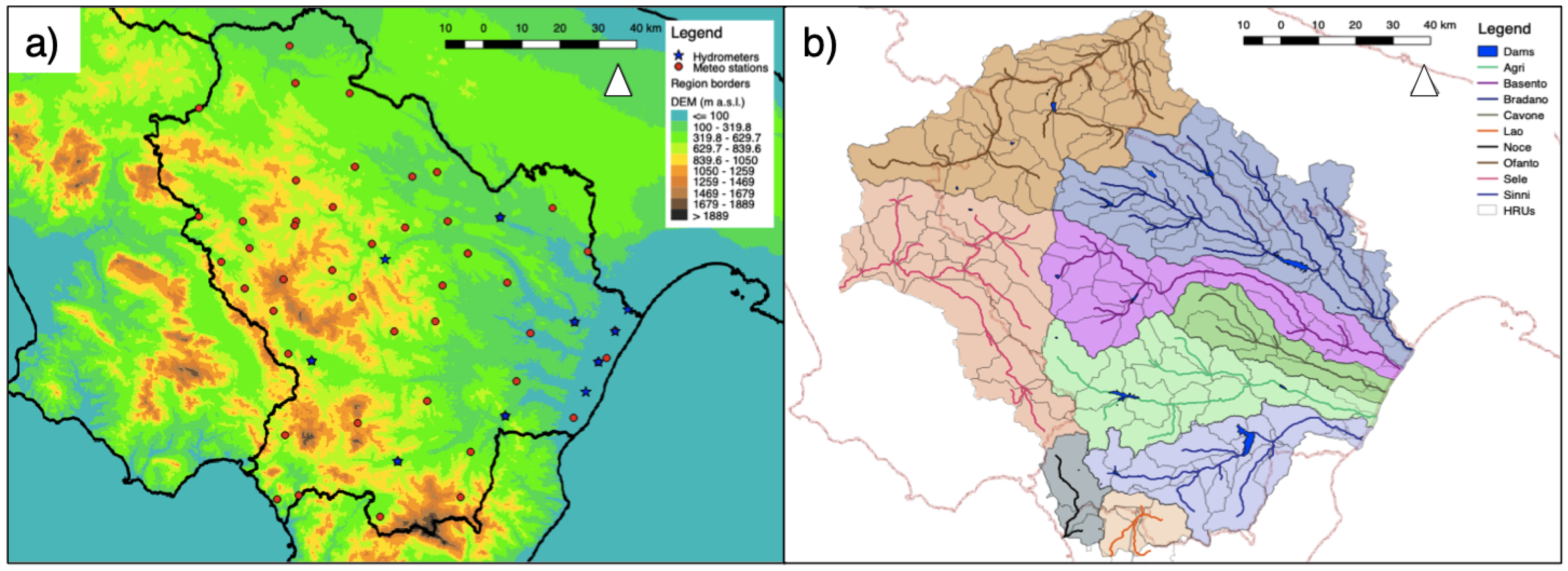
2. Case Study
- San Giuliano, Acerenza, Genzano, and Basentello on the Bradano River;
- Pertusillo and Marsico Nuovo on the Agri River;
- Monte Cotugno on the Sinni River;
- Rendina on the Ofanto River;
- Camastra on the Basento River.
3. Methodology
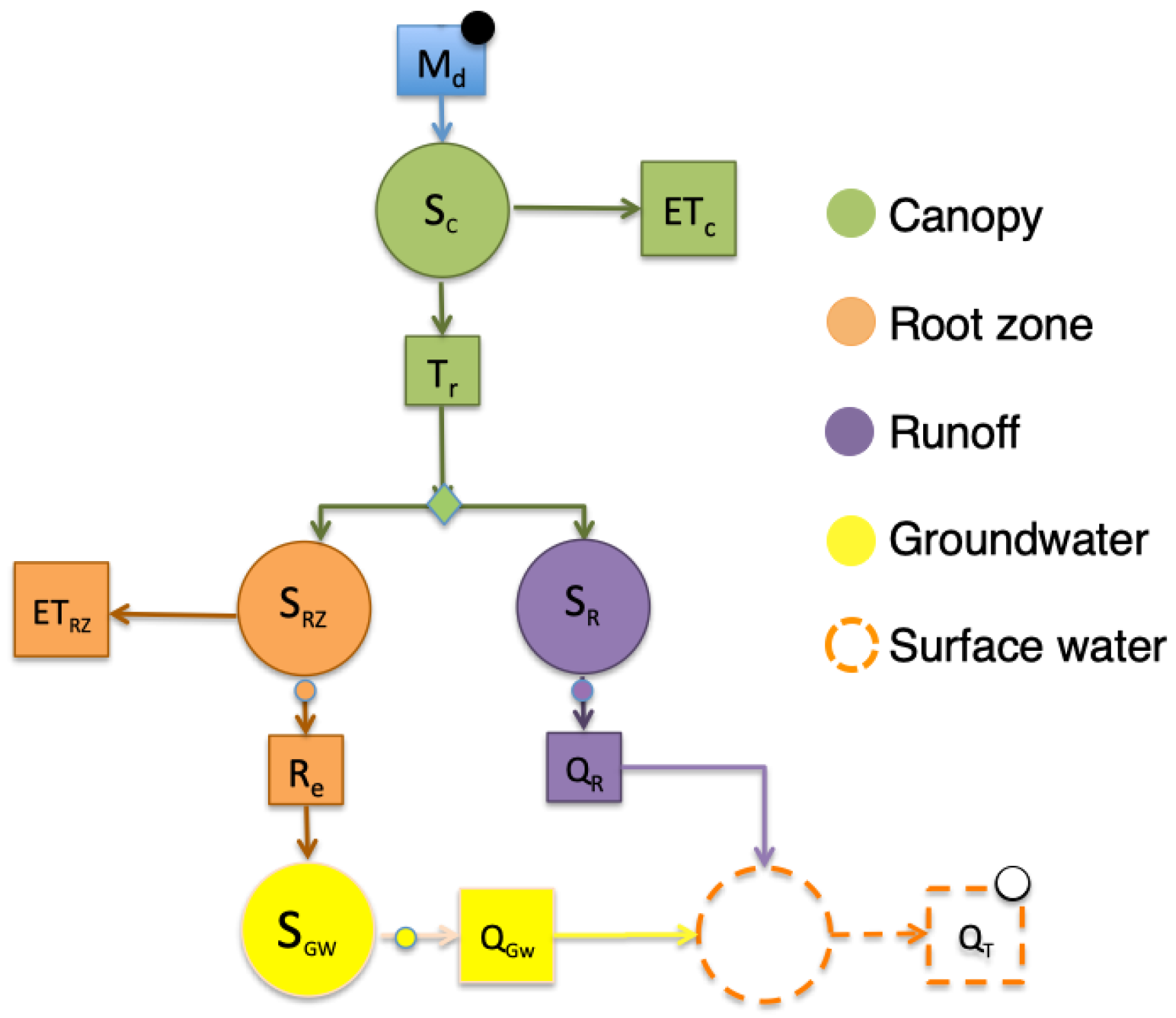
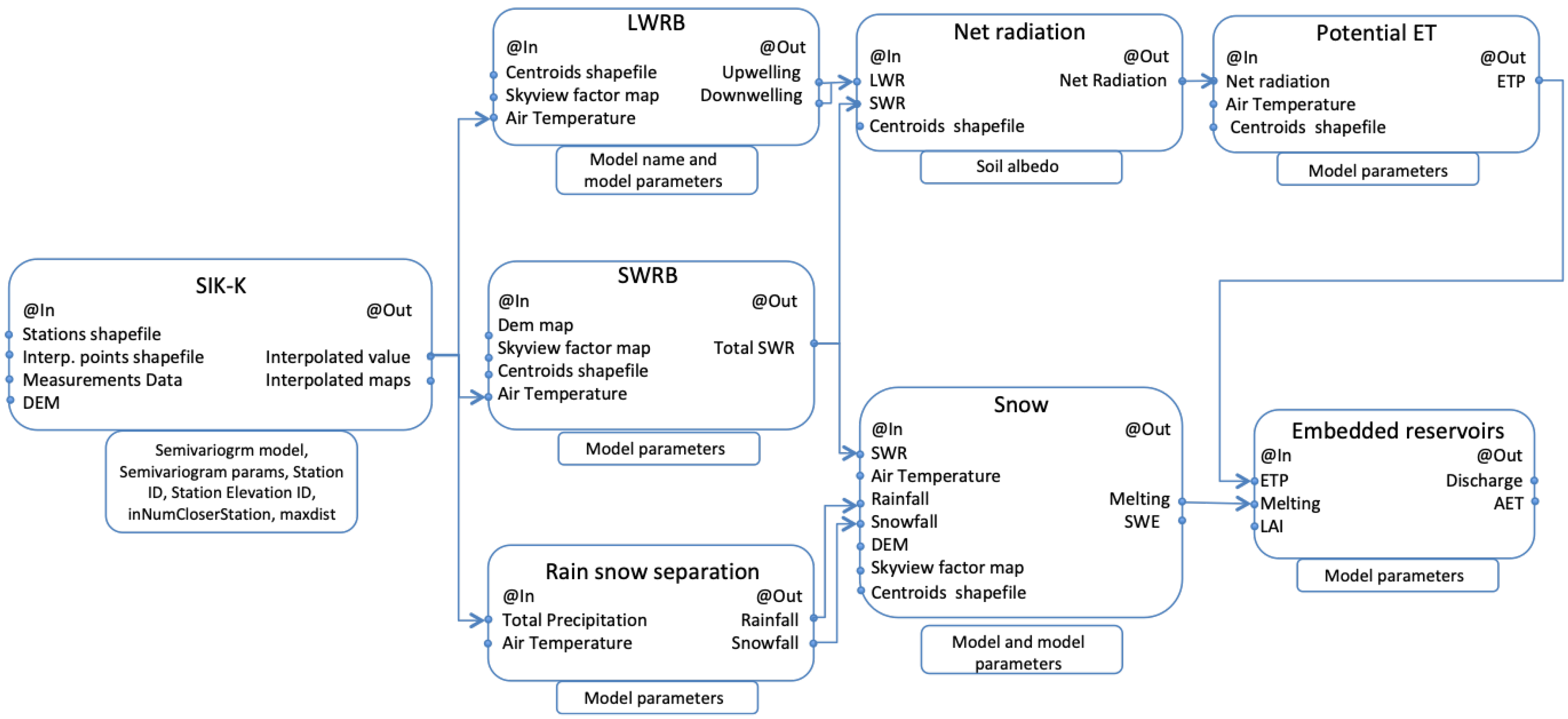
3.1. GEoframe-NewAGE and the NET3 Graph
- Geomorphic and DEM analyses;
- Spatial extrapolation/interpolation of meteorological variables;
- Estimation of the radiation budget;
- Estimation of evapotranspiration;
- Estimation of runoff production;
- Simulation of infiltration;
- Channel routing;
- Travel time analysis;
- Calibration algorithms.
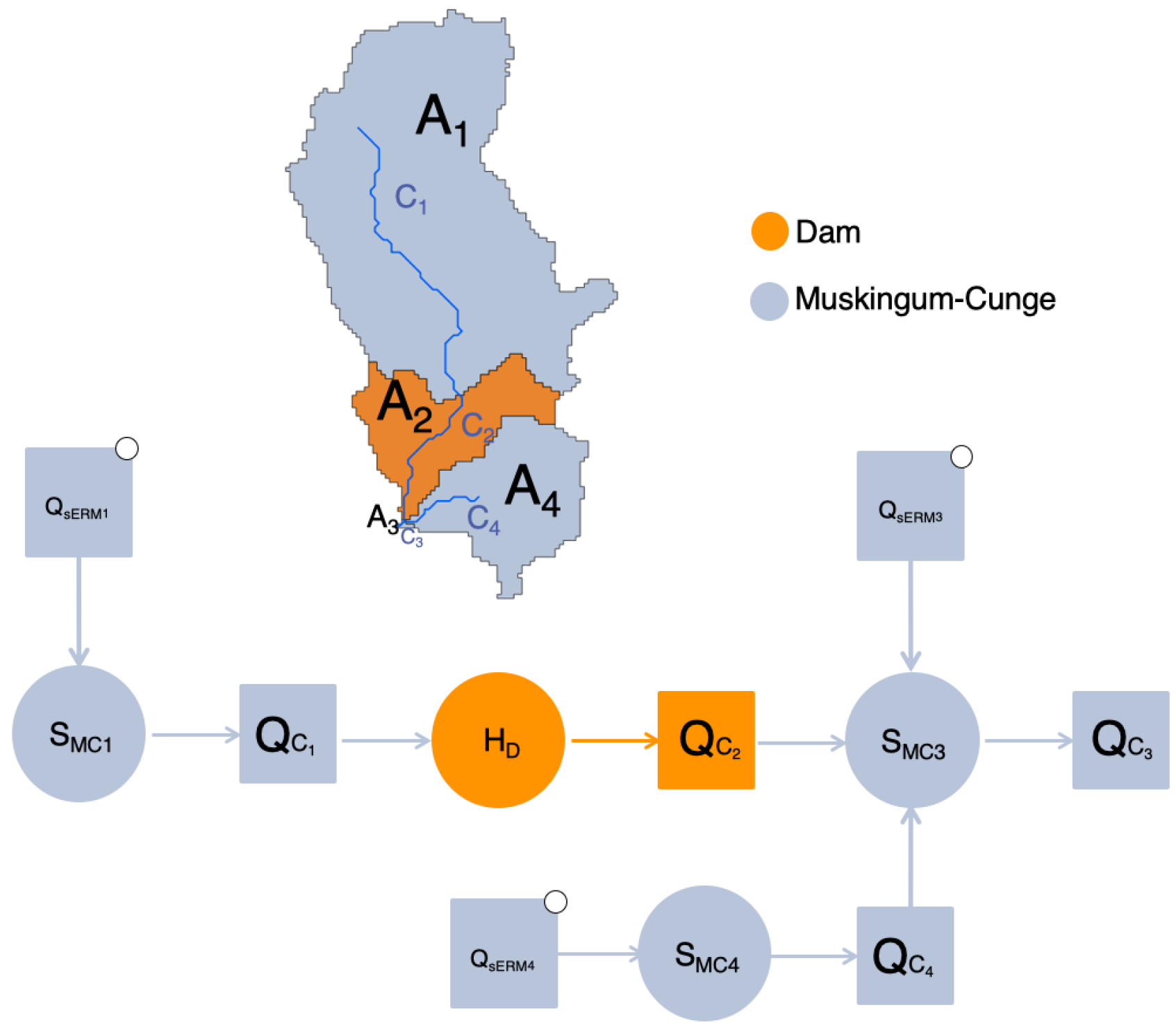
Simplified Embedded Reservoir Model
- the possibility to consider several representations of spatial variability and hydrologic connectivity;
- the possibility to simulate a broad range of hydrologic processes, with multiple options for individual processes.
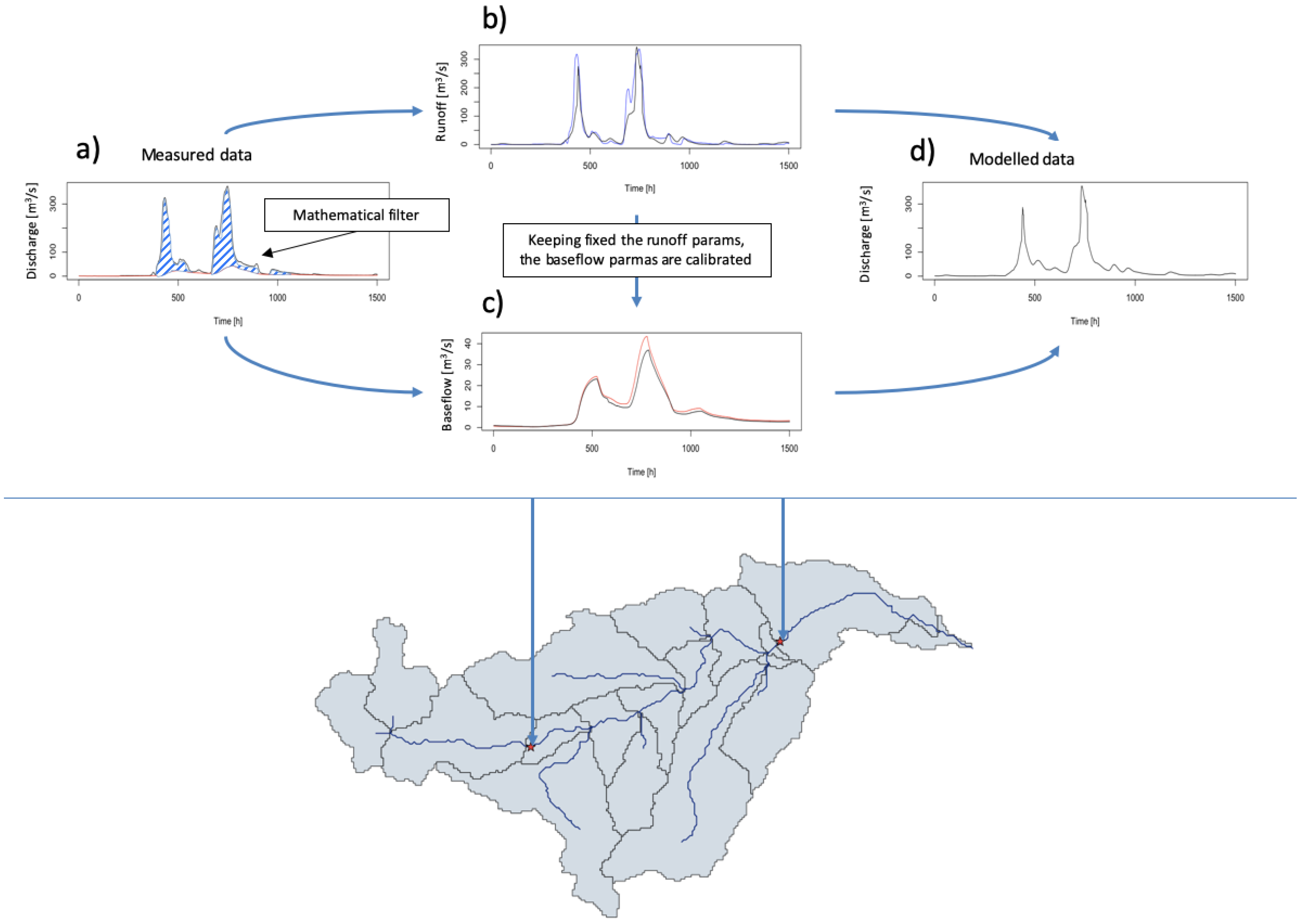
3.2. Calibration Strategies in a Data-Scarce Environment
- from the hourly total discharge, the baseflow was extracted using a mathematical filter, which connected the local minima (Figure 3a, red line);
- the runoff was extracted by subtracting the baseflow from the hourly total discharge (Figure 3a, blue line);
- the parameters of the root zone and runoff reservoirs were calibrated against the extracted runoff (Figure 3b);
- with the root zone and runoff reservoir maintaining fixed calibrated parameters, the parameters of the groundwater reservoir were calibrated against the extracted baseflow (Figure 3c);
- finally, the calibrated parameters previously obtained were further optimized against the hourly total discharge (Figure 3d).
3.3. Model Setup
3.3.1. HRU Scale
3.3.2. Catchment Scale
- Stage;
- Volumes;
- Inflows;
- Precipitation;
- Spillway volumes;
- Restitution downstream.
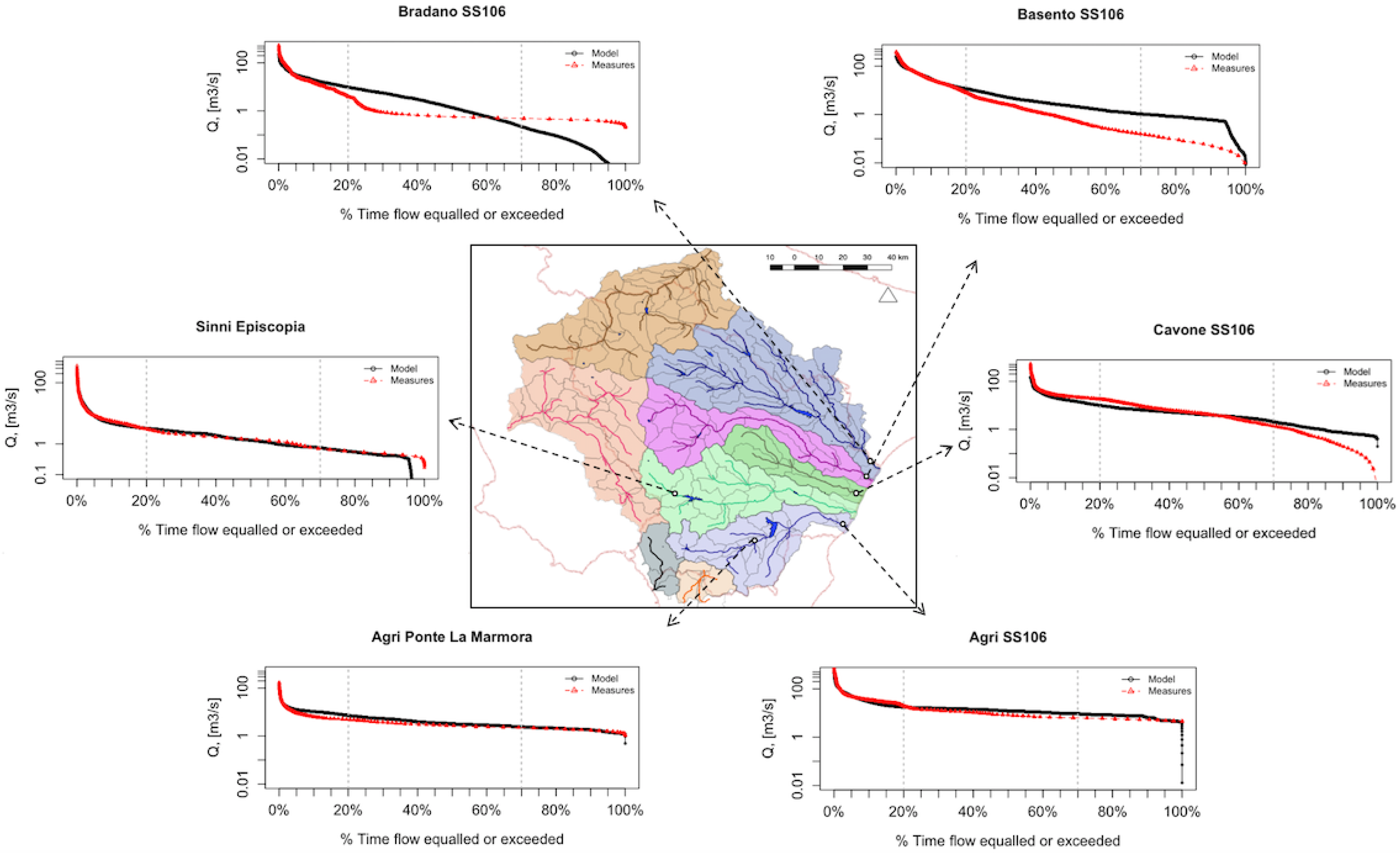
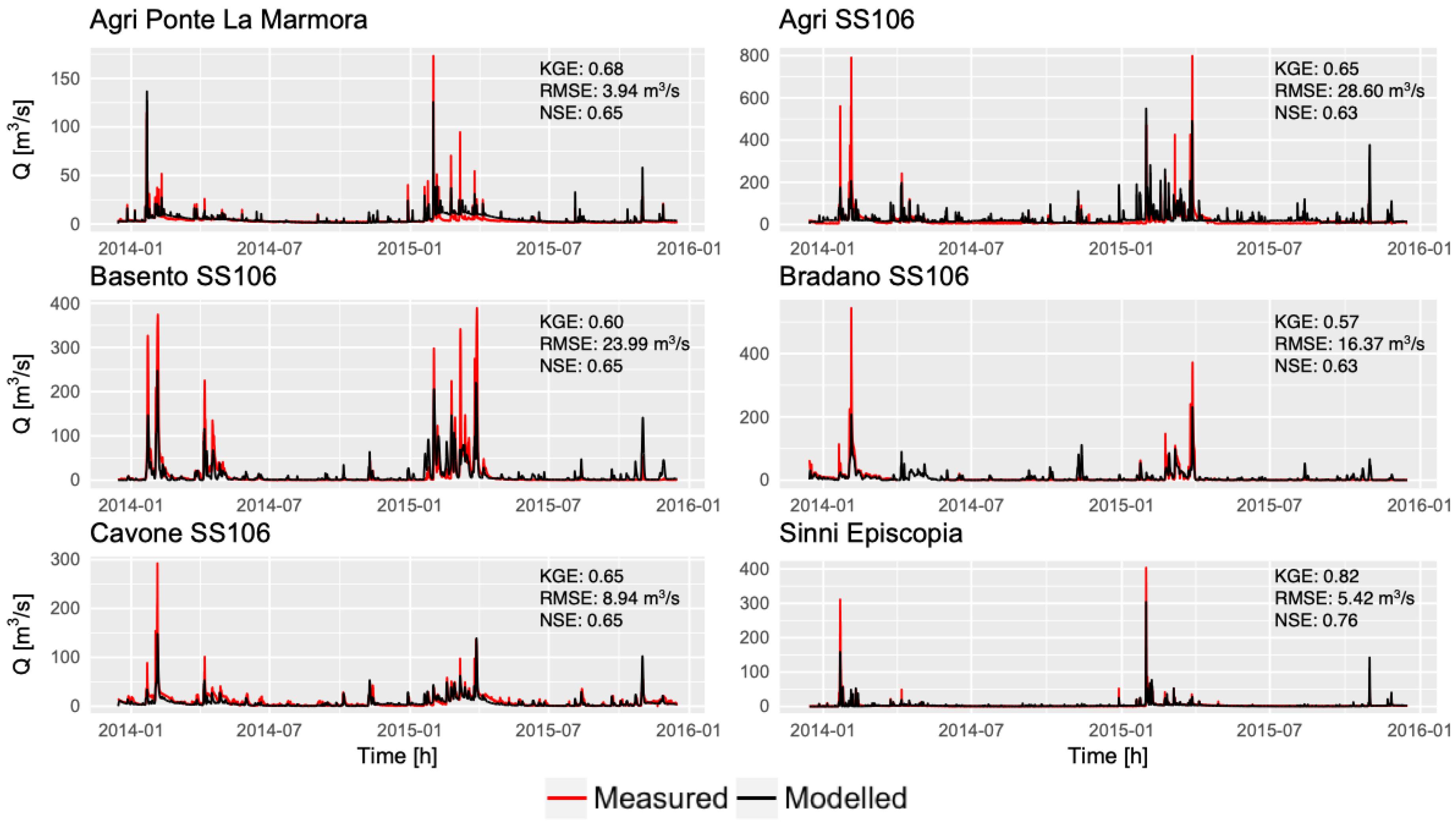
4. Results and Discussion
5. Conclusions
- the extraction of the flow-rating curves using a novel approach based on the velocity and wetted area measurements;
- the multi-calibrations versus the different components of the discharge, i.e., the runoff and the groundwater;
- the multi-site calibration in different closure sections, when available.
Author Contributions
Funding
Conflicts of Interest
Appendix A. The Early Warning System of the Basilicata Region
- The cumulative precipitation of the last 120 h (as recorded by the meteorological network) is spatialized using the inverse distance weighting method [68];
- The GRIB files with the forecasts are downloaded and pre-processed;
- For each duration (3, 6, 12, 18, 24, 48, 72, 96, 120 h), from the current time to the next 36 h, the DSS checks whether the threshold has been exceeded. Recorded precipitation and forecasts are accumulated for a time span of 3 h and compared with the critical values. If a threshold has been exceeded, then the area receives a critical alert level, and the related map is produced;
- A map with the highest expected criticality is produced for the following 12 and 36 h;
- The temperature data are downloaded from the sensor network and the LAI map is obtained from the MODIS satellite [69];
- GEOframe-NewAge is run to obtain the 36-h discharge and stage forecasts for each node of the network, considering the running conditions;
- A saturation degree map is produced for the current time;
- The expected stages are compared with thresholds with an assigned return time to verify final hydrological criticalities;
- A historical dataset of discharges and stages is updated, which is required for the definition of the running conditions for the simulation in the next hour.
Appendix B. The Budyko Model
Appendix C. The Flow Rating Curves Adopted
| Station | Method | FRC Expression | (cm) |
|---|---|---|---|
| Agri Ponte La Marmora | VA | ||
| Agri SS 106 | VA | ||
| Basento SS 106 | QH | ||
| Bradano SS 106 | VA | ||
| Cavone SS 106 | QH | ||
| Sinni Episcopia | VA |
Appendix D. Error Metrics Adopted
- Kling–Gupta efficiencyThe Kling–Gupta Efficiency (KGE) incorporates three different statistical measures (the correlation coefficient, r; the variability error, a ; and the bias error, b = ) of the relation between measured and simulated data into one objective function. and are the mean values of measured and simulated data, while and are the standard deviations.KGE = 1 indicates the maximum agreement between predicted and observed values.
- Nash–Sutcliffe efficiencyThe Nash–Sutcliffe Efficiency (NSE) is a normalized model efficiency coefficient. It determines the relative magnitude of the residual variance compared with the measured data variance.where and are the predicted and observed values at a given time step. The NSE varies from to 1, where 1 corresponds to the maximum agreement between predicted and observed values.
- Root-Mean-Square ErrorThe Root-Mean-Square Error (RMSE) is given bywhere M and S represent the measured and simulated time-series, respectively, and N is the number of components in the series.
- Percent BiasThe Percent Bias (PBIAS) measures the average tendency of the simulated values to overestimate (positive values) or underestimate (negative values) the observed values. PBIAS is given bywhere M and S represent the measured and simulated time-series, respectively, and N is the number of components in the series.
References
- Chen, W.; He, B.; Ma, J.; Wang, C. A WebGIS-based flood control management system for small reservoirs: A case study in the lower reaches of the Yangtze River. J. Hydroinform. 2016, 19, 299–314. [Google Scholar] [CrossRef]
- Shi, H.; Li, T.; Liu, R.; Chen, J.; Li, J.; Zhang, A.; Wang, G. A service-oriented architecture for ensemble flood forecast from numerical weather prediction. J. Hydrol. 2015, 527, 933–942. [Google Scholar] [CrossRef]
- Al-Sabhan, W.; Mulligan, M.; Blackburn, G.A. A real-time hydrological model for flood prediction using GIS and the WWW. Comput. Environ. Urban Syst. 2003, 27, 9–32. [Google Scholar] [CrossRef]
- Sivapalan, M.; Takeuchi, K.; Franks, S.; Gupta, V.; Karambiri, H.; Lakshmi, V.; Liang, X.; McDonnell, J.; Mendiondo, E.; O’connell, P.; et al. IAHS Decade on Predictions in Ungauged Basins (PUB), 2003–2012: Shaping an exciting future for the hydrological sciences. Hydrol. Sci. J. 2003, 48, 857–880. [Google Scholar] [CrossRef]
- Shi, H.; Li, T. Estimating hydrological parameters based on rainfall patterns in river basins with no long-term historical observations. J. Hydrol. 2017, 553, 651–661. [Google Scholar] [CrossRef]
- Blöschl, G.; Sivapalan, M.; Savenije, H.; Wagener, T.; Viglione, A. Runoff Prediction in Ungauged Basins: Synthesis across Processes, Places and Scales; Cambridge University Press: Cambridge, UK, 2013. [Google Scholar]
- Blöschl, G. Predictions in ungauged basins—Where do we stand? Proc. Int. Assoc. Hydrol. Sci. 2016, 373, 57–60. [Google Scholar]
- Wanders, N.; Karssenberg, D.; Roo, A.D.; De Jong, S.; Bierkens, M. The suitability of remotely sensed soil moisture for improving operational flood forecasting. Hydrol. Earth Syst. Sci. 2014, 18, 2343–2357. [Google Scholar] [CrossRef]
- Ruiz-Pérez, G.; González-Sanchis, M.; Del Campo, A.; Francés, F. Can a parsimonious model implemented with satellite data be used for modelling the vegetation dynamics and water cycle in water-controlled environments? Ecol. Model. 2016, 324, 45–53. [Google Scholar] [CrossRef]
- Manfreda, S.; Mita, L.; Dal Sasso, S.F.; Samela, C.; Mancusi, L. Exploiting the use of physical information for the calibration of a lumped hydrological model. Hydrol. Process. 2018, 32, 1420–1433. [Google Scholar] [CrossRef]
- Li, Y.; Grimaldi, S.; Pauwels, V.R.; Walker, J.P. Hydrologic model calibration using remotely sensed soil moisture and discharge measurements: The impact on predictions at gauged and ungauged locations. J. Hydrol. 2018, 557, 897–909. [Google Scholar] [CrossRef]
- Li, H.; Brunner, P.; Kinzelbach, W.; Li, W.; Dong, X. Calibration of a groundwater model using pattern information from remote sensing data. J. Hydrol. 2009, 377, 120–130. [Google Scholar] [CrossRef]
- De Lavenne, A.; Thirel, G.; Andréassian, V.; Perrin, C.; Ramos, M.H. Spatial variability of the parameters of a semi-distributed hydrological model. Proc. Int. Assoc. Hydrol. Sci. 2016, 373, 87–94. [Google Scholar] [CrossRef]
- Formetta, G.; Antonello, A.; Franceschi, S.; David, O.; Rigon, R. Hydrological modelling with components: A GIS-based open-source framework. Environ. Model. Softw. 2014, 55, 190–200. [Google Scholar] [CrossRef]
- Bancheri, M. A Flexible Approach to the Estimation of Water Budgets and Its Connection to the Travel Time Theory. Ph.D. Thesis, University of Trento, Trento, Italy, 2017. [Google Scholar]
- Clarke, M.; Rendell, H. Hindcasting extreme events: The occurrence and expression of damaging floods and landslides in Southern Italy. Land Degrad. Dev. 2006, 17, 365–380. [Google Scholar] [CrossRef]
- Lazzari, M. Note Illustrative Della Carta Inventario Delle Frane Della Basilicata Centroccidentale; Editore Zaccara: Lagonegro, Italy, 2011. [Google Scholar]
- Lazzari, M.; Piccarreta, M.; Manfreda, S. The role of antecedent soil moisture conditions on rainfall-triggered shallow landslides. Nat. Hazards Earth Syst. Sci. 2018. [Google Scholar] [CrossRef]
- Vita, M.; Gerardi, M.; Vecchio, G.L. La gestione della risorsa idrica in Basilicata. Geol. Territ. Ambiente 2010, 16, 10–16. [Google Scholar]
- Lazzari, M.; Geraldi, E.; Lapenna, V.; Loperte, A. Natural hazards vs human impact: An integrated methodological approach in geomorphological risk assessment on the Tursi historical site, Southern Italy. Landslides 2006, 3, 275–287. [Google Scholar] [CrossRef]
- Piccarreta, M.; Pasini, A.; Capolongo, D.; Lazzari, M. Changes in daily precipitation extremes in the Mediterranean from 1951 to 2010: The Basilicata region, southern Italy. Int. J. Climatol. 2013, 33, 3229–3248. [Google Scholar] [CrossRef]
- David, O.; Ascough, J.C., II; Lloyd, W.; Green, T.R.; Rojas, K.; Leavesley, G.H.; Ahuja, L.R. A software engineering perspective on environmental modeling framework design: The Object Modeling System. Environ. Model. Softw. 2013, 39, 201–213. [Google Scholar] [CrossRef]
- Argent, R.M. An overview of model integration for environmental applications—Components, frameworks and semantics. Environ. Model. Softw. 2004, 19, 219–234. [Google Scholar] [CrossRef]
- Van Ittersum, M.K.; Ewert, F.; Heckelei, T.; Wery, J.; Olsson, J.A.; Andersen, E.; Bezlepkina, I.; Brouwer, F.; Donatelli, M.; Flichman, G.; et al. Integrated assessment of agricultural systems—A component-based framework for the European Union (SEAMLESS). Agric. Syst. 2008, 96, 150–165. [Google Scholar] [CrossRef]
- Formetta, G.; Bancheri, M.; David, O.; Rigon, R. Performance of site-specific parameterizations of longwave radiation. Hydrol. Earth Syst. Sci. 2016, 20, 4641–4654. [Google Scholar] [CrossRef]
- Bancheri, M.; Serafin, F.; Bottazzi, M.; Abera, W.; Formetta, G.; Rigon, R. The design, deployment, and testing of kriging models in GEOframe with SIK-0.9. 8. Geosci. Model Dev. 2018, 11, 2189–2207. [Google Scholar] [CrossRef]
- Formetta, G.; Mantilla, R.; Franceschi, S.; Antonello, A.; Rigon, R. The JGrass-NewAge system for forecasting and managing the hydrological budgets at the basin scale: Models of flow generation and propagation/routing. Geosci. Model Dev. 2011, 4, 943–955. [Google Scholar] [CrossRef]
- Formetta, G.; Kampf, S.; David, O.; Rigon, R. The Cache la Poudre river basin snow water equivalent modeling with NewAge-JGrass. Geosci. Model Dev. Discuss. 2013, 6, 4447–4474. [Google Scholar] [CrossRef]
- Formetta, G.; Rigon, R.; Chávez, J.; David, O. Modeling shortwave solar radiation using the JGrass-NewAge system. Geosci. Model Dev. 2013, 6, 915–928. [Google Scholar] [CrossRef]
- Abera, W.; Formetta, G.; Borga, M.; Rigon, R. Estimating the water budget components and their variability in a pre-alpine basin with JGrass-NewAGE. Adv. Water Resour. 2017, 104, 37–54. [Google Scholar] [CrossRef]
- Abera, W.; Formetta, G.; Brocca, L.; Rigon, R. Modeling the water budget of the Upper Blue Nile basin using the JGrass-NewAge model system and satellite data. Hydrol. Earth Syst. Sci. 2017, 21, 3145. [Google Scholar] [CrossRef]
- Rigon, R.; Ghesla, E.; Tiso, C.; Cozzini, A. The HORTON Machine: A System for DEM Analysis the Reference Manual; Università degli Studi di Trento: Trento, Italy, 2006. [Google Scholar]
- Abera, W.; Antonello, A.; Franceschi, S.; Formetta, G.; Rigon, R. The uDig Spatial Toolbox for hydro-geomorphic analysis. Geomorphol. Tech. 2014, 2, 1–19. [Google Scholar]
- Goovaerts, P. Geostatistics for Natural Resources Evaluation; Oxford University Press: Oxford, UK, 1997. [Google Scholar]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop Evapotranspiration-Guidelines for Computing Crop Water Requirements-FAO Irrigation and Drainage Paper 56; FAO: Rome, Italy, 1998; Volume 300, p. 6541. [Google Scholar]
- Schymanski, S.J.; Or, D. Leaf-scale experiments reveal an important omission in the Penman-Monteith equation. Hydrol. Earth Syst. Sci. 2017, 21, 685–706. [Google Scholar] [CrossRef]
- Rigon, R.; Bancheri, M.; Formetta, G.; De Lavenne, A. The geomorphological unit hydrograph from a historical-critical perspective. Earth Surf. Process. Landf. 2016, 41, 27–37. [Google Scholar] [CrossRef]
- Rigon, R.; Bancheri, M.; Green, T.R. Age-ranked hydrological budgets and a travel time description of catchment hydrology. Hydrol. Earth Syst. Sci. Discuss. 2016, 2016, 1–22. [Google Scholar] [CrossRef]
- Hay, L.E.; Umemoto, M. Multiple-Objective Stepwise Calibration Using Luca; US Geological Survey: Reston, VA, USA, 2007.
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the IEEE International Conference on Neural Networks, Perth, Australia, 27 November–1 December 1995; Volume 4, pp. 1942–1948. [Google Scholar]
- Cunge, J.A. On the subject of a flood propagation computation method (Musklngum method). J. Hydraul. Res. 1969, 7, 205–230. [Google Scholar] [CrossRef]
- Ponce, V.M.; Yevjevich, V. Muskingum-Cunge method with variable parameters. J. Hydraul. Div. 1978, 104, 1663–1667. [Google Scholar] [CrossRef]
- Serafin, F.; Bancheri, M.; David, O.; Rigon, R. On complex networks representation and computation of hydrologycal quantities. In Proceedings of the AGU Fall Meeting Abstracts, New Orleans, LA, USA, 11–15 December 2017. [Google Scholar]
- Serafin, F. Enabling Modeling Frameworks with Surrogate Modelling Capabilities and Complex Networks. Ph.D. Thesis, University of Trento, Trento, Italy, 2019. [Google Scholar]
- Bancheri, M.; Serafin, F.; Formetta, G.; Rigon, R.; David, O. JGrass-NewAge hydrological system: An open-source platform for the replicability of science. In Proceedings of the EGU General Assembly Conference Abstracts, Vienna, Austria, 23–28 April 2017; Volume 19, p. 17109. [Google Scholar]
- Github. Github. Available online: https://github.com (accessed on 7 July 2019).
- GEOframe Source Code. GEOframe Source Code on Github. Available online: https://github.com/geoframecomponents (accessed on 7 July 2019).
- GEOframe OMS Projects. GEOframe OMS Projects on Github. Available online: https://github.com/GEOframeOMSProjects (accessed on 7 July 2019).
- Travis CI. Travis Continuous Integration Service. Available online: https://travis-ci.org (accessed on 7 July 2019).
- Gradle Build Tool. Gradle Build Tool. Available online: https://gradle.org (accessed on 7 July 2019).
- OSF. Open Science Framework. Available online: https://osf.io (accessed on 7 July 2019).
- OSF Page of GEOframe. Open Science Framework Page of GEOframe. Available online: https://osf.io/fk8ta/ (accessed on 7 July 2019).
- Fenicia, F.; Kavetski, D.; Savenije, H.H. Elements of a flexible approach for conceptual hydrological modeling: 1. Motivation and theoretical development. Water Resour. Res. 2011, 47. [Google Scholar] [CrossRef]
- Kavetski, D.; Fenicia, F. Elements of a flexible approach for conceptual hydrological modeling: 2. Application and experimental insights. Water Resour. Res. 2011, 47. [Google Scholar] [CrossRef]
- Clark, M.P.; Nijssen, B.; Lundquist, J.D.; Kavetski, D.; Rupp, D.E.; Woods, R.A.; Freer, J.E.; Gutmann, E.D.; Wood, A.W.; Brekke, L.D.; et al. A unified approach for process-based hydrologic modeling: 1. Modeling concept. Water Resour. Res. 2015, 51, 2498–2514. [Google Scholar] [CrossRef]
- Clark, M.P.; Nijssen, B.; Lundquist, J.D.; Kavetski, D.; Rupp, D.E.; Woods, R.A.; Freer, J.E.; Gutmann, E.D.; Wood, A.W.; Gochis, D.J.; et al. A unified approach for process-based hydrologic modeling: 2. Model implementation and case studies. Water Resour. Res. 2015, 51, 2515–2542. [Google Scholar] [CrossRef]
- Bancheri, M.; Serafin, F.; Rigon, R. The representation of hydrological dynamical systems using Extended Petri Nets (EPN). Water Resour. Res. 2019. under review. [Google Scholar] [CrossRef]
- Rutter, A.; Kershaw, K.; Robins, P.; Morton, A. A predictive model of rainfall interception in forests, 1. Derivation of the model from observations in a plantation of Corsican pine. Agric. Meteorol. 1971, 9, 367–384. [Google Scholar] [CrossRef]
- Dickinson, R.E. Modeling evapotranspiration for three-dimensional global climate models. Clim. Process. Clim. Sensit. 1984, 29, 58–72. [Google Scholar]
- Zhao, R.J. The xinanjiang model. In Proceedings of the Oxford Symposium, Oxford, UK, 15–19 April 1980. [Google Scholar]
- Manfreda, S.; Fiorentino, M.; Iacobellis, V. DREAM: A distributed model for runoff, evapotranspiration, and antecedent soil moisture simulation. Adv. Geosci. 2005, 2, 31–39. [Google Scholar] [CrossRef]
- Iacobellis, V.; Fiorentino, M. Derived distribution of floods based on the concept of partial area coverage with a climatic appeal. Water Resour. Res. 2000, 36, 469–482. [Google Scholar] [CrossRef]
- Manfreda, S. On the derivation of flow rating curves in data-scarce environments. J. Hydrol. 2018, 562, 151–154. [Google Scholar] [CrossRef]
- Budyko, M.I. Climate and Life; Academic Press: New York, NY, USA, 1971. [Google Scholar]
- Taylor, K.; Walker, G.; Abel, D. A framework for model integration in spatial decision support systems. Int. J. Geogr. Inf. Sci. 1999, 13, 533–555. [Google Scholar] [CrossRef]
- Idso, S.B. A set of equations for full spectrum and 8-to 14-μm and 10.5-to 12.5-μm thermal radiation from cloudless skies. Water Resour. Res. 1981, 17, 295–304. [Google Scholar] [CrossRef]
- Yuan, Y.; Cheng, Q. Integrating Web-GIS and hydrological model: A case study with Google Maps and IHACRES in the oak ridges moraine area, Southern Ontario, Canada. In Proceedings of the Geoscience and Remote Sensing Symposium, Barcelona, Spain, 23–27 July 2007; pp. 4574–4577. [Google Scholar]
- Ly, S.; Charles, C.; Degré, A. Different methods for spatial interpolation of rainfall data for operational hydrology and hydrological modeling at watershed scale: A review. Biotechnol. Agron. Soc. Environ. 2013, 17, 392–406. [Google Scholar]
- MODIS. MODIS LAI. Available online: https://modis.gsfc.nasa.gov/data/dataprod/mod15.php (accessed on 7 July 2019).
| Symbol | Name | Type | Unit |
|---|---|---|---|
| a | coefficient of the RZ non-linear reservoir model | P | (T−1) |
| b | exponent of the RZ non-linear reservoir model | P | (−) |
| bc | drainage coefficient | P* | (T−1) |
| c | coefficient of GW the non-linear reservoir model | P | (T−1) |
| d | exponent of GW the non-linear reservoir model | P | (−) |
| k | runoff coefficient | P | (TL−2β) |
| kc | LAI coefficient | P* | (L3) |
| p | free throughfall coefficient | P* | (−) |
| A | HRU area | (L2) | |
| D(t) | drainage from the canopy | F | (L3T−1) |
| ETc(t) | evapotranspiration from the canopy | F | (L3T−1) |
| ETp(t) | potential evapotranspiration | F | (L3T−1) |
| ETrz(t) | evapotranspiration from the root zone | F | (L3T−1) |
| LAI | leaf area index | (L2L−2) | |
| Md(t) | melting discharge/rain | F | (L3T−1) |
| QGW(t) | groundwater discharge | F | (L3T−1) |
| QR(t) | runoff discharge | F | (L3T−1) |
| Re(t) | recharge term of groundwater | F | (L3T−1) |
| Sc(t) | canopy storage | P | (L3) |
| canopy maximum retention storage | P | (L3) | |
| SGW(t) | groundwater storage | SV | (L3) |
| maximum groundwater storage | P | (L3) | |
| SR(t) | runoff storage | SV | (L3) |
| Srz(t) | root zone storage | SV | (L3) |
| maximum root zone storage | SV | (L3) | |
| Tr(t) | throughfall | F | (L3T−1) |
| α(t) | partitioning coefficient between root zone and surface runoff | SV | (−) |
| β | runoff exponent | P* | (−) |
| Symbol | Name | Expression |
|---|---|---|
| drainage from the canopy | ||
| evapotranspiration from the canopy | ||
| evapotranspiration from the root zone | ||
| groundwater discharge | ||
| runoff discharge | ||
| recharge term of groundwater | ||
| canopy storage | ||
| throughfall |
| Component | Parameter | Value | Units |
|---|---|---|---|
| Kriging on temperature | nugget | 0.28 | (°C) |
| range | 4.95 | (km) | |
| sill | 2.24 | (°C) | |
| Kriging on precipitation | nugget | 0.24 | (mm) |
| range | 4.93 | (km) | |
| sill | 0.15 | (mm) | |
| SWRB | vertical ozone layer thickness | 0.6 | (cm) |
| 0.9 | (-) | ||
| visibility | 80.0 | (km) | |
| LWRB | X param of [66) | 0.7 | (-) |
| Y param of [66) | 5.95 | (-) | |
| Net radiation | soil albedo | 0.26 | (-) |
| ETP | 0.8 | (-) | |
| Rain–snow separation | 1 | (-) | |
| 1 | |||
| melting temperature | 2 | (°C) | |
| Snow | freezing factor | (mm°C−1h−1) | |
| liquid water retention capacity coefficient | 0.69 | (-) | |
| melt factor | 0.25 | (mm°C−1h−1) | |
| melting temperature | 2 | (°C) | |
| radiation factor | (mm°C−1W−1h−1) |
| Symbol | Name | Type | Unit |
|---|---|---|---|
| surface area of the dam | (L2) | ||
| coefficient in area expression | P | (L1) | |
| known term in area expression | P | (L2) | |
| g | gravitational acceleration | P | (LT−2) |
| stage with respect to m a.s.l. | V | (L) | |
| stage at which the spillway activates | P | (L) | |
| K | storage coefficient in MC | P | (T) |
| l | spillway length | P | (L1) |
| generic channel flow | F | (L3T−1) | |
| input to the dam | F | (L3T−1) | |
| output from the dam | F | (L3T−1) | |
| regulated dam’s outflow | F | (L3T−1) | |
| spillway discharge | F | (L3T−1) | |
| discharge from the HRU | F | (L3T−1) | |
| t | time | V | (T) |
| x | weighting factor in MC | P | (-) |
| coefficient of the spillway | (-) |
| Symbol | Name | Expression |
|---|---|---|
| surface area of the dam | ||
| K | storage coefficient in MC | |
| output from the dam | ||
| spillway discharge |
| River | Budyko | Q(V,A) | Q(H) | MAPE (VA) | MAPE (Q(H)) |
|---|---|---|---|---|---|
| Agri Ponte La Marmora | 513 | 546 | 541 | 6 | 6 |
| Agri SS 106 | 387 | 330 | 308 | 15 | 20 |
| Basento SS 106 | 245 | 161 | 245 | 34 | 0 |
| Bradano SS 106 | 90 | 99 | 71 | 11 | 21 |
| Cavone SS 106 | 317 | 560 | 501 | 76 | 58 |
| Sinni Episcopia | 914 | 318 | 302 | 65 | 67 |
| River | Budyko | Q(V,A) | Q(H) | MAPE (VA) | MAPE (Q(H)) |
|---|---|---|---|---|---|
| Agri Ponte La Marmora | 750 | 510 | 508 | 32 | 32 |
| Agri SS 106 | 841 | 332 | 310 | 61 | 63 |
| Basento SS 106 | 348 | 157 | 250 | 55 | 28 |
| Bradano SS 106 | 90 | 64 | 55 | 29 | 39 |
| Cavone SS 106 | 436 | 520 | 459 | 19 | 5 |
| Sinni Episcopia | 1053 | 516 | 472 | 51 | 55 |
| Root Zone | Runoff | Groundwater | Muskingum–Cunge | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| River | B(-) | (mm) | a(h−1) | b(-) | k(h/km) | (mm) | c(h−1) | d(-) | x(-) | (m/s) |
| [0.1–0.4] | [100–500] | [0.01–10] | [1–10] | [0.05–0.5] | [100–2500] | [0.01–40] | [1–15] | [0.01–0.5] | [0.4–1.5] | |
| Agri (Up) | 0.10 | 110.22 | 1.80 | 8.96 | 0.23 | 1494.12 | 10.05 | 7.84 | 0.07 | 0.69 |
| Agri (Down) | 0.11 | 162.64 | 0.10 | 3.16 | 0.08 | 2039.01 | 0.49 | 13.89 | 0.06 | 1.26 |
| Basento | 0.10 | 143.62 | 0.02 | 8.66 | 0.29 | 137.44 | 25.89 | 9.52 | 0.01 | 0.65 |
| Bradano | 0.10 | 116.43 | 0.14 | 3.51 | 0.28 | 2491.35 | 0.01 | 13.43 | 0.10 | 0.68 |
| Cavone | 0.21 | 163.33 | 0.18 | 7.91 | 0.23 | 170.28 | 29.88 | 8.48 | 0.01 | 0.50 |
| Sinni | 0.13 | 233.05 | 0.14 | 3.17 | 0.29 | 204.03 | 0.01 | 14.75 | 0.38 | 0.40 |
| River | KGE (-) | NSE (-) | RMSE (m3/s) | PBIAS (%) |
|---|---|---|---|---|
| Agri (Up) | 0.68 | 0.65 | 3.94 | 26.6 |
| Agri (Down) | 0.65 | 0.63 | 28.6 | 12.3 |
| Basento | 0.60 | 0.65 | 23.99 | −3.4 |
| Bradano | 0.57 | 0.63 | 16.37 | −3 |
| Cavone | 0.65 | 0.65 | 8.94 | −21.2 |
| Sinni | 0.82 | 0.76 | 5.42 | −0.1 |
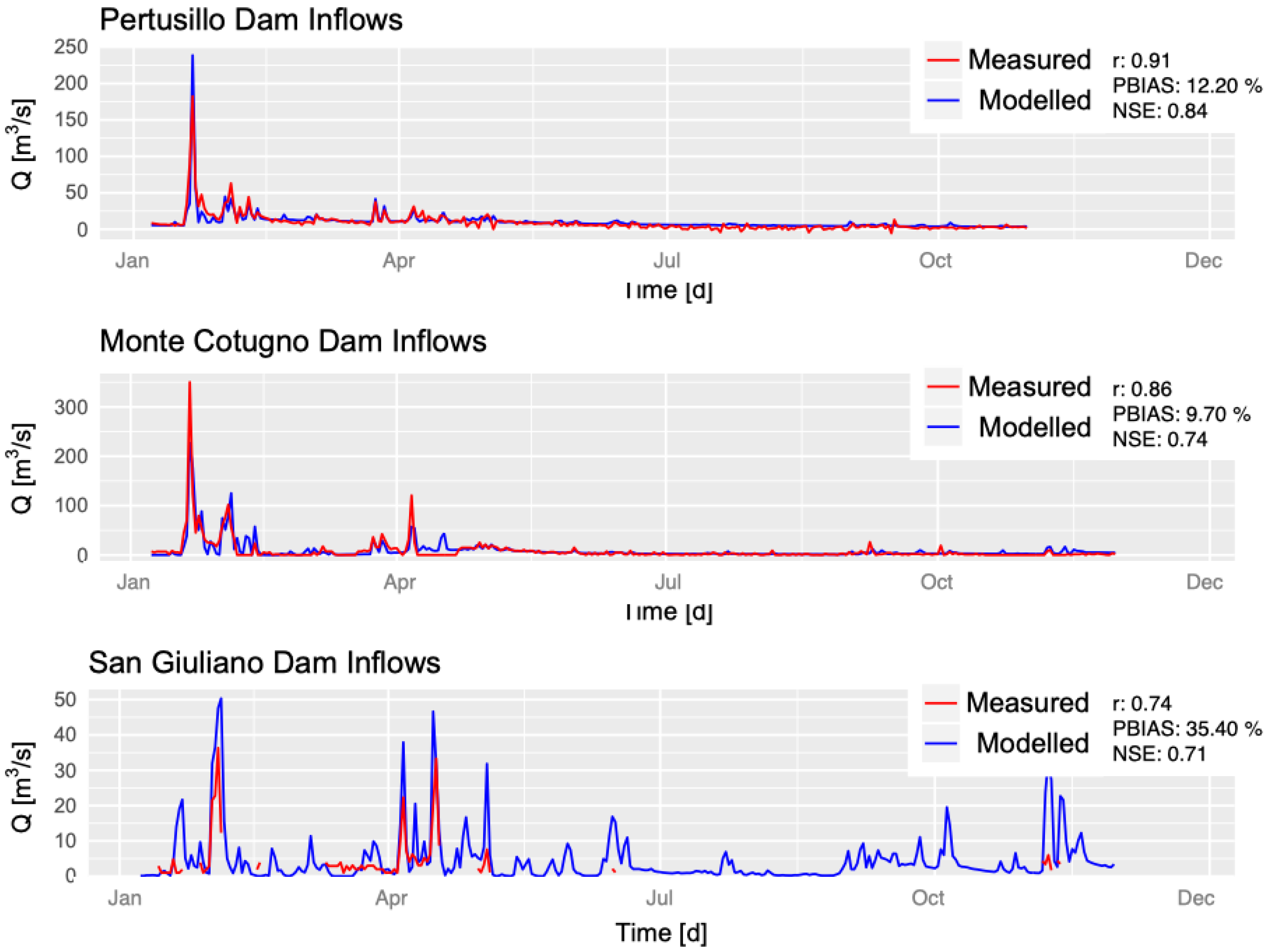
| Dam | Maximum Volume (m3) | Drainage Area (km2) | r (-) | NSE (-) | PBIAS (%) |
|---|---|---|---|---|---|
| Pertusillo | 1.59 × 109 | 530 | 0.91 | 0.84 | 12.20 |
| Monte Cotugno | 5.30 × 109 | 890 | 0.86 | 0.74 | 9.70 |
| San Giuliano | 1.07 × 109 | 1631 | 0.74 | 0.71 | 35.40 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bancheri, M.; Rigon, R.; Manfreda, S. The GEOframe-NewAge Modelling System Applied in a Data Scarce Environment. Water 2020, 12, 86. https://doi.org/10.3390/w12010086
Bancheri M, Rigon R, Manfreda S. The GEOframe-NewAge Modelling System Applied in a Data Scarce Environment. Water. 2020; 12(1):86. https://doi.org/10.3390/w12010086
Chicago/Turabian StyleBancheri, Marialaura, Riccardo Rigon, and Salvatore Manfreda. 2020. "The GEOframe-NewAge Modelling System Applied in a Data Scarce Environment" Water 12, no. 1: 86. https://doi.org/10.3390/w12010086
APA StyleBancheri, M., Rigon, R., & Manfreda, S. (2020). The GEOframe-NewAge Modelling System Applied in a Data Scarce Environment. Water, 12(1), 86. https://doi.org/10.3390/w12010086







