Abstract
Water scarcity is a mounting problem in arid and semi-arid regions such as the Mediterranean. Therefore, smarter and more effective water management is required, especially in irrigated agriculture. One of the most challenging uncertainties in the operation of on-demand collective Pressurized Irrigation Distribution Systems (PIDSs) is to know, a priori, the number and the position of hydrants in simultaneous operation. To this end, a model was developed to generate close to reality operating hydrants configurations, with 15, 30 or 60 min time steps, by estimating the irrigation scheduling for the entire irrigation season, using climatic, crop and soil data. The model is incorporated in an integrated DSS called Decision Support for Irrigation Distribution Systems (DESIDS) and links two of its modules, namely, the irrigation demand and scheduling module and the hydraulic analysis module. The latter is used to perform two types of analyses for the performance assessment and decision-making processes. The model was used in a real case study in Italy to generate hydrants’ operation taking into consideration irrigation scheduling. The results show that during the peak period, hydrants simultaneity topped 62%. The latter created pressure deficit in some hydrants, thus reducing the volume of water supplied for irrigation by up to 87 m3 in a single hydrant during the peak demand day. The developed model proved to be an important tool for irrigation managers, as it provides vital information with great flexibility and the ability to assess and predict the operation of PIDSs at any period during the irrigation season.
1. Introduction
On-demand irrigation delivery schedule gives farmers the ability to control the frequency, rate and duration of irrigation. Thus, it provides farmers with a high level of flexibility to better match their crop water needs with the amount of water delivered to farms. Pressurized Irrigation Distribution Systems (PIDSs) are designed to offer this type of schedule taking into account the minimum required pressure needed to appropriately operate on-farm irrigation systems. However, in most cases, the pipe networks are designed with a constraint to deliver a maximum discharge at the upstream end of the system which does not always guarantee 100% simultaneity of hydrants’ use (hydrants operating at the same time).
One of the most challenging uncertainties in the design of on-demand PIDSs is to know, a priori, the number and the position of hydrants in simultaneous operation and, thus, the discharges flowing in each section of the network. A widely used probabilistic approach proposed by Clément [1] for the calculation of such discharges has been contrasted in several studies that considered it appropriate for the design of on-demand irrigation networks [2]. However, this approach does not permit to take into consideration the variety of flow regimes occurring in an irrigation system.
The occurrence of spatial and temporal variability of hydrants’ simultaneity in relation to farmers’ decision over time depends on different factors including the cropping pattern, crops grown, meteorological conditions, on-farm irrigation efficiency and farmers’ behaviour [3]. The assumed factors at the design stage may change over time, increasing the demand uncertainties. Therefore, exceeding the design simultaneity (higher upstream discharge than the one presumed at the design stage) may occur. This will affect the performance of the distribution network, which may in return affects the performance of the on-farm systems and the yields of the irrigated crops. In fact, even when the simultaneity is not exceeded, hydrants may experience pressure and/or discharge failure depending on their position in the network and hydrants’ simultaneity [4,5].
In on-demand networks, the analysis of the performance is often carried out by generating random hydrants’ opening to simulate different scenarios. However, the ability to forecast farmers’ demand is fundamental to the real-time operational control of an on-demand water distribution system [6]. For irrigation managers, having the ability to simulate hydrants’ opening and the duration of their use can greatly help with the prediction of the performance of the network throughout the irrigation season, thus helping in the decision making for better management.
Many models and software are available to support decision making for water managers and farmers. Some of these models are limited to the calculation of Crop Water Requirements (CWRs) and determination of irrigation scheduling such as CROPWAT [7], GISAREG [8] and WISCHE [9]. Others are designed to simulate demand scenarios (hydrants opening) to be used for either the design of new irrigation distribution systems or for the analysis of existing ones.
Moreno et al. [10] developed the Random Daily Demand Curve (RDDC) method, which generates scenarios for open hydrants during a day and in the peak period to calculate the flow at the main pipe. The probability of a hydrant opening was calculated by considering the irrigation characteristics of each irrigation plot, such as the number of irrigation subunits per plot, irrigation time depending on CWRs, network daily operating time and irrigation interval. This method was improved by Córcoles et al. [11] to calculate the discharges from all pipes of the network, allowing the determination of the pressure at the pumping station required to guarantee a minimum pressure at the open hydrants.
Khadra and Lamaddalena [12] developed the WINGENERA model based on the soil water balance for generating daily demand hydrographs for the whole irrigation season in an on-demand irrigation system. The model considers a deterministic component represented by the equation of soil water balance and a stochastic component function of the uncertainties linked to the sowing date of the crops, the initial water reserve and the farmer’s management strategy. However, this model does not account for the hydraulic and physical limitations of the irrigation network. The HydroGEN model [13] is based on the aforementioned model and simulates the soil water balance for each cropped field (under regulated and deficit irrigation scenarios) supplied by water delivery hydrants and generates the demand hydrographs both at the hydrant level and at the inlet of the distribution networks.
Rodríguez Díaz et al. [14] also reported a simulation model based on water balance, taking into account farmers’ practices, the irrigation systems on the farms and any existing limitations such as flow rate. This model determines the flows that circulate in each section of a network for each period during the irrigation season, depending on the crop demand (the applied irrigation depth is constant and depends on the irrigation system) and irrigation practices.
The abovementioned models were developed to generate water demands to be used in the design stage of irrigation distribution systems. Therefore, rely on many stochastic approaches related to the determination of variables such as planting dates, assignation of hydrants to specific plots, irrigation methods used and hydrants’ opening time, etc. However, for existing networks, these approaches do not give water managers a lot of flexibly in controlling different known variables for determining these demands.
An on-demand network gives farmers the freedom to decide when and how much water to take from this network. However, irrigation managers have to be involved in monitoring the overall operations to ensure good performance of the network. Hence, the management of the network should be done with a coordinated process between the irrigation manager and the farmers. De Nys et al. [15] proposed a simulation tool for open channels called WaDI (water delivery for irrigation). The model is dedicated to the relations between the manager’s water supply and the farmers’ demand. It is used for analysing infrastructure and organizational constraints in specific periods; hence, it calculates water demand at the farm level on a weekly basis. Nevertheless, this tool simulates ‘‘what-if’’ scenarios providing flexibility and capacity to explore a large range of cases and potential solutions.
The objective of this work is to provide water managers with an effective tool that offers support for decision making to maintain satisfactory services to farmers. A prior knowledge of water deliveries to each hydrant, especially during the peak period, is a crucial information for water managers. Hence, this tool will help them understand the behaviour of the distribution network during failure conditions and take the proper decisions to improve the reliability of this network. The tool relies mostly on deterministic processes to be more representative of the actual situation. The only stochastic process can be the simulation of hydrants opening time so as to keep the network operating on demand.
2. Materials and Methods
To evaluate the performance of PIDSs and to take the appropriate decisions concerning the operation and management of these systems, it is necessary to know the allocation of water at the farm level. To this end, the irrigation demand and scheduling module was developed to simulate Crop Water Requirements (CWR) and irrigation scheduling for each field in an irrigation district. This model is incorporated in an integrated Decision Support System (DSS) called DESIDS (Decision Support for Irrigation Distribution Systems) [16]. The incorporation of this model in the DSS (see Figure 1) is imperative as it allows irrigation system managers to efficiently match the discharges and pressures supplied by the system to on-farm water use and take the necessary decisions to provide adequate PIDSs performance to meet the crop water demand. Irrigation demand and irrigation scheduling are determined following the approach of CROPWAT using climatic, crop and soil parameters. The estimation of irrigation requirements is one of the principal parameters for the planning, design and operation of PIDSs. In this module, monthly available data are used to estimate the crop water and irrigation requirements, especially during the peak period, for a proposed cropping pattern for the planning and design of a PIDS, while the daily data is very important in formulating the policy for optimal allocation of water as well as in decision making in the day-to-day operation and management of the systems.
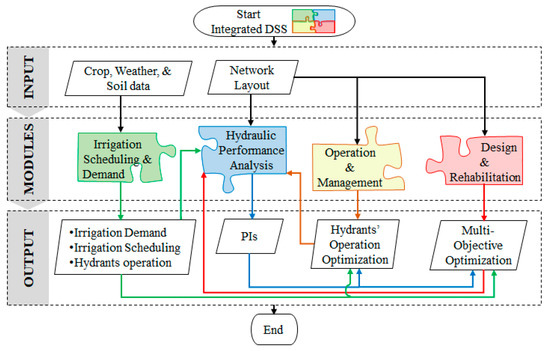
Figure 1.
Decision Support for Irrigation Distribution Systems (DESIDS) integrated modules.
2.1. Crop Water Requirements and Irrigation Scheduling
CWRs and irrigation scheduling are determined using the irrigation demand and scheduling module using climatic, crop and soil parameters. First, the daily ET0 is calculated using the FAO-56 Penman–Monteith [17]. ET0 can also be estimated using Hargreaves methods, depending on the availability of data. ETc is then determined by multiplying ET0 by the crop coefficient Kc. It is worth mentioning that in this module, the planting dates for all crops are pre-defined by the user and not generated randomly to mimic the actual behaviour of the irrigation network. In addition, the same crop can have different planting dates for different fields because not all farmers plant the same crop in the same day. CWRs are calculated then as the difference between ETc and the effective rainfall (Peff), which is estimated as 80% of the actual daily rainfall. The model can also estimate Peff using other options: (i) FAO formula for dependable rainfall, (ii) empirical formula and (iii) USDA Soil Conservation Service formula.
Concerning the determination of irrigation scheduling, net irrigation demands are estimated using daily soil water balance expressed in terms of depletion at the end of each day [17]:
where Ii is the net irrigation depth on day i, Dr,i is the root zone depletion at the end of day i, Dr,i−1 is water content in the root zone at the end of the previous day, i − 1, Pi is the actual rainfall on day i, ROi is the runoff from the soil surface on day i, CRi is the capillary rise from the groundwater table on day i, ETci is the crop evapotranspiration on day i, and DPi is the water loss out of the root zone by deep percolation on day i, all expressed in mm.
The initial depletion can be derived from measured soil water content and has to be entered by the user of the module. The latter also takes into consideration that ETc can be affected by water depletion from the root zone. Therefore, when depletion exceeds the readily available water (RAW), ETc is reduced and adjusted using a water stress coefficient, ks (dimensionless transpiration reduction factor). When the depletion is smaller than RAW, ks = 1. Otherwise,
where TAW is the total available water in mm, which is governed by the types of soil and the rooting depth. The module allows allocating different type of soils for each crop to account for soil heterogeneity in farms.
Gross irrigation demand (GIR) is then calculated by considering the on-farm irrigation efficiency (Eirr). The latter accounts for the losses of water incurred during irrigation application, which depends on the on-farm irrigation methods. GIR is then calculated as:
In this module, efficiency is assigned, separately, to each specific crop since different crops can be irrigated with a different type of irrigation even in the same farm. In addition, the module is set to permit the use of several irrigation management options for each specific crop (irrigate to field capacity, deficit irrigation and salt leaching, irrigate with fix interval, fixed irrigation depth, etc.), as farmers manage irrigation in different ways (Figure 2).
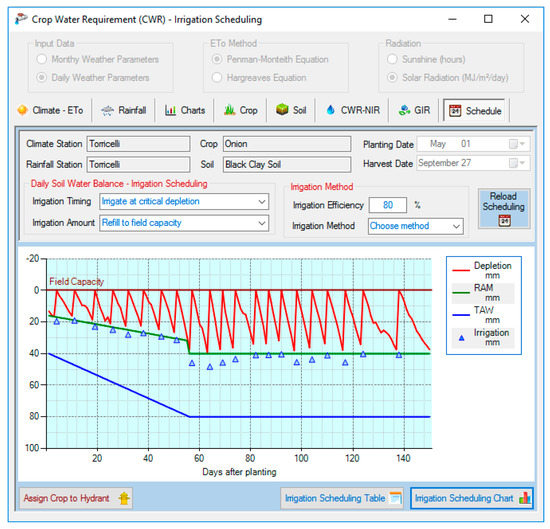
Figure 2.
Irrigation scheduling and demand module.
2.2. Generation of Hydrants Opening Configurations
The process of generating hydrants’ configurations (hydrants operating simultaneously) starts by allocating each crop to a specific hydrant in the distribution network. It should be noted that, hydrants are assigned to each field with a single crop and not to a farm, since farms can encompass more than one crop. Therefore, the module works with the assumption that farmers open hydrants to irrigate each crop separately.
Theoretically speaking, a hydrant can operate 24 h a day in an on-demand network. However, if more than one field are to be irrigated by the same hydrant, then the hydrant operating time has to be adjusted accordingly, since hydrants are set to irrigate one field at a time. This is a realistic assumption as farmers sharing the same hydrant usually agree to use it at different time of the day if they have to irrigate in the same day. Accordingly, irrigation scheduling for the whole season is adjusted to deliver the maximum possible irrigation depth during the agreed-upon hours of the day.
The irrigation starting time can either be fixed or generated randomly to keep the simulated network operating on-demand. In this process, the day is divided into 6 windows of 4 h, each window with a user pre-defined probability (proportional to its frequency of occurrence) that fits farmers’ behaviour in the irrigation district. In fact, there are hours of the day where farmers prefer to irrigate, according to their commitments, customary, social conditions and availability of pressure at their hydrants [18]. Therefore, initially, a field (crop) is assigned to a time window randomly. Then, the irrigation starting time is randomly generated, with a uniform distribution, within this time window (4 h) for the whole irrigation season. This approach is valid because even if the farmer prefers to start irrigation at a certain time of the day, irrigation will not start at the exact hour throughout the irrigation season.
To create a more realistic operation of hydrants in a PIDS, this module is set to generate hydrants’ configurations for the entire irrigation season or a pre-defined period such as the peak period, using 15-, 30- or 60-min time steps. Selecting a shorter time step provides more detailed and accurate information on the operation of the PIDS, but it requires additional calculation and data processing time after assigning each field in the irrigation district to a hydrant. The irrigation time can either be fixed by the user or generated randomly. In addition, the maximum irrigation time per day can be set to either mimic on-demand irrigation (satisfy irrigation requirements set by farmers) or limited (by irrigation mangers) if the PIDS is operated under rotation delivery schedule.
When it is time to irrigate, a hydrant j is opened and remains as such for the time of irrigation (tir,j), until the desired irrigation depth is delivered. On the other hand, when tir,j is greater than the operating time of the hydrant j, th,j (h), irrigation scheduling for the entire season is adjusted to deliver the maximum possible irrigation depth, Imax,j (mm), and to fully satisfy irrigation requirements:
where 0.36 is a unit adaptation coefficient, qj is the nominal discharge of hydrant j (ls−1), and Aj is the area irrigated by hydrant j (ha).
All fields and the hydrants that are used to irrigate them are added to a table representing the irrigation scheme. In this module, the determination of the seasonal peak period is achieved by applying the moving average method to the daily volumes of irrigation water, for periods pre-defined by the user. For instance, the moving average of a 10 day period is a series of successive averages of 10 days. In other words, the first average is the mean of 10 days starting from day 1 to day 10, while the second average is the mean of 10 days starting from day 2 to day 11. The final step is the generation of hydrants’ opening configuration for the entire irrigation season or the period defined by the user. These configurations can be saved in a file to be used by the hydraulic analysis module.
2.3. Hydraulic Analysis
The hydraulic analysis is carried out using another interlinked model called hydraulic analysis module, which is the core of DESIDS. This module combines the stochastic analysis capabilities for on-demand systems of COPAM [3] and the analysis of complex systems using EPANET [19] hydraulic solver to calculate unknown discharges and pressures for each operating hydrant in the considered PIDS.
The purpose from generating hydrants configurations using the irrigation demand and schedule module is to provide district managers with deterministic data that can be used to efficiently analyse the PIDS. In this work, the generated data is used to perform both, demand-driven analysis (DDA) and pressure-driven analysis (PDA). DDA assumes that the demands at the hydrants are constant regardless of the available pressure, and thus, it is not suitable for operating conditions with insufficient pressure [20], while PDA considers the variation of demands depending on the pressure status. Several researchers have highlighted the use of PDA for its ability to deliver realistic results under different pressure conditions [21,22,23].
The aim for the hydraulic analyses is to explore the difference between the outputs of the two abovementioned methods and their effects on the decision-making process. DDA is performed using the incorporated EPANET solver, which provides the hydraulic analysis module with the ability to perform “extended period simulations”, which is used here for the simulation of hydrants’ operation for long periods of time (peak period or the entire irrigation season), by means of a succession of steady states.
For this study, the use of PDA in PIDSs is particularly important to assess the reliability of these systems when referring to their ability to provide the required discharges needed to meet on-farm water demands. To achieve this goal, the non-iterative method suggested by [24] was applied in this module. This method was selected because it provides the possibility to perform PDA by directly using the EPANET toolkit with a single simulation. It was also compared to other similar methods and applied on three real-life cases where it proved to provide accurate and reliable results, reproducing the functioning of a network in the pressure-driven mode [25].
When the PDA option is selected for assessing the performance of a PIDS, the hydraulic analysis module automatically adds the abovementioned devices to all open hydrants following the procedure described in [24]. The method consists of adding artificial string of check valve (CV), flow control valve (FCV) and emitter, in series, at each hydrant to model pressure deficient PIDS as illustrated in Figure 3.

Figure 3.
Setting of the added devices for each open hydrant in the pressure-driven analysis (PDA).
Three Performance Indicators are used for the hydraulic performance analyses, namely:
- Relative Pressure Deficit RPD [3], which compares the actual pressure head for hydrant j (Hj) to the minimum pressure (Hmin,j).
- Reliability Re [3], which indicates the ability of a PIDS to provide an adequate level of service, referring to the pressure.where Ns,j is the number of times the pressure at hydrant j is satisfied, and No,j is the total number of times where hydrant j is open.
- Available Volume Fraction ADF [21]. The latter is only used in the PDA to measure the reliability of hydrants when taking into account the available discharges. This indicator compares the available discharge at hydrant j (qj,avl) with the required discharge (qj,req), at the same hydrant, set to meet the irrigation requirements at farm level. Hence, this indicator is used to estimate the fraction of the discharge that is actually delivered by hydrant j.
2.4. Case Study
The abovementioned methodology was applied to an irrigation scheme served by District 1-a irrigation system in Southern Italy. The district receives water through a pumping station located upstream of a branched distribution network, equipped with 74 hydrants having a nominal discharge of 10 ls−1, each supplying water to one or more cropped fields. The pumping station was designed to convey a peak discharge of 300 ls−1 and to ensure a constant pressure head of 65 m at the upstream end of the network. The layout of District 1-a system is depicted in Figure 4. This system is operated by a restricted-demand delivery schedule, in which all farmers take water at their convenience within the maximum allowed flow rate (nominal discharge) and not exceeding the maximum seasonal allocated shares out of the total water supply available from the dam. The system guarantees a minimum pressure of 20 m at each hydrant (which are equipped with flow limiters) to satisfy the operation of on-farm irrigation systems. The scheme under study covers an area of about 212 ha, with the main irrigated crops being tomatoes (35%) and asparagus (30%). The cropping pattern of the scheme is detailed in Table 1.
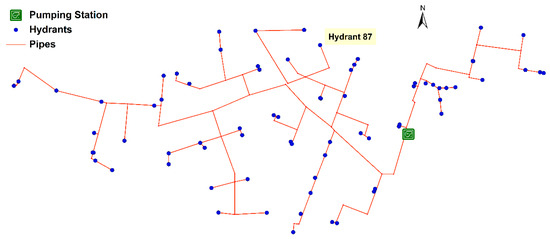
Figure 4.
Layout of District 1-a system.

Table 1.
Crop allocation in District 1-a.
3. Results and Discussions
3.1. Estimation of Irrigation Scheduling
Daily weather data for temperature, humidity, wind speed and radiation were used for the calculation of ET0. Subsequently, net irrigation requirements and irrigation scheduling were determined using the available crops and soil data. The irrigation scheduling for each crop is then assigned to a field in the irrigation scheme, served by the hydrants of District 1-a system.
The irrigation scheduling in each field, for the entire irrigation season, is adjusted taking into account the irrigated area of the field, the nominal discharge of the corresponding hydrant and the maximum allowable irrigation time. The selection of opening times of each hydrant is the only stochastic process in the tool. In this work, the opening time was determined by dividing the day into six windows of four hours, each window with a user pre-defined probability (proportional to its frequency of occurrence) that fits farmers’ behaviour in the irrigation district as depicted in Figure 5.
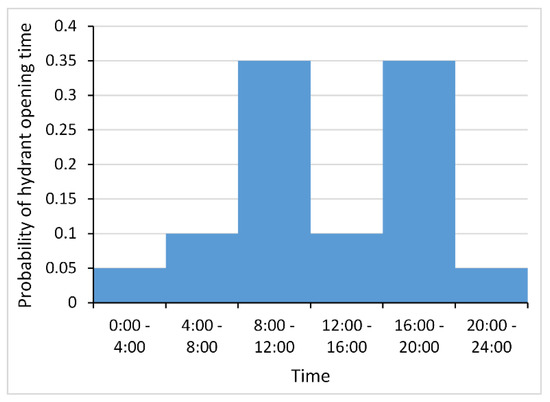
Figure 5.
Probability of hydrant opening time.
3.2. Generation of Hydrants’ Configurations
After the determination of irrigation scheduling for each field, the hourly operation of each corresponding hydrant is determined for the entire irrigation season. Using this data, the irrigation district manager can generate operating hydrants’ configurations for the entire irrigation season or a specific period, particularly the peak demand period. The latter is determined using the moving average method depending on pre-defined number of days. This is achieved by calculating the daily irrigation volumes demanded at the upstream end of the delivery network.
Figure 6 shows how the developed tool calculates the daily volumes and sorts the outcome according to the average demand volume for 10 days periods. In this work, the 10-day peak demand period is identified to be between July 2 and July 11 with an average irrigation volume of 18,900 m3.
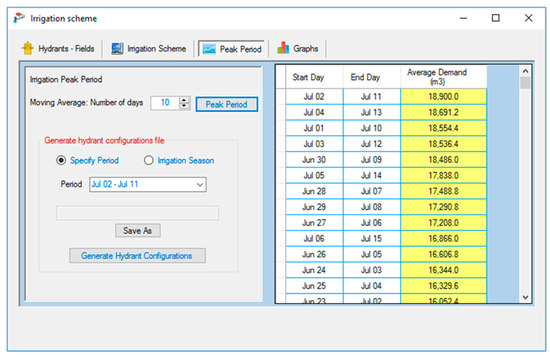
Figure 6.
Determination of the peak period.
It is important to mention that finding the peak period using the average volumes is significantly affected by the selected length, i.e., number of days, of the peak period to be simulated. For instance, when calculating the volume on a daily basis, the system supplied a volume of 14,112 m3 on 8 July, which is included in the 10-day peak period mentioned above. On the other hand, the daily volume recorded on 20 May amounts to 19,548 m3, ranking the fourth highest daily volume for the entire irrigation season. However, when considering a 10-day peak demand, this day is encompassed in the period between 19 May and 28 May with an average volume of 13,496 m3, which is ranked 37th highest 10-day average volume. Hence, to extend the ability of the manager to explore all possible scenarios, the developed tool was set to provide high level of flexibility for a thorough assessment of the functionality of the system throughout the irrigation season.
Figure 7 illustrates the hourly water demand volumes as well as the hourly hydrants simultaneity recorded during the 10-day peak period determined above. It is shown that the hourly irrigation volumes supplied by the system in the district are concentrated in the second half of the day and particularly in the late afternoon, compared to relatively low demand in the early morning hours. This is confirmed by the typical farmers’ behaviour in the area [26]. This information is vital for the district manager to take the appropriate decisions to deal with any unpredicted operation scenario of the system, which may cause insufficient discharge and pressure at hydrant level that may adversely affect the performance of the on-farm irrigation systems.
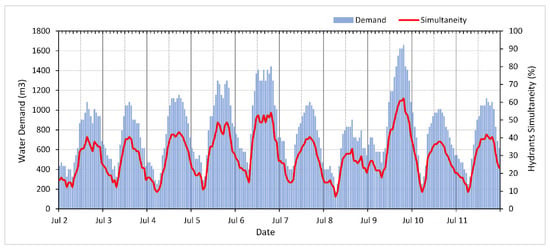
Figure 7.
Hourly water demand and hydrant simultaneity of the peak period.
It should be noted that it is important to consider the hourly operation of all hydrants and not just the daily volumes since a high daily water demand does not necessarily entail negative effects on the hydraulic performance of the system. In other words, even if the demand volume recorded during a day is high, this volume may have been supplied evenly throughout the same day. Contrarily, low daily volumes may cause performance problems if the supply is concentrated on a few hours a day. For this reason, hourly hydrants’ simultaneity is calculated by the developed tool and displayed as depicted in Figure 5.
This tool provides irrigation district managers with the option to track the progress of hydrants’ simultaneity every 15-, 30- or 60-min time steps, throughout the irrigation season. This is extremely important because the simultaneity has great impact on the hydraulic performance of the system. Thus, this option helps managers to take appropriate decisions to avoid high simultaneity, which can be achieved, for instance, by using the operation and management module through the optimization of irrigation periods [27].
3.3. Hydraulic Analysis
The purpose of generating hydrants configurations from irrigation scheduling is to realistically assess the hydraulic performance of PIDSs. The generated configurations for the specified period are saved to be used by the hydraulic analysis module in DESIDS. Two types of analyses can be carried out, DDA and PDA. The latter was added to the hydraulic analysis module to overcome the major drawback of the DDA, which is the failure to measure a partially failed network performance. In such cases, the DDA may produce very unrealistic results such as negative pressures. To shed the light on the importance of using PDA in PIDSs, the two analyses are performed for the peak demand day of the irrigation season, i.e., 9 July where the daily volume supplied by the system reached 24,840 m3 and the hydrants simultaneity topped 62%.
Figure 8 and Figure 9 display, respectively, the maximum RPD and reliability of all operating hydrants during the peak demand day. Both indicators show that in some hydrants, the values resulted from DDA demonstrate a greater hydraulic performance failure compared to the results of PDA. Hydrant 87 (highlighted in Figure 2) was selected to be studied in detail to compare the two analyses because it has the lowest performance in the network during the selected day. Even though the reliability of this hydrant is 0, i.e., it failed to deliver the required pressure during all its operating hours, DDA resulted in a lowest RPD with a value of −1.1 compared to −0.5 for PDA. This is due to the fact that DDA considers the required discharge at the hydrant fully supplied even if the pressure is lower than the minimum required. Therefore, the system is assumed to supply the full anticipated upstream discharge, which consequently leads to the overestimation of failures.
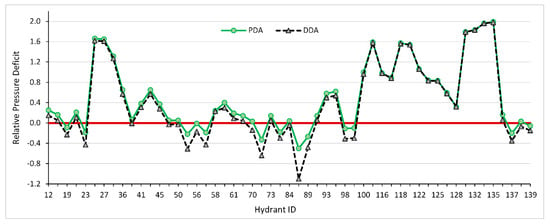
Figure 8.
Relative pressure deficit (RPD) indicator for demand-driven analysis (DDA) and pressure-driven analysis (PDA) for the peak demand day.
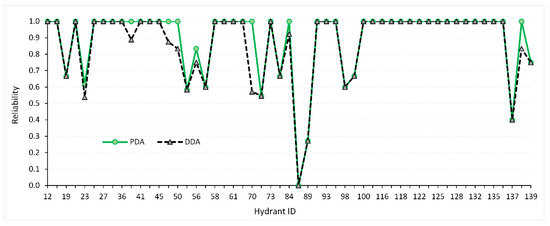
Figure 9.
Reliability indicator for DDA and PDA for the peak day.
On the other hand, PDA provides more realistic modelling of the hydraulic system since discharges are assumed to be driven by pressure. Hence, the actual upstream discharge of the system will be lower than the anticipated upstream discharge in the presence of pressure deficient hydrants. This is illustrated in Figure 10, which shows the influence of the available pressure at hydrant 87 on the discharge for both DDA and PDA. It is demonstrated that in the case of DDA, it is assumed that the required discharge at the hydrant is fulfilled while the pressure is lower than the minimum required, i.e., 20 m. In this case, the magnitude of the failure is overestimated resulting in negative pressure between 17:00 and 19:00. Conversely, in PDA, the discharge of the hydrant fluctuates depending on the available pressure. This has resulted in much lower pressure deficit compared to DDA. For instance, at 19:00, PDA recorded a pressure deficit of 10 m, which resulted in a discharge of 7 ls−1, i.e., lower than the required 10 ls−1, whereas DDA recorded a pressure deficit 22 m (negative pressure) while providing the required discharge of 10 ls−1.
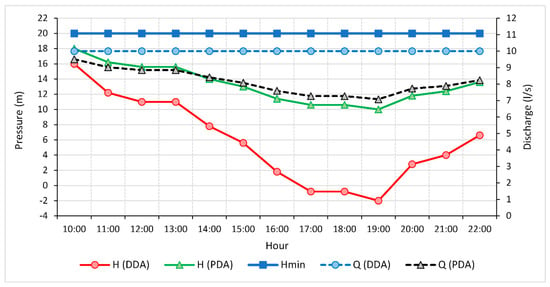
Figure 10.
Pressure and discharge at hydrant 87 resulted from DDA and PDA.
In PIDSs operation, the goal of the irrigation district manager is to guarantee farmers served by the distribution system the minimum pressure required for appropriate operation of on-farm systems and the required discharge to meet irrigation demand. The latter is an important issue that is usually ignored when dealing with the hydraulic analysis of PIDSs. The PDA used in the hydraulic analysis module provides an additional indicator, namely, ADF, used to assess the reliability of the hydrant to deliver the required discharge. Figure 11 illustrates the available discharge fraction at hydrant 87 during its operation in the peak demand day. ADF is shown to vary between 0.7 and 0.95 for this hydrant between 10:00 and 22:00. During the 13 h of operation, only 81% of the required volume of irrigation water was supplied by this hydrant, i.e., a deficit of 87 m3. This information is useful to estimate the impact of the reliability of the hydrant to deliver the expected demand throughout the irrigation season and to estimate potential crops’ yield reduction.
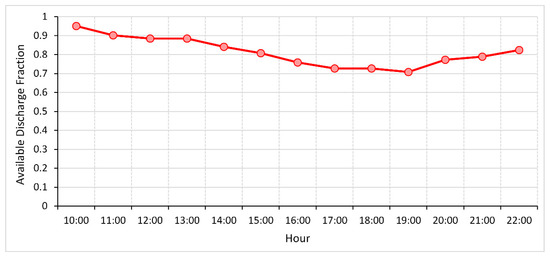
Figure 11.
ADF resulted from PDA of the peak demand day.
4. Conclusions
During peak demand periods, the discharge flowing in the system may exceed the design discharge of the system, causing insufficient pressure head at the hydrant level, which can adversely affect the discharges supplied for irrigation. In this work, DESIDS was used to analyse an existing PIDS by generating realistic hydrants configuration. A tool was developed to link two of its incorporated modules, namely, the irrigation demand and scheduling module and the hydraulic analysis module. The tool generates operating hydrants configurations, with 15-, 30- or 60-min time steps, by estimating the irrigation scheduling for each field served by the considered PIDS, using climatic, crop and soil data. Hence, it provides irrigation district managers with great flexibility and the ability to assess the operation of PIDSs at any period during the irrigation season. This is achieved by performing either DDA or PDA. This work has shown that using the latter is vital to determine not just pressure deficiencies in the network but a−o the impact of these deficiencies on the supplied discharges from hydrants. Thus, it estimates the potential negative impact of the overall performance of the PIDS on crops’ yield. This information is imperative as it gives irrigation district managers the ability to extend the management of the PIDS beyond the distribution structure and understand the real effect of their decisions on crops’ yield and farmers’ income. The information provided by the integration of the developed model into DESIDS and the ability of the latter to perform PDA is an innovative approach in the decision-making process for PIDSs operation and management. The existing models found in the literature do not provide such approach and lack the ability to estimate discharge deficit caused by the failure to provide the appropriate pressure at the hydrant level.
Author Contributions
Conceptualization, A.F.; methodology, A.F.; software, A.F.; validation, A.F. and J.A.R.D.; formal analysis, A.F.; data curation, A.F.; writing—original draft preparation, A.F.; writing—review and editing, A.F., J.A.R.D., and N.L.; visualization, A.F.; supervision, N.L. and J.A.R.D. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Clément, R. Calcul des débits dans les réseaux d’irrigation fonctionnant à la demande. La Houille Blanche 1966, 5, 553–576. [Google Scholar] [CrossRef]
- Granados, A.; Martín-Carrasco, F.J.; García de Jalón, S.; Iglesias, A. Adaptation of irrigation networks to climate change: Linking robust design and stakeholder contribution. Span. J. Agric. Res. 2015, 13, e1205. [Google Scholar] [CrossRef]
- Lamaddalena, N.; Sagardoy, J.A. Performance Analysis of On-Demand Pressurized Irrigation Systems; FAO Irrigation and Drainage Paper 59; Food and Agriculture Organization of the United Nations: Rome, Italy, 2000. [Google Scholar]
- Khadra, R.; Lamaddalena, N. Development of a decision support system for irrigation systems analysis. Water Re. Manag. 2010, 24, 3279–3297. [Google Scholar] [CrossRef]
- Lamaddalena, N.; Khadra, R.; Fouial, A. Use of localized loops for the rehabilitation of on-demand pressurized irrigation distribution systems. Irrig. Sci. 2015, 33, 453–468. [Google Scholar] [CrossRef]
- Pulido-Calvo, I.; Roldán, J.; López-Luque, R.; Gutiérrez-Estrada, J.C. Demand Forecasting for Irrigation Water Distribution Systems. J. Irrig. Drain. Eng. 2003, 129, 422–431. [Google Scholar] [CrossRef]
- Smith, M. CROPWAT: A Computer Program for Irrigation Planning and Management; FAO Irrigation and Drainage Paper 46; Food and Agriculture Organization of the United Nations: Rome, Italy, 1992. [Google Scholar]
- Fortes, P.S.; Platonov, A.E.; Pereira, L.S. GISAREG—A GIS based irrigation scheduling simulation model to support improved water use. Agric. Water Manag. 2005, 77, 159–179. [Google Scholar] [CrossRef]
- Almiñana, M.; Escudero, L.F.; Landete, M.; Monge, J.F.; Rabasa, A.; Sánchez-Soriano, J. WISCHE: A DSS for water irrigation scheduling. Omega 2010, 38, 492–500. [Google Scholar] [CrossRef]
- Moreno, M.; Planells, P.; Ortega, J.; Tarjuelo, J. New methodology to evaluate flow rates in on-demand irrigation networks. J. Irrig. Drain. Eng. 2007, 133, 298–306. [Google Scholar] [CrossRef]
- Córcoles, J.I.; Tarjuelo, J.M.; Moreno, M.A. Methodology to improve pumping station management of on-demand irrigation networks. Biosyst. Eng. 2016, 144, 94–104. [Google Scholar] [CrossRef]
- Khadra, R.; Lamaddalena, N. A Simulation Model to generate the Demand Hydrographs in Large-scale Irrigation Systems. Biosyst. Eng. 2006, 93, 335–346. [Google Scholar] [CrossRef]
- Zaccaria, D.; Lamaddalena, N.; Neale, C.M.U.; Merkley, G.P.; Palmisano, N.; Passarella, G. Simulation of peak-demand hydrographs in pressurized irrigation delivery systems using a deterministic–stochastic combined model. Part I: model development. Irrig. Sci. 2011, 1–16. [Google Scholar] [CrossRef]
- Rodríguez Díaz, J.; Camacho Poyato, E.; López Luque, R. Model to forecast maximum flows in on-demand irrigation distribution networks. J. Irrig. Drain. Eng. 2007, 133, 222–231. [Google Scholar] [CrossRef]
- De Nys, E.; Le Gal, P.-Y.; Raes, D.; Ana, E. WaDI (water delivery for irrigation): A simulation tool to address strategic interaction of water demand and supply in irrigation schemes. Agric. Water Manage. 2008, 95, 224–232. [Google Scholar] [CrossRef]
- Fouial, A.; García, I.F.; Bragalli, C.; Lamaddalena, N.; Diaz, J.A.R. Multi-Objective Optimization Model Based on Localized Loops for the Rehabilitation of Gravity-fed Pressurized Irrigation Networks. Water Res. Manage. 2017, 32, 465–480. [Google Scholar] [CrossRef]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop Evapotranspiration-Guidelines for Computing Crop Water Requirements; Food and Agriculture Organization of the United Nations: Rome, Italy, 1998. [Google Scholar]
- Khadra, R.; Moreno, M.A.; Awada, H.; Lamaddalena, N. Energy and hydraulic performance-based management of large-scale pressurized irrigation systems. Water Res. Manag. 2016, 30, 3493–3506. [Google Scholar] [CrossRef]
- Rossman, L.A. EPANET 2 Users Manual; National Risk Management Research Laboratory, U.S. Environmental Protection Agency: Cincinnati, OH, USA, 2000.
- Tanyimboh, T.T.; Templeman, A.B. Seamless pressure-deficient water distribution system model. Proc. Inst. Civ. Eng.-Water Manag. 2010, 163, 389–396. [Google Scholar] [CrossRef]
- Ozger, S.S.; Mays, L.W. A semi-pressure-driven approach to reliability assessment of water distribution networks. In Proceedings of the 30th IAHR Congress, Thessaloniki, Greece, 24–29 August 2003; pp. 345–352. [Google Scholar]
- D’Ercole, M.; Righetti, M.; Ugarelli, R.M.; Berardi, L.; Bertola, P. An integrated modeling approach to optimize the management of a water distribution system: Improving the sustainability while dealing with water loss, energy consumption and environmental impacts. Procedia Eng. 2016, 162, 433–440. [Google Scholar] [CrossRef]
- Giustolisi, O.; Laucelli, D.; Colombo, A.F. Deterministic versus Stochastic Design of Water Distribution Networks. J. Water Res.. Plan. Manage. 2009, 135, 484–492. [Google Scholar] [CrossRef]
- Abdy Sayyed, M.A.H.; Gupta, R.; Tanyimboh, T.T. Noniterative application of EPANET for pressure dependent modelling of water distribution systems. Water Res. Manage. 2015, 29, 3227–3242. [Google Scholar] [CrossRef][Green Version]
- Pacchin, E.; Alvisi, S.; Franchini, M. Analysis of non-iterative methods and proposal of a new one for pressure-driven snapshot simulations with EPANET. Water Res. Manage. 2016, 31, 75–91. [Google Scholar] [CrossRef]
- Daccache, A.; Lamaddalena, N.; Fratino, U. Assessing pressure changes in an on-demand water distribution system on drip irrigation performance—case study in Italy. J. Irrig. Drain. Eng. 2010, 136, 261–270. [Google Scholar] [CrossRef]
- Fouial, A.; Fernández García, I.; Bragalli, C.; Brath, A.; Lamaddalena, N.; Rodríguez Diaz, J.A. Optimal operation of pressurised irrigation distribution systems operating by gravity. Agric. Water Manage. 2017, 184, 77–85. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).