Abstract
In this study, numerical simulations were conducted in order to understand the role of wave-current interactions in wave deformation. The wave-current interaction mechanisms, wave reflection and energy loss due to currents, the effect of incident conditions on wave-current interactions, the advection-diffusion characteristics of saltwater, and the effect of density currents on wave-current interactions were discussed. In addition, the effect of saltwater–freshwater density on wave-current interactions was investigated under a hypopycnal flow field via numerical model testing. Turbulence was stronger under the influence of wave-current interactions than under the influence of waves alone, as wave-current interactions reduced wave energy, which led to decreases in wave height. This phenomenon was more prominent under shorter wave periods and higher current velocities. These results increase our understanding of hydrodynamic phenomena in estuaries in which saltwater–freshwater and wave-current pairs coexist.
1. Introduction
In the ocean, various continually interacting physical external forces. In particular, estuaries are characterized by freshwater flows from land and saltwater flows from the ocean, which meet and form a major pathway for material transportation. Estuaries are complex, therefore it is difficult to investigate their hydrodynamic characteristics. Thus, it is critical to analyze the dynamic interactions between complex estuary features, including wave-current interaction mechanisms. Furthermore, it is necessary to understand the effect of a density current, which is generated by density differences between saltwater and freshwater, on wave-current interactions.
In the estuary that exhibits highly complex hydraulic characteristics, the circulation type varies significantly according to vertical salinity distribution, tide, and wave [1,2]. However, if two fluids differing in density meet at the estuary, three types of flow and material transport patterns are largely exhibited [3,4]. As shown in Figure 1, homopycnal flow occurs in the case of no density difference, hypopycnal flow occurs when the influx flow has a lower density, and hyperpycnal flow occurs when the influx flow has a higher density. Hypopycnal flow generally occurs in the estuary when fresh river water flows in to ocean and interacts with ocean waves. However, most studies that attempted to analyze the wave-current interaction mechanism at the estuary region did not consider the density discrepancy between freshwater and saltwater, and were performed under homopycnal flow conditions. Meanwhile, due to the developments of measurement equipment, wave transformation, wave set-up, flow rate, salinity, and temperature at the estuary are being observed [5,6,7,8,9]. In some studies, a model of the estuary was composed in a three-dimensional experimental tank to measure wave variation based on wave-current interaction and vertical salinity distribution influenced by density current behavior at the estuary [10,11]. Onsite investigations or transport of three-dimensional experiment to the estuary requires significant time and money and only allows for limited information to be recorded at measurement points.
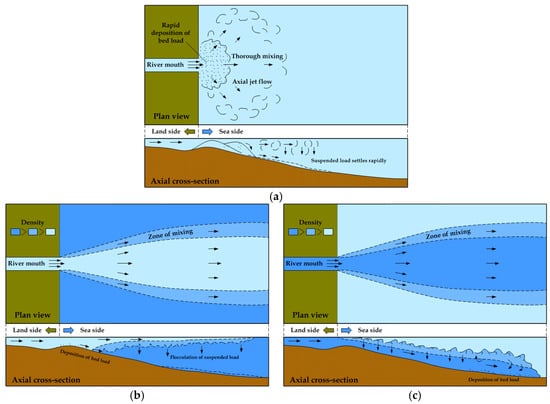
Figure 1.
Three types of estuarine hydrodynamics based on the density differences between river and sea/lake water (Modified from Bates [3] and Boggs [4]). (a) Homopycnal flow; (b) hypopycnal flow; (c) hyperpycnal flow.
Therefore, numerical simulations are frequently performed to analyze the hydraulic characteristics of the estuary. Most of studies have used the model based on the depth-averaged model [12,13,14] or the 3-D model based on σ-coordinate system [15,16]. This numerical model cannot directly simulate wave behavior due to a large discrepancy between the calculation grid and time. To consider the wave reaction, the wave radiation stress estimated from Simulating WAves Nearshore (SWAN [17]) or WAve Model (WAM [18]) are substituted into the momentum equations [14,19,20].
Various theoretical, experimental and observational studies on waves propagating with currents have previously been conducted in the field of coastal and ocean engineering [21,22,23,24,25]. In particular, there have been many studies on the effects of wave kinematics (changes in the wave number and frequency due to shoaling and refraction) and dynamics (changes in wave steepness and wave-action conservation) according to wave-current interaction [26,27,28,29]. Wave kinematics include the effects of depth and current in wavelength variation and dispersion (Doppler shift) according to opposing or following current. Wave dynamics include energy and action conservation and the variations in wave height and water level [24,30]. Umeyama [31] and Lee et al. [32] explored the vertical distribution of flow and turbulence structures under wave-current interactions in order to analyze wave-current interaction mechanisms. Smith et al. [10] investigated wave deformation by wave-current interactions in a 3-D experimental basin with an estuary model. However, these experimental studies were not able to define the mechanisms of wave deformation and energy loss due to wave-current interactions. Numerical studies have reproduced past experimental results, but have focused mostly on wave deformation, neglecting to analyze the mechanisms behind wave-current interactions. In addition, Umeyama [33] measured and analyzed the flow velocity and trace of water particles by combining them with the particle image velocimetry (PIV) and particle tracking velocimetry (PTV) when the wave and current have the same direction. Chen et al. [34] studied the trace of water particles using the electronic hydrometer when the wave and current have opposite directions. However, none of the experimental studies conducted so far describe the wave deformation phenomenon and the mechanism of energy decrease clearly. The abovementioned studies focus on the motion of water particles from the wave-current interaction instead of the characteristics of wave deformation. Fernando et al. [35] discussed the topographic change resulting from the wave-current crossing angle, and the characteristics of local and vertical distribution of flow velocity. However, it is difficult to extend this study to analyze the effect of the hydraulic pattern. Lim and Madsen [36] analyzed the vertical flow velocity structure and shear velocity for wave-current crossing angles of 30°, 60°, and 90° for conditions of smooth and uniform beds of fixed roughness. The results show that the fluid motion affects some topographic changes depending upon the wave-current crossing angle.
Wave reflection by the opposing current is known to be weakened under wave-current interactions. Longuet-Higgins and Stewart [37] built a theoretical background for wave reflection by currents upon which many researchers have expanded [38]. These theoretical backgrounds remain insufficient for defining reflection characteristics under wave-current interactions. Lee et al. [39] did not discuss wave reflection, although a partial standing wave field was formed by the wave-current interactions in their experiments. Rey et al. [40] measured wave reflection using a 3-D experiment basin in which the wave and current coexist, using the incidence and reflected wave separation method proposed by Drevard et al. [41]. Lee et al. [32] investigated the effect of turbulence on the reduced wave height in a river channel. They analyzed the coefficient of wave reflection due to the current in the partial standing wave field. However, a structure was installed in their experimental water tank, so the net wave reflection due to the wave and current cannot be known.
Currently, advances in computer technology have enabled 3-D numerical model experiments [42,43,44,45] using Navier–Stokes solvers with high calculation loads. In addition, Liu et al. [46] applied the homotopy analysis method (HAM) to the analysis of wave-current interaction to identify the utility and show the potential of solving the issue of strong wave-current interaction.
Previous studies [32] were performed under homopycnal flow conditions without considering the density discrepancy at the estuary. It is expected that hydraulic characteristics according to wave-current interaction and a decreased mechanism of wave height will show a difference at the actual estuary. In this study, it was necessary to improve the existing numerical wave water tank in order to analyze density current caused by temperature or salinity difference. Afterwards, the measured wave height distribution and density current propagation processes according to wave-current interaction in the existing experiment were compared and verified in order to check the validity and effectiveness. Subsequently, the wave height decrease mechanism, wave reflection, average water level, and turbulence energy caused by wave-current interaction were analyzed numerically. Further, from the numerical simulation model considering hypopycnal flow, the influence of density current, that is exhibited in the case of density difference between the river and ocean, on wave-current interaction was thoroughly investigated.
2. Numerical Model
The mechanism and hydrodynamic characteristics of the interactions between waves and currents were analyzed accounting for the densities of freshwater and seawater. For this purpose, a 3-D numerical analysis model [47,48] based on the existing 3-D numerical wave tank (NWT), LES-WASS-3D [49,50,51] was introduced to analyze density currents in this study.
LES-WASS-3D, which is based on the 3-D Navier–Stokes momentum equations, uses the volume of fluid (VOF) method to reproduce complicated free surfaces, including wave breaking, and the porous body model (PBM) to reflect energy dissipation by a permeable structure; the model was based on Hur and Mizutani [52] and Hur et al. [53]. In addition, to analyze sub-grid scale (SGS) turbulence, Smagorinsky turbulence model (STM [54]) for the large eddy simulation (LES) was adopted in the NWT [55]. By considering inertia [56], turbulence [57,58], and laminar flow resistance [58,59] according to porous medium characteristics (diameter, porosity, and shape), the model can directly analyze interactions among waves, structures, and the seabed [49,50,51].
The water density state equation (refer to Appendix A [60]) and kinematic viscosity coefficient (refer to Appendix B [61]) were applied herein to analyze the density current in view of salinity and temperature. Salinity and temperature were quantitatively calculated by simultaneously applying a 3-D advection-diffusion equation. Due to flow separation around structures, present LES turbulence models do not provide accurate calculations of turbulence, which significantly influences the diffusion coefficient applied in the advection-diffusion equation. Thus, a dynamic modeling procedure involving the application of the dynamic eddy viscosity model suggested by Germano et al. [62] and Lilly [63] was applied to re-evaluate Smagorinsky constant ().
2.1. Governing Equations
The basic set of calculations consists of the continuity equation (Equation (1)), which includes the source term that generates waves and currents without reflection in 3-D incompressible and viscous fluids, and a modified Navier–Stokes momentum equation (Equation (2)), in which the fluid resistance of the permeable structure is applied.
where is the Cartesian coordinate system (, , and ); is time; is the velocity components (, , and ); is the fluid density; is the fluid pressure; is the kinematic viscosity coefficient; is the eddy viscosity coefficient from the turbulence model; and are the volume and surface porosities, as shown in Figure 2; is the fluid resistance term for the porous media; is the acceleration of gravity; refers to the wave energy damping term (; where is the damping factor which equals 0 except for the added damping zones) for the vertical velocity only; Qi refers to the wave and current source terms (); and is the source term required to generate waves and currents, and it is defined as:
where is the flux density; is the grid size at the source position ().
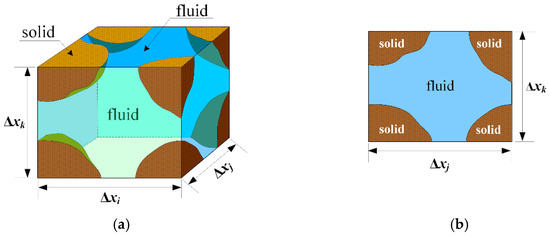
Figure 2.
Definition of the volume and surface porosities. Each cell is flagged as one of three types according to the value: an empty cell occupied by fluid ( ), an impermeable cell without fluid flow ( ), and a permeable cell containing both solid and fluid (), where and are the volume and surface area of solids in a cell, respectively. (a) ; (b) .
As suggested by Brorsen and Larsen [64], the flux density of the wave and current generation sources in Equation (3) is gradually increased during three wave periods starting with wave and current generation, as shown in Equation (4).
where is the horizontal velocity determined by incident condition (in case of wave, based on the 3rd-order Stokes wave theory); and is the intensity factor at the wave source (); is the water surface elevation at the source position, is the water surface elevation estimated using the 3rd-order Stokes wave theory, and is the water depth). The constant “2” accounts for two flows propagating to the left and right sides in NWT. The depth integrated quantity of is adjusted by to achieve the same quantity in the non-reflection condition [65].
is the volume of fluid (VOF) in each cell [66], which can be expressed as fluid conservation by applying an assumption of fluid incompressibility and a function volume based on PBM, as in Equation (5).
where is the VOF function. In the numerical simulation, each cell is assigned as one of three types by the VOF function value: fluid cell (), empty cell (), and free surface cell ().
2.2. Advection-Diffusion Equations
In density current analyses, quantitative decisions about influential factors are important in order to accurately calculate the fluid density and kinematic viscosity coefficient , which are substituted into the governing equations. The state equation used to calculate the density and kinematic viscosity coefficient of water is a function of temperature and salinity . Therefore, the 3-D advection-diffusion equations adopted herein include Equation (6) for temperature and Equation (7) for salinity.
where is temperature or salinity , and is the horizontal and vertical diffusion coefficients. In this study, , which is the Prandtl/Schmidt number, has a value of 1.0, as estimated from experimental results [67] and ocean observations [68,69].
2.3. Turbulence Model
In general, to reproduce complete turbulence, the calculation area must be larger than the representative scale of the fluid, and the grid must be set smaller than the minimum turbulence scale. It is essential to consider turbulence when modeling a 3-D phenomenon, therefore the grid number of (; Reynolds Number) is required. However, it is practically impossible conduct numerical analysis using this number of grids. Thus, the use of a turbulence model is practical for reproducing turbulence. To this end, the STM [54] was adopted in this study.
However, a model constant () must be applied in the eddy viscosity model for the fluid. For this, the appropriate can be calculated through the dynamic modeling procedure suggested by Germano et al. [62] and Lilly [63].
The dynamic modeling method expresses the physical quantity included in the analytical grid as functions of time and space. This method does not require prior designation of unknown model constants or fine tuning and can accurately predict laminar flow and asymptotic behavior near walls. In addition, the model constant has a negative value showing energy backscattering, as the model constant is applied temporally and spatially.
2.3.1. Eddy Viscosity Model
In the STM, length and speed are expressed as and , respectively. The speed calculation assumes that the pure dissipation equals the energy transferred from the large-scale to small-scale analytical grids, and that the eddy viscosity coefficient formula is expressed as:
where is the strain tensor for the grid size, and is the filter length scale.
2.3.2. Dynamic Eddy Viscosity Model
In the LES grid, the stress of the sub-grid scale can be modeled via Equation (12) and Equation (13) using STM.
where and have the same definition in the STM.
Likewise, the stress of the secondary stress can be modeled as Equations (14) and (15) by applying a secondary filter.
A secondary filter (the test filter) with width larger than is introduced. It is generally assumed that the width of the test filter is two times of that of the grid filter and that the of the two filters are the same. These assumptions are adopted in this study. and are related by the Germano identity.
Substituting the sub-grid scale stress from Equation (13) and secondary filter stress from Equation (15) into Equation (16) produces relationships such as those seen in Equation (18).
where is the ratio of the test and grid filters ().
There is only one unknown quantity, , in Equation (17). Both and are tensors, so Equation (17) is an overdetermined equation system. Applying a least-squares technique to Equation (17) produces a least error value for .
A critical problem exists in the determination of the space-temporal function . If exhibits severe fluctuations or negative values, numerical instability is induced, and it ultimately diverges. To prevent such numerical instability, a space mean in uniform direction of numerator and denominator is required locally for every calculation. In addition, a clipping of is also required so that can always be a positive (+) value. On following the above process, most of the limitations of STM can be overcome. Germano et al. [62] proposed 1/2 as the optimal value in flow calculation while applying the dynamic eddy viscosity model. We also apply in this study.
2.4. Non-Reflected Boundary
Figure 3 shows a schematic diagram of a numerical water basin with a variable grid system and damping factors in an added damping zone for non-reflected wave generation [70]. Each grid cell in the damping zone increases its size by a factor 1.03 with respect to the previous cell as they approach the open boundaries, as shown in Equation (21). This approach serves to make the analysis zone independent from the influence of the numerical water basin boundaries. In addition, wave reflection is controlled by setting the horizontal differences in physical quantities , such as velocity and the VOF function, to zero at the numerical water basin boundary, as shown in Equation (22).
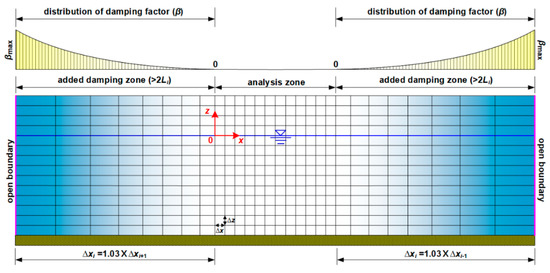
Figure 3.
Schematic diagram of grid system and damping factor in a numerical wave basin.
For the boundary condition of the impermeable slope in a quadrilateral mesh system according to spatial discretization based on finite difference method, the impermeable condition is adopted in the normal direction and slip condition is adopted in the tangential force for the inclined structure by applying the reasonable boundary [48,51] based on Petit et al. [71].
2.5. Numerical Water Basin Stability
Figure 4 presents the computed water surface profiles in the numerical water basin during one wave period. Figure 3 shows that the wave spatial envelope is gradually attenuated in both of the added damping zones by the numerical dispersion caused by the coarse grid system and the wave damping term included in the momentum equation; the wave spatial envelope vanishes after x/Li = 2. An added damping zone with a length over 2 Li was applied in this study. From numerical result such as those in Figure 3, one can conclude that the present non-reflected system works efficiently to absorb waves in the damping zone and release energy out of the open boundaries.
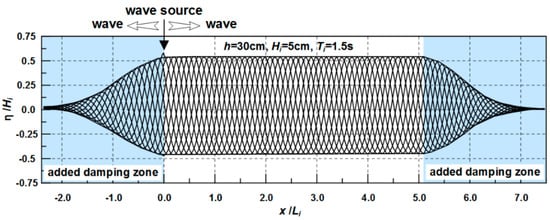
Figure 4.
Computed wave profiles for each time step and envelope in a numerical water basin.
2.6. Numerical Model Validation
2.6.1. Wave-Current Interaction
The hydraulic model experiment in Iwasaki and Sato [72] was simulated to verify the characteristics of wave deformation by wave-current interactions in an open channel. Figure 5 shows the numerical water tank simulated by Iwasaki and Sato [72]. Wave and current generation sources (without reflection) were deployed at each end of the analysis domain, and additional damping zones were included at both ends. For verification, a numerical calculation was conducted with an x direction grid size of 1 cm, a z direction grid size of 0.5 cm, and a time increment of 1/1000 s.
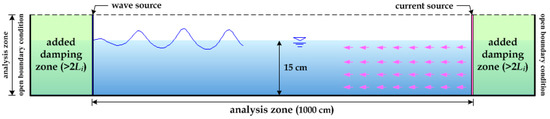
Figure 5.
The numerical water basin is modelled after the experimental campaign by Iwasaki and Sato [72].
Figure 6 shows the wave height distribution while the wave propagates over an opposing current, where (a) shows a current velocity of Vc = 6.3 cm/s and (b) shows a current velocity of Vc = 19 cm/s. Here, the black circle (●) and blue triangle (▲) indicate the experimental results, and black line (━) and blue line (━) represent the modelled values. Wave height damping due to wave-current interactions is observed in the experimental results and calculations shown in Figure 6. In this study, the experimental results are reproduced well by the calculations. Furthermore, the inclination of the wave height distribution is quite similar in the calculations and the experiments for wave deformations with coexisting wave-current fields. This indicates that the ratios of wave height damping due to wave-current interaction are similar. These results were used to determine the validity and effectiveness of the numerical model for wave transformation during an interaction with an opposing current.
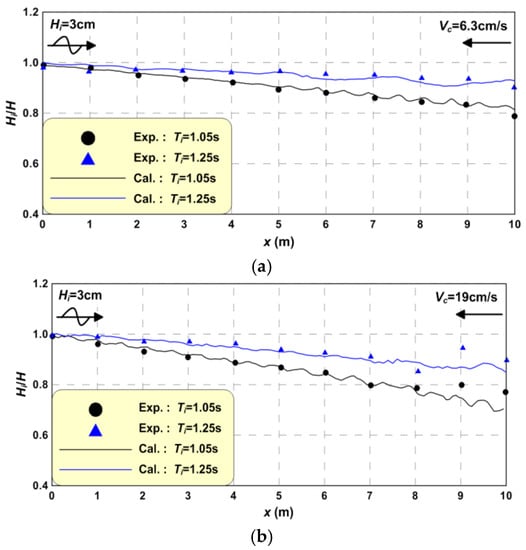
Figure 6.
Comparison between measured and calculated wave heights under wave-current interactions. (a) Vc = 6.3 cm/s; (b) Vc = 19 cm/s.
2.6.2. Salinity Advection
Figure 7 shows a numerical water tank based on the hydraulic model experiment in Huppert and Simpson [73]. The water tank was 960 cm long and 27 cm wide, and the water depth was 10 cm. A compartment of 30 cm long (x0) was installed in the water tank and filled with the density of saltwater (ρs) of 1.0115 g/cm3. The remaining area was filled with the density freshwater (ρf) of 0.9999 g/cm3. The density difference (Δρ) was 0.0116 g/cm3 and the reduced gravity g’ (= Δρg/ρf) was 11.4 cm/s2. The grid size for verification was Δx = 1 cm, Δy = 1 cm, and Δz = 0.25 cm, and the numerical calculation was carried out for Δt = 1/1000 s.
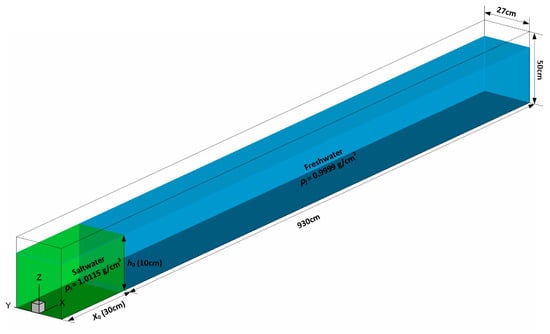
Figure 7.
The numerical water basin is modeled after the experimental campaign by Huppert and Simpson [73].
Figure 8 shows the temporal evolution of the salinity front due to the density difference. The upper picture shows the experimental results and the lower picture shows the calculated results. The figure also shows the saltwater shapes when (a) t = 4.4 s, (b) t = 6.8 s, (c) t = 9.7 s, and (d) t = 17.5 s after the partition was removed from the compartments.
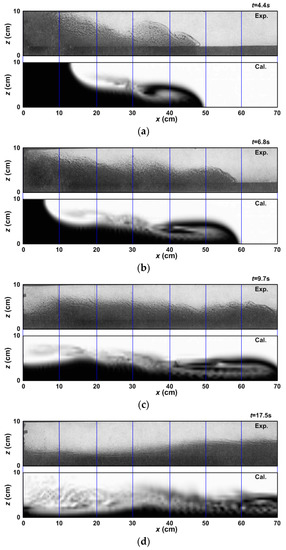
Figure 8.
Comparison between experimental (upper picture) and numerical (lower picture) results showing the evolution of advection-diffusion of a saltwater mass. (a) t = 4.4 s; (b) t = 6.8 s; (c) t = 9.7 s; (d) t= 17.5 s.
3. Numerical Results
3.1. Wave-Current Interactions without Density Current
3.1.1. Description of Numerical Water Basin and Incident Conditions
A numerical wave tank was defined as shown in Figure 9 in order to numerically investigate the mechanisms of wave-current interactions according to the velocity of the incident wave and current in an open channel. To generate waves based on 3rd-order Stokes waves and currents without reflection, wave and current sources were installed at each end of the analytical domain; damping zones were added at both ends to absorb wave energy. The length of the analytical domain was 5 Li of the incident wavelength, the width was 30 cm, and the water depth was 30 cm. In addition, the length of the damping zones was set to more than double the incident wavelength to absorb wave energy and minimize reflection.
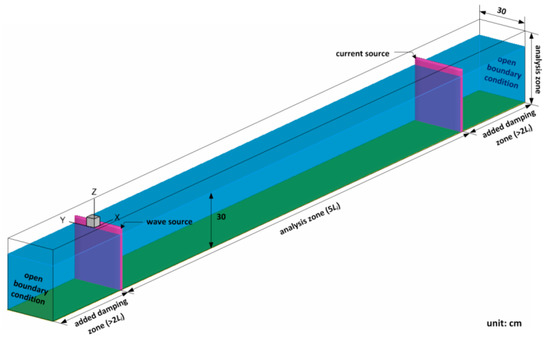
Figure 9.
Sketch of a numerical water basin for simulating wave-current interactions.
Wave-current interaction numerical simulations were performed for 63 different cases involving three incident wave heights (Hi = 3, 5, and 7 cm), three incident wave periods (Ti = 1.2, 1.5, and 1.8 s), and seven current velocities (Vc = 0, 5, 10, 15, 20, 25, and 30 cm/s). The wave celerity (Ci) is based on 3rd-order Stokes wave theory. The calculation grids were Δx = 2 cm, Δy = 2 cm, and Δz = 1 cm. In all simulations, the wave was generated after current generation in order to stabilize the flow field.
3.1.2. Distribution of Wave Heights
Figure 10 shows the wave height spatial distributions for various current velocity conditions when the incident wave (Ti) period was 1.2 s. As shown in Equation (23), the wave height was calculated using surface elevations (Equation (24)) from three periods and described via the non-dimensional wave height (H/Hi) after the flow and wave field stabilized.
where and represent the bottom and top of the NWT, and is the grid size in the z direction.
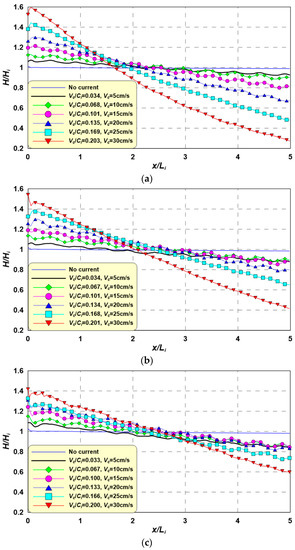
Figure 10.
Spatial distributions of wave heights for an incident wave period of 1.2 s according to Vc. (a) Hi = 3 cm, Ti = 1.2 s, Hi/Li = 0.017, Ur = 3.5; (b) Hi = 5 cm, Ti = 1.2 s, Hi/Li = 0.028, Ur=5.8; (c) Hi = 7 cm, Ti = 1.2 s, Hi/Li = 0.04, Ur = 8.1.
In Figure 10, for all the cases, the wave height is higher than the incident wave height (Hi) at x/Li = 0. The wave height gradually decreases with wave propagation. This phenomenon is more obvious as the ratio (Vc/Ci) between current velocity (Vc) and incident wave celerity (Ci) increases. A partial standing wave field is generally observed due to wave reflection by the wave-current interactions. These results are in agreement with the experimental results [32,39,74]. In addition, an intersecting point with a wave height of H/Hi = 1 is observed in (a–c); this point moves farther from x/Li = 0 as Hi increases because Ci increases, thus decreasing Vc/Ci.
Furthermore, as Vc/Ci increases, the partial standing wave wave-height distribution is marginally formed. In this case, the wave height is also relatively high at x/L = 0 in comparison to the point at which the partial standing wave forms. This phenomenon was also reported by Lee et al. [39], who found Hi = 5 cm, Ti = 1.0 s, and Vc = 60 cm/s. In other words, shorter wave periods, lower wave heights, and higher current velocities lead to lower wave orbital motion velocity. Therefore, this phenomenon appears to be a result of the predominance of wave energy loss over wave reflection. Nevertheless, further study is required to verify this mechanism.
Figure 11 shows the spatial distribution of the H/Hi according changes in the Vc under Ti = 1.5 s. This figure shows a tendency similar to that in Figure 10, which has Ti = 1.2 s. However, the Vc/Ci is small compared to the case with Ti = 1.2 s; thus, the effects caused by a decrease in wave height due to decreases in interactions decrease, and changes in the wave height rate become weaker. For this reason, points (H/Hi = 1) generally move far from x/Li = 0. The wave height distribution becomes narrower because the range over which Vc/Ci fluctuates is relatively narrow.
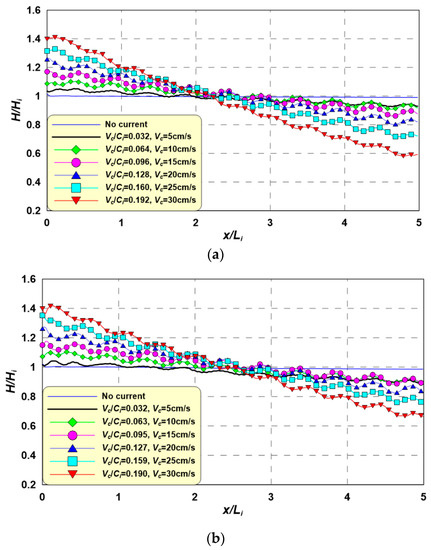
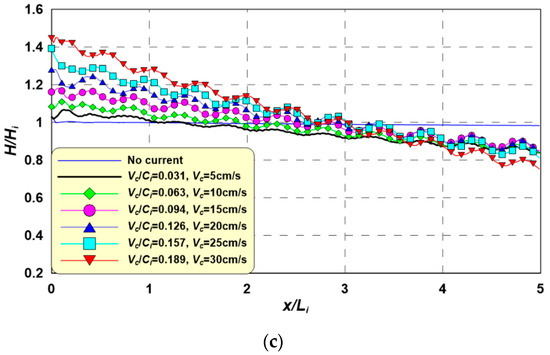
Figure 11.
Spatial distributions of wave heights for an incident wave period of 1.5 s according to Vc. (a) Hi = 3 cm, Ti = 1.5 s, Hi/Li = 0.013, Ur = 6.1; (b) Hi = 5 cm, Ti = 1.5 s, Hi/Li = 0.021, Ur = 10.2; (c) Hi = 7 cm, Ti = 1.5 s, Hi/Li = 0.03, Ur = 14.2.
Figure 12 shows the wave height spatial distribution with changes in the Vc under Ti = 1.8 s. This figure also shows a tendency similar to those in Figure 8 and Figure 9, and also shows prolonged wave-current interaction period characteristics. As the Ti increases, the range over which Vc/Ci fluctuates decreases, resulting in a narrower wave height distribution. In addition, as the incident wave period and wave height increase, the Ci increases and the decreases in wave height weaken, resulting in gentler inclinations in the wave height distribution.
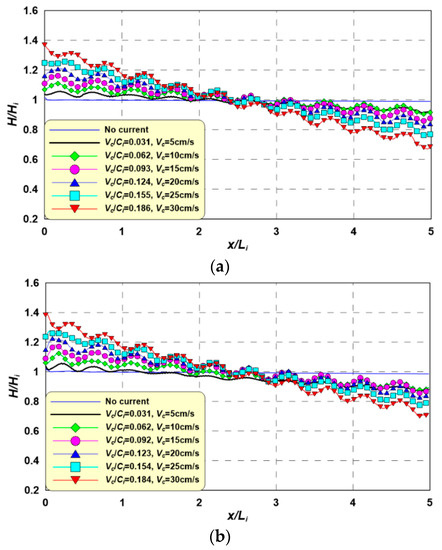
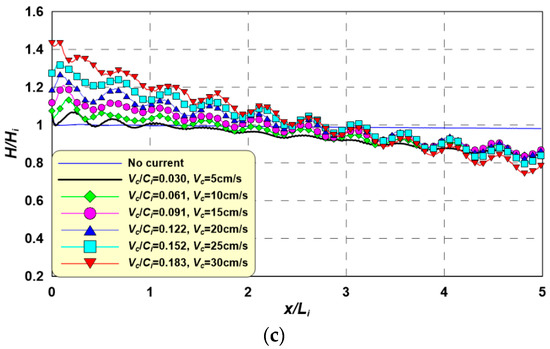
Figure 12.
Spatial distributions of wave heights for an incident wave period of 1.8 s according to Vc. (a) Hi = 3 cm, Ti = 1.8 s, Hi/Li = 0.01, Ur = 9.3; (b) Hi = 5 cm, Ti = 1.8 s, Hi/Li = 0.017, Ur = 15.5; (c) Hi = 7 cm, Ti = 1.8 s, Hi/Li = 0.024, Ur = 21.7.
Considering the above discussion of Figure 8, Figure 9 and Figure 10, the wave orbital motion velocity and current velocity have the same direction under the wave trough and different directions under the wave crest within the wave-current interaction. As confirmed in the existing experiment, more intense wave-current interactions occur in the wave crests than in the wave troughs. This leads to wave reflection and wave height decay.
3.1.3. Characteristics of Turbulent Kinitic Energy (TKE)
The mean phase-averaged TKE () is the average turbulence over ten wave periods, as shown in Equation (25). This TKE is calculated using Equations (26) and (27), as suggested by Christensen [75]. Equation (26) can be used to calculate the TKE of a grid scale () using the flow velocity calculated by the numerical model, and Equation (27) can be used to calculate TKE of a sub-grid scale () by applying the values calculated by LES. The center of the analysis zone is the measuring point.
where ,, and are turbulence components; is the eddy viscosity coefficient estimated using STM; is a model constant calculated by the dynamic eddy viscosity model; and is the filter length scale.
Figure 13 shows the vertical distribution of the according to the ratio of current velocity and wave celerity (Vc/Ci). This figure shows that the value of the mean phase-averaged TKE is larger with wave-current interactions than with waves alone. The intensity generally increases with higher Vc/Ci values. In particular, still water with higher velocity due to wave orbital motion shows higher TKE. Therefore, wave height decreases with increased TKE. The relationship between TKE and wave height decay in the coexisting wave-current field will be comprehensively discussed later, along with wave energy characteristics.
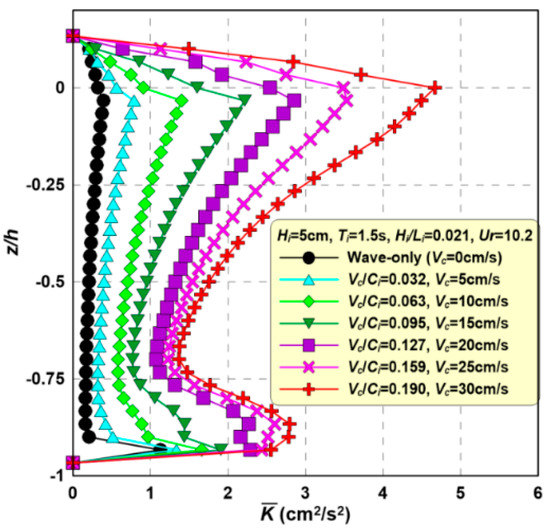
Figure 13.
Vertical distributions of mean phase-averaged turbulent kinitic energy (TKE) according to variations in Vc.
Figure 14 shows the vertical distribution of the according to the incident wave period (Ti). The mean phase-averaged TKE increases with increasing Hi, Hi/Li, and Ursell number (Ur). This increment is larger near still-water levels. In addition, with longer incident periods, the mean phase-averaged TKE increases in sections, except for those near the still-water level. Under the influence of wave-current interactions, TKE is closely related with velocity due to the orbital motion of waves and current velocity. That is, as the incident wave height and period increase, the velocity of water particles increases, and thus the TKE is increased by wave-current interactions.
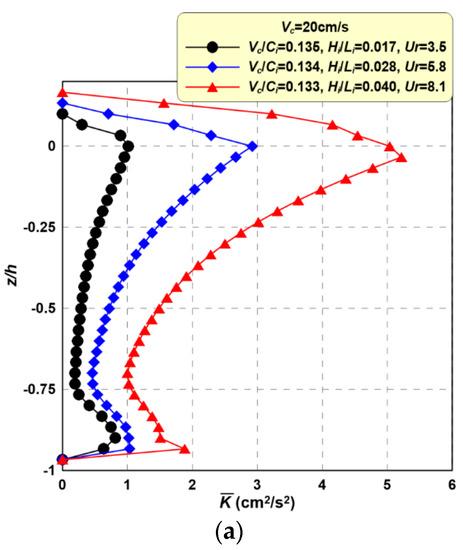
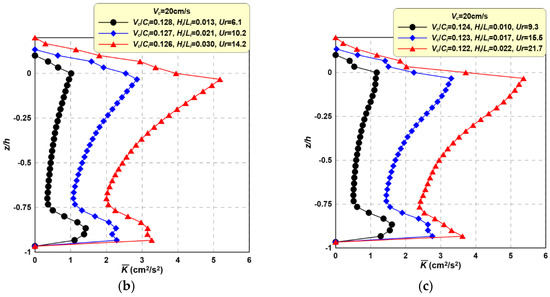
Figure 14.
Vertical distributions of mean phase-averaged TKE () according to variations in Hi. (a) Ti = 1.2 s; (b) Ti = 1.5 s; (c) Ti = 1.8 s.
Nevertheless, it is difficult to directly correlate TKE and the aforementioned wave height decay because they are not proportional. The wave energy conditions differ, therefore wave energy decay and wave height decay are not proportional to TKE. This relationship is closely related to the wave energy described later and will be discussed in more detail in the following section. Wave height decay is caused primarily by turbulence in the coexisting wave-current field, therefore the mechanism of wave attenuation will be analyzed by exploring changes in TKE, wave energy, and wave height decay.
3.1.4. Wave Energy Loss Characteristics
Wave energy () lost due to wave-current interactions is calculated by applying the simulated data in Equation (28) after a stable wave-current coexisting field is attained. In Equation (29), the mean energy loss () is calculated for three periods from the energy ratio of the prior and following waves. Subsequently, the average of five wavelengths is used to calculate the wavelength-averaged energy loss ().
Figure 15 shows the according to the Vc/Ci between current velocity and wave celerity under various wave conditions. Wave energy loss increases as Vc/Ci increases. This phenomenon can be explained with the fact that TKE increases as Vc/Ci increases, which results in increased energy loss. The energy decay rate was expected to increase because the TKE becomes larger as the incident wave height increases. The energy decay due to turbulence increases because higher wave energies accompany higher wave heights, but the general decay rate is relatively low compared to that for low wave heights.
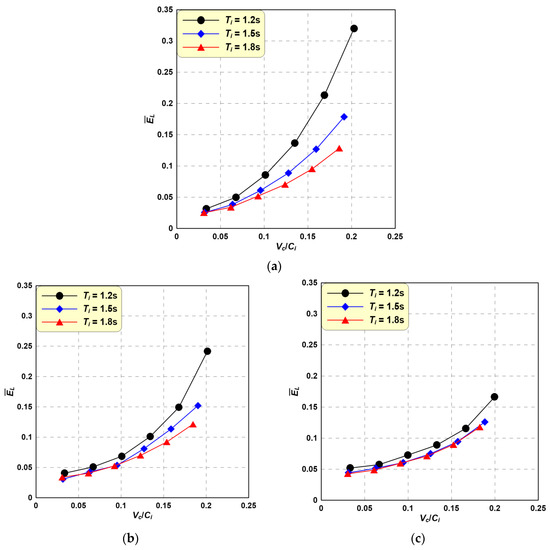
Figure 15.
Averaged energy loss according to variations in Vc. (a) Hi = 3 cm; (b) Hi = 5 cm; (c) Hi = 7 cm.
The aforementioned analytical results for wave height distribution, TKE, and wave energy show that the TKE increases with increasing Vc/Ci rate. This leads to wave energy and height decay. This numerical mechanism can be used to understand wave height decay due to wave-current interactions.
3.1.5. Wave Reflection Characteristics
Partial standing waves due to wave-current interactions are also found in the aforementioned wave height distribution. Equation (30), which was proposed by Healy [76], was used to calculate the reflection coefficient with the wave-current interactions. In addition, the values calculated for five partial standing wave field wavelengths were averaged to produce the average reflection coefficient.
where and are the wave heights at the node and the anti-node in a partial standing wave field, respectively.
Figure 16 shows the wavelength-averaged reflection coefficient () according to the ratio (Vc/Ci) between current velocity and wave celerity under various wave conditions. The wave reflection rate generally increases as Vc/Ci increases. Wave reflection due to current is generated by a strong interaction under the wave crest, where the wave orbital motion velocity and current velocity oppose each other. Therefore, the reflection rate increases as the current velocity increases. Meanwhile, (a–c), which feature the same incident wave height, show lower reflection rates with shorter incident wave periods. The wavelength is not long in waves with shorter periods, therefore the exposure time under the wave crest decreases. Therefore, the wave-current interaction time becomes shorter under an opposite flow velocity, resulting in a lower reflection rate. In addition, the current by the incident wave height does not appear to have strong effects on the wave reflection rate, which is similar to the reflective wave characteristics.
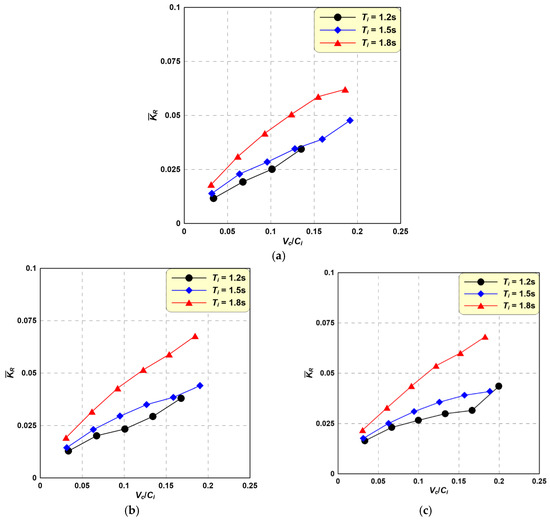
Figure 16.
Wavelength-averaged reflection coefficients according to variations in Vc. (a) Hi = 3 cm; (b) Hi = 5 cm; (c) Hi = 7 cm.
Wave reflection by currents, which was reported by an existing theoretical study to be insignificant [37], is therefore confirmed, and the mechanism is elucidated above. The reflection rate is up to 0.068 under the incident conditions applied herein. Such a wave reflection rate cannot be ignored when analyzing hydraulic phenomena in coexisting wave-current fields.
3.1.6. Mean Wave Level Characteristics
Figure 17 shows the spatial distribution of the mean water level according to the ratio between the current velocity and wave celerity, Vc/Ci. As shown in Equation (31), the mean water level was calculated using surface elevations (Equation (24)) from three periods and described via the non-dimensional mean level () after the wave and flow field stabilized.
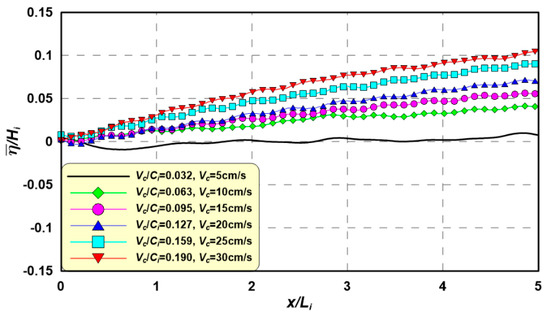
Figure 17.
Spatial distributions of mean water level under wave-current interaction according to variations in Vc.
In Figure 17, The mean water level also increases when Vc/Ci increases because the wave energy decreases due to wave-current interactions, which show a tendency to increase because the wave energy decreases further when Vc/Ci increases. Meanwhile, these types of wave level distributions create currents due to wave level differences; currents, in turn, increase the initial current velocity, which will accelerate wave height dissipation. To analyze this further, it is necessary to study the interactions between the flow field and the wave field.
3.2. Wave-Current Interactions with Density Current
The effect of current due to density differences between freshwater and saltwater must be considered, as estuaries contain both freshwater and saltwater. In the past, most studies on wave-current interactions did not consider density currents. Therefore, wave-current interactions under the influence of density differences were numerically simulated using a newly suggested numerical model in order to calculate density currents.
3.2.1. Description of Numerical Water Basin and Incident Conditions
A numerical water basin was prepared as shown in Figure 18 to evaluate the effect of density current on wave-current interactions in an estuary. To generate waves without reflection, wave and current sources were installed at both ends of the simulation domain, and damping zones were added to absorb the wave energy. The analysis zone featured a length of 5 Li of the incident wavelength, a width of 50 cm, and a water level of 30 cm; a 1:5 slope was installed to a water depth of 10 cm to serve as the current source.
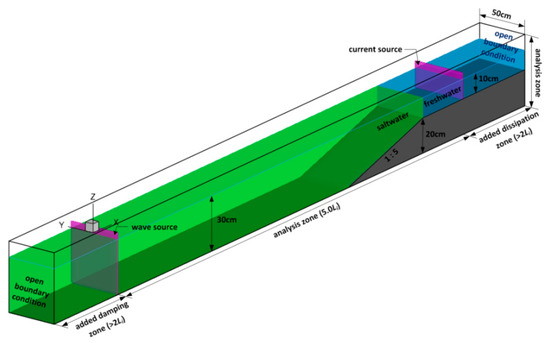
Figure 18.
Sketch of a numerical water basin for simulating wave-current interactions with included density differences.
The simulations were performed under fixed incident wave and current conditions and variable water density. The details are described in Table 1. Two major cases were considered: one with density differences under wave-current interactions, and another without density differences (ρw = ρc). The first major case was divided into three sub-experiments, which involved: high density water mass and low density current flows (ρw > ρc); low density water mass and high density current flows (ρw < ρc); and water mass with density stratification and middle density current flows (ρw1 < ρc < ρw2). Here, the reduced gravity (g’) is that the effective change in the acceleration of gravity acting on one fluid in contact with a fluid of different density due to buoyancy forces. For these, the calculation grids were Δx = 2 cm, Δy = 2 cm, and Δz = 1 cm. In all simulations, current was generated first, and waves were generated only after the flow field stabilized.

Table 1.
Incident wave and current conditions for simulating wave-current interactions with density differences.
3.2.2. Density Current Formation Characteristics
Figure 19 shows the flow fields for CASEs 1–4 in Table 1, in which current was generated without considering waves. In Figure 19, four different current shapes can be identified due to density differences, including (a) a uniform-depth current due to a lack of density difference, (b) an undercurrent due to a high-density current, (c) an upper current due to a low-density current, and (d) a middle current due to a middle-density current flowing into the density stratification. Based on these results, various currents may arise from various density difference structures. Therefore, the consideration of differences in density will affect the wave-current interactions in co-existing fields.
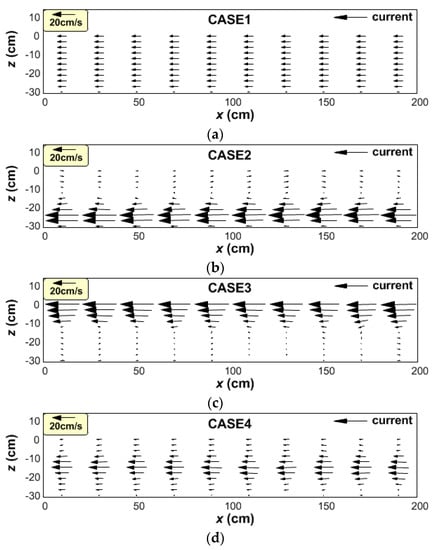
Figure 19.
Four types of density currents with varying density differences. (a) Depth-uniform current (ρw = ρc); (b) Undercurrent (ρw < ρc); (c) Upper current (ρw > ρc); (d) Middle current (ρw1 < ρc < ρw2).
3.2.3. Wave Height Variation
Figure 20 shows the wave height variations generated by wave-current interactions with density differences, including (a) interactions between the wave and four different current shapes due to density differences, (b) an interaction between the wave and undercurrent (ρw < ρc), and (c) an interaction between the wave and upper current (ρw > ρc).
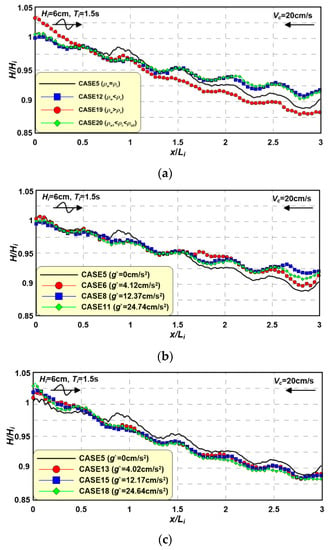
Figure 20.
Spatial distributions of wave height under various interactions between waves and currents. (a) According to type of density current; (b) According to the undercurrent (ρw < ρc); (c) According to the upper current (ρw > ρc).
All cases in Figure 20a show decreases in wave height due to wave energy loss caused by wave-current interactions. In particular, CASE 19 (ρw > ρc) shows considerable wave height decay because the inflowing current is concentrated near the water surface, where the velocity caused by wave orbital motion is large. Therefore, there may be stronger interactions near the water surface, which induce wave height decay due to wave energy loss. In addition, the wave height decay seen in CASE 12 (ρw < ρc) and wave height seen in CASE 20 (ρw1 < ρc < ρw2) are lower than those seen in CASE 5 (ρw = ρc) because the current flows in the lower-middle layers, which feature lower velocity caused by orbital motion, lead to less interaction between waves and currents, which results in less wave height decay than that in CASE 5 (ρw = ρc), in which differences in density are not considered.
In Figure 20b, CASEs 6, 8, and 11 show the same phenomenon and feature less wave height dissipation than in CASE 5, which has a uniform-depth current. Furthermore, CASEs 6, 8, and 11 show more wave height dissipation under smaller differences in salinity. This is because current generation is more similar to that under a uniform-depth current when the difference in density is small. In Figure 20c, there is more wave height decay in CASEs 13, 15, and 18 than in CASE 5. The cases with upper current also show a tendency toward higher wave height decay as density differences increase, although the effect is not very strong.
These results indicate that vertically varying currents affect wave deformation due to wave-current interactions. Therefore, density currents must be considered in order to effectively analyze wave-current interactions in areas with density differences.
3.2.4. Vertical Distribution of TKE
Figure 21 shows the vertical distribution of the mean phase-average TKE () under various wave-current interactions due to density differences, including (a) interactions between the wave and four different current shapes due to density differences, (b) an interaction between the wave and an undercurrent (ρw < ρc), and (c) an interaction between the wave and an upper current (ρw > ρc).
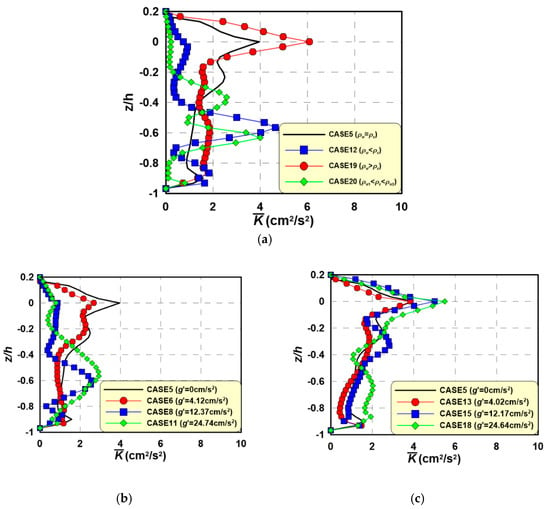
Figure 21.
Vertical profiles of the mean phase-averaged turbulence intensities under wave-current interactions. (a) According to the type of density current; (b) According to the undercurrent (ρw < ρc); (c) According to the upper current (ρw > ρc).
In Figure 21a, CASE 5 shows more balanced under the interactions between waves and a uniform-depth current than do the other cases. CASEs 12, 19, and 20 show strong generation at each current point generated by density differences. In particular, due to the wave-upper current interaction appears to be strong near the free surface in CASE 19, which features the highest wave height decay (Figure 18). In addition, CASE 5, which features a uniform-depth current, possesses higher than CASE 12, which features undercurrent and less wave height dissipation, and CASE 20, which features a middle current. This turbulence appears to be the major factor in the wave energy loss and height dissipation and can explain the formation mechanisms of the abovementioned wave height distributions. In Figure 21b, CASEs 8 and 11 feature stronger when larger salinity differences exist in the lower layer. However, CASE 6, which features the lowest salinity difference, shows a vertical distribution similar to that in CASE 5; this reduces the wave energy, resulting in the wave height distribution described above. In Figure 21c, CASEs 13, 15, and 18 possess stronger under larger salinity differences near the free surface. Under smaller salinity differences, vertical distributions similar to that in CASE 5, which features a uniform-depth current, are observed, which reduces wave energy, resulting in the wave height distribution discussed earlier.
Overall, wave-current interactions in cases with density differences appear different from those found in cases that do not consider density differences. Therefore, consideration of currents due to density differences is strongly recommended during analysis of wave-current interactions in water bodies with density differences, such as estuaries.
4. Conclusions
In the estuary, most of the laboratory experiments and numerical simulations for analysis of the wave-current interaction were performed under homopycnal flow conditions that do not consider the density discrepancy between the river and ocean. However, hypopycnal flow, which refers to river water spreading out to the upper layer of ocean, actually occurs in estuary. In this study, to simulate wave-current interaction under hypopycnal flow conditions, we have revised the NWT to reproduce the density current based on the existing numerical model. To confirm the effectiveness and validity of the improved numerical model, the model was compared with the results of hydraulic experiments [72,73]. These comparisons confirmed the validity and effectiveness of the newly suggested numerical model in wave-current interaction simulations in estuaries that contain density differences.
This study addressed wave attenuation, wave reflection, and wave energy reduction under wave-current interactions, which have not been addressed in previous studies. In addition, this study numerically explored the effects of current due to density differences on wave-current interactions in an open channel. Wave height decay and wave reflection mechanisms were analyzed in the coexisting wave-current field in terms of TKE and wave energy. The hydraulic characteristics of the numerically simulated wave-current interactions can be summarized as follows:
- When the ratio (Vc/Ci) between current velocity and wave celerity increases, wave height decay increases. Wave reflection by currents forms a partial standing wave field.
- When the Vc/Ci velocity ratio increases, the overall mean phase-average TKE increases. At higher incident wave heights, wave steepness, and Ursell numbers larger increases occur near still-water levels. Longer incident periods lead to larger increases, except near the still-water level.
- As a result of turbulence caused by wave-current interactions, wave energy increases as the Vc/Ci increases. When the incident wave height is high, TKE increases and the wave energy decay rate decreases. Higher wave heights have higher wave energy, therefore the energy decay rate is relatively low.
- The rate of wave reflection due to currents becomes larger as the Vc/Ci increases. With longer wave periods, the exposure time in wave troughs, in which the wave orbital motion velocity and current velocity are opposite in direction, is longer, and thus the wave reflection rate is increased. As a result, reflection rates of up to 0.068 were found under the incident conditions applied in this study.
- The mean water level increases more due to wave-current interactions as the velocity ratio Vc/Ci increases, which further reduces wave energy.
In conclusion, the flow velocity turbulence element is increased in the coexisting wave-current field by wave-current interactions, which decreases the wave energy. Consequently, the wave height decays and the water level increases. Wave reflection by currents occurs under the wave trough. Thus, the results provide an explanation wave height decay and wave reflection mechanisms due to wave-current interactions.
The influence of currents caused by density differences on wave-current interaction in an estuary can be described as follows:
- Various currents are generated depending on the density difference between two fluids.
- Wave height decay due to various current-wave interactions is highest in cases involving upper currents, in which strong interactions occur near still-water levels. Cases involving middle current and undercurrent feature less wave height decay than do cases with uniform-depth currents, which feature no density current.
- The mean phase-average TKE vertical distribution is broad near each type of current. Greater wave height decay values are accompanied by higher mean phase-average TKE.
In general, simulated wave-current interactions caused by density differences show different tendencies than cases that do not account for density differences. Therefore, currents arising from density differences must be considered when analyzing wave-current interactions in water bodies with density differences, such as estuaries.
Author Contributions
W.-D.L. and N.M. designed the study concept; W.-D.L. and D.-S.H. developed the code and performed the model simulations; All authors analyzed the results; W.-D.L. wrote the paper. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the National Research Foundation of Korea (NRF) grant funded by the Korea government (MSIT) (No. NRF-2018R1C1B6007461).
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. Fluid Density Equations
To analyze density current, it is important to estimate the density of a fluid accurately; thus, Equation (A1) was applied to estimate density according to temperature and salinity, as suggested by Gill [60]. Here, is the density of 4 °C freshwater. is the increase in density with temperature change and is expressed as Equation (A2). expresses the change in density with changing salinity and is expressed as Equation (A3). The empirical constants used in the density calculation are shown in Table A1.
where is the temperature (°C) and is the salinity (psu).

Table A1.
Density estimation coefficients.
Table A1.
Density estimation coefficients.
| ρ0 = 0.999842594 g/cm3 | a5 = 6.536332 × 10−12 | a10 = 5.38750 × 10−12 |
| a1 = 6.793952 × 10−5 | a6 = 8.244930 × 10−4 | a11 = 5.72466 × 10−6 |
| a2 = 9.095290 × 10−6 | a7 = 4.089900 × 10−6 | a12 = 1.02270 × 10−7 |
| a3 = 1.001685 × 10−7 | a8 = 7.643800 × 10−8 | a13 = 1.65460 × 10−9 |
| a4 = 1.120083 × 10−9 | a9 = 8.246700 × 10−10 | a14 = 4.83140 × 10−7 |
Appendix B. Kinematic Viscosity Coefficient Equations
The kinematic viscosity coefficient for the fluid is calculated using Equation (A4). Here, the calculated value of Equation (A1) is substituted for the density , and the viscosity coefficient is calculated using Equation (A5), which considers the water temperature and salinity, as suggested by Riley and Skirrow [61].
where, is the viscosity coefficient for 4 °C freshwater. indicates the change in the viscosity coefficient with a change in temperature and is expressed via Equation (A6). indicates the change in the viscosity coefficient with a change in salinity and is expressed via Equation (A7). The empirical constants used for the water viscosity coefficient are expressed in Table A2.

Table A2.
Viscosity estimation coefficients.
Table A2.
Viscosity estimation coefficients.
| μ0 = 1.802863 × 10−2 g/cm·s | b2 = 1.31419 × 10−5 | b4 = 2.15123 × 10−5 |
| b1 = 6.108600 × 10−4 | b3 = 1.35576 × 10−7 | b5 = 3.59406 × 10−10 |
References
- Geyer, W.R.; MacCready, P. The estuarine circulation. Annu. Rev. Fluid Mech. 2014, 46, 175–197. [Google Scholar] [CrossRef]
- Bolaños, R.; Brown, J.M.; Souza, A.J. Wave–current interactions in a tide dominated estuary. Cont. Shelf Res. 2014, 87, 109–123. [Google Scholar] [CrossRef]
- Bates, C.C. Rational theory of delta formation. Bull. Am. Assoc. Pet. Geol. 1953, 37, 2119–2162. [Google Scholar]
- Boggs, S. Principles of Sedimentology and Stratigraphy, 2nd ed.; Prentice Hall: Englewood Cliffs, NJ, USA, 1995; p. 774. [Google Scholar]
- Kang, K.R.; Iorio, D.D. Depth- and current-induced effects on wave propagation into the Altamaha River Estuary, Georgia. Estuar. Coast. Shelf Sci. 2006, 66, 395–408. [Google Scholar] [CrossRef]
- Zippel, S.; Thomson, J. Surface wave breaking over sheared currents: Observations from the Mouth of the Columbia River. J. Geophys. Res. Ocean. 2017, 122, 3311–3328. [Google Scholar] [CrossRef]
- Tanaka, H.; Nagabayashi, H.; Yamauchi, K. Observation of wave set-up height in a river mouth. In Proceedings of the 27th International Conference on Coastal Engineering, Sydney, Australia, 16–21 July 2000; pp. 3458–3471. [Google Scholar]
- Nguyen, X.T.; Tanaka, H.; Nagabayashi, H. Wave setup at river and inlet entrances due to an extreme event. In Proceedings of the International Conference on Violent Flows, Fukuoka, Japan, 20–22 November 2007. [Google Scholar]
- Donnell, J.O. Observations of near-surface currents and hydrography in the Connecticut River plume with the surface current and density array. J. Geophys. Res. Ocean. 1997, 102, 25021–25033. [Google Scholar] [CrossRef]
- Smith, J.M.; Seabergh, W.C.; Harkins, G.S.; Briggs, M.J. Wave Breaking on a Current at an Idealized Inlet, Coastal Inlets Research Program, Inlet Laboratory Investigations; Technical Report CHL-98-31; US Army Engineer Waterways Experiment Station: Vicksburg, MS, USA, 1998. [Google Scholar]
- Ibrahim, Z.; Latiff, A.A.A.; Halim, A.H.A.; Bakar, N.A.; Subramaniam, S. Experimental studies on mixing salt wedge estuary. Malays. J. Civ. Eng. 2008, 20, 188–199. [Google Scholar]
- Shi, F.; Dalrymple, R.A.; Kirby, J.T.; Chen, Q.; Kennedy, A. A fully nonlinear Boussinesq model in generalized curvilinear coordinates. Coast. Eng. 2001, 42, 337–358. [Google Scholar] [CrossRef]
- de Brye, B.; de Brauwere, A.; Gourgue, O.; Kärnä, T.; Lambrechts, J.; Comblen, R.; Deleersnijder, E. A finite-element, multi-scale model of the Scheldt tributaries, River, Estuary and ROFI. Coast. Eng. 2010, 57, 850–863. [Google Scholar] [CrossRef]
- Pascolo, S.; Petti, M.; Bosa, S. Wave–Current Interaction: A 2DH Model for Turbulent Jet and Bottom-Friction Dissipation. Water 2018, 10, 392. [Google Scholar] [CrossRef]
- Sutherlanda, J.; Walstrab, D.J.R.; Cheshera, T.J.; van Rijn, L.C.; Southgate, H.N. Evaluation of coastal area modelling systems at an estuary mouth. Coast. Eng. 2004, 51, 119–142. [Google Scholar] [CrossRef]
- Lesser, G.R.; Roelvink, J.A.; van Kester, J.A.T.M.; Stelling, G.S. Development and validation of a three-dimensional morphological model. Coast. Eng. 2004, 51, 883–915. [Google Scholar] [CrossRef]
- Booij, N.; Ris, R.C.; Holthuijsen, L.H. A third-generation wave model for coastal regions, Part I, Model description and validation. J. Geophys. Res. 1999, 104, 7649–7666. [Google Scholar] [CrossRef]
- The WAMDI Group. The WAM model—A third generation ocean wave prediction model. J. Phys. Oceanogr. 1988, 18, 1775–1810. [Google Scholar] [CrossRef]
- Zhang, Q.-H.; Tan, F.; Han, T.; Wang, X.-Y.; Hou, Z.-Q.; Yang, H. Simulation of sorting sedimentation in the channel of Huanghua harbor by using 3d multi-sized sediment transport model of EFDC. In Proceedings of the 32nd International Conference on Coastal Engineering, Shanghai, China, 30 June–5 July 2010; pp. 1604–1614. [Google Scholar]
- Liang, B.; Zhao, H.; Li, H.; Wu, G. Numerical study of three-dimensional wave-induced longshore current’s effects on sediment spreading of the Huanghe River mouth. Acta Oceanol. Sin. 2012, 31, 129–138. [Google Scholar] [CrossRef]
- Baddour, R.E.; Song, S. On the interaction between waves and currents. Ocean Eng. 1990, 17, 1–21. [Google Scholar] [CrossRef]
- Peregrine, D.H. Interaction of Water Waves and Currents. Adv. Appl. Mech. 1976, 16, 9–117. [Google Scholar]
- Jonsson, I.G.; Skougaard, C.; Wang, J.D. Interaction between waves and currents. Coast. Eng. 1970, 1, 489–507. [Google Scholar]
- Wolf, J.; Prandle, D. Some observations of wave–current interaction. Coast. Eng. 1999, 37, 471–485. [Google Scholar] [CrossRef]
- Gonzalez, F.I. A case study of wave-current-bathymetry interactions at the Columbia River Entrance. J. Phys. Oceanogr. 1984, 14, 1065–1078. [Google Scholar] [CrossRef]
- Grant, W.D.; Madsen, O.S. Combined wave and current interaction with a rough bottom. J. Geophys. Res. Ocean. 1979, 84, 1797–1808. [Google Scholar] [CrossRef]
- Fredsøe, J. Turbulent boundary layer in wave-current motion. J. Hydraul. Eng. 1984, 110, 1103–1120. [Google Scholar] [CrossRef]
- Christoffersen, J.B.; Jonsson, I.G. Bed friction and dissipation in a combined current and wave motion. Ocean Eng. 1985, 12, 387–423. [Google Scholar] [CrossRef]
- Soulsby, R.L.; Hamm, L.; Klopman, G.; Myrhaug, D.; Simons, R.R.; Thomas, G.P. Wave–current interaction within and outside the bottom boundary layer. Coast. Eng. 1993, 21, 41–69. [Google Scholar] [CrossRef]
- Jonsson, I.G. Wave–Current Interactions; The Sea; Le Méhauté, B., Hanes, D.M., Eds.; Wiley: New York, NY, USA, 1990; Volume 9, pp. 65–120. [Google Scholar]
- Umeyama, M. Reynolds stresses and velocity distributions in a wave-current coexisting environment. J. Waterw. Portcoast. Ocean Eng. 2005, 131, 203–212. [Google Scholar] [CrossRef]
- Lee, W.D.; Mizutani, N.; Hur, D.S. Experimental analysis of wave deformation and bottom flow under wave-current interaction in the river mouth. Ocean Eng. 2017, 140, 169–182. [Google Scholar] [CrossRef]
- Umeyama, M. Coupled PIV and PTV measurements of particle velocities and trajectories for surface waves following a steady current. J. Waterw. Portcoast. Ocean Eng. 2010, 137, 85–94. [Google Scholar] [CrossRef]
- Chen, Y.Y.; Hsu, H.C.; Hwung, H.H. Particle trajectories beneath wave-current interaction in a two-dimensional field. Nonlinear Process. Geophys. 2012, 19, 185–197. [Google Scholar] [CrossRef]
- Fernando, P.C.; Guo, J.; Lin, P. Wave-current interaction at an angle 1: Experiment. J. Hydraul. Res. 2011, 49, 424–436. [Google Scholar] [CrossRef]
- Lim, K.Y.; Madsen, O.S. An experimental study on near-orthogonal wave–current interaction over smooth and uniform fixed roughness beds. Coast. Eng. 2016, 116, 258–274. [Google Scholar] [CrossRef]
- Longuet-Higgins, M.S.; Stewart, R.W. The changes in amplitudes of short gravity waves on steady non-uniform currents. J. Fluid Mech. 1961, 10, 529–549. [Google Scholar] [CrossRef]
- Dingemans, M.W. Water Wave Propagation over Uneven Bottoms; Advanced Series on Ocean Engineering 13; World Scientific: London, UK, 1997; p. 1016. [Google Scholar]
- Lee, K.H.; Mizutani, N.; Komatsu, K.; Hur, D.S. Experimental study on wave-current interaction. In Proceedings of the 16th International Offshore and Polar Engineering Conference, San Francisco, CA, USA, 28 May–2 June 2006; pp. 600–606. [Google Scholar]
- Rey, V.; Charland, J.; Touboul, J. Wave–current interaction in the presence of a three-dimensional bathymetry: Deep water wave focusing in opposing current conditions. Phys. Fluids 2014, 26, 096601. [Google Scholar] [CrossRef]
- Drevard, D.; Rey, V.; Fraunie, P. Partially standing wave measurement in the presence of steady current by use of coincident velocity and/or pressure data. Coast. Eng. 2009, 56, 992–1001. [Google Scholar] [CrossRef]
- Mizutani, N.; Lee, K.H.; Komatsu, K.; Hur, D.S. Fundamental study on wave-current interaction. Proc. Coast. Eng. Conf. Jpn. Soc. Civ. Eng. 2005, 21, 307–312. (In Japanese) [Google Scholar]
- Mizutani, N.; Hur, D.S.; Maeda, Y. Numerical analysis of nonlinear wave-current interaction in side harbor. Proc. Coast. Eng. Conf. Jpn. Soc. Civ. Eng. 2002, 49, 51–55. (In Japanese) [Google Scholar]
- Lee, K.H.; Ohori, F.; Mizutani, N.; Kuwabara, S. A study on interactions between effluent currents and incoming waves near an estuary. Annu. J. Civ. Eng. Ocean. Soc. Civ. Eng. 2008, 24, 897–902. (In Japanese) [Google Scholar]
- Lee, W.D.; Mizutani, N.; Hur, D.S. Effect of crossing angle on interaction between wave and current in the river mouth. J. Jpn. Soc. Civ. Eng. Ser. B3 (Ocean Eng.) 2011, 67, 256–261. (In Japanese) [Google Scholar]
- Liu, Z.; Lin, Z.; Tao, L.; Lan, J. Nonlinear wave–current interaction in water of finite depth. J. Waterw. Portcoast. Ocean Eng. 2016, 142, 04016009. [Google Scholar] [CrossRef]
- Lee, W.D.; Jeong, Y.H.; Jeon, H.S. Groundwater flow analysis in a coastal aquifer with the coexistence of seawater and freshwater by using a non-hydrostatic pressure model. J. Coast. Res. 2019, 91, 121–125. [Google Scholar] [CrossRef]
- Lee, W.D.; Yoo, Y.J.; Jeong, Y.M.; Hur, D.S. Experimental and numerical analysis on hydraulic characteristics of coastal aquifers with seawall. Water 2019, 11, 2343. [Google Scholar] [CrossRef]
- Hur, D.S.; Lee, W.D.; Cho, W.C. Three-dimensional flow characteristics around permeable submerged breakwaters with open inlet. Ocean Eng. 2012, 44, 100–116. [Google Scholar] [CrossRef]
- Hur, D.S.; Lee, W.D.; Cho, W.C. Characteristics of wave run-up height on a sandy beach behind dual-submerged breakwaters. Ocean Eng. 2012, 45, 38–55. [Google Scholar] [CrossRef]
- Hur, D.S.; Lee, W.D.; Cho, W.C.; Jeong, Y.H.; Jeong, Y.M. Rip current reduction at the open inlet between double submerged breakwaters by installing a drainage channel. Ocean Eng. 2019, 193, 106580. [Google Scholar] [CrossRef]
- Hur, D.S.; Mizutani, N. Numerical estimation of the wave forces acting on a three-dimensional body on submerged breakwater. Coast. Eng. 2003, 47, 329–345. [Google Scholar] [CrossRef]
- Hur, D.S.; Mizutani, N.; Kim, D.S. Direct 3-d numerical simulation of wave forces on asymmetric structures. Coast. Eng. 2004, 51, 407–420. [Google Scholar] [CrossRef]
- Smagorinsky, J. General circulation experiments with the primitive equation. Mon. Weather Rev. 1963, 91, 99–164. [Google Scholar] [CrossRef]
- Hur, D.S.; Lee, K.H.; Yeom, G.S. The phase difference effects on 3-d structure of wave pressure acting on a composite breakwater. Ocean Eng. 2008, 35, 1826–1841. [Google Scholar] [CrossRef]
- Sakakiyama, T.; Kajima, R. Numerical simulation of nonlinear wave interacting with permeable breakwater. In Proceedings of the 23rd International Conference on Coastal Engineering, Venice, Italy, 4–9 October 1992; pp. 1517–1530. [Google Scholar]
- Ergun, S. Fluid flow through packed columns. Chem. Eng. 1952, 48, 89–94. [Google Scholar]
- van Gent, M.R.A. Wave Interaction with Permeable Coastal Structures. Ph.D. Thesis, Delft University, Delft, The Netherlands, 1995; p. 175. [Google Scholar]
- Liu, S.; Masliyah, J.H. Non-linear flows porous media. J. Non-Newton. Fluid Mech. 1999, 86, 229–252. [Google Scholar] [CrossRef]
- Gill, A.E. Atmosphere-Ocean Dynamics; Academic Press: New York, NY, USA, 1982; p. 662. [Google Scholar]
- Riley, J.P.; Skirrow, G. Chemical Oceanography 3; Academic Press: London, UK, 1965. [Google Scholar]
- Germano, M.; Piomelli, U.; Moin, P.; Cabot, W.H. A dynamic subgrid-scale eddy viscosity model. Phys. Fluids 1991, 3, 1760–1765. [Google Scholar] [CrossRef]
- Lilly, D.K. A proposed modification of the Germano subgrid-scale closure method. Phys. Fluids 1991, 4, 633–635. [Google Scholar] [CrossRef]
- Brorsen, M.; Larsen, J. Source generation of nonlinear gravity wave with boundary integral equation method. Coast. Eng. 1987, 11, 93–113. [Google Scholar] [CrossRef]
- Ohyama, T.; Nadaoka, K. Modeling the transformation of nonlinear waves passing over a submerged dike. In Proceedings of the 23rd International Conference on Coastal Engineering, Venice, Italy, 4–9 October 1992; pp. 526–539. [Google Scholar]
- Hirt, C.W.; Nichols, B.D. Volume of fluid (VOF) method for the dynamics of free boundaries. J. Comput. Phys. 1981, 39, 201–225. [Google Scholar] [CrossRef]
- Mellor, G.L.; Yamada, M. Development of a turbulence closure model for geophysical fluid problems. Rev. Geophys. 1982, 20, 851–875. [Google Scholar] [CrossRef]
- Gregg, M.C.; D’Asaro, E.A.; Shay, T.J.; Larson, N. Observations of persistent mixing and near-inertial internal waves. J. Phys. Oceanogr. 1986, 16, 856–885. [Google Scholar] [CrossRef]
- Peters, F.; Gregg, M.C.; Toole, J.M. On the parameterization of equatorial turbulence. J. Geophys. Res. 1988, 93, 1199–1218. [Google Scholar] [CrossRef]
- Hinatsu, M. Numerical simulation of unsteady viscous nonlinear waves using moving grid system fitted on a free surface. J. Kansai Soc. Nav. Archit. 1992, 217, 1–11. [Google Scholar]
- Petit, H.A.H.; Tonjes, P.; ven Gent, M.R.A.; van den Bosch, P. Numerical simulation and validation of plunging breakers using a 2D Navier–Stokes model. In Proceedings of the 24th International Conference on Coastal Engineering, Kobe, Japan, 23–28 October 1994; pp. 511–524. [Google Scholar]
- Iwasaki, T.; Sato, M. Energy damping of wave propagating against currents (2). Proc. Coast. Eng. Conf. Jpn. Soc. Civ. Eng. 1971, 18, 55–59. (In Japanese) [Google Scholar]
- Huppert, H.E.; Simpson, J.E. The slumping of gravity currents. J. Fluid Mech. 1980, 99, 785–799. [Google Scholar] [CrossRef]
- Sakai, S.; Saeki, H. Effects of opposing current on wave transformation on sloping sea bed. In Proceedings of the 19th International Conference on Coastal Engineering, Houston, TX, USA, 3–7 September 1984; pp. 1219–1232. [Google Scholar]
- Christensen, E.D. Large eddy simulation of spilling and plunging breakers. Coast. Eng. 2006, 53, 463–485. [Google Scholar] [CrossRef]
- Healy, J.J. Wave damping effect of beaches. In Proceedings, Minnesota International Hydraulic; St. Anthony Falls Hydraulic Laboratory: Minneapolis, MN, USA, 1952; pp. 213–220. [Google Scholar]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).