Drought in the Twenty-First Century in a Water-Rich Region: Modeling Study of the Wabash River Watershed, USA
Abstract
1. Introduction
2. Materials and Methods
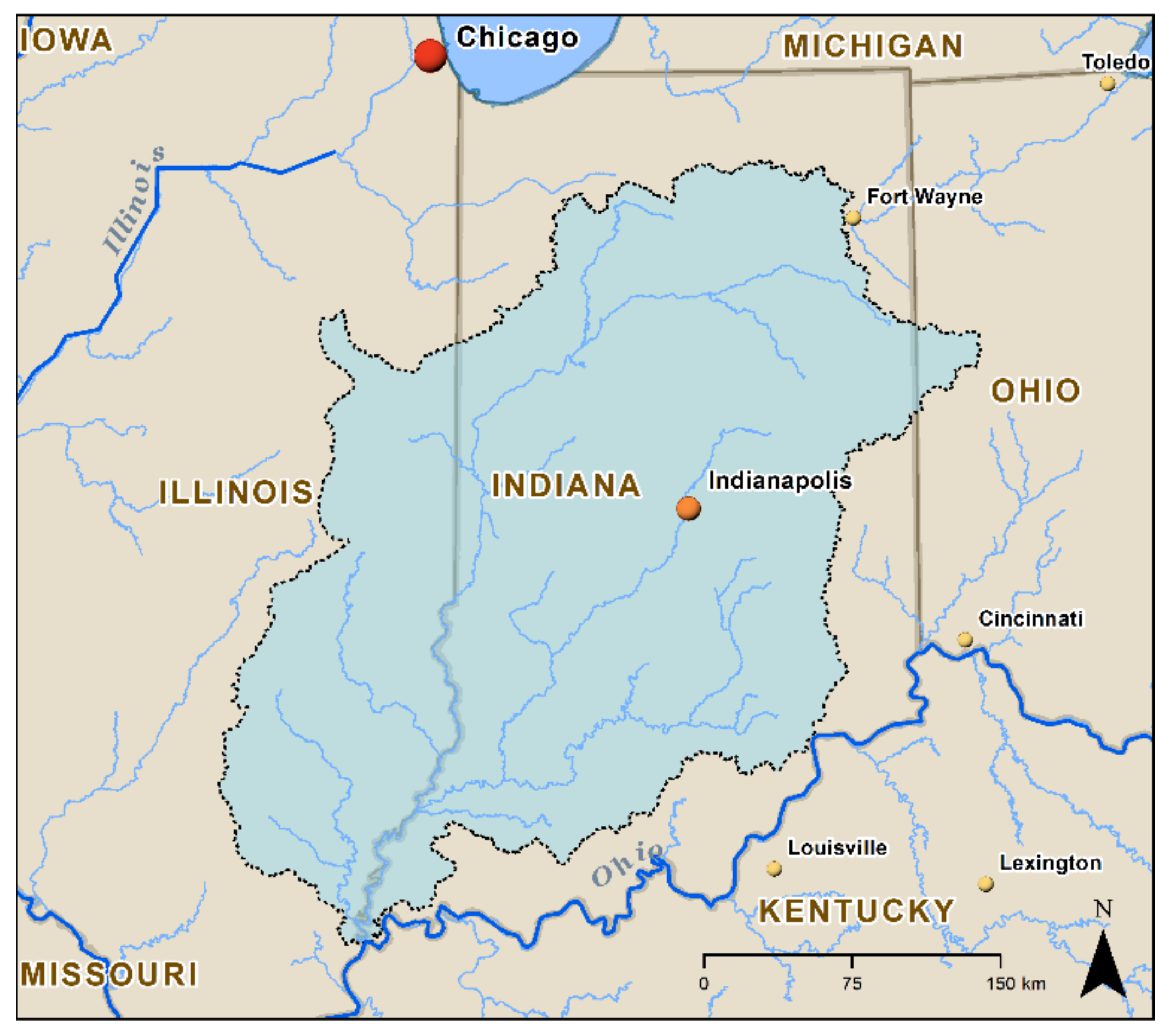
2.1. Study Area
2.2. Hydrologic Model
2.2.1. Model Inputs
2.2.2. Hydrological Response Unit (HRU) Definition
2.3. Model Calibration and Validation
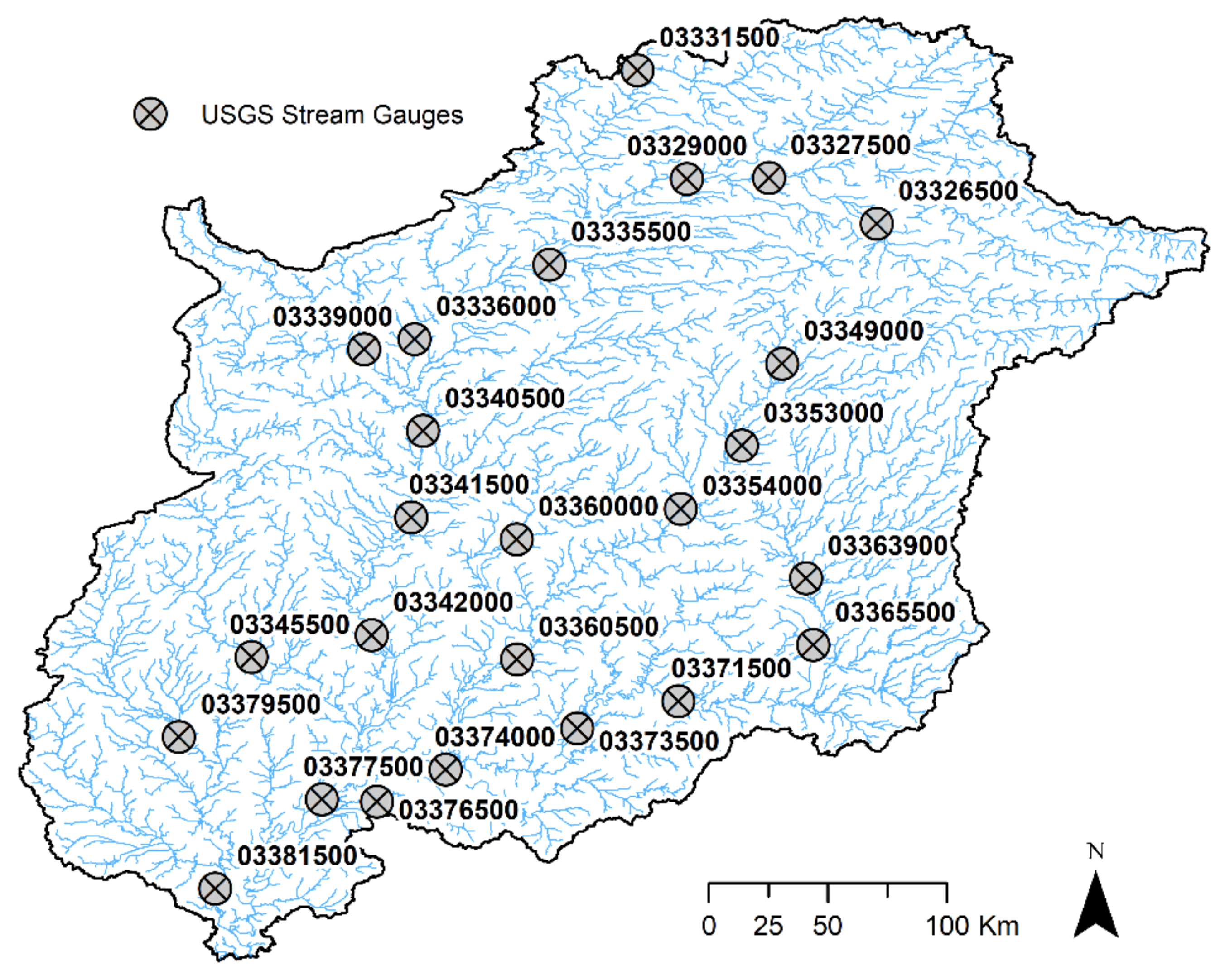
2.3.1. Stream Flow Calibration Sites
2.3.2. Multi-Criteria Objective Function
2.4. Quantification of Drought
- The time series of watershed-averaged precipitation, soil water content, and runoff were obtained from the SWAT model output for the historical baseline model simulation.
- The probability distributions of monthly precipitation, soil water content, and runoff were calculated separately for each month. Distribution fits were tested with the Shapiro–Wilk test. The gamma distribution produced a satisfactory fit for precipitation. No satisfactory distribution was found for soil moisture or runoff. Therefore, percentiles for soil moisture and runoff were estimated empirically, following recommendations in [56].
- Monthly time series of cumulative probabilities were calculated using the fitted distributions (for baseline and climate change scenarios) and then converted to z-values, representing the number of standard deviations below or above the mean of a normal distribution with a mean of 0 and a variance of 1.
3. Results
3.1. Model Calibration and Validation
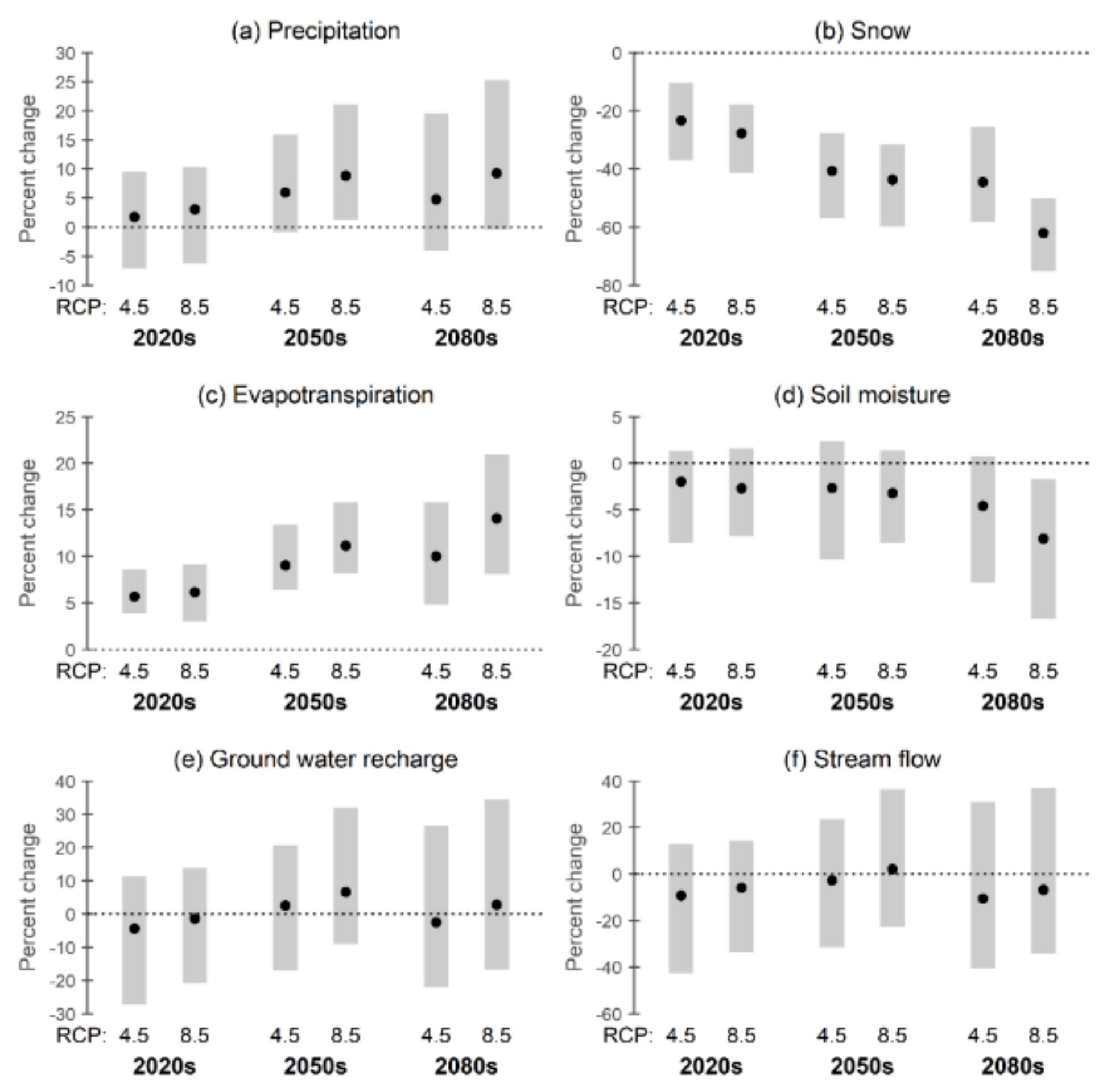
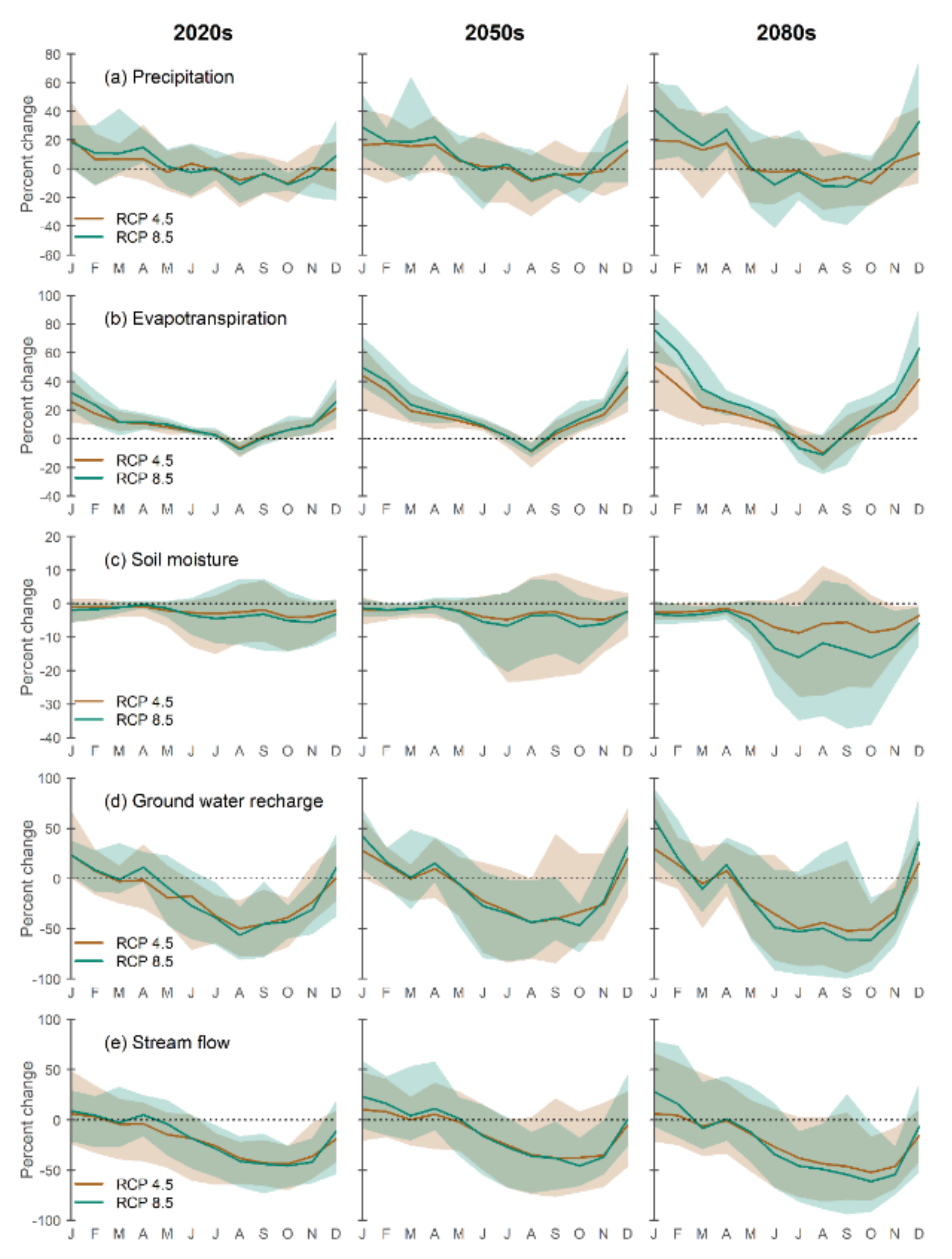
3.2. Climate Change Impacts on Annual and Intra-Annual Water Balance
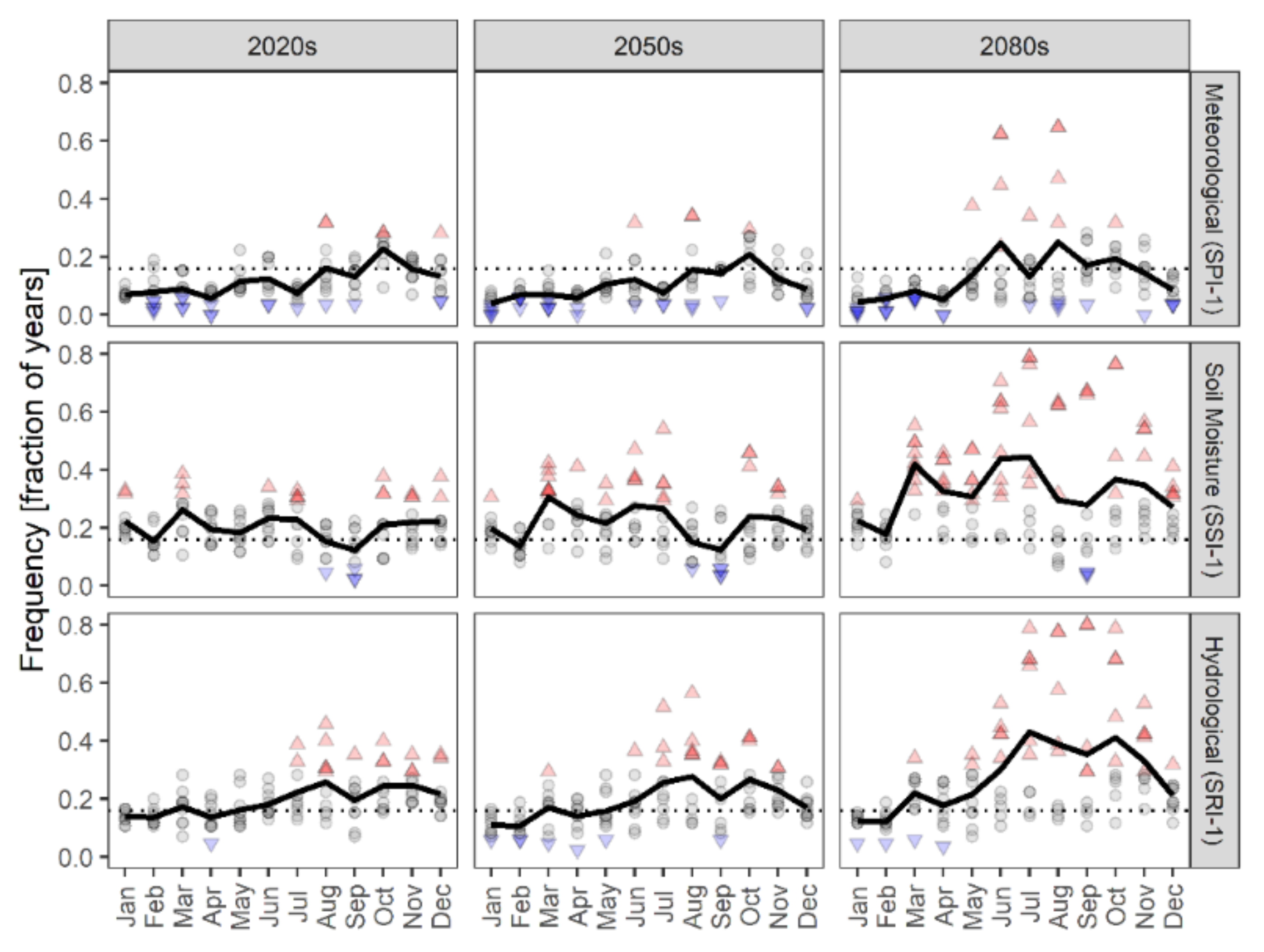
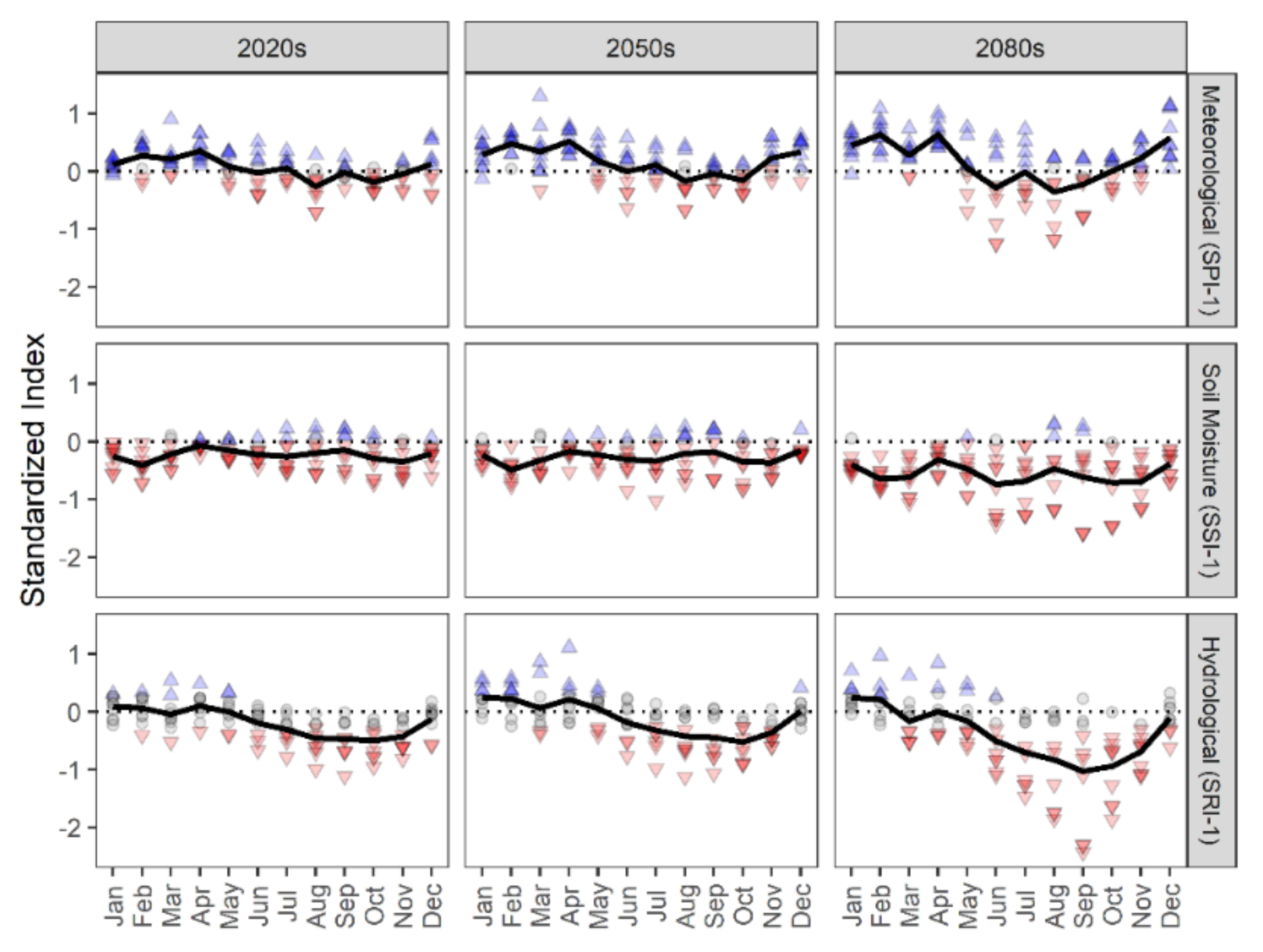
3.3. Projected Changes in Meteorological, Soil Moisture, and Hydrological Drought
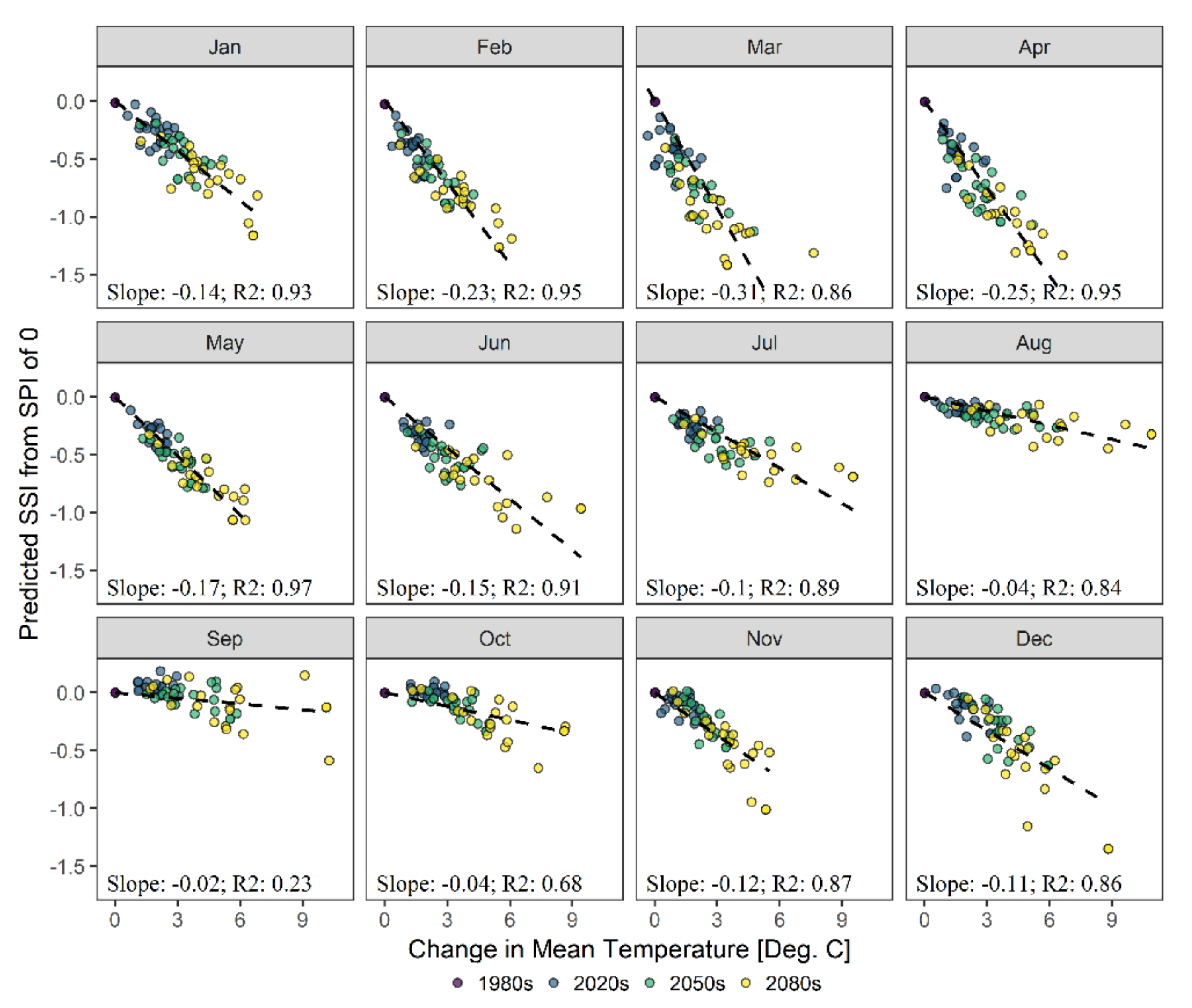
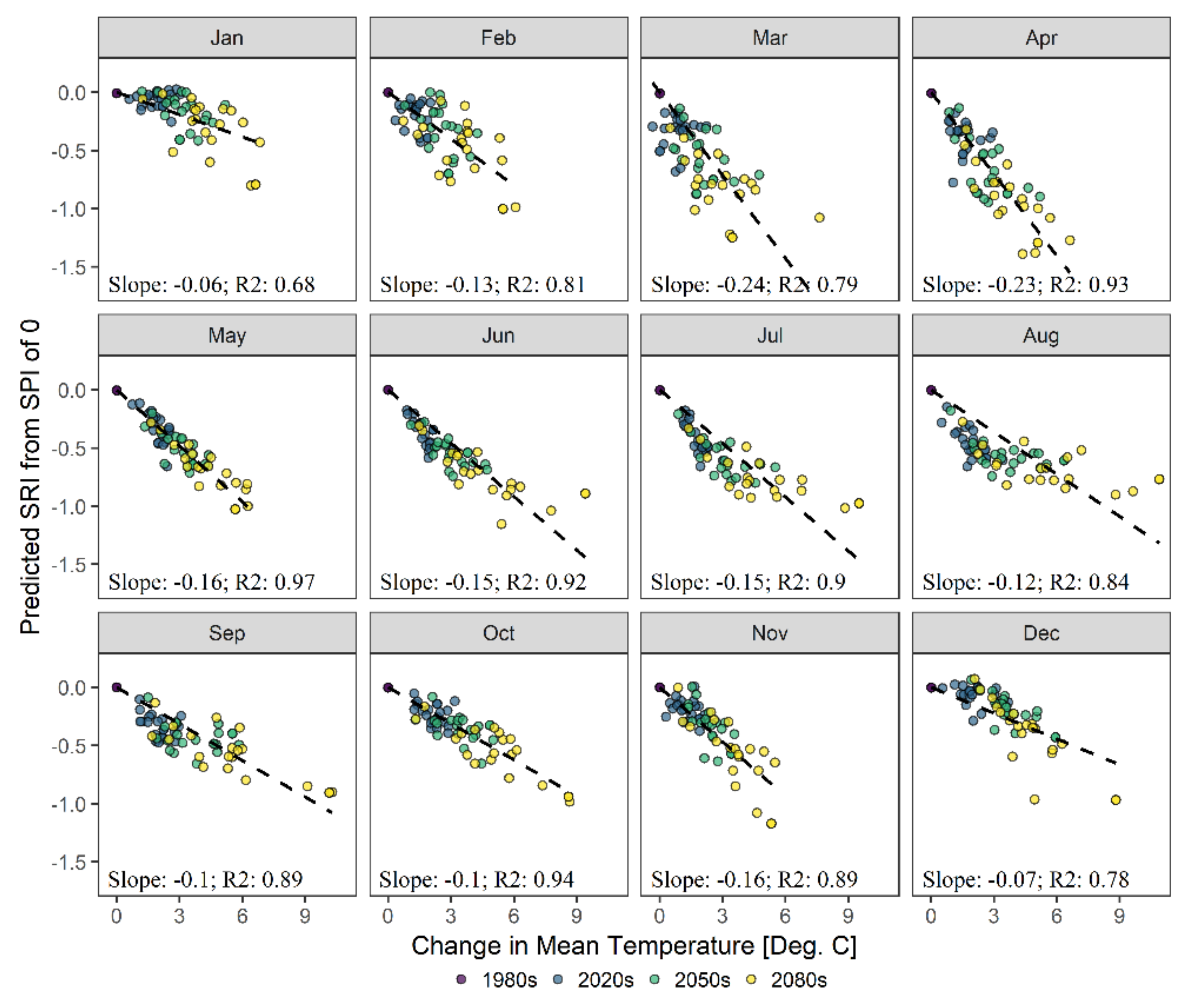
3.4. Climate Warming Impacts on Relationship between Drought Types
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Palmer, W.C. Meteorological Drought; United States Department of Commerce: Washington, DC, USA, 1965.
- Dracup, J.A.; Lee, K.S.; Paulson, E.G. On the definition of droughts. Water Resour. Res. 1980, 16, 297–302. [Google Scholar] [CrossRef]
- Van Loon, A.F. Hydrological drought explained. Wiley Interdiscip. Rev. Water 2015, 2, 359–392. [Google Scholar] [CrossRef]
- Rippey, B.R. The U.S. drought of 2012. Weather Clim. Extrem. 2015, 10, 57–64. [Google Scholar] [CrossRef]
- Sheffield, J.; Wood, E.F. Drought: Past Problems and Future Scenarios; Earthscan: London, UK, 2011. [Google Scholar]
- Feyen, L.; Dankers, R. Impact of global warming on streamflow drought in Europe. J. Geophys. Res. Atmos. 2009, 114, 1–17. [Google Scholar] [CrossRef]
- Dai, A. Drought under global warming in observations and models. Nat. Clim. Chang. 2013, 3, 52–58. [Google Scholar] [CrossRef]
- Intergovernmental Panel on Climate Change (IPCC). Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Stocker, T.F., Qin, G.-K., Plattner, M., Tignor, S.K., Allen, J., Boschung, A., Nauels, Y., Xia, V., Bex, D., Midgley, P.M., Eds.; Cambridge University Press: Cambridge, UK, 2013; p. 1535. [Google Scholar]
- Wehner, M. Projections of future drought in the continental United States and Mexico. J. Hydrometeorol. 2011, 12, 1359–1377. [Google Scholar] [CrossRef]
- Swain, S.; Hayhoe, K. CMIP5 projected changes in spring and summer drought and wet conditions over North America. Clim. Dyn. 2015, 44, 2737–2750. [Google Scholar] [CrossRef]
- Seager, R.; Ting, M.; Held, I.; Kushnir, Y.; Lu, J.; Vecchi, G.; Huang, H.; Harnik, N.; Leetmaa, A.; Lau, N.; et al. Model projections of an imminent transition to a more arid climate in southwestern North America. Science 2007, 316, 1181–1184. [Google Scholar] [CrossRef]
- Gutzler, D.S.; Robbins, T.O. Climate variability and projected change in the western United States: Regional downscaling and drought statistics. Clim. Dyn. 2011, 37, 835–849. [Google Scholar] [CrossRef]
- Wang, D.; Hejazi, M.; Cai, X.; Valocchi, A.J. Climate change impact on meteorological, agricultural, and hydrological drought in central Illinois. Water Resour. Res. 2011, 47, W09527. [Google Scholar] [CrossRef]
- Kang, H.; Sridhar, V. Combined statistical and spatially distributed hydrological model for evaluating future drought indices in Virginia. J. Hydrol. Reg. Stud. 2017, 12, 253–272. [Google Scholar] [CrossRef]
- Teuling, A.J.; Van Loon, A.F.; Seneviratne, S.I.; Lehner, I.; Aubinet, M.; Heinesch, B.; Bernhofer, C.; Grunwald, T.; Prasse, H.; Spank, U. Evapotranspiration amplifies European summer drought. Geophys. Res. Lett. 2013, 40, 2071–2075. [Google Scholar] [CrossRef]
- Diffenbaugh, N.S.; Swain, D.L.; Touma, D. Anthropogenic warming has increased drought risk in California. Proc. Natl. Acad. Sci. USA 2015, 112, 3931–3936. [Google Scholar] [CrossRef] [PubMed]
- Verdon-Kidd, D.C.; Kiem, A.S. Quantifying drought risk in a nonstationary climate. J. Hydrometeorol. 2010, 11, 1019–1031. [Google Scholar] [CrossRef]
- Smidt, S.J.; Kendall, A.D.; Hyndman, D.W. Increased dependence on irrigated crop production across the CONUS (1945–2015). Water 2019, 11, 1458. [Google Scholar] [CrossRef]
- Zipper, S.C.; Qiu, J.; Kucharik, C.J. Drought effects on US maize and soybean production: Spatiotemporal patterns and historical changes. Environ. Res. Lett. 2016, 11, 094021. [Google Scholar] [CrossRef]
- Arnold, J.G.; Williams, J.R.; Maidment, D.R. Continuous-time water and sediment-routing model for large basins. J. Hydraul. Eng. 1995, 121, 171–183. [Google Scholar] [CrossRef]
- Arnold, J.G.; Srinivasan, R.; Muttiah, R.S.; Williams, J.R. Large area hydrologic modeling and assessment part I: Model development. J. Am. Water Resour. Assoc. 1998, 34, 73–89. [Google Scholar] [CrossRef]
- Winchell, M.; Srinivasan, R.; Di Luzio, M.; Arnold, J. ArcSWAT Interface for SWAT 2005: User’s Guide; Blackland Research Center: Temple, TX, USA, 2008; pp. 1–453. [Google Scholar]
- United States Department of Agriculture (USDA). Urban Hydrology for Small Watersheds; Engineering Division, Soil Conservation Service, USDA: Washington, DC, USA, 1986.
- Monteith, J.L. Evaporation and environment. Symp. Soc. Exp. Biol. 1965, 19, 205–234. [Google Scholar]
- Ritchie, J.T. Model for predicting evaporation from a row crop with incomplete cover. Water Resour. Res. 1972, 8, 1204–1213. [Google Scholar] [CrossRef]
- Beik, S.E. Tile Drain Installation and Repair. In Indiana Drainage Handbook—October 1999 Update Package; Burke, C.B., Ed.; State of Indiana: Indianapolis, IN, USA, 1999; pp. 118–130. [Google Scholar]
- Kalita, P.; Algoazany, A.; Mitchell, J.; Cooke, R.; Hirschi, M. Subsurface water quality from a flat tile-drained watershed in Illinois, USA. Agric. Ecosyst. Environ. 2006, 115, 183–193. [Google Scholar] [CrossRef]
- Sugg, Z. Assessing U.S. Farm Drainage: Can GIS Lead to Better Estimates of Subsurface Drainage Extent? World Resources Institute. Available online: http://pdf.wri.org/assessing_farm_drainage.pdf (accessed on 29 October 2019).
- Srinivasan, R.; Zhang, X.; Arnold, J. SWAT ungauged: Hydrological budget and crop yield predictions in the Upper Mississippi River Basin. Trans. ASABE 2010, 53, 1533–1546. [Google Scholar] [CrossRef]
- Kalcic, M.M.; Frankenberger, J.; Chaubey, I. Spatial optimization of six conservation practices using SWAT in tile-drained agricultural watersheds. J. Am. Water Resour. Assoc. 2015, 51, 956–972. [Google Scholar] [CrossRef]
- Guo, T.; Gitau, M.; Merwade, V.; Arnold, J.; Srinivasan, R.; Hirschi, M.; Engel, B. Comparison of performance of tile drainage routines in SWAT 2009 and 2012 in an extensively tile-drained watershed in the Midwest. Hydrol. Earth Syst. Sci. 2018, 22, 89–110. [Google Scholar] [CrossRef]
- Homer, C.; Dewitz, J.; Fry, J.; Coan, M.; Hossain, N.; Larson, C.; Herold, N.; McKerrow, A.; VanDriel, J.N.; Wickham, J. Completion of the 2001 National Land Over Database for the conterminous United States. Photogramm. Eng. Remote Sens. 2007, 73, 337–341. [Google Scholar]
- Boryan, C.; Yang, Z.; Mueller, R.; Craig, M. Monitoring US Agriculture: The US Department of Agriculture, National Agricultural Statistics Service Cropland Data Layer Program. Geocarto Int. 2011, 26, 341–358. [Google Scholar] [CrossRef]
- Byun, K.; Hamlet, A.F. Projected changes in future climate over the Midwest and Great Lakes region using downscaled CMIP5 ensembles. Int. J. Climatol. 2018, 38, 531–553. [Google Scholar] [CrossRef]
- CMIP5 in CCIA. Available online: http://www.crc.nd.edu/~kbyun/CMIP5_IN_CCIA.html (accessed on 29 October 2019).
- Van Vuuren, D.P.; Edmonds, J.; Kainuma, M.; Riahi, K.; Thomson, A.; Hibbard, K.; Hurtt, G.C.; Kram, T.; Krey, V.; Lamarque, J.; et al. The representative concentration pathways: An overview. Clim. Chang. 2011, 109, 5–31. [Google Scholar] [CrossRef]
- Towns, J.; Cockerill, T.; Dahan, M.; Foster, I.; Gaither, K.; Grimshaw, A.; Hazlewood, V.; Lathrop, S.; Lifka, D.; Peterson, G.D.; et al. XSEDE: Accelerating scientific discovery. Comput. Sci. Eng. 2014, 16, 62–74. [Google Scholar] [CrossRef]
- Byun, K.; Chiu, C.-M.; Hamlet, A.F. Effects of 21st century climate change on seasonal flow regimes and hydrologic extremes over the Midwest and Great Lakes region of the US. Sci. Total Environ. 2019, 650, 1261–1277. [Google Scholar] [CrossRef]
- Gassman, P.W.; Reyes, M.R.; Green, C.H.; Arnold, J.G. The Soil and Water Assessment Tool: Historical development, applications, and future research directions. Trans. ASABE 2007, 50, 1211–1250. [Google Scholar] [CrossRef]
- Xue, X.; Zhang, K.; Hong, Y.; Gourley, J.J. New multisite cascading calibration approach for hydrological models: Case study in the Red River Basin using the VIC model. J. Hydrol. Eng. 2015, 21, 05015019. [Google Scholar] [CrossRef]
- Abbaspour, K.C.; Vejdani, M.; Haghighat, S. SWAT-CUP2: SWAT Calibration and Uncertainty Programs Manual Version 2. Department of Systems Analysis, Integrated Assessment and Modelling (SIAM); Eawag Swiss Federal Institute of Aquatic Science and Technology: Duebendorf, Switzerland, 2011; p. 106. [Google Scholar]
- R Development Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2014. [Google Scholar]
- Wittman, J. Water and Economic Development in Indiana: Modernizing the State’s Approach to A Critical Resource. INTERA for the Indiana Chamber of Commerce. 2014. Available online: https://www.indianachamber.com/wp-content/uploads/2017/09/WaterStudyReport2014LoRes.pdf (accessed on 29 October 2019).
- Gustard, A.; Demuth, S. Manual on Low-Flow Estimation and Prediction; Operational Hydrology Report No. 50; World Meteorological Organisation: Geneva, Switzerland, 2008; p. 136. [Google Scholar]
- Koffler, D.; Gauster, T.; Laaha, G. Lfstat: Calculation of Low Flow Statistics for Daily Stream Flow Data. R Package Version 0.9.4. Available online: https://cran.r-project.org/web/packages/lfstat/index.html (accessed on 29 October 2019).
- Carnell, R. Lhs: Latin Hypercube Samples. R Package Version 1.0.1. Available online: https://cran.r-project.org/web/packages/lhs/index.html (accessed on 29 October 2019).
- Chapman, T.B.; Maxwell, A. Baseflow separation—Comparison of numerical methods with tracer experiments. In Hydrology and Water Resources Symposium 1996: Water and the Environment: Preprints of Papers; Institution of Engineers: ACT, Australia, 1996. [Google Scholar]
- Eckhardt, K. How to construct recursive digital filters for baseflow separation. Hydrol. Process. 2005, 19, 507–515. [Google Scholar] [CrossRef]
- Ryberg, K.R.; Vecchia, A.V. Waterdata: Retrieval, Analysis, and Anomaly Calculation of Daily Hydrologic Time Series Data. R Package Version 1.0.8. Available online: https://cran.r-project.org/web/packages/waterData/ (accessed on 29 October 2019).
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models. Part I: A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Criss, R.E.; Winston, W.E. Do Nash values have value? Discussion and alternate proposals. Hydrol. Process. 2008, 22, 2723–2725. [Google Scholar] [CrossRef]
- Muleta, M.K. Model performance sensitivity to objective function during automated calibrations. J. Hydrol. Eng. 2012, 17, 756–767. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Arnold, J.G.; Van Liew, M.W.; Bingner, R.D.; Harmel, R.D.; Leith, T.L. Model evaluation guidelines for systematic quantification of accuracy in watershed simulations. Trans. ASABE 2007, 50, 885–900. [Google Scholar] [CrossRef]
- McKee, T.B.; Doesken, N.J.; Kleist, J. Drought Monitoring with Multiple Time Scales Proceeding of the Ninth Conference on Applied Climatology; American Meteorological Society: Boston, MA, USA, 1995. [Google Scholar]
- AghaKouchak, A. A baseline probabilistic drought forecasting framework using standardized soil moisture index: Application to the 2012 United States drought. Hydrol. Earth Syst. Sci. 2014, 18, 2485–2492. [Google Scholar] [CrossRef]
- Shukla, S.; Wood, A.W. Use of a standardized runoff index for characterizing hydrologic drought. Geophys. Res. Lett. 2008, 35, L02405. [Google Scholar] [CrossRef]
- Wilcoxon, F. Individual comparisons by ranking methods. Biom. Bull. 1945, 1, 80–83. [Google Scholar] [CrossRef]
- Mann, H.B.; Whitney, D.R. On a test of whether one of two random variables is stochastically larger than the other. Ann. Math. Stat. 1947, 18, 5–60. [Google Scholar] [CrossRef]
- Akaike, H. A new look at the statistical model identification. IEEE Trans. Autom. Control 1974, 19, 716–723. [Google Scholar] [CrossRef]
- Guttman, N.B. Accepting the standardized precipitation index: A calculation algorithm. J. Am. Water Resour. Assoc. 1999, 35, 311–322. [Google Scholar] [CrossRef]
- Leng, G.; Tang, Q.; Rayburg, S. Climate change impacts on meteorological, agricultural, and hydrological droughts in China. Glob. Planet. Chang. 2015, 126, 23–34. [Google Scholar] [CrossRef]
- Vicente-Serrano, S.M.; Lopez-Moreno, J.; Begueria, S.; Lorenzo-Lacruz, J.; Sanchez-Lorenzo, A.; Garcia-Ruiz, J.; Azorin-Molina, C.; Moran-Tejeda, E.; Revuelto, J.; Trigo, R.; et al. Evidence of increasing drought severity caused by temperature rise in southern Europe. Environ. Res. Lett. 2014, 9, 044001. [Google Scholar] [CrossRef]
- Cheng, L.; Hoerling, M.; AhaKouchak, A.; Livneh, B.; Quan, X.; Eischeid, J. How has human-induced climate change affected California drought risk? J. Clim. 2016, 29, 111–120. [Google Scholar] [CrossRef]
- Berg, A.; Sheffield, J.; Milly, P.C.D. Divergent surface and total soil moisture projections under global warming. Geophys. Res. Lett. 2017, 44, 235–244. [Google Scholar] [CrossRef]
| GCM | RCP |
|---|---|
| Community Earth System Model 1-Community Atmospheric Model 5 (CESM1-CAM5) | 4.5 and 8.5 |
| Geophysical Fluid Dynamics Laboratory Climate Model 3 (GFDL-CM3) | 4.5 and 8.5 |
| Geophysical Fluid Dynamics Laboratory Earth System Model 2 (GFDL-ESM2) | 4.5 and 8.5 |
| First Institute of Oceanography-Earth System Model (FIO-ESM) | 4.5 and 8.5 |
| Hadley Global Environment Model 2-Atmosphere-Ocean (HadGEM2-AO) | 4.5 and 8.5 |
| Hadley Global Environment Model 2-Carbon Cycle (HadGEM2-CC) | 4.5 and 8.5 |
| Community Climate System Model 4 (CCSM4) | 4.5 and 8.5 |
| Centro Euro-Mediterraneo sui Cambiamenti Climatici Climate Model (CMCC-CM) | 4.5 and 8.5 |
| Hadley Global Environment Model 2-Earth System (HadGEM2-ES) | 4.5 and 8.5 |
| Model for Interdisciplinary Research on Climate 5 (MIROC5) | 4.5 and 8.5 |
| ID | Name | Lat. | Lon. | Area (km2) | αgw 1 |
|---|---|---|---|---|---|
| 03363900 | Flatrock River at Columbus, IN | 39.24 | −85.93 | 1383 | 0.23 |
| 03326500 | Mississinewa River at Marion, IN | 40.58 | −85.66 | 1766 | 0.33 |
| 03376500 | Patoka River near Princeton, IN | 38.39 | −87.55 | 2129 | 0.62 |
| 03360000 | Eel River at Bowling Green, IN | 39.38 | −87.02 | 2150 | 0.86 |
| 03331500 | Tippecanoe River near Ora, IN | 41.16 | −86.56 | 2217 | 0.17 |
| 03349000 | White River at Noblesville, IN | 40.05 | −86.02 | 2222 | 0.24 |
| 03379500 | Little Wabash River below Clay City, IL | 38.63 | −88.30 | 2929 | 0.85 |
| 03339000 | Vermilion River near Danville, IL | 40.10 | −87.60 | 3341 | 0.27 |
| 03345500 | Embarras River at Ste. Marie, IL | 38.94 | −88.02 | 3926 | 0.27 |
| 03353000 | White River at Indianapolis, IN | 39.74 | −86.17 | 4235 | 0.35 |
| 03365500 | East Fork White River at Seymour, IN | 38.98 | −85.90 | 6063 | 0.23 |
| 03354000 | White River near Centerton, IN | 39.50 | −86.40 | 6330 | 0.28 |
| 03327500 | Wabash River at Peru, IN | 40.75 | −86.07 | 6957 | 0.56 |
| 03381500 | Little Wabash River at Carmi, IL | 38.06 | −88.16 | 8034 | 0.95 |
| 03329000 | Wabash River at Logansport, IN | 40.75 | −86.38 | 9788 | 0.51 |
| 03371500 | East Fork White River near Bedford, IN | 38.77 | −86.41 | 10,000 | 0.31 |
| 03360500 | White River at Newberry, IN | 38.93 | −87.02 | 12,142 | 0.26 |
| 03373500 | East Fork White River at Shoals, IN | 38.67 | −86.79 | 12,761 | 0.26 |
| 03335500 | Wabash River at Lafayette, IN | 40.42 | −86.90 | 18,821 | 0.32 |
| 03336000 | Wabash River at Covington, IN | 40.14 | −87.41 | 21,285 | 0.22 |
| 03340500 | Wabash River at Montezuma, IN | 39.79 | −87.37 | 28,796 | 0.21 |
| 03374000 | White River at Petersburg, IN | 38.51 | −87.29 | 28,814 | 0.21 |
| 03341500 | Wabash River at Terre Haute, IN | 39.47 | −87.42 | 31,766 | 0.20 |
| 03342000 | Wabash River at Riverton, IN | 39.02 | −87.57 | 34,087 | 0.19 |
| 03377500 | Wabash River at Mt. Carmel, IL | 38.40 | −87.76 | 74,164 | 0.22 |
| Metric | Description | Calibration Target 1 |
|---|---|---|
| RSR | Root mean square error/standard deviation of observed | ≤0.70 |
| PBIAS | Percent bias | ≤±25 |
| NSE | Nash–Sutcliffe Efficiency criterion | ≥0.50 |
| VE | Volumetric efficiency | ≥0.50 |
| Drought Index Value | Classification |
|---|---|
| <−2 | Extremely Dry |
| −1 to −1.5 | Severely Dry |
| −1.5 to −1 | Moderately Dry |
| −1 to +1 | Near normal |
| +1 to +1.5 | Moderately Wet |
| +1.5 to +2 | Severely Wet |
| >+2 | Extremely Wet |
| SPI-1 | SPI-2 | SPI-3 | SPI-4 | SPI-5 | SPI-6 | |
|---|---|---|---|---|---|---|
| SSI-1 | 0.49 | 0.67 | 0.69 | 0.68 | 0.66 | 0.65 |
| SRI-1 | 0.55 | 0.76 | 0.81 | 0.81 | 0.79 | 0.75 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dierauer, J.R.; Zhu, C. Drought in the Twenty-First Century in a Water-Rich Region: Modeling Study of the Wabash River Watershed, USA. Water 2020, 12, 181. https://doi.org/10.3390/w12010181
Dierauer JR, Zhu C. Drought in the Twenty-First Century in a Water-Rich Region: Modeling Study of the Wabash River Watershed, USA. Water. 2020; 12(1):181. https://doi.org/10.3390/w12010181
Chicago/Turabian StyleDierauer, Jennifer R., and Chen Zhu. 2020. "Drought in the Twenty-First Century in a Water-Rich Region: Modeling Study of the Wabash River Watershed, USA" Water 12, no. 1: 181. https://doi.org/10.3390/w12010181
APA StyleDierauer, J. R., & Zhu, C. (2020). Drought in the Twenty-First Century in a Water-Rich Region: Modeling Study of the Wabash River Watershed, USA. Water, 12(1), 181. https://doi.org/10.3390/w12010181





