Evaluating Evaporation Methods for Estimating Small Reservoir Water Surface Evaporation in the Brazilian Savannah
Abstract
1. Introduction
2. Materials and Methods
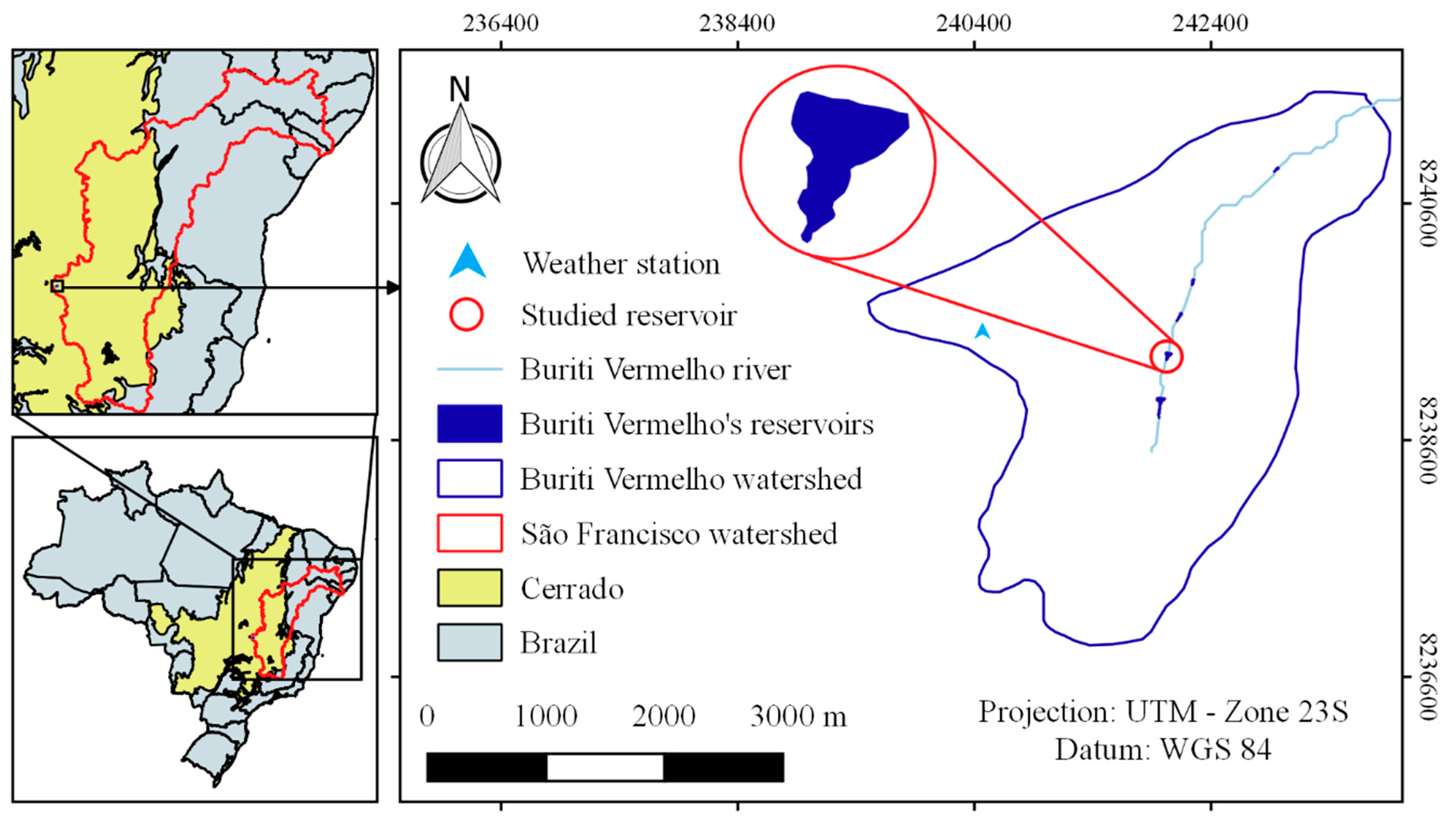
2.1. Study Area
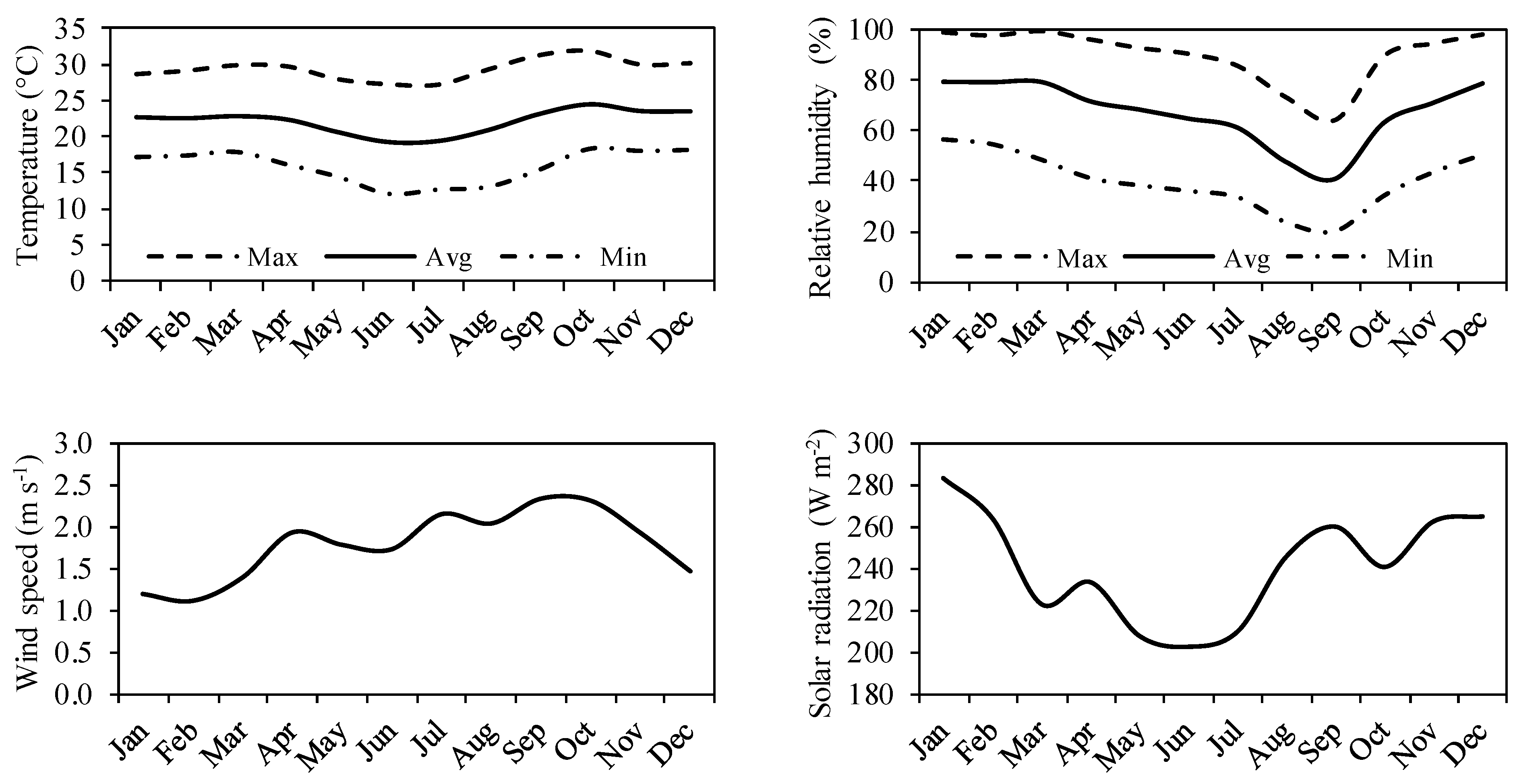
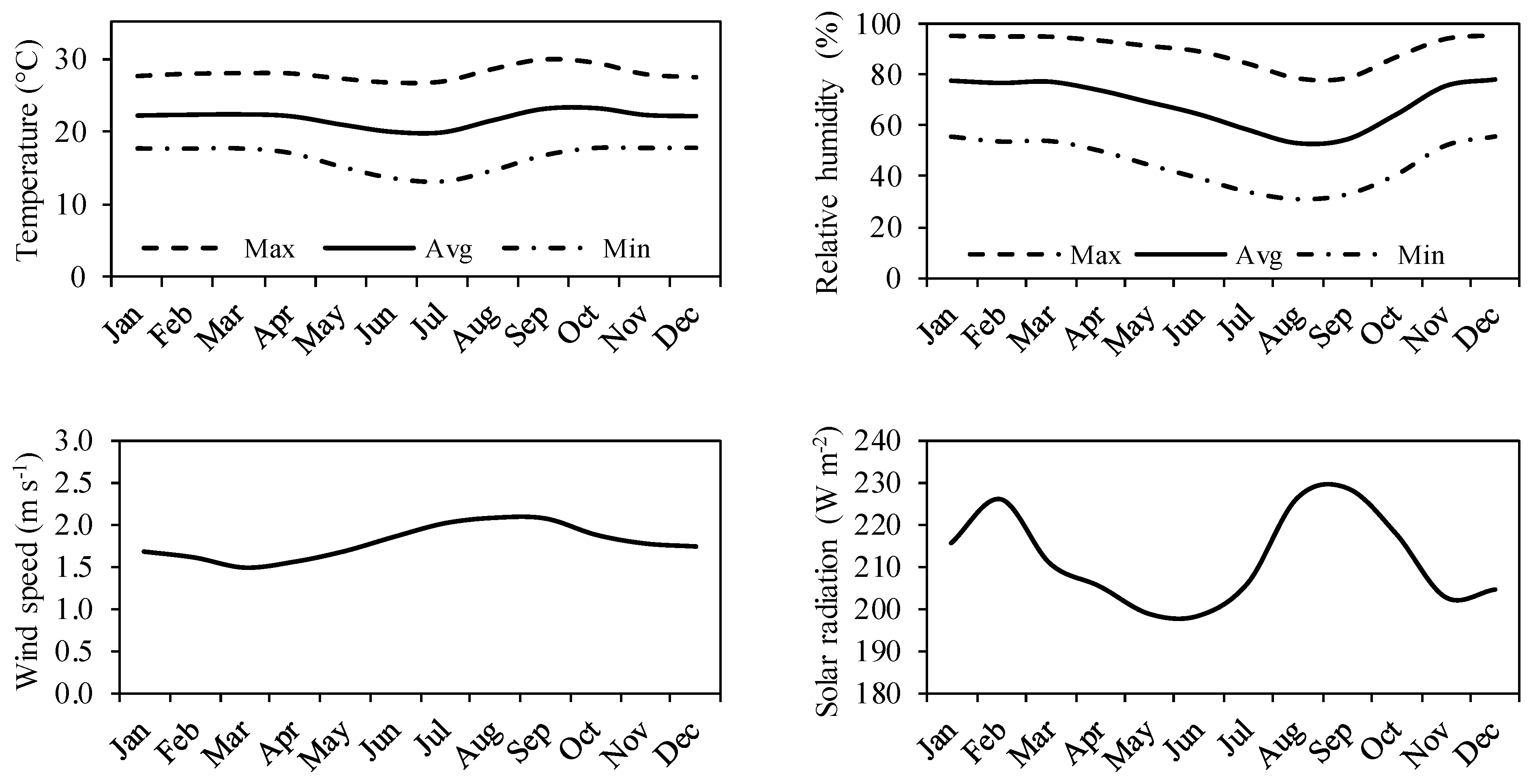
2.2. Data
2.3. Methods Used to Estimate Reservoir Evaporation
2.4. Performance Analysis of the Employed Equations
2.5. Elaboration of Reservoir Evaporation Frequency Curves
3. Results
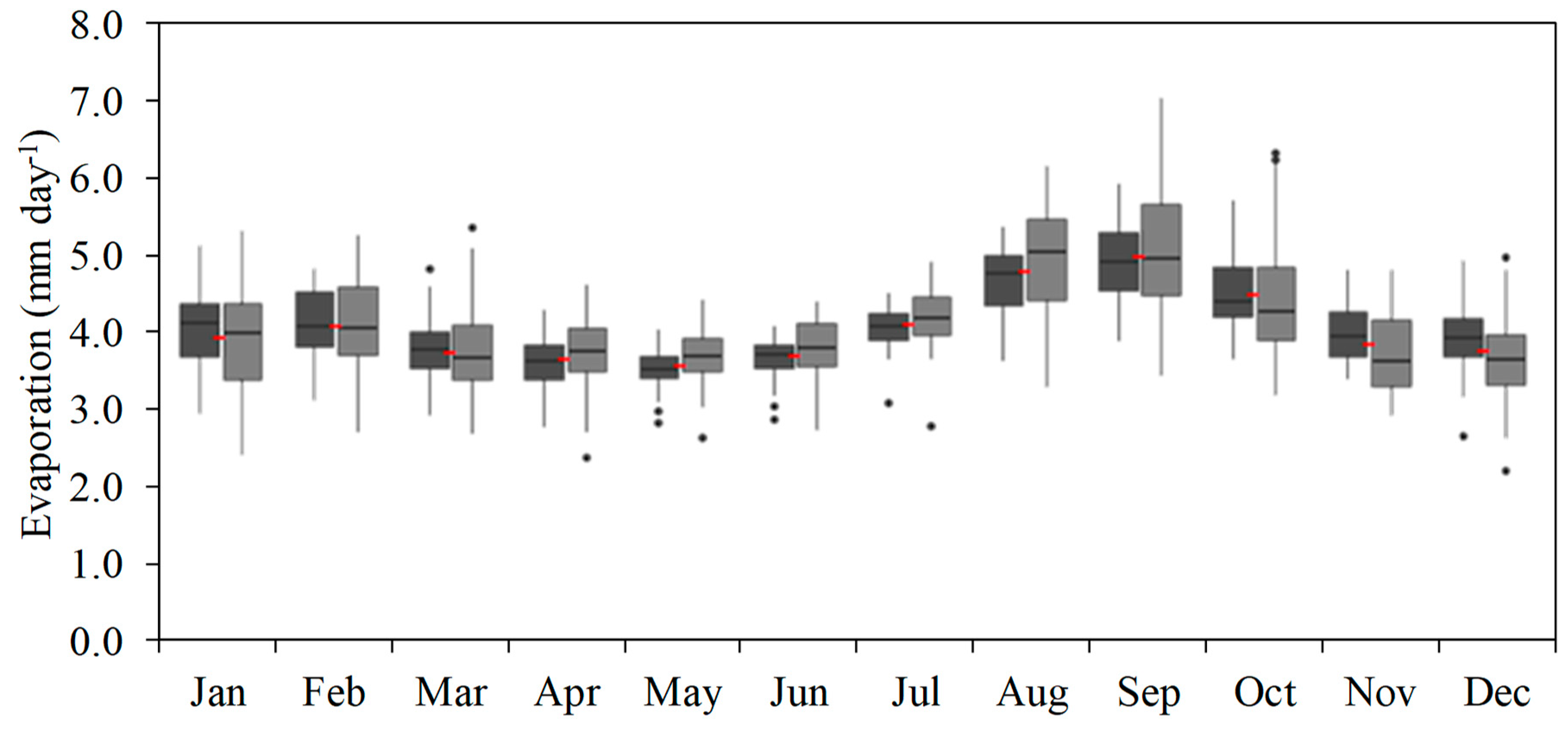
3.1. Evaluation of Observed Data
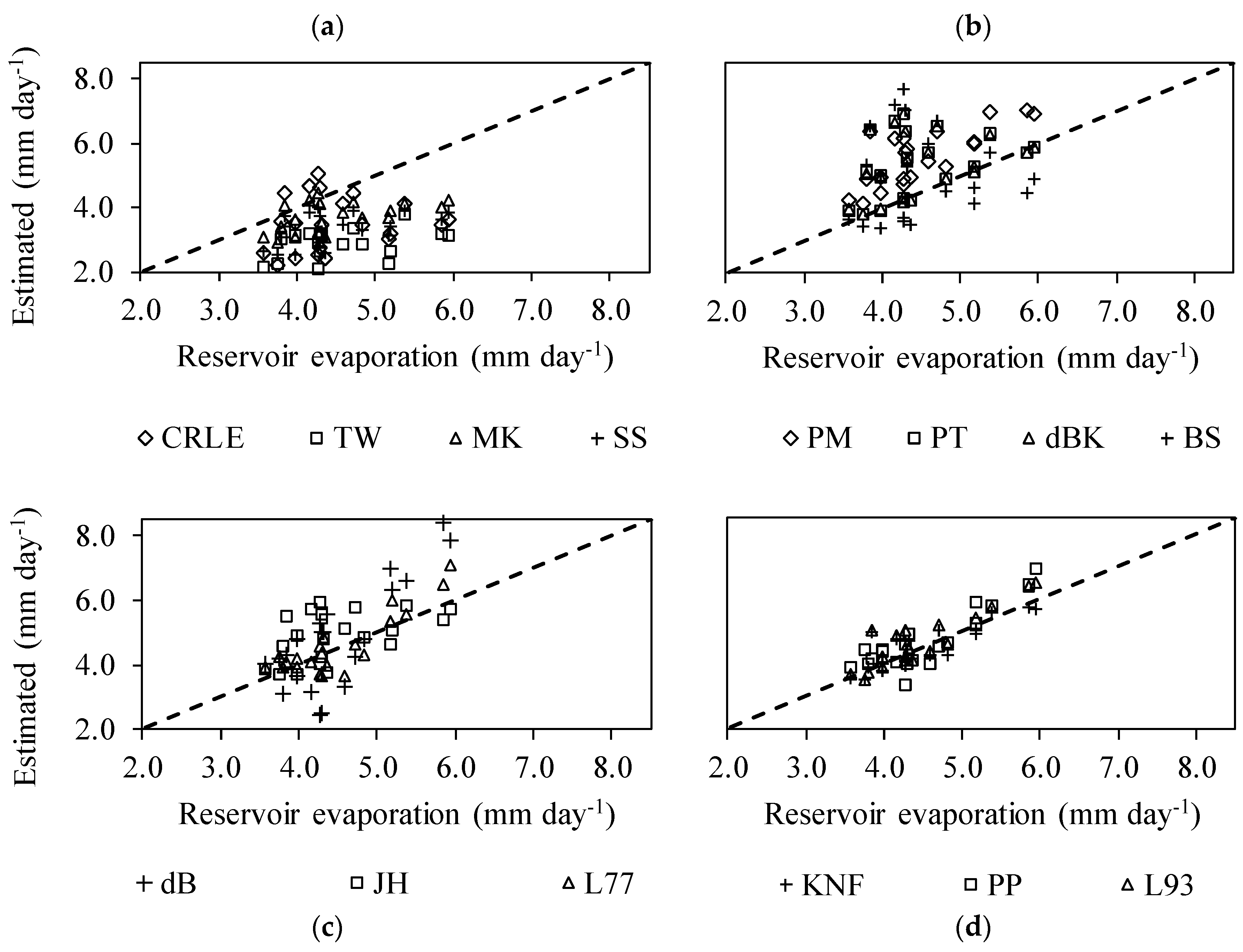
3.2. Performance of the Methods Used to Estimate Evaporation
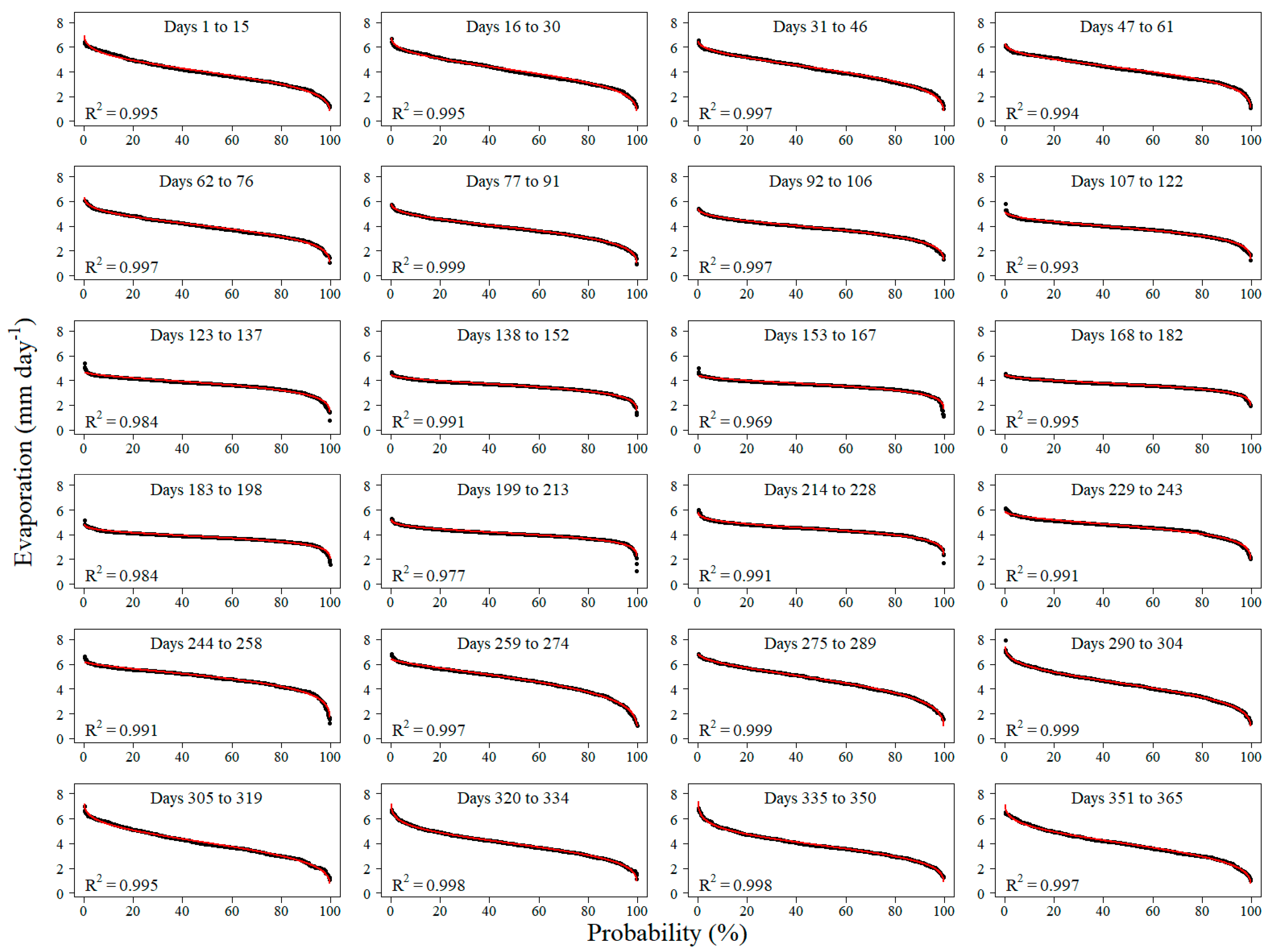
3.3. Reservoir Evaporation Frequency Curves
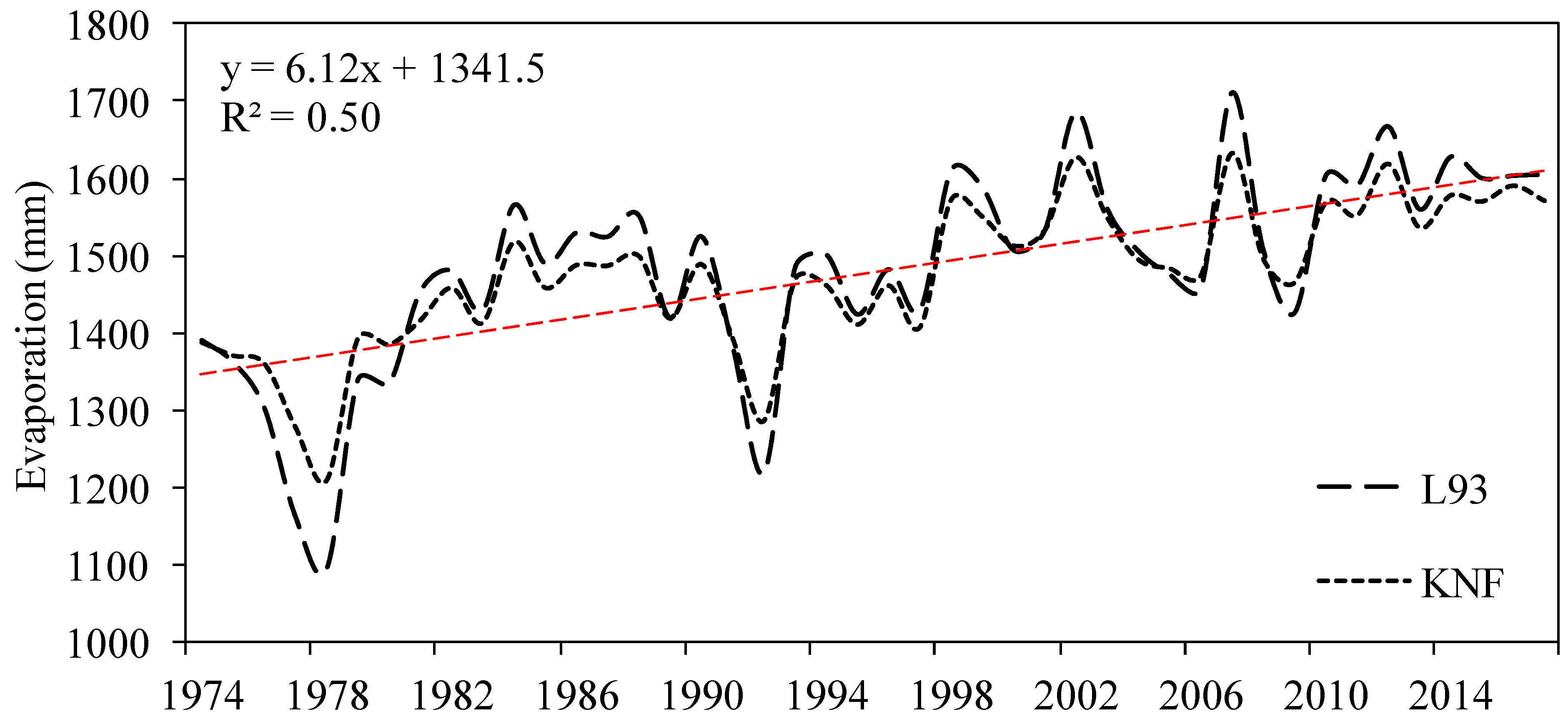
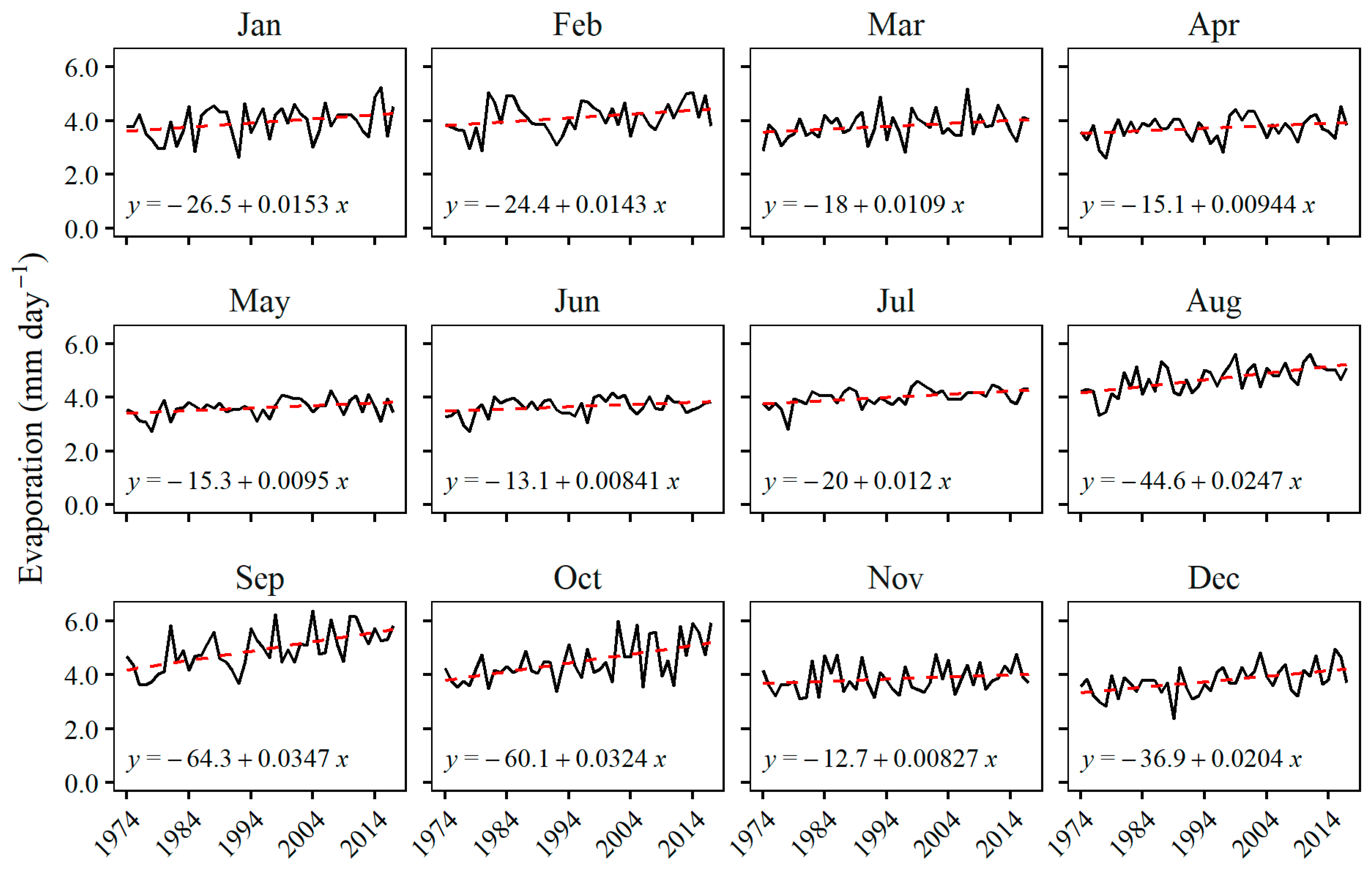
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Rosenberry, D.O.; Winter, T.C.; Buso, D.C.; Likens, G.E. Comparison of 15 evaporation methods applied to a small mountain lake in the northeastern USA. J. Hydrol. 2007, 340, 149–166. [Google Scholar] [CrossRef]
- Rodrigues, L.N.; Sano, E.E.; Steenhuis, T.S.; Passo, D.P. Estimation of small reservoir storage capacities with remote sensing in the Brazilian Savannah Region. Water Resour. Manag. 2012, 26, 873–882. [Google Scholar] [CrossRef]
- Klink, C.A. Policy intervention in the Cerrado Savannas of Brazil: Changes in the land use and effects on conservation. In Ecology and Conservation of the Maned Wolf: Multidisciplinary Perspectives; Consorte-McCrea, A.G., Ferraz Santos, E., Eds.; CRC Press: Boca Raton, FL, USA, 2014; pp. 293–308. [Google Scholar]
- Brito, L.T.L.; Cavalcanti, N.B.; Silva, A.S.; Pereira, L.A. Produtividade da água de chuva em culturas de subsistência no Semiárido Pernambucano. Eng. Agrícola 2012, 32, 102–109. [Google Scholar] [CrossRef]
- Poussin, J.-C.; Renaudin, L.; Adogoba, D.; Sanon, A.; Tazen, F.; Dogbe, W.; Fusillier, J.-L.; Barbier, B.; Cecchi, P. Performance of small reservoir irrigated schemes in the Upper Volta basin: Case studies in Burkina Faso and Ghana. Water Resour. Rural Dev. 2015, 6, 50–65. [Google Scholar] [CrossRef]
- Rodrigues, L.N.; Ramos, A.E.; Schaedler, H.A.R.; Lopes, A.V.; Figueiredo, G.C. Aspectos legais a serem considerados na construção de pequenas barragens. ITEM Irrig. E Tecnol. Mod. 2008, 80, 53–55. [Google Scholar]
- Friedrich, K.; Grossman, R.L.; Huntington, J.; Blanken, P.D.; Lenters, J.; Holman, K.D.; Gochis, D.; Livneh, B.; Prairie, J.; Skeie, E.; et al. Reservoir evaporation in the Western United States: Current science, challenges, and future needs. Bull. Am. Meteorol. Soc. 2018, 99, 167–187. [Google Scholar] [CrossRef]
- O’Reilly, C.M.; Sharma, S.; Gray, D.K.; Hampton, S.E.; Read, J.S.; Rowley, R.J.; Schneider, P.; Lenters, J.D.; McIntyre, P.B.; Kraemer, B.M.; et al. Rapid and highly variable warming of lake surface waters around the globe. Geophys. Res. Lett. 2015, 42, 10773–10781. [Google Scholar] [CrossRef]
- Wang, W.; Lee, X.; Xiao, W.; Liu, S.; Schultz, N.; Wang, Y.; Zhang, M.; Zhao, L. Global lake evaporation accelerated by changes in surface energy allocation in a warmer climate. Nat. Geosci. 2018, 11, 410–414. [Google Scholar] [CrossRef]
- Kang, M.; Park, S. Modeling water flows in a serial irrigation reservoir system considering irrigation return flows and reservoir operations. Agric. Water Manag. 2014, 143, 131–141. [Google Scholar] [CrossRef]
- Tinoco, V.; Willems, P.; Wyseure, G.; Cisneros, F. Evaluation of reservoir operation strategies for irrigation in the Macul Basin, Ecuador. J. Hydrol. Reg. Stud. 2016, 5, 213–225. [Google Scholar] [CrossRef][Green Version]
- Lowe, L.D.; Webb, J.A.; Nathan, R.J.; Etchells, T.; Malano, H.M. Evaporation from water supply reservoirs: An assessment of uncertainty. J. Hydrol. 2009, 376, 261–274. [Google Scholar] [CrossRef]
- Wurbs, R.A.; Ayala, R.A. Reservoir evaporation in Texas, USA. J. Hydrol. 2014, 510, 1–9. [Google Scholar] [CrossRef]
- Kaya, S.; Evren, S.; Dașcı, E. Comparison of various equations for estimating class a pan evaporation in semi-arid climate conditions. Ziraat Fakültesi Derg. Uludağ Üniversitesi 2016, 30, 1–9. [Google Scholar]
- Zhao, G.; Gao, H. Estimating reservoir evaporation losses for the United States: Fusing remote sensing and modeling approaches. Remote Sens. Environ. 2019, 226, 109–124. [Google Scholar] [CrossRef]
- Althoff, D.; Rodrigues, L.N.; da Silva, D.D.; Bazame, H.C. Improving methods for estimating small reservoir evaporation in the Brazilian Savanna. Agric. Water Manag. 2019, 216, 105–112. [Google Scholar] [CrossRef]
- Masoner, J.R.; Stannard, D.I.; Christenson, S.C. Differences in evaporation between a floating pan and Class A pan on land. JAWRA J. Am. Water Resour. Assoc. 2008, 44, 552–561. [Google Scholar] [CrossRef]
- Harwell, G.R. Estimation of Evaporation from Open Water: A Review of Selected Studies, Summary of US Army Corps of Engineers Data Collection and Methods, and Evaluation of Two Methods for Estimation of Evaporation from Five Reservoirs in Texas; U.S. Department of the Interior: Washington, DC, USA; U.S. Geological Survey: Reston, VA, USA, 2012.
- Penman, H.L. Natural evaporation from open water, bare soil and grass. Proc. R. Soc. Lond. Ser. A 1948, 193, 120–145. [Google Scholar]
- Antonopoulos, V.Z.; Gianniou, S.K.; Antonopoulos, A.V. Artificial neural networks and empirical equations to estimate daily evaporation: Application to Lake Vegoritis, Greece. Hydrol. Sci. J. 2016, 61, 2590–2599. [Google Scholar] [CrossRef]
- Kohler, M.; Nordenson, T.; Fox, W. Evaporation from Pans and Lakes; US Weather Bureau: Washington, DC, USA, 1955; p. 38.
- Thornthwaite, C.W.; Mather, J.R. The Water Balance; Drexel Institute of Technology, Laboratory of Climatology: Centerton, NJ, USA, 1955; p. 104. [Google Scholar]
- Linacre, E.T. A simple formula for estimating evaporation rates in various climates, using temperature data alone. Agric. Meteorol. 1977, 18, 409–424. [Google Scholar] [CrossRef]
- Linacre, E.T. Data-sparse estimation of lake evaporation, using a simplified Penman equation. Agric. For. Meteorol. 1993, 64, 237–256. [Google Scholar] [CrossRef]
- DeBruin, H.A.R.; Keijman, J.Q. The Priestley-Taylor evaporation model applied to a large, shallow lake in the Netherlands. J. Appl. Meteorol. 1979, 18, 898–903. [Google Scholar] [CrossRef]
- Morton, F.I. Operational estimates of areal evapotranspiration and their significance to the science and practice of hydrology. J. Hydrol. 1983, 66, 1–76. [Google Scholar] [CrossRef]
- Winter, T.C.; Rosenberry, D.O.; Sturrock, A.M. Evaluation of 11 equations for determining evaporation for a small lake in the north central United States. Water Resour. Res. 1995, 31, 983–993. [Google Scholar] [CrossRef]
- Leão, R.A.D.O.; Soares, A.A.; Teixeira, A.D.S.; Silva, D.D.D. Estimation of evaporation in the Banabuiú dam, in the state of Ceará, Brazil, by different combined methods, derived from the Penman equation. Eng. Agrícola 2013, 33, 129–144. [Google Scholar] [CrossRef]
- Stephens, J.C.; Stewart, E.H. A comparison of procedures for computing evaporation and evapotranspiration. Publication 1963, 62, 123–133. [Google Scholar]
- McGuinness, J.L.; Bordne, E.F. A Comparison of Lysimeter-Derived Potential Evapotranspiration with Computed Values; U.S. Department of Agriculture: Washington, DC, USA, 1972.
- Papadakis, J. Potential evapotranspiration. Soil Sci. 1965, 100, 76. [Google Scholar] [CrossRef]
- Thornthwaite, C.W. An approach toward a rational classification of climate. Geogr. Rev. 1948, 38, 55–94. [Google Scholar] [CrossRef]
- Priestley, C.H.B.; Taylor, R.J. On the assessment of surface heat flux and evaporation using large-scale parameters. Mon. Weather Rev. 1972, 100, 81–92. [Google Scholar] [CrossRef]
- DeBruin, H.A.R. A simple model for shallow lake evaporation. J. Appl. Meteorol. 1978, 17, 1132–1134. [Google Scholar] [CrossRef]
- Jensen, M.E.; Haise, H.R. Estimating evapotranspiration from solar radiation. Proc. Am. Soc. Civ. Eng. J. Irrig. Drain. Div. 1963, 89, 15–41. [Google Scholar]
- Brutsaert, W.; Stricker, H. An advection-aridity approach to estimate actual regional evapotranspiration. Water Resour. Res. 1979, 15, 443–450. [Google Scholar] [CrossRef]
- Coelho, C.D.; da Silva, D.D.; Sediyama, G.C.; Moreira, M.C.; Pereira, S.B.; Lana, Â.M.Q. Comparison of the water footprint of two hydropower plants in the Tocantins River Basin of Brazil. J. Clean. Prod. 2017, 153, 164–175. [Google Scholar] [CrossRef]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models part I—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Saleh, A.; Arnold, J.G.; Gassman, P.W.; Hauck, L.M.; Rosenthal, W.D.; Williams, J.R.; McFarland, A.M.S. Application of SWAT for the upper North Bosque River watershed. Trans. ASAE 2000, 43, 1077–1087. [Google Scholar] [CrossRef]
- Willmott, C.J.; Matsuura, K. Advantages of the mean absolute error (MAE) over the root mean square error (RMSE) in assessing average model performance. Clim. Res. 2005, 30, 79–82. [Google Scholar] [CrossRef]
- Richter, K.; Hank, T.B.; Atzberger, C.; Mauser, W. Goodness-of-fit measures: What do they tell about vegetation variable retrieval performance from Earth observation data. In Remote Sensing for Agriculture, Ecosystems, and Hydrology XIII; International Society for Optics and Photonics: Bellingham, WA, USA, 2011; Volume 8174, p. 81740R. [Google Scholar]
- Santhi, C.; Arnold, J.G.; Williams, J.R.; Dugas, W.A.; Srinivasan, R.; Hauck, L.M. Validation of the swat model on a large rwer basin with point and nonpoint sources. J. Am. Water Resour. Assoc. 2001, 37, 1169–1188. [Google Scholar] [CrossRef]
- Searcy, J.K. Flow-Duration Curves; US Government Printing Office: Washington, DC, USA, 1959.
- Shao, Q.; Zhang, L.; Chen, Y.D.; Singh, V.P. A new method for modelling flow duration curves and predicting streamflow regimes under altered land-use conditions. Hydrol. Sci. J. 2009, 54, 606–622. [Google Scholar] [CrossRef]
- Kimball, B.F. On the choice of plotting positions on probability paper. J. Am. Stat. Assoc. 1960, 55, 546–560. [Google Scholar] [CrossRef]
- Shao, Q.; Wong, H.; Xia, J.; Ip, W.-C. Models for extremes using the extended three-parameter Burr XII system with application to flood frequency analysis. Hydrol. Sci. J. 2004, 49, 685–702. [Google Scholar] [CrossRef]
- Moré, J.J. The Levenberg-Marquardt algorithm: Implementation and theory. In Numerical Analysis; Springer: Berlin/Heidelberg, Germany, 1978; pp. 105–116. ISBN 978-3-540-08538-6. [Google Scholar]
- Barnes, E.A.; Barnes, R.J. Estimating linear trends: Simple linear regression versus epoch differences. J. Clim. 2015, 28, 9969–9976. [Google Scholar] [CrossRef]
- Mudelsee, M. Trend analysis of climate time series: A review of methods. Earth Sci. Rev. 2019, 190, 310–322. [Google Scholar] [CrossRef]
- Garfinkel, C.I.; Waugh, D.W.; Polvani, L.M. Recent Hadley cell expansion: The role of internal atmospheric variability in reconciling modeled and observed trends. Geophys. Res. Lett. 2015, 42, 10824–10831. [Google Scholar] [CrossRef]
- Condie, S.A.; Webster, I.T. The influence of wind stress, temperature, and humidity gradients on evaporation from reservoirs. Water Resour. Res. 1997, 33, 2813–2822. [Google Scholar] [CrossRef]
- Warnaka, K.; Pochop, L. Analyses of equations for free water evaporation estimates. Water Resour. Res. 1988, 24, 979–984. [Google Scholar] [CrossRef]
- Cabrera, M.C.; Anache, J.A.A.; Youlton, C.; Wendland, E. Performance of evaporation estimation methods compared with standard 20 m2 tank. Rev. Bras. Eng. Agrícola E Ambient. 2016, 20, 874–879. [Google Scholar] [CrossRef]
- Pires, G.F.; Abrahão, G.M.; Brumatti, L.M.; Oliveira, L.J.; Costa, M.H.; Liddicoat, S.; Kato, E.; Ladle, R.J. Increased climate risk in Brazilian double cropping agriculture systems: Implications for land use in Northern Brazil. Agric. For. Meteorol. 2016, 228, 286–298. [Google Scholar] [CrossRef]
- Adrian, R.; O’Reilly, C.M.; Zagarese, H.; Baines, S.B.; Hessen, D.O.; Keller, W.; Livingstone, D.M.; Sommaruga, R.; Straile, D.; Donk, E.V.; et al. Lakes as sentinels of climate change. Limnol. Oceanogr. 2009, 54, 2283–2297. [Google Scholar] [CrossRef]
- Krol, M.S.; de Vries, M.J.; van Oel, P.R.; de Araújo, J.C. Sustainability of small reservoirs and large scale water availability under current conditions and climate change. Water Resour. Manag. 2011, 25, 3017–3026. [Google Scholar] [CrossRef]

| Methods (Reference) | Equation | Applied |
|---|---|---|
| Stephens and Stewart (1963)—SS [29] | Monthly | |
| Makkink (McGuinness et al. 1972)—MK [30] | Monthly | |
| Papadakis (1965)—PP [31] | Monthly | |
| Thornthwaite (1948)—TW [32] | Monthly | |
| Priestley and Taylor (1972)—PT [33] | >10 days | |
| DeBruin (1978)—dB [34] | >10 days | |
| Jensen and Haise (1963)—JH [35] | >5 days | |
| Penman (1948)—PM [19] | Daily | |
| Brutsaert and Stricker (1979)—BS [36] | Daily | |
| DeBruin and Keijman (1979)—dBK [25] | Daily | |
| Morton (1983)—CRLE [26] | Daily | |
| Linacre (1977)—L77 [23] | Daily | |
| Linacre (1993)—L93 [24] | Daily | |
| Kohler et al. (1955)—KNF [21] | Daily |
| Methods | NSE | R2 | RMSE | MAE | MBE |
| Daily Scale | |||||
| KNF | 0.58 | 0.61 | 0.68 | 0.54 | −0.18 |
| L93 | 0.54 | 0.66 | 0.71 | 0.56 | 0.14 |
| L77 | −0.01 | 0.43 | 1.06 | 0.83 | 0.22 |
| PM | −0.09 | 0.54 | 1.10 | 0.89 | 0.79 |
| dBK | −0.19 | 0.19 | 1.15 | 0.85 | 0.26 |
| BS | −1.50 | 0.01 | 1.66 | 1.35 | −0.26 |
| CRLE | −1.91 | 0.15 | 1.79 | 1.59 | −1.44 |
| Methods | NSE | R2 | RMSE | MAE | MBE |
| Monthly Scale | |||||
| KNF | 0.66 | 0.70 | 0.38 | 0.29 | 0.03 |
| L93 | 0.55 | 0.80 | 0.44 | 0.34 | 0.23 |
| PP | 0.43 | 0.75 | 0.49 | 0.42 | 0.19 |
| L77 | 0.41 | 0.76 | 0.50 | 0.40 | 0.09 |
| JH | −0.56 | 0.23 | 0.82 | 0.63 | 0.39 |
| MK | −1.32 | 0.26 | 1.00 | 0.85 | −0.81 |
| dB | −2.46 | 0.64 | 1.22 | 1.04 | 0.33 |
| PM | −2.55 | 0.56 | 1.23 | 1.09 | 1.09 |
| dBK | −2.71 | 0.11 | 1.26 | 0.87 | 0.82 |
| PT | −2.80 | 0.12 | 1.27 | 0.88 | 0.82 |
| SS | −3.25 | 0.23 | 1.35 | 1.21 | −1.21 |
| CRLE | −3.56 | 0.02 | 1.40 | 1.21 | −1.00 |
| BS | −4.77 | 0.01 | 1.57 | 1.26 | 0.56 |
| TW | −6.88 | 0.12 | 1.84 | 1.71 | −1.71 |
| Interval (Julian days) | Performance Criteria | Evaporation (mm day−1) | Distribution Coefficients | ||||
|---|---|---|---|---|---|---|---|
| NSE | RMSE | 20% * | 60% * | λ | β | α | |
| 1 to 15 | 0.995 | 0.08 | 4.91 | 3.68 | 4.358 | 0.006 | 0.252 |
| 16 to 30 | 0.995 | 0.08 | 5.05 | 3.82 | 4.577 | 0.120 | 0.258 |
| 31 to 46 | 0.997 | 0.06 | 5.13 | 3.93 | 4.766 | 0.252 | 0.261 |
| 47 to 61 | 0.994 | 0.07 | 5.01 | 3.97 | 4.644 | 0.168 | 0.218 |
| 62 to 76 | 0.997 | 0.05 | 4.75 | 3.73 | 4.305 | 0.011 | 0.211 |
| 77 to 91 | 0.999 | 0.03 | 4.55 | 3.61 | 4.186 | 0.110 | 0.213 |
| 92 to 106 | 0.997 | 0.04 | 4.41 | 3.63 | 4.116 | 0.119 | 0.180 |
| 107 to 122 | 0.993 | 0.06 | 4.34 | 3.65 | 4.101 | 0.159 | 0.164 |
| 123 to 137 | 0.984 | 0.08 | 4.18 | 3.59 | 4.045 | 0.351 | 0.156 |
| 138 to 152 | 0.991 | 0.05 | 3.95 | 3.45 | 3.802 | 0.240 | 0.133 |
| 153 to 167 | 0.969 | 0.09 | 3.98 | 3.51 | 3.845 | 0.264 | 0.123 |
| 168 to 182 | 0.995 | 0.03 | 3.98 | 3.55 | 3.814 | 0.086 | 0.102 |
| 183 to 198 | 0.984 | 0.06 | 4.14 | 3.70 | 3.925 | −0.110 | 0.094 |
| 199 to 213 | 0.977 | 0.07 | 4.43 | 3.95 | 4.195 | −0.141 | 0.094 |
| 214 to 228 | 0.991 | 0.05 | 4.85 | 4.30 | 4.573 | −0.151 | 0.099 |
| 229 to 243 | 0.991 | 0.07 | 5.18 | 4.50 | 4.966 | 0.218 | 0.136 |
| 244 to 258 | 0.991 | 0.08 | 5.61 | 4.78 | 5.502 | 0.491 | 0.177 |
| 259 to 274 | 0.997 | 0.06 | 5.67 | 4.53 | 5.627 | 0.602 | 0.264 |
| 275 to 289 | 0.999 | 0.04 | 5.68 | 4.45 | 5.386 | 0.346 | 0.252 |
| 290 to 304 | 0.999 | 0.04 | 5.33 | 4.05 | 4.762 | 0.005 | 0.240 |
| 305 to 319 | 0.995 | 0.08 | 5.05 | 3.73 | 4.482 | 0.040 | 0.271 |
| 320 to 334 | 0.998 | 0.05 | 4.86 | 3.68 | 4.269 | −0.111 | 0.229 |
| 335 to 350 | 0.998 | 0.05 | 4.74 | 3.56 | 4.098 | −0.202 | 0.225 |
| 351 to 365 | 0.997 | 0.07 | 4.93 | 3.64 | 4.348 | −0.001 | 0.263 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Althoff, D.; Rodrigues, L.N.; da Silva, D.D. Evaluating Evaporation Methods for Estimating Small Reservoir Water Surface Evaporation in the Brazilian Savannah. Water 2019, 11, 1942. https://doi.org/10.3390/w11091942
Althoff D, Rodrigues LN, da Silva DD. Evaluating Evaporation Methods for Estimating Small Reservoir Water Surface Evaporation in the Brazilian Savannah. Water. 2019; 11(9):1942. https://doi.org/10.3390/w11091942
Chicago/Turabian StyleAlthoff, Daniel, Lineu Neiva Rodrigues, and Demetrius David da Silva. 2019. "Evaluating Evaporation Methods for Estimating Small Reservoir Water Surface Evaporation in the Brazilian Savannah" Water 11, no. 9: 1942. https://doi.org/10.3390/w11091942
APA StyleAlthoff, D., Rodrigues, L. N., & da Silva, D. D. (2019). Evaluating Evaporation Methods for Estimating Small Reservoir Water Surface Evaporation in the Brazilian Savannah. Water, 11(9), 1942. https://doi.org/10.3390/w11091942






