Wall Stresses in Cylinder of Stationary Piped Carriage Using COMSOL Multiphysics
Abstract
1. Introduction
2. Theoretical Analysis
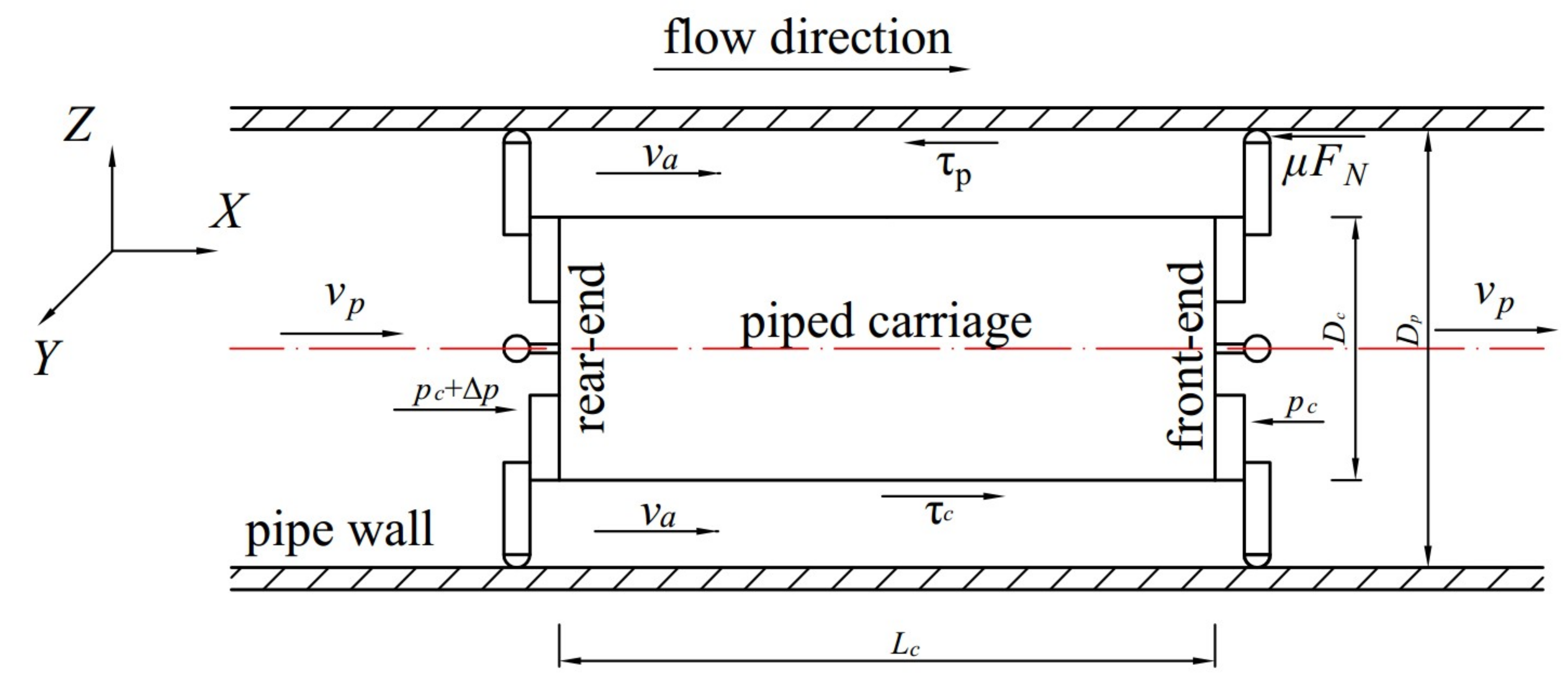
2.1. Piped Carriage Structure
2.2. Force Analysis
3. Methods
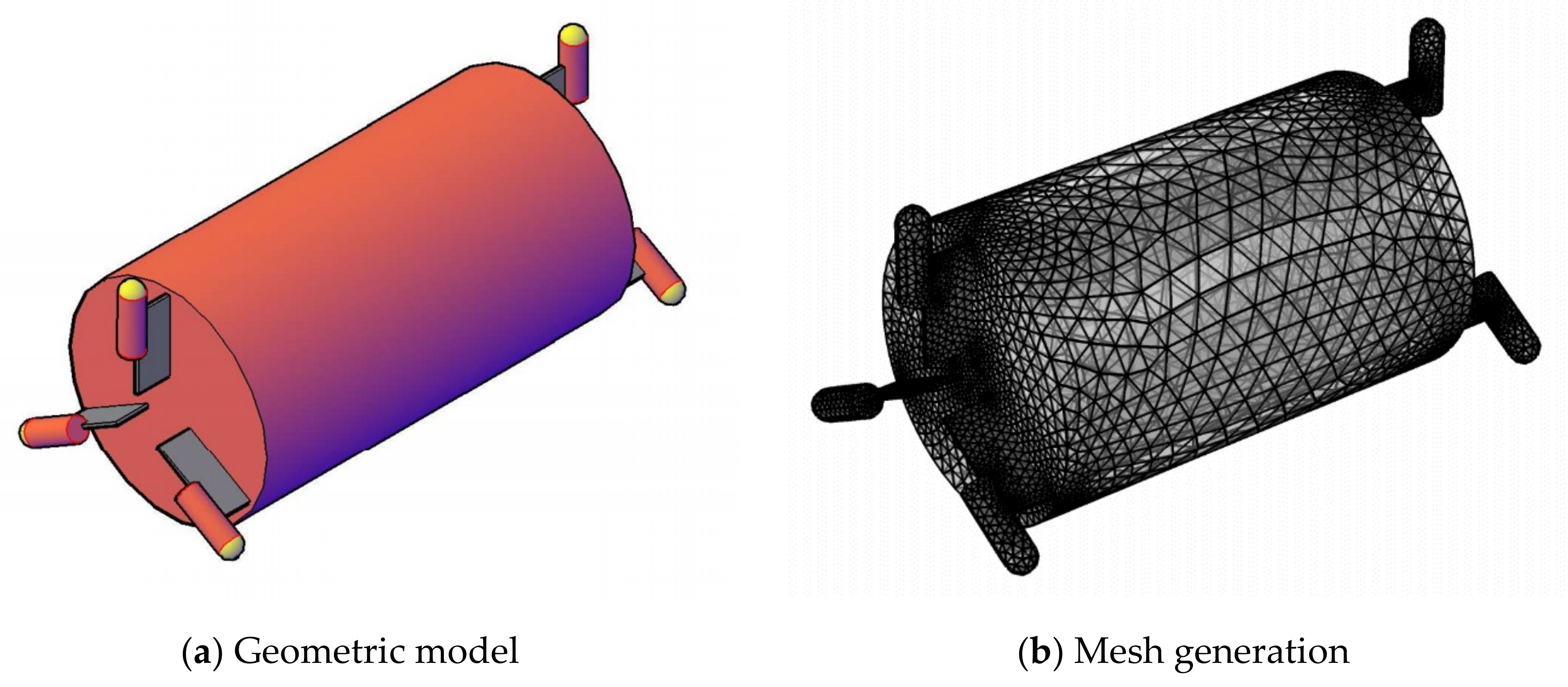
3.1. Model Setup in COMSOL Multiphysics
3.2. Definitions
3.2.1. Fluid Properties
3.2.2. Structure Properties
3.2.3. Interaction Conditions
3.3. Boundary Conditions
3.4. Finite Elements Mesh
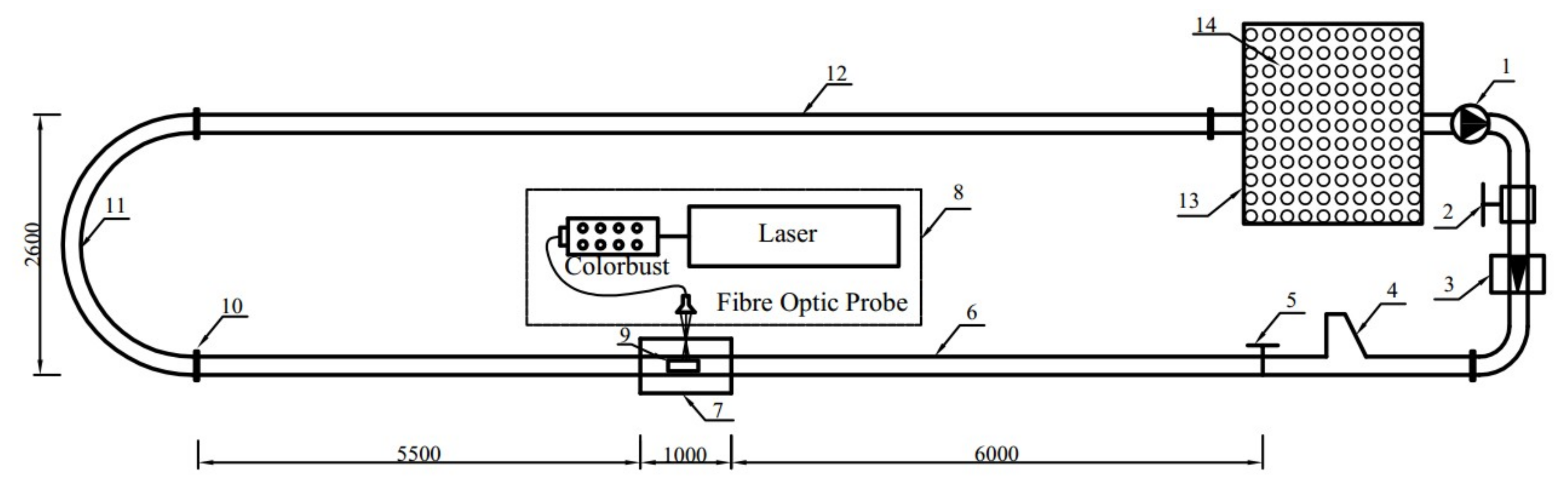
4. Experimental Setup and Conditions
4.1. Laser Doppler Velocimetry (LDV)
4.2. Piped Carriage Force Measuring System
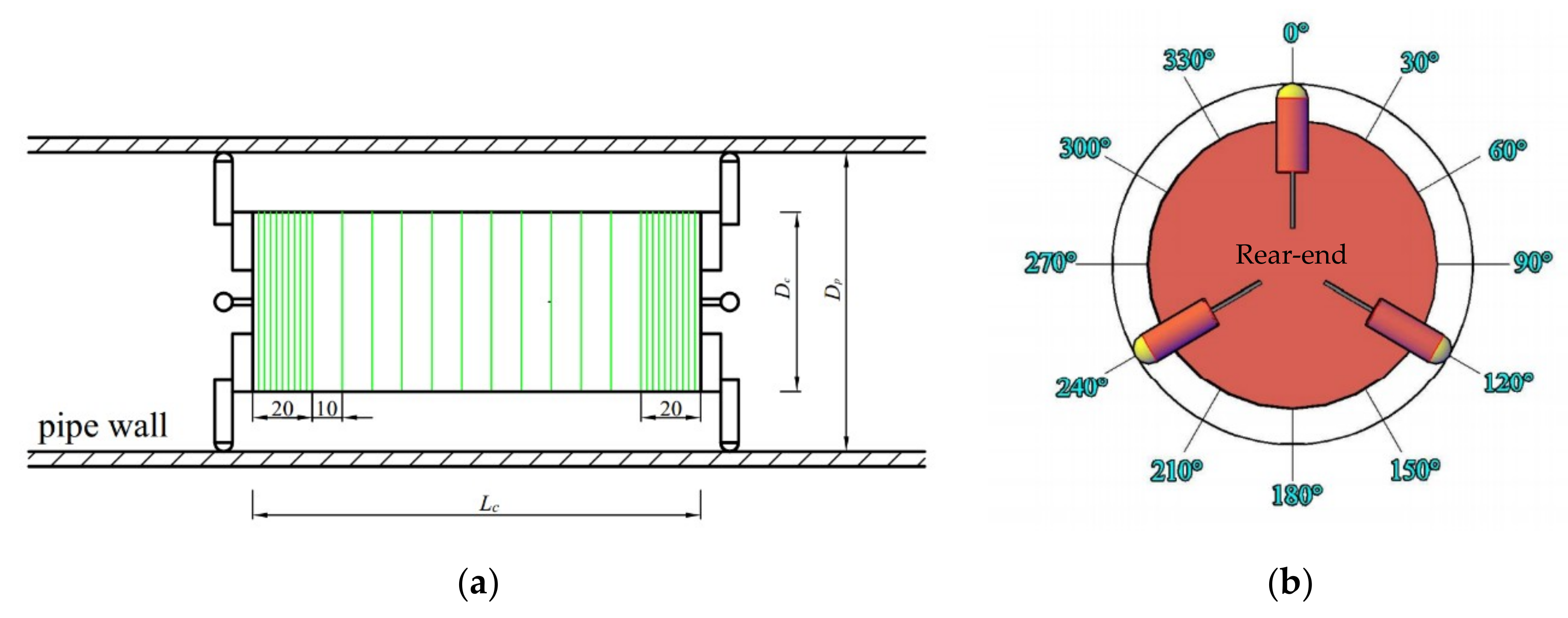
4.3. Selection of Cross Section and Layout of Measurement Points
4.3.1. The Layout of Measuring Points in LDV Measuring Flow Field Near the Cylinder Wall of Piped Carriage
4.3.2. The Layout of Measuring Points in Measuring the Principal Stress by Pipeline Force Measuring System
4.4. Design of Conditions
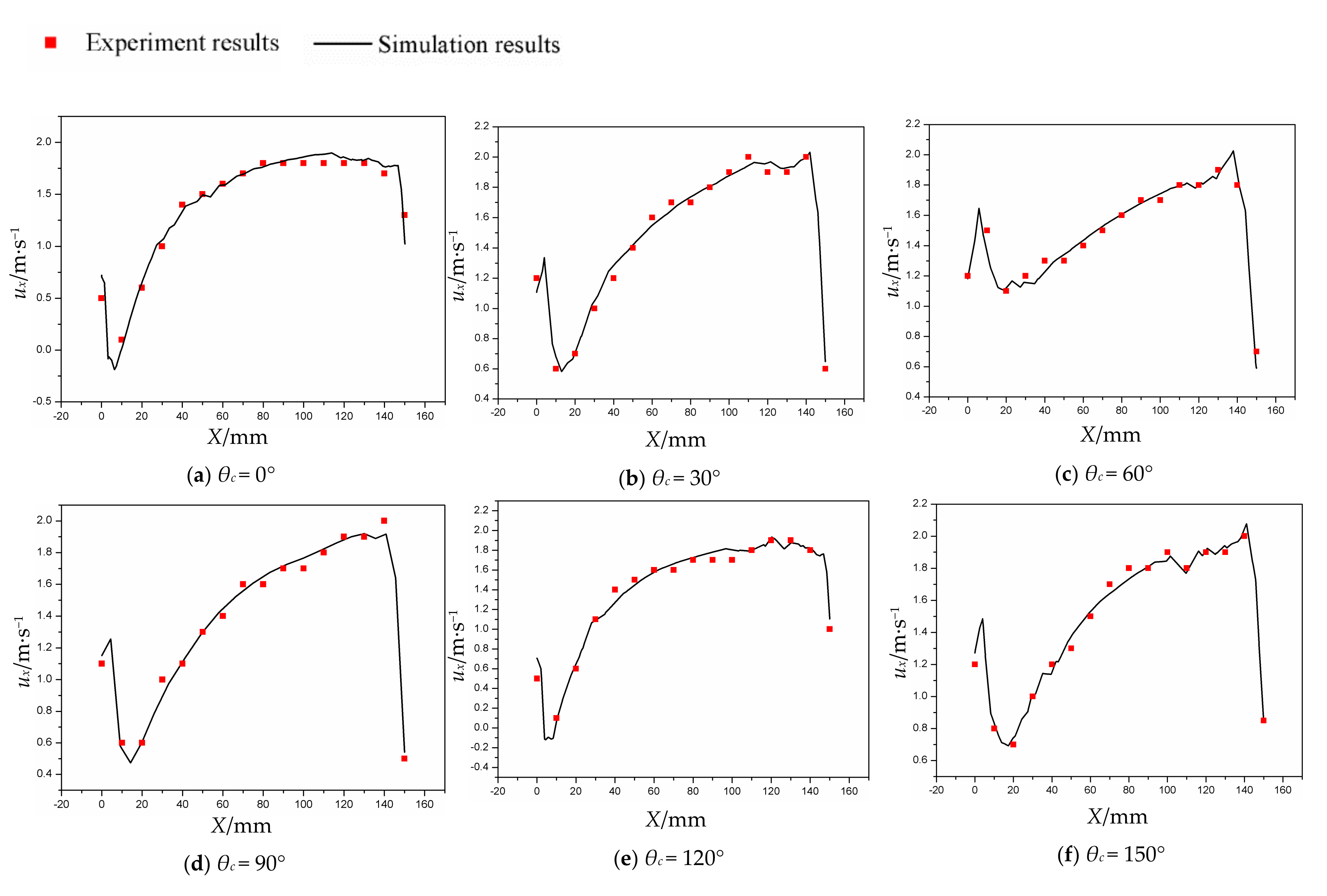
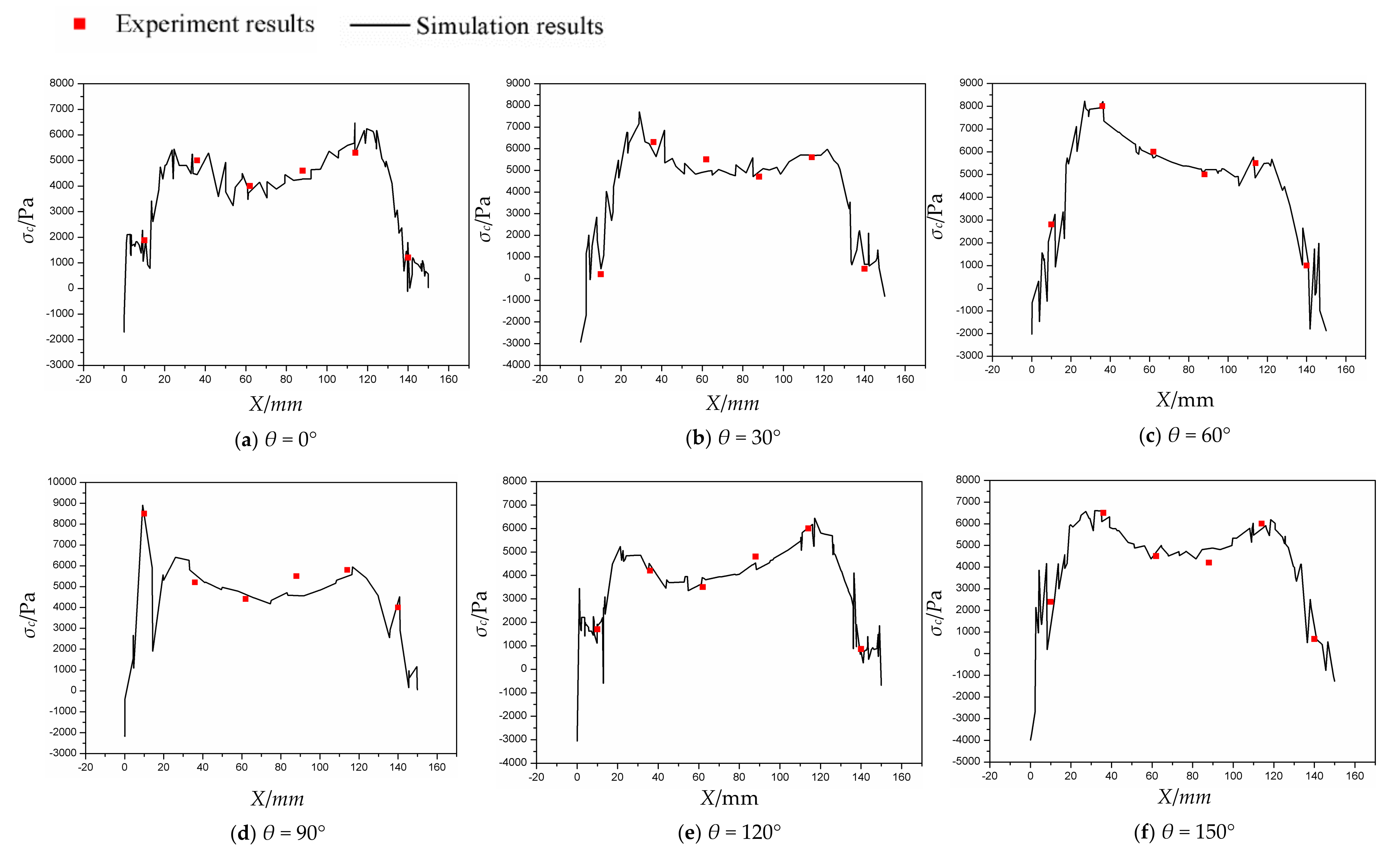
5. Validation of Simulated Results
5.1. Velocity Distribution
5.2. The Circumferential Component of the Principal Stress
6. Results and Discussion
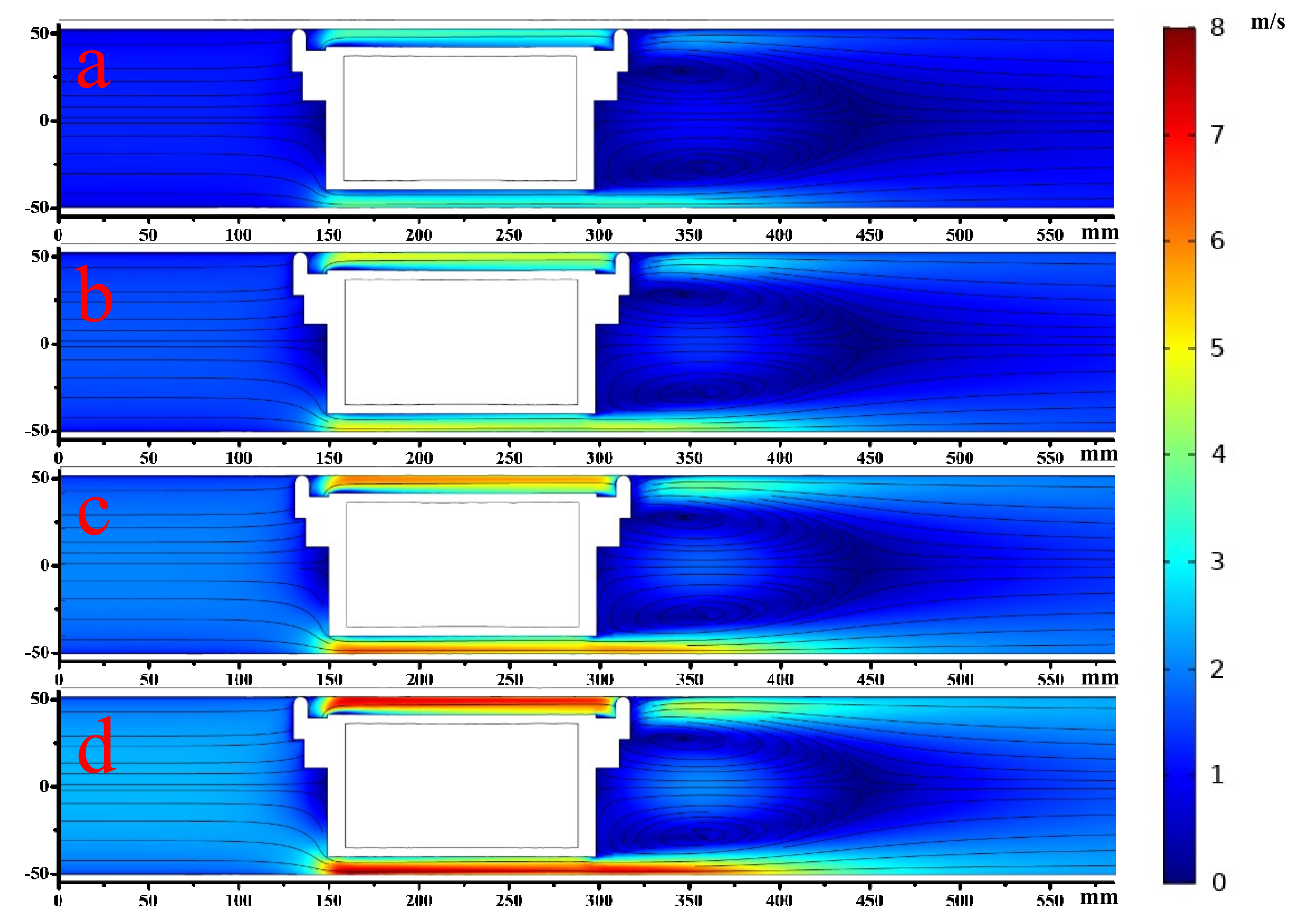
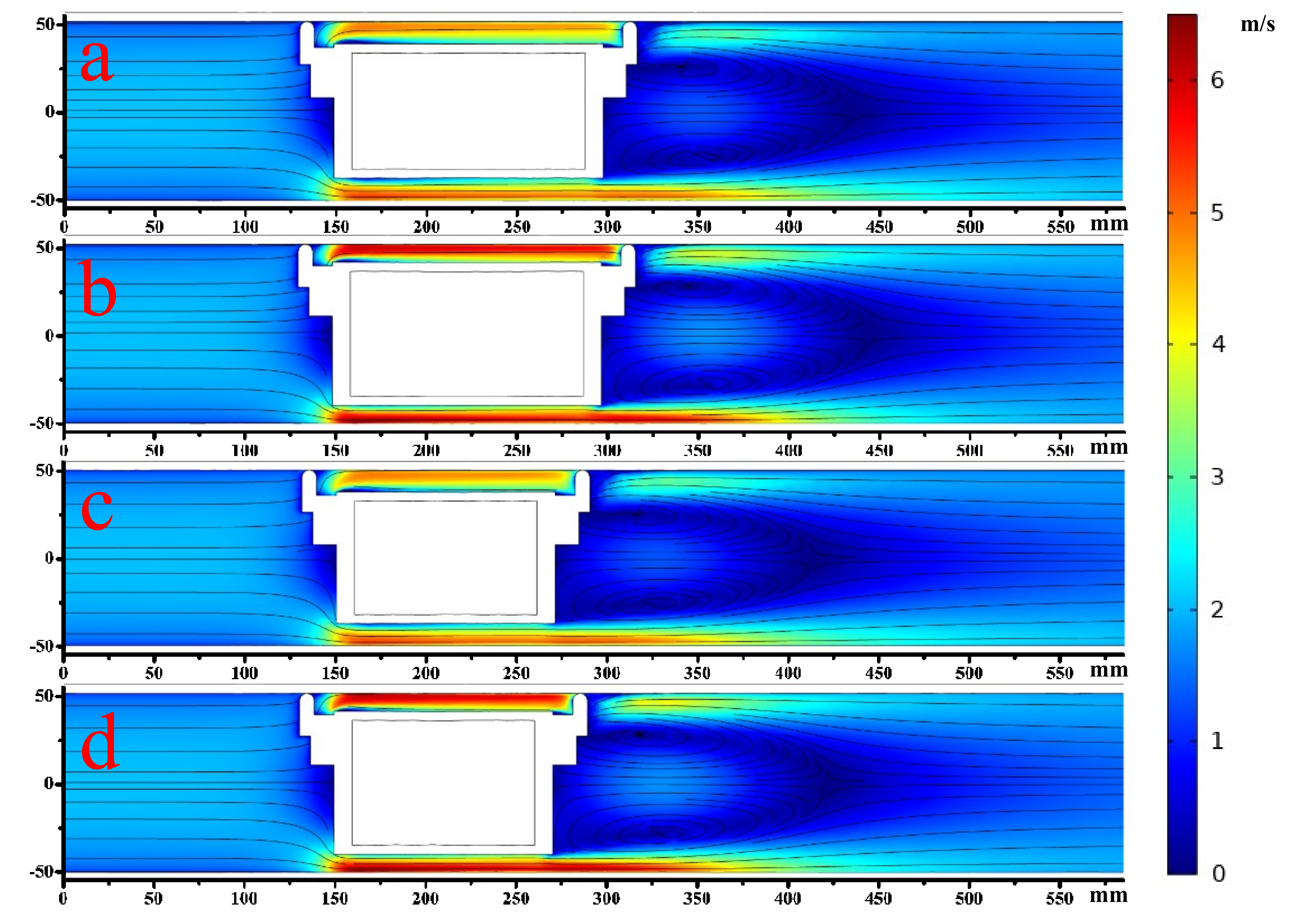
6.1. Velocity Distributions
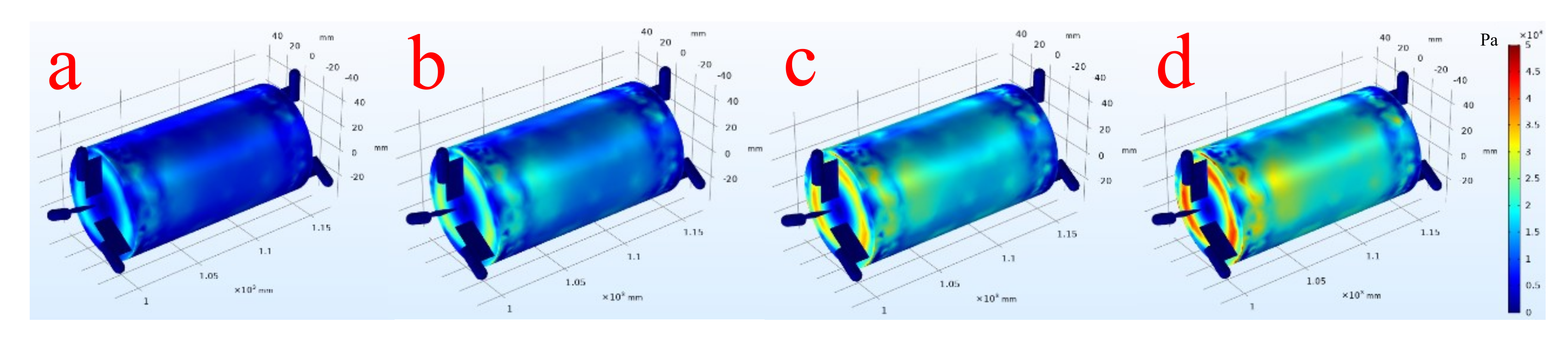
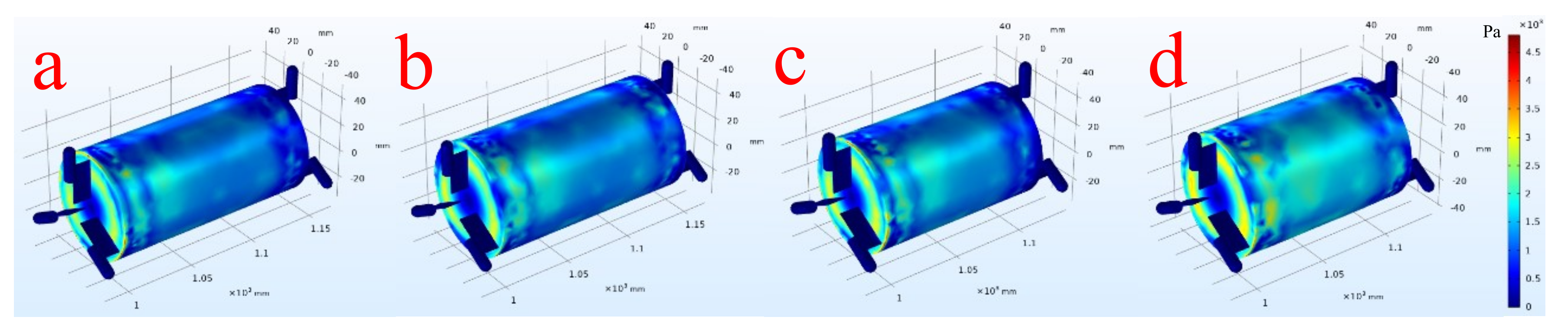
6.2. Wall Shear Stress Distributions
6.3. Principal Stress Distributions
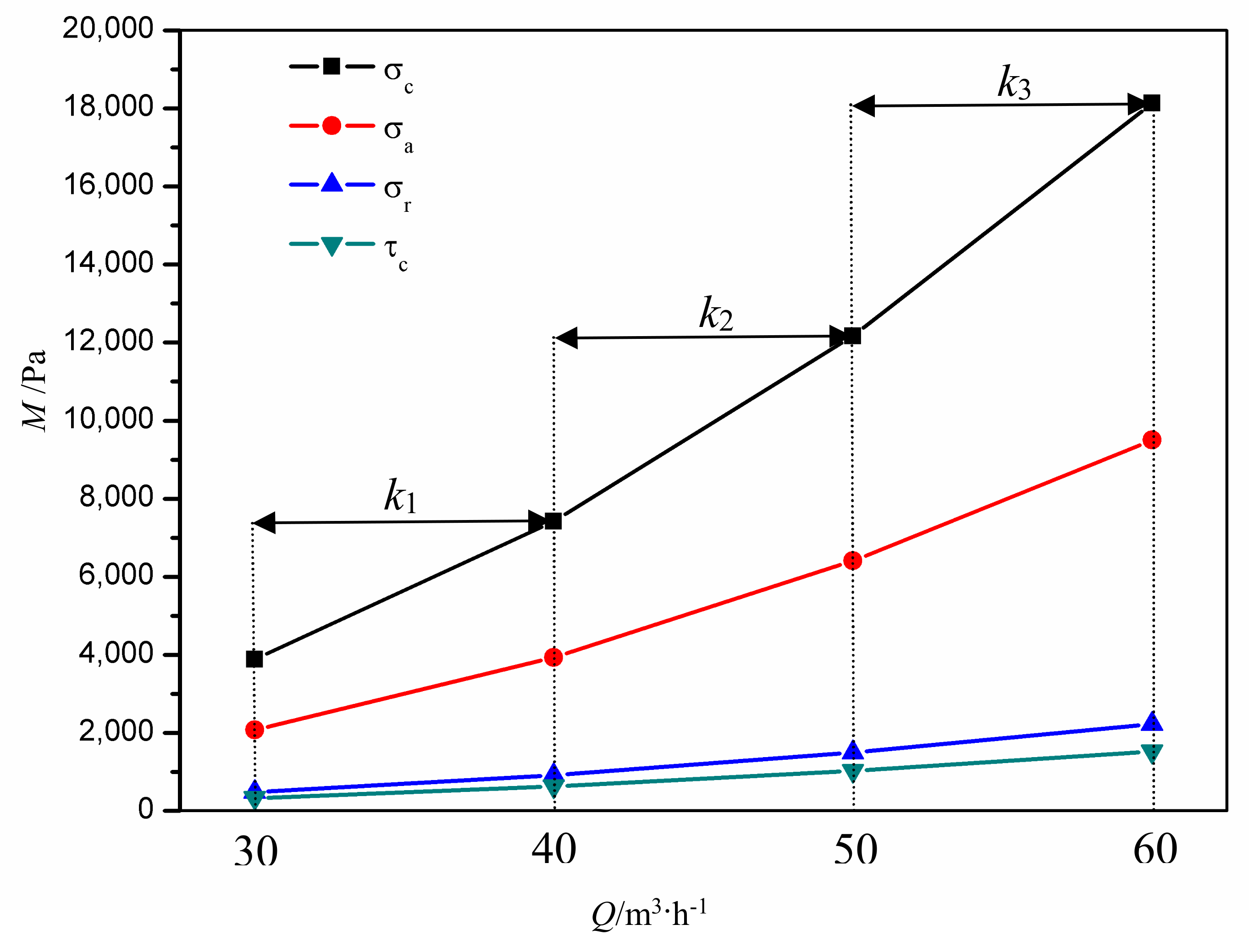
6.4. Effect of Discharge on the Wall Stress of Piped Carriage
7. Conclusions
- -
- With the increase of the discharge in the pipe, the flow velocity around the piped carriage increased obviously, especially in the region between the inner wall of the pipe and the piped carriage. The influence of the diameter of the cylinder Dc on the flow field around the piped carriage was greater than that of the length of the cylinder Lc.
- -
- The wall shear stress on cylinder of the piped carriage was greater than zero, that is, the wall shear stress along the direction of the pipe flow, and the maximum value appeared between the two groups of support feet in the middle and rear section of the cylinder. When the length of the cylinder Lc was fixed, the larger the diameter of cylinder Dc, the greater the wall shear stress.
- -
- The stress components on the cylinder wall of the piped carriage obeyed the rule as follow: σa > σc > σr. From the rear-end to the front-end of the piped carriage, the distribution of stress components shows the M type, first increased, then decreased, then increased and decreased. The minimum value appeared at the rear-end and front-end of the piped carriage, and it was negative. The maximum value appeared between the two groups of support feet 25 mm away from the rear-end of the cylinder. When the length of cylinder Lc was fixed, the larger the diameter Dc was, the greater were the three components of the corresponding principal stress. When the diameter of the cylinder, Dc, was a constant, the shorter the cylinder length Lc, the greater the three components of the principal stress.
- -
- The larger the flow, the greater the influence of unit flow on the wall shear stress and principal stress of the piped carriage, that is, k1 < k2 < k3. At the same time, the increase of the flow has the greatest influence on the circumferential component of the principal stress of the cylinder, followed by the axis component, and the smallest influence on the wall shear stress of the cylinder, i.e., > > > .
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Liu, H.; Assadollahbaik, M. Energy Conservation Value of Hydraulic Container Pipeline (HCP); U.S. Dept. of Energy, Division of Transportation Energy Conservation: Washington DC, USA, 1979.
- Liu, H.; Assadollahbaik, M. Feasibility of using hydraulic capsule pipeline to transport coal. J. Pipeline 1981, 1, 295–306. [Google Scholar]
- Liu, H.; Wu, J.P. Economic Feasibility of Using Hydraulic Pipeline to Transport Grain in the Midwest of the United States; Freight Pipeline (Proc. 6th Int. Symp, on Freight Pipelines); Hemisphere Publishing Corp: New York, NY, USA, 1990; pp. 135–140. [Google Scholar]
- Brown, R.A.S. Capsule pipeline research at the Alberta Research Council, 1985–1978. J. Pipeline 1987, 6, 75–82. [Google Scholar]
- Liu, H. Hydraulic Capsule Pipeline. J. Pipeline 1981, 1, 11–23. [Google Scholar]
- Liu, H.; Graze, H.R. Lift and drag on stationary capsule. J. Hydraul. Eng. 1983, 109, 28–47. [Google Scholar] [CrossRef]
- Liu, H.; Richards, J.L. Hydraulics of stationary capsule in pipe. J. Hydraul. Eng. 1994, 120, 22–40. [Google Scholar] [CrossRef]
- Gao, X.; Liu, H. Hydraulics predicting incipient velocity of capsules in pipe. J. Hydraul. Eng. 2000, 126, 470–473. [Google Scholar] [CrossRef]
- Cheng, C.C.; Liu, H. Tilt of stationary capsule in pipe. J. Hydraul. Eng. 1996, 12, 90–96. [Google Scholar] [CrossRef]
- Kroonenberg, H.H. Mathematical model for concentric horizontal capsule transport. Can. J. Chem. Eng. 1962, 56, 538–543. [Google Scholar] [CrossRef]
- Charles, M.E. The pipeline flow of capsules: Part 2: Theoretical analysis of the concentric flow of cylindrical forms. Can. J. Chem. Eng. 1963, 41, 46–51. [Google Scholar]
- Tomita, Y.; Yamamoto, M.; Funatsu, K. Motion of a single capsule in a hydraulic pipeline. J. Fluid Mech. 1986, 171, 495–508. [Google Scholar] [CrossRef]
- Latto, B.; Chow, K.W. Hydrodynamic transport of cylindrical capsules in a vertical pipeline. Can. J. Chem. Eng. 1982, 60, 713–722. [Google Scholar] [CrossRef]
- Michiyoshp, I.; Nakajima, T. Fully developed turbulent flow in a concentric annulus11. J. Nucl. Sci. Technol. 1968, 5, 354–359. [Google Scholar] [CrossRef]
- Nouri, J.M.; Umur, H.; Whitelaw, J.H. Flow of Newtonian and non-Newtonian concentric and eccentric annuli. J. Fluid Mech. 1993, 253, 617–641. [Google Scholar] [CrossRef]
- Quadrio, M.; Luchini, P. Direct numerical simulation of the turbulent flow in a pipe with annular cross section. Eur. J. Mech. 2002, 21, 413–427. [Google Scholar] [CrossRef]
- Khalil, M.F.; Kassab, S.Z.; Adam, I.G.; Samaha, M.A. Turbulent flow around single concentric long capsule in a pipe. Appl. Math. Model. 2010, 34, 2000–2017. [Google Scholar] [CrossRef]
- Asim, T.; Mishra, R.; Nearchou, A.; Ubbi, K. Effect of the length and diameter of a cylindrical capsule on the pressure drop in a horizontal pipeline. J. Phys. Conf. Ser. 2012, 1, 364. [Google Scholar] [CrossRef]
- Sun, X.H.; Li, Y.Y.; Yan, Q.F. Experimental study on starting conditions of the hydraulic transportation on the piped carriage. In Proceedings of the 20th National Conference on Hydrodynamics, Taiyuan, China, 23–25 August 2007; pp. 425–431. [Google Scholar]
- Li, Y.Y.; Sun, X.H. Hydraulic characteristics of transportation of different piped carriages in pipe. J. Drain. Irrig. Mach. Eng. 2010, 28, 174–178. [Google Scholar]
- Jing, Y.H. Characteristics of Slit Flow Velocity by the Formation of Stable Moving Piped Carriage with Different Diameter in Straight Piped Segments. Master’s Thesis, Taiyuan University of Technology, Taiyuan, China, 2014. [Google Scholar]
- Zhang, C.; Sun, X.; Li, Y.; Zhang, X.; Zhang, X.; Yang, X.; Li, F. Hydraulic characteristics of transporting a piped carriage in a horizontal pipe based on the bidirectional fluid-structure interaction. Math. Probl. Eng. 2018, 2018, 1–27. [Google Scholar] [CrossRef]
- Xiaoni, Y.; Yongye, L.; Xihuan, S. Analysis on hydraulic characteristics of hydrocyclone in horizontal straight pipeline under operation. J. Hydroelectr. Eng. 2015, 34, 98–102. [Google Scholar]
- Yang, X.N. Study on the Character of Spiral Flow Caused by Different Length Guide Vanes. Master’s Thesis, Taiyuan University of Technology, Taiyuan, China, 2013. [Google Scholar]
- Zhang, X.L.; Sun, X.H.; Li, Y.Y.; Xi, X.N.; Guo, F.; Zheng, L.J. Numerical investigation of the concentric annulus flow around a cylindrical body with contrasted effecting factors. J. Hydrodyn. 2015, 27, 273–285. [Google Scholar] [CrossRef]
- Zhang, C.; Sun, X.; Li, Y.; Zhang, X.; Zhang, X.; Yang, X.; Li, F. Effects of guide vane placement angle on hydraulic characteristics of flow field and optimal design of hydraulic capsule pipelines. Water 2018, 10, 1378. [Google Scholar] [CrossRef]
- Li, Y.Y.; Sun, X.H.; Yan, Q.F. Experimental research on the piped hydraulic transportation with the different diversion angle. J. Hydrodyn. 2008, 23, 86–89. [Google Scholar]
- Zhang, C.J.; Sun, X.H.; Li, Y.Y.; Zhang, X.Q. Effects of guide strip angles on hydraulic characteristics of moving boundary annular gap flow. J. Drain. Irrig. Mach. Eng. 2019, 37, 136–141,147. [Google Scholar]
- Xi, X.N. Research on Hydraulic Characteristics of the Pipe Hydraulic Transportation of Tube-Contained Raw Materials under Different Reynolds Numbers. Master’s Thesis, Taiyuan University of Technology, Taiyuan, China, 2012. [Google Scholar]
- Li, Y.Y.; Sun, X.H.; Yan, Y.F. Hydraulic characteristics of tube-contained raw material hydraulic transportation under different loads on the piped carriage. Trans. Chin. Soc. Agric. Eng. 2008, 39, 93–96. [Google Scholar]
- Ma, C.G.; Wu, J.; Lu, Y.F.; Li, Y.Y.; Zhang, X.L. Study on the characteristics of slot flow velocity at different flow conditions of same double piped carriages. Water Power 2018, 44, 90–93. [Google Scholar]
- Lu, Y.F. Research on the Numerical Simulation of the Velocity of the Concentric Annular Gap Spiral Flow around the Stationary Column in the Horizontal Straight Pipeline. Master’s Thesis, Taiyuan University of Technology, Taiyuan, China, 2018. [Google Scholar]
- Abdi, R.; Rezazadeh, N.; Abdi, M. Investigation of passive oscillations of flexible splitter plates attached to a circular cylinder. J. Fluid. Struct. 2019, 84, 302–317. [Google Scholar] [CrossRef]
- Souli, M.; Ouahsine, A.; Lewin, L. ALE formulation for fluid–structure interaction problems. Comput. Methods Appl. Mech. Eng. 2000, 190, 659–675. [Google Scholar] [CrossRef]
- Lee, J.S.; Lee, S.H. Fluid-structure interaction for the propulsive velocity of a flapping flexible plate at low Reynolds number. Comput. Fluids 2013, 71, 348–374. [Google Scholar] [CrossRef]
- Govier, G.W.; Aziz, K. The Flow of Capsules in Pipes. In The Flow of Complex Mixtures in Pipes; Van Nostrand-Reinhold: New York, NY, USA, 1972; pp. 712–757. [Google Scholar]
- Zhang, Z.C.; Li, G.D.; Li, Z.Q. Hydraulics; China Water & Power Press: Beijing, China, 2011; Volume 1. [Google Scholar]
- Fan, F.; Liang, B.C.; Li, Y.R.; Bai, Y.C.; Zhu, Y.J.; Zhu, Z.X. Numerical investigation of the influence of water jumping on the local scour beneath a pipeline under steady flow. Water 2017, 9, 642. [Google Scholar] [CrossRef]
- Yao, R.T.; Guo, D.P. Computational Fluid Dynamics Foundation and STAR-CD Engineering Application; National Defense Industry Press: Beijing, China, 2015. [Google Scholar]
- Turek, S.; Hron, J. Proposal for numerical benchmarking of fluid–structure interaction between an elastic object and laminar incompressible flow. In Fluid–Structure Interaction; Springer: Berlin/Heidelberg, Germany, 2006; pp. 371–385. [Google Scholar]
- Damiri, H.S.; Bardaweel, H.K. Numerical design and optimization of hydraulic resistance and wall shear stress inside pressure-driven microfluidic networks. Lab. Chip. 2015, 15, 4187–4196. [Google Scholar] [CrossRef]
- Thim, T.; Hagensen, M.K.; Falk, E.; Hørlyck, A.; Kim, W.Y.; Niemann, A.K.; Bøtker, H.E. Wall shear stress and local plaque development in stenosed carotid arteries of hypercholesterolemic minipigs. J. Cardiovasc. Dis. Res. 2012, 3, 76–83. [Google Scholar] [CrossRef] [PubMed]
- Santos, D.S.; Faia, P.M.; Garcia, F.A.P.; Rasteiro, M.G. Oil/water stratified flow in a horizontal pipe: Simulated and experimental studies using EIT. J. Petrol. Sci. Eng. 2019, 174, 1179–1193. [Google Scholar] [CrossRef]
- Zheng, D.S.; Jiang, Y.Z. Determination of optimum location of a right angle strain flower using optimization. J. Vib. Meas. Diag. 1997, 17, 53–56. [Google Scholar]
- Sundstrom, L.R.J.; Cervantes, M.J. Characteristics of the wall shear stress in pulsating wall-bounded turbulent flows. Exp. Therm. Fluid Sci. 2018, 96, 257–265. [Google Scholar] [CrossRef]
- Marusic, I.; Mckeon, B.J.; Monkewitz, P.A.; Nagib, H.M.; Smits, A.J.; Sreenivasan, K.R. Wall-bounded turbulent flows at high Reynolds numbers: Recent advances and key issues. Phys. Fluids 2010, 22, 1–58. [Google Scholar] [CrossRef]
- Ariyaratne, C. Design and Optimization of Swirl Pipes and Transition Geometries for Slurry Transport. Ph.D. Thesis, The University of Nottingham, Nottingham, UK, 2005. [Google Scholar]
- Asim, T.; Algadi, A.; Mishra, R. Effect of capsule shape on hydrodynamic characteristics and optimal design of hydraulic capsule pipelines. J. Pet. Sci. Eng. 2018, 161, 390–408. [Google Scholar] [CrossRef]
- Lin, J.Z.; Ruan, X.D.; Chen, B.G.; Wang, J.P.; Zhou, J.; Ren, A.L. Fluid Mechanics, 2nd ed.; Tsinghua University Press: Beijing, China, 2005. [Google Scholar]


| Runs | Dc × Lc (mm × mm) | Q (m3·h−1) | Up (m/s) | E (Pa) | νs | Re |
|---|---|---|---|---|---|---|
| 1 | 75 × 150 | 30/40/50/60 | 1.06/1.41/1.77/2.12 | 11.2 × 109 | 0.49 | 105,366/140,488/175,610/210,731 |
| 2 | 80 × 150 | |||||
| 3 | 75 × 120 | |||||
| 4 | 80 × 120 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, X.; Ma, J.; Li, Y.; Sun, X.; Jia, X.; Li, Y. Wall Stresses in Cylinder of Stationary Piped Carriage Using COMSOL Multiphysics. Water 2019, 11, 1910. https://doi.org/10.3390/w11091910
Yang X, Ma J, Li Y, Sun X, Jia X, Li Y. Wall Stresses in Cylinder of Stationary Piped Carriage Using COMSOL Multiphysics. Water. 2019; 11(9):1910. https://doi.org/10.3390/w11091910
Chicago/Turabian StyleYang, Xiaoni, Juanjuan Ma, Yongye Li, Xihuan Sun, Xiaomeng Jia, and Yonggang Li. 2019. "Wall Stresses in Cylinder of Stationary Piped Carriage Using COMSOL Multiphysics" Water 11, no. 9: 1910. https://doi.org/10.3390/w11091910
APA StyleYang, X., Ma, J., Li, Y., Sun, X., Jia, X., & Li, Y. (2019). Wall Stresses in Cylinder of Stationary Piped Carriage Using COMSOL Multiphysics. Water, 11(9), 1910. https://doi.org/10.3390/w11091910




