A Simple and Unified Linear Solver for Free-Surface and Pressurized Mixed Flows in Hydraulic Systems
Abstract
:1. Introduction
2. Methods
2.1. Governing Equations
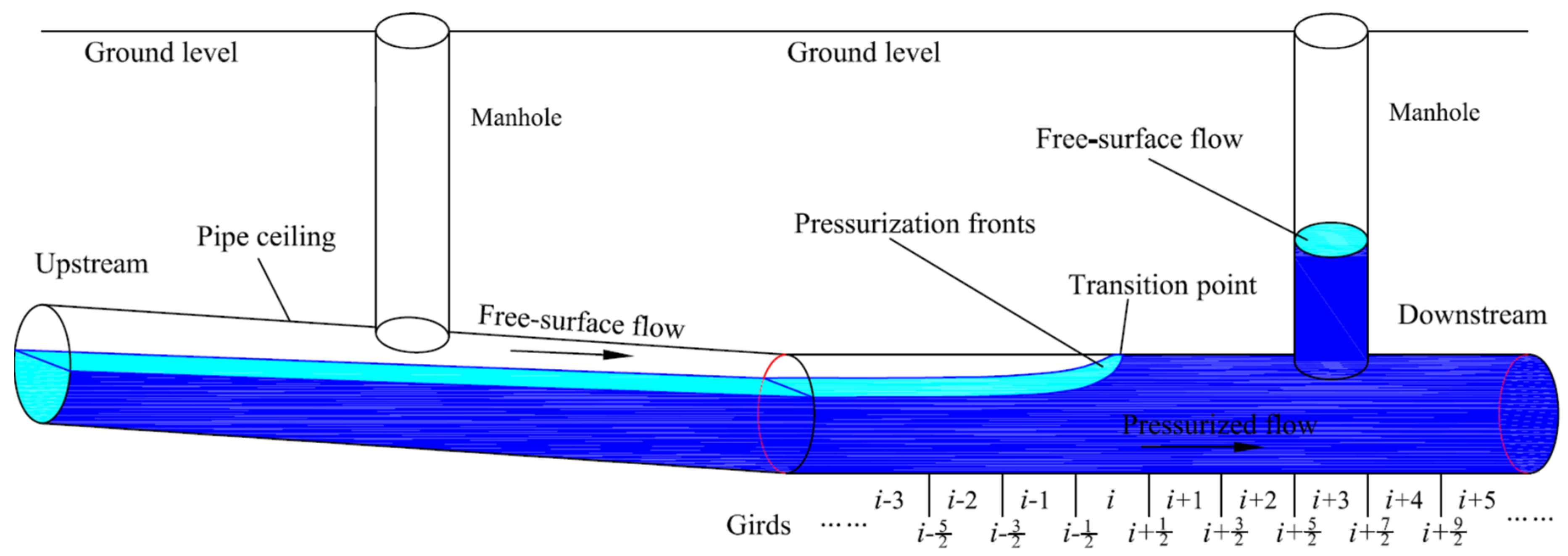
2.2. Computational Grid and Description of Mixed Flows
2.3. Numerical Formulation
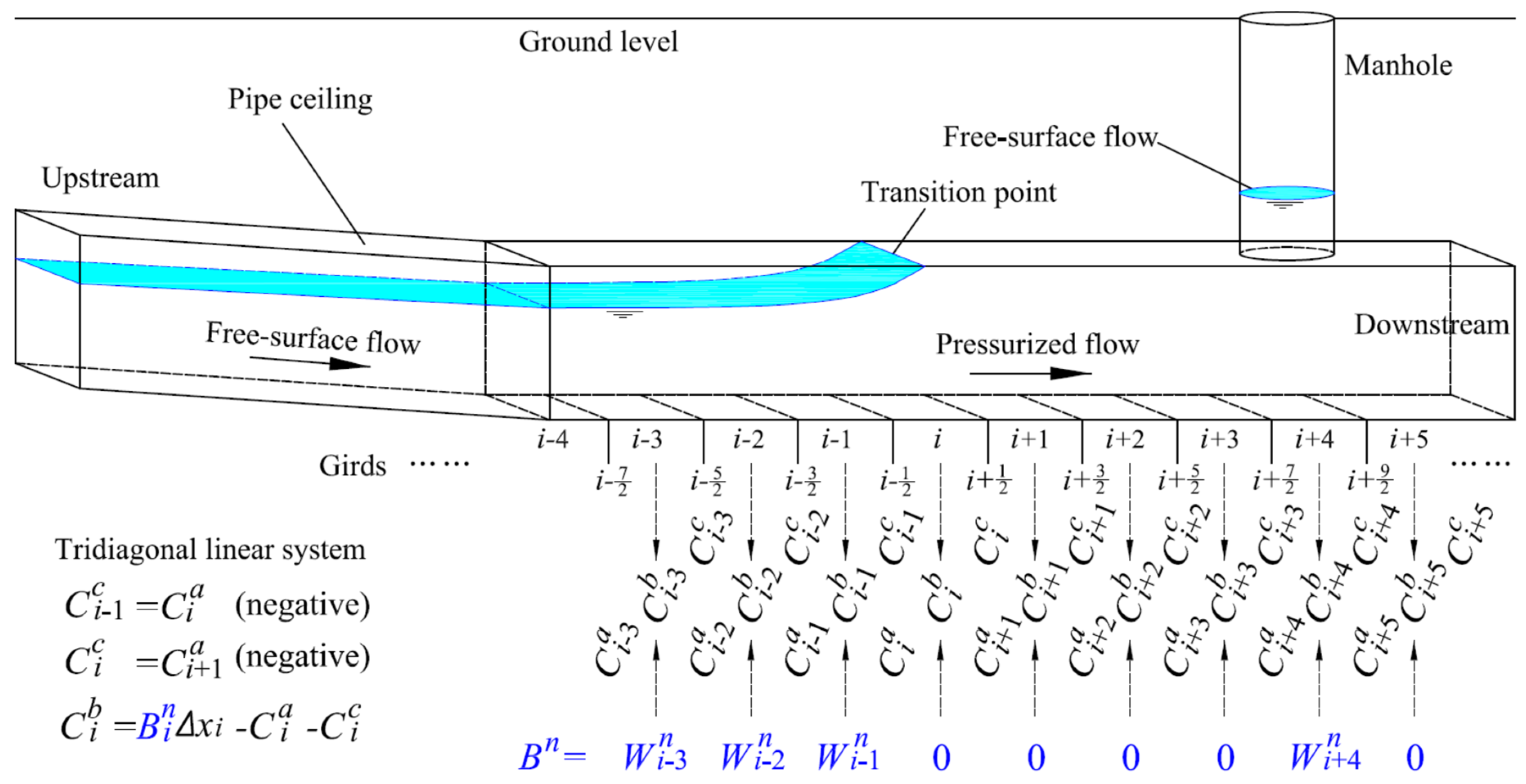
2.3.1. Discretization of Governing Equations
2.3.2. Solution of Velocity–Pressure Coupling
2.3.3. Considerations of Abrupt Change of Wet Surface Width in Mixed Flows
3. Results
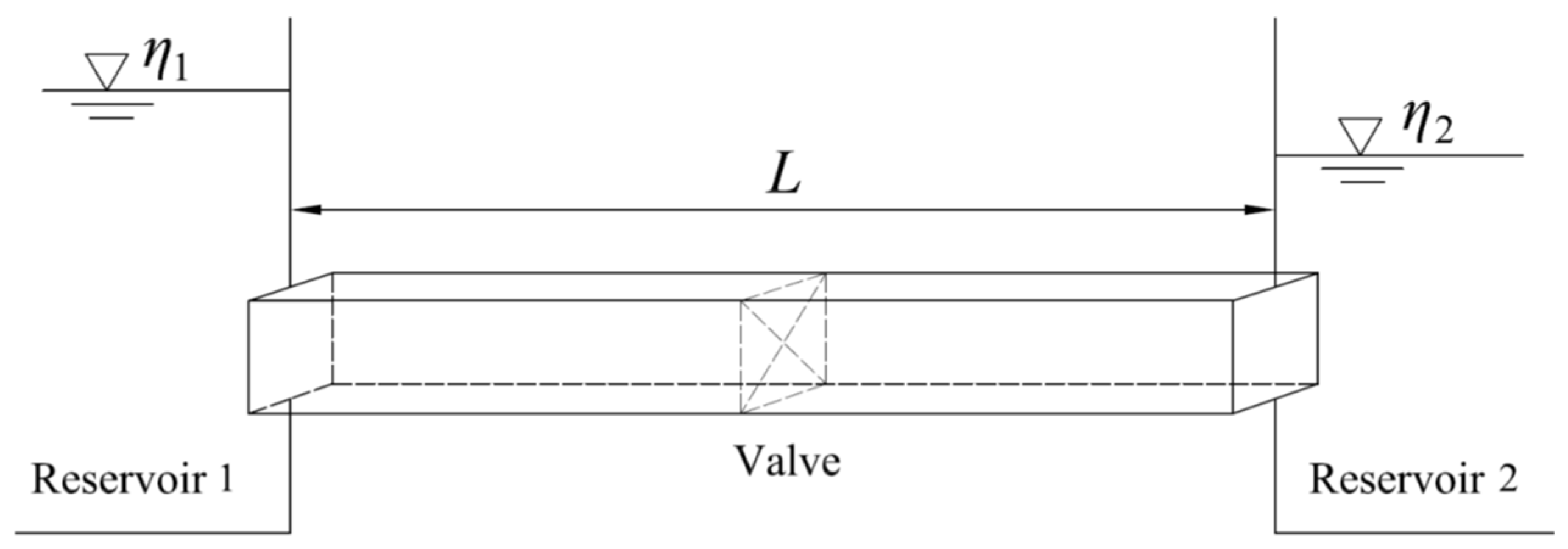
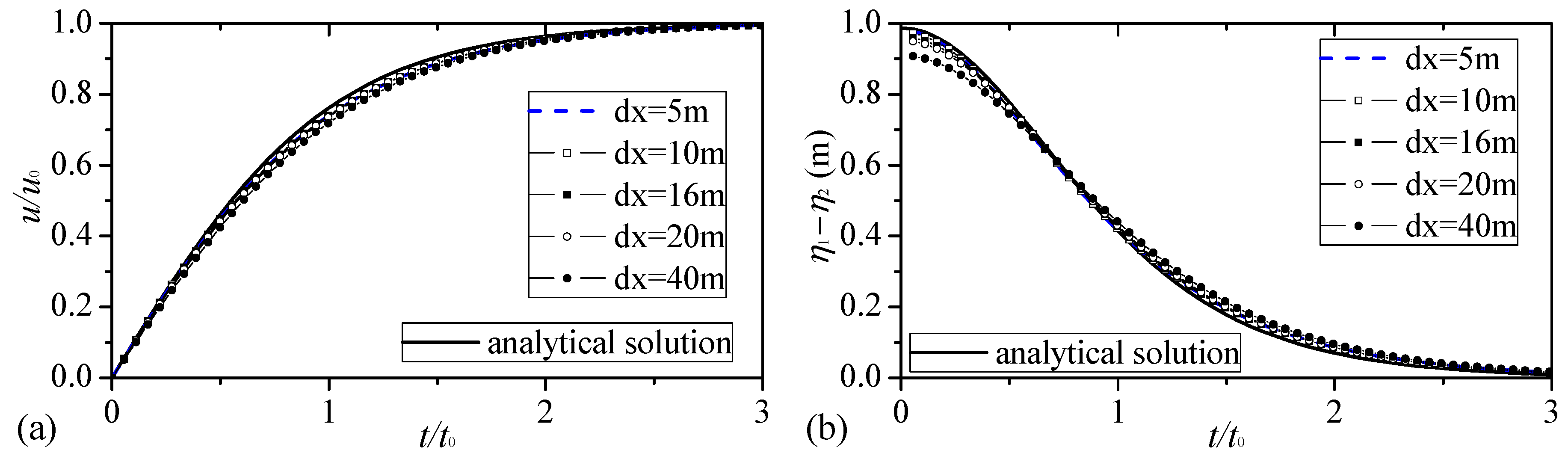
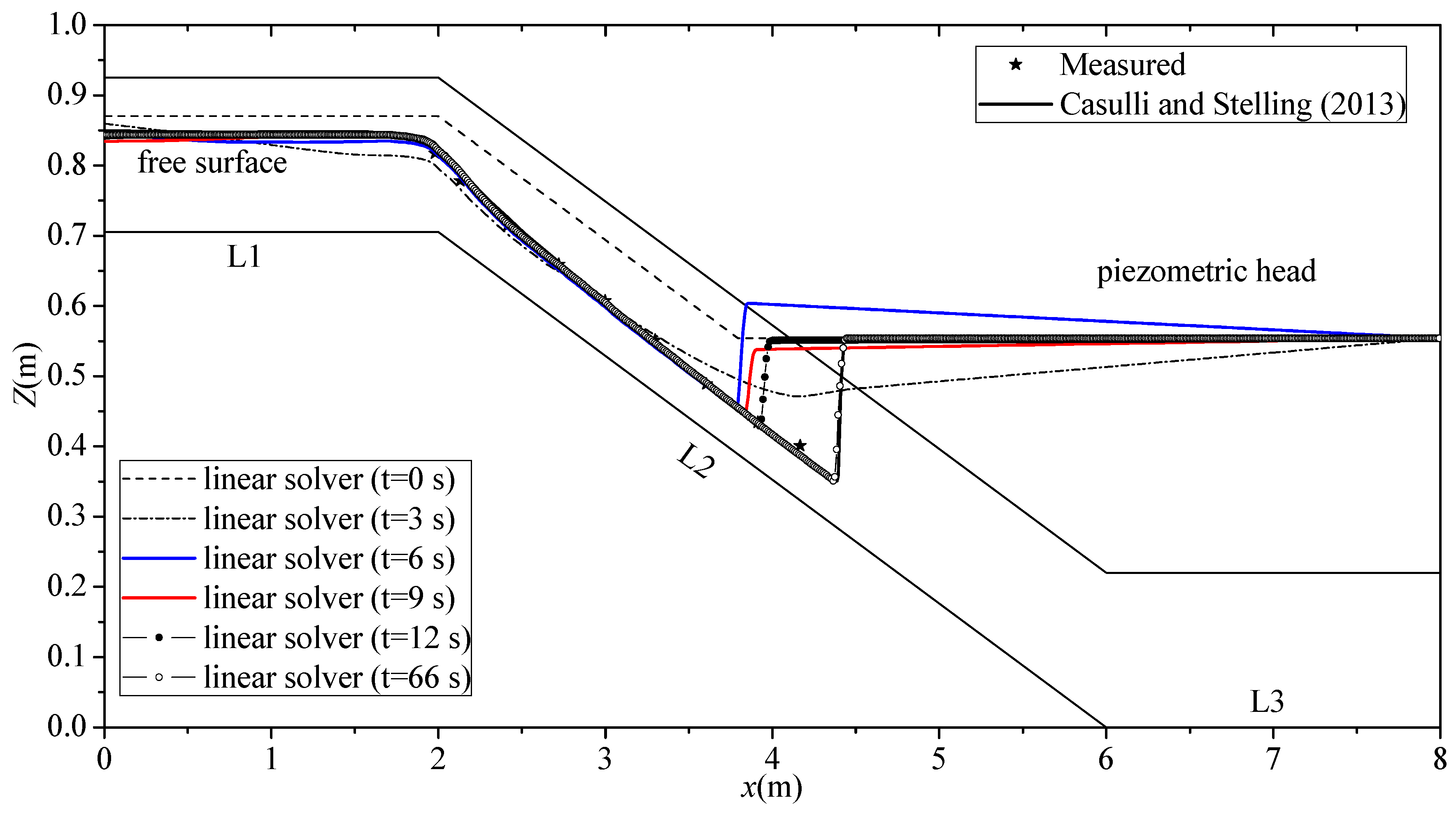
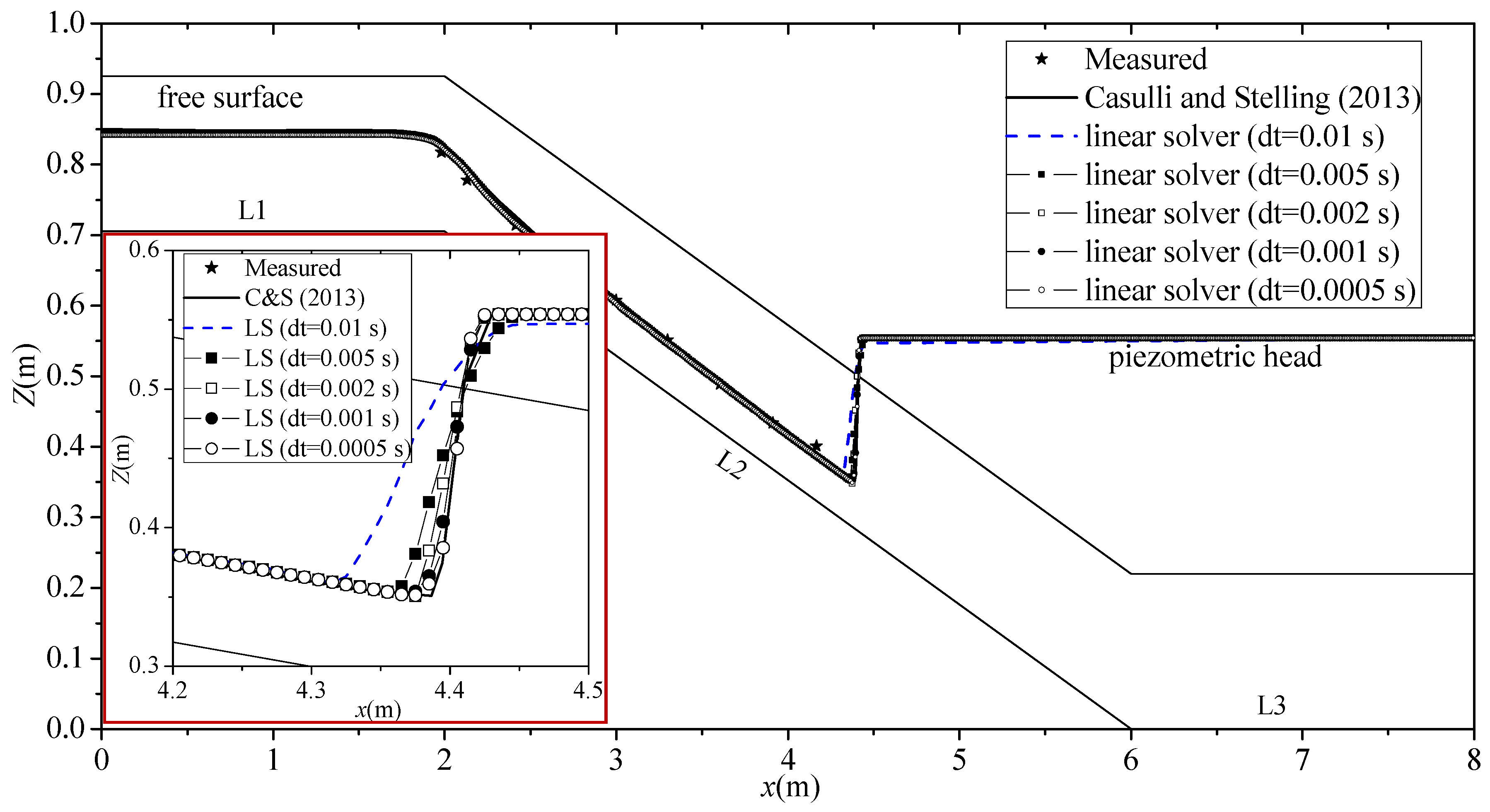
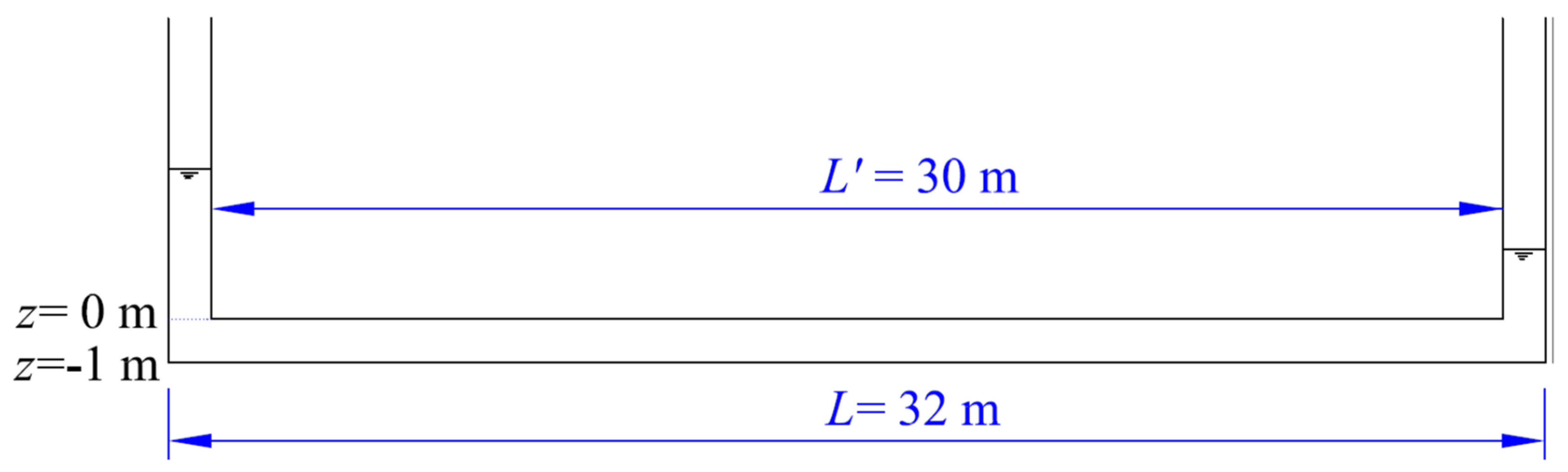
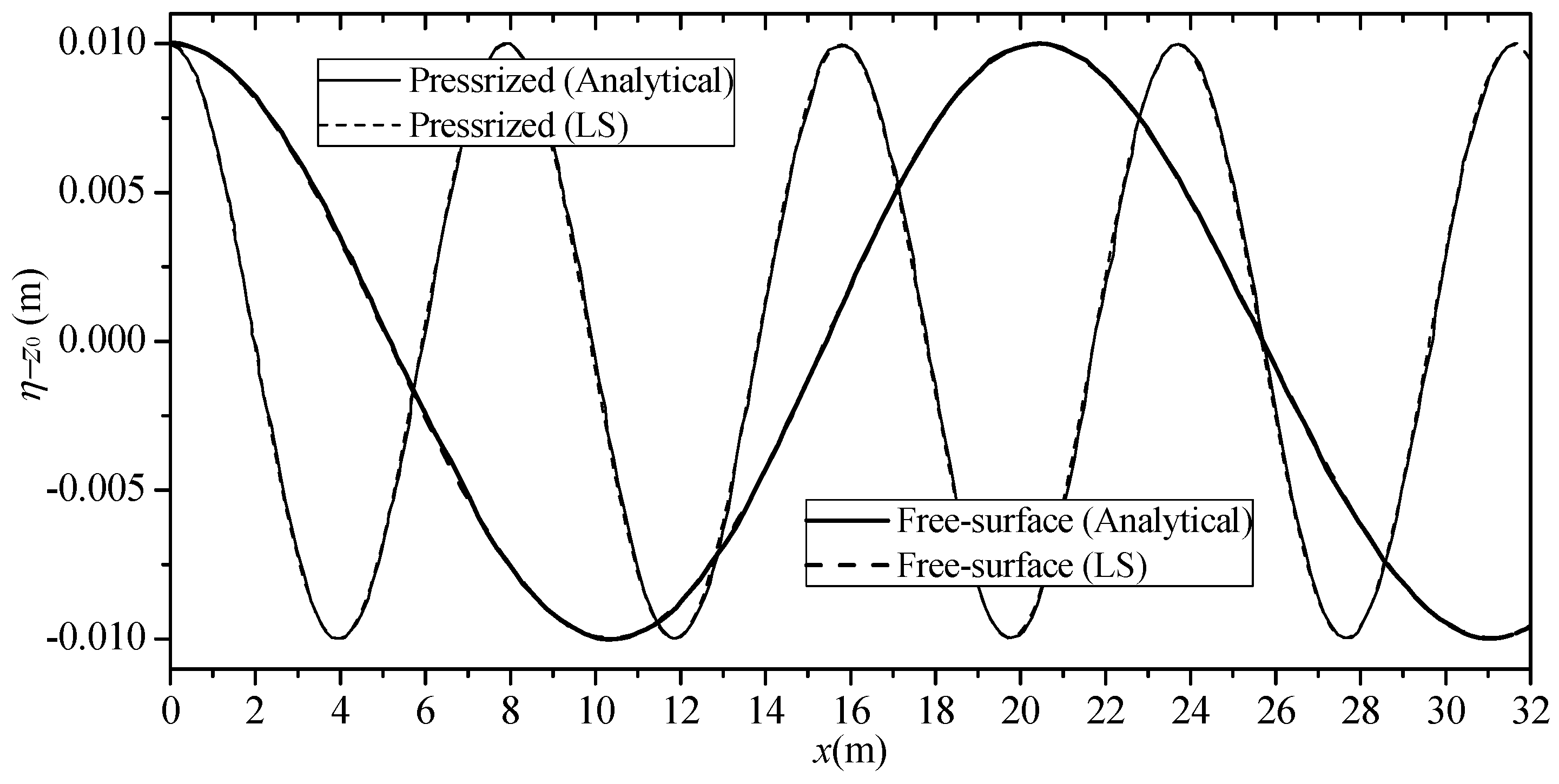
3.1. Test Case 1
3.2. Test Case 2
3.3. Test Case 3
4. Discussion
4.1. Differences between the New Model and Existing Models
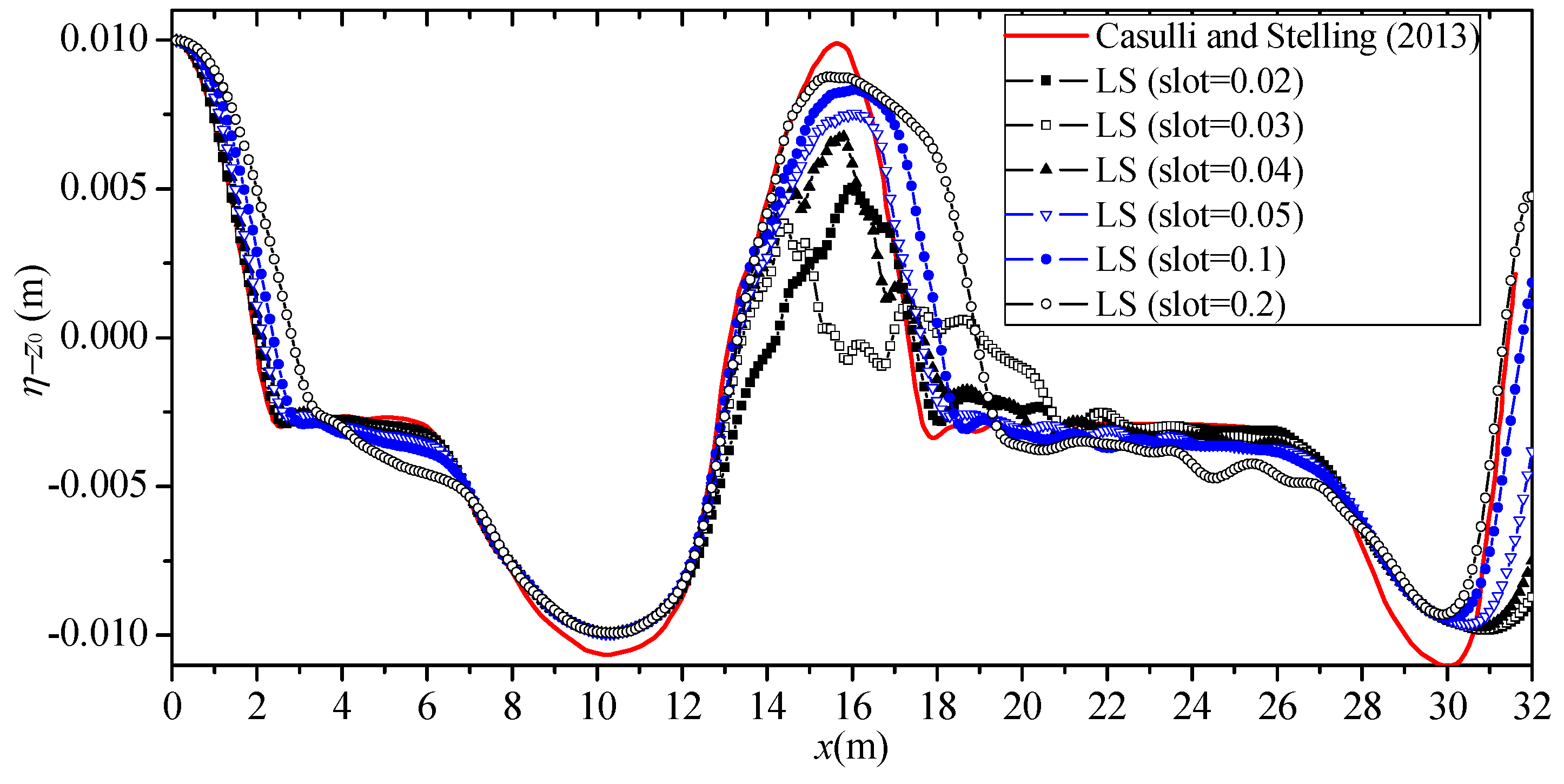
4.2. The DMDC Problem and the A-Slot Approach
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Notation
| A | Wetted cross-sectional area (conveyance area); |
| Ap | The area of the cross-section; |
| A-slot | Artificial slot for coping with the discontinuous main-diagonal coefficients problem |
| B | =, the wet surface width of a cross-section for the free-surface parts and is equal to 0 for the pressurized parts of a closed pipe; |
| g | Gravity acceleration; |
| ne | The quantities of cells; |
| ns | The quantities of sides; |
| nm | Manning’s roughness coefficient; |
| Nbt | The number of substeps of the ELM |
| R | Hydraulic radius; |
| t | Time; |
| u | Averaged velocity of cross-section; |
| ubt | Solution of the advection term uisng the ELM; |
| Wi | Representative width of the cross-section; |
| x | Longitudinal distance along the channel; |
| zc | The celling of the cross-section; |
| t | Time; |
| Δt | Time step |
| Δxi | The length of cell i; |
| Δxi+1/2 | The distance between the centers of cells i and i + 1; |
| θ | Implicit factor |
| η | Water level measured from an undisturbed reference water surface (for free-surface flows); piezometric head measured from an undisturbed reference water surface (for pressurized flows); |
| ε | The percent that the width of the A-slot account for the representative width |
| ASE | A single set of equations; |
| CLO | A mark which is used to distinguish closed and nonclosed reaches; |
| DMDC | Discontinuous main-diagonal coefficients |
| ELM | Eulerian–Lagrangian method; |
| PRE | A mark which is used to distinguish free-surface and pressurized reaches; |
| SVE | Saint–Venant equations |
| TSE | Two sets of equations; |
References
- Yen, B.C. Hydraulics of sewer systems. In Stormwater Collection Systems Design Handbook; McGraw-Hill: New York, NY, USA, 2001. [Google Scholar]
- Kerger, F.; Archambeau, P.; Erpicum, S.; Dewals, B.J.; Pirotton, M. A fast universal solver for 1D continuous and discontinuous steady flows in rivers and pipes. Int. J. Numer. Meth. Fluids 2011, 66, 38–48. [Google Scholar] [CrossRef]
- Hamam, M.A.; McCorquodale, J.A. Transient conditions in the transition from gravity to surcharged sewer flow. Can. J. Civ. Eng. 1982, 9, 189–196. [Google Scholar] [CrossRef]
- Li, J.; McCorquodale, A. Modeling mixed flow in storm sewers. J. Hydraul. Eng. 1999, 125, 1170–1180. [Google Scholar] [CrossRef]
- Zhou, F.; Hicks, F.E.; Steffler, P.M. Transient flow in a rapidly filling horizontal pipe containing trapped air. J. Hydraul. Eng. 2002, 28, 25–634. [Google Scholar] [CrossRef]
- Song, C.S.S.; Cardle, J.A.; Leung, K.S. Transient mixed flow models for storm sewers. J. Hydraul. Eng. 1983, 109, 1487–1504. [Google Scholar] [CrossRef]
- Cardle, J.A.; Song, C.S.S. Mathematical modeling of unsteady flow in storm sewers. Int. J. Eng. Fluid Mech. 1988, 1, 495–518. [Google Scholar]
- Guo, Q.; Song, C.S.S. Surging in urban storm drainage systems. J. Hydraul. Eng. 1990, 116, 1523–1537. [Google Scholar] [CrossRef]
- Fuamba, M. Contribution on transient flow modelling in storm sewers. J. Hydraul. Res. 2002, 40, 685–693. [Google Scholar] [CrossRef]
- Wang, K.H.; Shen, Q.; Zhang, B. Modeling propagation of pressure surges with the formation of an air pocket in pipelines. Comput. Fluids 2003, 32, 1179–1194. [Google Scholar] [CrossRef]
- Politano, M.; Odgaard, A.J.; Klecan, W. Case study: Numerical evaluation of hydraulic transients in a combined sewer overflow tunnel system. J. Hydraul. Eng. 2007, 133, 1103–1110. [Google Scholar] [CrossRef]
- Bousso, S.; Daynou, M.; Fuamba, M. Numerical Modeling of Mixed Flows in Storm Water Systems: Critical Review of Literature. J. Hydraul. Eng. 2013, 139, 385–396. [Google Scholar] [CrossRef]
- Garcia-Navarro, P.; Priestley, A.; Alcrudo, S. Implicit method for water flow modeling in channels and pipes. J. Hydraul. Res. 1994, 32, 721–742. [Google Scholar] [CrossRef]
- Capart, H.; Sillen, X.; Zech, Y. Numerical and experimental water transients in sewer pipes. J. Hydraul. Res. 1997, 35, 659–672. [Google Scholar] [CrossRef]
- Ji, Z. General hydrodynamic model for sewer/channel network systems. J. Hydraul. Eng. 1998, 124, 307–315. [Google Scholar] [CrossRef]
- Trajkovic, B.; Ivetic, M.; Calomino, F.; D’Ippolito, A. Investigation of transition from free surface to pressurized flow in a circular pipe. Water Sci. Technol. 1999, 39, 105–112. [Google Scholar] [CrossRef]
- Vasconcelos, J.G.; Wright, S.J.; Roe, P.L. Improved Simulation of Flow Regime Transition in Sewers: Two-Component Pressure Approach. J. Hydraul. Eng. 2006, 132, 553–562. [Google Scholar] [CrossRef]
- León, A.S.; Ghidaoui, M.S.; Schmidt, A.R.; García, M.H. Application of Godunov-type schemes to transient mixed flows. J. Hydraul. Res. 2009, 47, 147–156. [Google Scholar] [CrossRef]
- Bourdarias, C.; Gerbi, S. A conservative model for unsteady flows in deformable closed pipes and its implicit second-order finite volume discretisation. Comput. Fluids 2008, 37, 1225–1237. [Google Scholar] [CrossRef]
- Cunge, J.A.; Wegner, M. Numerical integration of Barre de Saint-Venant’s flow equations by means of implicit scheme of finite differences. Houille Blanche 1964, 19, 33–39. [Google Scholar] [CrossRef]
- Sanders, B.F.; Bradford, S.F. Network implementation of the two-component pressure approach for transient flow in storm sewers. J. Hydraul. Eng. 2011, 137, 158–172. [Google Scholar] [CrossRef]
- Aldrighetti, E. Computational Hydraulic Techniques for the Saint Venant Equations in Arbitrarily Shaped Geometry. Ph.D. Thesis, University of Trento, Trento, Italy, 2007. [Google Scholar]
- Casulli, V.; Stelling, G.S. A semi-implicit numerical model for urban drainage systems. Int. J. Numer. Meth. Fluids 2013, 73, 600–614. [Google Scholar] [CrossRef]
- Dumbser, M.; Iben, U.; Ioriattia, M. An efficient semi-implicit finite volume method for axially symmetric compressible flows in compliant tubes. Appl. Numer. Math. 2015, 89, 24–44. [Google Scholar] [CrossRef]
- Leskens, J.G.; Brugnach, M.; Hoekstra, A.Y.; Schuurmans, W. Why are decisions in flood disaster management so poorly supported by information from flood models? Environ. Model. Softw. 2014, 53, 53–61. [Google Scholar] [CrossRef]
- Storm Water Management Model (SWMM). Storm Water Management Model Reference Manual Volume II-Hydraulics; EPA/600/R-17/111; Rossman: Los Angeles, CA, USA; National Risk Management Laboratory: Cincinnati, OH, USA, 2017.
- Dimou, K. 3-D Hybrid Eulerian–Lagrangian/Particle Tracking Model for Simulating Mass Transport in Coastal Water Bodies. Ph.D. Thesis, Department of Civil Engineering, Massachusetts Institute of Technology, Cambridge, MA, USA, 1992. [Google Scholar]
- Casulli, V.; Zanolli, P. Semi-implicit numerical modeling of nonhydrostatic free-surface flows for environmental problems. Math. Comput. Model. 2002, 36, 1131–1149. [Google Scholar] [CrossRef]
- Zhang, Y.L.; Baptista, A.M.; Myers, E.P. A cross-scale model for 3D baroclinic circulation in estuary-plume-shelf systems, I. Formulation and skill assessment. Cont. Shelf Res. 2004, 24, 2187–2214. [Google Scholar] [CrossRef]
- Hu, D.C.; Zhong, D.Y.; Zhang, H.W.; Wang, G.Q. Prediction–Correction Method for Parallelizing Implicit 2D Hydrodynamic Models I Scheme. J. Hydraul. Eng. 2015, 141, 04015014. [Google Scholar] [CrossRef]
- Hu, D.C.; Zhong, D.Y.; Zhu, Y.H.; Wang, G.Q. Prediction–Correction Method for Parallelizing Implicit 2D Hydrodynamic Models II Application. J. Hydraul. Eng. 2015, 141, 06015008. [Google Scholar] [CrossRef]
- Pothof, I. Co–Current Air–Water Flow in Downward Sloping Pipes; Gildeprint Drukkerijen BV: Enschede, The Netherland, 2011; ISBN 978-90-8957-018-5. [Google Scholar]
- Lubbers, C.L. On Gas pockets in Wastewater Pressure Mains and Their Effect on Hydraulic Performance. Ph.D. Thesis, Department of Civil Engineering and Geosciences, University of Technology, Delft, The Netherlands, 2007. [Google Scholar]
- Ferreri, G.B.; Freni, G.; Tomaselli, P. Ability of Preissmann slot scheme to simulate smooth pressurisation transient in sewers. Water Sci. Technol. 2010, 62, 1848–1858. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, D.; Li, S.; Yao, S.; Jin, Z. A Simple and Unified Linear Solver for Free-Surface and Pressurized Mixed Flows in Hydraulic Systems. Water 2019, 11, 1979. https://doi.org/10.3390/w11101979
Hu D, Li S, Yao S, Jin Z. A Simple and Unified Linear Solver for Free-Surface and Pressurized Mixed Flows in Hydraulic Systems. Water. 2019; 11(10):1979. https://doi.org/10.3390/w11101979
Chicago/Turabian StyleHu, Dechao, Songping Li, Shiming Yao, and Zhongwu Jin. 2019. "A Simple and Unified Linear Solver for Free-Surface and Pressurized Mixed Flows in Hydraulic Systems" Water 11, no. 10: 1979. https://doi.org/10.3390/w11101979
APA StyleHu, D., Li, S., Yao, S., & Jin, Z. (2019). A Simple and Unified Linear Solver for Free-Surface and Pressurized Mixed Flows in Hydraulic Systems. Water, 11(10), 1979. https://doi.org/10.3390/w11101979




