Turbulence Characteristics before and after Scour Upstream of a Scaled-Down Bridge Pier Model
Abstract
:1. Introduction
2. Methodology
2.1. Experimental Setup
2.2. Experimental Procedure
3. Results and Discussion
3.1. Velocity Field
3.2. Temporal Variation of Flow and Turbulence Characteristics Upstream of the Bridge Pier
3.3. Flow Characteristics Upstream of the Bridge Pier
4. Summary and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Graf, W.H.; Istiarto, I. Flow pattern in the scour hole around a cylinder. J. Hydraul. Res. 2002, 40, 13–20. [Google Scholar] [CrossRef]
- Chang, W.; Lai, J.; Yen, C. Evolution of scour depth at circular bridge piers. J. Hydraul. Eng. 2007, 130, 905–913. [Google Scholar] [CrossRef]
- Gautam, P.; Eldho, T.I.; Mazumder, B.S.; Behera, M.R. Experimental study of flow and turbulence characteristics around simple and complex pier using PIV. Exp. Therm. Fluid Sci. 2019, 100, 193–206. [Google Scholar] [CrossRef]
- Dey, S. Sediment pick-up for evolving scour near circular cylinders. Appl. Math. Model. 1996, 20, 534–539. [Google Scholar] [CrossRef]
- Khaple, S.; Hanmaiahgari, P.; Gaudio, R.; Dey, S. Interference of an upstream pier on local scour at downstream piers. Acta Geophys. 2017, 65, 29–46. [Google Scholar] [CrossRef]
- Unger, J.; Hager, W. Down-flow and horseshoe vortex characteristics of sediment embedded bridge piers. Exp. Fluids 2007, 42, 1–19. [Google Scholar] [CrossRef]
- Dey, S.; Raikar, R.V. Characteristics of horseshoe vortex in developing scour holes at piers. J. Hydraul. Eng. 2007, 133, 399–413. [Google Scholar] [CrossRef]
- Dargahi, B. Turbulent flow field around a circular cylinder. Exp. Fluids 1989, 8, 12. [Google Scholar] [CrossRef]
- Simpson, R.L. Junction flows. Annu. Rev. Fluid Mech. 2001, 33, 415–443. [Google Scholar] [CrossRef]
- Melville, B.W. Local Scour at Bridge Sites. Ph.D. Thesis, School of Engineering, University of Auckland, Aukland, New Zealand, 1975. [Google Scholar]
- Baker, C.J. Theoretical approach to prediction of local scour around bridge piers. J. Hydraul. Res. 1980, 18, 12. [Google Scholar] [CrossRef]
- Nakagawa, H.; Suzuki, K. Application of stochastic model of sediment motion to local scour around a bridge pier. In Proceedings of the 16th Congress of the International Association for Hydraulic Research, Sao Paulo, Brazil, 24 July–6 August 1975; pp. 285–299. [Google Scholar]
- Einstein, H.A. Bed-load Function for Sediment Transportation in Open Channel Flows; Bulletin 1027 71, United States Department of Agriculture (USDA): Washington, DC, USA, 1950. [Google Scholar]
- Qadar, A. Vortex Scour Mechanism at Bridge Piers. Proc. Inst. Civ. Eng. 1981, 71, 739–757. [Google Scholar] [CrossRef]
- Kothyari, U.C.; Garde, R.J.; Ranga Raju, K.G. Temporal variation of scour around circular bridge piers. J. Hydraul. Eng. 1992, 118, 1091–1106. [Google Scholar] [CrossRef]
- Ram, S. A theroretical model to predict local scour at bridge piers in non-cohesive soils. In Proceedings of the The Seventh International Symposium on River Sedimentation, Hong Kong, China, 16–18 December 1998; pp. 173–178. [Google Scholar]
- Muzzammil, M.; Gangadhariah, T. Caracteristiques moyennes d’un vortex en fer a cheval au droit d’une pile cylindrique(The mean characteristics of horsehoe vortex at a cylindrical pier). J. Hydraul. Res. 2003, 41, 285–297. [Google Scholar] [CrossRef]
- Kirkil, G.; Constantinescu, S.; Ettema, R. Coherent structures in the flow field around a circular cylinder with scour hole. J. Hydraul. Eng. 2008, 134, 572–587. [Google Scholar] [CrossRef]
- Kirkil, G.; Constantinescu, G. Flow and turbulence structure around an instream rectangular cylinder with scour hole. Water Res. Res. 2010, 46, W11549. [Google Scholar] [CrossRef]
- Schanderl, W.; Jenssen, U.; Strobl, C.; Manhart, M. The structure and budget of turbulent kinetic energy in front of a wall-mounted cylinder. J. Fluid Mech. 2017, 827, 285–321. [Google Scholar] [CrossRef]
- Guan, D.; Chiew, Y.; Wei, M.; Hsieh, S. Characterization of horseshoe vortex in a developing scour hole at a cylindrical bridge pier. Int. J. Sediment Res. 2019, 34, 118–124. [Google Scholar] [CrossRef]
- Lee, S.; Sturm, T.W. Effect of sediment size scaling on physical modeling of bridge pier scour. J. Hydraul. Eng. 2009, 135, 793–802. [Google Scholar] [CrossRef]
- Hong, S.; Lee, S. Insight of Bridge Scour during Extreme Hydrologic Events by Laboratory Model Studies. KSCE J. Civ. Eng. 2018, 22, 2871–2879. [Google Scholar] [CrossRef]
- Lee, S.; Hong, S. Reproducing field measurements using scaled-down hydraulic model studies in a laboratory. Adv. Civ. Eng. 2018, 2018, 11. [Google Scholar] [CrossRef]
- Hong, S.; Abid, I. Scour around an erodible abutment with riprap apron over time. J. Hydraul. Eng. 2019, 145, 6. [Google Scholar] [CrossRef]
- Hong, S.; Sturm, T.W.; Stoesser, T. Clear water abutment scour in a compound channel for extreme hydrologic events. J. Hydraul. Eng. 2015, 141, 12. [Google Scholar] [CrossRef]
- Saha, R.; Lee, S.; Hong, S. A comprehensive method of calculating maximum bridge scour depth. Water 2018, 10, 1572. [Google Scholar] [CrossRef]
- Yoon, K.; Lee, S.; Hong, S. Time-averaged turbulent velocity flow field through the various bridge contractions during large flooding. Water 2019, 11, 13. [Google Scholar] [CrossRef]
- Chua, K.; Fraga, B.; Stoesser, T.; Hong, S.; Sturm, T.W. Effect of bridge abutment length on turbulence structure and flow through the opening. J. Hydraul. Eng. 2019, 145, 19. [Google Scholar]
- Ge, L.; Lee, S.; Sotiropoulos, F.; Sturm, T.W. 3D unsteady RANS modeling of complex hydraulic engineering flows. Part II: Model validation and flow physics. J. Hydraul. Eng. 2005, 131, 809–820. [Google Scholar] [CrossRef]
- Jones, J.S.; Kilgore, R.T.; Mistichelli, M.P. Effects of footing location on bridge pier scour. J. Hydraul. Eng. 1992, 118, 280–290. [Google Scholar] [CrossRef]
- Melville, B.W.; Raudkivi, A.J. Effects of foundation geometry on bridge pier scour. J. Hydraul. Eng. 1996, 122, 203–209. [Google Scholar] [CrossRef]
- Coleman, S.E. Clearwater local scour at complex piers. J. Hydraul. Eng. 2005, 131, 330–334. [Google Scholar] [CrossRef]
- Devenport, W.J.; Simpson, R.L. Time-dependent and time-averaged turbulence structure near the nose of a wing-body junction. J. Fluid Mech. 1990, 210, 23–55. [Google Scholar] [CrossRef]
- Paik, J.; Escauriaza, C.; Sotiropoulos, F. On the bimodal dynamics of the turbulent horseshoe vortex system in a wing-body junction. Phys. Fluids 2007, 19, 045107. [Google Scholar] [CrossRef]
- Keshavarzi, A.; Melville, B.; Ball, J. Three-dimensional analysis of coherent turbulent flow structure around a single circular bridge pier. Environ. Fluid Mech. 2014, 14, 821–847. [Google Scholar] [CrossRef]
- Marchioli, C.; Soldati, A. Mechanisms for particle transfer and segregation in a turbulent boundary layer. J. Fluid Mech. 2002, 468, 283–315. [Google Scholar] [CrossRef]
- Kundu, P.K. Fluid Mechanics; Academic Press: San Diego, CA, USA, 1990. [Google Scholar]


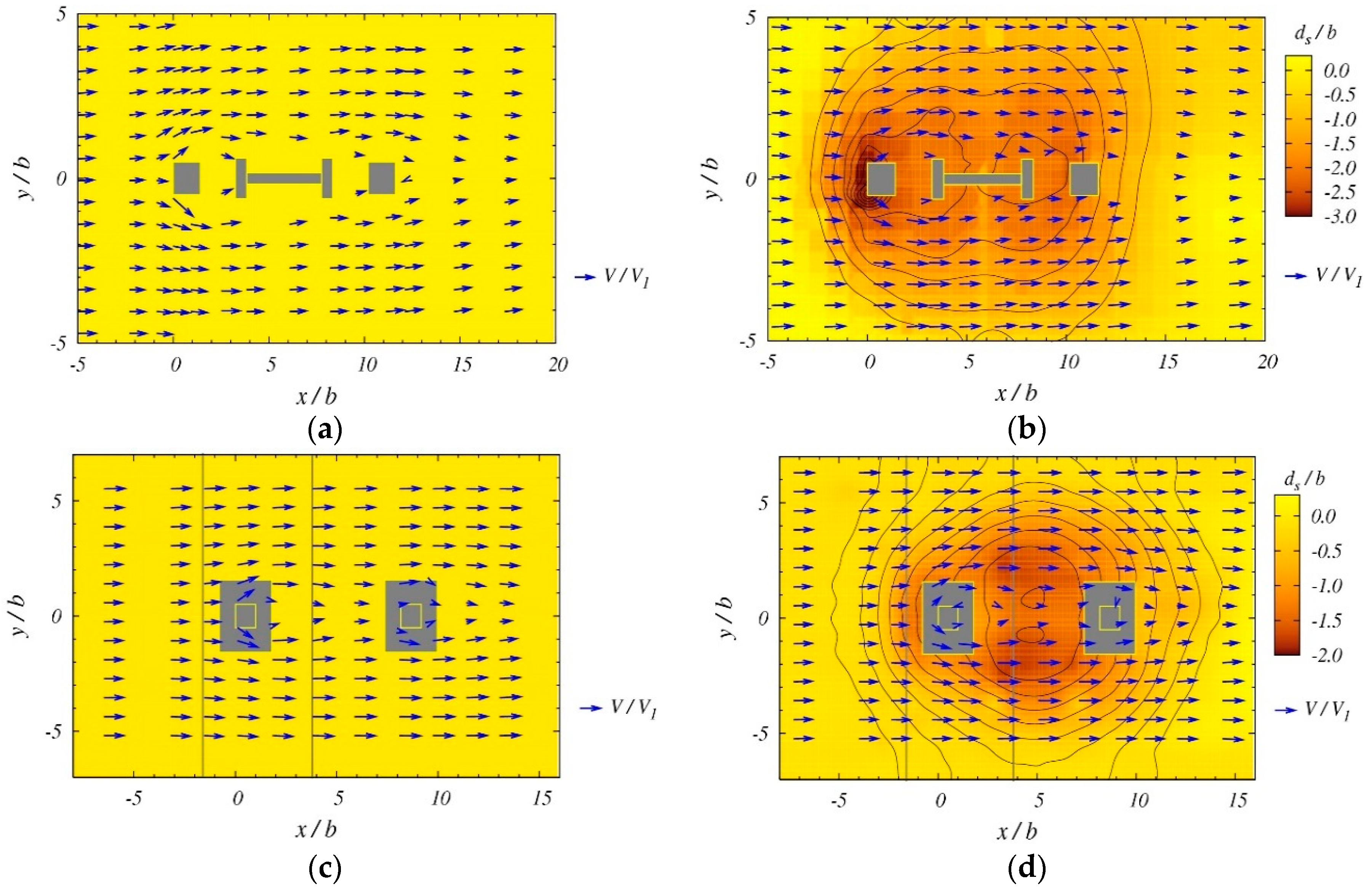
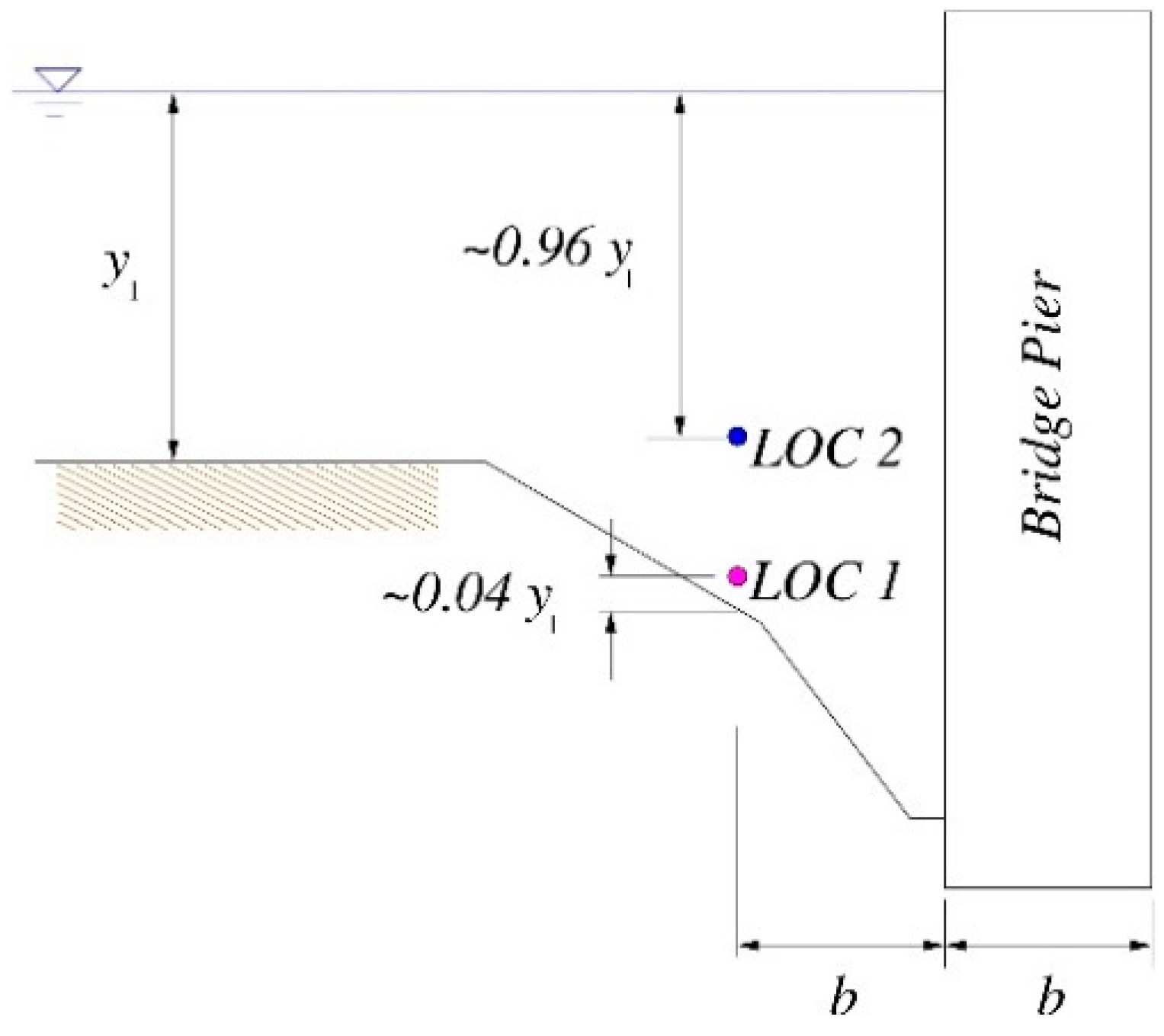

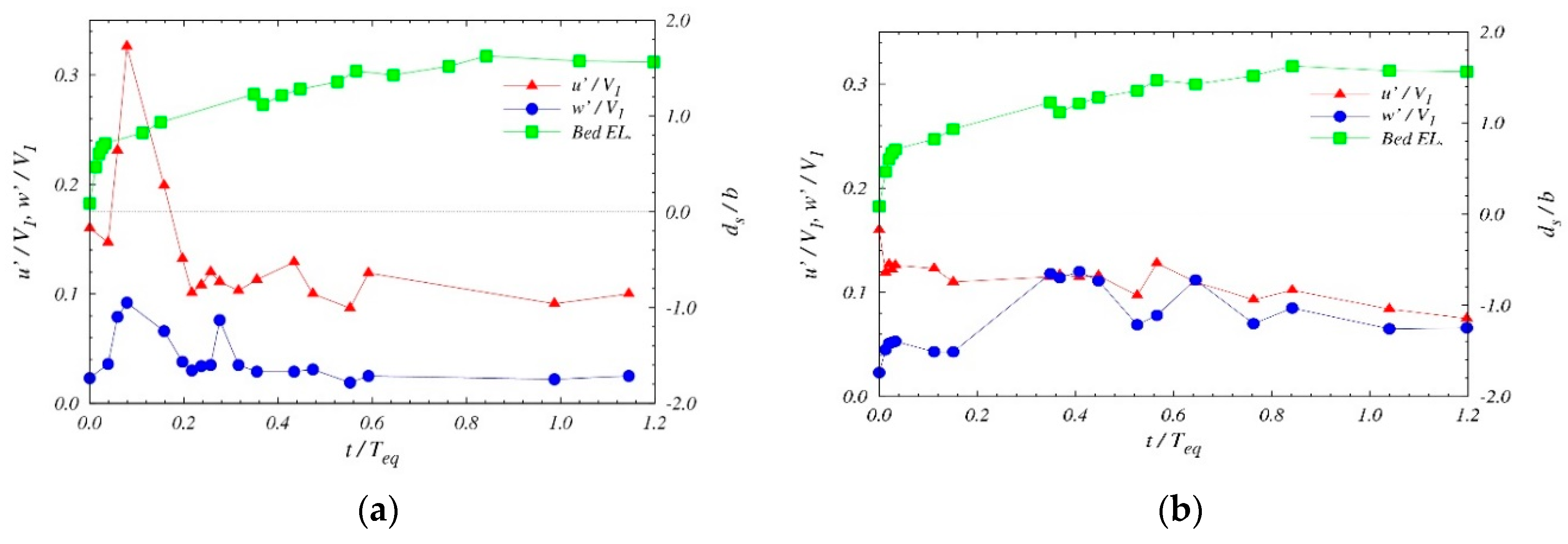


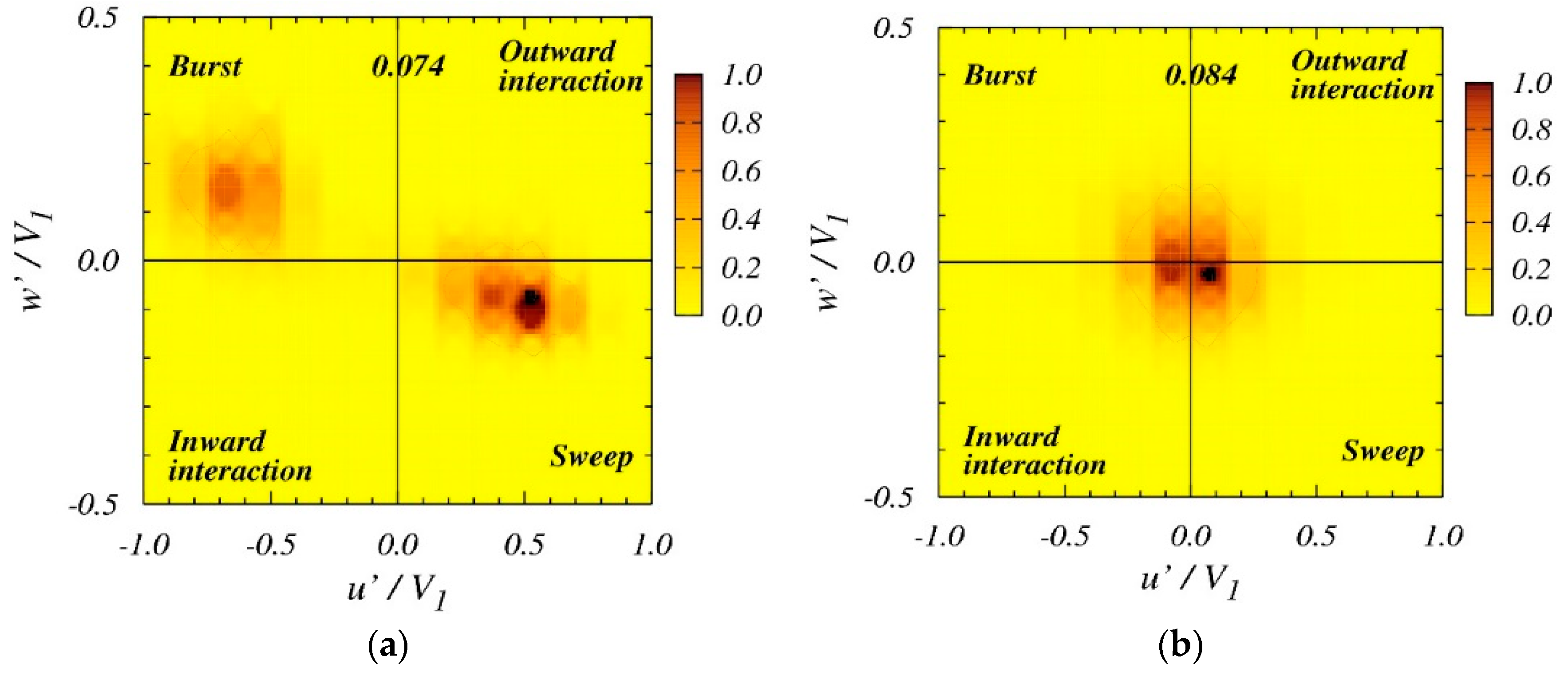
| Run | Model | Scale | Q (m3/s) | b (m) | y1 (m) | V1 (m/s) | Teq (h) | ds (m) | Conditions |
|---|---|---|---|---|---|---|---|---|---|
| 1 | CR | 1:23 | 0.051 | 0.046 | 0.191 | 0.257 | 30 | 0.093 | Fixed & Moveable-bed |
| 2 | 0.044 | 0.046 | 0.142 | 0.304 | 12 | 0.090 | |||
| 3 | FR | 1:33 | 0.054 | 0.055 | 0.241 | 0.215 | 48 | 0.046 | Fixed & Moveable-bed |
| 4 | 0.052 | 0.055 | 0.170 | 0.281 | 24 | 0.085 |
| Before Scour, Sec | After Scour, Sec | |
|---|---|---|
| Streamwise direction | 1.8 | 1.3 |
| Vertical direction | 4.3 | 0.7 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, S.O.; Hong, S.H. Turbulence Characteristics before and after Scour Upstream of a Scaled-Down Bridge Pier Model. Water 2019, 11, 1900. https://doi.org/10.3390/w11091900
Lee SO, Hong SH. Turbulence Characteristics before and after Scour Upstream of a Scaled-Down Bridge Pier Model. Water. 2019; 11(9):1900. https://doi.org/10.3390/w11091900
Chicago/Turabian StyleLee, Seung Oh, and Seung Ho Hong. 2019. "Turbulence Characteristics before and after Scour Upstream of a Scaled-Down Bridge Pier Model" Water 11, no. 9: 1900. https://doi.org/10.3390/w11091900
APA StyleLee, S. O., & Hong, S. H. (2019). Turbulence Characteristics before and after Scour Upstream of a Scaled-Down Bridge Pier Model. Water, 11(9), 1900. https://doi.org/10.3390/w11091900





