Turbulence in Wall-Wake Flow Downstream of an Isolated Dunal Bedform

Abstract

This study examines the turbulence in wall-wake flow downstream of an isolated dunal bedform. The streamwise flow velocity and Reynolds shear stress profiles at the upstream and various streamwise distances downstream of the dune were obtained. The results reveal that in the wall-wake flow, the third-order moments change their signs below the dune crest, whereas their signs remain unaltered above the crest. The near-wake flow is featured by sweep events, whereas the far-wake flow is controlled by the ejection events. Downstream of the dune, the turbulent kinetic energy production and dissipation rates, in the near-bed flow zone, are positive. However, they reduce as the vertical distance increases up to the lower-half of the dune height and beyond that, they increase with an increase in vertical distance, attaining their peaks at the crest. The turbulent kinetic energy diffusion and pressure energy diffusion rates, in the near-bed flow zone, are negative, whereas they attain their positive peaks at the crest. The anisotropy invariant maps indicate that the data plots in the wall-wake flow form a looping trend. Below the crest, the turbulence has an affinity to a two-dimensional isotropy, whereas above the crest, the anisotropy tends to reduce to a quasi-three-dimensional isotropy.

1. Introduction

Turbulent flow over dunal bedforms fascinates researchers. The topic is important not only from the viewpoint of intrinsic scientific reasons, but also owing to its far-reaching applications in engineering. In addition to its practical applications, it allows a significant theoretical understanding of wake flows. Despite impressive advances over the past years, an inclusive picture of the flow and turbulence characteristics over a dunal bedform remains far from complete [1]. The dunes are created by an interaction between the flow and bed sediment particles. Dunes are kind of bedforms that are found when the flow variables, such as flow velocity and bed shear stress over a sediment bed surpass their threshold values.

Over the decades, a large corpus of experimental and numerical studies has been reported to grasp the flow features over dunal bedforms. Researchers studied the velocity field over dunes to acquire an insight into the physical features, including the reattachment point, wake region and internal boundary layer [2,3]. The experimental observations of flow over a series of two- and three-dimensional dunes revealed that the two-dimensional dunes induce stronger turbulence compared to their three-dimensional counterparts [4,5]. However, the flow characteristics over a natural dune were found to be quite different from those over an artificial dune [6]. Best [7] found that over the dune crests, the ejections dominate the instantaneous flow field.

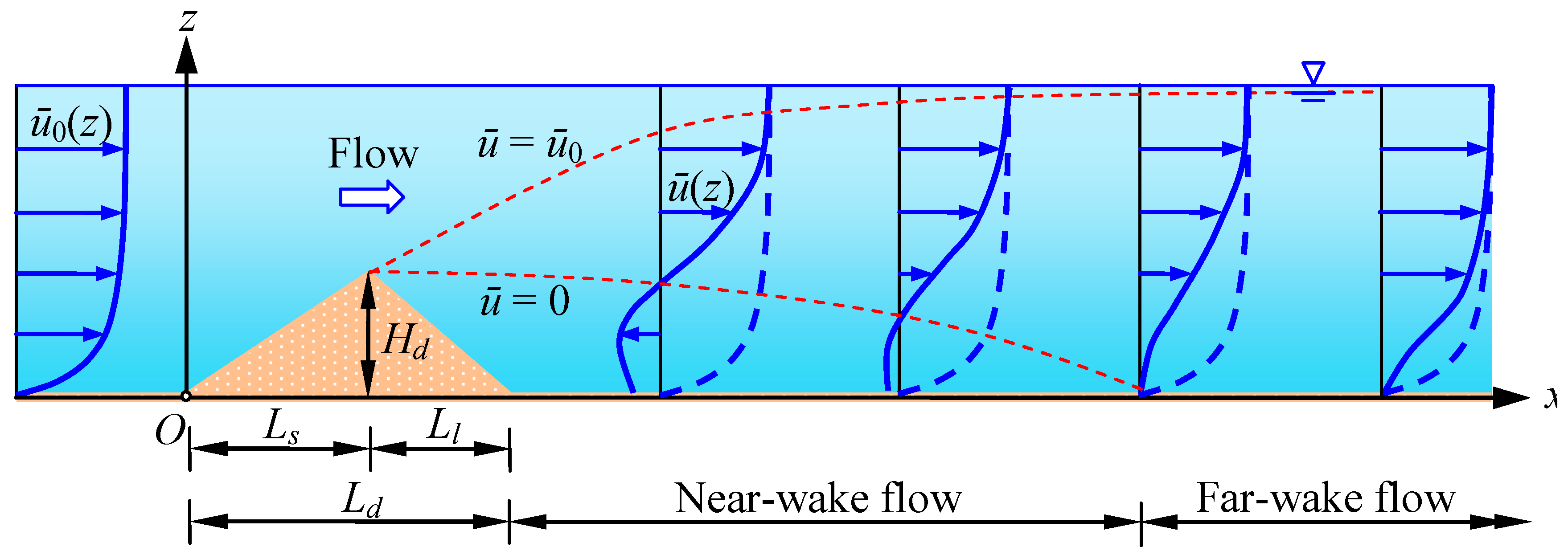
In a natural streamflow, an isolated dunal bedform acts as a bluff-body, producing wall-wake flow at its downstream. The wake flow downstream of an isolated dunal bedform persists up to a certain stretch until the local wake flow diffuses to and becomes the part of the undisturbed upstream flow. Figure 1 presents a conceptual representation of flow past an isolated dunal bedform in xz plane. Here, x is the streamwise distance measured from a convenient point O and z is the vertical distance from the bed. The dune length L_d comprises the stoss-side length L_s and the leeside length L_l (L_d = L_s + L_l). The dune height H_d is the vertical distance of the dune crest from the bed. Downstream of the dune, a flow reversal takes place, called the near-wake flow. Afterward, the flow is called the far-wake flow. In Figure 1, the lower dashed line denotes the locus of ū(z) = 0, whereas the upper dashed line signifies the boundary layer (ū = ū₀) in the wall-wake flow. Here, ū(z) is the time-averaged streamwise flow velocity in the wake flow and ū₀(z) is the time-averaged streamwise flow velocity in the undisturbed upstream flow. In the far downstream of the dunal bedform, the flow achieves the undisturbed upstream state, called the fully recovered open-channel flow.

In this context, it is pertinent to mention that for a shear-free flow, Schlichting [8] pioneered the similarity theory of the velocity defect profile in the free-wake flow downstream of a circular cylinder. The wall-wake flow downstream of an isolated dunal bedform in an approach wall-shear flow, being different from a free-wake flow, is rather intricate. The turbulence characteristics and the vortex shedding downstream of bed-mounted bluff-bodies in both near- and far-wake flows were studied by various researchers. Some of these bluff-bodies include plate [9,10], hemisphere [11], sphere [12,13], circular cylinder [14,15,16,17,18,19,20,21] and pebble cluster [22].

It is worth noting that most of the former studies were dedicated to understanding the flow features over a continuous train of dunes. In fact, little is known about the flow and turbulence characteristics over an isolated dunal bedform. This study specifically puts into focus the flow and turbulence characteristics downstream of an isolated two-dimensional dunal bedform over a rough bed in order to advance the present state-of-the-art. In addition to time-averaged streamwise flow velocity, the salient features of turbulence, including the Reynolds shear stress, turbulent bursting, turbulent kinetic energy budget and Reynolds stress anisotropy, are greatly discussed. It may be noted that the preliminary studies of flow and turbulence characteristics downstream of an isolated dunal bedform have been recently presented elsewhere [23,24].

2. Experimental Design

Experiments were performed in a re-circulatory flume, having a rectangular cross-section, at the Fluvial Mechanics Laboratory in the Indian Statistical Institute, Kolkata, India. The length, width and height of the flume were 20 m, 0.5 m and 0.5 m, respectively. The inflow discharge, supplied by a centrifugal pump, was measured by an electromagnetic gadget. The transparent sidewalls of the flume provided visual access to the flow. The flume bed, having a streamwise bed slope of 3 × 10^–4, was prepared by gluing uniform gravels of median size d₅₀ = 2.49 mm. In the experiments, two types of isolated two-dimensional dunal bedforms, classified as Runs 1 and 2, respectively (Figure 2), were mounted on the flume bed at a distance of 7 m from the inlet. In Runs 1 and 2, the dune heights H_d were 0.09 m and 0.03 m, whereas the dune lengths L_d were 0.4 m (L_S = 0.24 m and L_l = 0.16 m) and 0.3 m (L_S = 0.24 m and L_l = 0.06 m), respectively. In both the runs, the same approach uniform flow condition was maintained. The approach flow depth h and depth-averaged approach flow velocity Ū₀ were maintained as h ≈ 0.3 m and Ū₀ ≈ 0.44 m s⁻¹. The flow depth and the free surface profile were measured by a Vernier point gauge, having a precision of ±0.1 mm. The approach shear velocity u_* [= (τ₀/ρ)^0.5], obtained from the streamwise bed slope, was 0.03 m s⁻¹. Here, τ₀ is the bed shear stress and ρ is the mass density of fluid. However, the values of u_* in both Runs 1 and 2, determined from the Reynolds shear stress profiles, were 0.027 m s^–1 and 0.025 m s⁻¹, respectively. It is worth noting that to find the u_* from the Reynolds shear stress profiles, the profiles were extrapolated up to the bed. In both the runs, the flow Reynolds number was 528,000, whereas the flow Froude number was 0.256 (subcritical). The shear Reynolds number R_* (= d₅₀u_*/ν, where ν is the coefficient of kinematic viscosity of fluid) was preserved to be 74.7 (> 70), setting a hydraulically rough flow regime.

A 5 cm down-looking Vecrtino probe (acoustic Doppler velocimetry), also called Vectrino plus, was used to capture the instantaneous three-dimensional flow velocity components along the flume centreline at various relative streamwise distances x/L_d = −0.5, −0.25, 0, 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1, 1.1, 1.3, 1.7, 2.1, 2.5 and 3.3. The Vecrtino system, having a flexible sampling volume of 6 mm diameter and 1 to 4 mm height, was operated with 10 MHz acoustic frequency and 100 Hz sampling rate. The velocity components (u, v, w) correspond to (x, y, z), where y is the spanwise direction. It may be noted that up to the dune crest, the lowest sampling height was set as 1 mm, whereas beyond the crest, it was 2.5 mm. The closest measuring location of the data points was 2 mm. A sampling duration of 300 s was found to be adequate to obtain the time-independent flow velocity and turbulence quantities. The minimum signal-to-noise ratio was maintained as 18, whereas the minimum threshold of signal correlation was maintained as 70%. 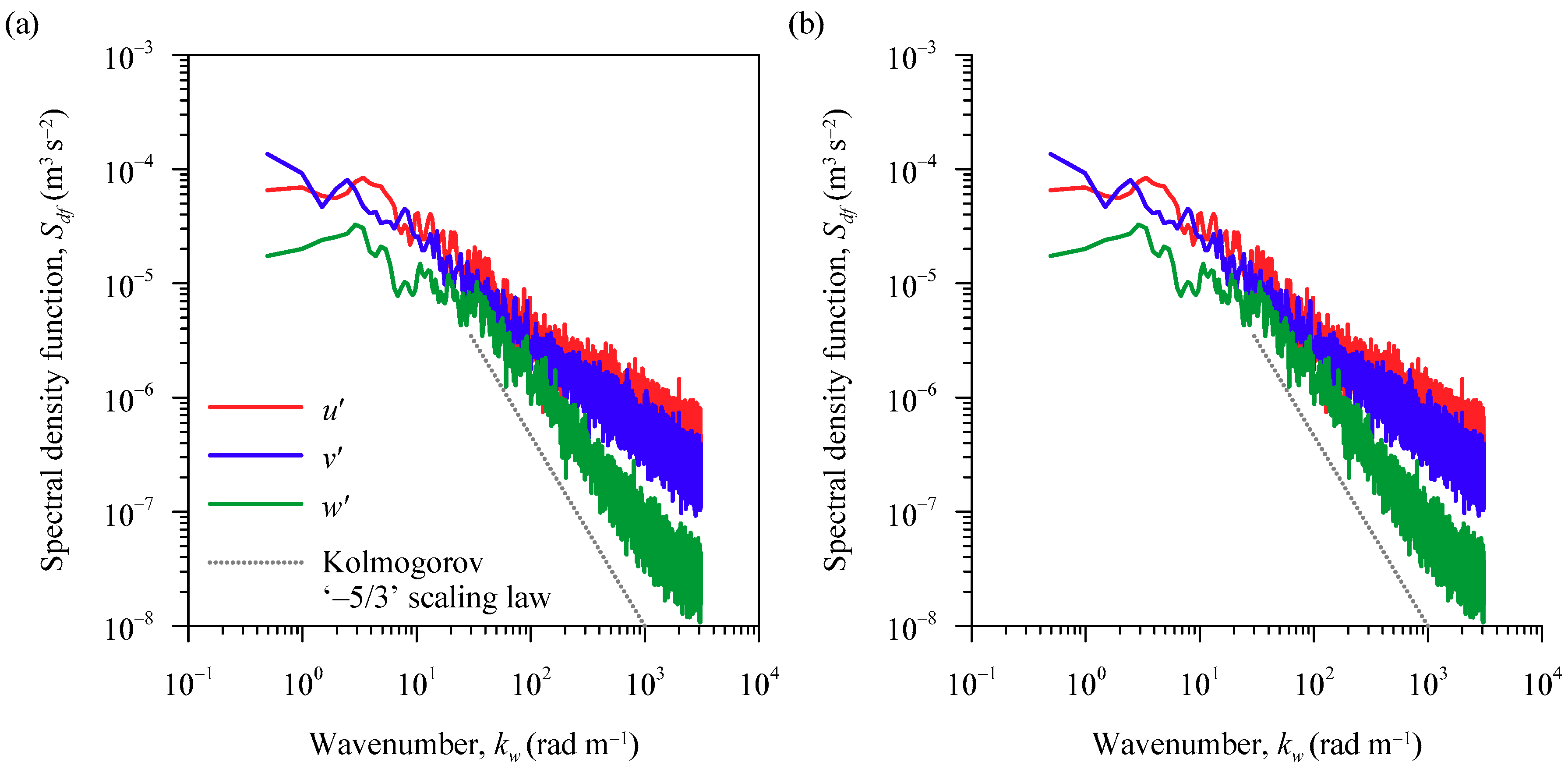The measured data were filtered whenever required applying the acceleration thresholding method [25]. This method could separate and substitute the unwanted data spikes in two phases. The threshold values of 1 to 1.5 for decontaminating the measured data were ascertained by satisfying Kolmogorov ‘–5/3’ scaling law in the inertial subrange for the spectral density function S_df(k_w) of streamwise velocity fluctuations u′. Here, k_w is the wavenumber (= 2πf/ū) and f is the frequency. Figure 3a,b illustrates the data plots of S_df(k_w) for velocity fluctuations (u′, v′, w′) in (x, y, z) before and after decontaminating the data in Run 1, respectively, at a relative streamwise distance x/L_d = 0.7 and a relative vertical distance z/L_d = 0.13. The S_df(k_w) curves of decontaminated signals compare well with Kolmogorov ‘–5/3’ scaling law in the inertial subrange for k_w ≥ 30 rad s⁻¹. In addition, it appears that the discrete spectral peaks are prominent for k_w < 30 rad s⁻¹. This indicates that the signals corresponding to k_w < 30 rad s⁻¹ contained large-scale turbulent structures, while those for k_w ≥ 30 rad s⁻¹ confirmed a pure turbulence. Therefore, a high-pass filter with a cut-off wavenumber of 30 rad s⁻¹ was used to filter the data.

In order to find the uncertainty of Vectrino data, 15 samples were collected at a sampling rate of 100 Hz for a duration of 300 s at a vertical distance z = 5 mm.

Table 1. Uncertainty estimation for Vectrino.

Ū (m s−1)	$\overline{\mathit{v}}$ (m s−1)	$\overline{\mathit{w}}$ (m s−1)	($\overline{{\mathit{u}}^{\prime }{\mathit{u}}^{\prime }}$)0.5 (m s−1)	($\overline{{\mathit{v}}^{\prime }{\mathit{v}}^{\prime }}$)0.5 (m s−1)	($\overline{{\mathit{w}}^{\prime }{\mathit{w}}^{\prime }}$)0.5 (m s−1)	τ (m2 s−2)
2.94 × 10−3 * (±2.93 × 10−2 †)	2.33 × 10−3 (±3.02 × 10−2)	1.75 × 10−3 (±3.95 × 10−2)	2.18 × 10−3 (±5.87 × 10−2)	1.34 × 10−3 (±6.72 × 10−2)	1.07 × 10−3 (±6.89 × 10−2)	4.37 × 10−5 (±7.48 × 10−4)

* Standard deviation. † Average of maximum (negative and positive) percentage error.

summarizes the results of uncertainty estimations of the time-averaged velocity components (ū, $\overline{v}$, $\overline{w}$) and the turbulence intensities [($\overline{u^{\prime }{u}^{\prime }}$)^0.5, ($\overline{v^{\prime }{v}^{\prime }}$)^0.5, ($\overline{w^{\prime }{w}^{\prime }}$)^0.5] in (x, y, z) and the Reynolds shear stress τ per unit mass density of fluid (= −$\overline{u^{\prime }{w}^{\prime }}$). It is pertinent to mention that to avoid bias and random errors, the samplings were done every time after resuming the experiments. The errors for the time-averaged velocity components, turbulence intensities and Reynolds shear stress were within ±4%, ±7% and ±8%, respectively. This confirmed the appropriateness of the data sampling with 100 Hz sampling rate. Further, it was necessary to ascertain the fully-developed undisturbed approach velocity profiles for both the Runs. 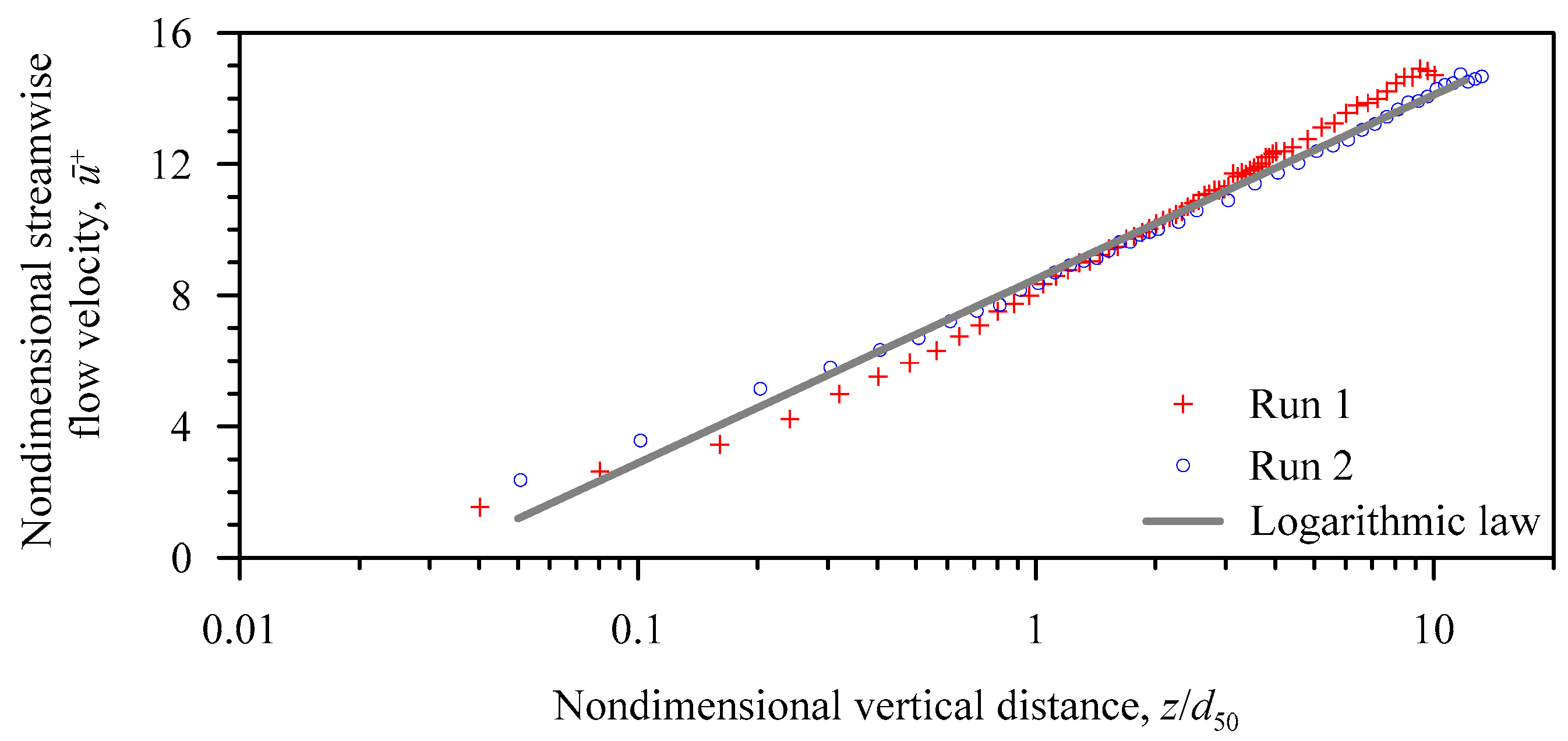Figure 4 shows the vertical profiles of nondimensional streamwise flow velocity ū⁺ (= ū/u_*) at the upstream of isolated dunal bedforms for both Runs 1 and 2. The data plots compare well with the classical logarithmic law ū/u_* = κ⁻¹ln(z/d₅₀) + 8.5 for a hydraulically rough flow regime. Here, κ is the von Kármán constant (= 0.41). This confirmed the acceptability of the fully-developed undisturbed approach flow velocity profiles for a hydraulically rough flow regime.

3. Time-Averaged Flow

3.1. Streamwise Flow Velocity

Figure 5 shows the vertical profiles of nondimensional streamwise flow velocity ū⁺ at upstream and various downstream relative streamwise distances x/L_d in Runs 1 and 2. Immediate downstream of the dune (x/L_d = 1), the wall-shear flow separates from the dune crest, giving rise to a flow reversal owing to negative streamwise flow velocity. The near-wake flow zone extends up to x/L_d ≈ 1.7. As the flow reaches further downstream, the flow reversal disappears. In addition, the streamwise flow velocity, having a velocity defect, starts to recover the undisturbed upstream velocity profile in the far-wake zone (x/L_d = 2.1 to 2.5). At x/L_d ≈ 3.3, the velocity profile appears to follow the undisturbed upstream velocity profile. It is also evident that above the relative vertical distance z/H_d = 1.5, the values of ū⁺ remain almost the same irrespective of x/L_d. However, the extents of the near- and far-wake flow zones in Runs 1 and 2 are different because of the effects of dune dimensions. It is worth mentioning that in wall-wake flows downstream of a sphere and a horizontal cylinder, the velocity profiles appear to follow their corresponding undisturbed upstream velocity profile at streamwise distances equaling roughly 8.5 and 7 times the diameter of sphere and cylinder, respectively [12,21].

3.2. Reynolds Shear Stress

Figure 6 presents the vertical profiles of nondimensional Reynolds shear stress τ⁺ (= τ/$u_{*}^2$) at the upstream and various downstream relative streamwise distances x/L_d in Runs 1 and 2. Upstream of the dune (x/L_d = −0.5), theτ⁺ profile follows a linear law. The τ⁺ is approximately unity at the relative vertical distance z/H_d = 0 and then, it reduces with an increase in relative vertical distance to become zero at the free surface (if the profiles would be extended up to the free surface). Immediate downstream of the dune (x/L_d = 1), the τ⁺ is negative in the near-bed flow zone. Thereafter, it increases with an increase in z/H_d, attaining a positive peak at the dune crest (z/H_d = 1). Above the crest, the τ⁺ decreases with an increase in z/H_d and attains almost similar pattern to the upstream profile for z/H_d > 1.5. It appears that for a given z/H_d, the τ⁺ decreases with an increase in x/L_d. In particular, at x/L_d ≈ 3.3, the τ⁺ profile becomes almost similar to the upstream profile at x/L_d = −0.5. It may be noted that for z/H_d > 1.75, the values of τ⁺ at various x/L_d are nearly similar. Therefore, it may be concluded that the Reynolds shear stress in the wall-wake flow is influenced by the dune up to a vertical distance of approximately 1.75 times the dune height and a streamwise distance of approximately 2.5 times the dune length.

4. Third-Order Moments

The third-order moments of velocity fluctuations offer relevant probabilistic information about the flux and the advection of Reynolds normal stresses. In addition, they give an indication of the predominance of turbulent bursting events [26]. The third-order moments, in the generalized form in xz plane, is expressed as m_jk = $\overline{{\tilde{u}}^j{\tilde{w}}^k}$, where $\tilde{u}$ = u′/($\overline{u^{\prime }{u}^{\prime }}$)^0.5, $\tilde{w}$ = w′/($\overline{w^{\prime }{w}^{\prime }}$)^0.5 and j + k = 3. Therefore, depending on the values of j and k, the third-order moments are given as, m₃₀ = $\overline{u^{\prime }{u}^{\prime }{u}^{\prime }}$/($\overline{u^{\prime }{u}^{\prime }}$)^1.5, m₀₃ = $\overline{w^{\prime }{w}^{\prime }{w}^{\prime }}$/($\overline{w^{\prime }{w}^{\prime }}$)^1.5, m₂₁ = $\overline{u^{\prime }{u}^{\prime }{w}^{\prime }}$/[($\overline{u^{\prime }{u}^{\prime }}$)×($\overline{w^{\prime }{w}^{\prime }}$)^0.5] and m₁₂ = $\overline{u^{\prime }{w}^{\prime }{w}^{\prime }}$/[($\overline{u^{\prime }{u}^{\prime }}$)^0.5×($\overline{w^{\prime }{w}^{\prime }}$)]. Here, the m₃₀ signifies the skewness of u′, indicating the streamwise flux of the streamwise Reynolds normal stress $\overline{u^{\prime }{u}^{\prime }}$. The m₀₃ defines the skewness of w′, suggesting the vertical flux of the vertical Reynolds normal stress $\overline{w^{\prime }{w}^{\prime }}$. In addition, the m₂₁ represents the advection of $\overline{u^{\prime }{u}^{\prime }}$ in the vertical direction, whereas the m₁₂ demonstrates the advection of $\overline{w^{\prime }{w}^{\prime }}$ in the streamwise direction.

Figure 7 shows the vertical profiles of m₃₀ and m₀₃ at the upstream and various downstream relative streamwise distances x/L_d in Runs 1 and 2. Upstream of the dune (x/L_d = −0.5), the m₃₀ and m_03, in the near-bed flow zone, are negative and positive, respectively. Then, they increase with an increase in relative vertical distance z/H_d without changing their signs. Downstream of the dune (x/L_d = 1 to 2.1), for a given x/L_d, the m₃₀ and m₀₃, in the near-bed flow zone, start with positive and negative values, respectively. Thereafter, they increase slowly with an increase in z/H_d until they attain their respective positive and negative peaks at z/H_d ≈ 0.75 and 0.5. As the z/H_d increases further, the m₃₀ and m₀₃ reduce quickly, changing their signs at z/H_d = 1, and for z/H_d > 1, they become independent of z/H_d. However, these features disappear gradually with an increase in x/L_d. It may be noted that the m₃₀ and m₀₃ profiles at x/L_d = 3.3 remain almost similar to those in the upstream.

Figure 8 depicts the vertical profiles of m₂₁ and m₁₂ at the upstream and various downstream relative streamwise distances x/L_d in Runs 1 and 2. It appears that upstream of the dune (x/L_d = −0.5), the m₂₁ and m₁₂, in the near-bed flow zone, attain positive and negative values, respectively. Then, they increase with an increase in relative vertical distance z/H_d up to a certain height. Subsequently, they reduce with an increase in z/H_d, becoming independent of z/H_d for z/H_d > 1.1. Downstream of the dune (x/L_d = 1 to 2.1), for a given x/L_d, the m₂₁ and m₁₂, in the near-bed flow zone, are negative and positive, respectively. Then, they increase with an increase in z/H_d attaining their respective peaks. Afterward, they reduce quickly, changing their signs at the dune crest (z/H_d = 1). Thereafter, the m₂₁ and m₁₂ profiles recover their upstream profiles. Downstream of the dune, an advection of $\overline{u^{\prime }{u}^{\prime }}$ in the upward direction and that of $\overline{w^{\prime }{w}^{\prime }}$ in the upstream direction prevail below the crest. In fact, below the crest, there appears a streamwise acceleration, which is linked with the downward flux causing sweeps with an advection of $\overline{u^{\prime }{u}^{\prime }}$ in the downward direction. By contrast, above the crest, the streamwise deceleration is associated with an upward flux producing ejections with an advection of $\overline{u^{\prime }{u}^{\prime }}$ in the upward direction.

5. Quadrant Analysis

Lu and Willmarth [27] suggested that the bursting events can be quantified by performing the quadrant analysis of velocity fluctuations u′ and w′ on a u′w′ plane. The turbulent bursting includes four events in four distinct quadrants i = 1 to 4, such as (i) Q1 events or outward interactions (i = 1 and u′, w′ > 0), (ii) Q2 events or ejections (i = 2 and u′ < 0, w′ > 0), (iii) Q3 events or inward interactions (i = 3 and u′, w′ < 0) and (iv) Q4 events or sweeps (i = 4 and u′ > 0, w′ < 0). Outside the hole size H, the contribution of ${\overline{u^{\prime }{w}^{\prime }}|}_{{}^{i,H}}$ from the quadrant i to $\overline{u^{\prime }{w}^{\prime }}$ is ascertained by averaging the quantity u′(t)w′(t)F_i,H over the sampling duration. Here, F_i,H is the detection function, defined as F_i,H = 1 if the pair (u′, w′) in the quadrant i satisfies the condition |u′w′|≥ H($\overline{u^{\prime }{u}^{\prime }}$)^0.5($\overline{w^{\prime }{w}^{\prime }}$)^0.5 and F_i,H = 0 otherwise. The relative fractional contributions S_i,H toward the Reynolds shear stress production is expressed as S_i,H = ${\overline{u^{\prime }{w}^{\prime }}|}_{{}^{i,H}}$/$\overline{u^{\prime }{w}^{\prime }}$. It turns out that for H = 0, the sum of S_1,0, S_2,0, S_3,0 and S_4,0 becomes unity.

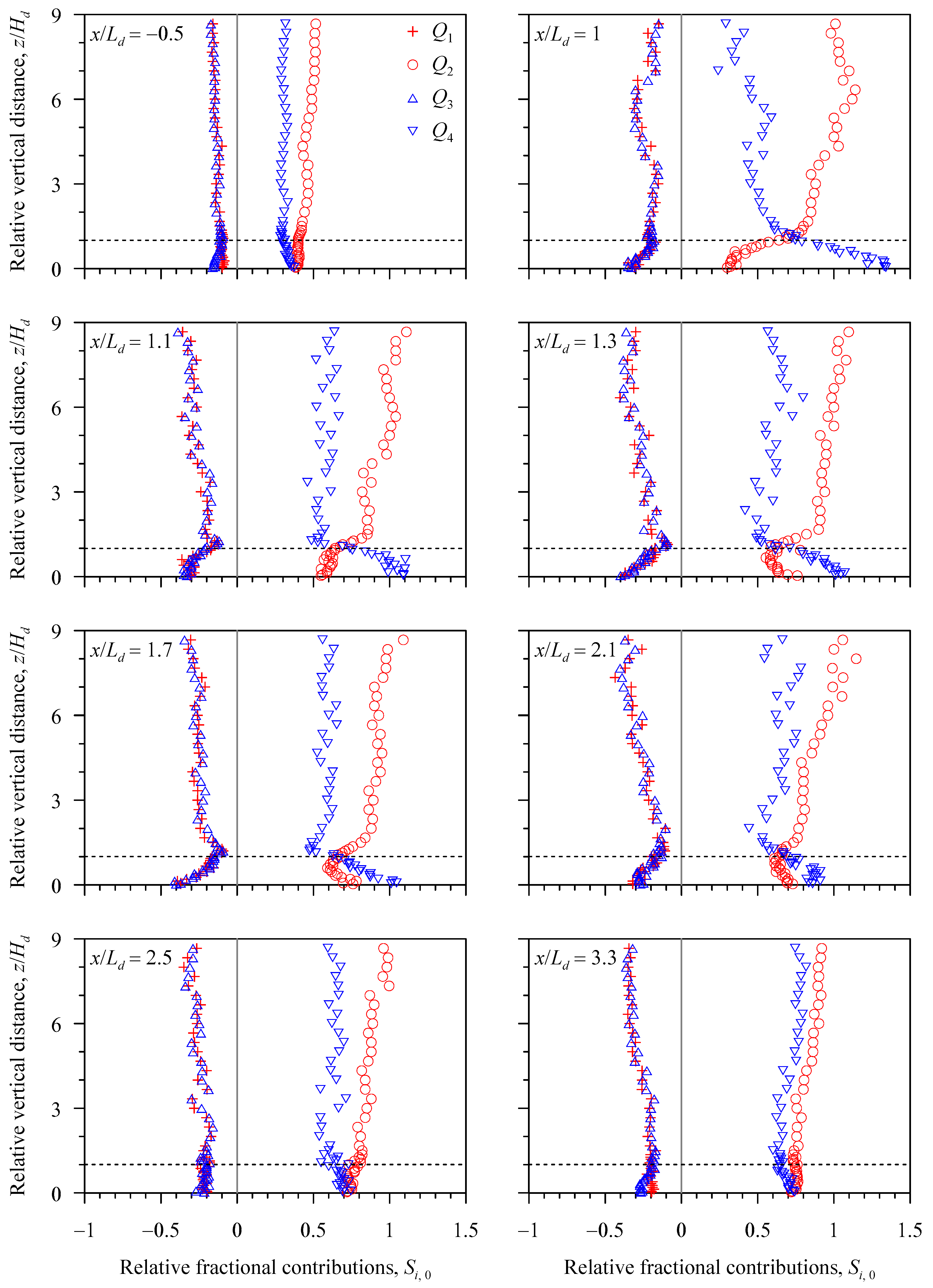
Figure 9 and Figure 10 show the vertical profiles of S_i,0 at the upstream and various downstream relative streamwise distances x/L_d in Runs 1 and 2, respectively. Upstream of the dune (x/L_d = –0.5), the Q2 and Q4 events remain the most and the second-most contributing events, respectively, to the production of Reynolds shear stress. However, the Q1 and Q3 events are trivial across the flow depth. Downstream of the dune (x/L_d = 1 to 2.1), all the four events contribute largely below the dune crest with prevailing Q4 events in the form of arrival of high-speed fluid streaks. At x/L_d = 2.5, contributions from the Q2 and Q4 events appear to be nearly equal below the crest. Further downstream (x/L_d = 3.3), the Q2 events dominate over Q4 events in the form of arrival of low-speed fluid streaks. It may be noted that above the crest (z/H_d > 1), the Q2 events are the most contributing events regardless of x/L_d.

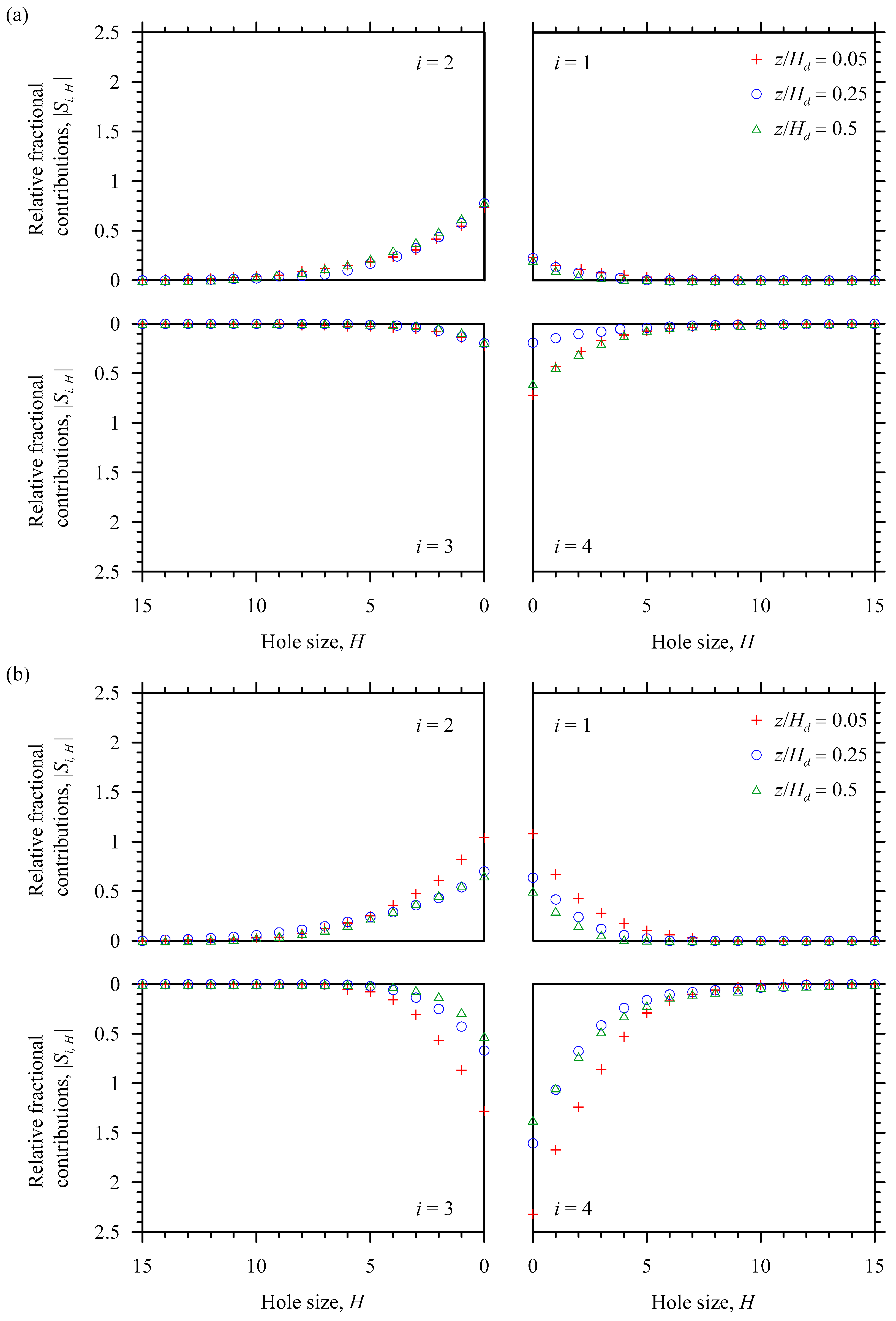
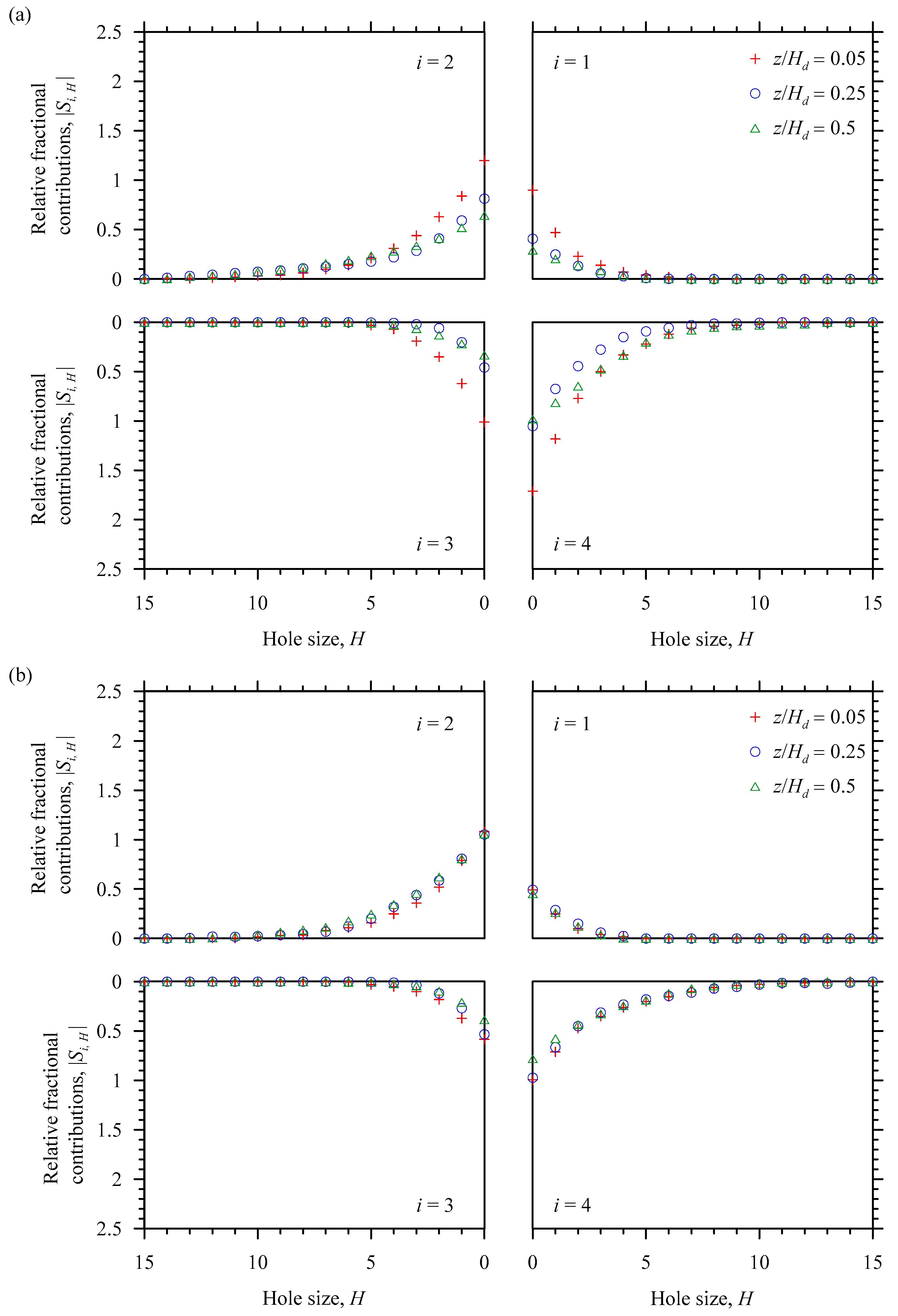
Figure 11a,b shows the variations of relative fractional contributions |S_i,H| with hole size H in Run 1 for different relative vertical distances z/H_d (=0.05, 0.25 and 0.5) at relative streamwise distances x/L_d = –0.5 (uninterrupted upstream flow) and 1 (near-wake flow), whereas Figure 12a,b shows those at x/L_d = 1.7 (far-wake flow) and 3.3 (near to fully recovered flow). It appears that upstream of the dune (x/L_d = –0.5), the Q1 and Q3 events for z/H_d = 0.05 contribute minimally to the Reynolds shear stress production as compared to the Q2 and Q4 events. However, for z/H_d = 0.05, the pairs (Q1, Q3) and (Q2, Q4) are equal, indicating that they mutually cancel the dominance of each other. At x/L_d = –0.5, the Q2 events remain dominant for z/D = 0.25 and 0.5. Immediate downstream of the dune (x/L_d = 1), the Q1 and Q3 events, for a given z/H_d, are smaller than Q2 and Q4 events. However, at the downstream, the Q4 remain the most dominant events for z/H_d = 0.05, 0.25 and 0.5. At x/L_d = 1.7, these features remain similar to those at x/L_d = 1, but with relatively smaller Q4 events. Far downstream of the dune (x/L_d = 3.3), the events, for a given z/H_d, follow the upstream trend. The contributions from the events are considerable for lower values of H. In essence, for H ≥ 12, all the events are trivial at different streamwise and vertical distances.

6. Turbulent Kinetic Energy Budget

The turbulent kinetic energy budget reads t_P = ε + t_D + p_D − v_D, where t_P is the turbulent kinetic energy production rate (= –$\overline{u^{\prime }{w}^{\prime }}$∂ū/∂z), ε is the turbulent kinetic energy dissipation rate, t_D is the turbulent kinetic energy diffusion rate (= ∂f_kw/∂z), f_kw is the vertical flux of turbulent kinetic energy, p_D is the pressure energy diffusion rate [= ρ⁻¹∂($\overline{p^{\prime }{w}^{\prime }}$)/∂z], p′ is the pressure fluctuations, v_D is the viscous diffusion rate (=ν∂²k/∂z²) and k is the turbulent kinetic energy. In an open channel flow, the v_D is insignificant compared to other components of the turbulent kinetic energy budget. In this study, Kolmogorov second hypothesis was applied to determine the ε from the velocity power spectra [28]. The t_P and t_D were determined from the experimental data, whereas the p_D was obtained from the relationship p_D = t_P − ε − t_D. In nondimensional form, the set of variables (t_P, ε, t_D, p_D) is expressed as (T_P, E_D, T_D, P_D) = (t_P, ε, t_D, p_D) × (H_d/$u_{*}^3$).

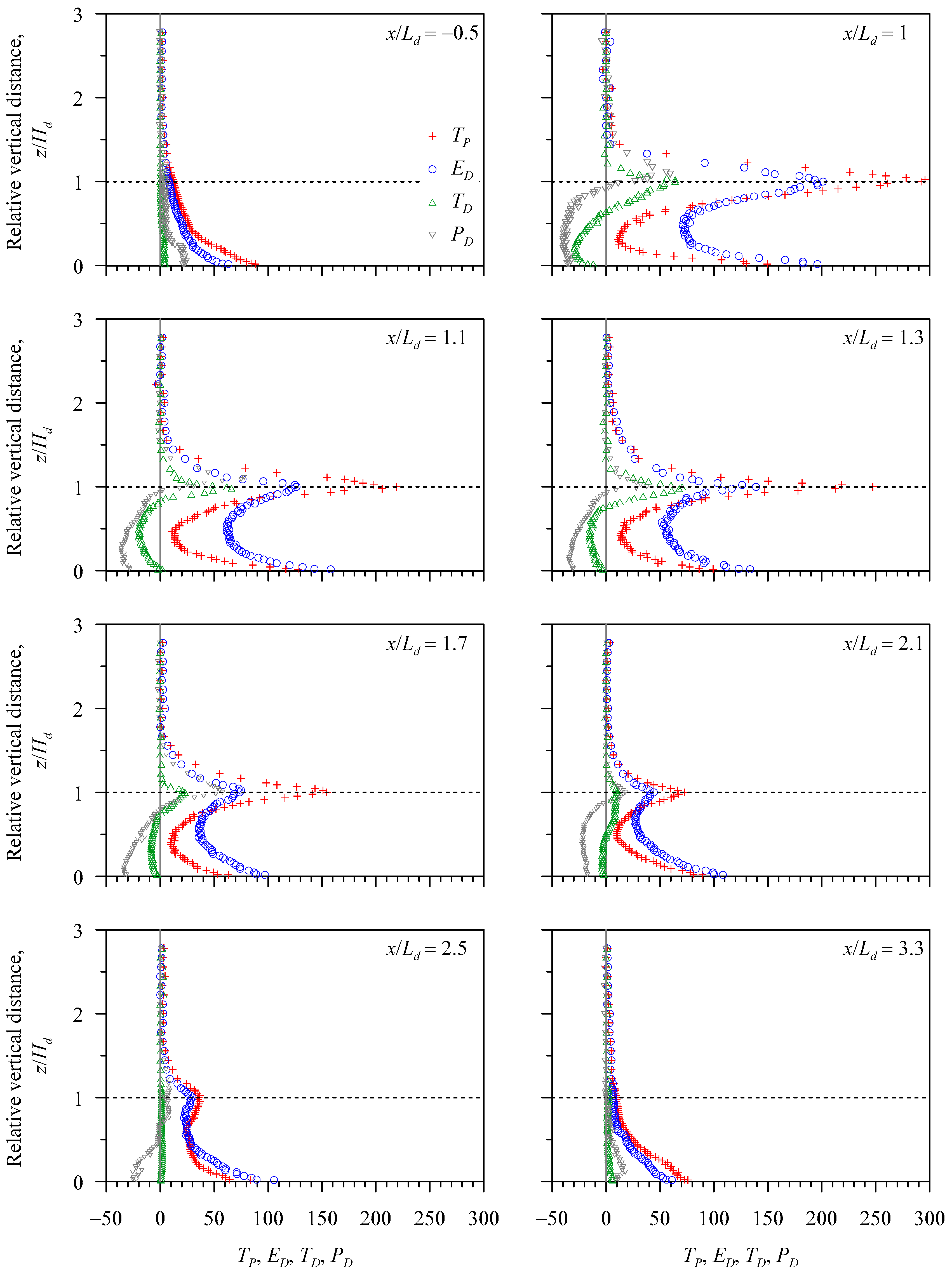
Figure 13 illustrates the vertical profiles of nondimensional components of the turbulent kinetic energy budget at various relative streamwise distances x/L_d in Run 1. Upstream of the dune (x/L_d = –0.5), all the components of the turbulent kinetic energy budget, in the near-bed flow zone, are positive with a sequence of magnitude T_P > E_D > P_D > T_D and then, they reduce with an increase in relative vertical distance z/H_d. Above the dune crest (z/H_d > 1), they are quite small. Downstream of the dune (x/L_d = 1 to 2.1), the peaks of T_P, E_D, P_D and T_D are found to appear at the crest. In the near-bed flow zone, the T_P and E_D are positive, whereas the P_D and T_D are negative for x/L_d = 1 to 2.1. Downstream of the dune, the absolute values of T_P, E_D, P_D and T_D decrease with an increase in x/L_d. In particular, at x/L_d = 3.3, the T_P, E_D, P_D and T_D profiles are almost similar to those of the undisturbed upstream flow at x/L_d = −0.5.

7. Reynolds Stress Anisotropy

An isotropic turbulence refers to an idealized condition, where the velocity fluctuations at a specific point remain invariant to the rotation of axes. In a lucid way, this condition indicates that the Reynolds normal stresses are identical (σ_x = σ_y = σ_z), where (σ_x, σ_y, σ_z) = ($\overline{u^{\prime }{u}^{\prime }}$, $\overline{v^{\prime }{v}^{\prime }}$, $\overline{w^{\prime }{w}^{\prime }}$). By contrast, in an anisotropic turbulence, the Reynolds normal stresses are dissimilar, because the velocity fluctuations ${u^{\prime }}_i$ [= (u′, v′, w′) for i = (1, 2, 3)] are directionally preferred.

The Reynolds stress anisotropy tensor b_ij is expressed as b_ij = $\overline{{u^{\prime }}_i{u^{\prime }}_j}$/(2k) − δ_ij/3, where δ_ij is the Kronecker delta function [δ_ij(i = j) = 1 and δ_ij(i ≠ j) = 0]. To ascertain the degree and the nature of anisotropy, the second and third principal invariants, I₂ (= –b_ijb_ij/2) and I₃ (= b_ijb_jkb_ki/3), respectively, are introduced. 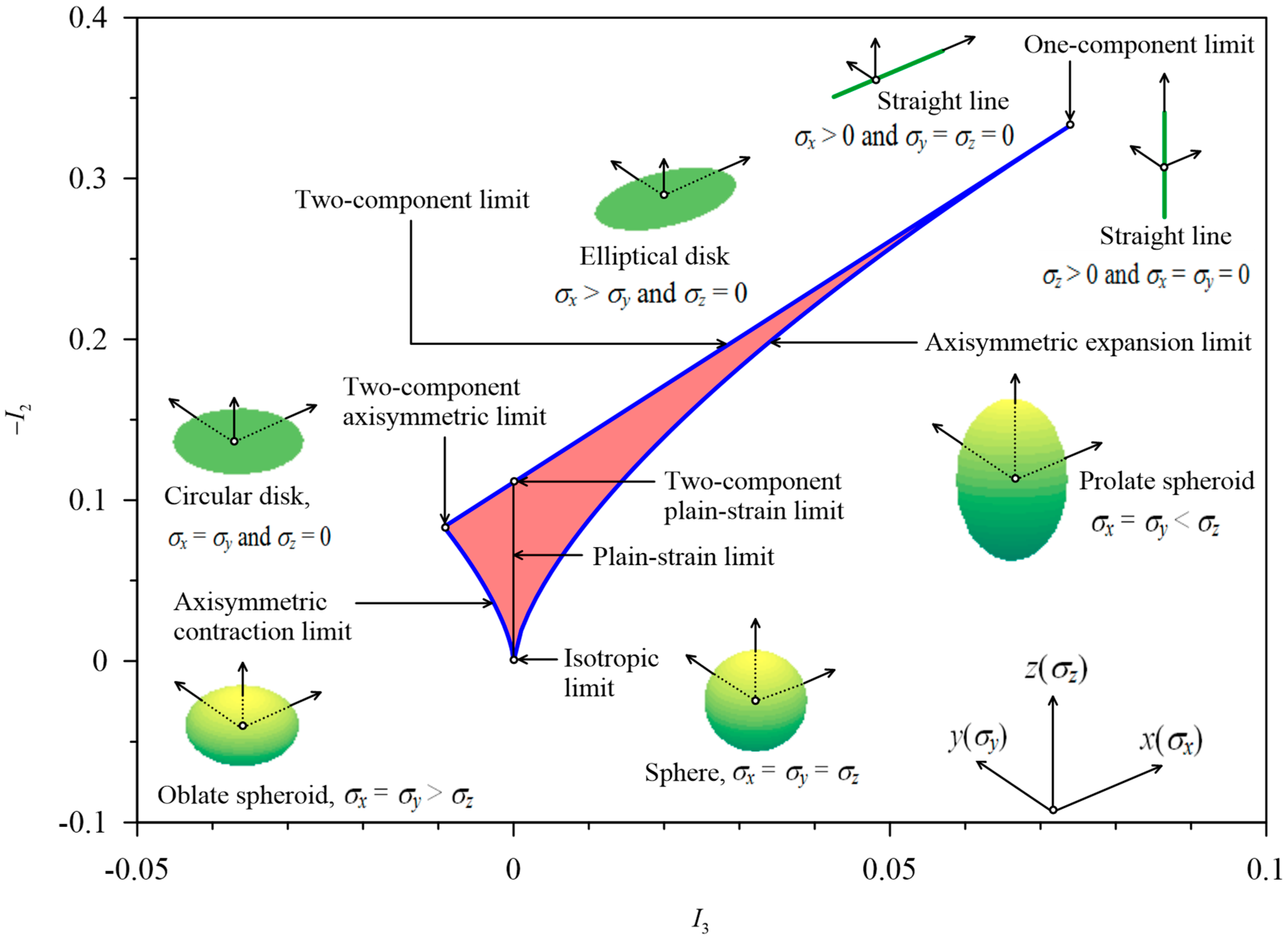The Reynolds stress anisotropy is determined by plotting –I₂ as a function of I₃, called the anisotropy invariant map (AIM). In an AIM, the possible turbulence states are confined to a triangle, called the Lumley triangle (Figure 14). The left-curved and the right-curved boundaries of the Lumley triangle, given by I₃ = ±2(−I₂/3)^3/2, are symmetric about the plane-strain limit (I₃ = 0). In addition, the top-linear boundary of the Lumley triangle obeys I₃ = −(9I₂ + 1)/27. Dey et al. [29] envisioned the Reynolds stress anisotropy from the perspective of the shape of ellipsoid formed by the Reynolds normal stresses (σ_x, σ_y, σ_z) in (x, y, z). In an isotropic turbulence (σ_x = σ_y = σ_z), the stress ellipsoid becomes a sphere (Figure 14). On the left-curved boundary, called the axisymmetric contraction limit, one component of Reynolds normal stress is smaller than the other two equal components (σ_x = σ_y > σ_z), forming the stress ellipsoid an oblate spheroid. On the left vertex, called the two-component axisymmetric limit, one component of Reynolds normal stress disappears (σ_x = σ_y and σ_z = 0) to make the stress ellipsoid a circular disc (Figure 14). On the right-curved boundary, called the axisymmetric expansion limit, one component of Reynolds normal stress is larger than the other two equal components (σ_x = σ_y < σ_z), making the stress ellipsoid a prolate spheroid (Figure 14). Further, on the top-linear boundary, called the two-component limit, one component of Reynolds normal stress is larger than the other component together with a third vanishing component (σ_x > σ_y and σ_z = 0), producing the stress ellipsoid an elliptical disk. The point of intersecting of the plain-strain limit and the two-component limit is called the two-component plain-strain limit. Moreover, on the right vertex of the Lumley triangle, called the one-component limit [(σ_x > 0, σ_y = σ_z = 0) or (σ_x = σ_y = 0, σ_z > 0)], only one component of Reynolds normal stress sustains to make the stress ellipsoid a straight line (Figure 14).

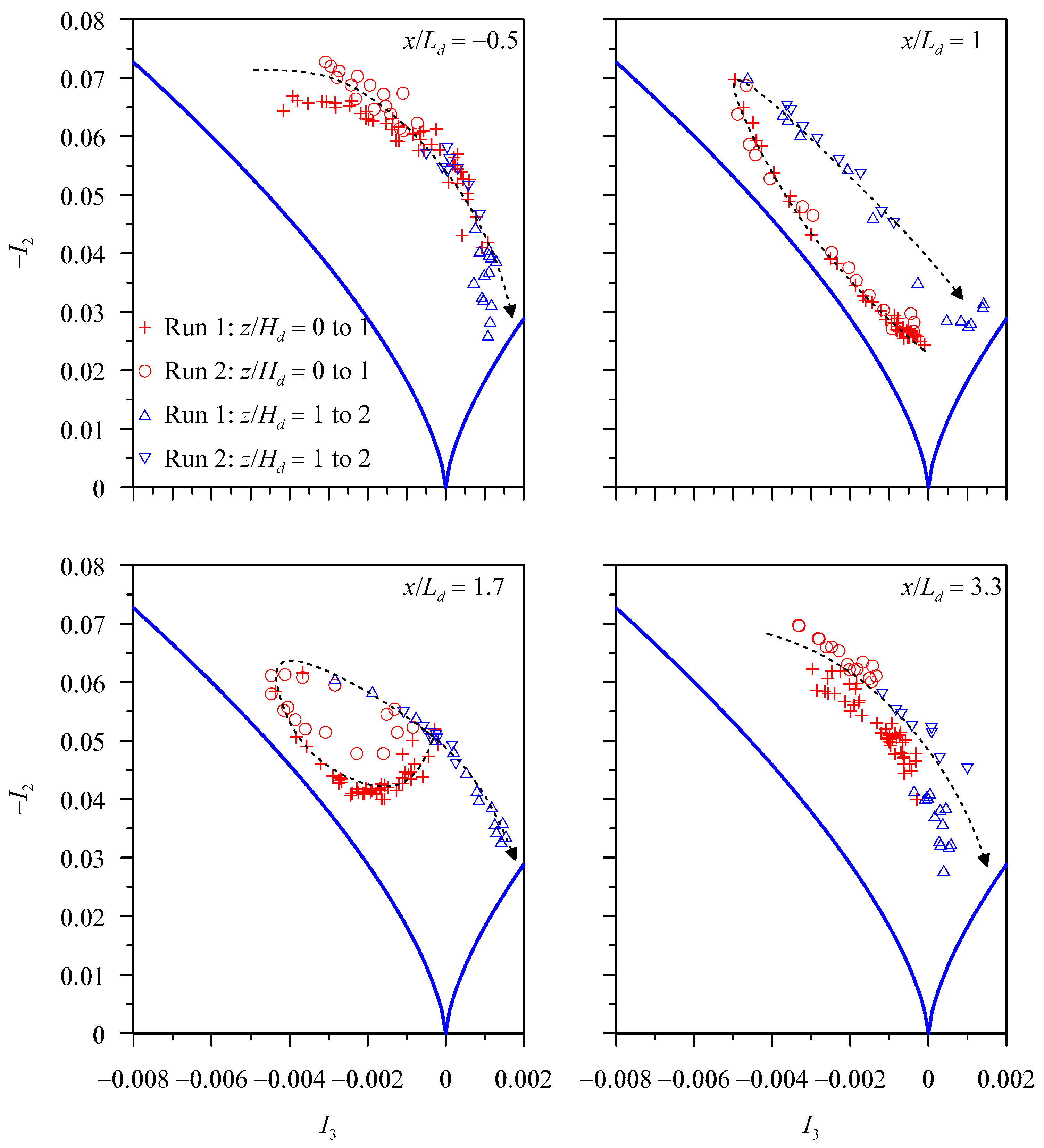
Figure 15 shows the data plots of −I₂ versus I₃, confined to the AIM boundaries, at various relative streamwise distances x/L_d in Runs 1 and 2. Upstream of the dune (x/L_d = −0.5), the data plots initiate from the near left vertex, moving toward the bottom cusp, and then, with an increase in vertical distance, they cross the plain-strain limit to shift toward the right-curved boundary. The trends of the data plots for both Runs 1 and 2 are almost monotonic. The AIM of the upstream indicates that as the vertical distance increases, the turbulence anisotropy tends to reduce to a quasi-three-dimensional isotropy. Immediate downstream of the dune, the data plots tend to create a stretched loop inclined to the left-curved boundary. However, below the dune crest (z/H_d < 1), the data plots in the near-bed flow zone initiate from the plain-strain limit and with an increase in vertical distance up to the crest, they shift toward the left vertex following the left-curved boundary. This suggests that the turbulence anisotropy has an affinity to a two-dimensional isotropy. Above the crest, the data plots turn toward the right and as the vertical distance increases further, they move toward the bottom cusp following the left-curved boundary. This demonstrates that the turbulence anisotropy tends to reduce to a quasi-three-dimensional isotropy. Further downstream (x/L_d = 1.7), the size of the loop created by the data plots reduces forming a tail, and the loop disappears at x/L_d = 3.3, signifying a recovery of the undisturbed upstream trend. It therefore appears that that below the crest, the turbulence has an affinity to a two-dimensional isotropy, whereas above the crest, a quasi-three-dimensional isotropy prevails.

From the perspective of the shape of stress ellipsoid, Figure 15 shows that below the dune crest, an oblate spheroid axisymmetric turbulence is predominant in the wall-wake flow. The line of plain-strain limit (I₃ = 0) is touched by the curve through the data plots in the near-bed flow zone. This reveals that the axisymmetric contraction to the oblate spheroid enhances as the vertical distance increases up to the crest. However, the axisymmetric contraction to oblate spheroid lessens with a further increase in vertical distance above the crest.

8. Conclusions

This study puts into focus the turbulence in wall-wake flow downstream of an isolated dunal bedform. The vertical profiles of streamwise flow velocity reveal that the near-wake flow zone extends up to 1.7 times the dune length, whereas the streamwise flow velocity profile follows the undisturbed upstream velocity profile beyond 3.3 times the dune length. The Reynolds shear stress in the wall-wake flow is affected by the dune up to a vertical distance of 1.75 times the dune height and a streamwise distance of 2.5 times the dune length. The third-order moment of velocity fluctuations reveal that downstream of the dune, a streamwise acceleration having a downward flux prevails below the dune crest, whereas a streamwise deceleration having an upward flux persists above the crest. Below the crest, the sweeps are found to be the predominant events, whereas above the crest, the ejections are the major events. The components of the turbulent kinetic energy budget reveal an amplification of the magnitudes of the turbulent parameters, which attain their maximum peaks at the crest. The anisotropy invariant maps show that the data plots in the wall-wake flow start from the plain-strain limit in the near-bed flow zone, shifting toward the left vertex of the Lumley triangle up to the crest to show an affinity to a two-dimensional isotropy. Above the crest, the data plots show an affinity to a quasi-three-dimensional isotropy.

In essence, this study advances the current understanding of flow and turbulence characteristics in wall-wake flow downstream of an isolated dunal bedform. The experimental results provide guidance to numerical simulations of wall-wake flow. In addition, this study may be helpful, at least qualitatively, to simulate the mobile-bed flow downstream of a dunal bedform.