Smooth Open Channel with Increasing Aspect Ratio: Influence on Secondary Flow

Abstract

A high-resolution particle image velocitmetry system is used to investigate the relationship between secondary flow and aspect ratio in a straight channel. Considering the symmetry of open channel flow, the flow parameters in half of the flume are measured. Since the variation of the aspect ratio has a direct impact on the intensity and structure of secondary flows, this study was conducted in a smooth open channel to study the influence of aspect ratio on the structure and strength of secondary flows with aspect ratio change from 3 to 7.5 under supercritical flow condition. Profiles and contour-maps of time-averaged stream-wise and vertical velocities were acquired using precise measuring instruments. The results show that there are several secondary flow cells in the cross section, and their structure affects the velocity distribution and energy distribution, which makes the velocity distribution deviate from the traditional logarithmic distribution, and the maximum velocity occur below the surface. The flow intensity of secondary flows is different under different aspect ratios. Results show great agreement with classical theory.

1. Introduction

Turbulent flow is a relatively common phenomenon in the engineering field, and studies on turbulence have been conducted in the field of hydraulic, shipping, and aeronautical engineering. A turbulent channel flow is always accompanied by transverse circulating currents, which are also called secondary flow. The study of secondary motion is of great importance because it is not only applied in hydraulic structures like open channel and duct flow, but also present in more complicated configurations that have been applied in engineering field, such as diffusers, turbine blades or wings [1]. To date, plenty of studies have been carried out to explain the generating mechanism of secondary flow, including a wide range of experiments [2,3,4] and numerical simulation in channel and duct flow [1,5,6,7]. On the basis of the different mechanisms of secondary flow production, Prandtl [8] classified secondary currents into two types: the first type is generated in a meandering channel and induced by a transverse pressure gradient or body force known as centrifugal force. The cross flow of this type plays an important role during riverbed evolution process. The second type occurs in a straight open channel flow due to the anisotropy of Reynolds shear stress. As Gessner [9] presented, transverse flow is directed towards the corner as a direct result of turbulent shear stress gradients that are normal to the bisector. Previous studies have shown that the channel flow presents 3D characteristics due to the influence of secondary flow on the main flow. Nezu and Nakagawa [2] indicated that two vortices exist in the cross section: free surface vortex and bottom vortex. These two counter rotating vortices change the shear stress and velocity distributions in the flow field. Duct flow is similar to open channel flow; two vortices exist in each corner region. Others have also pointed out that the secondary current appears due to nonzero near wall velocity gradient in the direction tangent to the wall [10,11]. Figure 1 shows the brief structure of secondary currents, which changes our traditional understanding of a simple 2D open channel flow pattern.

An open channel flow cannot be regarded as a simple 2D flow when secondary currents exist. Hu [12] conducted an investigation and concluded that the area of the 2D flow region increases with the aspect ratio. Additionally, with the increase in boundary roughness, the effect of sidewall on the main flow will become more evident. The flow can be approximated as 2D only under the condition of a relatively large aspect ratio. Therefore, depending on aspect ratio, the channel flow is divided into two types: one is a wide and shallow open-channel flow with an aspect ratio of higher than 5, and the other is a relatively deep and narrow open channel flow with an aspect ratio less than 5. In the cross section, secondary currents influence the convection and transport process of the energy, momentum, heat, and mass within the flow field, which complicates the investigation of open channel flow. Given the simple boundary condition and wide application of open-channel flow in the engineering field, pertinent studies relating to water supply, sediment transportation, and pollutant dispersion are of importance. Many existing studies have focused on the factors that influence the structure and strength of secondary flow, as well as the velocity and shear stress distributions under the effect of secondary flow. The influencing factors include: roughness of boundary condition (both bed and sidewall), aspect ratio, Reynolds number, and atmospheric condition over free surface [13,14,15]. Other researchers have also studied the influence of vegetation on the secondary flow [16,17,18].

Traditional studies on flow include theoretical analysis, numerical simulation, and experimental study, and these methods have been combined and verified to solve the actual problem [19,20,21,22,23,24,25,26]. Technically, the magnitude of flow in span-wise is relatively small, which only takes up 2–5% of the main flow [27]. Since secondary flow is relatively weak, any small error during velocity measurement and any defect in the measurement principle can render the result unreliable, and some features of secondary currents may not be captured. Studies have indicated that vertical velocity is essential in studying the structure of secondary currents [15], and the distribution of vortices along the corner region is closely related to the aspect ratio. The present study uses a measurement technique called particle image velocimetry (PIV) to acquire the flow parameters in open channel with $B/H$ (aspect ratio) changes from 3 to 7.5. As previously mentioned, the secondary flow is affected by the aspect ratio; however, the mechanism remains ambiguous. Therefore, the main purposes of this study are as follows: (1) to acquire an velocity profile at different distances from the side wall and analyze the relationship between the aspect ratio and velocity distribution; (2) to compare the strength of secondary flow at different aspect ratios, and study the influence of aspect ratio on secondary flow; (3) investigate the turbulence intensity distribution in the cross section under different aspect ratios. This paper presents a discussion of the velocity distribution and a brief analysis of the relationship between secondary currents and aspect ratio in a rectangular open channel.

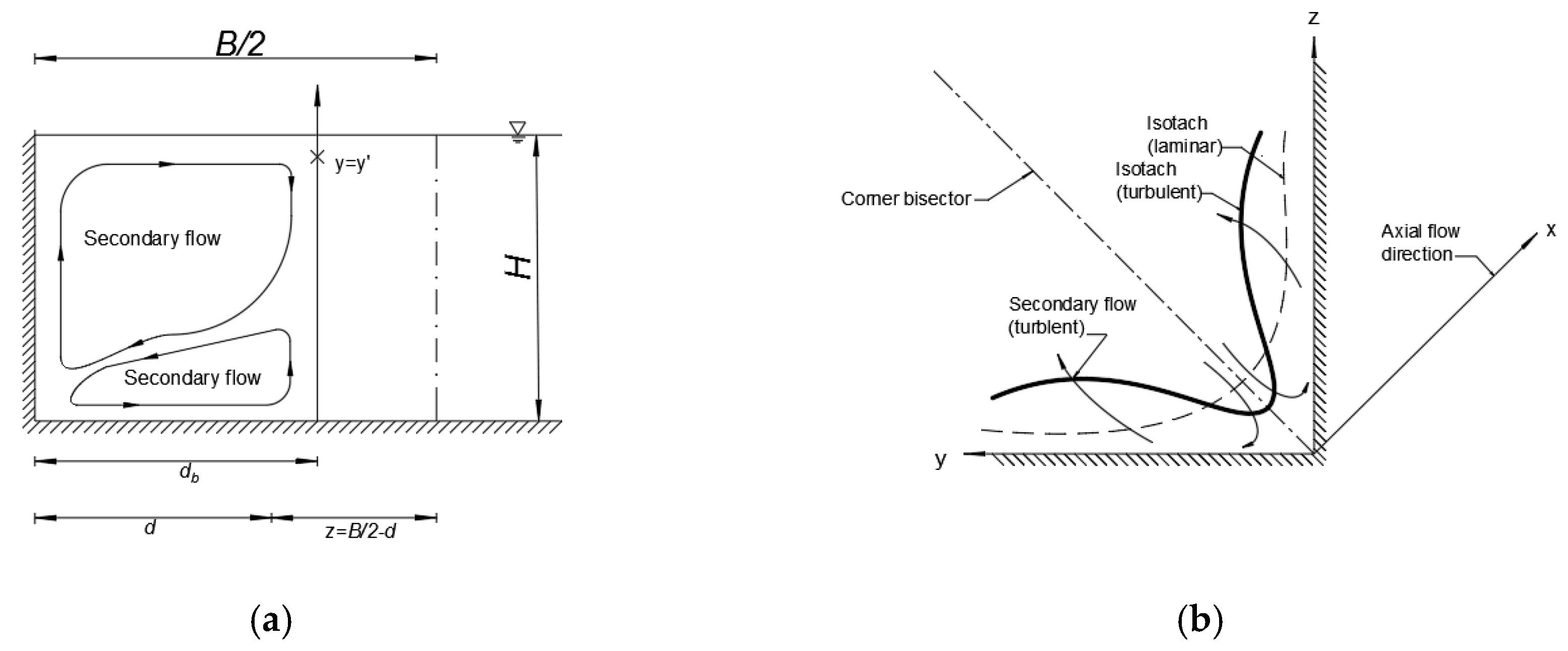
2. Experiment Setup

2.1. Hydraulic Model

The experiment was conducted in a recirculating hydraulic flume, which is 14 m long, 0.3 m wide, and 0.25 m high; the layout of the test flume and measuring sections are presented in Figure 2 and Figure 3. All three sides of the flume are made of transparent polymethyl methacrylate to facilitate PIV application. As shown in Figure 3, x, y, and z represent the stream-wise, vertical directions, and span-wise, respectively. While u, v, and w represent the instantaneous velocity, U, V, and W denote the time-averaged velocity in the x-, y-, and z-directions, respectively. Three honeycombs were placed at the flume entrance to dissipate energy of large scale structures and stabilize the flow. Water was circulated through a pump, via which the discharge can be adjusted to meet the requirements of experiment design. The measuring accuracy of the electromagnetic flow meter is less than 5%. To avoid upstream and downstream influences on the sampling area and ensure the full development of turbulent flow, the measuring section was set at x = 8.1 m downstream of the sink entrance, where the flow is sufficiently stable without significant fluctuation. The arrangement of laser device and camera is shown in Figure 3. The laser source was designed to move span-wise only.

2.2. PIV System

The experiment was performed via a PIV system with high spatiotemporal resolution developed by Tsinghua University, as shown in Figure 4. The image acquisition system is based on an advanced high-speed camera and continuous laser emitter. The flow field calculation system is based on multiple-interpretation, multi-grid iteration, and image deformation processing algorithms, with accuracy of less than 1%. The principle of the PIV system is to measure the movement distance of tiny particles in a fixed time period, which is sufficiently short. The movement velocity of the particle was calculated by applying the fast Fourier cross-correlation algorithm. A fan-shaped laser light was used to illuminate the particles in the fluid, thereby allowing the CCD camera to take pictures of the micelle particles. The light source was provided by a laser, which can create a 1 mm thick light. Dantec polyamide was used as tracer particle. The averaged diameter of seeding particles is 5 μm, and the density is 1.03 g/m³. The seeding particles are minuscule and thus show great following quality, the flow structure will not be affected, and the actual velocity of the particles in the stream-wise and vertical directions can be regarded as the flow velocity.

2.3. Test Program

As previously mentioned, the present study aims to investigate the characteristics of secondary flow in an open channel, particularly the influence of aspect ratio on the flow field. In a flume with fixed width, the flow depth was changed from 10 cm to 4 cm to meet the requirements of different aspect ratios; the value of aspect ratio changed from 3 to 7.5 respectively. The laser light source was designed to move along the z axis. Hence, the velocity distribution at different distances from the side wall can be acquired. For each flow depth, nine groups of stream wise and vertical velocity were obtained. Measuring section number 1 was set at 1 cm away from the side wall, measuring section number 2 was set 2 cm away from the side wall, and other sections were set up in the same pattern. Bed and side wall roughness remained unchanged and the flume can be regarded as a smooth open channel. Under different flow depths, a total of 10,000 pictures were obtained at each measuring section, and the sampling frequency was set to 800 Hz. Two consecutive pictures of the test section constitute one flow field, and particle displacement satisfies the rule for PIV correlation analysis that the maximum particle displacement less than one quarter of the calculation window [28]. The exposure rate was fixed at 1000 to ensure clear particle images. Bed slop was set at 0.5%, with a completely opened tailgate, and the pump was adjusted to obtain different flow depths.

Table 1. Hydraulic parameters for experiments.

Case	H (cm)	Ar	Q (m3/h)	$\overline{\mathbf{U}}$	${\mathbf{U}}_{*} (\mathbf{m}/\mathbf{s})$	$\mathit{F}\mathbf{r}$	$\mathit{R}\mathit{e}$
1	10	3	138.9	1.2861	0.0542	1.2992	76,402.64
2	8	3.75	104.8	1.2130	0.0506	1.3699	62,658.44
3	6	5	68.8	1.0617	0.0458	1.3846	50,552.67
4	4.62	6.5	47.9	0.9600	0.0416	1.4267	37,130.11
5	4	7.5	38.3	0.8866	0.0393	1.4260	30,015.53

shows detailed hydraulic parameters, where H represents the flow depth, Q denotes the discharge, $\overline{\mathrm{U}}$ represents the mean flow velocity, ${\mathrm{U}}_{*}$ is the frictional velocity, and Fr is the Froude number. The flow can be regarded as a supercritical turbulent flow for Fr > 1 and Re > 500 in all 5 cases.

3. Results

Considering that symmetry is a characteristic of open channel flow in the rectangular flume, this study only investigates half of the flume region. This section presents a detailed analysis of the experimental data.

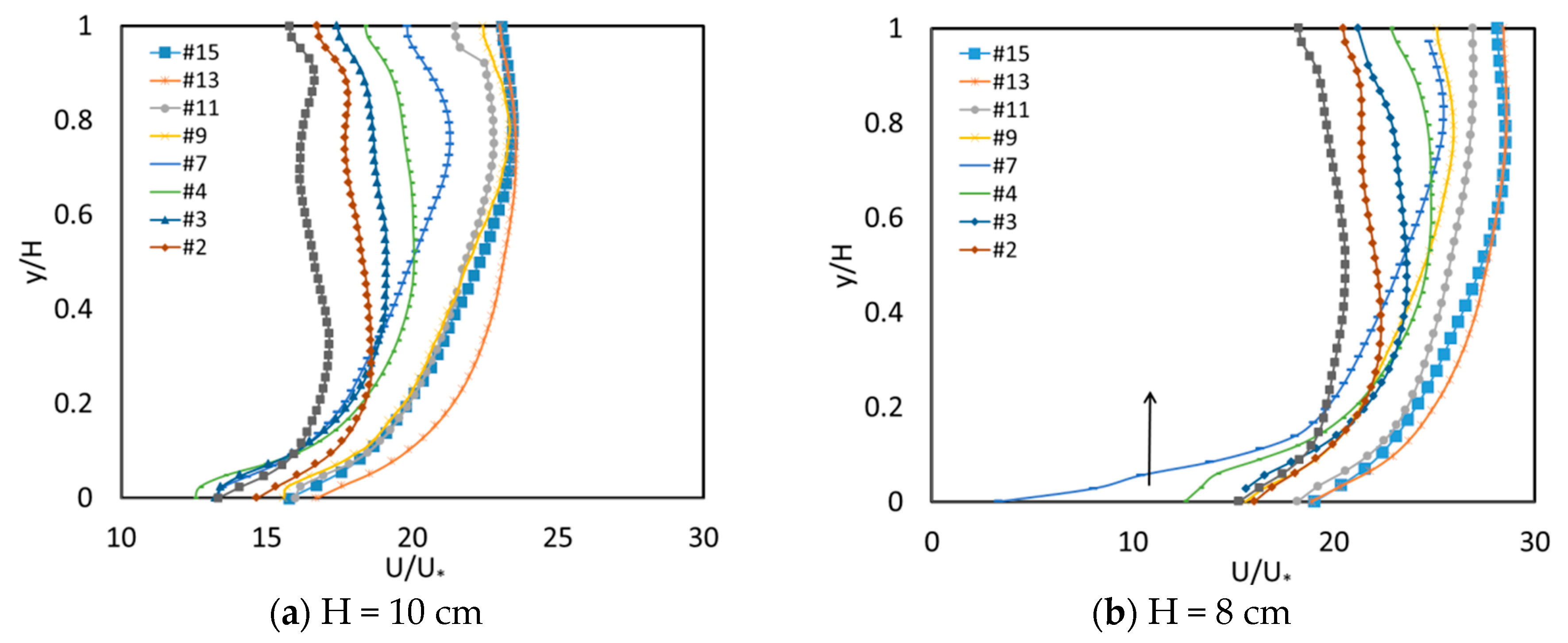
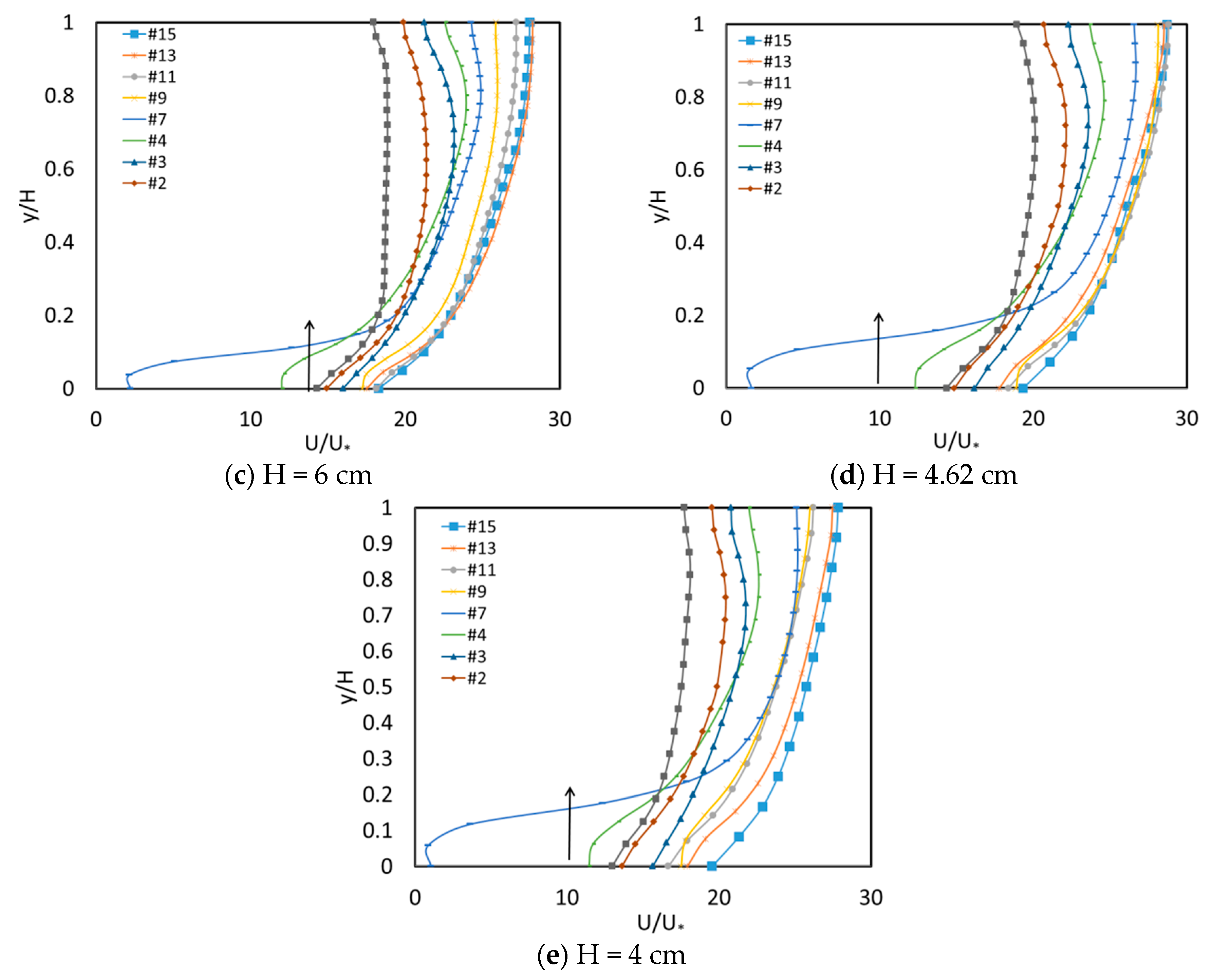
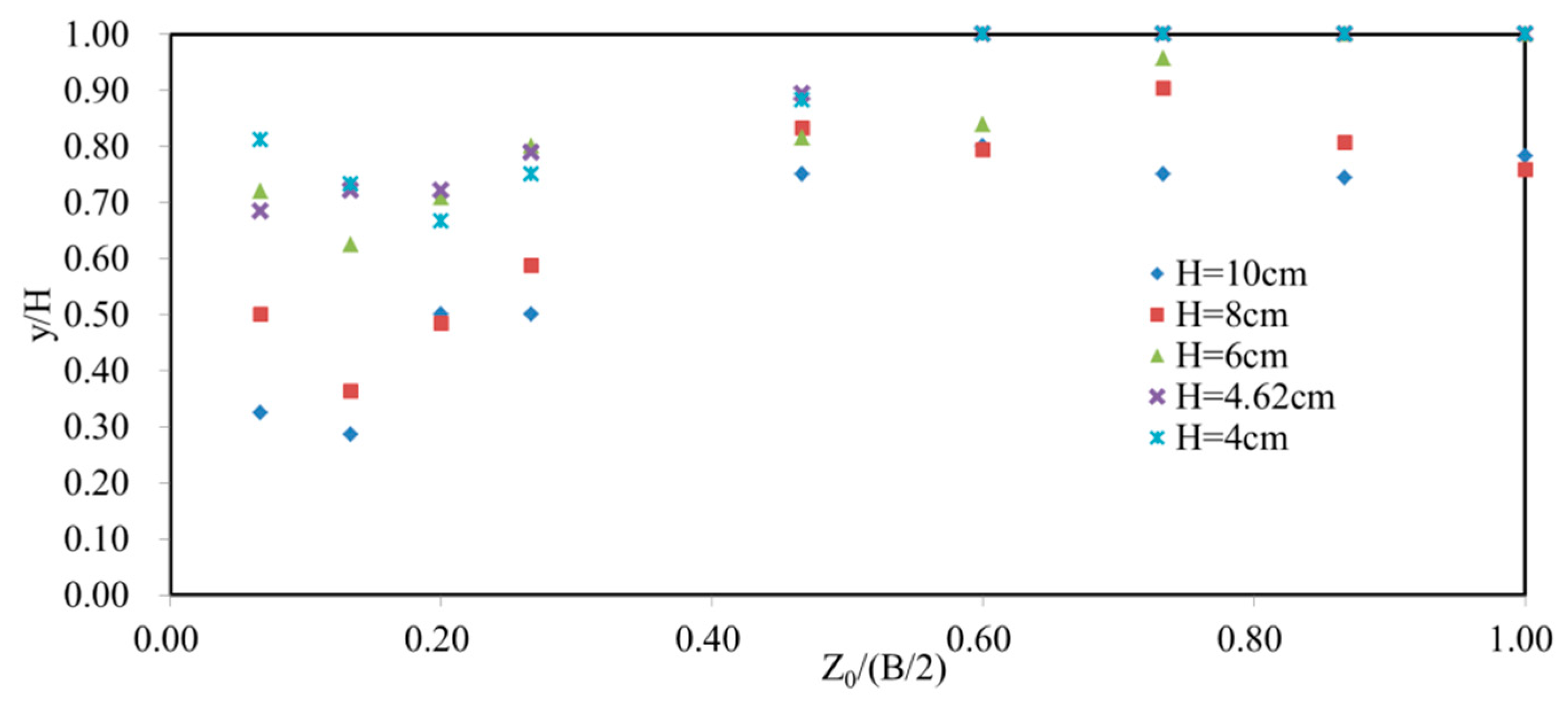
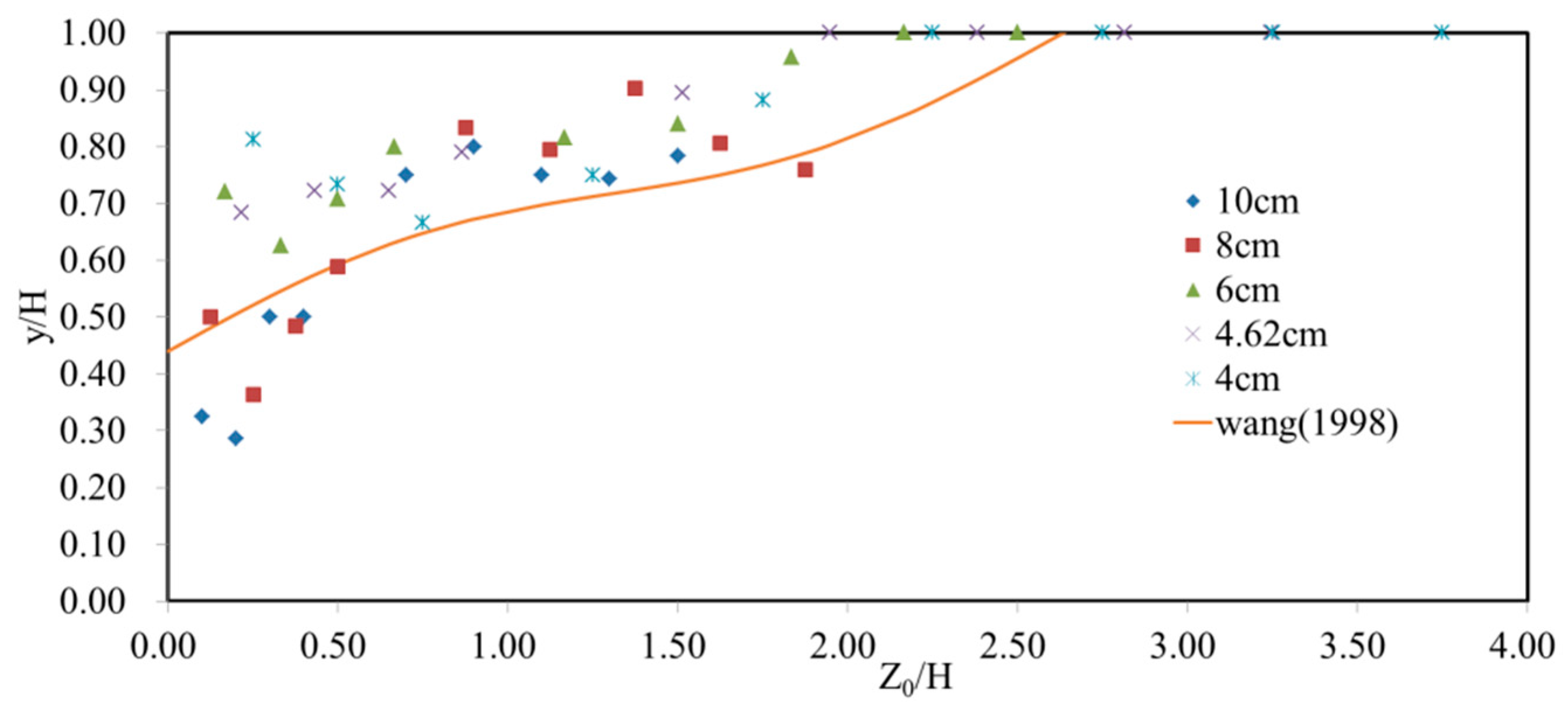
3.1. Effects of the Aspect Ratio on Stream-Wise Velocity Distribution

Figure 5 plots the stream wise velocity of cases 1 to 5 at different measuring sections against $y/H$, velocity was normalized by friction velocity. Figure 6 is the velocity contour map in the cross section. When the flow depth changes from 10 cm to 4 cm, stream-wise velocity profiles present a phenomenon of velocity dip, which indicates that the maximum velocity occurs below the surface. For H = 10 cm, 8 cm (in Figure 5a,b), the dip phenomenon appears in the entire cross section, which means that the flow can be regarded as completely 3D. With the decrease in flow depth, for H = 6 cm, 4.62 cm, and 4 cm (in Figure 5c–e), the dip phenomenon only occurs at the area near the side wall. The same phenomenon can also be seen in Figure 6. Previous studies have shown that the side wall effect increases with the distance from the central line. Therefore, in a relatively shallow and wide channel flow, a 2D flow region exists without the influence of side wall.

Velocity profiles in Figure 5 indicate that dip phenomenon closely relates to the distance from the side wall and also $B/H$ (aspect ratio). In Figure 7, the relative position of the maximum velocity of different measuring sections plotted against $Z_0/\left(B/2\right)$ in the cross section. For a given value of $B/H$, $\delta /H$ increase with $Z_0/\left(B/2\right)$. From Figure 7, under the influence of secondary flow, the position of the maximum velocity fluctuating along the horizontal axis. Velocity profiles acquired near the side wall present an evident feature of velocity dip. Combined with Figure 6, when $B/H$ is less than 5, the maximum velocity of the entire cross section occurs below the free surface, thereby presenting a completely 3D flow pattern. However, when $B/H$ is larger than 5, the near wall region is still under the influence of secondary flow, and a totally 2D flow only exists near the central line of the flume. The relative areas where 2D flow occurs expand with the aspect ratio. For a water depth of 6 cm, the dip phenomenon disappears when $Z_0/\left(B/2\right)\approx 0.8$, whereas for a water depth of 4 cm, the dip phenomenon disappears when $Z_0/\left(B/2\right)\approx 0.6$.

On the basis of numerous experimental data, Wang [29] proposed Equation (1) to predict the relative position of the maximum velocity. The influence of relative distance from the side wall and aspect ratio is considered and used as the parameter $Z_0/H$ which decides the dip position.

$$\frac{\delta }{H}=0.44+0.212\frac{Z_0}{H}+0.05\sin (\frac{2\pi }{2.6}\frac{Z_0}{H})$$

(1)

where $\delta$ represents the location of the maximum velocity. $Z_0$ is the distance from the sidewall. H denotes the flow depth. The above equation can be used under the condition that the aspect ratio is less than 5.2. The critical value of the aspect ratio is in consideration of the physical truth, when the aspect ratio is larger than 5.2, the calculated position of the maximum velocity will be above the free surface, which is inconsistent with the reality. Figure 8 presents the measured position of maximum velocity $y/H$ plotted against the value of $Z_0/H$ in half of the flume under different flow depth. The calculated value was presented for comparison. Comparing the experimental data with the calculated value, the application of sine function in Equation (1) obtains a desirable result. Figure 8 indicates that the dip phenomenon disappears at $Z_0/H$ = 2.25, that is, when $B/H$ ≥ 5, the side wall effect is too weak to exert influence on the stream-wise velocity distribution.

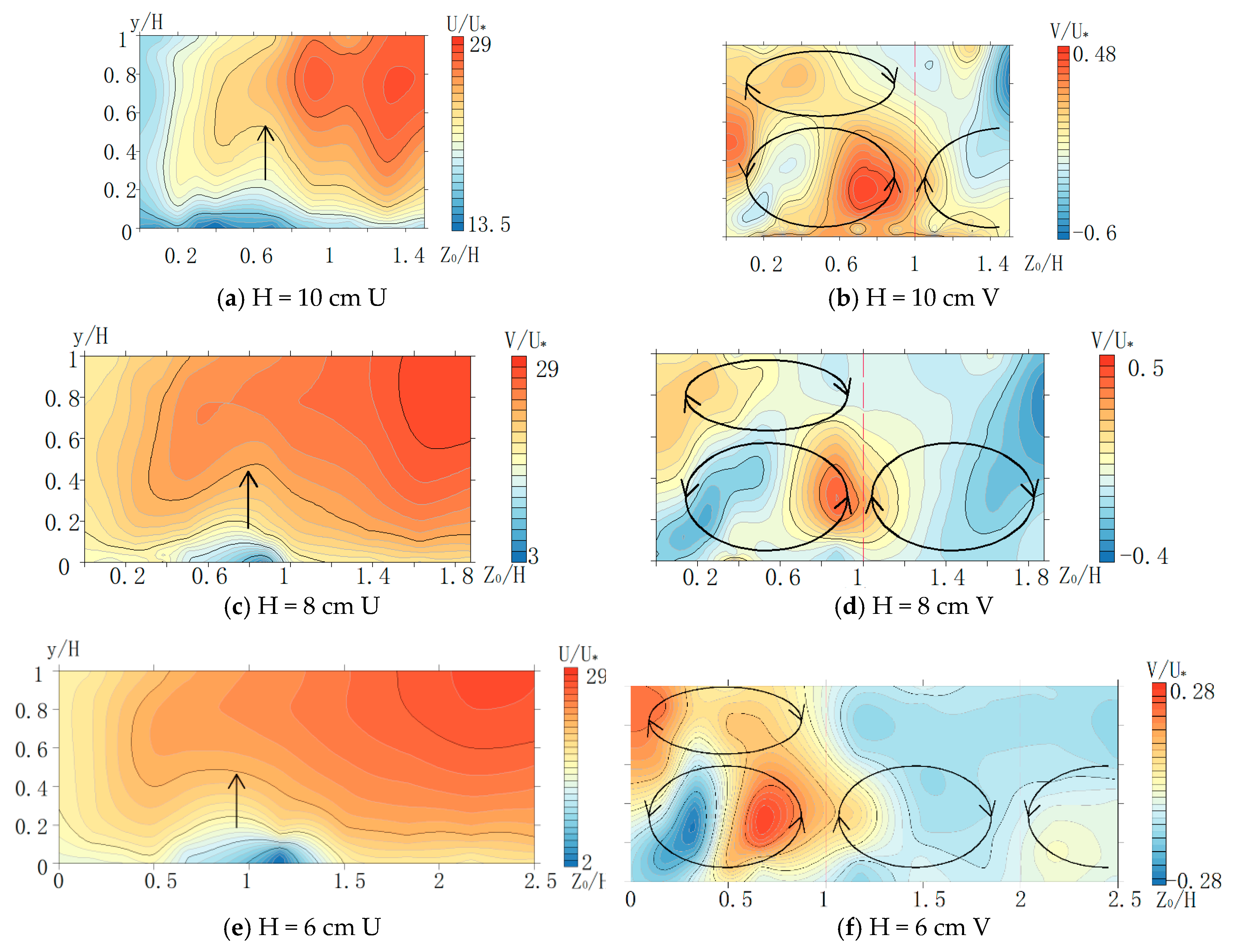
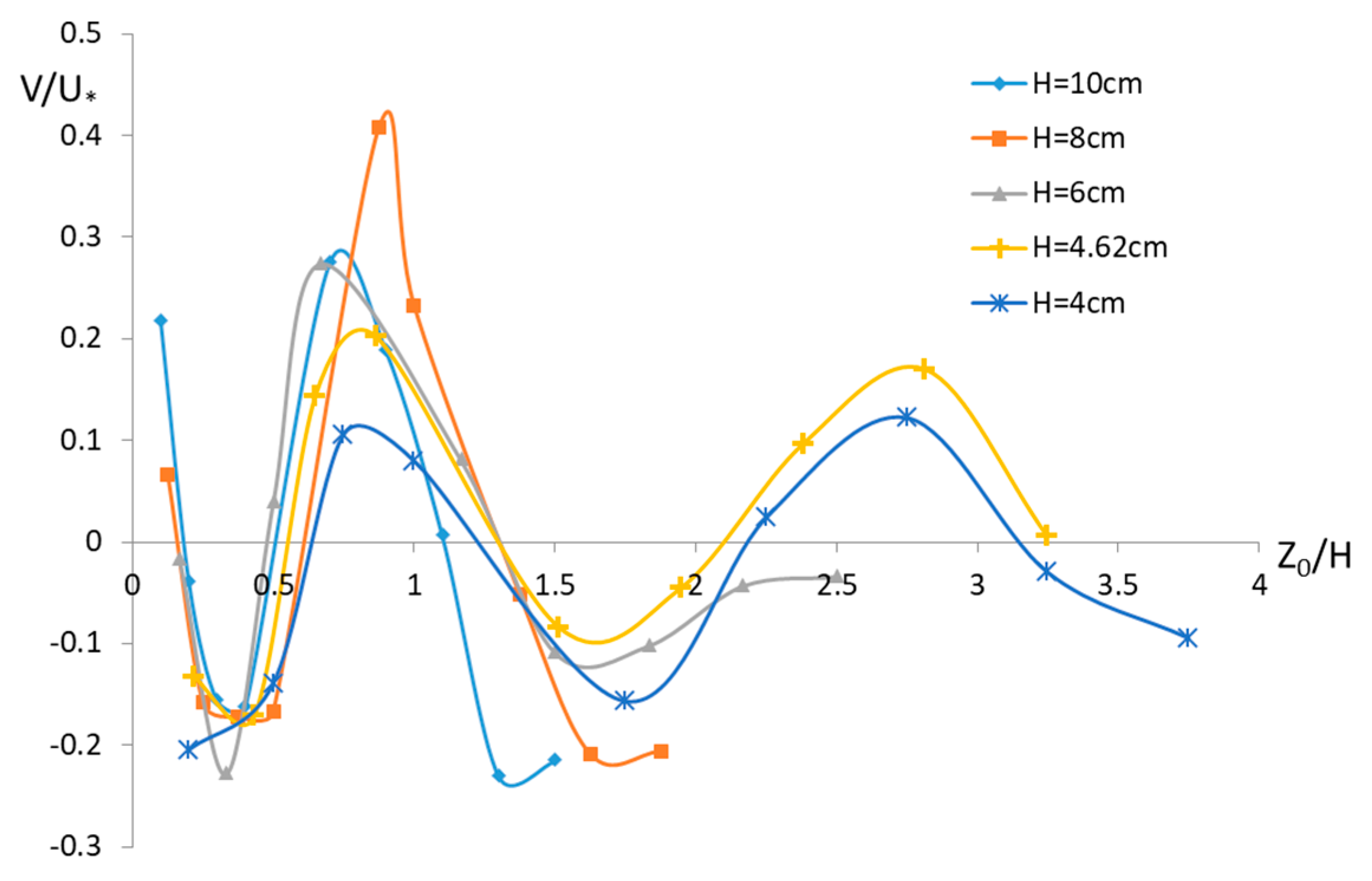
3.2. Effects of Aspect Ratio on Secondary Flow Cells

Nezu [2] stated that two vortices exist in the corner region, namely, upper and lower cells. High-speed fluid elements are carried by transverse motion through the surface toward the bed, and low-speed fluid elements are brought to the channel center. The distribution of vertical velocity which is normalized by friction velocity is shown in Figure 6b,f,h,j. Positive velocity value means upwards flow, whereas on the contrary, negative velocity value means downwards flow. A pair of upwards and downwards flow denotes the existence of a vortex in the corresponding region. In the light of this statement, the structure of secondary cells in the cross section is also represented by the curved line with an arrow in Figure 6.

In corner region, when flow depth changes from 10 cm to 4 cm (aspect ratio changes from 3 to 7.5), a pair of counter rotating vortices exist where the bottom one is larger than the upper one, leading to a three-dimensional flow pattern. However, just as Yang [10] proposed, the division-line that separates the neighboring secondary currents is not always identical to the bisector of the corner. Meanwhile, several upwelling and down-welling flow regions can be seen which distribute alternatively along the span wise. With the increase in aspect ratio, more up-welling and down-welling flow regions appear in the cross section, namely, multiple secondary cells. This finding is in accordance with the study of Christian’s in supercritical open channel flow [3] and Albayrak’s in open channel flow over rough bed [4]. Others applied direct numerical simulation in duct flow with increasing aspect ratio and they also found that the rich array of secondary vortices extending throughout the upper and lower walls of the duct [5,30]. Therefore, the effect of aspect ratio on the dynamics of secondary currents is significant. According to the distribution of up-welling and down-welling region, the brief structure of secondary cell is presented by curved line with arrow in Figure 6. Upwelling and downwelling region occur at the place with the same $Z_0/H$ value which means that the scale of secondary cell is controlled by flow depth. With the increase in aspect ratio, no obvious change in distribution pattern of secondary cells, and secondary cells do not stretch or compress significantly in span wise. The lateral dimension of the vortex is approximately equal to the flow depth. However, this is quite different from the result of direct numerical simulation in duct flow. Vinuesa [6,7] found that secondary vortices are much more elongated than the equivalent structures found in turbulent channel, and bottom vortex stretches toward the central line in a rectangular duct flow with the increase in aspect ratio.

Secondary currents exist in the cross section, which also slightly changes the isovel lines of stream wise velocity. In Figure 6, velocity contour lines ((a), (c), (e), (g), and (i)) are bugled near the bottom; this feature also happens in velocity profiles (Figure 5), which indicates the existence of secondary currents. In particular, comparing the velocity distributions in stream-wise and vertical directions in Figure 6, it can be seen that stream wise velocity isovel lines become bugled and concaved at places where upwelling and down-welling flows occur, respectively. Therefore, the contour map fluctuates laterally. However, with the increase in aspect ratio, isovel lines near the center region are smoothed without significant fluctuation. The reason is that the vertical flow intensity decreases with the distance from the side wall. When the aspect ratio is larger than 5, secondary currents near the flume center do not have an obvious effect on the main flow. Although the experiment ignores the influence of boundary roughness (side wall and bottom surface are both smooth), and the results remain consistent with those of previous studies. Although the number of secondary cells increases with the aspect ratio, the relative intensities of upwelling and down-welling flows are slightly decreased from the side wall to the flume center, and the effect of side wall on flow structure is reduced. Thus, when $Z_0/H$ > 5, no dip phenomenon occurs near the center region.

In Figure 6b,d,f,h,j, the maximum value of V appears around the place where $y/H$ = 0.4. Figure 9 plots the value of $\mathrm{V}/{\mathrm{U}}_{*}$ at $y/H$ = 0.4 along the span-wise direction for all five cases to investigate the influence of aspect ratio on secondary cells. By comparing the vertical velocity at $y/H$ = 0.4 in all 5 cases, the conclusion can be obtained that the strength of secondary flow is closely related to the aspect ratio. With the increase in aspect ratio, the value of $\mathrm{V}/{\mathrm{U}}_{*}$ decreases gradually, which means that upward and downward flows are weakened. Furthermore, the value of $\mathrm{V}/{\mathrm{U}}_{*}$ slightly decrease towards the flume center. Therefore, aspect ratio ($B/H$) and distance from the side wall ($Z_0/H$) exert a strong influence on secondary flow. The strength of secondary flow decreases with the increase in $B/H$ and $Z_0/H$.

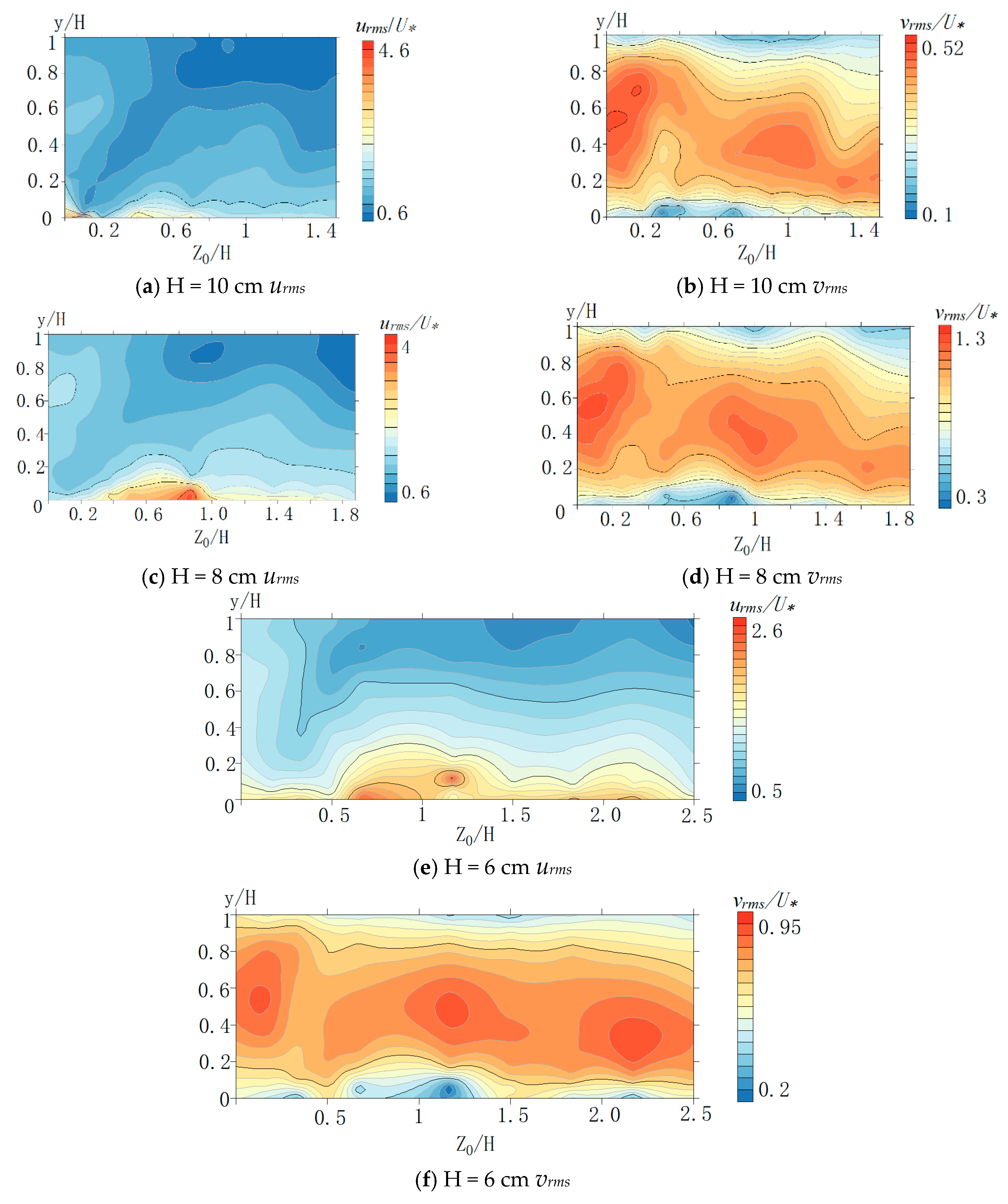
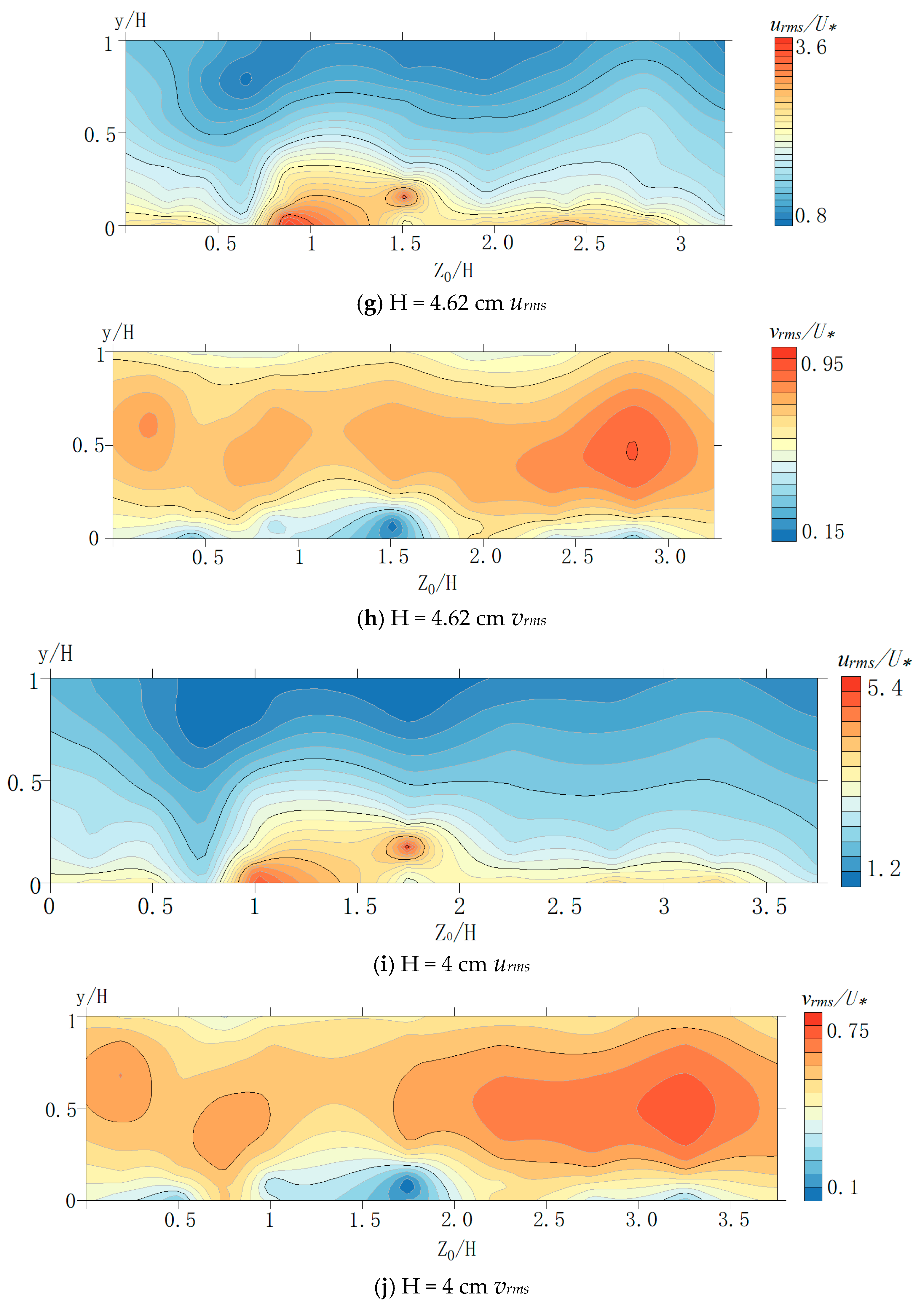
3.3. Effects of Aspect Ratio on Turbulence Intensity Distribution

The definition indicates that the value of turbulence intensity can be used as a characteristic value which can reflect the magnitude of velocity fluctuation. On the basis of the theory of statistics, the turbulence intensity is represented by the second-order central moment of the fluctuating velocity at any spatial point in the flow field, which can also be regarded as the degree of deviation of instantaneous velocity around the time-averaged velocity. Stream-wise and vertical turbulence intensity, expressed as $u_{rms}$ and $v_{rms}$ can be calculated by fluctuating velocity as follows:

$$u_{rms}=\sqrt{\frac{1}{N}{\displaystyle {\sum }_{i=1}^N{\left(u-U\right)}^2}}=\sqrt{\frac{1}{N}{\displaystyle {\sum }_{i=1}^{N}u{\prime }^2}}=\sqrt{\overline{u{\prime }^2}}$$

(2)

$$v_{rms}=\sqrt{\frac{1}{N}{\displaystyle {\sum }_{i=1}^N{\left(v-V\right)}^2}}=\sqrt{\frac{1}{N}{\displaystyle {\sum }_{i=1}^{N}v{\prime }^2}}=\sqrt{\overline{v{\prime }^2}}$$

(3)

As for the computing system of PIV, N denotes the sample size, i denotes the number of sampling points, $u$ and $v$ represent the instantaneous velocities of the sampling point, U and V represent the time-averaged velocities, $u_{rms}$ and $v_{rms}$ denote velocity fluctuating velocity in x and y direction respectively. Figure 10 plots the normalized turbulence intensity (both stream wise and vertical) of 5 cases in the cross section. Some conclusions are discussed in detail as follows.

The distribution of stream-wise turbulence intensity $u_{rms}$ increases from the free surface to the bottom and reaches the maximum value at $y/H$ = 0. This is different from the distribution of stream wise velocity U which increases with the distance from the bottom surface, whereas $u_{rms}$ presents a decrease tendency along this direction. This result is in accordance with the classical turbulence distribution and Zhong’s study in channel flow [31,32]. Turbulence intensity $u_{rms}$ is high in region with low stream wise velocity and low in region with high velocity. The isovel lines of turbulence intensity $u_{rms}$ are bulged near the bottom surface, which is similar to the velocity contour map in Figure 1b. This “bulging” feature is related to the secondary structure. The contour map of $v_{rms}$ distribution in the cross section at different water depths shows that the maximum vertical turbulence intensity occurs below the free surface, which is also in accordance with the experimental result of Zhong and Alamo [31,32]. This is what is called boundary restriction: (1) At the area near the free surface, upward and downward turbulence is restrained by surface wave and surface tension; therefore, turbulence intensity is decreased at the free surface. (2) At the area near the bottom surface, turbulence intensity $v_{rms}$ is also constrained due to the impenetrability of the boundary.

With the increase in aspect ratio ($B/H$), no evident difference of $u_{rms}$ and $v_{rms}$ distribution is observed in all 5 cases; therefore, $B/H$ do not exert great influences on the pattern of stream-wise turbulence intensity and vertical turbulence intensity distribution. However, secondary flows do have influence on the turbulence intensity. Secondary flow intensify the mixing of flow particles which intensify pressure fluctuating at each point. Pressure pulsation is the direct cause of turbulent kinetic energy redistribution. Therefore, considering the influence of secondary flow, secondary flow may be essential to the redistribution of turbulence intensity.

4. Conclusions

In this study, the dynamics of secondary currents in an open channel flow whose aspect ratio changes from $B/H$ = 3 to $B/H$ = 7.5 over a smooth bottom surface are investigated using the PIV system. Technically, secondary flows widely exist in turbulent channel and duct flow due to the effect of the side wall. The structure and intensity of secondary currents are influenced by boundary conditions, especially by aspect ratio. This paper mainly discussed the influence of aspect ratio on secondary flows. The results are in great agreement with previous theories and investigations, and the conclusions of this paper are as follow:

• The existence of secondary cells in the corner region is verified through PIV measurements: two counter-rotating vortices exist near the free surface and near the bottom. Dip phenomenon is observed wherein the maximum velocity occurs below the surface and the velocity contour is “bugled” near the bed at the corner region. When aspect ratio is $B/H$ ≤ 5, the velocity dip is present in the entire cross section; however, when aspect ratio is $B/H$ ≥ 5, the dip phenomenon disappears at $Z_0/H$ = 2.25.
• There are upwelling and down-welling regions that exist along the span-wise which indicates the structure of a secondary flow. Secondary flow cells are lined up along the span-wise and show an increasing tendency with the aspect ratio. Vertical velocity distribution for different water depths indicates that the aspect ratio does not have a significant effect on the structure of secondary flow cells. The vortices do not stretch or compress with the change in aspect ratio, and the size of secondary flow cells is closely related to the flow depth. For different $B/H$, upwelling and downwelling region occur at the place with the same $Z_0/H$ value which means that the scale of secondary cell is controlled by flow depth.
• Normalized vertical velocity is used to characterize the intensity of secondary flows. With the increase in aspect ratio, the strength of secondary flow decreases. Furthermore, when $B/H$ unchanged, the strength of secondary flow also decreases from the side wall to the flume center, therefore, no evident velocity dip phenomenon occurs at the center region when secondary flow does not have a significant effect on the main flow.
• The distribution of turbulence intensity is influenced by secondary flow. $u_{rms}$ increase from the surface towards the bottom and approach the maximum value at the $y/H$ = 0. $v_{rms}$ is restrained by bottom and free surface, the maximum value occurs below the surface.