An Adaptive Basin Management Rule to Improve Water Allocation Resilience under Climate Variability and Change—A Case Study in the Laja Lake Basin in Southern Chile
Abstract
1. Introduction
2. Methods
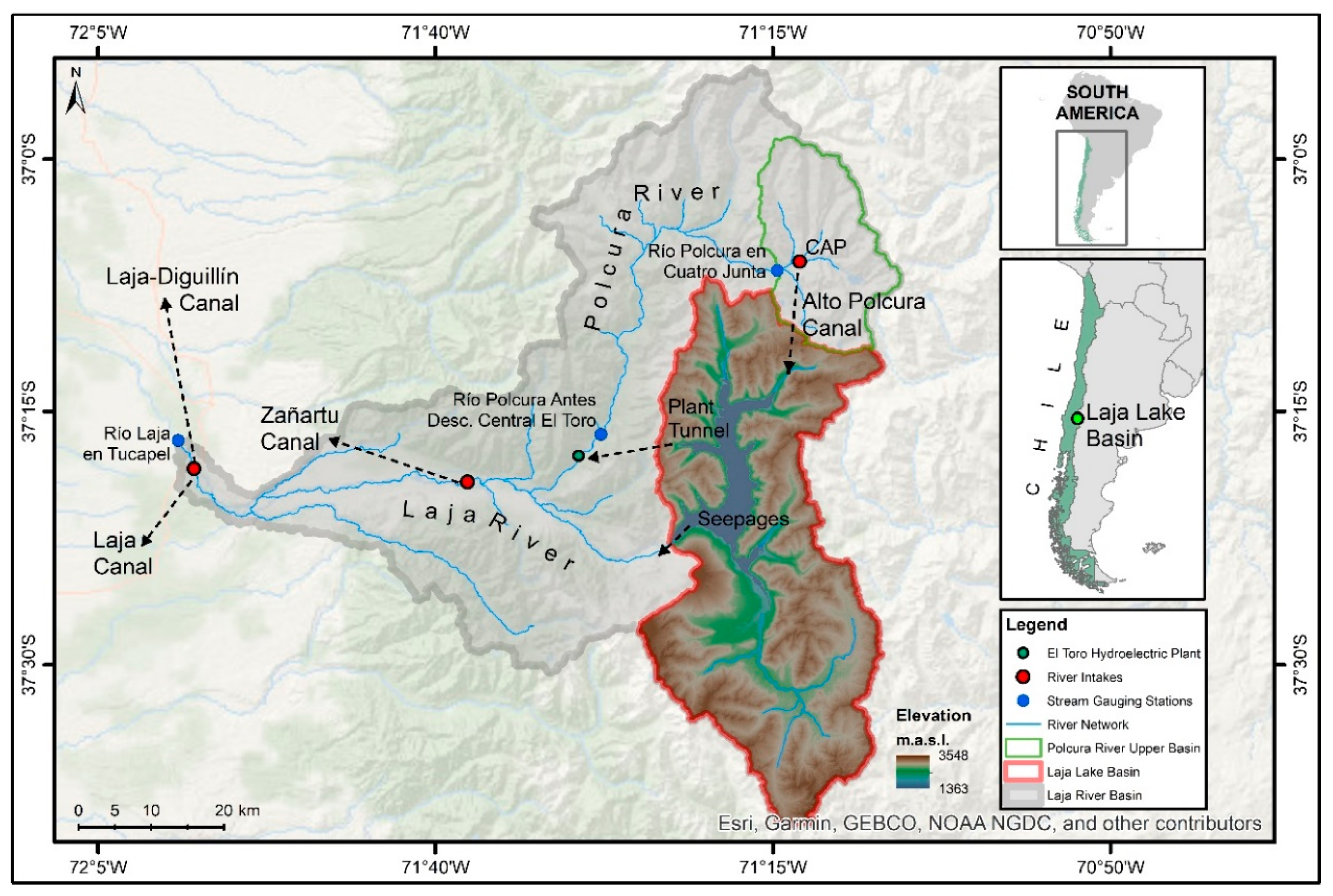
2.1. Study Area and Context
2.2. Description of the Former and New Operation Rule
- (i)
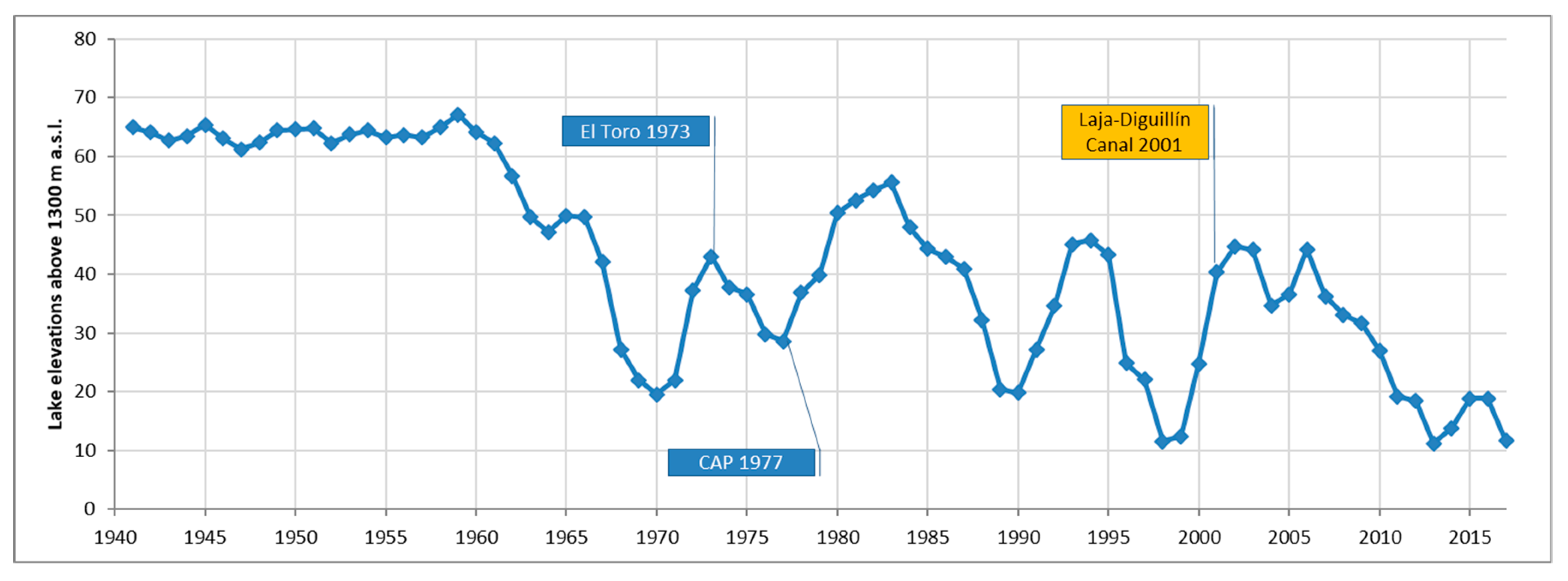
- Simulation of continuing under the current operation rule for water allocation: The 1958 agreement led to the current situation of the lake. Simulations showed the existence of an overallocation of water. Therefore, continuing under this water allocation rule would generate more conflicts among users, lower lake levels and greater uncertainties.
- (ii)
- Allocation based on predictions. The 1958 allocation rule was based on the prediction of the next hydrological year. However, such predictions are subject to high uncertainty due to climate variability and would constantly cause the overexploitation of the lake.
- (iii)
- Allocation based on current water availability. This analysis helped bring about a turning point in the discussion on a new agreement. Simulations of water allocation based on current water availability (not predictions) showed that system stability could be reached. From this point forward, the level of stability pursued was discussed.
- (iv)
- Lake stability and water security for Laja Lake users. Once a lake stability criterion was defined (point iii), the discussion moved to water security and priority of uses. As water for irrigation and other purposes is also used for energy, irrigation and tourism were seen as the most sensitive-to-conflict water uses. In addition, irrigation requires minimum water allocation security in order to plan investments and crops. Therefore, a minimum base of water allocation for irrigation and landscape (tourism) uses was defined, and after covering this minimum, a combined allocation for energy and irrigation was agreed upon. In the case of wet hydrological years and abundant water availability in the lake for water allocation, more water for energy would be allocated in order to not restrict energy production under favorable conditions.
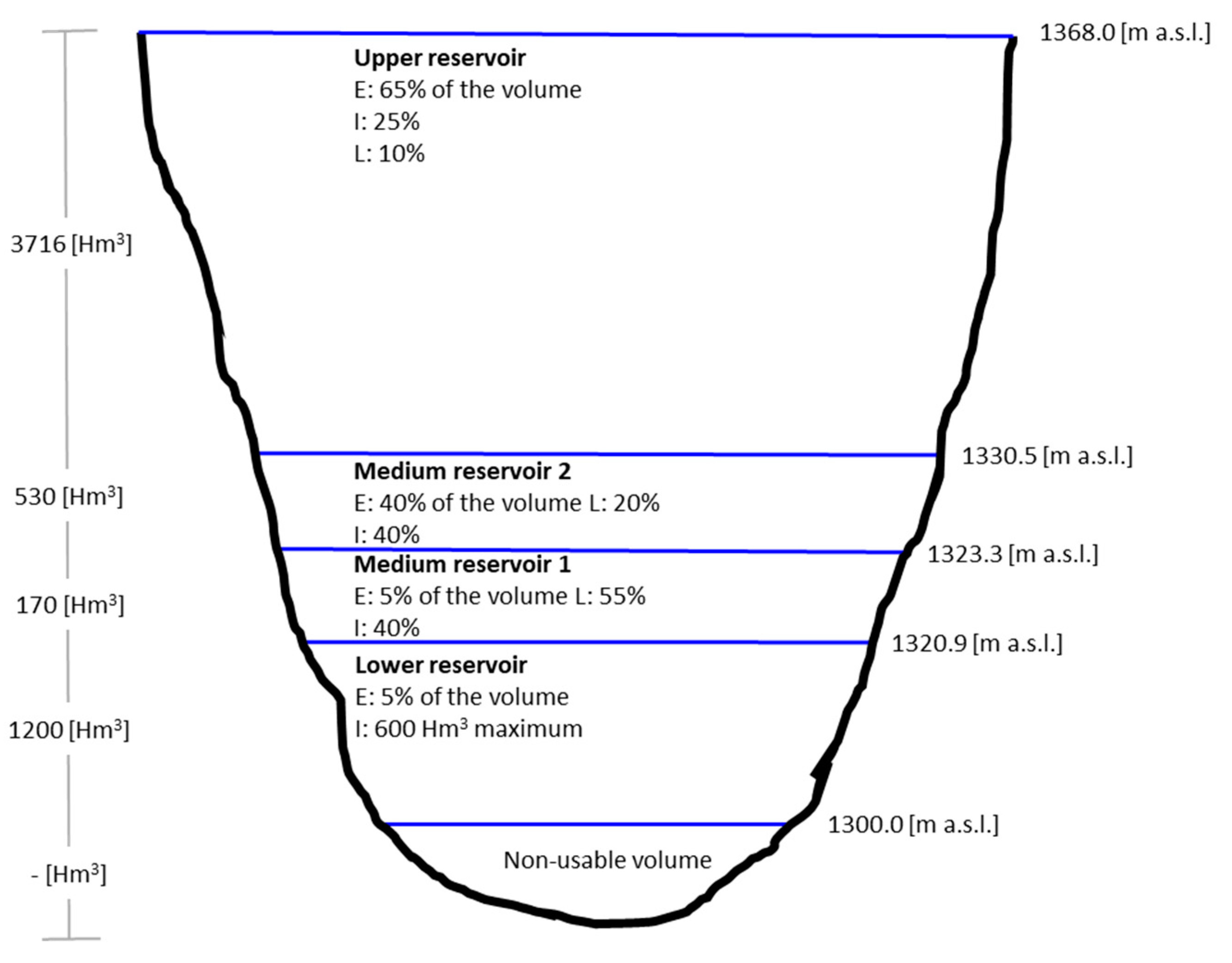
2.3. Water Balance Model Descrption
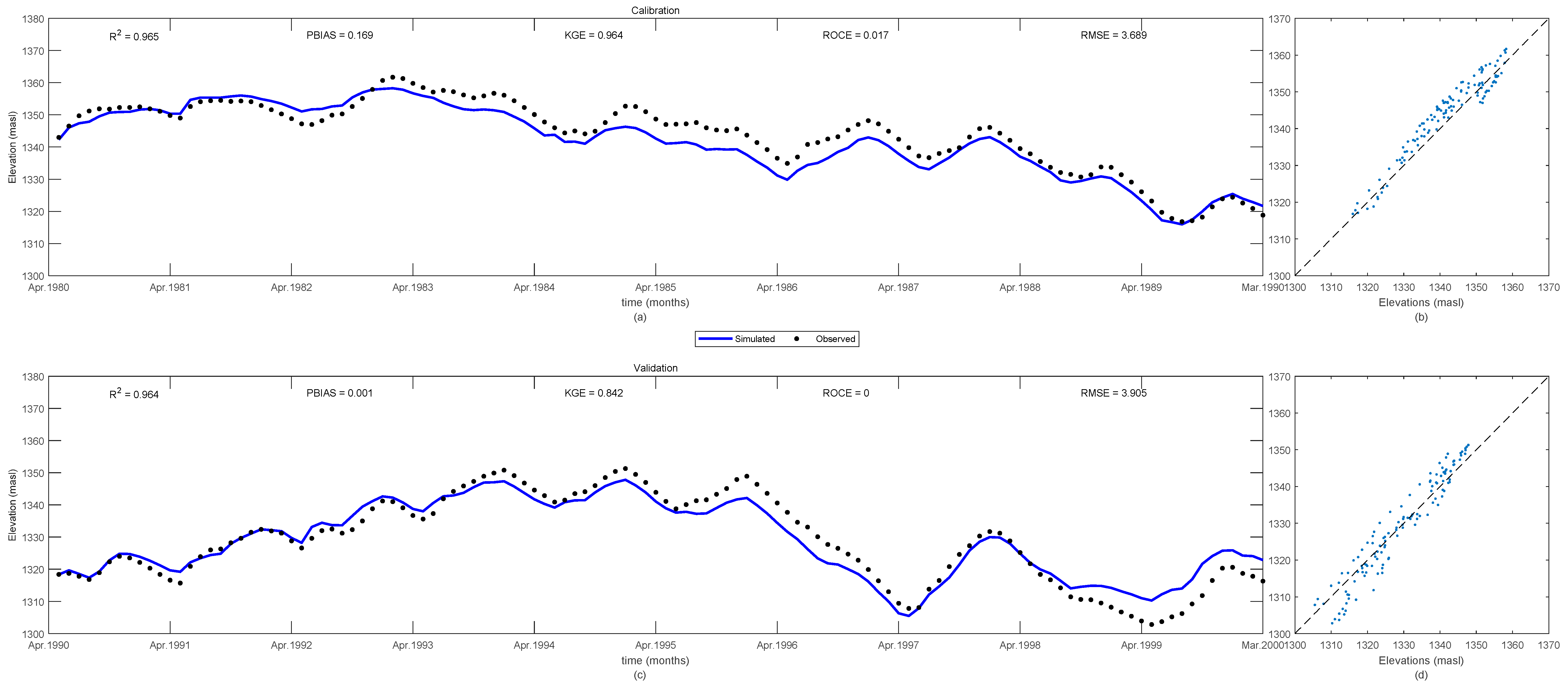
2.4. Modeling Approach and Data
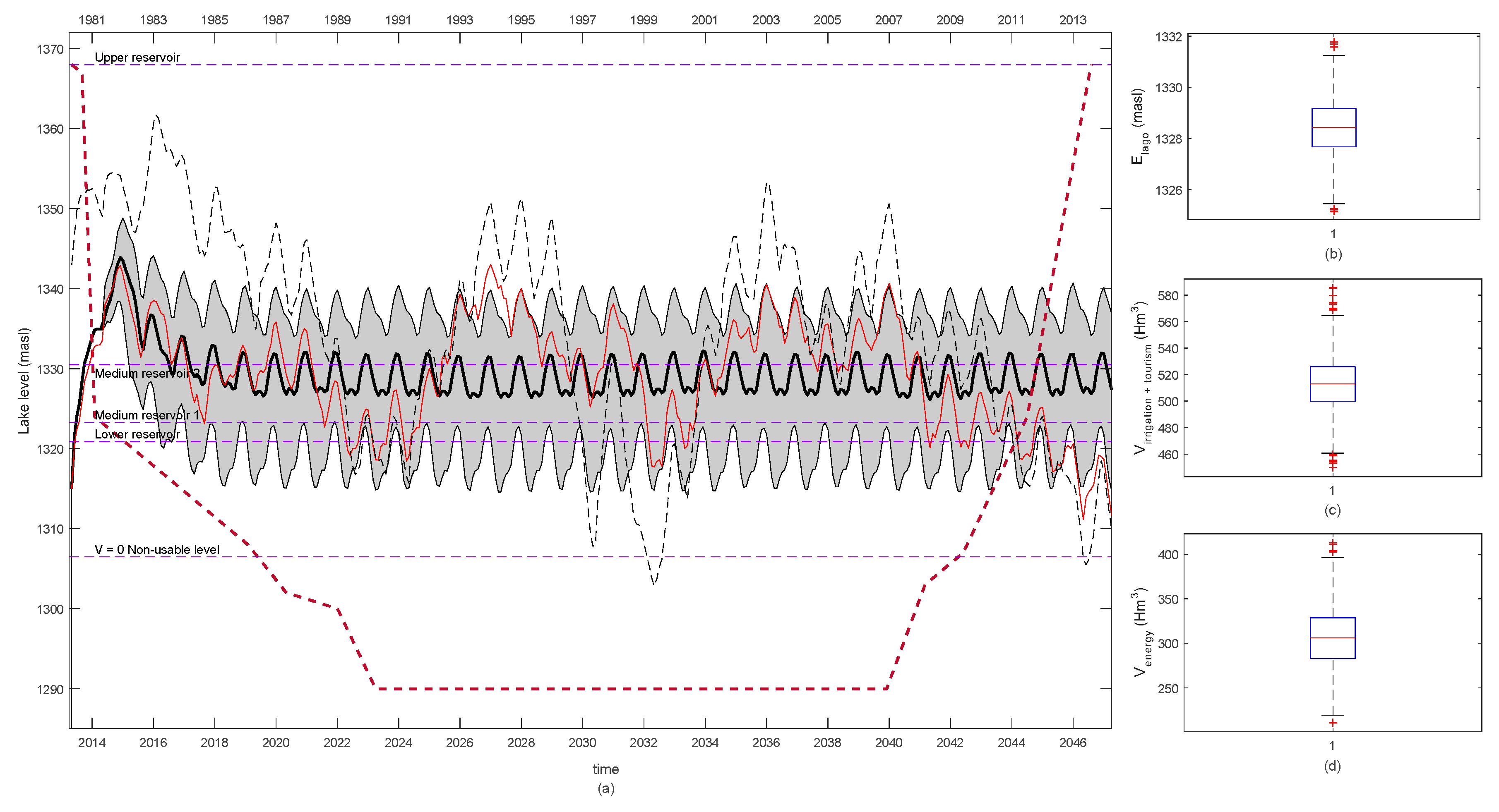
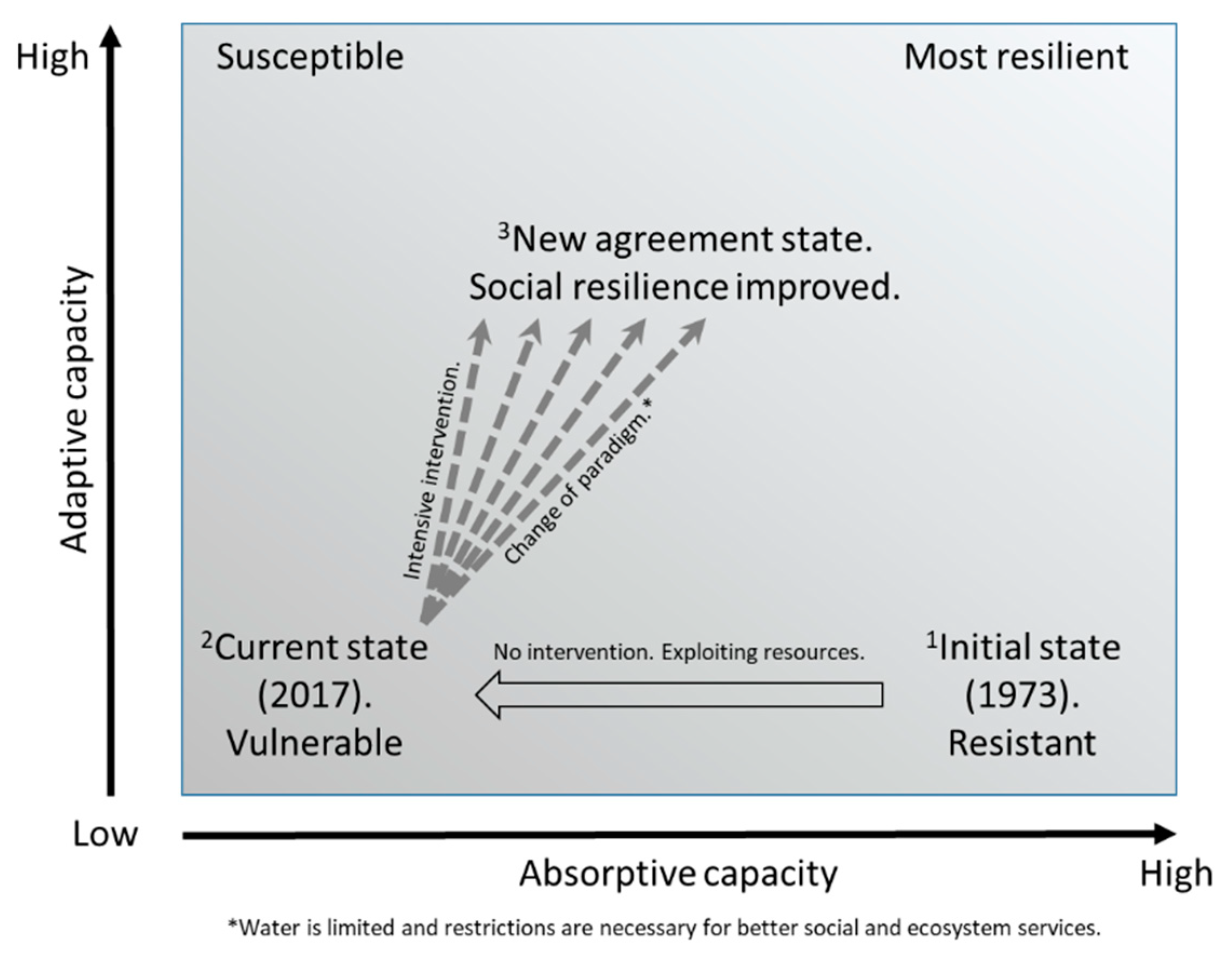
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Mishra, A.K.; Singh, V.P. A review of drought concepts. J. Hydrol. 2010, 391, 202–216. [Google Scholar] [CrossRef]
- Xu, J.; Ma, N.; Lv, C. Dynamic equilibrium strategy for drought emergency temporary water transfer and allocation management. J. Hydrol. 2016, 539, 700–722. [Google Scholar] [CrossRef]
- Muller, M. Adapting to climate change: Water management for urban resilience. Environ. Urban. 2007, 19, 99–113. [Google Scholar] [CrossRef]
- Piao, S.; Ciais, P.; Huang, Y.; Shen, Z.; Peng, S.; Li, J.; Zhou, L.; Liu, H.; Ma, Y.; Ding, Y.; et al. The impacts of climate change on water resources and agriculture in China. Nature 2010, 467, 43. [Google Scholar] [CrossRef]
- Vörösmarty, C.J.; Green, P.; Salisbury, J.; Lammers, R.B. Global water resources: Vulnerability from climate change and population growth. Science 2000, 289, 284–288. [Google Scholar] [CrossRef]
- Gosling, S.N.; Arnell, N.W. A global assessment of the impact of climate change on water scarcity. Clim. Chang. 2016, 134, 371–385. [Google Scholar] [CrossRef]
- Fischer, E.M.; Knutti, R. Anthropogenic contribution to global occurrence of heavy-precipitation and high-temperature extremes. Nat. Clim. Chang. 2015, 5, 560. [Google Scholar] [CrossRef]
- Grimm, A.M. Interannual climate variability in South America: Impacts on seasonal precipitation, extreme events, and possible effects of climate change. Stoch. Env. Res. Risk A 2011, 25, 537–554. [Google Scholar] [CrossRef]
- Li, M.; Guo, P.; Singh, V.P. An efficient irrigation water allocation model under uncertainty. Agric. Syst. 2016, 144, 46–57. [Google Scholar] [CrossRef]
- Moradkhani, H.; Sorooshian, S.; Gupta, H.; Houser, P.R. Dual state-parameter estimation of hydrological models using ensemble Kalman filter. Adv. Water Resour. 2005, 28, 135–147. [Google Scholar] [CrossRef]
- Renard, B.; Dmitri Kavetski, D.; Kuczera, G.; Thyer, M.; Franks, S.W. Understanding predictive uncertainty in hydrologic modeling: The challenge of identifying input and structural errors. Water Resour. Res. 2010, 46, W05521. [Google Scholar] [CrossRef]
- Beven, K. A manifesto for the equifinality thesis. J. Hydrol. 2006, 320, 18–36. [Google Scholar] [CrossRef]
- Muñoz, E.; Rivera, D.; Vergara, F.; Tume, P.; Arumí, J.L. Identifiability analysis: Towards constrained equifinality and reduced uncertainty in a conceptual model. Hydrol. Sci. J. 2014, 59, 1690–1703. [Google Scholar] [CrossRef]
- Speed, R.; Yuanyuan, L.; Zhiwei, Z.; Le Quesne, T.; Pegram, G. Basin Water Allocation Planning: Principles, Procedures and Approaches for Basin Allocation Planning; UNESCO: Paris, France, 2013. [Google Scholar]
- Xiao, Y.; Hipel, K.W.; Fang, L. Incorporating water demand management into a cooperative water allocation framework. Water Resour. Manag. 2016, 30, 2997–3012. [Google Scholar] [CrossRef]
- Han, Y.; Huang, Y.F.; Wang, G.Q.; Maqsood, I. A multi-objective linear programming model with interval parameters for water resources allocation in Dalian city. Water Resour. Manag. 2011, 25, 449–463. [Google Scholar] [CrossRef]
- Yang, Y.C.E.; Zhao, J.; Cai, X. Decentralized Optimization Method for Water Allocation Management in the Yellow River Basin. J. Water Resour. Plan. Manag. 2011, 138, 313–325. [Google Scholar] [CrossRef]
- Yang, Y.S.; Kalin, R.M.; Zhang, Y.; Lin, X.; Zou, L. Multi-objective optimization for sustainable groundwater resource management in a semiarid catchment. Hydrol. Sci. J. 2009, 46, 55–72. [Google Scholar] [CrossRef]
- Reis, L.; Bessler, F.; Walters, G.; Savic, D. Water supply reservoir operation by combined genetic algorithm–linear programming (GA-LP) approach. Water Resour. Manag. 2006, 20, 227–255. [Google Scholar] [CrossRef]
- Goyal, M.K.; Ojha, C.; Singh, R.; Swamee, P.; Nema, R. Application of ANN, fuzzy logic and decision tree algorithms for the development of reservoir operating rules. Water Resour. Manag. 2013, 27, 911–925. [Google Scholar] [CrossRef]
- Davijani, M.H.; Banihabib, M.E.; Anvar, A.N.; Hashemi, S.R. Multi-objective optimization model for the allocation of water resources in arid regions based on the maximization of socioeconomic efficiency. Water Resour. Manag. 2016, 30, 927–946. [Google Scholar] [CrossRef]
- Islam, Z.; Gan, T.Y. Water Allocation Challenges of South Saskatchewan River Basin under the Combined Impacts of Climate Change and El Nino Southern Oscillation. J. Water Resour. Plan. Manag. 2016, 142, 4016039. [Google Scholar] [CrossRef]
- Culley, S.; Noble, S.; Yates, A.; Timbs, M.; Westra, S.; Maier, H.R.; Giuliani, M.; Castelletti, A. A bottom-up approach to identifying the maximum operational adaptive capacity of water resource systems to a changing climate. Water Resour. Res. 2016, 52, 6751–6768. [Google Scholar] [CrossRef]
- Fiering, M.B. Streamflow Synthesis; Harvard University Press: Cambridge, MA, USA, 1967. [Google Scholar]
- Fiering, M.B. Forecasts with varying reliability. J. Sanit. Eng. Div. 1969, 95, 629–644. [Google Scholar]
- Fiering, M.B. Alternative indices of resilience. Water Resour. Res. 1982, 18, 33–39. [Google Scholar] [CrossRef]
- Fiering, M.B. Estimates of resilience indices by simulation. Water Resour. Res. 1982, 18, 41–50. [Google Scholar] [CrossRef]
- Fiering, M.B. Estimating resilience by canonical analysis. Water Resour. Res. 1982, 18, 51–57. [Google Scholar] [CrossRef]
- Rodina, L.; Baker, L.A.; Galvin, M.; Goldin, J.; Harris, L.; Manungufala, T.; Musemwa, M.; Sutherland, C.; Ziervogel, G. Water, equity and resilience in Southern Africa: Future directions for research and practice. Curr. Opin. Environ. Sustain. 2017, 26–27, 143–151. [Google Scholar] [CrossRef]
- Fiering, M.B.; Holling, C.S. Management and standards for perturbed ecosystems. Agro Ecosyst. 1974, 1, 301–321. [Google Scholar] [CrossRef]
- Fiering, M.B. The role of systems analysis in water program development. Nat. Resour. J. 1976, 16, 759–771. [Google Scholar]
- Hashimoto, T.; Stedinger, J.R.; Loucks, D.P. Reliability, resiliency, and vulnerability criteria for water resource system performance evaluation. Water Resour. Res. 1982, 18, 14–20. [Google Scholar] [CrossRef]
- Pimm, S.L. The complexity and stability of ecosystems. Nature 1984, 307, 321–326. [Google Scholar] [CrossRef]
- Quinlan, A.E.; Berbés-Blázquez, M.; Haider, L.J.; Peterson, G.D. Measuring and assessing resilience: Broadening understanding through multiple disciplinary perspectives. J. Appl. Ecol. 2016, 53, 677–687. [Google Scholar] [CrossRef]
- Shin, S.; Lee, S.; Judi, D.R.; Parvania, M.; Goharian, E.; McPherson, T.; Burian, S.J. A Systematic Review of Quantitative Resilience Measures for Water Infrastructure Systems. Water 2018, 10, 164. [Google Scholar] [CrossRef]
- Asefa, T.; Clayton, J.; Adams, A.; Anderson, D. Performance evaluation of a water resources system under varying climatic conditions: Reliability, resilience, vulnerability and beyond. J. Hydrol. 2014, 508, 53–65. [Google Scholar] [CrossRef]
- Chanda, K.; Maity, R.; Sharma, A.; Mehrotra, R. Spatiotemporal variation of long-term drought propensity through reliability-resilience-vulnerability based drought management index. Water Resour. Res. 2014, 50, 7662–7676. [Google Scholar] [CrossRef]
- Mao, F.; Clark, J.; Karpouzoglou, T.; Dewulf, A.; Buytaert, W.; Hannah, D. HESS Opinions: A conceptual framework for assessing socio-hydrological resilience under change. Hydrol. Earth Syst. Sci. 2017, 21, 3655–3670. [Google Scholar] [CrossRef]
- Holling, C.S. Adaptive Environmental Assessment and Management; Blackburn Press: Caldwell, New York, NY, USA, 1978. [Google Scholar]
- Pretty, J.N. Participatory learning for sustainable agriculture. World Dev. 1995, 23, 1247–1263. [Google Scholar] [CrossRef]
- Garreaud, R. The Andes climate and weather. Adv. Geosci. 2009, 7, 1–9. [Google Scholar] [CrossRef]
- Montecinos, A.; Aceituno, P. Seasonality of the ENSO-related rainfall variability in central Chile and associated circulation anomalies. J. Clim. 2003, 16, 281–296. [Google Scholar] [CrossRef]
- Thiele, R.; Moreno, H.; Elgueta, S.; Lahsen, A.; Rebolledo, S.; Petit-Breuilh, M.E. Evolución geológico-geomorfológica cuaternaria del tramo superior del valle del río Laja. Rev. Geol. Chile 1998, 25, 229–253. (In Spanish) [Google Scholar] [CrossRef]
- Dirección Nacional de Riego—Empresa Nacional de Electricidad SA. Convenio de Riego Ad-Referéndum sobre la regulación del Río Laja; Dirección Nacional de Riego—Empresa Nacional de Electricidad SA: Santiago, Chile, 1958. (In Spanish) [Google Scholar]
- Garreaud, R. Cambio Climático: Bases Físicas e Impactos en Chile. Rev. Tierra Adentro 2011, 93, 1–14. [Google Scholar]
- Garreaud, R.D.; Alvarez-Garreton, C.; Barichivich, J.; Boisier, J.P.; Duncan, C.; Galleguillos, M.; Zambrano-Bigiarini, M. The 2010–2015 megadrought in central Chile: Impacts on regional hydroclimate and vegetation. Hydrol. Earth Syst. Sci. 2017, 21, 6307–6327. [Google Scholar] [CrossRef]
- Ministerio de Obras Públicas (MOP). Guía Para la Explotación del Lago Laja; Gobierno de Chile, Ministerio de Obras Públicas, Dirección de Obras Hidráulicas-Endesa: Santiago, Chile, 2018. (In Spanish)
- Muñoz, E. Desarrollo de un Modelo Hidrológico como Herramienta de Apoyo Para la Gestión del Agua. Aplicación a la Cuenca del Río Laja, Chile. Master’s Thesis, Universidad de Cantabria, Santander, Cantabria, Spain, 2010. (In Spanish). [Google Scholar]
- Muñoz, E.; Acuña, M.; Lucero, J.; Rojas, I. Correction of Precipitation Records through Inverse Modeling in Watersheds of South-Central Chile. Water 2018, 10, 1092. [Google Scholar] [CrossRef]
- Parra, V.; Fuentes-Aguilera, P.; Muñoz, E. Identifying advantages and drawbacks of two hydrological models based on a sensitivity analysis: A study in two Chilean watersheds. Hydrol. Sci. J. 2018, 63, 1831–1843. [Google Scholar] [CrossRef]
- Muñoz, E.; Arumí, J.L.; Wagener, T.; Oyarzún, R.; Parra, V. Unraveling complex hydrogeological processes in Andean basins in south-central Chile: An integrated assessment to understand hydrological dissimilarity. Hydrol. Process. 2016, 30, 4934–4943. [Google Scholar] [CrossRef]
- Rango, A.; Martinec, J. Revisiting the degree-day method for snowmelt computations. J. Am. Water Resour. Assoc. 1995, 31, 657–669. [Google Scholar] [CrossRef]
- Ministerio de Obras Públicas (MOP). Guía Para la Explotación del Lago Laja; Gobierno de Chile, Ministerio de Obras Públicas, Dirección de Obras Hidráulicas-Endesa: Santiago, Chile, 2007. (In Spanish)
- Ministerio de Obras Públicas (MOP). Guía Para la Explotación del Lago Laj; Gobierno de Chile, Ministerio de Obras Públicas, Dirección de Obras Hidráulicas-Endesa: Santiago, Chile, 2014. (In Spanish)
- Gupta, H.V.; Kling, H.; Yilmaz, K.K.; Martinez, G.F. Decomposition of the mean squared error and NSE performance criteria: Implications for improving hydrological modelling. J. Hydrol. 2009, 377, 80–91. [Google Scholar] [CrossRef]
- Nash, J.E.; Sutcliffe, J.V. River Flow Forecasting Through Conceptual Models, Part I, A Discussion of Principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Wagener, T.; McIntyre, N.; Lees, M.J.; Wheater, H.S.; Gupta, H.V. Towards reduced uncertainty in conceptual rainfall-runoff modelling: Dynamic identifiability analysis. Hydrol. Process. 2003, 17, 455–476. [Google Scholar] [CrossRef]
- Yilmaz, K.; Vrugt, J.A.; Gupta, H.V.; Sorooshian, S. Model calibration in watershed hydrology. In Advances in Databased Approaches for Hydrologic Modeling and Forecasting; Sivakumar, B., Berndtsson, R., Eds.; World Scientific: Hackensack, NJ, USA, 2010; pp. 53–105. [Google Scholar]
- Garreaud, R.D.; Vuille, M.; Compagnucci, R.H.; Marengo, J. Present-day South American climate. Palaeogeogr. Palaeoclimatol. Palaeoecol. 2009, 281, 180–195. [Google Scholar] [CrossRef]
- Beven, K.; Binley, A. The future of distributed models: Model calibration and uncertainty prediction. Hydrol. Process. 1992, 6, 279–298. [Google Scholar] [CrossRef]
- Willmott, C.J.; Matsuura, K. Terrestrial Air Temperature and Precipitation: 1900–2014 Gridded Monthly Time Series, Version 4.01; University of Delaware: Newark, DE, USA, 2014. [Google Scholar]
- Muñoz, E.; Arumí, J.L.; Rivera, D.; Montecinos, A.; Bilib, M.; Álvarez, C. Gridded data for a hydrological model in a scarce-data basin. Proc. Inst. Civ. Eng. Water 2012, 167, 249–258. [Google Scholar] [CrossRef]
- Thornthwaite, C.W. An approach toward a rational classification of climate. Geogr. Rev. 1948, 38, 55–94. [Google Scholar] [CrossRef]
- Moriasi, D.; Arnold, J.; Van Liew, M.; Bingner, R.; Harmel, R.; Veith, T. Model evaluation guidelines for systematic quantification of accuracy in watershed simulations. Trans. ASABE 2007, 50, 885–900. [Google Scholar] [CrossRef]
- Kouchi, D.H.; Esmaili, K.; Faridhosseini, A.; Sanaeinejad, S.H.; Khalili, D.; Abbaspour, K.C. Sensitivity of Calibrated Parameters and Water Resource Estimates on Different Objective Functions and Optimization Algorithms. Water 2017, 9, 384. [Google Scholar] [CrossRef]
- Quintana, J. The drought in Chile and La Niña. In Drought Network News (1994–2001); International Drought Information Center and the National Drought Mitigation Center: Lincoln, NE, USA, 2000; p. 71. Available online: http://digitalcommons.unl.edu/droughtnetnews/71 (accessed on 10 May 2018).
- Valdés-Pineda, R.; Pizarro, R.; García-Chevesich, P.; Valdés, J.B.; Olivares, C.; Vera, M.; Balocchi, F.; Pérez, F.; Vallejos, C.; Fuentes, R.; et al. Water governance in Chile: Availability, management and climate change. J. Hydrol. 2014, 519, 2538–2567. [Google Scholar] [CrossRef]
- Meza, F.J.; Vicuña, S.; Jelinek, M.; Bustos, E.; Bonelli, S. Assessing water demands and coverage sensitivity to climate change in the urban and rural sectors in central Chile. J. Water Clim. Chang. 2014, 5, 192–203. [Google Scholar] [CrossRef]

| Module | Parameter | Description | Influence on | Range |
|---|---|---|---|---|
| Rainfall module parameters | Cmax | - Maximum runoff coefficient when the sub-surface layer is saturated. | - EI | 0.05–0.85 |
| PLim (mm) | - Rainfall limit above which PPD exists. | - PPD | 0–500 | |
| D | - Percentage of rainfall over PLim transformed into PPD. | - PPD | 0–100 | |
| Hmax (mm) | - Maximum capacity of the soil layer to retain water. | - Cmax and ER | 180–500 | |
| PORC | - Fraction of Hmax that defines the soil water content, restricting the evaporation processes. | - Hcrit and ER | 0–100 | |
| Ck | - Underground runoff coefficient. | - ES | 0.05–0.85 | |
| A | - Precipitation data adjustment factor. | - PM | 0.80–2.50 | |
| B | - Potential evapotranspiration data adjustment factor. | - PET and ER | 0.80–2.50 | |
| Snow module parameters | M (mm °C−1) | - Parameter of the degree-day method that defines the fraction of the snow storage that is melted. The method also considers a base temperature (Tb = 0 °C) at which melting starts. | - PSP, PS | 1–12 |
| DM | - Minimum melting rate when the monthly temperature is lower than Tb. | - PSP, PS | 0.00–0.50 | |
| F | - Fraction of the real snowmelt that goes to EI. | - EI | 0.00–1.00 |
| Objective Function | Equation | Performance Rating | |
|---|---|---|---|
| Satisfactory | Very Good | ||
| KGE | >0.50 | >0.90 | |
| NSE | >0.50 | >0.75 | |
| ROCE * (m3/s/mm) | - | - | |
| RMSE * (m3/s) | - | - | |
| PBIAS (%) | <|25%| | <|10%| | |
| R2 | >0.50 | >0.75 | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Muñoz, E.; Guzmán, C.; Medina, Y.; Boll, J.; Parra, V.; Arumí, J.L. An Adaptive Basin Management Rule to Improve Water Allocation Resilience under Climate Variability and Change—A Case Study in the Laja Lake Basin in Southern Chile. Water 2019, 11, 1733. https://doi.org/10.3390/w11081733
Muñoz E, Guzmán C, Medina Y, Boll J, Parra V, Arumí JL. An Adaptive Basin Management Rule to Improve Water Allocation Resilience under Climate Variability and Change—A Case Study in the Laja Lake Basin in Southern Chile. Water. 2019; 11(8):1733. https://doi.org/10.3390/w11081733
Chicago/Turabian StyleMuñoz, Enrique, Christian Guzmán, Yelena Medina, Jan Boll, Victor Parra, and José Luis Arumí. 2019. "An Adaptive Basin Management Rule to Improve Water Allocation Resilience under Climate Variability and Change—A Case Study in the Laja Lake Basin in Southern Chile" Water 11, no. 8: 1733. https://doi.org/10.3390/w11081733
APA StyleMuñoz, E., Guzmán, C., Medina, Y., Boll, J., Parra, V., & Arumí, J. L. (2019). An Adaptive Basin Management Rule to Improve Water Allocation Resilience under Climate Variability and Change—A Case Study in the Laja Lake Basin in Southern Chile. Water, 11(8), 1733. https://doi.org/10.3390/w11081733





