Physical Modeling of Ski-Jump Spillway to Evaluate Dynamic Pressure
Abstract
:1. Introduction
2. Materials and Methods
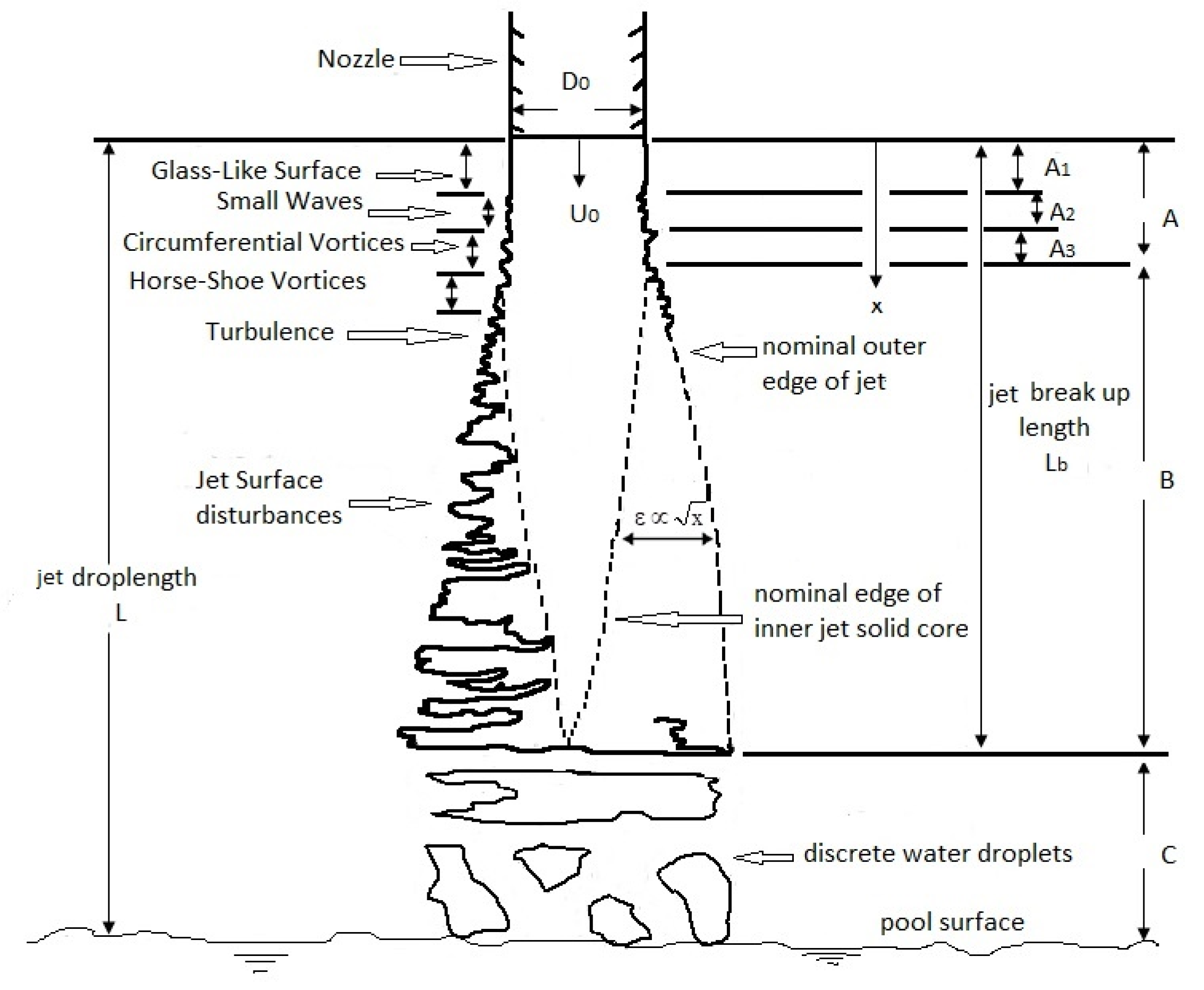
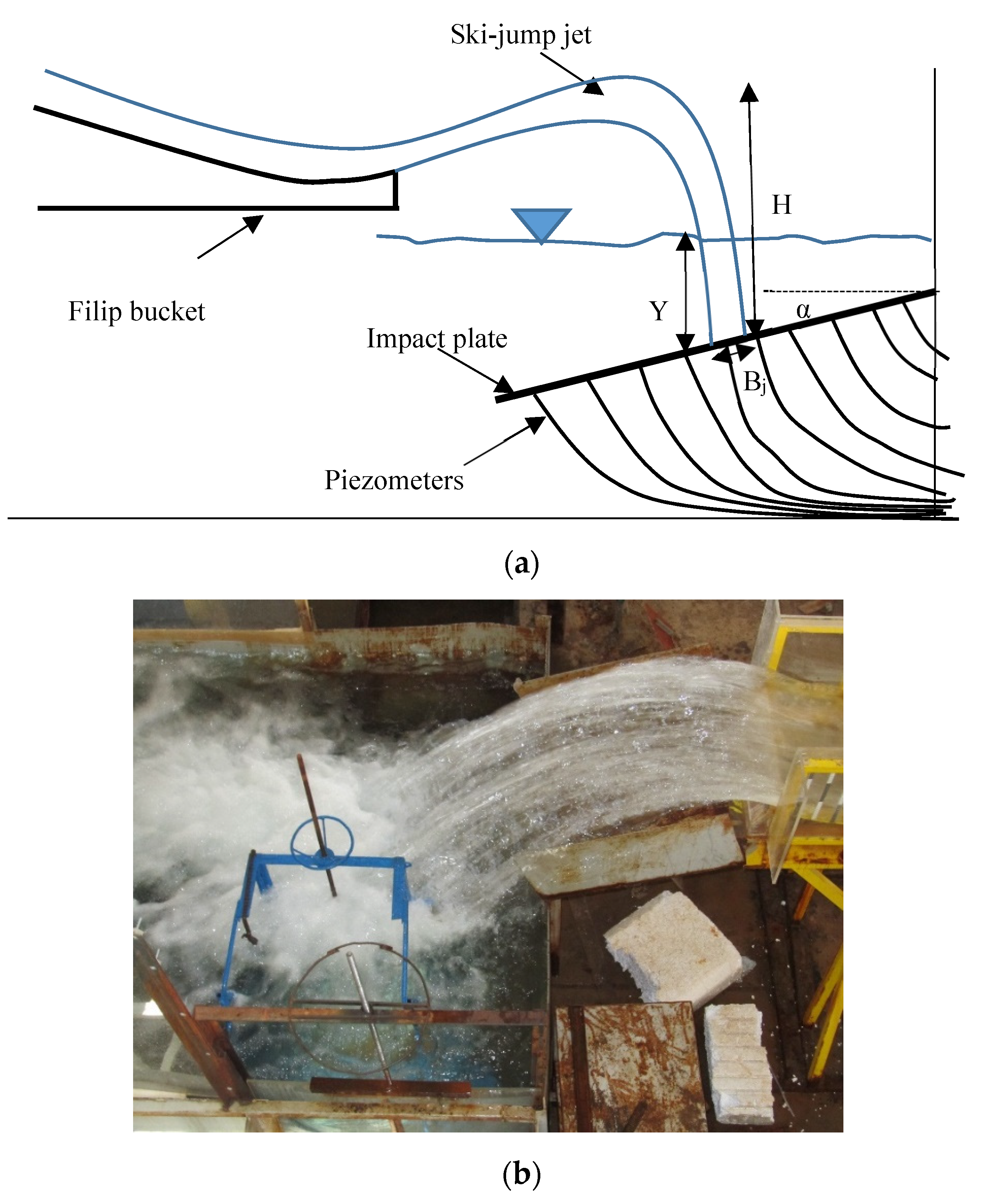
2.1. Mechanism and Effective Parameters
2.2. Dimensional Analysis
2.3. The Experiments and Models
2.4. Experiments’ Setup
2.5. Measurement of Dynamic Pressure
3. Results and Discussion
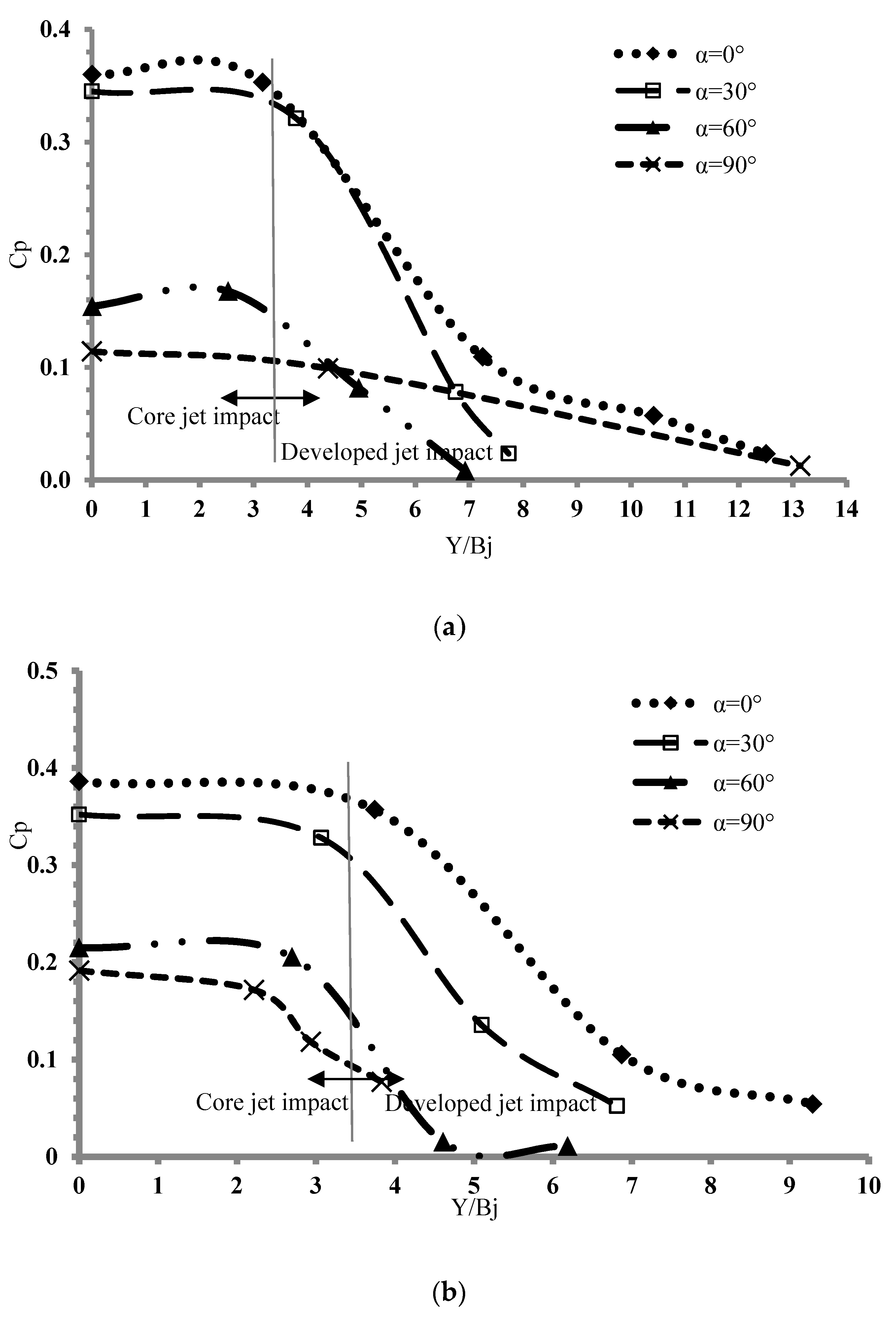
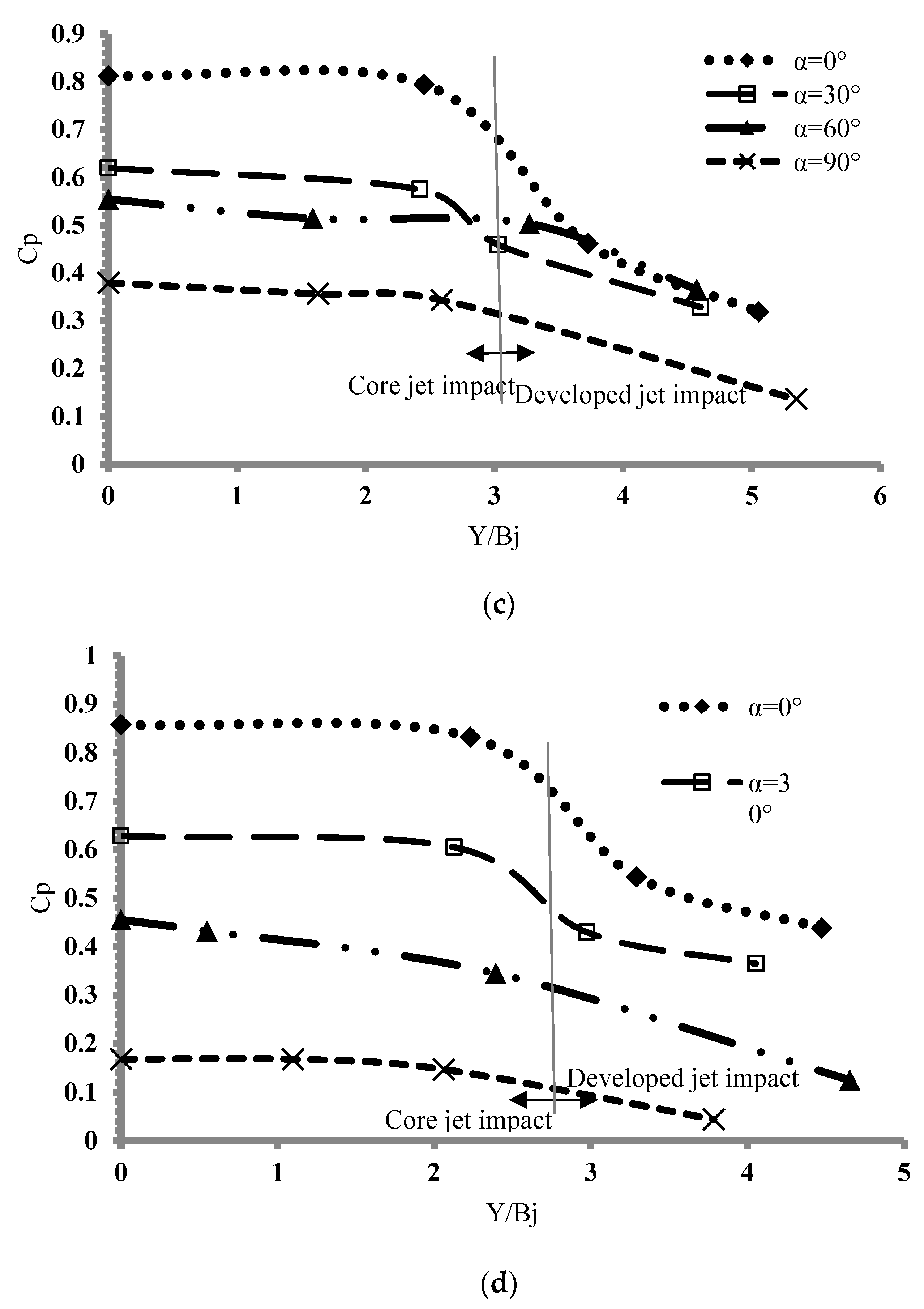
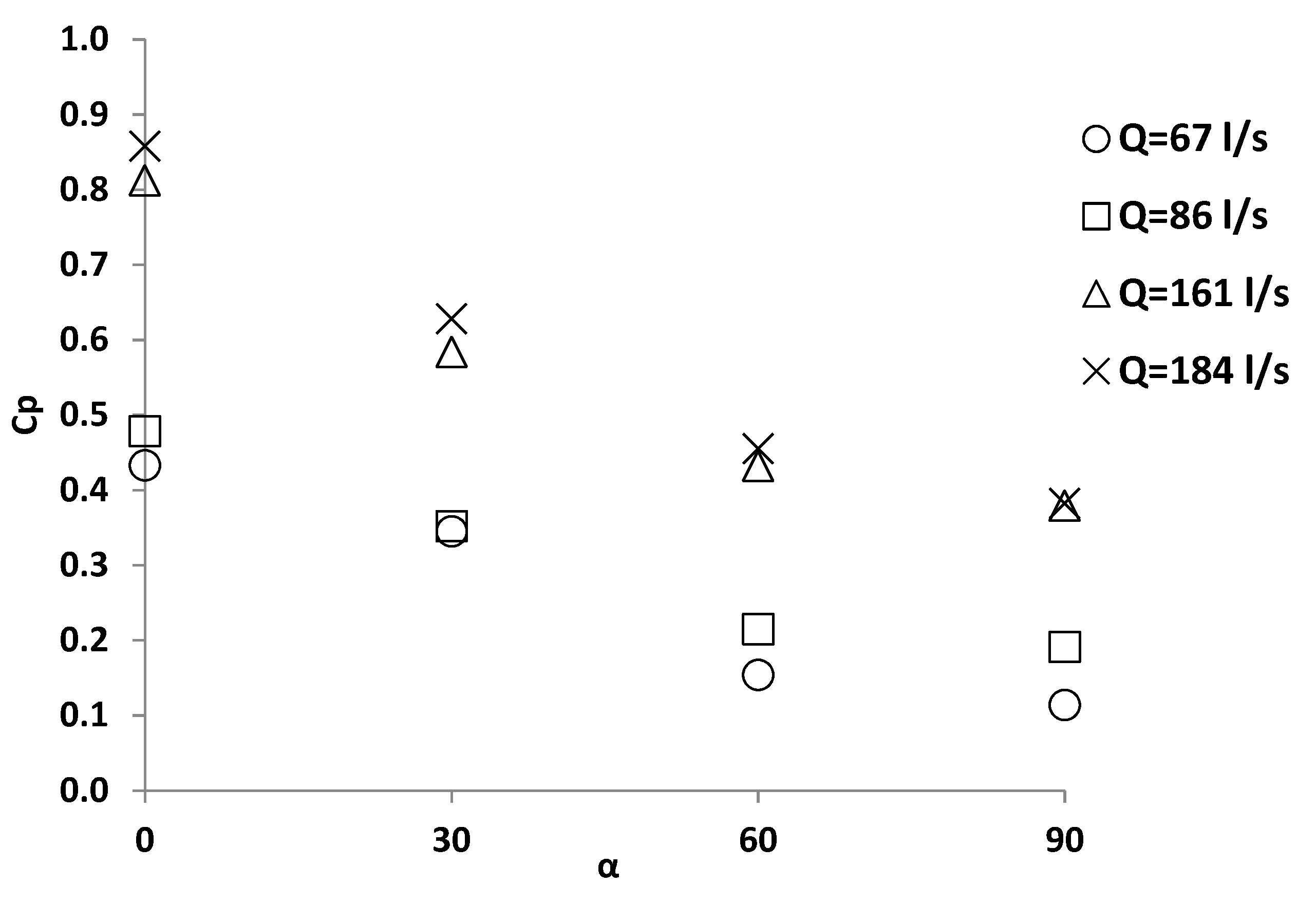
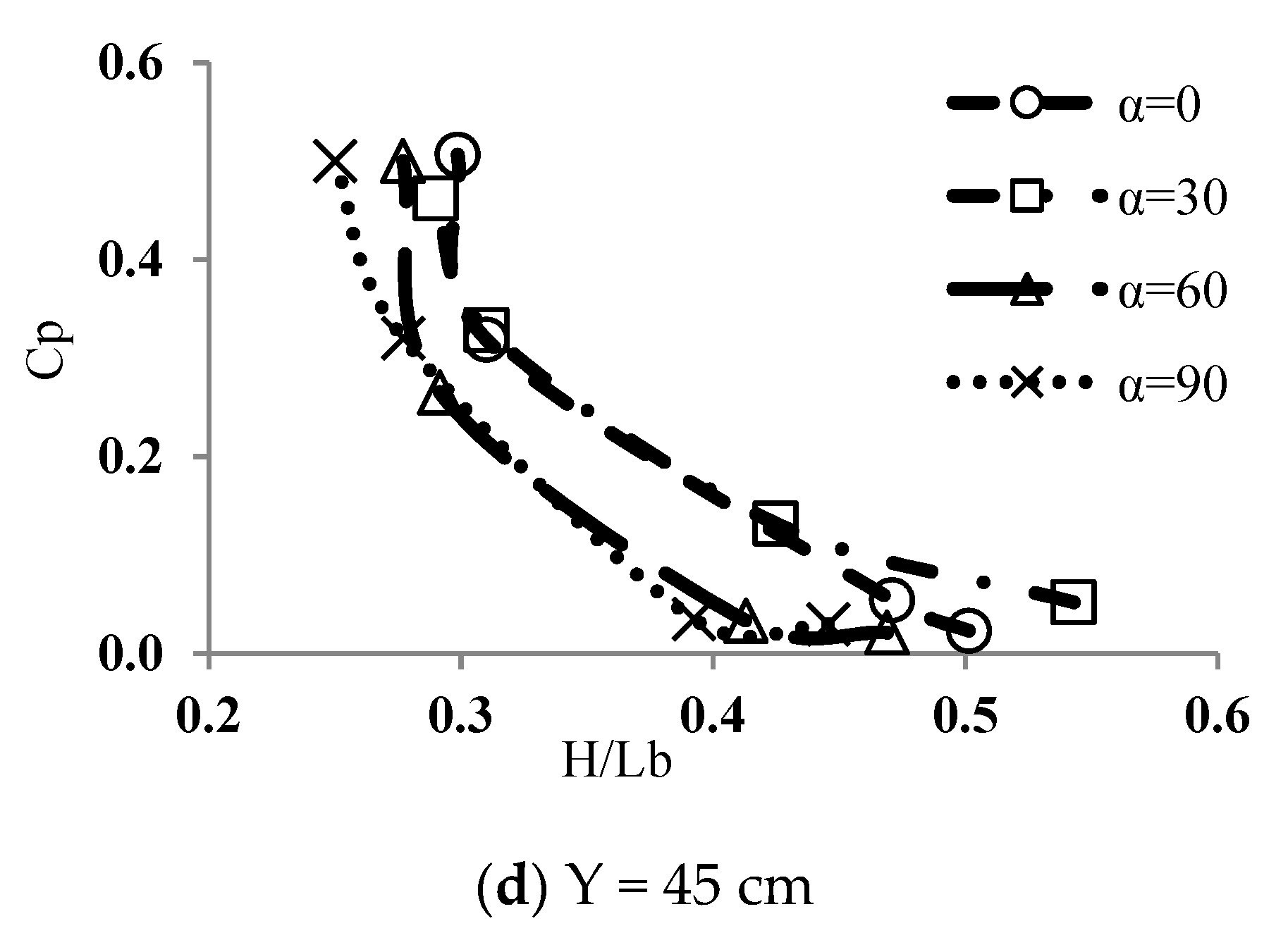
3.1. Mean Dynamic Pressure Coefficient
3.1.1. Effect of Plunging Depth
3.1.2. Effect of Jet Impact Angle
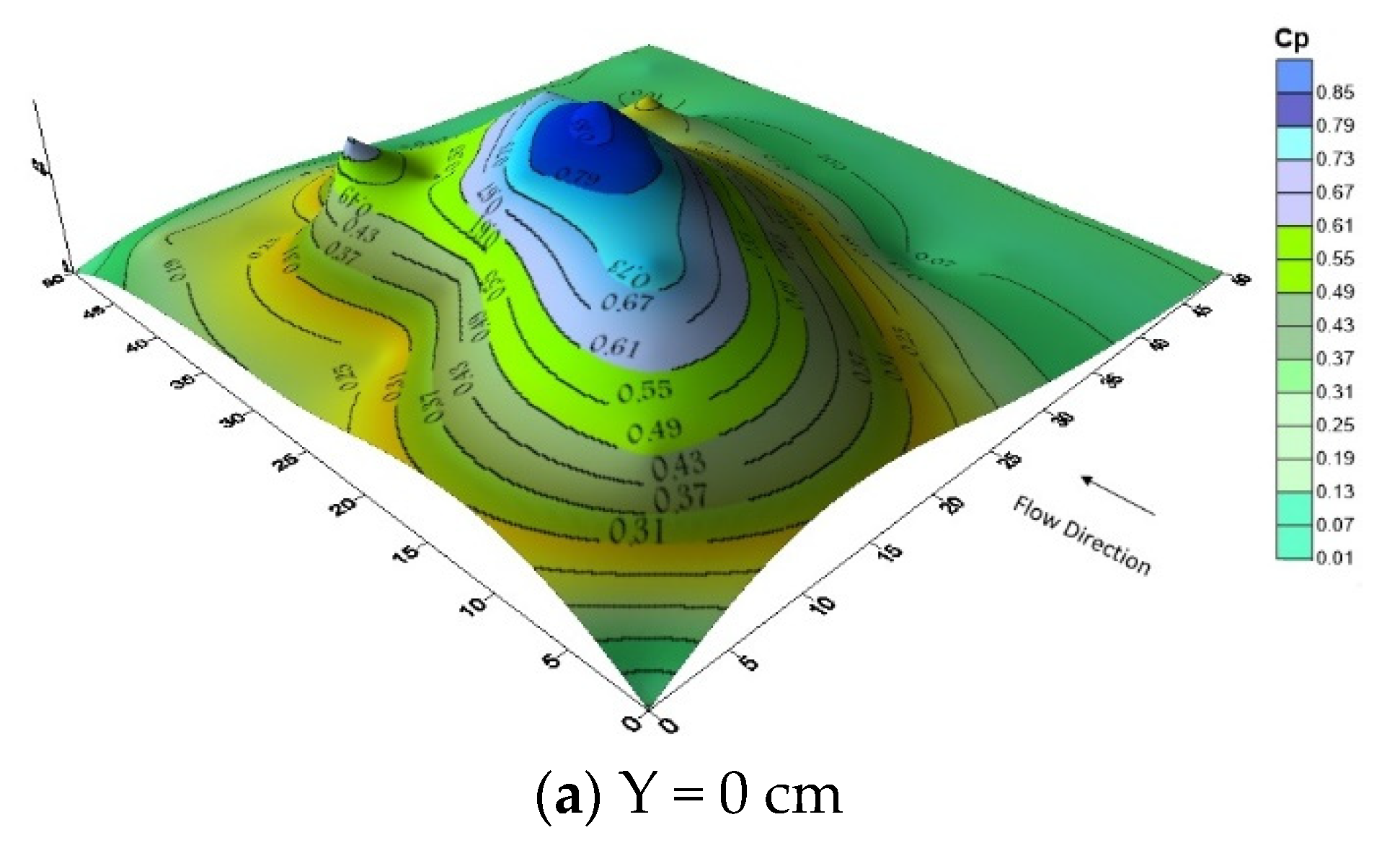
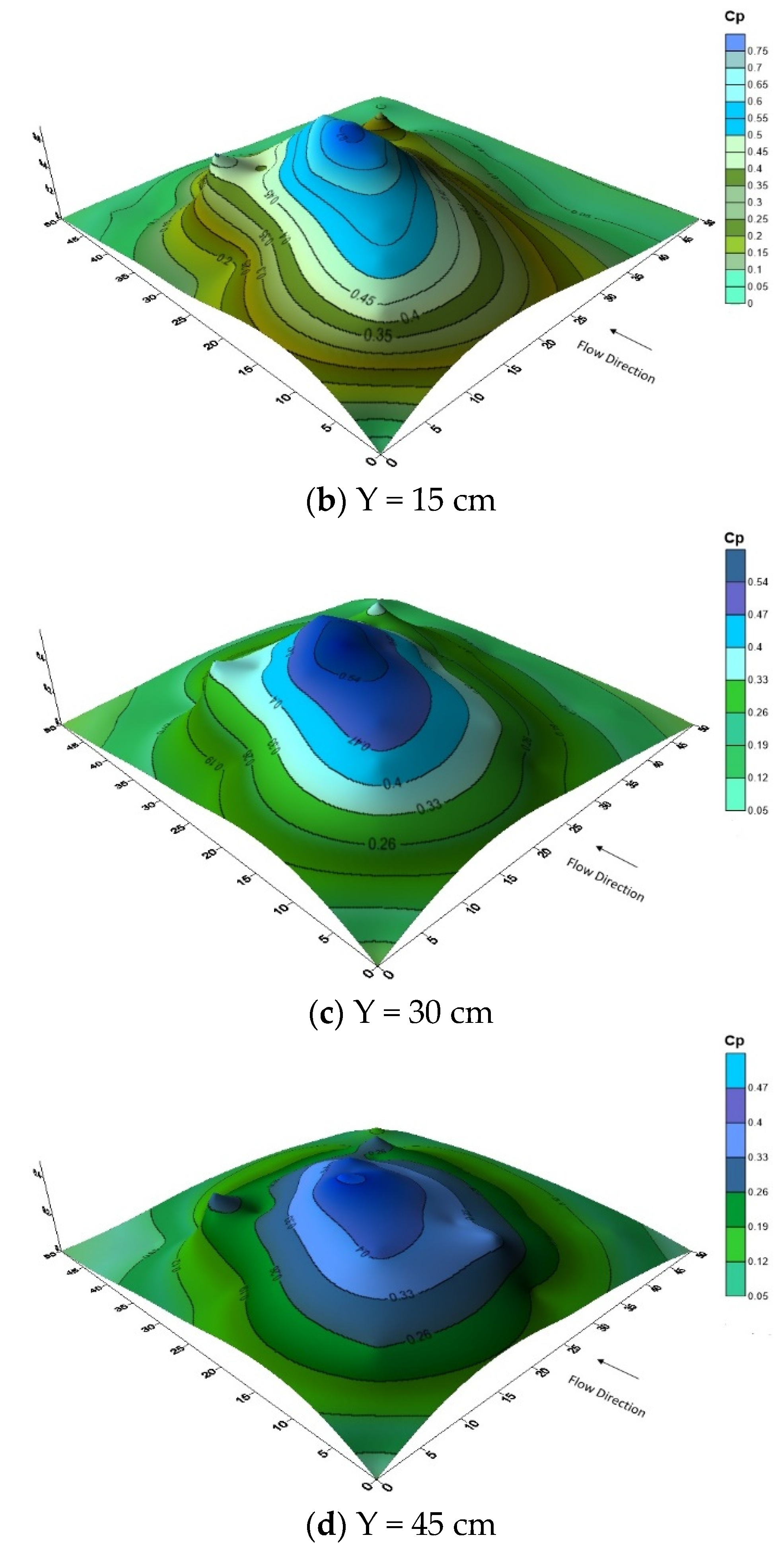
3.2. Distribution of Dynamic Pressure on Impact Plate
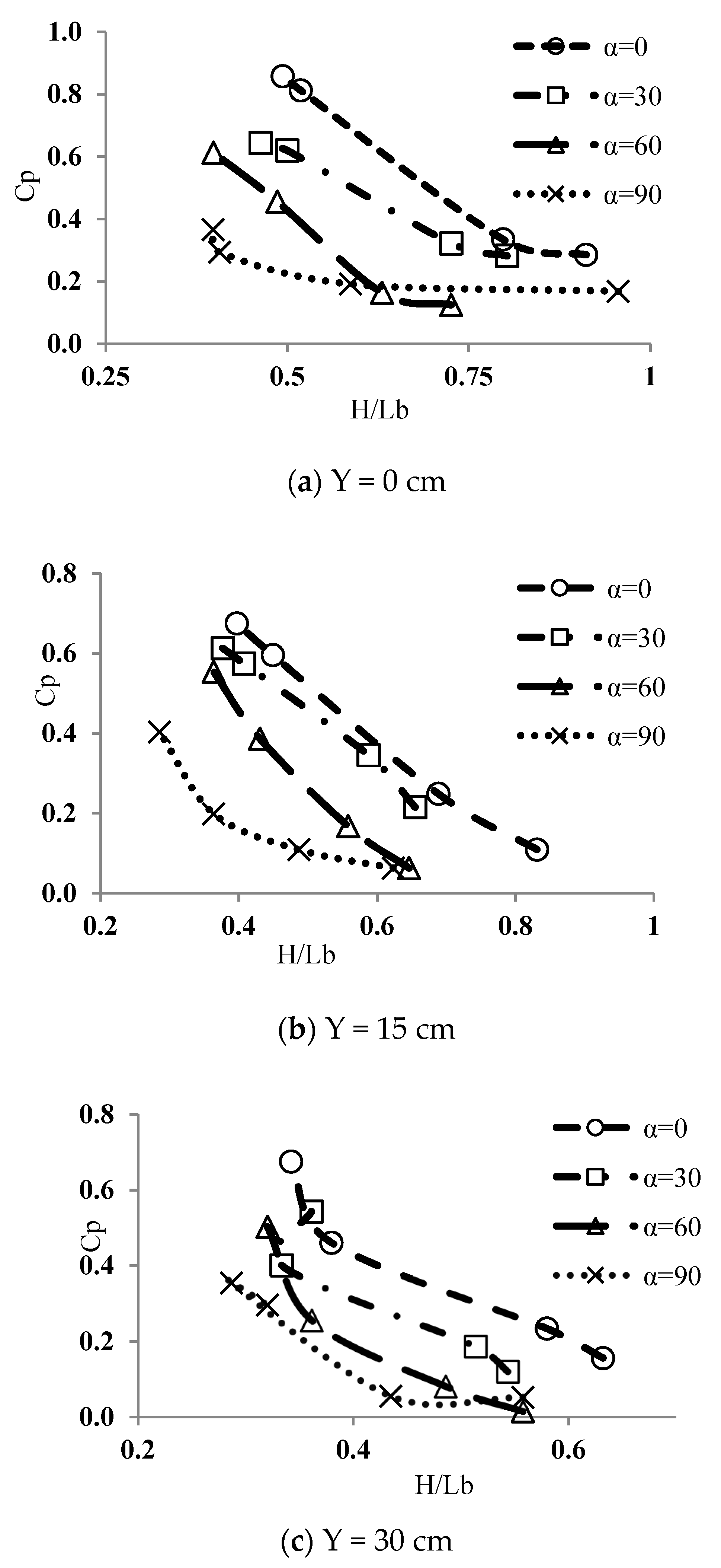
3.3. Mean Dynamic Pressure Coefficient and Break-Up Length
4. Conclusions
- At different discharges, with an increase in plunging depth, the mean dynamic coefficient of the pressure on the impact plate was primarily constant and then decreased.
- As the impact plate angle increased the mean dynamic pressure reduced, this reduction occurred more often from the angles of 0 to 60°.
- The greater the plunging depth, the less the effect of impact plate angle on the mean dynamic pressure was observed.
- A low plunging depth did not give a reduction of dynamic pressure on the walls. This depth was in effect at the time when it reached a certain limit. The bound was obtained as Y/Bj > 3 in this research.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Karami Moghadam, M.; Amini, A.; Keshavarzi, A. Intake design attributes and submerged vanes effects on sedimentation and shear stress. Water Environ. J. 2019, 1–7. [Google Scholar] [CrossRef]
- Eghbalzadeh, A.; Javan, M.; Hayati, M.; Amini, A. Discharge prediction of circular and rectangular side orifices using artificial neural networks. KSCE J. Civ. Eng. 2016, 20, 990–996. [Google Scholar] [CrossRef]
- Eklund, S. CFD modeling of ski-jump spillway in Stornnforsen. Master’s Thesis, Royal Institute of Technology, Stockholm, Sweden, 2017. [Google Scholar]
- Steiner, R.; Heller, V.; Hager, W.H.; Minor, H.E. Deflector ski jump hydraulics. J. Hydraul. Eng. 2008, 134, 562–571. [Google Scholar] [CrossRef]
- Jorabloo, M.; Maghsoodi, R.; Sarkardeh, H. 3D simulation of flow over flip buckets at dams. J. Am. Sci. 2011, 7, 931–936. [Google Scholar]
- Mahmoud, H.; Kriaa, W.; Mhiri, H.; Le Palec, G.; Bournot, P. Numerical analysis of recirculation bubble sizes of turbulent co-flowing jet. Eng. Appl. Comput. Fluid. 2012, 6, 58–73. [Google Scholar] [CrossRef]
- Chakravarti, A.; Jain, R.K.; Kothyari, U.C. Scour under submerged circular vertical jets in cohesionless sediments. ISH J. Hydraul. Eng. 2014, 20, 32–37. [Google Scholar] [CrossRef]
- Noori, R.; Hooshyaripor, F. Effective prediction of scour downstream of ski-jump buckets using artificial neural networks. Water Resour. 2014, 41, 8–18. [Google Scholar] [CrossRef]
- Husain, S.M.; Muhammed, J.R.; Karunarathna, H.U.; Reeve, D.E. Investigation of pressure variations over stepped spillways using smooth particle hydrodynamics. Adv. Water Resour. 2014, 66, 52–69. [Google Scholar] [CrossRef]
- Aricò, C.; Re, C.L. A non-hydrostatic pressure distribution solver for the nonlinear shallow water equations over irregular topography. Adv. Water Resour. 2016, 98, 47–69. [Google Scholar] [CrossRef] [Green Version]
- Simpiger, B.M.; Bhalerao, A.R. Estimation of throw distance in the design of ski-jump bucket. Int. J. Sci. Eng. Res. 2016, 7, 1214–1221. [Google Scholar]
- Aminoroayaie Yamini, O.; Kavianpour, M.R.; Mousavi, S.H.; Movahedi, A.; Bavandpour, M. Experimental investigation of pressure fluctuation on the bed of compound flip buckets. ISH J. Hydraul. Eng. 2018, 24, 45–52. [Google Scholar] [CrossRef]
- Wu, J.H.; Li, S.F.; Ma, F. Energy dissipation of slot-type flip buckets. J. Hydrodynam. 2018, 30, 365–368. [Google Scholar] [CrossRef]
- Ervine, D.A.; Flavey, H.R.; Withers, W. Pressure fluctuation on plunge pool floor. J. Hydraul. Res. IAHR. 1997, 35, 257–279. [Google Scholar] [CrossRef]
- Nazari, O.; Jabbari, E.; Sarkardeh, H. Dynamic pressure analysis at chute flip buckets of five dam model studies. J. Civ. Eng. Trans. A Civ. Eng. 2015, 13, 45–54. [Google Scholar] [CrossRef]
- Castillo, E.L.G. Aerated jets and pressure fluctuation in plunge pools. In Proceedings of the 7th ICHE, Philadelphia, PA, USA, 10–13 September 2006. [Google Scholar]
- Bollaert, E.; Schleiss, A. Scour of rock due to the impact of plunging high velocity jets. Part I: A state-of-the-art review. J. Hydraul. Res. 2003, 41, 451–464. [Google Scholar] [CrossRef]
- Bollaert, E.; Schleiss, A. Scour of rock due to the impact of plunging high velocity jets. Part II: Experimental results of dynamic pressures at pool bottoms and in one-and two-dimensional closed end rock joints. J. Hydraul. Res. 2003, 41, 465–480. [Google Scholar] [CrossRef]
- Castillo, E.L.G. Pressure characterization of undeveloped and developed jets in shallow and deep pool. In Proceedings of the 32nd Congress of IAHR, Venice, Italy, 1–6 July 2007. [Google Scholar]
- Castillo, E.L.G. Metodología experimental y numérica para la caracterización del campo de presiones en los disipadores de energía hidráulica. Aplicación al vertido en presas bóveda. Ph.D. Thesis, Universitat Politècnica de Catalunya, Barcelona, Spain, 1989. [Google Scholar]
- Cola, R. Energy dissipation of a high-velocity vertical jet entering a basin. In Proceedings of the 11th IAHR, Leningrad, Russia, Ex-USSR, 6–11 September 1965. [Google Scholar]
- Albertson, M.L.; Dai, Y.B.; Jenson, R.A.; Rouse, H. Diffusion of submerged jets. Trans. Am. Soc. Civ. Eng. 1950, 115, 639–664. [Google Scholar]


| α (deg.) | Y (cm) | Q (L/s) | |||
|---|---|---|---|---|---|
| 67 | 86 | 161 | 184 | ||
| CP | |||||
| 0 | 0 | 0.360 | 0.386 | 0.812 | 0.858 |
| 15 | 0.353 | 0.357 | 0.794 | 0.832 | |
| 30 | 0.109 | 0.105 | 0.461 | 0.544 | |
| 45 | 0.057 | 0.054 | 0.318 | 0.438 | |
| 30 | 0 | 0.345 | 0.352 | 0.619 | 0.628 |
| 15 | 0.321 | 0.328 | 0.574 | 0.605 | |
| 30 | 0.078 | 0.135 | 0.459 | 0.429 | |
| 45 | 0.023 | 0.052 | 0.328 | 0.365 | |
| 60 | 0 | 0.154 | 0.215 | 0.553 | 0.455 |
| 15 | 0.167 | 0.205 | 0.514 | 0.432 | |
| 30 | 0.082 | 0.015 | 0.503 | 0.345 | |
| 45 | 0.008 | 0.011 | 0.365 | 0.125 | |
| 90 | 0 | 0.114 | 0.191 | 0.379 | 0.168 |
| 15 | 0.099 | 0.171 | 0.356 | 0.168 | |
| 30 | 0.013 | 0.118 | 0.343 | 0.147 | |
| 45 | 0.012 | 0.077 | 0.136 | 0.044 | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Karami Moghadam, M.; Amini, A.; Malek, M.A.; Mohammad, T.; Hoseini, H. Physical Modeling of Ski-Jump Spillway to Evaluate Dynamic Pressure. Water 2019, 11, 1687. https://doi.org/10.3390/w11081687
Karami Moghadam M, Amini A, Malek MA, Mohammad T, Hoseini H. Physical Modeling of Ski-Jump Spillway to Evaluate Dynamic Pressure. Water. 2019; 11(8):1687. https://doi.org/10.3390/w11081687
Chicago/Turabian StyleKarami Moghadam, Mehdi, Ata Amini, Marlinda Abdul Malek, Thamer Mohammad, and Hasan Hoseini. 2019. "Physical Modeling of Ski-Jump Spillway to Evaluate Dynamic Pressure" Water 11, no. 8: 1687. https://doi.org/10.3390/w11081687
APA StyleKarami Moghadam, M., Amini, A., Malek, M. A., Mohammad, T., & Hoseini, H. (2019). Physical Modeling of Ski-Jump Spillway to Evaluate Dynamic Pressure. Water, 11(8), 1687. https://doi.org/10.3390/w11081687





