Spatial–Temporal Soil Water Dynamics beneath a Tree Monitored by Tensiometer-Time Domain Reflectometry Probes
Abstract
1. Introduction
- Are the spatial variability of soil water described by θ and ψ different?
- Could matrix flow and preferential flow underneath a tree be detected using the dataset of θ and ψ measured by the T-TDR probes in a short observation period?
- What are the main effects of roots on soil water dynamics during the wetting and drying processes?
2. Materials and Methods
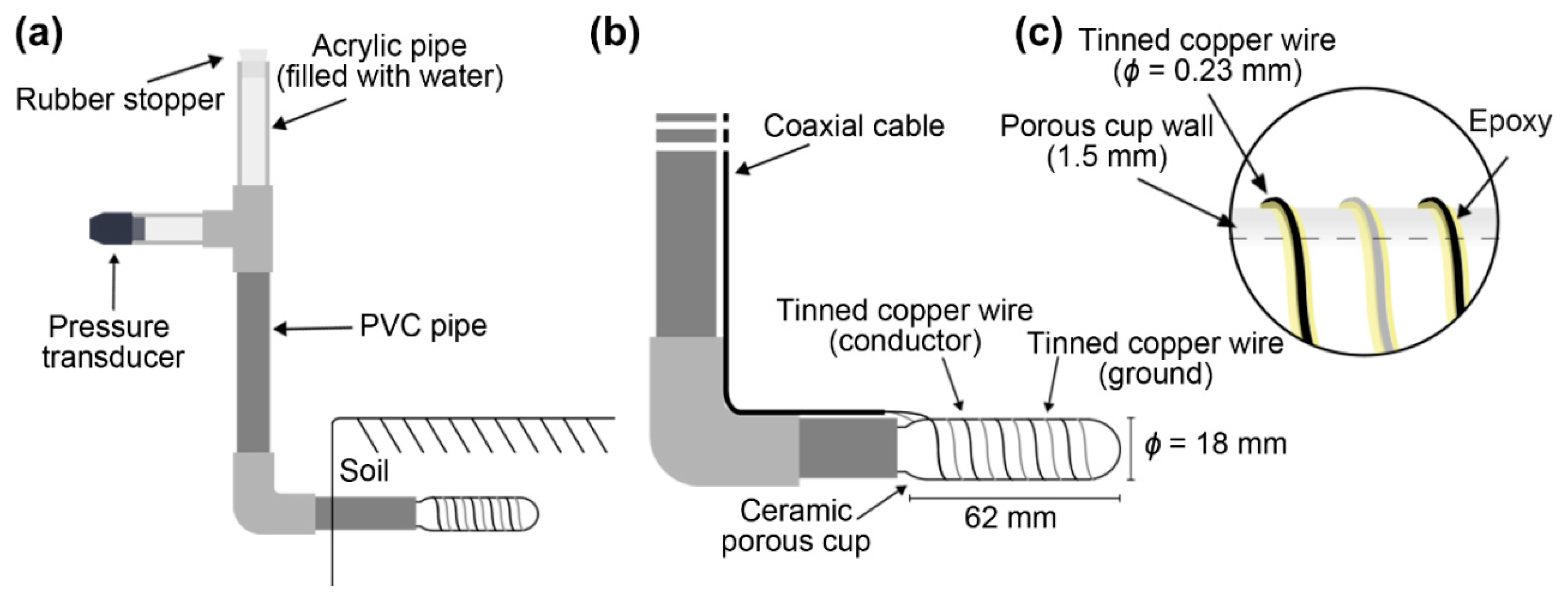
2.1. Design of a T-TDR Probe
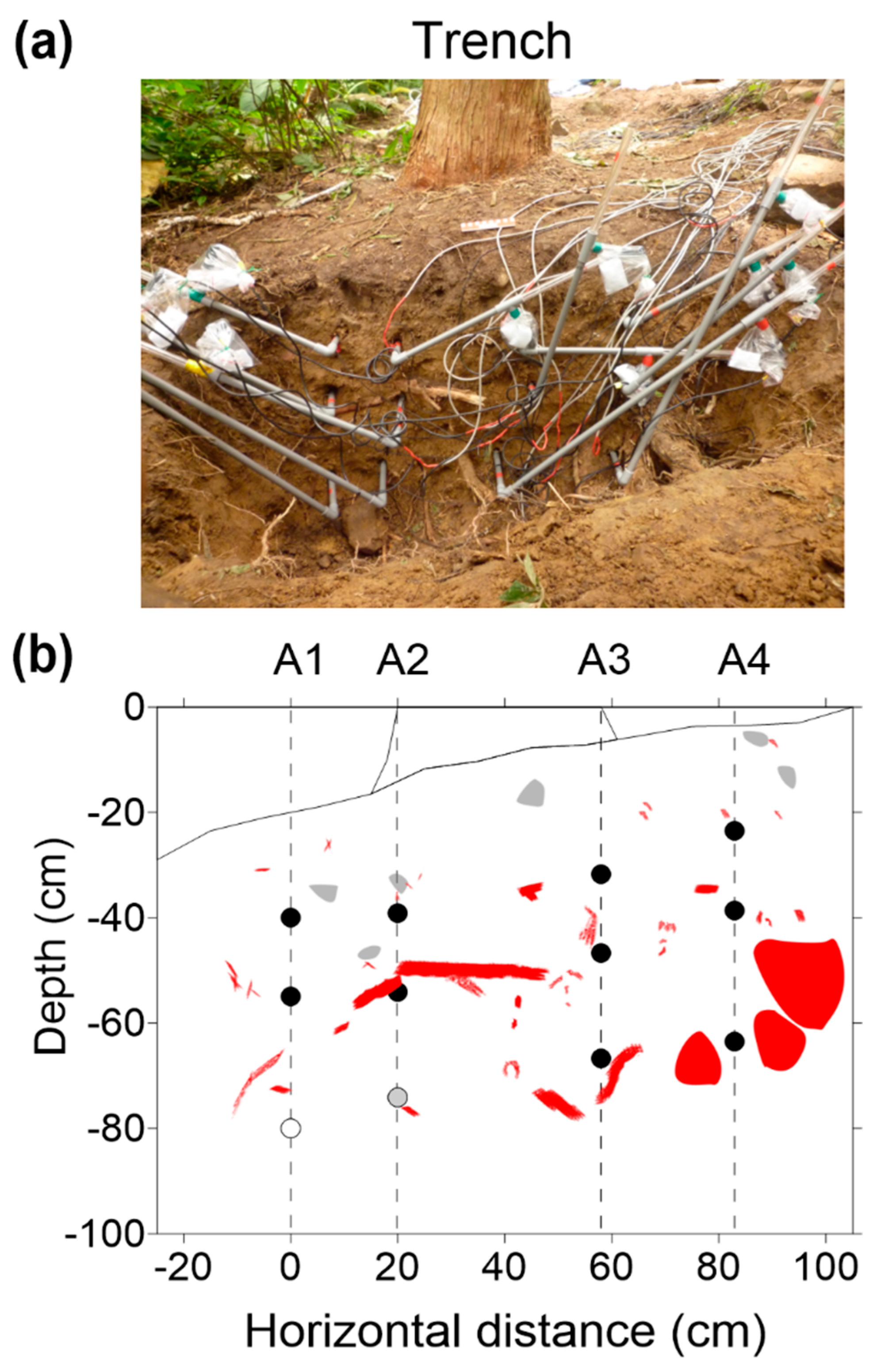
2.2. Study Area and Sensor Installation
2.3. Calibration of the T-TDR Probes
2.4. Data Analyses for Soil Water Dynamics
3. Results
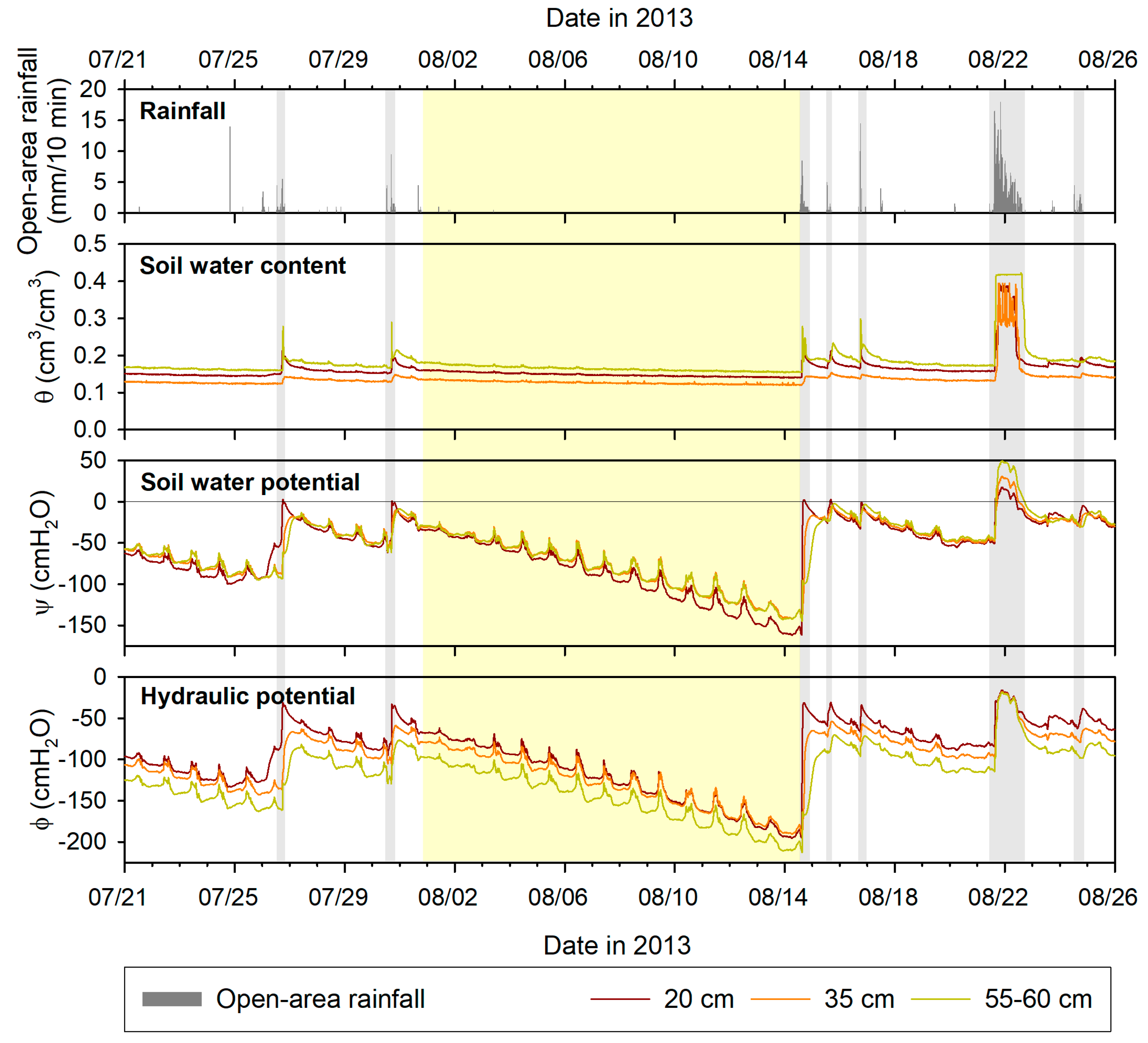
3.1. Temporal Variation in Soil Water Dynamics
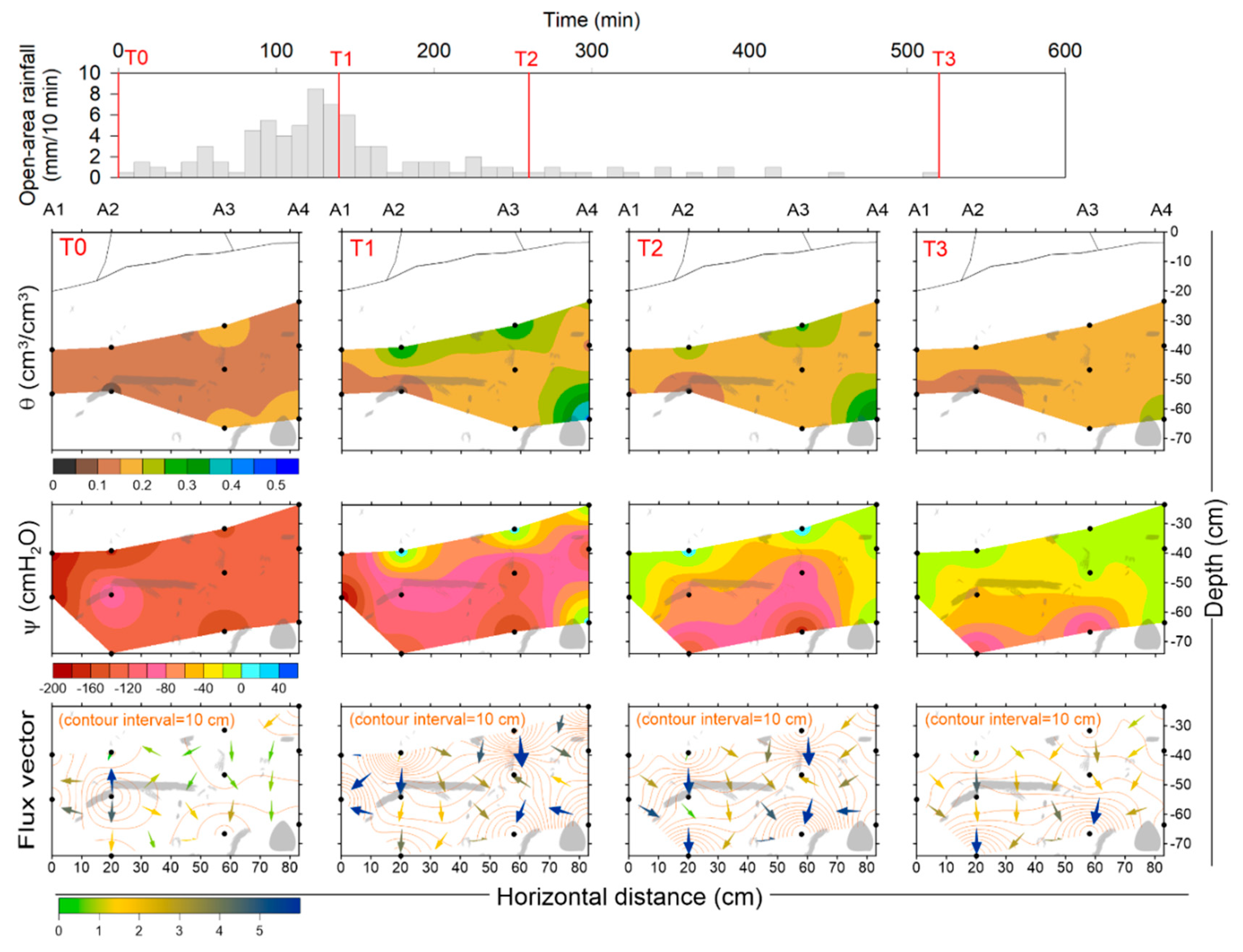
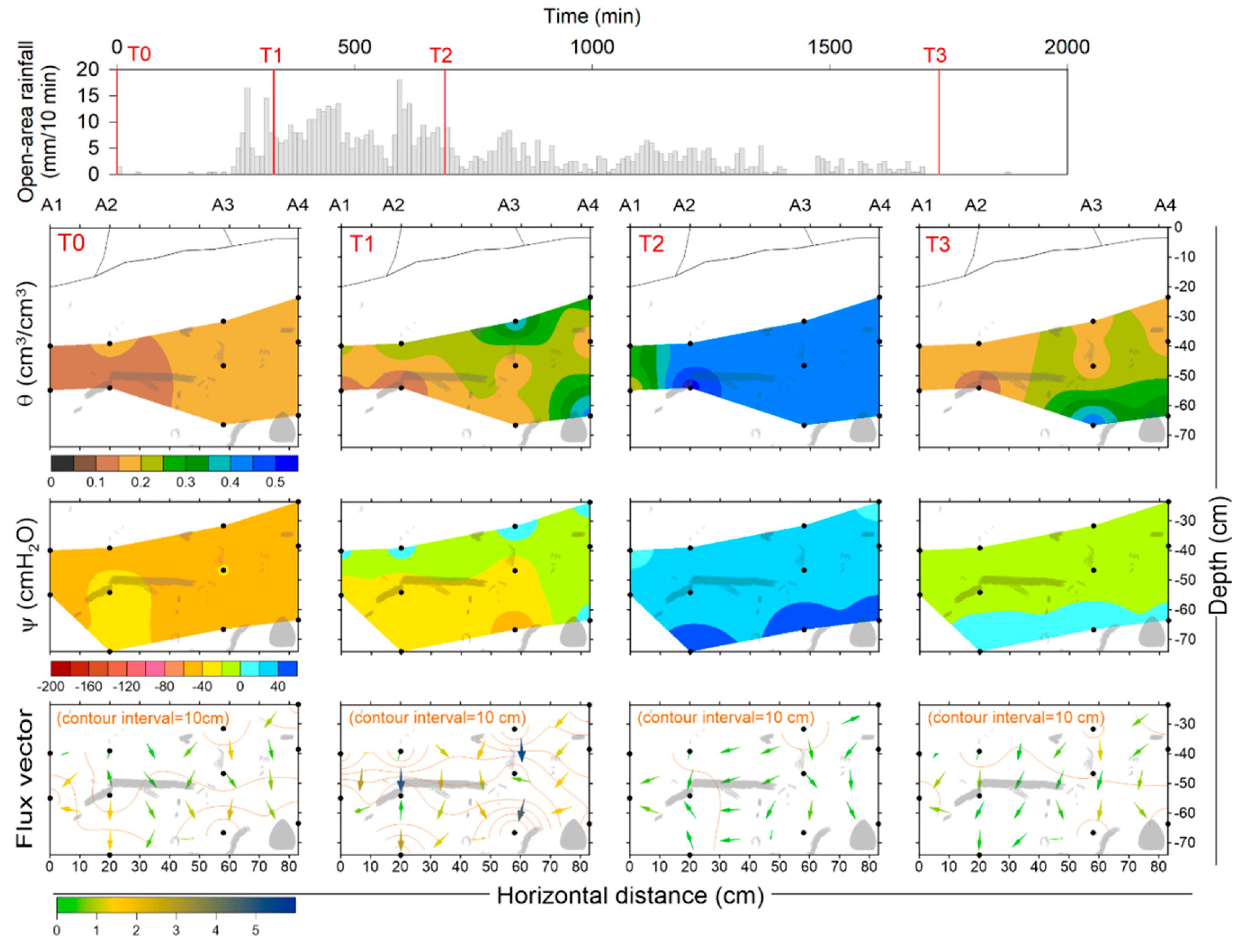
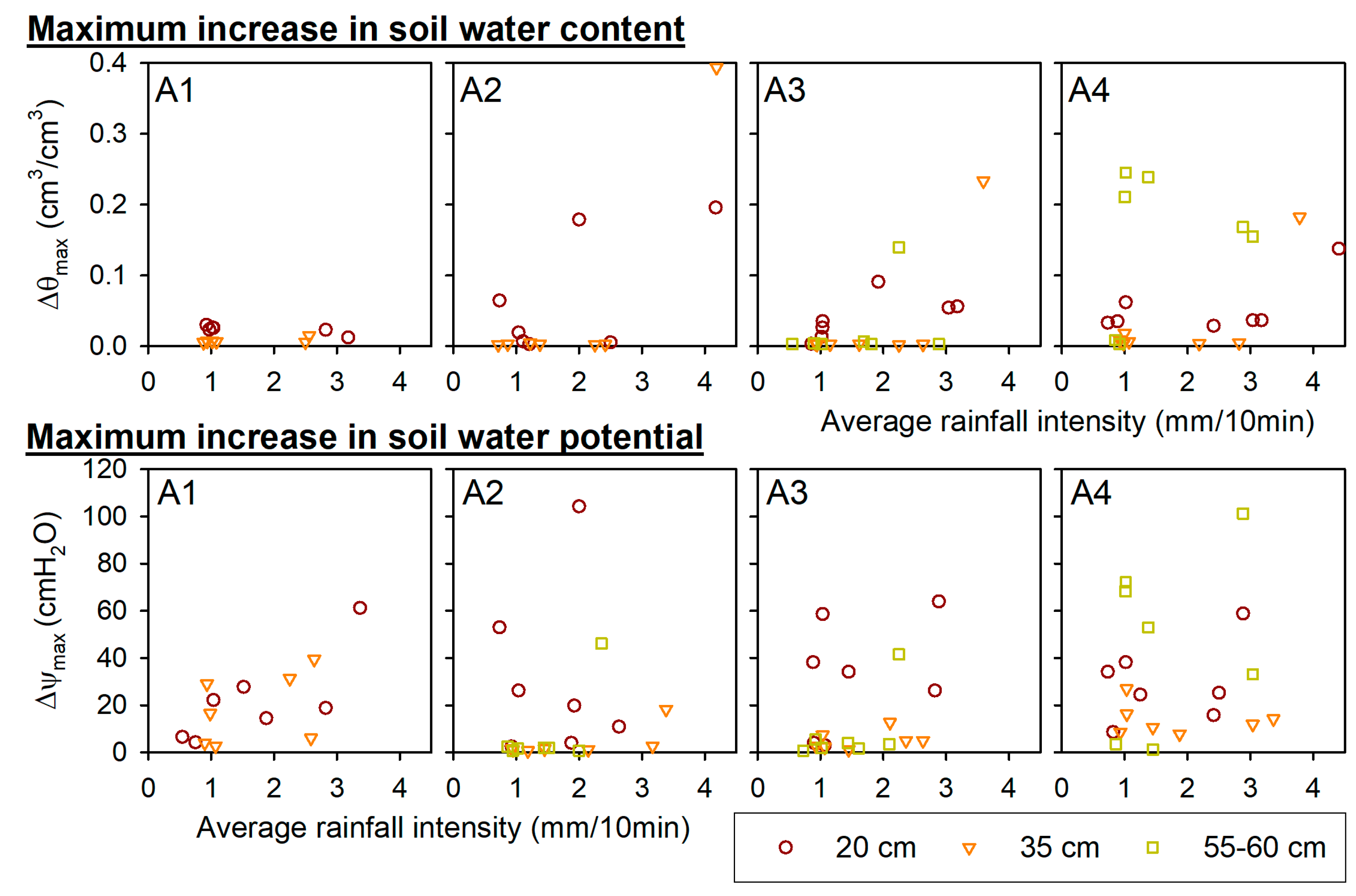
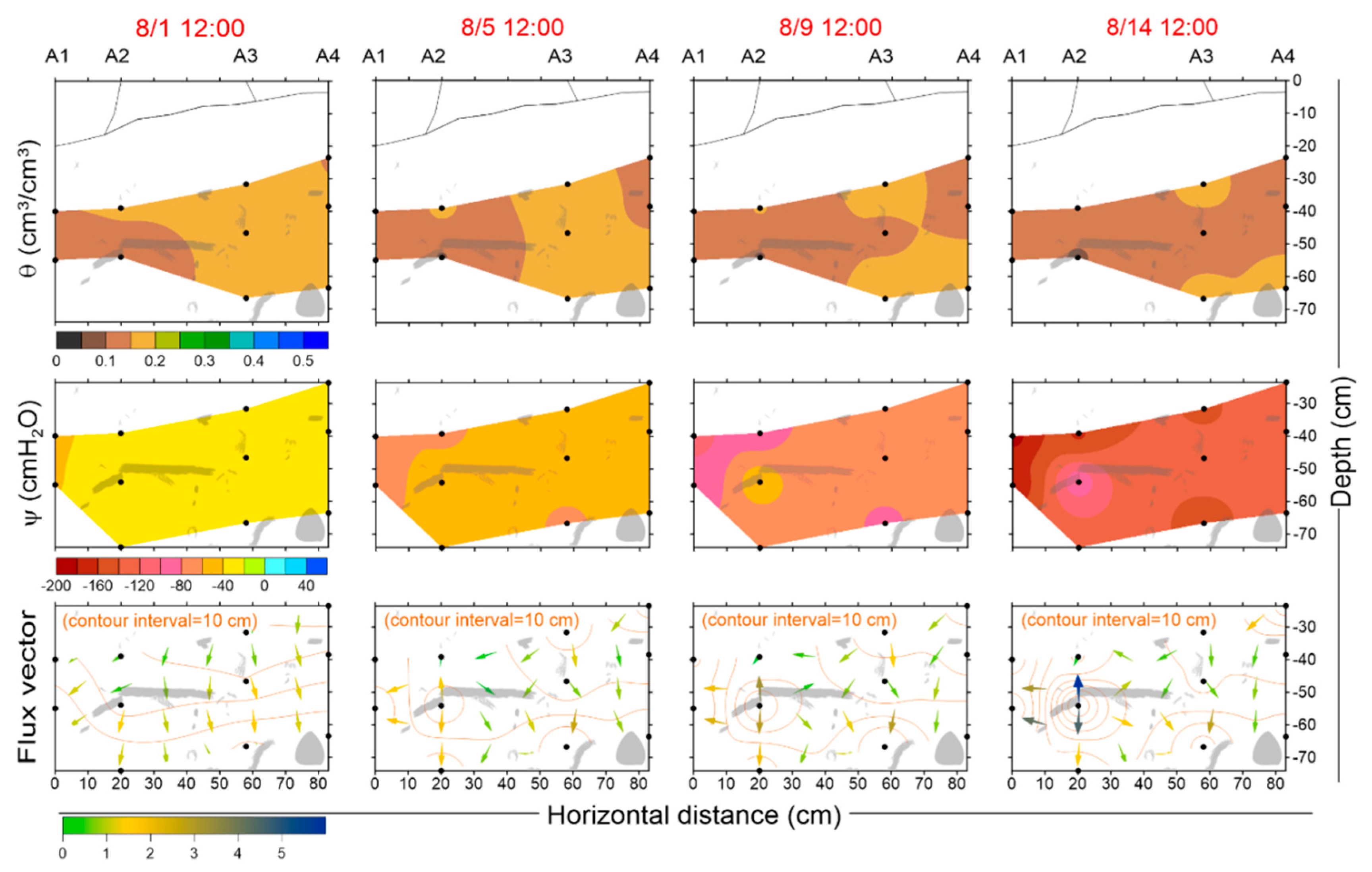
3.2. Spatial Variation in Soil Water Dynamics during Rainfall Events
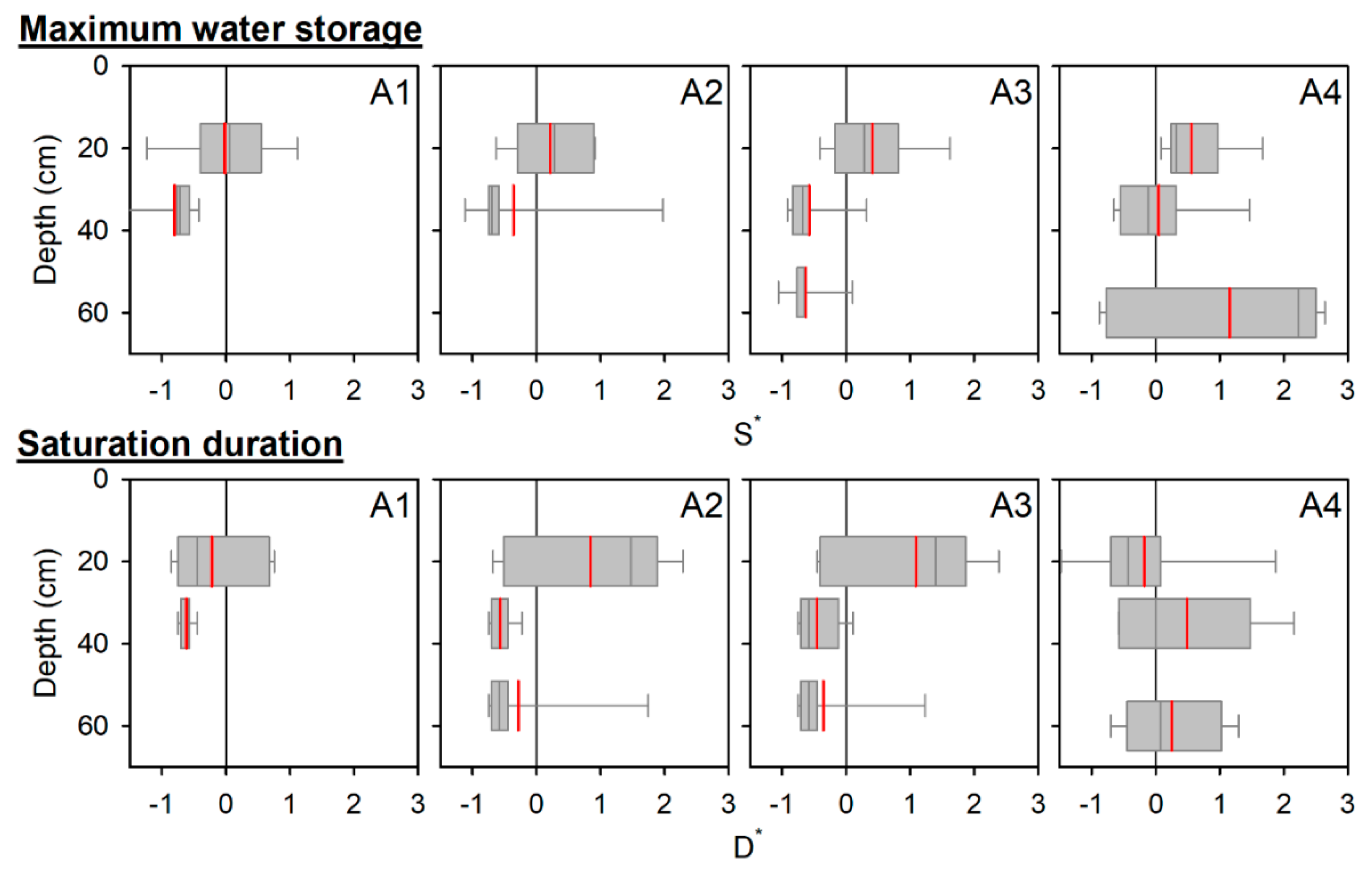
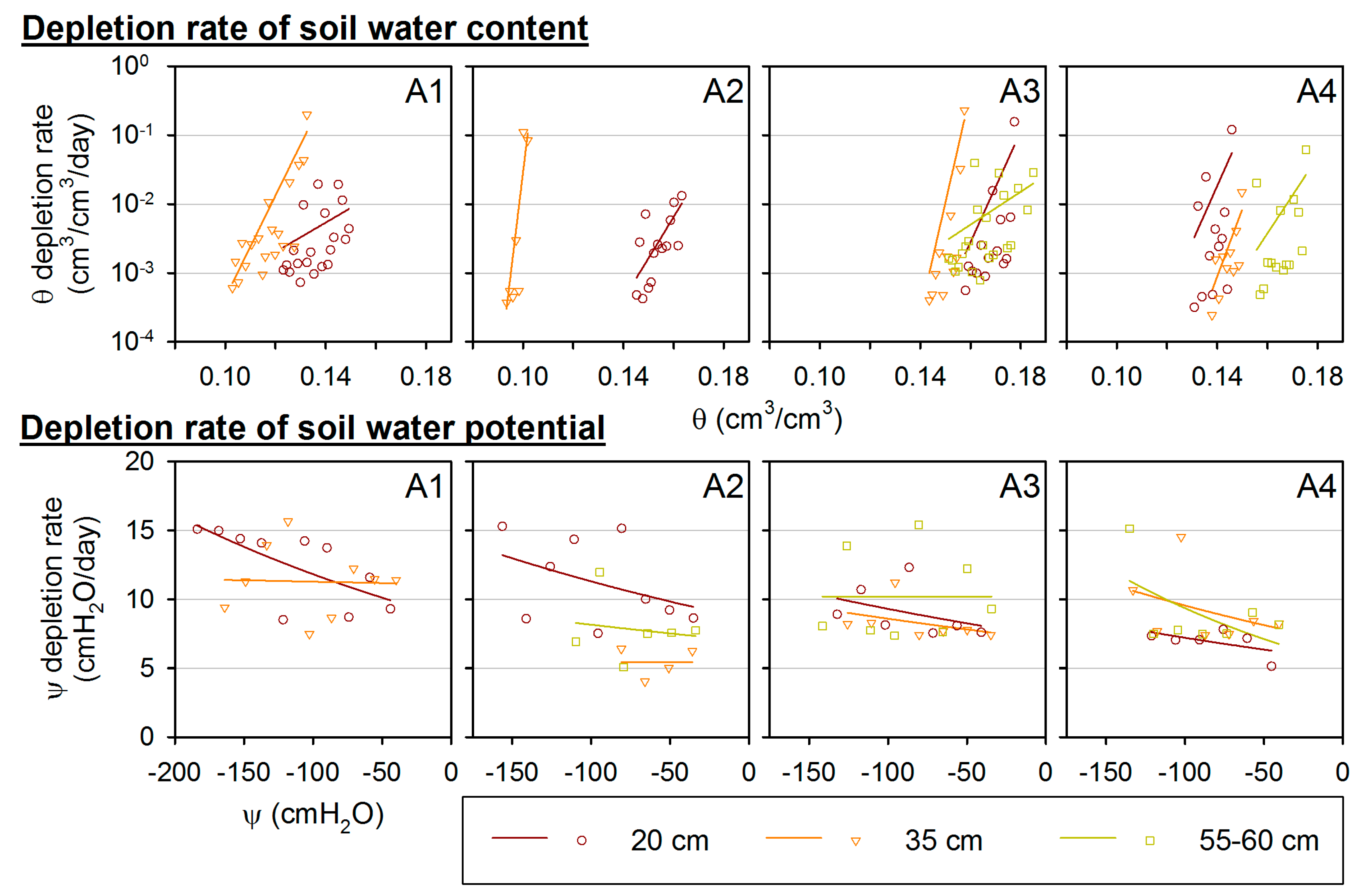
3.3. Spatial Variation in Soil Water Depletion during a Drying Period
4. Discussion
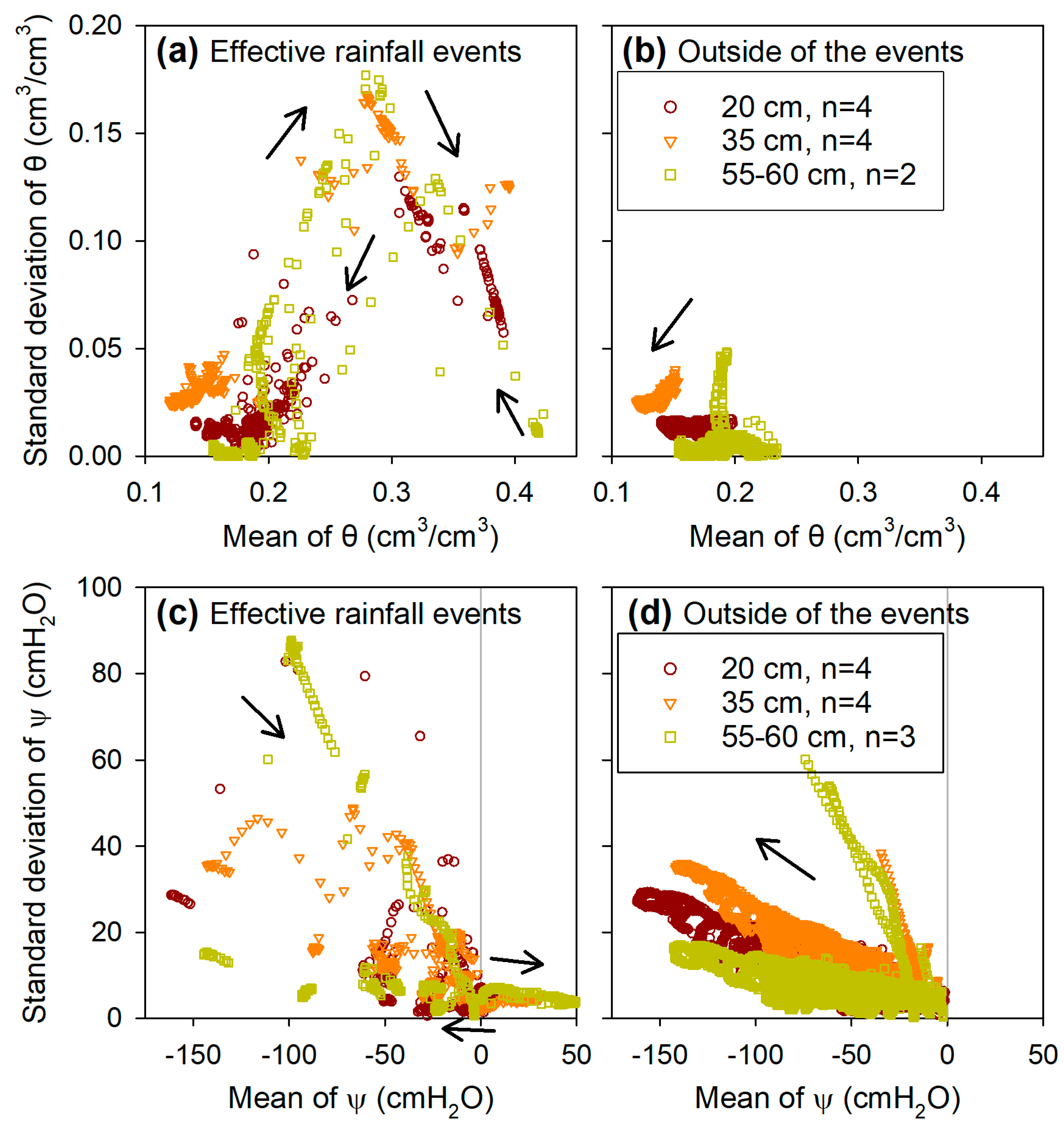
4.1. Relationships between the Mean and Standard Deviation of Soil Water Content and Soil Water Potential
4.2. Effects of Roots on Soil Water Dynamics underneath the Tree
5. Conclusions
- The relationship between the mean and standard deviation of spatial θ and ψ showed convex-upward shapes and negative curvilinear shapes, respectively. High spatial variability was observed at intermediate values of θ and small values of ψ, which indicates the need for θ measurement in wetter conditions and ψ measurement in drier conditions.
- Infiltration processes dominated by matrix flow and preferential flow accounted for 75% and 25% of observations taken beneath the tree, respectively. Although matrix flow dominated the infiltration process in the root environment, preferential flow could cause the average θ and ψ at all of the locations to reach their maxima.
- A coarse root served as a “hot spot” that exhibited sensitive responses to wetting, although this root-induced preferential flow acted only for a short time in rainfall events. A “cold spot” existed underneath a lateral root where the hydrological responses were insensitive.
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Liang, W.-L.; Kosugi, K.; Mizuyama, T. Characteristics of stemflow for tall stewartia (Stewartia monadelpha) growing on a hillslope. J. Hydrol. 2009, 378, 168–178. [Google Scholar] [CrossRef][Green Version]
- Keim, R.F.; Skaugset, A.E.; Weiler, M. Temporal persistence of spatial patterns in throughfall. J. Hydrol. 2005, 314, 263–274. [Google Scholar] [CrossRef]
- Levia, D.F.; Germer, S. A review of stemflow generation dynamics and stemflow-environment interactions in forests and shrublands. Rev. Geophys. 2015, 53, 673–714. [Google Scholar] [CrossRef]
- Beven, K.; Germann, P. Macropores and water flow in soils. Water Resour. Res. 1982, 18, 1311–1325. [Google Scholar] [CrossRef]
- Liang, W.-L.; Kosugi, K.; Mizuyama, T. Soil water dynamics around a tree on a hillslope with or without rainwater supplied by stemflow. Water Resour. Res. 2011, 47, W02541. [Google Scholar] [CrossRef]
- Germer, S. Development of near-surface perched water tables during natural and artificial stemflow generation by babassu palms. J. Hydrol. 2013, 507, 262–272. [Google Scholar] [CrossRef]
- Krämer, I.; Hölscher, D. Soil water dynamics along a tree diversity gradient in a deciduous forest in Central Germany. Ecohydrology 2010, 3, 262–271. [Google Scholar] [CrossRef]
- Liang, W.-L.; Kosugi, K.; Mizuyama, T. Soil water redistribution processes around a tree on a hillslope: The effect of stemflow on the drying process. Ecohydrology 2015, 8, 1381–1395. [Google Scholar] [CrossRef]
- Kulli, B.; Stamm, C.; Papritz, A.; Fluhler, H. Discrimination of flow regions on the basis of stained infiltration patterns in soil profiles. Vadose Zone J. 2003, 2, 338–348. [Google Scholar] [CrossRef]
- Noguchi, S.; Tsuboyama, Y.; Sidle, R.C.; Hosoda, I. Morphological characteristics of macropores and the distribution of preferential flow pathways in a forested slope segment. Soil Sci. Soc. Am. J. 1999, 63, 1413–1423. [Google Scholar] [CrossRef]
- Sander, T.; Gerke, H.H. Preferential flow patterns in paddy fields using a dye tracer. Vadose Zone J. 2007, 6, 105–115. [Google Scholar] [CrossRef]
- Lin, H.; Zhou, X. Evidence of subsurface preferential flow using soil hydrologic monitoring in the Shale Hills catchment. Eur. J. Soil Sci. 2008, 59, 34–49. [Google Scholar] [CrossRef]
- Lozano-Parra, J.; van Schaik, N.L.; Schnabel, S.; Gómez-Gutiérrez, Á. Soil moisture dynamics at high temporal resolution in a semiarid Mediterranean watershed with scattered tree cover. Hydrol. Process. 2016, 30, 1155–1170. [Google Scholar] [CrossRef]
- Gwak, Y.; Kim, S. Factors affecting soil moisture spatial variability for a humid forest hillslope. Hydrol. Process. 2017, 31, 431–445. [Google Scholar] [CrossRef]
- Bouten, W.; Schaap, M.G.; Bakker, D.J.; Verstraten, J.M. Modeling soil water dynamics in a forested ecosystem.1. A site specific evaluation. Hydrol. Process. 1992, 6, 435–444. [Google Scholar] [CrossRef]
- Gardenas, A.I.; Simunek, J.; Jarvis, N.; van Genuchten, M.T. Two-dimensional modelling of preferential water flow and pesticide transport from a tile-drained field. J. Hydrol. 2006, 329, 647–660. [Google Scholar] [CrossRef]
- Faybishenko, B. Comparison of laboratory and field methods for determining the quasi-saturated hydraulic conductivity of soils. In Proceedings of the Characterization and Measurement of the Hydraulic Properties of Unsaturated Porous Media, Riverside, CA, USA, 22–24 October 1997; pp. 279–292. [Google Scholar]
- Morgan, K.; Parsons, L.; Adair Wheaton, T. Comparison of laboratory- and field-derived soil water retention curves for a fine sand soil using tensiometric, resistance and capacitance methods. Plant. Soil 2001, 234, 153–157. [Google Scholar] [CrossRef]
- Pachepsky, Y.; Rawls, W.J.; Gimenez, D. Comparison of soil water retention at field and laboratory scales. Soil Sci. Soc. Am. J. 2001, 65, 460–462. [Google Scholar] [CrossRef]
- Basile, A.; Ciollaro, G.; Coppola, A. Hysteresis in soil water characteristics as a key to interpreting comparisons of laboratory and field measured hydraulic properties. Water Resour. Res. 2003, 39, 1355. [Google Scholar] [CrossRef]
- Lozano-Parra, J.; Schnabel, S.; Ceballos-Barbancho, A. The role of vegetation covers on soil wetting processes at rainfall event scale in scattered tree woodland of Mediterranean climate. J. Hydrol. 2015, 529, 951–961. [Google Scholar] [CrossRef]
- Metzger, J.C.; Wutzler, T.; Dalla Valle, N.; Filipzik, J.; Grauer, C.; Lehmann, R.; Roggenbuck, M.; Schelhorn, D.; Weckmüller, J.; Küsel, K.; et al. Vegetation impacts soil water content patterns by shaping canopy water fluxes and soil properties. Hydrol. Process. 2017, 31, 3783–3795. [Google Scholar] [CrossRef]
- Ghazavi, G.; Thomas, Z.; Hamon, Y.; Marie, J.C.; Corson, M.; Merot, P. Hedgerow impacts on soil-water transfer due to rainfall interception and root-water uptake. Hydrol. Process. 2008, 22, 4723–4735. [Google Scholar] [CrossRef]
- Leung, A.K.; Garg, A.; Coo, J.L.; Ng, C.W.W.; Hau, B.C.H. Effects of the roots of Cynodon dactylon and Schefflera heptaphylla on water infiltration rate and soil hydraulic conductivity. Hydrol. Process. 2015, 29, 3342–3354. [Google Scholar] [CrossRef]
- Seyfried, M.S.; Wilcox, B.P. Soil water storage and rooting depth: Key factors controlling recharge on rangelands. Hydrol. Process. 2006, 20, 3261–3275. [Google Scholar] [CrossRef]
- Vaz, C.M.P.; Hopmans, J.W.; Macedo, A.; Bassoi, L.H.; Wildenschild, D. Soil water retention measurements using a combined tensiometer-coiled time domain reflectometry probe. Soil Sci. Soc. Am. J. 2002, 66, 1752–1759. [Google Scholar] [CrossRef]
- Vaz, C.M.P.; Hopmans, J.W. Simultaneous measurement of soil penetration resistance and water content with a combined penetrometer–TDR moisture probe. Soil Sci. Soc. Am. J. 2001, 65, 4–12. [Google Scholar] [CrossRef]
- Kosugi, K.; Yamakawa, Y.; Masaoka, N.; Mizuyama, T. A combined penetrometer-moisture probe for surveying soil properties of natural hillslopes. Vadose Zone J. 2009, 8, 52–63. [Google Scholar] [CrossRef]
- Nissen, H.H.; Moldrup, P.; de Jonge, L.W.; Jacobsen, O.H. Time domain reflectometry coil probe measurements of water content during fingered flow. Soil Sci. Soc. Am. J. 1999, 63, 493–500. [Google Scholar] [CrossRef]
- Nissen, H.H.; Moldrup, P.; Henriksen, K. High-resolution time domain reflectometry coil probe for measuring soil water content. Soil Sci. Soc. Am. J. 1998, 62, 1203–1211. [Google Scholar] [CrossRef]
- Katsura, S.; Kosugi, K.; Mizuyama, T. Application of a coil-type TDR probe for measuring the volumetric water content in weathered granitic bedrock. Hydrol. Process. 2008, 22, 750–763. [Google Scholar] [CrossRef]
- Subedi, S.; Kawamoto, K.; Karunarathna, A.K.; Moldrup, P.; Wollesen de Jonge, L.; Komatsu, T. Mini tensiometer-time domain reflectometry coil probe for measuring soil water retention properties. Soil Sci. Soc. Am. J. 2013, 77, 1517–1528. [Google Scholar] [CrossRef]
- Toll, D.G.; Hassan, A.A.; King, J.M.; Asquith, J.D. New devices for water content measurement. In Proceedings of the 18th International Conference on Soil Mechanics and Geotechnical Engineering, Paris, France, 2–6 September 2013; pp. 1199–1202. [Google Scholar]
- Lai, Y.-J.; Chang, C.-S.; Tsao, T.-M.; Wey, T.-H.; Chiang, P.-N.; Wang, Y.-N. Preliminary assessment of soil erosion impact during forest restoration process using self-designed tiny weirs. J. Exp. For. Natl. Taiwan Univ. 2013, 27, 273–284, (In Chinese, with English abstract). [Google Scholar]
- Liang, W.-L.; Kosugi, K.; Mizuyama, T. Heterogeneous soil water dynamics around a tree growing on a steep hillslope. Vadose Zone J. 2007, 6, 879–889. [Google Scholar] [CrossRef]
- Penna, D.; Tromp-van Meerveld, H.J.; Gobbi, A.; Borga, M.; Dalla Fontana, G. The influence of soil moisture on threshold runoff generation processes in an alpine headwater catchment. Hydrol. Earth Syst. Sci. 2011, 15, 689–702. [Google Scholar] [CrossRef]
- Campbell. TDR100 Instruction Manual; Campbell Scientific Inc.: Logan, UT, USA, 2000. [Google Scholar]
- Takagi, K.; Lin, H.S. Temporal dynamics of soil moisture spatial variability in the shale hills critical zone observatory. Vadose Zone J. 2011, 10, 832–842. [Google Scholar] [CrossRef]
- Liang, W.-L.; Li, S.-L.; Hung, F.-X. Analysis of the contributions of topographic, soil, and vegetation features on the spatial distributions of surface soil moisture in a steep natural forested headwater catchment. Hydrol. Process. 2017, 31, 3796–3809. [Google Scholar] [CrossRef]
- Bogena, H.R.; Herbst, M.; Huisman, J.A.; Rosenbaum, U.; Weuthen, A.; Vereecken, H. Potential of wireless sensor networks for measuring soil water content variability. Vadose Zone J. 2010, 9, 1002. [Google Scholar] [CrossRef]
- Penna, D.; Borga, M.; Norbiato, D.; Dalla Fontana, G. Hillslope scale soil moisture variability in a steep alpine terrain. J. Hydrol. 2009, 364, 311–327. [Google Scholar] [CrossRef]
- Rosenbaum, U.; Bogena, H.R.; Herbst, M.; Huisman, J.A.; Peterson, T.J.; Weuthen, A.; Western, A.W.; Vereecken, H. Seasonal and event dynamics of spatial soil moisture patterns at the small catchment scale. Water Resour. Res. 2012, 48, W10544. [Google Scholar] [CrossRef]
- Garcia-Estringana, P.; Latron, J.; Llorens, P.; Gallart, F. Spatial and temporal dynamics of soil moisture in a Mediterranean mountain area (Vallcebre, NE Spain). Ecohydrology 2012, 6, 741–753. [Google Scholar] [CrossRef]
- Western, A.; Grayson, R.; Blöschl, G.; Wilson, D. Spatial variability of soil moisture and its implications for scaling. In Scaling Methods in Soil Physics; Pachepsky, Y., Radcliffe, D.E., Selim, H.M., Eds.; CRC Press: Boca Raton, FL, USA, 2003; pp. 119–142. [Google Scholar]
- Choi, M.; Jacobs, J.M. Soil moisture variability of root zone profiles within SMEX02 remote sensing footprints. Adv. Water Resour. 2007, 30, 883–896. [Google Scholar] [CrossRef]
- Famiglietti, J.S.; Ryu, D.; Berg, A.A.; Rodell, M.; Jackson, T.J. Field observations of soil moisture variability across scales. Water Resour. Res. 2008, 44, W01423. [Google Scholar] [CrossRef]
- Zucco, G.; Brocca, L.; Moramarco, T.; Morbidelli, R. Influence of land use on soil moisture spatial–temporal variability and monitoring. J. Hydrol. 2014, 516, 193–199. [Google Scholar] [CrossRef]
- Greminger, P.J.; Sud, Y.K.; Nielsen, D.R. Spatial variability of field-measured soil-water characteristics. Soil Sci. Soc. Am. J. 1985, 49, 1075–1082. [Google Scholar] [CrossRef]
- Yeh, T.C.J.; Gelhar, L.W.; Wierenga, P.J. Observations of spatial variability of soil-water pressure in a field soil. Soil Sci. 1986, 142, 7–12. [Google Scholar] [CrossRef]
- Yu, H.; Yang, P.; Lin, H. Spatiotemporal patterns of soil matric potential in the Shale Hills Critical Zone Observatory. Vadose Zone J. 2015, 14. [Google Scholar] [CrossRef]
- Liang, W.-L.; Chan, M.-C. Spatial and temporal variations in the effects of soil depth and topographic wetness index of bedrock topography on subsurface saturation generation in a steep natural forested headwater catchment. J. Hydrol. 2017, 546, 405–418. [Google Scholar] [CrossRef]
- Ghestem, M.; Sidle, R.C.; Stokes, A. The influence of plant root systems on subsurface flow: Implications for slope stability. BioScience 2011, 61, 869–879. [Google Scholar] [CrossRef]
- Yunusa, I.; Mele, P.; Rab, M.; Schefe, C.; Beverly, C. Priming of soil structural and hydrological properties by native woody species, annual crops, and a permanent pasture. Aust. J. Soil Res. 2002, 40, 207–220. [Google Scholar] [CrossRef]
- Weiler, M. Macropores and preferential flow-a love-hate relationship. Hydrol. Process. 2017, 31, 15–19. [Google Scholar] [CrossRef]
| Depth (cm) | Particle Density (g/cm−3) | Bulk Density (g/cm−3) | Porosity (%) | Sand (%) | Silt (%) | Clay (%) |
|---|---|---|---|---|---|---|
| 20 | 2.18 | 1.32 | 39.6 | 33.8 | 35.6 | 30.6 |
| 35 | 2.27 | 1.46 | 35.8 | 36.3 | 34.4 | 29.4 |
| 60 | 2.23 | 1.40 | 37.4 | 34.1 | 33.2 | 32.7 |
| Event | Start | End | Duration (hr) | Total Rainfall (mm) | Max. Rainfall Intensity (mm/10 min) |
|---|---|---|---|---|---|
| 1 | 26 July 2013 12:30 | 26 July 2013 19:40 | 7.2 | 40.0 | 5.5 |
| 2 | 30 July 2013 12:30 | 30 July 2013 20:20 | 7.8 | 40.5 | 9.5 |
| 3 | 14 August 2013 13:10 | 14 August 2013 21:50 | 8.7 | 75.0 | 8.5 |
| 4 | 15 August 2013 12:30 | 15 August 2013 17:00 | 4.5 | 23.0 | 5.0 |
| 5 | 16 August 2013 16:10 | 16 August 2013 22:30 | 6.3 | 45.0 | 14.5 |
| 6 | 21 August 2013 10:30 | 22 August 2013 17:50 | 31.3 | 637.0 | 18.0 |
| 7 | 24 August 2013 12:10 | 24 August 2013 20:10 | 8.0 | 40.0 | 4.5 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, S.-L.; Liang, W.-L. Spatial–Temporal Soil Water Dynamics beneath a Tree Monitored by Tensiometer-Time Domain Reflectometry Probes. Water 2019, 11, 1662. https://doi.org/10.3390/w11081662
Li S-L, Liang W-L. Spatial–Temporal Soil Water Dynamics beneath a Tree Monitored by Tensiometer-Time Domain Reflectometry Probes. Water. 2019; 11(8):1662. https://doi.org/10.3390/w11081662
Chicago/Turabian StyleLi, Sheng-Lun, and Wei-Li Liang. 2019. "Spatial–Temporal Soil Water Dynamics beneath a Tree Monitored by Tensiometer-Time Domain Reflectometry Probes" Water 11, no. 8: 1662. https://doi.org/10.3390/w11081662
APA StyleLi, S.-L., & Liang, W.-L. (2019). Spatial–Temporal Soil Water Dynamics beneath a Tree Monitored by Tensiometer-Time Domain Reflectometry Probes. Water, 11(8), 1662. https://doi.org/10.3390/w11081662





