Simulating the Overtopping Failure of Homogeneous Embankment by a Double-Point Two-Phase MPM
Abstract
1. Introduction
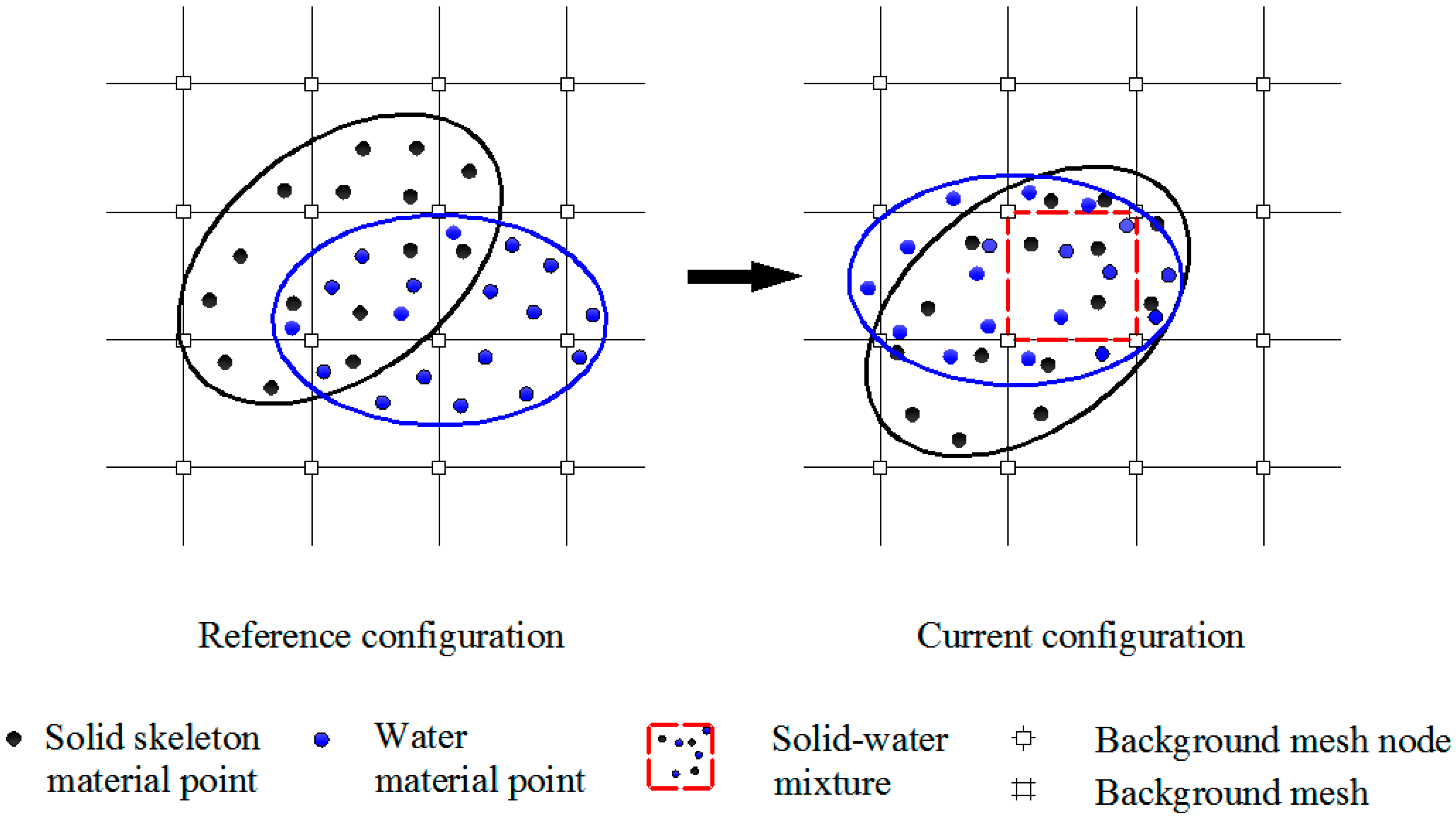
2. Mathematical Formulation
3. Numerical Examples
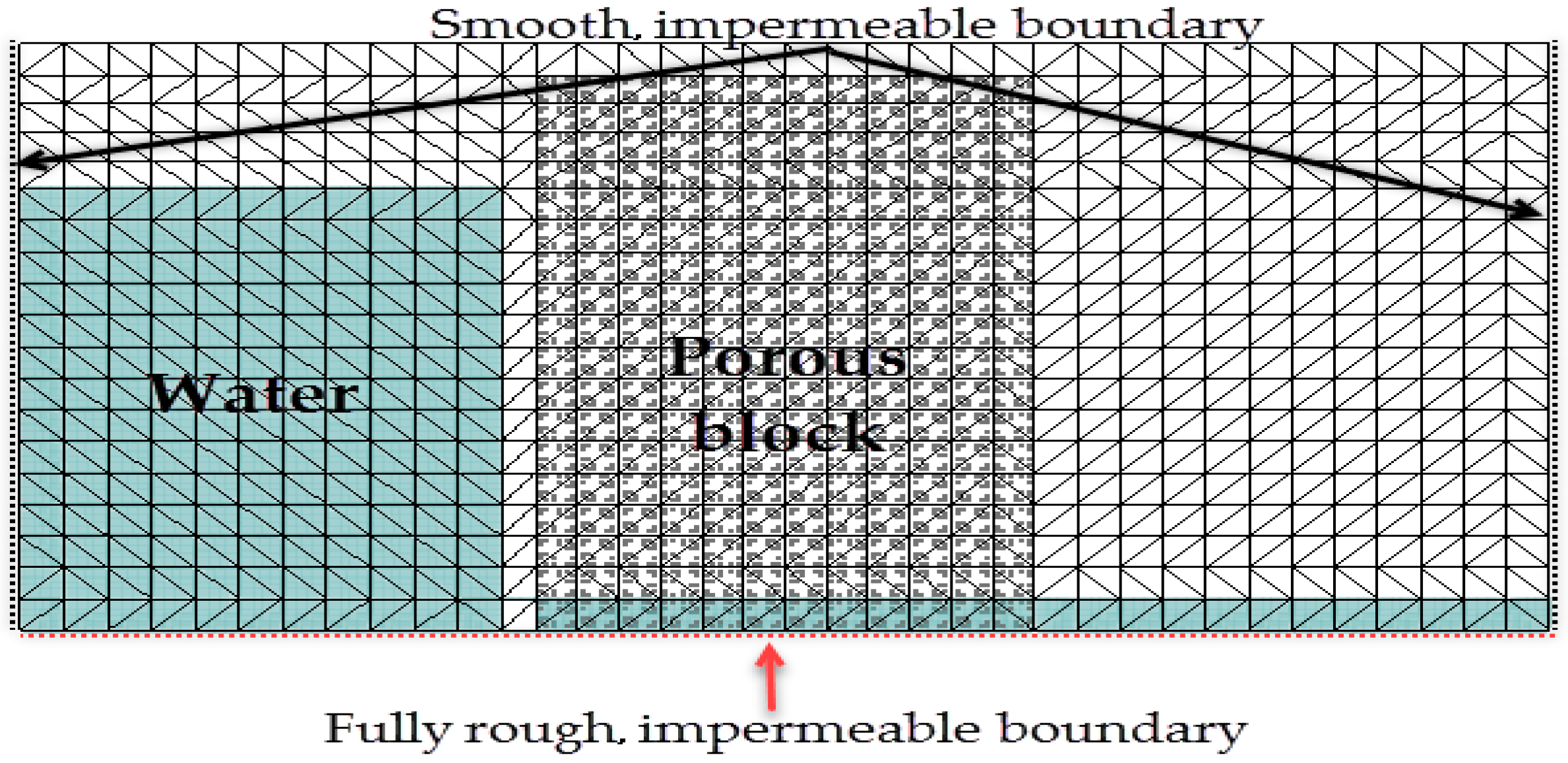
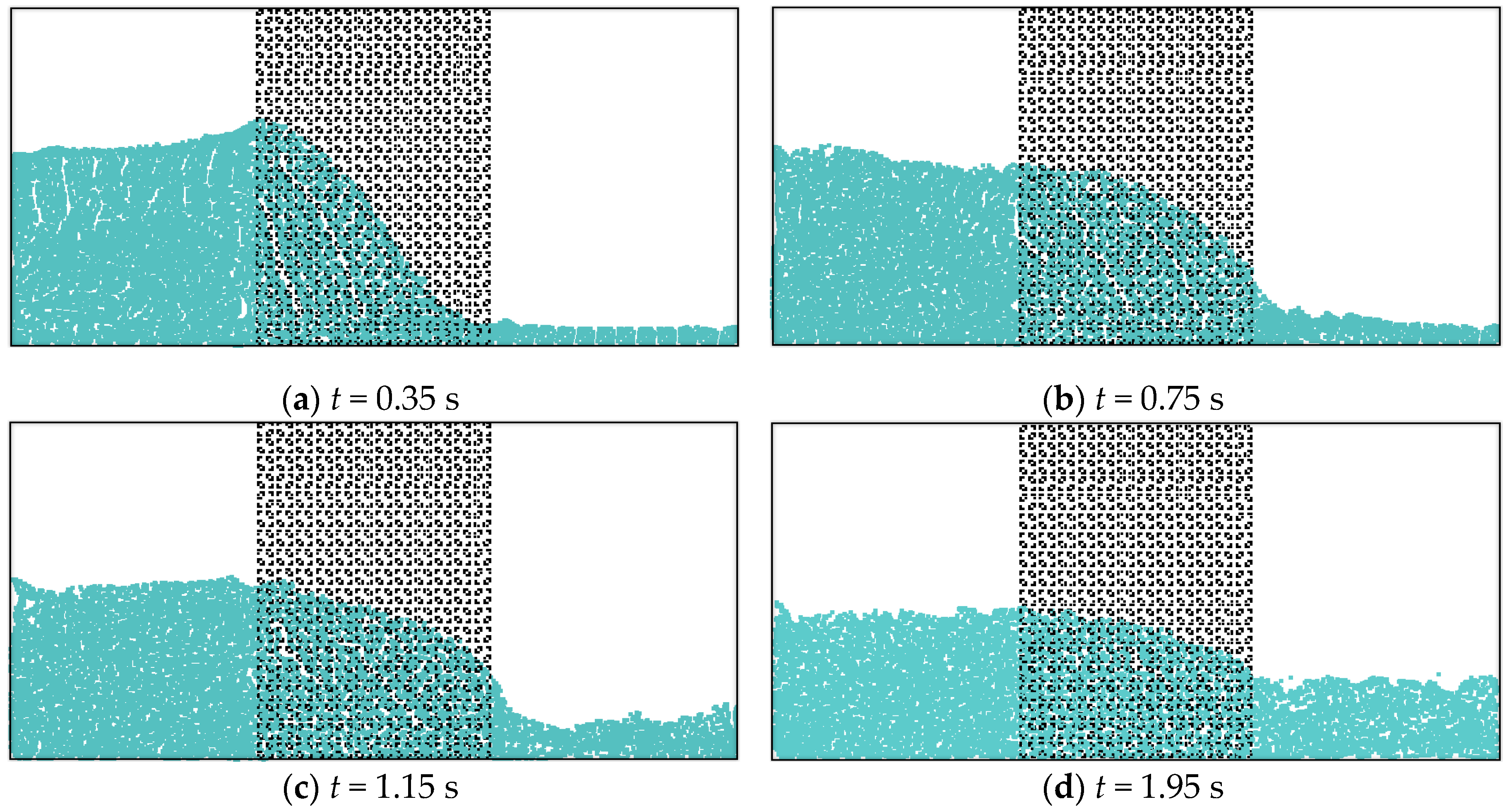
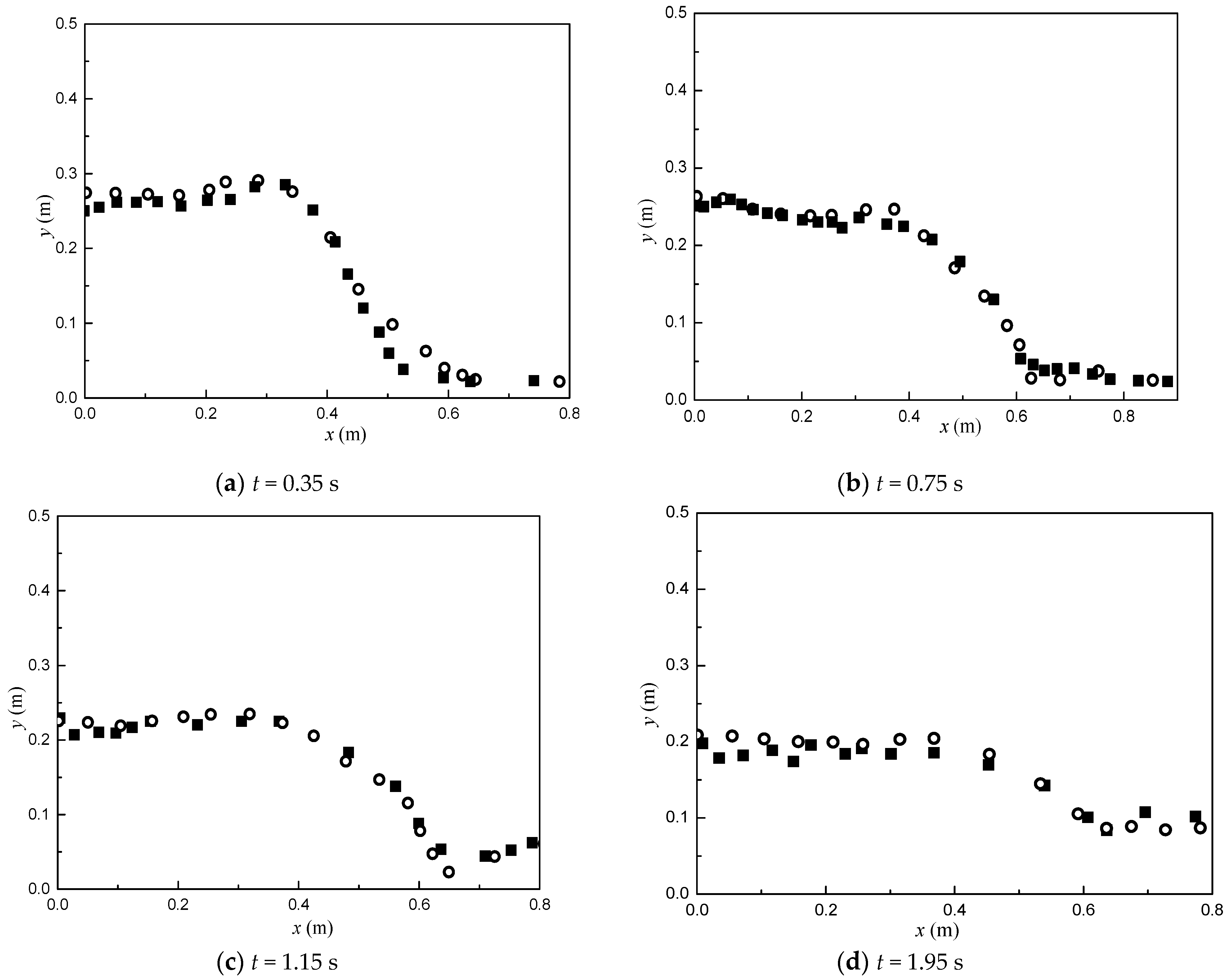
3.1. Flow through a Porous Block
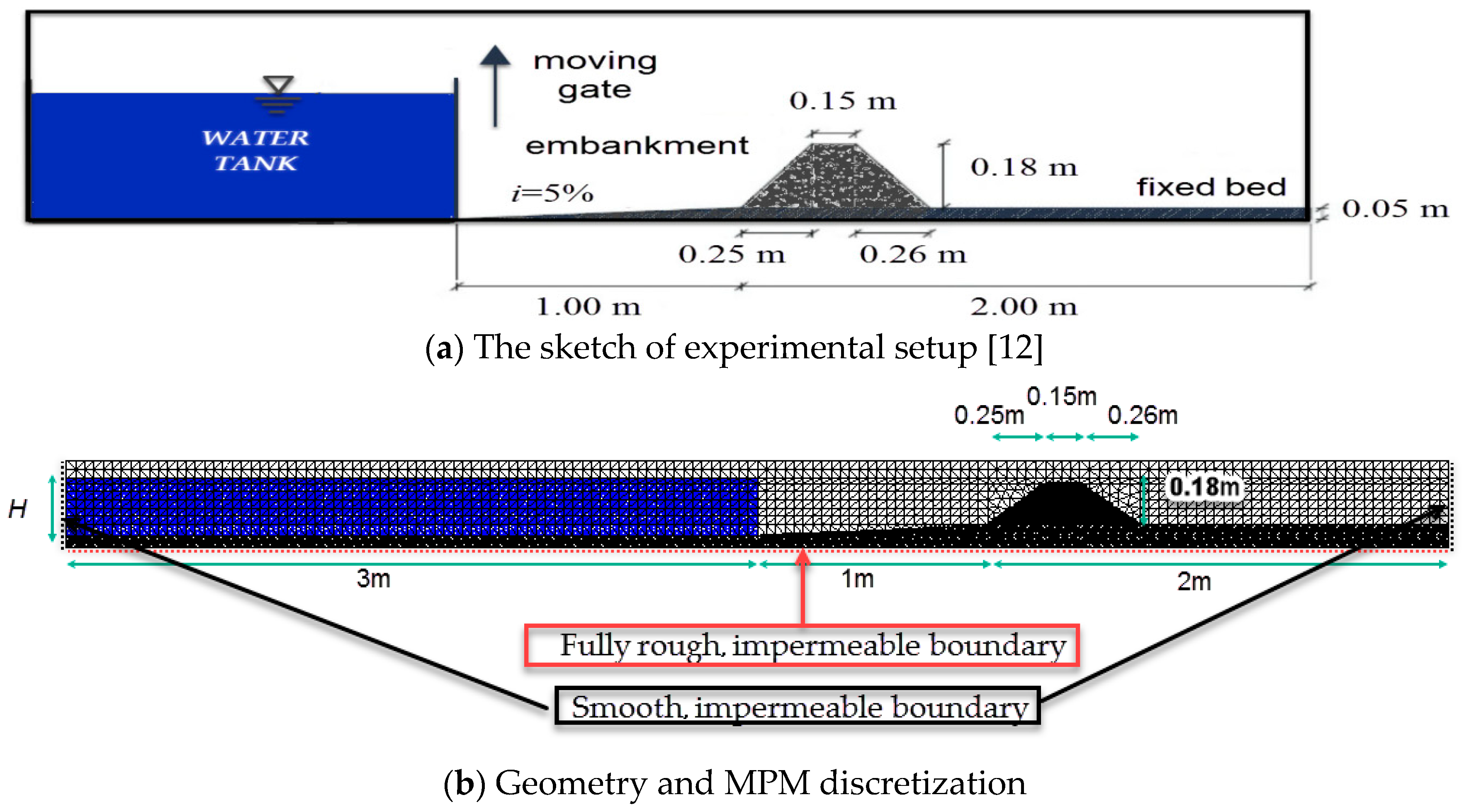
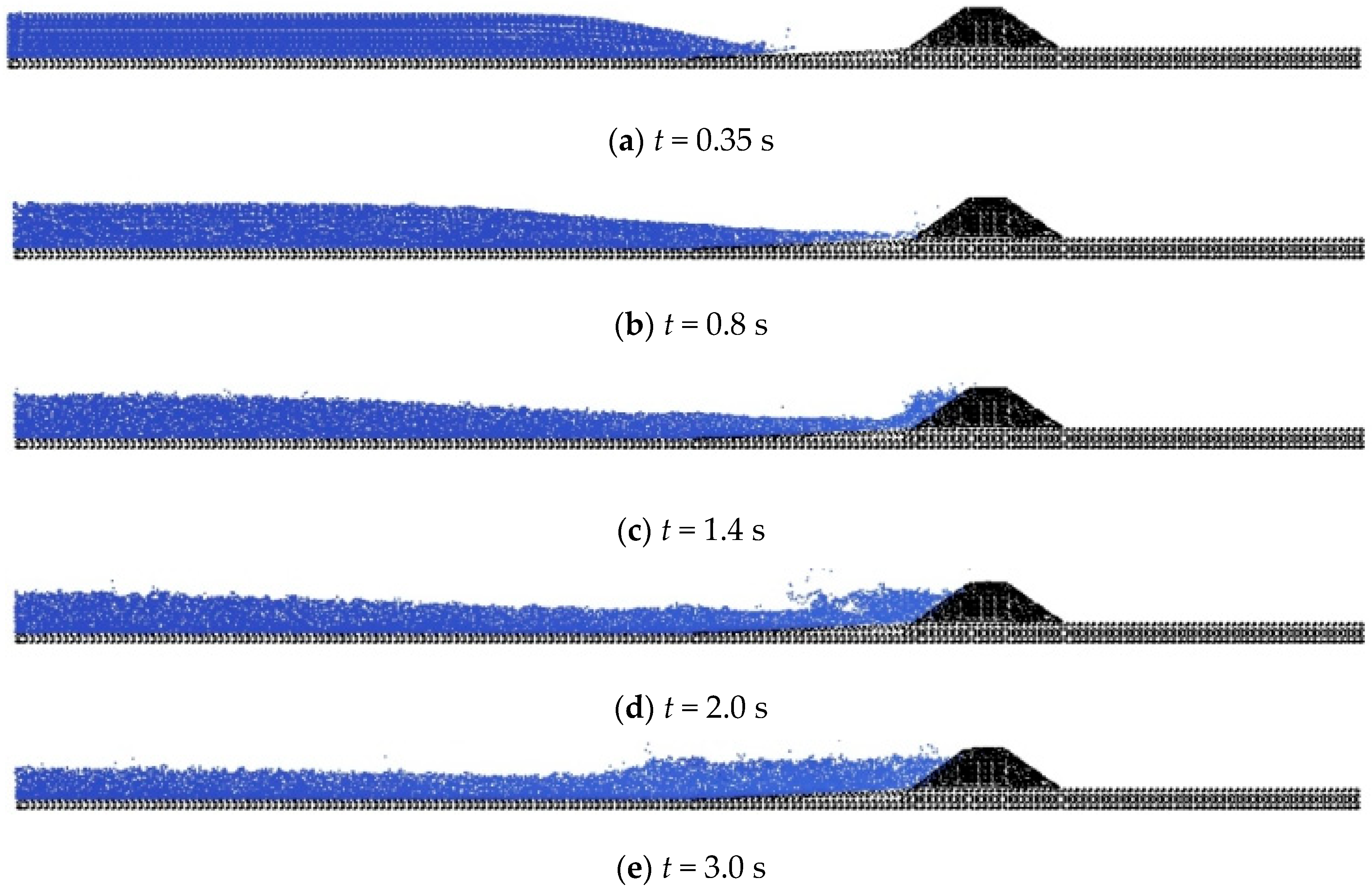
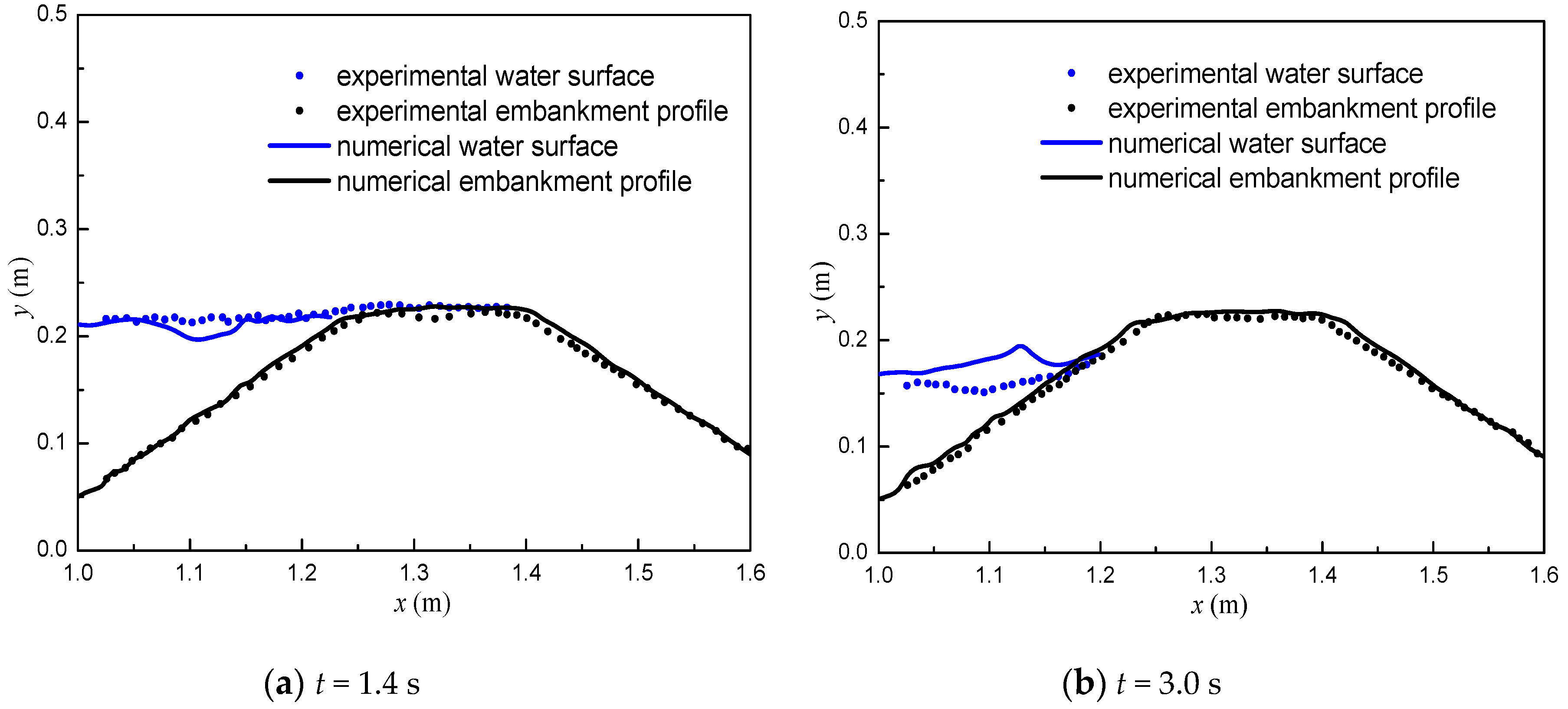
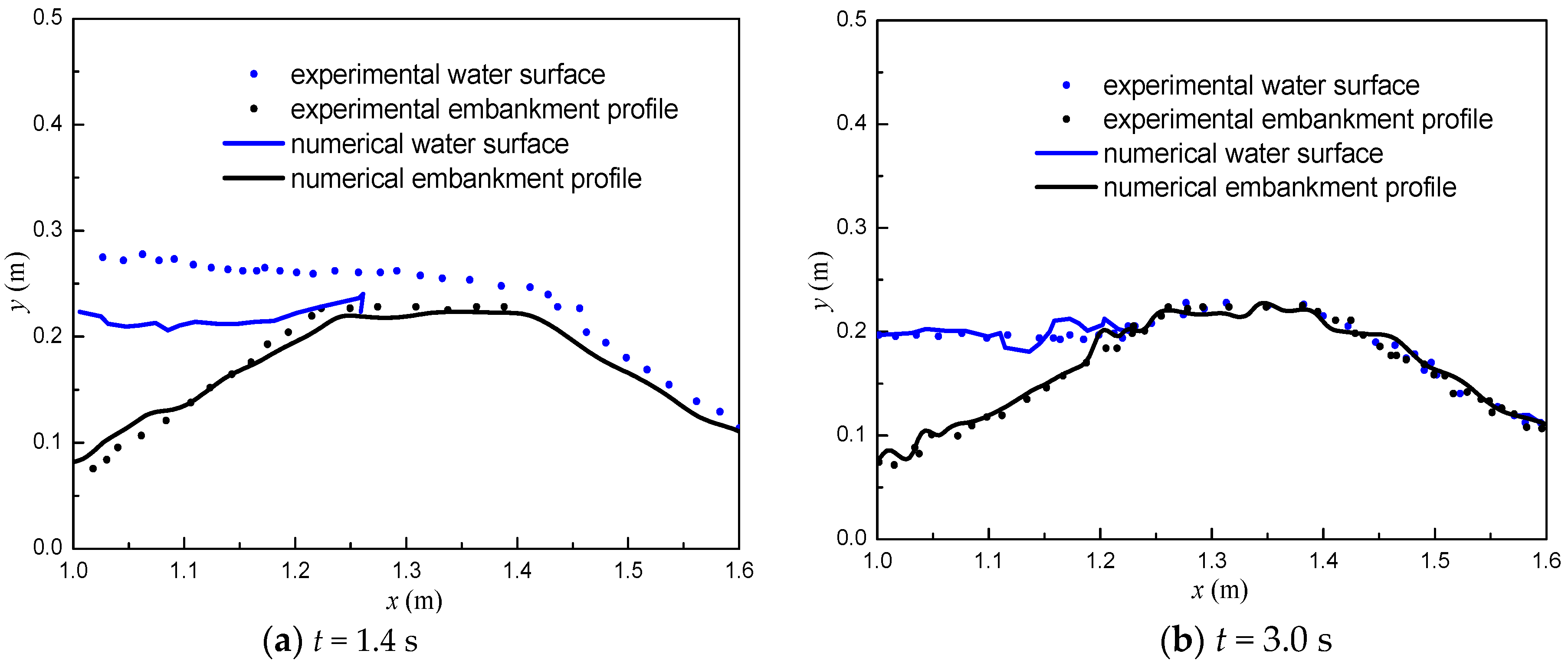
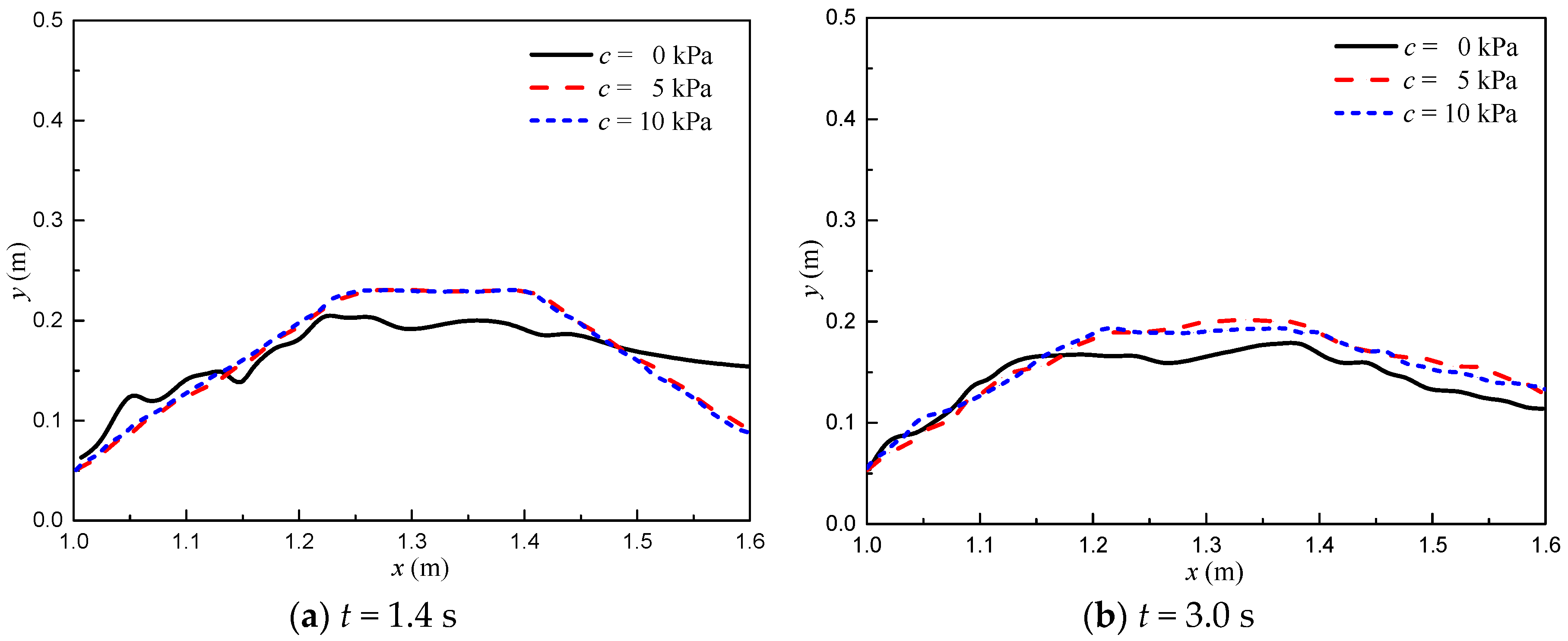
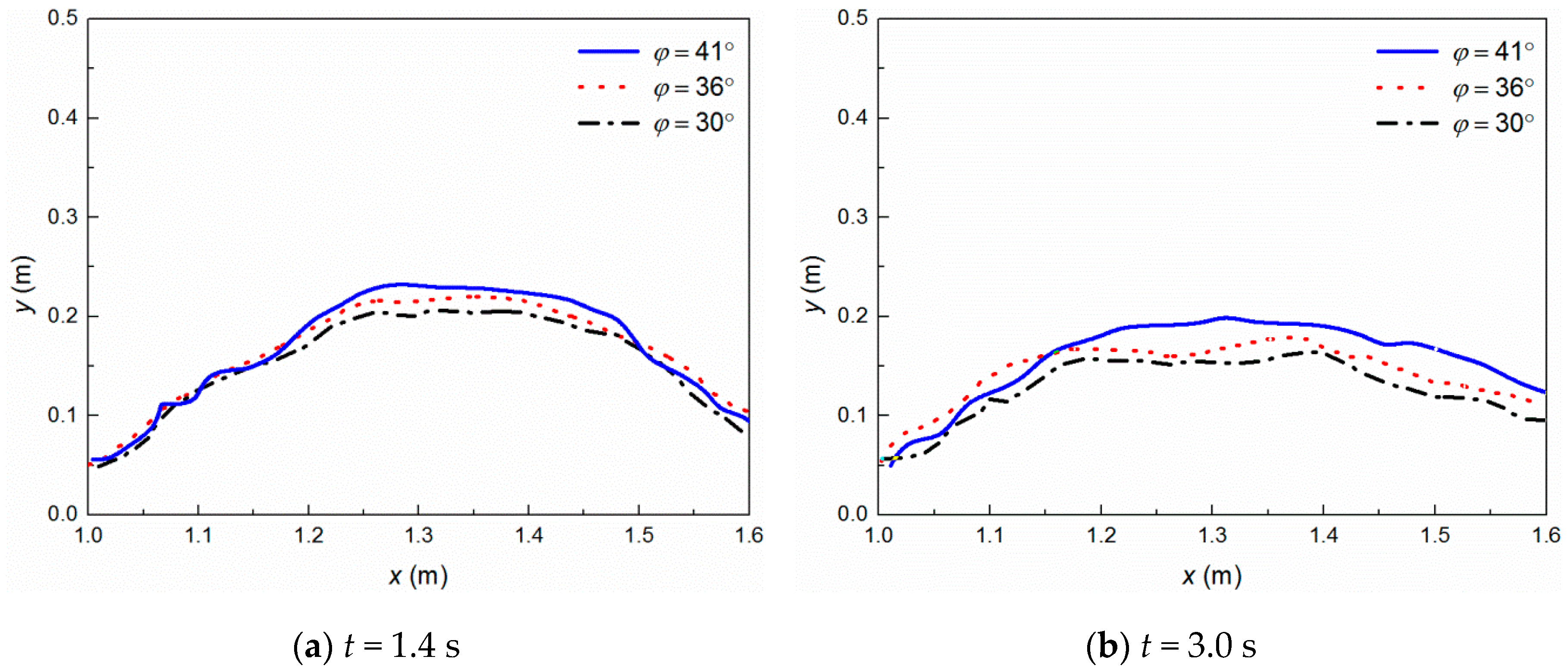
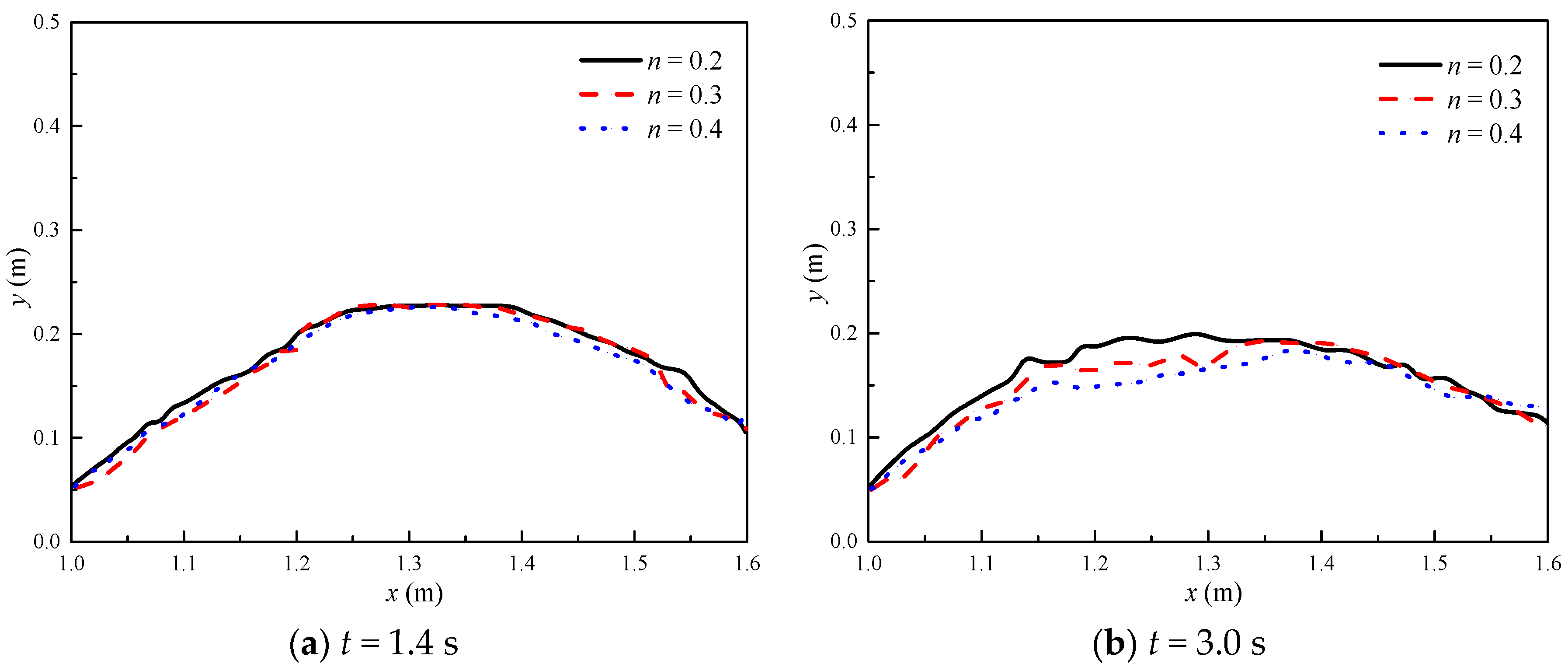
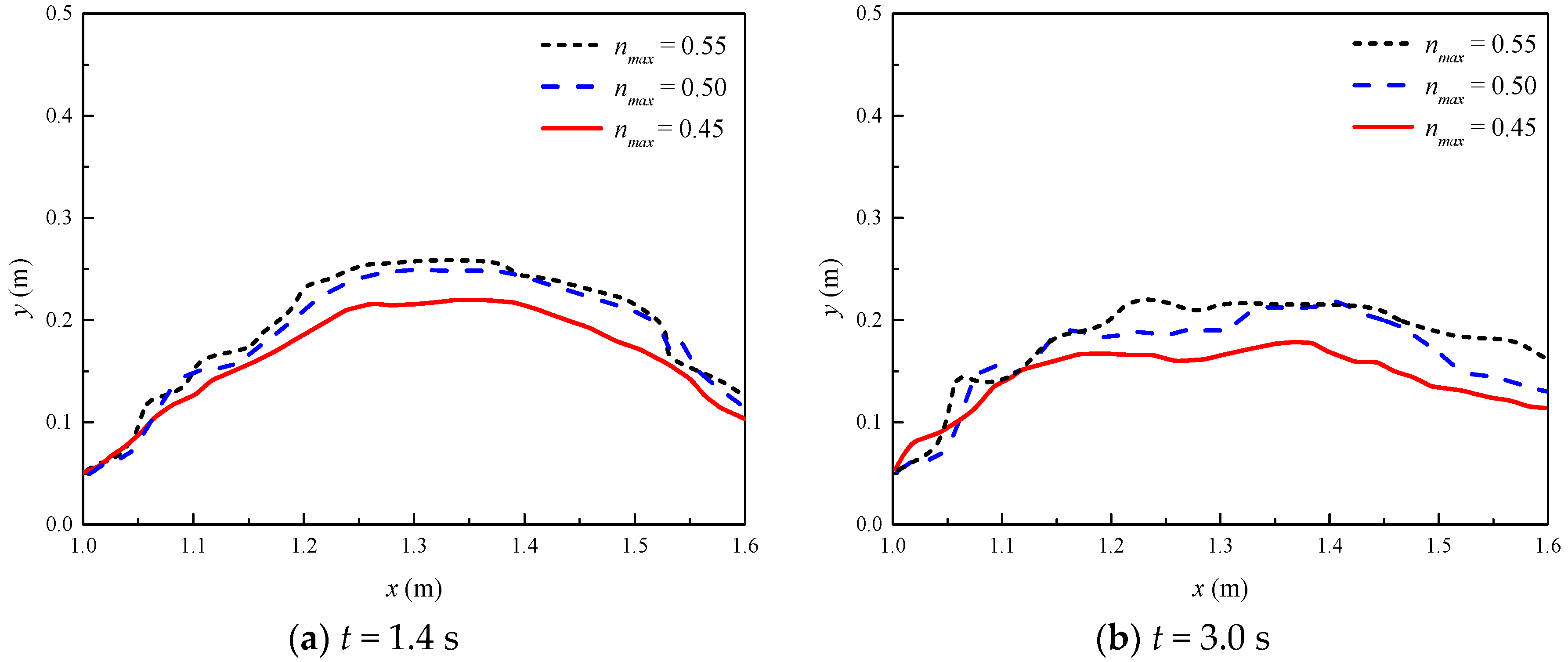
3.2. Overtopping Failure of Homogeneous Embankments
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Confalonieri, U.B.; Menne, R.; Akhtar, K.L.; Ebi, M.; Hauengue, R.S.K. Climate Change 2007: Impacts, Adaptation and Vulnerability; Contribution of Working Group II to the Fourth Assessment Report of the Intergovernmental Panel on Climate Change; Parry, M.L., Canziani, O.F., Palutikof, J.P., van der Linden, P.J., Hanson, C.E., Eds.; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
- Larese, A.; Rossi, R.; Oñate, E.; Toledo, M.Á.; Morán, R.; Campos, H. Numerical and experimental study of overtopping and failure of rockfill dams. Int. J. Geomech. 2015, 15, 1–23. [Google Scholar] [CrossRef]
- Powledge, G.R.; Ralston, D.C.; Miller, P.; Chen, Y.H.; Clopper, P.E.; Temple, D.M. Mechanics of overflow erosion on embankments. II: Hydraulic and design considerations. J. Hydraul. Eng. 1989, 115, 1056–1075. [Google Scholar] [CrossRef]
- Tingsanchali, T.; Chinnarasri, C. Numerical modeling of dam failure due to overtopping. Hydrol. Sci. J. 2001, 46, 113–130. [Google Scholar] [CrossRef]
- Chinnarasri, C.; Tingsanchali, T.; Weesakul, S.; Wongwises, S. Flow patterns and damage of dike overtopping. Int. J. Sediment Res. 2003, 18, 301–309. [Google Scholar]
- Leopardi, A.; Oliveri, E.; Greco, M. Numerical simulation of gradual earth-dam failure. In Proceedings of the 2nd International Conference New Trends in Water and Environmental Engineering for Safety and Life: Eco-Compatible Solutions for Aquatic Environments, Capri, Italy, 24–28 June 2002. [Google Scholar]
- Pontillo, M.; Schmocker, L.; Greco, M.; Hager, W.H. 1D numerical evaluation of dike erosion due to overtopping. J. Hydraul. Res. 2010, 48, 573–582. [Google Scholar] [CrossRef]
- Volz, C.; Rousselot, P.; Vetsch, D.; Faeh, R. Numerical modelling of non-cohesive embankment breach with the dual-mesh approach. J. Hydraul. Res. 2012, 50, 587–598. [Google Scholar] [CrossRef]
- Mizutani, H.; Nakagawa, H.; Yoden, T.; Kawaike, K.; Zhang, H. Numerical modelling of river embankment failure due to overtopping flow considering infiltration effects. J. Hydraul. Res. 2013, 51, 681–695. [Google Scholar] [CrossRef]
- Guan, M.; Wright, N.; Sleigh, P. 2D Process-Based Morphodynamic Model for Flooding by Noncohesive Dyke Breach. J. Hydraul. Eng. 2014, 140, 04014022. [Google Scholar] [CrossRef]
- Kakinuma, T.; Shimizu, Y. Large-scale experiment and numerical modeling of a riverine levee breach. J. Hydraul. Eng. 2014, 140, 04014039. [Google Scholar] [CrossRef]
- Evangelista, S. Experiments and Numerical simulations of dike erosion due to a wave impact. Water 2015, 7, 5831–5848. [Google Scholar] [CrossRef]
- Gingold, R.A.; Monaghan, J.J. Smoothed particle hydrodynamics: Theory and applications to non-spherical stars. Mon. Not. R. Astron. Soc. 1977, 181, 375–389. [Google Scholar] [CrossRef]
- Lucy, L. A numerical approach to testing the fission hypothesis. Astron. J. 1977, 81, 1013–1024. [Google Scholar] [CrossRef]
- Koshizuka, S.; Oka, Y. Moving-particle semi-implicit method for fragmentation of incompressible fluid. Nucl. Sci. Eng. 1996, 123, 421–434. [Google Scholar] [CrossRef]
- Belytschko, T.; Lu, Y.Y.; Gu, L. Element free Galerkin methods. Int. J. Numer. Meth. Eng. 1994, 37, 229–256. [Google Scholar] [CrossRef]
- Sulsky, D.; Chen, Z.; Schreyer, H.L. A particle method for history-dependent materials. Comput. Methods Appl. Mech. Eng. 1994, 118, 176–196. [Google Scholar] [CrossRef]
- Sulsky, D.; Zhou, S.J.; Schreyer, H.L. Application of a particle-in-cell method to solid mechanics. Comput. Phys. Commun. 1995, 87, 236–252. [Google Scholar] [CrossRef]
- Gotoh, H.; Hyashi, M.; Oda, K.; Sakai, T. Gridless analysis of slope failure of embankment by overflow. Ann. J. Hydraul. Eng. JSCE 2002, 46, 439–444. [Google Scholar] [CrossRef]
- Gotoh, H.; Ikari, H.; Tanioka, H.; Yamamoto, K. Numerical simulation of river-embankment erosion due to overflow by particle method. Proc. Hydraul. Eng. 2008, 52, 979–984. [Google Scholar] [CrossRef]
- Li, L.; Rao, X.; Amini, F.; Tang, H.W. SPH Modeling of Hydraulics and Erosion of HPTRM Levee. J. Adv. Res. Ocean Eng. 2015. [Google Scholar] [CrossRef]
- Zhang, W.; Maeda, K.; Saito, H.; Li, Z.; Huang, Y. Numerical analysis on seepage failures of dike due to water level-up and rainfall using a water–soil-coupled smoothed particle hydrodynamics model. Acta Geotech. 2016, 11, 1401–1418. [Google Scholar] [CrossRef]
- Liu, C.J.; Ning, B.H.; Ding, L.Q.; Zhang, S.F. Simulation of piping erosion process of dike foundation with element free method. Water Resour. Power 2012, 30, 58–61. [Google Scholar]
- Nikolic, M.; Ibrahimbegovic, A.; Miscevic, P. Discrete element model for the analysis of fluid-saturated fracturedporo-plastic medium based on sharp crack representation with embedded strong discontinuities. Comput. Methods Appl. Mech. Eng. 2016, 298, 407–427. [Google Scholar] [CrossRef]
- Zhao, X.Y.; Liang, D.F. MPM modelling of seepage flow through embankments. In Proceedings of the Twenty-Sixth International Ocean and Polar Engineering Conference, Rhodes, Greece, 26 June–1 July 2016. [Google Scholar]
- Martinelli, M.; Rohe, A.; Soga, K. Modeling dike failure using the Material Point Method. Procedia Eng. 2017, 175, 341–348. [Google Scholar] [CrossRef]
- Ma, S.; Zhang, X.; Qiu, X.M. Comparison study of MPM and SPH in modeling hypervelocity impact problems. Int. J. Impact Eng. 2009, 36, 272–282. [Google Scholar] [CrossRef]
- Mackenzie-Helnwein, P.; Arduino, P.; Shin, W.; Moore, J.A.; Miller, G.R. Modeling strategies for multiphase drag interactions using the material point method. Int. J. Numer. Methods Eng. 2010, 83, 295–322. [Google Scholar] [CrossRef]
- Abe, K.; Soga, K.; Bandara, S. Material Point Method for Coupled Hydromechanical Problems. J. Geotech. Geoenviron. Eng. 2013, 140, 04013033. [Google Scholar] [CrossRef]
- Bandara, S.; Soga, K. Coupling of soil deformation and pore fluid flow using material point method. Comput. Geotech. 2015, 63, 199–214. [Google Scholar] [CrossRef]
- Fern, J.; Rohe, A.; Soga, K.; Alonso, E. The Material Point Method for Geotechnical Engineering: A Practical Guide; CRC Press, Taylor & Francis Group: Boca Raton, FL, USA, 2019. [Google Scholar]
- Soga, K.; Alonso, E.; Yerro, A.; Kumar, K.; Bandara, S. Trends in large-deformation analysis of landslide mass movements with particular emphasis on the material point method. Géotechnique 2015, 66, 1–26. [Google Scholar]
- Martinelli, M. Soil-Water Interaction with Material Point Method; Technical Report; Deltares: Delft, The Netherlands, 2016. [Google Scholar]
- Ceccato, F.; Yerro, A.; Martinelli, M. Modelling Soil-Water Interaction with the Material Point Method. Evaluation of single-point and double-point formulations. In Proceedings of the NUMGE, Porto, Portugal, 25–29 June 2018. [Google Scholar]
- Liu, L.-F.; Lin, P.Z.; Chuang, K.-A.; Sakakiyama, T. Numerical modelling of wave interaction with porous structures. J. Waterw. Port Coast. Ocean. Eng. ASCE 1999, 125, 322–330. [Google Scholar] [CrossRef]
- Lauber, G.; Hager, W.H. Experiments to dambreak wave: Horizontal channel. J. Hydraul. Res. 1998, 36, 291–307. [Google Scholar] [CrossRef]




| Material | Parameter | Value |
|---|---|---|
| Porous block | Density (kg/m3) | 2700 |
| Young modulus (kPa) | 1000 | |
| Poisson’s ratio | 0.3 | |
| Initial porosity | 0.49 | |
| Mean diameter (mm) | 15.9 | |
| Water | Density (kg/m3) | 1000 |
| Bulk modulus (kPa) | 2.15 × 104 | |
| Dynamic viscosity (kPa·s) | 1 × 10−6 |
| Material | Parameter | Value |
|---|---|---|
| Sand | Density (kg/m3) | 2680 |
| Young modulus (kPa) | 1000 | |
| Poisson’s ratio | 0.3 | |
| Internal friction angle (°) | 36 | |
| Cohesion (kN) | 0 | |
| Initial porosity Maximum porosity | 0.40 0.45 | |
| Mean diameter (mm) | 0.2 | |
| Water | Density (kg/m3) | 1000 |
| Bulk modulus (kPa) | 2.15 × 104 | |
| Dynamic viscosity (kPa·s) | 1 × 10−6 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, Y.-S.; Yang, T.-T.; Qiu, L.-C.; Han, Y. Simulating the Overtopping Failure of Homogeneous Embankment by a Double-Point Two-Phase MPM. Water 2019, 11, 1636. https://doi.org/10.3390/w11081636
Yang Y-S, Yang T-T, Qiu L-C, Han Y. Simulating the Overtopping Failure of Homogeneous Embankment by a Double-Point Two-Phase MPM. Water. 2019; 11(8):1636. https://doi.org/10.3390/w11081636
Chicago/Turabian StyleYang, Yong-Sen, Ting-Ting Yang, Liu-Chao Qiu, and Yu Han. 2019. "Simulating the Overtopping Failure of Homogeneous Embankment by a Double-Point Two-Phase MPM" Water 11, no. 8: 1636. https://doi.org/10.3390/w11081636
APA StyleYang, Y.-S., Yang, T.-T., Qiu, L.-C., & Han, Y. (2019). Simulating the Overtopping Failure of Homogeneous Embankment by a Double-Point Two-Phase MPM. Water, 11(8), 1636. https://doi.org/10.3390/w11081636





