Determining the Relation between Groundwater Flow Velocities and Measured Temperature Differences Using Active Heating-Distributed Temperature Sensing
Abstract
1. Introduction
2. Materials and Methods
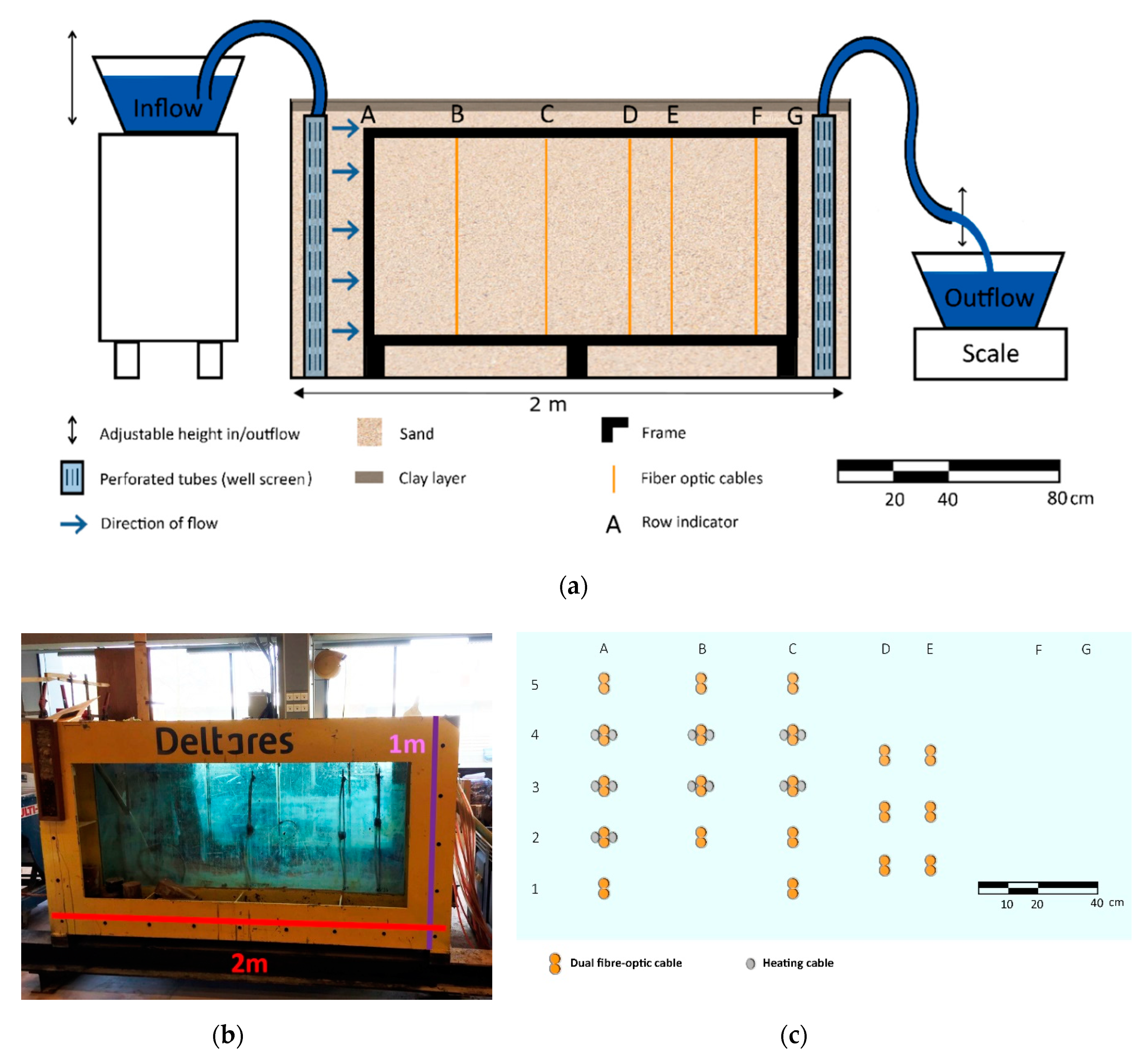
2.1. Laboratory Setup Flow Simulator
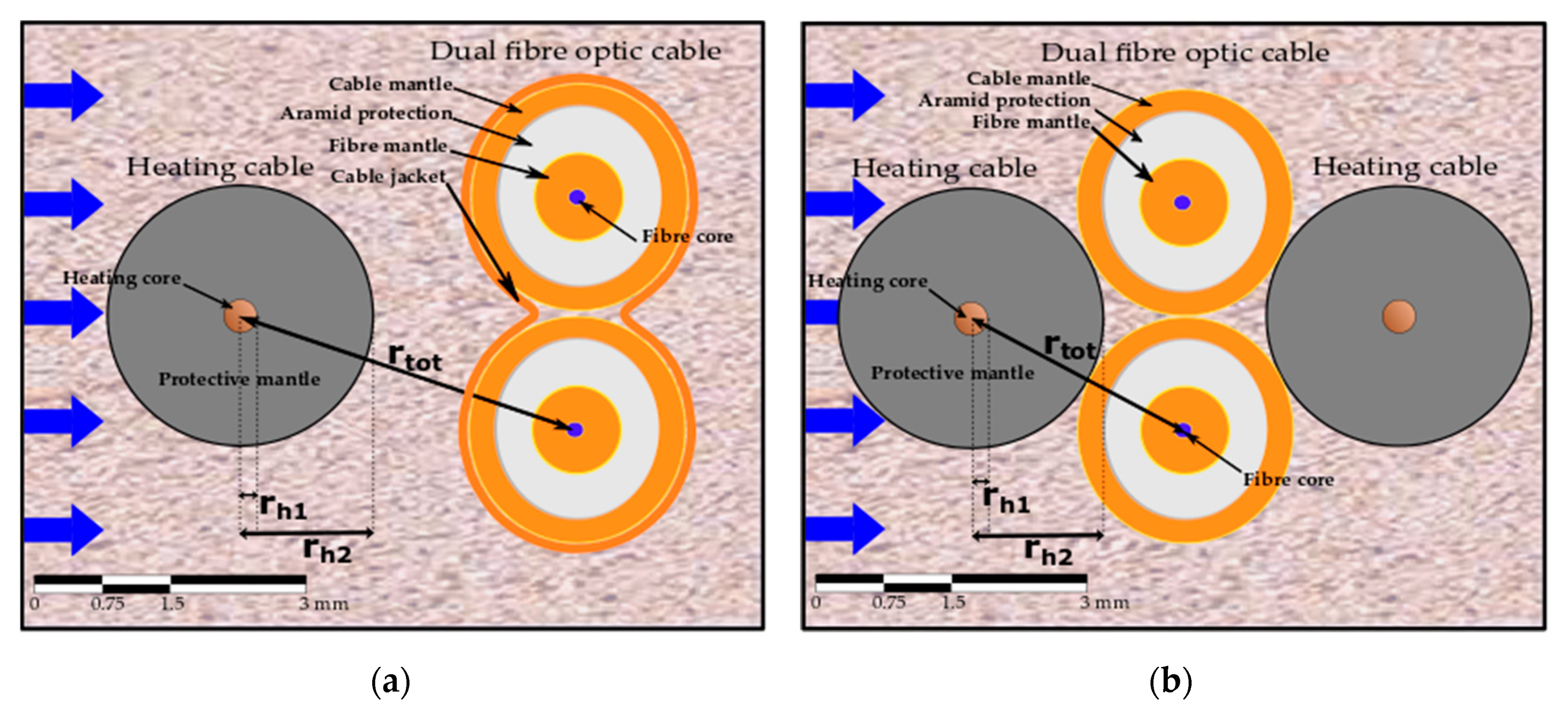
2.2. Measuring Temperature Using AH-DTS
2.3. Numerical Modeling
2.4. Analytical Solution for Direct Groundwater Flow Velocity Estimation Using
3. Results
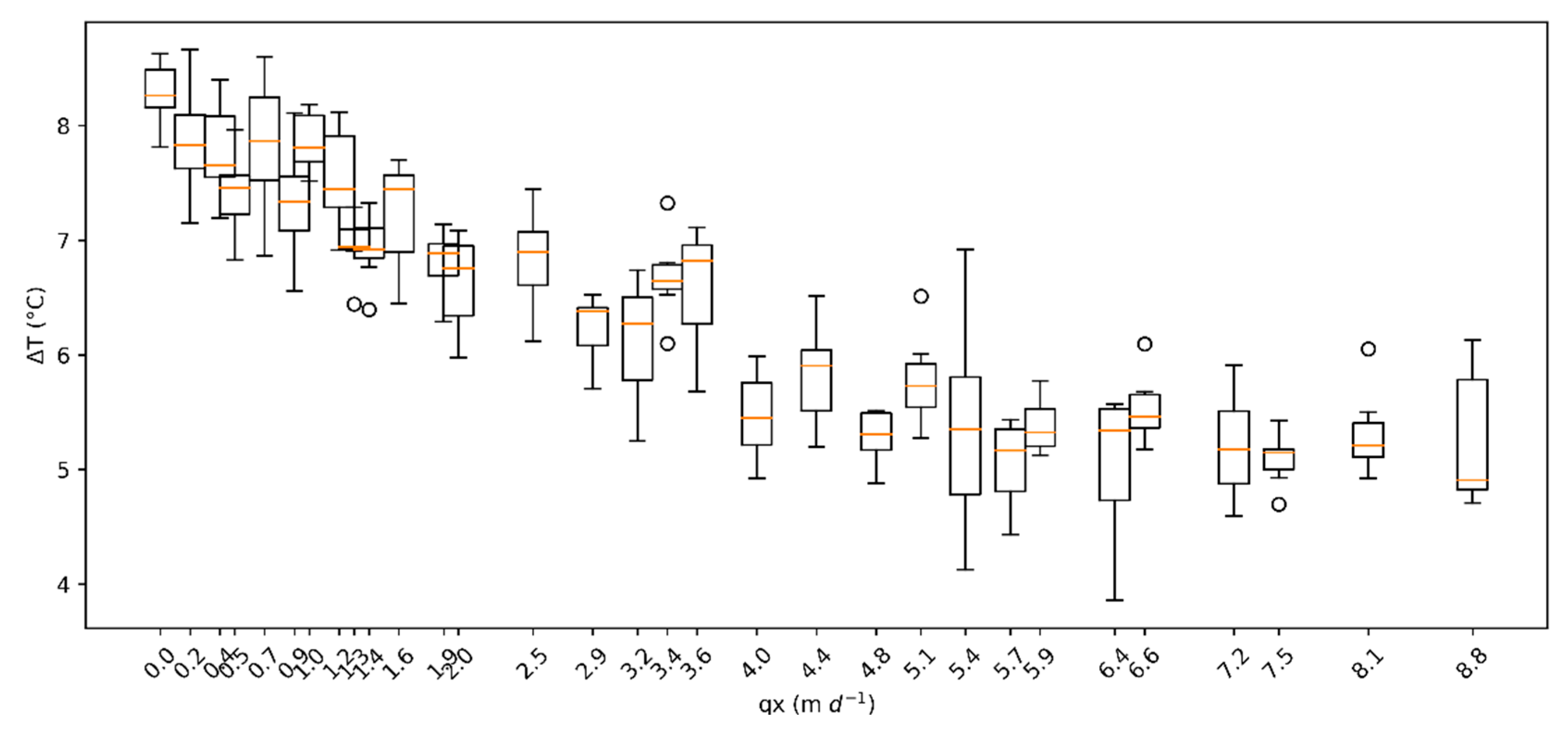
3.1. Experimental Results
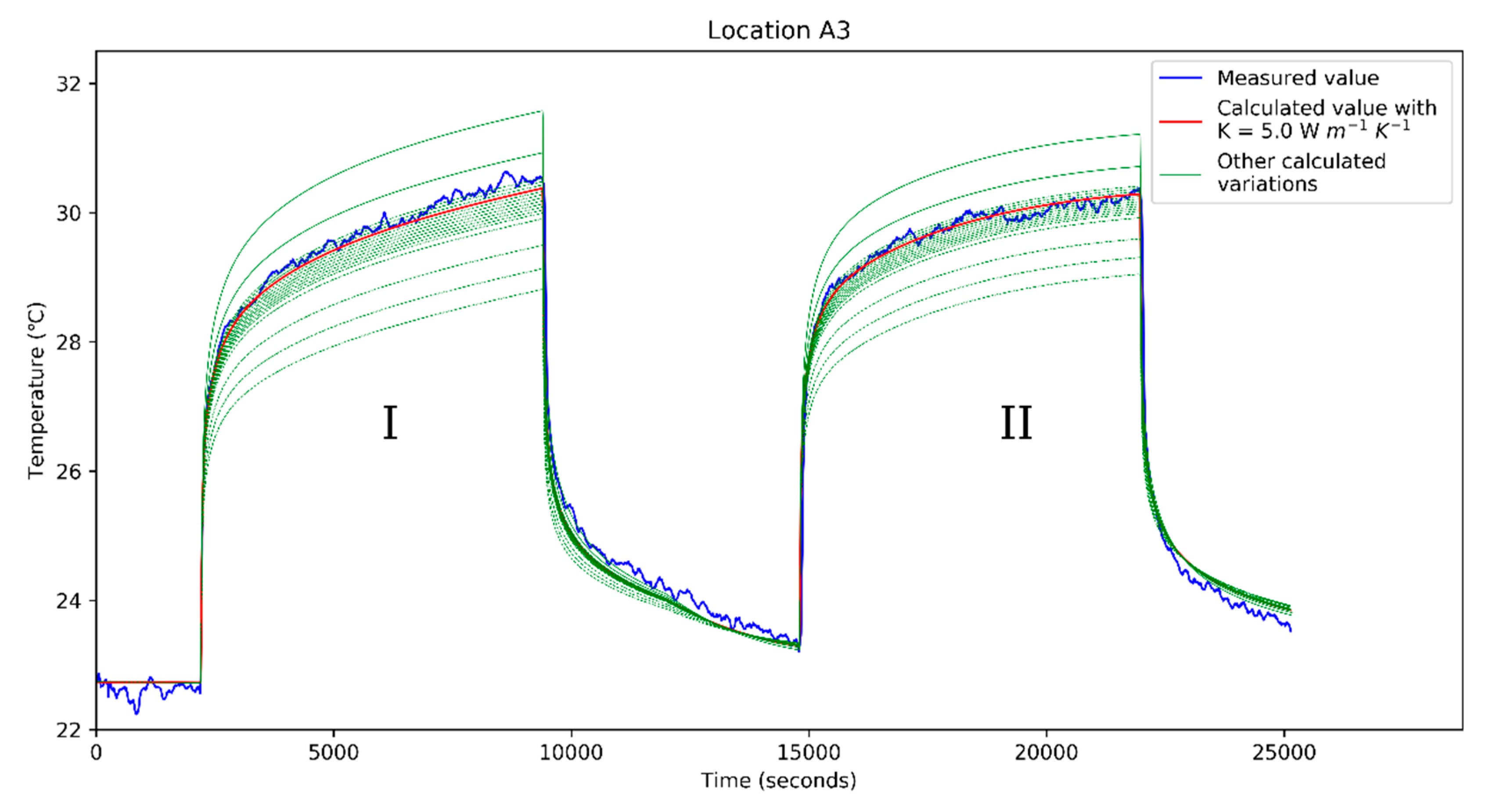
3.2. Analyzing Results with a Numerical Modeling Code (FlexPDE)
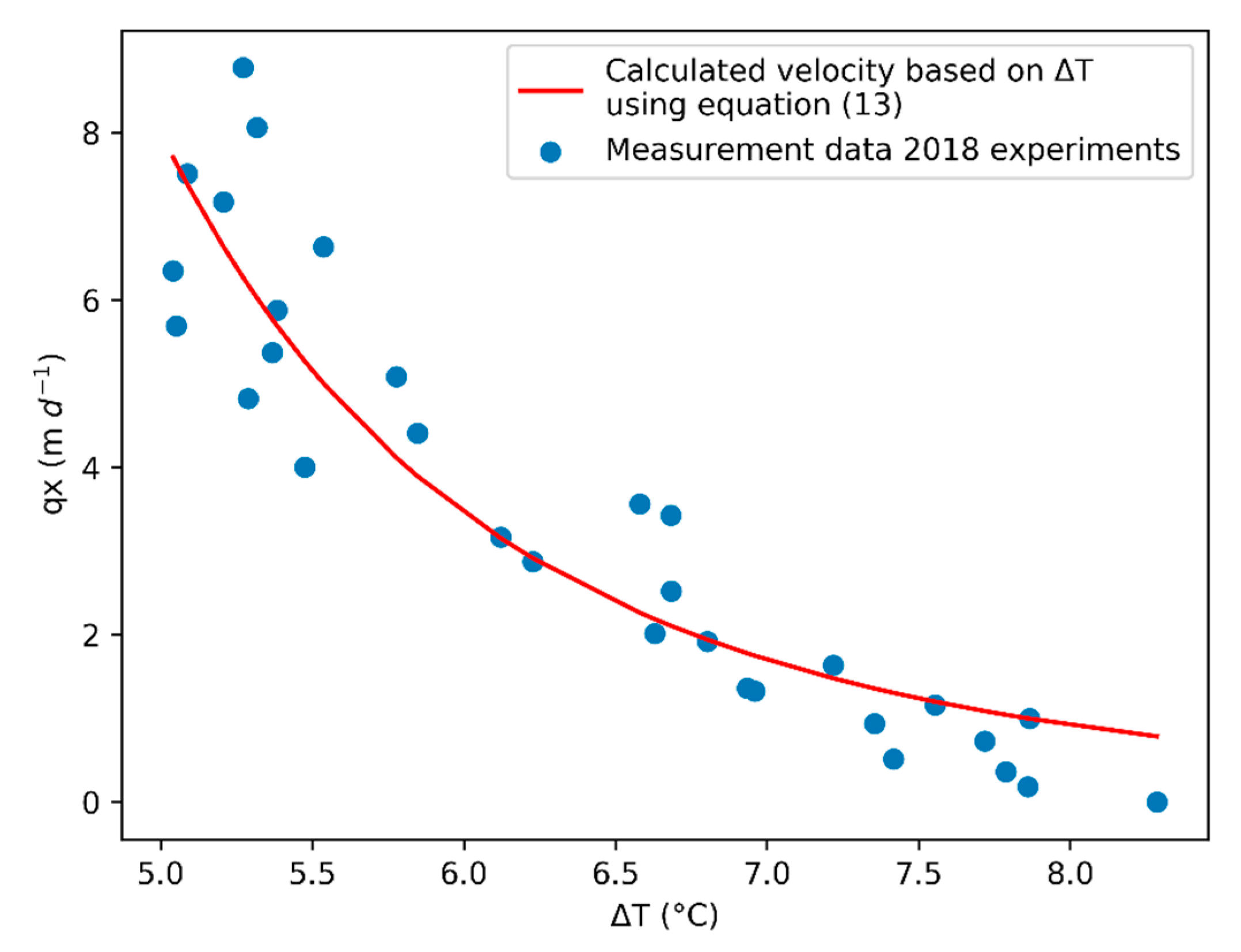
3.3. Applying Analytical Solution (Equation (13)) for Flow Velocity Estimation
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Equation (13) Derived Based on Equation (6)
- as heat input to the cable (W m−1),
- the radius of the heating part of the heating cable (m),
- the total radius of the heating cable (m),
- is the sum of the radii of the heating cable, the distance through the sediment and the radius of the fiber-optic cable used to measure temperature change combined (m),
- ∆T as the temperature change due to heating (°C), and
- is the combined thermal conductivity calculated (harmonic mean) as materials in series [26]:
- ○
- and are the thermal conductivity and fraction of thickness in respect to the total radius of the heating cable core,
- ○
- and are the thermal conductivity and fraction of thickness in respect to the total radius of the heating cable protection,
- ○
- and are the thermal conductivity and fraction of thickness in respect to the total radius of the DTS cable jacket,
- ○
- and are the thermal conductivity and fraction of thickness in respect to the total radius of the DTS cable aramid protection,
- ○
- and are the thermal conductivity and fraction of thickness in respect to the total radius of the DTS fiber mantle,
- ○
- and are the thermal conductivity and fraction of thickness in respect to the total radius of the DTS fiber,
- ○
- and are the thermal conductivity and fraction of thickness in respect to the total radius of the saturated sediment.
- Parameter is the heat transfer coefficient defined by [6]:
- ○
- L is the characteristic length of the flow (m),
- ○
- Nu the Nusselt number (-),
- ○
- the combined thermal conductivity of sediment and water as given by [18]:
- ▪
- is the porosity
- ▪
- and the thermal conductivity of the water and the sediment solid material.
- The Nusselt number is given by
- ○
- is the Reynolds number (-)
- ▪
- the density of the water (in kg m−3)
- ▪
- the groundwater flow velocity (in m s−1)
- ▪
- the dynamic viscosity of the water (kg m−1 s−1)
- ▪
- the kinematic viscosity of the water (in m2 s−1)
- ○
- is de Prandtl number (-)
- ▪
- the specific heat capacity of the fluid (in J kg−1 °C−1)
- ▪
- is the thermal conductivity of the fluid (in W m−1 °C−1)
- ○
- and are constants which are determined empirically and standard values for and are available depending on the values for and (Hilpert, 1933; Bergman et al., 2011).
References
- Burnett, B.; Chanton, J.; Christoff, J.; Kontar, E.; Krupa, S.; Lambert, M.; Moore, W.; O’Rourke, D.; Paulsen, R.; Smith, C.; et al. Assessing methodologies for measuring groundwater discharge to the ocean. Eos Trans. Am. Geophys. Union (Wash. DC) 2002, 83, 117–123. [Google Scholar] [CrossRef]
- Sommer, W.; Valstar, J.; Leusbrock, I.; Grotenhuis, T.; Rijnaarts, H. Optimization and spatial pattern of large-scale aquifer thermal energy storage. Appl. Energy 2015, 137, 322–337. [Google Scholar] [CrossRef]
- Greswell, R. High-Resolution in Situ Monitoring of Flow between Aquifers and Surface Waters; Environment Agency: Rio House, Waterside Drive, Aztec West, Almondsbury Bristol, UK, 2005. [Google Scholar]
- Brouyère, S.; Batlle-Aguilar, J.; Goderniaux, P.; Dassargues, A. A new tracer technique for monitoring groundwater fluxes: The Finite Volume Point Dilution Method. J. Contam. Hydrol. 2008, 95, 121–140. [Google Scholar] [CrossRef] [PubMed]
- Drost, W.; Klotz, D.; Koch, A.; Moser, H.; Neumaier, F.; Rauert, W. Point dilution methods of investigating ground water flow by means of radioisotopes. Water Resour. Res. 1968, 4, 125–146. [Google Scholar] [CrossRef]
- Read, T.; Bour, O.; Selker, J.S.; Bense, V.; Le Borgne, T.; Hochreutener, R.; Lavenant, N. Active-distributed temperature sensing to continuously quantify vertical flow in boreholes. Water Resour. Res. 2014, 50, 3706–3713. [Google Scholar] [CrossRef]
- Bakker, M.; Caljé, R.; Schaars, F.; Van Der Made, K.-J.; De Haas, S. An active heat tracer experiment to determine groundwater velocities using fiber optic cables installed with direct push equipment. Water Resour. Res. 2015, 51, 2760–2772. [Google Scholar] [CrossRef]
- Aufleger, M.; Conrad, M.; Goltz, M.; Perzlmaier, S.; Porras, P. Innovative dam monitoring tools based on distributed temperature measurement. Jordan J. Civ. Eng. 2007, 1, 29–37. [Google Scholar]
- Bense, V.; Read, T.; Bour, O.; Le Borgne, T.; Coleman, T.; Krause, S.; Chalari, A.; Mondanos, M.; Ciocca, F.; Selker, J.S. Distributed Temperature Sensing as a downhole tool in hydrogeology. Water Resour. Res. 2016, 52, 9259–9273. [Google Scholar] [CrossRef]
- Pehme, P.; Parker, B.; Cherry, J.; Greenhouse, J. Improved Resolution of Ambient Flow through Fractured Rock with Temperature Logs. Ground Water 2010, 48, 191–205. [Google Scholar] [CrossRef] [PubMed]
- Banks, E.W.; Shanafield, M.A.; Cook, P.G. Induced Temperature Gradients to Examine Groundwater Flowpaths in Open Boreholes. Ground Water 2014, 52, 943–951. [Google Scholar] [CrossRef] [PubMed]
- Read, T.; Bour, O.; Bense, V.; Le Borgne, T.; Goderniaux, P.; Klepikova, M.; Hochreutener, R.; Lavenant, N.; Boschero, V. Characterizing groundwater flow and heat transport in fractured rock using fiber-optic distributed temperature sensing. Geophys. Res. Lett. 2013, 40, 2055–2059. [Google Scholar] [CrossRef]
- Selker, F.; Selker, J.S. Investigating Water Movement Within and Near Wells Using Active Point Heating and Fiber Optic Distributed Temperature Sensing. Sensors 2018, 18, 1023. [Google Scholar] [CrossRef] [PubMed]
- Tombe, B.F.D.; Bakker, M.; Smits, F.; Schaars, F.; Made, K.; Van Der Made, K.-J.; Tombe, B.F.D. Estimation of the Variation in Specific Discharge Over Large Depth Using Distributed Temperature Sensing (DTS) Measurements of the Heat Pulse Response. Water Resour. Res. 2019, 55, 811–826. [Google Scholar] [CrossRef]
- Van Weesep, R. Modelling Groundwater Flow Velocity Using Temperature Change Data from Active Distributed Temperature Sensing Measurements in Laboratory Experiments. Master’s Thesis, University of Utrecht, Utrecht, The Netherlands, 2017. [Google Scholar]
- Hausner, M.B.; Suarez, F.; Glander, K.E.; Van De Giesen, N.; Selker, J.S.; Tyler, S.W. Calibrating Single-Ended Fiber-Optic Raman Spectra Distributed Temperature Sensing Data. Sensors 2011, 11, 10859–10879. [Google Scholar] [CrossRef] [PubMed]
- LEONI. Available online: www.leoni-fiber-optics.com (accessed on 15 May 2019).
- Anderson, M.P. Heat as a Ground Water Tracer. Groundwater 2005, 43, 951–968. [Google Scholar] [CrossRef] [PubMed]
- Farouki, O.T. Thermal Properties of Soils; U.S. Army Cold Regions Research and Engineering Laboratory: Hanover, NH, USA, 1981.
- Hamdhan, I.N.; Clarke, B. Determination of thermal conductivity of coarse and fine sand soils. In Proceedings of the World Geotherm, Bali, Indonesia, 25–29 April 2010; pp. 1–7. [Google Scholar]
- Abu-Hamdeh, N.H. Thermal Properties of Soils as affected by Density and Water Content. Biosyst. Eng. 2003, 86, 97–102. [Google Scholar] [CrossRef]
- Sim, L.; Ramanan, S.; Ismail, H.; Seetharamu, K.; Goh, T. Thermal characterization of Al2O3 and ZnO reinforced silicone rubber as thermal pads for heat dissipation purposes. Thermochim. Acta 2005, 430, 155–165. [Google Scholar] [CrossRef]
- Tomlins, P.E.; Rides, M.; Dawson, A.; Gee, M.; Dean, G.; Hobbs, C.; Allen, C.; Gnaniah, S.; Calver, A.; Darling, R. Physical Characterisation of Soft-Touch Polymers; National Physical Laboratory: Teddington, UK, 2005. [Google Scholar]
- Dupont. Kevlar Aramid Fiber Technical Guide; Dupon: Richmond, VA, USA, 2017; Available online: www.dupont.com (accessed on 14 February 2019).
- André, P.; Rocha, A.; Domingues, F.; Facão, M. Thermal Effects in Optical Fibres. In Developments in Heat Transfer; InTech: Haverhill, MA, USA, 2011; Volume 1987, Available online: http://www.intechopen.com/books/developments-in-heat-transfer/thermal-effects-in-optical-fibres (accessed on 4 August 2019).
- Bergman, T.L.; Incropera, F.P.; Lavine, A.S.; DeWitt, D.P. Fundamentals of Heat and Mass Transfer; John Wiley & Sons: Hoboken, NJ, USA, 2011; ISBN 978-0470501979. [Google Scholar]
- Hilpert, R. Wärmeabgabe von geheizten Drähten und Rohren im Luftstrom. Forsch. Ing. 1933, 4, 215–224. [Google Scholar] [CrossRef]
- Powell, R.W.; Ho, C.Y.; Liley, P.E. Thermal Conductivity of Selected Materials; U.S. Department of Commerce: Washington, DC, USA, 1966.
- Tarnawski, V.R.; Momose, T.; Leong, W.H. Thermal Conductivity of Standard Sands II. Saturated Conditions. Int. J. Thermophys. 2011, 32, 984–1005. [Google Scholar] [CrossRef]



| Parameter | Parameter | Reference |
|---|---|---|
| Heat input Q (W m−1) | 33.33 | Based on measured voltage input and cable resistance |
| Horizontal hydraulic conductivity (m d−1) | 40 | Determined in laboratorial experiments |
| Effective porosity (-) | 0.41 | Determined in laboratorial experiments |
| Medium | Thermal Conductivity (W m−1 K−1) | Specific Heat (J kg−1 K−1) | Density (g cm−3) | Reference |
|---|---|---|---|---|
| Sand | 5.1 1 | 830 | 2.65 | [19,20,21] |
| Water | 0.591 | 4186 | 0.99 | [19] |
| Heating cable core | 390 | 385 | 8.96 | |
| Heating cable protection material | 0.2 | 100 | 1.2 | [22] |
| DTS protective jacket | 0.196 | 1565 | 1.121 | [23] |
| DTS aramid protection | 0.04 | 1420 | 1.44 | [24] |
| DTS fiber mantle | 0.196 | 1565 | 1.121 | [23] |
| DTS fiber | 2 | 1430 | 2.2 | [25] |
| Thermal Conductivity (W m−1 K−1) | Location A4 (°C) | Location A3 (°C) |
|---|---|---|
| 4.0 | 0.670 | 0.596 |
| 4.5 | 0.372 | 0.323 |
| 5.0 | 0.149 | 0.172 |
| 5.5 | 0.322 | 0.382 |
| 6 | 0.523 | 0.581 |
| 6.5 | 0.700 | 0.758 |
| 7 | 0.857 | 0.914 |
| Thermal Conductivity (W m−1 K−1) | Location A4 (°C) | Location A3 (°C) |
|---|---|---|
| 4.85 | 0.192 | 0.164 |
| 4.9 | 0.172 | 0.159 |
| 4.95 | 0.156 | 0.162 |
| 5.0 | 0.149 | 0.172 |
| 5.05 | 0.152 | 0.188 |
| 5.1 | 0.163 | 0.207 |
| 5.15 | 0.178 | 0.227 |
| 5.2 | 0.195 | 0.249 |
| 5.25 | 0.215 | 0.271 |
| 5.3 | 0.236 | 0.294 |
| 5.35 | 0.257 | 0.316 |
| 5.4 | 0.279 | 0.338 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bakx, W.; Doornenbal, P.J.; van Weesep, R.J.; Bense, V.F.; Oude Essink, G.H.P.; Bierkens, M.F.P. Determining the Relation between Groundwater Flow Velocities and Measured Temperature Differences Using Active Heating-Distributed Temperature Sensing. Water 2019, 11, 1619. https://doi.org/10.3390/w11081619
Bakx W, Doornenbal PJ, van Weesep RJ, Bense VF, Oude Essink GHP, Bierkens MFP. Determining the Relation between Groundwater Flow Velocities and Measured Temperature Differences Using Active Heating-Distributed Temperature Sensing. Water. 2019; 11(8):1619. https://doi.org/10.3390/w11081619
Chicago/Turabian StyleBakx, Wiecher, Pieter J. Doornenbal, Rebecca J. van Weesep, Victor F. Bense, Gualbert H. P. Oude Essink, and Marc F. P. Bierkens. 2019. "Determining the Relation between Groundwater Flow Velocities and Measured Temperature Differences Using Active Heating-Distributed Temperature Sensing" Water 11, no. 8: 1619. https://doi.org/10.3390/w11081619
APA StyleBakx, W., Doornenbal, P. J., van Weesep, R. J., Bense, V. F., Oude Essink, G. H. P., & Bierkens, M. F. P. (2019). Determining the Relation between Groundwater Flow Velocities and Measured Temperature Differences Using Active Heating-Distributed Temperature Sensing. Water, 11(8), 1619. https://doi.org/10.3390/w11081619





