Assessing Controls on the Displacement of Tracers in Gravel-Bed Rivers
Abstract
1. Introduction
2. Materials and Methods
2.1. Rationale
2.2. Data Set Compilation and Grouping
2.3. Data Analysis
3. Results
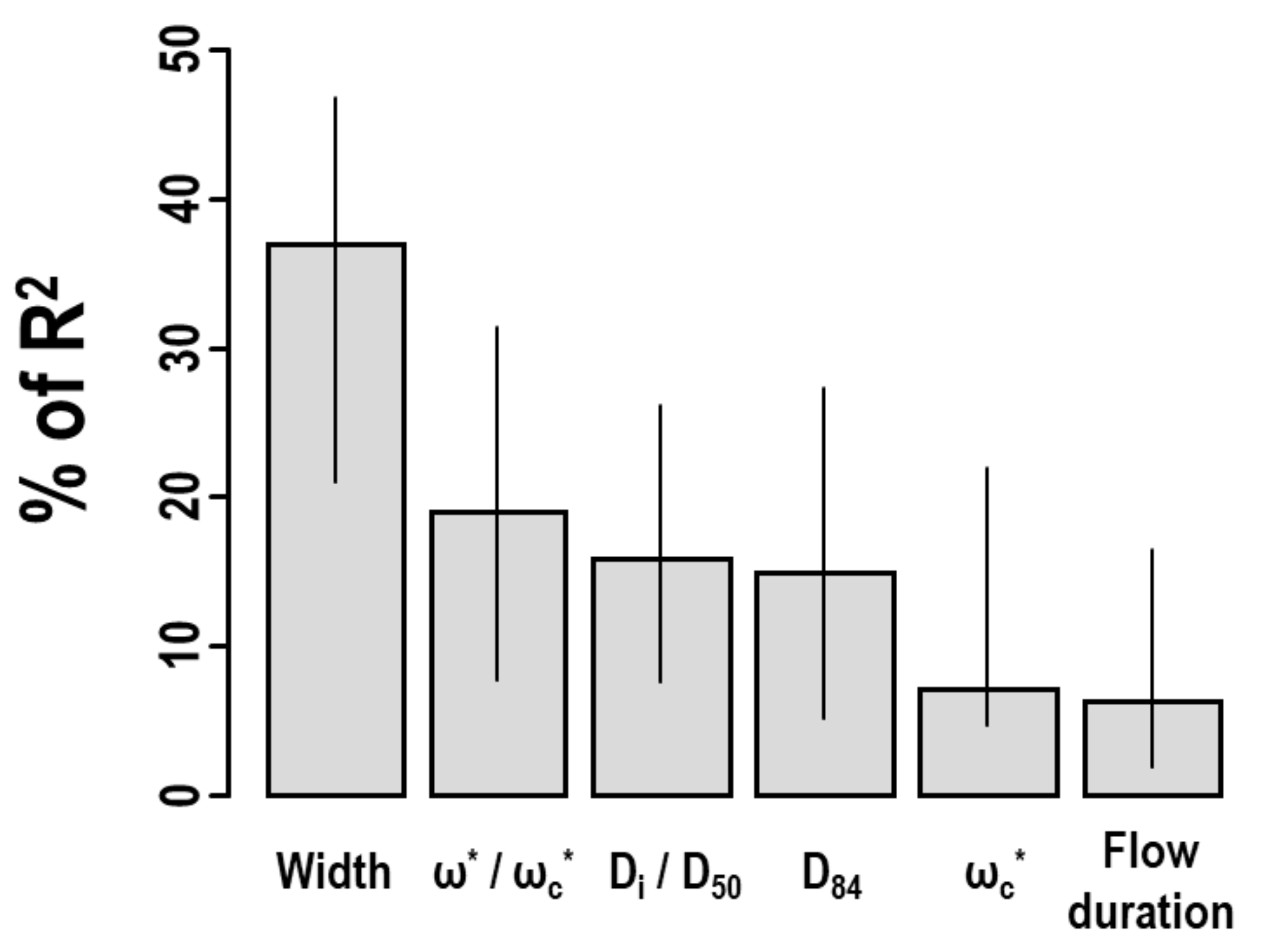
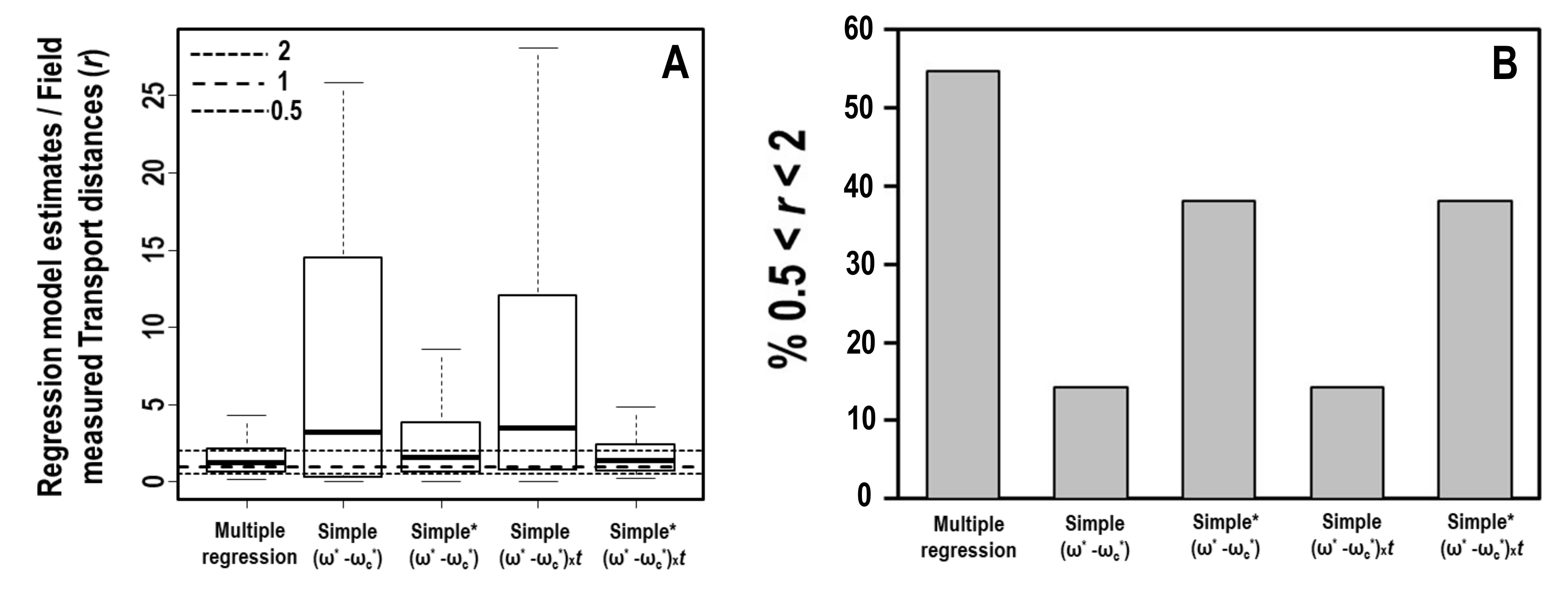
3.1. Regression Model
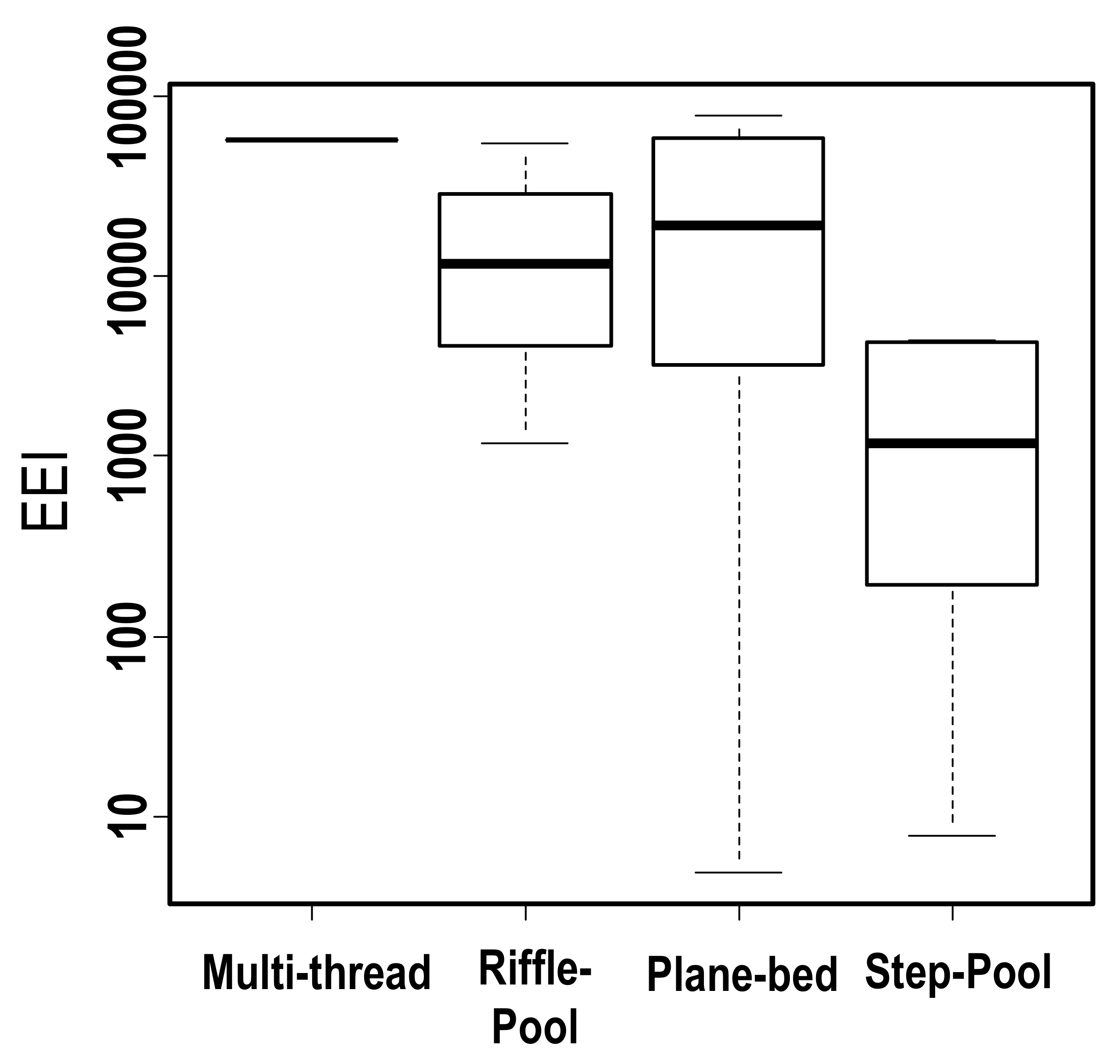
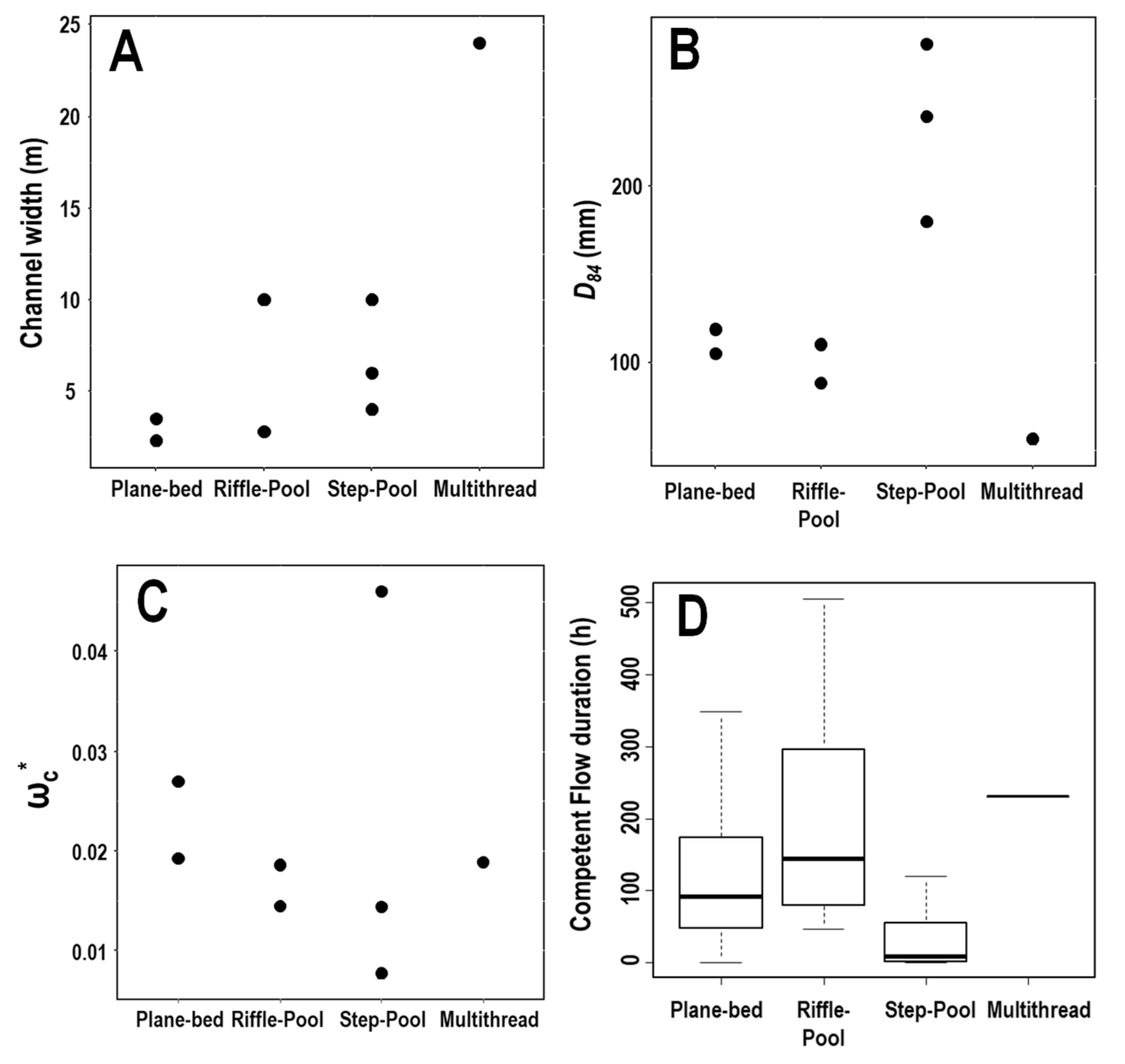
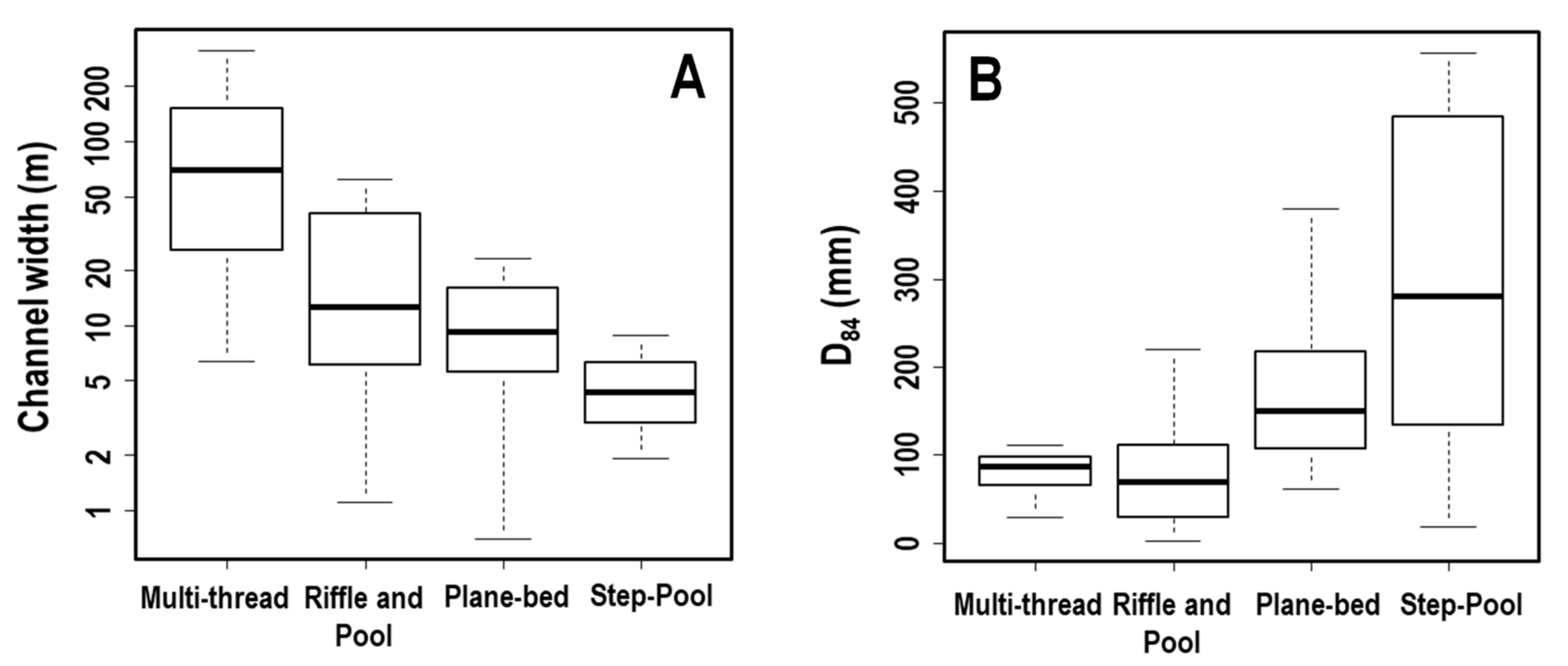
3.2. Influence of Channel Morphology and Experimental Conditions
4. Discussion
4.1. Variability in Particle Travel Distances
4.2. Morphological Control of Travel Length
4.3. Structural Controls on Travel Length
4.4. Methodological Uncertainties
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| b | Model coefficient defining how travel lengths scale to the tracer size |
| c | Model coefficient defining how travel lengths scale to ωc* |
| d | Model coefficient defining how travel lengths scale to ω*/ωc* |
| Di | Tracer size |
| D50 | Median diameter of the surface grain-size distribution |
| D84 | 84-th percentile of the surface grain-size distribution |
| γH | Parameter multiplying D84 and characterizing the active layer depth |
| e | Model coefficient defining how travel lengths scale to t |
| f | Model coefficient defining how travel lengths scale to WT |
| g | Gravity acceleration |
| h | Average depth of the active layer |
| l | Model coefficient defining how travel lengths scale to D84 |
| L | Average distance travelled by the bedload |
| LDi | Average transport distance of individual grains of diameter Di |
| LD50 | Average transport distance of the median grain-size |
| p | Fractional porosity of channel sediment |
| Q | Water discharge |
| Qc | Threshold discharge for incipient sediment motion |
| qs | Average bedload rate of the transport episode |
| Qs | Event-based bedload volumes |
| S | Channel slope |
| t | Time duration of the competent flow |
| Wa | Mean active channel width |
| WT | Total channel width |
| γW | Fraction of the total channel width involved in the bedload |
| ω | Specific stream power |
| ωc | Threshold value of ω for incipient sediment motion |
| ω* | Dimensionless specific stream power |
| ωc* | Threshold value of ω* for incipient sediment motion |
References
- Church, M. Bed material transport and the morphology of alluvial river channels. Annu. Rev. Earth Planet. Sci. 2006, 34, 325–354. [Google Scholar] [CrossRef]
- Rice, S.; Johnson, M.F.; Reid, I. Animals and the geomorphology of gravel-bed rivers. In Gravel-bed Rivers: Processes, Tools, Environments; Church, M., Biron, P., Roy, A.G., Eds.; Wiley and Sons: Chichester, UK, 2012; pp. 225–241. [Google Scholar]
- Recking, A. An analysis of nonlineary effects on bedload transport prediction. J. Geophys. Res. Earth Surf. 2013, 118, 1264–1281. [Google Scholar] [CrossRef]
- Ferguson, R.I. The missing dimension: Effects of lateral variation on 1-D calculations of fluvial bedload transport. Geomorphology 2003, 56, 1–14. [Google Scholar] [CrossRef]
- Parker, G. Chapter 3: Transport of gravel and sediment mixtures. In Manual 110. Sedimentation Engineering: Processes, Measurements, Modelling and Practice; García, M., Ed.; American Society of Civil Engineers: Reston, VA, USA, 2008; pp. 165–244. [Google Scholar]
- Yager, E.M.; Venditti, J.G.; Smith, H.J.; Schmeeckle, M.W. The trouble with shear stress. Geomorphology 2018, 323, 41–50. [Google Scholar] [CrossRef]
- Gomez, B.; Naff, R.L.; Hubell, D.W. Temporal variations in bedload transport associated with the migration of bedforms. Earth Surf. Process. Landf. 1989, 14, 135–156. [Google Scholar] [CrossRef]
- Hoey, T.B. Temporal variations in bedload transport rates and sediment storage in gravel-bed rivers. Prog. Phys. Geogr. 1992, 16, 319–338. [Google Scholar] [CrossRef]
- Kuhnle, R.A. Chapter 5: Unsteady transport of sand and gravel mixtures. In Advances in Fluvial Dynamics and Stratigraphy; Carling, P.A., Dawson, M.R., Eds.; John Wiley and Sons Ltd.: Hoboken, NJ, USA, 1996; pp. 183–201. [Google Scholar]
- Recking, A.; Liébault, F.; Peteuil, C.; Jolimet, T. Testing several bedload transport equations with consideration of time scales. Earth Surf. Process. Landf. 2012, 37, 774–789. [Google Scholar] [CrossRef]
- Laronne, J.B.; Carson, M. Interrelationships between bed morphology and bed material transport for a small, gravel-bed channel. Sedimentology 1976, 23, 67–85. [Google Scholar] [CrossRef]
- Hassan, M.; Schick, A.; Laronne, J. The recovery of flood-dispersed coarse sediment particles. Catena suppl. 1984, 5, 53–162. [Google Scholar]
- Ashworth, P.J. Bedload Transport and Channel Change in Gravel-Bed Rivers. Ph.D. Thesis, University of Stirling, Scotland, UK, 1987. [Google Scholar]
- Sear, D. Sediment transport processes in pool–riffle sequences. Earth Surf. Process. Landf. 1996, 21, 241–262. [Google Scholar] [CrossRef]
- Hassan, M.A.; Ergenzinger, P. Use of Tracers in Fluvial Geomorphology. In Tools in Fluvial Geomorphology; Kondolf, G.M., Piegay, H., Eds.; John Wiley and Sons: Hoboken, NJ, USA, 2003. [Google Scholar]
- Hassan, M.A.; Roy, A. Use of Tracers in Fluvial Geomorphology. In Tools in Fluvial Geomorphology, 2nd ed.; Kondolf, G.M., Piegay, H., Eds.; John Wiley and Sons: Hoboken, NJ, USA, 2015. [Google Scholar]
- Hassan, M.; Bradley, D.N. Geomorphic controls on tracer particle dispersion in gravel-bed rivers. In Gravel-Bed Rivers. Processes and Disasters; Tsutsumi, D., Laronne, J.B., Eds.; Wiley-Blackwell: Chichester, UK, 2017; pp. 439–466. [Google Scholar]
- Cassel, M.; Dépret, T.; Piegay, H. Assessment of a new solution for tracking pebbles in rivers based on active RFID. Earth Surf. Process. Landf. 2017, 42, 1938–1951. [Google Scholar] [CrossRef]
- Wong, M.; Parker, G.; DeVries, P.; Brown, T.M.; Burges, J.S. Experiments on dispersion of tracer stones under lower-regime plane-bed equilibrium bedload transport. Water Resour. Res. 2007, 43. [Google Scholar] [CrossRef]
- Reid, I.; Layman, J.T.; Frostick, L.E. The continuous measurement of bedload discharge. J. Hydraul. Res. 1980, 18, 243–279. [Google Scholar] [CrossRef]
- Helly, E.J.; Smith, W. Development and Calibration of a Pressure-Difference Bedload Sampler. US Geological Survey Open-File Report; U. S. Dept. of the Interior, Geological Survey, Water Resources Division: Menlo Park, CA, USA, 1971.
- Hassan, M.A.; Church, M.; Ashworth, P.J. Virtual rate and mean distance of travel of individual clasts in gravel-bed channels. Earth Surf. Process. Landf. 1992, 17, 617–627. [Google Scholar] [CrossRef]
- Lenzi, M.A. Displacement and transport of marked pebbles, cobbles and boulders during floods in a steep mountain stream. Hydrol. Process. 2004, 18, 1899–1914. [Google Scholar] [CrossRef]
- Lamarre, H.; Roy., A.G. The role of morphology on the displacement of particles in a step–pool river system. Geomorphology 2008, 99, 270–279. [Google Scholar] [CrossRef]
- Haschenburger, J.K. Tracing river gravels: Insights into dispersion from a long-term field experiment. Geomorphology 2013, 200, 121–131. [Google Scholar] [CrossRef]
- Schneider, J.; Turowski, J.; Rickenmann, D.; Hegglin, R.; Arrigo, S.; Mao, L.; Kirchner, J. Scaling relationships between bedload volumes, transport distances, and stream power in steep mountain channels. J. Geophys. Res. Earth Surf. 2014, 119, 533–549. [Google Scholar] [CrossRef]
- Phillips, C.B.; Martin, R.L.; Jerolmack, D.J. Impulse framework for unsteady flows reveals superdiffusive bedload transport. Geophys. Res. Lett. 2013, 40, 1328–1333. [Google Scholar] [CrossRef]
- Phillips, C.B.; Jerolmack, D.J. Dynamics and mechanics of bed-load tracer particles. Earth Surf. Dyn. 2014, 2, 513–530. [Google Scholar] [CrossRef]
- Vázquez-Tarrío, D.; Recking, A.; Liébault, F.; Tal, M.; Menéndez-Duarte, R. Particle transport in gravel-bed rivers: Revisiting passive tracer data. Earth Surf. Process. Landf. 2019, 44, 112–128. [Google Scholar]
- Beechie, T.J. Empirical predictors of annual bedload travel distance, and implications for salmonid habitat restoration and protection. Earth Surf. Process. Landf. 2001, 26, 1025–1034. [Google Scholar] [CrossRef]
- Milan, D.J.; Heritage, G.L.; Large, A.R.G. Tracer pebble entrainment and deposition loci: Influence of flow character and implications for riffle-pool maintenance. In Sediment Flux to Basins: Causes, Controls and Consequences; Jones, S.J., Frostick, L.E., Eds.; Geological Society of London Special Publications 191; The Geological Society: London, UK, 2002; pp. 133–148. [Google Scholar]
- Pyrce, R.S.; Ashmore, P.E. The relation between particle path length distributions and channel morphology in gravel-bed streams: A synthesis. Geomorphology 2003, 56, 167–187. [Google Scholar] [CrossRef]
- Pyrce, R.S.; Ashmore, P.E. Particle path length distributions in meandering gravel-bed streams: Results from physical models. Earth Surf. Process. Landf. 2003, 28, 951–966. [Google Scholar] [CrossRef]
- Pyrce, R.S.; Ashmore, P.E. Bedload path length and point bar development in gravel-bed river models. Sedimentology 2005, 52, 839–857. [Google Scholar] [CrossRef]
- Milan, D.J. Sediment routing hypothesis for pool-riffle maintenance. Earth Surf. Process. Landf. 2013, 38, 1623–1641. [Google Scholar] [CrossRef]
- Hassan, M.A.; Church, M.; Schick, A.P. Distance of movement of coarse particles in gravel-bed streams. Water Resour. Res. 1991, 27, 503–511. [Google Scholar] [CrossRef]
- Milan, D.J. Virtual velocity of tracers in a gravel-bed river using size-based competence duration. Geomorphology 2013, 198, 107–114. [Google Scholar] [CrossRef]
- Brayshaw, A.C.; Frostick, L.E.; Reid, I. The hydrodynamics of particle clusters and sediment entrainment in coarse alluvial channels. Sedimentology 1983, 30, 137–143. [Google Scholar] [CrossRef]
- Reid, I.; Frostick, L.E.; Brayshaw, A.C. Microform roughness elements and the selective entrainment and entrapment of particles in gravel-bed rivers. In Dynamics of Gravel-Bed Rivers; Billi, P., Hey, R.D., Thorne, C.R., Tacconi, P., Eds.; Wiley: Chichester, UK, 1992; pp. 253–266. [Google Scholar]
- Powell, D.M.; Ashworth, P.J. Spatial pattern of flow competence and bedload transport in a divided gravel-bed river. Water Resour. Res. 1995, 31, 741–752. [Google Scholar] [CrossRef]
- Church, M.; Hassan, M.A.; Wolcott, J.F. Stabilizing self-organized structures in gravel-bed stream channels: Field and experimental observations. Water Resour. Res. 1998, 34, 3169–3179. [Google Scholar] [CrossRef]
- Turowski, J.; Yager, E.M.; Badoux, A.; Rickenmann, D.; Molnar, P. The impact of exceptional events on erosion, bedload transport and channel stability in a step-pool channel. Earth Surf. Process. Landf. 2009, 34, 1661–1673. [Google Scholar] [CrossRef]
- Ockelford, A.; Haynes, H. The impact of stress history on bed structure. Earth Surf. Process. Landf. 2013, 38, 717–727. [Google Scholar] [CrossRef]
- Mao, L.; Dell’Agnese, A.; Surian, N. Sediment motion and velocity in a glaciar-fed stream. Geomorphology 2017, 291, 69–79. [Google Scholar] [CrossRef]
- Mao, L. The effects of flood history on sediment transport in gravel-bed rivers. Geomorphology 2018, 322, 196–205. [Google Scholar] [CrossRef]
- Masteller, C.C.; Finnegan, N.J.; Turowski, J.M.; Yager, E.M.; Rickenmann, D. History-dependent threshold for motion revealed by continuous bedload transport measurements in a steep mountain stream. Geophys. Res. Lett. 2019, 46, 2583–2591. [Google Scholar] [CrossRef]
- Ferguson, R.I.; Bloomer, D.J.; Hoey, T.B.; Werritty, A. Mobility of river tracer pebbles over different timescales. Water Resour. Res. 2002, 38, 1045. [Google Scholar] [CrossRef]
- Ballio, F.; Pokrajac, D.; Radice, A.; Hosseini Sadabadi, S.A. Lagrangian and Eulerian description of bedload transport. J. Geophys. Res. Earth Surf. 2018, 123, 384–408. [Google Scholar] [CrossRef]
- Klösch, M.; Habersack, H. Deriving formulas from an unsteady virtual velocity of bedload tracers. Earth Surf. Process. Landf. 2018, 43, 1529–1541. [Google Scholar]
- Parker, G. Tracer stones moving as bedload in gravel-bed streams. 1D Sediment Transport Morphodynamics with Applications to Rivers and Turbidity Currents. Ebook. 2004. Available online: http://hydrolab.illinois.edu/people/parkerg/morphodynamics_e-book.htm.
- Fernandez Luque, R.; Van Beek, R. Erosion and Transport of Bed-Load Sediment. J. Hydraul. Res. 1976, 14, 127–144. [Google Scholar] [CrossRef]
- Laronne, J.B.; Outhet, D.N.; Duckham, J.L.; Mc Cabe, T.J. Determining event bedload volumes for evaluation of potential degradation site due to gravel extraction N.S.W., Australia. In Erosion and Sediment Transport Monitoring Programmes in River Basins, Proceedings of the Oslo Symposium, N.S.W., Australia, 24–28 August 1992; No. 210; IAHS Publication: Wallingford, UK, 1992; pp. 87–94. [Google Scholar]
- Martin, Y.; Church, M. Bed-material transport estimated from channel surveys: Vedder River, British Columbia. Earth Surf. Process. Landf. 1995, 20, 347–361. [Google Scholar] [CrossRef]
- Haschenburger, J.K.; Church, M. Bed material transport estimated from the virtual velocity of sediment. Earth Surf. Process. Landf. 1998, 23, 791–808. [Google Scholar] [CrossRef]
- Liébault, F.; Laronne, J.B. Factors affecting the evaluation of bedload transport in gravel-bed rivers using scour chains and painted tracers: The case of the Esconavette Torrent. Geodin. Acta 2008, 21, 23–34. [Google Scholar]
- Vázquez-Tarrío, D. Transporte de Sedimentos Como Carga de Fondo en la Cuenca del Río Narcea (Vertiente Norte de la Cordillera Cantábrica). Ph.D. Thesis, University of Oviedo, Oviedo, Spain, 2013. [Google Scholar]
- Vázquez-Tarrío, D.; Menéndez-Duarte, R. Bedload transport rates for coarse-bed streams in an Atlantic region (Narcea River, NW Iberian Peninsula). Geomorphology 2014, 217, 1–14. [Google Scholar]
- Vericat, D.; Wheaton, J.M.; Brasington, J. Revisiting the morphological approach: Opportunities and challenges with repeat high-resolution topography. In Gravel-Bed Rivers. Processes and Disasters; Tsutsumi, D., Laronne, J.B., Eds.; Wiley-Blackwell: Chichester, UK, 2017; pp. 121–158. [Google Scholar]
- Gomez, B.; Church, M. An assessment of bedload sediment transport formulae for gravel-bed rivers. Water Resour. Res. 1989, 25, 1161–1186. [Google Scholar] [CrossRef]
- Pitlick, J.; Cui, Y.; Wilcock, P. Manual for Computing Bedload Transport Using BAGS; USDA, Forest Service, Rocky Mountain Research Station: Fort Collins, CO, USA, 2009.
- Vázquez-Tarrío, D.; Menéndez-Duarte, R. Assessment of bedload equations using data obtained with tracers in two coarse-bed mountain streams (Narcea River basin, NW Spain). Geomorphology 2015, 238, 78–93. [Google Scholar]
- Eaton, B.; Church, M. A rational sediment transport scaling relation based on dimensionless stream power. Earth Surf. Process. Landf. 2011, 36, 901–910. [Google Scholar] [CrossRef]
- Church, M.; Hassan, M.A. Size and distance of travel of unconstrained clasts on a streambed. Water Resour. Res. 1992, 28, 299–303. [Google Scholar] [CrossRef]
- Hassan, M.A.; Church, M. The movement of individual grains on the streambed. In Dynamics of Gravel Bed Rivers; Bill, P., Hey, C.R., Thorne, C.R., Tacconi, P., Eds.; John Wiley & Sons: Chichester, UK, 1992. [Google Scholar]
- DeVries, P. Bedload Layer Thickness and Disturbance Depth in Gravel Bed Streams. J. Hydraul. Eng. 2002, 128, 983–991. [Google Scholar] [CrossRef]
- Recking, A. Simple method for calculating reach-averaged bed-load transport. J. Hydraul. Eng. 2013, 139, 70–75. [Google Scholar] [CrossRef]
- McKenzie, L.G.; Eaton, B.C.; Church, M. Breaking from the average: Why large grains matter in gravel-bed streams. Earth Surf. Process. Landf. 2018, 43, 3190–3196. [Google Scholar] [CrossRef]
- Haschenburger, J.K. A Probability model of scour and fill depths in gravel-bed channels. Water Resour. Res. 1999, 35, 2857–2869. [Google Scholar] [CrossRef]
- Montgomery, D.R.; Buffington, J.M. Channel-reach morphology in mountain drainage basins. Geol. Soc. Am. Bull. 1997, 109, 596–611. [Google Scholar] [CrossRef]
- Papangelakis, E.; Hassan, M. The role of channel morphology on the mobility and dispersion of bed sediment in a small gravel-bed stream. Earth Surf. Process. Landf. 2016, 41, 2191–2206. [Google Scholar] [CrossRef]
- Gintz, D.; Hassan, M.A.; Schmidt, K.H. Frequency and magnitude of bedload transport in a mountain river. Earth Surf. Process. Landf. 1996, 21, 433–445. [Google Scholar] [CrossRef]
- Bradley, D.N.; Tucker, G.E. Measuring gravel transport and dispersion in a mountain river using passive radio tracers. Earth Surf. Process. Landf. 2012, 37, 1034–1045. [Google Scholar] [CrossRef]
- Liébault, F.; Bellot, H.; Chapuis, M.; Klotz, S.; Deschàtres, M. Bedload tracing in a high-sediment-load mountain stream. Earth Surf. Process. Landf. 2012, 37, 385–399. [Google Scholar]
- Dell’Agnese, A.; Brardinoni, F.; Toro, M.; Mao, L.; Engel, M.; Comiti, F. Bedload transport in a formerly glaciated mountain catchment constrained by particle tracking. Earth Surface Dynamics 2015, 3, 527–542. [Google Scholar]
- Miller, D.M. Reducing transformation bias in curve fitting. Am. Stat. 1984, 38, 124–126. [Google Scholar]
- James, G.; Witten, D.; Hastie, T.; Tibshirani, R. An Introduction to Statistical Learning: With Applications in R; Springer Publishing Company, Incorporated: Berlin/Heidelberg, Germany, 2014. [Google Scholar]
- Lindeman, R.H.; Merenda, P.F.; Gold, R.Z. Introduction to Bivariate and Multivariate Analysis; Scott Foresman & Co: Glenview, IL, USA, 1980. [Google Scholar]
- Quenouille, M.H. Problems in Plane Sampling. Ann. Math. Stat. 1949, 20, 355–375. [Google Scholar] [CrossRef]
- Tukey, J.W. Bias and confidence in not quite large samples. Ann. Math. Stat. 1958, 29, 614. [Google Scholar]
- Phillips, C.B.; Hill, K.M.; Paola, C.; Singer, M.B.; Jerolmack, D.J. Effect of flood hydrograph duration, magnitude, and shape on bedload transport dynamics. Geophys. Res. Lett. 2018, 45, 8264–8271. [Google Scholar]
- Francalanci, S.; Solari, L.; Toffolon, M.; Parker, G. Do alternate bars affect sediment transport and flow resistance in gravel-bed rivers? Earth Surf. Process. Landf. 2012, 37, 866–875. [Google Scholar] [CrossRef]
- Recking, A.; Piton, G.; Vázquez-Tarrío, D.; Parker, G. Quantifying the morphological print of bedload transport. Earth Surf. Process. Landf. 2016, 41, 809–822. [Google Scholar] [CrossRef]
- Kasprak, A.; Wheaton, J.M.; Ashmore, P.E.; Hensleigh, J.W.; Peirce, S. The relationship between particle travel distance and channel morphology: Results from physical models of braided rivers. J. Geophys. Res. Earth Surf. 2015, 120, 55–74. [Google Scholar] [CrossRef]
- Schmidt, K.; Ergenzinger, P. Bedload entrainment, travel lengths, step lengths, rest periods—Studied with passive (iron, magnetic) and active (radio) tracer techniques. Earth Surf. Process. Landf. 1992, 17, 147–165. [Google Scholar] [CrossRef]
- Sawada, T.; Ashida, K.; Takahashi, T. Relationship between channel pattern and sediment transport in a steep gravel-bed river. Zeitschrift für Geomorphologie Suppl. 1983, 16, 55–66. [Google Scholar]
- Lamarre, H.; Roy, A.G. A field experiment on the development of sedimentary structures in a gravel-bed river. Earth Surf. Process. Landf. 2008, 33, 1064–1081. [Google Scholar] [CrossRef]
- Klingeman, P.C.; Emmett, W.W. Gravel bedload transport processes. In Gravel Bed Rivers: Fluvial Processes, Engineering and Management; Hey, R.D., Bathurst, J.C., Thorne, C.R., Eds.; Wiley: Chichester, UK, 1982; pp. 141–169. [Google Scholar]
- Reid, I.; Frostick, L.E. Particle interaction and its effect on the thresholds of initial and final bedload motion in coarse alluvial channels. In Sedimentology of Gravels and Conglomerates; Memoir 10; Canadian Society of Petroleum Geologists: Calgary, AB, Canada, 1984; pp. 61–68. [Google Scholar]
- Turowski, J.M.; Badoux, A.; Rickenmann, D. Start and end of bedload transport in gravel-bed streams. Geophys. Res. Lett. 2011, 38. [Google Scholar] [CrossRef]
- Piton, G.; Recking, A. The concept of travelling bedload and its consequences for bedload computation in mountain streams. Earth Surf. Process. Landf. 2017, 42, 1505–1519. [Google Scholar] [CrossRef]
- Piton, G.; Vázquez-Tarrío, D.; Recking, A. Can bed-load help to validate hydrology studies in mountainous catchment? The case study of the Roize (Voreppe–FR). E3S Web Conf. 2016, 7, 04020. [Google Scholar] [CrossRef]
- Hassan, M.A.; Church, M. Vertical mixing of coarse particles in gravel bed rivers: A kinematic model. Water Resour. Res. 1994, 30, 1173–1186. [Google Scholar] [CrossRef]
- Ferguson, R.I.; Wathen, S.J. Tracer-pebble movement along a concave river profile: Virtual velocity in relation to grain size and shear stress. Water Resour. Res. 1998, 34, 2031–2038. [Google Scholar] [CrossRef]
- Ferguson, R.; Hoey, T. Long-term slowdown of river tracer pebbles: Generic models and implications for interpreting short-term tracer studies. Water Resour. Res. 2002, 38, 1142. [Google Scholar] [CrossRef]

| Data Set | W (m) | S | D50 (mm) | L (m) | Measuring Procedure | Observations | Recovery (%) | Q (m3/s) | Qc (m3/s) [Estimation Method] | Seeding Procedure | Survey Duration | Stream Type | Source |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Lainbach | 10.0 | 0.020 | 120 | 15–451 | No information | Mean distances estimated for all tracers and for moving tracers only | 17–100 | 3.2–165.0 | 3 [First tracer movements] | Tracers seeded on pools, steps, bars, and the toss side of large boulders | 4 years | Step-pool | [71]: Gintz et al. (1996) |
| Spruce creek | 6.0 | 0.120 | 86 | 163.8–513.9 | Straight line distance between the initial location and the point of the final deposition | Mean distances estimated for moving tracers only | 83–92 | 1.2–2.0 | 1 [Discharge above 25% of clasts are mobile] | Tracers seeded along cross sections on the channel bed | 3.5 years | Step-pool | [24]: Lamarre and Roy (2008) |
| Halfmoon Creek | 2.2 | 0.010 | 57 | 10.0–144.8 | Distances along and away from the channel centerline | Mean distances estimated for all tracers and for moving tracers only | 93–98 | 5.6–14.5 | 3.5 [Estimate based on critical shields stress] | A grid of 893 tracers in rows across the channel with 0.5 m between each tracer and each row | 4 years | Riffle-pool | [72]: Bradley and Tucker (2012) |
| Bouinenc river | 24.0 | 0.020 | 20 | 299.0–775.0 | Distances measured along the axis of the main low flow channel | Mean distances estimated for all tracers and for moving tracers only | 65–88 | 33.4–41.1 | 2.5 [Estimate based on critical shields stress] | Tracers seeded along transverse lines crossing several morphological units | 3 years | Multithread channel | [73]: Liebault et al. (2012) |
| Strimm Creek | 3.5–4.0 | 0.080-0.150 | 62–76 | 0.2–185.0 | Distances measured along the thalweg | Mean distances estimated for moving tracers only | 54–100 | 0.32–1.81 | 0.3–0.4 [Discharges able to mobilize clasts from all size classes] | Tracers seeded along transverse ribs on the streambed | 4 years | Step-pool/Plane- bed/Cascade | [74]: Dell’Agnese et al. (2015) |
| East Creek | 2.3–2.8 | 0.018-0.020 | 49–55 | 0.3–35.7 | Distances measured along the thalweg | Mean distances estimated for moving tracers only | 77–88 | 0.9–4.7 | 0.5 [Discharge at which ¡ mobility is initiated for the median grain size] | Tracers seeded on the surface in rows spanning the entire width of the channel | 8 years | Riffle-pool/Plane-bed | [70]: Papangelakis and Hassan (2016) |
| Variable | Coefficient | Standard Error | t | p-value | VIF 1 |
|---|---|---|---|---|---|
| Intercept | 1170.146 | 2.686 | 3.47 | 0.001 ++ | |
| 1-log10(Di/D50) | 4.859 | 1.516 | 3.204 | 0.003 ++ | 4.574 |
| D84 | 3.239 | 0.455 | 7.12 | 2.68 × 10−8 ++ | 2.431 |
| Width | 3.878 | 0.51 | 7.608 | 6.38 × 10−9 ++ | 6.239 |
| ω*/ωc* | 1.931 | 0.278 | 6.945 | 4.49 × 10−8 ++ | 1.908 |
| Flow duration | 0.167 | 0.084 | 1.991 | 0.054 + | 1.908 |
| ωc* | 2.742 | 0.554 | 4.952 | 1.85 × 10−5 ++ | 4.002 |
| Model | Intercept | b1 | c2 | d3 | e4 | f5 | l6 | R2 |
|---|---|---|---|---|---|---|---|---|
| Equation (13) (all) | 13406.86 | 4.859 | 2.742 | 1.931 | 0.167 | 2.878 | 3.239 | 0.87 |
| (ω*−ωc*) (all) | 0.81 | 0.82 | 0.18 | |||||
| (ω*−ωc*) (RP) | 0.21 | 0.81 | 0.12 | |||||
| (ω*−ωc*) (PB) | 0.18 | 0.57 | 0.43 | |||||
| (ω*−ωc*) (SP) | 0.54 | 1.04 | 0.46 | |||||
| (ω*−ωc*) × t (all) | 2.99 | 0.14 | 0.03 | |||||
| (ω*−ωc*) × t (RP) | 0.00 | 1.24 | 0.72 | |||||
| (ω*−ωc*) × t (PB) | 0.02 | 0.26 | 0.37 | |||||
| (ω*−ωc*) × t (SP) | 0.35 | 0.30 | 0.27 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vázquez-Tarrío, D.; Batalla, R.J. Assessing Controls on the Displacement of Tracers in Gravel-Bed Rivers. Water 2019, 11, 1598. https://doi.org/10.3390/w11081598
Vázquez-Tarrío D, Batalla RJ. Assessing Controls on the Displacement of Tracers in Gravel-Bed Rivers. Water. 2019; 11(8):1598. https://doi.org/10.3390/w11081598
Chicago/Turabian StyleVázquez-Tarrío, Daniel, and Ramon J. Batalla. 2019. "Assessing Controls on the Displacement of Tracers in Gravel-Bed Rivers" Water 11, no. 8: 1598. https://doi.org/10.3390/w11081598
APA StyleVázquez-Tarrío, D., & Batalla, R. J. (2019). Assessing Controls on the Displacement of Tracers in Gravel-Bed Rivers. Water, 11(8), 1598. https://doi.org/10.3390/w11081598





