Abstract
Rainfall data is frequently used as input and analysis data in the field of hydrology. To obtain adequate rainfall data, there should be a rain gauge network that can cover the relevant region. Therefore, it is necessary to analyze and evaluate the adequacy of rain gauge networks. Currently, a complex network analysis is frequently used in network analysis and in the hydrology field, Pearson correlation is used as strength of link in constructing networks. However, Pearson correlation is used for analyzing the linear relationship of data. Therefore, it is now suitable for nonlinear hydrological data (such as rainfall and runoff). Thus, a possible solution to this problem is to apply mutual information that can consider nonlinearity of data. The present study used a method of statistical analysis known as the Brock–Dechert–Scheinkman (BDS) statistics to test the nonlinearity of rainfall data from 55 Automated Synoptic Observing System (ASOS) rain gauge stations in South Korea. Analysis results indicated that all rain gauge stations showed nonlinearity in the data. Complex networks of these rain gauge stations were constructed by applying Pearson correlation and mutual information. Then, they were compared by computing their centrality values. Comparing the centrality rankings according to different thresholds for correlation showed that the network based on mutual information yielded consistent results in the rankings, whereas the network, which based on Pearson correlation exhibited much variability in the results. Thus, it was found that using mutual information is appropriate when constructing a complex network utilizing rainfall data with nonlinear characteristics.
1. Introduction
Rainfall data are important in various fields such as hydrology, water resources, environment, and ecology. These data are analyzed through the analysis of rainfall characteristics such as rainfall intensity, variability, statistical characteristics, and trends [1,2,3,4,5,6]. Moreover, they have been widely used as input data in runoff analysis, estimation of flood discharge and flood elevation, calculation of the vulnerability index, computation of the drought index, and so on [7,8,9,10]. In rainfall-related research, it is important to collect appropriate data and determine the relationships that can be obtained in the data. For analysis of rainfall and related phenomena, it is necessary to have an adequate amount of data that covers the relevant region. To obtain such data, it is necessary to construct a network of rain gauge stations that cover the entire region under investigation. This rain gauge network aims at collecting rainfall data, and the evaluation of such a rain gauge network includes the assessment of the clustering and importance of rain gauges [11]. It must be conducted to determine the exact amount of available water resources, and also to properly estimate the area-average rainfall that is used as input data in rainfall–runoff analyses [12]. If the rain gauge network does not attain the adequate levels in these assessments, it will generate errors in estimating the area-average rainfall because of insufficient rainfall data, and even larger errors in the rainfall–runoff analysis results that use the area-average rainfall as input data [13]. It will also cause the further problem of greatly reducing the accuracy of analyses that use the estimated rainfall as input data. Therefore, the evaluation and analysis of rain gauge networks is an important prerequisite in the field of hydrology. Spatial connectivity between rain gauge stations, which is one of the elements in the analysis of rain gauge networks, is a key component in analysis because it can be used as a basis for interpolation, classification, and prediction in ungauged basins [14,15,16]. In analyzing the connectivity between rain gauge stations, complex networks, based on graph theory, are currently being used.
Complex networks are based on graph theory, which was first created by Leonhard Euler in connection with the Königsberg bridge problem. Graph theory analyzes graphs, which are mathematical structures that model pairwise relationships between objects to determine the characteristics of a given set of data [17]. After Euler, the basic concepts and theories related to graph theory were established by Francis Guthrie, Arthur Cayley, and William Thomas Tutte, among others. Through complex network analysis, it is possible to determine the relationships between data points, and to know how one element affects the entire system. Moreover, the analysis enables us to determine the dynamic characteristics of the overall data by identifying their network structure, and to clearly grasp this structure by simplifying a network consisting of a complex array of numerous data points [18]. Due to the advantages of such complex network analysis, it is applied in diverse fields such as linguistics, physics, biology, sociology, engineering, economics, and ecology [19,20,21,22].
In the field of hydrology, Yazdani et al. [23] analyzed the structure and vulnerability of the water supply system by constructing a network based on correlations between the supply system and related factors (such as hierarchy, evolution, performance reliability, and vulnerability). Boer et al. [24] identified the climatic linkages of extreme rainfall and the spatial characteristics of extreme rainfall synchronicity by analyzing the South American Monsoon System (SAMS), and provided a classification of rainfall on this basis. Sivakumar and Woldemeskel [25] used complex networks to determine the spatial connections between streamflow gauging stations. Halverson and Fleming [26] applied the complex network method to stream flow gauges to check the applicability of the method in hydrology data. Jha et al. [15] used the complex network anaylsis for rainfall modeling to check the spatial connections. However, the above studies used Pearson correlation as the method of determining relationships in the construction of complex networks. Pearson correlation is an index that shows linear relationships between factors by analyzing the trends between them and, thus, has the disadvantage of showing incorrect relationships when it is applied to nonlinear data. Using Pearson correlation can cause an error to work out the relationships between target factors because rainfall data is a representative case of nonlinear data. Mutual information can be a suitable solution to take into account the nonlinearity of hydrological time series data.
Mutual information is an indicator that shows the mutual dependence between two variables. With respect to two random variables X and Y, it measures how much our knowledge about one variable X tells us about another variable Y. It is based on probability theory and information theory, and has the advantage of taking into account the nonlinearity in the relationship between two variables [27]. Due to this advantage, mutual information is utilized as a useful method for determining the dimension to reconstructing the state space data in chaos analysis, and several studies have shown that it yields better results in relation to nonlinear data [28,29]. Among studies that have applied complex networks, Donges et al. [30] in climate research, Wang et al. [31] in economics, and Zhang et al. [32] in neuroscience have constructed complex networks using both mutual information and Pearson correlation, and found that mutual information is more adequate through indices and prediction models that analyzed the networks. Therefore, given that mutual information as a method for analyzing relationships can take into account the nonlinearity of rainfall data in constructing complex networks, the purpose of this study is to determine the applicability of mutual information to rain gauge networks. For this purpose, Section 2 describes the Brock–Dechert–Scheinkman (BDS) statistic, which is used to identify linearity and nonlinearity, and explains complex networks. Section 3 compares the results of applying mutual information and Pearson correlation in relation to actual synoptic weather stations in the Republic of Korea. Section 4, as the last section, summarizes the results of this study.
2. Basic Theory
2.1. BDS Statistic and Nonlinearity Test
The classification of data characteristics relies on various criteria. Among these criteria, linearity and nonlinearity are often taken into account. Linear data can be expressed as a straight line, and refers to data that has certain characteristics such as the superposition principle and so on [33]. Therefore, it can be easily analyzed and predicted with statistical methods. Data with the opposite characteristics is nonlinear. The relationship between data is not simply static or directly proportional to the input but instead is dynamic and variable. It is a property of chaotic systems, characterized by approximation, random behavior, and unpredictability [34]. There are several methods for classifying the linearity and nonlinearity of data, but among these, the BDS statistic is the method that can clearly distinguish linear and nonlinear data. The BDS statistic was proposed by Brock et al. [14,35], and it is one of the methods for testing the null hypothesis that a given set of time series data follows a random distribution. The BDS statistic is a particularly useful statistical technique for distinguishing between linear and nonlinear systems [36,37]. Assuming that the data points of a time series are mutually independent and have the same probability distribution, in short, independent and identically distributed (IID), when m > 1, the BDS statistic is expressed as follows.
In here,
Here N = The number of data points.
- M = N (m − 1): The number of state vector points in m-dimensional (m = embedding dimension).
- r: Radius for determining the number of state vectors points.
- : the sup-norm.
When the values evaluated in the confidence interval set by the researchers exceed the interval, the null hypothesis is rejected, and the data is judged to be nonlinear [38,39,40].
2.2. Pearson Correlation and Mutual Information
Pearson correlation is an indicator used in various fields to determine the relationship between two variables. With respect to two variables (x, y), it describes the relationship between the two by comparing the trends in their changing values.
Pearson correlation has a value between −1 and 1, such that indicates a strong negative correlation between the two variables x and y, and indicates a strong positive correlation. However, Pearson correlation is an index expressing a linear relationship and, thus, has the disadvantage of failing to reflect any nonlinearity in the data.
Mutual information, on the other hand, is an indicator that shows the relationship between two variables on the basis of probability theory and information theory. With respect to two variables (x, y), it quantifies the extent to which we can know about y through x, and shows it as information content.
Mutual information has a value between , and a value of 0 indicates that the two variables are statistically independent of each other. Mutual information has the advantage of reflecting nonlinearity in the data, and this was confirmed in several studies. Moreover, it is not affected much by outliers, and can be computed even when the two variables in question have different ranges [2]. Due to these advantages, mutual information is used frequently in studies of nonlinear phenomena. In particular, it is utilized as a useful technique in setting the optimal dimension for reconstructing the data in chaos analysis. In this study, both mutual information and Pearson correlation were applied to determine the strength of links in constructing complex networks.
2.3. Graph Theory and Complex Network
2.3.1. General
Complex network is based on the graph theory. In graph theory, a graph is a network constituted by nodes and links. Mathematically, a graph can be expressed as , constituted by the node set = { with number of nodes, and the link set with number of links [25]. For instance, the graph in Figure 1 is constituted by six nodes () and nine links (. The graph shown below is a simple kind of network. In the real world, however, there are very complex networks formed by numerous factors, such as (i) when various kinds of nodes and links are involved in forming a network, (ii) when various factors are additionally applied (e.g., weights) to each node or link, (iii) when the links have directionality, and (iv) when a network is constituted by multi-links, self-links, hyperlinks, and so on. It can be applied to actual cases because it has various complex forms. When applying the methodology, the node and link must be defined firstly. After making a network with defined node and link, researchers analyze the shape of network and apply many indicators for checking the characteristic of target.
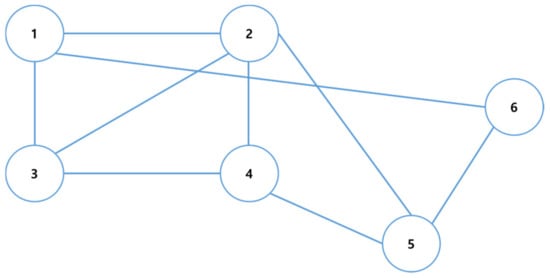
Figure 1.
Simplest form of network.
The most important thing in forming a complex network is link. Link is a node connection element and is used to calculate various indicators for analyzing complex networks such as centrality, clustering coefficient, and so on. Thus, the results may vary depending on how the link is defined. In the hydrology field, the strength of link was calculated using the correlation coefficient.
2.3.2. Centrality
There are various indices for determining the characteristics of a complex network. These indices include centrality, clustering coefficient, adjacency, distance, and community structure. These indices are used to quantify and evaluate the characteristics of a given network. Centrality is the most basic indicator for quantifying the characteristics of a network, and it is used to determine the importance of each node in a network. It was first used in regard to the community networks discussed by Bavelas [41] and Leavitt [42], and Jeong et al. [43] and Newman [44] were the first to apply degree of centrality to complex networks. The centrality can be computed for each node, and this can show which nodes are more important (or more influential) compared to other nodes. The node that has the highest degree of centrality in a network is the most important node, whereas the node that has the lowest degree of centrality is the least important. In a network consisting of number of nodes, the degree of centrality of the node is calculated by dividing the number of directly connected nodes ( by the number of nodes that can be connected to the (). The number of directly connected nodes can be calculated according to some given threshold.
3. Application and Results
3.1. Study Area and Data
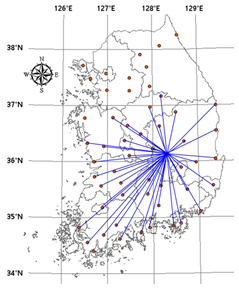
In this study, complex networks were constructed for the Automated Synoptic Observing System (ASOS) weather stations in South Korea. ASOS weather stations are managed by the Korean government and they have highly qualified observation data. In the ASOS weather stations, weather stations on Jeju Island were excluded from the networks because they are situated far away from the stations in mainland Korea, and various intervening factors, such as the sea, exist in between (Figure 2). Among the data from each synoptic weather station, daily rainfall data was used. To cover as many weather stations as possible, daily rainfall data from 1980 to 2019 was selected, and as a result, 55 ASOS stations were used in the complex networks (Latitude: 34.3959–38.2509° N, Longitude: 126.3812–129.4128° E). Table 1 explained the basic statistics of observed data (In the Supplementary Materials, Appendix A, basic statistic of each stations were written.). Through the Figure 2 and Table 2, location, number and name of station can be indentified.
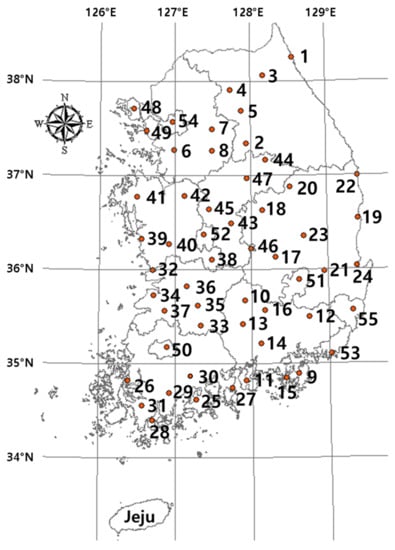
Figure 2.
The 55 rainfall gauge stations in the study area (Latitude: 34.3959–38.2509° N, Longitude: 126.3812–129.4128° E).

Table 1.
Basic statistics of daily rainfall series of 55 rainfall gaging stations: all basic statistics of each station are in Supplementary Materials, Appendix A.

Table 2.
Numbers of rainfall gauge stations.
3.2. Nonlinearity of Rainfall
To determine the nonlinearity of the rainfall data, the BDS statistic was applied. To apply the BDS statistic, the and values must be carefully selected. After conducting various kinds of analyses, Brock et al. [14] proposed that the suitable value for is , and for r, (here, is the standard deviation). In this study, and were applied in determining the nonlinearity of rainfall data. These values were applied to the above mentioned 55 weather stations, and the data was tested for nonlinearity at the 95% confidence interval. Applying the BDS statistic showed that all the values exceeded the 95% confidence interval, thus indicating that the rainfall data is nonlinear (the result is shown in Supplementary Materials, Appendix B). One result for Geoje station is shown in Table 3 and the other stations also showed the same result, in which the rainfall data has nonlinear characteristics.

Table 3.
Brock–Dechert–Scheinkman (BDS) statistic results of observed daily rainfall (09: Geoje): all values of BDS statistics results are out of Confidence Interval. The null hypothesis is rejected, and observation data is determined as nonlinear data. The results of the other stations are shown in the Supplementary Materials, Appendix B.
3.3. Analysis and Results
Complex network analysis was applied to a total of 55 weather stations. Each station was represented as a node in the networks, and the correlation coefficients between stations were represented as the links between the nodes. The strength of the links was determined using the Pearson Correlation Matrix () and the Mutual Information Matrix (), which were computed by means of Pearson correlation and mutual information, respectively. We attempted to compare the two matrices, but as shown in Figure 3, the matrixes have a different range of values (Pearson coefficient: 0.000 to 1.000, mutual information: 0.000 to 2.339). Therefore, we sought to compare the two matrices by shape of graph and centrality, which is an indicator for analyzing complex networks
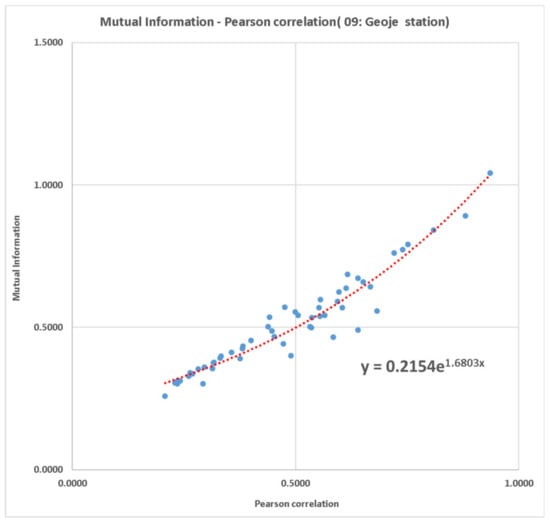
Figure 3.
Mutual information—Pearson correlation graph (09: Geoje): The X-axis is the Pearson coefficient and the Y-axis is the mutual information. In the graph, the two axes have different ranges (X: 0.0–1.0, Y: 0.0–1.5).
In calculating the degree of centrality, two nodes were judged to be connected when the calculated strength of the link between nodes was larger than the threshold set by the researchers. There has been much research on setting the threshold, but there is still no specific method for setting the appropriate threshold [30]. In this study, we established the threshold 0.1 to 0.9 at 0.1 intervals. Then we calculated the number of links according to the threshold and drew the graph (Figure 4.). Through the graph, we found the range which showed the dramatic change of links according to the threshold. This is because we believed that the key to comparing the two networks, given the different ranges of the strength of links in these networks, is to analyze the changes in each network by identifying the points where drastic changes occur. With respect to the two matrices, the threshold was applied at 0.1 intervals from 0.1 to 0.9, and the number of links was calculated. The results of these calculations are represented in the graph below (Figure 4.).
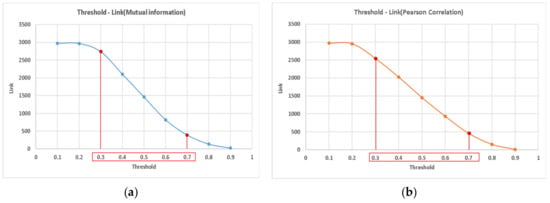
Figure 4.
The number of links according to threshold: (a) mutual information; (b) Pearson correlation.
The number of links at each threshold was compared to those of others, and those thresholds that show a difference of 10% or higher were set as the interval where drastic changes occur. Namely, as shown in Figure 4a, the complex network where mutual information was applied showed drastic changes in the number of links from 0.3 to 0.7, and the one where Pearson correlation was applied showed drastic changes in the same interval. Therefore, the network links were calculated by applying the thresholds in the interval (0.3, 0.4, 0.5, 0.6, 0.7) where the number of links changes drastically, and the complex networks were constructed on this basis (Figure 5).
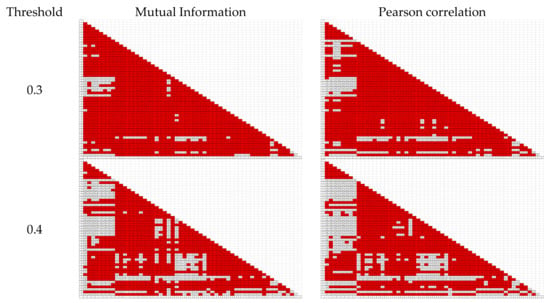

Figure 5.
Selection of links according to threshold: the mutual information and Pearson coefficient between stations are calculated as links. According to the threshold, the values, which is bigger than threshold, are filled with red color and the others remain as white color.
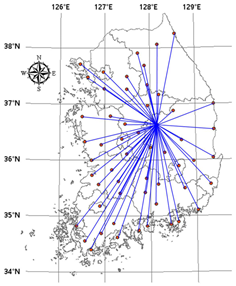
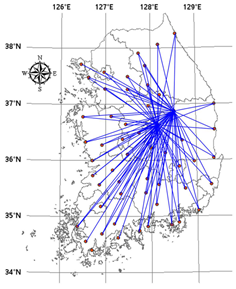
Looking at the changes in the number of links according to the threshold, it can be seen that the same kind of change occurs in the case of both complex networks. As the threshold increases, the number of links decreases at certain points. As for differences, we can see that the network based on Pearson correlation has more links than the one based on mutual information at all thresholds. Figure 6 shows the complex networks when the threshold is set at 0.7. When the two networks are compared, it shown that the network based on Pearson correlation has more links, and the stations in geographically similar locations are mostly connected together. By contrast, the network based on mutual information shows that in some cases, stations in geographically similar locations are not connected together. In particular, these differences can be clearly seen in the case of the stations located on the eastern coast of the Korean Peninsula (i.e., Station 19 (Yeongdeok), Station 22 (Uljin), Station 24 (Pohang), and Station 55 (Ulsan)). Looking at the links between them, it can be seen that the network based on Pearson correlation shows these stations to be connected to one another and also with other stations located inland, whereas in the network based on mutual information, these stations are unconnected not only to inland stations but also to one another. In the Korean Peninsula, there is a large mountain range (i.e., Taebaek Mountains) stretching along the eastern seaboard, and, thus, the coastal stations have rainfall characteristics that are different from those of inland stations on the other side of the mountain range. Therefore, there should be little correlation between the stations on either side of the mountain range, and the network based on mutual information reflects this, whereas the one based on Pearson correlation does not.
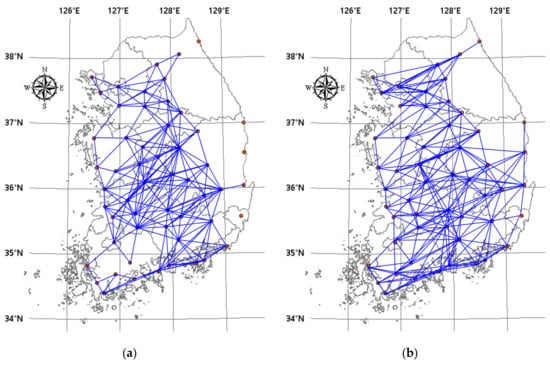
Figure 6.
Complex network connected by threshold 0.7: (a) mutual information; (b) Pearson correlation.
The centrality values were computed for these two networks. Based on these computed values, each station was ranked according to its importance (Figure 7 and Figure 8). If we examine the ranks of stations according to threshold values, the rank by mutual information is less sensitive to threshold than that by Pearson correlation. Especially, Pearson correlation shows large variability in the ranks of stations according to threshold values rather than data characteristics. Therefore, there is the problem of using Pearson correlation for analyzing the importance of stations. However, mutual information that is not sensitive to threshold values can be used for the evaluation of rain gauge networks.
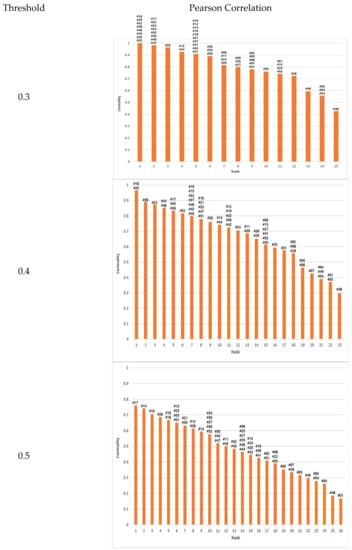
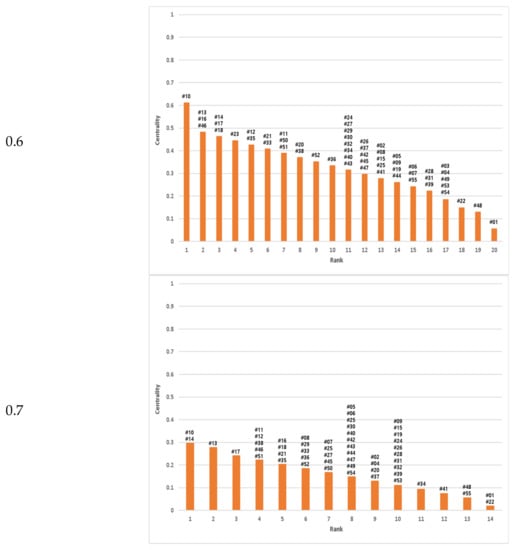
Figure 7.
Estimation of centrality and rank of station by Pearson correlation: The X-axis mean the rank of station and the Y-axis is the values of centrality. The number upon the bar mean the stations which belong to the rank.
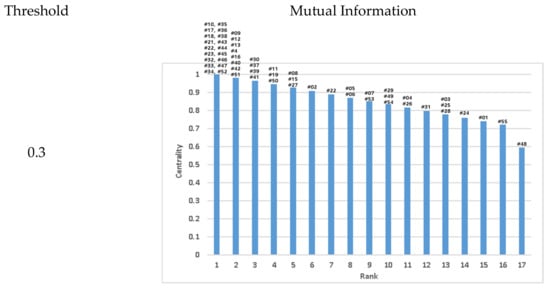
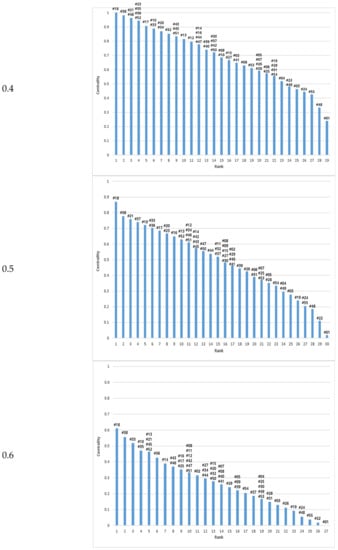
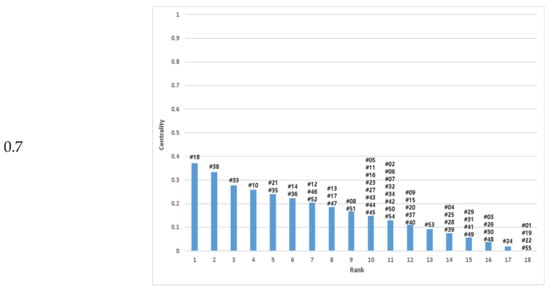
Figure 8.
Estimation of centrality and rank of station by mutual information: on the X-axis is the rank of station and on the Y-axis are the values of centrality. The number upon the bar mean the stations which belong to the rank.
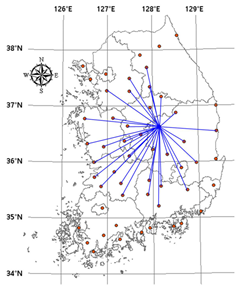
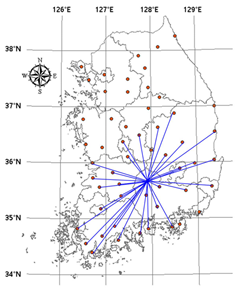
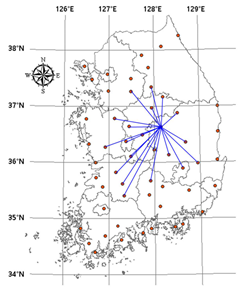
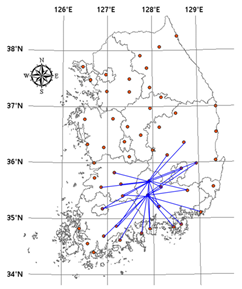
Table 4 shows the stations that were ranked as the most important and the links connecting them with other stations. When the threshold is set at 0.3, however, the station ranked as the most important is connected to all the other 54 stations, making it difficult to identify its characteristics and both cases have the same shape of network; therefore, this was excluded. In the network based on mutual information, the changes according to the threshold show that as the threshold increases, the number of links connecting the most important station with outer stations decreases. In particular, the number of links with coastal stations decreases. Moreover, it can be seen that the network constructed around the most important node forms a gauge network that covers most of the southern half of the Korean Peninsula. In the network based on Pearson correlation, the changes according to the threshold show that the network constructed around the most important node grows from inland to coastal areas, and that this network covers a lesser area in the Korean Peninsula.

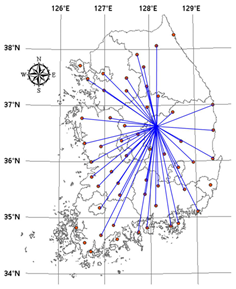
Table 4.
The first station of centrality and links. The most important stations and their links are expressed in the map according to the threshold (0.4 to 0.7). In the case of threshold 0.3, many stations are selected and each of the chosen stations connected with all stations in both cases (mutual information and Pearson coefficient).
3.4. Discussion
In this study, two complex networks were constructed using the daily rainfall data from 55 ASOS weather stations in the Republic of Korea. These complex networks were generated by applying mutual information and Pearson correlation. It was impossible to compare these networks directly because they had values with mutually different ranges; therefore, they were evaluated using the degree of centrality index. To compare the two networks using the degree of centrality index, it is necessary to set the threshold, but there is currently no established method for setting the threshold. Therefore, in this study, we computed the changes in the number of links according to different thresholds, and identified the interval where there is at least 10% difference in the number of links compared to the preceding threshold as the interval where drastic changes occur. This is the interval where drastic changes occur in the network structure due to the drastic changes in the number of links, thus changing the characteristics of the network and of each node. As it is possible to analyze all the characteristics of the network within this interval, we selected it as the threshold interval. To compare the characteristics of the two networks constructed via the two different methods, we compared their node rankings according to the centrality. The figure below shows the geographical locations of the stations ranked as the most important (Figure 9).
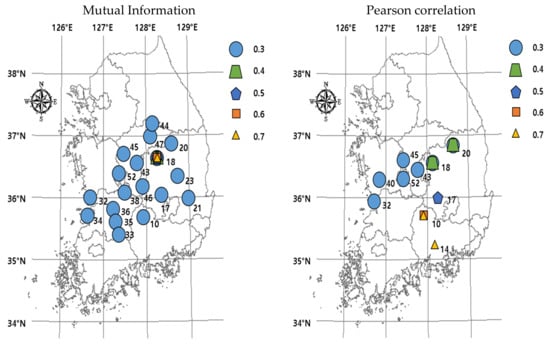
Figure 9.
Locations of the most important station according to the threshold. The stations that have the highest value of centrality are expressed in the map according to the threshold (0.3, 0.4, 0.5, 0.6, 0.7). The location of the station in the case of mutual information is in the central of the Korean peninsula. The result of Pearson correlation shows that locations of the highest ranked station are moving into the south part of the Korean peninsula.
As shown above (Table 5), in the network based on mutual information, it can be seen that Station 18 (Mungyeong) is ranked as the most important at all threshold values except 0.3. Here, it can be noted that the geographical location of Station 18 is at the center of the southern half of the Korean Peninsula. By contrast, in the network based on Pearson correlation, it can be seen that the most important station varies according to the threshold. When we locate the most important stations on the map, it can be noted that their locations are skewed to the south except when the threshold is 0.3 or 0.4. In terms of geographical location, therefore, it is difficult to accept that the stations ranked as the most important in the Pearson correlation-based network are indeed the most important. Moreover, in the network based on Pearson correlation, the most important station varied according to the threshold, thus showing that the network is sensitive to the choice of threshold. As the rankings of all the stations vary according to changes in the threshold, the evaluation of the gauge network is highly dependent on the choice of threshold, and it is difficult to determine which stations are important. By contrast, the network based on mutual information yields the same results even when the threshold changes, and, thus, it is adequate for evaluating rain gauge networks. Therefore, if mutual information is used in constructing complex networks, we expect that it will contribute to solving the extant problem of choosing which threshold to apply.

Table 5.
The most important station according to threshold. The stations which have the highest value of centrality are chosen according to the threshold (0.3, 0.4, 0.5, 0.6, 0.7). The mutual information results have consistent results, but the Pearson correlation results have variability.
4. Conclusions
In this paper, we recommended the use of mutual information, that can consider nonlinearity, instead of Pearson correlation, which was frequently applied in previous studies using complex networks to analyze relationships in the field of hydrology. First, a useful statistical method known as the BDS statistic was used to determine the nonlinearity of rainfall data. Using the 95% confidence interval, the null hypothesis was rejected in all cases, thus observed daily rainfall data was determined as the nonlinearity of the data. Next, both Pearson correlation and mutual information were used to calculate the strength of the links in complex networks. As the two resulting networks have values in mutually different ranges, it was impossible to compare them directly, so the two networks were compared using degree of centrality. However, the degree of centrality varies its numerator according to changes in the threshold; therefore, the number of links was compared according to the threshold, and a threshold interval in which the number of links undergoes drastic changes was identified. Then, the two networks were compared, and the results indicated that the network based on mutual information is consistent in its ranking of stations, whereas the network based on Pearson correlation varied its ranking according to changes in the threshold. Moreover, a comparison of stations ranked as the most important station indicated that the network based on Pearson correlation assigned high ranking to geographically skewed stations, whereas the one based on mutual information assigned high ranking to a centrally located station. Furthermore, mutual information has the advantage of factoring in nonlinearity and being relatively free from the influence of outliers [28]. Therefore, when constructing complex networks involving rainfall data, which have nonlinearity, using mutual information is more suitable than Pearson coefficient.
Supplementary Materials
The following are available online at https://www.mdpi.com/2073-4441/11/8/1578/s1, Appendix A. Basic statistic of observed daily rainfall data in each station. Appendix B. Results of BDS statistics.
Author Contributions
This research was carried out in collaboration among all authors. H.S.K. and H.J. had the original idea and led the research; D.H., and S.K. performed the data processing and analysis; and K.K. and T.L. edited the final manuscript. All authors reviewed and approved the manuscript.
Funding
This research was funded by the National Research Foundation of Korea (NRF) grant funded by the Korean government (MSIT) (No. 2017R1A2B3005695).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Burgueno, A.; Vilar, E.; Puigcerver, M. Spectral Analysis 49 Years of Rainfall Rate and Relation to Fade Dynamics. IEE Trans. Commun. 1990, 9, 1359–1366. [Google Scholar] [CrossRef]
- Goyal, M.K. Monthly rainfall prediction using wavelet regression and neural network: An analysis of 1901–2002 data, Assam, India. Theor. Appl. Climatol. 2014, 118, 25–34. [Google Scholar] [CrossRef]
- Kyoung, M.S.; Kim, H.S.; Sivakumar, B.; Singh, V.P.; Ahn, K.S. Dynamic characteristics of monthly rainfall in the Korean Penisula under climate change. Stoch. Environ. Res. Risk Assess. 2011, 25, 613–625. [Google Scholar] [CrossRef]
- Olayide, O.E.; Alabi, T. Between rainfall and food poverty: Assessing vulnerability to climate change in an agricultural economy. J. Clean. Prod. 2018, 198, 1–10. [Google Scholar] [CrossRef]
- DehghanSh, K.S.; Eslamian, S.; Gandomkar, A.; Marani-Barzani, M.; Amoushahi-Khouzani, M.; Singh, V.P.; Ostad-Ali-Askari, K. Change in Temperature and Precipitation with the Anaylsis of Geomorphic Basin Chaos in Shiranz. Iran Int. J. Constr. Res. Civ. Eng. (IJCRCE) 2017, 3, 50–57. [Google Scholar] [CrossRef]
- Krajewski, W.F.; Ciach, G.J.; Habib, E. An analysis of small-scale rainfall variability in different climatic regimes. Hydrol. Sci. J. 2002, 48, 151–162. [Google Scholar] [CrossRef]
- Di Piazza, A.; Conti, F.L.; Noto, L.V.; Viola, F.; La Loggia, G. Comparative analysis of different techiques for spatial interpolation of rainfall data to creat a serially complete monthly time series of precipitation for Sicily, Italy. Int. J. Appl. Earth Obs. Geoinf. 2011, 13, 396–408. [Google Scholar] [CrossRef]
- Tokar, A.S.; Markus, M. Precipiation-Runoff Modelling using Artificial Neural Networks and Conceptual Models. J. Hydrol. Eng. 2000, 5, 156–161. [Google Scholar] [CrossRef]
- Duffourg, F.; Ducrocq, V. Assessment of the water supply to Mediterranean heavy precipitation: A method based on finely designed water budgets. Atmos. Sci. Lett. 2013, 14, 133–138. [Google Scholar] [CrossRef]
- Binti Sa’adin, S.L.; Kaewunruen, S.; Jaroszweski, D. Heavy rainfall and flood vulnerability of Singapore-Malaysia high speed rail system. Aust. J. Civ. Eng. 2016, 14, 123–131. [Google Scholar] [CrossRef]
- David, C.C.; Dotson, H.W. Rain Gage Network Size for Automated Flood Warning System, Conference Proceeding of Engineering Hydrology; ASCE: Reston, VA, USA, 1993. [Google Scholar]
- Ministry of Land, Infrastructure and Transport (MLIT). Han River Watershed Research Hydraulic and Hydrological Research Report; MLIT: Tokyo, Japan, 2004.
- Dyck, G.E.; Gray, D.M. Spatial Characteristics of Prairie Rainfall; American Meteorological Society: Tronoto, ON, Canada, 1997; pp. 25–27. [Google Scholar]
- Brock, W.A.; Heish, D.A.; Lebaron, B. Nonlinear Dynamics Chaos and Instability Statistical Theory and Economic Evidence; The MIT Press Publisher: Cambridge, MA, USA, 1991. [Google Scholar]
- Jha, S.K.; Zhao, H.; Woldemeskel, F.M.; Sivakumar, B. Network Theory and spatial rainfall connections: An Interpretation. J. Hydrol. 2015, 527, 13–19. [Google Scholar] [CrossRef]
- Luk, K.C.; Ball, J.E.; Sharma, A. A Study of optimal model lag and spatial inputs to artificial neural network for rainfall forecasting. J. Hydrol. 2000, 227, 56–65. [Google Scholar] [CrossRef]
- Boccaletti, S.; Latora, V.; Moreno, Y.; Chavez, M.; Hwang, D.U. Complex networks:Structure and dynamics. Phys. Rep. 2006, 424, 175–308. [Google Scholar] [CrossRef]
- Latora, V.; Nicosia, V.; Russo, G. Complex Networks Principles, Methods and Applications; Cambridge University Press: Cambridge, UK, 2017. [Google Scholar]
- Schweitzer, F.; Fagiolo, G.; Sornette, D.; Vega-Redondo, F.; Vespignani, A.; White, D.R. Economic Networks: The New Challenges. Science 2009, 325, 422–425. [Google Scholar] [CrossRef] [PubMed]
- Pagani, G.A.; Aiello, M. The Power Grid as a complex Netowrk: A survey. Physica A: Stat. Mech. Appl. 2013, 392, 2688–2700. [Google Scholar] [CrossRef]
- Mason, O.; Verwoerd, M. Graph theory and networks in Biology. IET Syst. Biol. 2007, 1, 89–119. [Google Scholar] [CrossRef]
- Milo, R.; Shen-Orr, S.; Itzkovitz, S.; Kashtan, N.; Chklovskii, D.; Alon, U. Network Motifs: Simple Building Block of Complex Networks. Science 2002, 298, 824–827. [Google Scholar] [CrossRef]
- Yazdani, A.; Jeffrey, P. Complex network analysis of water distributuion systems. Chaos 2011, 21, 01611. [Google Scholar] [CrossRef] [PubMed]
- Boers, N.; Bookhagen, B.; Marwan, N.; Kurths, J.; Marengo, J. Complex networks identiy spatial patterns of extreme rainfall events of the South American Monsoon System. Geophys. Reasearch Lett. 2013, 40, 4386–4392. [Google Scholar] [CrossRef]
- Sivakumar, B.; Woldemeskel, F.M. Complex networks for streamflow dynamics. Hydrol. Earth Syst. Sci. 2014, 11, 4565–4578. [Google Scholar] [CrossRef]
- Halverson, J.M.; Fleming, S.W. Complex network theory, streamflow, and hydrometric monitoring system design. Hydrol. Earth Syst. Sci. 2015, 19, 3301–3318. [Google Scholar] [CrossRef]
- Cover, T.M.; Tomas, J.A. Elements of Information Theory, 2nd ed.; Schilling, D.L., Ed.; Wiley Series in Telecommunications Press: New York, NY, USA, 2006. [Google Scholar]
- Numata, J.; Ebenhöh, O.; Knapp, E.W. Measuring correlation in Metabolomic networks with Mutual Information. Genome Inform. Ser. 2008, 20, 112–122. [Google Scholar] [CrossRef]
- Dadgostar, M.; Einalou, Z.; Setarehdam, S.K.; Keskin-Ergen, H.Y.; Akin, A. Comparison of Mutual Information and Partial Correlation for Functional Connectivity in fNIRS. In Proceedings of the 21th Iranian Conference on Electric Engineering, Mashhad, Iran, 14–16 May 2013. [Google Scholar]
- Donges, J.F.; Zou, Y.; Marwan, N.; Kurths, J. Complex networks in climate dynamics Comparing linear and nonlinear network construction methods. Eur. Phys. J. Spec. Top. 2009, 174, 157–179. [Google Scholar] [CrossRef]
- Wang, J.; He, J.M. Correlation and Interdependence Structure in Stock Market: Based on Information Theory and Complex Networks. In Proceedings of the 17th International Conference on Control, Automation and Systmes (ICCAS 2017), Jeju, Korea, 18–21 October 2017. [Google Scholar]
- Zhang, W.; Ma, J.; Ideker, T. Classifying tumors by supervised networks propagation. Bioinformatics 2018, 34, 484–493. [Google Scholar] [CrossRef] [PubMed]
- Kroll, M.H.; Emancipator, K. A Theoretical Evaluation of Linearity. Clin. Chem. 1993, 39, 405–413. [Google Scholar] [PubMed]
- Strogatz, S.H. Nonlinear Dynamics and Chaos with Application to Physics, Biology, Chemistry and Engineering; Westview Press: Philadelphia, PA, USA, 2015. [Google Scholar]
- Brock, W.A.; Scheinkman, J.A.; Dechert, W.D.; LeBaron, B. A test for independence based on the correlation dimension. Econom. Rev. 1996, 15, 197–235. [Google Scholar] [CrossRef]
- Kim, H.S.; Eykholt, R.; Salas, J.D. Delay time window and plateau onset of the correlation dimension for small data sets. Phys. Rev. E 1998, 58, 5676–5682. [Google Scholar] [CrossRef]
- Kim, H.S.; Eykholt, R.; Salas, J.D. Nonliear dynamics, delay times and embedding windows. Phys. D 1999, 127, 48–60. [Google Scholar] [CrossRef]
- Kim, S.; Noh, H.; Kang, N.; Lee, K.; Kim, Y.; Lim, S.; Lee, D.R.; Kim, H.S. Noise Reduction Analysis of Radar Rainfall Using Chaotic Dynamics and Filtering Techniques; Hindawi Publishing Corporation: London, UK, 2014; pp. 1–10. [Google Scholar]
- Kim, H.S.; Kang, D.S.; Kim, J.H. The BDS statistic Application to Hydrologic Data. J. Korea Water Resour. Assoc. 2003, 31, 769–777. [Google Scholar]
- Kim, K.H.; Han, D.G.; Kim, J.W.; Lim, J.H.; Lee, J.S.; Kim, H.S. Modelling and Residual Analysis for Water Level Series of Upo Wetland. J. Wetl. Res. 2018, 21, 66–76. [Google Scholar] [CrossRef]
- Bavelas, A. A mathematical model for group structure. Hum. Org. 1948, 7, 16–30. [Google Scholar] [CrossRef]
- Leavitt, H.J. Some effects of certain communication patterns on group performance. J. Abnorm. Soc. Psych. 1951, 46, 38–50. [Google Scholar] [CrossRef]
- Jeong, H.; Tomber, B.; Albert, R.; Oltavi, Z.N.; Barabási, A.L. The large-scale organization of metabolic networks. Nature 2000, 40, 651–654. [Google Scholar] [CrossRef] [PubMed]
- Newman, M.E.J. The structure of scientific collaboration networks. Proc. Natl. Acad. Sci. USA 2001, 98, 404–409. [Google Scholar] [CrossRef] [PubMed]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).