Development of Threshold Levels and a Climate-Sensitivity Model of the Hydrological Regime of the High-Altitude Catchment of the Western Himalayas, Pakistan
Abstract
1. Introduction
2. Methodology
2.1. Study Area and Data Collection
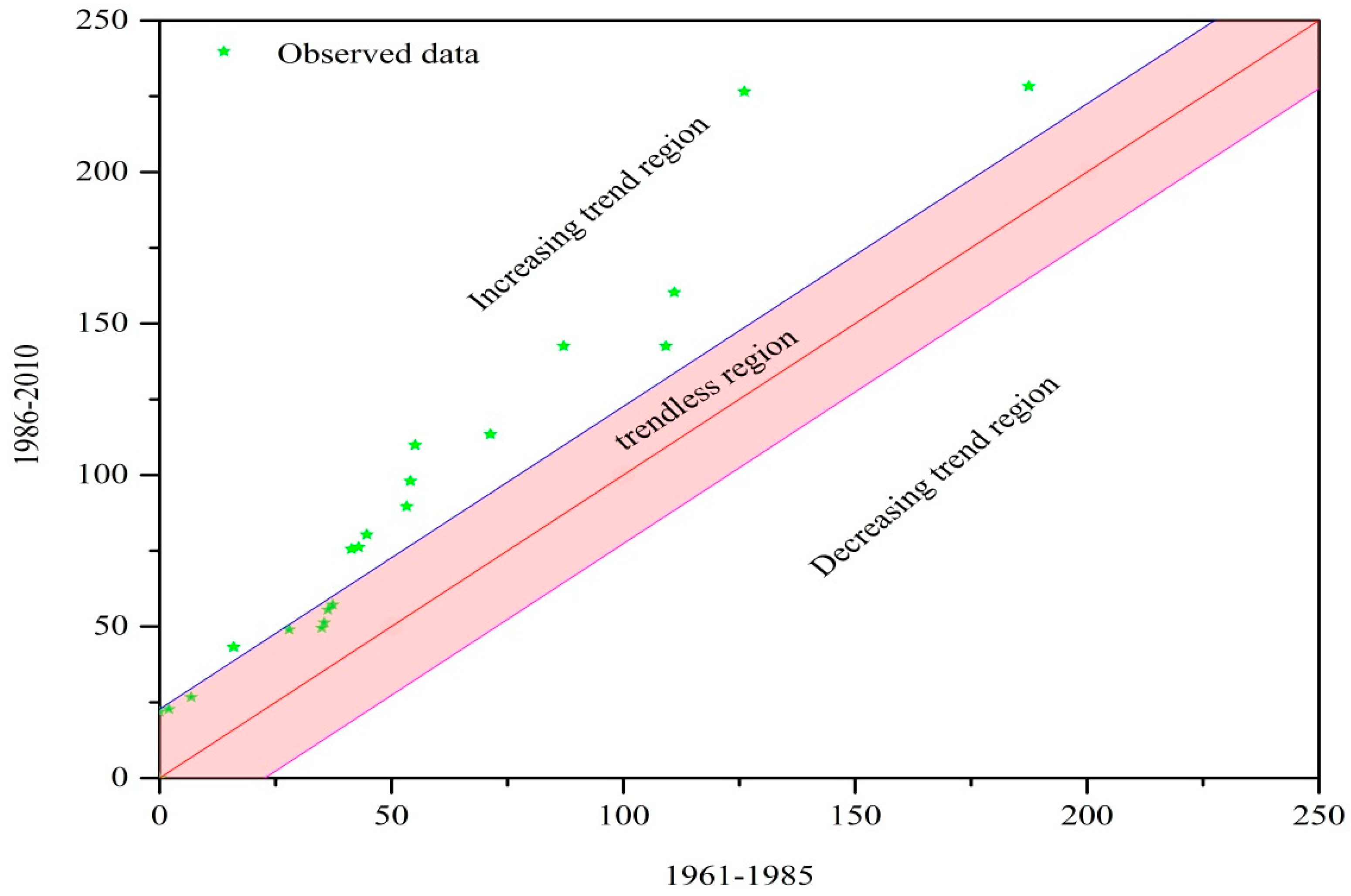
2.2. Innovative Trend Detection Test
2.3. Hydrological Regime Variability
2.4. Accumulated Difference Curve for Trend Detection
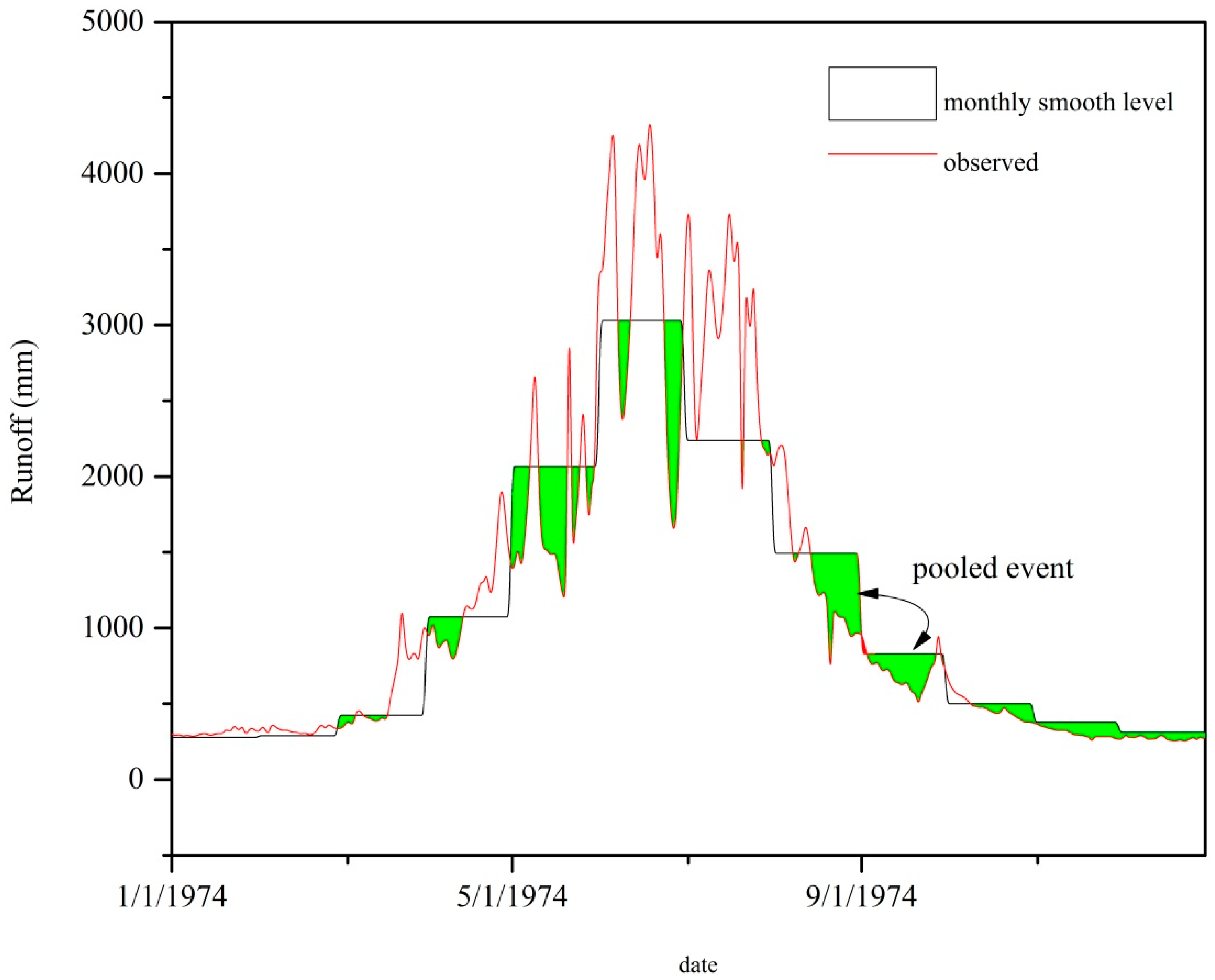
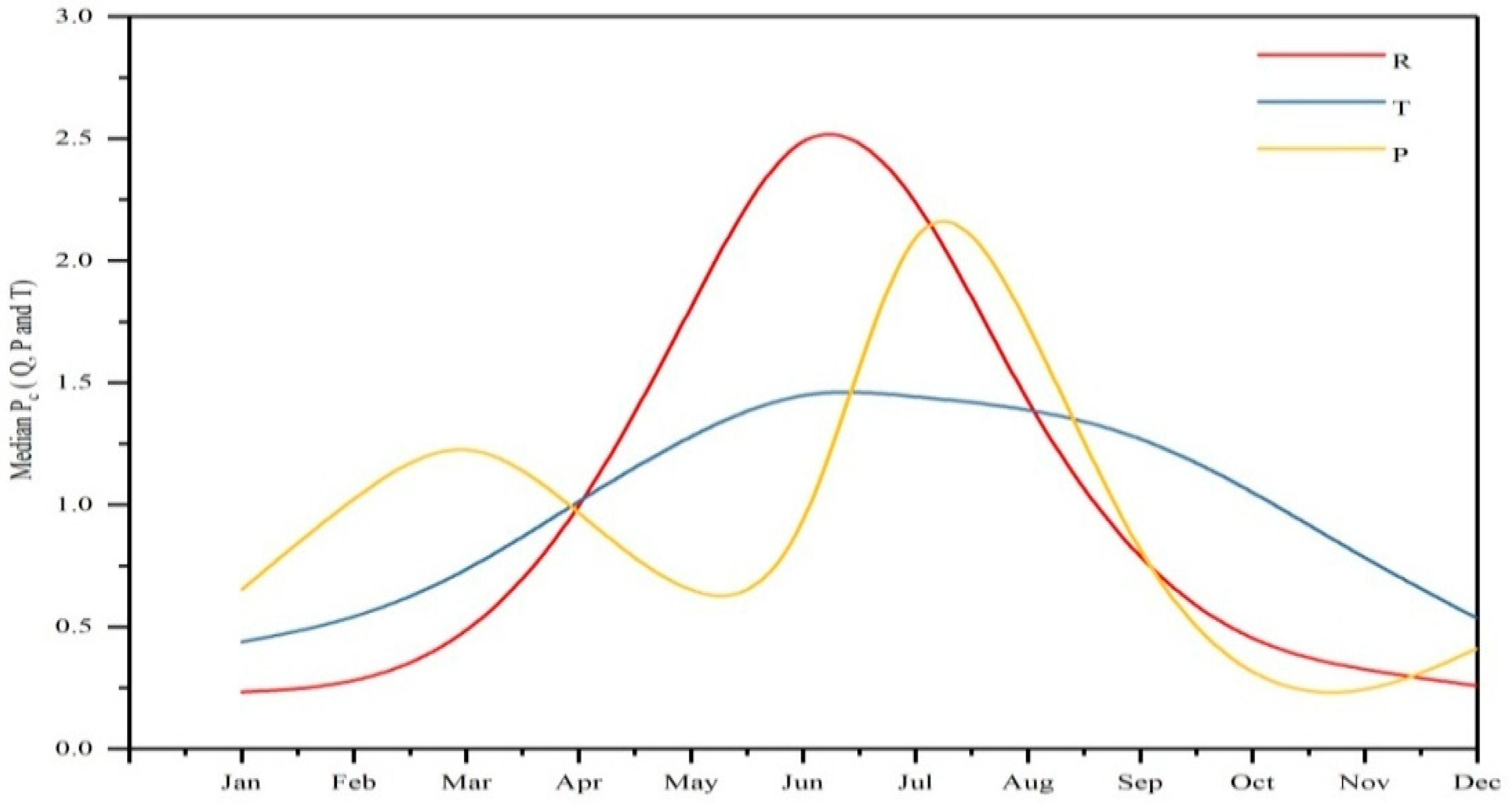
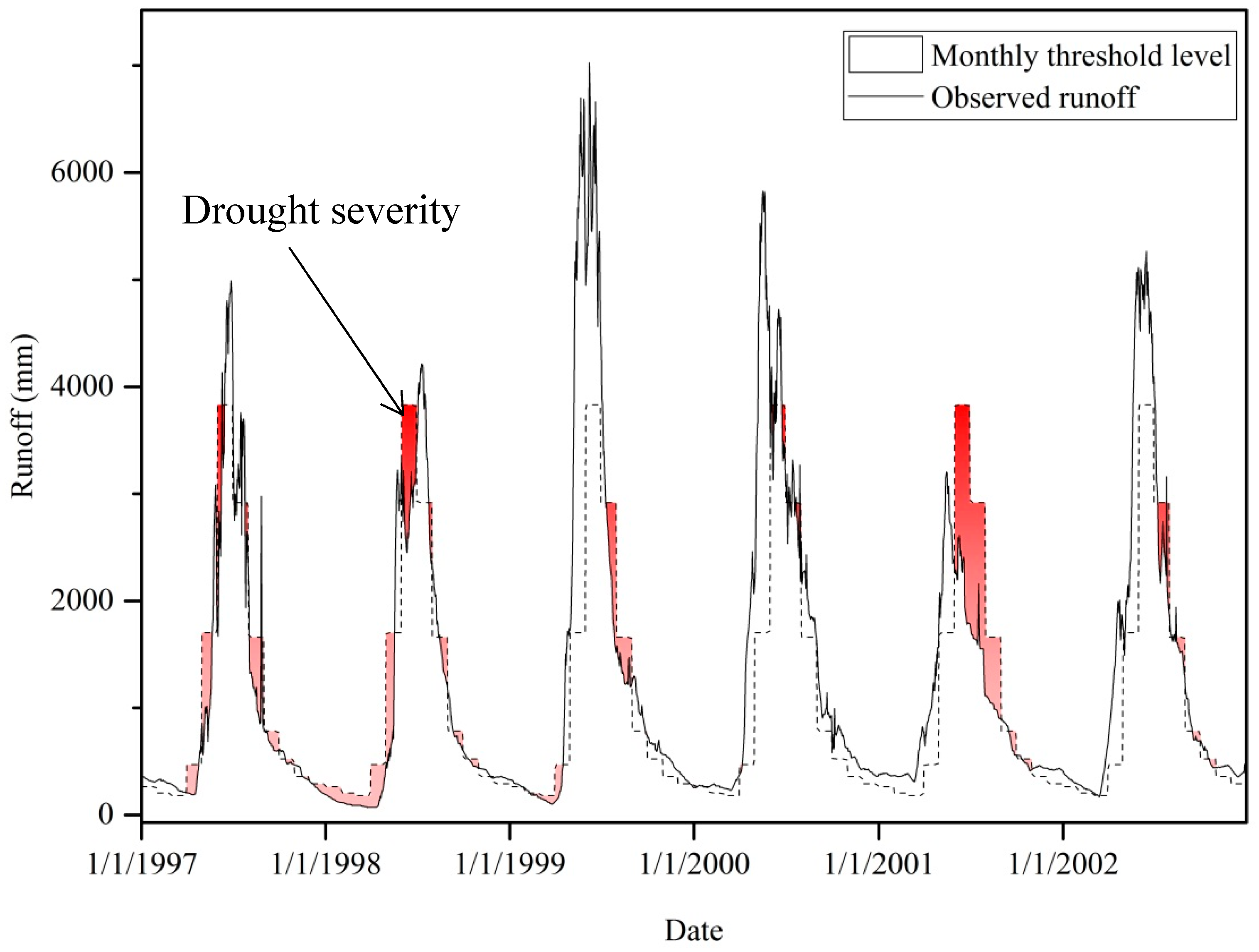
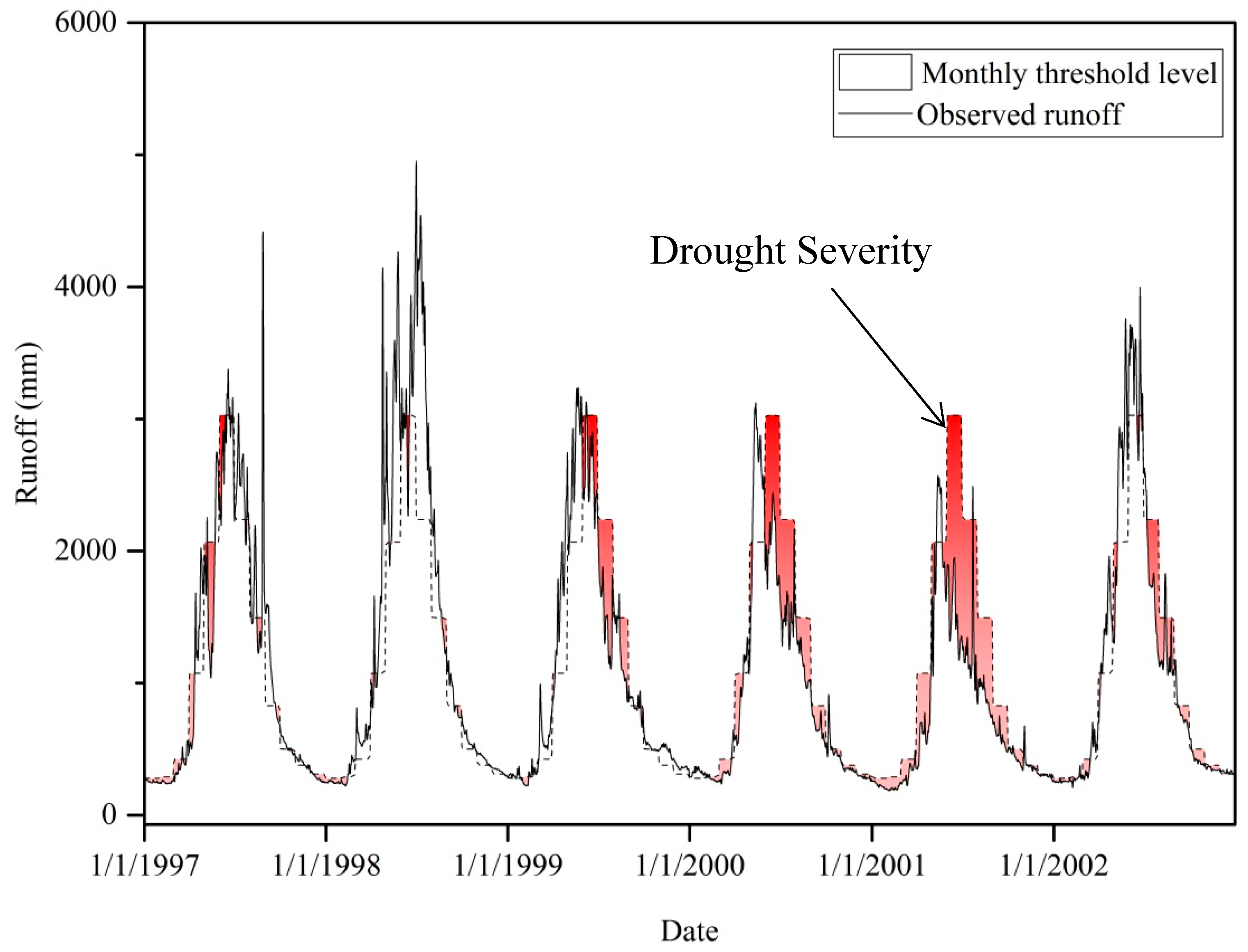
2.5. Development of Threshold Levels for a Hydrological Regime
2.6. Sensitivity of Hydrological Regime to Climate
3. Results and Discussion
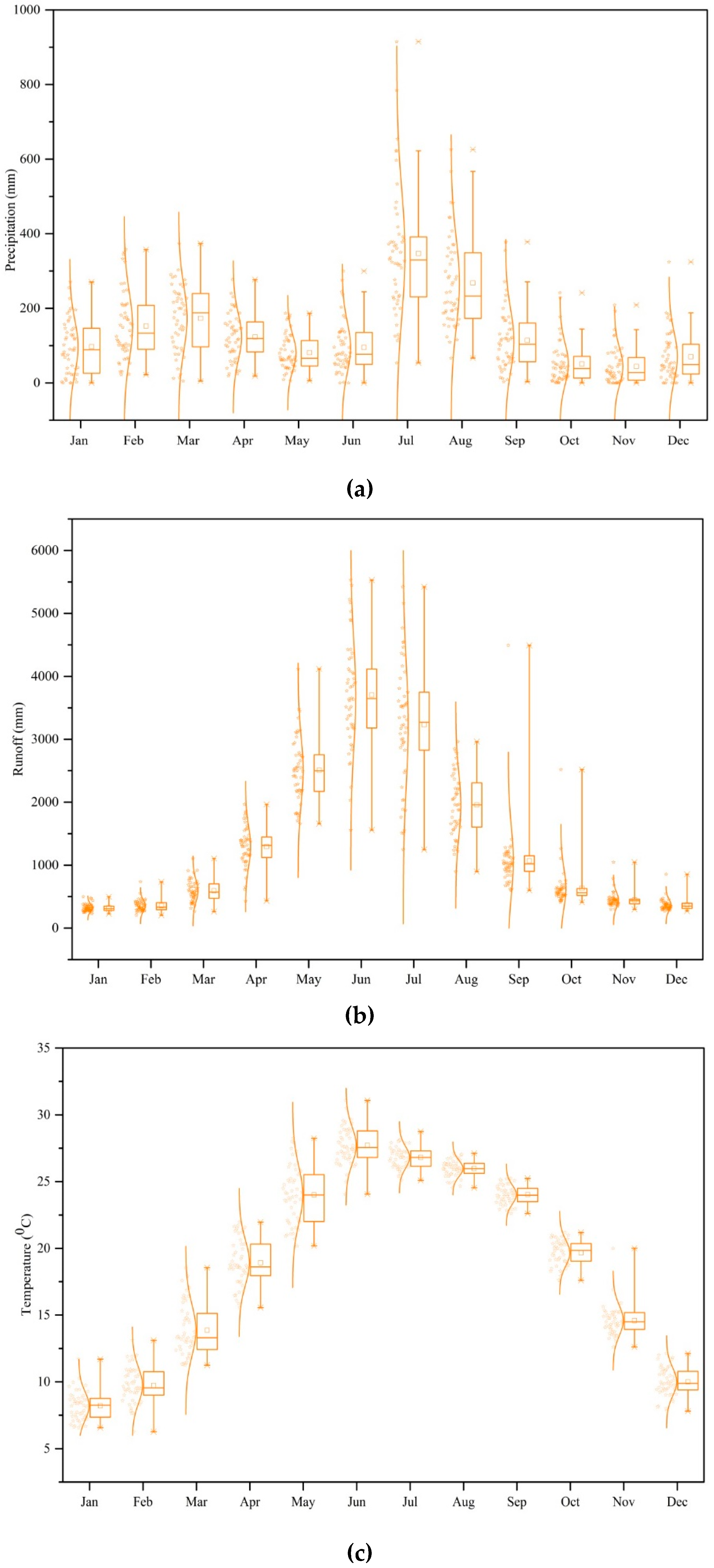
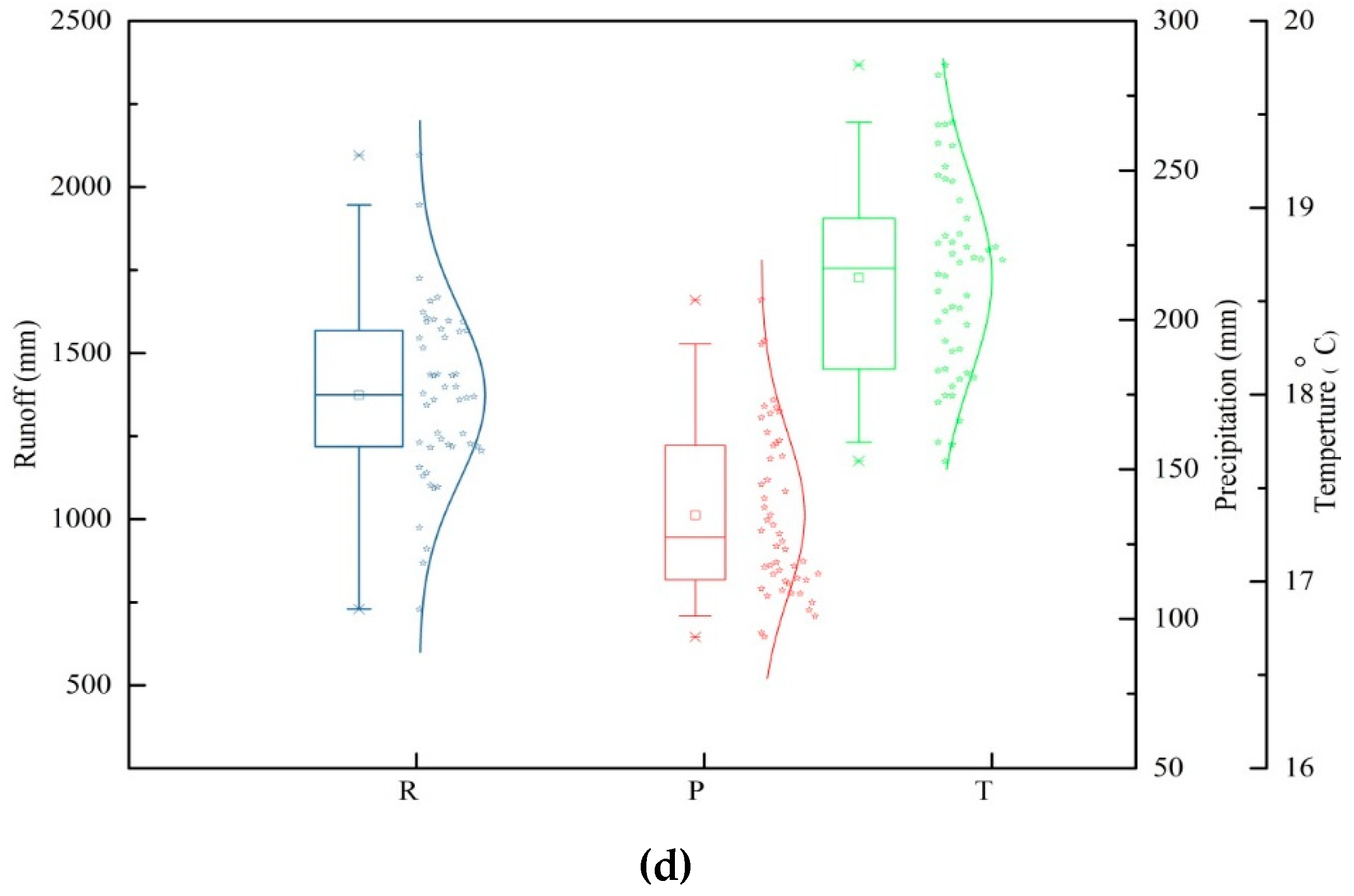
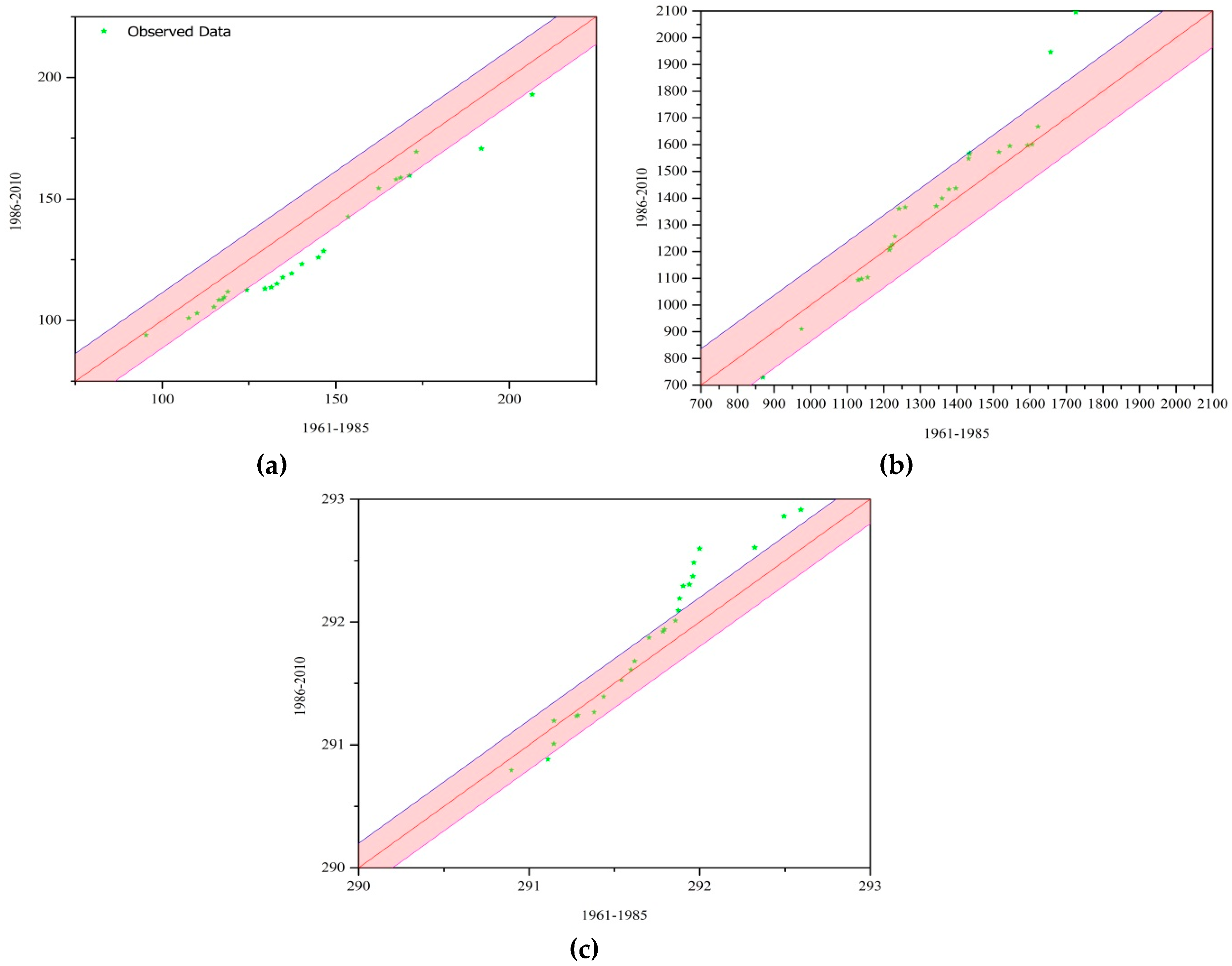
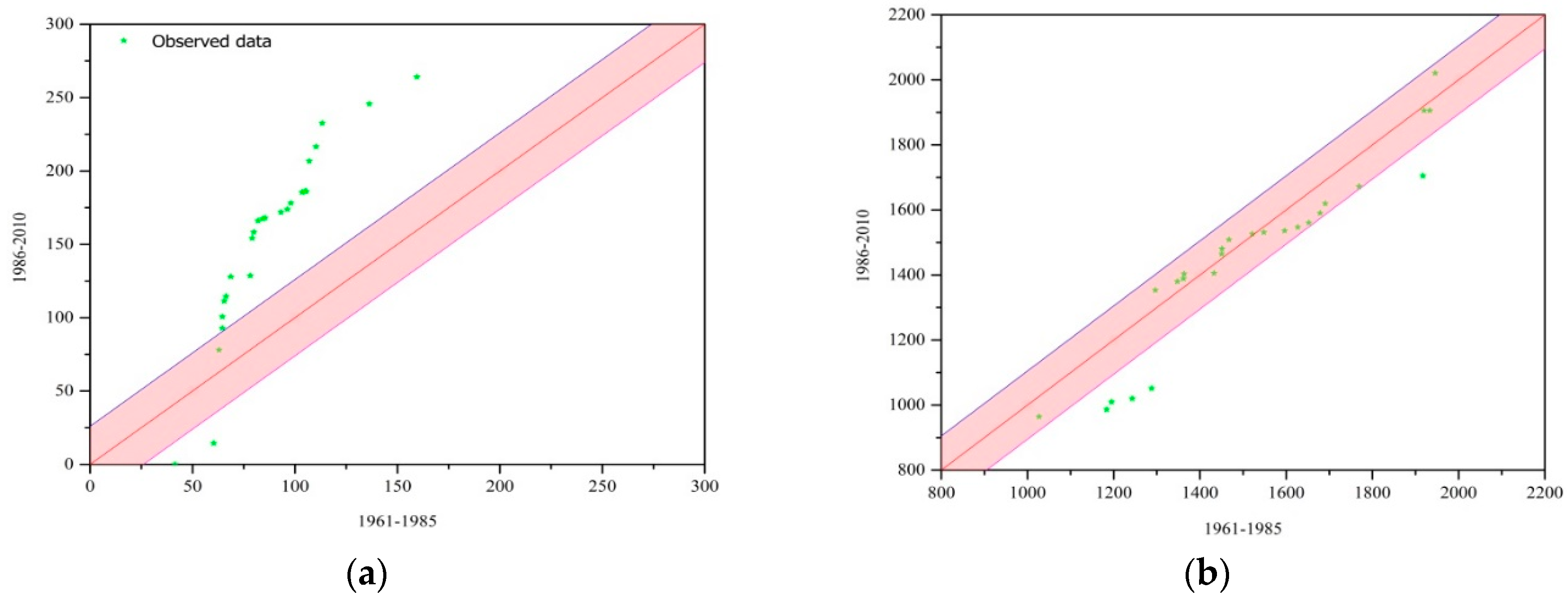
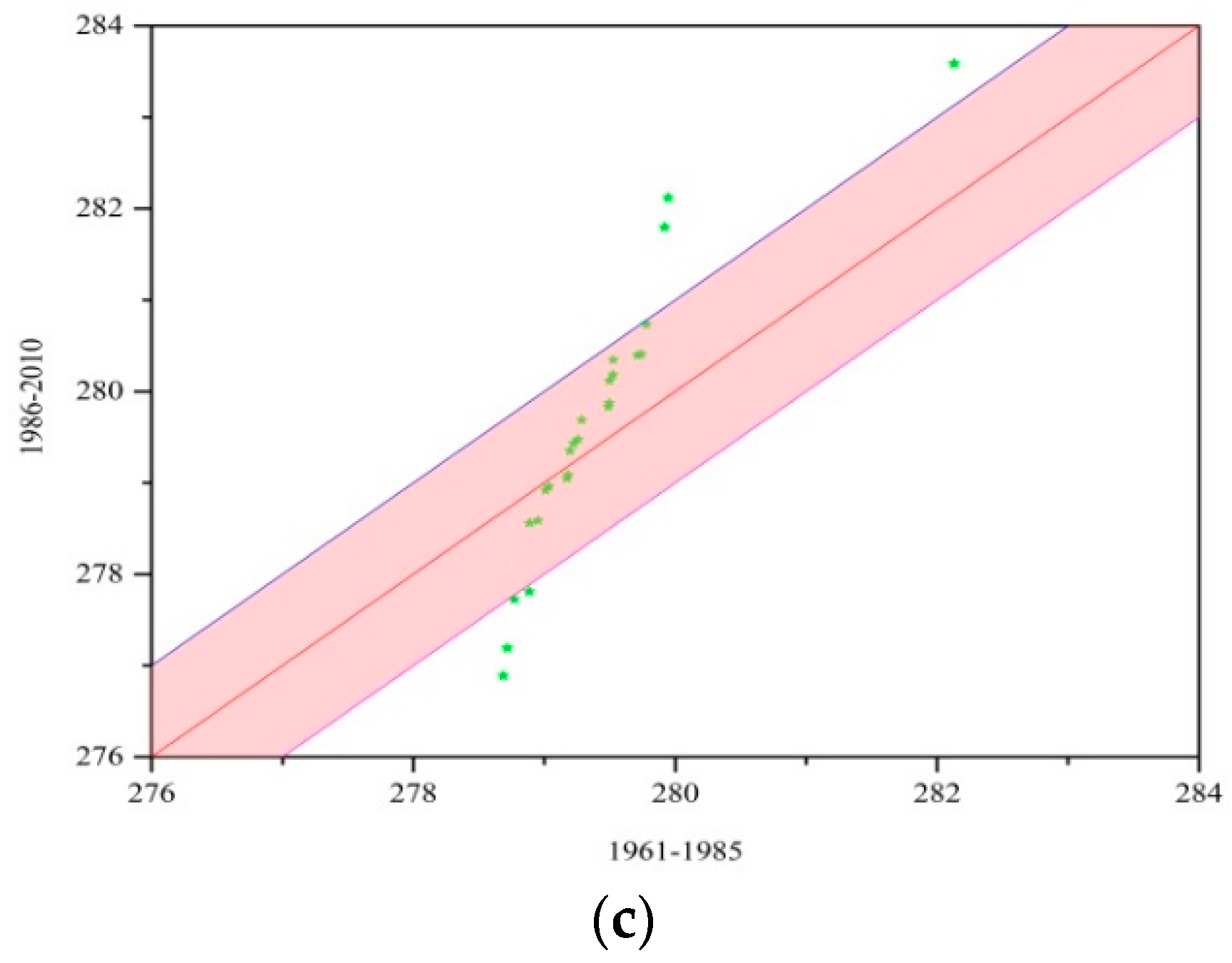
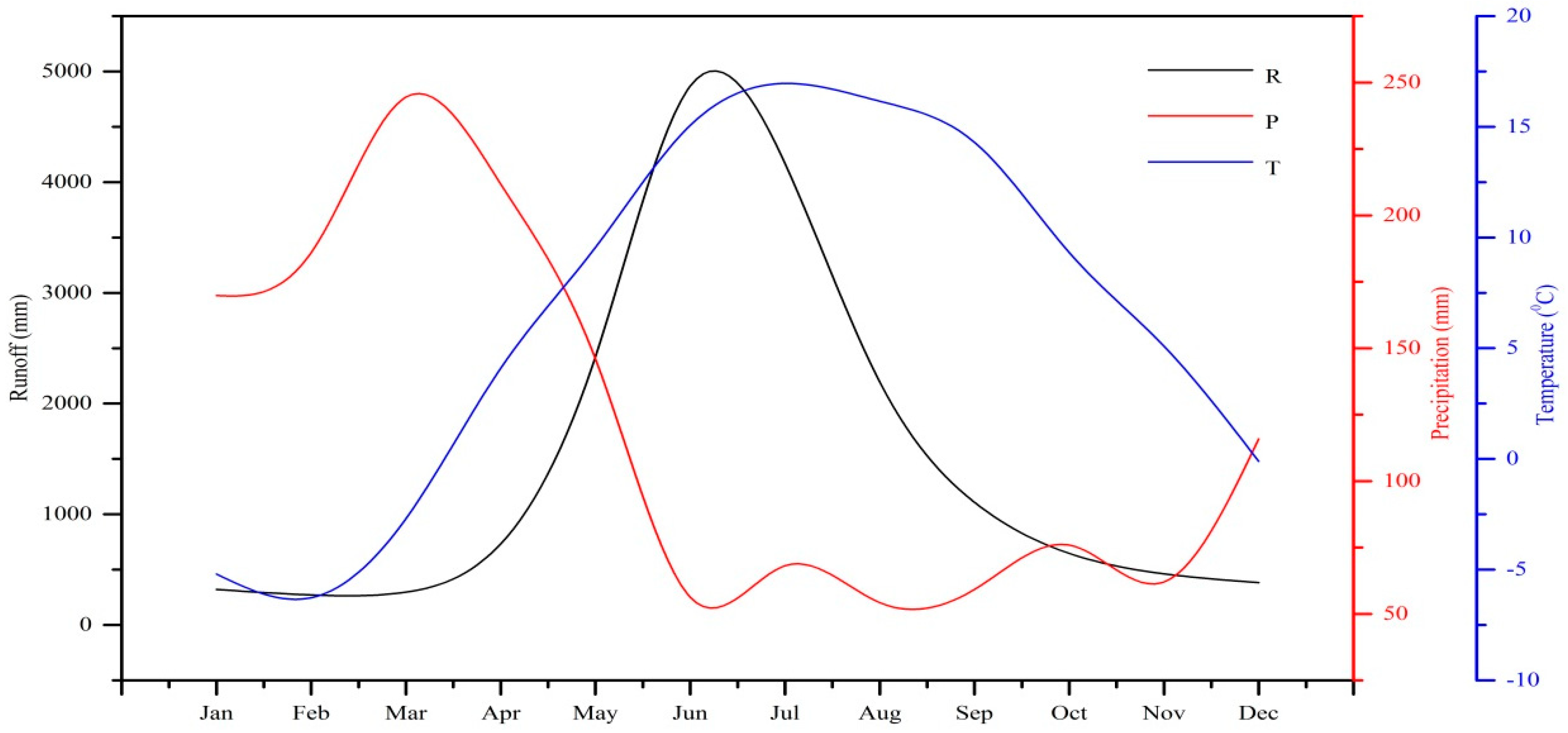
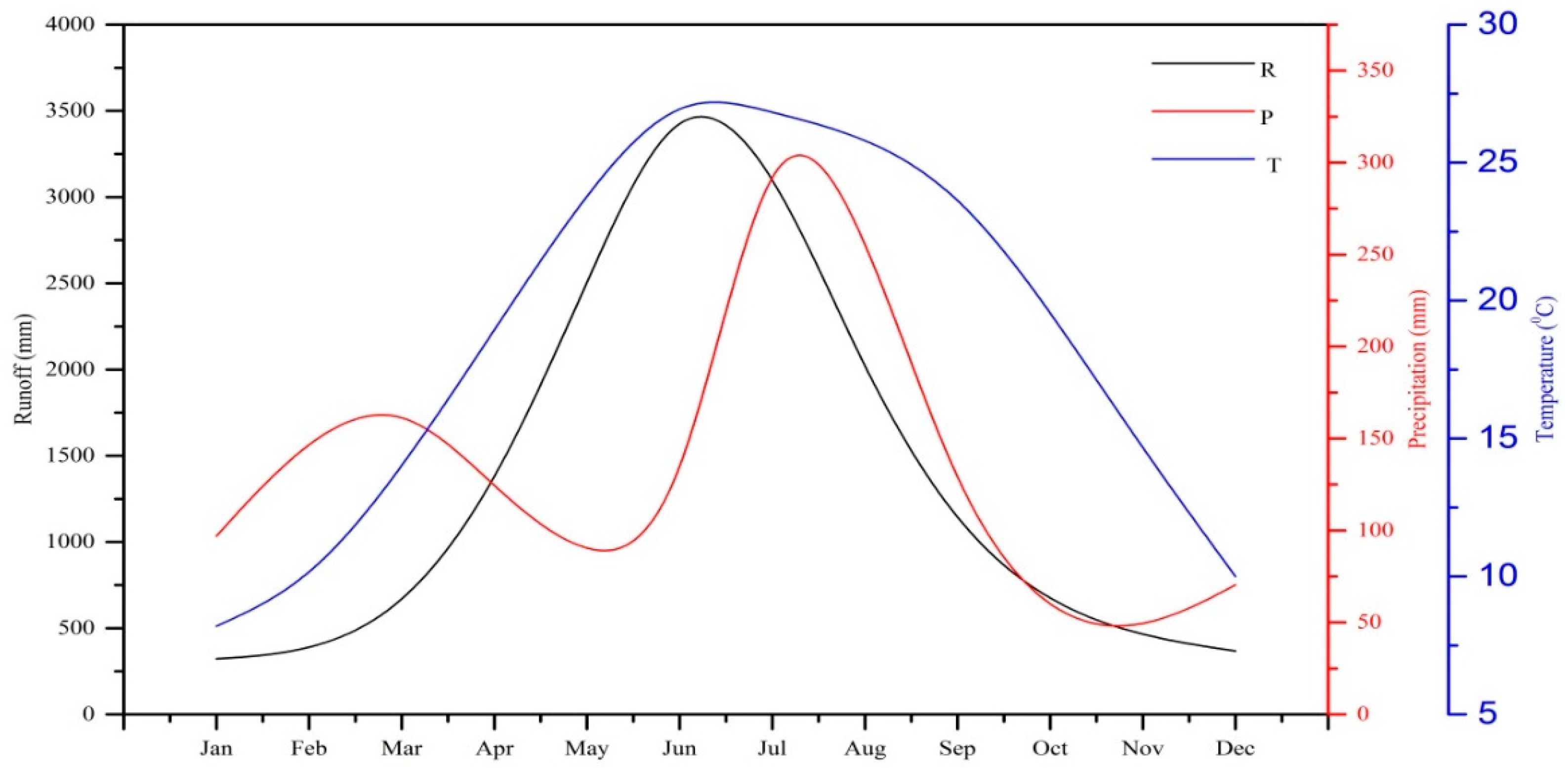
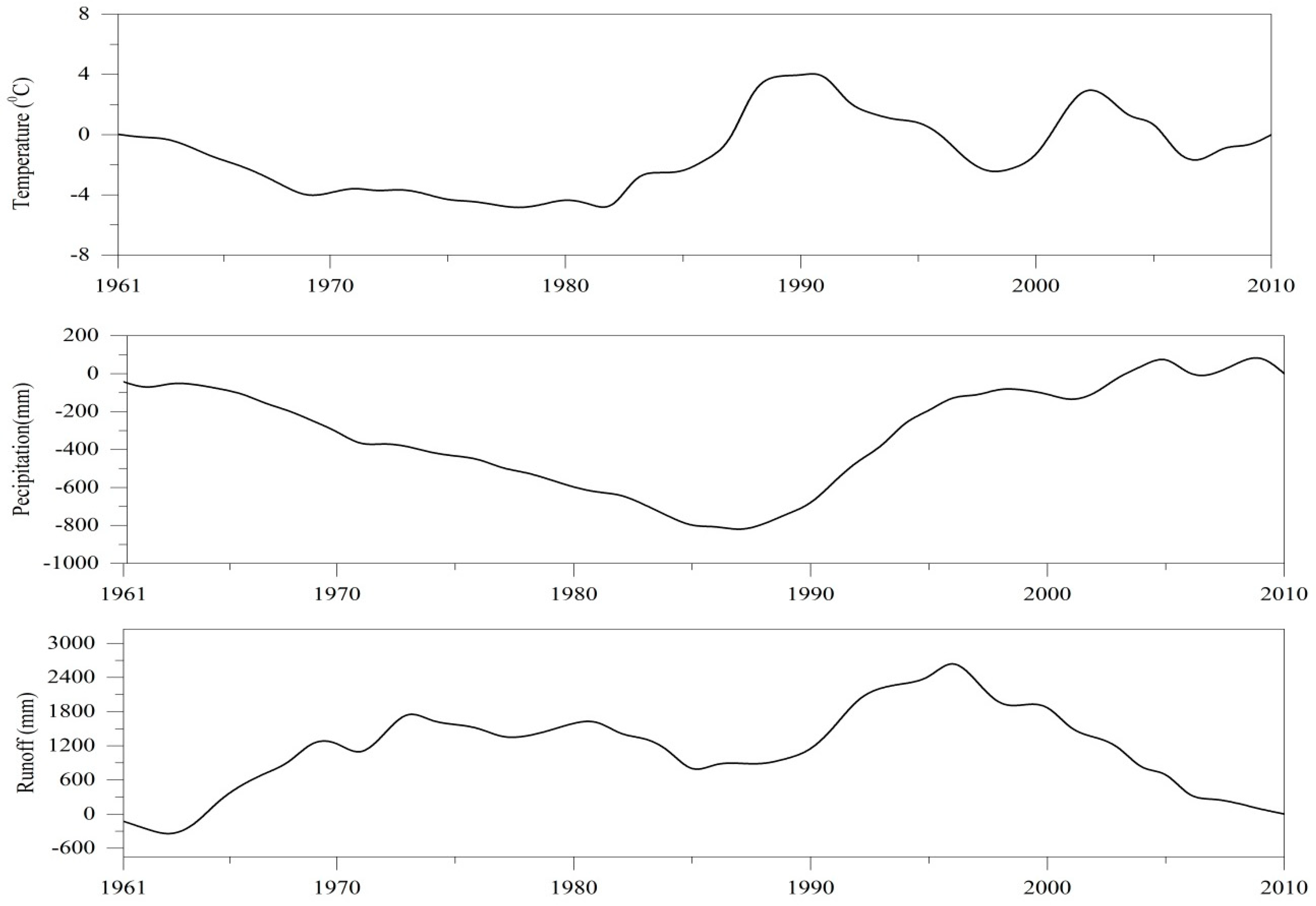
3.1. Spatial and Temporal Characteristics of Precipitation, Temperature and Runoff
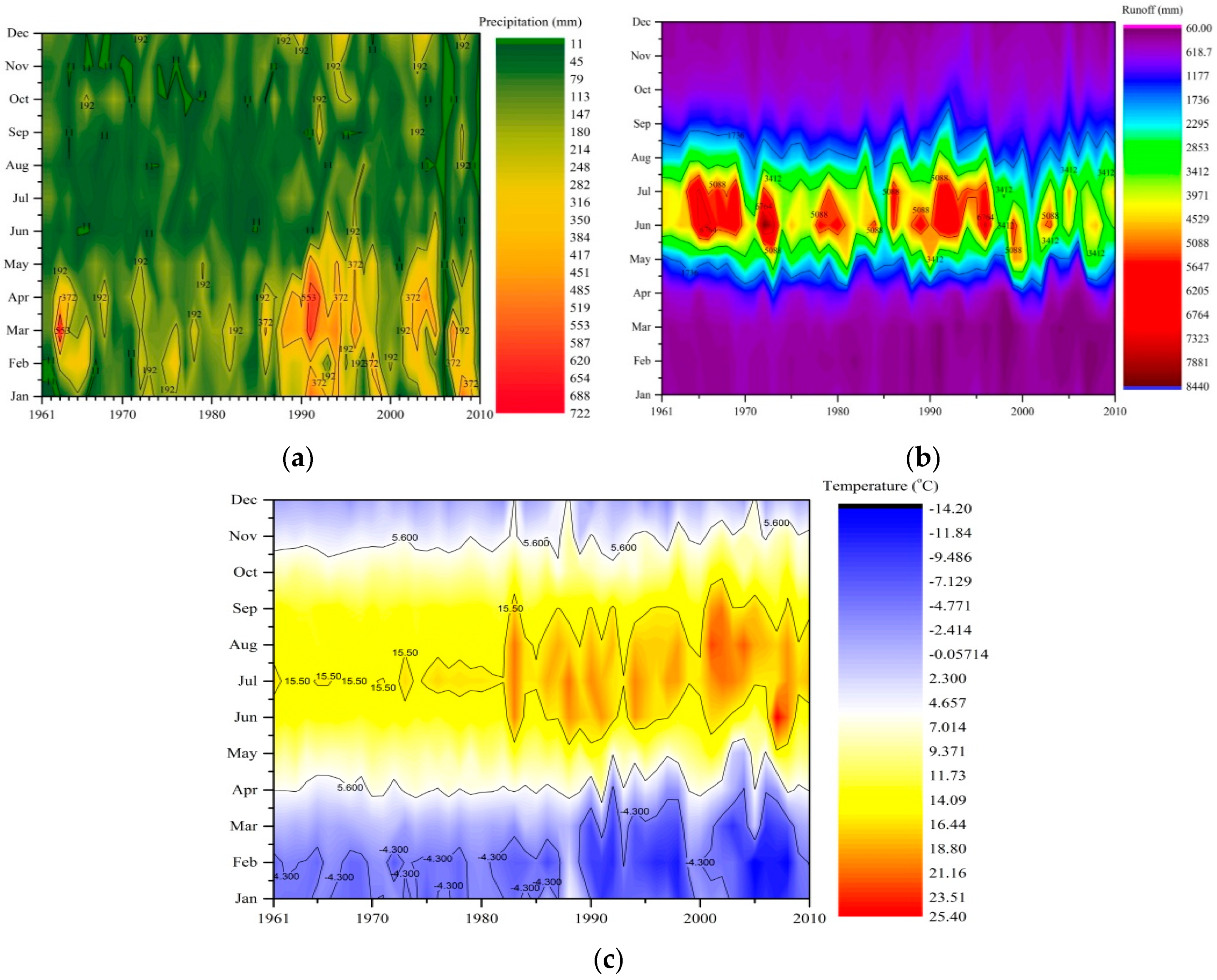
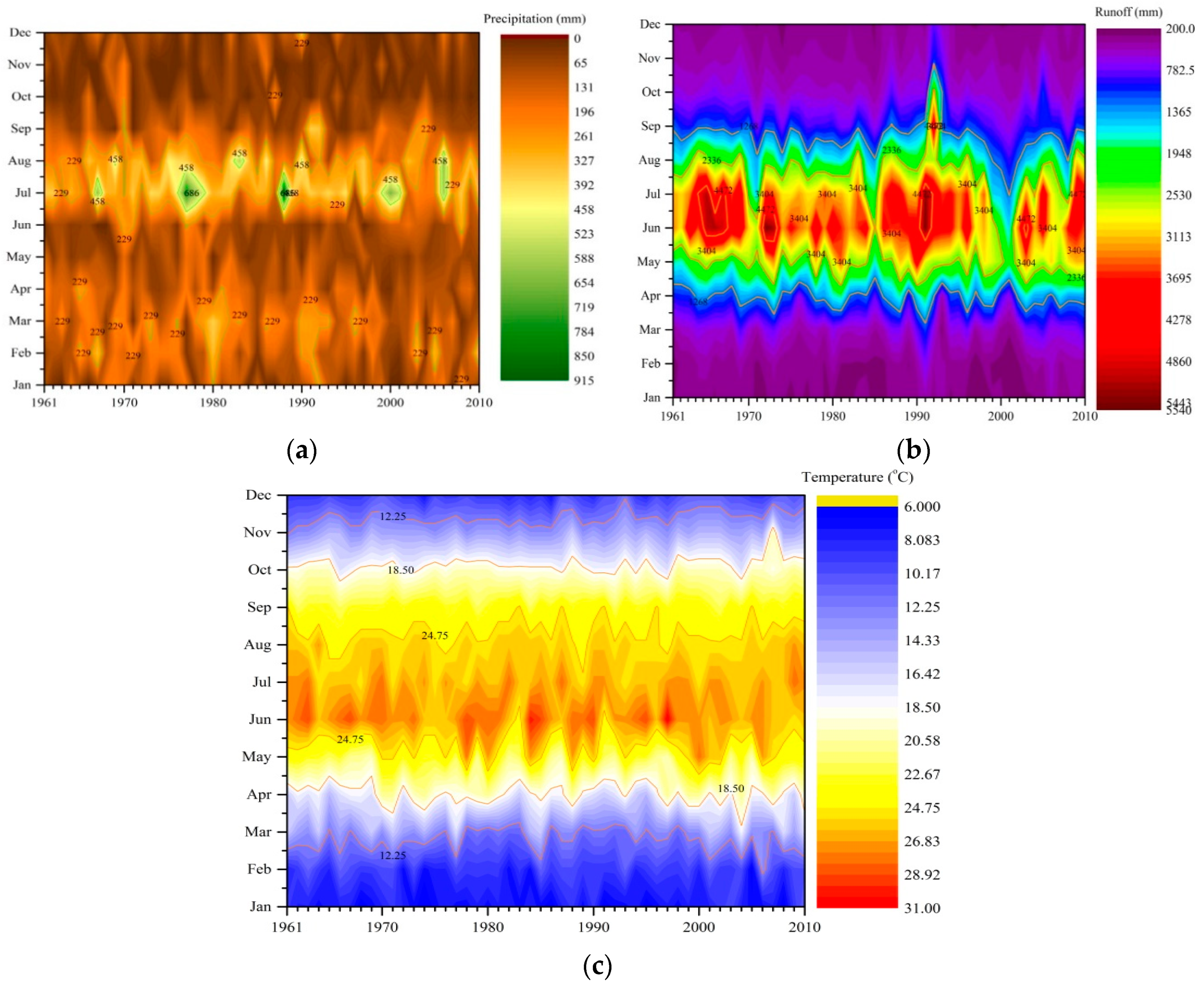
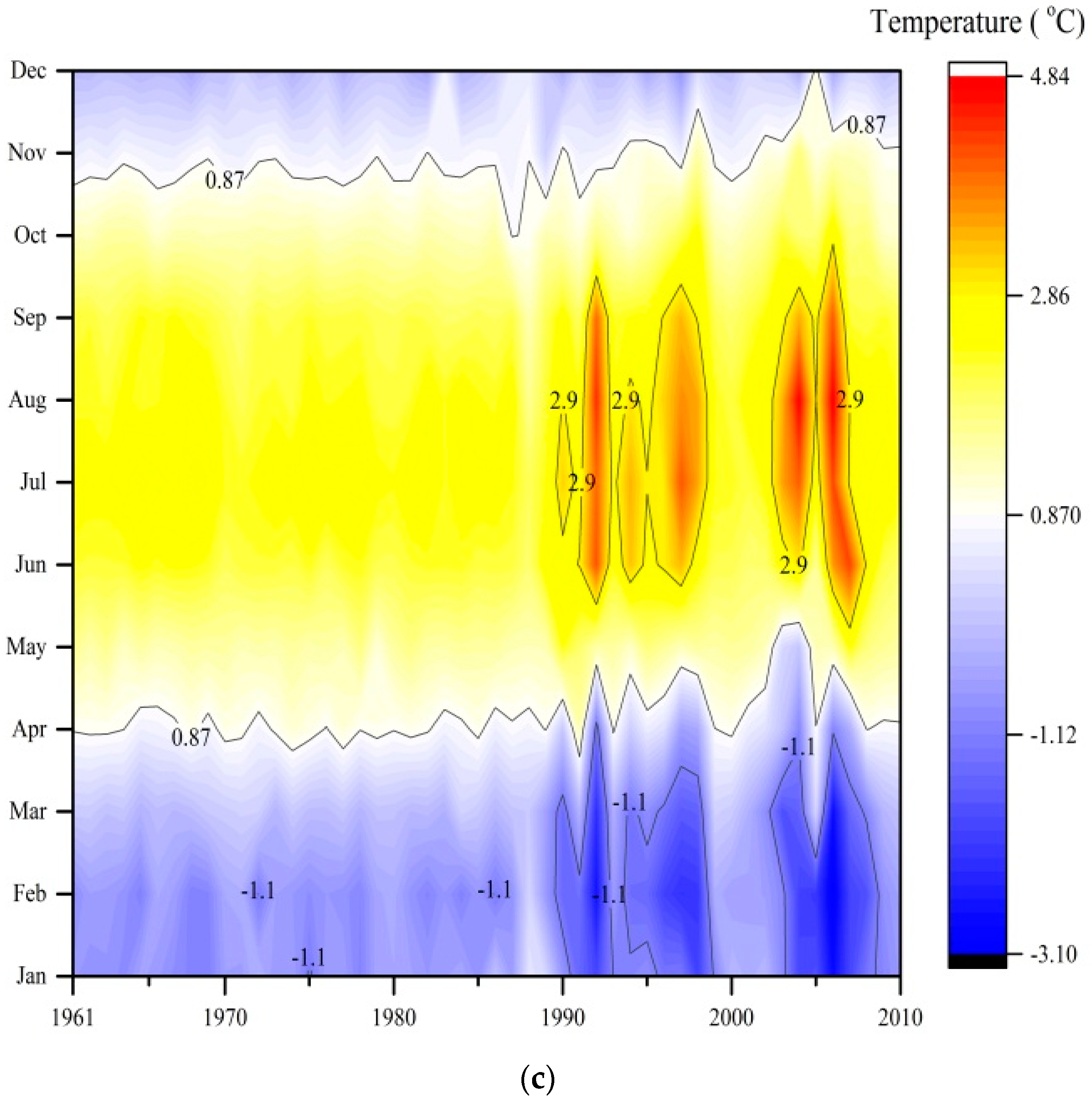
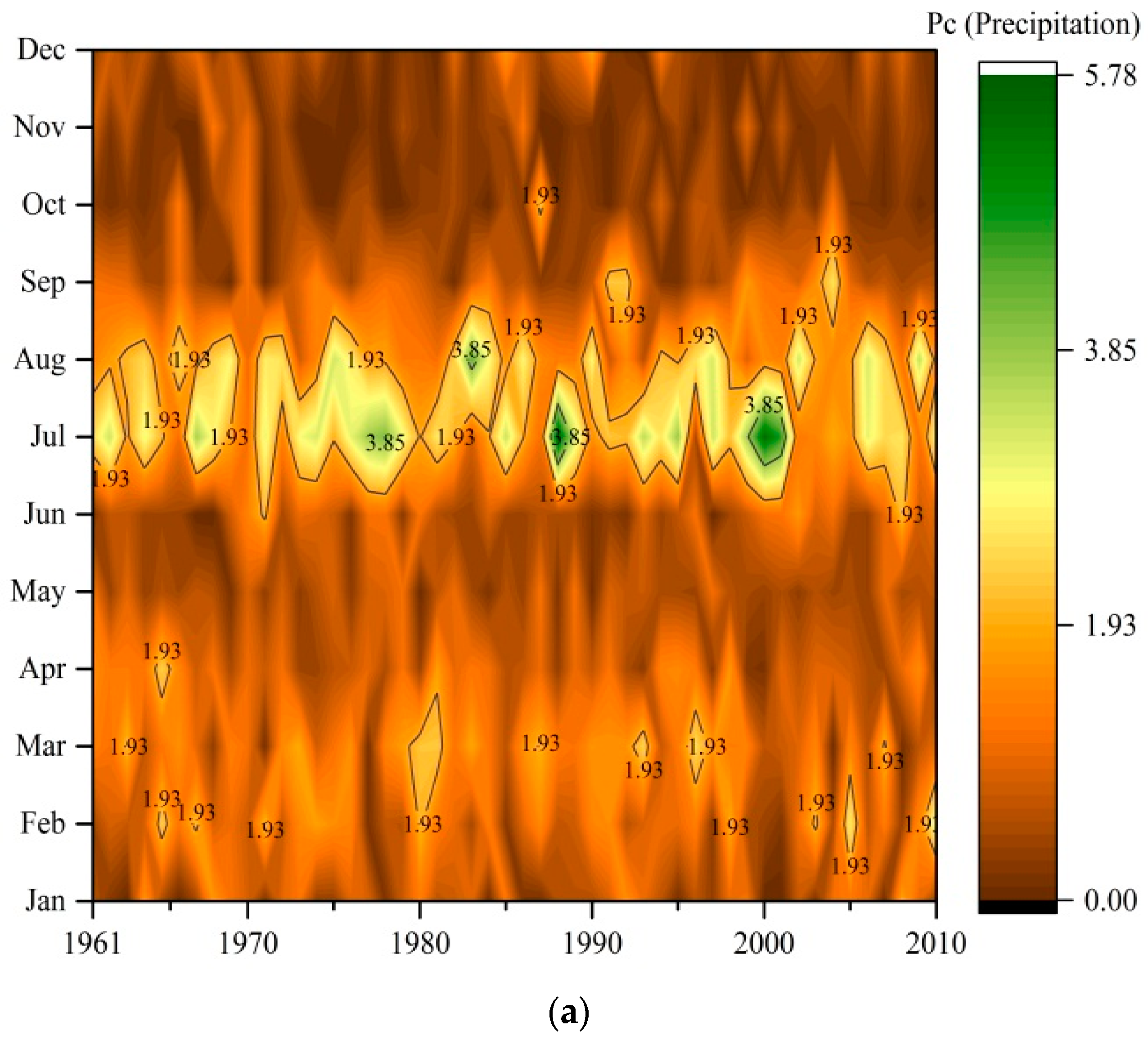
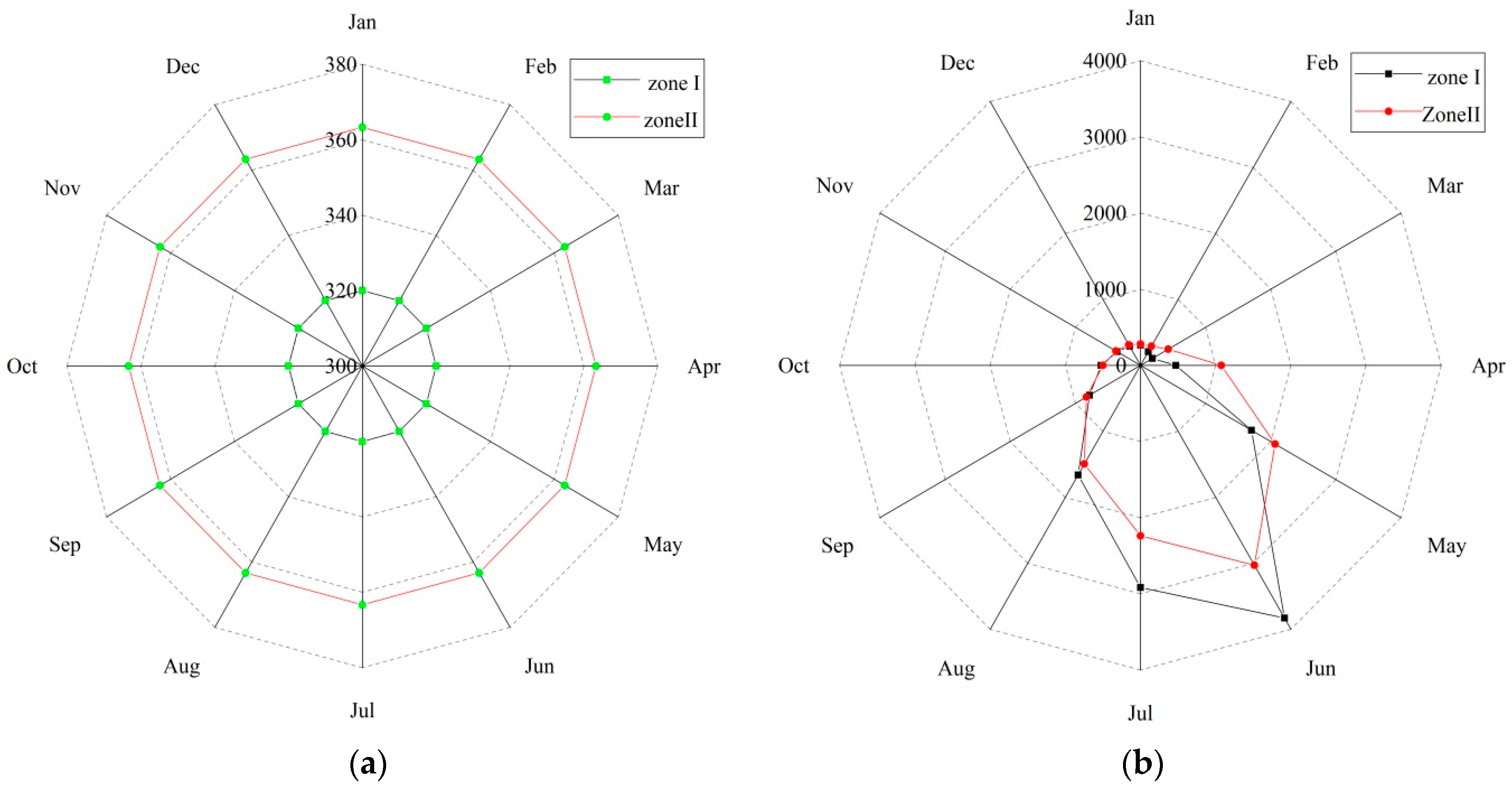
3.2. Iso-Plots of Precipitation, Temperature and Runoff
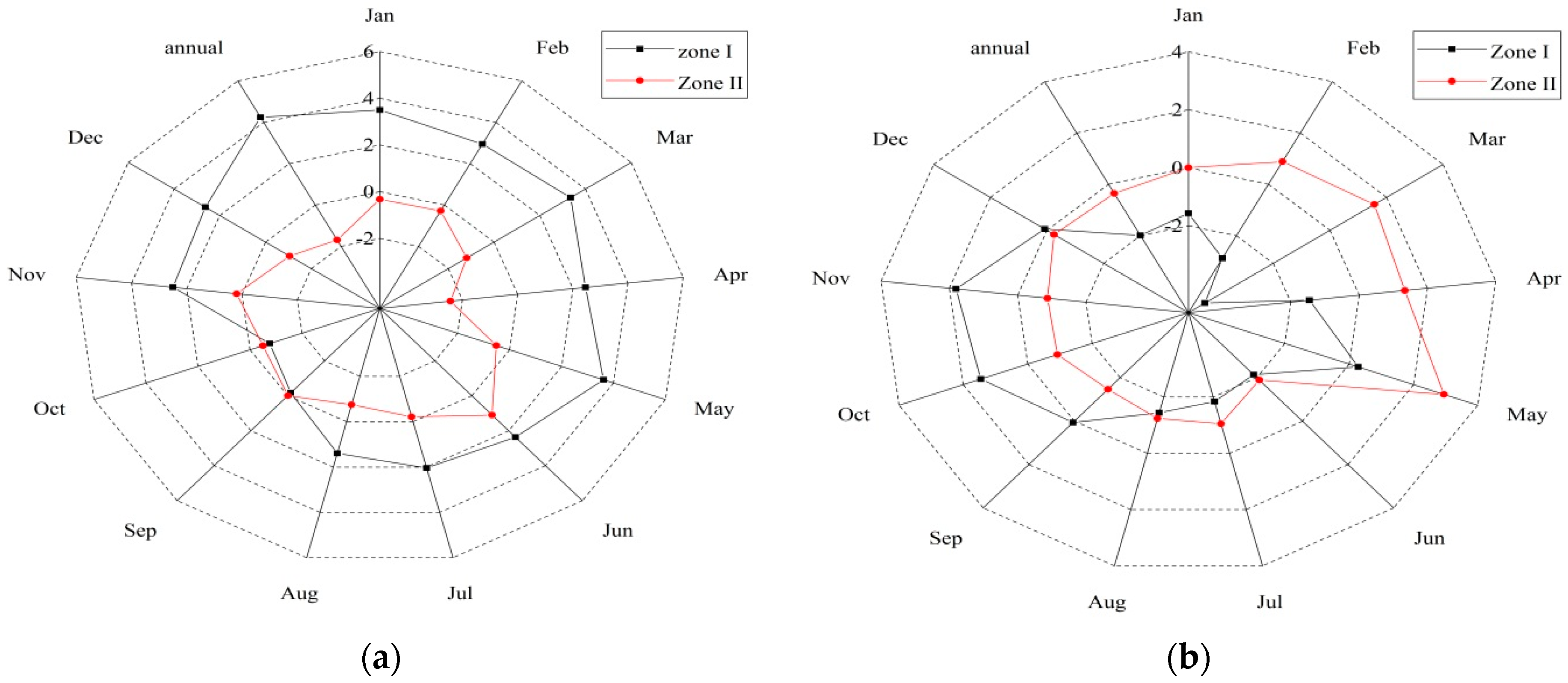
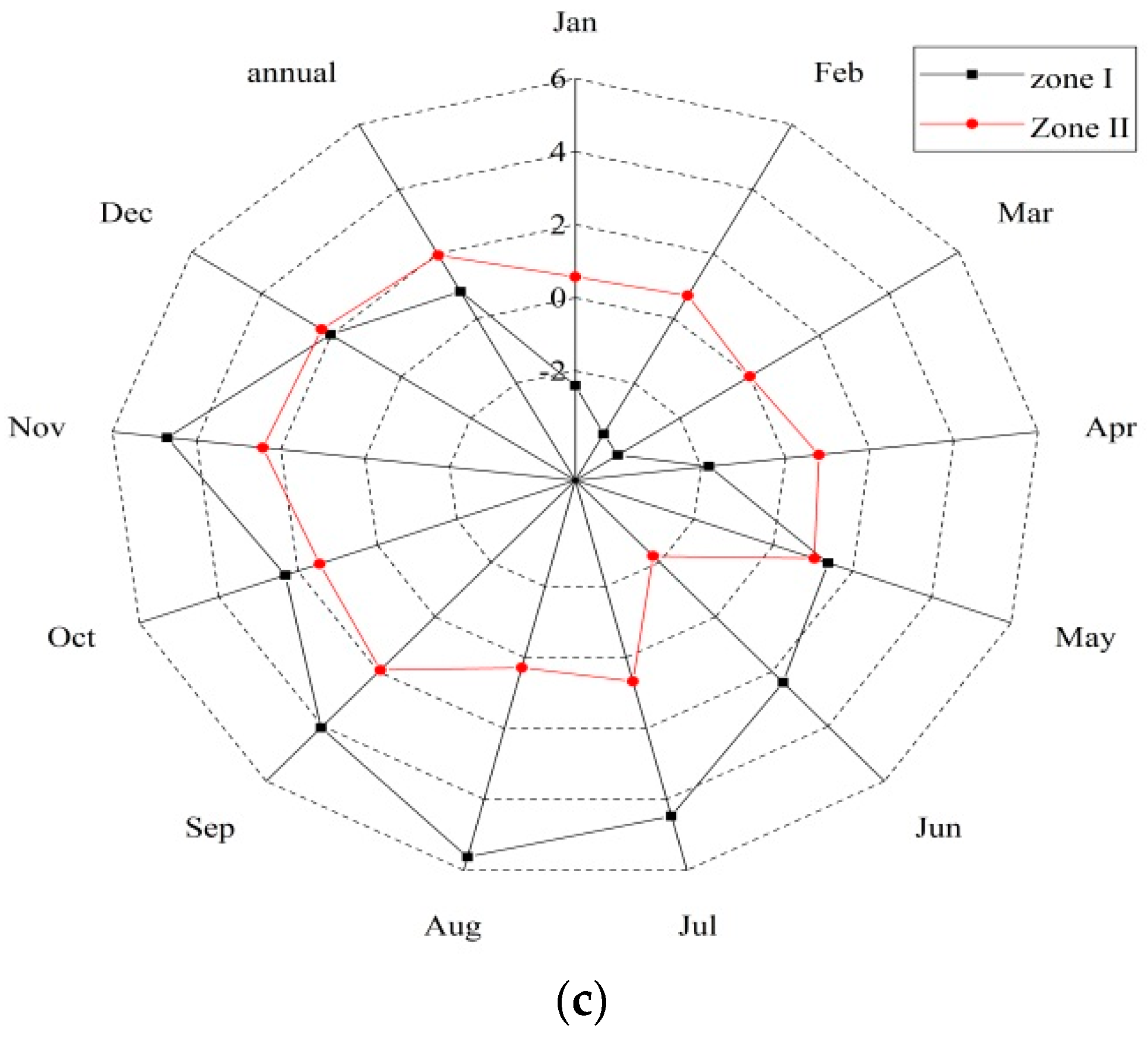
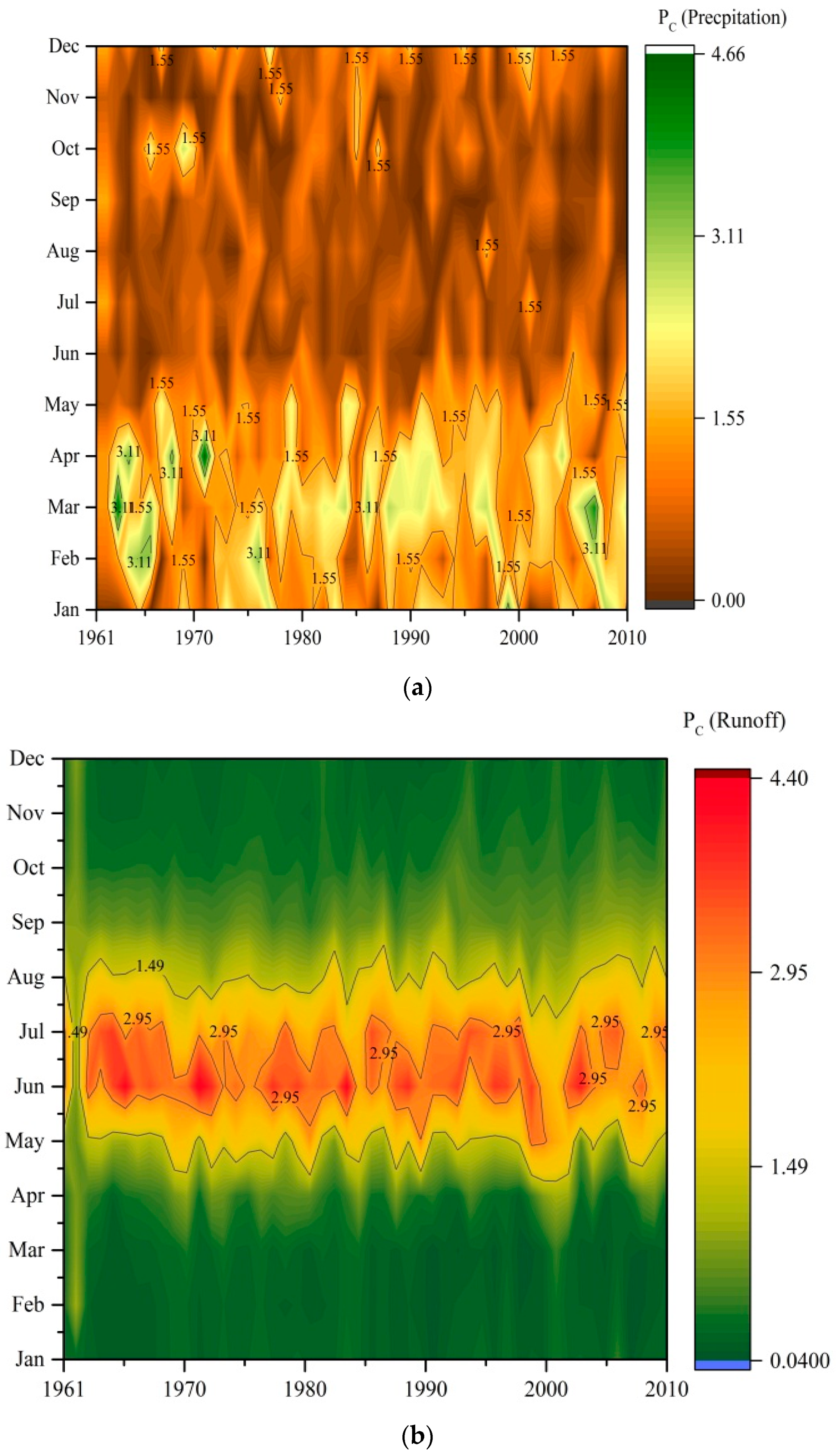
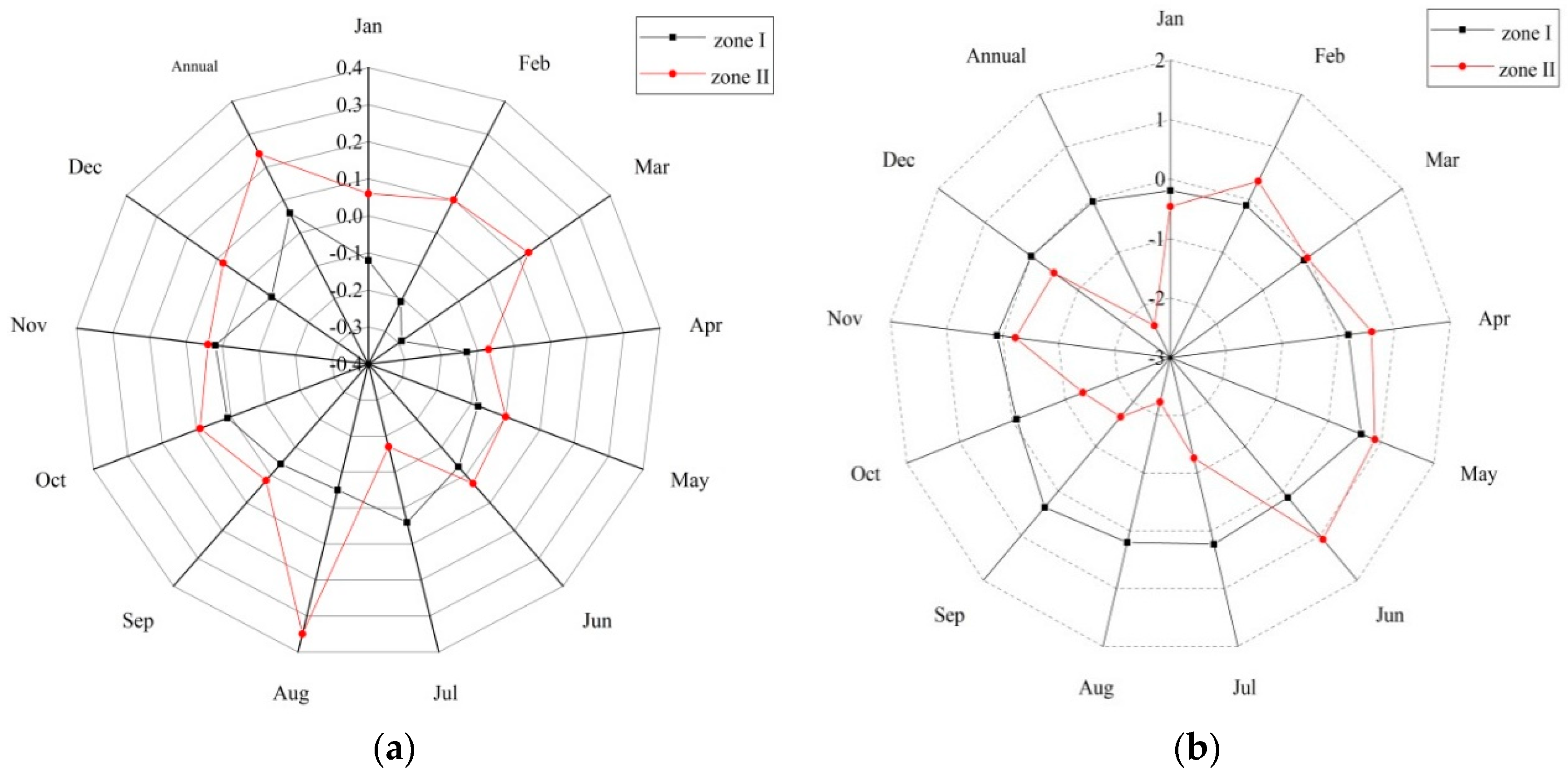
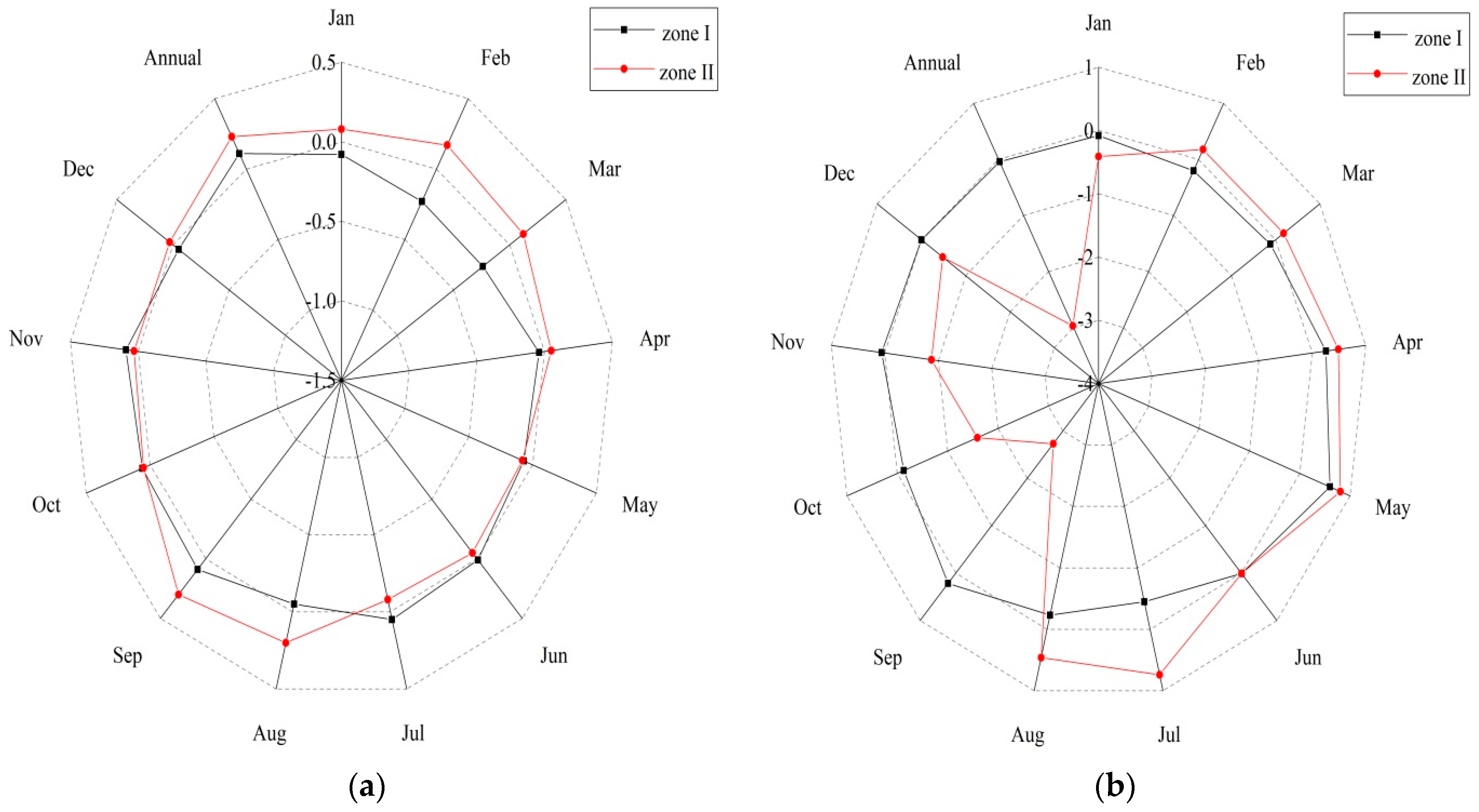
3.3. Hydrological-Regime Variability
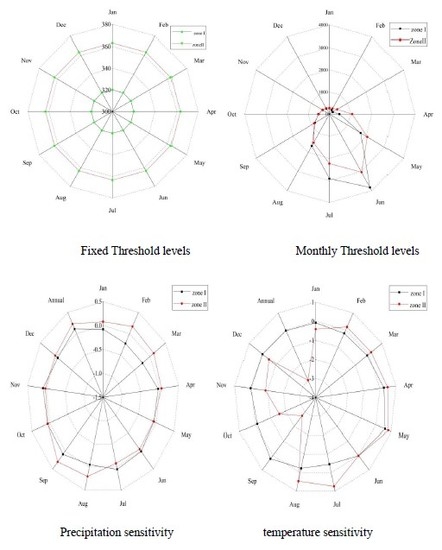
3.4. Threshold Levels of the Kunhar River
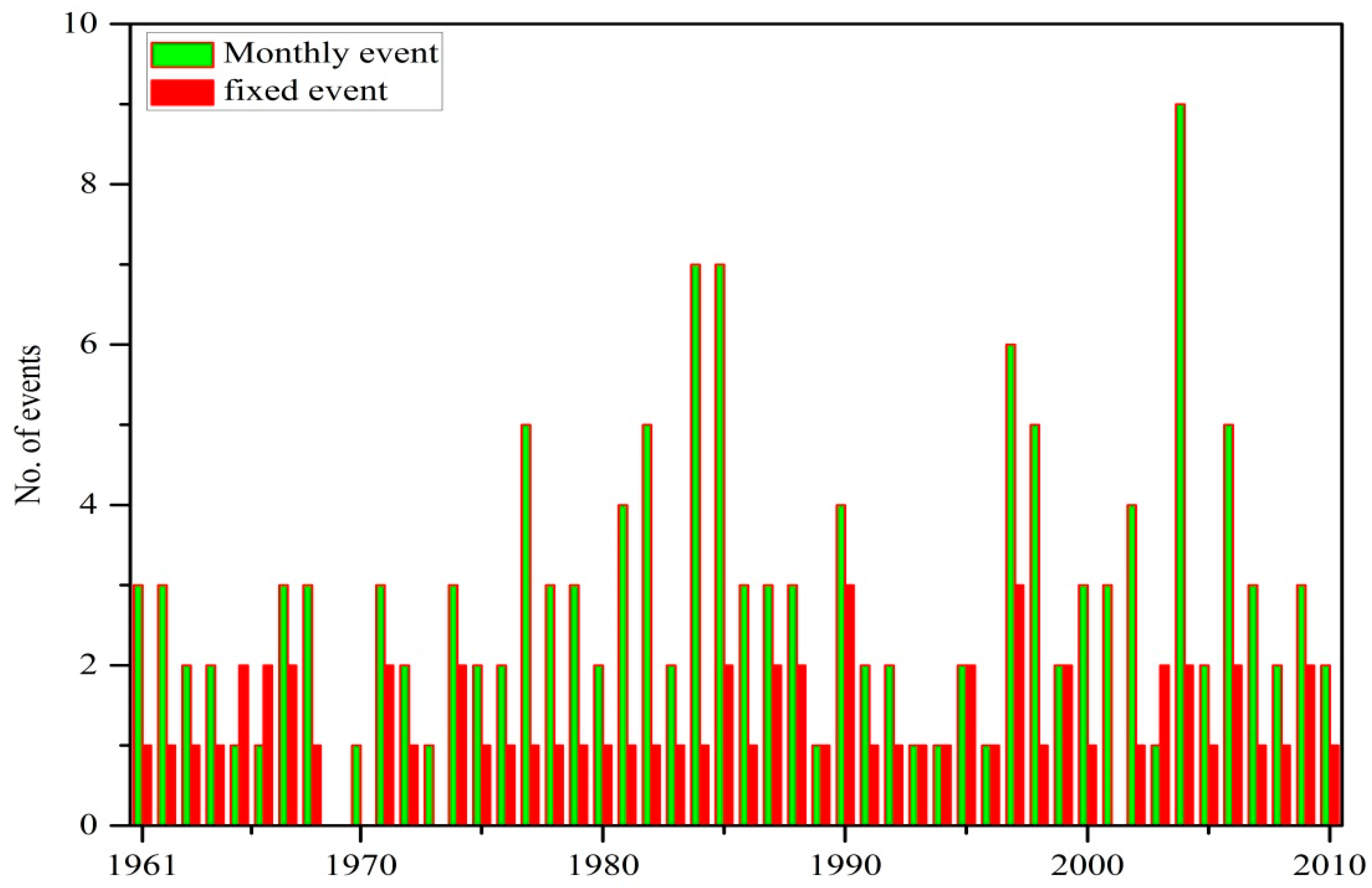
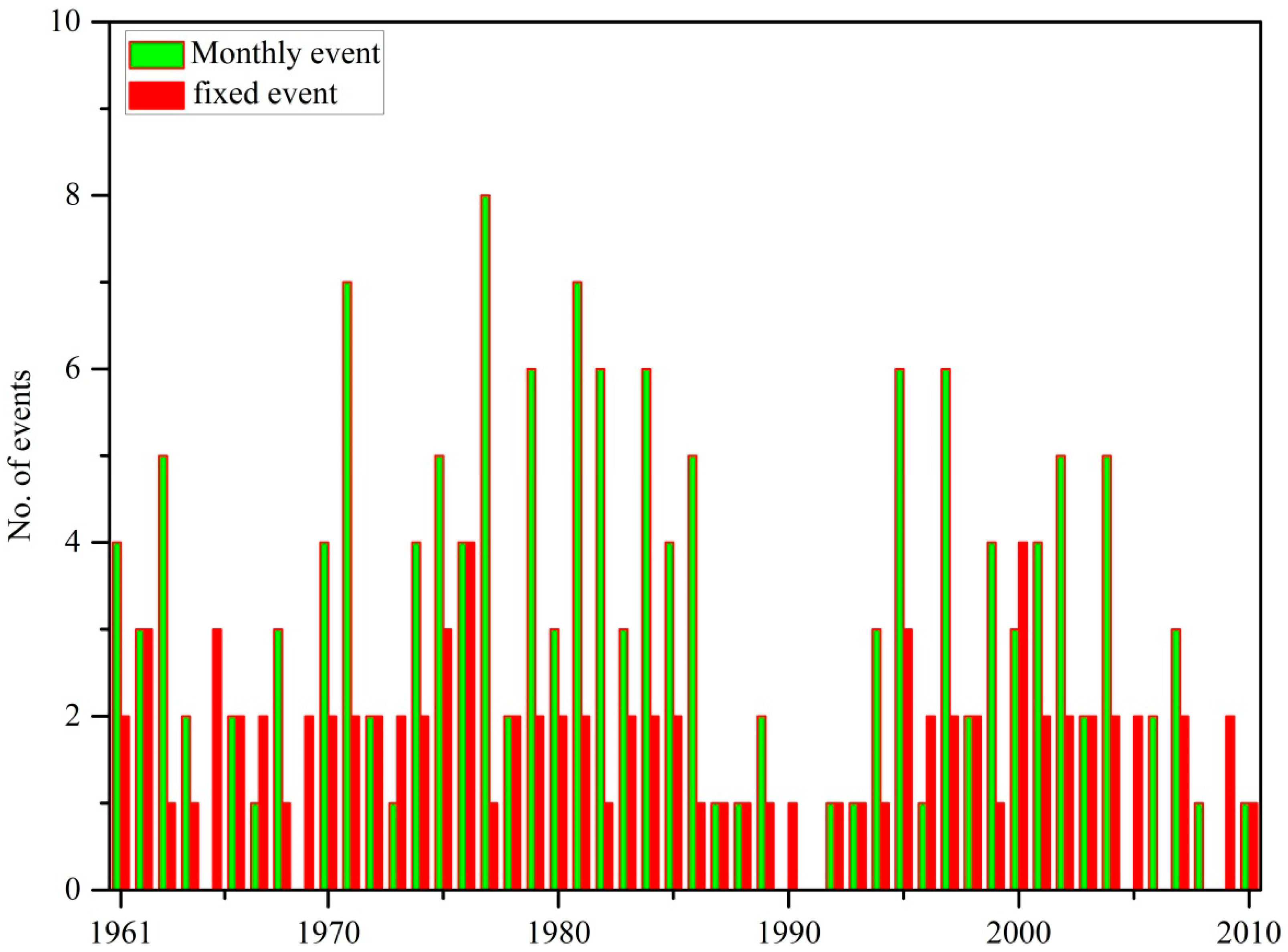
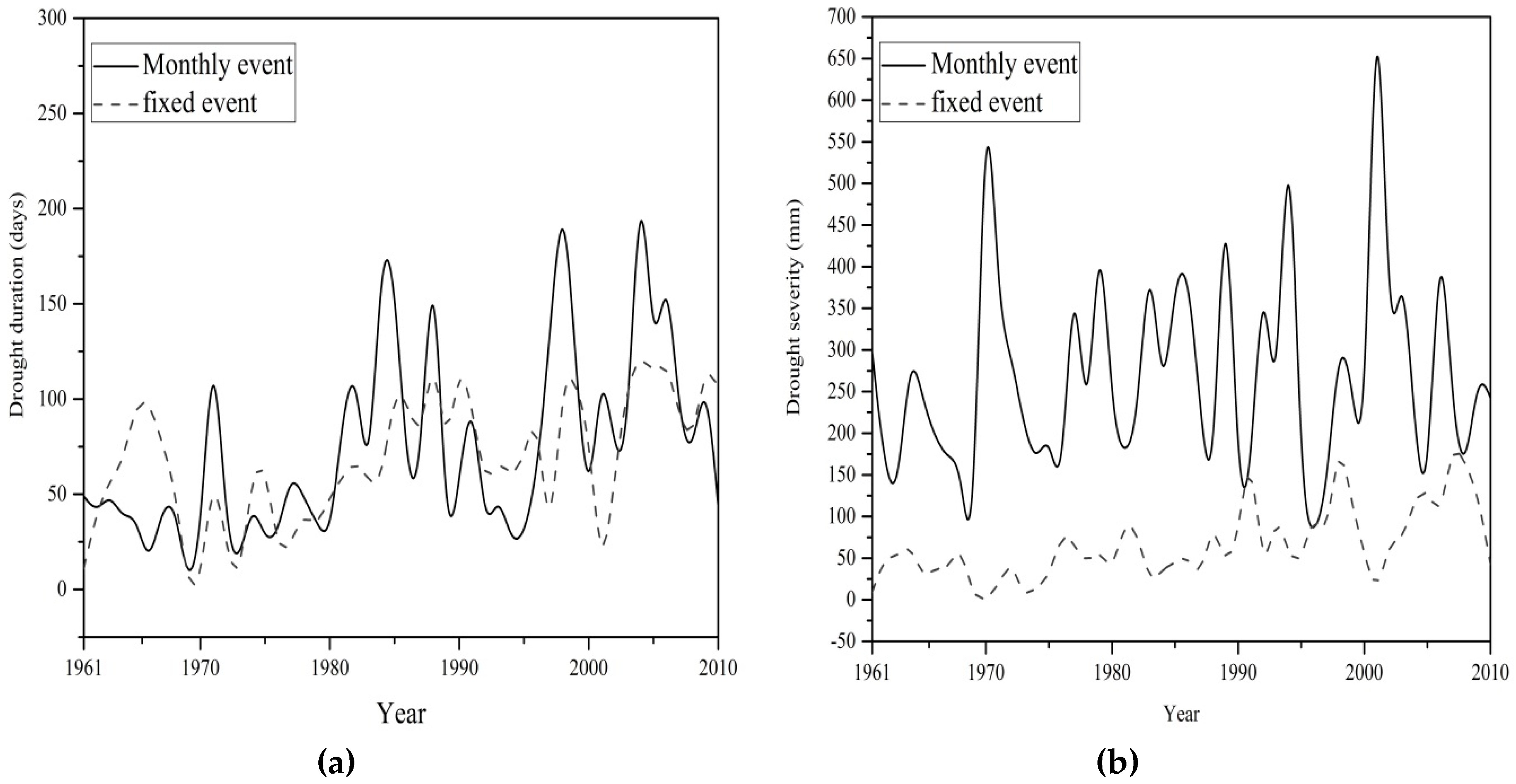
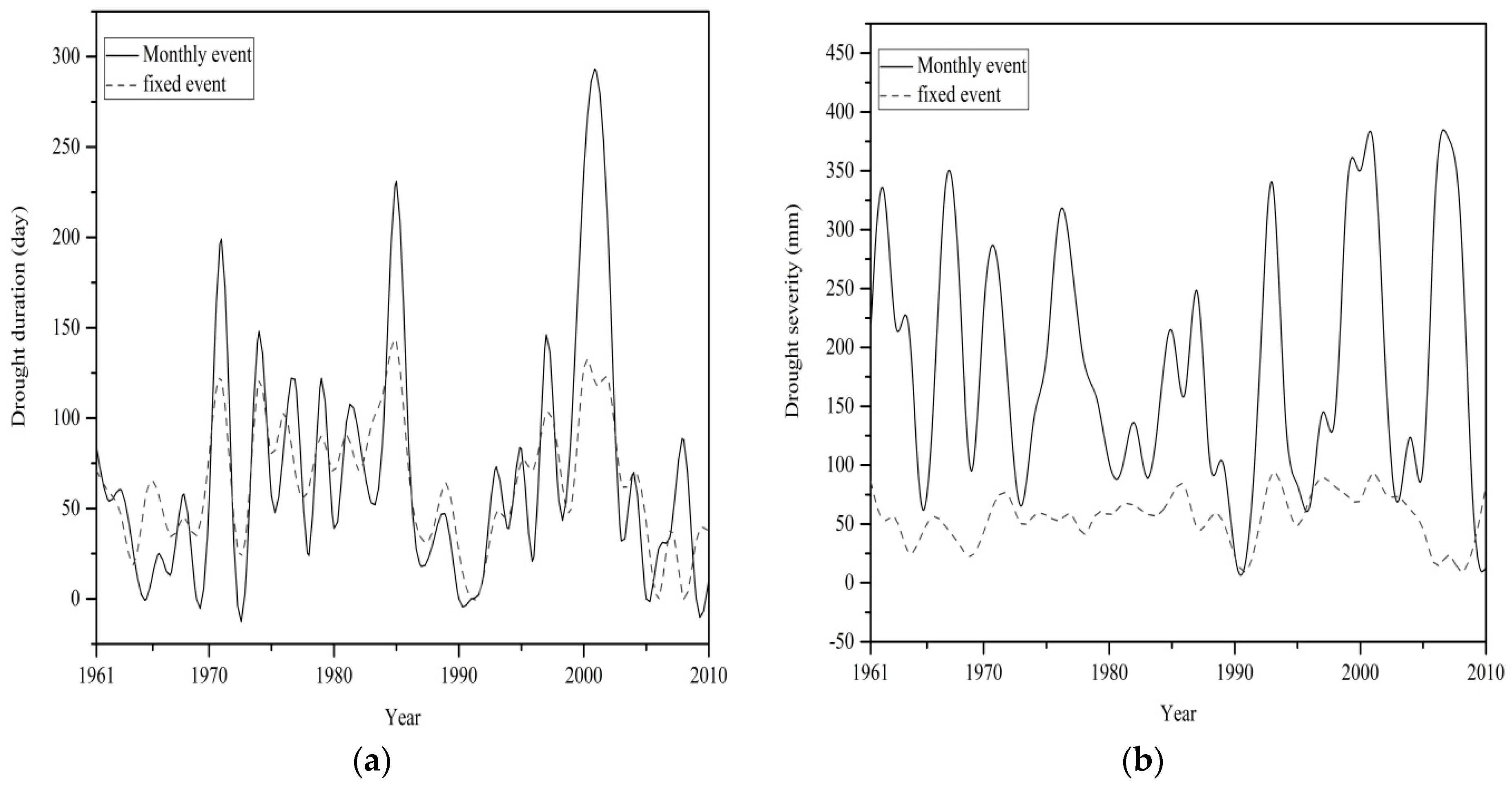
3.5. Hydrological Drought Analysis: 1961/1962–2009/2010
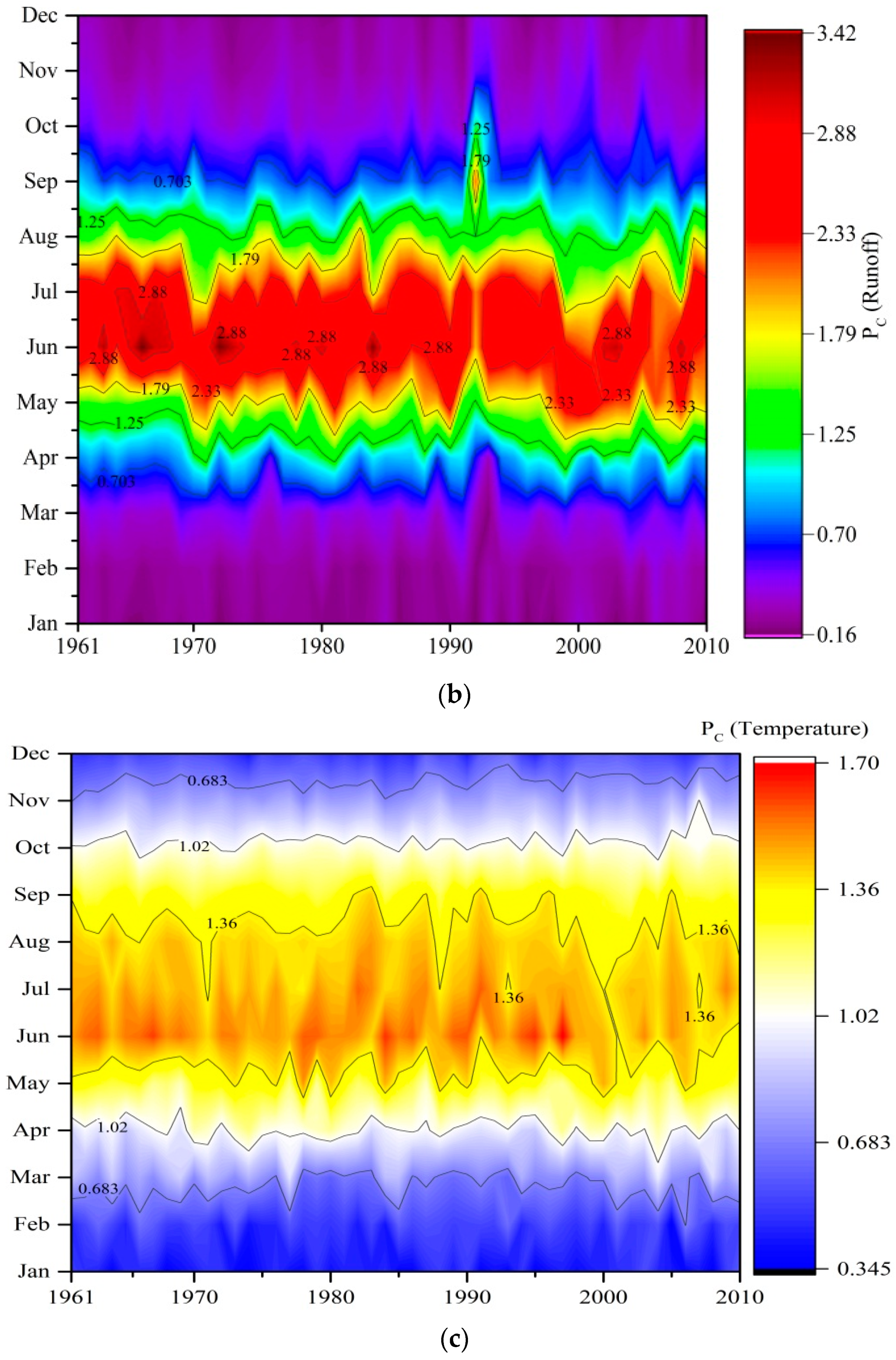
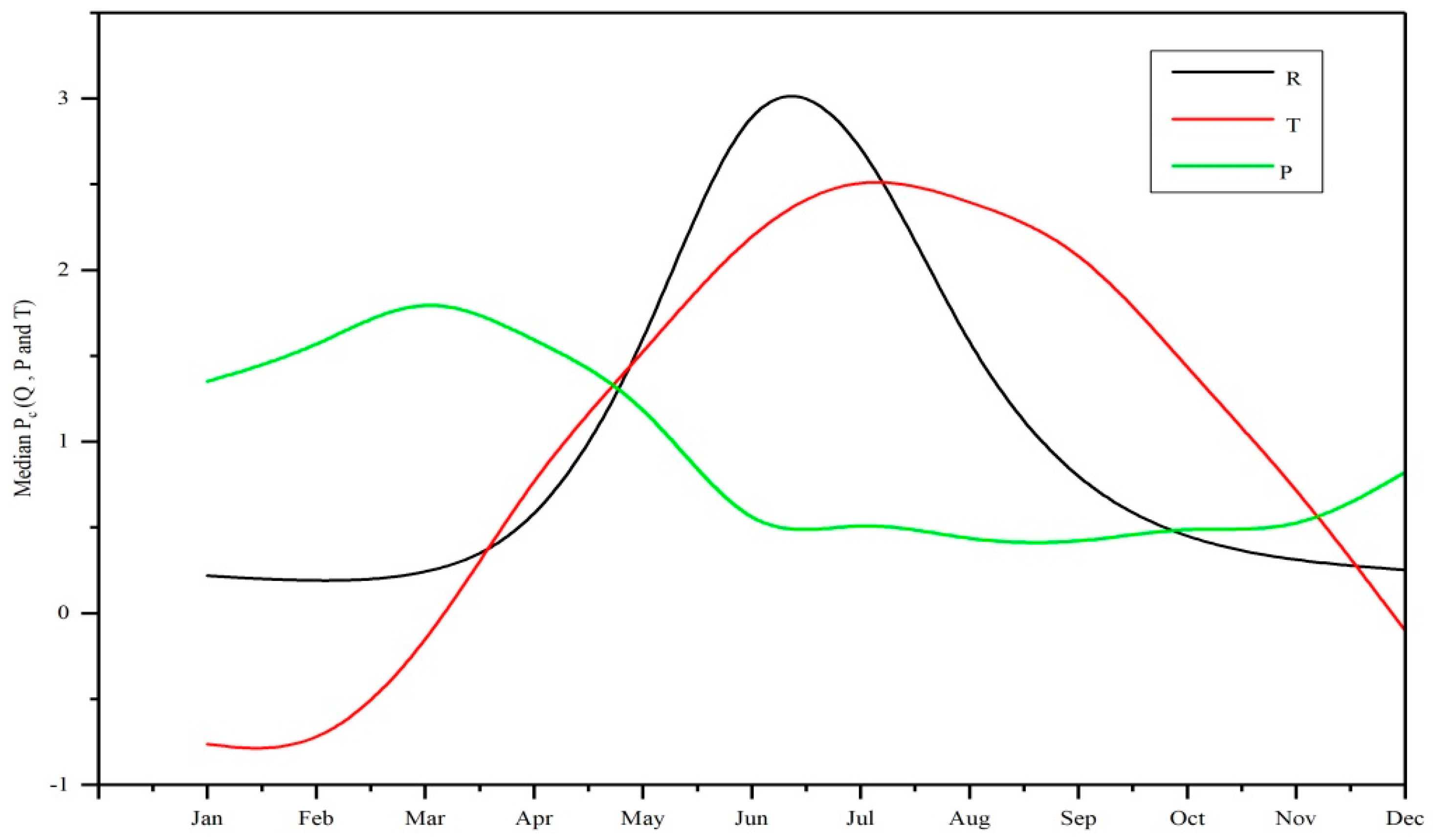
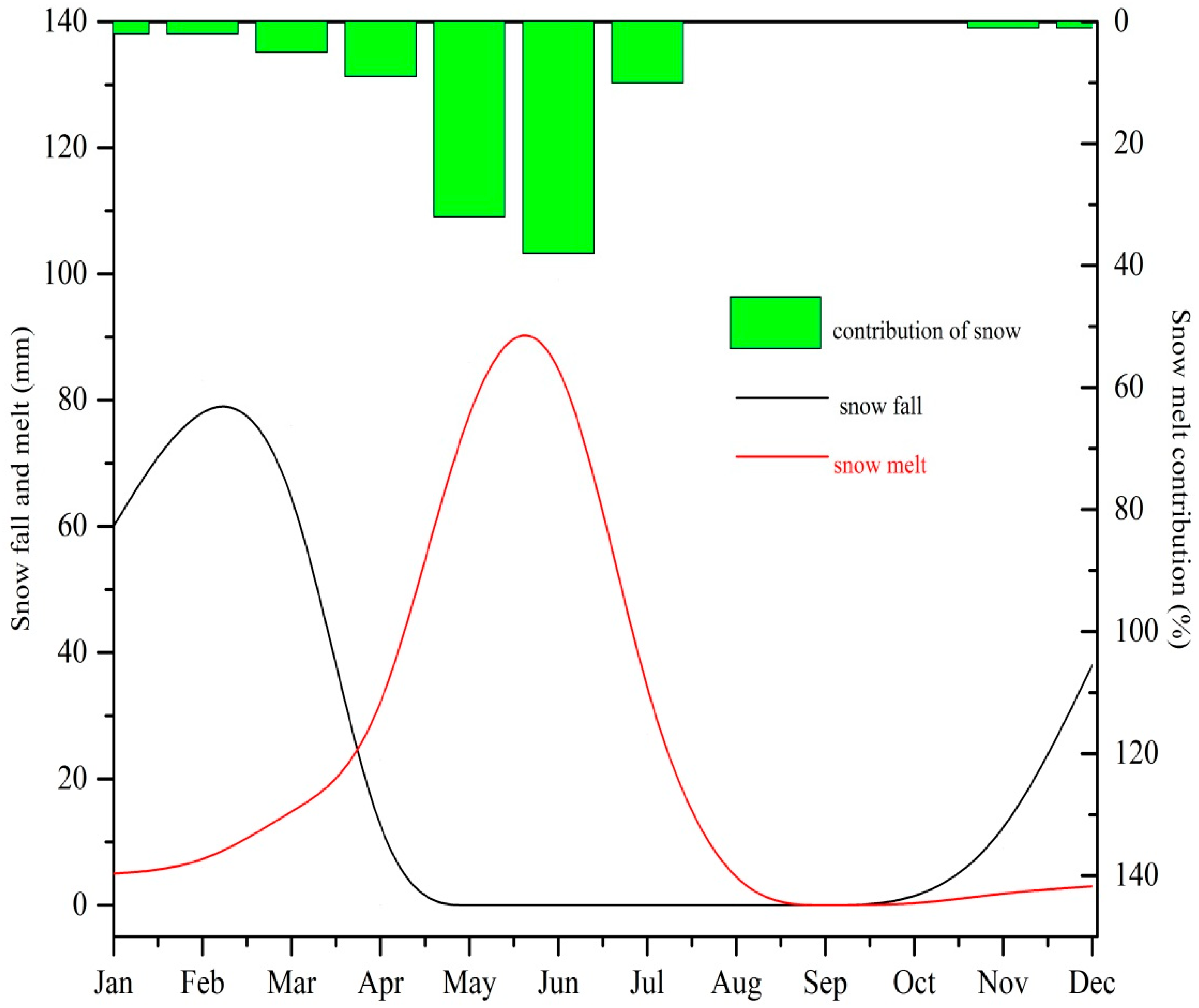
3.6. Sensitivity of Hydrological Regime to Climate
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
References
- Mahmood, R.; Jia, S.; Babel, M. Potential Impacts of Climate Change on Water Resources in the Kunhar River Basin, Pakistan. Water 2016, 8, 23. [Google Scholar] [CrossRef]
- Tahir, A.A.; Chevallier, P.; Arnaud, Y.; Ashraf, M.; Bhatti, M.T. Snow cover trend and hydrological characteristics of the Astore River basin (Western Himalayas) and its comparison to the Hunza basin (Karakoram region). Sci. Total Environ. 2015, 505, 748–761. [Google Scholar] [CrossRef] [PubMed]
- Shrestha, M.; Koike, T.; Hirabayashi, Y.; Xue, Y.; Wang, L.; Rasul, G.; Ahmad, B. Integrated simulation of snow and glacier melt in water and energy balance-based, distributed hydrological modeling framework at Hunza River Basin of Pakistan Karakoram region. J. Geophys. Res. Atmos. 2015, 4889–4919. [Google Scholar] [CrossRef]
- Farhan, S.B.; Zhang, Y.; Aziz, A.; Gao, H.; Ma, Y.; Kazmi, J.; Nasir, J.; Shahzad, A.; Hussain, L.; Mansha, M.; et al. Assessing the impacts of climate change on the high altitude snow- and glacier-fed hydrological regimes of Astore and Hunza, the sub-catchments of Upper Indus Basin. J. Water Clim. Chang. 2018. [Google Scholar] [CrossRef]
- Zheng, H.; Zhang, L.; Zhu, R.; Liu, C.; Sato, Y.; Fukushima, Y. Responses of streamflow to climate and land surface change in the headwaters of the Yellow River Basin. Water Resour. Res. 2009, 45. [Google Scholar] [CrossRef]
- Merz, R.; Blöschl, G. A regional analysis of event runoff coefficients with respect to climate and catchment characteristics in Austria. Water Resour. Res. 2009, 45. [Google Scholar] [CrossRef]
- Zou, L.; Xia, J.; She, D. Analysis of Impacts of Climate Change and Human Activities on Hydrological Drought: A Case Study in the Wei River Basin, China. Water Resour. Manag. 2017, 32, 1421–1438. [Google Scholar] [CrossRef]
- Zhang, Y.; Engel, B.; Ahiablame, L.; Liu, J. Impacts of Climate Change on Mean Annual Water Balance for Watersheds in Michigan, USA. Water 2015, 7, 3565–3578. [Google Scholar] [CrossRef]
- Tsai, Y. The multivariate climatic and anthropogenic elasticity of streamflow in the Eastern United States. J. Hydrol. Reg. Stud. 2017, 9, 199–215. [Google Scholar] [CrossRef]
- Milano, M.; Reynard, E.; Bosshard, N.; Weingartner, R. Simulating future trends in hydrological regimes in Western Switzerland. J. Hydrol. Reg. Stud. 2015, 4, 748–761. [Google Scholar] [CrossRef]
- Zelenhasić, E.; Salvai, A. A Method of Streamflow Drought Analysis. Water Resour. Res. 1987, 23, 156–168. [Google Scholar] [CrossRef]
- Carroll, N.; Frijters, P.; Shields, M.A. Quantifying the costs of drought: New evidence from life satisfaction data. J. Popul. Econ. 2009, 22, 445–461. [Google Scholar] [CrossRef]
- Wanders, N.; Wada, Y. Human and climate impacts on the 21st century hydrological drought. J. Hydrol. 2015, 526, 208–220. [Google Scholar] [CrossRef]
- Rivera, J.A.; Araneo, D.C.; Penalba, O.C. Threshold level approach for streamflow drought analysis in the Central Andes of Argentina: A climatological assessment. Hydrol. Sci. J. 2017, 62, 1949–1964. [Google Scholar] [CrossRef]
- Van Loon, A.F.; Laaha, G. Hydrological drought severity explained by climate and catchment characteristics. J. Hydrol. 2015, 526, 3–14. [Google Scholar] [CrossRef]
- Saifullah, M.; Li, Z.; Li, Q.; Zaman, M.; Hashim, S. Quantitative Estimation of the Impact of Precipitation and Land Surface Change on Hydrological Processes through Statistical Modeling. Adv. Meteorol. 2016, 2016, 1–15. [Google Scholar] [CrossRef]
- Sung, J.H.; Chung, E.S. Development of streamflow drought severity–duration–frequency curves using the threshold level method. Hydrol. Earth Syst. Sci. 2014, 18, 3341–3351. [Google Scholar] [CrossRef]
- Liu, Y.; Ren, L.; Zhu, Y.; Yang, X.; Yuan, F.; Jiang, S.; Ma, M. Evolution of Hydrological Drought in Human Disturbed Areas: A Case Study in the Laohahe Catchment, Northern China. Adv. Meteorol. 2016, 2016, 1–12. [Google Scholar] [CrossRef]
- Jiang, S.; Ren, L.; Yong, B.; Singh, V.P.; Yang, X.; Yuan, F. Quantifying the effects of climate variability and human activities on runoff from the Laohahe basin in northern China using three different methods. Hydrol. Process. 2011, 25, 2492–2505. [Google Scholar] [CrossRef]
- Tsakiris, I.N.G. Assessment of Hydrological Drought Revisited. Water Resour. Manag. 2009, 881–897. [Google Scholar] [CrossRef]
- Van Loon, A.F.; Van Lanen, H.A.J. A process-based typology of hydrological drought. Hydrol. Earth Syst. Sci. 2012, 16, 1915–1946. [Google Scholar] [CrossRef]
- Razmkhah, H. Comparing Threshold Level Methods in Development of Stream Flow Drought Severity-Duration-Frequency Curves. Water Resour. Manag. 2017, 31, 4045–4061. [Google Scholar] [CrossRef]
- Tallaksen, L.M.; Madsen, H.; Clausen, B. On the definition and modelling of streamflow drought duration and deficit volume. Hydrol. Sci. J. 1997, 42, 15–33. [Google Scholar] [CrossRef]
- Khan, M.I.; Liu, D.; Fu, Q.; Faiz, M.A. Detecting the persistence of drying trends under changing climate conditions using four meteorological drought indices. Meteorol. Appl. 2018, 25, 184–194. [Google Scholar] [CrossRef]
- Kjeldsen, T.R.; Lundorf, A.; Rosbjerg, D. Use of a two-component exponential distribution in partial duration modelling of hydrological droughts in Zimbabwean rivers. Hydrol. Sci. J. 2000, 45, 285–298. [Google Scholar] [CrossRef]
- Sankarasubramanian, A.; Vogel, R.M. Annual hydro climatology of the United States. Water Resour. Res. 2002, 38, 19-1–19-12. [Google Scholar] [CrossRef]
- Bormann, H. Runoff regime changes in German rivers due to climate change. Erdkunde 2010, 64, 257–279. [Google Scholar] [CrossRef]
- Wang, S.; Yan, Y.; Yan, M.; Zhao, X. Quantitative estimation of the impact of precipitation and human activities on runoff change of the Huangfuchuan River Basin. J. Geogr. Sci. 2012, 22, 906–918. [Google Scholar] [CrossRef]
- Sankarasubramanian, A.; Vogel, R.M.; Limbrunner, J.F. Climate elasticity of streamflow in the United States. Water Resour. Res. 2001, 37, 1771–1781. [Google Scholar] [CrossRef]
- Saifullah, M.; Li, Z.; Li, Q.; Hashim, S.; Zaman, M. Quantifying the Hydrological Response to Water Conservation Measures and Climatic Variability in the Yihe River Basin, China. Outlook Agric. 2015, 44, 273–282. [Google Scholar] [CrossRef]
- Shahid, M.; Cong, Z.; Zhang, D. Understanding the impacts of climate change and human activities on streamflow: A case study of the Soan River basin, Pakistan. Theor. Appl. Climatol. 2017, 134, 205–219. [Google Scholar] [CrossRef]
- Zhai, R.; Tao, F. Contributions of climate change and human activities to runoff change in seven typical catchments across China. Sci. Total Environ. 2017, 605–606, 219–229. [Google Scholar] [CrossRef]
- Xu, Y.; Wang, S.; Bai, X.; Shu, D.; Tian, Y. Runoff response to climate change and human activities in a typical karst watershed, SW China. PLoS ONE 2018, 13, e0193073. [Google Scholar] [CrossRef]
- Saifulllah, M.; Li, Z.J.; Li, Q.L.; Hashim, S.; Zaman, M.; Liu, K.L. Assessment the impacts of land surface change on the hydrological process based on similar hydro-meteorological conditions with SWAT. Fresenius Environ. Bull. 2016, 25, 3071–3082. [Google Scholar]
- Li, B.; Su, H.; Chen, F.; Li, H.; Zhang, R.; Tian, J.; Chen, S.; Yang, Y.; Rong, Y. Separation of the impact of climate change and human activity on streamflow in the upper and middle reaches of the Taoer River, northeastern China. Theor. Appl. Climatol. 2013, 118, 271–283. [Google Scholar] [CrossRef]
- Li, B.; Chen, F. Using the aridity index to assess recent climate change: A case study of the Lancang River Basin, China. Stoch. Environ. Res. Risk Assess. 2014, 29, 1071–1083. [Google Scholar] [CrossRef]
- Kundzewicz, Z.W.; Merz, B.; Vorogushyn, S.; Hartmann, H.; Duethmann, D.; Wortmann, M.; Huang, S.; Su, B.; Jiang, T.; Krysanova, V. Analysis of changes in climate and river discharge with focus on seasonal runoff predictability in the Aksu River Basin. Environ. Earth Sci. 2014, 73, 501–516. [Google Scholar] [CrossRef]
- Wang, W.; Zhang, Z.; Duan, L.; Wang, Z.; Zhao, Y.; Zhang, Q.; Dai, M.; Liu, H.; Zheng, X.; Sun, Y. Response of the groundwater system in the Guanzhong Basin (central China) to climate change and human activities. Hydrogeol. J. 2018, 26, 1429–1441. [Google Scholar] [CrossRef]
- Chiew, F.H.; Peel, M.C.; McMahon, T.A.; Siriwardena, L.W. Precipitation elasticity of streamflow in catchments across the world. Climate Variability and Change—Hydrological Impacts. In Proceedings of the Fifth Friend World Conference, Havana, Cuba, 27 November–1 December 2006. [Google Scholar]
- Ma, H.; Yang, D.; Tan, S.K.; Gao, B.; Hu, Q. Impact of climate variability and human activity on streamflow decrease in the Miyun Reservoir catchment. J. Hydrol. 2010, 389, 317–324. [Google Scholar] [CrossRef]
- Forsythe, N.; Fowler, H.J.; Blenkinsop, S.; Burton, A.; Kilsby, C.G.; Archer, D.R.; Harphamc, C.; Hashmi, M.Z. Application of a stochastic weather generator to assess climate change impacts in a semi-arid climate: The Upper Indus Basin. J. Hydrol. 2014, 517, 1019–1034. [Google Scholar] [CrossRef]
- Mahmood, R.; Babel, M.S. Evaluation of SDSM developed by annual and monthly sub-models for downscaling temperature and precipitation in the Jhelum basin, Pakistan and India. Theor. Appl. Climatol. 2013, 113, 27–44. [Google Scholar] [CrossRef]
- Babur, M.; Babel, M.; Shrestha, S.; Kawasaki, A.; Tripathi, N. Assessment of Climate Change Impact on Reservoir Inflows Using Multi Climate-Models under RCPs—The Case of Mangla Dam in Pakistan. Water 2016, 8, 389. [Google Scholar] [CrossRef]
- Azmat, M.; Liaqat, U.W.; Qamar, M.U.; Awan, U.K. Impacts of changing climate and snow cover on the flow regime of Jhelum River, Western Himalayas. Reg. Environ. Chang. 2017, 17, 813–825. [Google Scholar] [CrossRef]
- Şen, Z. Innovative Trend Analysis Methodology. J. Hydrol. Eng. 2012, 17, 1042–1046. [Google Scholar] [CrossRef]
- Şen, Z. Trend Identification Simulation and Application. J. Hydrol. Eng. 2014, 19, 635–642. [Google Scholar] [CrossRef]
- Saplıoğlu, K.; Kilit, M.; Yavuz, B.K. Trend analysis of streams in the western Mediterranean basin of Turkey. Fresenius Environ. Bull. 2014, 23, 1–12. [Google Scholar]
- Yue, S.; Hashino, M. Long term trends of annual and monthly precipitation in Japan. Am. Water Resour. Assoc. 2003, 39, 587–596. [Google Scholar] [CrossRef]
- Mann, H. Nonparametric Tests against Trend. Econometrica 1945, 13, 245–259. [Google Scholar] [CrossRef]
- Sen, P.K. Estimates of the Regression Coefficient Based on Kendall’s Tau. J. Am. Stat. Assoc. 1968, 63, 1379–1389. [Google Scholar] [CrossRef]
- Theil, H. A rank-invariant method of linear and polynomial regression analysis. Mathematics 1992, 23, 345–381. [Google Scholar]
- Pardé, M. Quelques notes sur l’hydrologie du Brahmapoutre, du Gange et de l’Indus. Revue de. Géographie Alpine 1940, 28, 157–198. [Google Scholar] [CrossRef]
- Parde, M. Fleuves et Rivières. Rev. Géogr. Alp. 1933, 214, 851–854. [Google Scholar]
- Amo-Boateng, M.; Li, Z.; Guan, Y. Inter-annual variation of streamflow, precipitation and evaporation in a small humid watershed (Chengcun Basin, China). Chin. J. Oceanol. Limnol. 2013, 32, 455–468. [Google Scholar] [CrossRef]
- Hao, X.; Chen, Y.; Xu, C.; Li, W. Impacts of Climate Change and Human Activities on the Surface Runoff in the Tarim River Basin over the Last Fifty Years. Water Resour. Manag. 2007, 22, 1159–1171. [Google Scholar] [CrossRef]
- Yao, J.Q.; Zhao, Q.D.; Liu, Z.H. Effect of climate variability and human activities on runoff in the Jinghe River Basin, Northwest China. J. Mt. Sci. 2015, 12, 358–367. [Google Scholar] [CrossRef]
- Fu, G.; Charles, S.P.; Chiew, F.H. A two-parameter climate elasticity of streamflow index to assess climate change effects on annual streamflow. Water Resour. Res. 2007, 43. [Google Scholar] [CrossRef]
- Roderick, M.L.; Farquhar, G.D. A simple framework for relating variations in runoff to variations in climatic conditions and catchment properties. Water Resour. Res. 2011, 47. [Google Scholar] [CrossRef]
- Mátyás, K.; Bene, K. Comparison of Annual Prediction Methods for Spring Flow in the Aggtelek Region. Acta Tech. Jaurinensis 2017, 10, 70–73. [Google Scholar] [CrossRef][Green Version]
- Olsson, O.; Gassmann, M.; Wegerich, K.; Bauer, M. Identification of the effective water availability from streamflows in the Zerafshan river basin, Central Asia. J. Hydrol. 2010, 390, 190–197. [Google Scholar] [CrossRef]
- Rasul, G. Climate Data Modelling and Analysis of the Indus Ecoregion; World Wide Fund Nature Pak: Lahore, Pakistan, 2012; pp. 26–27. [Google Scholar]
- Andréassian, V.; Coron, L.; Lerat, J.; Le Moine, N. Climate elasticity of streamflow revisited—An elasticity index based on long-term hydrometeorological records. Hydrol. Earth Syst. Sci. 2016, 20, 4503–4524. [Google Scholar] [CrossRef]
- Wang, D.; Alimohammadi, N. Responses of annual runoff, evaporation, and storage change to climate variability at the watershed scale. Water Resour. Res. 2012, 48. [Google Scholar] [CrossRef]
- Khan, M.; Zaidi, A.Z. Run-of-River Hydropower Potential of Kunhar River, Pakistan. Pakistan J. Meteorol. 2015, 12, 25–32. [Google Scholar]
- Ali, A.F.; Zhang, X.P.; Adnan, M.; Iqbal, M.; Khan, G. Projection of future streamflow of the Hunza River Basin, Karakoram Range (Pakistan) using HBV hydrological model. J. Mt. Sci. 2018, 15, 2218–2235. [Google Scholar] [CrossRef]
- Saifullah, M.; Zaman, M.; Li, Z.; Nasir, A. Impacts of hydro climatic variables trends on water resources of Yihe River Basin during the past 50 years. In Proceeding of the International Conference on Hydropower—A Vital Source of Sustainable Energy for Pakistan 2017, Washington, DC, USA, 19–20 December 2017; pp. 42–46. [Google Scholar]
- De Scally, F.A. Relative importance of snow accumulation and monsoon rainfall data for estimating annual runoff, Jhelum basin, Pakistan. Hydrol. Sci. 1994, 39, 199–216. [Google Scholar] [CrossRef]
- Chen, X.; Alimohammadi, N.; Wang, D. Modeling inter-annual variability of seasonal evaporation and storage change based on the extended Budyko framework. Water Resour. Res. 2013, 49, 6067–6078. [Google Scholar] [CrossRef]
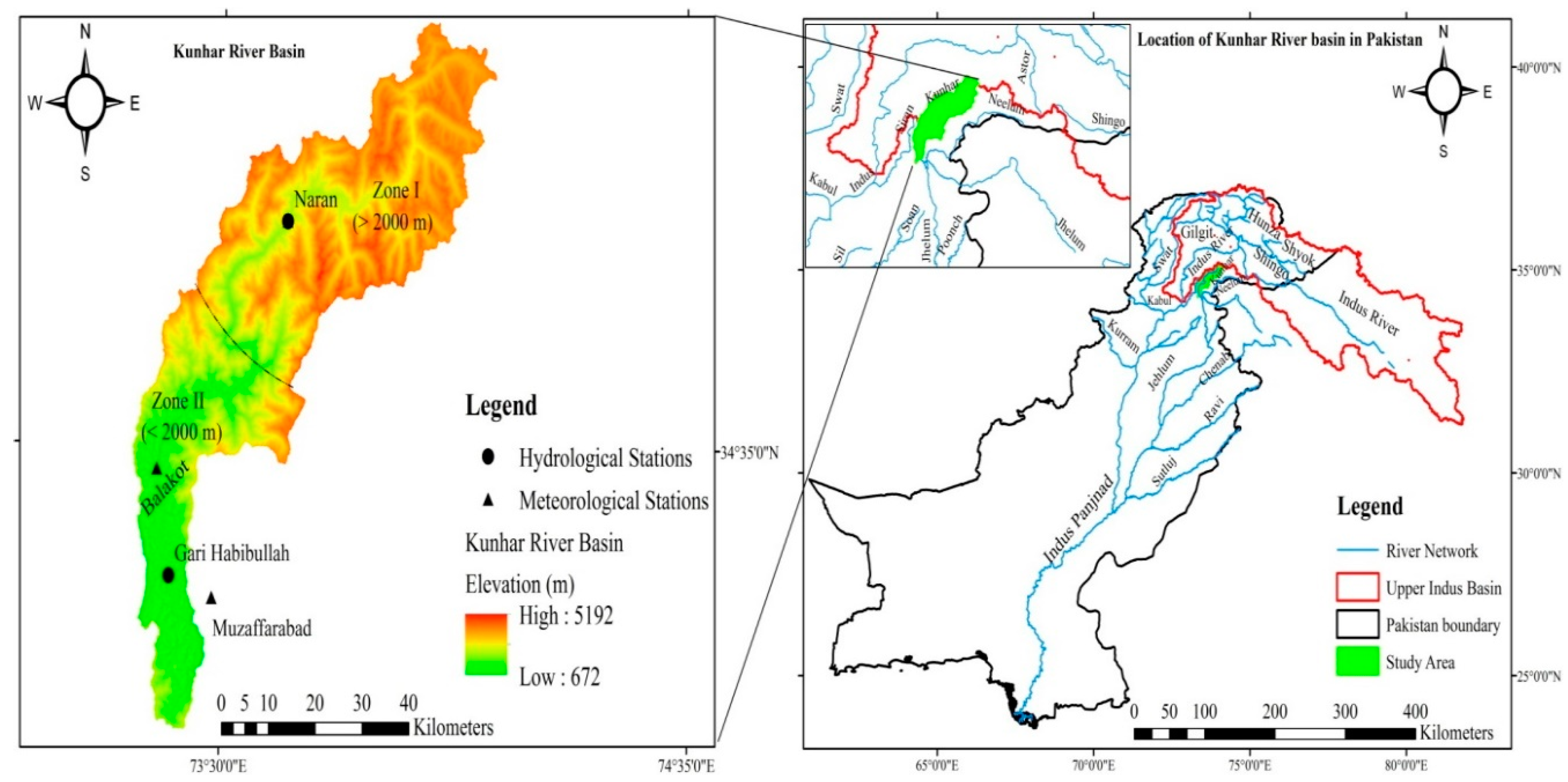




| Sr. # | Station | Lat (°N) | Long (°E) | Altitude (m ASL) | Period (Years) |
|---|---|---|---|---|---|
| Meteorological station | |||||
| 1 | Naran | 34.9 | 73.65 | 2421 | 1961–2010 |
| 2 | Balakot | 34.55 | 73.35 | 995 | Same period |
| 3 | Muzzafarabad | 34.37 | 73.48 | 702 | Same period |
| Hydrological station | |||||
| 1 | Naran | 34.9 | 73.65 | 2362 | 1961–2010 |
| 2 | Gari Habibullah | 34.40 | 73.38 | 810 | Same period |
| Month | β (%) | S (%) | ITA | ||||||
|---|---|---|---|---|---|---|---|---|---|
| R | P | T | R | P | T | R | P | T | |
| Jan | −17.92 | 42.8 | −1.06 | −2.07 | 36.64 | −0.09 | ↓ | ↑ | ↓ |
| Feb | −38.65 | 62.5 | −2.19 | −4.11 | 15.13 | −0.20 | ↓ | ↑ | ↔ |
| Mar | −76.18 | 57.3 | −2.45 | −6.39 | 16.86 | −0.28 | ↓ | ↑ | ↓ |
| Apr | −29.40 | 50.8 | −0.63 | −1.15 | 21.27 | −0.19 | ↓ | ↑ | ↓ |
| May | 6.11 | 26.5 | 0.53 | 0.08 | 29.82 | 0.02 | ↔ | ↑ | ↑ |
| Jun | −31.75 | 67.9 | 0.68 | −0.12 | 15.13 | 0.14 | ↔ | ↑ | ↑ |
| Jul | −29.83 | 62.2 | 0.92 | −0.04 | 38.48 | 0.12 | ↔ | ↑ | ↑ |
| Aug | −17.33 | 40.8 | 1.83 | 0.03 | 38.42 | 0.19 | ↔ | ↔ | ↑ |
| Sep | 1.18 | −5.7 | 1.05 | 0.59 | 18.63 | 0.12 | ↔ | ↔ | ↑ |
| Oct | 14.14 | −22.4 | 0.60 | 1.68 | −1.38 | 0.07 | ↑ | ↔ | ↑ |
| Nov | 17.77 | 60.0 | 1.12 | 2.28 | 50.46 | 0.11 | ↔ | ↑ | ↑ |
| Dec | 1.11 | 50.2 | 0.64 | −0.23 | 39.81 | 0.08 | ↔ | ↑ | ↑ |
| annual | −16.11 | 58.9 | 0.16 | −0.12 | 30.28 | 0.01 | ↓ | ↑ | ↑ |
| Month | β (%) | S (%) | ITA | ||||||
|---|---|---|---|---|---|---|---|---|---|
| R | P | T | R | P | T | R | P | T | |
| Jan | −0.22 | −11.25 | 0.11 | 1.12 | −6.36 | 0.02 | ↑ | ↓ | ↔ |
| Feb | 8.67 | −14.13 | 0.16 | 1.58 | −2.18 | 0.02 | ↑ | ↓ | ↔ |
| Mar | 24.46 | −31.31 | 0.00 | 1.31 | −2.56 | −0.02 | ↑ | ↓ | ↓ |
| Apr | 16.60 | −60.92 | 0.21 | 0.25 | −11.00 | 0.00 | ↔ | ↓ | ↔ |
| May | 30.07 | −12.53 | 0.35 | 0.31 | −10.73 | 0.01 | ↑ | ↓ | ↔ |
| Jun | −21.17 | 37.84 | −0.50 | −0.11 | −3.28 | −0.03 | ↓ | ↔ | ↓ |
| Jul | −17.79 | −4.39 | 0.12 | −0.03 | −0.29 | 0.08 | ↔ | ↔ | ↔ |
| Aug | −17.55 | −14.50 | 0.02 | 0.01 | −2.37 | 0.00 | ↔ | ↓ | ↔ |
| Sep | −13.07 | −1.20 | 0.24 | 0.66 | 5.16 | 0.02 | ↔ | ↔ | ↑ |
| Oct | −8.38 | −16.98 | 0.25 | 1.93 | −11.36 | 0.01 | ↔ | ↓ | ↔ |
| Nov | −4.69 | 0.00 | 0.36 | 1.53 | −18.30 | 0.05 | ↑ | ↔ | ↑ |
| Dec | −2.34 | −34.32 | 0.43 | 1.85 | 0.63 | 0.04 | ↔ | ↔ | ↑ |
| annual | −2.56 | −15.04 | 0.17 | 0.14 | −3.16 | 0.01 | ↑ | ↓ | ↑ |
| Month | Runoff Amplitude (RA) | Precipitation Amplitude (PA) | Temperature Amplitude (TA) | |||
|---|---|---|---|---|---|---|
| Zone I | Zone II | Zone I | Zone II | Zone I | Zone II | |
| Jan | 0.41 | 0.20 | 3.39 | 1.90 | 3.26 | 0.23 |
| Feb | 1.05 | 0.21 | 3.24 | 2.96 | 3.32 | 0.34 |
| March | 0.86 | 0.44 | 4.04 | 2.42 | 3.04 | 0.37 |
| April | 0.94 | 1.15 | 4.45 | 2.19 | 2.82 | 0.31 |
| May | 2.49 | 1.53 | 2.49 | 1.17 | 2.48 | 0.40 |
| June | 3.55 | 1.47 | 1.59 | 2.10 | 2.65 | 0.36 |
| July | 2.67 | 1.57 | 1.56 | 5.31 | 2.25 | 0.24 |
| August | 1.29 | 1.03 | 1.76 | 3.72 | 3.20 | 0.18 |
| Sep | 0.70 | 1.62 | 1.55 | 2.54 | 2.72 | 0.23 |
| Oct | 0.54 | 0.87 | 2.73 | 2.20 | 1.86 | 0.21 |
| Nov | 0.58 | 0.32 | 1.81 | 1.24 | 1.71 | 0.35 |
| Dec | 0.80 | 0.22 | 2.69 | 1.90 | 1.82 | 0.22 |
| Parameters | Fixed Method | Variable Method | ||
|---|---|---|---|---|
| Q80 | Monthly | |||
| I | II | I | II | |
| Total drought events | 46 | 87 | 140 | 151 |
| No. of drought per year | 0.9 | 1.74 | 2.8 | 3.02 |
| Mean duration (days) | 78.28 | 63.64 | 26.39 | 78.98 |
| Max duration (days) | 153 | 142 | 138 | 292 |
| Mean severity (mm) | 79.95 | 55.61 | 270.11 | 207.64 |
| Max severity (mm) | 285.16 | 260.66 | 2539.02 | 1882.54 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Saifullah, M.; Liu, S.; Tahir, A.A.; Zaman, M.; Ahmad, S.; Adnan, M.; Chen, D.; Ashraf, M.; Mehmood, A. Development of Threshold Levels and a Climate-Sensitivity Model of the Hydrological Regime of the High-Altitude Catchment of the Western Himalayas, Pakistan. Water 2019, 11, 1454. https://doi.org/10.3390/w11071454
Saifullah M, Liu S, Tahir AA, Zaman M, Ahmad S, Adnan M, Chen D, Ashraf M, Mehmood A. Development of Threshold Levels and a Climate-Sensitivity Model of the Hydrological Regime of the High-Altitude Catchment of the Western Himalayas, Pakistan. Water. 2019; 11(7):1454. https://doi.org/10.3390/w11071454
Chicago/Turabian StyleSaifullah, Muhammad, Shiyin Liu, Adnan Ahmad Tahir, Muhammad Zaman, Sajjad Ahmad, Muhammad Adnan, Dianyu Chen, Muhammad Ashraf, and Asif Mehmood. 2019. "Development of Threshold Levels and a Climate-Sensitivity Model of the Hydrological Regime of the High-Altitude Catchment of the Western Himalayas, Pakistan" Water 11, no. 7: 1454. https://doi.org/10.3390/w11071454
APA StyleSaifullah, M., Liu, S., Tahir, A. A., Zaman, M., Ahmad, S., Adnan, M., Chen, D., Ashraf, M., & Mehmood, A. (2019). Development of Threshold Levels and a Climate-Sensitivity Model of the Hydrological Regime of the High-Altitude Catchment of the Western Himalayas, Pakistan. Water, 11(7), 1454. https://doi.org/10.3390/w11071454