Revisiting SWAT as a Saturation-Excess Runoff Model
Abstract
:1. Introduction
2. Background for Changing SWAT-2012 to a Saturation-Excess Model
2.1. SWAT-2012
2.2. SWAT-wil
3. Materials and Methods
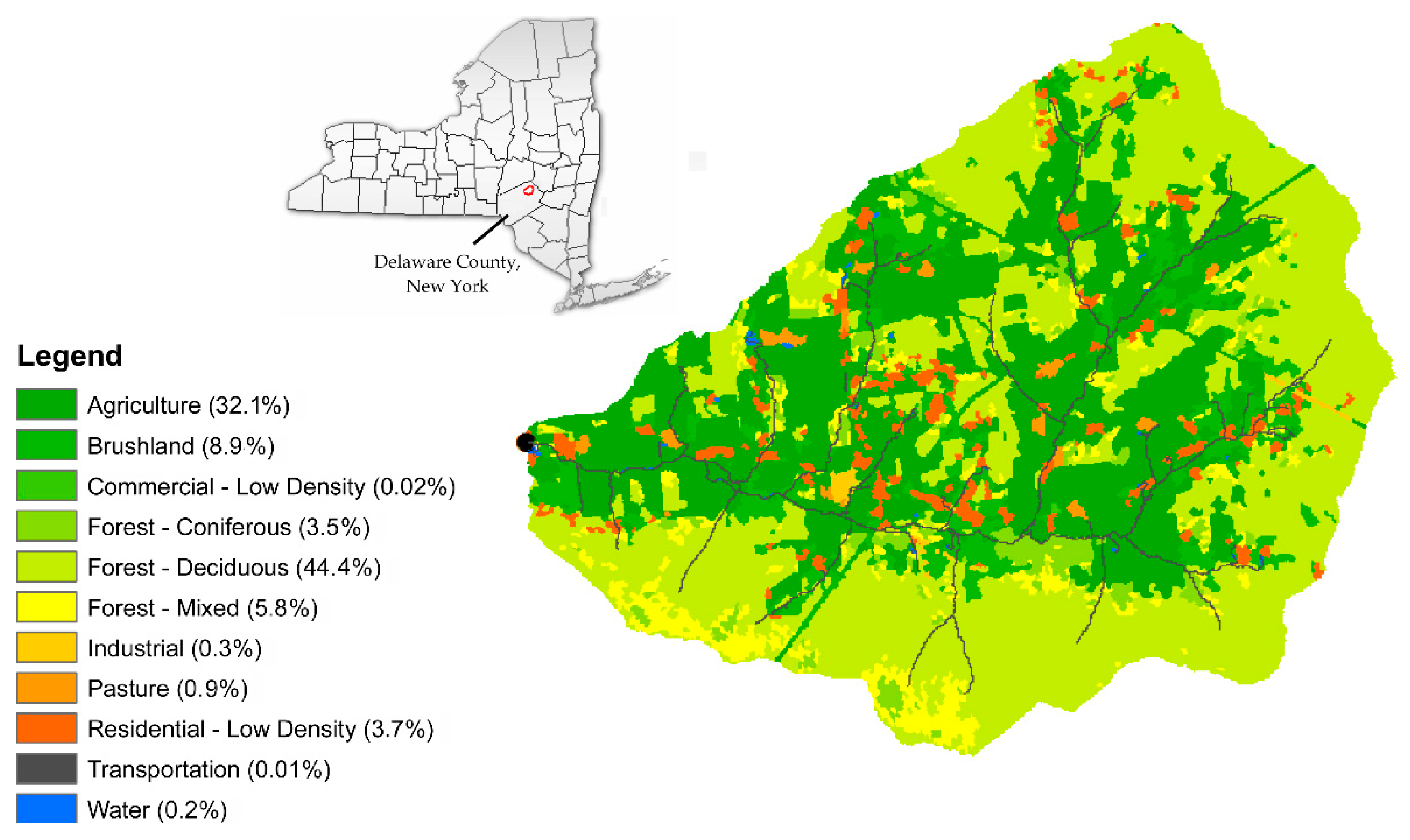
3.1. Town Brook Watershed
3.2. Description of SWAT-Hillslope
3.3. Model Setup for SWAT-wil
3.4. Model Calibration
3.5. Code Changes
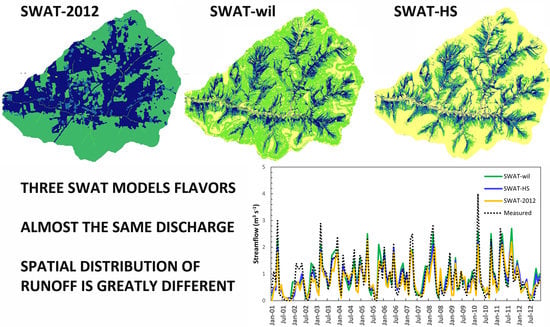
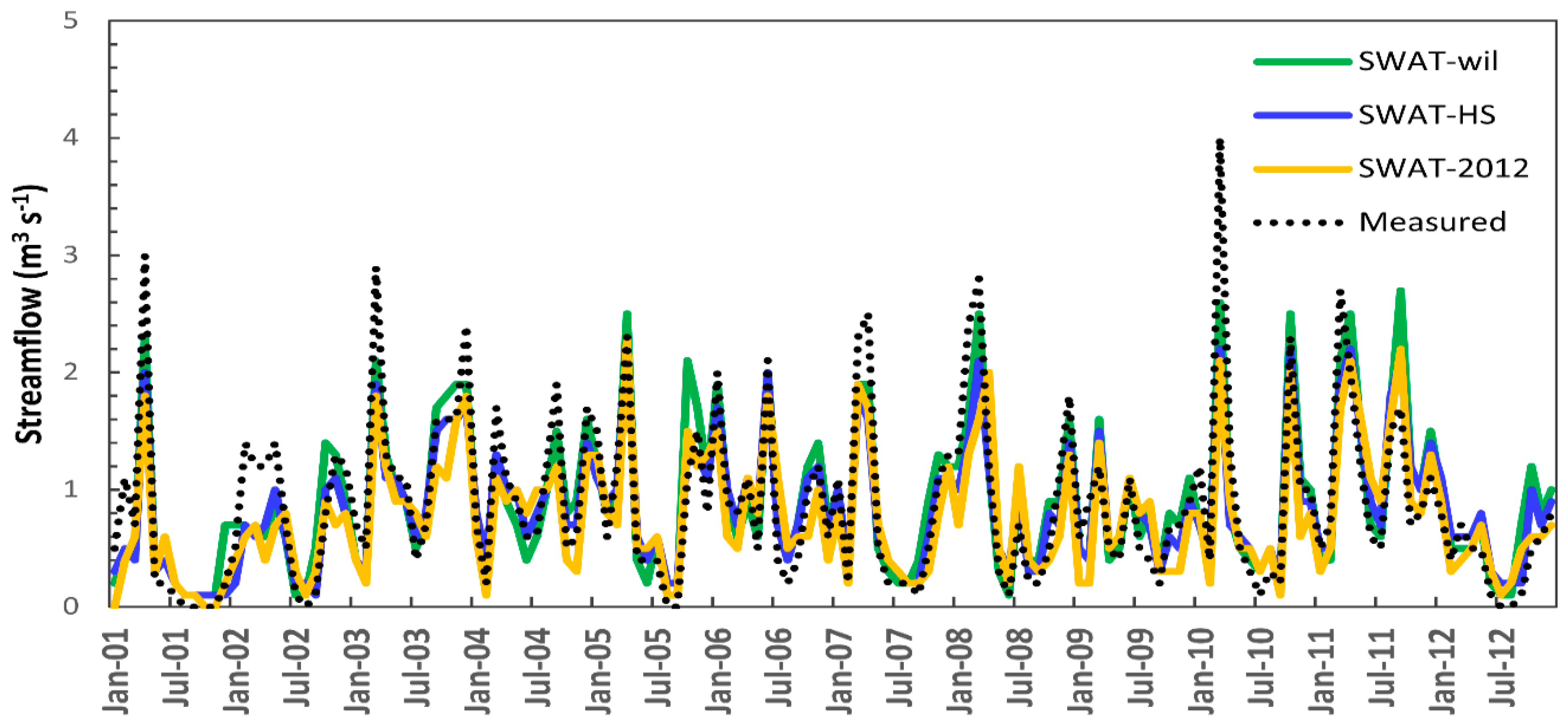
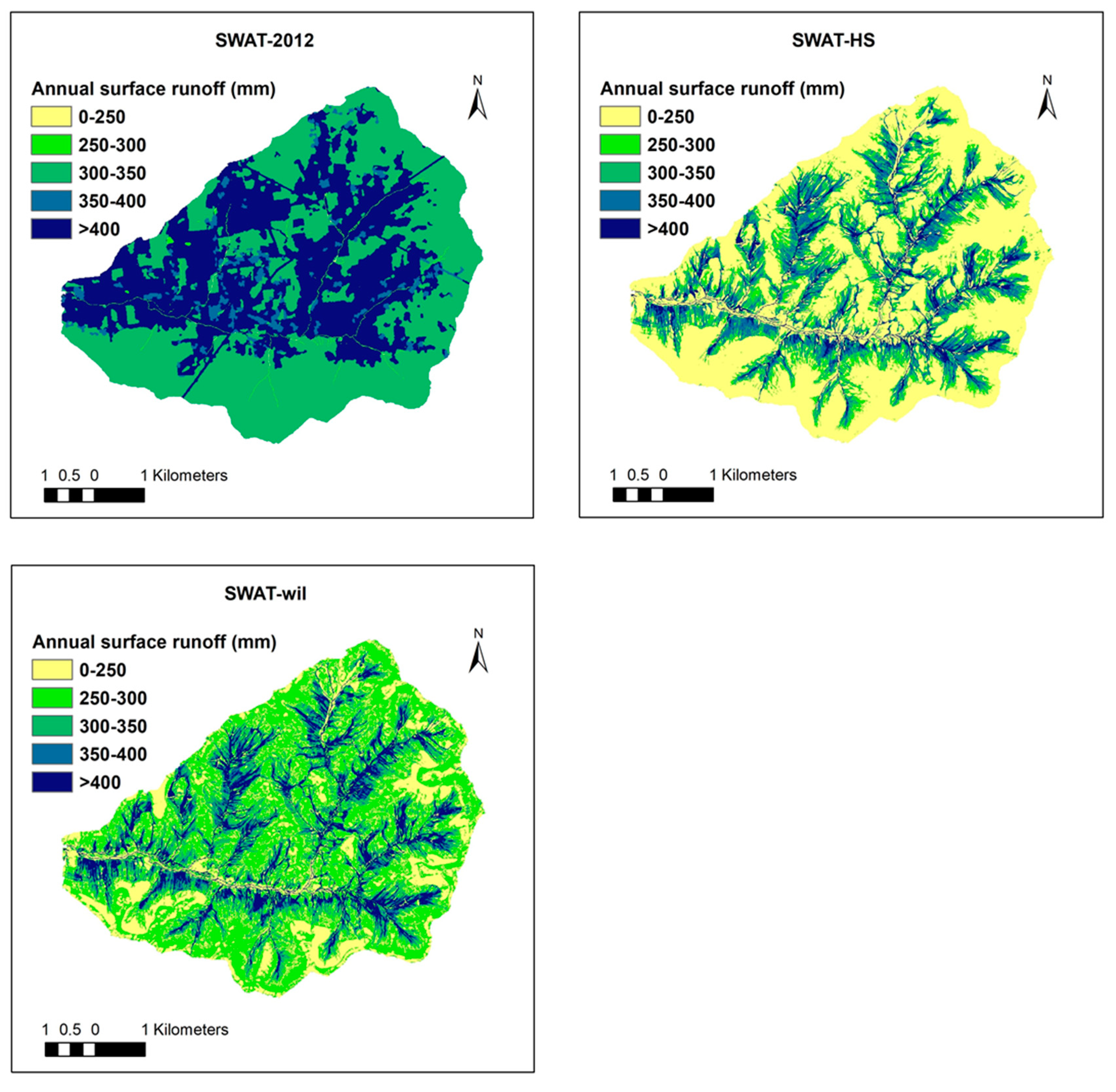
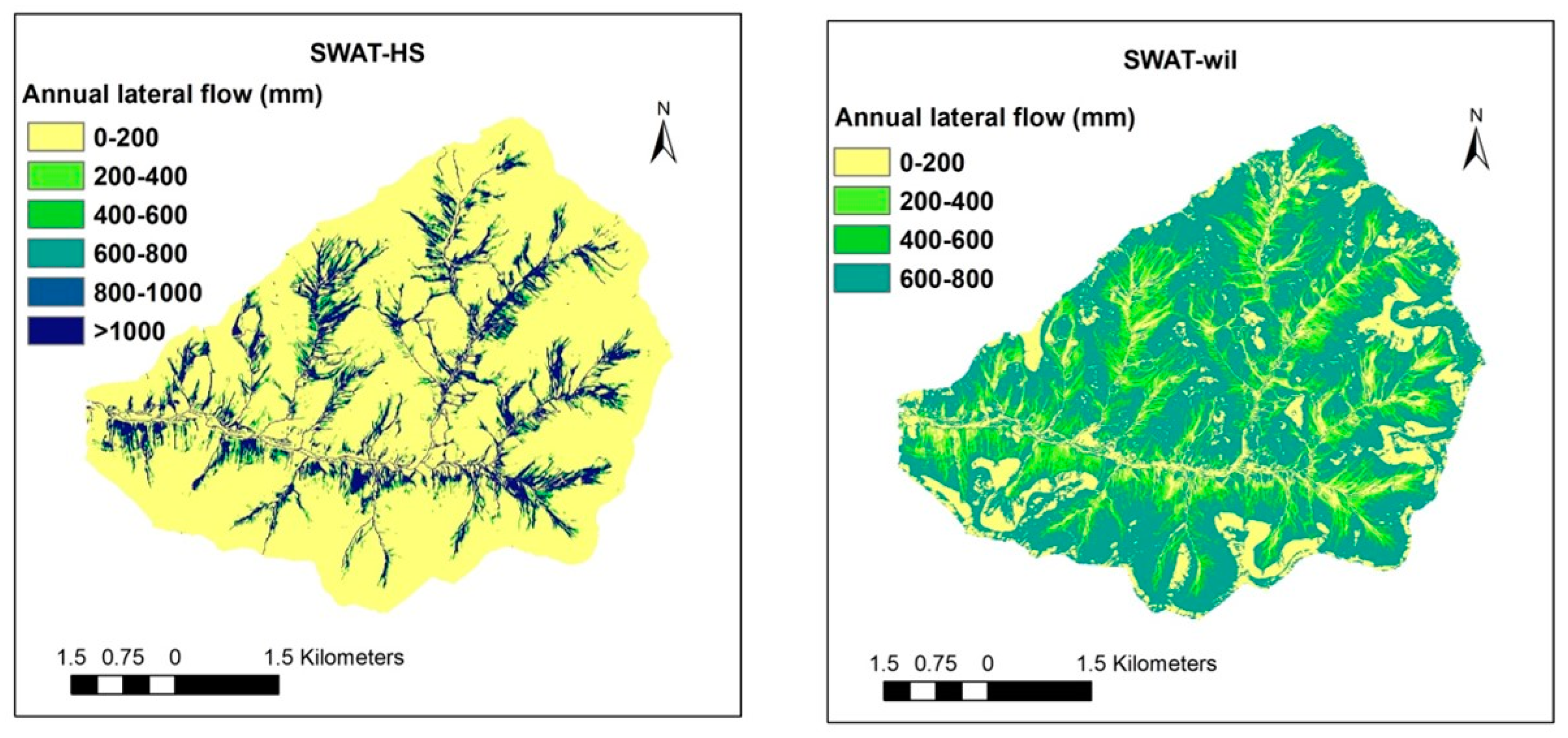
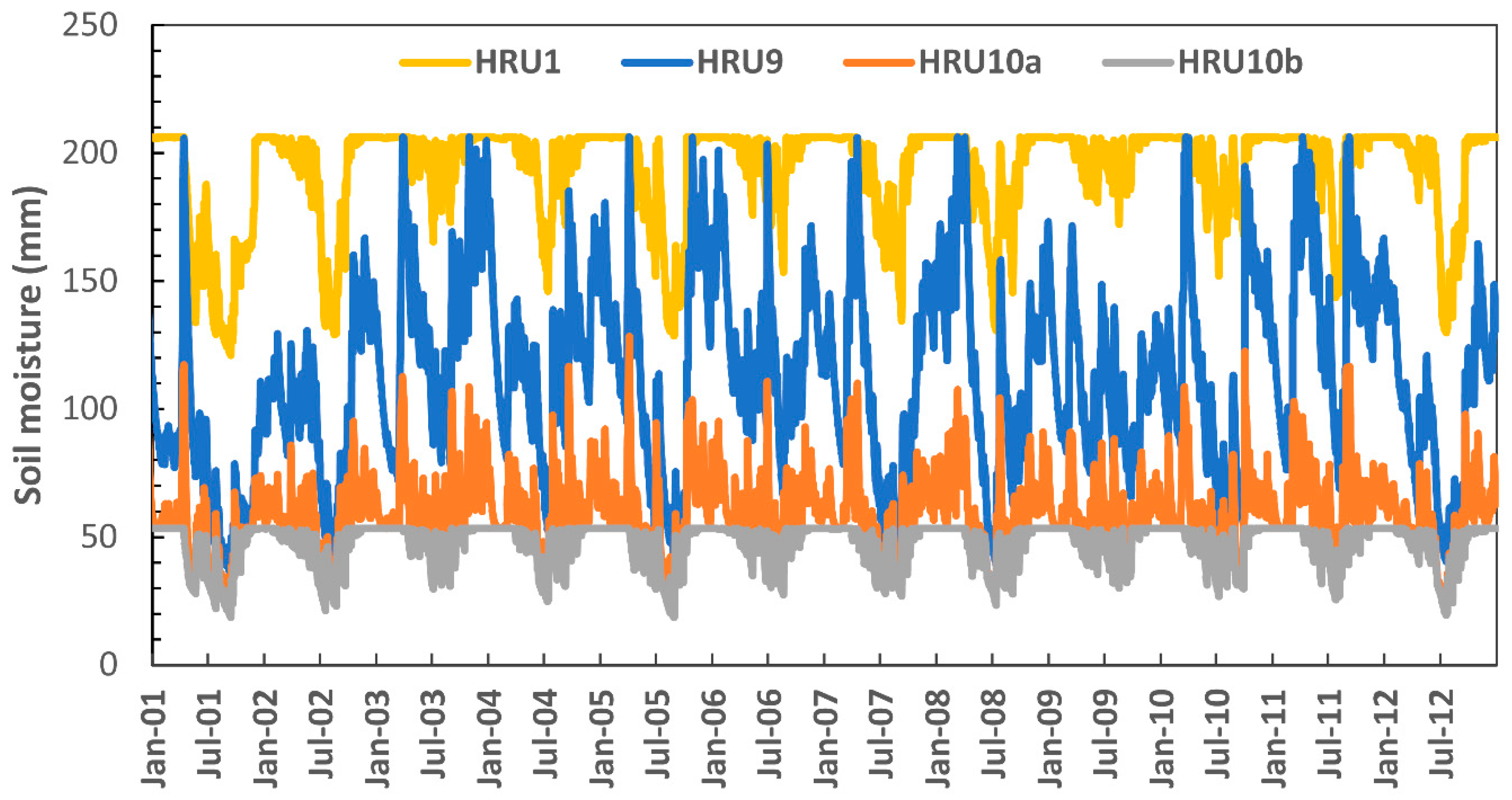
4. Results
5. Discussion
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Arnold, J.G.; Srinivasan, R.; Muttiah, R.S.; Williams, J.R. Large area hydrological modelling and assessment Part I: Model development. J. Am. Water Works Assn. 1998, 34, 73–89. [Google Scholar] [CrossRef]
- Bieger, K.; Arnold, J.G.; Rathjens, H.; White, M.J.; Bosch, D.D.; Allen, P.M.; Volk, M.; Srinivasan, R. Introduction to SWAT+, a completely restructured version of the soil and water assessment tool. J. Am. Water Resour. Assoc. 2017, 53, 115–130. [Google Scholar] [CrossRef]
- Walega, A.; Salata, T. Influence of land cover data sources on estimation of direct runoff according to SCS-CN and modified SME methods. Catena 2019, 172, 232–242. [Google Scholar] [CrossRef]
- Merwin, I.A.; Stiles, W.C.; van Es, H.M. Orchard Groundcover Management Impacts on Soil Physical Properties. J. Am. Soc. Hortic. Sci. 1994, 119, 216–222. [Google Scholar] [CrossRef] [Green Version]
- Tilahun, S.A.; Mukundan, R.; Demisse, B.A.; Engda, T.A.; Guzman, C.D.; Tarakegn, B.C.; Easton, Z.M.; Collick, A.S.; Zegeye, A.D.; Schneiderman, E.M. A saturation excess erosion model. T ASABE 2013, 56, 681–695. [Google Scholar] [CrossRef]
- Brooks, E.S.; Boll, J.; McDaniel, P.A. A hillslope-scale experiment to measure lateral saturated hydraulic conductivity. Water Resour. Res. 2004, 40, W04208. [Google Scholar] [CrossRef]
- Rittenburg, R.A.; Squires, A.L.; Boll, J.; Brooks, E.S.; Easton, Z.M.; Steenhuis, T.S. Agricultural BMP Effectiveness and Dominant Hydrological Flow Paths: Concepts and a Review. J. Am. Water Resour. Assoc. 2015, 51, 305–329. [Google Scholar] [CrossRef]
- Hewlett, J.D.; Hibbert, A.R. Factors affecting the response of small watersheds to precipitation in humid areas. In Forest Hydrology; Pergamon Press: New York, NY, USA, 1967. [Google Scholar] [CrossRef]
- Kane, D.L. Snowmelt infiltration into seasonally frozen soils. Cold Regions Sci. Tech. 1980, 3, 153–161. [Google Scholar] [CrossRef]
- Stähli, M.; Jansson, P.-E.; Lundin, L.-C. Soil moisture redistribution and infiltration in frozen sandy soils. Water Resour. Res. 1999, 35, 95–103. [Google Scholar] [CrossRef]
- Al-Houri, Z.; Barber, M.; Yonge, D.; Ullman, J.; Beutel, M. Impacts of frozen soils on the performance of infiltration treatment facilities. Cold Regions Sci. Tech. 2009, 59, 51–57. [Google Scholar] [CrossRef]
- Moges, M.A.; Schmitter, P.; Tilahun, S.A.; Langan, S.; Dagnew, D.C.; Akale, A.T.; Steenhuis, T.S. Suitability of Watershed Models to Predict Distributed Hydrologic Response in the Awramba Watershed in Lake Tana Basin. Land Degrad. Dev. 2017, 28, 1386–1397. [Google Scholar] [CrossRef]
- Bosch, D.; Arnold, J.; Volk, M.; Allen, P. Simulation of a low-gradient coastal plain watershed using the SWAT landscape model. T ASABE 2010, 53, 1445–1456. [Google Scholar] [CrossRef]
- Arnold, J.; Allen, P.; Volk, M.; Williams, J.; Bosch, D. Assessment of different representations of spatial variability on SWAT model performance. T ASABE 2010, 53, 1433–1443. [Google Scholar] [CrossRef]
- White, E.D.; Easton, Z.M.; Fuka, D.R.; Collick, A.S.; Adgo, E.; McCartney, M.; Awulachew, S.B.; Selassie, Y.G.; Steenhuis, T.S. Development and application of a physically based landscape water balance in the SWAT model. Hydrol. Process. 2011, 25, 915–925. [Google Scholar] [CrossRef]
- Easton, Z.M.; Fuka, D.R.; Walter, M.T.; Cowan, D.M.; Schneiderman, E.M.; Steenhuis, T.S. Re-conceptualizing the soil and water assessment tool (SWAT) model to predict runoff from variable source areas. J. Hydrol. 2008, 348, 279–291. [Google Scholar] [CrossRef]
- Hoang, L.; Schneiderman, E.M.; Moore, K.E.; Mukundan, R.; Owens, E.M.; Steenhuis, T.S. Predicting saturation-excess runoff distribution with a lumped hillslope model: SWAT-HS. Hydrol. Process. 2017, 31, 2226–2243. [Google Scholar] [CrossRef]
- Winter, T.C. The Concept of Hydrologic Landscapes. J. Am. Water Resour. Assoc. 2001, 37, 335–349. [Google Scholar] [CrossRef]
- McDonnell, J.J.; Sivapalan, M.; Vaché, K.; Dunn, S.; Grant, G.; Haggerty, R.; Hinz, C.; Hooper, R.; Kirchner, J.; Roderick, M.L.; et al. Moving beyond heterogeneity and process complexity: A new vision for watershed hydrology. Water Resour. Res. 2007, 43. [Google Scholar] [CrossRef] [Green Version]
- Savenije, H.H.G. HESS Opinions “Topography driven conceptual modelling (FLEX-Topo)”. Hydrol. Earth Syst. Sci. 2010, 14, 2681–2692. [Google Scholar] [CrossRef]
- Steenhuis, T.S.; Collick, A.S.; Easton, Z.M.; Leggesse, E.S.; Bayabil, H.K.; White, E.D.; Awulachew, S.B.; Adgo, E.; Ahmed, A.A. Predicting discharge and sediment for the Abay (Blue Nile) with a simple model. Hydrol. Process. 2009, 23, 3728–3737. [Google Scholar] [CrossRef]
- Steenhuis, T.S.; Winchell, M.; Rossing, J.; Zollweg, J.A.; Walter, M.F. SCS runoff equation revisited for variable-source runoff areas. J. Irrigat. Drain. Eng. 1995, 121, 234–238. [Google Scholar] [CrossRef]
- Schneiderman, E.M.; Steenhuis, T.S.; Thongs, D.J.; Easton, Z.M.; Zion, M.S.; Neal, A.L.; Mendoza, G.F.; Todd Walter, M. Incorporating variable source area hydrology into a curve-number-based watershed model. Hydrol. Process. 2007, 21, 3420–3430. [Google Scholar] [CrossRef]
- Frankenberger, J.R.; Brooks, E.S.; Walter, M.T.; Walter, M.F.; Steenhuis, T.S. A GIS-based variable source area hydrology model. Hydrol. Process. 1999, 13, 805–822. [Google Scholar] [CrossRef]
- Western, A.W.; Zhou, S.-L.; Grayson, R.B.; McMahon, T.A.; Blöschl, G.; Wilson, D.J. Spatial correlation of soil moisture in small catchments and its relationship to dominant spatial hydrological processes. J. Hydrol. 2004, 286, 113–134. [Google Scholar] [CrossRef]
- Beven, K. Rainfall Runoff Modeling: The Primer; John Wiley & Sons, Ltd.: Chichester, London, UK, 2001; p. 360. [Google Scholar] [CrossRef]
- Beven, K.J.; Kirkby, M.J. A physically based, variable contributing area model of basin hydrology/Un modèle à base physique de zone d’appel variable de l’hydrologie du bassin versant. Hydrol. Sci. J. 1979, 24, 43–69. [Google Scholar] [CrossRef]
- Bayabil, H.K.; Tilahun, S.A.; Collick, A.S.; Yitaferu, B.; Steenhuis, T.S. Are runoff processes ecologically or topographically driven in the (sub) humid Ethiopian highlands? The case of the Maybar watershed. Ecohydrology 2010, 3, 457–466. [Google Scholar] [CrossRef] [Green Version]
- Dahlke, H.E.; Easton, Z.M.; Lyon, S.W.; Todd Walter, M.; Destouni, G.; Steenhuis, T.S. Dissecting the variable source area concept—Subsurface flow pathways and water mixing processes in a hillslope. J. Hydrol. 2012, 420–421, 125–141. [Google Scholar] [CrossRef]
- Harpold, A.A.; Lyon, S.W.; Troch, P.A.; Steenhuis, T.S. The hydrological effects of lateral preferential flow paths in a glaciated watershed in the northeastern USA. Vadose Zone J. 2010, 9, 397–414. [Google Scholar] [CrossRef]
- Zimale, F.A.; Tilahun, S.A.; Tebebu, T.Y.; Guzman, C.D.; Hoang, L.; Schneiderman, E.M.; Langendoen, E.J.; Steenhuis, T.S. Improving watershed management practices in humid regions. Hydrol. Process. 2017, 31, 3294–3301. [Google Scholar] [CrossRef]
- Hewlett, J.D.; Nutter, W.L. The Varying Source Area of Streamflow. In Proceedings of the symposium on interdisciplinary aspects of watershed management 1970, Bozeman, MT, USA, 3–6 August 1970. [Google Scholar]
- Liang, X.; Lettenmaier, D.P.; Wood, E.F.; Burges, S.J. A simple hydrologically based model of land surface water and energy fluxes for general circulation models. J. Geophys. Res. Atmos. 1994, 99, 14415–14428. [Google Scholar] [CrossRef]
- Wigmosta, M.S.; Lettenmaier, D.P. A comparison of simplified methods for routing topographically driven subsurface flow. Water Resour. Res. 1999, 35, 255–264. [Google Scholar] [CrossRef]
- Mehta, V.K.; Walter, M.T.; Brooks, E.S.; Steenhuis, T.S.; Walter, M.F.; Johnson, M.; Boll, J.; Thongs, D. Application of SMR to Modeling Watersheds in the Catskill Mountains. Environ. Model. Assess. 2004, 9, 77–89. [Google Scholar] [CrossRef]
- Brinson, M.M. A Hydrogeomorphic Classification for Wetlands; Technical Report WRP-DE-4; US Army Corps of Engineers Waterways Experiment Station: Vicksburg, MS, USA, 1993. [Google Scholar]
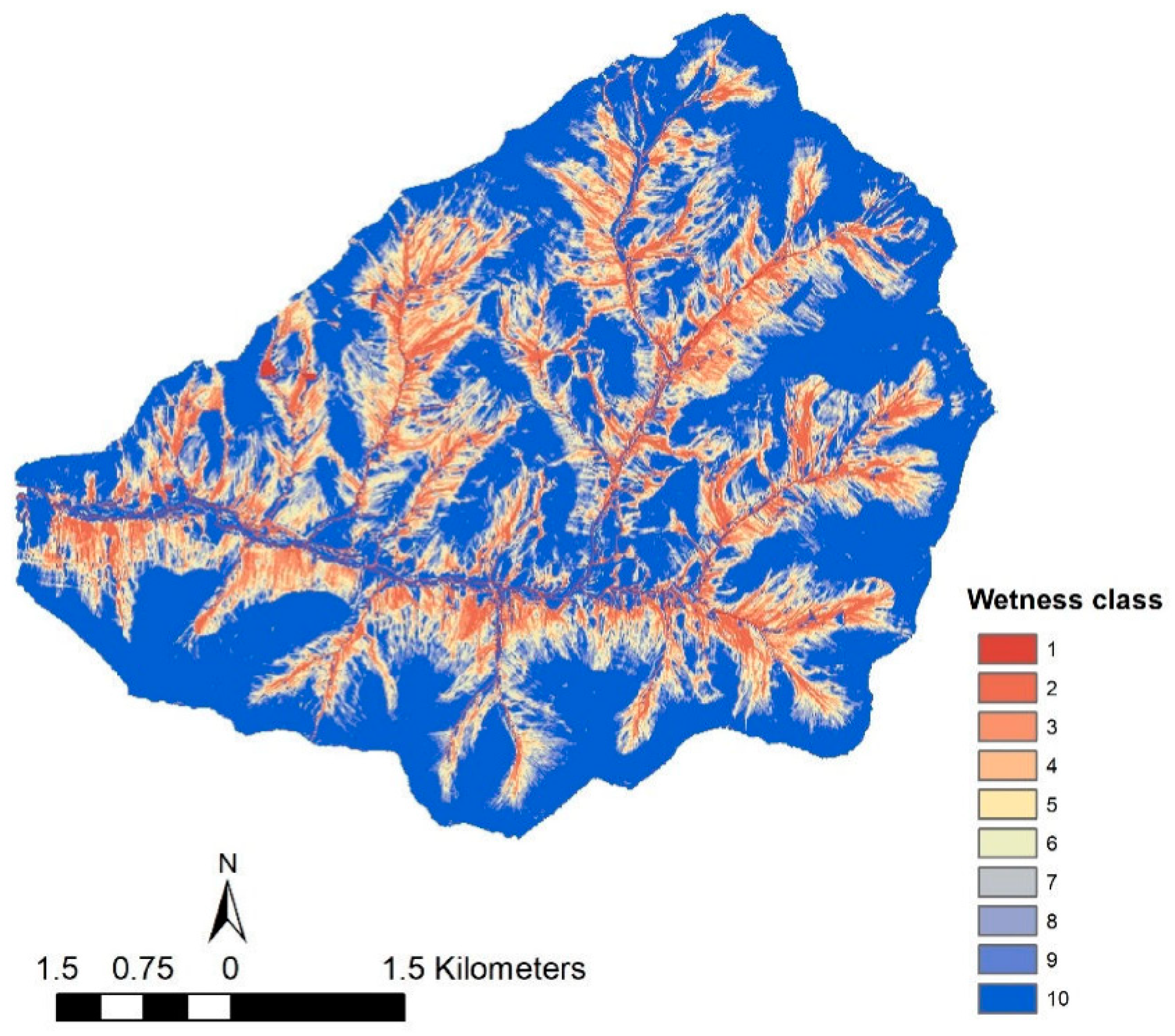
| HRU | Topographic Index λ | AreaHRU % | DEPIMP mm | KSAT mm h−1 | HRUSLP mm mm−1 | SLSOIL m | CN2 | R2ADJ |
|---|---|---|---|---|---|---|---|---|
| 1 | >17.7 | 0.59 | 457 | 33 | 0.040 | 1662 | - | 100 |
| 2 | 16.7–17.7 | 6.06 | 457 | 33 | 0.093 | 307 | - | 100 |
| 3 | 15.8–16.7 | 6.24 | 457 | 33 | 0.116 | 135 | - | 100 |
| 4 | 14.8–15.8 | 6.18 | 457 | 33 | 0.128 | 87 | - | 100 |
| 5 | 13.8–14.8 | 6.37 | 457 | 33 | 0.141 | 65 | - | 100 |
| 6 | 12.9–13.8 | 6.20 | 457 | 33 | 0.152 | 51 | - | 100 |
| 7 | 11.9–12.9 | 6.90 | 457 | 33 | 0.167 | 43 | - | 100 |
| 8 | 10.9–11.9 | 6.67 | 457 | 33 | 0.183 | 36 | - | 100 |
| 9 | 10.0–10.9 | 6.04 | 457 | 33 | 0.198 | 31 | - | 100 |
| 10a | 10–7.6 | 33.7 | 457 | 33 | 0.263 | 21 | 35 | 1 |
| 10b | <7.6 | 15 | 6000 | 33 | 0.116 | 1600 | - | 100 |
| Hydrologic Component | Parameter | SWAT-wil Value | SWAT-HS Value |
|---|---|---|---|
| Snow | SFTMP | −0.58 | −0.58 |
| SMTMP | 1.10 | 1.10 | |
| SMFMX | 7.62 | 7.62 | |
| SMFMN | 2.68 | 2.68 | |
| TIMP | 0.022 | 0.022 | |
| ET | ESCO | 1.00 | 0.691 |
| EPCO | 0.10 | 0.989 | |
| Overland Flow | SURLAG | 2.20 | 4.00 |
| Groundwater Flow | ALPHA_BF | 0.37 | 0.05 |
| GW_DELAY | 3.45 | 31.00 | |
| Lateral flow | LAT_TTIME | 0.22 | n.a. |
| SWAT-2012 | SWAT-wil | SWAT-HS | |||||
|---|---|---|---|---|---|---|---|
| Time Step | NSE | R2 | NSE | R2 | NSE | R2 | |
| 2001–2008 | Daily | 0.53 | 0.54 | 0.61 | 0.61 | 0.65 | 0.64 |
| 2001–2008 | Monthly | 0.67 | 0.73 | 0.81 | 0.82 | 0.80 | 0.86 |
| 2009–2012 | Daily | 0.50 | 0.50 | 0.51 | 0.52 | 0.53 | 0.54 |
| 2009–2012 | Monthly | 0.68 | 0.68 | 0.73 | 0.74 | 0.73 | 0.74 |
| Flow Component | SWAT-2012 (mm/day) | SWAT-wil (mm/day) | SWAT-HS (mm/day) |
|---|---|---|---|
| Surface runoff | 1.20 | 0.36 | 0.22 |
| Lateral flow | 0.26 | 1.34 | 1.25 |
| Groundwater flow | 0.29 | 0.30 | 0.29 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Steenhuis, T.S.; Schneiderman, E.M.; Mukundan, R.; Hoang, L.; Moges, M.; Owens, E.M. Revisiting SWAT as a Saturation-Excess Runoff Model. Water 2019, 11, 1427. https://doi.org/10.3390/w11071427
Steenhuis TS, Schneiderman EM, Mukundan R, Hoang L, Moges M, Owens EM. Revisiting SWAT as a Saturation-Excess Runoff Model. Water. 2019; 11(7):1427. https://doi.org/10.3390/w11071427
Chicago/Turabian StyleSteenhuis, Tammo S., Elliot M. Schneiderman, Rajith Mukundan, Linh Hoang, Mamaru Moges, and Emmet M. Owens. 2019. "Revisiting SWAT as a Saturation-Excess Runoff Model" Water 11, no. 7: 1427. https://doi.org/10.3390/w11071427
APA StyleSteenhuis, T. S., Schneiderman, E. M., Mukundan, R., Hoang, L., Moges, M., & Owens, E. M. (2019). Revisiting SWAT as a Saturation-Excess Runoff Model. Water, 11(7), 1427. https://doi.org/10.3390/w11071427