Abstract
Ion-selective membranes are an important component of electrodialysis stacks for desalination. Manufacturing imperfections or slight inhomogeneity of the material can lead to minute membrane surface imperfections. Two-dimensional solutions of the coupled Poisson–Nernst–Planck and Navier–Stokes equations were sought for a perfectly smooth membrane and for membranes with well-defined small-amplitude harmonic surface roughness. The simulations were carried out with the validated rheoEFoam solver by Pimenta and Alves. In the overlimiting regime, the electric field is strong enough for an electrokinetic instability to occur. The instability leads to disturbance growth and the formation of electro-convection cells, which strongly increase the current density. The present simulations show that with an increasing ion concentration and applied voltage, the instability becomes stronger and the overlimiting regime is reached earlier. The limiting current density shows a noticeable dependence on the wavelength of the surface roughness. When the wavelength of the surface roughness is incommensurate with the wavelength of the naturally occurring instability, the limiting current density is increased. Since production membranes will always have some degree of surface roughness, this suggests that membrane surface treatments which favor certain wavelengths may have an effect on the overall membrane performance.
1. Introduction
Desalination of alternative waters, such as brackish water, seawater, municipal, and industrial wastewater, has become a critical strategy to expand traditional water supplies and to alleviate water shortages [1]. Electrodialysis (ED) is a membrane desalination technology that uses semi-permeable ion-exchange membranes (IEMs) to selectively separate salt ions in water under the influence of an electric field [2]. An ED stack consists of pairs of anion-exchange membranes (AEMs) and cation-exchange membranes (CEMs) arranged alternatingly between an anode and a cathode (Figure 1). The positively charged cations migrate toward the cathode, pass the negatively charged CEM, and are rejected by the positively charged AEM. The opposite occurs when the negatively charged anions migrate toward the anode. This results in an alternatively increasing ion concentration in one compartment (concentrate) and decreasing salt concentration in the other (diluate). The process can be viewed as a dialysis process, where the ion diffusion across the membranes is amplified and orientated by an electric field. Electrodialysis reversal (EDR) is a modified ED process, where the electrical polarity of the electrodes is reversed periodically. This results in a reversal in the direction of the ion transport so that the concentrated stream becomes the diluate stream and vice versa. This self-flushing of scale forming ions and fouling matter in concentrate compartments allows EDR to operate at a higher water recovery than ED.
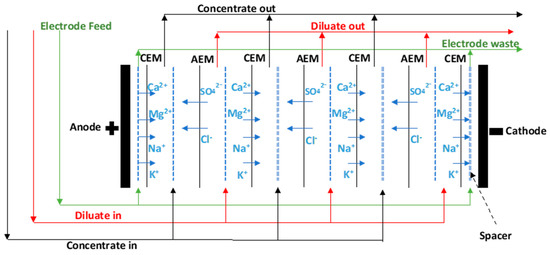
Figure 1.
Schematic diagram of electrodialysis stack.
Electrodialysis and EDR have been utilized for decades to desalinate brackish water, treat municipal and industrial wastewater, and produce NaCl from seawater [1]. It has also found applications in chemical processes, as well as the food, beverage, and drug industries. Despite the broad application of ED/EDR, the number of experiments and simulations concerned with the thermodynamics and fluid dynamics of the ED process is very limited [3]. For example, a key parameter for the design and operation of ED is the limiting current density (LCD). It is typically identified as the diffusion-limited current density, corresponding to the complete solute depletion in the layer adjacent to the membrane surface [2]. The limiting regime in ED is associated with the appearance of electroconvective structures near the membranes [3]. The structures are caused by an electrokinetic instability (EKI). The phenomena involved in the limiting region are not yet fully understood. Any improvement of the effectiveness of the ED process based on a reduction of the energy losses (e.g., Chehayeb and Lienhard [3]) and methods that overcome inherent operating limitations have strong implications for environmental sustainability and the water, food, and chemical industries.
This paper is concerned with the factors governing the onset of the overlimiting regime in ED. Of particular interest are the effects of the applied voltage, salt concentration, and membrane surface geometry on the onset of the EKI. Towards that end, simulations of the phenomena near a CEM were carried out for a binary electrolyte solution. Because the hydrodynamics and ion transport for CEMs and AEMs are similar, the present findings transfer over to AEMs. The paper starts out with a discussion of the onset of the overlimiting regime and how it is related to the EKI. This section is followed by a discussion of the governing equations, the setup of the simulations, and the defining parameters. Instantaneous visualizations and time histories of the current density are employed to investigate the onset of the EKI. The paper concludes with a brief discussion of the results and their relevance for ED.
2. Overlimiting Regime and Electrokinetic Instability
When the voltage is low enough, the cations in the diffusion layer are drawn to the CEM surface by both migration and diffusion. For the anions, the diffusive and electromigration fluxes cancel each other out. The solution remains locally charge neutral with the exception of a thin electric double layer (EDL) with a thickness of tens of micrometers that forms on the selective membrane surface. As the voltage and hence the concentration gradients are increased, the electroneutrality condition demands very small anion concentrations near the CEM surface. For some limiting voltage, the electroneutrality condition in the diffusion layer is violated and another layer emerges between the EDL and the diffusion layer, which is known as extended space charge layer. Beyond a critical voltage, an instability sets in (here referred to as electrokinetic instability, EKI) and disturbance amplification results in the formation of organized flow structures and electroconvection. The flow structures eject fluid and charge density away from the membrane and substantially increase the current density. For mono-valent binary solutions, the magnitude of the limiting current density is inversely proportional to the boundary layer thickness [4]. The electroconvective structures are similar to those arising from the Rayleigh–Bénard instability, which is driven by opposing gravity and buoyancy forces.
Based on experiments, Rubinstein et al. [5] made a connection between the onset of the overlimiting regime, which is associated with an unsteadiness of the current density, and the occurrence of the EKI. Later, simulations and stability investigations followed (e.g., Demekhin et al. [6], Rubinstein and Zaltzman [7,8]). A review on electroconvective micro-structures and related phenomena was provided by Chang et al. [9]. Despite the small length-scales associated with electroconvection, the instability can lead to broad spectra and an energy cascade similar to those observed in turbulent flows. Dye visualizations by Yossifon et al. [10] revealed vortices with an initial wavelength of 10 to (close to the thickness of the boundary layer). As the vortices grow in size they merge and the wavelength is reduced. For narrow microchannels, the channel height determines the final vortex size [10]. When fully developed, the size of the structures is of the order of the distance between the membranes, which is typically less than . For very narrow channels, the vortices never form, which, of course, suggests that the instability is suppressed.
The simulation of reverse osmosis (RO) and even more so ED processes is challenging because of the complex flow physics and the large spread of length-scales from nanometer-sized pores to millimeter-sized spacers. For liquids, the continuum assumption breaks down for length scales around . Although some researchers argue that lattice Boltzmann methods should be employed to describe the flow in ED stacks (because of the small scales), the general consensus is that the continuous flow model (Navier–Stokes equations) is accurate enough. Aside from the Navier–Stokes (N–S) equations, for ED processes additional conservation equations for the molar concentrations, , of the ions, the Nernst–Planck (N–P) equations, have to be solved. Diffusion and electromigration dominate the ionic transport in the boundary layer. Since the water flux through the IEMs in ED is typically insignificant, the convection terms are often neglected. For example, Kim et al. [11] developed a mathematical model for the steady-state transport of three ion species through an ED cell based on diffusion and migration.
Research aimed at understanding the physics of the boundary layer near the IEMs has to consider the complete N–P equations. Druzgalski et al. [12] solved the coupled two-dimensional (2-D) N–P and N–S equations to investigate the EKI for a binary electrolyte between an IEM and a reservoir (water flow channel). They also presented a framework for the development of ensemble-averaged models (similar to Reynolds-averaged Navier–Stokes models) for the inclusion of the resulting electroconvective-driven mixing processes. Similar simulations were performed by Zourmand et al. [13] and Enciso et al. [14]. Enciso et al. [14] performed experiments and found a 16% difference between the computed and measured mass transfer coefficients. Pimenta and Alves [15] developed an OpenFOAM solver, rheoEFoam, which is part of the rheoTool suite, for the simulation of electrically-driven flows. Importance was placed on the conservation of the ionic species, numerical robustness, and an overall second-order-accuracy of the discretization. RheoEFoam was validated by comparison with the binary electrolyte problem by Druzgalski et al. [12].
Demekhin et al. [16] carried out three-dimensional (3-D) simulations of a reservoir-membrane configuration and found three typical flow structures arising from the EKI: Two-dimensional (2-D) counter-rotating rolls, regular hexagonal (“bee hive”) structures, and more chaotic 3-D structures. The onset of the instability and the type of the resulting flow structures were found to depend on the applied voltage and a coupling coefficient, , between the hydrodynamics and the electrostatics. Here, is the permittivity, is the electric potential, is the dynamic viscosity, and is the ionic diffusivity. When the voltage exceeded a first critical value, counter-rotating rolls formed. When the voltage was increased further beyond a second critical value, hexagonal structures arose. Finally, for very large voltages, the flow became chaotic and the spectra filled up. Druzgalski and Mani [17] employed 3-D simulations to investigate the fully chaotic regime. They found short-lived high-current-density spots that appeared randomly on the membrane surface and contributed significantly to the mean current density.
Rubinstein and Zaltzman [8] showed that the EKI leads to the growth of disturbances with a preferred natural wavelength whose initial amplitude can be increased by imparting a minute waviness on the membrane surface. This paper is concerned with the dependence of the current density on the wavelength of the waviness of the membrane surface. The present effort has been motivated by research in fluid dynamics that has shown that the growth of instability waves can be influenced. Saric et al. [18] investigated crossflow transition on swept wings. By adding micro-sized roughness elements that were spaced at a wavelength below the most unstable (natural) wavelength of the instability, the growth rate of the steady crossflow mode could be reduced and transition to turbulence could be delayed. Embacher and Fasel [19] stabilized a secondary instability by forcing the primary instability at a wavelength that was incommensurate with the most amplified natural wavelength. Finally, streamwise riblets with a spanwise wavelength close to the wavelength of the naturally occurring near-wall streaks in turbulent boundary layers (the wavelength can be as small as ) were found to reduce the turbulent skin-friction drag [20].
This paper shows that by transferring these ideas to ED applications, the onset of the EKI and the overlimiting regime can be delayed. Of particular relevance for the present investigations are the results for wavy membranes by Rubinstein and Zaltzman [8] and the crossflow instability research by Saric et al. [18]. As will be shown later, the required dimensions of the membrane surface structures will be much smaller than what has already been considered in the literature (e.g., Güler et al. [21]). All of the present simulations were carried out with the rheoEFoam code, which was developed by Pimenta and Alves [15]. The majority of the simulations are 2-D. The concentration and the strength of the electric field were varied. For one case, a 3-D simulation was carried out to demonstrate the relevance of the 2-D simulations.
3. Methodology
3.1. Governing Equations
The equations governing the unsteady, incompressible, isothermal, single-phase, laminar flow of a Newtonian fluid under the action of an electric field were solved with rheoEFoam by Pimenta and Alves [15]. Within rheoEFoam, after the initialization of the field variables, a Poisson equation for the electric potential, , with unit , is solved:
where is the electric permittivity in and is the charge density in . Here, is Faraday’s constant, and and are the charge valences or charge numbers and molar concentrations (in ) of species . Updated molar concentrations, , are obtained from the Nernst–Planck equation:
where is the velocity vector in , are the diffusion coefficients in , and = are the electrical mobilities in . Here, is the elementary charge, is the Boltzmann constant, and is the temperature in . RheoEFoam converges Equations (1) and (2) before solving the Navier–Stokes equations:
to obtain updates for the velocities, , and pressure, (in ). The mixture density, in , is computed from the molar masses, , in . is the dynamic viscosity in . For the computation of the electric force per unit volume, in , the electric permittivity is assumed as constant. Finally, is the electric field in . Once Equations (3) and (4) are solved, rheoEFoam goes back to computing Equations (1) and (2) until the entire system of Equations (1)–(4) converges.
3.2. Boundary Conditions
The present simulations were set up according to the 2-D problem by Druzgalski et al. [12]. This two-species problem is defined by a reservoir at the top surface and a CEM at the bottom surface that allows cationic species to pass (Figure 2). An electric field () is applied in the direction perpendicular to the reservoir and the membrane.

Figure 2.
Generic problem of a 2-D reservoir with a cation-selective membrane (CEM).
The CEM was placed at y = 0. The membrane was modeled by no-slip and no-penetration conditions for the velocities, , a zero normal pressure gradient, a zero potential, , a fixed cation concentration, , and a no-flux condition for the anions. No-slip and no-penetration conditions for the velocities and a zero normal gradient for the pressure were also applied at the reservoir boundary at . The potential, , at the reservoir boundary was set according to the applied voltage differential, . The cation and anion concentrations, and , at the reservoir boundary were held constant. Periodic (i.e., cyclic) boundary conditions were employed at all other boundaries.
3.3. Defining Parameters
A case with very low NaCl concentration () matching that of an earlier simulation by Pimenta and Alves [15] was chosen as the baseline. In addition, cases with higher salt concentrations matching slightly and moderately brackish water (low and medium), as well as seawater (high concentration), were considered. The concentrations for the different cases are listed in Table 1. The temperature was set to room temperature, , the diffusion coefficients were set to . According to Vitagliano and Lyons [22], the diffusion coefficient for NaCl solutions has the same order of magnitude and varies slightly with concentration. The mixture density was (i.e., water), the dynamic viscosity was taken as , and the kinematic viscosity was .

Table 1.
Simulated cases.
3.4. Computational Grid and Timestep
Structured computational grids with equidistant line spacing in the direction parallel to the membrane were created with OpenFoam blockMesh (an example is shown in Figure 3). Grid line clustering was employed near the membrane to properly resolve the boundary layer. The domain dimensions (width × height × depth) are denoted as . It was found that the grid resolution and the timestep had to be adjusted depending on the concentrations and electric field strength to resolve all relevant scales and maintain numerical stability. The domain dimensions as well as the number of cells and the computational timestep are listed in Table 2. The computational timestep is dictated by numerical stability and was found through trial and error. All simulations were carried out on a 24-core Dell Precision T5600 desktop computer. As in the work by Pimenta and Alves [15], a one-dimensional (1-D) solution was computed first. The 1-D solution was then extended in the second and third dimension and a 1% random disturbance was added to the concentrations to raise the initial disturbance amplitudes.

Figure 3.
Zoom-in of computational grid near membrane.

Table 2.
Details of computational grids and timestep.
For the baseline case, 2-D simulations with a wavy wall were carried out to investigate the effect of the membrane surface geometry on the current density (Figure 4). The 2-D roughness was periodic along the width of the domain. The average domain height, , width, and depth of the domain as well as the number of cells in all three directions were left unchanged. The wavy wall geometry was defined with splines in blockMesh. The amplitude of the roughness, , was either (for the majority of the cases; peak to peak) or peak to peak).

Figure 4.
Outline of computational domain with wavy wall.
3.5. Non-Dimensionalization
In the following, tildes identify dimensionless quantities. The voltage:
was made dimensionless with the thermal voltage, . Time was made dimensionless with the diffusion coefficient and the domain height:
Finally, the dimensionless current density is:
4. Results
4.1. Effect of Dimensionless Potential
As two representative cases for the baseline ( NaCl concentration) 2-D simulations, in Figure 5 and Figure 6, instantaneous visualizations of the anion concentration, vertical velocity, and electric potential are shown for dimensionless voltages of = 30 and 40. Initially, at = 0.0008 for = 30 and = 0.0004 for = 40, the solutions are very close to the 1-D initial condition. However, the vertical velocity iso-contours reveal that disturbances are growing as a result of the EKI. The instability sets in earlier for the higher voltage. Once the disturbance amplitude is above a certain threshold, periodic structures can be discerned above the membrane. The structures are also seen in the anion concentration but less so in the electrical potential. As time progresses, the disturbances are growing and for = 0.01 (= 30) and 0.0008 ( = 40) they are strong enough to result in a significant distortion of the electrical potential. The merging of neighboring structures results in the formation of larger structures such as seen for the last two time instances for = 40.
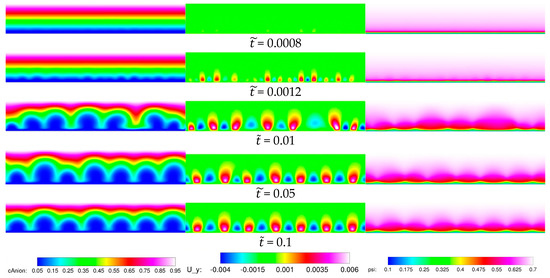
Figure 5.
Baseline 2-D case, = 30. Smooth membrane. From left to right: Anion concentration, vertical velocity in , electric potential in .
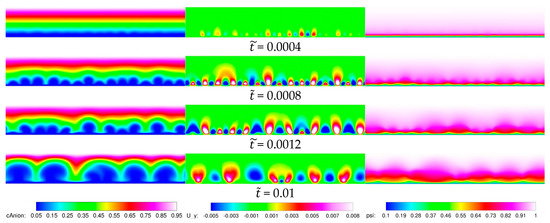
Figure 6.
Baseline 2-D case, = 40. Smooth membrane. From left to right: Anion concentration, vertical velocity in , electric potential in .
When the voltage is increased to = 120, the instability is stronger, the disturbances grow faster, and the structures show up much earlier (compare anion concentrations in Figure 5, Figure 6 and Figure 7). For = 0.001, smaller structures have coalesced into bigger structures in a process similar to vortex merging in fluid mechanics. For = 0.001 and = 0.1, the solution appears chaotic and much of the ion transfer across the height of the domain is accomplished by convection instead of diffusion.

Figure 7.
Baseline 2-D case ( concentration), = 120. Smooth membrane. Anion concentration.
In Figure 8, the current density, averaged over the surface area of the membrane, for six different voltages is plotted versus time. For voltages of = 10 and 20, the current density remains steady around , which suggests that no instability occurs. As the voltage is increased to = 30, the current density shoots up to around = 0.004. At this time instant, the near-membrane structures are growing strongly as a result of the primary instability. The current density then drops slowly to an average value of and remains essentially constant apart from a weak unsteadiness (Figure 8). Figure 5 reveals nearly steady structures (= 0.05 and 0.1). The structures increase the current density. An observed slight “wobble” of the structures leads to the minute oscillation of the current density. For voltages of = 40 and above, the current density also exhibits an initial overshoot and then settles on a lower value. The oscillations are, however, much stronger and more stochastic than for = 30. Based on a comparison of Figure 5 and Figure 6, it can be concluded that for , the structures become unsteady (in a fluid dynamics context, this would be referred to as the onset of secondary instability). In the simulations, the unsteadiness grows from truncation and machine roundoff errors. In experiments, slight imperfections of the experimental setup or environmental factors can provide the initial disturbances. The unsteadiness appears random (randomness would typically be associated with turbulence) and the amplitude of the unsteadiness grows when the electric field strength is increased.

Figure 8.
Baseline 2-D case. Area-averaged current density for the smooth membrane.
For the baseline case, a 3-D simulation was also performed for a voltage of = 120. Instantaneous visualizations for are shown in Figure 9. As for the 2-D simulation, the EKI leads to the appearance of large-scale structures that effectively transport ions from the membrane to the reservoir. The wavelengths of the dominant structures for the 2-D and 3-D simulation are similar (Figure 7 and Figure 9) and the initial rise of the current density is almost identical (Figure 10). Because of this close similarity and the high cost of the 3-D simulation, it was decided to exclusively employ 2-D simulations for the following investigations.
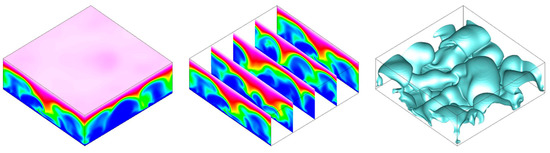
Figure 9.
Baseline 3-D case, = 120. Smooth membrane. Iso-contours of anion concentration and iso-surfaces of anion concentration of 0.2 for .

Figure 10.
Baseline case, = 120. Area-averaged current density for the smooth membrane.
The dimensionless current density, , obtained from the 2-D simulations was averaged for (Figure 11). Similar to experimental J-V curves (e.g., [9,23,24]), three distinct regimes can be observed for the smooth membrane. (i) For the Ohmic regime, the current density scales linearly with the applied voltage; (ii) in the limiting regime, the rate of increase of the current density decreases and the current density approaches an asymptotic value that is determined by the diffusion-limited transport of ions; and (iii) for the overlimiting regime, the current density increases again with the applied voltage. The existence of the overlimiting regime has been commonly attributed to electroconvection, which refers to the generation of vertical flow structures near the membrane. These structures, which are also observed in the present simulations for , facilitate a very effective convective mixing, which overcomes the diffusion-limited transport of ions. As a result, the current density increases dramatically. In the present simulations, the transition from the limiting regime to the overlimiting regime occurred at . A fine mesh simulation with a smooth membrane (black “x” in Figure 11) was carried out for . Since the current density for the coarse and fine mesh were almost identical, the conclusion was drawn that the present results are grid-converged.

Figure 11.
Baseline 2-D case. Time- and area-averaged current density.
4.2. Effect of Salt Concentration
The NaCl concentration was raised to and (simulating slightly and moderately brackish water), and finally (seawater). For the medium and high concentration cases, the grid extent was decreased by a factor of 10 in all directions. Since the number of cells was kept constant, this resulted in a factor of 10 increase of the grid resolution and the electric field strength. As the concentration was increased, the structures appeared earlier and their size was reduced. The same mesh dimensions ( were employed for the 1 and simulations (Figure 5, Figure 6 and Figure 7 and Figure 12a). For the latter, the initial structures were much smaller and appeared earlier. Similar observations can be made for the 100 and 400 concentration cases, which were both computed on a mesh (Figure 12b,c). This suggests that the onset of the instability is also (in addition to the voltage) dependent on the ion concentration and that the wavelength of the most unstable disturbances scales with the concentration.

Figure 12.
Two-dimensional simulations for = 120 and (a) , (b) , and (c) . Smooth membrane. Anion concentration.
4.3. Wavy Membrane
The main emphasis of the present investigation is on the effect of surface roughness on the current density. According to Rubinstein and Zaltzman [8], by making the membrane surface wavy, the initial wavelength of the disturbances can be controlled. All simulations with wavy membrane are for the baseline case with a concentration. It was decided to first try a membrane waviness with an amplitude of and a wavelength of . Iso-contours of the anion concentration for a dimensionless voltage of = 120 are shown in Figure 13. Compared to the smooth membrane results in Figure 7, the structures form much earlier and up to = 0.00016 have a pronounced periodicity that is dictated by the wall waviness. Especially for = 0.00012 and 0.00016, the structures are mushroom-shaped and similar in appearance to the structures resulting from buoyancy-driven instability. For , the initial periodicity is lost and the flow is more chaotic.

Figure 13.
Baseline 2-D case, = 120. Wavy membrane with and . Anion concentration.
The wall waviness raises the initial amplitudes of the disturbances, which dominate at the beginning. As the mode saturates and stops growing, other modes are still growing and reach comparable amplitudes, which makes the anion concentration field appear chaotic. The earlier onset of the EKI suggests that the waviness increased the initial amplitude of an unstable mode. The decision was made to lower the amplitude of the membrane waviness to and to investigate a broader range of wavelengths.
The wavelength of the waviness was varied from (40 periods per domain width; 12 grid intervals per period) to 20 (3 periods per domain width; 120 grid intervals per period). Instantaneous visualizations of the anion concentration for five cases are provided in Figure 14 and Figure 15. Despite the very small amplitude of the membrane waviness, for , , and , the wavelength of the primary structures resulting from the EKI is identical to the wavelength of the waviness (Figure 14). For and , the structures maintain the same wavelength up to = 0.00016, after which the flow becomes chaotic. For , the structures sustain their initial wavelength only up to = 0.0008, after which they split up in two (halving of wavelength). The halving of the wavelength implies that the higher harmonic, , grows more strongly.
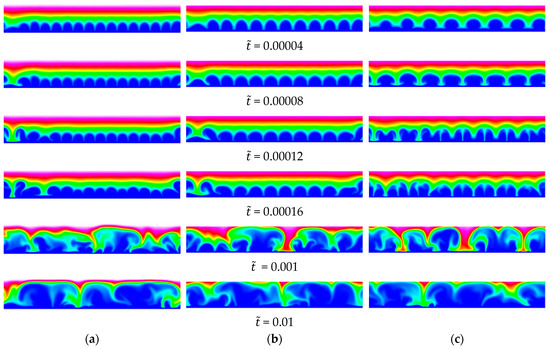
Figure 14.
Baseline 2-D case, = 120. Wavy membrane with and (a) , (b) and (c) . Anion concentration.
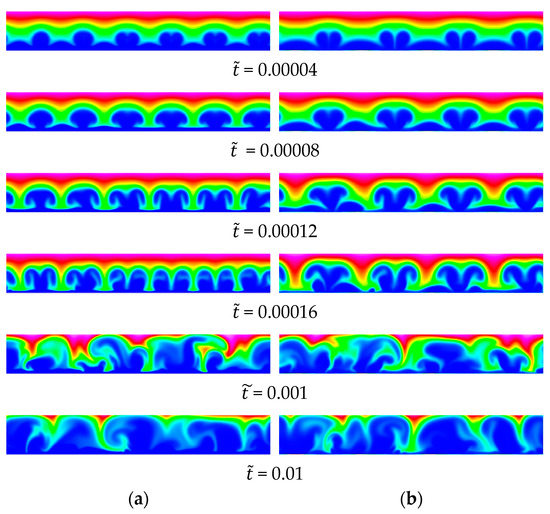
Figure 15.
Baseline 2-D case, = 120. Wavy membrane with and (a) and (b) . Anion concentration.
For the larger wavelengths of and , the visualizations for = 0.00004 provide clear evidence that, although the disturbance that is directly related to the forcing is present, higher harmonics grow more strongly (Figure 15). For , the wavelength is reduced to (and interestingly not ) for = 0.00016. This provides supporting evidence that the wavelength of the most amplified disturbance is close to . For , each structure splits up into two structures with a wavelength of approximately (subharmonic of ).
In Figure 16, the dimensionless current density for is plotted versus time. Compared to the smooth membrane (Figure 8), the initial overshoots occur earlier, which implies that the structures form sooner. For = 20, the current density is increased for , suggesting that the wavy membrane leads to the formation of structures for a voltage where no structures form for the smooth membrane. This means that the overlimiting regime starts at a lower voltage as also seen in Figure 11. Irrespective of the applied voltage, the average current density for is noticeably higher, which, in accordance with Rubinstein and Zaltzman [8], suggests that the waviness enhances the electroconvection. This is also seen in Figure 11 (compare the value for with the value for the smooth membrane).

Figure 16.
Baseline 2-D case. Area-averaged current density for the wavy membrane with and .
In Figure 17, the time- and area-averaged current density for the baseline 2-D case is plotted versus the wavelength, , of the membrane waviness. For very short wavelengths, , the current density matches that of the smooth membrane, , and the waviness (i.e., surface roughness) has no effect. For a minimal increase to (wavelength of the most amplified structures), the current density is strongly increased (). Even stronger maxima of the current density are observed for integer multiples of this wavelength, and . By introducing wavelengths that are incommensurate with this natural disturbance wavelength (similar to Saric et al. [18]), the growth of the disturbance waves can be reduced. As a result, the current density is reduced. Figure 17 displays a strong reduction of the current density for and .

Figure 17.
Baseline 2-D case, = 20 (transition from limiting to overlimiting regime). Time- and area-averaged current density.
5. Discussion
The overlimiting regime in electrodialysis (ED) is associated with the appearance of electroconvective structures near the membranes. The structures are caused by an electrokinetic instability (EKI). The present two-dimensional (2-D) simulations of a generic two-species problem with a smooth ion-selective membrane on the bottom and a water flow channel (reservoir) on the top indicate a dependence of the onset of the EKI on the applied voltage and concentration. With an increasing applied voltage and concentration, the instability becomes stronger and the structures form earlier. The initial perturbations were found to have a well-defined wavelength that is inversely related to the concentration. For very low ion concentrations (), the wavelength was of the order of . For ion concentrations of (moderately brackish water) and (seawater), the wavelength was in the order of .
For ED applications, it is desirable to delay the onset of the overlimiting regime. Similar to hydrodynamic stability problems in fluid mechanics, it was speculated that a favored natural most-amplified wavelength exists. Related research by Saric et al. [18] of the crossflow instability on swept wings has shown that by forcing a wavelength that is incommensurate with the wavelength of the most amplified natural disturbances, the appearance of nonlinear flow structures can be delayed. Whether the same idea can be transferred to ED applications was investigated. In the present simulations, disturbances were introduced through a 2-D periodic waviness of the membrane surface. It was found that a very minute waviness amplitude had a large effect on the initial growth of the disturbances and the time- and area-averaged current density. When the wavelength was , , or , in agreement with Rubinstein and Zaltzman [8], the current density increased and the overlimiting regime set in at a lower voltage. It was speculated that for these cases, the initial amplitude of the naturally occurring unstable mode was increased. Forcing with a wavelength of and , on the other hand, delayed the formation of the structures and the onset of the overlimiting regime. When the wavelength of the membrane waviness was below approximately , it had no effect on the current density and the smooth membrane result was recovered.
Membranes are never perfectly smooth. The proposed simulations show a clear dependence of the minimum voltage for the onset of the EKI and thus the overlimiting regime on the geometric surface properties of the membrane. The membrane fine structure (order of for low concentrations and for higher concentrations) has implications for the onset of the overlimiting regime and the current density. It was found that by adding fine-scale structures to the membrane surface, the onset of the instability can be controlled. Compared to Güler et al. [21], the wavelength is several orders of magnitude smaller and the control is based on a different physical mechanism. Whether such membrane surface modifications are feasible remains to be seen. Finally, the 2-D assumption was made for the present parameter study. The extension to 3-D will be explored in the future.
Author Contributions
Conceptualization and methodology, A.G., X.X., and P.X.; investigation, software, formal analysis, and visualization, A.M. and P.C.G.; writing—original draft, A.G. and P.X.; writing—review and editing, A.G., X.X., and P.X.; funding acquisition, project administration, and supervision, A.G. and P.X.
Funding
This work was supported by a New Mexico State University College of Engineering mini-grant, and the National Science Foundation Engineering Research Center ReNUWIt (EEC-1028968).
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
References
- Xu, P.; Cath, T.Y.; Robertson, A.P.; Reinhard, M.; Leckie, J.O.; Drewes, J.E. Critical Review of Desalination Concentrate Management, Treatment and Beneficial Use. Environ. Eng. Sci. 2013, 30, 502–514. [Google Scholar] [CrossRef]
- Xu, P.; Capito, M.; Cath, T.Y. Selective removal of arsenic and monovalent ions from brackish water reverse osmosis concentrate. J. Hazard. Mater. 2013, 260, 885–891. [Google Scholar] [CrossRef] [PubMed]
- Chehayeb, K.M.; Lienhard, J.H. Entropy Generation Analysis of Electrodialysis. Desalination 2017, 413, 184–198. [Google Scholar] [CrossRef]
- Campione, A.; Gurreri, L.; Ciofalo, M.; Micale, G.; Tamburini, A.; Cipollina, A. Electrodialysis for water desalination: A critical assessment of recent developments on process fundamentals, models and applications. Desalination 2018, 434, 121–160. [Google Scholar] [CrossRef]
- Rubinstein, I.; Staude, E.; Kedem, O. Role of the membrane surface in concentration polarization at ion-exchange membrane. Desalination 1988, 69, 101–114. [Google Scholar] [CrossRef]
- Demekhin, E.A.; Shapar, E.M.; Lapchenko, V.V. Initiation of electroconvection in semipermeable electric membranes. Dokl. Phys. 2008, 53, 450–453. [Google Scholar] [CrossRef]
- Rubinstein, I.; Zaltzman, B. Electro-convective versus electroosmotic instability in concentration polarization. Adv. Colloid Interface Sci. 2007, 134, 190–200. [Google Scholar] [CrossRef] [PubMed]
- Rubinstein, I.; Zaltzman, B. Electro-osmotically induced convection at a permselective membrane. Phys. Rev. E 2000, 62, 2238. [Google Scholar] [CrossRef]
- Chang, H.-C.; Yossifon, G.; Demekhin, E.A. Nanoscale Electrokinetics and Microvortices: How Microhydrodynamics Affects Nanofluidic Ion Flux. Ann. Rev. Fluid Mech. 2012, 44, 401–426. [Google Scholar] [CrossRef]
- Yossifon, G.; Mushenheim, P.; Chang, H.-C. Controlling the nanoslot overlimiting current by varying the micro-chamber depth. Europhys. Lett. 2010, 90, 64004. [Google Scholar] [CrossRef]
- Kim, Y.; Walker, W.S.; Lawler, D.F. Electrodialysis with spacers: Effects of variation and correlation of boundary layer thickness. Desalination 2011, 274, 54–63. [Google Scholar] [CrossRef]
- Druzgalski, C.L.; Andersen, M.B.; Mani, A. Direct numerical simulation of electroconvective instability and hydrodynamic chaos near an ion-selective surface. Phys. Fluids 2013, 25, 110804. [Google Scholar] [CrossRef]
- Zourmand, Z.; Faridirad, F.; Kasiri, N.; Mohammadi, T. Mass transfer modeling of desalination through an electrodialysis cell. Desalination 2015, 359, 41–51. [Google Scholar] [CrossRef]
- Enciso, R.; Delgadillo, J.A.; Dominguez, O.; Rodríguez-Torres, I. Analysis and validation of the hydrodynamics of an electrodialysis cell using computational fluid dynamics. Desalination 2017, 408, 127–132. [Google Scholar] [CrossRef]
- Pimenta, F.; Alves, M.A. Numerical simulation of electrically-driven flows using OpenFOAM. arXiv 2018, arXiv:Physics/1802.02843v2. [Google Scholar]
- Demekhin, E.A.; Nikitin, N.V.; Shelistov, V.S. Three-dimensional coherent structures of electrokinetic instability. Phys. Rev. E 2014, 90, 013031. [Google Scholar]
- Druzgalski, C.L.; Mani, A. Statistical analysis of electroconvection near an ion-selective membrane in the highly chaotic regime. Phys. Rev. Fluids 2016, 1, 073601. [Google Scholar] [CrossRef]
- Saric, W.S.; Carpenter, A.L.; Reed, H.L. Passive control of transition in three-dimensional boundary layers, with emphasis on discrete roughness elements. Philos. Trans. R. Soc. A 2011, 369, 1352–1364. [Google Scholar] [CrossRef]
- Embacher, M.; Fasel, H.F. Direct numerical simulations of laminar separation bubbles: Investigation of absolute instability and active flow control of transition to turbulence. J. Fluid Mech. 2014, 747, 141–185. [Google Scholar] [CrossRef]
- Walsh, M.J. Riblets as a viscous drag reduction technique. AIAA J. 1983, 21, 485–486. [Google Scholar] [CrossRef]
- Güler, E.; Elizen, R.; Saakes, M.; Nijmeijer, K. Micro-structured membranes for electricity generation by reverse electrodialysis. J. Membr. Sci. 2014, 458, 136–148. [Google Scholar] [CrossRef]
- Vitagliano, V.; Lyons, P.A. Diffusion Coefficients for Aqueous Solutions of Sodium Chloride and Barium Chloride. J. Am. Chem. Soc. 1956, 78, 1549–1552. [Google Scholar] [CrossRef]
- Rubinstein, I.; Shtilman, L. Voltage against current curves of cation exchange membrane. J. Chem. Soc. Faraday Trans. 2 Mol. Chem. Phys. 1979, 75, 231–246. [Google Scholar] [CrossRef]
- Krol, J.J.; Wessling, M.; Strathmann, H. Concentration polarization with monopolar ion exchange membranes: Current-voltage curves and water dissociation. J. Membr. Sci. 1999, 162, 145–154. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).