Tsunami Intrusion and River Ice Movement
Abstract
1. Introduction
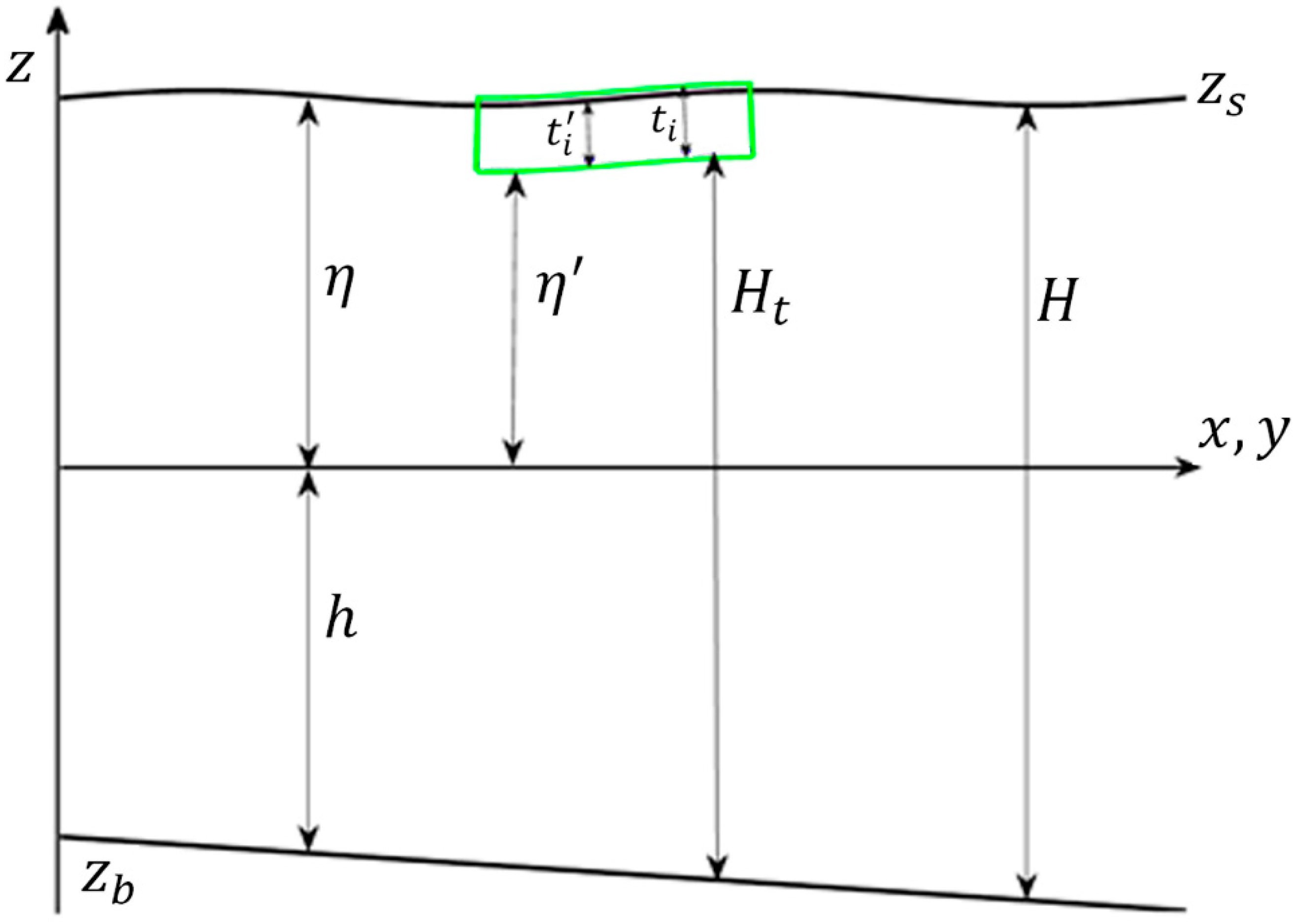
2. Model Formulation
2.1. Hydrodynamics Equations
2.2. Numerical Method
2.3. Ice Dynamic Model
3. Model Validations
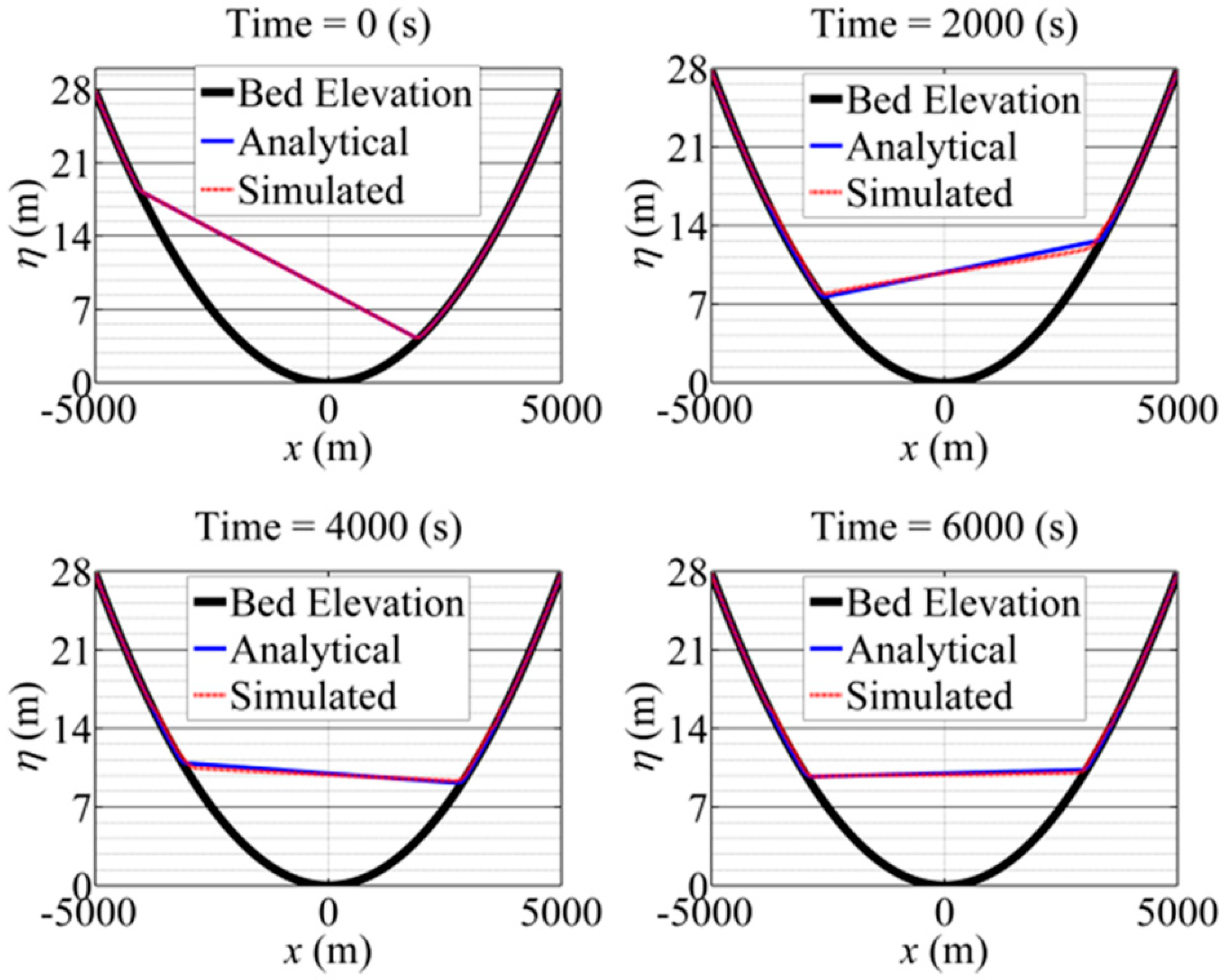
3.1. Case I: Oscillation in a Parabolic Container
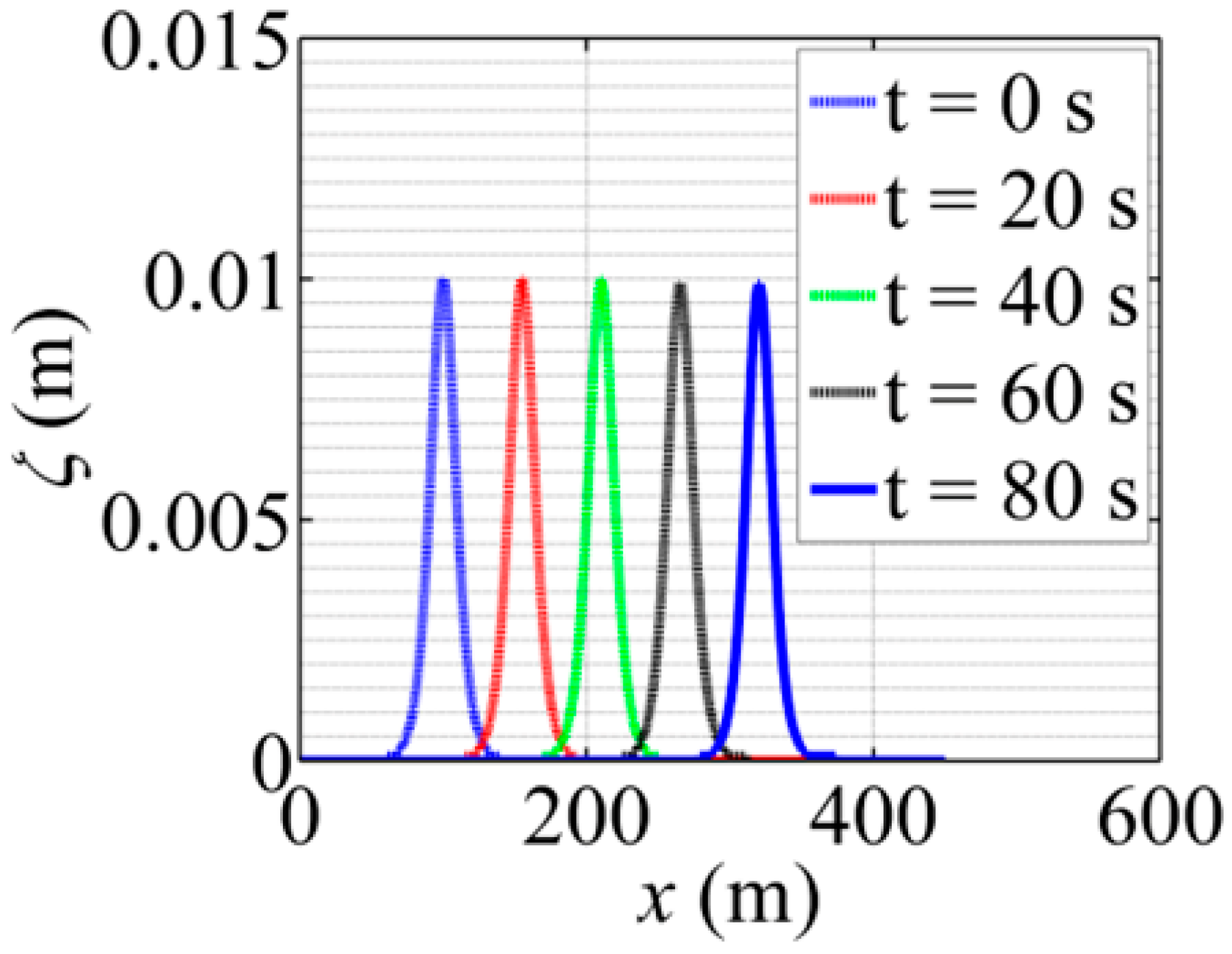
3.2. Case II: Conservation of Solitary Wave Propagation
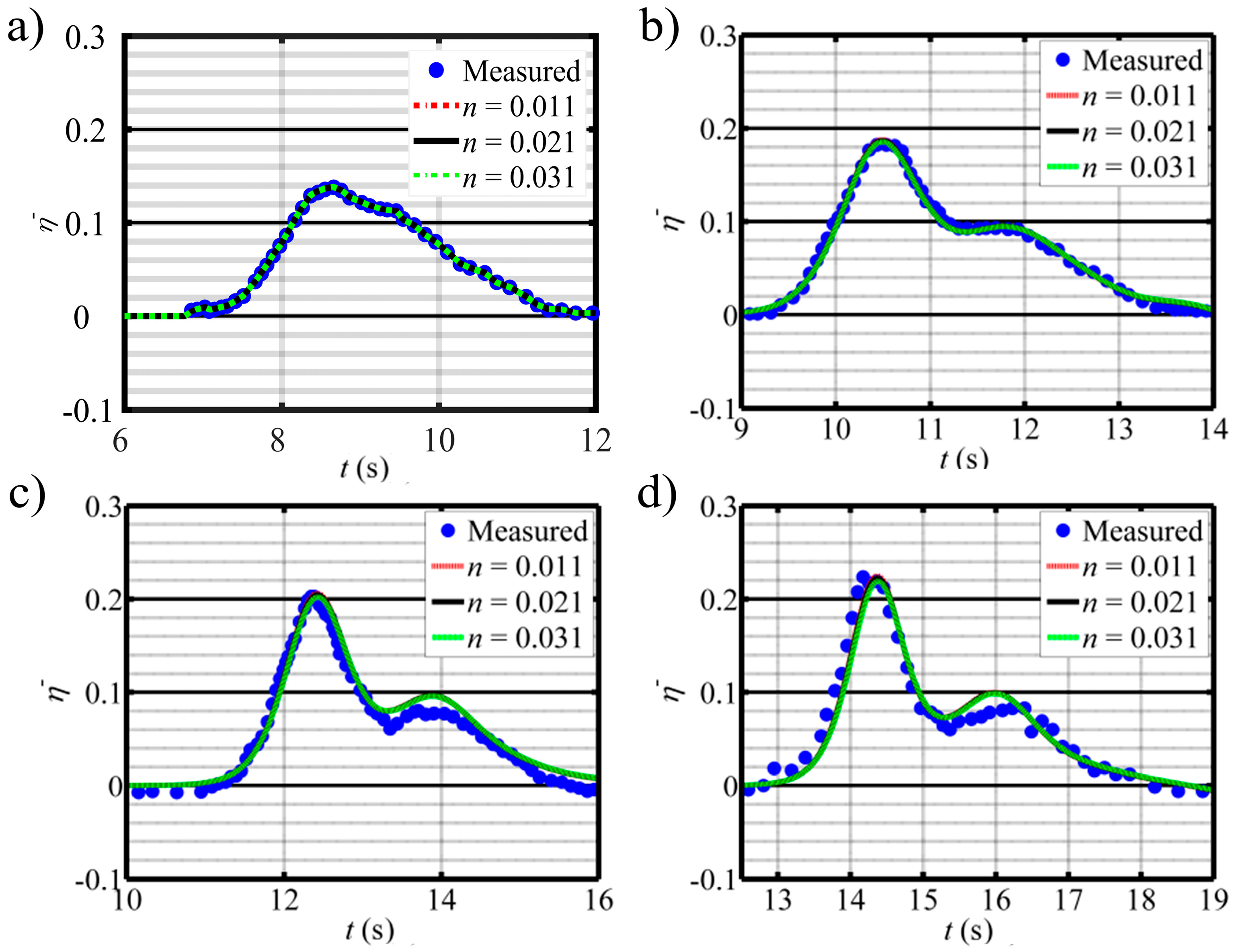
3.3. Case III: Tsunami Wave in a Laboratory Flume
4. Model Applications
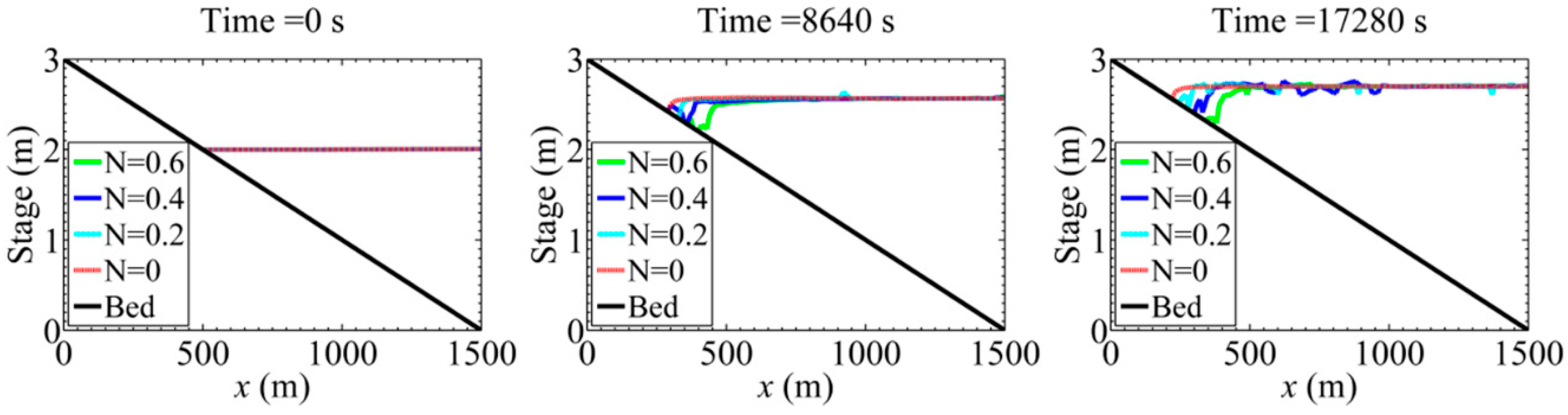
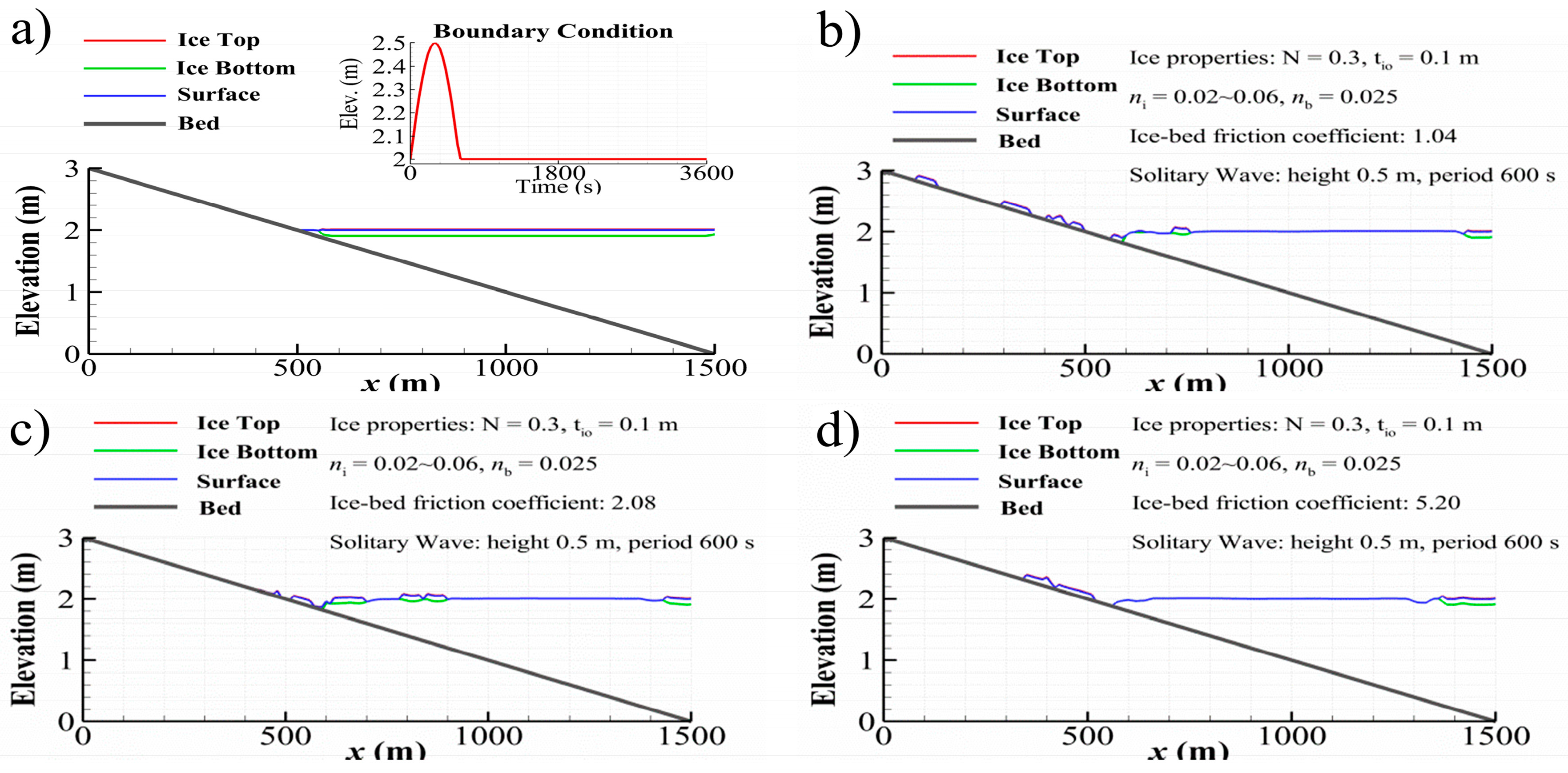
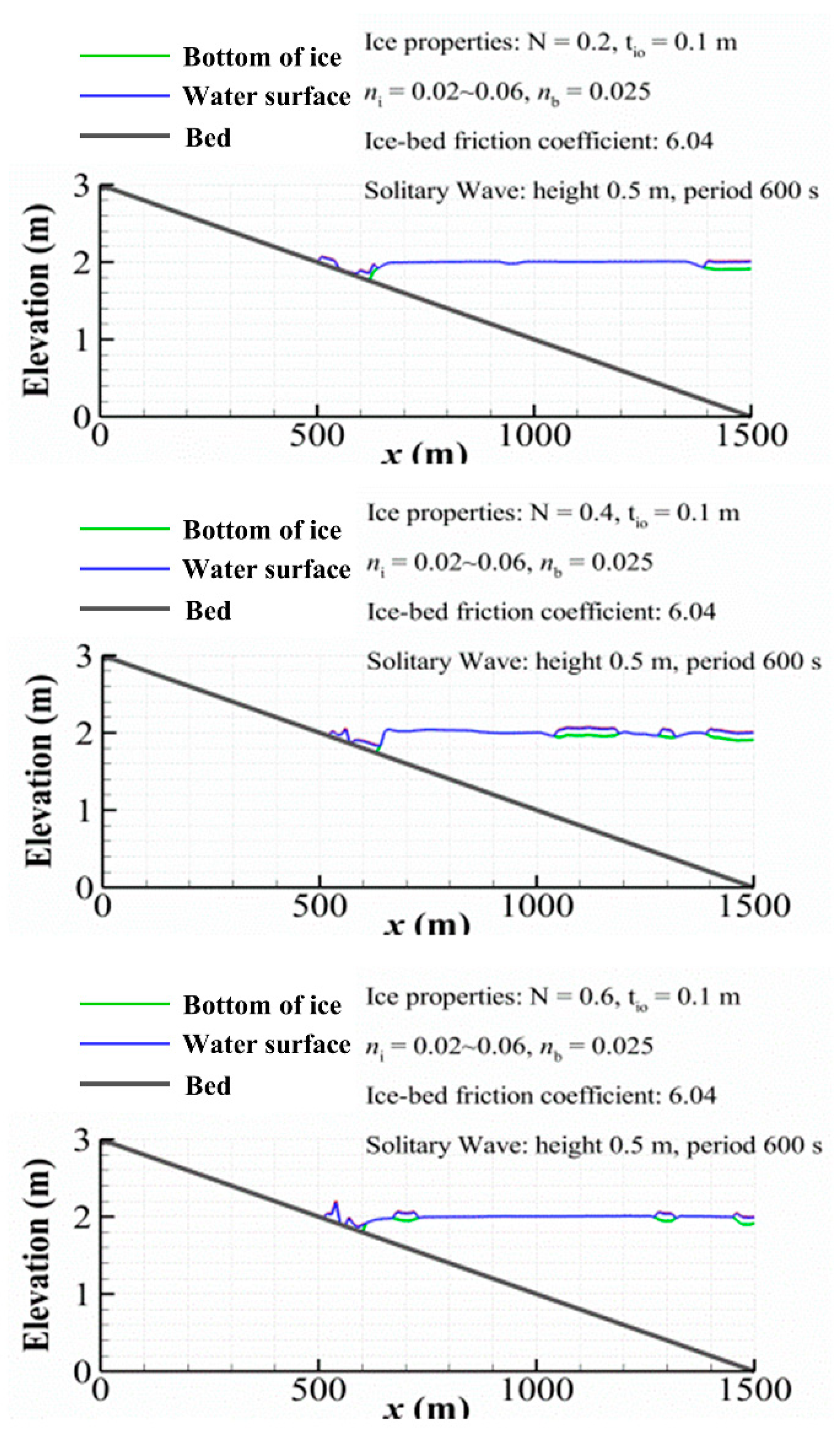
4.1. Ice Effect on Tsunami Wave Propagations over a Beach
4.2. Ice Deposition on the Beach
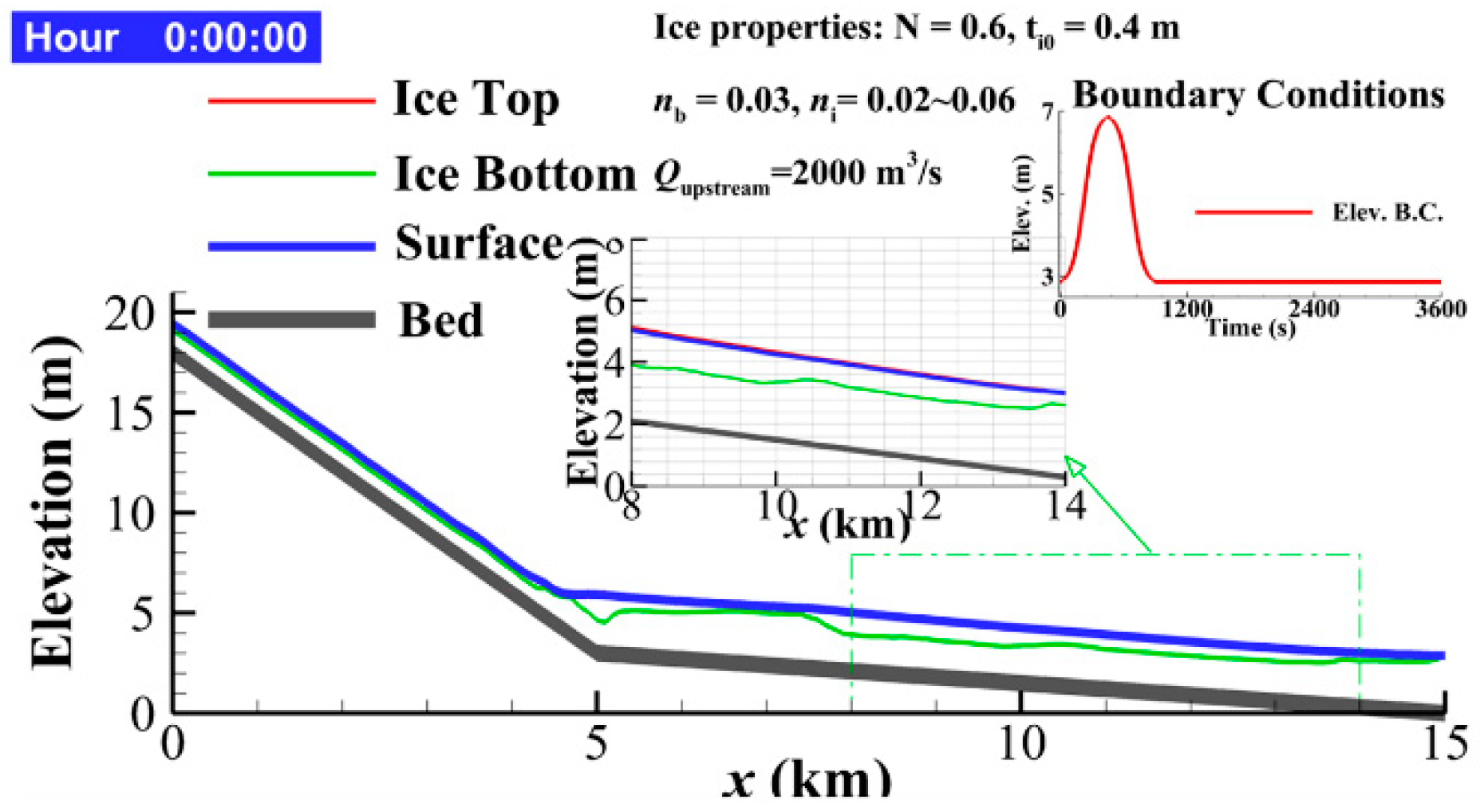
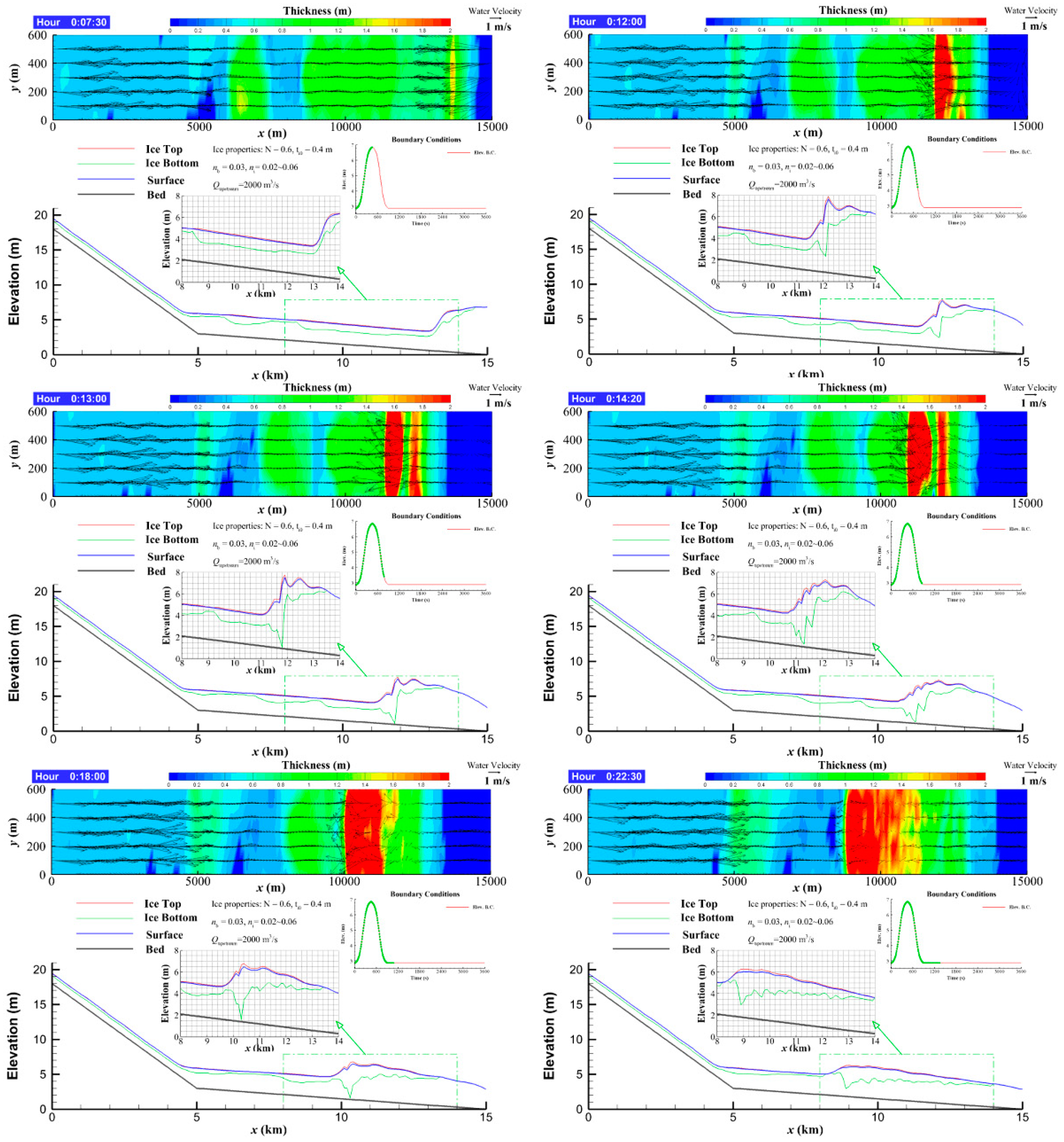
4.3. Ice jamming in River Channel with Incoming Tsunami Wave
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Peregrine, D. Long waves on a beach. J. Fluid Mech. 1967, 27, 815–827. [Google Scholar] [CrossRef]
- Madsen, P.A.; Murray, R.; Sørensen, O.R. A new form of the Boussinesq equations with improved linear dispersion characteristics. Coast. Eng. 1991, 15, 371–388. [Google Scholar] [CrossRef]
- Nwogu, O. Alternative form of Boussinesq equations for nearshore wave propagation. J. Waterwy. Port Coast. Ocean. Eng. 1993, 119, 618–638. [Google Scholar] [CrossRef]
- Wei, G.; Kirby, J.T. Time-dependent numerical code for extended Boussinesq equations. J. Waterway. Port Coast. Ocean. Eng. 1995, 121, 251–261. [Google Scholar] [CrossRef]
- Madsen, P.A.; Schäffer, H.A. Higher–order Boussinesq–type equations for surface gravity waves: Derivation and analysis. Philos. Trans. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 1998, 356, 3123–3181. [Google Scholar] [CrossRef]
- Agnon, Y.; Madsen, P.A.; Schäffer, H. A new approach to high-order Boussinesq models. J. Fluid Mech. 1999, 399, 319–333. [Google Scholar] [CrossRef]
- Zou, Z.L. Higher order Boussinesq equations. Ocean. Eng. 1999, 26, 767–792. [Google Scholar] [CrossRef]
- Gobbi, M.F.; Kirby, J.T.; Wei, G.E. A fully nonlinear Boussinesq model for surface waves. Part 2. Extension to O(kh)4. J. Fluid Mech. 2000, 405, 181–210. [Google Scholar] [CrossRef]
- Madsen, P.A.; Fuhrman, D.R. High-order Boussinesq-type modelling of nonlinear wave phenomena in deep and shallow water. In Advances in Numerical Simulation of Nonlinear Water Waves; World Scientific: Singapore, 2010; Volume 11, pp. 245–285. [Google Scholar]
- Shi, F.; Kirby, J.T.; Harris, J.C.; Geiman, J.D.; Grilli, S.T. A high-order adaptive time-stepping TVD solver for Boussinesq modeling of breaking waves and coastal inundation. Ocean. Model. 2012, 43, 36–51. [Google Scholar] [CrossRef]
- Debsarma, S.; Das, K.P.; Kirby, J.T. Fully nonlinear higher-order model equations for long internal waves in a two-fluid system. J. Fluid Mech. 2010, 654, 281–303. [Google Scholar] [CrossRef]
- Fang, K.; Zou, Z.; Dong, P.; Liu, Z.; Gui, Q.; Yin, J. An efficient shock capturing algorithm to the extended Boussinesq wave equations. Appl. Ocean. Res. 2013, 43, 11–20. [Google Scholar] [CrossRef]
- Yao, Y.; Huang, Z.; Monismith, S.G.; Lo, E.Y.M. 1DH Boussinesq modeling of wave transformation over fringing reefs. Ocean. Eng. 2012, 47, 30–42. [Google Scholar] [CrossRef]
- Gaeta, M.; Bonaldo, D.; Samaras, A.; Carniel, S.; Archetti, R. Coupled wave-2D hydrodynamics modeling at the Reno River Mouth (Italy) under climate change scenarios. Water 2018, 10, 1380. [Google Scholar] [CrossRef]
- Petti, M.; Bosa, S.; Pascolo, S. Lagoon sediment dynamics: A coupled model to study a medium-term silting of tidal channels. Water 2018, 10, 569. [Google Scholar] [CrossRef]
- Li, Y.; Song, Z.; Peng, G.; Fang, X.; Li, R.; Chen, P.; Hong, H. Modeling hydro-dynamics in a Harbor Area in the Daishan Island, China. Water 2019, 11, 192. [Google Scholar] [CrossRef]
- Brunt, K.M.; Okal, E.A.; MacAyeal, D.R. Antarctic ice-shelf calving triggered by the Honshu (Japan) earthquake and tsunami, March 2011. J. Glaciol. 2011, 57, 785–788. [Google Scholar] [CrossRef]
- Kaistrenko, V.; Razjigaeva, N.; Kharlamov, A.; Shishkin, A. Manifestation of the 2011 Great Tohoku Tsunami on the coast of the Kuril Islands: A tsunami with Ice. Pure Appl. Geophys. 2013, 170, 1103–1114. [Google Scholar] [CrossRef]
- Shen, H.T.; Wang, D.S.; Lal, A.W. Numerical simulation of river ice processes. J. Cold Reg. Eng. 1995, 9, 107–118. [Google Scholar] [CrossRef]
- Shen, H.T.; Su, J.; Liu, L. SPH simulation of river ice dynamics. J. Comput. Phys. 2000, 165, 752–770. [Google Scholar] [CrossRef]
- Knack, I.M.; Shen, H.T. A numerical model study on Saint John River ice breakup. Can. J. Civ. Eng. 2016, 45, 817–826. [Google Scholar] [CrossRef]
- Shen, H.T.; Liu, L. Shokotsu River ice jam formation. Cold Reg. Sci. Technol. 2003, 37, 35–49. [Google Scholar] [CrossRef]
- Kolerski, T.; Shen, H.T. Possible effects of the 1984 St. Clair River ice jam on bed changes. Can. J. Civ. Eng. 2015, 42, 696–703. [Google Scholar] [CrossRef]
- Madsen, P.A.; Sørensen, O.R. A new form of the Boussinesq equations with improved linear dispersion characteristics. Part 2. A slowly-varying bathymetry. Coast. Eng. 1992, 18, 183–204. [Google Scholar] [CrossRef]
- Tonelli, M.; Petti, M. Shock-capturing Boussinesq model for irregular wave propagation. Coast. Eng. 2012, 61, 8–19. [Google Scholar] [CrossRef]
- Liang, Q.; Borthwick, A.G.L. Adaptive quadtree simulation of shallow flows with wet-dry fronts over complex topography. Comput. Fluids 2009, 38, 221–234. [Google Scholar] [CrossRef]
- Tonelli, M.; Petti, M. Numerical simulation of wave overtopping at coastal dikes and low-crested structures by means of a shock-capturing Boussinesq model. Coast. Eng. 2013, 79, 75–88. [Google Scholar] [CrossRef]
- Toro, E.F. Riemann Solvers and Numerical Methods for Fluid Dynamics: A Practical Introduction; Springer: Berlin/Heidelberg, Germany, 2009; Volume 16, p. 724. [Google Scholar]
- Erduran, K.; Ilic, S.; Kutija, V. Hybrid finite-volume finite-difference scheme for the solution of Boussinesq equations. Int. J. Numer. Methods Fluids 2005, 49, 1213–1232. [Google Scholar] [CrossRef]
- Shen, H.T. Mathematical modeling of river ice processes. Cold Reg. Sci. Technol. 2010, 62, 3–13. [Google Scholar] [CrossRef]
- Ji, S.-Y.; Shen, H.T.; Wang, Z.-L.; Shen, H.H.; Yue, Q. A viscoelastic-plastic constitutive model with Mohr-Coulomb yielding criterion for sea ice dynamics. Acta Oceanol. Sin. Engl. Ed. 2005, 24, 54. [Google Scholar]
- Orszaghova, J.; Borthwick, A.G.; Taylor, P.H. From the paddle to the beach—A Boussinesq shallow water numerical wave tank based on Madsen and Sørensen’s equations. J. Comput. Phys. 2012, 231, 328–344. [Google Scholar] [CrossRef]
- Yasuda, H. One-dimensional study on propagation of tsunami wave in river channels. J. Hydraul. Eng. 2010, 136, 93–105. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pan, J.; Shen, H.T. Tsunami Intrusion and River Ice Movement. Water 2019, 11, 1290. https://doi.org/10.3390/w11061290
Pan J, Shen HT. Tsunami Intrusion and River Ice Movement. Water. 2019; 11(6):1290. https://doi.org/10.3390/w11061290
Chicago/Turabian StylePan, Jiajia, and Hung Tao Shen. 2019. "Tsunami Intrusion and River Ice Movement" Water 11, no. 6: 1290. https://doi.org/10.3390/w11061290
APA StylePan, J., & Shen, H. T. (2019). Tsunami Intrusion and River Ice Movement. Water, 11(6), 1290. https://doi.org/10.3390/w11061290





