Managing Municipal Wastewater Treatment to Control Nitrous Oxide Emissions from Tidal Rivers
Abstract
1. Introduction
2. Materials and Methods
2.1. Water Quality Simulation Model
2.1.1. The Flow Model
2.1.2. Transport Model
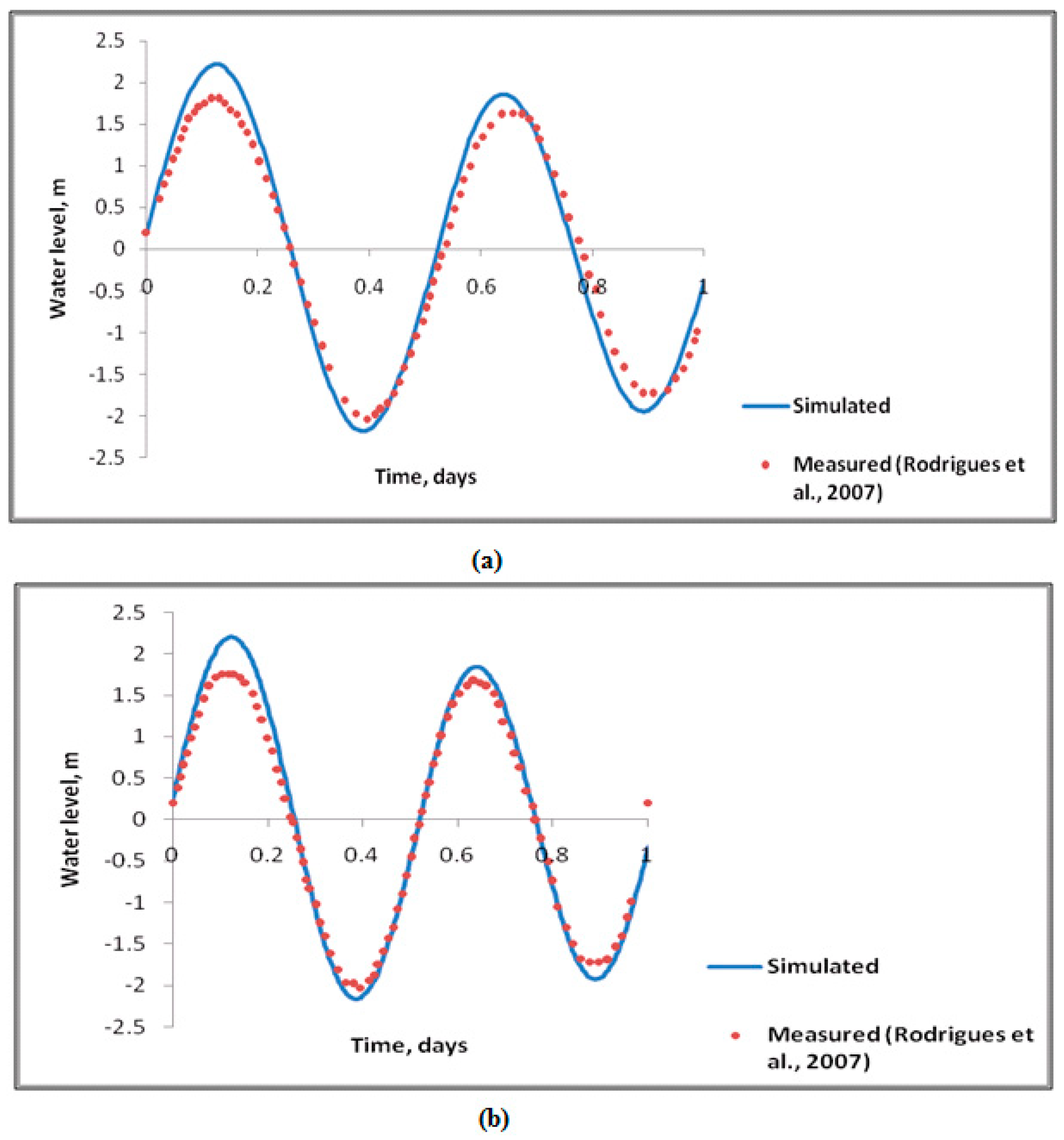
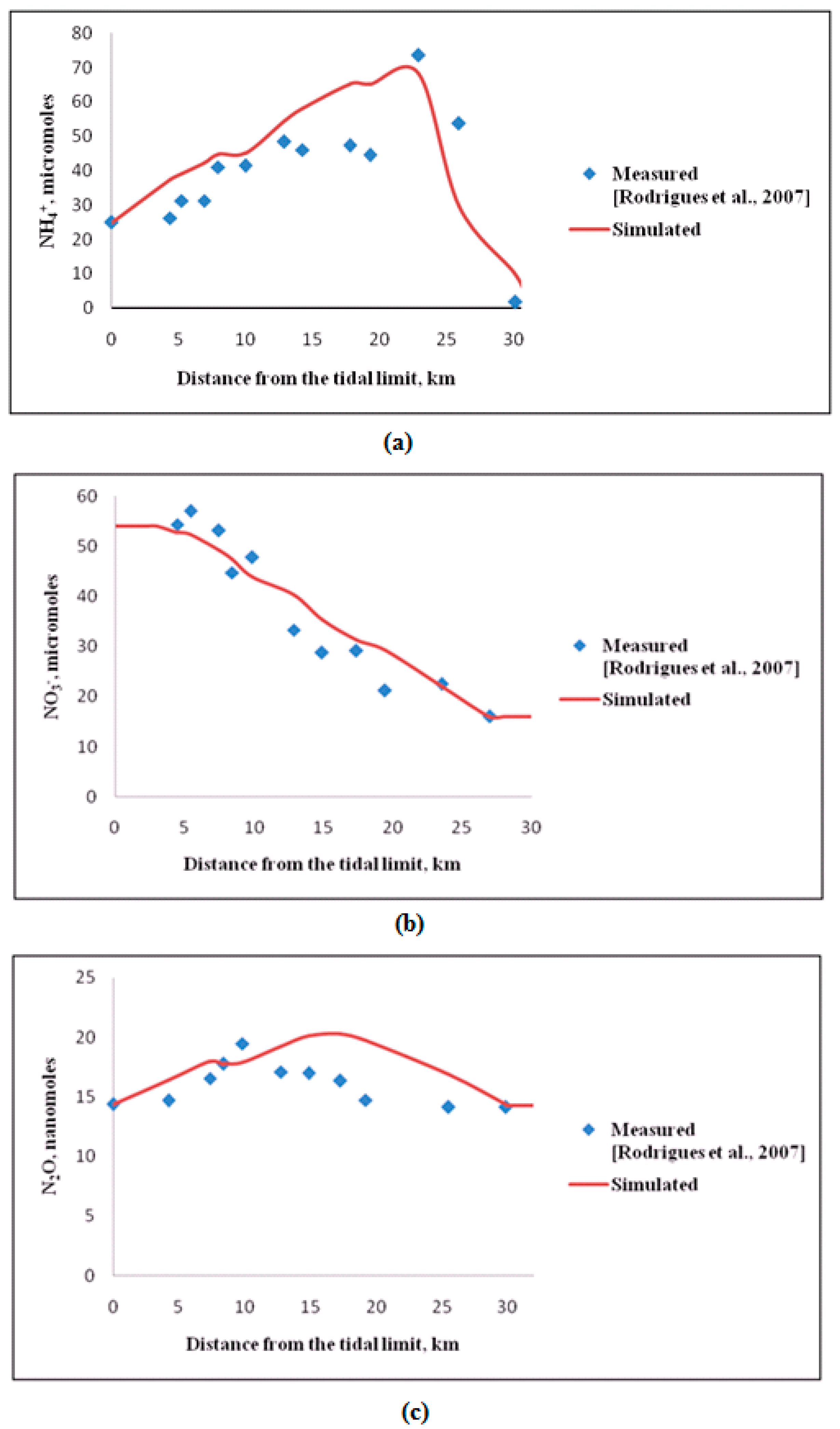
2.2. Validation of the Simulation Model
2.3. Optimisation Models
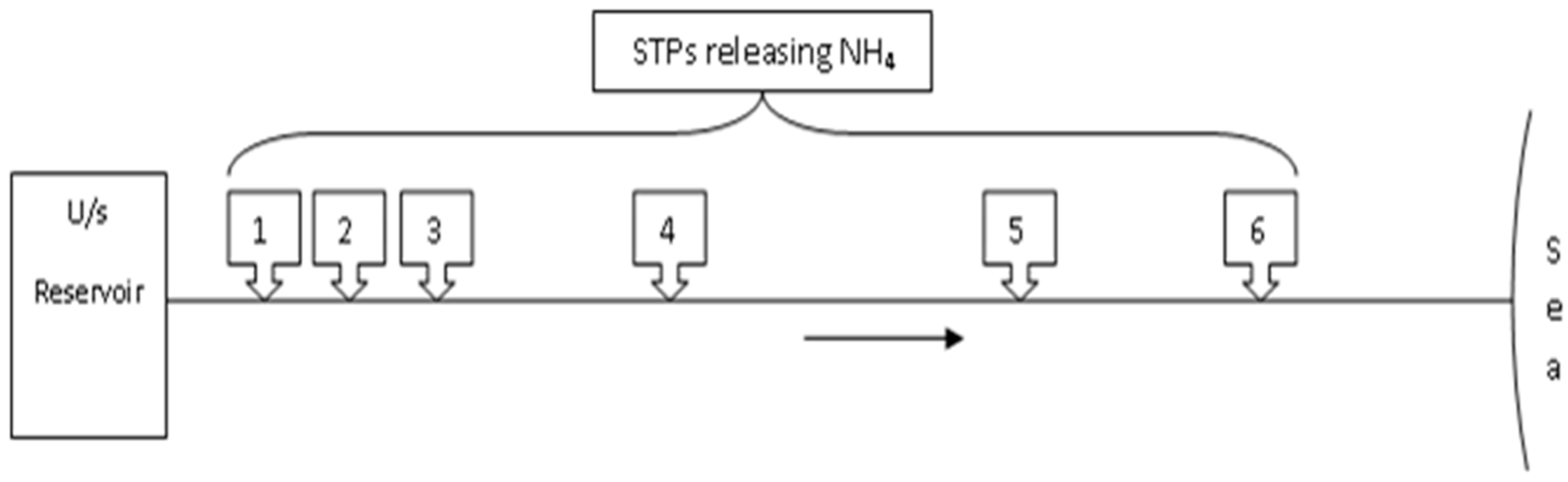
2.3.1. Management Model-I (MM-I)
Decision Vector
Objective Function
Constraints
- Constraint on emission: The total amount of N2O emission from the entire river during the operation horizon, should be lesser than a maximum specified value, .is calculated as summation of N2O emissions at each location i along the length of the river over each time step .where, = rate of nitrogen emission from a single reach of length Δx in mg/L/s during the time period of Δt, = surface area of the reach = and hi,t = average depth in the reach. is calculated using the Equation (12).
- Simulation constraint: The concentration of N2O in any reach “i” at any instant “t” depends on upstream release of water, tidal variation, channel characteristics, and concentration of ammonium in the effluent from STPs discharging into the river.
- Treatment limits: There may be upper and lower limits for treatment fraction at STPs. Lower limit represents a completely untreated case, and the upper limit represents a maximum possible efficiency of ammonium removal in STP based on practical conditions [40].
2.3.2. Management Model-II (MM-II)
Decision Vector
Objective Function
Constraints
- Constraint on emission
- Simulation constraint
- Treatment limits
- Reservoir release constraint: Upstream reservoir release at any time should not be lesser than a minimum value, Qmin and not more than a maximum value, Qmax.
2.3.3. Management Model-III (MM-III)
Decision Vector
Objective Function
Constraints
3. Results and Discussion
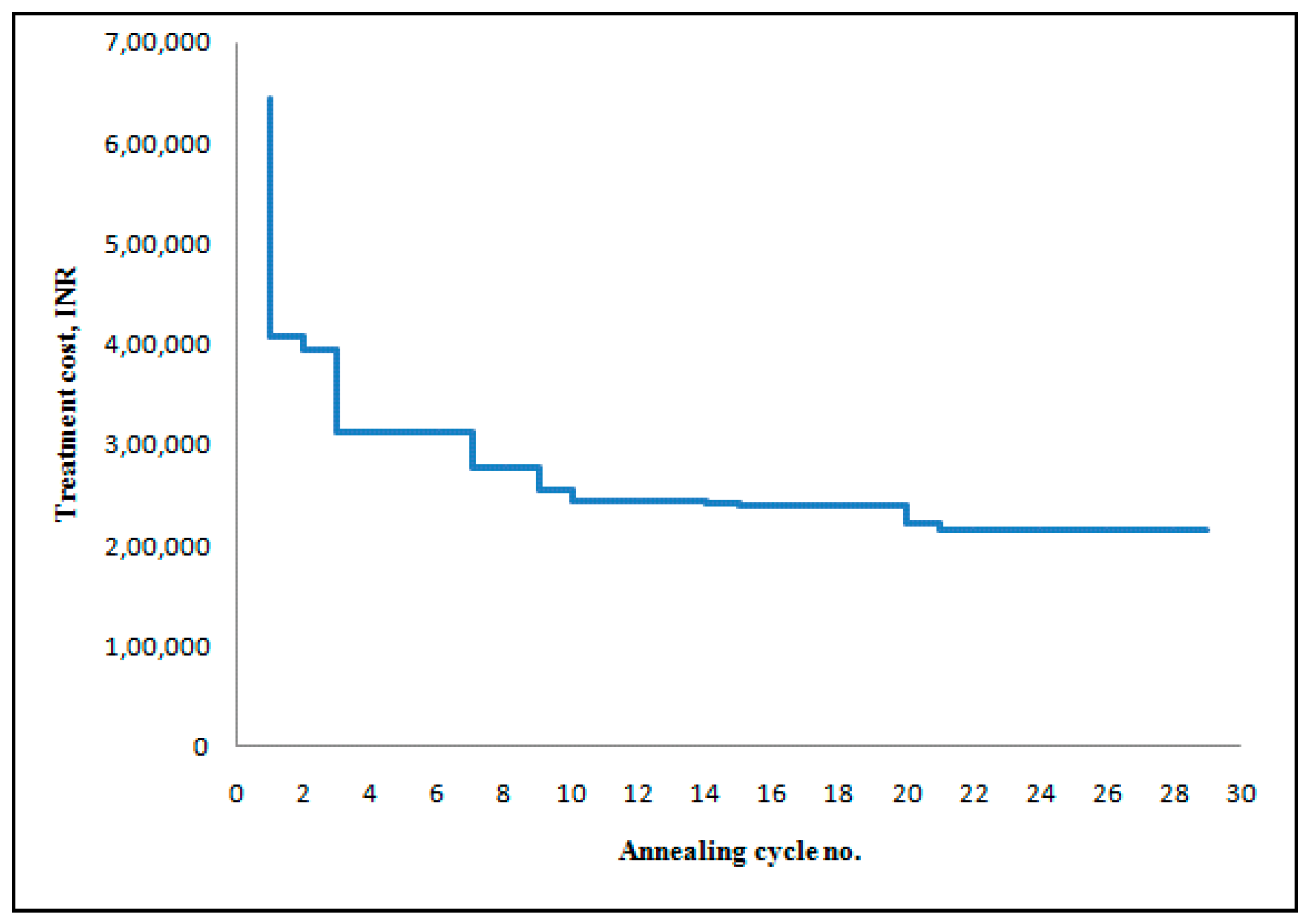
3.1. Illustration of Manage Model-I (MM-I)
Case 1: Constant treatment level throughout the time period
Case 2: Different treatment levels during high and low tides
Case 3: Effect of upstream release on optimal treatment cost
3.2. Illustration of Manage Model-II (MM-II): Case-IV and Case-V
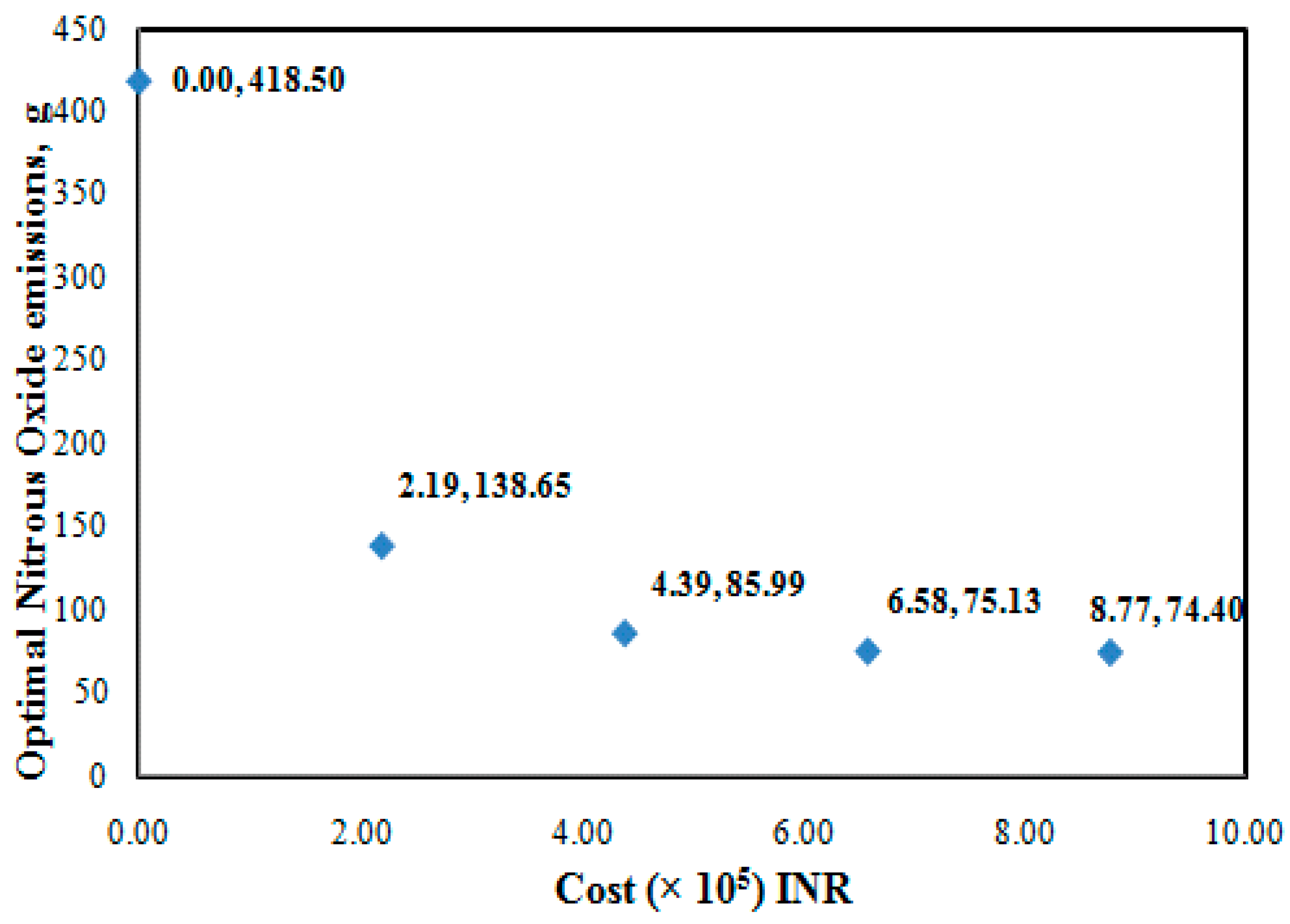
3.3. Illustration of Manage Model-III (MM-III)
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Forster, P.; Ramaswamy, V.; Artaxo, P.; Berntsen, T.; Betts, R.; Fahey, D.W.; Haywood, J.; Lean, J.; Lowe, D.C.; Myhre, G.; et al. Changes in Atmospheric Constituents and in Radiative Forcing; Solomon, S., Qin, D., Manning, M., Marquis, M., Averyt, K., Tignor, M.M.B., LeRoy Miller, H., Jr., Chen, Z., Eds.; Cambridge University Press: Cambridge, UK, 2007; p. 234. [Google Scholar]
- Galloway, J.N. The global nitrogen cycle: Changes and consequences. Environ. Pollut. 1998, 102 (Suppl. 1), 15–24. [Google Scholar] [CrossRef]
- Battle, M.; Bender, M.; Sowers, T.; Tans, P.; Butler, J.; Elkins, J.; Ellis, J.; Conway, T.; Zhang, N.; Lang, P. Atmospheric gas concentrations over the past century measured in air from firn at the South Pole. Nature 1996, 383, 231. [Google Scholar] [CrossRef]
- Steinfeld, H.; Gerber, P.; Wassenaar, T.; Castel, V.; Rosales, M.; De Haan, C. Livestock’s Long Shadow—Environmental Issues and Options; Food and Agriculture Organization (FAO) of the United Nations: Rome, Italy, 2006. [Google Scholar]
- Nitrous Oxide Emissions. U.S. Environmental Protection Agency. 2016. Available online: https://www.epa.gov/ghgemissions/overview-greenhouse-gases#nitrous-oxide (accessed on 11 April 2019).
- Kumar, S.; Smith, S.R.; Fowler, G.; Velis, C.; Kumar, S.J.; Arya, S.; Rena; Kumar, R.; Cheeseman, C. Challenges and opportunities associated with waste management in India. R. Soc. Open Sci. 2017, 4, 160764. [Google Scholar] [CrossRef] [PubMed]
- McMahon, P.; Dennehy, K. N2O emissions from a nitrogen-enriched river. Environ. Sci. Technol. 1999, 33, 21–25. [Google Scholar] [CrossRef]
- Marzadri, A.; Tonina, D.; Bellin, A.; Tank, J. A hydrologic model demonstrates nitrous oxide emissions depend on streambed morphology. Geophys. Res. Lett. 2014, 41, 5484–5491. [Google Scholar] [CrossRef]
- Beaulieu, J.J.; Nietch, C.T.; Young, J.L. Controls on nitrous oxide production and consumption in reservoirs of the Ohio River Basin. J. Geophys. Res. Biogeosci. 2015, 120, 1995–2010. [Google Scholar] [CrossRef]
- Middelburg, J.J.; Nieuwenhuize, J.; Iversen, N.; Høgh, N.; De Wilde, H.; Helder, W.; Seifert, R.; Christof, O. Methane distribution in European tidal estuaries. Biogeochemistry 2002, 59, 95–119. [Google Scholar] [CrossRef]
- Rajkumar, A.N.; Barnes, J.; Ramesh, R.; Purvaja, R.; Upstill-Goddard, R. Methane and nitrous oxide fluxes in the polluted Adyar River and estuary, SE India. Mar. Pollut. Bull. 2008, 56, 2043–2051. [Google Scholar] [CrossRef]
- Liu, X.-L.; Bai, L.; Wang, Z.-L.; Li, J.; Yue, F.-J.; Li, S.-L. Nitrous oxide emissions from river network with variable nitrogen loading in Tianjin, China. J. Geochem. Explor. 2015, 157, 153–161. [Google Scholar] [CrossRef]
- Burgos, M.; Sierra, A.; Ortega, T.; Forja, J. Anthropogenic effects on greenhouse gas (CH4 and N2O) emissions in the Guadalete River Estuary (SW Spain). Sci. Total Environ. 2015, 503, 179–189. [Google Scholar] [CrossRef]
- Wang, L.; Zhang, G.; Zhu, Z.; Li, J.; Liu, S.; Ye, W.; Han, Y. Distribution and sea-to-air flux of nitrous oxide in the East China Sea during the summer of 2013. Cont. Shelf Res. 2016, 123, 99–110. [Google Scholar] [CrossRef]
- He, Y.; Wang, X.; Chen, H.; Yuan, X.; Wu, N.; Zhang, Y.; Yue, J.; Zhang, Q.; Diao, Y.; Zhou, L. Effect of watershed urbanization on N2O emissions from the Chongqing metropolitan river network, China. Atmos. Environ. 2017, 171, 70–81. [Google Scholar] [CrossRef]
- Kroeze, C.; Seitzinger, S.P. Nitrogen inputs to rivers, estuaries and continental shelves and related nitrous oxide emissions in 1990 and 2050: A global model. Nutr. Cycl. Agroecosyst. 1998, 52, 195–212. [Google Scholar] [CrossRef]
- Denman, K.L.; Brasseur, G.; Chidthaisong, A.; Ciais, P.; Cox, P.M.; Dickinson, R.E.; Hauglustaine, D.; Heinze, C.; Holland, E.; Jacob, D.; et al. Couplings Between Changes in the Climate System and Biogeochemistry. Chapter 7; IPCC Working Group I, National Oceanic and Atmospheric Administration NOAA, DSRC R/AL/8, 325 Broadway, Boulder, CO 80305 (United States); Cambridge University Press: Cambridge, UK, 2007; pp. 499–587. [Google Scholar]
- Musenze, R.S.; Werner, U.; Grinham, A.; Udy, J.; Yuan, Z. Methane and nitrous oxide emissions from a subtropical estuary (the Brisbane River estuary, Australia). Sci. Total Environ. 2014, 472, 719–729. [Google Scholar] [CrossRef] [PubMed]
- Hu, B.; Wang, D.; Zhou, J.; Meng, W.; Li, C.; Sun, Z.; Guo, X.; Wang, Z. Greenhouse gases emission from the sewage draining rivers. Sci. Total Environ. 2018, 612, 1454–1462. [Google Scholar] [CrossRef] [PubMed]
- Cébron, A.; Garnier, J.; Billen, G. Nitrous oxide production and nitrification kinetics by natural bacterial communities of the lower Seine river (France). Aquat. Microb. Ecol. 2005, 41, 25–38. [Google Scholar] [CrossRef]
- Akbarzadeh, Z.; Laverman, A.M.; Rezanezhad, F.; Raimonet, M.; Viollier, E.; Shafei, B.; Van Cappellen, P. Benthic nitrite exchanges in the Seine River (France): An early diagenetic modeling analysis. Sci. Total Environ. 2018, 628, 580–593. [Google Scholar] [CrossRef] [PubMed]
- Radwan, M.; Willems, P.; El-Sadek, A.; Berlamont, J. Modelling of dissolved oxygen and biochemical oxygen demand in river water using a detailed and a simplified model. Int. J. River Basin Manag. 2003, 1, 97–103. [Google Scholar] [CrossRef]
- Chapra, S.C.; Pelletier, G.J.; Tao, H. QUAL2K: A Modeling Framework for Simulating River and Stream Water Quality, Version 2.11; Documentation and Users Manual; Department of Civil and Environmental Engineering, Tufts University: Medford, OR, USA, 2008. [Google Scholar]
- Ambrose, R.B.; Wool, T.A. WASP7 Stream Transport. Model. Theory and User’s Guide; U.S. Environmental Protection Agency: Athens, Greece, 2009.
- Regnier, P.; O’kane, J.; Steefel, C.; Vanderborght, J.-P. Modeling complex multi-component reactive-transport systems: Towards a simulation environment based on the concept of a Knowledge Base. Appl. Math. Model. 2002, 26, 913–927. [Google Scholar] [CrossRef]
- Rodrigues, P.; Barnes, J.; Upstill-Goddard, R. Simulating estuarine nitrous oxide production by means of a dynamic model. Mar. Pollut. Bull. 2007, 54, 164–172. [Google Scholar] [CrossRef]
- Garnier, J.; Billen, G.; Cébron, A. Modelling nitrogen transformations in the lower Seine river and estuary (France): Impact of wastewater release on oxygenation and N2O emission. Hydrobiologia 2007, 588, 291–302. [Google Scholar] [CrossRef]
- Burn, D.H.; Yulianti, J.S. Waste-load allocation using genetic algorithms. J. Water Resour. Plan. Manag. 2001, 127, 121–129. [Google Scholar] [CrossRef]
- Maier, H.R.; Lence, B.J.; Tolson, B.A.; Foschi, R.O. First-order reliability method for estimating reliability, vulnerability, and resilience. Water Resour. Res. 2001, 37, 779–790. [Google Scholar] [CrossRef]
- Mujumdar, P.P.; SubbaraoVemula, V. Fuzzy waste load allocation model: Simulation-optimization approach. J. Comput. Civ. Eng. 2004, 18, 120–131. [Google Scholar] [CrossRef]
- Yandamuri, S.; Srinivasan, K.; Murty Bhallamudi, S. Multiobjective optimal waste load allocation models for rivers using nondominated sorting genetic algorithm-II. J. Water Resour. Plan. Manag. 2006, 132, 133–143. [Google Scholar] [CrossRef]
- Mostafavi, S.A.; Afshar, A. Waste load allocation using non-dominated archiving multi-colony ant algorithm. Procedia Comput. Sci. 2011, 3, 64–69. [Google Scholar] [CrossRef]
- Belayneh, M.Z.; Bhallamudi, S.M. Optimization model for management of water quality in a tidal river using upstream releases. J. Water Resour. Prot. 2012, 4, 149. [Google Scholar] [CrossRef]
- Zewdie, M.; Bhallamudi, S.M. Multi-objective management model for waste-load allocation in a tidal river using archive multi-objective simulated annealing algorithm. Civ. Eng. Environ. Syst. 2012, 29, 222–230. [Google Scholar] [CrossRef]
- Niksokhan, M.; Ardestani, M. Multi-objective waste load allocation in river system by MOPSO. Int. J. Environ. Res. 2015, 9, 69–76. [Google Scholar]
- Nikoo, M.R.; Beiglou, P.H.B.; Mahjouri, N. Optimizing multiple-pollutant waste load allocation in rivers: An interval parameter game theoretic model. Water Resour. Manag. 2016, 30, 4201–4220. [Google Scholar] [CrossRef]
- Chaudhry, M.H. Open-Channel Flow, 2nd ed.; Springer: New York, NY, USA, 2008; p. 523. [Google Scholar]
- Broecker, W.S.; Peng, T.H. Tracers in the Sea; Eldigio Press: New York, NY, USA, 1982. [Google Scholar]
- Park, J.; James, A. A unified method of estimating longitudinal dispersion in estuaries. In Water Pollution Research and Control Brighton; Elsevier: Amsterdam, The Netherlands, 1988; pp. 981–993. [Google Scholar]
- Delgadillo-Mirquez, L.; Lopes, F.; Taidi, B.; Pareau, D. Nitrogen and phosphate removal from wastewater with a mixed microalgae and bacteria culture. Biotechnol. Rep. 2016, 11, 18–26. [Google Scholar] [CrossRef] [PubMed]
- Stare, A.; Vrečko, D.; Hvala, N.; Strmčnik, S. Comparison of control strategies for nitrogen removal in an activated sludge process in terms of operating costs: A simulation study. Water Res. 2007, 41, 2004–2014. [Google Scholar] [CrossRef] [PubMed]
- Cornish, G.; Bosworth, B.; Perry, C.; Burke, J.J. Water Charging in Irrigated Agriculture: An Analysis of International Experience; Food & Agriculture Organization: Rome, Italy, 2004; Volume 28. [Google Scholar]
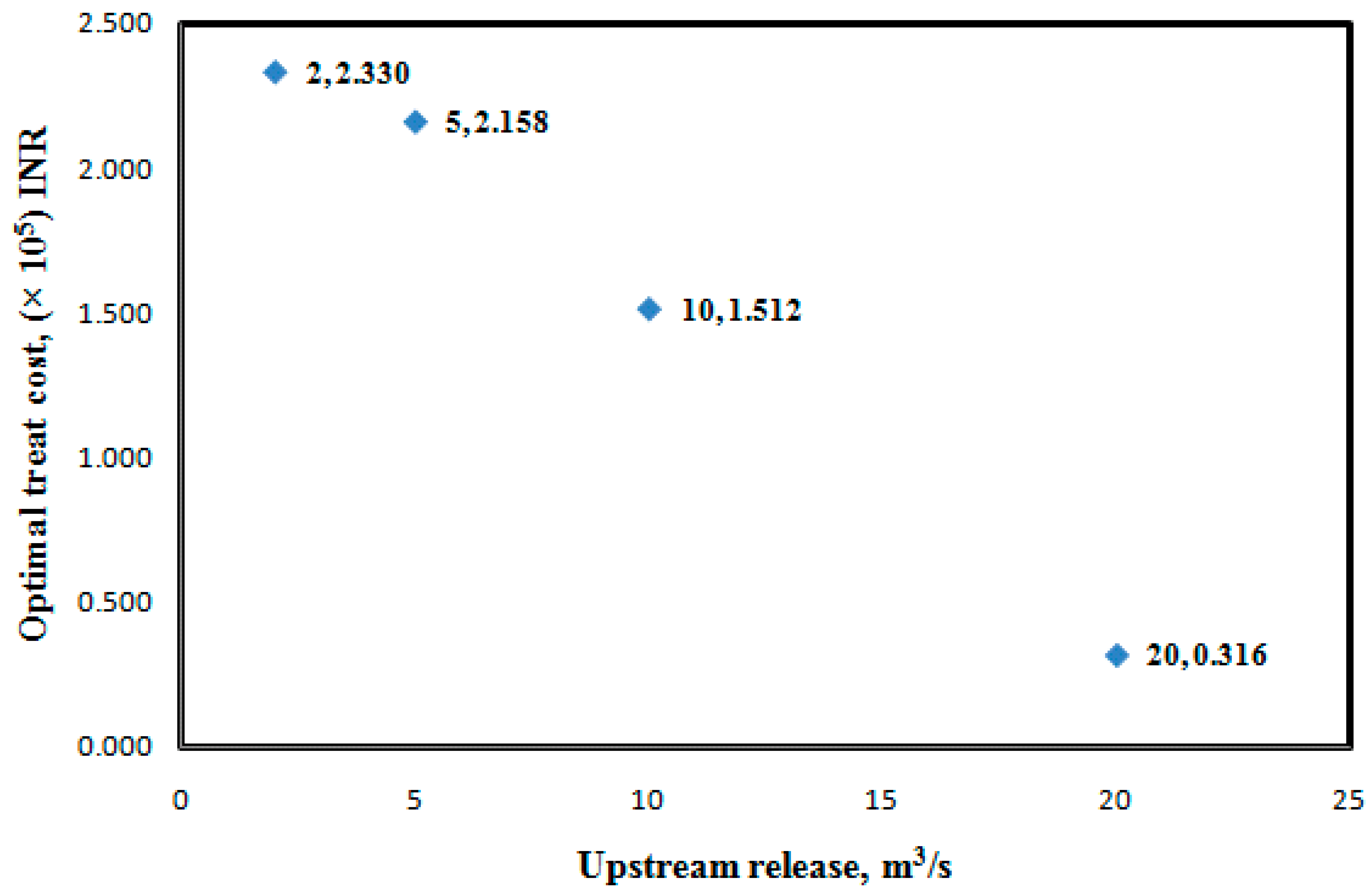
| Location | 4 km | 6 km | 8 km | 13 km | 23 km | 27 km | N2O, g | Optimal Treatment Cost, INR | |
|---|---|---|---|---|---|---|---|---|---|
| Case-1 | HT | 0.88 | 0.27 | 0.54 | 0.34 | 0.00 | 0.04 | 188 | 236,593 |
| LT | 0.88 | 0.27 | 0.54 | 0.34 | 0.00 | 0.04 | |||
| Case-2 | HT | 0.66 | 0.73 | 0.41 | 0.16 | 0.10 | 0.24 | 188 | 151,280 |
| LT | 0.02 | 0.07 | 0.18 | 0.00 | 0.05 | 0.02 | |||
| Qmin | Tidal Period | 4 km | 6 km | 8 km | 13 km | 23 km | 27 km | Qu, m3/s | Optimal Cost, INR | N2O, g | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 10 | 0.01 | HT | 0.61 | 0.04 | 0.00 | 0.02 | 0.02 | 0.05 | 18.42 | 54,637 | 188 |
| LT | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 14.67 | ||||
| 0.1 | HT | 0.18 | 0.27 | 0.27 | 0.00 | 0.35 | 0.00 | 17.69 | 128,766 | 189 | |
| LT | 0.02 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 10.00 | ||||
| 5 | 0.1 | HT | 0.81 | 0.78 | 0.79 | 0.00 | 0.00 | 0.00 | 6.63 | 154,941 | 190 |
| LT | 0.00 | 0.00 | 0.00 | 0.02 | 0.00 | 0.00 | 5.28 |
| Limiting Cost (×105) INR | Tidal Ceriod | 4 km | 6 km | 8 km | 13 km | 23 km | 27 km | Qu, m3/s | Optimal N2O, g | % Water Cost |
|---|---|---|---|---|---|---|---|---|---|---|
| 6.6 | HT | 0.90 | 0.90 | 0.90 | 0.90 | 0.90 | 0.65 | 20.00 | 75.13 | 42 |
| LT | 0.31 | 0.57 | 0.55 | 0.10 | 0.11 | 0.44 | 7.68 | |||
| 4.4 | HT | 0.89 | 0.90 | 0.90 | 0.82 | 0.73 | 0.00 | 17.09 | 85.99 | 45 |
| LT | 0.00 | 0.31 | 0.27 | 0.85 | 0.00 | 0.01 | 5.29 | |||
| 2.2 | HT | 0.90 | 0.90 | 0.87 | 0.07 | 0.00 | 0.01 | 10.38 | 138.65 | 62 |
| LT | 0.00 | 0.00 | 0.06 | 0.00 | 0.00 | 0.10 | 5.00 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Akella, C.S.; Bhallamudi, S.M. Managing Municipal Wastewater Treatment to Control Nitrous Oxide Emissions from Tidal Rivers. Water 2019, 11, 1255. https://doi.org/10.3390/w11061255
Akella CS, Bhallamudi SM. Managing Municipal Wastewater Treatment to Control Nitrous Oxide Emissions from Tidal Rivers. Water. 2019; 11(6):1255. https://doi.org/10.3390/w11061255
Chicago/Turabian StyleAkella, Chandra Sekhar, and S. Murty Bhallamudi. 2019. "Managing Municipal Wastewater Treatment to Control Nitrous Oxide Emissions from Tidal Rivers" Water 11, no. 6: 1255. https://doi.org/10.3390/w11061255
APA StyleAkella, C. S., & Bhallamudi, S. M. (2019). Managing Municipal Wastewater Treatment to Control Nitrous Oxide Emissions from Tidal Rivers. Water, 11(6), 1255. https://doi.org/10.3390/w11061255





