A Preliminary Study on a Pumping Well Capturing Groundwater in an Unconfined Aquifer with Mountain-Front Recharge from Segmental Inflow
Abstract
:1. Introduction
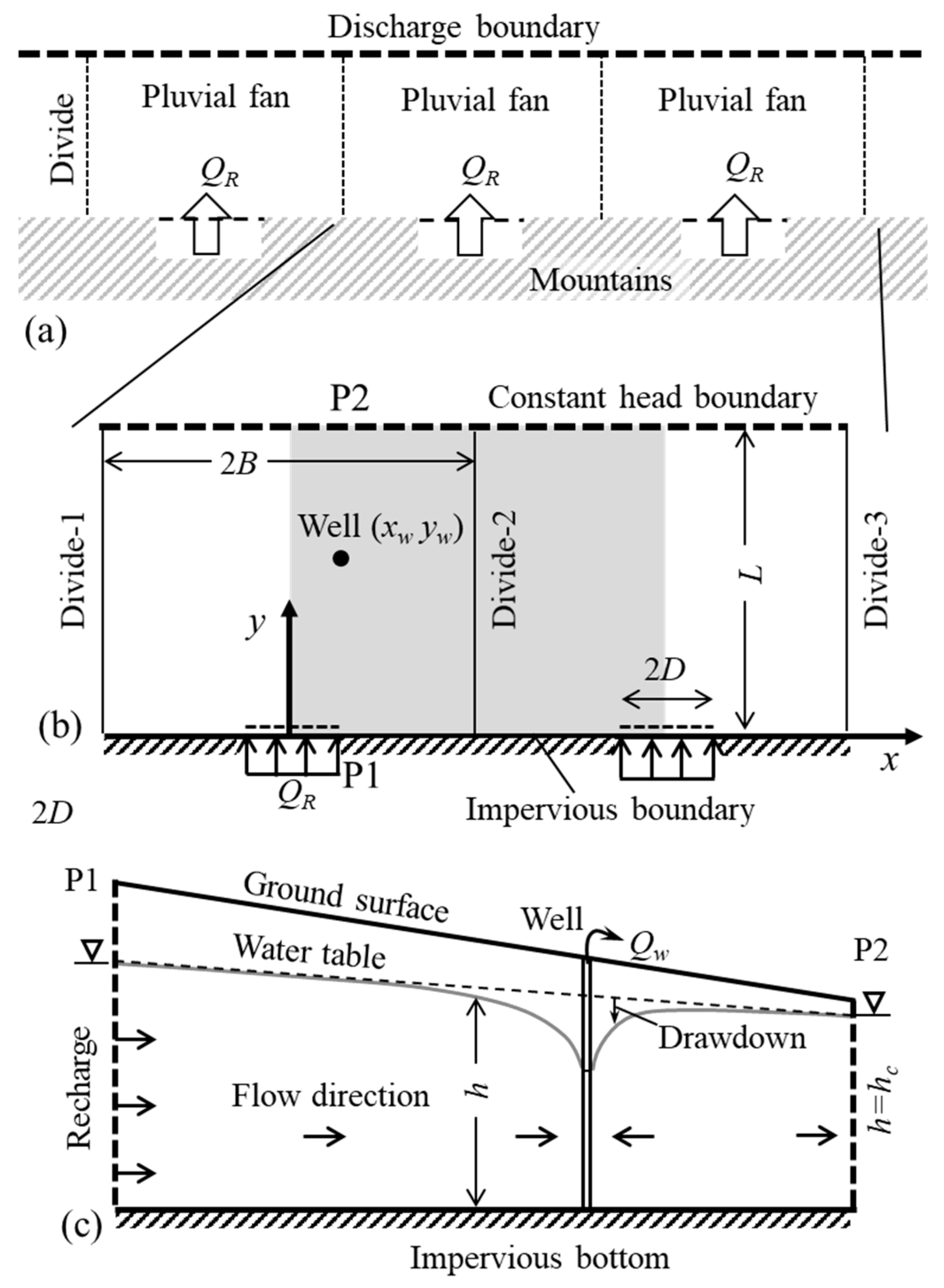
2. Conceptual and Mathematical Models of Groundwater Flow
2.1. Conceptual Model with Simplifications
2.2. Mathematical Model and Lumped Parameters
3. Numerical Methods
3.1. Numerical Solution of Groundwater Flow
3.2. Particle Tracking Method for Streamlines and Travel Time
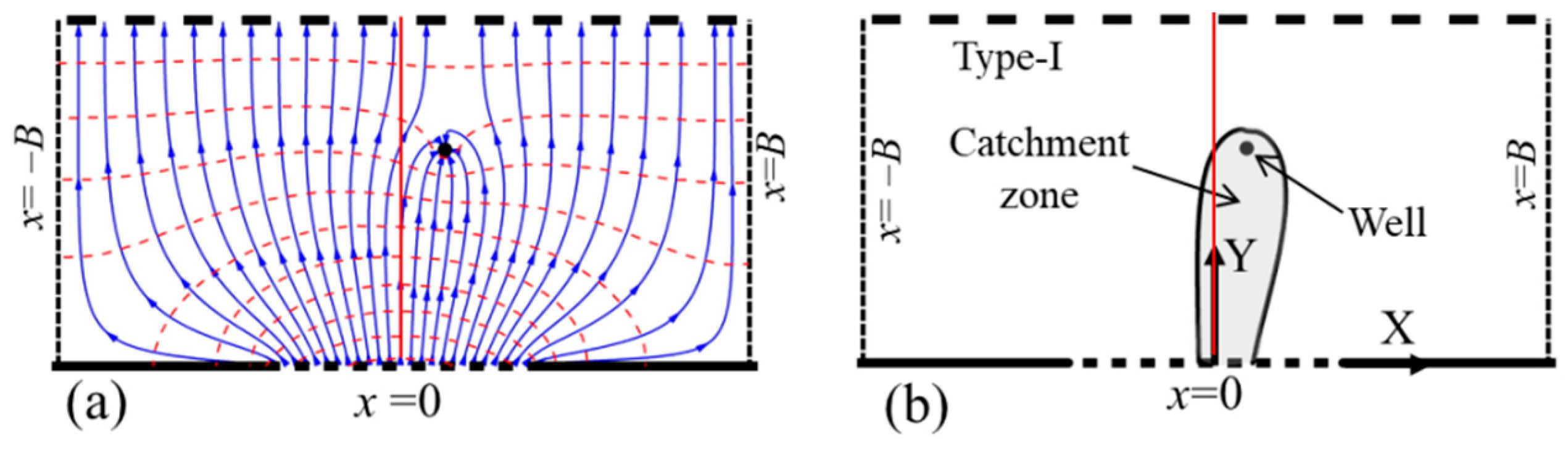
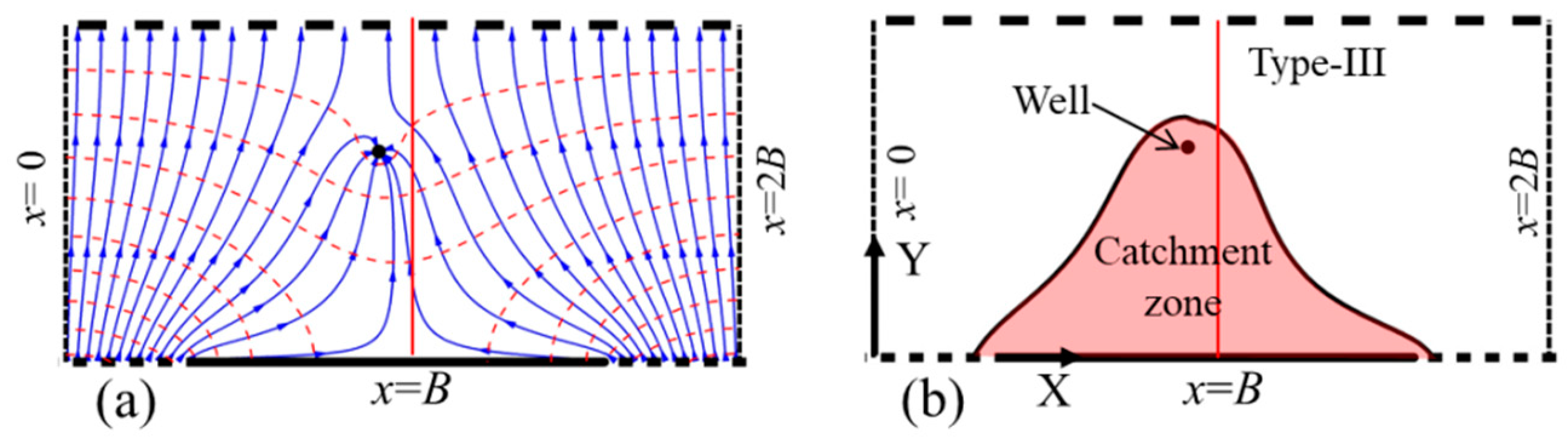
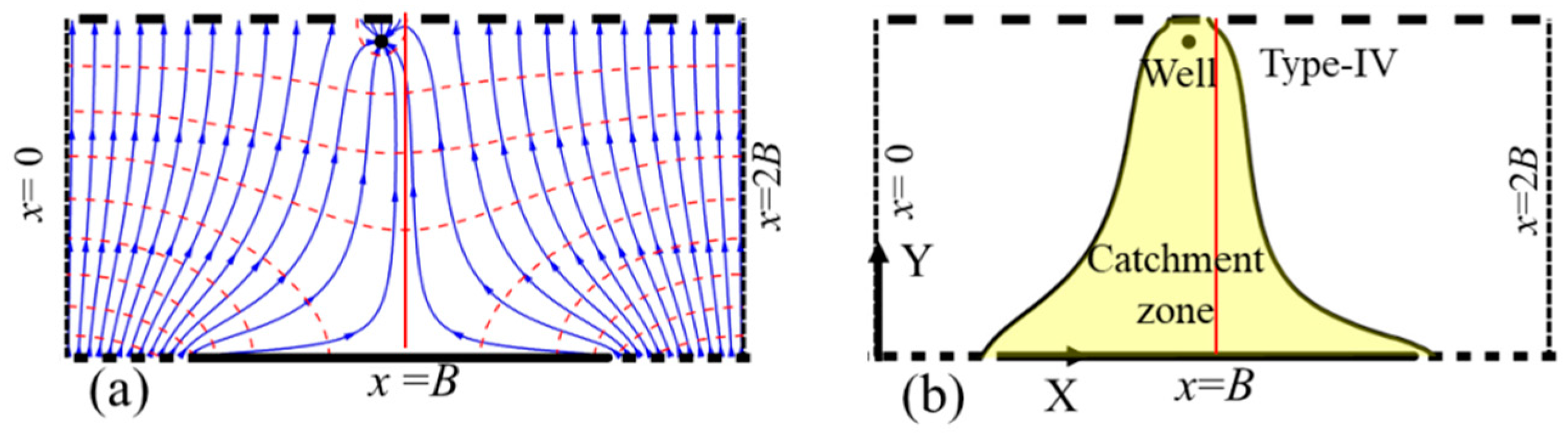
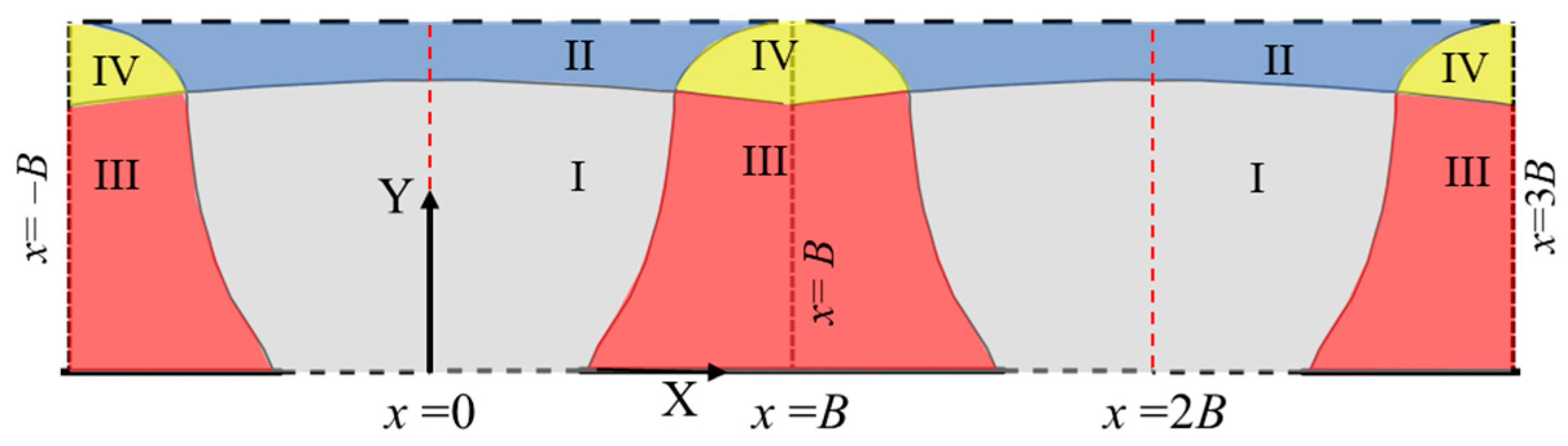
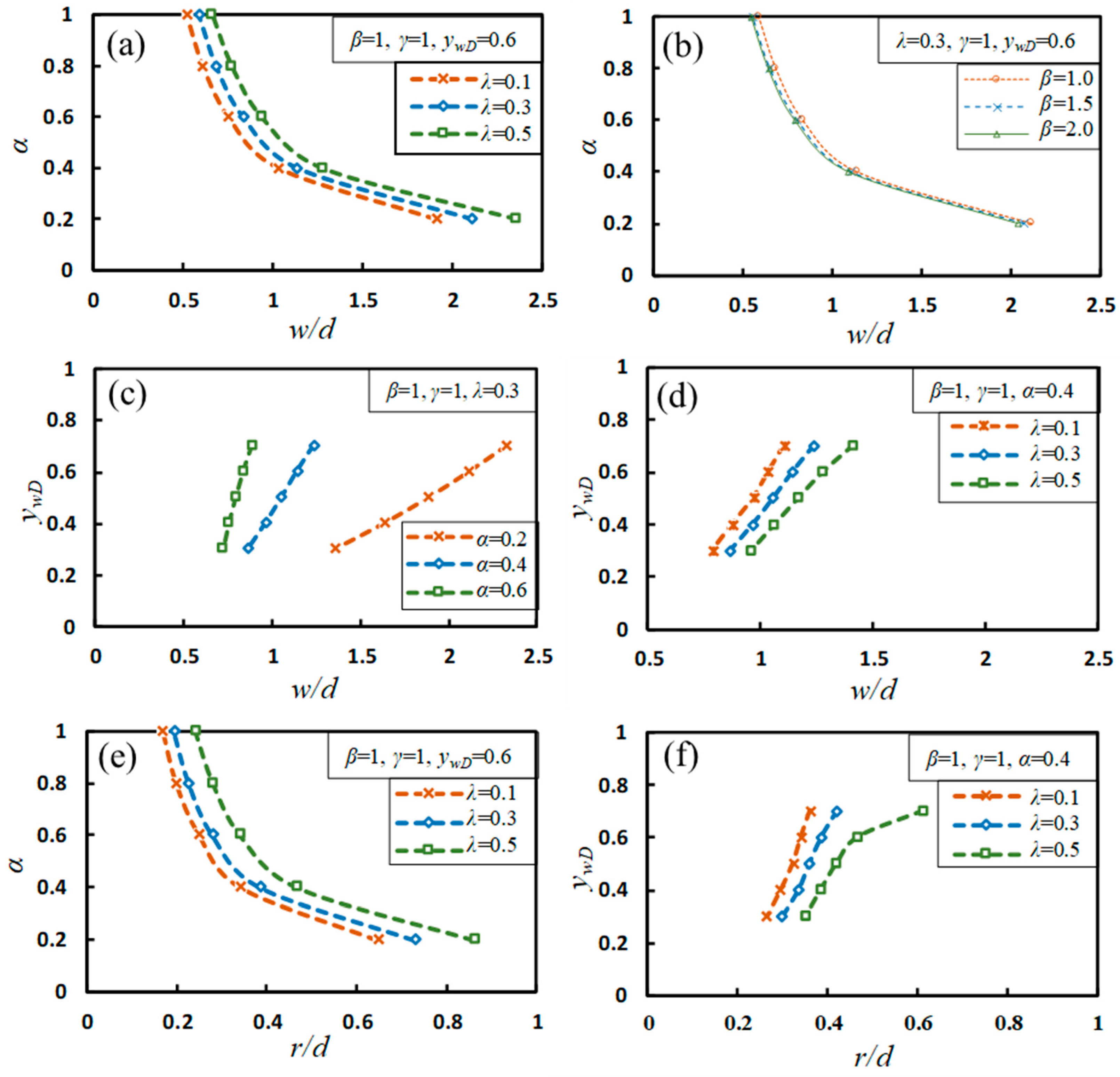
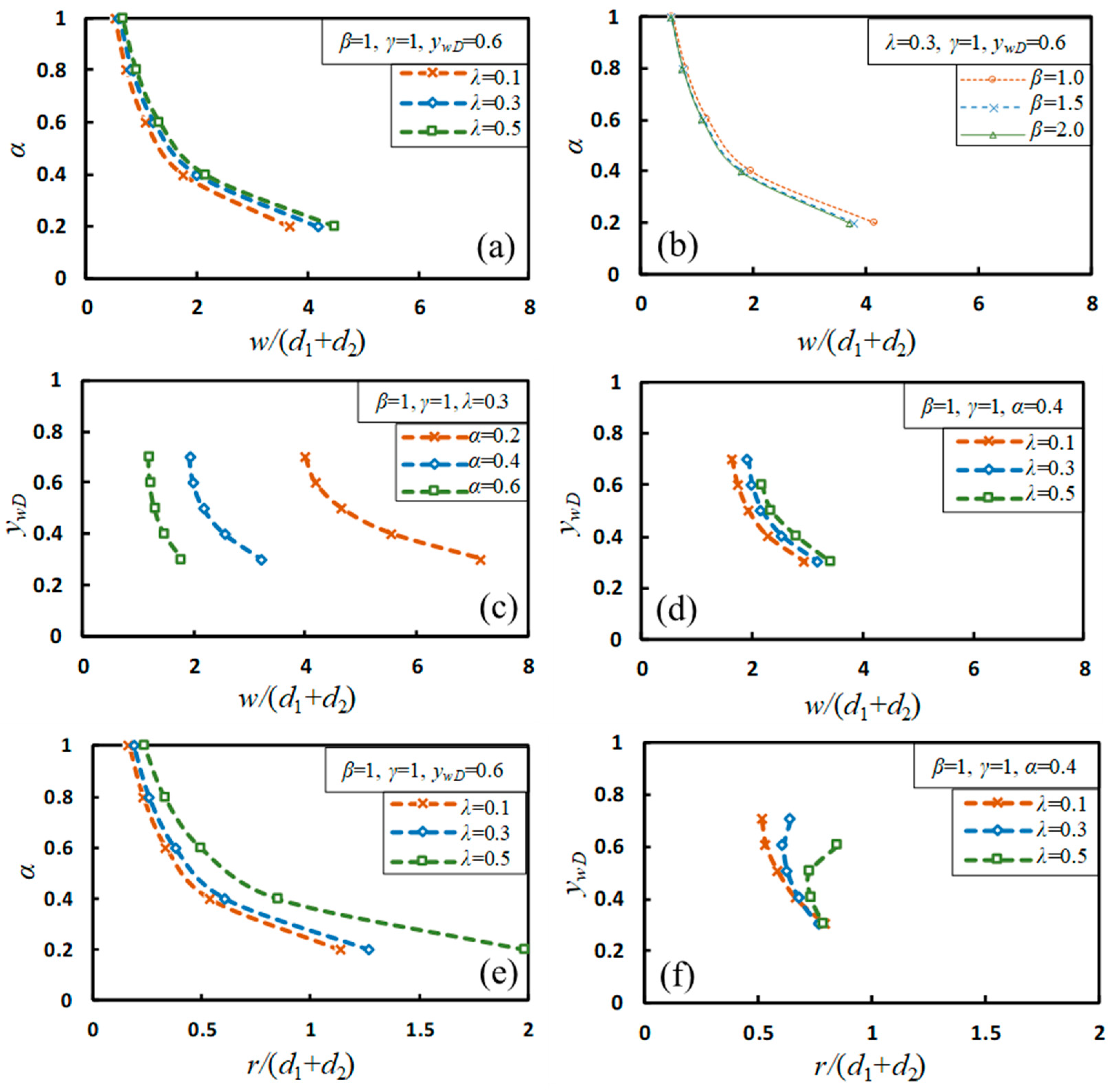
4. Results of the Catchment Zone
4.1. General Shape and Classification
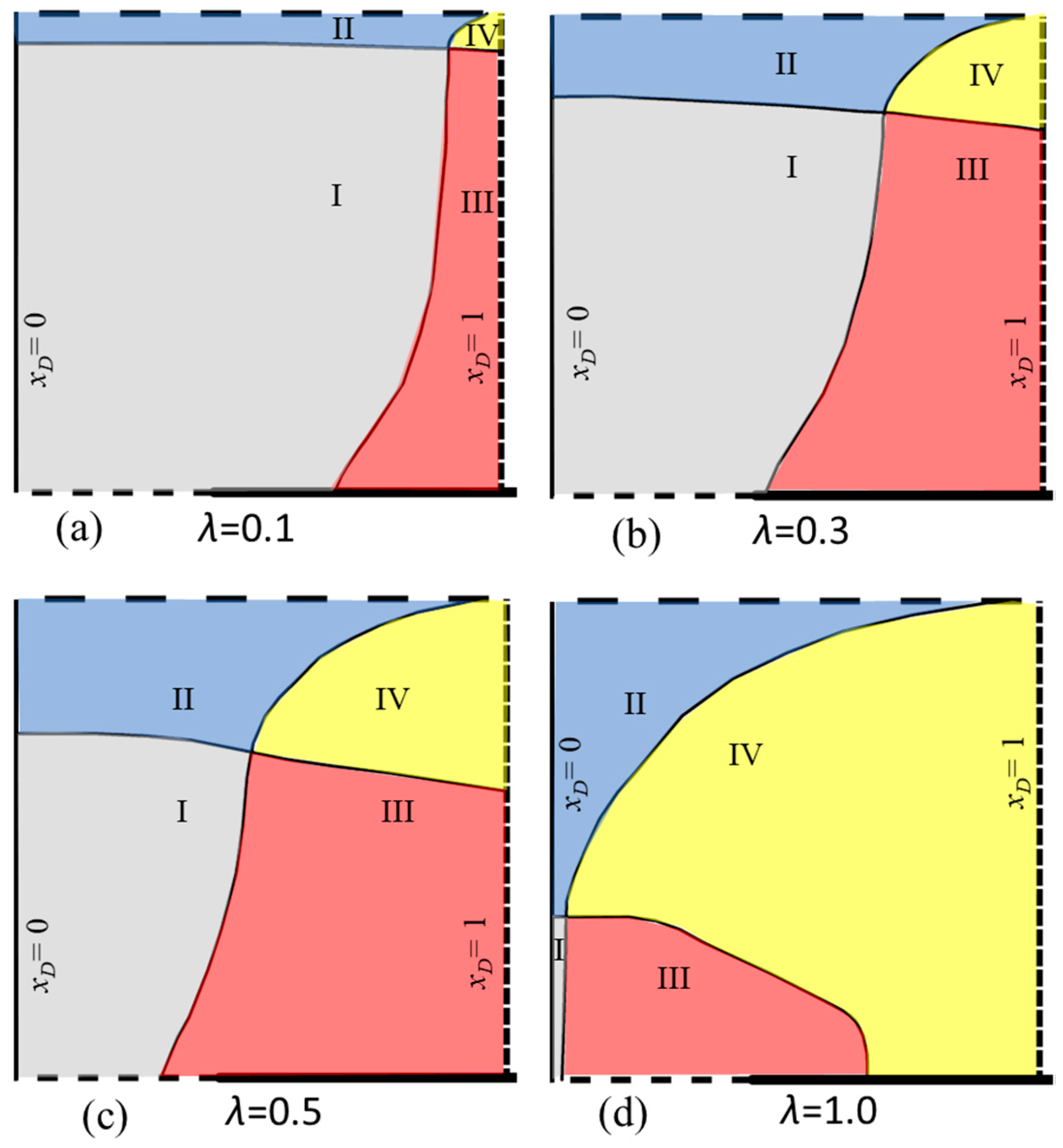
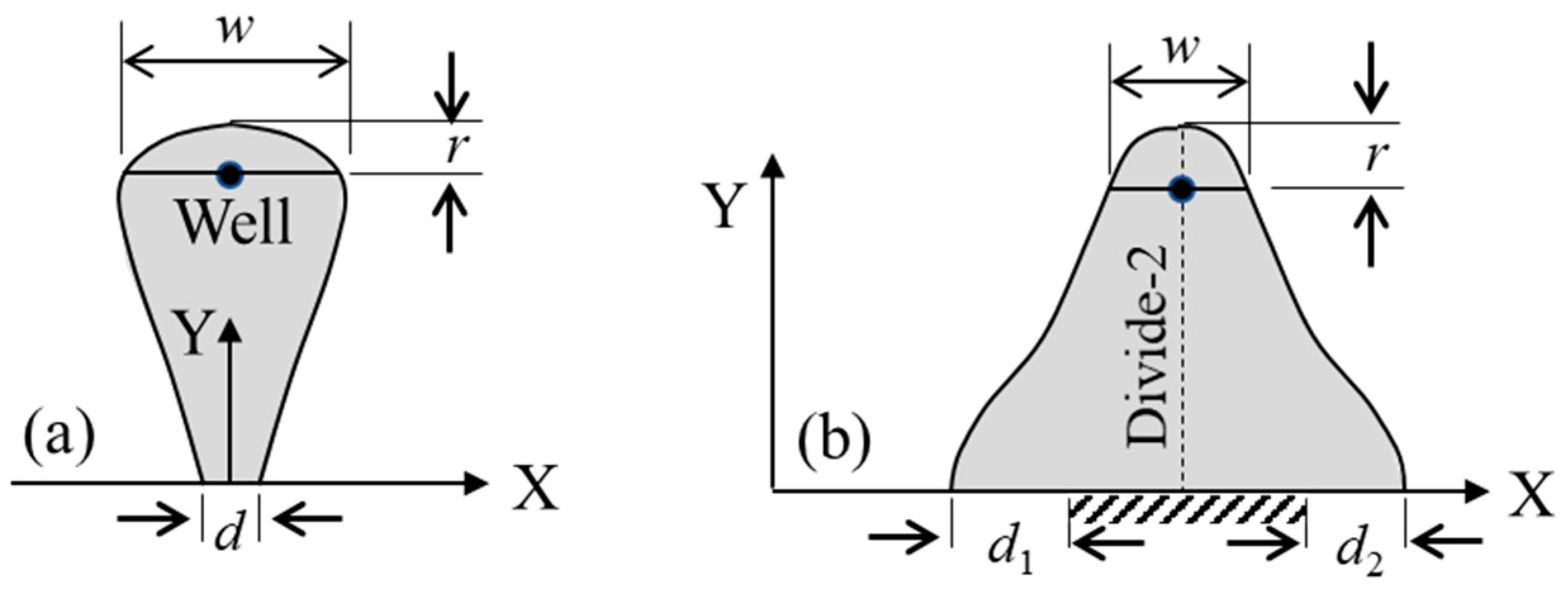
4.2. Dependency of Shape Factors on Controls
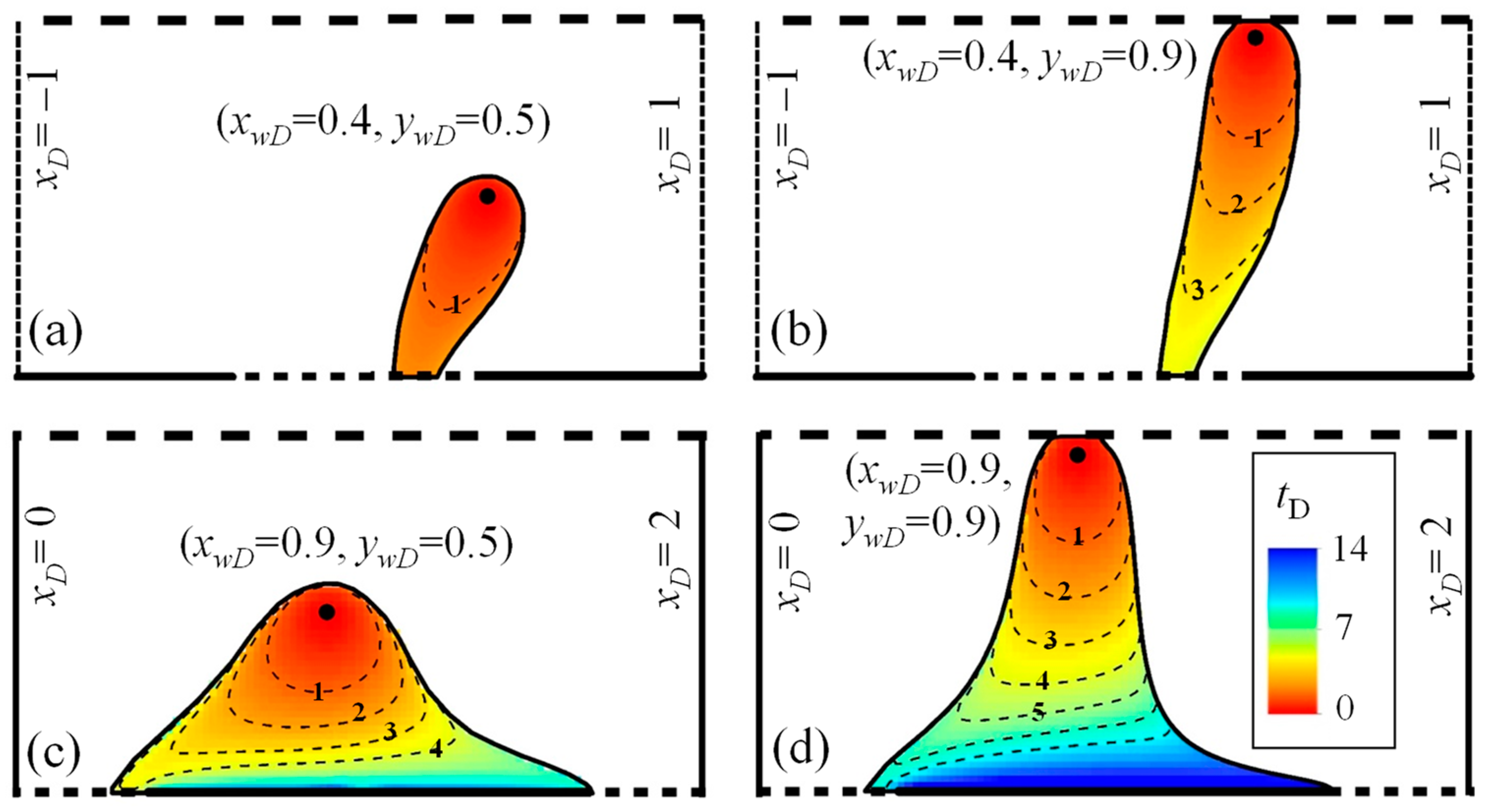
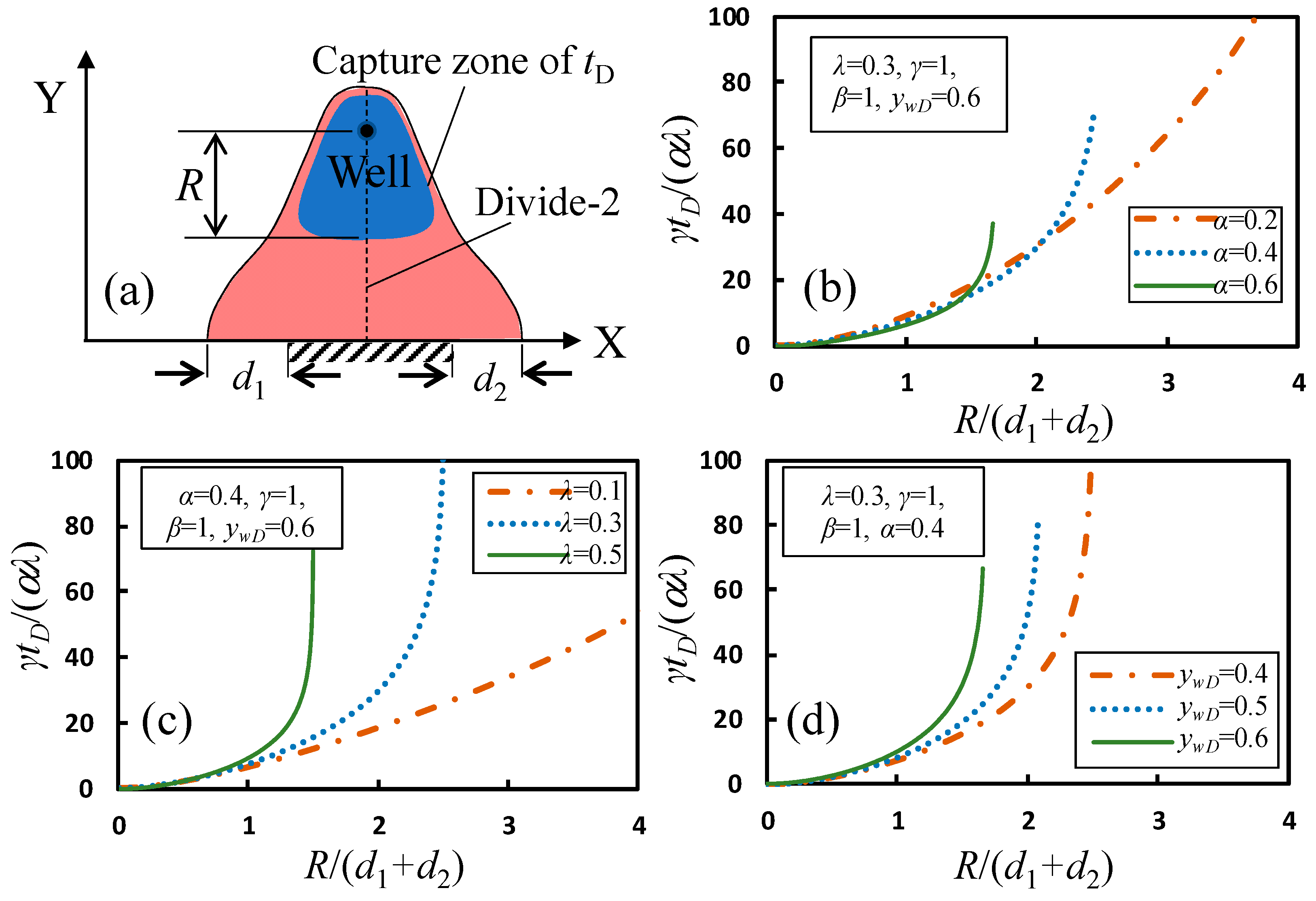
5. Travel Time Analyses for Capture Zones
5.1. General Travel Time Distribution
5.2. The Relationship between the Travel Time and the Size Factor
6. Discussions on the Application
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- De Smedt, F. Analytical solution for capture and catchment zones of a well located on a groundwater divide. Water Resour. Res. 2014, 50, 736–740. [Google Scholar] [CrossRef]
- Muskat, M.; Meres, M.W. The flow of homogeneous fluids through porous media. Physics 1936, 7, 346–363. [Google Scholar] [CrossRef]
- Bear, J. Hydraulics of Groundwater; McGraw-Hill: New York, NY, USA, 1979; 567p. [Google Scholar]
- Javandel, I.; Tsang, C.F. Capture-zone type curves: A tool for aquifer cleanup. Groundwater 1986, 24, 616–625. [Google Scholar] [CrossRef]
- Shan, C. An analytical solution for the capture zone of two arbitrarily located wells. J. Hydrol. 1999, 222, 123–128. [Google Scholar] [CrossRef]
- Grubb, S. Analytical model for estimation of steady-state capture zones of pumping wells in confined and unconfined aquifers. Groundwater 1993, 31, 27–32. [Google Scholar] [CrossRef]
- Newsom, J.M.; Wilson, J.L. Flow of ground water to well near a stream-effect of ambient ground-water flow direction. Groundwater 1989, 26, 703–711. [Google Scholar] [CrossRef]
- Asadi-Aghbolaghi, M.; Rakhshandehroo, G.R.; Kompani-Zare, M. Analytical solutions for the capture zone of a pumping well near a stream. Hydrogeol. J. 2011, 19, 1161–1168. [Google Scholar] [CrossRef]
- Intaraprasong, T.; Zhan, H. Capture zone between two streams. J. Hydrol. 2007, 338, 297–307. [Google Scholar] [CrossRef]
- Samani, N.; Zarei-Doudeji, S. Capture zone of a multi-well system in confined and unconfined wedge-shaped aquifers. Adv. Water Resour. 2012, 39, 71–84. [Google Scholar] [CrossRef]
- De Smedt, F. Analytical solution for the catchment zone of a well located near a groundwater divide in a recharged semi-confined aquifer. J. Hydrol. 2014, 519, 1271–1277. [Google Scholar] [CrossRef]
- Simpson, M.J.; Clement, T.P.; Yeomans, F.E. Analytical model for computing residence times near a pumping well. Groundwater 2003, 41, 351–354. [Google Scholar] [CrossRef]
- Chapuis, R.P.; Chesnaux, R. Travel time to a well pumping an unconfined aquifer without recharge. Groundwater 2006, 44, 600–603. [Google Scholar] [CrossRef]
- Zhou, Y.X.; Haitjema, H. Approximate solutions for radial travel time and capture zone in unconfined aquifers. Groundwater 2012, 50, 799–803. [Google Scholar] [CrossRef] [PubMed]
- Shafer, J.M. Reverse pathline calculation of time-related capture zones in nonuniform flow. Groundwater 1987, 25, 283–298. [Google Scholar] [CrossRef]
- Pollock, D.W. Semianalytical computation of path lines for finite-difference models. Groundwater 1988, 26, 743–750. [Google Scholar] [CrossRef]
- Wang, Y.; Guo, H.; Li, J.; Huang, Y.; Liu, Z.; Liu, C. Survey and Assessment on Groundwater Resources and Relevant Environmental Problems in the Qaidam Basin; Geological Publishing House: Beijing, China, 2008. (In Chinese) [Google Scholar]
- Wilson, J.L.; Guan, H. Mountain-block hydrology and mountain-front recharge. In Groundwater Recharge in a Desert Environment: The Southwestern United States; Phillips, F.M., Hogan, J., Scanlon, B., Eds.; The American Geophysical Union: Washington, DC, USA, 2004. [Google Scholar]
- McDonald, M.G.; Harbaugh, A.W. Techniques of Water-Resources Investigations of the United States Geological Survey Chapter A1: A Modular Three-Dimensional Finite Difference Ground-Water Flow Model; United States Government Printing Office: Washington, DC, USA, 1988.
- Harbaugh, A.W.; McDonald, M.G. User’s Documentation for MODFLOW-96, an Update to the U.S. Geological Survey Modular Finite-Difference Ground-Water Flow Model; Office of Ground Water U.S. Geological Survey: Reston, VA, USA, 1996; p. 56.
- Hill, M.C. Preconditioned Conjugate-Gradient 2 (PCG2): A Computer Programfor Solving Ground-Water Flow Equations; U.S. Geological Survey: Denver, CO, USA, 1990; p. 43.
- Pollock, D.W. Documentation of Computer Programs to Compute and Display Pathlines Using Results from the U.S. Geological Survey Modular Three-Dimensional Finite Difference Ground-Water Flow Model; U.S. Geological Survey: Reston, VA, USA, 1989.
- Pollock, D.W. User Guide for MODPATH Version 6—A Particle-Tracking Model for MODFLOW; U.S. Geological Survey: Reston, VA, USA, 2012.


| B (km) | D (km) | L (km) | hc (m) |
|---|---|---|---|
| 6–11 | 2–4 | 8–11 | 100–160 |
| QR (×104 m3/d) | q0 (m2/d) | K (m/d) | Porosity |
| 28–36 | 35–90 | 30–90 | 0.25–0.31 |
| Qw (×104 m3/d) | xw | yw | |
| 6.0–10.0 | 1.8 | 4.7 | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, H.; Wang, X.-s. A Preliminary Study on a Pumping Well Capturing Groundwater in an Unconfined Aquifer with Mountain-Front Recharge from Segmental Inflow. Water 2019, 11, 1243. https://doi.org/10.3390/w11061243
Li H, Wang X-s. A Preliminary Study on a Pumping Well Capturing Groundwater in an Unconfined Aquifer with Mountain-Front Recharge from Segmental Inflow. Water. 2019; 11(6):1243. https://doi.org/10.3390/w11061243
Chicago/Turabian StyleLi, Haixiang, and Xu-sheng Wang. 2019. "A Preliminary Study on a Pumping Well Capturing Groundwater in an Unconfined Aquifer with Mountain-Front Recharge from Segmental Inflow" Water 11, no. 6: 1243. https://doi.org/10.3390/w11061243
APA StyleLi, H., & Wang, X.-s. (2019). A Preliminary Study on a Pumping Well Capturing Groundwater in an Unconfined Aquifer with Mountain-Front Recharge from Segmental Inflow. Water, 11(6), 1243. https://doi.org/10.3390/w11061243





